Teaching Robot Navigation Behaviors to Optimal RRT Planners

Abstract

This work presents an approach for learning navigation behaviors for robots using Optimal Rapidly-exploring Random Trees (RRT$^{*}$) as the main planner. A new learning algorithm combining both Inverse Reinforcement Learning and RRT$^{*}$ is developed to learn the RRT$^{*}$’s cost function from demonstrations. A comparison with other state-of-the-art algorithms shows how the method can recover the behavior from the demonstrations. Finally, a learned cost function for social navigation is tested in real experiments with a robot in the laboratory.

1 Introduction

Today, more and more mobile robots are coexisting with us in our daily lives. As a result, the creation of motion plans for robots that share space with humans in dynamic environments is a subject of intense investigation in robotics. Robots must respect human social conventions, guarantee the comfort of surrounding persons, and maintain legibility so that humans can understand the robot’s intentions [15]. This is called human-aware navigation.

This problem was initially tackled by including pre-programmed costs and constraints related to human-awareness into motion planners to obtain socially acceptable paths [11, 36]. However, hard-coded social behaviors might be inappropriate [5]. In many implementations (for instance [12, 24]), these costs are grounded in Proxemics theory [8]. However, as shown in [19], Proxemics is focused on people interaction, and it could not be suitable for navigating among people.

All in all, it is easier to demonstrate socially acceptable behaviors than mathematically defining them. Therefore, learning these social behaviors from data seems a more principled approach. In particular, we consider in this paper the application of telepresence robots [33] (see Fig. 1). Our goal is to increase the autonomy of such robots, freeing the users from the low-level navigation tasks. In this setup, it is very natural to collect navigation data online from the users controlling the telepresence robot. Then, this data is easily reproducible off-line and thus, used as examples to learn social navigation behaviors during idle times of the robot.

Fig. 1

Image of the telepresence robot developed in the TERESA project http://teresaproject.eu

Thus, we present in the paper a new approach to learn navigation behaviors from demonstrations. We make use of Inverse Reinforcement Learning (IRL) concepts [21] and sampling-based costmap planners, like Optimal-RRTs (RRT$^{*}$)[10], to identify the RRT cost function that best fits the example trajectories. Many IRL approaches for robot navigation are based on discrete Markov Decision Process (MDPs) to frame the problem [9, 28, 37]. MDPs allow dealing with uncertain outcomes of actions. However, MDPs present some disadvantages for robot motion planning, like poor scalability with the involved large (and typically continuous) state spaces, which leads to high computational complexity. The proposed method, which we have called Rapidly-exploring random Trees Inverse Reinforcement Learning (RTIRL), makes use of the RRT$^{*}$ instead of an MDP. It exploits the advantages of the RRT$^{*}$ to deal with continuous state and control spaces and to scale with the state size. It is also general enough to be applied in different scenarios.

The contribution of this paper is threefold: a new method for learning robot navigation behaviors from demonstrations that employs widely-used navigation planners like RRT*; a comparison with other approaches from the state of the art that shows how the method adequately recovers the demonstrated behavior; and the application of the method to the human-aware navigation problem.

The paper is structured as follows. After a summary of the related work, next section describes the algorithm for learning from demonstrations using RRT$^{*}$. Then, Sect. 3 describes the particular problem of social navigation considered in the paper. Section 4 presents a benchmarking evaluation of the method, including a comparison with other algorithms from the state of the art. In Sect. 5, a set of experiments with a real robot using a learned cost function for social navigation is presented. Finally, Sect. 6 summarizes the paper contribution and outlooks future work.

1.1 Related Work

In the last years, several contributions have been presented regarding the application of learning to the problem of human-aware navigation, and in particular, an interesting approach is Learning from Demonstrations (LfD) [2]. One successful technique to do that is Inverse Reinforcement Learning (IRL) [21]: the observations of an expert demonstrating the task are used to recover the reward (or cost) function the demonstrator was attempting to maximize (minimize). Then, the reward can be used to obtain a similar robot policy. Other LfD techniques that directly learn maps from inputs to actions, like Behavioral Cloning [35], are in general more adequate for learning low-level control policies than for planning [2]. An interesting characteristic of IRL techniques is that they try to learn the underlying behavior that the demonstrator is showing, and therefore, they allow to generalize to different scenarios or situations where to perform the learned task. Furthermore, the learned reward functions can be transferred to different planners.

The literature tackles the IRL problem from different points of view. The initial projection method proposed by Abbeel [1] was followed by other well-known approximations. A probabilistic method based on the principle of maximum entropy is presented in [39], or a maximum margin structured prediction based on subgradients is employed in [30, 31]. In [27], a Bayesian perspective is taken to solve the problem.

In most of the existing models, the IRL technique makes use of MDPs as the underlying process. However, it is complex to encode general problems with MDPs due to its computational complexity which scales poorly with high dimensionality and large state spaces.

Different solutions have been considered to deal with the main MDP drawbacks. The computational cost is managed in [20] by using a Bayesian nonparametric mixture model to divide the observations and obtain a group of simpler reward functions to learn. In [18], deterministic MDPs with large, continuous state and action spaces are handled by considering only the shape of the learned reward function in the neighborhood of the experts demonstrations. Furthermore, neural networks are applied in [38] to learn non-linear policies. In [23], a socially normative behavior is learned using flexible graph-based representation to model the underlying MDP.

Other authors try to replace or represent the MDP by another process according to the aim of the task. In [30], the MDP can be replaced by an A$^{*}$ search algorithm. Different car driving styles are learned in [16] by modeling the car dynamics using a time-continuous spline representation instead of an MDP. Another example is [14], where the cooperative navigation behavior of humans is learned using Hamiltonian Markov chain Monte Carlo sampling to compute the feature expectations over high-dimensional continuous distributions.

While the previous approaches show promising results, they employ representations tailored to the problem at hand. In this paper, we present an algorithm for learning robot navigation behaviors from demonstrations using RRT$^{*}$ as main planner [10]. RRT* planners are very common in robotics applications; they are asymptotically optimal, can cope with continuous state and action spaces and kinodynamic constraints, reason implicitly about obstacles and can be easily extended to spaces with higher dimensions. We aim at creating a new learning algorithm combining both IRL and RRT$^{*}$ techniques to extract the proper weights of the cost function from demonstration trajectories. This cost function can be used later in a regular RRT$^{*}$ to allow the robot reproducing the desired behavior at different scenarios. A similar idea of ours is recently presented in [34] where the Maximum Margin Planning (MMP) method is extended to learn RRT$^{*}$ cost functions.

This work is an extension of the work initially presented in [25]. The paper has been significantly extended, including a thorough evaluation of the learning performance through a comparison with similar state-of-the-art approximations; the application of the method to the social navigation problem considering a wider set of features; and a comparison of the resultant navigation behavior with respect to non human-aware planners.

2 Learning a RRT* Cost Function

2.1 IRL Formulation with RRT* Planners

RRT$^{*}$ is a technique for optimal motion planning employed extensively in robotics [10]. It is flexible and easily adapted to different scenarios and problems. RRT$^{*}$ approaches reason about collisions with obstacles at moderate computational cost even in high dimensionality. They explore the configuration space to obtain optimal paths on cost spaces, and the kinodynamic extension allows reasoning about the robot dynamics.

The RRT$^{*}$ algorithm considers that a cost function is associated with each point x in the configuration space of the robot. The algorithm seeks to obtain the trajectory $\zeta ^{*}$ that minimizes the total cost along the path $C(\zeta )$. It does so by randomly sampling the configuration space and creating a tree towards the goal. The paths are then represented by a finite set of configuration points $\zeta =\{x_1,x_2,\ldots ,x_N\}$.

Without loss of generality, we can assume that the cost for each point x can be expressed as a weighted linear combination of a set of J functions $f_j(x)$:

$$\begin{aligned} c(x)=\sum _{j=1}^{J} \omega _j f_j(x) = \omega ^{T} f(x) \end{aligned}$$

(1)

The function $f(x)=[f_1(x), f_2(x), \ldots , f_J(x)]^{T}$ is based on J measurable characteristics that will be called features. The particular features will depend on the task to be learned, and are used to extract the information from the robot configurations that are relevant for that particular task. While not explicitly indicated, the value of the features will depend also on the scenario s (given by the position of obstacles, people, goals and any other relevant information external to the robot) where the planning takes place.

The cost of a path is then the sum of the cost for all points in it. Particularly, in the RRT$^{*}$, the cost of a path is the sum of the sub-costs of moving between pairs of points in the path:

$$\begin{aligned} C(\zeta )&= \sum ^{N-1}_{i=1} \frac{c(x_i)+c(x_{i+1})}{2}\Vert x_{i+1} - x_i \Vert \end{aligned}$$

(2)

$$\begin{aligned}&=\omega ^{T}\underbrace{\sum ^{N-1}_{i=1} \frac{f(x_i)+f(x_{i+1})}{2}\Vert x_{i+1} - x_i \Vert }_{f(\zeta )} \end{aligned}$$

(3)

$$\begin{aligned}&=\omega ^{T}f(\zeta ) \end{aligned}$$

(4)

where $f(\zeta )$ is called the feature count vector of path $\zeta$. Thus, for a given weights vector $\omega$, the algorithm will return trajectories that try to minimize this cost.

Given a set of demonstration trajectories by an expert,

$$\begin{aligned} \mathcal {D}=\{\zeta _1, \zeta _2,\ldots ,\zeta _D \} \end{aligned}$$

(5)

and the definition of the feature function f(x) in (1), the problem of learning from demonstrations, in this setup, means to determine the weights $\omega$ that lead our planner to behave similarly to these demonstrations.

The concept of similarity in this context is ambiguous. One may want to reproduce exactly the same trajectories in the same situations. However, it is necessary to learn a representation that can generalize to other cases. As in [1, 16], this can be achieved by using the mentioned features as a measure of similarity. The objective is then to model the underlying trajectory distribution of the expert $p(\zeta | \omega )$ with the constraint that the expected value of the features for the path generated by the model is the same as the expected value of the features for the given demonstrated trajectories:

$$\begin{aligned} \mathbb {E}(f(\zeta )) = \frac{1}{D}\sum _{i=1}^{D}f(\zeta _i) \end{aligned}$$

(6)

There are many distributions $p(\zeta | \omega )$ that achieve the previous constraint. Applying the Maximum Entropy Principle [13, 39] to the IRL problem leads to the following form for the probability density for the trajectories returned by the demonstrator:

$$\begin{aligned} p(\zeta | \omega ) = \frac{1}{Z(\omega )} e^{-\omega ^{T}f(\zeta )} \end{aligned}$$

(7)

where the partition function $Z(\omega )=\int e^{-\omega ^{T}f(\zeta )} d\zeta$ is a normalization function that does not depend on $\zeta$. Thus, this model assumes that the expert is exponentially more likely to chose a trajectory with lower cost $\omega ^{T}f(\zeta )$.

Under this model, the (log-)likelihood of the demonstrated trajectories is given by:

$$\begin{aligned} \mathcal {L}(\mathcal {D}|\omega ) = -D\log (Z(\omega ) ) + \sum _{i=1}^{D}(-\omega ^{T}f(\zeta _i)) \end{aligned}$$

(8)

The gradient of this log-likelihood with respect to $\omega$ is given by:

$$\begin{aligned} \frac{\partial \mathcal {L}(\mathcal {D}|\omega )}{\partial \omega }&= D\underbrace{\frac{1}{Z(\omega )}\int f(\zeta )e^{-\omega ^{T}f(\zeta )} d\zeta }_{\mathbb {E}(f(\zeta )) } - \sum _{i=1}^{D}f(\zeta _i) \end{aligned}$$

(9)

$$\begin{aligned}&= D(\mathbb {E}(f(\zeta ))-\frac{1}{D}\sum _{i=1}^{D}f(\zeta _i)) \end{aligned}$$

(10)

We arrive at the original constraint in (6) by setting this gradient to zero. This means, as indicated in [17], that the IRL problem under the Maximum Entropy distribution is equivalent to maximizing the likelihood of the demonstrations when assuming an exponential distribution.

Maximizing the likelihood (8) to obtain the set of weights cannot be solved analytically. But the gradient (10) can be used to apply gradient ascend techniques to solve this problem. As mentioned in [16], this gradient can be intuitively explained. If the value of one of the features for the trajectories returned by the planner is higher than the value in the demonstrated trajectories, the corresponding weight should be increased to penalize those trajectories.

The main problem with the computation of the previous gradient is that it requires to estimate the expected value of the features $\mathbb {E}(f(\zeta ))$ for the generative distribution (7) over the continuous space of trajectories.

$$\begin{aligned} \mathbb {E}(f(\zeta )) = \frac{1}{Z(\omega )}\int f(\zeta )e^{-\omega ^{T}f(\zeta )} d\zeta \end{aligned}$$

(11)

In [13], a probabilistic generative model for trajectories is derived from data, and the expectation is computed by Monte Carlo Chain sampling methods, which are very computationally demanding. One option is to approximate the previous expectation by the features of the most likely trajectory [16]. In our case, we will approximate the expert by the RRT$^{*}$ planner on board the robot. Being an asymptotically optimal planner, for some given weights, the RRT$^{*}$ will provide the trajectory that minimizes the cost (the most likely) given infinite time. As the planning time is limited, the RRT$^{*}$ will provide trajectories with some variability on the features, and thus the feature expectation $\mathbb {E}(f(\zeta ))$ is computed by running several times the planner between the start and goal configurations. This is then used to calculate the gradient and adapt the weights employed in the RRT$^{*}$ planner.

The experimental results will show that the method can recover the behaviors taught by the expert.

Fig. 2

General learning scheme proposed to adjust the weights of the cost function of a RRT$^{*}$ planner

2.2 RTIRL Algorithm

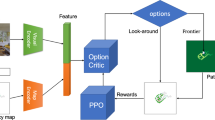
The general scheme of the learning algorithm proposed is presented in Fig. 2. First, we define a scenario as a particular situation where to perform the task proposed (for instance, a particular position of the obstacles, people positions and orientations, starting and goal positions, for the task of social navigation). So, for each different scenario $s \in \mathcal {S}$ present in the demonstrations, we plan a path to the respective goal using the RRT$^*$ planner. The planner has a limited time to plan, so small variations of the resulting path can arise. So, as commented before, we deal with that by repeating the plan some times and calculating the average values over the number of repetitions. Then, the feature count of the demonstration paths and the RRT$^*$ paths are calculated and averaged over all the scenarios. The difference between these values is used to update the weights of the cost function at each iteration. Thus, we get the weights that make the cost function fit better the demonstration paths as output of the algorithm.

The approximation is described in more detail in Algorithm 1. First, in Line 1 we obtain the average feature count $\overline{f}_{\mathcal {D}}=\frac{1}{D}\sum _{i=1}^{D}f(\zeta _i)$ from the example trajectories in $\mathcal {D}$ scenarios. The feature counts are obtained as the addition of the feature values of pairs of nodes of the trajectory evaluated similarly to Eq. (3).

Then we initialize the weights with a random value (Line 2). It is noteworthy that the weights are being normalized during the learning iterations and the features values for each node are also normalized for the sake of clarity of representation, but this is not a requirement of the algorithm.

The key point is the gradient given by (10), which requires a comparison of the features counts obtained from the example trajectories and the expected value from the RRT$^{*}$ planner. The latter is obtained by running $rrt\_repetitions$ times the planner for the current weight values for each scenario considered (Line 6), and estimating and normalizing the features counts (Line 7). In Lines 9 and 11, the averaged values are computed.

Based on this comparison the weights of the cost function are updated using gradient descent (line 13):

$$\begin{aligned} \omega _{i+1} \leftarrow \omega _i - \frac{\lambda }{\phi }*\nabla \mathcal {L}_i \end{aligned}$$

(12)

where $\phi$ is a value for stabilization which is being incremented after each iteration, $\lambda$ is an adjusting factor of the equation and $\nabla \mathcal {L}_i=\frac{\partial \mathcal {L}(\mathcal {D}|\omega )}{\partial \omega _i}$ is the i-th component of the gradient.

Finally, the learning process finishes when the variations of the weight values keep under a certain convergence value $\epsilon$.

3 Features for Social Navigation

The general learning approach presented above can be applied to any task that can be solved with a RRT$^*$ planner and by defining the adequate features that describe the task properly. From this section on, we apply the algorithm to learn the particular task of human-aware navigation. So, a set of features specially designed for that task is presented here.

The social navigation task considered involves the robot navigating in different house environments like rooms and corridors where some persons stand in various positions so that the robot has to avoid them to reach the goal.

The selection of the adequate features involved in the social navigation task is not trivial [29]. A review and analysis of the most used features in the literature are presented in [37]. Taking into account these previous works, a set of commonly-used features have been considered here. In particular, they are the distance to the goal, the distance to the closest obstacle, and the distance from the robot to the people in the scene and the angle of the robot position with respect to the people $\alpha$, as depicted in Fig. 3. We are not using dynamic features as velocities or accelerations here, which we will leave for future work.

Fig. 3

Some of the features employed in the social cost function learned. $d_{}1$, distance to the goal. $d_{2}$, distance to the closest obstacle. $d_{3}$, distance from the people to the robot. $\alpha$, angle between the person front and the robot location. The three Gaussian functions deployed over the people are also represented

Thus, five functions based on the features presented are combined to obtain the cost function employed in the RRT$^{*}$ planner. The functions are computed for each sample $x_k$ of the configuration space. The first one is just the computation of the Euclidean distance from the robot position to the goal:

$$\begin{aligned} f_1(x_k) = \Vert x_k, x_{goal}\Vert \end{aligned}$$

(13)

The second feature function uses the distance to the closest obstacle for each node $x_k$, with the aim of motivating the robot to keep some distance from the obstacles. This value grows when the distance to the obstacle decreases. A distance transform function is employed to obtain the distance to the closest obstacle for each sample [3]. Then, a normalized value is obtained by using this distance according to Eq. (14).

$$\begin{aligned} f_2(x_k) = \frac{a_{1}}{\gamma *(\Vert x_k, x_{closest\_obs\_k}\Vert +a_{2})} \end{aligned}$$

(14)

where $a_1$ and $a_2$ are the parameters that define the function and take the values 2 and 0.2 respectively. $\gamma$ is a normalization parameters that takes the value 10 in this case.

Then, other three feature functions representing a proxemics cost with respect to the people in the environment are employed. These cost functions are defined by Gaussian functions and are inspired by the model used by Kirby et al. [12]. One Gaussian function is placed in the front of the person, another one in the back, and the last one in the right side of the person. The shape of these Gaussian functions can be seen in Fig. 3. These cost functions p depend on the distance ($d_{jk}$) and relative angle ($\alpha _{jk}$) of the robot position $x_k$ with respect to each person j in the scenario. The costs due to all persons in the scenario are integrated according to the next expressions, where $\mathcal {P}$ represents the set of people:

$$\begin{aligned} f_3(x_k)= & {} max \{ p_{front}(d_{jk} , \alpha _{jk}), \forall j \in \mathcal {P} \} \end{aligned}$$

(15)

$$\begin{aligned} f_4(x_k)= & {} max \{ p_{back}(d_{jk} , \alpha _{jk}), \forall j \in \mathcal {P} \} \end{aligned}$$

(16)

$$\begin{aligned} f_5(x_k)= & {} max \{ p_{right\_side}(d_{jk} , \alpha _{jk}), \forall j \in \mathcal {P} \} \end{aligned}$$

(17)

The first Gaussian function is asymmetric and placed in the front of the person with $\sigma _h = 1.20~(\mathrm{m})$ being the variance in the direction the person is facing, and considering a smaller variance towards the sides $\sigma _s = \sigma _h /1.5$. The second Gaussian is placed in the back of the person with $\sigma _h = \sigma _s = 0.8$. Finally, a third Gaussian is placed in the right side of the person with $\sigma _h = 0.8$ and $\sigma _s = 0.8/2.5$. This function can be useful in corridor scenarios where, usually in Europe, the people usually walk on the right-hand side [15]. Another one could be placed on the left side, so the system should learn the correct weight for each side.

The values of the J (5 in this case) feature functions are normalised and the cost function for each node $x_k$ is built adding its weighted values $c(x_k) = \sum _{i=1}^{J} \omega _i f_{i}(x_k)$ where $\omega _i \in [0,1]$ and $\sum _{i} \omega _i = 1$.

Finally, the total cost of the N nodes of the path $\zeta$ is obtained based on the motion-cost function employed by the RRT$^{*}$ algorithm to calculate the cost of moving from one node to the next one according to Eq. (2).

4 Experimental Results

In this section, we validate the ability of the proposed RTIRL algorithm to recover the cost function and the behavior implicitly encoded by the demonstrations. To do so, a ground-truth cost function is employed to obtain a set of demonstration trajectories from a motion planner optimizing such function. Then, these trajectories are used by the proposed learning algorithm. This way, the learnt cost function can be directly compared with the ground-truth one.

Fig. 4

Some of the scenarios employed in the validation (scenario 9 and scenario 19 respectively). The green cylinders represent the people in the scene indicating their orientations with an arrow. A low-resolution coloured costmap is also shown

Moreover, we present a comparison with two learning from demonstration algorithms of the state-of-the-art: the Maximum Margin Planning algorithm (MMP) [30], which uses an A$^{*}$ algorithm as a planner, and a new learning algorithm called Rapidly Exploring Learning Trees (RLT$^{*}$) [34], which adapts MMP to use a RRT$^{*}$ as a planner. These algorithms have been chosen because they follow the same idea of using a planning algorithm instead of an MDP, and these planning algorithms are also two of the most used planners in robot navigation.

The MMP is a method for learning to plan which attempts to automate the mapping from perception features to costs (or rewards) as well as IRL tries to find the weights of a cost (or reward) function of an MDP. The idea behind MMP is to determine the set of weights that makes that the cost of the demonstrated trajectories are lower than any other path between the same start and goal configurations. For better generalization, the cost function is augmented by a margin that reduces the costs of paths far from the demonstrations. The notion of closeness to demonstrations is defined by a loss-function $\mathcal {L} : \zeta \times \zeta _D \rightarrow \mathbb {R}_{+}$ which defines for each path $\zeta$ how much the learner pays for failing to match the example behavior $\zeta _D$. This loss function value is inverted $(1-\mathcal {L}(\zeta (k), \zeta _D))$ and added to the cost function. This way, the algorithm tries to make any demonstrated path better than any other path by a margin that scales with the size of the loss.

The loss-function employed in the A*-based MMP algorithm [30] counts the number of states that the planner visits but the teacher did not. It is also recommended to relax this function so that nearby paths are also admissible. In the case of RLT$^{*}$ the loss-function used takes into account the nearby paths but it is not explicitly specified [34]. Therefore, in our implementation, we have followed the idea of admitting also nearby path by defining a loss-function, used in both methods (MMP and RLT$^{*}$), which add a cost for each point of the evaluated path based on the Euclidean distance from that point to the closest point of the demonstrated path according to:

$$\begin{aligned} \mathcal {L}(\zeta (k), \zeta _D) = \left\{ \begin{array}{ll} 1 &{}\quad \text{ if } d_{min}(\zeta (k),\zeta _D) > 1 \\ d_{min}(\zeta (k),\zeta _D) &{}\quad \text{ otherwise } \end{array} \right. \nonumber \\ \end{aligned}$$

(18)

where the function $d_{min}$ calculates the Euclidean distance between the point k of the path $\zeta$ and the closest point of the demonstration path $\zeta _D$.

4.1 Algorithm Validation

In order to validate the algorithm performance, we have used a set of demonstration trajectories obtained by a planner optimizing a given ground-truth cost function unknown to the learner. That is, the demonstration trajectories have been recorded by the planner using a cost function with the features explained in Sect. 3 and a known set of weights. This way, we can compare the weights learned with the ground-truth weights and the path costs of the demonstrations and the learned paths. The paths generated with the cost function computed with the learning algorithm are expected to recover the behavior of the demonstration trajectories. Moreover, we should obtain approximately the same weights of the cost function used to generate the demonstration trajectories, our ground-truth, in case that a unique set of weights can replicate the desired behavior.

Particularly, we have employed the ground-truth cost function to record 30 trajectories, each one in a different demonstration scenario (different initial robot position, goal position and person positions in different parts or rooms in a house map). Also, we varied the number of persons in the scenes from 1 to 3. These demonstrations have been recorded by using the RRT$^{*}$ planner with the ground-truth cost function proposed. All the trajectories are performed in a fixed area of $100~\mathrm{m}^{2}$ with the robot in the center. And the time for plan calculation employed is 10 s, which have been seen that it is enough to converge close to the optimum given the space for planning.

Testing and validation of the approximation will be based on splitting the 30 different demonstration trajectories into 20 trajectories to learn the weights of each cost function, and 10 configurations to compare the resultant paths. An example of the scenarios employed in the validation can be seen in Fig. 4 where the scenarios 9 and 19 are presented. In order to have small well-defined sets of trajectories in different enough scenarios, we have grouped the trajectories used for learning and evaluation in three trials for cross-validation according to Table 1.

Table 1 Demonstration trials

The time the RRT$^{*}$ is allowed to plan a path during the execution of the learning algorithms RLT$^*$ y RTIRL is 3 s (other times are also considered in Sect. 4.2). In the case of the MMP learning, the resolution of the discretization of the state space for the A$^{*}$ planning is $0.05~\mathrm{m}$, which is considered a good resolution to get a smooth A$^{*}$ path. Finally, 100 iterations of each learning algorithm have been performed. As the ground-truth weights are known ($\omega _{gt}$), we can calculate the relative errors committed in the final weights learned according to:

$$\begin{aligned} RE_{\omega } = \frac{\Vert \omega _{gt} - \omega \Vert }{\Vert \omega _{gt}\Vert } \end{aligned}$$

(19)

These relative errors obtained in the weights by each algorithm for the 3 trials are shown in Table 2. As can be seen, the RTIRL approximation can recover the ground-truth weights with a small error for all the trials committing a final average error much lower than the other approximations.

Table 2 Relative error in the weights committed by the learning algorithms in the three trials

Fig. 5

Dissimilarity values for the 10 configurations for evaluation of the 3 trials

Fig. 6

Visual comparison of the paths learned in some of the scenarios for evaluation of the three trials

Once the learning phase has finished, we can compare the 10 trajectories reserved for evaluation of the 3 trials with the trajectories computed by the RRT$^{*}$ (and A$^{*}$ planner in case of MMP) with the estimated cost functions in order to visualize how close to the trajectories are in other scenarios. The planning time for the RRT$^{*}$ planner and the space discretization for the A$^{*}$ planner are the same that the ones employed in the learning phase. To overcome the randomness of the RRT$^{*}$ algorithm, 5 paths are planned and an average computation over these paths is performed. The comparison is performed using the following metrics:

4.1.1 Path Dissimilarity Comparison

The first metric, that we called dissimilarity, is used to compare how different are two given paths. This metric is an estimation of the area contained between two paths $\zeta _1$ and $\zeta _2$ by employing the Riemann’s summation:

$$\begin{aligned}&dissimilarity(\zeta _1, \zeta _2) = \nonumber \\&\quad \frac{\sum _{k=1}^{N-1} \frac{d(\zeta _1(k), \zeta _2) + d(\zeta _1({k+1}), \zeta _2)}{2} \Vert \zeta _1(k) - \zeta _1(k+1)\Vert }{\delta } \end{aligned}$$

(20)

where the function d calculates the Euclidean distance between the point k of the path $\zeta _1$ and its closest point of the path $\zeta _2$. $\delta$ is the number of divisions that we performed in the path $\zeta _1$. In this case, we have split the paths into slots of 10 cm in which we calculate the area. The paths are more similar when the dissimilarity approaches zero.

Figure 5 shows the dissimilarity values (along with the standard errors in the case of the 5 paths of RRT$^{*}$-based approximations) for the trials 1,  2 and 3 respectively. As can be seen, for trial 1, the dissimilarity of the RTIRL method is the lowest in most of the cases. The other algorithms lead to big dissimilarity values in some scenarios while the RTIRL method keep a low dissimilarity except for scenarios 5 and 6 where none of the algorithms is able to lead to a good path. In the case of the trial 2, the same happens again. The MMP weight set is not able to reproduce correctly the behavior in scenarios 2, 8 and 10. The RLT$^*$ weight set fails in scenarios 3 and 8. The RTIRL algorithm only partially fails in scenario 8 because some of the 5 paths take another homotopy. Finally, for trial 3, the RTIRL was able to reproduce very well all the evaluation paths while the MMP and RLT$^*$ cost functions lead to paths farther from the ground-truth in scenarios 1, 4 and 8, and 4 and 6 respectively.

For a better understanding of the dissimilarity values, Fig. 6 shows a visual comparison of the paths corresponding with some of the worst cases of the scenarios for evaluation observed in the dissimilarity comparison presented in the Fig. 5. As can be seen, the weight set learned by the RTIRL approximation (blue lines) leads the paths closer to the demonstrated ones (green circles) in most of the cases.

Table 3 summarizes the dissimilarity values for the 3 trials. The results obtained by the weights learned with the RTIRL algorithm are better than the state-of-the-art methods.

Table 3 Dissimilarity means and standard errors committed by the learning algorithms in the three trials

Fig. 7

Relative error in the feature counts for the 10 configurations for evaluation of the 3 trials

4.1.2 Feature Count Comparison

Another interesting comparison is the feature count of the paths $f(\zeta )$, obtained according to Eq. (3). Figure 7 shows the relative errors committed in the feature counts of the paths with respect to those of the demonstration paths. Again, the RTIRL method commits the lowest errors in most of the cases while the other methods fail strongly in some cases. These results are stated in Table 4, which averages the results of the 3 trials. As can be seen, the RTIRL method reaches significant better results than the RLT$^*$ and MMP methods which performance is quite similar according to this metric.

4.1.3 Path Cost Comparison

Finally, as the weights of the ground-truth cost function are known, we can also compare the costs of the learned paths and the demonstration paths. To do that, we can calculate the relative error in the cost of the paths according to:

$$\begin{aligned} RE_{costs}(\zeta ^{i}_{l}, \zeta ^{i}_d) = \frac{\omega ^{T}_{gt}(f(\zeta ^{i}_l) - f(\zeta ^{i}_d))}{\omega ^{T}_{gt} f(\zeta ^{i}_d)} \end{aligned}$$

(21)

where $\zeta ^{i}_{l}$ is the path obtained in the scenario i with the cost function learned and $\zeta ^{i}_{d}$ is the demonstration path in the scenario i. $\omega _{gt}$ is the weight vector of the ground-truth function.

The relative errors in the costs of the paths for the evaluation scenarios of the 3 trials is shown in Fig. 8. As can be seen, the results are quite similar to those obtained for the relative error in the feature count, where the error committed by the RTIRL algorithm is much lower than the error reached by the other approximations. Moreover, the average results for the trials in presented in Table 5. Again, the RTIRL clearly improves the results of the RLT$^{*}$ and MMP methods.

4.1.4 Statistical Significance

A Welch’s T-test is employed to compare the results of the methods in the 3 trials. Table 6 shows the results of the t-tests when comparing the different metrics along with the p-values obtained. As can be observed, the better results reached by the RTIRL method can be considered significant (for a 0.05 level) whereas the differences between the RLT$^*$ and the MMP method can be neglected in the setup presented.

Table 4 Mean relative errors in the feature counts of the paths with the standard errors committed by the learning algorithms in the three trials

Fig. 8

Relative error in the cost of the paths for the 10 configurations for evaluation of the 3 trials

4.2 Learning with Different RRT* Planning Times

We also evaluate the performance of the proposed learning algorithm regarding the time that the RRT$^{*}$ planner is allowed to plan a path during the learning process (this time may be different from that used in execution after learning) and the number of repetitions of the planning. Table 7 shows the average relative error committed in the weights for the methods RTIRL y RLT$^*$ according to different planning times of the RRT$^*$ planner (0.5, 3 and 9 s) and different number of planning repetitions (10 repetitions, 5 repetitions and 1 repetition respectively). As can be observed, the algorithm behaves well even for short planning times. The relative error in the weights just varies around a $3\%$ in both algorithms. These results highlights the importance of the number of repetitions. Even if the time for planning is short, we can still have a good estimation of the average features values if we repeat the plan several times. The results also show that the RTIRL is all in all more efficient in terms error versus planning time than the RLT* algorithm.

Table 5 Mean relative errors in the path costs with the standard errors committed by the learning algorithms in the three trials

Table 6 Results of the Welch’s t-test

Table 7 Average relative error in the learned weights committed by the learning algorithms according to different planning times of the RRT$^*$ planner used in the learning phase

5 Evaluation of the Social Navigation

In this section, the cost function for social navigation learned using the RTIRL algorithm is evaluated by performing real experiments with the TERESA robot in the laboratory. We perform a comparison between the social capabilities of a navigation system employing the cost function learned from a set of demonstrations (which we will denote Social Navigation System (SNS)) and a standard navigation stack where all entities in the scene are considered as simple obstacles. For the latter we employ the popular move_base framework from ROS¹ [26] (denoted Non-Social Navigation System (Non-SNS)). The default configuration parameters have been used but the related ones to the robot footprint, velocities and accelerations than have been adjusted to the TERESA robot.

The library of RRT algorithms and the rest of necessary modules for the SNS have been developed by the authors and are available in the Github of the Service Robotics Lab² under BSD license. A RRT$^*$ replanning each 0.5 s in a local area surrounding the robot and using the learned costs is employed for motion planning, and a simple controller derived from the Dynamic Windows Approach algorithm [7] is used to follow the RRT path.

5.1 Metrics

A set of simple metrics for a social evaluation used in the literature [22], some of them based on the Proxemics theory [8], has been considered here:

• Time to reach the goal ($T_{p}$) Time since the robot start the navigation until the goal is correctly reached.

  $$\begin{aligned} T_{p} = (T_{goal} - T_{ini}) \end{aligned}$$

  (22)

• Path length ($L_{p}$) The length of the path followed by the robot from the initial point to the goal position.

  $$\begin{aligned} L_{p} = \sum _{i=1}^{N-1} \Vert x_r^i - x_r^{i+1} \Vert _2 \end{aligned}$$

  (23)

• Cumulative heading changes (CHC) It counts the cumulative heading changes of in the robot trajectory measured by angles between successive waypoints. It gives a simple way to check on smoothness of path and energy [22] so a low value is desirable.

  $$\begin{aligned} \textit{CHC} = \sum _{i=1}^{N-1} (h_r^i - h_r^{i+1}) \end{aligned}$$

  (24)

  where $h_r^i$ indicates the heading of the robot in the position i. The angles and their difference are normalized between $-\pi$ and $\pi$.

• Average distance to closest person ($CP_{avg}$) A measure of the mean distance from the robot to the closest person along the trajectory.

  $$\begin{aligned} \textit{CP}_{avg} = \frac{1}{N} \sum _{i=1}^{N} (\Vert x_r^i - x_{cp}^i \Vert _2) \end{aligned}$$

  (25)

  where $x_{cp}^i$ indicates the position of the closest person to the robot at step i.

• Minimum and maximum distance to people ($CP_{min}$ and $CP_{max}$ respectively) The values of the minimum and the maximum distances from the robot to the people along the trajectory. It can give an idea of the dimension of the robot trajectory with respect to the people in the space.

  $$\begin{aligned} \textit{CP}_{min}= & {} \min \{ \Vert x_r^i - x_{cp}^i \Vert _2 \mid \forall i \in N\} \end{aligned}$$

  (26)
  $$\begin{aligned} \textit{CP}_{max}= & {} \max \{ \Vert x_r^i - x_{cp}^i \Vert _2 \mid \forall i \in N\} \end{aligned}$$

  (27)

• Personal space intrusions ($CP_{prox}$) This metric is based on the Proxemics theory which define personal spaces around people for interaction [8]. These areas are defined as:

  • Intimate. Distance shorter than 0.45 m.

  • Personal. Distance between 0.45 and 1.2 m.

  • Social. Distance between 1.2 and 3.6 m.

  • Public. Distance longer than 3.6 m.

  Thus, the metric classifies the distance between the robot and the closest person at each time step in one of the Proxemics spaces (in our case we use only three: Intimate, Personal and Social+Public), and obtain a percentage of the time spent in each space for the whole trajectory:

  $$\begin{aligned} \textit{CP}_{prox}^k= \left( \frac{1}{N} \sum _{j=1}^N \mathcal {F} (\Vert x_r^j - x_{cp}^j \Vert _2 < \delta ^k)\right) *100 \end{aligned}$$

  (28)

  where N is the total number of time steps in the trajectory, $\delta$ defines the distance range for classification defined by $k=\{Intimate,~Personal,~Social+Public\}$, and $\mathcal {F}(\cdot )$ is the indicator function. The desirable behavior should lead the robot to spend most of the time in the Social or Public distance range, but this depends on the dimensions of the space and the density of people in the area. So, for a small area shared with people, intrusions in the Personal area are acceptable whereas for a big open space the robot should stay in the Social and Public distances. In any case, the intrusions in the Intimate space should be avoided.

• Interaction space intrusions ($\textit{IS}_{prox}$) This metric is inspired by the work of Okal and Arras [22] in formalizing social normative robot behavior, and it is related to groups of interacting persons. It measures the percentage of time spent by the robot in the three Proxemics spaces considered with respect to an interaction area formed by a group of people that are interacting with each other. The detection of the interaction area of the group is based on the detection of F-formations. A F-formation arises whenever two or more people sustain a spatial and orientational relationship in which the space between them is one to which they have equal, direct, and exclusive access [4, 32].

  $$\begin{aligned} \textit{IS}_{prox}^k= \left( \frac{1}{N} \sum _{j=1}^N \mathcal {F} (\Vert x_r^j - x_{f}^j \Vert _2 < \delta ^k)\right) *100 \end{aligned}$$

  (29)

  where $x_{f}^j$ determines the center of the closest formation or group of people f to the robot at step j.

5.2 Experiments

The social navigation behavior learned using the proposed learning algorithm RTIRL is evaluated here. A cost function using the features described in Sect. 3 has been learnt from navigation demonstrations in static scenarios. The demonstrations were recorded in the Robotics Lab and some scenarios of the TERESA project (an elderly care center in Troyes, France, see Fig. 1). The planning time for the RRT$^*$ employed during the learning phase was 3 s. The learned cost function is then used by the Social Navigation System.

Two sets of experiments have been performed. One in a static scenario (the learning is performed from static scenes) and another one in a dynamic scenario, to check the behavior in scenarios with moving pedestrians.

These evaluation experiments have been recorded in the Robotics Lab of the Pablo de Olavide University. The room has an approximate dimension of $4.60\times 7.60~\mathrm{m}$ and it is equipped with an Optitrack Motion Capture System. This system has been used to accurately estimate the position of the robot and persons involved in the experiments so that results cannot be biased by localization errors.

Fig. 9

Capture of the real experiments for the social navigation evaluation in the University Pablo de Olavide

Fig. 10

Static scenario for social evaluation along with some of the paths obtained by the SNS and non-SNS. Left: Two persons, represented by magenta circles with the blue arrow indicating their orientation, are forming a group. Right: Two persons are facing the walls (not a group). The red line shows the path followed by the TERESA social navigation system (SNS). The blue line shows the path of the move_base non-social system (Non-SNS)

5.2.1 Experiments in Static Scenarios

In the static scenario we have considered two different situations: first, a small group of two people talking to each other in the middle of the scene, as can be seen in Fig. 9; second, there are two persons in the scenario, but they are not interacting each other. Figure 10 shows two examples of the scenarios proposed, where the robot paths and the people position and orientation are shown. As can be seen, the Social Navigation System (SNS) avoid interfering with the group indicating a more acceptable behavior than the Non-Social Navigation System (Non-SNS) from the social point of view.

Tables 8 and 9 shows the metrics, with their standard deviations, obtained for four runs of each navigation system in the static scenario with a group of interacting people, and another four runs in the scenario with two non-interacting individuals respectively.

In the case of two people not forming a group, the metrics do not present many significant differences as can be observed in Table 8 (note that the $IS_{prox}$ metric is not applicable because there is not interaction space). This is because of, in this particular setup, the social taught behaviors lead the robot to similar paths of the Non-SNS. Nevertheless, some metrics can be highlighted: the minimum distance to people is higher in the case of the SNS which indicates that the system always was able to keep some distance to the person; and the SNS was able to spend less time in the Personal space in favor of the time in the Social space which indicates a better social behavior.

Furthermore, the case of a group of people presents clearer differences. The Non-SNS performs clear intrusions in the Intimate space with respect to the closest person and also to the interaction space of the group. Again, the minimum distance to people is higher in the case of SNS. These results show that the SNS is more respectful of the people spaces and the interaction space of the group from a social point of view.

Table 8 Results for social navigation evaluation with a static scenario with two people

Table 9 Results for social navigation evaluation with a static group of two people

Fig. 11

Representation of the paths followed in the dynamic free run experiment. Left: paths followed by the robot using the SNS (red) and Non-SNS (blue). Right: Paths followed by the two people in the scenario

Table 10 Results for social navigation evaluation of a free run with two people moving in the scenario

5.2.2 Experiments in Dynamic Scenarios

Another test has been recorded in a dynamic situation. The aim is to check whether the social cost function learned for static situations is still able to behave in a socially acceptable way in an environment with moving pedestrians. To do that, the RRT$^*$ re-plans at a frequency of 2 Hz. In this scenario, two people are walking freely in the scenario, sometimes forming a group and sometimes walking alone. At the same time, the robot is receiving waypoints that lead it to cross the room avoiding the people around. One long run for each navigation system was performed. Figure 11 shows the paths followed by the people in one of the runs (right) and the paths followed by the robot with the SNS and the Non-SNS (left). As can be seen, the SNS tried to deal with the people adapting its paths to the individuals in a social way unlike the Non-SNS, which tried to perform the same direct trajectory to the goal many times.

Table 10 shows the metrics obtained in the experiment. In this case, the total time $T_{p}$ indicates the total duration of the run being the recording of the SNS case a bit longer than the Non-SNS recording. Under this condition, the path length metric $L_{p}$ indicates the total length traveled by the robot (all the trajectories), and, as can be seen, it was longer in the SNS case. This fits with the paths shown in Fig. 11 left, and explains the higher value in the cumulative heading changes (CHC) since the SNS tried to adapt its paths to the people in the scene. Again the most relevant and significant metrics are the intrusions in the Proxemics spaces of the closest person ($CP_{prox}$) and the interaction area ($IS_{prox}$). The intrusions in the intimate spaces are much lower in the case of SNS, what states the effort on minimizing the disturbance of people. As a general result, we can say that the behavior of the SNS is more socially acceptable than the behavior showed by the Non-SNS as expected.

6 Conclusions

This paper presented an approach for teaching a robot social navigation behaviors using demonstrations. To this end, a method based on IRL has been implemented and linked with a regular RRT$^{*}$ to learn the weights of its cost function, so the planner behaves similarly to the demonstrated behaviors. The method is simple to implement and allows to overcome the typical problems associated to IRLs based on MDPs. The proposed method allows to deal with continuous state spaces and is capable of dealing with larger scenarios (in terms of persons and features) than previous discrete-MDP-based approaches for human-aware navigation [28]. It also simplifies the generalization of the behavior thanks to the inherent benefits of RRTs. The approach has been validated using demonstrations provided from a ground-truth cost function. The results show that it is able to properly approximate the demonstrated cost function, and to obtain behaviors more similar to the demonstrations than related algorithms from the state-of-art. Furthermore, Sect. 5 has shown how the taught behaviors lead to more socially appropriate motion than methods not considering the learned costs.

The proposed method has been applied to a telepresence robot. While the learning approach is offline, this setup allows to gather additional data whenever the user employs the robot in teleoperated mode, and thus to update the learned costs iteratively when new data is available, considering new scenarios.

Future work will consider including kinodynamic constraints of the robot in the RRT$^{*}$ planner and the use of a richer set of features also employing the velocities of the robot and persons. Additionally, we will also evaluate learning the relevant features from the demonstrations. For that, recent approaches of deep learning for IRL [6] will be considered. Finally, a further mathematical analysis of the distributions of path costs followed by the RRT$^{*}$ planner as well as other optimization techniques to solve the problem will be considered.