1 Introduction

Crowd movement modeling is currently a challenging problem in various fields, from architecture and civil engineering to entertainment and visual effects. Its applications are numerous: studying the flow of people in confined spaces, creating realistic models of crowds for use in movies, validating human behavior models in psychology/sociology under different environmental conditions like panic situations etc.. The wide variation in walking styles, the complex behavior of each individual, and the large number of individuals potentially interacting with each other make difficult any rigorous formalization of crowd phenomena. Nevertheless, in response to the complexity of human behavior, numerous models have been proposed in recent years with the goal of representing a precise crowd behavior or situation. Two main types of pedestrian models can be found: the macroscopic models and the microscopic ones. For the first category, the crowd is described with fluid-like properties, giving rise to macroscopic approaches. These models describe how the density and the velocity of the pedestrian flow change over time, using partial differential equations. This approach is based on some analogies with fluid behavior observed at medium and high crowd densities. While this approach could be partially confirmed, it is does not take into consideration certain particular interactions (i.e. avoidance and deceleration maneuvers). The attention was then shifted to modeling individual pedestrian motion. The second category which concerns microscopic and agent-based models is now the main focus of pedestrian research. These models are the best suited to treat decentralized decision making, local-global interactions, self-organization, emergence and effects of heterogeneity in a complex system. The most well-known types of agent-based models are the force-based models [9, 16, 27, 38], cellular automata [3, 4, 6, 14, 23], and artificial intelligence-based models [15, 34]. The main differences between these models lie in the representation of the environment (discrete or continuous) and the level of complexity and the nature of pedestrian–pedestrian interactions (force-based, rule-based, cognitive, etc.).

A 2D microscopic approach in which the movement of each pedestrian is represented in time and in space was recently proposed in [30, 32, 33]. It is therefore an agent-based model with a continuous representation of the environment. To control the crowd movement on the ground, three aspects are addressed: (1) multiple simultaneous collisions, i.e. to detect and to handle each local interaction, such as pedestrian–pedestrian and pedestrian-obstacle; (2) the desire of each pedestrian to move in a particular direction with a specific speed at each time; (3) the possibility to add different levels of complexity for a more realistic behavior of the pedestrians (social forces, subgroup forces, fields of vision, heuristics, etc.). The main contribution of the model is its ability to treat collisions without any interpenetration between the agents or between the agents and the obstacles by using an original approach based on the theory of rigid body collisions in a rigorous thermodynamics context [13]. In future work, the particles will be rendered deformable which will allow us to study the pressure exerted on each pedestrian at very high densities. Another contribution of the model is a new approach to model pedestrians who hold hands. Only by integrating the rotation of the pedestrians about their vertical axis in the 2D model [2], which is rarely done in literature [1, 26], we were able to take into account the interactions between rigid particles as an at-a-distance deformation velocity [7]. This is necessary to ensure the cohesion of a group of particles and maintain the links between its members. As a result, our model is able to represent a particular subgroup behavior: the holding hands pedestrians. Few approaches are able to model this behavior [29, 36] which is crucial when parents and children are present in a crowd.

The aim of this paper is to briefly present the 2D microscopic model developed in [2, 30, 32, 33] and to calibrate its main parameters for a pedestrian–pedestrian collision and the repulsive force parameters [17] for the experiment done in [35]. Since one of the objectives behind crowd modeling is to improve elements of pedestrian facilities, we have chosen to study a typically problematic area: the bottleneck. A bottleneck can include entrance corridors, escalators, stairways, turnstiles and revolving doors.

The paper is organized as follows. In Sect. 2, the 2D discrete model is presented. Then, the parameters of the model are calibrated for a pedestrian–pedestrian collision in Sect. 3. Section 4 describes the setup of an evacuation experiment of a corridor with a bottleneck exit. In addition, a parametric study of our model is performed and the numerical simulations are presented. Finally, the results are discussed and analyzed in the last section.

2 The 2D crowd movement model

The proposed 2D crowd movement model has already been introduced in detail in [30, 32, 33] and more recently in [2]. In this section, we only recall it along with its adaptation to crowd movement. The aim is to help the readers that discover this approach for the first time.

2.1 A non-smooth microscopic model based on Frémond’s approach for collision modeling

In the following, scalars are written in normal font. Vectors and matrices are written in bold font and are represented by lower case and upper case respectively unless precised. Frémond’s approach have originally been developed for granular media. However, this article deals with pedestrian modeling and thus the corresponding terminology will be used (e.g. pedestrian instead of particle). Let us consider a system of N pedestrians represented by circular disks moving in a horizontal plane each defined by:

  • a mass \(m_i\)

  • a moment of inertia \(I_i\) about its vertical axis

  • a radius \(r_i\)

  • a center of gravity \(G_i\), whose position with respect to a reference system with axes \(x-y\) and origin O, is described by the vector \(^t {\mathbf {q}}_i(t) = (q^x_i(t) , q^y_i(t), \theta_i(t)) \in {\mathbb {R}}^3\)

  • a velocity denoted by \(^t{\mathbf {v}}_i(t)=({\mathbf {u}}_i(t), {\dot{\theta}}_i(t))=(u^x_i(t) , u^y_i(t), {\dot{\theta}}_i(t))\)

where \(\theta_i(t) \in [-\pi ,\pi ]\) represents the walking direction of the pedestrians about the \({\mathbf {e}}_z\)-axis (\(\theta_i(t)=0\) when the individual’s walking direction is parallel to the x-axis in the positive direction and \(\theta_i(t)>0\) when the individual turns counterclockwise) and \({\dot{\theta }}_i(t)=d\theta_i/dt\) their rotational velocity. Contacts between agents are assumed to be pointwise. For the sake of notation simplicity, we shall omit the time dependence in the following, unless this leads to ambiguities.

The description of the behavior of this collection of discrete bodies is based on the consideration that the global system they constitute is deformable even if each disk is rigid. Making use of the principle of virtual work, the equations describing the regular (smooth) as well as the discontinuous (non-smooth collisions) evolutions of the movement of the system can be obtained. The deformation velocity involving the ith and jth pedestrians at the contact point A is given by:

$$\begin{aligned} \varvec{\varDelta }_{ij}({\mathbf {v}} ) ={\mathbf {u}}_{i}+{\dot{\theta}}_i{\mathbf {e}}_z\times {\mathbf {G}}_{i} {\mathbf {A}} -({\mathbf {u}}_{j}+ {\dot{\theta}}_j{\mathbf {e}}_z\times {\mathbf {G}}_{j} {\mathbf {A}} ) \end{aligned}$$
(1)

where \(^t{\mathbf {v}} =(^t{\mathbf {v}}_i,^t{\mathbf {v}}_j)\) collects the velocities of all the agents evolving in the studied system and \(\times\) the cross product.

A different form of the deformation velocity allows to represent a particular case of subgroup: pedestrians holding hands. While existing methods depict the cohesion of a subgroup with forces [29, 36], the proposed method to describe this particular type of subgroups uses an at-a-distance deformation velocity. Inspired by the works of Caselli and Frémond [7], an at-a-distance interaction between rigid particles is introduced to model the effects of the subgroup as a continuous deformation of the system constituted by all the linked pedestrians. The at-a-distance deformation velocity is a scalar quantity defined by the derivative with respect to time of the squared distance between linked shoulders, i.e. for pedestrians i and j points \(A_i\) and \(A_j\) are considered and illustrated in Fig. 1.

Fig. 1
figure 1

Two holding hands pedestrians—example of linked shoulders

Full size image

For a group of two individuals, the at-a-distance deformation velocity is expressed as:

$$\begin{aligned} \varDelta_{ij}^{*}\left( {\mathbf {v}} \right) =2\left( {\mathbf {u}}_{i}+{\dot{\theta}}_i{\mathbf {e}}_z\times {\mathbf {G}}_{i} {\mathbf {A}}_{i}-\left( {\mathbf {u}}_{j}+{\dot{ \theta}}_{j} {\mathbf {e}}_z\times {\mathbf {G}}_{j} {\mathbf {A}}_{j}\right) \right) \cdot {\mathbf {A}}_{j} {\mathbf {A}}_{i} \end{aligned}$$
(2)

where \(\cdot\) is the dot product. The dynamics equations for the set of all pedestrians can be written as follows:

$$\mathbf{M}{\dot{\mathbf{v}}}=-\mathbf{f}^{int}+\mathbf{f}^{ext}$$
(3)
$$\mathbf{M}({\mathbf{v}^{+}}-{\mathbf{v}^{-}})=-\mathbf{p}^{int}+\mathbf{p}^{ext}$$
(4)

where \({\mathbf {M}}\) is the \(3N\times 3N\) inertial matrix of the set of individuals; \({\mathbf {f}} ^{ext}\) (resp. \({\mathbf {f}} ^{int}\)) is the external force vector (resp. internal force vector) of dimension 3N applied to the deformable system of all the pedestrians; \({\mathbf {v}} ^{-}\) and \({\mathbf {v}} ^{+}\) are the agent’s velocities before and after a collision. For instance, the social repulsion force introduced by Helbing [17] would be considered as an external force, while the force driving an individual to a certain destination would be introduced as an internal one.

The existence of a solution of the system given by Eqs. (3) and (4) is proven in [8, 11, 13]. Eq. (3) describes the smooth evolution of the multi-particles system whereas Eq. (4) describes its non-smooth evolution during a collision. Hence, Eq. (3) applies almost everywhere, except at the instant of collision, where it is replaced by Eq. (4).

When a contact is detected, the velocities of colliding pedestrians become discontinuous. Therefore, Eq. (4), where the interior and exterior percussions (\({\mathbf {p}} ^{int}\) and \({\mathbf {p}} ^{ext}\) respectively) are introduced, is used to calculate the velocity after the shock. By definition, percussions have the dimension of a linear momentum: a force multiplied by time (kg m s\(^{-1}\)). The \({\mathbf {p}} ^{int}\) percussions are unknown; they take into account the dissipative interactions between the colliding agents (dissipative percussions \({\mathbf {p}} ^{d}\)) and the reaction forces that permit the avoidance of overlapping among pedestrians (reactive percussions \({\mathbf {p}} ^{reac}\)), and hence \({\mathbf {p}} ^{int}={\mathbf {p}} ^{d}+{\mathbf {p}} ^{reac}\). Frémond [12, 13] defined the deformation velocity \(\mathscr {D}(\frac{\mathbf{v }^{+}+\mathbf{v }^{-}}{2})\) in duality with \({\mathbf {p}} ^{int}\) according to the work of internal forces, where \(\mathscr {D}({\mathbf {v}} )=(\varvec{\varDelta }({\mathbf {v}} ),\varDelta ^{*}({\mathbf {v}} ))\), \(\varvec{\varDelta }({\mathbf {v}} )\) represents the vector containing all the velocities of deformation of all the individuals in contact, and \(\varDelta ^{*}({\mathbf {v}} )\) represents the vector containing all the at-a-distance deformation velocities of the pedestrians belonging to groups. He then introduced a pseudopotential of dissipation \(\varPhi =\varPhi (\mathscr {D})\), which allows us to express \({\mathbf {p}} ^{int}\) as:

$$\begin{aligned} {\mathbf{p}}^{int}\in \partial {\varPhi }\left( \mathscr {D}\left( \frac{{\mathbf{v}}^{+}+{\mathbf{v}}^{-}}{2}\right) \right) \end{aligned}$$
(5)

where the symbol \(\partial\) denotes the sub differential of the functional in the sense of convex analysis, which generalizes the derivative for convex functions [13]. We recall that a pseudo-potential, in the definition by Moreau, is a non-negative convex function, which is zero for zero dissipation.

The convex function \(\varPhi\) is defined as the sum of two pseudopotentials [28]:

$$\begin{aligned} \varPhi =\varPhi ^d+\varPhi ^r \, , \end{aligned}$$
(6)

where \(\varPhi ^d\) and \(\varPhi ^r\) characterize respectively the dissipative and reactive interior percussions.

The introduced system (Eqs. 4–6) leads to a constrained minimization problem:

$$\begin{aligned} {\mathbf {X}} =\arg \min_\mathbf{Y \in \mathbb {R}^{3N_c}}\Big [\,^{t} {\mathbf {Y}} \,{\mathbf {M}} \,{\mathbf {Y}} +\varPhi \left( \mathscr {D}({\mathbf {Y}} )\right) -^{t}\left( 2{\mathbf {v}} ^{-}+{\mathbf {M}} ^{-1} {\mathbf {p}} ^{ext}\right) {\mathbf {M}} \,{\mathbf {Y}} \Big ] \end{aligned}$$
(7)

with \({\mathbf{Y}}=\frac{\mathbf{v }^{+}+\mathbf{v }^{-}}{2}\) and \(N_c\) the number of pedestrians in contact. \({\mathbf {X}}\) and \({\mathbf {Y}}\) are vectors. The solution is given by \({\mathbf{X}}=\frac{\mathbf{v }^{+}+{\mathbf{v}}^{-}}{2}\) [13]. A proof of the existence and uniqueness of the velocity \({\mathbf {v}} ^{+}\) after the simultaneous collisions of several rigid solids, as well as the dissipative nature of the collisions, is presented in [11–13].

2.2 Choice of the pseudopotentials

The reactive percussion \({\mathbf {p}} ^{reac}\) ensures the non-interpenetration between agents. It is equal to 0 if contact is not maintained after collision (i.e., \(\varDelta_{ij}({\mathbf {v}} ^{+})\cdot {\mathbf {e}} ^n_{ij}<0\)) and positive if contact is maintained after collision (i.e., \(\varDelta_{ij}({\mathbf {v}} ^{+})\cdot {\mathbf {e}} ^n_{ij}=0\)). These conditions allow us to define \({\mathbf {p}} ^{reac}\) using the indicator function \(\varPhi ^r=I_{\mathbb {R}^-}(\varDelta_{ij}({\mathbf {v}} ^{+})\cdot {\mathbf {e}} ^n_{ij})\) such that \({\mathbf {p}} ^{reac} \in \partial \varPhi ^r\) [13]. Since \(\varOmega\) is convex and contains the origin, \(I_\varOmega\) can be considered as a pseudopotential of dissipation.

By giving \(\varPhi ^d\) different expressions, a large variety of behaviors after impact can be obtained [8, 13]. In [10], different types of collisions (collision with adhesion, perfectly elastic, inelastic and perfectly inelastic collisions) were studied and analyzed. A quadratic pseudopotential gives the same classical results obtained by using the coefficient of restitution for the case of a single collision between two bodies. For the case of multiple simultaneous collisions, only the approach using a pseudopotential has been proved to ensure the existence and the unicity of a solution and the dissipative nature of the collision [10]. In the following, a quadratic pseudopotential \(\varPhi ^d\) is chosen :

$$\begin{aligned} \varPhi ^{d}\left( \mathscr {D}({\mathbf {v}} )\right)= & \frac{1}{2}\sum_{1\le i\le j\le N}\left[ K_{n}\left( \,^{t}\varvec{\varDelta }_{ij}\left( {\mathbf {v}} \right) \cdot {\mathbf {e}} ^n_{ij}\right) ^{2}+K_{tg}\left( \,^{t}\varvec{\varDelta }_{ij}\left( {\mathbf {v}} \right) \cdot {\mathbf {e}} ^{tg}_{ij}\right) ^{2}\right] \\&+\sum_{1\le i\le j\le N_{subgroup}}\frac{1}{2}K_{v}\left( \,\varDelta ^{*}_{ij}\left( {\mathbf {v}} \right) \right) ^{2} \end{aligned}$$
(8)

where \({\mathbf {e}} ^{tg}_{ij}={\mathbf {e}}_z\times {\mathbf {e}} ^n_{ij}\) and \(N_{subgroup}\) is the number of pedestrians that belong to groups. The dissipation coefficient \(K_n\) (in kg) for the normal component of the dissipative percussion characterizes the inelastic nature of the collisions between agents; an infinite value of \(K_n\) implies a perfectly elastic collision. \(K_{tg}\) (in kg) is the dissipation coefficient for the tangential component of the percussion while \(K_v\) (in kg m\(^{-2}\)) is the coefficient of viscous dissipation. The higher its value is, the more rigid the link between the pedestrians forming a group is. In other words, for a high value of \(K_v\), a free agent colliding with a group of pedestrians won’t be able to break their bond.

In the discrete element method (DEM) instead of pseudopotentials, forces are introduced to treat the overlapping problem. In this smooth approach, which is used by Helbing [17] without considering rotation, a slight overlapping between pedestrians is allowed in order to introduce a “body force” (Eq. 9) counteracting body compression (preventing overlapping) and a “sliding friction force” (Eq. 10) impeding relative tangential motion:

$$\begin{aligned} {\mathbf {f}}_{b,i}= & -\kappa 'g(r_i+r_j-\parallel {\mathbf {q}}_i-{\mathbf {q}}_j\parallel ){\mathbf {e}} ^n_{ij} \end{aligned}$$
(9)
$$\begin{aligned} {\mathbf {f}}_{s,i}= & -\kappa ''g(r_i+r_j-\parallel {\mathbf {q}}_{i}-{\mathbf {q}}_{j}\parallel ) \varDelta u_{ij}^{tg} \cdot {\mathbf {e}} ^{tg}_{ij} \end{aligned}$$
(10)

where \(\kappa '=1.2 \times 10^5\) kg s\(^{-2}\), \(\kappa ''=2.4\times 10^5\)  kg m\(^{-1}\) s\(^{-1}\) [17] and the function g(s) is 0 if the pedestrians are not in contact, otherwise equal to the argument s. The tangential velocity difference between pedestrians i and j is given by \({\varDelta } u_{ij}^{tg}=-({\mathbf {u}}_{j}-{\mathbf {u}}_{i})\cdot {\mathbf {e}} ^{tg}_{ij}\). The contact forces \({\mathbf {f}}_{b,j}\) and \({\mathbf {f}}_{s,j}\) acting on the agent j are equal and opposite to the forces \({\mathbf {f}}_{b,i}\) and \({\mathbf {f}}_{s,i}\) respectively. With the aforementioned value of \(\kappa '\), the human body acts like a very stiff string that resists penetration. At the same time, this value of \(\kappa '\) results in a very high contact force capable of crushing an individual [25]. In this approach, only perfectly elastic pedestrian–pedestrian collisions can be obtained.

It is important to note that \(K_n\) and \(K_{tg}\) should not be confounded with \(\kappa '\) and \(\kappa ''\). The parameters \(K_n\) and \(K_{tg}\) are dissipative coefficients that determine the nature of a collision (from perfectly inelastic to perfectly elastic) in an approach that does not allow any overlapping between the colliding pedestrians that are represented by rigid disks. We are currently working on rendering the agents deformable in our model to study body compression. On the other hand, \(\kappa '\) and \(\kappa ''\) are stiffness coefficients defined in an approach that allows overlapping between the colliding agents. The overlapping distance and the stiffness coefficients are then used to generate a force to counteract body compression leading to purely elastic collisions. That is why \(K_n\) and \(K_{tg}\) on one side and \(\kappa '\) and \(\kappa ''\) don’t necessarily have the same values or the same order of magnitude.

2.3 Adaptation to crowd movement

In our 2D model a pedestrian is represented by a circular particle having a “willingness”, i.e. a desire to move in a particular direction with a specific speed at each time [17, 30, 32, 33]. In this article, we are interested in the egress scenarios under normal conditions. We don’t deal with other scenarios like pedestrian movement in a train station or a commercial center.

The first step of the approach is to give a desired trajectory to each pedestrian. Several definitions of the desired trajectory of a pedestrian are possible: (1) the most comfortable trajectory, where the individual exerts the least effort, e.g. by avoiding stairs or making the fewest changes in direction, etc.; (2) the shortest path; or (3) the fastest one [19]. It is possible to combine two strategies in the same simulation or to change the preferred strategy for any reason during the simulation. In the current model, pedestrians use the shortest path to get to the exit. To do so, we consider a wavefront that starts at the exit \(\partial \varUpsilon\) of a 2D environment \(\varUpsilon\) where the areas occupied by obstacles are represented by \(\varGamma\). As the wavefront propagates in \(\varUpsilon\), its arrival times can be found for each node of the discretized space. These arrival times form a scalar function T(x, y) whose values can be obtained by solving the eikonal equation [5] given by :

$$\begin{aligned} \mid \mid \varvec{\nabla } T(x,y)\mid \mid= & \frac{1}{V(x,y)} \quad \text {for} \ (x,y)\ \in \varUpsilon \end{aligned}$$
(11)
$$\begin{aligned} T(x,y)= & 0 \quad \text {for} \ (x,y)\ \in \partial \varUpsilon \end{aligned}$$
(12)

where V(x, y) is the velocity of the wavefront. By setting \(V(x,y)=0\) in \(\varGamma\), the wavefront cannot penetrate this area. In this way, areas that cannot be accessed by pedestrians can be defined (obstacles, walls, …). By setting \(V(x,y)=1\) m/s in \(\varUpsilon \backslash \varGamma\), the arrival times T(x, y) coincide with the Euclidean distances to the exit. In this way, the shortest path from one point to another can be calculated. By setting \(0<V(x,y)<1\) in \(\varUpsilon \backslash \varGamma\), areas that are not frequently used by pedestrians can be defined (areas near to obstacles and walls, wet floor, streets…). Several numerical methods exist to solve the eikonal equation, for example the Fast Marching Method [22] and the Fast Iterative Method [21]. In our model we set \(V(x,y) =1\) in \(\varUpsilon \backslash \varGamma\) and \(V(x,y) =0\) in \(\varGamma\). Then by using the Fast Marching Algorithm to solve the eikonal equation, a geodesic map is obtained that can be used to find \({\mathbf {e}}_{d,i}\), the desired direction [17] of an individual i towards the exit using the shortest path :

$$\begin{aligned} {\mathbf {e}}_{d,i}=-\frac{\varvec{\nabla } T(x,y)}{\mid \mid \varvec{\nabla } T(x,y)\mid \mid } \end{aligned}$$
(13)

The desired velocity is then defined by \({\mathbf {u}}_{d,i}=\parallel \mathbf{u_{d,i}}\parallel \,\cdot \,{\mathbf {e}}_{d,i}\) where \(\parallel \mathbf{u_{d,i}}\parallel\) represents the amplitude of the desired velocity at which the ith pedestrian wants to move. For normal conditions, this speed is chosen to be following a normal distribution with an average of 1.34 m s\(^{-1}\) and a standard deviation of 0.26 m s\(^{-1}\) [18].

The second step is to introduce the desired velocity into the original discrete model to simulate crowd movement. Let \({\mathbf {f}} ^{int}={\mathbf {h}} ^a\), where \({\mathbf {h}} ^a\) gives the desired direction, the amplitude of the velocity and the walking direction of each pedestrian. Each vector \({\mathbf {h}}_i^a\) associated with pedestrian i represents a component of the vector \(^{t} {\mathbf {h}} ^a=(^{t} {\mathbf {h}}_{1}^a,^{t} {\mathbf {h}}_{2}^a,\ldots ,^{t} {\mathbf {h}}_{N}^a)\) of dimension 3N. It can be expressed as \(^{t} {\mathbf {h}} ^a_i=(^{t} {\mathbf {f}}_{i}^a,l_{i}^a)\), where \({\mathbf {f}}_{i}^a\) (in kg m s\(^{-2}\)) is the so-called acceleration force [17] giving the desired direction and amplitude of the velocity of the ith pedestrian. \({\mathbf {f}}_{i}^a\) is defined in [17, 30, 32, 33] by:

$$\begin{aligned} \mathbf{f }_{i}^a=m_i\frac{\mathbf{u }_i - \parallel \mathbf{u }_{d,i}\parallel \mathbf{e }_{d,i}}{\tau_i} \end{aligned}$$
(14)

where \({\mathbf {u}}_{i}\) (in m s\(^{-1}\)) is the actual velocity and \(\tau_i\) (in s) is the relaxation time, which specifies how long the pedestrian will take to recover his desired velocity after a contact or after a sudden change in path. For example, Helbing [17] chose \(\tau_i=0.5\) s in his numerical simulations. When the value of \(\tau_i\) is less than or equal to 0.5 s, the pedestrians walk “aggressively” and several contacts may occur successively. Its influence has been studied in [33].

As for \(l_i^a\) (in kg m\(^{2}\) s\(^{-2}\)), it represents the restoring torque in order to return the pedestrian to his desired direction after a perturbation. It is modeled as the combination of a linear rotational spring and of a linear rotational damper [2], and is defined for the i-th pedestrian by:

$$\begin{aligned} l_{i}^a=k_i\left( \theta_i-\theta_{d,i}\right) +c_i{\dot{\theta}}_i=-I_i\ddot{\theta }_i \end{aligned}$$
(15)

where \(\theta_{d,i}\) is the angle between \({\mathbf {e}}_{d,i}\) and the reference direction \({\mathbf {e}}_x=[1;0]\), \(I_i\) (in kg m\(^2\)) is the moment of inertia, \(k_i\) (in kg m\(^{2}\) s\(^{-2}\) rd\(^{-1}\)) is the torsional stiffness, \(c_i\) (in kg m\(^2\) s\(^{-1}\) rd\(^{-1}\)) is the rotational damping, and \(\omega_i=\sqrt{\frac{k_i}{I_i}}\) (in rd s\(^{-1}\)) is the undamped resonant frequency for pedestrian i. After a perturbation, a pedestrian returns the fastest without oscillations to its desired direction when its rotation is critically damped (\(\zeta_i=\frac{c_i}{2\sqrt{I_i\, k_i}}=1\)). For \(\zeta_i>1\), the individual returns more slowly to its desired position. For \(\zeta_i<1\), it oscillates before returning to its desired direction. In Fig. 2, the collision occurs at \(t=0.1\) s and the time step is \(\varDelta t =0.01\) s. The solid line plotted inside the agent represents the pedestrian’s desired direction while the dotted line represents his current walking direction. We have chosen \(\zeta_i=1\). The choice of \(k_i\) will be discussed later. As we have mentioned earlier, adding rotation to the pedestrians’ movement is essential to model subgroup behavior.

Fig. 2
figure 2

Pedestrian–pedestrian interaction without repulsive forces: the left column shows the pedestrian’s movement after “collision” for \(\zeta_i=1\) (top) and \(\zeta_i=0\) (bottom), where \(\theta_{d,i}=0\). The right column is a plot of the pedestrian’s rotation as a function of time

Full size image

2.4 Pedestrian–pedestrian interaction

Among the different types of pedestrian interaction, the act of avoidance stands out as an essential component of the coordination of collective movement. This action constitutes a central element of the majority of pedestrian movement models. Experimental studies exist to compare predictions from a model with certain observed global characteristics, such as flow intensity, velocity distribution or emerging collective arrangements. However, the lack of control of the observed situations in these experiments creates a major obstacle for the process of identifying the interaction laws and validating the underlying assumptions. In a natural environment, the result of an interaction on a pedestrian’s spontaneous behavior is difficult to quantify, given that the observer neither controls the terms of the interaction nor knows the pedestrian’s desired direction, attention level, or comfort velocity.

In the classical crowd movement models, the pedestrians’ behavior can be enriched by adding social forces [17, 29, 33] so as to become more realistic (repulsive force, attractive force, group force, etc.). Among the social forces, the sociopsychological or the social repulsion force is essential to reproduce human behavior. It reflects an individual’s tendency to avoid collisions with other pedestrians and obstacles keeping a certain distance from them (Fig. 3). This force was introduced by Helbing and was given by the following form in [17]:

$$\begin{aligned} {\mathbf {f}}_{ij}=-Ae^{\left( (R_{ij}-d_{ij})/B\right) }\left( \varLambda +(1-\varLambda )\frac{1+\text {cos}\phi_{ij}}{2}\right) \,{\mathbf {e}} ^n_{ij} \end{aligned}$$
(16)

where \(R_{ij}=r_i+r_j\) is the sum of the radii of pedestrians i and j, \(d_{ij}\) is the distance between their centers, A and B are constant parameters of the model representing the magnitude of the maximum sociopsychological force and its fall-off length respectively, \(\varLambda\) with \(0<\varLambda <1\) is a parameter which grows with the effect of interactions behind an individual, and \(\phi_{ij}\) is the angle between the desired direction \({\mathbf {e}}_{d,i}\) and the vector \(-{\mathbf {e}} ^n_{ij}\). The social force \({\mathbf {f}}_{ij}\) acts on pedestrian i. The force acting on pedestrian j reads: \({\mathbf {f}}_{ji}=-{\mathbf {f}}_{ij}\).

Fig. 3
figure 3

Pedestrian–pedestrian interaction, a without and b with introducing the repulsive force (for \(A=2000\) N and \(B=0.15\) m)

Full size image

In [17], Helbing chose \(A=2000\) kg m s\(^{-2}\) and \(B=0.08\) m. In [25], it is shown that for these values of A and B, a pedestrian’s maximum deceleration exceed the acceleration of gravity by almost 40 %. A value that does not seem realistic.

3 Calibrating the parameters that govern a collision

3.1 Velocity after collision

In the proposed model, the main parameter controlling the velocity after a collision between two individuals is \(K_n\) (in kg). Let us consider a head on collision of two points of masses \(m_1\) and \(m_2\) respectively, illustrated in Fig. 4, where \(K_{tg}=K_v=0\) and rotation is not considered. The after collision velocities \({\mathbf {u}}_{1}^{+}\) and \({\mathbf {u}}_{2}^{+}\) of the masses \(m_1\) and \(m_2\) respectively, can be found analytically by solving the following system (derived from Eqs. 4 and 5):

$$\left\{ \begin{array}{ll} m_{1}({\mathbf {u}}_1^{+}-{\mathbf {u}} _{1}^{-})=-{\mathbf {p}} ^{int}=-\frac{K_{n}}{2}({\mathbf {u}} _{1}^{+}-{\mathbf {u}}_{2}^{+}+{\mathbf {u}}_{1}^{-}-{\mathbf {u}} _{2}^{-})-{\mathbf {p}} ^{reac}\\ m_{2}({\mathbf {u}} _2^{+}-{\mathbf {u}}_{2}^{-})={\mathbf {p}} ^{int} \\ {\mathbf {p}} ^{reac} \in \partial I_{\mathbb {R}^-}\left( {\mathbf{u}} _{1}^{+}-{\mathbf {u}}_{2}^{+}\right) \end{array}.\right.$$

The solution of this system can be found [13]:

  • If \(K_n \le \frac{m_1 m_2}{m_1+m_2}\) then

    $$\begin{aligned} {\mathbf {u}}_1^{+}={\mathbf {u}}_2^{+}=\frac{m_1{\mathbf {u}}_1^{-}+m_2{\mathbf {u}}_2^{-}}{m_1+m_2} \end{aligned}$$
    (17)

  • If \(K_n \ge \frac{m_1 m_2}{m_1+m_2}\) then

    $$\begin{aligned} \begin{aligned} {\mathbf {u}}_{1}^{+}&=\frac{(m_{1}m_{2}+K_{n}m_{1}-K_{n}m_{2}){\mathbf {u}}_{1}^{-}+2K_{n}m_{2} {\mathbf {u}}_{2}^{-}}{m_{1}m_{2}+K_{n}m_{1}+K_{n} m_{2}}\\ {\mathbf {u}}_{2}^{+}&=\frac{(m_{1}m_{2}+K_{n}m_{2}-K_{n}m_{1}){\mathbf {u}}_{2}^{-}+2K_{n}m_{1} {\mathbf {u}}_{1}^{-}}{m_{1}m_{2}+K_{n}m_{1}+K_{n}m_{2}} \end{aligned} \end{aligned}$$

It can be noticed in Eq. (17) that when \(K_{n} \le \frac{m_1 m_2}{m_1+m_2}\), the after collision velocities are not dependent on \(K_{n}\) and when \(K_{n} > \frac{m_1 m_2}{m_1+m_2}\), the agents move in opposite directions after colliding. Finally when \(K_{n}\) tends towards infinity, the after collision velocities become:

$$\begin{aligned} {\mathbf {u}}_{1}^{+}= & \frac{(m_{1} - m_{2}){\mathbf {u}}_{1}^{-} + 2 m_{2} {\mathbf {u}}_{2}^{-}}{m_{1} + m_{2}}\\ {\mathbf {u}}_{2}^{+}= & \frac{(m_{2}-m_{1}){\mathbf {u}}_{2}^{-} + 2m_{1} {\mathbf {u}}_{1}^{-}}{m_{1}+m_{2}} \end{aligned}$$
(18)

and in the case of \(m_1=m_2\), Eq. (18) can be simplified:

$$\begin{aligned} {\mathbf {u}}_{1}^{+}= & {\mathbf {u}}_{2}^{-} \\ {\mathbf {u}}_{2}^{+}= & {\mathbf {u}}_{1}^{-} \end{aligned}$$
(19)
Fig. 4
figure 4

Two colliding pedestrians. The dotted line represents each pedestrian’s current walking direction

Full size image

In this paragraph, we compare between the analytical and numerical solutions. The collision illustrated in Fig. 4 has been studied for two cases. In the first case, \(m_1=m_2=62 \, kg\) and \(\mid {\mathbf {u}}_{1}^{-} \mid =\mid {\mathbf {u}}_{2}^{-} \mid =1\) m/s while in the second one \(m_1=62\) kg, \(m_2=20\) kg, \(\mid {\mathbf {u}}_{1}^{-} \mid =2\) m/s and \(\mid {\mathbf {u}}_{2}^{-}\mid = 0.5\) m/s. The plot of \({u}_{i}^+\) as a function of \(\text {log}_{10}(K_n)\) illustrated in Fig. 5, shows the validity of the used scheme and the influence of the normal coefficient of dissipation on the after collision velocities. It can be observed that for \(K_n>10^4\) kg the collisions become perfectly elastic. The nature of the pedestrian–pedestrian collision controls the choice of \(K_n\). In [2, 30, 32, 33], the author chose \(K_n=10^5\) kg which results in perfectly elastic collisions when social forces are not considered. The simulations done using this value for \(K_n\) gave satisfying results for the case of emergency evacuation.

Fig. 5
figure 5

Velocity after a head on collision of two pedestrians for a \(m_1=m_2=62\) kg and \(\mid {\mathbf {u}}_{1}^{-} \mid =\mid {\mathbf {u}}_{2}^{-} \mid =1\) m/s and b \(m_1=62\) kg, \(m_2=20\) kg, \(\mid {\mathbf {u}}_{1}^{-} \mid =2\) m/s and \(\mid {\mathbf {u}}_{2}^{-}\mid = 0.5\) m/s

Full size image

3.2 Pedestrian’s rotation

In the available crowd models, pedestrians’ rotation is seldom treated. Since it must be introduced in our model if we want to model subgroup behavior, we will study its effect on evacuation. By solving Eq. (15), we obtain the rotation time-evolution of an individual about himself:

$$\begin{aligned} \theta_i(t)={\dot{\theta}}_{0}(K_{tg},K_n)te^{-\omega_i t}+\theta_{d,i} \end{aligned}$$
(20)

where \({\dot{\theta}}_{0}(K_{tg},K_n)\) is calculated by the model (by solving Eq. 7) after a shock takes place and \(k_i=I_i\cdot \omega ^2_i\), the torsional stiffness (Eq. (15), is introduced by the user (\(k_i=k\) for the sake of simplicity). Figure 6 shows that the value of \({\dot{\theta}}_{0}\), calculated after a shock, varies with \(K_{tg}\) and is independent of \(K_n\) for values greater than \(2\times 10^3\) kg. From Eq. (20), we can easily obtain the expression of \(\theta_{max}\):

$$\begin{aligned} \theta_{max}=\frac{{\dot{\theta}}_{0}(K_{tg})}{\omega_i \cdot e}+\theta_{d,i} \end{aligned}$$
(21)

By varying k (in kg m\(^{2}\) s\(^{-2}\) rd\(^{-1}\)) in the interval [0.5,18.5], and for each value of \({\dot{\theta}}_{0}\) obtained from Fig. 6 (each value of \({\dot{\theta}}_{0}\) corresponds to a value of \(K_{tg}\)), Eq. (21) gives the surface illustrated in Fig. 7. Now the user can specify the desired value of \(\theta_{max}\) by choosing from Fig. 7 a point (\({\dot{\theta}}_{0},k\)) which corresponds to a couple (\(K_{tg},k\)). The couple must be on or below the isoline representing the chosen value of the maximal rotation.

Fig. 6
figure 6

Variation of \({\dot{\theta}}_{0}\) as a function of \({\text {log}}_{10}(K_{tg})\)

Full size image
Fig. 7
figure 7

Variation of \(\theta_{max}\) as a function of \({\dot{\theta}}_{0}\) and k

Full size image

4 Application to pedestrian flow through bottlenecks

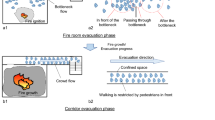
In this section, we are interested in testing the performance of our model for the case of an evacuation through a bottleneck. Several experiments have been conducted in order to measure the influence of the bottleneck width on the pedestrian flow [24, 35, 37]. We will simulate the experiment set up presented in [35]. Its configuration is shown in Fig. 8a.

Fig. 8
figure 8

Experimental setup (a) and the configuration of 60 pedestrians reproduced by our model (b)

Full size image

In [35], for every value of the bottleneck width \(b \in [0.8\,\mathrm{m}, 1.2\,\mathrm{m}]\) with increments of 0.1 m, three runs are performed with \(N=20, 40\), and 60 pedestrians respectively. The pedestrians are located in the holding area in a way that the density of each of the three sections is \(\rho =3.3\) individuals/m\(^{2}\) (Fig. 8). It is important to note that the participants in this experiment were advised not to push and to walk with a normal velocity.

To compare different tests, the authors introduced the specific flow \(J_s\) that was calculated for every run. The specific flow \(J_s\) is defined by the ratio of the flow J on the bottleneck width b:

$$J_s= \frac{J}{b}=\frac{ N_b}{{\varDelta} t\cdot b}$$
(22)

where J is defined here as a time-averaged flow equal to the ratio between the number of pedestrians \(N_b\) passing a certain facility and the duration \(\varDelta t\) measured starting from the instant where the first individual exits and ending when the last one does.

Table 1 Experimental specific flow \(J_{s,exp}\) (individuals m\(^{-1}\) s\(^{-1})\) [35]
Full size table

In [35], the specific flow \(J_s\) was calculated for three different group sizes \(N_b\) and five different values of the width b of the bottleneck as seen in Table 1. It allows to examine the influence of the dimensions of this type of exits on the evacuation procedure. In previous versions of our model, by fixing certain parameters (\(K_n=10^5\) kg, \(K_{tg}=0\) kg), several qualitative aspects of pedestrian dynamics was reproduced such as, lane formation, the arch phenomenon, oscillations at bottleneck exits, etc. In the following section, we will examine the quantitative results obtained using the same aforementioned parameter values.

4.1 A quantitative study

In this section, we study the quantitative results obtained by our model using the values of \(K_n\) and \(K_{tg}\) used in previous studies [2, 31–33]. We first study the effect of introducing rotation to the pedestrian’s movement. We then introduce the repulsive forces [17].

4.1.1 Adding rotation to the pedestrians’ movement

For \(K_n=10^5\) kg and \(K_{tg}=0\) kg, we calculate \(J_s\) for two cases: with and without rotation. We aim to verify, when friction between pedestrians is not considered, if their rotations have any effect on the flow. For each case, we ran fifty simulations, with different random initial pedestrian positions, and \(J_s\) is calculated for each one. The average value and the standard deviation of the specific flow are then calculated. The same procedure was repeated for the values of the parameters \((b,N_b)\) found in Table 1. The results are illustrated in Fig. 9 along with the experimental ones [35]. They show that the agents’ rotation introduced into our model does not affect the flow values. The reason behind this expected result is that we have not connected the agent’s rotational motion to its translational one (pedestrians move even if they are not looking in the range of the direction of motion). As mentioned earlier, the interest of integrating the rotational motion was to be able to reproduce subgroup behavior. Further investigation of the relation between the rotational and translational motion of a pedestrian will be done in order to study the effect of the rotational motion on the flow values.

Fig. 9
figure 9

Values of \(J_{s}\) obtained with or without introducing the rotation for N = (a) 20, b 40, and c 60. The social force is not considered

Full size image

4.1.2 Introducing the repulsive forces: a sensitivity analysis

Since the experiment in [35] is held in normal conditions, introducing repulsive forces in our model is necessary to be able to approach the experimental data. However, the values of the parameters \(A_i\)(kg m s\(^{-2})\) and \(B_i(m)\) (Eq. 16) have to be adapted to the scenario under study (flow through a bottleneck, multi-directional flows, stairs…). For this reason, we have decided to perform a sensitivity analysis to find the values of \(A_i\)(kg m s\(^{-2})\) and \(B_i(m)\) of the pedestrian–pedestrian repulsive force that will best reproduce the flow through a bottleneck under normal conditions (Eq. 16). The parameters will be identical for all pedestrians: \(A_i=A\) and \(B_i=B\). Therefore, for twenty linearly spaced values of A and B in the intervals [10; 1000] and [0.01; 0.2] respectively, all the runs conducted in [35] were simulated (400 simulations for each run). An example of the configuration of the participants (N = 60) along with the different parameters used in the simulations are shown in Fig. 8b and Table 2 respectively. The parameters that vary from one simulation to another are A, B, N and b.

Table 2 Parameters used in the simulations for pedestrian flow through a bottleneck
Full size table

For each \(N_b^j\), an error criterion in the least mean squares sense has been studied:

$$\varepsilon_j \left( A, B \right) =\frac{1}{n_b} \sum ^{n_b}_{i=1} \left( \frac{{J_s}(A, B, b_i, N_b^j)}{J_{s,exp}(b_i, N_b^j)}-1\right) ^2$$
(23)

where \(n_b\) is the number of bottleneck widths considered (see Table 1), \(J_{s,exp}\) the experimental value of the specific flow found in Table 1, and \({J_s}\) the value of the specific flow obtained by our model.

It should be noted that Eq. (23) represents the variance of \({J_s}(A, B, b_i, N_b^j)/J_{s,exp}(b_i, N_b^j)\) where the mean is equal to one. The \(n_b\) corresponding errors are then added together in a way to conserve the value of the mean, and the global error is given by:

$$\varepsilon_T \left( A, B \right) =\frac{1}{n_g\, n_b}\, \sum_{j=1}^{n_g} \sum_{i}^{n_b} \left( \frac{{J_s}(A, B, b_i, N_b^j)}{J_{s,exp}(b_i, N_b^j)}-1\right) ^2$$
(24)

where \(n_g\) is the number of participants groups. The optimized values \({\tilde{A}}\) and \({\tilde{B}}\) are obtained by minimizing \(\varepsilon_T\) in the least mean squares sense:

$$\left( {\tilde{A}}, {\tilde{B}} \right) = \arg \min \varepsilon_T \left( A, B \right)$$
(25)

By plotting \(\varepsilon_T\) as a function of A and B, the surface illustrated in Fig. 10 is obtained. After interpolating and smoothing the surface, using the curve fitting toolbox of Matlab, several functions that fit the local minima represented by red circles in Fig. 10 can be found. The best fit was achieved by the exponential function shown in Fig. 10. We ran simulations for three points of the curve and got the specific flow values illustrated in Fig. 11. The first point was chosen so as to use the same value of B found in [17]. The other two were chosen to be around the latter. Figure 11 shows that the specific flow values obtained for the three points are in good agreement with the experimental results.

Fig. 10
figure 10

The surface representing \(\varepsilon_T\) as a function of A and B. The curve is given by the exponential function \(A=1501*e^{-7.98B}\)

Full size image
Fig. 11
figure 11

Specific flow measurements obtained by our model (considering the social repulsive force) in comparison with empirical data [35] for N = a 20, b 40, and c 60

Full size image

Another validation of our model comes from the density measurements inside and in front of the bottleneck. The results are also in good agreement with the experimental data (Fig. 12).

Fig. 12
figure 12

Density measurements for 60 pedestrians obtained by the experiment [35] and by our model (\(A=790\) N, \(B=0.08\) m): a density in front of the entrance of the bottleneck and b density inside the bottleneck

Full size image

4.1.3 Linear dependence of the flow on the bottleneck-width

In [35], the relationship between the flow and the width of a bottleneck is examined. Using the experimental findings of [35] along with several others, it is argued that the relationship is linear rather than stepwise, as suggested by [20]. To verify which J–b relationship (\(J=J_s\cdot b\)) would be obtained by our model using one of the values of (A, B) found in the previous section, i.e. \(A=790\) N and \(B=0.08\) m, we calculated the flow for each b. The results of the simulations and the experimental data [35] along with their linear regressions are plotted in Fig. 13. The norm of residuals of the linear regressions are presented in Table 3. It is clear that the flow values given by our model increase rather linearly with the bottleneck width. We can also notice that the difference between the simulation and experimental results decrease as N increases. This can be explained by the fact that, for small N, the time allotted to the experiment was not enough to reach a stationary state [35].

Fig. 13
figure 13

Flow values obtained by the 2D discrete model (\(A=790\) N, \(B=0.08\) m) compared to the experimental data [35] for N = a 20, b 40, and c 60

Full size image

4.2 Lane formation inside the bottleneck

In [24, 35, 37], pedestrians formed lanes inside the bottleneck. The number of lanes depends on the bottleneck width. In order to verify if our model can reproduce the same phenomenon, we ran fifty simulations for each bottleneck width b and for \(N=60\).

Table 3 Norms of residuals of the linear regressions plotted in Fig. 13
Full size table

For each run, we saved the probability of finding a pedestrian at position x inside the bottleneck (see Fig. 8). The probability is given by \(X_i/(\sum_{j=1}^{m}X_j)\) where \(X_i\) represents the number of times pedestrians were detected in an interval centered at position x of magnitude 0.01 m and \(\sum_{j=1}^{m}X_j\) represents the total number of detections made inside the bottleneck. The probabilities were plotted in Fig. 14. Lane formation is illustrated by the double peak structure in the probability distribution of the positions for \(b\ge 0.9\) m. Starting with one lane for \(b=0.8\) m and ending with two lanes for \(b=1.2\) m, it is clear that the lanes continue to separate with the width of the bottleneck.

Fig. 14
figure 14

The probability of finding a pedestrian at position x for 50 runs with \(N=60\), \(A=790\) N, \(B=0.08\) m, and b = a 0.8, b 0.9, c 1, d 1.1, and e 1.2

Full size image

4.3 Discussion

In this section, we discuss and analyze results obtained by the 2D model for the simulation of the movement of pedestrians through a bottleneck. The discussed results concern the specific flow and the lane formation. We show that they agree with the findings of several bottleneck experiments.

Concerning the specific flow \(J_s\), two criteria are to be examined: the value of \(J_s\) for each bottleneck width and its variation. Without introducing the social force, the specific flow values obtained by our model were very far from the experimental ones found in [35]. The main reason behind this expected result is the different pedestrian behavior in the two studies. While in [35] the participants are asked not to push and to move normally, pedestrians were clearly more aggressive in our model (Fig. 15). This behavior might increase the flow for some bottleneck widths and decrease it for others (clogging phenomenon). For this reason, we repeated the study after introducing the social force. The obtained results approach the experimental ones better than the case without the repulsive forces. However, the sudden drop of the specific flow value for \(b=1.1\) m and \(N=20\) (Fig. 13), that was not explained in [35], was not reproduced for all the simulations we ran. This could be explained by the fact that, for small N, the time allotted to the experiment was not enough to reach a stationary state. This means that the value of \(J_s\) found in [35] might not be representative of the specific flow value for \(b=1.1\) m and \(N=20\). The difference between the characteristics of the pedestrians in each study might have also contributed to the small gap between the results obtained by our model and the empirical ones. As for the variation of the flow (\(J=b\cdot J_s\)), we have found that it increases rather linearly with the bottleneck width.

Fig. 15
figure 15

Pedestrian behavior when \(N=40\) at \(t=2.5\) s, a without and b with the social repulsive force

Full size image

The second result obtained by the 2D model was the lane formation inside the bottleneck. This phenomenon was found in all the experiments done on the bottleneck with a difference in the number of lanes formed. The simulation results conform with what was obtained experimentally in [35] except for the shift of the lanes towards one half of the bottleneck and the asymmetry of the lane formation (see Fig. 14). This outcome can be explained by the slight shift of the initial pedestrian configuration as seen in Fig. 8b.

5 Conclusions and perspectives

A parametric study of a 2D discrete model based on Frémond’s approach for collisions modeling has been done to examine the effect of model parameters on pedestrian–pedestrian collisions and evacuation times. Starting with collisions, it has been found that the smaller the value of \(K_n\) is the more inelastic shocks are. As for k and \(K_{tg}\), they have to be chosen as a couple that limits the value of the pedestrian’s maximal rotation. The case of a unidirectional pedestrian stream through a bottleneck was studied. We first showed that the rotation we added to the pedestrians’ movement in order to model subgroups had no effect on evacuation times and flow values. Then, using the 2D discrete model, we did a parametric study and found a series of values of the social repulsive force parameters (A and B) that allowed us to obtain simulation results (specific flow, flow rate, density inside and outside the bottleneck) close to the experimental ones found in [35]. It was also shown that our model is capable of reproducing the lane formation phenomenon inside bottleneck that was observed in several experiments [24, 35, 37].

In this paper, a simple parametric study was done by varying only a few parameters of our model. For future work, we will implement an experimental design technique. First, a study will be performed to determine which parameters could be correlated. Then by varying all the parameters, we will find the optimal parameter set that enables us to obtain simulation results that approach the experimental ones for a particular scenario.