1 Introduction

Linear programming techniques (LPTs) based on fuzzy sets or other versions have much importance and popularity while solving real-life optimization problems. Many LPTs are available for the solution of real-life optimization problems. Practically, optimization problems such as transportation problems, assignment problems, supply chain management, engineering problems, etc. can not be with a single goal. Thus, an optimization problem having multiple conflicting objectives under constraints is called a MOLOP. In MOLOP, it is not always possible to get a single solution that fulfills each objective efficiently. However, a compromise solution is possible that fulfills each goal at the same time. Therefore the concept of compromise solution is important and leads in search of the global optimality requirements. In literature, a tremendous amount of research is available in the context of MOLOP. Here, a better approach based on newly invented HIFS deals properly than existing ones. The main contributions of the present paper that may make it popular are given below:

  • The hesitant intuitionistic fuzzy is one of the recent extensions of fuzzy sets and explained by current adverse circumstances: the physical distancing during COVID-19.

  • The paper introduces a new hesitant intuitionistic fuzzy set-theoretic operation that minimizes the computational complexity of real-life optimization problems.

  • A set of possible interval-valued membership and non membership degrees are defined to tackle the uncertainty and hesitation of MOLOP rather than single fixed degrees.

  • The hesitant intuitionistic Pareto optimal solution is introduced in this paper.

  • I develop a new computational algorithm to deal with MOLOP with uncertainty and hesitation.

  • The profit obtained from the proposed method is more than some existing methods.

  • Obtained decisions are more realistic and unbiased due to several experts’ opinions.

  • The proposed optimization technique is a generalization of both fuzzy and intuitionistic fuzzy optimization techniques.

  • The proposed algorithm searches for a better optimal solution with best membership and worst nonmembership degrees.

  • The HIFS would be a perfect tool to deal with any real life problem in the context of uncertainty and hesitation.

The rest of the paper is organized as follows: Sect. 2 reviews the literature on algorithms for multiobjective optimization problems and explained the associated shortcomings. Section 3 recalls some concept of HIFS and illustrated HIFS. For the practical point of view, a computational algorithm is developed in Sect. 4, and it is an extension of both fuzzy and intuitionistic fuzzy optimization techniques. In Sect. 5, stepwise procedures are described, and for the validity and performance of the proposed algorithm, an illustrative example is presented in Sect. 6. The obtained results are discussed in Sect. 7. Conclusions and future scope are presented in Sects. 8 and 9 respectively.

2 Literature review

Many multiobjective optimization problems appear to modeling and making decision of engineering and management sectors, where objectives are conflicting in nature. It was Charnes and Cooper (1977) who presented the concept of goal programming (GP). Furthermore, Evans and Steuer (1973) proposed a necessary and sufficient condition for a point to be an efficient solution of a multiobjective linear programming problem. For this, they stated some lemma and theorems that help to find an efficient solution to a multiobjective linear programming problem. Further, for the solution of multiobjective linear programming, a revised simplex algorithm is developed. Zionts and Wallenius (1976) proposed a practical man-machine interactive programming for the solution of optimization problems under some restrictions containing multiple objective functions. Here, feasible space is a convex set over which the concave objective functions are to be maximized. It also interesting to note that the classical method of optimization assumes, all the parameters and goals of an optimization problem are precisely known and fixed. But, in many real-life optimization problems, there are uncertainty and hesitation about input data. Particularly, in MOLOP, the goal values for the different objectives cannot be defined precisely. Fuzzy set Zadeh (1965) is one of the best available decision-making tool that finds the solution of the such uncertain problem.

To deal MOLOP with imprecision, the fuzzy programming technique (FPT) based on fuzzy sets (FS) has been introduced by Zimmermann (1983). In FPT, uncertainty is resolved by defining linear membership function on the basis of aspiration and tolerance levels. Then, a compromise solution is obtained by using maximin approach. But some of the cases, tolerances cannot be defined precisely. To deal this difficulty, goal programming technique (GPT) in fuzzy scenario has been investigated by Narasimhan (1980). Furthermore, the GPT has been extensively intended by Hannan (1981), Tiwari et al. (1987), Pal et al. (2003), and the work is to demonstrate how fuzzy,or imprecise goals of the decision-maker may be incorporated into a standard goal programming formulation. The new problem can then be solved by using the properties of piecewise linear and continuous functions and by goal programming deviational variables. For this, a methodology for the solution of the fuzzy goal programming problem is presented. The main objective of this paper is to find an efficient solution to the multiobjective programming problem with fuzzy goals. Further, FPT has been widely studied and various modifications and generalizations have presented. One of them is the concept of interval-valued fuzzy programming technique (IV FPT), has been extended by Hongmei and Nianwei (2010), furthermore, Shih et al. (2008) presented a method to find optimal solution of multiobjective programming in interval-valued fuzzy environment where multiobjective programming converted into an interval-valued fuzzy programming using interval-valued fuzzy membership functions for each crisp inequalities.

In the situation where the degree of acceptance is defined simultaneously with the degree of rejection and when both these degrees are not complementary to each other then FS does not deal properly. It was Atanassov (1986) who invented intuitionistic fuzzy sets (IFS). An intuitionistic fuzzy set is a simple generalization of Zadeh’s fuzzy sets. In IFS, an element has membership and nonmembership degrees in [0, 1]. Many research works such as Mahajan and Gupta (2019), Kumar (2018, 2020), Malhotra and Bharati (2016) are carried out using IFS. Angelov (1997) developed a computational technique based on the intersection of intuitionistic fuzzy sets for the solution of an optimization problem which is a very popular technique and it is an extended version of fuzzy optimization technique. Here an illustration of the transportation problem is presented. In this paper, a new concept of the optimization problem with uncertainty and hesitation is proposed. It is an extension of fuzzy optimization in which the degrees of rejection of objective(s) and constraints are considered together with the degrees of satisfaction. This approach is an application of the intuitionistic fuzzy (IF) set concept to optimization problems. An approach to solving such problems is proposed and illustrated with a simple numerical example. It converts the introduced intuitionistic fuzzy optimization (IFO) problem into the crisp (non-fuzzy) one. The advantage of the IFO problems is twofold: they give the richest apparatus for the formulation of optimization problems and, on the other hand, the solution of IFO problems can satisfy the objective(s) with a bigger degree than the analogous fuzzy optimization problem and the crisp one. Further, it is observed that the hesitation factor of real-life problems can be not tackled by using fuzzy sets. IFS is further extended to an interval-valued intuitionistic fuzzy set by Atanassov and Gargov (1989), where the membership degree and nonmembership degree of an element in an IVIFS are, respectively, represented by intervals in [0, 1] rather than fixed real numbers between 0 and 1. Both interval-valued intuitionistic and hesitant fuzzy sets have successful applications in decision-making. Recently, Bharati and Singh (2019); Bharati (2021); Bharati and Singh (2018) studied interval-valued intuitionistic fuzzy sets and their various properties. From the practical point of view, a computational algorithm is developed and it is an extension of both fuzzy and intuitionistic fuzzy optimization techniques.

Torra and Narukawa (2009); Torra (2010) introduced the concept of hesitant fuzzy sets which is an extension of ordinary fuzzy sets and it can be considered as a useful tool allowing more possible degrees of an element to a set. The degree of an element in hesitant fuzzy sets is a subinterval of [0, 1]. Recently, several researchers have studied hesitant fuzzy sets and applied them to various fields (Bharati 2018a, b). Further based upon the same logic Zhang (2013) introduced the concept of interval-valued intuitionistic fuzzy sets. Linear programming is a very famous tool to make the best decision on real-life optimization problems. But every real-life problem cannot be restricted to a single objective. Hence the appearance of multiobjective in literature is a natural phenomenon. Recently, Bharati (2021, 2022) presented new approaches to deal MOLOP in a better way.

3 The hesitant intuitionistic fuzzy sets

The uncertainty and hesitation occur in every real-life problem and therefore it is very necessary to explain it. Researchers have little attention on hesitant intuitionistic fuzzy sets, and therefore, in this section, we present an illustration of the hesitant intuitionistic fuzzy sets based on physical distancing during the COVID-19 pandemic. For this, suppose that X represents a set of 100 peoples of a village and if we ask about a number of people who follow Physical Distancing during COVID-19 pandemic. The natural answer is that we get our \(30, 40, \ldots\), etc. And the number of people who do not follow Physical Distancing is \(5, 10, \ldots ,\), etc. In the same manner, let \(X=\{x_1, x_2,\ldots ,x_N \}\) be the set of N people in a village. And let the number of people who follow Physical Distancing during the COVID-19 pandemic can be different because of different experts.

According to first expert \(E^1\) be \(m^{E^1}(x)\) and number of people who do not follow be \(n^{E^1}(x).\)

According to second expert \(E^2\) be \(m^{E^2}(x)\) and number of people who do not follow be \(n^{E^2}(x).\)

According to third expert \(E^3\) be \(m^{E^3}(x)\) and number of people who do not follow be \(n^{E^3}(x).\) similarly,

According to \(k^{th}\) expert \(E^k\) be \(m^{E^k}(x)\) and number of people who do not follow be \(n^{E^k(x)}.\)

Then \(m^{E^1}(x)+n^{E^1}(x)\le N\)

\(\Rightarrow \frac{m^{E^1}(x)+n^{E^1}(x)}{N} \le 1,\) since \(N>0,\) hence following inequalities make sense

\(\Rightarrow \frac{m^{E^1}(x)}{N}+\frac{n^{E^1}(x)}{N} \le 1\)

similarly,

\(\frac{m^{E^2}(x)}{N}+\frac{n^{E^2}(x)}{N}\le 1\)

\(\frac{m^{E^3}(x)}{N}+\frac{n^{E^3}(x)}{N}\le 1\)

\(\vdots\)

\(\vdots\)

\(\frac{m^{E^k}(x)}{N}+\frac{n^{E^k}(x)}{N}\le 1\)

Therefore

\(\{ \langle x, (\frac{m^{E^1}(x)}{N},\frac{n^{E^1}(x)}{N})\rangle ;\langle x, (\frac{m^{E^2}(x)}{N},\frac{n^{E^2}(x)}{N})\rangle ; \cdots \langle x, (\frac{m^{E^k}(x)}{N},\frac{n^{E^k}(x)}{N})\rangle \}\) is a hesitant intuitionistic fuzzy set. Now, we shall represent the formal definition of hesitant intuitionistic fuzzy sets.

Definition 1

(Hesitant fuzzy sets) Torra and Narukawa (2009) and Torra (2010) invented a new tool which is the hesitant fuzzy sets (HFSs) and which permit the membership degree of an object to a set of several possible values. The HFS can be expressed hesitant fuzzy sets in the following way:

Let X be a fixed set, then a hesitant fuzzy sets is represented as \(A=\{(x, h_A(x))|x\in X\}\) where \(h_A(x)\) is denoting the possible membership degrees of the element \(x \in X\) to the set A. \(h_A\) is called hesitant element. Further, Xia and Xu (2011, 2011) used it in their research works.

Definition 2

(Hesitant intuitionistic fuzzy sets) When a decision-maker makes a decision, he may hesitate to choose the exact membership and nonmembership degrees in [0, 1]. For such a circumstance where there are many membership and nonmembership degrees of one element to a set, the HIFS, which is a kind of generalized FS where the membership and nonmembership degrees of an element to a certain set can be illustrated several different values between 0 and 1. The HIFS is perfect at dealing with situations where people have disagreements or hesitancy when deciding something. Let X be a fixed set, then a hesitant intuitionistic fuzzy sets is represented as \(A=\{(x, h_A(x))|x\in X\}\) where \(h_A(x)\) is a set of some intuitionistic fuzzy sets in X, denoting the possible membership degree intervals and non-membership degree intervals of the element \(x \in X\) to the set A. \(h_A\) is called hesitant intuitionistic fuzzy element.

Definition 3

(Hesitant intuitionistic fuzzy sets theoretic operations) Let \(H_1,\) and \(H_2\) be two hesitant intuitionistic fuzzy sets and \(h_1\in H_1, h_2\in H_2\). Then, some popular operations among HIFS are:

  • \(H^c=\{h^c:h\in H\}\)

  • \(H_1 \cup H_2=\{ max(h_1, h_2):h_1\in H_1, h_2 \in H_2\},\) where \(h_1 \cup h_2=\{max(\mu _{h_1},\mu _{h_2}),min(\nu _{h_1}, \nu _{h_2}) \}\)

  • \(H_1 \cap H_2=\{ min(h_1, h_2):h_1\in H_1, h_2 \in H_2\},\) where \(h_1 \cap h_2=\{min(\mu _{h_1},\mu _{h_2}),max(\nu _{h_1}, \nu _{h_2}) \}\)

4 Development of the algorithm

Definition 4

(Multiobjective linear optimization problem) Practically, it had observed that a linear programming problem can not be restricted to a single objective, and consequently, a multiobjective linear optimization problem had explored. Symbolically, a multiobjective linear optimization problem with n decision variables and m constraints represented as:

$$\begin{aligned} \begin{aligned} \text {Maximize} \ Z =\{f_1, f_2, \ldots , f_K\} \\ \text {Such that} \ g_i(x) \le 0 \\ x_j \ge 0,\ j= 1,2,\ldots ,n \\ \text {where} \ x=\{x_1,x_2,\ldots , x_n \} \\ \end{aligned} \end{aligned}$$
(1)

The set \(\Omega =\{x : \ g_i(x) \le 0, x_j \ge 0; \ i= 1,2, \ldots ,\ m; \ j=1, 2, \ldots ,\ n\}\) is called a basic feasible space of the problem (1).

Definition 5

(Pareto-optimal solution) An optimal solution that is obtained from a single objective may or may not satisfy all the conflicting objectives simultaneously. But it is impossible to obtain a solutions that simultaneously optimizes all of the objective and satisfies all the restrictions, called the Pareto-optimal solutions. Mathematically, a basic feasible solution \(x_0 \in \Omega\) is called a Pareto-optimal solution of the problem (1) if and only if there is no \(x \in \Omega\) such that \(f_k(x)\ge f_k(x_0) \ \forall k\) and \(f_{k_0}(x)> f_{k_0}(x_0)\) for at least one \(k_0.\)

Definition 6

(Hesitant intuitionistic fuzzy Pareto-optimal solution) For the hesitant intuitionistic fuzzy optimization, the Pareto-optimal solutions can be defined in the following manners:

A solution \(X_0\) is called a Pareto optimal solution for (1) if there does not exist another X such that \(f_k(x)\ge f_k(X_0)\) with \(\mu ^{E^k}_k(f_k(X))\ge \mu ^{E^k}_k(f_k(X_0))\) and \(\nu ^{E^k}_k(f_k(X))\le \nu ^{E^k}_k(f_k(X_0))\) and \(f_{K_0}(x)> f_{K_0}(X_0)\) with \(\mu ^{E^{K_0}}_{K_0}(f_{K_0}(X)) > \mu ^{E^{K_0}}_{K_0}(f_{K_0}(X_0))\) and \(\nu ^{E^{K_0}}_{K_0}(f_{K_0}(X))< \nu ^{E^{K_0}}_{K_0}(f_{K_0}(X_0))\) for at least one \(K_0\in \{1, 2, \ldots , K\}.\)

Definition 7

(Hesitant intuitionistic fuzzy programming) Assuming that the decision maker uses unclear aspiration levels such as, objective function should be greater than or equal to some value \(\lessapprox g^o_k, k=1, 2, \ldots , K\). Therefore, the problem (1) can be restated as:

$$\begin{aligned} \begin{aligned} \text {Find} \ X =\{x_1, x_2, \ldots ,x_n \} \\ \text {Such that} \ f_k \lessapprox g^o_k, k=1, 2, \ldots , K \\ \ g_j(x) \le 0 \\ x_j \ge 0,\ j= 1, 2, \ldots , n \\ \text {where} \ x=\{x_1,x_2, \ldots , x_n \} \\ \end{aligned} \end{aligned}$$
(2)

where \(g^o_k\) is goal for \(k^{th}\) objective and \(\lessapprox\) is uncertain type of \(\le\), and has been represented by various version of fuzzy set, further, it is presented in Fig. 3.

Definition 8

Zimmermann (1983) fuzzy optimization technique for the uncertain multiobjective linear optimization problem (1). Here, each expression is represented by FS known as fuzzy goal, whose membership \(\mu _k(f_k(x)),\ \mu _k:\mathbb {R}\rightarrow [0,1],\) provides the satisfaction degree \(\alpha _k\) to which the \(k^{th}\) fuzzy inequality is fulfilled. Further, to construct the membership function \(\mu _k(f_k(x)),\) the decision maker has provide the tolerance margins \(g_k+t_k\) that he willing to accept. The final version of fuzzy optimization technique is represented below as:

$$\begin{aligned} \begin{aligned} \text {Maximize} \ \alpha \\ \text {subject to} \ \alpha \le \mu _{k}{(x)}, \ k=1,2,\ldots ,K \\ 0\le \alpha \le 1 \\ x \in X. \end{aligned} \end{aligned}$$
(3)

Definition 9

Angelov (1997) fuzzy optimization technique for the uncertain multiobjective linear optimization problem (1) is stated below:

$$\begin{aligned} \begin{aligned} \text {Maximize} \ (\alpha -\beta )\\ \text {subject to} \ \alpha \le \mu _{k}{(x)}, \ k=1,2,\ldots , K \\ \beta \ge \nu _{k}{(x)}, \ k=1,2,\ldots ,K \\ \alpha +\beta \le 1 \\ \alpha \ge \beta , \beta \ge 0 \\ x \in X. \end{aligned} \end{aligned}$$
(4)

4.1 Construction of hesitant fuzzy membership functions

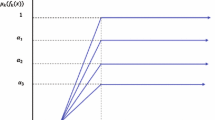
A decision-maker can not achieve a goal fully due to undeniable uncertainty and hesitation, and single membership degree does not deal properly. For such a circumstance, there are several membership degrees of one element to a set are selected. Now, let upper and lower bounds for the hesitant fuzzy membership functions be \(\mu _{k}(f_{k}(x)),\ k=1, 2,\ldots , K.\) Then hesitant fuzzy membership functions for each objectives are presented below and can be visualized in Fig. 1.

Fig. 1
figure 1

Hesitant membership of objectives

Full size image
$$\begin{aligned} \mu ^{E^1}_k(f_k(x)) = {\left\{ \begin{array}{ll} 0,\ if \ f_k(x)\le L_k^\mu \\ \alpha _1 \frac{f_k(x)-L_k^\mu }{U_k^\mu -L_k^\mu }, \ if \ L_k^\mu \le f_k(x)\le U_k^\mu \\ 1, if \ f_k(x)\ge L_k^\mu \\ \end{array}\right. } \end{aligned}$$
(5)
$$\begin{aligned} &\mu ^{E^2}_k(f_k(x)) = {\left\{ \begin{array}{ll} 0,\ if \ f_k(x)\le L_k^\mu \\ \alpha _2 \frac{f_k(x)-L_k^\mu }{U_k^\mu -L_k^\mu }, \ if \ L_k^\mu \le f_k(x)\le U_k^\mu \\ 1, if \ f_k(x)\ge L_k^\mu \\ \end{array}\right. }\\ &\ldots\\ &\ldots \end{aligned}$$
(6)
$$\begin{aligned} \mu ^{E^n}_k(f_k(x)) = {\left\{ \begin{array}{ll} 0,\ if \ f_k(x)\le L_k^\mu \\ \alpha _n \frac{f_k(x)-L_k^\mu }{U_k^\mu -L_k^\mu }, \ if \ L_k^\mu \le f_k(x)\le U_k^\mu \\ 1, if \ f_k(x)\ge L_k^\mu \end{array}\right. } \end{aligned}$$
(7)

where \(0 \le \alpha _1, \alpha _2,\ldots ,\alpha _n \le 1.\)

4.2 Construction of hesitant fuzzy nonmembership functions

A decision-maker can not achieve a goal fully due to undeniable uncertainty and hesitation, and further he may hesitate to choose the exact nonmembership degree in [0, 1]. For such a circumstance, there are several nonmembership degrees of one element to a set are constructed. Now, let upper and lower bounds for the hesitant fuzzy nonmembership functions are \(\nu _{k} (f_{k}(x)),\ k=1, 2,\ldots , K.\) Then hesitant fuzzy nonmembership functions for each objective are presented below and can be visualized in Fig. 2.

Fig. 2
figure 2

Hesitant nonmembership of objectives

Full size image
$$\begin{aligned} \nu ^{E^1}_k(f_k(x)) = {\left\{ \begin{array}{ll} 0,\ if \ f_k(x)\ge \phi \times U_k^\mu \\ \alpha _1 \frac{f_k(x)-L_k^\mu }{\phi \times U_k^\mu -L_k^\mu }, \ if \ L_k^\mu \le f_k(x)\le U_k^\mu \\ 1, if \ f_k(x)\le L_k^\mu \\ \end{array}\right. } \end{aligned}$$
(8)
$$\begin{aligned} &\nu ^{E^2}_k(f_k(x)) = {\left\{ \begin{array}{ll} 0,\ if \ f_k(x)\ge \phi \times U_k^\mu \\ \alpha _2 \frac{f_k(x)-L_k^\mu }{\phi \times U_k^\mu -L_k^\mu }, \ if \ L_k^\mu \le f_k(x)\le \phi \times U_k^\mu \\ 1, if \ f_k(x)\le L_k^\mu \\ \end{array}\right. }\\ & \ldots\\ & \ldots \end{aligned}$$
(9)
$$\begin{aligned} \nu ^{E^n}_k(f_k(x)) = {\left\{ \begin{array}{ll} 0,\ if \ f_k(x)\ge U_k^\mu \\ \alpha _n \frac{f_k(x)-L_k^\mu }{\phi \times U_k^\mu -L_k^\mu }, \ if \ L_k^\mu \le f_k(x)\le \phi \times U_k^\mu \\ 1, if \ f_k(x)\le L_k^\mu \\ \end{array}\right. } \end{aligned}$$
(10)

where, \(0 \le \alpha _1, \alpha _2,\ldots ,\alpha _n \le 1.\)

Step 9 In this step, we present uncertain and imprecise objectives of MOLP by using the following linear hesitant membership functions \(\mu ^{E^1}_k(f_k(x))\):

$$\begin{aligned} \mu ^{E^1}_k(f_k(x)) = {\left\{ \begin{array}{ll} 0,\ if \ f_k(x)\le L_k^\mu \\ \alpha _1 \frac{f_k(x)-L_k^\mu }{U_k^\mu -L_k^\mu }, \ if \ L_k^\mu \le f_k(x)\le U_k^\mu \\ 1, if \ f_k(x)\ge L_k^\mu \\ \end{array}\right. } \end{aligned}$$
(11)
$$\begin{aligned} \mu ^{E^2}_k(f_k(x)) = {\left\{ \begin{array}{ll} 0,\ if \ f_k(x)\le L_k^\mu \\ \alpha _2 \frac{f_k(x)-L_k^\mu }{U_k^\mu -L_k^\mu }, \ if \ L_k^\mu \le f_k(x)\le U_k^\mu \\ 1, if \ f_k(x)\ge L_k^\mu \\ \end{array}\right. }\\ & \ldots\\ & \ldots \end{aligned}$$
(12)
$$\begin{aligned} \mu ^{E^n}_k(f_k(x)) = {\left\{ \begin{array}{ll} 0,\ if \ f_k(x)\le L_k^\mu \\ \alpha _n \frac{f_k(x)-L_k^\mu }{U_k^\mu -L_k^\mu }, \ if \ L_k^\mu \le f_k(x)\le U_k^\mu \\ 1, if \ f_k(x)\ge L_k^\mu \\ \end{array}\right. } \end{aligned}$$
(13)

where, \(0 \le \alpha _1,\ \alpha _2,\ldots ,\alpha _n \le 1.\)

Let \(h_D(x)\) be the hesitant intuitionistic fuzzy decision, then

\(h_D(x)=\langle \mu ^{E^1}_1(f_k(x)),\ \mu ^{E^2}_1(f_k(x)),\ \mu ^{E^3}_1(f_k(x)) \rangle \bigcap \langle \mu ^{E^1}_2(f_k(x)),\ \mu ^{E^2}_2(f_k(x)),\ \mu ^{E^3}_2(f_k(x)) \rangle \bigcap \langle \mu ^{E^1}_3(f_k(x)),\ \mu ^{E^2}_3(f_k(x)),\ \mu ^{E^3}_3(f_k(x)) \rangle ,\) where

$$h_D(x)=\langle min \{\mu ^{E^1}_1(f_k(x)),\ \mu ^{E^1}_2(f_k(x)) \}, \ min \{\mu ^{E^1}_1(f_k(x)),\ \mu ^{E^2}_2(f_k(x)) \}, min \{\mu ^{E^1}_1(f_k(x)), \ \mu ^{E^2}_3(f_k(x)) \}, \ min \{\mu ^{E^1}_1(f_k(x)),\ \mu ^{E^3}_1(f_k(x)) \}, min \{\mu ^{E^1}_1(f_k(x)), \ \mu ^{E^2}_3(f_k(x))\}, \ min \{\mu ^{E^1}_1(f_k(x)),\ \mu ^{E^3}_3(f_k(x)) \}, min \{\mu ^{E^2}_1(f_k(x)), \ \mu ^{E^1}_2(f_k(x)) \}, \ min \{\mu ^{E^2}_1(f_k(x)),\ \mu ^{E^2}_2(f_k(x)) \}, min \{\mu ^{E^2}_1(f_k(x)),\ \mu ^{E^3}_2(f_k(x)) \}, \ min \{\mu ^{E^2}_1(f_k(x)),\ \mu ^{E^1}_3(f_k(x)) \}, min \{\mu ^{E^2}_1(f_k(x)),\ \mu ^{E^2}_3(f_k(x)) \}, \ min \{\mu ^{E^2}_1(f_k(x)),\ \mu ^{E^3}_3(f_k(x)) \}, min \{\mu ^{E^3}_1(f_k(x)),\ \mu ^{E^1}_2(f_k(x)) \}, \ min \{\mu ^{E^3}_1(f_k(x)),\ \mu ^{E^3}_2(f_k(x)) \}, min \{\mu ^{E^3}_1(f_k(x)),\ \mu ^{E^3}_2(f_k(x)) \}, \ min \{\mu ^{E^3}_1(f_k(x)),\ \mu ^{E^1}_3(f_k(x)) \}, min \{\mu ^{E^3}_1(f_k(x)),\ \mu ^{E^2}_3(f_k(x)) \}, \ min \{\mu ^{E^3}_1(f_k(x)),\ \mu ^{E^3}_3(f_k(x))\}, min \{\mu ^{E^1}_2(f_k(x)),\ \mu ^{E^1}_3(f_k(x)) \}, \ min \{\mu ^{E^1}_2(f_k(x)),\ \mu ^{E^2}_3(f_k(x)) \}, min \{\mu ^{E^1}_2(f_k(x)),\ \mu ^{E^3}_3(f_k(x)) \}, \ min \{\mu ^{E^2}_2(f_k(x)),\ \mu ^{E^1}_3(f_k(x)) \}, min \{\mu ^{E^2}_2(f_k(x)),\ \mu ^{E^2}_3(f_k(x))\}, \ min \{\mu ^{E^2}_2(f_k(x)),\ \mu ^{E^3}_3(f_k(x))\}, min \{\mu ^{E^3}_2(f_k(x)),\ \mu ^{E^1}_3(f_k(x))\}, \ min\{\mu ^{E^3}_2(f_k(x)),\ \mu ^{E^2}_3(f_k(x))\} min \{\mu ^{E^3}_2(f_k(x)),\ \mu ^{E^3}_3(f_k(x))\}, max\{\nu ^{E^1}_1(f_k(x)), \ \nu ^{E^1}_2(f_k(x)) \}, max \{\nu ^{E^1}_1(f_k(x)),\ \nu ^{E^2}_2(f_k(x)) \}, max \{\nu ^{E^1}_1(f_k(x)),\ \mu ^{E^3}_2(f_k(x)) \}, \ max \{\nu ^{E^1}_1(f_k(x)),\ \nu ^{E^1}_3(f_k(x)) \}, max \{\nu ^{E^1}_1(f_k(x)),\ \nu ^{E^2}_3(f_k(x)) \},\ max \{\nu ^{E^1}_1(f_k(x)),\ \nu ^{E^3}_3(f_k(x)) \}, max \{\nu ^{E^2}_1(f_k(x)),\ \nu ^{E^1}_2(f_k(x)) \},\ max \{\nu ^{E^2}_1(f_k(x)),\ \nu ^{E^2}_2(f_k(x)) \}, max \{\nu ^{E^2}_1(f_k(x)),\ \nu ^{E^3}_2(f_k(x)) \},\ max \{\nu ^{E^2}_1(f_k(x)),\ \nu ^{E^1}_3(f_k(x)) \}, max \{\nu ^{E^2}_1(f_k(x)),\ \nu ^{E^2}_3(f_k(x)) \},\ max \{\nu ^{E^2}_1(f_k(x)),\ \nu ^{E^3}_3(f_k(x)) \}, max \{\nu ^{E^3}_1(f_k(x)),\ \nu ^{E^1}_2(f_k(x)) \},\ max \{\nu ^{E^3}_1(f_k(x)),\ \nu ^{E^2}_2(f_k(x)) \}, max \{\nu ^{E^3}_1(f_k(x)),\ \nu ^{E^3}_2(f_k(x)) \},\ max \{\nu ^{E^3}_1(f_k(x)),\ \nu ^{E^1}_3(f_k(x)) \}, max \{\nu ^{E^3}_1(f_k(x)),\ \nu ^{E^2}_3(f_k(x)) \},\ max \{\nu ^{E^3}_1(f_k(x)),\ \nu ^{E^3}_3(f_k(x)) \}, max \{\nu ^{E^1}_2(f_k(x)),\ \nu ^{E^1}_3(f_k(x)) \},\ max \{\nu ^{E^1}_2(f_k(x)),\ \nu ^{E^2}_3(f_k(x)) \}, max \{\nu ^{E^1}_2(f_k(x)),\ \nu ^{E^3}_3(f_k(x)) \},\ max \{\nu ^{E^2}_2(f_k(x)),\ \nu ^{E^1}_3(f_k(x)) \}, max \{\nu ^{E^2}_2(f_k(x)),\ \nu ^{E^2}_3(f_k(x))\}, \ max \{\nu ^{E^2}_2(f_k(x)),\ \nu ^{E^3}_3(f_k(x))\}, max \{\nu ^{E^3}_2(f_k(x)),\ \nu ^{E^1}_3(f_k(x))\}, \ max \{\nu ^{E^3}_2(f_k(x)),\ \nu ^{E^2}_3(f_k(x))\}, max \{\nu ^{E^3}_2(f_k(x)),\ \nu ^{E^3}_3(f_k(x))\} \rangle$$

.

Let us introduce new variables that representing min and max values:

$$\delta _1=min \{\mu ^{E^1}_1(f_k(x)),\ \mu ^{E^1}_2(f_k(x)) \},\ \delta _2=min \{\mu ^{E^1}_1(f_k(x)),\ \mu ^{E^2}_2(f_k(x)) \}, \delta _3=min \{\mu ^{E^1}_1(f_k(x)),\ \mu ^{E^2}_3(f_k(x)) \}, \ \delta _4=min \{\mu ^{E^1}_1(f_k(x)),\ \mu ^{E^3}_1(f_k(x)) \}, \delta _5=min \{\mu ^{E^1}_1(f_k(x)),\ \mu ^{E^2}_3(f_k(x))\}, \ \delta _6= min \{\mu ^{E^1}_1(f_k(x)),\ \mu ^{E^3}_3(f_k(x)) \}, \delta _7=min \{\mu ^{E^2}_1(f_k(x)),\ \mu ^{E^1}_2(f_k(x)) \}, \ \delta _8=min \{\mu ^{E^2}_1(f_k(x)),\ \mu ^{E^2}_2(f_k(x)) \}, \delta _9=min \{\mu ^{E^2}_1(f_k(x)),\ \mu ^{E^3}_2(f_k(x)) \}, \ \delta _{10}=min \{\mu ^{E^2}_1(f_k(x)),\ \mu ^{E^1}_3(f_k(x)) \}, \delta _{11}=min \{\mu ^{E^2}_1(f_k(x)),\ \mu ^{E^2}_3(f_k(x)) \},\ \delta _{12}=min \{\mu ^{E^2}_1(f_k(x)),\ \mu ^{E^3}_3(f_k(x)) \}, \delta _{13}=min \{\mu ^{E^3}_1(f_k(x)),\ \mu ^{E^1}_2(f_k(x)) \},\ \delta _{14}=min \{\mu ^{E^3}_1(f_k(x)),\ \mu ^{E^3}_2(f_k(x)) \}, \delta _{15}=min \{\mu ^{E^3}_1(f_k(x)),\ \mu ^{E^3}_2(f_k(x)) \},\ \delta _{16}=min \{\mu ^{E^3}_1(f_k(x)),\ \mu ^{E^1}_3(f_k(x)) \}, \delta _{17}=min \{\mu ^{E^3}_1(f_k(x)),\ \mu ^{E^2}_3(f_k(x)) \},\ \delta _{18}=min \{\mu ^{E^3}_1(f_k(x)),\ \mu ^{E^3}_3(f_k(x))\}, \delta _{19}= min \{\mu ^{E^1}_2(f_k(x)),\ \mu ^{E^1}_3(f_k(x)) \},\ \delta _{20}=min \{\mu ^{E^1}_2(f_k(x)),\ \mu ^{E^2}_3(f_k(x)) \}, \delta _{21}=min \{\mu ^{E^1}_2(f_k(x)),\ \mu ^{E^3}_3(f_k(x)) \},\ \delta _{22}=min \{\mu ^{E^2}_2(f_k(x)),\ \mu ^{E^1}_3(f_k(x)) \}, \delta _{23}=min \{\mu ^{E^2}_2(f_k(x)),\ \mu ^{E^2}_3(f_k(x))\},\ \delta _{24}=min \{\mu ^{E^2}_2(f_k(x)),\ \mu ^{E^3}_3(f_k(x))\}, \delta _{25}=min\{\mu ^{E^3}_2(f_k(x)),\ \mu ^{E^1}_3(f_k(x))\},\ \delta _{26}=min\{\mu ^{E^3}_2(f_k(x)),\ \mu ^{E^2}_3(f_k(x))\} \delta _{27}=min \{\mu ^{E^3}_2(f_k(x)),\ \mu ^{E^3}_3(f_k(x))\}.$$
$$\gamma _1=max \{\nu ^{E^1}_1(f_k(x)),\ \nu ^{E^1}_2(f_k(x)) \},\ \gamma _2=max \{\nu ^{E^1}_1(f_k(x)),\ \nu ^{E^2}_2(f_k(x)) \}, \gamma _3=max \{\nu ^{E^1}_1(f_k(x)),\ \mu ^{E^3}_2(f_k(x)) \},\ \gamma _4=max \{\nu ^{E^1}_1(f_k(x)),\ \nu ^{E^1}_3(f_k(x)) \}, \gamma _5=max \{\nu ^{E^1}_1(f_k(x)),\ \nu ^{E^2}_3(f_k(x)) \},\ \gamma _6=max \{\nu ^{E^1}_1(f_k(x)),\ \nu ^{E^3}_3(f_k(x)) \}, \gamma _7=max \{\nu ^{E^2}_1(f_k(x)),\ \nu ^{E^1}_2(f_k(x)) \},\ \gamma _8=max \{\nu ^{E^2}_1(f_k(x)),\ \nu ^{E^2}_2(f_k(x)) \}, \gamma _9=max \{\nu ^{E^2}_1(f_k(x)),\ \nu ^{E^3}_2(f_k(x)) \},\ \gamma _{10}=max \{\nu ^{E^2}_1(f_k(x)),\ \nu ^{E^1}_3(f_k(x)) \}, \gamma _{11}=max \{\nu ^{E^2}_1(f_k(x)),\ \nu ^{E^2}_3(f_k(x)) \}, \ \gamma _{12}=max \{\nu ^{E^2}_1(f_k(x)),\ \nu ^{E^3}_3(f_k(x)) \}, \gamma _{13}=max \{\nu ^{E^3}_1(f_k(x)),\ \nu ^{E^1}_2(f_k(x)) \},\ \gamma _{14}=max \{\nu ^{E^3}_1(f_k(x)),\ \nu ^{E^2}_2(f_k(x)) \}, \gamma _{15}=max \{\nu ^{E^3}_1(f_k(x)),\ \nu ^{E^3}_2(f_k(x)) \},\ \gamma _{16}=max \{\nu ^{E^3}_1(f_k(x)),\ \nu ^{E^1}_3(f_k(x)) \}, \gamma _{17}=max \{\nu ^{E^3}_1(f_k(x)),\ \nu ^{E^2}_3(f_k(x)) \},\ \gamma _{18}=max \{\nu ^{E^3}_1(f_k(x)),\ \nu ^{E^3}_3(f_k(x)) \}, \gamma _{19}=max \{\nu ^{E^1}_2(f_k(x)),\ \nu ^{E^1}_3(f_k(x)) \},\ \gamma _{20}=max \{\nu ^{E^1}_2(f_k(x)),\ \nu ^{E^2}_3(f_k(x)) \}, \gamma _{21}=max \{\nu ^{E^1}_2(f_k(x)),\ \nu ^{E^3}_3(f_k(x)) \},\ \gamma _{22}=max \{\nu ^{E^2}_2(f_k(x)),\ \nu ^{E^1}_3(f_k(x)) \}, \gamma _{23}=max \{\nu ^{E^2}_2(f_k(x)),\ \nu ^{E^2}_3(f_k(x))\},\ \gamma _{24}=max \{\nu ^{E^2}_2(f_k(x)),\ \nu ^{E^3}_3(f_k(x))\}, \gamma _{25}=max \{\nu ^{E^3}_2(f_k(x)),\ \nu ^{E^1}_3(f_k(x))\}, \ \gamma _{26}=max \{\nu ^{E^3}_2(f_k(x)),\ \nu ^{E^2}_3(f_k(x))\}, \gamma _{27}=max \{\nu ^{E^3}_2(f_k(x)),\ \nu ^{E^3}_3(f_k(x))\}.$$

Here, we ignore repeated hesitant membership and nonmembership functions to get feasible solutions and complexity of the equivalent linear programming problems.

Step 10 Now the hesitant intuitionistic fuzzy an optimization technique for multiple objective linear optimizations (1) with linear membership and nonmembership functions Fig. 3 are:

Fig. 3
figure 3

Hesitant intuitionistic fuzzy representation of objectives

Full size image
$$\begin{aligned} \begin{aligned} \text {Maximize} \ \delta _1+\delta _2+\cdots +\delta _n\\ \text {Minimize} \ \gamma _1+\gamma _2+\cdots +\gamma _n\\ \text {Such that} \ \mu ^{E_1}_{k}{(x)}\ge \delta _1, \ \text {for all} \ k\\ \mu ^{E_2}_{k}{(x)}\ge \delta _2, \ \text {for all} \ k\\ \ldots \\ \ldots \\ \mu ^{E_n}_{k}{(x)}\ge \delta _n, \ \text {for all} \ k\\ 0\le \delta _1, \delta _2,\ldots , \delta _n \le 1, \\ \nu ^{E_1}_{k}{(x)}\le \gamma _1, \ \text {for all} \ k\\ \nu ^{E_2}_{k}{(x)}\le \gamma _2, \ \text {for all} \ k\\ \cdots \\ \cdots \\ \nu ^{E_n}_{k}{(x)}\le \gamma _n, \ \text {for all} \ k\\ 0\le \gamma _1, \gamma _2,\ldots , \gamma _n \le 1 \\ \delta _1 \ge \gamma _1\\ \delta _2 \ge \gamma _2\\ \cdots \\ \cdots \\ \delta _n \ge \gamma _n\\ \gamma _i \ge 0, i=1,2,\ldots n\\ g_j(x)\le 0, j= 1,2,\ldots ,q \\ x\ge 0. \end{aligned} \end{aligned}$$
(14)
$$\begin{aligned} \begin{aligned} \text {Maximize} \ \left( \delta _1+\delta _2+\cdots +\delta _n \right) -\left( \gamma _1+\gamma _2+\cdots +\gamma _n\right) \\ \text {Such that} \ \mu ^{E_1}_{k}{(x)}\ge \delta _1, \ \text {for all} \ k\\ \mu ^{E_2}_{k}{(x)}\ge \delta _2, \ \text {for all} \ k\\ \ldots \\ \ldots \\ \mu ^{E_n}_{k}{(x)}\ge \delta _n, \ \text {for all} \ k\\ 0\le \delta _1, \delta _2,\ldots , \delta _n \le 1, \\ \nu ^{E_1}_{k}{(x)}\le \gamma _1, \ \text {for all} \ k\\ \nu ^{E_2}_{k}{(x)}\le \gamma _2, \ \text {for all} \ k\\ \cdots \\ \cdots \\ \nu ^{E_n}_{k}{(x)}\le \gamma _n, \ \text {for all} \ k\\ 0\le \gamma _1, \gamma _2,\ldots , \gamma _n \le 1 \\ \delta _1 \ge \gamma _1\\ \delta _2 \ge \gamma _2\\ \cdots \\ \cdots \\ \delta _n \ge \gamma _n\\ \gamma _i \ge 0, i=1,2,\ldots n\\ g_j(x)\le 0, j= 1,2,\ldots ,q \\ x\ge 0. \end{aligned} \end{aligned}$$
(15)
$$\begin{aligned} \begin{aligned} \text {Maximize} \ \left( \delta _1-\gamma _1\right) +\left( \delta _2-\gamma _2\right) +\cdots +\left( \delta _n-\gamma _n\right) \\ \text {Such that} \ \mu ^{E_1}_{k}{(x)}\ge \delta _1, \ \text {for all} \ k\\ \mu ^{E_2}_{k}{(x)}\ge \delta _2, \ \text {for all} \ k\\ \ldots \\ \ldots \\ \mu ^{E_n}_{k}{(x)}\ge \delta _n, \ \text {for all} \ k\\ 0\le \delta _1, \delta _2,\ldots , \delta _n \le 1, \\ \nu ^{E_1}_{k}{(x)}\le \gamma _1, \ \text {for all} \ k\\ \nu ^{E_2}_{k}{(x)}\le \gamma _2, \ \text {for all} \ k\\ \cdots \\ \cdots \\ \nu ^{E_n}_{k}{(x)}\le \gamma _n, \ \text {for all} \ k\\ 0\le \gamma _1, \gamma _2,\ldots , \gamma _n \le 1 \\ \delta _1 \ge \gamma _1\\ \delta _2 \ge \gamma _2\\ \cdots \\ \cdots \\ \delta _n \ge \gamma _n\\ \gamma _i \ge 0, i=1,2,\ldots n\\ g_j(x)\le 0, j= 1,2,\ldots ,q \\ x\ge 0. \end{aligned} \end{aligned}$$
(16)
$$\begin{aligned} \begin{aligned} \text {Maximize} \ \left( \delta _1-\gamma _1\right) +\left( \delta _2-\gamma _2\right) +\cdots +\left( \delta _n-\gamma _n\right) \\ \text {Such that} \ \mu ^{E_1}_{k}{(x)}\ge \delta _1, \ \text {for all} \ k\\ \mu ^{E_2}_{k}{(x)}\ge \delta _2, \ \text {for all} \ k\\ \ldots \\ \ldots \\ \mu ^{E_n}_{k}{(x)}\ge \delta _n, \ \text {for all} \ k\\ 0\le \delta _1, \delta _2,\ldots , \delta _n \le 1, \\ \nu ^{E_1}_{k}{(x)}\le \gamma _1, \ \text {for all} \ k\\ \nu ^{E_2}_{k}{(x)}\le \gamma _2, \ \text {for all} \ k\\ \cdots \\ \cdots \\ \nu ^{E_n}_{k}{(x)}\le \gamma _n, \ \text {for all} \ k\\ 0\le \gamma _1, \gamma _2,\ldots , \gamma _n \le 1, \\ \delta _1 \ge \gamma _1\\ \delta _2 \ge \gamma _2\\ \cdots \\ \cdots \\ \delta _n \ge \gamma _n\\ \gamma _i \ge 0, i=1,2,\ldots n\\ g_j(x)\le 0, j= 1,2,\ldots ,q \\ x\ge 0. \end{aligned} \end{aligned}$$
(17)

Theorem

A unique optimal solution \((x^*, \delta ^*, \gamma ^*)\) of the problem (17) is also a Pareto-optimal solution for the problem (1), where \(\delta ^*=(\delta ^*_1, \delta ^*_2,\ldots , \delta ^*_n)\) and \(\gamma ^*=(\gamma ^*_1, \gamma ^*_2,\ldots , \gamma ^*_n).\)

Proof

Let \((x^*, \delta ^*, \gamma ^*)\) be an optimal solution of the problem (17). Then \((\delta ^* - \gamma ^*) > (\delta - \gamma )\) for any \((x, \delta , \gamma )\) feasible to the problem (17).

On the contrary, suppose that \((x^*, \delta ^*, \gamma ^*)\) is not an optimal solution of the problem (1). Then there exists another feasible solution \(x^{**}\) of the problem (1), such that \(f_k (x^*)\le f_k (x^{**})\) for all \(k=1, 2,\ldots , K\) and \(f_k (x^*)< f_k (x^{**})\) for at least one k.

Therefore, I have \(\frac{f_k(x^*)-L_k^\mu }{U_k^\mu -L_k^\mu } \le \frac{f_k(x^{**})-L_k^\mu }{U_k^\mu -L_k^\mu }\) for all \(k=1, 2, \ldots , K\) and \(\frac{f_k(x^*)-L_k^\mu }{U_k^\mu -L_k^\mu } < \frac{f_k(x^{**})-L_k^\mu }{U_k^\mu -L_k^\mu }\) for at least \(k \in \{1, 2, \ldots , K \}.\)

Hence, Max\(_k\) \(\frac{f_k(x^*)-L_k^\mu }{U_k^\mu -L_k^\mu }\) \(\le\) Max\(_k\) \(\frac{f_k(x^{**})-L_k^\mu }{U_k^\mu -L_k^\mu }\) and Max\(_k\) \(\frac{f_k(x^*)-L_k^\mu }{U_k^\mu -L_k^\mu }\) < Max\(_k\) \(\frac{f_k(x^{**})-L_k^\mu }{U_k^\mu -L_k^\mu }\) for at least one \(k\in \{1, 2, \ldots , K\}.\)

Similarly, Min\(_k\) \(\frac{f_k(x^*)-L_k^\mu }{\phi \times U_k^\mu -L_k^\mu }\) \(\ge\) Min\(_k\) \(\frac{f_k(x^{**})-L_k^\mu }{\phi \times U_k^\mu -L_k^\mu }\) and Min\(_k\) \(\frac{f_k(x^*)-L_k^\mu }{\phi \times U_k^\mu -L_k^\mu }\) > Min\(_k\) \(\frac{f_k(x^{**})-L_k^\mu }{\phi \times U_k^\mu -L_k^\mu }\) for at least one \(k\in \{1, 2, \ldots , K\}.\)

Now, suppose that Max\(_k\) \(\frac{f_k(x^*)-L_k^\mu }{U_k^\mu -L_k^\mu }=\delta ^*\) and Max\(_k\) \(\frac{f_k(x^*)-L_k^\mu }{U_k^\mu -L_k^\mu }=\delta ^{**},\) \(\frac{f_k(x^*)-L_k^\mu }{\phi \times U_k^\mu -L_k^\mu }=\gamma ^*\) and Max\(_k\) \(\frac{f_k(x^*)-L_k^\mu }{\phi \times U_k^\mu -L_k^\mu }=\gamma ^{**}.\)

Then \(\delta ^*\le (<) \delta ^{**}.\) and \(\gamma ^* \ge (>) \gamma ^{**}.\)

and this implies \((\delta ^* - \gamma ^*) < (\delta ^{**} - \gamma ^{**}).\)

Thus, I have reached at a contradiction with the fact that \((x^*, \delta ^*, \gamma ^*)\) be an optimal solution of the problem (17). Therefore our supposition is wrong and \((x^*, \delta ^*, \gamma ^*)\) be an optimal solution of the problem (1). This completes the proof. \(\square\)

5 The hesitant intuitionistic fuzzy algorithm

Step 1 Select a single objective function from a set of K objectives of the problem and solve it as a single objective subject to the given constraints. Find basic feasible solutions and the value of objective functions.

Step 2 Compute values of the remaining \((k-1)\) objectives at basic feasible solutions that are obtained from step 1.

Step 3 Repeat the step 1 and step 2 for remaining \((k-1)\) objective functions.

Step 4 Tabulate values of objective functions obtained from step 1, step 2, and step 3 to form a Table 1 and these are known as positive ideal solutions.

Table 1 Positive ideal solution
Full size table

Step 5 From step 5, find the lower and upper bounds for each objective function, where \(f_k^*\) and \(f_k^,\) are the maximum, minimum values of \(f_k\) respectively.

Step 6 Here, we denote and define upper and lower bounds by \(U_k^\mu = max(Z_k(X_r))\) and \(L_k^\mu = min(Z_k(X_r)), 1\le r\le p\) respectively for each uncertain and imprecise objective functions of multiple objective linear optimization problems.

Step 7 Set upper and lower bounds for each objective for hesitant degree of acceptance and hesitant degree of rejection corresponding to the set of solutions obtained in step 4.

For hesitant membership functions: Upper and lower bound for hesitant membership functions

\(U^{\mu }_{k}=\text {Max}(f_k(X_r))\) and \(L^{\mu }_{k}=\text {Min}(f_k(X_r)), 1\le r\le K, k=1, 2,\ldots , K.\)

For hesitant nonmembership function: Upper and lower bound for hesitant membership functions

\(U^{\nu }_{k}=\phi \times U^{\mu }_{k}\) and \(L^{\nu }_{k}=L^{\mu }_{k}, \ \phi \in \left[ 1, 3 \right] , k=1, 2,\ldots , K,\) where \(\phi\) is a hesitant parameters.

Step 8 In this step, we present uncertain and imprecise objectives of MOLP by using the following linear hesitant membership functions \(\mu ^{E^1}_k(f_k(x)).\)

Step 9 In this step, we present uncertain and imprecise objectives of MOLP by using the following linear hesitant non membership functions \(\nu ^{E^1}_k(f_k(x)).\)

Step 10 In this step, we apply a hesitant intuitionistic fuzzy optimization technique to get the solution to the multiobjective optimization problem.

$$\begin{aligned} \begin{aligned} \text {Maximize} \ \left( \delta _1-\gamma _1\right) +\left( \delta _2-\gamma _2\right) +\cdots +\left( \delta _n-\gamma _n\right) \\ \text {Such that} \ \mu ^{E_1}_{k}{(x)}\ge \delta _1, \ \text {for all} \ k\\ \mu ^{E_2}_{k}{(x)}\ge \delta _2, \ \text {for all} \ k\\ \ldots \\ \ldots \\ \mu ^{E_n}_{k}{(x)}\ge \delta _n, \ \text {for all} \ k\\ 0\le \delta _1, \delta _2,\ldots , \delta _n \le 1, \\ \nu ^{E_1}_{k}{(x)}\le \gamma _1, \ \text {for all} \ k\\ \nu ^{E_2}_{k}{(x)}\le \gamma _2, \ \text {for all} \ k\\ \cdots \\ \cdots \\ \nu ^{E_n}_{k}{(x)}\le \gamma _n, \ \text {for all} \ k\\ 0\le \gamma _1, \gamma _2,\ldots , \gamma _n \le 1, \\ \delta _1 \ge \gamma _1\\ \delta _2 \ge \gamma _2\\ \cdots \\ \cdots \\ \delta _n \ge \gamma _n\\ \gamma _i \ge 0, i=1,2,\ldots n\\ g_j(x)\le 0, j= 1,2,\ldots ,q \\ x\ge 0. \end{aligned} \end{aligned}$$
(18)

Hesitant membership and nonmembership functions for each uncertain objective are defined below in the next section.

Step 11 The above linear programming problem (14) can be easily solved by the above simplex method.

6 Application of proposed algorithm

6.1 Production planning problem

In MOLOP, a small violation in given constraints or conditions may lead to a more efficient solution to the problem. Such situations appear frequently in real-life modeling, as a matter of fact in optimization problems; many times it is not practical to fix accurate parameters as many of these are obtained through approximation or some kind of human observation. For example in a production optimization problem, not all the products need to be of good quality and are completely sellable at a fixed price. There is a possibility that some of the products may be defective and are not sellable at the fixed price. Further, prices of raw material, as well as the market price of the finished product, may vary depending on its surplus/deficiency in the market due to some uncontrollable situations. Thus it is evident that prices and/or productions are not purely deterministic but in general, these are imprecise or non-deterministic and thus such problems of optimization are to be dealt with help of some non-classical methods. Consider a park of six machine types whose capacities are to be devoted to the production of three products. A current capacity portfolio is available, measured in machine hours per weak for each machine capacity unit priced according to machine type. The necessary data in Table 2 is summarized below:

Table 2 Physical parameter values
Full size table

Let \(x_1,\ x_2,\ x_3\) denote three products, then the complete the mathematical formulation of the above-mentioned problem as a multiobjective linear optimization problem is given as:

$$\begin{aligned} \begin{aligned} \text {Maximize} \ f_1(x)=50 x_1+100 x_2+17.5 x_3 \ \text {(Profit)} \\ \text {Maximize} \ f_2(x)=92 x_1+75 x_2+50 x_3 \ \text { (Quality)} \\ \text {Maximize} \ f_3(x)=25 x_1+100x_2+75 x_3 \text {(Worker satisfaction)} \ \ \ \ \ \ \ \ \\ \text {Subject to the constraints} \\ 12 x_1+17 x_2 \le 1400 \\ 3 x_1+9 x_2+8 x_3 \le 1000 \\ 10 x_1+13 x_2+15 x_3 \le 1750 \\ 6 x_1+16 x_3 \le 1325 \\ x_1,x_2,x_3 \ge 0. \\ \end{aligned} \end{aligned}$$
(19)

A stepwise numerical verification of the proposed iterative method is presented below:

Step 1 In this step, we solve MOLOP as a single linear programming problem:

$$\begin{aligned} \begin{aligned} \text {Maximize} \ f_1(x)=50 x_1+100 x_2+17.5 x_3\\ \text {Subject to the constraints} \\ 12 x_1+17 x_2 \le 1400\\ 3 x_1+9 x_2+8 x_3 \le 100\\ 10 x_1+13 x_2+15 x_3 \le 1750\\ 6 x_1+16 x_3 \le 1325\\ 12 x_2+7 x_3 \le 900\\ 9.5 x_1+9.5 x_2+4 x_3 \le 1075\\ x_1,x_2,x_3 \ge 0. \end{aligned} \end{aligned}$$
(20)

Solving single objective linear programming problem (20), we get the following optimum solutions:

\(x_1=44.93,x_2=50.63, x_3=41.77, (f_1)_1=8041.14.\)

Step 2 With these decision variables, computed values of other remaining objective functions are: \((f_2)_1=10020.33, (f_3)_1=9319.25.\)

Step 3 Step 1 and Step 2 are repeated for other objective functions \(f_2,\ f_3.\)

Step 4 The Positive Ideal Solution obtained are placed in Table 3.

Step 5 I find the upper and lower bounds and these are given below:

Table 3 Positive ideal solution
Full size table

Step 6 In this step, we calculate lower and upper bounds for each objective functions:

\(L_1^\mu =5452.63, U_1^\mu =8041.14\)

\(L_2^\mu =10020.33, U_2^\mu =10950.59\)

\(L_3^\mu =9355.90, U_3^\mu =5903.00\)

Step 7 Use following linear membership function \(\mu ^{E^1}_k(f_k(x)), k=1,2,\ldots ,9\) for each objective functions:

$$\begin{aligned} \mu ^{E^1}_1(50x_1+100x_2+17.5x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 50x_1+100x_2+17.5x_3\le 5452.63\\ 0.96 \frac{50x_1+100x_2+17.5x_3-5452.63}{8041.14-5452.63}, \\ \text {if} \ \ 5452.63 \le 50x_1+100x_2+17.5x_3 \le 8041.14\\ 1, \text {if} \ \ 50x_1+100x_2+17.5x_3 \ge 5452.63 \\ \end{array}\right. } \end{aligned}$$
(21)
$$\begin{aligned} \mu ^{E^2}_2(50x_1+100x_2+17.5x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 50x_1+100x_2+17.5x_3\le 5452.63\\ 0.98 \frac{50x_1+100x_2+17.5x_3-5452.63}{8041.14-5452.63}, \\ \text {if} \ \ 5452.63 \le 50x_1+100x_2+17.5x_3 \le 8041.14\\ 1, \text {if} \ \ 50x_1+100x_2+17.5x_3 \ge 5452.63 \\ \end{array}\right. } \end{aligned}$$
(22)
$$\begin{aligned} \mu ^{E^3}_3(50x_1+100x_2+17.5x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 50x_1+100x_2+17.5x_3\le 5452.63\\ \frac{50x_1+100x_2+17.5x_3-5452.63}{8041.14-5452.63}, \\ \text {if} \ \ 5452.63 \le 50x_1+100x_2+17.5x_3 \le 8041.14\\ 1, \text {if} \ \ 50x_1+100x_2+17.5x_3 \ge 5452.63 \\ \end{array}\right. } \end{aligned}$$
(23)
$$\begin{aligned} \mu ^{E^1}_4( 92x_1+75x_2+50x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 92x_1+75x_2+50x_3 \le 10020.33\\ 0.96 \frac{ 92x_1+75x_2+50x_3-10020.33}{10950.59-10020.33}, \\ \text {if} \ \ 10020.33 \le 92x_1+75x_2+50x_3 \le 10950.59\\ 1, \text {if} \ \ 92x_1+75x_2+50x_3 \ge 10020.33 \\ \end{array}\right. } \end{aligned}$$
(24)
$$\begin{aligned} \mu ^{E^2}_5( 92x_1+75x_2+50x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 92x_1+75x_2+50x_3 \le 10020.33\\ 0.98\frac{ 92x_1+75x_2+50x_3-10020.33}{10950.59-10020.33}, \\ \text {if} \ \ 10020.33 \le 92x_1+75x_2+50x_3 \le 10950.59\\ 1, \text {if} \ \ 92x_1+75x_2+50x_3 \ge 10020.33 \\ \end{array}\right. } \end{aligned}$$
(25)
$$\begin{aligned} \mu ^{E^3}_6( 92x_1+75x_2+50x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 92x_1+75x_2+50x_3 \le 10020.33\\ \frac{ 92x_1+75x_2+50x_3-10020.33}{10950.59-10020.33}, \\ \text {if} \ \ 10020.33 \le 92x_1+75x_2+50x_3 \le 10950.59\\ 1, \text {if} \ \ 92x_1+75x_2+50x_3 \ge 10020.33 \\ \end{array}\right. } \end{aligned}$$
(26)
$$\begin{aligned} \mu ^{E^1}_7(25x_1+100x_2+75x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 25x_1+100x_2+75x_3\le 5903.00\\ 0.96\frac{25x_1+100x_2+75x_3-5903.00}{9355.90-5903.00}, \\ \text {if} \ \ 5903.00 \le 25x_1+100x_2+75x_3 \le 9355.90\\ 1, \text {if} \ \ 25x_1+100x_2+75x_3 \ge 5903.00 \\ \end{array}\right. } \end{aligned}$$
(27)
$$\begin{aligned} \mu ^{E^2}_8(25x_1+100x_2+75x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 25x_1+100x_2+75x_3\le 5903.00\\ 0.98 \frac{25x_1+100x_2+75x_3-5903.00}{9355.90-5903.00}, \\ \text {if} \ \ 5903.00 \le 25x_1+100x_2+75x_3 \le 9355.90\\ 1, \text {if} \ \ 25x_1+100x_2+75x_3 \ge 5903.00 \\ \end{array}\right. } \end{aligned}$$
(28)
$$\begin{aligned} \mu ^{E^3}_9(25x_1+100x_2+75x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 25x_1+100x_2+75x_3\le 5903.00\\ \frac{25x_1+100x_2+75x_3-5903.00}{9355.90-5903.00}, \\ \text {if} \ \ 5903.00 \le 25x_1+100x_2+75x_3 \le 9355.90\\ 1, \text {if} \ \ 25x_1+100x_2+75x_3 \ge 5903.00 \\ \end{array}\right. } \end{aligned}$$
(29)

Use following linear non membership function \(\nu ^{E^1}_k(f_k(x)), k=1,2,\ldots ,9\) for each objective functions:

$$\begin{aligned} \nu ^{E^1}_1(50x_1+100x_2+17.5x_3) ={\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 50x_1+100x_2+17.5x_3\ge \phi \times 8041.14\\ 0.96 \frac{\phi \times 8041.14-50x_1+100x_2+17.5x_3}{\phi \times 8041.14-5452.63}, \\ \text {if} \ 5452.63 \le 50x_1+100x_2+17.5x_3 \le \phi \times 8041.14\\ 1, \text {if} \ \ 50x_1+100x_2+17.5x_3 \le 5452.63 \\ \end{array}\right. } \end{aligned}$$
(30)
$$\begin{aligned} \nu ^{E^2}_2(50x_1+100x_2+17.5x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 50x_1+100x_2+17.5x_3\ge \phi \times 8041.14\\ 0.98 \frac{\phi \times 8041.14-50x_1+100x_2+17.5x_3}{\phi \times 8041.14-5452.63}, \\ \text {if} \ \ 5452.63 \le 50x_1+100x_2+17.5x_3 \le \phi \times 8041.14\\ 1, \text {if} \ \ 50x_1+100x_2+17.5x_3 \le 5452.63 \\ \end{array}\right. } \end{aligned}$$
(31)
$$\begin{aligned} \nu ^{E^3}_3(50x_1+100x_2+17.5x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 50x_1+100x_2+17.5x_3\ge \phi \times 8041.14\\ \frac{\phi \times 8041.14-50x_1+100x_2+17.5x_3}{\phi \times 8041.14-5452.63}, \\ \text {if} \ \ 5452.63 \le 50x_1+100x_2+17.5x_3 \le \phi \times 8041.14\\ 1, \text {if} \ \ 50x_1+100x_2+17.5x_3 \le 5452.63 \\ \end{array}\right. } \end{aligned}$$
(32)
$$\begin{aligned} \nu ^{E^1}_4( 92x_1+75x_2+50x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 92x_1+75x_2+50x_3 \ge \phi \times 10950.59\\ 0.96 \frac{\phi \times 10950.59- 92x_1+75x_2+50x_3}{\phi \times 10950.59-10020.33}, \\ \text {if} \ \ 10020.33 \le 92x_1+75x_2+50x_3 \le \phi \times 10950.59\\ 1, \text {if} \ \ 92x_1+75x_2+50x_3 \le 10020.33 \\ \end{array}\right. } \end{aligned}$$
(33)
$$\begin{aligned} \nu ^{E^2}_5( 92x_1+75x_2+50x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 92x_1+75x_2+50x_3 \ge \phi \times 10950.59\\ 0.98\frac{\phi \times 10950.59- 92x_1+75x_2+50x_3}{\phi \times 10950.59-10020.33}, \\ \text {if} \ \ 10020.33 \le 92x_1+75x_2+50x_3 \le \phi \times 10950.59\\ 1, \text {if} \ \ 92x_1+75x_2+50x_3 \le 10020.33 \\ \end{array}\right. } \end{aligned}$$
(34)
$$\begin{aligned} \nu ^{E^3}_6( 92x_1+75x_2+50x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 92x_1+75x_2+50x_3 \ge \phi \times 10950.59\\ \frac{\phi \times 10950.59- 92x_1+75x_2+50x_3}{\phi \times 10950.59-10020.33}, \\ \text {if} \ \ 10020.33 \le 92x_1+75x_2+50x_3 \le \phi \times 10950.59\\ 1, \text {if} \ \ 92x_1+75x_2+50x_3 \le 10020.33 \\ \end{array}\right. } \end{aligned}$$
(35)
$$\begin{aligned} \nu ^{E^1}_7(25x_1+100x_2+75x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 25x_1+100x_2+75x_3\ge \phi \times 9355.90\\ 0.96\frac{\phi \times 9355.90-25x_1+100x_2+75x_3}{\phi \times 9355.90-5903.00}, \\ \text {if} \ \ 5903.00 \le 25x_1+100x_2+75x_3 \le \phi \times 9355.90\\ 1, \text {if} \ \ 25x_1+100x_2+75x_3 \le 5903.00 \\ \end{array}\right. } \end{aligned}$$
(36)
$$\begin{aligned} \nu ^{E^2}_8(25x_1+100x_2+75x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 25x_1+100x_2+75x_3\ge \phi \times 9355.90\\ 0.98 \frac{\phi \times 9355.90-25x_1+100x_2+75x_3}{\phi \times 9355.90-5903.00}, \\ \text {if} \ \ 5903.00 \le 25x_1+100x_2+75x_3 \le \phi \times 9355.90\\ 1, \text {if} \ \ 25x_1+100x_2+75x_3 \le 5903.00 \\ \end{array}\right. } \end{aligned}$$
(37)
$$\begin{aligned} \nu ^{E^3}_9(25x_1+100x_2+75x_3) = {\left\{ \begin{array}{ll} 0,\ \text {if} \ \ 25x_1+100x_2+75x_3 \ge \phi \times 9355.90\\ \frac{\phi \times 9355.90-25x_1+100x_2+75x_3}{\phi \times 9355.90-5903.00}, \\ \text {if} \ \ 5903.00 \le 25x_1+100x_2+75x_3 \le 9355.90\\ 1, \text {if} \ \ 25x_1+100x_2+75x_3 \le 5903.00 \\ \end{array}\right. } \end{aligned}$$
(38)

where \(1 \le \phi \le 3\)

Step 8 In this step linear programming problem in hesitant intuitionistic fuzzy sense is solved. \(x_1=46.5607, x_2=48.0942, x_3=43.9445,\)

\(\delta _1=0.910062, \delta _2=0.929023, \delta _3=0.94798,\)

\(\delta _4=0.0697091,\delta _5=0.282288,\delta _6=0.0726135,\)

\(\delta _7=0.935917,\delta _8=0.955417,\delta _9=0.974913,\)

\(\gamma _1=0.0121611, \gamma _2=0.0124145, \gamma _3=0.0126678,\)

\(\gamma _4=0.069709, \gamma _5=0.0711613,\gamma _6=0.0726135,\)

\(\gamma _7=0.000000,\gamma _8=0.000000,\gamma _9=0.000000.\)

Table 4 Optimal Solutions based on proposed algorithm
Full size table
Fig. 4
figure 4

Membership and non membership degrees

Full size image
Table 5 Optimal values of objectives obtained by various algorithms
Full size table

7 Results discussion

Obtained solutions are placed in Table 4 and corresponding hesitant intuitionistic degrees are presented graphically in Fig. 4. In this section, I compare the proposed algorithm with previous algorithms, which are based on fuzzy sets and its other versions. The results are summarized in Table 5. Here, I present the obtained results by two ways, firstly with respect to similarity among methods and secondly, the difference between and existing algorithms. The similarity is presented below:

Proposed algorithm: \(f_2^0> f_3^0> f_1^0.\)

FS-algorithm: \(f_2^0> f_3^0> f_1^0.\)

IFS-algorithm: \(f_2^0> f_3^0> f_1^0.\)

IFS-algorithm: \(f_2^0> f_3^0> f_1^0.\)

HFS-algorithm: \(f_2^0> f_3^0> f_1^0.\)

For the difference between the proposed algorithm and previous algorithms, I calculate total values of objectives. Moreover, \(f_{Proposed-algorithm}> f_{HFS-algorithm}>f_{IVFS-algorithm}>f_{IFS-algorithm}>f_{FS-algorithm}.\) Further, it is very interesting to note that the total value \(f_{Proposed-algorithm}\) is larger than other existing algorithms, and it makes to algorithm stronger algorithm than others. Also, the comparison is presented graphically in Fig. 5.

Fig. 5
figure 5

Comparisons

Full size image

8 Conclusions

In recent years, dealing with real-life problems under uncertainty and hesitation is one of the main topics of researchers. The present paper focuses on a newly invented tool, the hesitant intuitionistic fuzzy sets, and their various properties. The paper discusses multiobjective linear optimization problems under uncertainty and hesitation with their solutions in the hesitant intuitionistic fuzzy scenarios, and for this, a computational algorithm is developed. Moreover, the developed algorithm is implemented in an industrial optimization problem. The proposed algorithm searched the best optimal solution as compared to some popular techniques, and the comparison is placed in Table 5 and appeared graphically in Fig. 5. The proposed algorithm is an extension of both fuzzy and intuitionistic fuzzy optimization techniques. The proposed algorithm searches the best optimal solution with a maximum degree of acceptance and a minimum degree of rejection, and it is in Fig. 4. Therefore, the presented algorithm can be used in several other real-life optimization problems too. Some merits and demerits that pointed out in this study are as follows:

  • The HIFS easily is restated and explained by using physical distancing during COVID-19.

  • A set of possible membership and nonmembership functions are defined to tackle the uncertainty and hesitation of MOLOP rather than a single.

  • The proposed approach properly deals with a MOLOP in uncertainty and hesitation scenarios.

  • The profit obtained from the proposed method is more than the existing methods.

  • Obtained decisions are more realistic and unbiased due to several expert’s opinions.

  • The proposed method is a generalization of both fuzzy and intuitionistic fuzzy optimization techniques.

  • It may be time-consuming while solving nonlinear multiobjective optimization problems.

  • It searches for the best optimal solution with a maximum membership and minimum nonmembership degrees.

9 Future research scope

The present approach is developed based on a newly invented set and hence it can be generalized in the following directions as well:

  • To solve a class of nonlinear optimization problems with uncertainty and hesitation.

  • To solve various types of multiple objective transportations and assignment problems.

  • It can be used to get a better solution of agricultural, industrial and health management etc.

  • It can be extended to deal with multiple objective fractional programming problems.

  • Game theory with uncertainty and hesitation can deal as well.