1 Introduction

In recent competitive industrial environment, a manufacturer should be able to produce qualitative products with on time delivery to the customers. So, designing a manufacturing environment including production department, machines’ layout, etc. is an important issue to reach the goals like better quality and on-time delivery. An effective way to have such design is to establish and balance a production (assembly) line. An assembly line consists of some tasks to be performed in a given order for producing the final product. The order of tasks is determined according to their precedence graph which defines the relationships among the tasks. The line is balanced when the tasks are assigned to some stations in order to optimize a given criterion (or set of criteria). The stations are usually connected with a conveyor and the parts and semi-products are moved among the stations on the conveyor to be completed at the end of the line. In a balanced line, each station consists of one or more tasks to be operated by usually one (in some cases more than one) worker in a given common time for all stations called cycle time of the line. The cycle time forces the line to send out a product from its last station in each cycle time. The order of stations and assigning the tasks to them must be determined in a way to respect to the precedence relationships of the tasks (precedence graph). The usual criteria used in an optimization problem of an assembly line balancing can be cycle time minimization, number of stations minimization, equipment purchasing cost minimization, worker-related cost minimization, etc. As a line balancing problem, one or more than one of these criteria may be considered for an assembly line. As an instance given by Fig. 1, assuming an assembly line which contains 8 tasks, the precedence relationships among the tasks is shown by graph (a). In this figure, the graphs (b) and (c) represent two feasible solutions which assign the tasks to 4 and 3 stations, respectively.

Fig. 1
figure 1

[source: Heydari et al. (2016)]

A graphical illustration of input (a) and output (b, c) for a straight assembly line balancing problem

Full size image

Assembly lines are classified from different aspects. Of physical point of view, a line can have different shapes. A line can have straight shape (Heydari et al. 2016) if there is enough straight available space. On the other hand it can be a U-shaped line for the case of small available spaces (Baybars 1986). Moreover, the stations may be placed on one or both sides of any assembly line. As another physical issue, use of parallel stations may be of interest for the cases that there is a task with operating time longer than the cycle time of the line. From product variety point of view, a line can be designed to produce one type product (single model) or being capable of producing more than one type of products (mixed-model). As another classification, a line can be designed to employ one worker in each station or working with more than one worker in each station. An important classification of assembly lines can be considered according to the deterministic and uncertain nature of the parameters. According to this classification, the parameters like task times, cycle time, cost values, etc. can be either of deterministic or uncertain nature. The uncertainty can be reflected by stochastic programming, fuzzy theory, interval programming, etc.

Although the literature of assembly line balancing problem is full of interesting studies, some of its most recent studies are reported here. Lei and Guo (2016) studied a two-sided assembly line balancing problem for cycle time minimization purpose. Yuguang et al. (2016) applied a PSO meta-heuristic algorithm for a typical multi-objective hull assembly line balancing problem to minimize the goals like cycle time, static load balancing between workstations, dynamic load balancing in all workstations, and multi-station associated complexity. Sepahi and Jalali Naini (2016) modeled a two-sided assembly line balancing problem considering parallel performance of tasks. A typical two-sided assembly line balancing problem (see also Tuncel and Aydin 2014) with mixed-model products (see also Kucukkoc and Zhang 2014; Ramezanian and Ezzatpanah 2015; Yang and Gao 2016) was studied by Kucukkoc and Zhang (2016) where they used a flexible agent-based ant colony optimization solution approach. Buyukozkan et al. (2016) applied artificial bee colony and tabu search meta-heuristic approaches for a typical two-sided assembly line balancing problem. As an interesting field of assembly line balancing problems, the number of U-shaped line related studies has been increased recently (see Ogan and Azizoglu 2015; Fattahi and Turkay 2015; Hazir and Dolgui 2015; Alavidoost et al. 2016). Moreover, multi-objective assembly line balancing problems in certain and uncertain environments (Khanjani Shiraz et al. 2015; Niroomand et al. 2016a, b; Mahmoodirad et al. 2017; Mosallaeipour et al. 2017; Salehi et al. 2017) have been of interest by the studies such as Alavidoost et al. (2015), (2016), Samouei et al. (2016), Zacharia and Nearchou (2016), etc. As an interesting problem, ergonomic issues of workers were considered in assembly line balancing problems by Battini et al. (2015). As an interesting study, Oksuz et al. (2017) considered the workers’ skills and performance levels in U-shaped assembly lines.

In this study, as a new assembly line balancing problem, the objectives average quality performance of workers, equipment purchasing cost and worker time-dependent wage are considered to be optimized simultaneously in a straight assembly line. This problem is studied in a stochastic environment where some parameters like task performing times and task performing qualities are determined stochastically with normal probability distribution with known parameters. The average quality performance of workers as a non-linear objective function is linearized using a modified version of the technique of Charnes and Cooper (1962). As a multi-objective problem (Tavana et al. 2014a; Jablonsky 2014), we propose a new hybrid goal programming solution approach which has a superior performance comparing to the existing methods of the literature in the case of the problem of this study.

The rest of this paper is organized as follows. In Sect. 2, the new multi-objective assembly line balancing formulation is proposed. In Sect. 3, a new solution approach is proposed to solve the problem of Sect. 2. In Sect. 4, some detailed computational experiments are performed. Finally, the paper ends with conclusion in Sect. 5.

2 Problem definition and formulation

As mentioned earlier, this paper focuses on a multi-objective straight assembly line balancing problem, where the following assumptions are to be respected in the mathematical formulation of the problem;

  • A single model product is to be assembled.

  • A constant cycle time is given.

  • A maximum number of potential stations are given which all or some of them may be opened.

  • Assigning a task to a station means that the required equipment of that task must be assigned to that station as well.

  • It is assumed that the workers of the potential stations are assigned in advance. Therefore, if a station is not opened, its worker will be applied in other departments of the company.

  • As the workers of the stations are determined in advance, each task is processed in different stations with different quality or dis-quality levels depending on the workers’ skills. Quality level and dis-quality level of a task in a station lies in the interval \(\left( {0,1} \right)\). For example if a task in a given station is performed by quality level of 0.85, it means that this task in that station is performed by dis-quality level of \(1 - 0.85 = 0.15\).

  • Each equipment has a purchasing cost.

  • According to the difficulty of the tasks, they have different time dependent processing cost. Therefore, the wage of a worker has two parts of fixed wage and variable wage. The variable wage of a worker is determined according to the most expensive task which is assigned to him/her multiplied by the cycle time (see Amen 2001, 2006).

  • The total variable wage of all stations is to be minimized.

  • The total equipment purchasing cost of all stations is to be minimized.

  • The average of minimum quality level of the stations is to be maximized.

  • The task processing times are uncertain. Those are of normal distribution with known means and variances.

  • The task dis-quality levels in the stations are uncertain. Those are of normal distribution with known means and variances.

Beyond the above-mentioned assumptions, the notations of Table 1 are used in all formulations of this section of the paper.

Table 1 The notations used in the formulations of the paper
Full size table

In the following sub-sections, first a non-linear deterministic formulation of the problem is introduced. Then the constraints with uncertainty are crisped using a stochastic chance-constrained technique. Finally, the equivalent linear form of the crisp version of the model is introduced.

2.1 Deterministic formulation

According to the above-mentioned assumptions, the following formulation is proposed for the multi-objective straight assembly line balancing problem that described above.

$${\text{Objective}}\;{\text{ function}}\;1{:}\;OF_{1} = \hbox{min} \;\sum\limits_{l = 1}^{L} {\sum\limits_{k = 1}^{K} {ec_{l} Z_{lk} } }$$
(1)
$${\text{Objective}}\;{\text{ function}}\;2{:}\;OF_{2} = \hbox{min} \;ct\sum\limits_{k = 1}^{K} {C_{k} }$$
(2)
$${\text{Objective}}\;{\text{ function}}\;3{:}\;OF_{3} = \hbox{max} \;\frac{{\sum\nolimits_{k = 1}^{K} {\left( {1 - DQ_{k} } \right)} }}{{\sum\nolimits_{k = 1}^{K} {W_{k} } }}$$
(3)

subject to

$$X_{ik} \le \frac{{\sum\nolimits_{{j \in P_{i} }} {\sum\nolimits_{r \le k} {X_{jr} } } }}{{\left| {P_{i} } \right|}}\quad \forall i,k$$
(4)
$$\sum\limits_{k = 1}^{K} {X_{ik} = 1} \quad \forall i$$
(5)
$$W_{k} \ge X_{ik} \quad \forall i,k$$
(6)
$$\sum\limits_{i = 1}^{I} {t_{i} X_{ik} \le ct} \quad \forall k$$
(7)
$$c_{i} X_{ik} \le C_{k} \quad \forall k$$
(8)
$$dq_{ik} X_{ik} \le DQ_{k} \quad \forall i,k$$
(9)
$$X_{ik} \le \frac{{\sum\nolimits_{{l \in Tl_{i} }} {Z_{lk} } }}{{\left| {Tl_{i} } \right|}}\quad \forall i,k$$
(10)
$$X_{ik} ,Z_{lk} ,W_{k} \in \left\{ {0,1} \right\}\quad \forall i,k,l$$
(11)
$$C_{k} ,DQ_{k} \ge 0\quad \forall k$$
(12)

The objective function (1) minimizes total purchasing cost of the equipment. The objective function (2) minimizes total time dependent task processing cost by the workers of the line. The objective function (3) maximizes a typical average quality level over the stations of the line. The constraint set (4) respects to the precedence relationships of the tasks. The notation \(\left| {P_{i} } \right|\) shows the number of predecessors of task i. According to this constraint task i can be assigned to station k if and only if its predecessors are assigned to station k or earlier stations. The constraint set (5) ensures that each task can be assigned to only one station. The constraint set (6) determines the value of \(W_{k}\) for all stations. Equation (7) upper bounds the processing time of each station by given cycle time. The constraint set (8) determines the time dependent cost of performing the tasks of each station according to the assumptions of the problem. Equation (9) determines the minimum dis-quality level of the tasks of each station according to the assumptions of the problem. Using the constraint set (10) the required tools of each station is assigned where \(\left| {Tl_{i} } \right|\) denotes the number of equipment required for performing task i. The last two constraint sets define the type of each variable.

More explanation on the objective function (3) may be of interest. Considering the term \(\sum\nolimits_{k = 1}^{K} {\left( {1 - DQ_{k} } \right)}\) and the constraint sets (6) and (9) together, for the stations that remain closed on the line, the quality level (the term \(1 - DQ_{k}\)) is equal to 1. This means that if more number of stations remain closed, the value \(\sum\nolimits_{k = 1}^{K} {\left( {1 - DQ_{k} } \right)}\) becomes greater, and the value \(\sum\nolimits_{k = 1}^{K} {W_{k} }\) becomes smaller. Therefore, the objective function (3) gets higher value. In fact, this objective function covers two purposes simultaneously; (1) maximizing average quality level of the line and (2) minimizing total number of opened stations of the line.

2.2 Uncertainty modeling of the deterministic formulation

In this sub-section a chance constrained modeling approach (see Agpak and Gokcen 2007) is proposed to cope with the uncertainty of the parameters of the model (1)–(12). As mentioned earlier in the assumptions of the problem, the parameters \(t_{i}\) and \(dq_{ik}\) are uncertain with normal probability distribution as \(t_{i} \sim N( {\mu_{t,i} ,\sigma_{t,i}^{2} } )\) and \(dq_{ik} \sim N( {\mu_{dq,ik} ,\sigma_{dq,ik}^{2} } )\) respectively. According to these uncertainties, the constraints (7) and (9) are uncertain.

To cope with the uncertainty of constraint (7), we first assume that \(H = \sum\nolimits_{i = 1}^{I} {t_{i} }\) where \(H \sim N\left( {\sum\nolimits_{i = 1}^{I} {\mu_{t,i} } ,\sum\nolimits_{i = 1}^{I} {\sigma_{t,i}^{2} } } \right)\). Now, as a chance constraint, it is claimed that the probability of satisfying constraint (7) must be at least \(\alpha\) (where \(0.5 < \alpha \le 1\)). This expression is shown by the chance constraint \(P(H \le ct) \ge \alpha\). This constraint, using Z transformation, is converted to the following constraint

$$P\left( {Z \le \frac{{ct - \sum\nolimits_{i = 1}^{I} {\mu_{t,i} } }}{{\sqrt {\sum\nolimits_{i = 1}^{I} {\sigma_{t,i}^{2} } } }}} \right) \ge \alpha$$
(13)

\(P(Z \le z_{\alpha } ) = \alpha\) and \(z_{\alpha }\) is \(100\alpha\) percentile of the standard normal distribution. Therefore the following relations are obtained accordingly,

$$z_{\alpha } \le \frac{{ct - \sum\nolimits_{i = 1}^{I} {\mu_{t,i} } }}{{\sqrt {\sum\nolimits_{i = 1}^{I} {\sigma_{t,i}^{2} } } }}$$
(14)

or

$$\sum\limits_{i = 1}^{I} {\mu_{t,i} } + z_{\alpha } \sqrt {\sum\limits_{i = 1}^{I} {\sigma_{t,i}^{2} } } \le ct$$
(15)

Applying \(X_{ik}\) variables in the constraint (15), the below crisp inequality is obtained that is used instead of the constraint (7).

$$\sum\limits_{i = 1}^{I} {\mu_{t,i} } X_{ik} + z_{\alpha } \sqrt {\sum\limits_{i = 1}^{I} {\sigma_{t,i}^{2} X_{ik} } } \le ct\quad \forall k$$
(16)

A similar procedure happens when coping with uncertainty of the constraint (9). As \(dq_{ik} \sim N( {\mu_{dq,ik} ,\sigma_{dq,ik}^{2} })\), satisfying the constraint (9) happens with the probability of \(\beta\) is shown by the expression \(P\left( {dq_{ik} \le DQ_{k} } \right) \ge \beta\) for \(\forall i,k\). This constraint is converted to the following one using Z transformation,

$$P\left( {Z \le \frac{{DQ_{k} - \mu_{dq,ik} }}{{\sigma_{dq,ik} }}} \right) \ge \beta \quad \forall i,k$$
(17)

\(P(Z \le z_{\beta } ) = \beta\) and \(z_{\beta }\) is \(100\beta\) percentile of the standard normal distribution. Therefore, similarly to the procedure of constraint (7) the following relations are obtained accordingly,

$$z_{\beta } \le \frac{{DQ_{k} - \mu_{dq,ik} }}{{\sigma_{dq,ik} }}\quad \forall i,k$$
(18)

and

$$\left( {\mu_{dq,ik} + z_{\beta } \sigma_{dq,ik} } \right)X_{ik} \le DQ_{k} \quad \forall i,k$$
(19)

So, the crisp constraint (19) is applied instead of the constraint (9) in the formulation (1)–(12). Replacing the crisp constraints (16) and (19) with (7) and (9) of the formulation (1)–(12), the following crisp model is obtained for the model (1)–(12),

$${\text{Objective}}\;{\text{ function}}\;1{:}\;OF_{1} = \hbox{min} \;\sum\limits_{l = 1}^{L} {\sum\limits_{k = 1}^{K} {ec_{l} Z_{lk} } }$$
(20)
$${\text{Objective}}\;{\text{ function}}\;2{:}\;OF_{2} = \hbox{min} \;ct\sum\limits_{k = 1}^{K} {C_{k} }$$
(21)
$${\text{Objective}}\;{\text{ function}}\;3{:}\;OF_{3} = \hbox{max} \;\frac{{\sum\nolimits_{k = 1}^{K} {\left( {1 - DQ_{k} } \right)} }}{{\sum\nolimits_{k = 1}^{K} {W_{k} } }}$$
(22)

subject to

$$X_{ik} \le \frac{{\sum\nolimits_{{j \in P_{i} }} {\sum\nolimits_{r \le k} {X_{jr} } } }}{{\left| {P_{i} } \right|}}\quad \forall i,k$$
(23)
$$\sum\limits_{k = 1}^{K} {X_{ik} = 1} \quad \forall i$$
(24)
$$W_{k} \ge X_{ik} \quad \forall i,k$$
(25)
$$\sum\limits_{i = 1}^{I} {\mu_{t,i} } X_{ik} + z_{\alpha } \sqrt {\sum\limits_{i = 1}^{I} {\sigma_{t,i}^{2} X_{ik} } } \le ct\quad \forall k$$
(26)
$$c_{i} X_{ik} \le C_{k} \quad \forall k$$
(27)
$$\left( {\mu_{dq,ik} + z_{\beta } \sigma_{dq,ik} } \right)X_{ik} \le DQ_{k} \quad \forall i,k$$
(28)
$$X_{ik} \le \frac{{\sum\nolimits_{{l \in Tl_{i} }} {Z_{lk} } }}{{\left| {Tl_{i} } \right|}}\quad \forall i,k$$
(29)
$$X_{ik} ,Z_{lk} ,W_{k} \in \left\{ {0,1} \right\}\quad \forall i,k,l$$
(30)
$$C_{k} ,DQ_{k} \ge 0\quad \forall k$$
(31)

The formulation (20)–(31) has high degree of non-linearity in the objective function (22) and the constraint set (26) where the terms \({{\sum\nolimits_{k = 1}^{K} {( {1 - DQ_{k} } )}}/{\sum\nolimits_{k = 1}^{K} {W_{k} } }}\) and \(\sqrt {\sum\nolimits_{i = 1}^{I} {\sigma_{t,i}^{2} X_{ik} } }\) are the sources of such non-linearity. In the next sub-section, linearization approaches to the formulation (20)–(31) are introduced.

2.3 Linearization techniques

In this sub-section, we focus to linearize the non-linearities of the objective function (22) and the constraint (26) of the formulation (20)–(31). The procedure of this linearization is described in the following sub-sections.

2.3.1 Linearization of the non-linear objective function

To linearize this objective function a modification of the method introduced by Charnes and Cooper (1962) is used. To do so, first a new continuous variable \(B = 1 /\sum\nolimits_{k = 1}^{K} W_{k}\) is defined and its upper bound is denoted by \(\bar{b}\). As the minimum number of stations of the assembly line balancing problem considered in this study cannot be less than 1, so, \(\frac{1}{K} \le B \le 1\) or \(0 \le B \le 1\), therefore, \(\bar{b} = 1\). This new variable defines the following new non-linear constraint.

$$\sum\limits_{k = 1}^{K} {B\left( {W_{k} } \right)} = 1$$
(32)

To further linearize the constraint (32), we define the new continuous variable \(V_{k} = B\left( {W_{k} } \right)\) and the constraint (32) is replaced by the following set (33)–(37). Obviously, the feasible solutions obtained by both of them are the same.

$$\sum\limits_{k = 1}^{K} {V_{k} } = 1$$
(33)
$$V_{k} \le \bar{b}W_{k} \quad \forall k$$
(34)
$$V_{k} \le B\quad \forall k$$
(35)
$$V_{k} \ge B - \bar{b}\left( {1 - W_{k} } \right)\quad \forall k$$
(36)
$$V_{k} \ge 0\quad \forall k$$
(37)

On the other hand, considering the relation \(B = 1 / \sum\nolimits_{k = 1}^{K} W_{k}\) and a new continuous variable \(Y_{k} = B\left( {DQ_{k} } \right)\), the following new versions of the objective function (22) and the constraint set (28) are obtained respectively.

$$OF_{3} = \hbox{max} \;\sum\limits_{k = 1}^{K} {\left( {B - Y_{k} } \right)}$$
(38)
$$\left( {\mu_{dq,ik} + z_{\beta } \sigma_{dq,ik} } \right)B\left( {X_{ik} } \right) \le Y_{k} \quad \forall i,k$$
(39)

To further linearize the constraint (39), we define the new continuous variable \(U_{ik} = B\left( {X_{ik} } \right)\) and the constraint set (39) is replaced by the following sets of constraints. Obviously, the feasible solution obtained by the linear constraints (40)–(44) is exactly the same as the feasible solution obtained by the non-linear constraint (39).

$$\left( {\mu_{dq,ik} + z_{\beta } \sigma_{dq,ik} } \right)U_{ik} \le Y_{k} \quad \forall i,k$$
(40)
$$U_{ik} \le \bar{b}X_{ik} \quad \forall i,k$$
(41)
$$U_{ik} \le B\quad \forall i,k$$
(42)
$$U_{ik} \ge B - \bar{b}\left( {1 - X_{ik} } \right)\quad \forall i,k$$
(43)
$$U_{ik} \ge 0\quad \forall i,k$$
(44)

Therefore, to linearize the objective function (22), the following changes are made in the formulation (20)–(31),

  • the objective function (22) is replaced by the objective function (38),

  • the constraint sets (33)–(37) are added to the formulation (20)–(31),

  • the constraint set (28) is replaced by the constraint sets (40)–(44).

2.3.2 Linearization of the non-linear constraints

In order to linearize the constraint (26), the inequality (14) is used. According to the inequality (14) and the inequality \(| {z_{\alpha } } | \le | {{{( {ct - \sum\nolimits_{i = 1}^{I} {\mu_{t,i} } } )} /{\sqrt {\sum\nolimits_{i = 1}^{I} {\sigma_{t,i}^{2} } } }}} |\), the following constraint is obtained,

$$\left( {z_{\alpha } } \right)^{2} \le {{\left( {ct - \sum\limits_{i = 1}^{I} {\mu_{t,i} X_{ik} } } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {ct - \sum\limits_{i = 1}^{I} {\mu_{t,i} X_{ik} } } \right)^{2} } {\left( {\sqrt {\sum\limits_{i = 1}^{I} {\sigma_{t,i}^{2} X_{ik} } } } \right)^{2} }}} \right. \kern-0pt} {\left( {\sqrt {\sum\limits_{i = 1}^{I} {\sigma_{t,i}^{2} X_{ik} } } } \right)^{2} }}$$
(45)

where,

$$ct - \sum\limits_{i = 1}^{I} {\mu_{t,i} X_{ik} } \ge 0$$
(46)

Considering the inequality \(\left( {z_{\alpha } } \right)^{2} \left( {\sum\nolimits_{i = 1}^{I} {\sigma_{t,i}^{2} X_{ik} } } \right) \le \left( {ct - \sum\nolimits_{i = 1}^{I} {\mu_{t,i} X_{ik} } } \right)^{2}\) from the constraint (45), its right-hand side is extended as,

$$\left( {ct - \sum\limits_{i = 1}^{I} {\mu_{t,i} X_{ik} } } \right)^{2} = ct^{2} - 2ct\sum\limits_{i = 1}^{I} {\mu_{t,i} X_{ik} } + \left( {\mu_{t,1}^{2} X_{1k}^{2} + \mu_{t,1} X_{1k} \mu_{t,2} X_{2k} + \mu_{t,1} X_{1k} \mu_{t,3} X_{3k} + \cdots + \mu_{t,I}^{2} X_{Ik}^{2} } \right)$$
(47)

To further linearize right-hand side of the Eq. (47), a new binary variable \(Q_{ijk} = X_{ik} X_{jk}\) is defined and the following sets of constraints are introduced to relate the value of \(Q_{ijk}\) and the term \(X_{ik} X_{jk}\).

$$X_{ik} + X_{jk} \le 1 + Q_{ijk} \quad \forall i,j,k$$
(48)
$$X_{ik} + X_{jk} \ge 2Q_{ijk} \quad \forall i,j,k$$
(49)

Finally, considering the constraints (45)–(49), the linearized version of the non-linear constraint (26) is shown by the following constraint sets.

$$ct^{2} - 2ct\sum\limits_{i = 1}^{I} {\mu_{t,i} X_{ik} } + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{I} {\mu_{t,i} \mu_{t,j} Q_{ijk} } } \ge \left( {z_{\alpha } } \right)^{2} \left( {\sum\limits_{i = 1}^{I} {\sigma_{t,i}^{2} X_{ik} } } \right)\quad \forall k$$
(50)
$$X_{ik} + X_{jk} \le 1 + Q_{ijk} \quad \forall i,j,k$$
(51)
$$X_{ik} + X_{jk} \ge 2Q_{ijk} \quad \forall i,j,k$$
(52)

2.4 Overall formulation

Based on the linearization techniques presented in the previous sub-section, the linearized version of the formulation (20)–(31) is summarized as follows,

$${\text{Objective}}\;{\text{function}}\;1{:}\;OF_{1} = \hbox{min} \;\sum\limits_{l = 1}^{L} {\sum\limits_{k = 1}^{K} {ec_{l} Z_{lk} } }$$
(53)
$${\text{Objective}}\;{\text{function}}\;2{:}\;OF_{2} = \hbox{min} \;ct\sum\limits_{k = 1}^{K} {C_{k} }$$
(54)
$${\text{Objective}}\;{\text{function}}\;3{:}\;OF_{3} = \hbox{max} \;\sum\limits_{k = 1}^{K} {\left( {B - Y_{k} } \right)}$$
(55)

subject to

$$X_{ik} \le \frac{{\sum\nolimits_{{j \in P_{i} }} {\sum\nolimits_{r \le k} {X_{jr} } } }}{{\left| {P_{i} } \right|}}\quad \forall i,k$$
(56)
$$\sum\limits_{k = 1}^{K} {X_{ik} = 1} \quad \forall i$$
(57)
$$W_{k} \ge X_{ik} \quad \forall i,k$$
(58)
$$ct^{2} - 2ct\sum\limits_{i = 1}^{I} {\mu_{t,i} X_{ik} } + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{I} {\mu_{t,i} \mu_{t,j} Q_{ijk} } } \ge \left( {z_{\alpha } } \right)^{2} \left( {\sum\limits_{i = 1}^{I} {\sigma_{t,i}^{2} X_{ik} } } \right)\quad \forall k$$
(59)
$$X_{ik} + X_{jk} \le 1 + Q_{ijk} \quad \forall i,j,k$$
(60)
$$X_{ik} + X_{jk} \ge 2Q_{ijk} \quad \forall i,j,k$$
(61)
$$c_{i} X_{ik} \le C_{k} \quad \forall k$$
(62)
$$\left( {\mu_{dq,ik} + z_{\beta } \sigma_{dq,ik} } \right)U_{ik} \le Y_{k} \quad \forall i,k$$
(63)
$$U_{ik} \le \bar{b}X_{ik} \quad \forall i,k$$
(64)
$$U_{ik} \le B\quad \forall i,k$$
(65)
$$U_{ik} \ge B - \bar{b}\left( {1 - X_{ik} } \right)\quad \forall i,k$$
(66)
$$X_{ik} \le \frac{{\sum\nolimits_{{l \in Tl_{i} }} {Z_{lk} } }}{{\left| {Tl_{i} } \right|}}\quad \forall i,k$$
(67)
$$\sum\limits_{k = 1}^{K} {V_{k} } = 1$$
(68)
$$V_{k} \le \bar{b}W_{k} \quad \forall k$$
(69)
$$V_{k} \le B\quad \forall k$$
(70)
$$V_{k} \ge B - \bar{b}\left( {1 - W_{k} } \right)\quad \forall k$$
(71)
$$X_{ik} ,Z_{lk} ,W_{k} ,Q_{ijk} \in \left\{ {0,1} \right\}\quad \forall i,j,k,l$$
(72)
$$C_{k} ,DQ_{k} ,V_{k} ,U_{ik} ,B \ge 0\quad \forall i,k$$
(73)

The formulation (53)–(73) is the final form of the multi-objective straight assembly line balancing problem defined in the beginning of this section. The formulation is in a mixed integer linear form with three different scaled objective functions. To tackle such a problem we need to apply multi-objective optimization approaches like fuzzy programming, goal programming, etc. which are usually used in multi-objective optimization. These approaches are used to provide efficient solutions to multi-objective problems. In the next section a solution approach based on goal programming method is proposed to tackle the formulation (53)–(73) of this paper.

3 Solution methodology

The aim of this section is to introduce a new solution approach to tackle the multi-objective formulation (53)–(73) for finding an efficient solution. For more information on the concepts of an efficient solution, the study of Abd El-Wahed and Lee (2006) can be referred. Generally, dealing with multi-objective optimization problems is difficult as satisfying all the objectives from the decision maker (DM) point of view is not easy. The methods of finding efficient solutions for multi-objective problems can be generally classified as the followings,

  • Interactive approaches,

  • Non-interactive approaches,

  • Goal programming approach,

  • Fuzzy programming approach.

In the interactive approaches DM plays an important role as he/she controls the solution procedure for finding a satisfactory solution from his/her point of view. So that, an objective function may be more focused by DM to be optimized in the solution procedure. In the classic version of this approach, an efficient solution is generated. If the solution does not satisfy DM, in the optimization direction selected by DM, another efficient solution is generated. This procedure is continued until DM’s satisfaction is obtained. For the interactive approaches the studies of Climaco et al. (1993) and Tamiz et al. (1998) can be of interest. In the non-interactive approaches, first, a pool of efficient solutions is generated and then DM selects one of the solutions according to his/her preferences. For the non-interactive approaches, the studies of Aneja and Nair (1979) and Kasana and Kumar (2000) can be of interest. In the goal programming approach (for a rich survey on goal programming approach, the study of Colapinto et al. (2017) can be referred), DM determines a goal for each objective function and tries to find a solution which satisfies the goals. Of course, all of the goals may not be achieved. In this approach, the obtained solutions can be analyzed by DM considering the aspiration level of the objective functions. For the goal programming approach the studies of Romero (1991), Abd El-Wahed and Lee (2006), etc. can be of interest. Zimmermann (1996) for the first time applied the fuzzy programming approach (max–min operator) to solve a multi-objective model. This method is an effective tool for the cases that the preferences of DM are not completely clear. As a shortcoming, this solution approach may not give efficient solutions in some cases (Alavidoost et al. 2016). This weakness of fuzzy programming approach later was focused in some studies. In order to overcome it, several hybrid versions of the fuzzy programming method like the approaches of Selim and Ozkarahan (2008), Torabi and Hassini (2008), Demirli and Yimer (2008), Alavidoost et al. (2016), etc. were introduced. Some other approaches of multi-objective optimization can be of interest such as Jablonsky (2007), Tavana et al. (2014b, 2016), etc.

3.1 The proposed hybrid goal programming approach

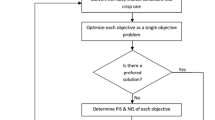
In this sub-section a solution approach hybridizing fuzzy programming and goal programming approaches is proposed to solve the multi-objective formulation (53)–(73). This new approach tries to cover the above-mentioned shortcomings of the classic approaches like the fuzzy programming and the goal programming. This proposed approach consists of two main phases such as (1) applying a hybrid fuzzy programming approach for finding a good efficient solution, and (2) applying a goal programming approach if the obtained efficient solution does not satisfy DM. These phases are explained in the following sub-sections.

3.1.1 Phase 1: the hybrid fuzzy programming

As the first phase of the proposed approach, the multi-objective formulation (53)–(73) is solved with a hybrid fuzzy programming approach without considering DM’s preferences. Therefore, in this hybrid version of the fuzzy programming approach, the objective functions are weighted equally. The steps of this phase which are mainly common in the most of the multi-objective optimization approaches (see Selim and Ozkarahan 2008; Torabi and Hassini 2008; Demirli and Yimer 2008; Alavidoost et al. 2016) are described as follows,

Step 1.1 In the formulation (53)–(73) , determine the probability levels \(\alpha\) and \(\beta\) where \(0.5 < \alpha ,\beta \le 1\).

Step 1.2 Solve the following sub-problems to find positive ideal solution (\(SOL_{q}^{PIS}\) where \(q \in \left\{ {1,2,3} \right\}\)) and its related objective value (\(OF_{q}^{PIS}\) where \(q \in \left\{ {1,2,3} \right\}\)) for each objective function separately.

$$\begin{aligned} {\text{Sub{-}problem}}\;1{:}\; & OF_{1}^{PIS} = \hbox{min} \;\sum\limits_{l = 1}^{L} {\sum\limits_{k = 1}^{K} {ec_{l} Z_{lk} } } \\ & {\text{subject}}\;{\text{to}} \\ & {\text{Constraints}}\;(56){-}(73) \\ \end{aligned}$$
(74)
$$\begin{aligned} {\text{Sub{-}problem}}\;2{:}\; & OF_{2}^{PIS} = \hbox{min} \;ct\sum\limits_{k = 1}^{K} {C_{k} } \\ & {\text{subject}}\;{\text{to}} \\ & {\text{Constraints}}\;(56){-}(73) \\ \end{aligned}$$
(75)
$$\begin{aligned} {\text{Sub{-}problem}}\;3{:}\; & OF_{3}^{PIS} = \hbox{max} \;\sum\limits_{k = 1}^{K} {\left( {B - Y_{k} } \right)} \\ & {\text{subject}}\;{\text{to}} \\ & {\text{Constraints}}\;(56){-}(73) \\ \end{aligned}$$
(76)

Now, using each obtained positive ideal solution, calculate the value of each objective function (for example \(OF_{1} \left( {SOL_{2}^{PIS} } \right)\), etc.) to construct the payoff table represented by Table 2.

Table 2 The payoff table to find the negative and positive ideal objective function values
Full size table

For the minimization type objective functions find the positive and negative ideal objective values (\(OF_{q}^{PIS}\) and \(OF_{q}^{NIS}\)) from Table 2 as,

$$OF_{q}^{PIS} = \mathop {\hbox{min} }\limits_{p} \left\{ {OF_{q} \left( {SOL_{p}^{PIS} } \right)} \right\}\quad \forall q \in \{ 1,2\}$$
(77)
$$OF_{q}^{NIS} = \mathop {\hbox{max} }\limits_{p} \left\{ {OF_{q} \left( {SOL_{p}^{PIS} } \right)} \right\}\quad \forall q \in \{ 1,2\}$$
(78)

For the maximization type objective functions find the positive and negative ideal objective values from Table 2 as,

$$OF_{q}^{PIS} = \mathop {\hbox{max} }\limits_{p} \left\{ {OF_{q} \left( {SOL_{p}^{PIS} } \right)} \right\}\quad q = 3$$
(79)
$$OF_{q}^{NIS} = \mathop {\hbox{min} }\limits_{p} \left\{ {OF_{q} \left( {SOL_{p}^{PIS} } \right)} \right\}\quad q = 3$$
(80)

Step 1.3 Using the results of Step 1.2, for the objective function \(i\) (\(q \in \left\{ {1,2,3} \right\}\)), determine a membership function as follows, where \(\mu_{q} \left( {OF_{q} } \right)\) calculates the satisfaction level (degree) of \(q -\) th objective function.

$$\mu_{q} \left( {OF_{q} } \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {OF_{q} \text{ < }OF_{q}^{PIS} } \hfill \\ {\frac{{OF_{q}^{NIS} - OF_{q} }}{{OF_{q}^{NIS} - OF_{q}^{PIS} }}} \hfill & {OF_{q}^{PIS} \le OF_{q} \le OF_{q}^{NIS} \quad \forall q \in \left\{ {1,2} \right\}} \hfill \\ 0 \hfill & {OF_{q} \text{ > }OF_{q}^{NIS} } \hfill \\ \end{array} } \right.$$
(81)
$$\mu_{q} \left( {OF_{q} } \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {OF_{q} \text{ < }OF_{q}^{NIS} } \hfill \\ {\frac{{OF_{q} - OF_{q}^{NIS} }}{{OF_{q}^{PIS} - OF_{q}^{NIS} }}} \hfill & {OF_{q}^{NIS} \le OF_{q} \le OF_{q}^{PIS} \quad q = 3} \hfill \\ 1 \hfill & {OF_{q} \text{ > }OF_{q}^{PIS} } \hfill \\ \end{array} } \right.$$
(82)

Step 1.4 Solve the following single objective model to find an efficient solution for the multi-objective formulation (53)–(73).

$$\begin{aligned} &\hbox{max} \;\gamma \lambda_{0} + \left( {1 - \gamma } \right)\frac{{\sum\nolimits_{q = 1}^{3} {\mu_{q} \left( {OF_{q} } \right)} }}{3} \hfill \\ &{\text{subject}}\;{\text{to}} \hfill \\ &\lambda_{0} \le \mu_{q} \left( {OF_{q} } \right)\quad \forall q \in \{ 1,2,3\} \hfill \\ &\gamma ,\lambda_{0} \in \left[ {0,1} \right] \hfill \\ &{\text{Constraints}}\;(56){-}(73) \hfill \\ \end{aligned}$$
(83)

where \(\lambda_{0}\) is the minimum satisfaction degree among the objectives and \(\gamma\) is the coefficient for controlling the compromise degree of the objective functions and \(\lambda_{0}\). The optimal value of \(\gamma\) can be obtained experimentally, but according to the similar approaches of the literature it is set to 0.4.

Step 1.5 If the solution obtained in Step 1.4 satisfies DM, the solution is accepted and the procedure stops here. Otherwise, DM can consider her/his preferences e.g. considering lower and upper limit for the objective functions that does not meet the preferences. These preferences are actually the goals of the objective functions. Therefore, each objective function has a lower limit and an upper limit for its goal, if DM is not satisfied with its value obtained by Step 1.4. This issue is focused in Phase 2 of the proposed solution approach which is analyzed in the following sub-section.

3.1.2 Phase 2: the fuzzy goal programming

As mentioned above, if DM is satisfied with the solution of Phase 1, the procedure stops and the solution is reported as a satisfying efficient solution of the formulation (53)–(73). Otherwise, DM may be interested to apply interval goals for the values of the objective functions which do not satisfy him/her. Let us to consider an interval of the form \(\left[ {LG_{q} ,UG_{q} } \right]\) for the objective function q which do not satisfy DM. Of course, this interval is introduced by DM. The values \(LG_{q}\) and \(UG_{q}\) are the lower and upper bounds for the goal value of the objective function q which do not satisfy DM (the set of objective functions satisfying DM is represented by S, while the set of objective functions not satisfying DM is noted by NS). To cope with this type of goals, we used a fuzzy goal programming technique in this section. Based on the above-introduced interval goal, the following equations for all of the objective function values are introduced,

$$\frac{{UG_{q} - OF_{q} }}{{UG_{q} - LG_{q} }} - d_{q}^{ + } + d_{q}^{ - } = 1\quad \forall q \in \left\{ {\left\{ {1,2} \right\} \cap NS} \right\}$$
(84)
$$\frac{{OF_{q} - LG_{q} }}{{UG_{q} - LG_{q} }} - d_{q}^{ + } + d_{q}^{ - } = 1\quad \forall q \in \left\{ {\left\{ 3 \right\} \cap NS} \right\}$$
(85)
$$\left( {\mu_{q} \left( {OF_{q} } \right) = \frac{{OF_{q}^{NIS} - OF_{q} }}{{OF_{q}^{NIS} - OF_{q}^{PIS} }}} \right) - d_{q}^{ + } + d_{q}^{ - } = 1\quad \forall q \in \left\{ {\left\{ {1,2} \right\} \cap S} \right\}$$
(86)
$$\left( {\mu_{q} \left( {OF_{q} } \right) = \frac{{OF_{q} - OF_{q}^{NIS} }}{{OF_{q}^{PIS} - OF_{q}^{NIS} }}} \right) - d_{q}^{ + } + d_{q}^{ - } = 1\quad \forall q \in \left\{ {\left\{ 3 \right\} \cap S} \right\}$$
(87)

where \(d_{q}^{ - }\) and \(d_{q}^{ + }\) (these variables are non-negative and at most one of them can be positive at the same time) are negative and positive derivations from the membership function values which are at the left side of the Eqs. (84)–(87). These equations can be rewritten as the following equations,

$$OF_{q} + \left( {UG_{q} - LG_{q} } \right)d_{q}^{ + } - \left( {UG_{q} - LG_{q} } \right)d_{q}^{ - } = LG_{q} \quad \forall q \in \left\{ {\left\{ {1,2} \right\} \cap NS} \right\}$$
(88)
$$OF_{q} - \left( {UG_{q} - LG_{q} } \right)d_{q}^{ + } + \left( {UG_{q} - LG_{q} } \right)d_{q}^{ - } = UG_{q} \quad \forall q \in \left\{ {\left\{ 3 \right\} \cap NS} \right\}$$
(89)
$$\mu_{q} \left( {OF_{q} } \right) - d_{q}^{ + } + d_{q}^{ - } = 1\quad \forall q \in \left\{ {\left\{ {1,2,3} \right\} \cap S} \right\}$$
(90)

Applying Eqs. (88)–(91) in the single objective formulation (83), the following fuzzy goal programming formulation is obtained,

$$\begin{aligned} &\hbox{max} \;\gamma \lambda_{0} + \left( {1 - \gamma } \right)\frac{{\sum\nolimits_{q = 1}^{3} {\mu_{q} \left( {OF_{q} } \right)} }}{3} \hfill \\& {\text{subject}}\;{\text{to}} \hfill \\ &\lambda_{0} \le \mu_{q} \left( {OF_{q} } \right)\quad \forall q \in \left\{ {\left\{ {1,2,3} \right\} \cap S} \right\} \hfill \\ &\lambda_{0} \le \frac{{UG_{q} - OF_{q} }}{{UG_{q} - LG_{q} }}\quad \forall q \in \left\{ {\left\{ {1,2} \right\} \cap NS} \right\} \hfill \\ &\lambda_{0} \le \frac{{OF_{q} - LG_{q} }}{{UG_{q} - LG_{q} }}\quad \forall q \in \left\{ {\left\{ 3 \right\} \cap NS} \right\} \hfill \\& OF_{q} + \left( {UG_{q} - LG_{q} } \right)d_{q}^{ + } - \left( {UG_{q} - LG_{q} } \right)d_{q}^{ - } = LG_{q} \quad \forall q \in \left\{ {\left\{ {1,2} \right\} \cap NS} \right\} \hfill \\ &OF_{q} - \left( {UG_{q} - LG_{q} } \right)d_{q}^{ + } + \left( {UG_{q} - LG_{q} } \right)d_{q}^{ - } = UG_{q} \quad \forall q \in \left\{ {\left\{ 3 \right\} \cap NS} \right\} \hfill \\ &\mu_{q} \left( {OF_{q} } \right) - d_{q}^{ + } + d_{q}^{ - } = 1\quad \forall q \in \left\{ {\left\{ {1,2,3} \right\} \cap S} \right\} \hfill \\ &\gamma ,\lambda_{0} \in \left[ {0,1} \right] \hfill \\& d_{q}^{ + } ,d_{q}^{ - } \ge 0\quad \forall q \in \left\{ {1,2,3} \right\} \hfill \\& {\text{Constraints}}\;(56){-}(73) \hfill \\ \end{aligned}$$
(91)

Solving (91), a new solution is obtained, different from the solution of Phase 1. In the new solution, the goals are respected, while the value of the satisfying objective functions from Phase 1 are forced to be close to their previous values. But, generally, when the objective functions not satisfying DM with respect to the goals of Phase 2, the other objective functions might be worse comparing to their values from Phase 1.

4 Computational experiments

In order to show the performance of the proposed approach, some benchmark problems are considered in this section. In the rest of this section first a benchmark with 12 tasks is explained in detail and the obtained result is analyzed. Then, some other benchmarks with different number of tasks are applied. Notably, as the problem of this study is new, all of the benchmarks are generated randomly. As an alternative solution approach, the interactive fuzzy goal programming approach developed by Abd El-Wahed and Lee (2006), is re-implemented for the problem of this study. We compare the result obtained by the proposed approach and those obtained by the approach of Abd El-Wahed and Lee (2006).

4.1 Benchmark 1 with 12 tasks

Benchmark 1 consists of balancing a line with 12 tasks, 4 types of equipment, and 8 potential stations. The data of this benchmark are shown by Fig. 2, Tables 3, 4 and 5. Furthermore, cycle time (\(ct\)) of the line is 14, and the equipment purchasing costs (\(ec_{l}\)) are 1000, 2000, 3000, and 4000 dollars for the equipment 1 to 4, respectively.

Fig. 2
figure 2

The precedence graph of benchmark 1

Full size image
Table 3 Time, cost and required tools for the tasks of benchmark 1
Full size table
Table 4 The data for mean dis-quality level (\(\mu_{dq,ik}\)) of benchmark 1
Full size table
Table 5 The data for variance of dis-quality level (\(\mu_{dq,ik}\)) of benchmark 1
Full size table

The required formulations of the proposed solution procedure for solving this benchmark is coded in GAMS solver and was run on a computer with an Intel Pentium Dual 2.53 GHz processor and 4 GB RAM.

To perform the computations, the probability levels \(\alpha\) and \(\beta\) are selected from the set \(\left\{ {0.6,0.7,0.8,0.9,1} \right\}\). Notably, in each treatment \(\alpha\) and \(\beta\) take the same value. As initial computations, the values of Table 6 are obtained for the positive and negative ideal objective function values.

Table 6 The negative and positive ideal objective function values obtained for benchmark 1 in different probability levels
Full size table

Using the ideal objective function values of Table 6, the result of the first phase of the proposed approach and the approach of Abd El-Wahed and Lee (2006) is obtained as reported by Table 7.

Table 7 The results obtained for benchmark 1 in different probability levels by the first phase of the proposed approach and the approach of Abd El-Wahed and Lee (2006)
Full size table

Comparing the results of Tables 6 and 7, some issues can be concluded. When \(\alpha\) and \(\beta\) take value of 0.6, the values of second and third objective functions are very close to their positive ideal solutions, while the value of first objective function is not close to its positive ideal solution. Therefore, it is logical to say that DM is not satisfied with the first objective function. For this reason, the preferences of DM for this objective function is considered by the second phase of the proposed solution approach (the formulation (91) where \(\left[ {LG_{1} ,UG_{1} } \right] = \left[ {27000,30000} \right]\)). Applying the same logic, the not satisfying objective functions in any level of \(\alpha\) and \(\beta\) were determined and the preferences of DM were considered for them as reported by Table 8.

Table 8 The preferences set by DM for the not satisfying objective functions
Full size table

To further improve the not satisfying objective functions, the second phase of the proposed approach and also the approach of Abd El-Wahed and Lee (2006) were applied using the preferences of Table 8. The results of this phase are shown in Table 9.

Table 9 The results obtained for benchmark 1 in different probability levels by the second phase of the proposed approach and the approach of Abd El-Wahed and Lee (2006)
Full size table

The results of Table 9 are interpreted for each probability level separately. For the probability level of 0.6, considering the results of Tables 7 and 9 simultaneously, it is concluded that both approaches perform similarly in the case of the first and second objective functions while the proposed approach outperforms the approach of Abd El-Wahed and Lee (2006) in the case of third objective function. When the probability levels are set to 0.7, both approaches perform similarly to the case of the second objective function, while the proposed approach outperforms the approach of Abd El-Wahed and Lee (2006) in the case of the first and third objective functions. When the probability levels are set to 0.8, both approaches perform similarly to the case of the first objective function, while the proposed approach outperforms the approach of Abd El-Wahed and Lee (2006) in the case of the second and third objective functions. For the probability level of 0.9, both approaches perform similarly in the case of the first and second objective functions while the proposed approach outperforms the approach of Abd El-Wahed and Lee (2006) in the case of the third objective function. Finally, for the probability level of 1, the proposed approach outperforms the approach of Abd El-Wahed and Lee (2006) in the case of the first and third objective functions, while an inverse performance happens for the case of second objective function.

4.2 Other benchmarks

In order to further analyze the performance of the proposed solution approach, we provided three more benchmarks with 16, 21, and 35 tasks. All of them contain 4 number of equipment with 10, 12, and 20 available stations respectively. The detailed data set of these benchmarks can be seen in “Appendix” section. By applying the proposed solution approach and the approach of Abd El-Wahed and Lee (2006), the results of Tables 10, 11 and 12 were obtained.

Table 10 The results obtained for the benchmark with 16 tasks in different probability levels by the proposed approach and the approach of Abd El-Wahed and Lee (2006)
Full size table
Table 11 The results obtained for the benchmark with 21 tasks in different probability levels by the proposed approach and the approach of Abd El-Wahed and Lee (2006)
Full size table
Table 12 The results obtained for the benchmark with 35 tasks in different probability levels by the proposed approach and the approach of Abd El-Wahed and Lee (2006)
Full size table

For the case of the benchmark with 16 tasks, according to the results of Table 10, in the first phase, the proposed approach absolutely performs better than the approach of Abd El-Wahed and Lee (2006), as for two out of three objective functions the better value is obtained by the proposed approach. Then, for the objective functions that do not satisfy DM (because their value is far from the objective function value of PIS), the goal values are determined by DM, and the second stage of both approaches. In the second phase, the proposed approach absolutely performs better than the approach of Abd El-Wahed and Lee (2006) as for two out of three objective functions the better value is obtained by the proposed approach. Of course, both of the approaches limit the not satisfying objective functions by the proposed goal intervals.

For the case of the benchmark with 21 tasks, according to the results of Table 11, in the first phase, the proposed approach absolutely performs better than the approach of Abd El-Wahed and Lee (2006) as for two out of three objective functions the better value is obtained by the proposed approach. Then, for the objective functions that do not satisfy DM (because their value is far from the objective function value of PIS), the goal values are determined by DM and the second stage of both approaches. In the second phase, the proposed approach absolutely performs better than the approach of Abd El-Wahed and Lee (2006) as for two out of three objective functions the better value is obtained by the proposed approach. Of course, both of the approaches limit the not satisfying objective functions by the proposed goal intervals.

For the case of the benchmark with 35 tasks, according to the results of Table 11, in the first phase, the proposed approach absolutely performs better than the approach of Abd El-Wahed and Lee (2006) as for two out of three objective functions the better value is obtained by the proposed approach. Then, by setting the necessary goal values, the second phase is performed. In the second phase, the proposed approach absolutely performs better than the approach of Abd El-Wahed and Lee (2006) as for two out of three objective functions the better value is obtained by the proposed approach. Of course, both of the approaches limit the not satisfying objective functions by the proposed goal intervals.

5 Concluding remarks

We addressed a new multi-objective assembly line balancing problem in this study. The objectives like equipment purchasing cost, worker time dependent wage, and average task performing quality of the assembly line were to be optimized simultaneously in existence of stochastic task times and task performing quality levels which are distributed normally. A mixed integer non-linear formulation was proposed for the problem. Applying a chance-constrained modeling approach and some linearization techniques the model was converted to a crisp multi-objective mixed integer linear formulation. To tackle such a problem a hybrid goal programming approach was proposed which combines a proposed hybrid fuzzy programming method and a typical goal programming approach. The computational experiments of the study proved the superiority of the proposed approach comparing to the literature.

Some limitations that may influence the difficulty of assembly line balancing problems are physical shape of assembly line, consumer centric assembly lines, various uncertainty type used for the data (like fuzzy theory, interval theory, other probability distribution functions than Normal distribution, etc.), multi-objectivity, non-polynomial run times, etc. Considering any of these limitations for the present problem can stand as a future case for research.