1 Introduction

In traditional economic order quantity (EOQ) model, it is assumed that the procurement cost must be paid for the items as soon as the items were received. But in today’s competitive business market, the supplier/retailer will allow a certain period (namely credit period) for settling the amount that the supplier owes to the retailer for the items supplied or the retailer owes to the customer for the items delivered. Before the end of the trade credit period, the retailer can sell the goods and accumulate revenue and earn interest. Also an interest is charged if the payment is not settled at the end of the trade credit period. Therefore, both of the retailer and the customer can take advantages of credit period without any additional charges. In this regard, a large number of models has been developed for inventory replenishment policies involving trade credit policy under varying condition in last few decays.

Goyal (1985) first studied an EOQ model under the conditions of permissible delay in payments. After that Chung (1998) facilitated Goyal’s (1985) exploration for the optimal solution. Again, Shinn et al. (1996) enhanced Goyal’s model considering quantity discount for freight cost. An ordering policy for deteriorating items was developed by Aggarwal and Jaggi (1995) under permissible delay in payments. Shah (1993) explored an EOQ model with constant deterioration rate for the products and also considering delay in payments. Further, Hwang and Shinn (1997) developed a model for determining the retailer’s optimal price and lot-size simultaneously when the supplier gives permission for delay payments and the demand rate is of constant price elasticity. Recently, Das et al. (2013) developed an integrated model for deteriorating items with procurement cost depended credit period.

On literature review, it is seen that most of the research works have been developed in inventory system assuming only one credit period which either the supplier provides to the retailer or the manufacturer provides to the supplier/retailer. But, it may also be happened that a retailer offers a credit period to his/her end customers to draw more attention in purchasing. That means, there exist two level trade credit periods, one of which manufacturer/supplier gives to his/her buyer and the another delay in payment facility is offered by the buyer to his/her customers i.e., both the manufacture/suppler and the buyer can take the advantages of the credit period to increase his/her customers’ demand. Huang (2003) developed a model where the retailer provides a credit period to the end customer. Recently, Shah and Cardenas-Barron (2015) formulated an EOQ for deteriorating items in which a supplier offers a order-linked credit period or cash discount to a retailer and also the retailer offers credit period to a customer. But, by literature survey on credit periods, it is studied that almost all research works have considered that retailer offers credit period to only one end customer. Practically, it is seen that there are so many end customers to purchase the items from the retailer. Ho (2011) established an inventory model with price and credit linked demand where all end customers are allowed to have the same credit during the total cycle. Lashgari et al. (2016) invented an inventory control problem under two levels of trade credit linked to the order quantity with back-ordering and financial considerations. And that’s why in this paper, two level trade credit periods have been considered where all end customers can take the advantages of credit period up-to a limited period. Also, some recent research works on one level or two levels of trade credit financing are Taleizadeh et al. (2008), Taleizadeh et al. (2016), Lashgari et al. (2016), Das et al. (2017) etc.

In our daily life, it is observed that there are so many products which deteriorate naturally as time goes on such as cold drinks, medicine, juice etc. So, the loss of items due to deterioration should not be neglected. Ghare and Schrader (1963) established a model for an exponentially decaying inventory. After that, Covert and Philip (1973) extended Ghare and Schrader’s constant deterioration rate to a two parameter Weibull distribution. Also, an integrated production inventory model was established by Yang and Wee (2003) considering deterioration of items. Again, Mishra and Mishra (2011) worked on fuzzified deterioration under cob-web phenomenon and permissible delay in payment. An EOQ model for perishable items was developed by Taleizadeh and Nematollahi (2014) under back-ordering and delay in payment assuming constant deterioration rate. Other relevant papers related on deterioration are by Taleizadeh et al. (2013a), Taleizadeh (2014), Wu and Chan (2014), Banu and Mondal (2016), Diabat et al. (2017) etc.

Usually, it is seen that most of the researchers have considered different parameters involving in inventory models as either constant or dependent on time or probabilistic in nature for the development of the EOQ model. But, the real business world is full of uncertainties in non-stochastic sense. In such cases, it may happen that some parameters cannot be defined definitely, that means some parameters have a flutter from their ground or could be prescribed orally. To tackle the uncertainties fuzzy set theory has been conceded as an important tool. In this regard, introduction of fuzzy set theory and basic ideas of fuzziness were described by Zimmermann (1991). After that a lot of research works have been conveyed to explore the appliance of fuzzy set theory in inventory models. For example, Maiti and Maiti (2006) discussed fuzzy inventory model with two warehouses under possibility constraints. Mondal and Maiti (2002) and Mahata and Goswami (2007) developed inventory models in the fuzzy sense by considering different parameters as fuzzy parameters. Shekarian et al. (2014) invented a fuzzified version of production model for a single-stage system with defective items and rework where they have assumed rate of defects and the demand rate as fuzzy parameters. Again Kazemi et al. (2015) described the concepts of learning in fuzziness to an EOQ model for imperfect quality. Also some recent works on inventory models in fuzzy sense are Taleizadeh et al. (2010, 2011, 2013b), Kazemi et al. (2010, 2015, 2016a, b), Shekarian et al. (2016, 2017) etc. Now, it is noticed that credit period takes an important role in today’s business concern, but there is no specific rules for assigning the value of a credit period. So, it may be fuzzy in nature. In this regard, Das et al. (2015) developed an integrated model for deteriorating items with fuzzy credit period in multiple sessional markets. Reviewing the literatures, it is seen that fuzziness of the parameters have been tackled by either triangular or trapezoidal or parabolic fuzzy number. That is, linear or non linear membership function has been used separately to remove the fuzziness of the parameters. Till now, there is no consideration of a membership function of fuzzy number by which both linear and non-linear sense have been adopted.

Table 1 Comparison of articles
Full size table

Also from Table 1, it is seen that no researcher has worked on EOQ model for deteriorating items with a demand function considering the duration of offering credit period in fuzzy environment.

In this paper, we have proposed an EOQ model with deteriorating items where the supplier offers a fuzzy credit period to the retailer. The fuzziness of this credit period has been defined as a new fuzzy number known as q-fuzzy number where depending on the value of q the fuzzy number becomes linear or non-linear. Here, the retailer also offers a delay payment facility to all customers up-to a certain duration to settle his/her account. Also, here we have discussed about the model when the retailer gives no credit to the customers. Finally, an algorithm is developed for defuzzification of the fuzzy model and also numerical examples are carried out to illustrate the theoretical results. The rest of this paper is organized as follows: Sect. 2 describes the problem for the model. In Sect. 3, mathematical formulations of the model have been provided. In Sect. 4, numerical examples have been shown to illustrate the model. Section 5, sensitivity analysis and managerial insights have been performed based on the numerical results. Finally, Sect. 6 provides some conclusions and future research direction.

2 Problem description

2.1 Notations

For convenience, the following notations have been used in the development of the proposed inventory model:

  1. (i)

    I(t): the inventory level at time t.

  2. (ii)

    T: the retailer’s replenishment cycle time in years (a decision variable).

  3. (iii)

    A: retailer’s ordering cost per order.

  4. (iv)

    p: retailer’s purchase cost per unit item.

  5. (v)

    s: retailer’s selling price per unit item.

  6. (vi)

    h: retailer’s holding cost per unit per unit time.

  7. (vii)

    \(I_e\): rate of interest earned.

  8. (viii)

    \(I_c\): rate of interest charged for the remaining stock from M to T to the supplier, after offered credit period.

  9. (ix)

    M: the retailer’s trade credit period offered by the supplier in years.

  10. (x)

    N: the customer’s credit period offered by the retailer in years, where \(N\le M\) (a decision variable).

  11. (xi)

    \(\theta\): rate of deterioration.

  12. (xii)

    Q: the retailer’s order quantity.

  13. (xiii)

    D(t): the demand function at time t.

  14. (xiv)

    TP1, TP2: the retailer’s total profit per unit time with and without credit period offered by the retailer respectively.

  15. (xv)

    \(N^*\): customer’s optimal credit period.

  16. (xvi)

    \(T^*\): the retailer’s optimal cycle length.

  17. (xvii)

    \(TP1^*\), \(TP2^*\): the retailer’s optimal profit with and without credit period offered by the retailer respectively.

2.2 Problem definition

In this model, an EOQ inventory model for a supplier and a retailer has been established in infinite time horizon for deteriorating items. Here, the retailer orders Q amount items to the supplier and after receiving the amounts he/she fulfills the demands of his/her customers from the stock during the time period [0, T]. It is assumed that the product is deteriorate at a constant rate. Also here, both the retailer and the supplier offer credit period to his/her customers, one of which is fuzzy and another one is taken as decision variable. But, the retailer offers credit up-to a limited period in which all customers take the facilities and after that no credit period isn’t given by the retailer. Because of credit period, the customers’ demand rate are considered as credit length dependent. Figure 1 shows the retailer’s inventory level for the model. Now to formulate the above described problem the following assumptions have been used.

Fig. 1
figure 1

Retailer’s inventory level

Full size image

2.3 Assumptions

  1. (i)

    The inventory system deals with only one item over infinite time planning horizon.

  2. (ii)

    The replenishment occurs instantaneously at an infinite rate.

  3. (iii)

    Shortages are not allowed.

  4. (iv)

    The items deteriorate at a constant rate of deterioration \(\theta\), where \(0<\theta <1\). There is no repair or replacement of deteriorated units during the planning horizon.

  5. (v)

    Here, two credit periods have been considered in each cycle. One (M) of them is offered by a supplier to the retailer and another one (N) is offered by the retailer to each customer in such a way that each customer must pay within the period of the credit period (M) offered by the supplier to the retailer. It is also assumed that the customer’s credit period is less than or equal to the retailer’s credit period i.e., \(N\le M\).

  6. (vi)

    Practically, it is seen that sometimes credit period offered by supplier changes due to various factors of his/her business policy. So, it is vague in nature. That is why, here the credit period offered by supplier i.e., M has been considered as a q-fuzzy number which is newly defined in this paper discussed in Sect. 3.2.1.

  7. (vii)

    It is assumed that the credit period (M) offered by supplier must be within each replenishment period (T) i.e., \(M\le T\).

  8. (viii)

    Here, it has been assumed that the payments to the supplier is carried out at the end of business cycle. So, the retailer has to pay an interest to the supplier at a rate of \(I_c\) on the remaining amount of stock after the credit period M.

  9. (ix)

    In this model, a retailer intends to offer a credit period (N) to each customer in certain duration to increase his/her demand (D(t)). Practically, it is seen that the longer credit period attracts more customers. So, to increase the length of credit period increases the customers’ demand. Here, the demand function depends on amount of credit period and the duration of the offering credit period. The duration of credit period is proposed in such a way that the last end customer who takes the facility of credit period pay his/her dues at the time of credit period (M) offered by the supplier. Therefore, all end customers take this facility who comes during the period \([0,M-N]\) in each cycle. As \(M-N\) is large, so number of customers take this privilege. That is why, the demand depends on both N and \(M-N\). For these reasons, the demand function D(t) has been considered as a exponential function of time in respect of \(N(M-N)\) which is defined as follows:

    $$\begin{aligned} D(t)=\left\{ \begin{array}{ll} D_0 e^{b_1N(M-N)t}; &{}\text{ when }\qquad \quad 0\le t\le (M-N) \\ D_0e^{b_2N(M-N)^2};&{}\text{ when }\qquad \quad (M-N) \le t\le T \end{array}\right. \end{aligned}$$

    where \(D_0>0\) is a scaling parameter and \(b_1\), \(b_2\) (\(b_1\ge b_2\)) are positive, which are known as effective parameters for credit periods.

3 Model formulation

In this section, we have formulated models considering the retailer’s credit period as crisp and also fuzzy. Also here, we have developed a model considering the case when there is no credit for the end customers. Now, during the period [0, T], the inventory level of the retailer is depleted gradually by demand and deterioration only.

3.1 Crisp model including two level credit periods

The differential equation of the inventory level I(t) at time t for the retailer in each cycle is given by

$$\begin{aligned} \frac{dI(t)}{dt}=-D(t)-\theta {I(t)};\qquad \quad 0\le t\le T \end{aligned}$$
(1)

with the boundary conditions

$$\begin{aligned} I(0)=Q , I(T)=0 \end{aligned}$$

Solving the differential Eq. (1) we get, [see “Appendix 2”]

$$\begin{aligned} I(t)=\left\{ \begin{array}{ll} Qe^{-\theta t}-\frac{D_0}{b_{1}N(M-N)+\theta }\{e^{b_{1}N(M-N)t}-e^{\theta t}\};&{}\text{ when }\quad 0\le t \le (M-N) \\ \frac{D_0}{\theta }e^{b_{2}N(M-N)^2}\{e^{\theta (T-t)}-1\};&{}\text{ when }\quad (M-N) \le t \le T\ \end{array}\right. \nonumber \\ \text{where }\,\,Q=\frac{D_0}{b_{1}N(M-N)+\theta }\left[ e^{(b_{1}N(M-N)+\theta )(M-N)}-1\right] +\frac{D_0}{\theta }e^{b_{2}N(M-N)^2}\left[ e^{\theta T}-e^{\theta (M-N)}\right] \end{aligned}$$
(2)

Retailer’s average sales revenue (ASR) is given by

$$\begin{aligned} ASR &= \frac{s}{T}\int _{0}^{T}D(t)dt\nonumber \\&= \frac{sD_0}{T}\bigg [\int _{0}^{M-N}e^{b_1N(M-N)t}dt+e^{b_2N(M-N)^2}\int _{M-N}^{T}dt\bigg ]\nonumber \\&= \frac{sD_0}{T}\bigg [\frac{e^{b_1N(M-N)^2}-1}{b_1N(M-N)}+(T-M+N)e^{b_2N(M-N)^2}\bigg ] \end{aligned}$$
(3)

Retailer’s average purchase cost (APC) is given by

$$\begin{aligned} APC&= \frac{p}{T}I(0)\nonumber \\&= \frac{pQ}{T}\nonumber \\&= \frac{pD_0}{T}\bigg [\frac{e^{(b_{1}N(M-N)+\theta )(M-N)}-1}{b_{1}N(M-N)+\theta }+e^{b_{2}N(M-N)^2}\frac{e^{\theta T}-e^{\theta (M-N)}}{\theta }\bigg ]\ \end{aligned}$$
(4)

Retailer’s average ordering cost (AOC) is given by

$$\begin{aligned} AOC=\frac{A}{T} \end{aligned}$$
(5)

Retailer’s average holding cost (AHC) is given by

$$\begin{aligned} AHC&= \frac{h}{T}\int _{0}^{T}I(t)dt\nonumber \\&= \frac{h}{T}\int _{0}^{M-N}\bigg [Qe^{-\theta t}-\frac{D_0}{b_{1}N(M-N)+\theta }\left\{ e^{b_{1}N(M-N)t}-e^{\theta t}\right\} dt\bigg ] +\frac{hD_0}{T\theta }\int _{M-N}^{T}e^{b_{2}N(M-N)^2}\left\{ e^{\theta (T-t)}-1\right\} dt\nonumber \\&= \frac{h}{T}\bigg [\frac{Q}{\theta }\left( 1-e^{-\theta (M-N)}\right) -\frac{D_0}{b_1N(M-N)+\theta }\left\{ \frac{e^{b_1N(M-N)^2}-1}{b_1N(M-N)}+\frac{e^{-\theta (M-N)}}{\theta }\right\} \nonumber \\ &\quad +\frac{D_0}{\theta }e^{b_2N(M-N)^2}\bigg \{\frac{e^{\theta (T-M+N)}-1}{\theta }-T+M-N\bigg \}\bigg ]\ \end{aligned}$$
(6)

Retailer’s average interest earned (AIE) is given by

$$\begin{aligned} AIE&= \frac{sI_e}{T}\bigg [\int _{0}^{M-N}[T-(t+N)]D(t)dt+\int _{M-N}^{T}(T-t)D(t)dt\bigg ]\nonumber \\&= \frac{sI_eD_0}{T}\bigg [\int _{0}^{M-N}[T-(t+N)]e^{b_1N(M-N)t}dt+e^{b_2N(M-N)^2}\int _{M-N}^{T}(T-t)dt\bigg ]\nonumber \\&= \frac{sI_eD_0}{T}\bigg [(T-N)\int _{0}^{M-N}e^{b_1N(M-N)t}dt-\int _{0}^{M-N}te^{b_1N(M-N)t}dt+e^{b_2N(M-N)^2}\int _{M-N}^{T}(T-t)dt\bigg ]\nonumber \\&= \frac{sI_eD_0}{T}\bigg [\frac{T-N}{b_1N(M-N)}[e^{b_1N(M-N)^2}-1] -\frac{(M-N)e^{b_2N(M-N)^2}}{b_1N(M-N)}+\frac{1}{[b_1N(M-N)]^2}[e^{b_1N(M-N)^2}-1]\nonumber \\&\quad +e^{b_2N(M-N)^2}\bigg \{T^2-\frac{T^2}{2}-T(M-N)+\frac{(M-N)^2}{2}\bigg \}\nonumber \\&= \frac{sI_eD_0}{T[b_1N(M-N)]}\bigg [\left\{ T-N+\frac{1}{b_1N(M-N)}\right\} \{e^{b_1N(M-N)^2}-1\}-(M-N)e^{b_1N(M-N)^2}\bigg ]\nonumber \\&\quad +\frac{sI_eD_0}{2T}e^{b_2N(M-N)^2}(T-M+N)^2.\ \end{aligned}$$
(7)

Retailer’s average interest charged (AIC) is given by

$$\begin{aligned} AIC&= \frac{pI_c}{T}\int _{M}^{T}I(t)dt\nonumber \\&= \frac{pI_cD_0}{\theta T}\int _{M}^{T}e^{b_2N(M-N)^2}[e^{\theta (T-t)}]dt\nonumber \\&= \frac{pI_cD_0}{\theta T}e^{b_2N(M-N)^2}{\bigg [-\frac{e^{\theta (T-t)}}{\theta }-t\bigg ]_M}^T\nonumber \\&= \frac{pI_cD_0}{\theta T}e^{b_2N(M-N)^2}\bigg [\frac{1}{\theta }-T+e^{\theta (T-M)+M}\bigg ]\nonumber \\&= \frac{pI_cD_0}{T\theta }e^{b_2N(M-N)^2}\bigg [\frac{e^{\theta (T-M)}}{\theta }+M-T\bigg ]\ \end{aligned}$$
(8)

Therefore the retailer’s average total profit TP1(N, T) is given by

$$\begin{aligned} TP1(N,T)&= ASR-APC-AHC-AIC+AIE-AOC\nonumber \\&= \frac{D_0}{T}\bigg [\frac{e^{b_1N(M-N)^2}-1}{b_1N(M-N)}+(T-M+N)e^{b_2N(M-N)^2}\bigg ]-\frac{pQ}{T}\nonumber \\&\quad -\frac{h}{T}\bigg [\frac{Q}{\theta }(1-e^{-\theta (M-N)}) -\frac{D_0}{b_1N(M-N)}\left\{ \frac{e^{b_1N(M-N)^2}-1}{b_1N(M-N)} +\frac{e^{-\theta (M-N)}}{\theta }\right\} \nonumber \\&\quad +\frac{D_0}{\theta }e^{b_2N(M-N)^2}\bigg \{\frac{e^{\theta (T-M+N)}-1}{\theta }-T+M-N\bigg \}\bigg ]-\frac{pI_cD_0}{T\theta }e^{b_2N(M-N)^2}\bigg [\frac{e^{\theta (T-M)}}{\theta }+M-T\bigg ]\nonumber \\&\quad +\frac{sI_eD_0}{T[b_1N(M-N)]}\bigg [\left\{ T-N+\frac{1}{b_1N(M-N)}\right\} \{e^{b_1N(M-N)^2}-1\}-(M-N)e^{b_1N(M-N)^2}\bigg ]\nonumber \\&\quad +\frac{sI_eD_0}{2T}e^{b_2N(M-N)^2}(T-M+N)^2-\frac{A}{T}\ \end{aligned}$$
(9)

3.2 Fuzzy model including two level credit periods

According to assumption (vi), the supplier offers a fuzzy credit period \((\tilde{M})\) to the retailer. Here, the credit period \((\tilde{M})\) is represented in two different forms such as linear fuzzy number and non-linear fuzzy number. Therefore, due to fuzzy credit period \((\tilde{M})\), the optimum profit function TP1(N, T) will be different for different values of M with some degree of belongingness. Therefore, the profit function will be fuzzy in nature and is denoted by \(TP1_{(N,T)}\tilde{(M)}\), where

$$\begin{aligned} TP1_{(N,T)}\tilde{(M)}&= \frac{D_0}{T}\bigg [\frac{e^{b_1N(\tilde{M}-N)^2}-1}{b_1N(\tilde{M}-N)}+(T-\tilde{M}+N)e^{b_2N(\tilde{M}-N)^2}\bigg ]-\frac{pQ}{T}\nonumber \\&\quad -\frac{h}{T}\bigg [\frac{Q}{\theta }(1-e^{-\theta (\tilde{M}-N)})-\frac{D_0}{b_1N(\tilde{M}-N)}\left\{ \frac{e^{b_1N(\tilde{M}-N)^2}-1}{b_1N(\tilde{M}-N)}+\frac{e^{-\theta (\tilde{M}-N)}}{\theta }\right\} \nonumber \\&\quad +\frac{D_0}{\theta }e^{b_2N(\tilde{M}-N)^2}\bigg \{\frac{e^{\theta (T-\tilde{M}+N)}-1}{\theta }-T+\tilde{M}-N\bigg \}\bigg ]-\frac{pI_cD_0}{T\theta }e^{b_2N(\tilde{M}-N)^2} \bigg [\frac{e^{\theta (T-\tilde{M})}}{\theta }+\tilde{M}-T\bigg ]\nonumber \\&\quad +\frac{sI_eD_0}{T[b_1N(\tilde{M}-N)]}\bigg [\left\{ T-N+\frac{1}{b_1N(\tilde{M}-N)}\right\} \{e^{b_1N(\tilde{M}-N)^2}-1\}-(\tilde{M}-N)e^{b_1N(\tilde{M}-N)^2}\bigg ]\nonumber \\&\quad +\frac{sI_eD_0}{2T}e^{b_2N(\tilde{M}-N)^2}(T-\tilde{M}+N)^2-\frac{A}{T}.\ \end{aligned}$$
(10)

3.2.1 q-fuzzy number

Recently, in the most business concern, it is seen that offering of a credit period has an important role to run the business smoothly. In this paper, the supplier offers a credit period (M) to the retailer. It is also observed that due to existence of different factors involved with the real business world, it is comprised with uncertainties in non-stochastic sense which leads to estimation of different parameters as fuzzy numbers. Since, there does not exist any specific rules for assigning a credit period, hence at different times its amount may be different. Basically, this is completely own strategy of supplier. In that sense, it is not a deterministic value. So here, it has been considered as fuzzy number (\(\tilde{M}\)). Now, to remove the uncertainty of the fuzzy parameter, different types of fuzzy number have been used like as triangular, trapezoidal, parabolic etc whose membership functions are either linear or non-linear. But on literature review, it is seen that separate membership functions have been used to represent different fuzzy numbers. There is no single representation of a membership function by which both the linear and non-linear uncertainties can be studied. That is why here, a new fuzzy number has been introduced as q-fuzzy number which is defined as follows:

Definition

The q-fuzzy number \(\tilde{M}\) is represented in the form of \((M_1, M_2, M_3; W, q)\), i.e., \(\tilde{M}=(M_1, M_2, M_3; W, q)\) whose the membership function denoted by \(\mu _{\tilde{M}}(x)\) is defined as follows:

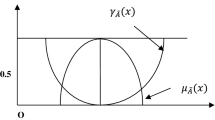
$$\begin{aligned} \mu _{\tilde{M}}(x) =\left\{ \begin{array}{ll} W(\frac{x-M_1}{M_2-M_1})^q;&{}\text{ if }\,\,M_1\le x \le M_2 \\ W(\frac{M_3-x}{M_3-M_2})^q; &{}\text{ if }\,\,M_2\le x \le M_3\\ 0; &{}\text{ otherwise }\ \end{array}\right. \end{aligned}$$

where W is the height of this fuzzy number, the linearity and non-linearity of the membership function, \(\mu _{\tilde{M}}(x)\) depend on the value of q. When \(q=1\), \(\mu _{\tilde{M}}(x)\) be linear, otherwise it be non-linear. So, by this consideration we can easily represent a fuzzy number as linear or non-linear just changing the value of q and also for this, numerical calculations can be easily handled regarding fuzzy number. Figure 2 shows the representation of the q-fuzzy number.

Fig. 2
figure 2

q-fuzzy number \(\tilde{M}\)

Full size image

Here, we have considered the fuzzy number \(\tilde{M}\) as normal fuzzy number i.e., here \(W=1\).

Theorem 1

The centroid value\((M^*)\)ofq-fuzzy number\(\tilde{M}\)is given by

$$\begin{aligned} M^*=(M_1+M_3-M_2)+\frac{q+1}{q+2}(2M_2-M_1-M_3) \end{aligned}$$
(11)

Proof

We know, the centroid value is formulated as

$$\begin{aligned} M^*&= \frac{\int _{-\infty }^{\infty }x\mu _{\tilde{M}}(x)dx}{\int _{-\infty }^{\infty }\mu _{\tilde{M}}(x)dx} \end{aligned}$$

Now,

$$\begin{aligned} \int _{-\infty }^{\infty }x\mu _{\tilde{M}}(x)dx &= \int _{M_1}^{M_2} x\left( \frac{x-M_1}{M_2-M_1}\right) ^qdx+\int _{M_2}^{M_3} x\left( \frac{M_3-x}{M_3-M_2}\right) ^qdx\\ &= \frac{1}{q+1}(M_3-M_1)(M_3+M_1-M_2)+\frac{1}{q+2}(M_3-M_1)(2M_2-M_1-M_3) \end{aligned}$$

Again,

$$\begin{aligned} \int _{-\infty }^{\infty }\mu _{\tilde{M}}(x)dx &= \int _{M_1}^{M_2} \left( \frac{x-M_1}{M_2-M_1}\right) ^qdx+\int _{M_2}^{M_3} \left( \frac{M_3-x}{M_3-M_2}\right) ^qdx\\ &= \frac{1}{q+1}(M_3-M_1) \end{aligned}$$

[Detailed calculation shown in “Appendix 3”].

Now,

$$\begin{aligned} M^* &= \frac{\frac{1}{q+1}(M_3-M_1)(M_3+M_1-M_2)+\frac{1}{q+2}(M_3-M_1)(2M_2-M_1-M_3)}{\frac{1}{q+1}(M_3-M_1)}\\ &= (M_1+M_3-M_2)+\frac{q+1}{q+2}(2M_2-M_1-M_3) \end{aligned}$$

[Detailed calculation shown in “Appendix 3”].

Therefore, the centroid value, \(M^*=(M_1+M_3-M_2)+\frac{q+1}{q+2}(2M_2-M_1-M_3)\).

Using the extension principle in fuzzy set theory, the membership function of \(TP1_{(N,T)}(\tilde{M})\), denoted by \(\mu _{TP1_{\tilde{M}}}(y)\) can be obtained as

$$\begin{aligned} \mu _{TP1_{\tilde{M}}}(y) =\left\{ \begin{array}{ll} \sup \limits _{x\in TP1_{(N,T)}^{-1}(y)}\mu _{\tilde{M}}(x); &{}\,\text{ if }\,\,y=TP1_{(N,T)}(x)\,\, and \,\, TP1_{(N,T)}^{-1}(y)\ne \phi \\ 0; &{}\,\,\text{ if }\,\, y=TP1_{(N,T)}(x) \,\,and \,\, TP1_{(N,T)}^{-1}(y)=\phi \\ \end{array}\right. \end{aligned}$$

i.e.,

$$\begin{aligned} \mu _{TP1_{\tilde{M}}}(y) =\left\{ \begin{array}{ll} \left( \frac{TP1_{(N,T)}^{-1}(y)-M_1}{M_2-M_1}\right) ^q &{} \text{ if }\,\, y_1\le y \le y_2 \\ \left( \frac{M_3-TP1_{(N,T)}^{-1}(y)}{M_3-M_2}\right) ^q &{}\text{ if }\,\,y_2\le y \le y_3\\ 0; &{}\text{ otherwise }\ \end{array}\right. \end{aligned}$$

where \(y_1=TP1_{(N,T)}(M_1)\), \(y_2=TP1_{(N,T)}(M_2)\),\(y_3=TP1_{(N,T)}(M_3)\).

Now, according to Theorem 1 the centroid value of \(TP1_{(N,T)}(\tilde{M})\) denoted by \(CV_{TP1}\) can be determined as follows:

$$\begin{aligned} CV_{TP1} &= \frac{\int _{-\infty }^{\infty }y\mu _{TP_{\tilde{M}}}(y)dy}{\int _{-\infty }^{\infty }\mu _{TP_{\tilde{M}}}(y)dy}\nonumber \\ i.e., CV_{TP1} &= (y_1+y_3-y_2)+\frac{q+1}{q+2}(2y_2-y_1-y_3)\ \end{aligned}$$
(12)

\(\square\)

3.2.2 Defuzzification algorithm

To get the defuzzified value of the fuzzy profit in proposed model with fuzzy credit the following steps are necessary:

  1. Step 1:

    At first get the expression for crisp profit TP1(N, T).

  2. Step 2:

    Input the values of the associated crisp parameters of the model.

  3. Step 3:

    Again input the values of \(M_1\), \(M_2\), \(M_3\) of fuzzy credit period \(\tilde{M}=(M_1, M_2, M_3; W, q)\).

  4. Step 3:

    Calculate the value of \(y_1\), \(y_2\) and \(y_3\) where \(y_1=TP1_{(N,T)}(M_1)\), \(y_2=TP1_{(N,T)}(M_2)\), \(y_3=TP1_{(N,T)}(M_3)\).

  5. Step 4:

    Calculate the centroid value \(CV_{TP1}\) of \(TP1_{(N,T)}(\tilde{M})\) according to formula (12) which is defuzzified value of the fuzzy profit \(TP1_{(N,T)}(\tilde{M})\).

3.3 Crisp model including one level credit period when no credit period is offered by the retailer

In this case, we assume that the retailer offers no credit period to the customers i.e., \(N=0\). So, here the demand function becomes constant and total profit TP2 becomes only function of T. Thus the retailer’s model for constant demand when the retailer offers no credit period to the customers will be formed when \(N\rightarrow 0\). Therefore, following will be hold:

Retailer’s average sales revenue is given by Eq. (3) as follows:

$$\begin{aligned} ASR1 &= \lim _{N \rightarrow 0} \frac{sD_0}{T}\bigg [\frac{e^{b_1N(M-N)^2}-1}{b_1N(M-N)}+(T-M+N)e^{b_2N(M-N)^2}\bigg ]\\ &= \frac{sD_0}{T}\bigg [\lim _{N \rightarrow 0}\frac{e^{b_1N(M-N)^2}-1}{b_1N(M-N)}+\lim _{N \rightarrow 0}(T-M+N)e^{b_2N(M-N)^2}\bigg ]\\ &= sD_0 \end{aligned}$$

Retailer’s average purchase cost is given by Eq. (4) as follows:

$$\begin{aligned} APC1 &= \lim _{N \rightarrow 0}\frac{pD_0}{T}\bigg [\frac{e^{(b_{1}N(M-N)+\theta )(M-N)}-1}{b_{1}N(M-N)+\theta }+e^{b_{2}N(M-N)^2}\frac{e^{\theta T}-e^{\theta (M-N)}}{\theta }\bigg ]\\ &= \frac{pD_0}{T}\bigg [\lim _{N \rightarrow 0}\frac{e^{(b_{1}N(M-N)+\theta )(M-N)}-1}{b_{1}N(M-N)+\theta }+\lim _{N \rightarrow 0}e^{b_{2}N(M-N)^2}\frac{e^{\theta T}-e^{\theta (M-N)}}{\theta }\bigg ]\\ &= \frac{pD_0}{T}\left[ \frac{e^{\theta T}-1}{\theta }\right] \end{aligned}$$

Retailer’s average holding cost is given by Eq. (6) as follows:

$$\begin{aligned} AHC1 &= \lim _{N \rightarrow 0}\frac{h}{T}\bigg [\frac{Q}{\theta }(1-e^{-\theta (M-N)})-\frac{D_0}{b_1N(M-N)+\theta } \left\{ \frac{e^{b_1N(M-N)^2}-1}{b_1N(M-N)}+\frac{e^{-\theta (M-N)}}{\theta }\right\} \\&+\frac{D_0}{\theta }e^{b_2N(M-N)^2}\bigg \{\frac{e^{\theta (T-M+N)}-1}{\theta }-T+M-N\bigg \}\bigg ]\\&=\frac{hD_0}{\theta }\bigg [\frac{e^{\theta T}-1}{\theta T}-1\bigg ] \end{aligned}$$

Retailer’s average interest earned is given by Eq. (7) as follows:

$$\begin{aligned} AIE1 &= \lim _{N \rightarrow 0}\bigg [\frac{sI_eD_0}{T[b_1N(M-N)]} \bigg [\left\{ T-N+\frac{1}{b_1N(M-N)}\right\} \{e^{b_1N(M-N)^2}-1\}-(M-N)e^{b_1N(M-N)^2}\bigg ]\\&\quad +\frac{sI_eD_0}{2T}e^{b_2N(M-N)^2}(T-M+N)^2\bigg ]\\ &= \lim _{N \rightarrow 0}\frac{sI_eD_0}{T[b_1N(M-N)]} \bigg [\left\{ T-N+\frac{1}{b_1N(M-N)}\right\} \{e^{b_1N(M-N)^2}-1\}-(M-N)e^{b_1N(M-N)^2}\bigg ]\\&\quad +\lim _{N \rightarrow 0}\frac{sI_eD_0}{2T}e^{b_2N(M-N)^2}(T-M+N)^2\\ &= \frac{sIeD_0T}{2} \end{aligned}$$

Retailer’s average interest charged is given by Eq. (8) as follows:

$$\begin{aligned} AIC1 &= \lim _{N \rightarrow 0}\frac{pI_cD_0}{T\theta }e^{b_2N(M-N)^2}\bigg [\frac{e^{\theta (T-M)}-1}{\theta }+M-T\bigg ]\\ &= \frac{pI_cD_0}{T\theta }\bigg [\frac{e^{\theta (T-M)}-1}{\theta }+M-T\bigg ] \end{aligned}$$

Therefore, the retailer’s average total profit for constant demand is as follows:

$$\begin{aligned} TP2(T) &= ASR1-APC1-AHC1-AIC1+AIE1-AOC\nonumber \\ &= sD_0-\frac{pD_0}{T}\left[ \frac{e^{\theta T}-1}{\theta }\right] -\frac{hD_0}{\theta }\bigg [\frac{e^{\theta T}-1}{\theta T}-1\bigg ]-\frac{pI_cD_0}{T\theta }\bigg [\frac{e^{\theta (T-M)}-1}{\theta }+M-T\bigg ]\nonumber \\&\quad +\frac{sIeD_0T}{2}-\frac{A}{T}\ \end{aligned}$$
(13)

Theorem 2

The profit functionTP2(T) satisfies the optimality condition analytically when the retailer offers no credit to customers provided that\(h+pI_c+p\theta -sI_e>0\).

Proof

Naturally, the rate of deterioration \(\theta\) is usually very small. So, by the Taylor series expansion for the exponential term, we have

$$\begin{aligned} e^{\theta T} &= 1+\theta T+\frac{\theta ^2 T^2}{2}\\ e^{\theta (T-M)} &= 1+\theta (T-M)+\frac{\theta ^2 (T-M)^2}{2}. \end{aligned}$$

Using the above approximation, the total profit function TP2(T) can be written as

$$\begin{aligned} TP2(T)=sD_0+\frac{sI_eD_0T}{2}-pD_0(1+\frac{\theta T}{2})-\frac{pI_cD_0}{2}(T-2M+\frac{M^2}{T})-\frac{hD_0T}{2}-\frac{A}{T} \end{aligned}$$
(14)

The necessary condition for optimality condition of Eq. (14) is \(\frac{dTP2(T)}{dT}=0\) [see “Appendix 3”], which gives,

$$\begin{aligned} \frac{D_0}{2}\left[sI_e-p\theta -pI_c\left(1-\frac{M^2}{T^2}\right)\right]-\frac{hD_0}{2}+\frac{A}{T^2}=0 \end{aligned}$$

This equation gives the optimal value of T,

$$\begin{aligned} T^* &= \sqrt{\frac{pI_cD_0M^2+2A}{(h+pI_c+p\theta -sI_e)D_0}} \text{ provided } \text{ that } h+pI_c+p\theta -sI_e>0 \end{aligned}$$

Now, the second order derivative of Eq. (14) at \(T=T^*\) is given by [see “Appendix 3”]

$$\begin{aligned} \frac{d^2TP2(T)}{dT^2}=-\frac{pI_cD_0M^2+2A}{T^{*3}}<0 \end{aligned}$$

Therefore TP2(T) is a concave function of T which shows that the profit function TP2(T) is optimum. So, \(T^*\) is the optimal value of T. \(\square\)

4 Numerical illustrations

To illustrate the above model, the following numerical examples have been considered.

4.1 Result for crisp model with exponential demand including two level credit period

Problem 1

Pal and Sons’ company supplies ready-made garments to a retailer according to the retailer’s requirement. For per unit item, the company takes \(\$10\) from the retailer. But the company gives 0.16 year time relaxation for the payment of the purchasing amount. In this business system, the retailer pays his/her all dues at the end of replenishment cycle and for this reason, the company charges an interest at a rate of \(8\%\) of the remaining stock after the delay period. The retailer bears a cost \(\$2\) for per unit price to hold the products at a rented house. The items are deteriorate at a rate of \(5\%\). After getting the time relaxation, the retailer also offers same credit N to all his/her customers up-to a limited period such that all the customers must pay their dues within the retailer’s time relaxation period. The retailer accumulates sales revenue at a rate of \(4\%\). The retailer pays \(\$500\) for ordering the products to the supplier. Here, the retailer’s objective is to maximize the total profit. Find also the optimal replenishment cycle length and the optimal credit period N offered by the retailer.

Solution

The values of the parameters regarding the problem are as follows in their appropriate units:

\(b_1=10\), \(b_2=5\), \(A=500\), \(D_0=1000\), \(\theta =0.05\), \(s=20\), \(p=10\), \(h=2\), \(M=0.16\); \(I_e=0.04\), \(I_c=0.08\).

Fig. 3
figure 3

Concavity of TP1

Full size image

Since the objective function TP1 of the proposed model is highly non-linear, therefore this cannot be optimized analytically. So, the standard Lingo software has been used to get the optimum solution. From Fig. 3, it has been shown that TP1 is a concave function of N and T. This implies that for these parametric values we get the optimum results. The obtained optimal results are as follows:

the optimal credit period of the customers: \(N^*=0.0482\) years, the optimal cycle length: \(T^*=0.6326\) years, the maximum profit: \(TP1^*=\$8542.38\).

Fig. 4
figure 4

N versus TP1

Full size image

Now, the question is why we take N as a decision variable or if we increase the value of N, is there any possibility to increase the value of TP1? According to assumption (ix), we see that the demand is function of both the credit period N which is offered by the retailer and the duration of the offering credit period, \(M-N\). So, if we increase N then for fixed M the length \(M-N\) decreases. This shows that for large N (\(<M\)), the length \(M-N\) becomes too small. On other hand, lower value of N increases the length \(M-N\). That is, the demand will be more when both effects of N and \(M-N\) will be maximum. Thus higher value of N is not always responsible to increase the profit. This phenomena has been shown in Fig. 4. This figure shows that we get a optimum value of N to get the optimum value of TP1.

4.2 Result for crisp model when no credit period is offered by the retailer

Problem 2

The problem is same as Problem-1 except here, the retailer does not offer any credit period to the customers i.e., here for this problem \(N=0\).

Solution

Using Lingo software, we have the following optimal results when the retailer offers no credit to the customers, the optimum cycle length for the business period \(T^*=0.6309\) years and the retailer’s optimum profit \(TP2^*=\$8521.16\) which satisfy Theorem 2, the required optimality condition.

Table 2 Results for different values of \(b_1\)
Full size table

From the above two results for Problems 1 and 2, it can be seen that the model with exponential demand including two level credit periods is more profitable than the model including one level credit period when the retailer offers no credit period to the customers for the above parametric values. But, is the model offering credit period by the retailer always profitable than the model offering no credit period to the customers by the retailer? For this regard, we discuss the nature of effective parameters \(b_1\) and \(b_2\). Now, it is seen that for offering no credit period to the customers the demand function becomes constant and for this reason there have no effect of the effective parameters. On other hand, for exponential demand considering two level credit periods we consider the value \(b_1=10\) and \(b_2=5\). Now from Table 2, we see that if the value of effective parameters be \(b_1=3\) and \(b_2=1\) then the optimum profit \(TP1^*=8521.71\) which is same as \(TP2^*\) though for this case the retailer offers a credit to the customers. So, it can be concluded that not only the customers’ credit period but also the effective parameters are responsible to increase the retailer’s total profit.

4.3 Result for fuzzy model with exponential demand including two level credit period

Problem 3

The problem is same as Problem-1 except the credit period (M) offered by the supplier. In this problem, it is considered as a q-fuzzy number such as \((\tilde{M})=(0.11,0.16,0.22;1,q)\).

Table 3 Optimal results for the fuzzy model
Full size table

Solution

For this problem, all values of the parameters involved in the system are same as the Problem-1 except the retailer’s credit period (M) offered by the supplier. In this problem, M has been considered as q-fuzzy number \((\tilde{M})=(M_1,M_2,M_3;W,q)\) where \(M_1=0.11\), \(M_2=0.16\), \(M_3=0.22\), \(W=1\) and for q, we have shown the result taking \(q=1\), \(q=2\) and \(q=3\). In this paper, the membership function of \(\tilde{M}\) has been defined newly in such a way that depending on the value of parameter q, the membership function shows different types: linear and non-linear. That is, when \(q=1\) it becomes linear fuzzy number known as triangular fuzzy number, otherwise it is non-linear. The optimum results of this fuzzy model have been shown in Table 3.

From Table 3, it is noted that the objective value \(CV_{TP1}\) is less for \((\tilde{M})=(0.11,0.16,0.22;1,2)\) and \((\tilde{M})=(0.11,0.16,0.22;1,3)\) than the objective value \(CV_{TP1}\) for \((\tilde{M})=(0.11,0.16,0.22;1,1)\). Again, it is also observed that for non-linear fuzzy number \(CV_{TP1}\) is less for higher value of q that means higher degree of non-linearity gives less result than the lower one. Now, what is the reason for this difference though they have same spread? The reason of this difference is the centroid values of these two fuzzy numbers. Since the centroid value of the fuzzy number \((\tilde{M})=(0.11,0.16,0.22;1,1)\) is \(M^*=0.1633\) which is higher than \(M^*= 0.1625\) for the fuzzy number \((\tilde{M})=(0.11,0.16,0.22;1,2)\) and \(M^*= 0.1620\) for the fuzzy number \((\tilde{M})=(0.11,0.16,0.22;1,3)\). So, it can be concluded that higher centroid value of \(M^*\) is responsible for the maximum objective value. And that is why \(CV_{TP1}\) be greater for \((\tilde{M})=(0.11,0.16,0.22;1,1)\) than for \((\tilde{M})=(0.11,0.16,0.22;1,2)\) and \((\tilde{M})=(0.11,0.16,0.22;1,3)\) which is discussed in sensitivity analysis section.

4.4 Result for fuzzy model when no credit is offered by the retailer

Problem 4

The problem is same as Problem-2 when supplier’s offered credit period is a q-fuzzy number \((\tilde{M})=(0.11,0.16,0.22; W,q)\) and the retailer offers no credit to the customers.

Table 4 Optimal results for the fuzzy model when \(N=0\)
Full size table

Solution

For this problem also, all values of the parameters involved in the system are same as the Problem-2 except the retailer’s credit period (M) offered by the supplier. The obtained results for this model taking \(q=1,2,3\) are shown in Table 4.

Table 4 also shows the same results as previous though the differences between different values of \(CV_{TP2}\) for \(q=1,2,3\) are so small.

Now, in fuzzy environment from the above results, it is also seen that the case when the retailer offers credit to the customers is more profitable. The different results for different values of \(M^*\) are discussed in sensitivity analysis section.

Table 5 Results for Problem-3 when \(q=1\)
Full size table
Table 6 Results for Problem-3 when \(q=2\)
Full size table
Table 7 Results for Problem-4 when \(q=1\)
Full size table
Table 8 Results for Problem-4 when \(q=2\)
Full size table
Table 9 Effect of changes in different parameters
Full size table

Now, in order to analyze the effects of different parameters on the fuzzy and crisp model a sensitivity analysis has been carried out in Tables 2, 5, 6, 7, 8 and 9.

5 Sensitivity analysis and managerial insights

Fig. 5
figure 5

\(\theta\) versus N

Full size image
Fig. 6
figure 6

\(\theta\) versus T

Full size image
Fig. 7
figure 7

M versus N

Full size image
Fig. 8
figure 8

M versus T

Full size image

Now, in order to analyze the effects of different parameters on the optimal solutions of the fuzzy and crisp model sensitivity analysis have been carried out for the case mainly when the retailer offers credit period. The following deduction can be drawn from Tables 2, 5, 6, 7, 8 and 9 and from the Figs. 5, 6, 7 and 8.

  1. 1.

    Now, from Table 5 it is observed that with increase of the difference \(\Delta =\Delta _2-\Delta _1\) where \(\Delta _1=M_2-M_1\) and \(\Delta _2=M_3-M_2\), the centroid value (\(M^*\)) of the fuzzy credit period increases. Also it is seen that the optimal cycle length \((T^*)\), the optimal customers’ credit period \((N^*)\) and the centroid value of the fuzzy profit (i.e., \(CV_{TP1}\)) all are directly proportional to \(M^*\). Again, it is also seen that the centroid value i.e., \(CV_{TP1}\) is higher with respect to the total profit \(TP1^*\). It is noted that Table 6 is showing the same phenomena as Table 5. Again, it is noted that Tables 7 and 8 are showing the same characteristics as Table 5 discussed in earlier except that in these cases the total profit \(TP2^*\) is higher than the centroid value \(CV_{TP2}\).

  2. 2.

    Comparing Tables 5 and 6, it is observed that at beginning of the Table 6 the values of \(M^*\) and \(CV_{TP1}\) are greater than the corresponding values in Table 5. But this phenomena is reversed at the end of the tables i.e., the values of \(M^*\) and \(CV_{TP1}\) in Table 6 are less than the corresponding values in Table 5. Now, the question is why the results have this opposite phenomena. From Tables 5 and 6, it is noted that at beginning of Table 5, \(\Delta _1(=M_2-M_1)\) is greater than \(\Delta _2(=M_3-M_2)\) i.e., left spread is greater than right spread and then at the end, \(\Delta _2(=M_3-M_2)\) is greater than \(\Delta _1(=M_2-M_1)\) i.e., right spread is greater than left spread. So, it is concluded that depending on the longer tail of the fuzzy numbers \((M_1, M_2, M_3; 1, 1)\) and \((M_1, M_2, M_3; 1, 2)\) either Table 5 or 6 gives the greater results. That is, the profit be maximum with q-fuzzy number for \(q=1\) than \(q=2\) when right tail be longer than left tail.

  3. 3.

    Table 9 shows the results for the changes of the different parameters for the fuzzy model. Now, it is observed that higher value of \(b_1\) implies less customers’ credit and cycle length but more profit. Also, it is concluded that when deterioration rate increases then cycle length, customers’ credit and profit all decrease. Again, from Table 9 it is seen that higher rate of ordering cost increases the customers’ credit and cycle length but decreases the profit. So, the retailer should keep a watch on the ordering cost.

  4. 4.

    Figures 5 and 6 plot the graph of optimal credit period and the cycle length with respect to deterioration rate for the crisp model which shows that both the cycle length and the credit period decrease gradually when the deterioration rate increases and this is obvious case.

  5. 5.

    Again from Table 2 for the crisp model, it is observed that for fixed value of \(b_2\), the customers’ credit period and the total profit increase, but the total business cycle length decreases with the increase of the effective parameter \(b_1\).

  6. 6.

    Now, Figs. 7 and 8 show the graphical representations of the customers’ credit period and the cycle length with respect to the retailer’s credit period respectively. From the figures it is observed that if the retailer gains more credit from the supplier then he is able to offer more credit to the customers and also the total business period increases with the higher value of M. As it is seen that credit period affects a positive impact on profit, so getting more credit one would like to offer more credit to his customers to increase his demand to get maximum profit. So, this phenomena is obvious.

6 Conclusion

This paper considers an EOQ model for deteriorating items with two level credit periods, one of which is offered by the supplier to the retailer and the another one is offered by the the retailer to the customers. Also, this paper counters the retailer’s credit period as fuzzy parameter and the customers’ credit period as the decision variable. Again introducing q-fuzzy number, we have discussed both types of linear and non-linear membership functions by a single representation for the fuzzy parameter. And depending on the value of q, we can change the degree of non-linearity of membership function. Further, we have illustrated the model without consideration of the customers’ credit period. The result section shows the crisp as well as fuzzy results for the both cases and also compares the results with respect to consideration of customers’ credit period. Also, some sensitivity analysis are given both for the fuzzy and crisp models. The numerical examples amplify that (1) customers’ credit period have a good impact to increase the retailer’s profit. (2) For the fuzzy model with q-fuzzy number, the retailer’s profit be maximum considering \(q=1\) than \(q=2\) when right tail of the fuzzy number be longer than the left tail. (3) The retailer should maintain the ordering cost to get maximum profit. (4) The retailer should keep watch on both the credit periods.

Now, by the q-fuzzy number, for \(q=1\), we can study the linear uncertainty which is same as triangular fuzzy number and for \(q>1\), this shows different degree of non-linear uncertainties. Therefore in this model, linear uncertainty such as trapezoidal fuzzy number cannot be studied. Further, one can study upon this limitation of this paper and also this model can be studied in different ways like considering pricing strategy, different demand structure, quantity discounts, incorporate inflation rate on various cost and others.