A fuzzy collaborative intelligence approach for estimating future yield with DRAM as an example

Abstract

To increase the ecological sustainability of manufacturing, enhancing the yield of each product is a critical task that eliminates waste and increases profitability. An equally crucial task is to estimate the future yield of each product so that the majority of factory capacity can be allocated to products that are expected to have higher yields. To this end, a fuzzy collaborative intelligence (FCI) approach is proposed in this study. In this FCI approach, a group of domain experts is formed. Each expert constructs an artificial neural work (ANN) to fit an uncertain yield learning process for estimating the future yield with a fuzzy value; in past studies, however, uncertain yield learning processes were modeled only by solving mathematical programming problems. In this research, fuzzy yield estimates from different experts were aggregated using fuzzy intersection. Then, the aggregated result was defuzzified with another ANN. A real dynamic random access memory case was utilized to validate the effectiveness of the proposed methodology. According to the experimental results, the proposed methodology outperformed five existing methods in improving the estimation accuracy, which was measured in terms of the mean absolute error and the mean absolute percentage error.

1 Introduction

Yield is the percentage of jobs that pass the fabrication process successfully. Yield has been recognized as an essential factor to the competitiveness and sustainable development of a factory (Chen and Wang 2014). Elevating yield is also a critical task for green manufacturing, because a high yield minimizes scrap and rework, conserving materials, energy, time, and labor (Rusinko 2007; Zhang et al. 2016; Huerta et al. 2016). For these reasons, all factories have sought to enhance yield. To achieve this goal, yield must be estimated in advance. A common managerial practice is to allocate the majority of capacity to products that are estimated to have relatively high yields. The results of yield estimation can also be fed back to adjust the settings of machines (Moyne et al. 2014).

The yield of a product can be estimated in two ways: micro yield modeling (MiYM) and macro yield modeling (MaYM) (Mullenix et al. 1997). In MiYM, the probability density function of defects is fitted for specific wafers intended to produce a specific product in order to estimate the asymptotic yield of the product. By contrast, in MaYM, wafers are not examined individually, but as a whole, and relevant statistics are calculated to track the fluctuation in the average yield over time. MiYM is a challenging task because numerous assumptions must be made; however, such assumptions may be violated. Therefore, this study involves MaYM. Fitting the improvement in yield with a learning model is a mainstream technique in this field (Chen and Wang 1999, 2014; Chen and Chiu 2015). However, considerable uncertainty exists in the yield learning process of a product (Chen and Wang 1999), which must be expressed using stochastic or fuzzy methods (Lin 2012). The research trends in this field include the following:

• 1. Estimating the yield of a product of which the fabrication is to be delivered to another factory (Ahmadi et al. 2015).

• 2. Using a yield model other than Gruber’s general yield model (Gruber 1992, 1994) to model the improvement in the yield of a product. Gruber’s general yield model is perhaps the most commonly used yield learning model that features an exponentially decaying failure rate (Chen 2009; Weber 2004).

• 3. Proposing a sophisticated method such as a fuzzy collaborative intelligence (FCI) approach to fit a yield learning process (Chen and Lin 2008).

In an FCI approach, a fuzzy yield learning model is first established to estimate the future yield. Subsequently, the opinions from multiple domain experts are considered to convert the fuzzy learning model into various optimization problems (Chen and Chiu 2015) such as quadratic programming (QP) or nonlinear programming (NLP) problems, which is not easy for the following reasons:

• 1. A nonconvex QP problem is widely considered to be difficult to optimize (Chen and Wang 2013).

• 2. Some settings of the model parameters result in no feasible solution.

• 3. The global optimal solution to a NLP problem is not easy to obtain. Therefore, Chen and Wang (2013) established a systematic procedure to approximate an NLP problem with a QP problem.

• 4. Managers require another viewpoint for fitting a yield learning process.

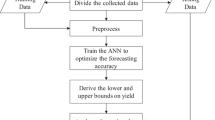
To facilitate resolving these difficulties, in this study, a fuzzy yield learning model is fitted with various artificial neural networks (ANNs) to provide more feasible managerial insights and more flexibility. Similar approaches have not been employed in past studies. The results of these fuzzy optimization problems represent the experts’ estimates of the future yield. These estimates are aggregated using fuzzy intersection (FI). The aggregation result is then defuzzified using another ANN (Ahmadi et al. 2015). The procedure for the proposed FCI approach is shown in Fig. 1.

Fig. 1

Procedure for the proposed FCI approach

The remainder of this paper is organized as follows. The concept of a fuzzy yield learning model is reviewed in Sect. 2. The FCI approach for fitting a fuzzy yield learning process is then described in Sect. 3. To illustrate the proposed methodology and compare with other existing methods, a real case of a dynamic random access memory (DRAM) product is detailed in Sect. 4. Subsequently, this study is concluded in Sect. 5.

The variables and parameters used in this study are defined as follows:

• 1. $\eta$: the learning rate; $0 \le \eta \le 1$.

• 2. $\tilde{\theta }$: the threshold on the output node.

• 3. $\Delta \tilde{\theta }_{t}$: the modification to be made to $\tilde{\theta }$ when considering the t-th example only.

• 4. $\delta_{t}$: the deviation between the network output and the actual value.

• 5. $a_{t}$: the actual value.

• 6. $\hat{b}$ (or $\tilde{b}$): the yield learning rate; $\hat{b}$ (or $\tilde{b}$) ≥ 0.

• 7. $\tilde{o}_{t}$: the ANN output for the t-th example.

• 8. t: the time index; t = 1,…, T.

• 9. $\tilde{w}$: the weight of the connection between the input node and the output node.

• 10. $\Delta \tilde{w}_{t}$: the modification to be made to $\tilde{w}$ when considering the t-th example only.

• 11. $x_{t} :$ the input to the ANN within period t.

• 12. $\hat{Y}_{0}$ (or $\tilde{Y}_{0}$): the asymptotic yield to which $Y_{t}$ will converge when t → ∞; $\hat{Y}_{0}$ (or $\tilde{Y}_{0}$) ∈ [0, 1]. $\hat{Y}_{0}$ (or $\tilde{Y}_{0}$) can be estimated by analyzing the distribution of defects.

• 13. $Y_{\hbox{max} }$: an upper bound on $\tilde{Y}_{0}$.

• 14. $Y_{\hbox{min} }$: a lower bound on $\tilde{Y}_{0}$.

• 15. $Y_{t}$: the actual (average) yield within period t.

• 16. $\hat{Y}_{t}$ (or $\tilde{Y}_{t}$): the estimated (average) yield within period t; $\hat{Y}_{t}$ (or $\tilde{Y}_{t}$) ∈ [0, 1].

• 17. $( - )$: fuzzy subtraction.

2 Fuzzy yield learning models

The improvement in the yield of a product can be traced with a learning model as (Gruber 1994)

$$\hat{Y}_{t} = \hat{Y}_{0} e^{{ - \frac{{\hat{b}}}{t} + r(t)}}$$

(1)

r(t) is a homoscedastic, serially noncorrelated error term satisfying the following assumption (Chen and Wang 1999):

$$r(t)\sim{\text{Normal}}\, ( 0 ,\sigma^{ 2} ),\,\hat{r}(t) = 0\,{\text{for}}\,{\text{all}}\,t$$

(2)

The yield learning model in (2) has been applied in numerous studies on yield estimation and management (Chen and Wang 1999, 2013, 2014; Chen and Chiu 2015; Gruber 1994; Chen 2009; Weber 2004; Chen and Lin 2008). In addition, according to numerous empirical analyses, such as those of Gruber (1994) and Weber (2004), the failure rate of semiconductor manufacturing follows an exponentially decaying process. The yield learning model also conforms to this requirement. Recently, Tirkel (2013) used the model to describe the survival rate after each step, which is called the step yield. Then, the yield after the whole fabrication process was described with a combination of the models. This again supported the applicability of the yield learning model to semiconductor manufacturing. For these reasons, the yield learning model is considered suitable for tracking the improvement in the yield of semiconductor manufacturing in this study.

After converting the parameters and variables in (1) into logarithms,

$${ \ln }\hat{Y}_{t} = \ln \hat{Y}_{0} - \frac{{\hat{b}}}{t} + r(t)$$

(3)

which is a linear regression (LR) problem that can be solved by minimizing the sum of the squared deviations:

$${\text{Min}}\,\sum\limits_{t = 1}^{T} {(Y_{t} - } \hat{Y}_{t} )^{2}$$

(4)

which leads to the following two equations:

$$\hat{b} = - \frac{{\sum\nolimits_{t = 1}^{T} {\frac{{\ln Y_{t} }}{t}} - T\left( {\overline{{\frac{1}{t}}} } \right)\left( {\overline{{\ln Y_{t} }} } \right)}}{{\sum\nolimits_{t = 1}^{T} {\frac{1}{{t^{2} }}} - T\left( {\overline{{\frac{1}{t}}} } \right)^{2} }}$$

(5)

$$\hat{Y}_{0} = e^{{\overline{{\ln Y_{t} }} + \hat{b}\overline{{\frac{1}{t}}} }}$$

(6)

However, optimizing another measure such as the mean absolute error (MAE) or the mean absolute percentage error (MAPE), is not straightforward. Optimizing certain measures requires a solution for complex mathematical programming problems.

In considering the uncertainty of the yield learning process, the parameters can be given in triangular fuzzy numbers (TFNs) (Chen and Wang 1999):

$$\tilde{Y}_{0} = e^{{(y_{1} ,y_{2} ,y_{3} )}}$$

(7)

$$\tilde{b} = (b_{1} ,b_{2} ,b_{3} )$$

(8)

As a result,

$$\tilde{Y}_{t} = \tilde{Y}_{0} e^{{ - \frac{{\tilde{b}}}{t} + r(t)}} = e^{{\left( {y_{1} - \frac{{b_{3} }}{t},y_{2} - \frac{{b_{2} }}{t},y_{3} - \frac{{b_{1} }}{t} + r(t)} \right)}} .$$

(9)

Lognormalizing (9) yields the following:

$$\ln \tilde{Y}_{t} = \ln \tilde{Y}_{0} ( - )\frac{{\tilde{b}}}{t} + r(t) = \left( {y_{1} - \frac{{b_{3} }}{t},y_{2} - \frac{{b_{2} }}{t},y_{3} - \frac{{b_{1} }}{t}} \right)\,+\,r(t)$$

(10)

$( - )$ denotes fuzzy subtraction. TFNs have been extensively used in various fields, including management performance evaluation (Wang et al. 2016), user influence measurement (Xiao et al. 2015), and ocean platform risk evaluation (Feng et al. 2016). Because TFNs have been widely successful, they are used in the proposed methodology. The proposed model can be easily modified to incorporate other types of fuzzy numbers, including trapezoidal fuzzy numbers, Gaussian fuzzy numbers, generalized bell fuzzy numbers, and others. However, if fuzzy numbers with nonlinear membership functions are used, the mathematical programming models for solving the parameters will also be nonlinear, causing difficulties in searching for global optimal solutions.

Equation (10) is a fuzzy linear regression (FLR) problem that can be solved in various ways. For example, Tanaka and Watada (1988) minimized the sum of spreads (or ranges) by solving a linear programming (LP) problem. Peters (1994) maximized the average satisfaction level by solving a NLP problem. By combining the previous two approaches, Donoso et al. (2006) minimized the weighted sum of both the central tendency and the sum of spreads. Recently, Roh et al. (2012) constructed a polynomial neural network to fit an FLR equation. However, most of the parameters of a yield learning process are constrained. Whether the method of Roh et al. (2012) can be directly applied is questionable. Chen and Lin (2008) modified Tanaka and Watada’s model and Peters’s model to incorporate nonlinear objective functions or constraints.

3 The proposed methodology

In the proposed methodology, a group of domain experts is formed. To this end, product engineers, quality control engineers, or industrial engineers from the factory who are responsible for monitoring or accelerating the quality improvement progress of the product will be invited. Each expert constructs an ANN to estimate the future yield of a product. An ANN is used because of the following reasons:

• 1. An ANN is much different from the mathematical programming models used in the existing methods; hence, an ANN provides a different point of view in fitting the yield learning process.

• 2. It is easier to find a feasible solution to an ANN than to the NLP problems in the existing methods.

• 3. An ANN is a well-known tool for fitting any nonlinear function, whereas the mathematical programming models used in the existing methods are not problem free.

3.1 ANN

The ANNs used by the experts are based on the same architecture; however, they have different settings and undergo separate training processes, resulting in different yield estimates that must be aggregated (Fig. 2).

Fig. 2

The ANN architecture used by each domain expert

The ANN has two layers. At first, the reciprocal of the time index is entered into the input layer as follows:

$$x_{t} = 1/t$$

(11)

After the input has been multiplied by the connection weight, the product is passed to the output layer. Here the connection weight is set to the learning constant:

$$\tilde{w} = \tilde{b}$$

(12)

On the output node, the received signal is compared with a threshold that is equal to the logarithm of the asymptotic yield:

$$\tilde{\theta } = \ln \tilde{Y}_{0}$$

(13)

Subsequently, the result is transformed into the network output. To this end, the common log-sigmoid function (Bonnans et al. 2006) is adopted:

$$y = \frac{1}{{1 + e^{ - x} }}$$

(14)

By setting $x$ in (14) to $\tilde{w}x_{t} ( - )\tilde{\theta }$ to derive the network output $\tilde{o}_{t}$,

$$\begin{aligned} \tilde{o}_{t} = & \frac{1}{{1 + e^{{ - (\tilde{w}x_{t} ( - )\tilde{\theta })}} }} \\ = \frac{1}{{1 + e^{{ - (\frac{{\tilde{b}}}{t}( - )\ln \tilde{Y}_{0} )}} }} \\ = \frac{1}{{1 + \tilde{Y}_{0} e^{{ - \frac{{\tilde{b}}}{t}}} }} \\ = \frac{1}{{1 + \tilde{Y}_{t} }} \\ \end{aligned}$$

(15)

or equivalently,

$$\tilde{Y}_{t} = \frac{1}{{\tilde{o}_{t} }} - 1$$

(16)

For a comparison, the actual value can be set to the following equation:

$$a_{t} = \frac{1}{{1 + Y_{t} }}$$

(17)

and the training of the ANN aims to minimize the following objective function:

$${\text{Min}}\,\sum\limits_{t = 1}^{T} {(o_{t2} - a_{t} )^{2} } = \sum\limits_{t = 1}^{T} {\left( {\frac{1}{{1 + Y_{t2} }} - \frac{1}{{1 + Y_{t} }}} \right)^{2} }$$

(18)

which forces $Y_{t2}$ to be close to $Y_{t}$ in a distinct way. In addition, (18) is different from (4), meaning that it is a new viewpoint for fitting an uncertain yield learning process. However, no absolute rule exists for judging whether (18) is better than (4), or vice versa. The objective function (18), minimizing the sum of squared error (SSE), is a common objective function for ANN training. In addition, the algorithm proposed in this study for training the ANN is modified from the existing gradient descent algorithm that also aims to minimize the SSE. Many other existing training algorithms also minimize the same objective function. For these reasons, the objective function (18) is chosen in the proposed methodology.

The following theorems are conducive to determining the optimal values of the network parameters.

Property 1

The lower bound of the network output, $o_{t1}$ , is associated with $Y_{03}$ and $b_{1}$ . Conversely, $o_{t3}$ , is associated with $Y_{01}$ and $b_{3}$.

Theorem 1

A reasonable choice of $b_{1}$ is $\mathop {\hbox{min} }\limits_{t} \left\{ { - t\ln \left( {\frac{{\frac{1}{{a_{t} }} - 1}}{{Y_{\hbox{max} } }}} \right)} \right\}$ if the asymptotic yield is expected to be less than $Y_{\hbox{max} }$.

Proof

$o_{t1}$ is a lower bound on $a_{t}$,

$$o_{t1} \le a_{t}$$

(19)

According to Property 1,

$$\frac{1}{{1 + Y_{03} e^{{ - \frac{{b_{1} }}{t}}} }} \le a_{t}$$

(20)

$$Y_{03} e^{{ - \frac{{b_{1} }}{t}}} \ge \frac{1}{{a_{t} }} - 1$$

(21)

If the asymptotic yield is expected to be less than $Y_{\hbox{max} }$,

$$Y_{\hbox{max} } \ge Y_{03}$$

(22)

Substituting (21) into (22), the following equations are obtained:

$$Y_{\hbox{max} } e^{{ - \frac{{b_{1} }}{t}}} \ge Y_{03} e^{{ - \frac{{b_{1} }}{t}}} \ge \frac{1}{{a_{t} }} - 1$$

(23)

$$b_{1} \le - t\ln \left( {\frac{{\frac{1}{{a_{t} }} - 1}}{{Y_{\hbox{max} } }}} \right)$$

(24)

Therefore,

$$b_{1} \le \mathop {\hbox{min} }\limits_{t} \left\{ { - t\ln \left( {\frac{{\frac{1}{{a_{t} }} - 1}}{{Y_{\hbox{max} } }}} \right)} \right\}$$

(25)

The larger $o_{t1}$ is, the better it is, and likewise, the larger $b_{1}$ is, the better it is. Therefore, it is reasonable to set

$$b_{1}^{*} = \mathop {\hbox{min} }\limits_{t} \left\{ { - t\ln \left( {\frac{{\frac{1}{{a_{t} }} - 1}}{{Y_{\hbox{max} } }}} \right)} \right\}$$

(26)

Theorem 1 is proved.

Theorem 2

A reasonable choice of $b_{3}$ is $\mathop {\hbox{max} }\limits_{t} \left\{ { - t\ln \left( {\frac{{\frac{1}{{a_{t} }} - 1}}{{Y_{\hbox{min} } }}} \right)} \right\}$ if the asymptotic yield is expected to be greater than $Y_{\hbox{min} }$.

Proof

This theorem can be proved according to Property 1, with a proof similar to that of Theorem 1.

Theorem 3

After determining the value of $b_{1}$ , a reasonable choice of $\theta_{3}$ is $\ln \mathop {\hbox{max} }\nolimits_{t} \left\{ {\left( {\frac{1}{{a_{t} }} - 1} \right)e^{{\frac{{b_{1}^{*} }}{t}}} } \right\}$.

Proof

According to (21)

$$Y_{03} e^{{ - \frac{{b_{1}^{*} }}{t}}} \ge \frac{1}{{a_{t} }} - 1$$

(27)

$$Y_{03} \ge \left( {\frac{1}{{a_{t} }} - 1} \right)e^{{\frac{{b_{1}^{*} }}{t}}}$$

(28)

$$Y_{03} \ge \mathop {\hbox{max} }\limits_{t} \left\{ {\left( {\frac{1}{{a_{t} }} - 1} \right)e^{{\frac{{b_{1}^{*} }}{t}}} } \right\}$$

(29)

The smaller $Y_{03}$ is, the better it is. Therefore, it is reasonable to set

$$Y_{03}^{*} = \mathop {\hbox{max} }\limits_{t} \left\{ {\left( {\frac{1}{{a_{t} }} - 1} \right)e^{{\frac{{b_{1}^{*} }}{t}}} } \right\}$$

(30)

$$\theta_{3}^{*} = \ln (Y_{03}^{*} ) = \ln \mathop {\hbox{max} }\limits_{t} \left\{ {\left( {\frac{1}{{a_{t} }} - 1} \right)e^{{\frac{{b_{1}^{*} }}{t}}} } \right\}$$

(31)

Theorem 3 is proved.

Theorem 4

After determining the value of $b_{3}$ , a reasonable choice of $\theta_{1}$ is $\ln \mathop {\hbox{min} }\nolimits_{t} \left\{ {\left( {\frac{1}{{a_{t} }} - 1} \right)e^{{\frac{{b_{3}^{*} }}{t}}} } \right\}$.

Proof

This theorem can be proved in a manner similar to that of Theorem 3.

3.2 Training algorithm

The network parameters $\tilde{\theta }$ and $\tilde{w}$ are constrained to be nonpositive and nonnegative, respectively. However, previously published algorithms for training an ANN, such as the gradient descent algorithm, the conjugate gradient algorithm, the scaled conjugate gradient algorithm, and the Levenberg–Marquardt (LM) algorithm, assume that parameters are unconstrained real numbers. For this reason, previously published training algorithms cannot be directly applied to train the ANN used in the FCI approach. Instead, the following algorithm is proposed to train the ANN:

• 1. Determine the number of epochs, the SSE threshold for the network convergence, and the learning rate $0 \le \eta \le 1$.

• 2. Estimate the lower and upper bounds on the asymptotic yield as $Y_{\hbox{min} }$ and $Y_{\hbox{max} }$, respectively.

• 3. Specify the initial values of the network parameters ($w_{1} \ge 0$; $\theta_{3} \le 0$).

• 4. Input the next example $x_{t1} = 1/t$ to the ANN and derive the output $\tilde{o}_{t}$ according to (15).

• 5. Calculate the deviation between the network output and the actual value as follows:

$$\delta_{t} = a_{t} - o_{t2} = \frac{1}{{1 + Y_{t} }} - o_{t2}$$

(32)

• 6. Calculate the additional modifications that must be made to the network parameters as follows:

$$\Delta w_{t2} = - \eta \delta_{t} x_{t}$$

(33)

$$\Delta \theta_{t2} = - \eta \delta_{t}$$

(34)

• 7. If all examples have been learned, proceed to Step 8; otherwise, return to Step 4.

• 8. Evaluate the learning performance in terms of SSE:

$${\text{SSE}} = \sum\limits_{t = 1}^{T} {\delta_{t}^{2} }$$

(35)

• 9. Add the modifications to the corresponding network parameters:

$${\text{New}}\,w_{2} = w_{2} + \sum\limits_{t = 1}^{T} {\Delta w_{t2} }$$

(36)

$${\text{New}}\,\theta_{2} = \theta_{2} + \sum\limits_{t = 1}^{T} {\Delta \theta_{t2} }$$

(37)

• 10. Record the values of the network parameters if

  • (i) $w_{3} \ge w_{2} \ge w_{1} \ge 0$; and

  • (ii) $\theta_{1} \le \theta_{2} \le \theta_{3} \le 0$; and

  • (iii) The SSE is lower than the smallest SSE that has been recorded.

• 11. If the number of epochs has been reached or the SSE is already lower than the SSE threshold, proceed to Step (12); otherwise, return to Step (4).

• 12. Modify $w_{1}$ and $w_{3}$ as

$${\text{New}}\,w_{1} = \mathop {\hbox{min} }\limits_{t} \left\{ { - t\ln \left( {\frac{{\frac{1}{{a_{t} }} - 1}}{{Y_{\hbox{max} } }}} \right)} \right\}$$

(38)

$${\text{New}}\,w_{3} = \mathop {\hbox{max} }\limits_{t} \left\{ { - t\ln \left( {\frac{{\frac{1}{{a_{t} }} - 1}}{{Y_{\hbox{min} } }}} \right)} \right\}$$

(39)

• 13. Modify $\theta_{1}$ and $\theta_{3}$ as

$${\text{New}}\,\theta_{1} = \ln \mathop {\hbox{min} }\limits_{t} \left\{ {\left( {\frac{1}{{a_{t} }} - 1} \right)e^{{\frac{{b_{3} }}{t}}} } \right\}$$

(40)

$${\text{New}}\,\theta_{3} = \ln \mathop {\hbox{max} }\limits_{t} \left\{ {\left( {\frac{1}{{a_{t} }} - 1} \right)e^{{\frac{{b_{1} }}{t}}} } \right\}$$

(41)

3.3 Aggregation

FI is a well-known function for deriving a consensus of fuzzy judgements. For example, the widely applied Mamdani fuzzy inference system (Mamdani 1974) uses FI to aggregate the results of satisfying multiple conditions. In the viewpoint of Silvert (2000), FI can integrate different types of observations in a manner that permits a good balance between favorable and unfavorable observations. Recently, Parreiras et al. (2012) mentioned that FI can obtain a global consensus when solving multicriteria problems. FI has been extensively applied in FCI (Chen and Wang 2013, 2014; Chen and Chiu 2015; Chen and Lin 2008; Parreiras et al. 2012).

The fuzzy yield estimates by various experts are aggregated using FI (i.e., the minimal T-norm) $\tilde{I}(\{ \tilde{Y}_{t} (g)|g = 1 \sim G\} )$:

$$\mu_{{\tilde{I}(\{ \tilde{Y}_{t} (g)|g = 1 \sim G\} )}} (x) = \hbox{min} (\mu_{{\tilde{Y}_{t} (1)}} (x), \ldots ,\mu_{{\tilde{Y}_{t} (G)}} (x)),$$

(42)

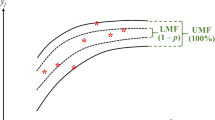
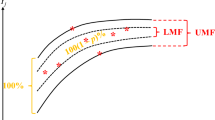
where $\tilde{Y}_{t} (g)$ is the yield estimate for period t by expert g. Because these fuzzy yield estimates are given in TFNs, the fuzzy intersection is a polygon-shaped fuzzy number (Fig. 3), the width of which determines the narrowest range of the yield.

Fig. 3

Result of fuzzy intersection

To derive a single representative (crisp) value from the aggregation result, another ANN is constructed with the following configuration:

• 1. Inputs are the corners of the polygon-shaped fuzzy number.

• 2. A single hidden layer has twice as many nodes as the number of inputs. Independent inputs to the ANN are aggregated on each node in the hidden layer. In this way, interactions between them can be considered.

• 3. The training algorithm is the Levenberg–Marquardt (LM) algorithm (Bonnans et al. 2006). The LM algorithm is a well-known algorithm for fitting a nonlinear relationship to minimize the SSE. The LM algorithm trains an ANN at a second-order speed without computation of the Hessian matrix; the LM algorithm is much faster than various other algorithms, such as the gradient descent algorithm.

4 A DRAM product case

A DRAM product case was used to illustrate the applicability of the proposed methodology. The data were collected from a DRAM factory in Hsinchu Science Park, Taiwan. The data specify the yields of the DRAM product during 10 periods (see Table 1). The first seven periods of the collected data were used to train the ANN. The remaining three periods were used to evaluate the estimation performance.

Table 1 DRAM product case

Three domain experts convened to estimate the future yield of the DRAM product collaboratively. We did not invite more experts because the collaboration process would have been prolonged and hostile experts would probably have been involved.

The experts assigned different initial values to the ANN parameters and established different lower and upper bounds for the asymptotic yield, as summarized in Table 2.

Table 2 Initial settings by the experts

The stopping criteria were established as follows:

• 1. Mean squared error (MSE) <10⁻⁴; or

• 2. 100 epochs have been run; or

• 3. The training process has become stuck in a local optimum.

The first criterion was chosen because it corresponded to an RMSE of 0.01 or 1%, which was obviously adequate. Because a small data set was involved and the relationship was not expected to be very complicated, 100 epochs were run. Nevertheless, more epochs could have been run if the estimation performance had not been adequate. In addition, when the training was stuck in a local optimum, the most practical action was to restart the training process.

The fuzzy yield learning models fitted by the experts were as follows: (Expert A)

$$\tilde{Y}_{t} = (0.870,0.876,\;1.000)e^{{ - \frac{(0.986,\;1.072,\;1.718)}{t}}}$$

(43)

(Expert B)

$$\tilde{Y}_{t} = (0.900,\;0.960,\;0.980)e^{{ - \frac{(0.966,\;1.490,\;1.888)}{t}}}$$

(44)

(Expert C)

$$\tilde{Y}_{t} = (0.920,\;0.926,\;0.960)e^{{ - \frac{(0.945,\;1.294,\;1.998)}{t}}}$$

(45)

For the training data, all fuzzy yield estimates generated by these fuzzy yield learning models contained the actual values. The fuzzy yield estimates by the three experts were aggregated using FI to determine the narrowest range of yield. The results are summarized in Table 3. According to the experimental results, each aggregation result; that is, each polygon-shaped fuzzy number, at the most, had seven corners. Therefore, the aggregation result was fed into an ANN with the following configuration to derive the representative (crisp) value:

Table 3 The narrowest range of yield determined using FI

• 1. The fourteen inputs included the values and memberships of the corners.

• 2. A single hidden layer had 28 nodes.

• 3. The training algorithm was the LM algorithm.

• 4. The learning rate was (η) = 0.2.

• 5. The stopping criteria were MSE < 5 × 10⁻³ or when 1000 epochs had been run.

The results are shown in Fig. 4.

Fig. 4

The representative values

The three fitted fuzzy yield learning models were applied to the testing data, and the results are shown in Table 4. The fuzzy yield estimates by the three experts were then aggregated using FI and defuzzified with the ANN defuzzifier to evaluate the estimation accuracy in terms of MAE, MAPE, and root mean squared error (RMSE). In addition, five existing methods, Gruber’s crisp yield learning method (1994), Tanaka and Watada’s FLR method (Chen and Wang 1999), Peters’s FLR method (1994), the FLR method of Donoso et al. (2006), and Chen and Lin’s FCI method (2008) were also applied to the collected data for a comparison.

Table 4 Results of applying the method to the testing data

Gruber’s model was built by fitting a logistic regression, and the result was

$$\hat{Y}_{t} = 0.810e^{{ - \frac{0.773}{t}}}$$

(46)

Tanaka and Watada’s FLR method tried to minimize the sum of spreads of fuzzy yield estimates, subject to the premise that the membership of each actual value in the corresponding fuzzy yield estimate was greater than a threshold that was set to 0.3 here. Conversely, Peters’s FLR methods maximized the sum of the memberships of the actual values by requesting the average spread of fuzzy yield estimates to be less than another threshold that was set to 1.0. Combining the previous two viewpoints, Donoso et al.’s FLR method minimized the weighted sum of the square of the deviation from the core and the square of the spread. Here the two weights were set to be equal. Chen and Lin’s FCI method was based on the collaboration of multiple experts. Each expert configured two NLP problems with different settings to generate fuzzy yield estimates that were not the same and were aggregated using FI. The settings by the experts were shown in Table 5. The aggregation result was then defuzzified with an ANN to arrive at a representative value. The performances of various methods were compared in Table 6.

Table 5 The settings by the experts

Table 6 Comparison of the performances of various methods

According to the experimental results,

• 1. The estimation accuracy using the proposed methodology, in terms of MAE or MAPE, was clearly better than that using the existing methods. Regarding RMSE, the proposed methodology also achieved a fair level of performance.

• 2. The most notable advantage occurred when the estimation accuracy was measured in terms of MAE. In this respect, the proposed methodology surpassed the existing methods by 26% on average.

• 3. FCI methods, including Chen and Lin’s method and the proposed methodology, achieved better performances than noncollaborative methods did, which revealed the importance of analyzing uncertain yield data from various viewpoints.

However, the proposed methodology was not compared with agent-based FCI methods, such as in Chen and Wang (2014), where the values of parameters were set arbitrarily and might not be valuable in practice.

5 Conclusions

Optimizing the yield of each product is a critical task for green manufacturing; it reduces waste and increases profitability. Every factory strives to estimate the future yield of each product in order to optimize yield. Therefore, this study proposed an FCI approach to estimate the future yield of a product in a wafer fab. The FCI approach starts from the modeling of an uncertain yield learning process with an ANN, which is a novel attempt in this field. In the FCI approach, a group of domain experts is formed. Each expert constructs a separate ANN to estimate the future yield with a fuzzy value. The fuzzy yield estimates from the experts are aggregated using FI. The aggregation result is then defuzzified with another ANN.

After utilizing a real DRAM case to validate the effectiveness of the proposed methodology, the following conclusions were drawn:

• 1. The proposed methodology was superior to five existing methods in improving the accuracy of the future yield estimates of the DRAM product.

• 2. The FCI methods demonstrated noteworthy advantages over noncollaborative methods in coping with the uncertainty of a yield learning process.

• 3. Fitting a yield learning process with an ANN was shown to be a meaningful effort.

However, the algorithm used to train the ANN is essentially a modification of the gradient descent algorithm, and can be improved to accelerate the ANN convergence process. Further, the ANN used in the proposed FCI approach has a simple architecture. A more sophisticated ANN, with hidden layers to portray the interactions among factors, may be employed in the future.