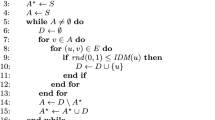On the optimal solution of budgeted influence maximization problem in social networks

Abstract

The budgeted influence maximization problem is a challenging stochastic optimization problem defined on social networks. In this problem, the objective is identifying influential individuals who can influence the maximum number of members within a limited budget. In this work an integer program that approximates the original problem is developed and solved by a sample average approximation (SAA) scheme. Experimental analyses indicate that SAA method provides better results than the greedy method without worsening the solution time performance.

1 Introduction

The budgeted influence maximization problem (BIMP) $\{\max \, \sigma (S): c(S) \le {} B; S \subset {} V\}$ is defined on a directed stochastic network, where V is the set of nodes, S is a subset of V with a cost of c(S) which is limited by a budget B and lastly $\sigma (S)$ is a function measuring the expected number of nodes activated in V when a cascade is initialized by the seed set S. In BIMP the aim is to identify a subset of nodes (representing individuals in a social network) with arbitrary costs such that when selected they can activate (influence) the largest number of nodes in the network within the available budget B.

The research in the field of online social networks has attracted a great amount of interest recently (Heidemann et al. 2012). The concept of using individuals in the spreading process of a certain message, idea or a product is frequently exploited by companies or marketers under the concept of “viral marketing” (Brown and Hayes 2008) and determining the most effective individuals (also called influentials) is of great importance. Although the research on this topic started earlier, the first mathematical optimization problem is provided by Kempe et al. (2003) and the phenomenon is named as “Influence Maximization”. By using various popular mathematical diffusion models they formulate it as a discrete optimization problem. Aside from its viral marketing applications, the same concept is studied in network security, computer virus detection, infrastructure planning, habitat conservation and wireless sensor networks (Leskovec et al. 2007; Lee et al. 2015; Sheldon et al. 2010; Chen et al. 2010).

BIMP is an extension of the traditional influence maximization problem (IMP). Different than IMP, in BIMP activating each node i has an arbitrary cost $c_{i}$. This cost can be assumed to be the marketing cost spent or discount given for persuading an individual to start spreading a viral message or advertisement to its peers. The total cost of any initial set S is represented by the cost function c(S) and the total available budget to be spent to recruit initial influentials is assumed to be B.

It is proven that the objective function $\sigma (S)$ is submodular under certain diffusion models (Kempe et al. 2003) and the greedy algorithm guarantees a $(1-1/e)$ approximation to the optimal solution of IMP (Nemhauser et al. 1978). Similarly, an approximation guarantee of $1/2(1-1/e)$ is proven for BIMP (Leskovec et al. 2007). Krause and Guestrin (2005) show that this bound can be improved to $(1 -1/\sqrt{e})$ with slight changes in the greedy algorithm. Finally a more inefficient and involved algorithm can achieve the $(1-1/e)$ approximation ratio (Khuller et al. 1999). The objective function of BIMP cannot be evaluated exactly in a computationally tractable way (see Sect.  2.1), so these constant factor results actually apply when the objective function is submodular and when exact calculation is possible.

Although performing well, due to the requirement of computing the influence function $\sigma (S)$ many times, the greedy algorithm is computationally unsatisfactory. To overcome this, researchers focused on different heuristics that determine the seed set faster. Nguyen and Zheng (2013) developed two algorithms that convert a general network into a directed-acyclic network (DAG), whereas Han et al. (2014) propose a balanced seed selection algorithm which utilizes three different selection mechanisms. In Wang et al. (2013) a graphic-SEIR (susceptible, exposed, infected and resistant) scheme is developed and four algorithms are provided to solve BIMP. Another popular strategy is splitting the network into smaller sub-networks by identifying communities using clustering techniques (Mandala et al. 2013).

In this study, our first contribution is providing a mathematical formulation to model the BIMP with independent cascade diffusion model as a mixed integer linear program. Next, a sample average approximation (SAA) scheme is applied to solve BIMP effectively. SAA method has been successfully used to solve stochastic optimization problems efficiently (Shapiro 2008). It not only determines an approximation of the optimal solution but also provides an upper bound on the optimal objective function value. Therefore, we provide results about the optimal solution of BIMP and the actual performance of the greedy method on BIMP, both of which have been open questions so far. SAA does not guarantee a worst-case bound like the greedy method, however the quality of the approximation can be quantified statistically (see Sect. 3). The organization of the paper is as follows: In Sect. 2, the details of the BIMP and the mathematical formulation is provided. In Sect. 3 the SAA Method is explained. In Sect. 4 experimental studies and results are presented. The last section concludes the paper.

2 Budgeted influence maximization problem

BIMP is defined on a directed and weighted network ${\mathcal {N}}=(V,A,W)$. Here V is the set of nodes, which are the individuals or members of the social network with a size of $\vert V\vert =n$. The set of arcs is shown by A and they correspond to any kind of a connection scheme in a social network, e.g. being friends, followers, common-link sharers. W represents the weights on arcs, where each arc $(i,j)\in A$ from node i to j has a corresponding weight $p_{ij}\in W$. These weights represent the influence probabilities between individuals. So $p_{ij}$ means the probability of i influencing j when i takes an action in the social network. In general these probabilities are assumed to be asymmetric, i.e. $p_{ij} \ne p_{ji}$. The number of arcs is $\vert A \vert = \vert W \vert =m$. Finally each node has an arbitrary cost $c_i$ which incurs only if node i is included in the seed set and a total budget of B is available to be spent. Given a seed set i.e., an initial set of active nodes S, the expected number of activated or influenced nodes is computed by the function $\sigma (S)$. The BIMP tries to determine the optimal seed set whose total cost $c(S)=\sum \nolimits _{i\in S} c_i$ does not exceed the budget B and when the diffusion starts with the nodes in S the influence function $\sigma (S)$ is maximized. We assume that the information disseminates through the network according to independent cascade (IC) diffusion model. More details on diffusion models can be found in (Kempe et al. 2003) and (Chen et al. 2010).

2.1 Evaluation of influence

The influence of a seed set $S\subset V$ is defined to be the expected number of active nodes at the end of the diffusion process and it is denoted as $\sigma (S)$, which is a real valued function defined on the power set of V; i.e. $\sigma : 2^V \rightarrow {\mathbb {R}}$. Chen et al. (2010) show that it is #P-hard to calculate the influence function $\sigma (S)$ exactly. $\sigma (S)$ is identical to the expected number of nodes that can be reached by the seed set S in a corresponding uncertain graph. Similar to the computation of reliability or reachability, there are two methods for exact evaluation of $\sigma (S)$ according to Hu et al. (2014). The first is the graph-based method: For a given uncertain graph ${\mathcal {N}}=(V,A,W)$ with n nodes and m arcs, there are a total of $2^m$ possible certain graphs. Therefore, the cost of calculating $\sigma (S)$ where $\vert S \vert =K$ is in $O(K \times n \times 2^m)$. The second one is the path-based method which determines all the simple paths from S to other nodes in uncertain graph ${\mathcal {N}}$ and it also has an exponential-time complexity.

2.2 Mathematical formulation of BIMP

The budgeted influence maximization problem can be formulated as $\{\max \, \sigma (S): c(S)\le {} B; S \subset {} V\}$. Kempe et al. (2003) prove that the unit cost version, i.e. IMP with the constraint $\left| S\right| = K$ instead of $c(S) \le {} B$ is NP-hard by showing a correspondence to the Stochastic Set Covering problem. When each $c_i=1$ and $B=\left| S\right|$, BIMP reduces to IMP so it is NP-hard as well. Thus, finding the optimal solution for large problems within reasonable durations is difficult. Even exactly calculating the objective function $\sigma (S)$ is proven to be #P-hard.

The above form of BIMP is not favorable for mathematical optimization approaches. However, it can be reformulated as a discrete optimization problem by considering all possible realizations of the network. Each realization corresponds to a subset of active arcs in the network. An arc (i, j) is said to be active if it exists in the network, which has a probability of $p_{ij}$. In the independent cascade diffusion model each arc (i, j) is active with the given weight $p_{ij}$ or inactive with probability $(1-p_{ij})$. Since the network has finitely many arcs, the number of possible realizations is also finite. Let r be the index representing a realization and let ${\mathcal {R}}$ be the set of all realizations with an exponential size of $\vert {\mathcal {R}}\vert =2^{m}$. Also, let $\mu _r$ be the probability of occurrence of realization r. It can be calculated by multiplying all the $p_{ij}$ values for the active arcs and $1-p_{ij}$ values for the inactive arcs of the given realization $r \in {\mathcal {R}}$. Lastly, we define $N_{r}(i) \subseteq V$ as the set of neighbours (predecessors) of node i for a given realization r.

Two sets of decision variables are required; one for capturing the initial seed set and the next for representing all activated nodes throughout the diffusion process. Let y be a $0-1$ vector of nodes in V and when node i is selected as an initial influential $y_{i}$ becomes one and zero otherwise. Also let X(y) be the set of random variables showing the outcome of the diffusion process initiated by y. Each $X_{i}(y)$ is again a $0-1$ variable indicating whether node i is activated in the diffusion process or not. The elements of X(y) consist of the initially active nodes plus the nodes that are activated later during the diffusion process and the probability distribution that governs the activation of the arcs (therefore the latter nodes) does not depend on y. The objective function $\sigma (S)$ can be equivalently written as $\sigma (S) = f(y) = \sum _{i \in V}E[X_i(y)] =\sum _{r \in {\mathcal {R}}}\sum _{i \in V} \mu _r X_{ir}(y)$. Here the function f has the same meaning with $\sigma$ but its domain is the set $\left\{ 0,1\right\} ^m$. Now $X_{ir}(y)$ shows if node i is reachable from the initially activated nodes in y through active arcs in realization r.

Given these definitions, the budgeted influence maximization binary integer program (BIMBP) with independent cascade diffusion model is presented below:

BIMBP:

$$\begin{aligned} \max \,\,z&=\sum \limits _{r\in {\mathcal {R}}}\sum \limits _{i\in V}\sum \limits _{t\in {\mathcal {T}}_{ir}}\mu _{r}x_{irt} \end{aligned}$$

(1)

$$\begin{aligned} \text {s.t.}&\quad\begin{array}{cc} \sum \limits _{i\in V}c_{i}y_{i}\le B&\end{array} \end{aligned}$$

(2)

$$\begin{aligned}&\begin{array}{cc} x_{ir1}\le y_{i}&\, i \in V, r \in {\mathcal {R}} \end{array} \end{aligned}$$

(3)

$$\begin{aligned}&\begin{array}{cc} x_{irt}\le \sum \limits _{j\in N_r(i)}x_{jr(t-1)}&\, i\in V, r \in {\mathcal {R}}, t\in {\mathcal {T}}_{ir}-\{1\} \end{array} \end{aligned}$$

(4)

$$\begin{aligned}&\begin{array}{cc} \sum \limits _{t\in {\mathcal {T}}_{ir}}x_{irt} \le 1&\, i \in V, r \in {\mathcal {R}} \end{array} \end{aligned}$$

(5)

$$\begin{aligned}&\begin{array}{cc} x_{irt}, y_i \in \{0,1\}&\,i\in V, r \in {\mathcal {R}}, t\in {\mathcal {T}}_{ir} \end{array} \end{aligned}$$

(6)

In BIMBP $y_{i}$ are binary variables showing if the i-th node is selected as an initial influential node or not. $x_{irt}$ are again binary decision variables, and if node i is activated at the t-th step of the independent cascade diffusion process in network realization r, then it is equal to one and otherwise equal to zero. Since the cascading process runs iteratively a new index $t \in {\mathcal {T}}_{ir}$ is introduced to identify the step in which a node is activated. The maximum number of steps to activate a node is equal to the depth of the r-th realization of the network. Therefore, a node can be activated only in one of the steps between 1 (meaning it is selected as an influential at the initial step) and $T_{ir}^{max}$, where $T_{ir}^{max}$ is the maximum number of steps (arcs) to access every reachable node through active arcs starting from node i. The set ${\mathcal {T}}_{ir}$ contains the time index from 1 to $T_{ir}^{max}$ and can be determined by running a breadth-first search initiated at node i for each realization r. The objective function (1) maximizes the expected number of activated nodes. The first constraint (2) limits the amount spent on initially activated nodes to the available budget B. The second set of constraints (3) show that the nodes that are activated in the beginning of the diffusion process which will trigger the cascade are those nodes that are selected as the initial influentials. The constraints (4) dictate that to activate node i in step t of the cascade, at least one of its neighbours should be activated in the previous step. Observe that these constraints exist only when $T_{ir}^{max}>1$. Also notice that in each realization the members of the neighbourhood may change depending whether the arcs connecting node i to its neighbours are active or not. The constraints (5) tell that a node can be activated only in one of the steps of cascade. The formulation ends with binary restrictions on the decision variables (6).

This formulation is valid even for networks with circuits. In such networks, when no precautions are taken in the formulation, a solution may contain some nodes becoming active without any of them being connected to an initial active node because of the circuits. Such solutions are unacceptable and it can be avoided by including a time index as done in this formulation. When the underlying stochastic network ${\mathcal {N}}$ is a directed acyclic graph (DAG), then there is no risk of having solutions with circuits and the formulation can be simplified by dropping the time index. Also constraints (5) are not necessary any more. A similar formulation to the simplified version of our mathematical model for the IMP on DAGs with independent cascade diffusion model is given in (Sheldon et al. 2010) to determine the best locations to be purchased in habitat conservation planning of endangered species.

3 A sample average approximation approach to solve BIMP

Solving BIMBP to optimality is almost impossible for even small networks because of the excessive number of possible realizations $\vert {\mathcal {R}}\vert$. One remedy is approximating $\sigma (S)$ by creating random realizations of the network through sampling. In other words, by flipping a biased coin for each arc (i, j) in the IC diffusion model, an instance of the network ${\mathcal {N}}$ is obtained. As a result, the r-th realization of the network ${\mathcal {N}}_{r} = (V,A_{r})$ contains only the active arcs according to the sampling outcome. Let ${\mathcal {R}}'$ be the set of the realizations through sampling and let $f_{r}(y)$ be the expected number of nodes reachable in network realization ${\mathcal {N}}_{r}$ given the seed vector y. One can create a total of $r=1,\ldots ,R$ realizations of the network $N_{1},\ldots ,N_{R}$ by sampling as described above and define $f_R(y)=\frac{1}{R}\sum \nolimits _{r=1}^R f_r(y)$, which is an unbiased estimate of the original objective function $\sigma (S)$. Notice that we interchangeably use the seed set S and the seed vector y both containing the initially active nodes.

Then the optimization problem BIMBP becomes:

BIMBP-SAA:

$$\begin{aligned} \max \,\,z&=\frac{1}{R}\sum \limits _{r\in {\mathcal {R}}'}\sum \limits _{i\in V}\sum \limits _{t\in {\mathcal {T}}_{ir}}x_{irt}\end{aligned}$$

(7)

$$\begin{aligned} \text {s.t.}&\,(2){\text {-}}(6) \end{aligned}$$

(8)

Note that in all the constraints (2)–(6) of BIMBP-SAA, the index $r\in {\mathcal {R}}'$ (not ${\mathcal {R}}$), which is the set of realizations created by sampling. The quality of approximations of $f_R(y)$ depends on the number of realizations R as well as how they are created. Applying crude Monte Carlo simulation, which has been the classical method for most of the previous research, requires huge values for R. Kempe et al. (2003) report that the solutions of the greedy method stabilize when $R = 10{,}000$ for the co-authorship network they tested in their experimental analysis, which results in long computation times.

Using crude Monte Carlo sampling with $R=10{,}000$ for BIMBP-SAA leads to a very large integer program and makes it difficult to solve. Therefore, it is preferred to use the SAA scheme, which solves many number of integer programs with much smaller sample sizes. Also the SAA method provides both an approximate upper bound and a feasible (hopefully near optimal) solution with a good lower bound on the true optimal solution. In the following subsections the details of determining these bounds are explained. The general SAA procedure presented is adopted from the independent random number streams procedure provided by Mak et al. (1999) but the estimation of the lower bounds use the extended procedure provided in Linderoth et al. (2006).

3.1 Estimation of upper bounds

Let $z^*$ and $f^*_R$ be the optimal objective values of the original problem (BIMBP) and the SAA problem (BIMBP-SAA), respectively. Norkin et al. (1998) proved that $z^*\le {\mathbf {E}}[f^*_{R}]$ by using the notion of expectation relaxation. Therefore, the solution of BIMBP-SAA can be used in estimating an upper bound for the true optimum. For this purpose, M independent BIMBP-SAA samples (or sometimes called replications (Cao et al. 2014) are created, each of which has a sample size of $R_{1}$. Each of these M integer programs are solved using deterministic optimization techniques to obtain M separate solutions. Let these solutions be ${\hat{y}}_{i}$, $i=1,\ldots ,M$ with corresponding objective function values $f_{1i}$. The average of these M solutions; i.e., ${\bar{f}}_1=\frac{1}{M}\sum \nolimits ^{M}_{i=1} f_{1i}$ is an unbiased estimator of ${\mathbf {E}}[f^*_R]$ and it converges to ${\mathbf {E}}[f^*_R]$ with probability one when $M\rightarrow \infty$ (Shapiro 2008). Also, when these M samples are iid, by the Central Limit Theorem

$$\begin{aligned} \sqrt{M}({\bar{f}}_1-{\mathbf {E}}[f^*_R]) \Longrightarrow {\mathbf {N}}(0,\nu ^2)\quad\;\text {as M}\rightarrow \infty . \end{aligned}$$

(9)

Here $\nu ^2$ is the variance of $f^*_R$ and “$\Longrightarrow$” denotes convergence in distribution. The variance $\nu ^2$ can be estimated by using $s^2_M=\frac{1}{M-1}\sum \nolimits ^{M}_{i=1}(f_{1i}-{\bar{f}}_1)^2$. In addition, a $(1-\alpha )$-confidence interval for ${\mathbf {E}}[f^*_R]$ can be constructed by

$$\begin{aligned} \left[ {\bar{f}}_{1}-\frac{z_{\alpha /2}s_M}{\sqrt{M}}, {\bar{f}}_{1}+\frac{z_{\alpha /2}s_M}{\sqrt{M}}\right] \end{aligned}$$

(10)

Observe that the confidence interval is also approximate because of the asymptotic result (9) and for small values of M one can use the t-distribution statistic instead of z with $M-1$ degrees of freedom (Linderoth et al. 2006).

3.2 Estimation of the optimal solution

The solutions ${\hat{y}}_{i}$, $i=1,\ldots ,M$ are all feasible solutions for BIMBP. Therefore, they can be used to estimate lower bounds to the original problem. When ${\hat{y}}_{i}$ is fixed, then computing $f_R(y)$ is a very simple process and it just involves counting the number of reachable nodes through the active nodes in the network starting from the seed set ${\hat{y}}_{i}$. Similar to the estimation of the upper bounds, we create T independent batches of samples but this time with a much larger sample size $R_2$ and the objective function value for each fixed solution ${\hat{y}}_{i}$ is evaluated. Formally, we compute $f_{2ij}({\hat{y}}_i)$ for the fixed solutions ${\hat{y}}_{i}$ using $R_{2}\gg R_{1}$ realizations and $j=1,\ldots ,T$.

With the greatly increased sample size $R_2$, the objective function values are more accurately calculated compared to the upper bound estimates. The averages ${\bar{f}}_{2i}({\hat{y}})=\frac{1}{T} \sum \nolimits ^{T}_{j=1}f_{2ij}({\hat{y}}_{i})$ are calculated for each solution ${\hat{y}}_{i}$. Next, the solution yielding the highest objective function value among ${{\bar{f}}_{2i}}({\hat{y}})$ is identified. Let this solution be ${{\hat{y}}}^*$. It is the best estimate of the SAA procedure to the optimal solution of the original problem. In the last step of the SAA procedure, the objective function value is re-evaluated for only the solution ${{\hat{y}}}^*$ one more time by using T independent batches of samples with a sample size of $R_{3}$, which is usually taken close to $R_{2}$ (Linderoth et al. 2006). The average ${\bar{f}}_3({\hat{y}}^*)=\frac{1}{T}\sum \nolimits ^{T}_{j=1} f_{3j}({\hat{y}}^*)$ is computed. The final objective function value ${\bar{f}}_3({\hat{y}}^*)$ is the output of the SAA method as an approximation to the true optimal value $z^*$.

Note that we use T batches, each of which have $R_{2}$ or $R_{3}$ replications within each batch. As we sample in an i.i.d. manner, we could simply use sample means with a total of $T \cdot R_{2}$ and $T \cdot R_{3}$ realizations, respectively. However, we prefer to state the procedure in this manner because it allows for non-i.i.d. sampling with each batch, as is explored using Latin hypercube sampling in Linderoth et al. (2006).

Since all ${{\hat{y}}}_i$ are feasible solutions to BIMBP then so is ${{\hat{y}}}^*$. Therefore, the relation ${\mathbf {E}}[{\bar{f}}_3({\hat{y}}^*)]\le {}z^*\le {} {\mathbf {E}}[{\bar{f}}_1]$ holds as the sample size converges to infinity. The difference, ${\bar{f}}_1-{\bar{f}}_3({\hat{y}}^*)$ is a statistical upper bound on the true optimality gap $z^*-{\mathbf {E}}[{\bar{f}}_3({\hat{y}}^*)]$ and as the number of samples and realizations increase the estimated optimality gap converges to the true optimality gap. Consequently, the choice for the values of M, T, $R_{1}$, $R_{2}$ and $R_{3}$ becomes an important issue as it effects the trade-off between solution quality and solution time performance. Notice one more time that, in the SAA procedure, only in the first step integer programs are solved. In the second and third steps, $f_{2ij}({\hat{y}}_i)$ and $f_{3j}({\hat{y}}^*)$ are algorithmically computed by simulating the diffusion process, which is computationally less costly then solving an integer program with the same sample size. The steps of the SAA algorithm are summarized in Algorithm 1.

4 Experimental results

In this section details of the experimental results are provided. First, information about the data set is presented. Next, we provide SAA upper bounds and make an analysis on the closeness of both Greedy and SAA methods to optimality. To the best of our knowledge this is the first study to provide such information on the BIMP. We also provide the comparison of the solution qualities of the greedy method and SAA method. Finally, the computation time performance of both methods are compared.

4.1 Dataset and experiment setup

Our testbed consists of the available data from arXiv, which is the same source used in the experimental studies of (Kempe et al. 2003; Chen et al. 2010). In this data set each node is an author and the arcs show the co-authorship relation. Although the network is undirected, we assumed the arcs to be directed and the first authors are assumed to be tails and second authors are assumed to be heads.

There are 37,153 nodes (authors) and 231,507 arcs (co-authorship relationships) in the network. As seen in Fig. 1, the co-authorship network’s characteristics are similar to that of a typical scale-free network, where a few nodes (authors) have high number of connections and most nodes have low number of connections (Yan and Ding 2009). The average out-degree of the network is 4.86 and the maximum out-degree is 152. Also the relationship between the outdegree of a node and its frequency matches a decay function and its log-log graph displays the power-law relationship on the degree distribution (Barabasi 2016).

Fig. 1

Frequency versus outdegree graph of arXiv co-authorship network. (a) Normal graph, (b) Log-log graph

We create different size networks by randomly selecting arcs from this master data set. Since the complexity depends on number of arcs, the size of the sample networks are fixed with respect to the number of arcs, i.e. $m=500, 1000, 2000, 5000, 10{,}000, 20{,}000, 50{,}000$. Also 16 different budget levels $B=5, 10, 15, 20, 25, 30, 40, 50, 60, 70, 80, 90, 100, 125, 150, 200$ are used resulting in a total of 112 different scenario combinations and each scenario is repeated 5 times and the averages are reported.

The weights on arcs (influence probabilities) are sampled uniformly from [0, 1] and the activation costs $c_{i}$ are randomly selected from [0,100]. For the SAA method $M=25$, $T=100$ and $R_1=100$, $R_{2}=R_{3}=10{,}000$. For the greedy method two different settings are tested. In the first case, to have a fair comparison with the SAA method, the greedy method is applied with a similar setting of the SAA approach, where the seeds sets are determined $M=25$ times with $R=100$ samples. Next, the best of these 25 solutions’ objective function values are re-evaluated with $R_{2}=10{,}000$ samples. Finally, the solution with the best objective function value is re-evaluated on more time with $R_{3}$ samples. In the second setting the classical approach used by other authors is used, where the greedy algorithm is run a single time with a sample size of $R=10{,}000$ and the solution is reported. We implemented the CELF (cost-effective lazy forward) version of the greedy method, which is much efficient than the naive one (Leskovec et al. 2007).

All experiments are carried out on Dell PowerEdge 2400 with two 64-bit, 2.66-GHz Xeon 5355 Quad Core processors and 28GB SD Ram memory, operating within Windows 2008 Server environment. CPLEX 12.6 is used with default settings for solving the integer programs of the first step of SAA method (ILOG-CPLEX 2013).

The case $n=12{,}133, m=50{,}000$ leads to the largest integer programs. Because of the scale free network structure, $T_{ir}^{max}$ are only large for very few nodes (maximum observed value is 30) and very low for most of the nodes. In the largest problem there are approximately 2.33 million variables and 2.85 million constraints, meaning that average size for the set ${\mathcal {T}}_{ir}$ is about 2. All the integer programs are solved to optimality, where none of them run longer than 1 h.

4.2 Analysis of solution quality

The lower and upper bounds on the optimal objective function value of the original problem for various different scenarios are presented in Table 1. The first two columns display the number of nodes and arcs in the sample network, whereas the third column displays the available budget. Column four displays the upper bound estimates ${\bar{f}}_{1}(y)$ (shown as UB) together with a $95\%$ confidence interval. Since $M=25$, we used t-distribution values with degrees of freedom 24. Similarly, lower bound estimates, which are also the best feasible solutions of the SAA procedure, ${\bar{f}}_{3}({\hat{y}}^*)$ (shown as $Z_{SA}$), are displayed again with a $95\%$ confidence interval in column five. The last column provides the estimated optimality gap using the formula: $100 \times (UB-Z_{SA})/UB$.

Table 1 Lower and upper bound estimates for $z^*$

The results show that, using SAA method one can obtain promising results for the BIMP. Notice that in almost all problems the optimality gap is within $1\%$ and the lower bound estimate is always inside the $95\%$ confidence interval of the upper bound. In some of the results, the optimality gap is negative which is not uncommon in SAA analysis (Linderoth et al. 2006; Mak et al. 1999). This is due to the larger variance in the estimation of the upper bound.

Next, as presented in Fig. 2, the seed set sizes at the best SAA solutions are displayed. They vary from 2 (for three cases when B = 5 and m = 500, 2000, 5000) to 111 (B = 200 and m = 50,000). Note that the seed set size is directly dependent on the choice of budget B and node activation costs $c_{i}$. In Kempe et al. (2003) the seed set sizes vary from 1 to 30 and in Chen et al. (2010) it is from 1 to 50. In Nguyen and Zheng (2013) budget levels range from 10 to 100. Therefore our choice for B and $c_{i}$ are reasonable.

Lastly, the mean of the best lower bounds of the SAA method are compared with the results obtained by the two different settings of the greedy method. Figure 3 shows the optimality gaps, i.e., the average optimality gap of SAA method and average optimality gaps of the two greedy methods are shown. In the figure, CELF-100x25 represents the average optimality gaps with respect to the Greedy method with SAA setting and CELF-10K show the results obtained by the Greedy method with the classical setting. They are determined by averaging over seven different network sizes’ optimality gap values for each budget level. It is clear that in most cases SAA method outperforms the greedy method with an average optimality gap ranging between 0.18 and $0.79\%$. Notice that the best objective function values obtained by the greedy method is also very close to the estimated upper bound with an average optimality gap range of 0.32–1.40% for CELF-10K and 0.45–2.34% for CELF-100x25, respectively.

Given these results we can comment on an open question in the literature: For the social network samples used in this study, the greedy algorithm performs very well and provides close-to-optimum solutions. Remember that the worst-case bound for the greedy method is $1/2(1-1/e)$, which is approximately $36.78\%$. A similar conclusion is available in Lee et al. (2015). In their study, they formulate a slightly different problem where the aim is minimizing the detection time of a virus in a network. After re-formulating the problem into a maximization form with a sub-modular objective function, they test the performances of the greedy algorithm and SAA method. In their results, in most of the cases greedy outperforms the SAA method with close-to-optimal solutions.

Fig. 2

Optimal seed set sizes with respect to budget and network size

Fig. 3

Comparison of optimality gaps

When the solutions (seed sets) obtained by the two methods (SAA and greedy) are analyzed, in $83\%$ of the cases the seed sets of SAA and Greedy-10K are exactly the same. This value drops to $21\%$ when the seed sets of SAA method are compared with that of Greedy-100x25. For the cases where the seed sets are exactly the same, the estimates of the optimality gap of both methods are very close to each other and the difference is a result due to sampling, where each method use their own stream of samples. Although one can never be sure of the real optimum seed set without enumerating $2^m$ realizations, we provide statistical statements ensuring that the solutions are near optimal. For the remaining $17\%$ (SAA vs Greedy-10K) and $79\%$ (SAA vs Greedy-100x25) of the cases, the seed sets do not match and the solution with the higher objective function can be considered as a better solution. However, its statistical significance should be tested via statistical (paired) t-test (Linderoth et al. 2006) and it is planned as a future research topic.

4.3 Analysis of solution time performance

The average CPU time performances of both methods are provided in Fig. 4. Here, the CPU times are calculated by taking the average over 16 CPU values of the corresponding budget levels and displayed for each one of the seven network sizes. For small size problems SAA method is much faster than the greedy method. In small networks SAA is almost 2–10 times faster than the Greedy method. This is a promising result and needs further discussion.

The benefit of the SAA method over greedy comes from various facts. First, due to the essence of the SAA method integer programs are constructed with considerably smaller number of samples and they are solved very fast when the network size is small. The second fact is related to the structure of simulation of the diffusion process. Both the greedy and SAA methods have to carry out a costly objective function estimation subroutine that simulates the diffusion process of a given seed set. However, the number of calls of greedy method is much more than that of SAA. The number of calls for SAA method is constant at (M + 1)T times ((25 + 1) × 100 = 2600 times in our setting) to calculate $f_{2ij}({\hat{y}}_i)$ and $f_{3j}({{\hat{y}}}^*)$. However greedy calls it in O(nkT) times where k is the number of nodes in the optimal seed set. The increase in CPU time due to increased budget (therefore seed set size) is larger for greedy compared to SAA. Lastly the network structure may have an effect on CPU times. The co-authorship network resembles a typical scale-free network. Here, few nodes have high number of connections (high outdegree) and most nodes have a small number of connections. This results in a sparse matrix structure and probably CPLEX benefits from it and solves the integer programs very efficiently.

As a summary, when the network is small the integer programs are solved very quickly and the time spent on objective function evaluation subroutine dominates the overall CPU time. In this case SAA performs better than greedy. However, when the network size increases and the solution time to solve the integer programs grows faster and it starts to dominate the overall CPU time. In that latter case SAA method’s performance decreases drastically and greedy method starts to outperform.

Fig. 4

Comparison of solution times

5 Conclusion

In this work the budgeted influence maximization problem is studied. Contrary to most studies in the literature we focus on the solution quality rather than solution time performance of BIMP. We provide a binary-integer program to formulate BIMP assuming the Independent Cascade diffusion model. Since the original problem is too complicated to be solved exactly, a sample average approximation (SAA) scheme is proposed. Experimental results over different size networks and budget levels show that SAA works very well and provide approximate optimal solutions. We also observed that the greedy method can find approximately optimal solutions for BIMP, which has been an open question until now. As for the future research directions, different versions of BIMP can be tested with different diffusion models and different type of networks such as random or small world networks. Finally, the SAA method can be further fine-tuned to improve both the solution quality and solution time performance.