Some Qualitative Features of the Isosceles Trapezoidal Four-Body Problem

Abstract

In this article, we present a novel survey of known qualitative features of the isosceles trapezoidal four-body problem, that has three degrees of freedom, as well as its two subsystems with two degrees of freedom, namely, the symmetric collinear four-body problem and the rectangular four-body problem. We use the configurations space to display the “full picture” that allows us to visualize all admissible configurations on the reduced space, homeomorphic to a three-sphere, called the shape sphere.

1 Introduction

In 1988, R. Moeckel [10] performed a qualitative study of the three-body problem getting what he called a “big picture”. Following these very inspiring ideas we fulfill a similar study for the isosceles trapezoidal four-body problem (IT4BP).

The isosceles trapezoidal four-body problem was first introduced by E. Lacomba in two articles published in 1981 and 1983 ([5] and [6], respectively). Since then, the attention has been mainly directed to study its two subsystems: the symmetrical collinear four-body problem (CS4BP) and the rectangular four-body problem (R4BP), and much information has been obtained from them, see among others [1, 2, 7, 8, 12, 13, 15]. However, a topic that has been left aside is the way on how to include information of the subsystems into the IT4BP in order to have a better picture on the dynamical behavior in this problem.

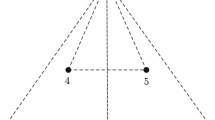
This paper deals with the isosceles trapezoidal four-body problem, where two mass point have equal masses $\mu$, while the remaining two have masses equal to m, see Fig. 1. If the particles lie initially at the vertices of an trapezoid with velocities symmetric with respect to its axis of symmetry, then they will always keep a symmetric trapezoidal configuration when moving under the newtonian law of attraction.

The aim of the present article is to give a step forward on the knowledge of the global dynamics for the IT4BP from its subproblems.

The manuscript is prepared as follows: the isosceles trapezoidal four-body problem is stated in Sect. 2. The regularization of the binary collision have been performed in Sect. 3. In Sect. 4 we carry out a wide review of the known results about the IT4BP and its subsystems, while in Sect. 5 the reduced configuration space is introduced. Finally, we gather from a global perspective all the dynamical features of the IT4BP, the collinear symmetric and the rectangular four-body problems.

2 Setting of the Problem

Let x be the semidistance between the upper pair of bodies with masses $\mu$, y the semidistance between the other two bodies of the trapezoid, both with masses m, and let z be the signed distance between the centers of mass of both binaries. These coordinates x, y, z can be seen as a Jacobi-like system of coordinates. Thus, the positions of the particles are given by

$$\begin{aligned} \begin{array}{cc} q_1 = \displaystyle {\left( x,\frac{m}{m+\mu }z \right) },&{} q_2 =\displaystyle {\left( -x,\frac{m}{m+\mu }z \right) },\\ q_3 = \displaystyle {\left( y,-\frac{\mu }{m+\mu }z \right) }, &{} q_4=\displaystyle {\left( -y,-\frac{\mu }{m+\mu }z \right) }, \end{array} \end{aligned}$$

(2.1)

where the the center of mass remains fixed at the origin. Consequently, the IT4BP is a three degrees of freedom problem. Later, this fact will play a key feature.

Fig. 1

Isosceles trapezoidal configuration

The equations of motion are

$$\begin{aligned} \begin{aligned} x''=&-\frac{\mu }{4x^2}-\frac{m(x-y)}{\left[ (x-y)^2+z^2\right] ^{3/2}}-\frac{m(x+y)}{\left[ (x+y)^2+z^2\right] ^{3/2}},\\ y''=&-\frac{m}{4y^2}+\frac{\mu (x-y)}{\left[ (x-y)^2+z^2\right] ^{3/2}}-\frac{\mu (x+y)}{\left[ (x+y)^2+z^2\right] ^{3/2}},\\ z''=&-(\mu +m)\left[ \frac{1}{\left[ (x-y)^2+z^2\right] ^{3/2}}+\frac{1}{\left[ (x+y)^2+z^2\right] ^{3/2}}\right] , \end{aligned} \end{aligned}$$

(2.2)

where $'=\frac{d}{dt}$.

From [1] we know that the all singularities in the IT4BP are due to collisions. These are given by total collision, two single binary collisions, those of the upper binaries ($x=0$ with y positive, and no restriction on z) and the collision of the bottom binary ($y=0$ with x positive, and no restriction on z), and two simultaneous binary collisions, one being symmetric ($x=y\ne 0$ and $z=0$) while the second one not necessarily symmetric with respect to the real line ($x=y=0$ and $z\ne 0$). See Fig. 2.

Fig. 2

Non total collisions for the isosceles trapezoidal problem.

The Hamiltonian of the system is

$$\begin{aligned} H(x,y,z,p_x,p_y,p_z)=\frac{p_x^2}{4\mu }+\frac{p_y^2}{4m}+\frac{p_z^2}{4M}-U(x,y,z) \end{aligned}$$

(2.3)

where $p_x=2\mu x',p_y=2m y'$ and $p_z=2M z'$ are the momenta, $M=\frac{\mu m}{\mu +m}$ and the potential U is given by

$$\begin{aligned} U(x,y,z)=\frac{\mu ^2}{2x}+\frac{m^2}{2y}+\frac{2\mu m}{\sqrt{(x-y)^2+z^2}}+\frac{2\mu m}{\sqrt{(x+y)^2+z^2}}. \end{aligned}$$

(2.4)

By taking $q=(x,y,z)$, $p=(p_x,p_y,p_z)$ and $A=\text{ diag }\left\{ 2\mu ,2m,2M\right\}$, the Hamiltonian (2.3) becomes

$$\begin{aligned} H=K(p)-U(q), \end{aligned}$$

(2.5)

where $K(p)=\frac{1}{2}p^TA^{-1}p$ is the kinetic energy.

3 Regularization of the Binary Collision

In order to study the behavior of solutions that eject or go to total collision, or pass close to total collision, a classical tool is to blow up the singularity associated to the collision of all particles, which was introduced by McGehee in [9] to study the collinear three-body problem. This is given by a polar-like change of coordinates in the configuration space together with a consistent change in the momenta, and a time reparametrization so that it infinitely slows down the physical time, the new time variable turns out to be a fictitious time.

We define $r=\sqrt{q^TAq}$, such that $r^2=I$ is the momentum of inertia of the particles. Let

$$\begin{aligned} S= \{ q : r^2 = q^TAq=1\} \end{aligned}$$

be the ellipsoid in the configuration space in the norm given by the moment of inertia. We now consider the McGehee’s set of coordinates

$$\begin{aligned} \begin{array}{cc} r=\sqrt{q^TAq}, &{} s=r^{-1}q,\\ v=r^{1/2}\langle p,s\rangle ,&{}\qquad w=r^{1/2}\left( A^{-1}p -\langle p,s\rangle s\right) , \end{array} \end{aligned}$$

(3.1)

together with the rescaling of time given by $dt=r^{3/2}d\tau$.

We remark that coordinate s gives us the shape of the configuration and $q=rs$ provides us with all of the configurations that are homothetic to configuration s.

At this stage, we would point out that as mass matrix A allows us to consider a norm in the configuration space, it also endows the configuration space with the norm $\Vert w\Vert ^2=w^TAw$, see [9].

In McGehee’s coordinates, the motion equations can be written as

$$\begin{aligned} \dot{r}= & {} rv,\nonumber \\ \dot{v}= & {} \Vert w\Vert ^2+\frac{1}{2}v^2-U(s),\nonumber \\ \dot{s}= & {} w, \nonumber \\ \dot{w}= & {} -\frac{1}{2}vw-\Vert w\Vert ^2s+\; \text{ Grad }\, U(s), \end{aligned}$$

(3.2)

where $\cdot =\frac{d}{d\tau }$, $\text {Grad} \,U(s)=U(s)s+A^{-1}\nabla U(s)$ is the gradient vector field at $s\in S$ of the restriction of U to S. The energy relation (2.3) becomes

$$\begin{aligned} \frac{1}{2}\left( v^2+\Vert w\Vert ^2\right) -U(s)=rh. \end{aligned}$$

(3.3)

By taking $r=0$ in the energy relation (3.3) we obtain the set

$$\begin{aligned} \mathcal {C}=\left\{ (s,v,w) \;| \; \frac{1}{2}\left( v^2+\Vert w\Vert ^2\right) =U(s)\right\} , \end{aligned}$$

(3.4)

called the total collision manifold, which is a common boundary for all energy manifolds [4]. The total collision manifold can be though as the spine of a book and each sheet corresponds to a fixed level of energy. Straightforward calculations show that if $r=0$, the first equation in (3.2) becomes $\dot{r}=0$, so $\mathcal C$ is an invariant set under the flow. Indeed, the set $\mathcal {C}$ is also obtained by taking $h=0$ in (3.3).

Once we carry out the change to McGehee coordinates, the singularity associated to the collision of all the particles of the system is replaced by the invariant manifold $\mathcal {C}$, and the flow has been extended to $\mathcal {C}$, that is, to $r=0$. Thus, the singularities for Eq. (3.2) are associated to the non total collisions.

Lets us denote $\hat{s}_1=2x$ the distance between the bodies of the top binary as well as $\hat{s}_2=2y$ the distance between the bodies of the bottom binary. The singularities due to binary collisions of the isosceles trapezoidal configuration can be regularized.

We show that collision of the upper binary can be regularized. It is well-known, that simultaneous binary collisions can be regularized [14]. To regularize explicitly this binary collision we use the change of coordinates associated to the Levi-Civita regularization method given by

$$\begin{aligned} \hat{s}_1=\xi ^2, \qquad \hat{w}_1=\frac{{\eta }}{2\xi }, \end{aligned}$$

(3.5)

together the time reparametrization given by $\displaystyle {\frac{d\tau }{ds}=4\xi ^2}$.

Under the new coordinates, the equations of motion (3.2) transform into

$$\begin{aligned} \frac{dr}{d\tau }= & {} rv,\nonumber \\ \frac{dv}{d\tau }= & {} \frac{\mu }{2\xi ^2}(\eta ^2+1)+2mw_2^2+2Mw_3^2+\frac{1}{2}v^2+\frac{m^2}{2s_2}+f(\xi ^2,s_2,s_3),\nonumber \\ \frac{d\xi }{d\tau }= & {} \frac{\eta }{4\xi ^2},\nonumber \\ \frac{ds_2}{d\tau }= & {} w_2,\nonumber \\ \frac{ds_3}{d\tau }= & {} w_3, \nonumber \\ \frac{d\eta }{d\tau }= & {} \frac{\eta ^2}{4\xi ^2}\frac{1}{\xi }-\frac{v\eta }{4} -\xi \left[ \frac{\mu \eta ^2}{2} +\left( 2mw_2^2+2Mw_3^2\right) +\frac{1}{2\mu }\left( \frac{\mu ^2}{2}\right) \right] \\- & {} \xi \left[ \left( \frac{\mu ^2}{2s_2}+f(\xi ^2,s_2,s_3)\right) \xi ^2+\nabla _{s_1}U(\xi ^2,s_2,s_3)\right] \nonumber \\ \frac{dw_2}{d\tau }= & {} -\frac{1}{2}(vw_2+\mu \eta ^2) -2\xi ^2\left( mw_2^2+Mw_3^2\right) \nonumber \\- & {} \,\frac{1}{2m}\left[ \frac{\mu ^2}{2}+\xi ^2\left( \frac{m^2}{2s_2}+f(\xi ^2,s_2,s_3)\right) +\nabla _{s_2}U(\xi ^2,s_2,s_3)\right] ,\nonumber \\ \frac{dw_3}{d\tau }= & {} - \frac{1}{2}(vw_3+\mu \eta ^2)-2\xi ^2 (mw_2^2+Mw_3^2)\nonumber \\- & {} \,\frac{1}{2M}\left[ \frac{\mu ^2}{2}+\xi ^2\left( \frac{m^2}{2s_2}+f(\xi ^2,s_2,s_3)\right) +\nabla _{s_3}U(\xi ^2,s_2,s_3)\right] \nonumber \end{aligned}$$

(3.6)

and the energy relation (3.3) becomes

$$\begin{aligned} rh-\frac{1}{2}v^2-mw_2^2-Mw_3^2+\frac{m^2}{2s_2}+f(\xi ^2,s_2,s_3)= \frac{\mu }{4\xi ^2}(\eta ^2-2\mu ), \end{aligned}$$

(3.7)

where

$$\begin{aligned} f(\xi _1^2,s_2,s_3)=\frac{\mu m}{\sqrt{(4\xi ^2-s_2)^2+s_3^2}}+\frac{\mu m}{\sqrt{ (4\xi ^2+s_2)^2+s_3^2}} \end{aligned}$$

is an analytical function in a neighborhood of the simple binary collision $\hat{s}_1=0$.

Observe that last equations still have singularities at $\xi _1=0$. Introducing the new time coordinate through $\displaystyle \frac{d\tau }{ds}=4\xi ^2$, the set of Eq. (3.6) are now regular.

The regularization of the below binary collision $s_2=0$ is done in a similar way.

We remark that if we multiply (3.7) by $\displaystyle \frac{1}{4\xi ^2}$, we have that $\eta \rightarrow \sqrt{2\mu }$ as $\xi \rightarrow 0$.

Another singularity corresponds to the symmetric simultaneous collisions of the pairs of bodies at the lateral sides of the trapezoid. It occurs when $x=y\ne 0$ and $z=0$.

4 Rectangular and Collinear Symmetric Four-Body Subsystems of the Isosceles Trapezoidal Problem

In this section review known results concerning the IT4BP as well as its subsystems, namely, the CS4BP and the R4BP.

Proposition 4.1

[6] For a fixed level of energy, the set of collision orbits in the IT4BP is given by the union of several submanifolds, two of dimension three corresponding to convex central configurations, and two of dimension two, associated to the configurations of Moulton (collinear), and another manifold of dimension two, related to total ejection orbits.

The two subsystems of the IT4BP have two degrees of freedom, they are given by the CS4BP and the R4BP. These subproblems are obtained when the four bodies always keep a collinear configuration ($z=0$) or, when the bodies lie at the vertices of a rectangle $(x=y)$, see Fig. 1. Observe that, in order to preserve this rectangular configuration under evolution all the masses must be equal, and for the CS4BP, the masses of the inner pair have to be equal and the masses of the remaining two particles are required to be equal in order to preserve the collinear symmetric configuration under time evolution.

Proposition 4.2

[2, 7, 8] For the CS4BP and the R4BP, their corresponding total collision manifolds are two-dimensional manifolds, independent of the total energy h, invariant under the flow and topologically equivalent to a sphere minus four points. On each total collision manifold there are two hyperbolic equilibrium points $E^+$ and $E^-$, which have associated their corresponding stable $W^s$ and unstable manifolds $W^u$. For any energy level there is an heteroclinic connection between the equilibria given by a unique homothetic orbit, that is, an orbit that is contained in the intersection of the manifolds $W^u(E^+)\cap W^s(E^-).$

For the two subsystems there is more information for invariant negative energy surfaces. In the case of the R4BP, there are two ways to escape, the binaries to the left and right of the rectangular configuration go to infinity in a horizontal way, such binaries may experience simultaneous binary collisions and the heigh of the rectangle remains bounded, or the top and bottom binaries escape vertically suffering simultaneous binary collisions while the width of the rectangle stays bounded. Moreover,

Proposition 4.3

[8] There are two ejecting orbits that reach infinity, one does it parabolically, while the other reaches infinity in a hyperbolic way.

The authors use this result to prove the following.

Proposition 4.4

[8] For the R4BP and a fixed negative level of energy, there are oscillatory trajectories passing close to total collapse and infinity.

These oscillatory orbits are trajectories that pass close to total collision, go to infinity with rectangular configuration of a infinite height and bounded width, go back close to total collapse, may repeat this behavior or reach infinity again as a rectangle with a unbounded width and infinite height and continue its oscillatory motion following this behavior.

Equally, the CS4BP presents interesting motions as the following results show. In particular, in [7], the authors proved in an analytical way the existence of a very rich family of orbits.

Proposition 4.5

[7] For any of negative energy level in the CS4BP, there are orbits that eject from total collision, perform a finite sequence of non simple collisions, binary collisions of the inner pair of bodies and/or symmetric double binary collisions to finally end in total collapse

These orbits can be regarded as heteroclinic connections between the equilibrium points, points which lie on the total collision manifold.

In addition, for the CS4BP, Alvarez-Ramírez et al. [2] studied analytical and numerically orbits that eject from (or collide to) total collision and escape to infinity or eject from it. They proved the next analytical result.

Proposition 4.6

[2] There are ejection-direct escape orbits that after being ejected perform a sequence of only one of the possible non total collisions; that is, binary collisions of the inner pair or symmetric simultaneous binary collisions.

Besides, for a fixed value of the mass parameter they found numerically orbits that directly escape to (come from) infinity and show a unique type of non total collisions. Moreover, they gave a method that can be used for any value of the mass parameter. We recall that in this subsystem there are two ways for an orbit to escape: the outer bodies escape in a symmetric manner while the motion of the inner pair remains bounded and perhaps performing single binary collisions or all of the particles escape performing symmetric double binary collisions.

5 The Reduced Configuration Space and the Shape Sphere

5.1 Reduction Through Classical Conserved Quantities

The differential equations that model the n-body problem give rise to a dynamical system that is high dimensional, it is possible to reduce the problem to a lower number of dimensions by using the the classical first integrals of motion: the total momentum

$$\begin{aligned} p_1+p_2+\cdots +p_n, \end{aligned}$$

(5.1)

the center of mass

$$\begin{aligned} \frac{1}{\mathcal {M}}\left( m_1q_1+m_2q_2+\cdots +m_nq_n\right) \end{aligned}$$

(5.2)

where $\mathcal {M}=\sum _{i=1}^n m_i$, the total angular momentum

$$\begin{aligned} \omega =q_1\times p_1+q_2\times p_2+\cdots +q_n\times p_n, \end{aligned}$$

(5.3)

and the total energy $H=K-U$.

After these reductions we obtain a space where energy and angular momentum are constant, whose topology depend on the energy, angular momentum and the masses of the bodies. Even with this reduction on the number of dimensions, the remaining number of dimensions is still too many.

5.2 Reduction via McGehee Coordinates and Configuration Space for IT4BP

The adoption of the McGehee coordinates [9] becomes convenient to study our problem from a geometrical setting. We restrict to the planar four-body problem and consider the moment of inertia I about the origin, this is plausible since the center of mass is set at the origin. In fact, the square root of the moment of inertia $r=\sqrt{I}$ measures the size of the configuration and can be seen as the radial component of the polar-like set of coordinates and $r=0$ corresponds to the total collision of all particles. We use the size of the configuration to normalize the configuration $q=(q_1,\ldots , q_4)$ formed by the particles. The coordinate $s=\frac{1}{r}q$ normalizes the positions and gives a measure of the “angular component” of the configuration. It is immediate to show that $s^TAs=1$. Thus, the set of all non trivial possible shapes is parametrized by an ellipsoid, that corresponds to the sphere of unit radius $\mathbb {S}^2$ under the metric defined by the matrix of masses A. By using coordinate s, we miss the size of the configuration but we keep the shape of the configuration.

In order to deal in an adequate way with the total energy and angular momentum it is convenient to make the transformation in the momenta given by $z=\sqrt{r} p,$ where $p=(p_1,p_2,p_3,p_4)$. In terms of coordinates $(s,z)=(s_1,s_2,s_3,s_4,z_1,z_2,z_3,z_4)$ the energy and angular momentum can be written as

$$\begin{aligned} hr=H(s,z)=\frac{1}{2}z^{T}Az-U(s)\quad \text{ and }\quad \sum _{i=1}^4 z_i\times s_i=\frac{1}{\sqrt{r}}\omega . \end{aligned}$$

(5.4)

Proposition 5.1

In terms of coordinates $(s,z)=(s_1,s_2,s_3,s_4,z_1,z_2,z_3,z_4)$ the energy and angular momentum can be written as

$$\begin{aligned} hr=H(s,z)=\frac{1}{2}z^{T}Az-U(s)\quad and\quad \sum _{i=1}^4 z_i\times s_i=\frac{1}{\sqrt{r}}\omega . \end{aligned}$$

(5.5)

The known integrals give rise to invariant sets described in terms of coordinates r, s, z. Given prescribed values for $\omega$ and h for the angular moment and energy, respectively, we obtain the invariant set

$$\begin{aligned} M(\omega ,h)= \left\{ (r,s,z) \; | \; r\ge 0, \quad \sum _{i=1}^4 m_is_i=0 \quad \text{ and } \quad (5.5)\right\} . \end{aligned}$$

(5.6)

that is still high dimensional.

There is another way to study our problem, a more geometrical one, where we take into account the geometry of the shapes of the configurations under study. For the IT4BP each configuration is associated to a trapezoid, and to rely on this geometric feature is more intuitive than to take also into consideration the behavior of the momenta. This is a very good reason to direct our attention only to the set of configurations.

Definition 5.2

The configuration space for the IT4BP is given by

$$\begin{aligned} V=\left\{ (q_1, q_2,q_3,q_4)\in \left( \mathbb {R}^2\right) ^4\; | \; \mu q_1+\mu q_2+mq_3+mq_4=0 \right\} , \end{aligned}$$

(5.7)

where the positions are given by (2.1), and the centre of mass is fixed at the origin.

5.3 The Quotient Map and the Shape Sphere

Moeckel [10], Montgomery [11] and Chen [3] used Jacobi-like systems of coordinates in the planar three-body problem (P3BP) and the parallelogram four-body problem (P4BP) to reduce the dimension of the space of configurations to identify the admissible configurations through the Hopf fibration. Since the IT4BP, P3BP and the P4BP have three degrees of freedom, we shall follow this approach for the IT4BP.

Now, we rely on complex coordinates to state Jacobi-like coordinates for the isosceles trapezoidal four-body problem and define

$$\begin{aligned} (z_1,z_2):=(q_4-q_2,q_1-q_2)\in \mathbb {C}^2. \end{aligned}$$

(5.8)

These Jacobi-like coordinates are a convenient way to parametrize the configuration space V and they are shown in Fig. 3.

Fig. 3

Jacobi-like coordinates for the isosceles trapezoidal configuration

The reduced configuration space $\tilde{V}$ is obtained by identifying $(z_1,z_2)\in \mathbb {C}^2$ with $(\tilde{z}_1,\tilde{z}_2)\in \mathbb {C}^2$ if there exists $\theta \in \mathbb {R}/\mathbb {Z}\cong \mathbb {S}^1$ so that $(\tilde{z}_1,\tilde{z}_2)=e^{i\theta }(z_1,z_2)$. In this way, this reduced space is $\mathbb {S}^1$-invariant. Let $[(z_1,z_2)]$ be the equivalence class associated to $(z_1,z_2)$ under this equivalence relation. Through this, we identify two isosceles trapezoidal configurations if they are rotationally equivalent. So, we have that $V/SO(2)\cong \mathbb {C}^2/\mathbb {S}^1$.

Next, we shall identify V/SO(2) with $\mathbb {R}^3$ by means of the Hopf fibration. To do so, consider the Hopf map

$$\begin{aligned} \Pi : \mathbb {C}^2\rightarrow \mathbb {R}\times \mathbb {C}\cong \mathbb {R}^3 \end{aligned}$$

(5.9)

defined as

$$\begin{aligned} \mathcal {\Pi }(z_1,z_2)=(|z_1|^2-|z_2|^2, 2\overline{z}_1z_2). \end{aligned}$$

(5.10)

This map takes the unit three sphere $\mathbb {S}^3$ in $\mathbb {C}^2$ into the unit sphere in $\mathbb {R}^3$. Consider $(w_1,w_2,w_3)\in \mathbb {R}^3$, where $w_1=|z_1|^2-|z_2|^2, w_2=\text{ Re }(2\overline{z}_1z_2)$ and $w_3=\text{ Im }(2\overline{z}_1z_2)$. If $z_1=a+ib$ and $z_2=c+id$, then we have that $w_1=(a^2+b^2)-(c^2+d^2)$, $w_2=2(ac+bd)$, $w_3=2(ad-bc)$. A straightforward computation shows that the image of $\mathbb {S}^3$ in $\mathbb {C}^2$ is the unit sphere $\mathbb {S}^2\subset \mathbb {R}^3.$

We denote by $\Pi$ to the extension of the Hopf map to $\mathbb {C}^2$, that is $\Pi :\mathbb {C}^2\rightarrow \mathbb {R}^3$. It is worthwhile to observe that $\Pi$ is invariant under the equivalence relation given by rotations $e^{i\theta }$, that is, ${\Pi }(z_1,z_2)=\Pi (e^{i\theta }z_1,e^{i\theta }z_2)$.

As a consequence, we have that the dynamics of the evolution of the trapezoids can be seen as motions of points in the three dimensional space through the compositions of maps

$$\begin{aligned} (q_1,q_2,q_3,q_4)\mapsto (z_1,z_2)\mapsto \left[ (z_1,z_2)\right] \mapsto (w_1,w_2,w_3). \end{aligned}$$

Next, we use spherical coordinates

$$\begin{aligned} (w_1,w_2,w_3)=(r^2\cos \phi \cos \theta , r^2\cos \phi \sin \theta , r^2\sin \phi ) \end{aligned}$$

(5.11)

in the reduced space $\mathbb {R}^3$. As we vary radius r we obtain different spheres, each containing a full set of equivalence classes of shapes, so we choose the sphere with $r=1$ as a model, and refer to it as shape sphere.

Fig. 4

Shape sphere for the isosceles trapezoidal problem.

5.4 Similarity Classes of Trapezoids

It is a tool that helps us to get another insight on the planar isosceles trapezoidal four-body problem, where for each point on the shape sphere we associate to it an oriented similarity class of trapezoids. Next, we give a description of the of the points on the shape sphere in terms of the possible configurations for a trapezoid.

The shape sphere has several distinguished points, some corresponding to central configurations and others corresponding to simple collisions. The following observations give us some geometric features for points on the shape sphere. See Fig. 4.

Fig. 5

Reduced configuration space

• The equator of the sphere represents to all the isosceles trapezoidal collinear configurations. This follows from the fact that $w_3=2\,\mathbb {I}m(\tilde{z}_1z_2)$ is equal to twice the area of the parallelogram generated by $z_1$ and $z_2$. So, $w_3=0$ means that $z_1$ and $z_2$ are collinear and the four bodies at $q_1,q_2,q_3$ and $q_4$ form a collinear configuration.

• Observe that $\frac{1}{2} w_2=ac+bd$ is the scalar product of $z_1=q_4-q_2$ and $z_2=q_1-q_2$, seen as vectors in $\mathbb {R}^2$. So, $z_1$ and $z_2$ are perpendicular when $w_2=0$. For this reason, under condition $w_2=0$, the corresponding trapezoids are rectangular configurations. Hence, the great circle with $w_2=0$ corresponds to the set of all rectangular configurations.

• In the equator we must also find the simultaneous double collisions of the top and bottom binaries, represented by point $SC_{t,b}$; point SBC in the equator represents the symmetric simultaneous binary collision of the lateral binaries, see Fig. 5. Also, the two collinear central configurations $E_1$ and $E_2$ ([6]) lie on this equator and their positions depend on the values of the masses.

• The trapezoids on the upper hemisphere, that is, having $w_3=\frac{1}{2}(ad-bc)$ positive and vertices $q_1,q_2,q_3,q_4$ are positively oriented, that is, $(q_4-q_2)\times (q_1-q_2)=z_1\times z_2$ is a positive multiple of the area generated by the canonical vectors $e_1$ and $e_2$ in the plane, while the trapezoids in the lower hemisphere correspond to the negatively oriented trapezoids.

• The two non-collinear central configurations, represented by points $NC_1$ and $NC_2$ must lie on the circle $w_2=0$ of rectangular configurations, see [6]. The point $NC_1$ is associated to the configuration of the positively oriented square is found in the upper hemisphere, while $NC_2$ in the lower hemisphere is associated to the negatively oriented square. As a square configuration is obtained when $\Vert z_1\Vert =\Vert z_2\Vert$, that is $w_1=0$. Hence, $NC_1$ and $NC_2$ correspond the north and south poles, respectively.

• When considering the two simple binary collisions, where the first one corresponds to collision of the bodies of the top binary and the second to collision of the bodies of the bottom binary. These collisions can not be seen on the shape sphere since they give rise to isosceles triangles associated to degenerate trapezoidal configurations

In polar-like coordinates, the Hill region is determined by restrictions imposed by the energy relation in (5.5). Since the kinetic energy is non-negative it follows that $U(s)\ge hr$, then for a given shape $s_0$, it is satisfied $U(s_0)/|h|\ge r$. The geometry of the Hill region is shown in Fig. 5, it looks like a shirt with several arms.

The reduced configuration space is obtained when we delete the points associated to non total collision points and has the form (topologically) of a shirt with four arms or two pants glued by the waist. Each hole corresponds to one of the non total collisions, the binary collision of the upper binary, collision of the inferior binary, simultaneous collision of the upper and bottom binary and the symmetric simultaneous binary collisions of the pairs of bodies to the right and left side of the trapezoidal configuration.

6 On the Global Dynamics of the IT4BP

Next, we gather together the known information, given in Sect. 4, on the isosceles trapezoidal problem and its two subsystems in the case of negative energy in order to have a better understanding on the global dynamical picture for this three degrees of freedom problem. We use the reduced configuration space, that is, the space that lie between the shape sphere and the four arms shirt, see Fig. 6. From now on, for our analysis we shall appeal to it.

Since 1974, McGehee coordinates [9] have been the main tool in the study of behavior of orbits ejecting, reaching or passing nearby total collision in the N-body problem, where this singularity is replaced by an invariant manifold. This is precisely the procedure used by Lacomba in [5] to study of total collision for the IT4BP and continued in [6]; as we know, orbits ejecting from (or going to) total collision end at a central configuration. He showed, see Proposition 4.1, that the IT4BP has four of them, two collinear and two non-collinear, each collinear one has associated one invariant manifold of dimension two and each non-collinear central configuration has associated one three dimensional manifold. So, any orbit that starts at (or ends in) total collapse must belong to any of these manifolds, in our figure we show some of these orbits.

Concerning both subsystems, from Proposition 4.2, there exist two homothetic orbits that are ejection-collision orbits that keep their shape unchanged, but not their size, that grow from zero to a maximum and then go back to total collapse, they can be viewed as orbits homoclinic to quadruple collision, one is related to the R4BP and the other to the CS4BP. Thus, these homohetic orbits appear in the figure as four line segments with one end on the shape sphere, going to the outer surface and living on a rays passing through the central configuration at which they are associated.

Fig. 6

Some geometric features on the global dynamics.

From Proposition 4.3, we know that for the R4BP and a negative energy surface there are two orbits that escape to infinity after been ejected from total collapse, one escapes parabolically and the other does it in a hyperbolic way. We see one of them in the figure, where it ejects from a non collinear central configuration and afterwards escapes along the lower arm. Also, we see two other orbits, one goes from the shape sphere to infinity along the upper arm and then goes back close to the shape sphere, and the second one travels from the upper arm to the lower arm, connecting both infinities and passing close to the shape sphere. They correspond, respectively, to a homoclinic and a heteroclinic oscillatory orbits that get close to infinity when escaping in the two possible ways, either by becoming a very tall and thin rectangle or a very wide and short one, see Proposition 4.4.

We also see an orbit that is ejected from the collinear central configuration $E_1$ and then goes back to the same central configuration performing, in the meantime, a sequence of simple binary collisions or symmetric simultaneous binary collisions. The existence of such type of orbits for the CS4BP is assured by Proposition 4.5. In the same figure we show an orbit of this type as one that ejects from total collapse, may go along the left arm, reaches a maximum distance from total collision, and then goes back to total collision.

Finally, on one hand, from Proposition 4.1, there is a manifold of dimension two consisting of direct escape orbits for the IT4BP, and for the other hand, for the CS4BP (Proposition 4.6) there are direct escape orbits presenting a sequence of only collisions of the inner pair of particles or a sequence of simultaneous binary collisions. These orbits must belong to the manifold of direct escape orbits for the IT4BP. In Fig. 6 we show an orbit of this kind, emerging from point $E_2$ and escaping along the right arm.

7 Conclusions

A complete understanding of the IT4BP remains as a problem far from being achieved, the progress accomplished in this direction seems small, we need to have a better comprehension of the features of its subsystems and to find the way they are connected in order to get closer to having a “big picture” of what is going on in the full problem. For instance, are there any connections between the infinities of R4BP and CS4BP?