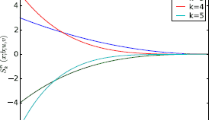Rational Parameterizations Approach for Solving Equations in Some Dynamical Systems Problems

Abstract

We show how the use of rational parameterizations facilitates the study of the number of solutions of many systems of equations involving polynomials and square roots of polynomials. We illustrate the effectiveness of this approach, applying it to several problems appearing in the study of some dynamical systems. Our examples include Abelian integrals, Melnikov functions and a couple of questions in Celestial Mechanics: the computation of some relative equilibria and the study of some central configurations.

1 Introduction

A very common way to solve equations involving polynomials and square roots of polynomials consists in squaring them several times until they become polynomials and look for their zeros using a numerical method. Besides the fact that the degree of such polynomials increases with any squaring, there exists a second inconvenience (harder than the first one): there appear many spurious solutions that must be discarded. This is usually done numerically, that is, finding (with a given precision) all the real roots of the final polynomial equation, replacing them into the original equation and imposing the final value to be smaller than a given tolerance. Of course, this is not a rigorous proof and to get a correct solution, one has to follow these two steps using interval arithmetic (see for instance the first example of this Sect. 1). The problem becomes more complicated when, instead of working with an equation, we deal with systems of equations of similar features. Is this the best convenient procedure to follow?: The answer is “no” and we will illustrate how rational parameterizations can be, in many cases, used to approach this kind of problems. As it will be seen, this method eliminates the spurious solutions and determines a well-posed domain containing the actual ones. This assertion will be supported on several examples.

The use of rational parameterizations to study the solutions of equations containing square roots is, in fact, an already known technique (see for example [1, 10, 20] and references therein). Although a few authors have introduced its use in dynamical systems (see, for instance [18]). In our opinion it has not received an special attention and its use in this setting is still infrequent.

The aim of this work is to show, by means of some examples, that the use of rational parameterizations is more than an alternative method to find the number of solutions in problems appearing in dynamical systems. Indeed, it permits, in some cases, to reduce the original question to a well-posed polynomial problem. Once this is moved into a polynomial setting, there are standard tools to approach its solutions, like the use of resultants or Gröbner basis (see for instance [23]).

The fundamental idea in the method is to impose that any expression appearing inside the square root symbol is equal to some new squared variable. This condition can be rewritten as an algebraic expression of the form $F_\lambda (x,y)=0,$ where $\lambda \in {\mathbb {R}}^k$ is a set of parameters. Cayley–Riemann’s Theorem ([2]) ensures that this algebraic curve can be rationally parameterized if and only if its genus is zero. Moreover, in such case there are effective methods to find a parameterization (see [21, Chapters 4 & 5]). In fact, many programs of symbolic calculus have implemented some of these methods and algorithms. The situation where $F_\lambda (x,y)=0$ has genus zero is the one that will appear henceforth in the examples and results presented in this work.

Let us begin with a simple well-known toy problem, that of the two leaning ladders (see for instance [5, 13]). It reads as follows: consider two ladders, of length A and B, leaning in opposite directions between two parallel walls. Assume that both of them contact the base of the opposite wall and that they cross in a point at distance h from the ground floor. Can we determine the distance w between both walls? And the distances a and b between the ground floor and the point where each ladder contacts its corresponding wall? (see Fig. 1).

Fig. 1

The two leaning ladders problem

Applying Thales’ Theorem it follows that the relation $1/h=1/a+1/b$ must be satisfied or, using Pythagoras, that

$$\begin{aligned} \frac{1}{h} = \frac{1}{\sqrt{A^2 - W}} + \frac{1}{\sqrt{B^2 - W}}, \end{aligned}$$

(1)

where $W=w^2.$ Squaring this equation, recurrently, one gets the final polynomial equation of degree 4, 

$$\begin{aligned} P(W):= & {} {W}^{4}+ \left( -2 {A}^{2}-2 {B}^{2}+4 {h}^{2} \right) {W}^{3}\\&\ \quad + \left( {A}^{4}+4 {A}^{2}{B}^{2}-6 {A}^{2}{h}^{2}+{B}^{4}-6 {B}^{2} {h}^{2} \right) {W}^{2}\\&\ \quad +\,\left( -2 {A}^{4}{B}^{2}+2 {A}^{4}{h}^{2}-2 {A}^{2}{B}^{4}+8 {A}^{2}{B}^{2}{h}^{2}+2 {B}^{4}{h}^{2} \right) {W}\\&\ \quad +\,{B}^{4}{A}^{4}-2 {B}^{2}{h}^{2}{A}^{4}+{h}^{4}{A}^{4}-2 {B}^{4 }{h}^{2}{A}^{2}-2 {B}^{2}{h}^{4}{A}^{2}+{B}^{4}{h}^{4}=0. \end{aligned}$$

Depending on the values of the parameters A,  B,  and h, one should look for positive zeros of this polynomial. It can be seen that it has more than one of these positive zeros. Afterwards, one must substitute them into Eq. (1) to decide whether or not they are in fact solutions.

An alternative way to solve (1) is to seek for a new variable t,  such that W is a rational function of t and in such a way that the equivalent problem has no spurious solutions. To find such change of variables, we notice that from $a^2= A^2 - W$, $b^2= B^2 -W$ the variables (a, b) move on the hyperbola $b^2 - a^2 = B^2 - A^2.$ This curve, in the (a, b)-plane, has genus zero and so, by Cayley–Riemann’s Theorem, it can be rationally parameterized. Indeed, let us find a rational parameterization for it. Having in mind that $b^2-a^2 = (b+a)(b-a),$ we introduce a real parameter t such that

$$\begin{aligned} b+a=t, \qquad b-a= \frac{B^2-A^2}{t}. \end{aligned}$$

Isolating a and b in terms of t we get

$$\begin{aligned} a=\frac{t^2 +A^2-B^2}{2t}, \qquad b=\frac{t^2 +B^2-A^2}{2t}. \end{aligned}$$

(2)

Since $a,b>0,$ it follows that $t>\sqrt{|A^2-B^2|}$ and we can parametrise W in terms of t as

$$\begin{aligned} W= & {} A^2-a^2=A^2-\left( \frac{t^2 +A^2- B^2}{2t}\right) ^2 \nonumber \\= & {} -\frac{(A^2-B^2)^2}{4t^2}+\frac{A^2+B^2}{2}-\frac{t^2}{4}=:\varphi (t). \end{aligned}$$

(3)

Therefore to study $P(W)=0$ is equivalent to consider $P(\varphi (t))=0$, where

$$\begin{aligned} P\left( \varphi (t)\right)= & {} \frac{ t^4 - 4ht^3 - \left( A^2 - B^2 \right) ^2}{h(t^2+A^2-B^2)(t^2-A^2+B^2)}\\=: & {} \frac{Q(t)}{h(t^2+A^2-B^2)(t^2-A^2+B^2)}. \end{aligned}$$

Hence, instead of solving $P(W)=0,$ we can solve $Q(t)=0.$ Each of the positive roots of this second equation produces, by using (3), a unique W which is a solution of (1). In fact, taking into account Bolzano’s Theorem and Descartes’ rule (it exhibits one change of sign when moving over its coefficients), it follows the existence of a unique positive root of Q, $t=t^*$ such that $w^*=\sqrt{W^*}=\sqrt{\varphi (t^*)}$ is the unique solution of our initial problem. The values of a and b are also unique and they can be determined similarly from (2).

To illustrate the advantages of this approach, we provide the details in a particular case. So, take for instance $A=7,$$B=6,$ and $h=3.$ Then,

$$\begin{aligned} P(W)={W}^{4}-134{W}^{3}+6163{W}^{2}-106326W+426465=0 \end{aligned}$$

has two positive solutions, $W_1\simeq 5.635917$ and $W_2\simeq 33.066465$. The actual solution is $W_1,$ since one can discard analytically the spurious solution $W_2$ using simple inequalities. Indeed, by Bolzano’s Theorem, we know that $33<W_2<331/10.$ Hence, from Eq. (1), it follows that

$$\begin{aligned} \frac{1}{h} -\frac{1}{\sqrt{A^2 - W_2}} -\frac{1}{\sqrt{B^2 - W_2}}= & {} \frac{1}{3} -\frac{1}{\sqrt{49 - W_2}} -\frac{1}{\sqrt{36 - W_2}}\\< & {} \,\frac{1}{3} -\frac{1}{\sqrt{49 - 33}} -\frac{1}{\sqrt{36 - 33}}=\frac{1}{12}-\frac{\sqrt{3}}{3}<0, \end{aligned}$$

and so $W_2$ is not a solution of (1). It has artificially appeared when squaring the formulas. Notice that in general discarding spurious solutions using interval arithmetic computation can be quite complicated (see for instance the last example in Sect. 3).

On the other hand our approach provides a direct answer: in the new variable t,  we get that

$$\begin{aligned} Q(t)=t^4-12t^3-169=0 \end{aligned}$$

has a unique positive root, $t_1^*\simeq 12.095502,$ and then

$$\begin{aligned} \varphi (t_1^*)=\left. \left( -\frac{169}{4t^2}+\frac{85}{2}-\frac{t^2}{4}\right) \right| _{t=t_1^*}=W_1. \end{aligned}$$

Hence, the solution of our problem is $w=\sqrt{W_1}\simeq 2.374008.$

Another easy application of the rational parameterization is to prove identities involving square roots. For instance the one appearing in [17], which says that for $x>y>0$ it holds that

$$\begin{aligned} \sqrt{x\pm y}=\sqrt{\frac{x}{2}+\frac{\sqrt{x^2-y^2}}{2}}\pm \sqrt{\frac{x}{2}-\frac{\sqrt{x^2-y^2}}{2}}, \end{aligned}$$

follows straightforwardly from the parameterization

$$\begin{aligned} x=\frac{t^2+s^2}{2t},\qquad y=\frac{t^2-s^2}{2t}, \end{aligned}$$

with $t>s>0.$ Indeed,

$$\begin{aligned} \sqrt{x+y}=\frac{t}{\sqrt{t}},\quad \sqrt{x-y}=\frac{s}{\sqrt{t}}\quad \text{ and }\quad \sqrt{\frac{x}{2}\pm \frac{\sqrt{x^2-y^2}}{2}}= \frac{t\pm s}{2\sqrt{t}}. \end{aligned}$$

This useful parameterization is obtained again from a genus zero planar curve. As before, it is natural to impose that $x^2-y^2=s^2,$ for some unknown value s. Hence the planar curve $F_s(x,y)=x^2-y^2-s^2,$ for $s\ne 0$, is irreducible and has genus zero. Therefore it admits a rational parameterization. The one given above is the simplest one.

These two simple examples show the advantages of using rational parameterizations to solve equations involving square roots. Along the paper some more applications of this use are presented. We briefly describe its contents. In Sect. 2 we recall with a simple example how to deal with 1-parameter families of polynomials systems, a common final situation after applying rational parameterizations. We will focus our attention on three particular types of applications. The first one, in Sect. 3, deals with polynomial expressions with two square roots of polynomials. These equations arise in the study of the number of zeros for some Abelian integrals (see [15]). The second one, in Sect. 4, handles with central configuration problems in Celestial Mechanics. Here, square roots appear due to the Euclidean distances among the bodies. Two examples are presented: one concerning critical points of a certain potential (see [6]) and a second one dealing with central configurations (see [7, 22]). And the third type, in Sect. 5, where we seek for estimates for the number of limit cycles of planar non-autonomous differential equations by studying the zeros of some Melnikov functions. The problem considered was proposed in [9].

2 Preliminary Results: Systems of Polynomial Equations

The well-known Bezout’s Theorem asserts that, generically and taking into account the solutions at infinity, the number of complex solutions $x\in \mathbb {C}^k$ that a polynomial system $\left\{ F_j(x)=0\right\} _{j=1,\ldots ,k}$ has is $\prod _{j=1}^k \deg (F_j)$. Moreover, this number only changes when some of these degrees vary. This situation is drastically different when one is interested only in its real solutions. In this sense, we focus our attention on 1-parameter families of polynomial systems and we are concerned about knowing when the number of their simple real solutions vary. To this end we introduce the following definition:

Definition 2.1

Let $F_i(x,\lambda )$ be real polynomials in $x\in \mathbb {R}^k,$$i=1,\ldots ,k,$ and $\lambda \in {\mathbb {R}}.$ An effective bifurcation value is a real value $\lambda ^*$ such that the number of simple real solutions of the system $\{F_i(x,\lambda ^*+\varepsilon )=0\}_i$ is different for $\varepsilon >0$ than for $\varepsilon <0,$ for any small enough $\varepsilon$.

Next example illustrates how these effective bifurcation values can be obtained by applying the techniques developed in [23]. In this particular example, both polynomials have degree 2 and effective bifurcations occur.

Proposition 2.1

The effective bifurcation values for the number of simple real solutions of the system of polynomial equations

$$\begin{aligned} F(x,y,\lambda )&=(- \lambda +1) x^2+3 \lambda y^2-x- \lambda y=0,\nonumber \\ G(x,y,\lambda )&=\lambda x^2+(2 \lambda +1) y^2-2 y+ \lambda x=0, \end{aligned}$$

(4)

are the four real roots of the polynomial $P_8(\lambda )=107\lambda ^8-1190\lambda ^7 +2525\lambda ^6-3222\lambda ^5+3307\lambda ^4+568\lambda ^3-868\lambda ^2+160\lambda - 4,$ namely,

$$\begin{aligned} \lambda _1\simeq -0.5081,\quad \lambda _2\simeq 0.02967, \quad \lambda _3\simeq 1.7826,\quad \lambda _4\simeq 8.7774. \end{aligned}$$

Moreover, the number of simple real solutions in the intervals $(-\infty , \lambda _1), ( \lambda _1, \lambda _2),$$( \lambda _2, \lambda _3),$$( \lambda _3, \lambda _4),$$( \lambda _4,+\infty )$ is 2, 4, 2, 4, 2,  respectively (see Fig. 2).

Fig. 2

$N(\widetilde{\lambda })$ denotes the number of real solutions of system (4) for $\lambda =\widetilde{\lambda }$

Proof

The first step consists on computing the resultants of F and G with respect to x and y. This is based on the fact that ${\text {Res}}(p(x),q(x),x)=0$ if and only p(x) and q(x) have a common root (see [23]). Thus,

$$\begin{aligned} R_x(y)= & {} {\text {Res}}(F,G, x)=y((5\lambda ^2-\lambda -1)^2y^3-2(5\lambda ^2-\lambda -1)(\lambda ^2+2\lambda -2 )y^2\\&\quad +\,(-2\lambda ^4+8\lambda ^3+3\lambda ^2-6\lambda +4)y+\lambda (\lambda -2)(\lambda ^2+2 )),\\ R_y(x)= & {} {\text {Res}}(F,G, y)=x((5\lambda ^2-\lambda -1)^2x^3+2(3\lambda ^2+2\lambda +1)(5\lambda ^2-\lambda - 1)x^2\\&\quad +\,(11\lambda ^4+11\lambda ^3-4\lambda ^2+14\lambda +1)x+\lambda (2\lambda -5)(\lambda ^ 2+2)). \end{aligned}$$

Afterwards, we define $\widehat{R}_x(y)$ and $\widehat{R}_y(x)$ as the polynomials containing the same factors as $R_x(y)$ and $R_y(x)$ but with simple multiplicity. In our case, there are no multiple factors in the polynomials $R_x(y)$ and $R_y(x),$ so we have $\widehat{R}_x(y)=R_x(y)$ and $\widehat{R}_y(x)=R_y(x).$ Next, following the approach proposed in [11, 12], we consider double resultants (see [16] for a general introduction to this setting). Computing them we get

$$\begin{aligned} R_{xy}(\lambda )= & {} {\text {Res}}\left( \widehat{R}_x(y), \widehat{R}_x'(y),y\right) \\= & {} \lambda ^4(\lambda ^2+2)^2(5\lambda ^2-\lambda -1)^4 (\lambda -2)^4P_8(\lambda ),\\ R_{yx}(\lambda )= & {} {\text {Res}}\left( \widehat{R}_y(x), \widehat{R}_y'(x), x\right) \\= & {} \lambda ^4(\lambda ^2+2)^2(5\lambda ^2-\lambda -1)^4 (2\lambda -5)^4P_8(\lambda ), \end{aligned}$$

where $P_8$ is given in the statement. The real roots of each of these polynomials are the only candidates to provide the effective bifurcation values we are looking for. So, all these values are contained in the set of real roots of the polynomial

$$\begin{aligned} R_{FG}(\lambda )= \lambda (5\lambda ^2-\lambda -1)(\lambda -2)(2\lambda -5)(\lambda ^2+2)P_8(\lambda ). \end{aligned}$$

The real roots of $P_8(\lambda )$ are $\lambda _1\simeq -0.5081$, $\lambda _2\simeq 0.02967$, $\lambda _3\simeq 1.7826$, and $\lambda _4\simeq 8.7774$, and the ones of $5\lambda ^2-\lambda -1$ are $\lambda _5\simeq -0.3582$ and $\lambda _6\simeq 0.5582.$ Hence, the (ordered) real roots of $R_{FG}$ are

$$\begin{aligned} \lambda _1<\lambda _5<0<\lambda _2<\lambda _6<\lambda _3<2<5/2<\lambda _4. \end{aligned}$$

To determine whether they are or not effective bifurcation values, we study the number of simple real solutions of the system on each one of the ten intervals defined by these nine real roots of $R_{FG}.$ To do this, it suffices to fix a rational value of $\lambda$ in each interval and compute the number of real solutions for that specific value (see Fig. 2). It follows that only four of them are effective bifurcation values, which correspond to the ones given in the statement. $\square$

3 Polynomial Expressions with Two Square Roots

Let us consider the following system of ordinary differential equations

$$\begin{aligned} \dot{x}= & {} -y(x-c)(y-d)+\varepsilon P(x,y),\\ \dot{y}= & {} \phantom {-}x(x-c)(y-d)+\varepsilon Q(x,y), \end{aligned}$$

with $c>0,$$d>0$, and P and Q polynomials. For $\varepsilon =0,$ this system has a linear center at the origin and a couple of straight lines of equilibrium points (precisely, $x=c$ and $y=d$). Then, all the circles centered at the origin of radius less than $\min (c,d)$ define a continuum of periodic orbits. It is well-known that the limit cycles that bifurcate from them come from the simple zeros of the Poincaré–Melnikov–Pontryagin function

$$\begin{aligned} I(r)=\int _{x^2+y^2=r^2}\frac{Q(x,y)\,dx-P(x,y)\,dy}{(x-c)(y-d)} \end{aligned}$$

(see for instance [8]). Using polar coordinates, it admits the equivalent expression

$$\begin{aligned} I(r)=\int _{0}^{2\pi }\frac{r(Q(r\cos \theta ,r\sin \theta )\sin \theta -P(r\cos \theta ,r\sin \theta )\cos \theta )}{(r\cos \theta -c)(r\sin \theta -d)} \, d\theta . \end{aligned}$$

As a direct consequence of Lemma 2.2 in [15], this function can be written as

$$\begin{aligned} I(r)=U(r^2)+\frac{1}{c^2+d^2-r^2}\left( \frac{V(r^2)}{\sqrt{c^2-r^2}} +\frac{W(r^2)}{\sqrt{d^2-r^2}}\right) , \end{aligned}$$

for some suitable polynomials U, V,  and W. Writing $z=-r^2,$ the form of the function $(c^2-r^2)(d^2-r^2)I(r)$ motivates the study of the number of zeros of functions of type

$$\begin{aligned} P_{n_0}(z) + P_{n_1}(z) \sqrt{z+a} + P_{n_2}(z) \sqrt{z+b}, \end{aligned}$$

(5)

with $P_{n_j}(z)$, arbitrary polynomials of degree $n_j,$ for $j=0,1,2,$ and $a,b \in {\mathbb {R}}.$

The problem of estimating the maximal number of zeros of these functions was studied in [14]. They were considered as elements of a family which is, in fact, an Extended Complete Chebyshev system. A rather different question is, given a particular function of this type (5), to compute effectively its zeros. The following theorem and example show how rational parameterizations are an efficient way to do it. However, the proof of the theorem does not work when the number of square roots involved is larger than 2, or the degrees of the polynomials inside the square roots are higher than 1.

Theorem 3.1

Let us consider polynomials $P_{n_j}$ of degree $n_j$, $j=0,1,2$, with no common factors. Then, the study of the number of zeros of the function

$$\begin{aligned} F(x):=P_{n_0}(x) + P_{n_1}(x) \sqrt{x+a} + P_{n_2}(x) \sqrt{x+b} \end{aligned}$$

in $x \ge -a>-b,$ is equivalent to the study of the number of positive zeros of the polynomial Q(t),  of degree 2m,  given by the numerator of $F(\varphi (t)),$ where $m:=\max (2n_0,2n_1+1,2n_2+1)$ and

$$\begin{aligned} \varphi (t)= {\frac{b{t}^{2} \left( 2+t \right) ^{2}-a \left( 2+2t+{t}^{2} \right) ^{2}}{4 \left( 1+t \right) ^{2}}}=\frac{R(t)}{(1+t)^2}. \end{aligned}$$

Proof

We look for (u, v), with $u,v\ge 0,$ satisfying $x+a=v^2$, $x+b=u^2$. These equalities imply that they must move on the hyperbola $u^2-v^2=b-a=:c>0$. To find a rational parameterization for this genus zero curve, first we take $\tau$ such that $u-v=\tau$, $u+v=c/\tau$, which leads to $u=(c+\tau ^2)/2\tau$, $v=(c-\tau ^2)/2\tau$ for $\tau \in (0,\sqrt{c}]$. The transformation $\tau = \sqrt{c}/(t+1)$ provides the rational parameterization for $t \in [0,+\infty )$:

$$\begin{aligned} u=\frac{2+2t+t^2}{2(1+t)}\sqrt{c},\quad v=\frac{t(2+t)}{2(1+t)}\sqrt{c}. \end{aligned}$$

(6)

Using this transformation we obtain that $x=v^2-a=u^2-b=\varphi (t),$ with the function $\varphi$ given in the statement. Hence

$$\begin{aligned} F(\varphi (t))= & {} P_{n_0}(\varphi (t)) + P_{n_1}(\varphi (t)) \sqrt{\varphi (t)+a} + P_{n_2}(\varphi (t)) \sqrt{\varphi (t)+b}\\= & {} P_{n_0}\left( \frac{R(t)}{(1+t)^2}\right) + P_{n_1}\left( \frac{R(t)}{(1+t)^2}\right) \frac{t(2+t)}{2(1+t)}\sqrt{c}\\&\quad + P_{n_2}\left( \frac{R(t)}{(1+t)^2}\right) \frac{2+2t+t^2}{2(1+t)}\sqrt{c} = \frac{Q(t)}{(1+t)^m} , \end{aligned}$$

where R(t) is the polynomial of degree 4 provided by the statement and Q(t) is a suitable polynomial of degree 2m. Notice that there is a one-to-one correspondence between zeros of F(x) and zeros of Q(t),  that is, no false zeros are added. Furthermore, the final domain $[0,+\infty )$ of Q(t) is very convenient to apply polynomial standard techniques.$\square$

Let us illustrate how our approach works with a particular example of function F(x).

Example 3.1

Consider, for $x\ge 0$, the following function:

$$\begin{aligned} F_{\alpha }(x)=A(x) + B(x) \sqrt{x} + C(x) \sqrt{x+1}, \end{aligned}$$

with A, B, C the polynomials

$$\begin{aligned}&A(x)=38340 + \alpha + 5760\,x, \quad B(x)= -69993 - 144298\,x,\\&\quad C(x)=23400 - 143702 \,x, \end{aligned}$$

and $\alpha$ being a real parameter. Then, $F_{\alpha }(x)$ has no real solutions for $\alpha <-61740$ and it has exactly one for $\alpha \ge -\,61740$.

Proof

In this case $a=0$ and $b=1$ in the statement of Theorem 3.1. Taking the rational parameterization (6),

$$\begin{aligned} x =\varphi (t)= \left( \frac{t(2+t)}{2(1+t)} \right) ^2, \qquad t\ge 0, \end{aligned}$$

(7)

we get that the numerator of $F_{\alpha }(\varphi (t))$ is

$$\begin{aligned} Q_{\alpha }(t)= & {} \, -72000 \, t^6 - 429120 \, t^5 - 968044 \, t^4 + (2\alpha - 950056) \, t^3\\&\quad +\,(6\alpha - 232009) \, t^2 + (6\alpha + 230454) \, t + (2\alpha + 123480), \end{aligned}$$

defined for $t\in [0,+\infty )$. To apply Descartes’ rule, we consider the values of $\alpha$ that produce changes in the sign of the coefficients of $Q_{\alpha }(t)$. Namely, they are

$$\begin{aligned} -\,61740, \quad -\,\frac{115227}{3}, \quad \frac{232009}{6}, \quad 475028. \end{aligned}$$

It is straightforward to verify that there is no change in the sign of the coefficients of $Q_{\alpha }(t)$ if $\alpha < -\,61740$ and one change otherwise. Thus we can assert that $Q_{\alpha }(t)$ has no real roots for $t\in (0,+\infty )$ in the first case and has at most one in the second case. Moreover, if $\alpha \ge -\,61740$ then $Q_{\alpha }(0) \ge 0$ and since $\lim _{t \rightarrow +\infty } Q_{\alpha }(t) = -\,\infty$ the existence of this zero $t_{\alpha }>0$ follows. From expression (7) we obtain the value $x_{\alpha }=\varphi (t_\alpha )$ such that $F_{\alpha }(x_{\alpha })=0$.$\square$

Finally, let us show with a fixed value of $\alpha$ the advantage of using our approach instead of the classical recurrent squaring process to solve $F_\alpha (x)=0.$ With this classical approach, the corresponding polynomial equation is

$$\begin{aligned} G_\alpha (x)=\left( A^2(x)+(x+1) C^2(x)- xB^2(x)\right) ^2 -4(x+1) A^2(x) C^2(x)=0. \end{aligned}$$

Consider, for instance, $\alpha =2$. Then

$$\begin{aligned} G_2(x)= & {} 29463035904000000 x^6-597819133749657600 x^5 \\ \quad&+\,4274549116862945536 x^4 - 13150960109956884832 x^3 \\ \quad&+ 16873855567372135585 x^2 - 7555772293001326152 x \\ \quad&+ 851096590977473296. \end{aligned}$$

Its roots, $z_1,z_2,\ldots ,z_6$, are located approximately at:

$$\begin{aligned} 0.1676387, \ 0.5656784, \ 1.731563, \ 3.713337, \ 5.502619, \ 8.609643. \end{aligned}$$

They all are candidates to be zeros of the function $F_2(x),$ but only the first one, $z_1,$ is an actual root. The others can be discarded, for example, using interval arithmetics. Let us do it, for instance, for the second one, $z_2\simeq 0.5656784.$ Indeed, it satisfies $1/2<z_2<3/5$ and it holds that

$$\begin{aligned} F_2(z)= & {} 38342+5760z- \left( 69993+144298z \right) \sqrt{z}+ \left( 23400 -143702z \right) \sqrt{z+1}\\< & {} 38342+5760\,\frac{3}{5}-\left( 69993+144298\,\frac{1}{2} \right) \sqrt{\frac{1}{2}}+ \left( 23400 -143702\,\frac{1}{2} \right) \\&\quad \sqrt{\frac{1}{2}+1}=41798-71071\sqrt{2}-\frac{48451}{2}\sqrt{6}<0. \end{aligned}$$

Similar computations can be done for the rest of solutions.

However, if we apply the rational parameterization provided by (7), we obtain

$$\begin{aligned} Q_{2}(t)= & {} -72000 t^6-429120 t^5-968044 t^4 - 950052 t^3-231997 t^2 \\ \quad&+ 230466 t + 123484. \end{aligned}$$

This polynomial has exactly one zero in $[0,+\infty )$, at the point $t_2\simeq 0.4900103$. Substituting this value into (7) one obtains $x_2=\varphi (t_2)\simeq 0.1676387$, an approximation of the unique zero of $F_2(x)$.

4 Applications to Celestial Mechanics

Distances among bodies and, therefore, square roots appear often in equations modeling many problems in Celestial Mechanics. In this section we show two applications of rational parameterization and polynomial tools in this field: a first one concerning critical points of a certain potential (see [6]) and a second one dealing with central configurations in a system of four charged particles (see [7, 22]).

4.1 Relative Equilibria in the Schwarzschild Isosceles Three Body Problem

The so-called Schwarzschild isosceles three body problem with masses $m_1=m_2=M>0$ and $m_3=1$ is introduce in detail in [6]. In particular, in cylindrical coordinates, it has the following reduced Hamiltonian

$$\begin{aligned} H_{\text {red}}=\frac{1}{M} P_R^2 +\frac{2M+1}{4M}P_z^2+U, \end{aligned}$$

(8)

with potential

$$\begin{aligned} U(R,z)= \frac{C^2}{M R^2}-\frac{A}{R}-\frac{B}{R^3}- \frac{4A_1}{\sqrt{R^2+4 z^2}}-\frac{16B_1}{(R^2+4 z^2)^{3/2}}, \end{aligned}$$

where $A,A_1,B,B_1,$ and C are positive parameters. This model extends to a three mass point system the classical Schwarzschild model of interaction between two mass points, with potential $U(r)=-A/r-B/r^3$, where r is the relative distance between them.

The solutions where the three mass points are steadily rotating about their common center of mass are called relative equilibria. In particular, for the Hamiltonian system defined by (8) they correspond to the critical points of U,  that is

$$\begin{aligned} \frac{\partial U}{\partial R}=0, \qquad \frac{\partial U}{\partial z} =0. \end{aligned}$$

(9)

In [6] it is studied, joint to other problems, the number of solutions of (9) on $z=0$ for positive values of $A,A_1,B,$ and $B_1$ in terms of C. In this case, there is only one bifurcation value, $C_2$ in the next result, that distinguish the cases with 0, 1 or 2 relative equilibria. The following result extends the study of the number of solutions of (9), also in terms of C, for arbitrary non-zero values of $A,A_1,B,$ and $B_1$. We show that the effective bifurcation set is bigger. In the proof it can be seen that there are values with more than two solutions. It is not restrictive to assume $C\ge 0.$

Theorem 4.1

For non-vanishing values of $A, A_1, B, B_1,$ and M the C-effective bifurcation values for the number of solutions of (9) belong to the set $E_C=\{C_1,C_2,C_3\}\cap {\mathbb {R}},$ where

$$\begin{aligned}&C_1=\root 4 \of {-\frac{3 M^2 (4 A B_1-A_1 B)^2}{16 A_1 B_1}},\\&C_2=\root 4 \of {3 M^2 (B+16 B_1)(A+4A_1)},\quad C_3=\root 4 \of { 3AB M^2}. \end{aligned}$$

Moreover, there exist values of the parameters such that $E_C$ is, actually, the C-effective bifurcation set.

Proof

To eliminate the square roots in system (9) we write $R^2+4z^2=r^2,$ for some new positive variable r. The family of planar curves $F_r(R,z)=R^2+4z^2-r^2=0$ has genus zero and can be rationally parameterized as

$$\begin{aligned} R=\frac{r (1-t^2)}{1+t^2}, \qquad z= \frac{rt}{1+t^2}, \end{aligned}$$

for $t\in {\mathbb {R}}$ and $r>0.$ Observe that the origin ($r=0$) has been removed since it is a singular point of (9). In the parameters (r, t), Eq. (9) are equivalent to

$$\begin{aligned} \frac{\partial U}{\partial r} = \frac{P_8(r,t)}{Mr^3 (t-1)^3 (t+1)^3}=0, \qquad \frac{\partial U}{\partial t}= \frac{Q_7(r,t)}{Mr^3 (t-1)^4 (t+1)^4}=0, \end{aligned}$$

where

$$\begin{aligned} P_8(r,t)= & {} \left( (A r^2 -4 A_1 r^2+3 B -48 B_1)t^6 -(A r^2-12 A_1 r^2-9 B-144 B_1) t^4\right. \\&\left. \quad -(A r^2 +12 A_1 r^2 -9 B+144 B_1)t^2 +A r^2+4 A_1 r^2+3 B+48 B_1 \right) M\\&\quad +\,2 C^2 r (t^4-1),\\ Q_7(r,t)= & {} t \left( (A r^2 +3 B )t^4-(2 A r^2-6 B)t^2+A r^2+3 B\right) M+2 C^2 r t (t^4-1). \end{aligned}$$

To solve them we follow the procedure presented in Sect. 2: we compute the resultants

$$\begin{aligned} R_r(t)= & {} {\text {Res}}(P_8,Q_7,r)=2^4 3 M^2 t^2 (t^2-1)^6 V_8(t), \\ R_t(r)= & {} {\text {Res}}(P_8,Q_7,t)=2^{20} 3^6 B^6 M^{10}(A_1 r^2 + 12 B_1)^4 W_2(r), \end{aligned}$$

where

$$\begin{aligned} V_8(t)= & {} 3(4 A B_1 t^4-A_1 B t^4-8 A B_1 t^2-2 A_1 B t^2+4 A B_1-A_1 B)^2 M^2\\&\quad +\,16 A_1 B_1 C^4 (t^4-1)^2,\\ W_2(r)= & {} \left( (4A_1+1)r^2 +3(B+16B_1)\right) M - 2C^2 r, \end{aligned}$$

and take

$$\begin{aligned} \widehat{R}_r(t)= & {} t(t^2-1) V_8(t), \\ \widehat{R}_t(r)= & {} (A_1 r^2 + 12 B_1) W_2(r), \end{aligned}$$

which contain all the terms in the preceding functions, but without multiplicity. Now,

$$\begin{aligned} R_{rt}= & {} {\text {Res}}(\widehat{R}_r(t), \widehat{R}_r'(t),t)\\= & {} 2^{118} 3^8 A^4 B^{12} A_1^{25} B_1^{17} M^{16} C^{16} (C^4-C_1)^5 (C^4-C_3)^4,\\ R_{tr}= & {} {\text {Res}}(\widehat{R}_t(r), \widehat{R}_t'(r),r)\\= & {} -2^{14} 3^3 A_1^4 B_1^3 (A+4A_1)(C^4-C_1)^2(C^4-C_2), \end{aligned}$$

where $C_1,C_2,$ and $C_3$ are the constants given at the statement. Thus, the product of the factors of $R_{rt}$ and $R_{tr}$ with no multiplicity, namely

$$\begin{aligned} C( C^4 - C_1 ) (C^4 - C_2 )( C^4 - C_3 ) =0, \end{aligned}$$

divides the positive real line in four different intervals having the same number of real simple solutions of system (9). The case $A+4A_1=0$ becomes $C_2=0$ and the set $E_C$ does not vary.

Finally, taking for instance $A=2,$$B=3,$$A_1=-1/3,$$B=1/5,$ and $M=2$ we get $0<C_2<C_3<C_1.$ The number of zeros on the intervals that they define is, respectively, 0, 2, 6,  and 2. In consequence, for these values of the parameters, $E_C$ is the C-effective bifurcation set.$\square$

Remark 4.1

• (i) From this proof it is not difficult to see that, when all the parameters are positive and one restricts himself to the surface $z=0$, the C-effective bifurcation set reduces to $\{C_2\},$ recovering the result of [6]. Indeed, $C_1$ is not real since $- 3 M^2 (4 A B_1-A_1 B)^2/(16 A_1 B_1)<0$. The condition $z=0$ implies $t=0$ in the rational parameterization (since $r>0$). This means that $Q_7(r,0)=0$ and $P_8(r,0)=(Ar^2+4A_1r^2+3B+48B_1)M-2C^2r$. The discriminant of $P_8(r,0)$ is $-3ABM^2-48A B_1 M^2-12 A_1 B M^2 -192 A_1 B_1 M^2 +C^4$, whose unique positive real root (there is one real negative and two conjugate pure imaginary) is $C_2.$

• (ii) Taking $A=2,$$B=3,$$A_1=-1,$$B=4,$ and $M=2$ it can be proved that the C-effective bifurcation set is $\{C_3\}.$ In fact, for $0<C<C_3$ the number of equilibria is 1. Even though on each of the intervals $C_3<C<C_1$ and $C>C_1$ this number is 3, their corresponding relative position changes between aligned and triangular-shaped.

• (iii) There exist values of the parameters whose C-effective bifurcation set is $E_C$, exhibiting different number of equilibria. Indeed, taking $A=5,$$B=3,$$A_1=-1,$$B_1=4,$ and $M=2,$ the respective number of equilibria is 0, 4, 6,  and 4.

4.2 Central Configurations

The equations governing the charged Newton’s planar n-body problem are

$$\begin{aligned} m_i \ddot{q}_i=-\sum _{j\ne i} \frac{m_i m_j}{|q_i - q_j|^3} \left( q_i - q_j \right) , \qquad i=1,\ldots , n. \end{aligned}$$

Here the units have been suitably taken, |q| denotes the Euclidean norm of q, and $m_i\in {\mathbb {R}}{\setminus }0.$ We will assume that the center of mass of the n charged particles is located at the origin. Then, they form a spatial charged central configuration if there exists a constant $\lambda \in {\mathbb {R}}$ such that

$$\begin{aligned} \lambda q_i=-\sum _{j\ne i} \frac{m_j}{|q_j - q_i|^3} \left( q_j - q_i \right) , \qquad i=1\ldots , n, \end{aligned}$$

(10)

(see [19] and references therein). Actually, the geometric configuration (up to dilations and rotations) of the particles is such that the position vectors are always parallel to the acceleration ones.

For a fixed set of masses, to find all possible central configurations is a very hard problem. Two of the main obstructions to solve system (10) are the large number of unknowns and to deal with equations involving square roots. Usual reductions of this problem come from assuming symmetries and restrictions on the dimension of the spatial positions. One of the most studied reduction is the planar non-collinear.

In some cases, the method of rational parameterization transforms this problem into seeking for zeros of polynomials in several variables. This is the approach used by Leandro in [18]. He studies the finiteness of central configurations when the d masses are in a plane and two more stay in the orthogonal line to this plane passing through the origin, where is located the center of masses of the system. The restriction to four masses moving on a plane is known as a kite central configuration. The case with three equal masses has been tackled in [7, 22] and the case of two couples of equal masses in [4]. Both cases, in the more general situation of charged masses, have been considered in [3].

Fig. 3

Kite configuration, where $\circ$ denotes the (charged) mass m

The aim of this section is to describe the number of different kite central configurations in the first frame, charged or not, using rational parameterizations. Without loss of generality we can fix $m_1=m_2=m_3=1$ and $m_4=m\in {\mathbb {R}}{\setminus }0.$ Moreover, we locate them as in Fig. 3. That is, with the charged mass at the point with coordinates $(0,\ell )$ and satisfying $k+\ell >0.$ In this setting, following [7], Eq. (10) reduces to

$$\begin{aligned} F_1(k,\ell ,m)= & {} m \left( k+\ell \right) \left( (k+\ell )^{-3}- \left( {\ell }^{2}+1 \right) ^{-3/2} \right) \nonumber \\&\quad +\,2\,k \left( \left( {k}^{2}+1 \right) ^{-3/2}-1/8 \right) =0,\nonumber \\ F_2(k,\ell )= & {} \left( k+\ell \right) \left( \left( k+\ell \right) ^{-3}- \left( {k}^{2}+ 1 \right) ^{-3/2} \right) \nonumber \\&\quad +\,2\,\ell \left( \left( {\ell }^{2}+1 \right) ^{-3/2}-1/8 \right) =0. \end{aligned}$$

(11)

Solutions of (11) correspond to different kite central configurations. The non-charged problem ($m>0$) is studied in [7, 22] where the authors show that the effective bifurcation set is formed by only one value. In the charged problem, as it will be seen in the next result, the bifurcation set is increased by two negative values of m. Our proof for the non-charged problem is also shorter.

Theorem 4.2

The effective bifurcation set for the number of solutions of system (11) is $\{-1,-1/4, m^*\}$ where $m^*\approx 1.00266054757261$ is the closest to 1 root of a suitable irreducible polynomial with integer coefficients and degree 240. Indeed, in the intervals $(-\infty ,-1),$$(-1,-1/4),$$(-1/4,m^*),$ and $(m^*,+\infty )$ this number is 3, 4, 5,  and 3,  respectively.

Proof

To eliminate the square roots in (11) we impose that $k^2+1=u^2$ and $\ell ^2+1=v^2,$ for some new variables u and v. Again, both planar curves have genus zero and can be parameterized through the rational parameterizations

$$\begin{aligned} (k,u)=\left( \frac{s^2-1}{2s}, \frac{s^2+1}{2s}\right) , \qquad (\ell ,v)=\left( \frac{t^2-1}{2t}, \frac{t^2+1}{2t}\right) , \end{aligned}$$

with $s,t>0.$ Substituting them into Eq. (11) they become

$$\begin{aligned} \widetilde{F}_1(s,t,m)= & {} \frac{P_{20}(s,t,m)}{(s^2+1)^3 (t^2+1)^3 (t+s)^2 (st-1)^2 s}=0,\\ \widetilde{F}_2(s,t)= & {} \frac{Q_{20}(s,t)}{(t^2+1)^3 (s^2+1)^3 (t+s)^2 (s t-1)^2 t}=0, \end{aligned}$$

where $P_{20},Q_{20}$ are polynomials with integer coefficients of degree 20 in s, t. Moreover $P_{20}$ has degree 1 on m. Recall that we only need to study the number of intersections of the algebraic curves $\widetilde{F}_1(k,\ell ,m)=0,$$\widetilde{F}_1(k,\ell )=0$ when $k+\ell >0.$ To do it we use the procedure explained in Sect. 2.

First we compute the resultants

$$\begin{aligned} R_s(t)= & {} {\text {Res}}(P_{20},Q_{20},s)= t^{20} (t^2+1)^{51} (3t^2-1)U_{100}(t),\\ R_t(s)= & {} {\text {Res}}(P_{20},Q_{20},t)= s^{20} (s^2+1)^{51} (3s^2-1)V_{100}(s). \end{aligned}$$

Afterwards we consider the functions (with no multiple roots)

$$\begin{aligned} \widehat{R}_s(t)= & {} t(3t^2-1)U_{100}(t),\\ \widehat{R}_t(s)= & {} s(3s^2-1)V_{100}(s), \end{aligned}$$

and get the new two resultants

$$\begin{aligned} R_{st}(m)= & {} {\text {Res}}\left( \widehat{R}_s(t), \widehat{R}_s'(t),t\right) \\= & {} m^{16}(4m-1)^{24}(4m+1)^{24}(m-1)^{60}(m+1)^{64} (m+2)^{24}\\&\quad (249m^2-162m-23)^2P_{18}^2(m)P_{240}(m)P_{644}^2(m),\\ R_{ts}(m)= & {} {\text {Res}}\left( \widehat{R}_t(s), \widehat{R}_t'(s),s\right) \\= & {} m^{1076}(4m-1)^{7}(4m+1)^{7}(m-1)^{60}(m+1)^{64} (m+2)^{78}\\&\quad (249m^2-162m-23)^2P_{240}(m)P_{408}^2(m), \end{aligned}$$

$P_i$ being polynomials of degree i,  irreducibles in $\mathbb {Q}(t).$ They are not explicitly written because of their big size. Finally, we consider a polynomial containing all the simple factors appearing in ${R}_{st}$ and ${R}_{ts}$, that is,

$$\begin{aligned} R_{PQ}(m)= & {} m(4m-1)(4m+1)(m-1)(m+1)(m+2) \\&\quad (249m^2-162m-23)P_{18}(m)P_{240}(m)P_{644}(m)P_{408}(m). \end{aligned}$$

This polynomial has 74 simple real roots. We analyze these roots taking rational values of the parameter m just before and after them and studying if an effective change in their behavior undergoes. We select those with such effective change, i.e., the effective bifurcation values. In this problem they are just three: $-1,-1/4,m^*$, with $m^*$ being the real root of $P_{240}$ which is closest to 1.$\square$

5 Zeros of Melnikov Functions

In this section we start with a similar question as the one posed in Sect. 3. Indeed, we consider a planar non-autonomous periodic differential equation with a continuum of periodic orbits and we study how many of these periodic solutions remain after small perturbations. Those which remain are isolated (limit cycles) and are closely related to the simple zeros of its corresponding Melnikov function. In [9], the following system of coupled generalized Abel equations is considered:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{r}=a(t)r^2+\varepsilon f(t)r^ns^m,\\ \dot{s}=b(t)s^2+\varepsilon g(t)r^ps^q, \end{array} \right. \end{aligned}$$

with $n+m\ge 3$, $p+q\ge 3,$ and a, b, f and g,  T-periodic trigonometric polynomials. Using a variational approach, the authors derive the corresponding Melnikov function:

$$\begin{aligned} M(\rho )=\left( \begin{array}{c}\displaystyle \rho _1^n\rho _2^m \int _0^{T} \dfrac{f(t)}{(1-A(t)\rho _1)^{n-2} (1-B(t)\rho _2)^m}\,dt \\ \displaystyle \rho _1^p\rho _2^q \int _0^{T} \dfrac{g(t)}{(1-A(t)\rho _1)^{p}(1-B(t)\rho _2)^{q-2}}\,dt \end{array} \right) , \end{aligned}$$

(12)

where $\rho =(\rho _1,\rho _2)\in {\mathbb {R}}^2,$$A(t)=\int _0^t a(s)\,ds,$$B(t)=\int _0^t b(s)\,ds,$ and $A(T)=B(T)=0.$

Motivated by this problem, it seems interesting to study the number of limit cycles arising from a system of type

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{r} &{}=&{} (\cos t) r^2 + \varepsilon \left( F_0 + F_1 \sin t +\cdots + F_n \sin ^n t \right) r s^2, \\ \dot{s} &{}=&{} (\cos t) s^2 + \varepsilon \left( G_0 + G_1 \sin t +\cdots + G_n \sin ^n t \right) r^2 s,\\ \end{array} \right. \end{aligned}$$

(13)

where $F_i,G_i$ are real constants such that $F_nG_n\ne 0$, $\varepsilon$ is an small parameter and $n\in \mathbb {N}$. The case $n=2$ was already considered in [9].

It is not restrictive (rescaling if necessary) to assume $F_n=G_n=1$. Denote $F=(F_0,F_1,\ldots ,F_{n-1})$ and $G=(G_0,G_1,\ldots ,G_{n-1}).$ We know that simple real zeros of (12) in $\mathcal {D}=\{|\rho _i|<1, \quad i=1,2 \text { and } \rho _1\rho _2\ne 0\}$ provide limit cycles of (13) for small enough $\varepsilon$. Several computations, that we omit for the sake of shortness, prove that system $M(\rho )=0$ in $\mathcal {D}{\setminus }\rho _1\rho _2\ne 0$ is equivalent to

$$\begin{aligned} \left\{ \begin{array}{rcl} P_F(\rho _1,\rho _2) + Q_F(\rho _1,\rho _2) \sqrt{1-\rho _2^2} &{}=&{}0, \\ P_G(\rho _1,\rho _2) + Q_G(\rho _1,\rho _2) \sqrt{1-\rho _1^2} &{}=&{}0, \end{array} \right. \end{aligned}$$

(14)

for some polynomial systems $P_F,P_G,Q_F, Q_G.$ In [9, Prop. 11], for $n=2$ and a suitable choice of the parameters F, G,  it is showed, by squaring the latter equations, that the system (14) has four simple solutions. Namely, they fix $F=F_*=(-1/2,-1/10),$$G=G_*=(-3/5,3/10)$ and get, using Gröbner Basis, that the squared system

$$\begin{aligned} \left\{ \begin{array}{rcl} \Phi _1(\rho _1,\rho _2)&{}=&{}P_{F_*}^2(\rho _1,\rho _2) - Q_{F_*}^2(\rho _1,\rho _2) \left( 1 - \rho _2^2 \right) =0, \\ \Phi _2(\rho _1,\rho _2)&{}=&{}P_{G_*}^2(\rho _1,\rho _2) - Q_{G_*}^2(\rho _1,\rho _2) \left( 1 - \rho _1^2 \right) =0. \end{array} \right. \end{aligned}$$

has 10 solutions in $\mathcal {D}$ from whose only 4 are actual solutions of (14).

Let us show how our method works for $n=2$ and with the same choice of the parameters F, G. Introducing the new variables $s_i$ as $1-\rho _i^2=s_i^2,$$i=1,2$ we have once more two genus zero curves for which rational parameterizations exist. Plugging in system (14) the rational parameterizations $\rho _i=2\sigma _i/(1+\sigma _i^2)$ and $s_i=(1-\sigma _i^2)/(1+\sigma _i^2),$ for $\sigma _i\in (-1,1),$$i=1,2$ we obtain an equivalent polynomial system $\mathcal {S},$ with rational coefficients and degree 6 in $\sigma _1,\sigma _2.$ This system is triangularized again by using Gröbner Basis, proving that there exist polynomials f and g,  of degree 13, 14, respectively, such that the system $\mathcal {S}$ is equivalent to $\{\sigma _1=f(\sigma _2),\, g(\sigma _2)=0\}.$ The polynomial g has only 6 zeros in $(-1,1).$ Using interval arithmetic it is easy to prove that only 4 of them belong to $\mathcal {D}$: for the values $\sigma _2$ such that $g(\sigma _2)=0$ one checks if $f(\sigma _2)\in (-1,1).$ We again find a clear advantage with respect to the previous method: no spurious solutions appear.

The study of the number of limit cycles of (13) for small $\varepsilon$ but arbitrary n presents some main difficulties. The most important one is that the complexity increases with the degree n. A second one is how to choose suitable parameters F and G giving rise to the highest number of limit cycles. Using the preceding procedure, the following result provides high lower bounds for small values of n.

Theorem 5.1

For $n=1,\ldots , 16,$ there exist values of F and G such that system (13) has $n^2$ limit cycles, for small enough values of $\varepsilon$.

Proof

However the result is asserted and proved for $n=1,\ldots ,16$, we strongly believe that the same procedure is applicable to larger values of n. The real limitation to that is its high computational cost. We describe the method for a general n without providing explicit expressions of the polynomials appearing during the process.

First, consider the same change as above: $\rho _i=2\sigma _i/(1+\sigma _i^2),$ for $i=1,2.$ So, system (14) reads

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{(\sigma _2^2+1)^2}{(\sigma _1^2+1)(\sigma _2^2-1)^3}\Lambda _1(\sigma _1, \sigma _2)=0, \\ \dfrac{(\sigma _1^2+1)^2}{(\sigma _2^2+1)(\sigma _1^2-1)^3}\Lambda _2(\sigma _1, \sigma _2)=0, \end{array} \right. \end{aligned}$$

where $\Lambda _1(\sigma _1,\sigma _2)$ and $\Lambda _2(\sigma _1,\sigma _2)$ are polynomials of degree $n+4.$ Thus, our problem becomes to find the number of real solutions of $\mathcal {S}=\{\Lambda _1(\sigma _1,\sigma _2)=0,\Lambda _2(\sigma _1,\sigma _2)=0\}$ in the open square $(-1,1)^2.$

Second, we look for values $F_*$ and $G_*$ such that the polynomial system $\mathcal {S}$ has n solutions, for instance, at the points $(-1+2j/(n+1),-1+2j/(n+1))$ with $j=1,\ldots ,n$.

Using again Gröbner basis, the system $\mathcal {S}$ is written as the union of systems of type $\{\sigma _1=f(\sigma _2),\, g(\sigma _2)=0\}$ for some polynomials f and g. A detailed study with interval arithmetic shows that $\mathcal {S}$ has in fact $n^2-n$ more simple solutions, having $n^2$ simple solutions in total.$\square$

We finish this section with a simple example of 1-parameter bifurcation in Eq. (14) with $n=2$, whose number of limit cycles varies with the parameter. Let consider $F=(-1/2,-1/3)$ and $G=(-3/4+2/3\lambda ,\lambda ).$ Thus, performing the change of variables $\rho _i=2\sigma _i/(1+\sigma _i^2),$ for $i=1,2,$ system (14) reads

$$\begin{aligned} \left\{ \begin{array}{l} 3 \sigma _1 ^ 2 \sigma _2 ^ 4 -6 \sigma _1 \sigma _2 ^ 5 -2 \sigma _1 \sigma _2 ^ 4 -9 \sigma _1 ^ 2 \sigma _2 ^ 2 +12 \sigma _1 \sigma _2 ^ 3 +3 \sigma _2 ^ 4-4 \sigma _1 ^ 2 \sigma _2 +8 \sigma _1 \sigma _2 ^ 2+6 \sigma _1 \sigma _2\\ \quad -9 \sigma _2 ^ 2+2 \sigma _1 -4 \sigma _2 =0,\\ 12 \lambda \sigma _1 ^ 4 \sigma _2 -12 \sigma _1 ^ 5 \sigma _2 +6 \sigma _1 ^ 4 \sigma _2 ^ 2 -8 \sigma _1 ^ 2 \sigma _2 ^ 2 \lambda -48 \lambda \sigma _1 ^ 2 \sigma _2 +24 \lambda \sigma _1 \sigma _2 ^ 2 + 6 \sigma _1 ^ 4 +24 \sigma _1 ^ 3 \sigma _2\\ \quad -15 \sigma _1 ^ 2 \sigma _2 ^ 2 -8 \lambda \sigma _1 ^ 2 +32 \lambda \sigma _1 \sigma _2 -8 \lambda \sigma _2 ^ 2 +24 \lambda \sigma _1 -12 \lambda \sigma _2 - 15 \sigma _1 ^ 2\\ \quad +3 \sigma _2 ^ 2 -8 \lambda +3=0. \end{array} \right. \end{aligned}$$

Using the procedure described in Sect. 2, it can be proved that its effective bifurcation values are $\lambda =-3/20$ and $\lambda =3/4$. In particular, for small enough $\varepsilon$, if $-3/20<\lambda <3/4$ the system (13) has four limit cycles while only two if $\lambda <-3/20$ or $\lambda >3/4$.