First Integrals and Phase Portraits of Planar Polynomial Differential Cubic Systems with the Maximum Number of Invariant Straight Lines

Abstract

In the article Llibre and Vulpe (Rocky Mt J Math 38:1301–1373, 2006) the family of cubic polynomial differential systems possessing invariant straight lines of total multiplicity 9 was considered and 23 such classes of systems were detected. We recall that 9 invariant straight lines taking into account their multiplicities is the maximum number of straight lines that a cubic polynomial differential systems can have if this number is finite. Here we complete the classification given in Llibre and Vulpe (Rocky Mt J Math 38:1301–1373, 2006) by adding a new class of such cubic systems and for each one of these 24 such classes we perform the corresponding first integral as well as its phase portrait. Moreover we present necessary and sufficient affine invariant conditions for the realization of each one of the detected classes of cubic systems with maximum number of invariant straight lines when this number is finite.

1 Introduction and Preliminaries

Polynomial differential systems on the plane are systems of the form

$$\begin{aligned} \dot{x} = P(x,y),\quad \dot{y} = Q(x,y), \end{aligned}$$

(1)

where $P,Q\in {\mathbb {R}}[x,y]$, i.e., P and Q are the polynomials over ${\mathbb {R}}$. We can associate to systems (1) the vector field

$$\begin{aligned} \mathbb {X}=P(x,y)\dfrac{\partial }{\partial x}+Q(x,y)\dfrac{\partial }{\partial y}. \end{aligned}$$

(2)

We call cubic system a cubic polynomial differential system (1) with degree $m=\max \{\deg P,$ $\deg Q \}=3$.

There are several open problems on polynomial differential systems, especially on the class of all cubic systems (1) (we denote in the following by ${\mathbb {CS}}$ the whole class of such systems). In this paper we are concerned with the algebraic integrability in the sense of Darboux and the classification of all phase portraits of ${\mathbb {CS}}$. These problems are very hard even in the simplest case of quadratic differential systems.

A straight line $f(x,y)=ux+vy+w=0$, $(u,v)\ne (0,0)$ satisfies

$$\begin{aligned} {\mathbb X}(f)=uP(x,y)+vQ(x,y)=(ux+vy+w)K(x,y) \end{aligned}$$

for some polynomial K(x, y) if and only if it is invariant under the flow of ${\mathbb X}$. If some of the coefficients u, v, w of an invariant straight line belongs to ${\mathbb C}{\setminus }{\mathbb R}$, then we say that the straight line is complex; otherwise the straight line is real. Note that, since systems (1) are real, if a system has a complex invariant straight line $ux+vy+w=0,$ then it also has its conjugate complex invariant straight line ${\bar{ux}}+{\bar{vy}}+{\bar{w}}=0.$

To a line $f(x,y)=ux+vy+w=0$, $(u,v)\ne (0,0)$ we associate its projective completion $F(X,Y,Z)=uX+vY+wZ=0$ under the embedding ${\mathbb C}^2\hookrightarrow \mathbf{P}_2({\mathbb C})$, $(x,y)\mapsto [x:y:1]$. The line $Z=0$ in $\mathbf{P}_2({\mathbb C})$ is called the line at infinity of the affine plane ${\mathbb C}^2$. It follows from the work of Darboux (see, for instance, [12]) that each system of differential equations of the form (1) over ${\mathbb C}$ yields a differential form on the complex projective plane $\mathbf{P}_2({\mathbb C})$ which is the compactification of the differential form $Q dx-P dy=0$ in ${\mathbb C}^2$. The line $Z=0$ is an invariant straight line of this complex form.

Definition 1

[25] We say that an invariant affine straight line $f(x,y)=ux+vy+w=0$ (respectively the line at infinity $Z=0$) for a cubic vector field ${\mathbb X}$ has multiplicity m if there exists a sequence of real cubic vector fields ${\mathbb X}_k$ converging to ${\mathbb X}$, such that each ${\mathbb X}_k$ has m (respectively $m-1$) distinct invariant affine straight lines $f^j_i=u^j_ix+v^j_iy+w^j_i=0$, $(u^j_i,v^j_i)\ne (0,0)$, $(u^j_i,v^j_i,w^j_i )\in {\mathbb C}^3$, converging to $f=0$ as $k\rightarrow \infty$ (with the topology of the coefficients), and this does not occur for $m+1$ (respectively m).

We remark that the above definition is a particular case of the definition of geometric multiplicity given in paper [11], and namely the notion of “strong geometric multiplicity” with the restriction, that the corresponding perturbations belong to the same class of cubic systems.

The set ${\mathbb {CS}}$ of cubic differential systems depends on 20 parameters and for this reason people began by studying particular subclasses of ${\mathbb {CS}}$. Here we deals with ${\mathbb {CS}}$ possessing invariant straight lines. We mention some papers devoted to polynomial differential systems possessing invariant straight lines. For quadratic systems see [13, 21, 22, 25–29]; for cubic systems see [4–9, 15, 16, 18, 19, 23, 32, 32, 33]; for quartic systems see [31, 34].

The existence of sufficiently many invariant straight lines of planar polynomial systems could be used for integrability of such systems. During the last 15 years several articles were published on this theme. Investigations concerning polynomial differential systems possessing invariant straight lines were done by Artes, Dai Guo Ren, Gassul, Kooij, Llibre, Popa, Schlomiuk, Sibirski, Sokulski, Vulpe, Zhang Xi Kang as well as Dolov and Kruglov.

According to [1] the maximum number of invariant straight lines taking into account their multiplicities for a polynomial differential system of degree m is 3m when we also consider the infinite invariant straight line, and when this number is finite. This bound is always reached if we consider the real and the complex invariant straight lines, see [11].

So the maximum number of the invariant straight lines (including the line at infinity $Z=0$) for cubic systems with non-degenerate infinity is 9. A classification of all cubic systems possessing the maximum number of invariant straight lines taking into account their multiplicities has been made in [16]. The authors used the notion of configuration of invariant lines for cubic systems (as introduced in [25], but without indicating the multiplicities of real singularities) and detected 23 such configurations. Moreover using invariant polynomials with respect to the action of the group $Aff(2,{\mathbb {R}})$ of affine transformations and time rescaling in that paper, the necessary and sufficient conditions for the realization of each one of 23 configurations were detected. A new class of cubic systems omitted in [16] was constructed in [4].

Definition 2

[29] Consider a planar cubic system (1). We call configuration of invariant straight lines of this system, the set of (complex) invariant straight lines (which may have real coefficients) of the system, each endowed with its own multiplicity and together with all the real singular points of this system located on these invariant straight lines, each one endowed with its own multiplicity.

It was observed that the configurations of invariant straight lines which were detected for various families of systems (1) using Poincaré compactification (see for details [10]), could serve as a base to complete the whole phase portrait of the system in the Poincaré disc, i.e. to give the full topological classification of such systems. For example, in papers [26, 28] for quadratic systems with invariant straight lines grater than or equal to 4, it was proved that the existence of 57 distinct configurations of invariant straight lines leads to the existence of 135 topologically distinct phase portraits. In [23, 24, 32, 33] for cubic systems with invariant straight lines of total parallel multiplicity six or seven (see definition of parallel multiplicity in the quoted papers), taking into consideration constructed configurations of invariant straight lines it was proved the existence of 113 topologically distinct phase portraits.

In this paper we approach the earlier mentioned problems for a specific class of cubic systems, i.e. ${\mathbb {CS}}$ possessing invariant straight lines of total multiplicity 9, including the line at infinity and considering their multiplicities (we denote this family by ${\mathbb {CSL}}_9$).

The goal of this article is to present a full study of this class by:

• improving the classification theorem from [16] of systems belonging to ${\mathbb {CSL}}_9$ (we construct the necessary and sufficient conditions for the realization of the detected class of systems);

• constructing the integrating factors and the first integrals (rational) for systems belonging to ${\mathbb {CSL}}_9$ via the method of Darboux;

• determining all topologically distinct phase portraits of the systems in this class together with the invariant criteria for their realization (we have 18 such phase portraits).

Let $\mathbb {C}[x,y]$ denote the ring of polynomials in two variables x and y with complex coefficients. The method of integration of Darboux uses multiple-valued complex functions of the form:

$$\begin{aligned} F=e^{G(x,y)}f_1(x,y)^{\lambda _1}\ldots f_s(x,y)^{\lambda _s},\ G=G_1/G_2,\ G_i\in \mathbb {C}[x,y], \end{aligned}$$

(3)

and $f_i$ irreducible polynomials over $\mathbb {C}[x,y]$. It is clear that F(x, y) is well defined at least in the points $(x,y)\in \mathbb {C}^2{\setminus } \big (\{G_2(x,y)=0\} \cup \{f_1(x,y)=0\}\cup \ldots \cup \{f_s(x,y)=0\}\big )$.

Suppose that (1) has a solution curve which is not a singular point, contained in an algebraic curve $f(x, y) = 0$. It is clear that the derivative of f with respect to t must vanish on the algebraic curve $f(x, y) = 0$, so $\dfrac{df}{d t}|_{f =0}=\big (\dfrac{d f}{\partial x}P(x,y)+ \dfrac{d f}{\partial y}Q(x,y)\big )|_{f=0}=0$. By the Hilbert’s Nullstellensatz theorem this is equivalent to the existence of a polynomial $K=K(x,y)$ such that ${\mathbb X}(f)=Kf$.

In 1878 Darboux introduced the notion of the invariant algebraic curve for differential equations on the complex projective plane. This notion can be adapted for systems (1). According to [12] the next definition follows.

Definition 3

An algebraic curve $f(x, y) = 0$ in $\mathbb {C}^2$ with $f\in \mathbb {C}[x, y]$ is an invariant algebraic curve (an algebraic partial integral) of a polynomial system (1) if $\mathbb {X}(f) =K f$ for some polynomial $K(x,y)\in \mathbb {C}[x, y]$ called the cofactor of the invariant algebraic curve $f(x, y) = 0$.

It could be observed that for the points of the curve $f(x, y) = 0$ the right hand side of (1) is zero. This means that the gradient $(\partial f/\partial x, \partial f/\partial y)$ is orthogonal to the vector field $\mathbb {X} = (P,Q)$ at these points. Therefore the vector field $\mathbb {X}$ is tangent to the curve $f = 0$. This explains why the algebraic curve $f = 0$ is invariant under the flow of the vector field $\mathbb {X}$.

The next proposition shows that we can work with irreducible invariant algebraic curves.

Proposition 1

We suppose that $f\in \mathbb {C}[x,y]$ and let $f=f_1^{n_1}\cdots f_r^{n_r}$ be its factorization in irreducible factors over $\mathbb {C}[x,y]$. Then, for a polynomial system (1), $f=0$ is an invariant algebraic curve with the cofactor $K_{f}$ if and only if $f_i=0$ is an invariant algebrain curve for each $i=1,\ldots ,r$ with cofactor $K_{f_i}$. Moreover $K_f=n_1K_{f_1}+\cdots +n_rK_{f_r}$.

Darboux showed that if a system (1) possesses a sufficient number of such invariant algebraic solutions $f_i(x,y)=0,\ f_i\in \mathbb {C}[x,y],\ i=1,2,\ldots ,s$, then the system has a first integral of the form (3).

According to [12], we say that a system (1) has a Darboux first integral (respectively Darboux integrating factor) if it admits a first integral (respectively integrating factor) of the form $\ {\prod _{i=1}^s f_i(x,y)^{\lambda _i}},$ where $f_i\in \mathbb {C}[x,y]$, $\deg f_i\ge 1$, $i=1,2,\ldots ,s$, $f_i$ irreducible over $\mathbb {C}[x,y]$ and $\lambda _i\in \mathbb {C}$.

Let $\mathbb {C}(x,y)$ be the set of all rational functions with coefficients in $\mathbb {C}$. According to [10] the notion of Darboux first integral was extended as follows. From now on a Darboux first integral is a function of the form

$$\begin{aligned} e^{G(x,y)}\prod _{i=1}^s f_i(x,y)^{\lambda _i}, \end{aligned}$$

(4)

where $G(x,y)\in \mathbb {C}(x,y)$ and $f_i\in \mathbb {C}[x,y]$, $\deg f_i\ge 1$, $i=1,2,\ldots ,s$, $f_i$ irreducible over $\mathbb {C}[x,y]$ and $\lambda _i\in \mathbb {C}$. If a system (1) has an integrating factor (or first integral) of the form (4) then $\forall i\in \{1,\ldots ,s\}$, $f_i=0$ is an algebraic invariant curve of (1).

In [12] Darboux proved the following remarkable theorem of integrability using invariant algebraic solutions of systems (1):

Theorem 2

Consider a differential system (1) with $P,Q\in \mathbb {C}[x,y]$. Assume that $m=\max (\deg P,\, \deg Q)$ and that this system admits s algebraic solutions $f_i(x,y)=0$, $i=1,2,\ldots ,s$ ($\deg f_i\ge 1$). Then we have:

• I. If $s=m(m+1)/2$ then there exists $\lambda =(\lambda _1,\ldots ,\lambda _s)\in \mathbb {C}^s{\setminus }\{0\}$ such that $\ R=\prod _{i=1}^s f_i(x,y)^{\lambda _i}$ is an integrating factor of (1).

• II. If $s\ge m(m+1)/2+1$ then there exists $\lambda =(\lambda _1,\ldots ,\lambda _s)\in \mathbb {C}^s{\setminus }\{0\}$ such that $\ F=\prod _{i=1}^s f_i(x,y)^{\lambda _i} \$ is a first integral of (1).

The Darboux theory of integrability stated in Theorem 2 has been improved using the notion of exponential factor, see for details [10].

Let $h,g\in \mathbb {C}[x,y]$ and assume that h and g are relatively prime in the ring $\mathbb {C}[x,y]$. Then the function $\exp (g/h)$ is called an exponential factor of the polynomial system (1) if for some polynomial $K\in \mathbb {C}[x,y]$ of degree at most $n-1$ it satisfies equation

$$\begin{aligned} \mathbb {X}\left( \exp \left( \frac{g}{h}\right) \right) =K\exp \left( \frac{g}{h}\right) . \end{aligned}$$

As before we say that K is the cofactor of the exponential factor $\exp (g/h)$.

Theorem 3

Suppose that a polynomial system (1) of degree m admits p invariant algebraic curves $f_i=0$ with cofactors $K_i$ for $i=1,\ldots ,p,$ q exponential factors $\exp (g_j/h_j)$ with cofactors $L_j$ for $j=1,\ldots ,q$.

• (a) If there exists $\lambda _i,\mu _j \in \mathbb {C}$ not all zero such that ${\sum _{i=1}^p\lambda _i K_i+\sum _{j=1}^q\mu _j L_j=0}$, then the (multi-valued) function

  $$\begin{aligned} f_1^{\lambda _1}\ldots f_p^{\lambda _p}\left( \exp \left( \frac{g_1}{h_1}\right) \right) ^{\mu _1}\ldots \left( \exp \left( \frac{g_q}{h_q}\right) \right) ^{\mu _q} \end{aligned}$$

  (5)

  is a first integral of the system (1).

• (b) If there exists $\lambda _i,\mu _j\!\in \! \mathbb {C}$ not all zero such that $\sum _{i=1}^p\lambda _i K_i\!+\!\sum _{j=1}^q\mu _j L_j = -div(P,Q)$, then function (5) is an integrating factor of system (1).

In 1979 Jouanolou proved the next theorem which improves part II of Darboux’s Theorem.

Theorem 4

Consider a polynomial differential system (1) over $\mathbb {C}$ and assume that it has s algebraic solutions $f_i(x,y)=0$, $i=1,2,\ldots ,s$ ($\deg f_i\ge 1$). Suppose that $s\ge m(m+1)/2+2$. Then there exists $(n_1,\ldots ,n_s)\in \mathbb {Z}^s{\setminus }\{0\}$ such that $F=\prod _{i=1}^s f_i(x,y)^{n_i}$ is a first integral of (1). In this case $F\in \mathbb {C}(x,y)$, i.e. F is rational function over $\mathbb {C}$.

The following theorem from [11, 17] improves the Darboux theory of integrability and the above result of Jouanolou taking into account not only the invariant algebraic curves (especially invariant straight lines) but also their algebraic multiplicities.

Theorem 5

[11, 17] Assume that the polynomial vector field $\mathbb {X}$ in $\mathbb {C}^2$ of degree $d >0$ has invariant algebraic curves.

• (a) If some of these irreducible invariant algebraic curves has no defined algebraic multiplicity, then the vector field $\mathbb {X}$ has a rational first integral.

• (b) Suppose that all the irreducible invariant algebraic curves $f_i = 0$ have defined algebraic multiplicity $q_i$ for $i = 1,\ldots , p$.

  • ($b_1$) If $\sum _{i=1}^p{q_i\ge N+1}$, then the vector field $\mathbb {X}$ has a Darboux first integral, where $N=(_2^{2+d-1})$

  • ($b_2$) If $\sum _{i=1}^p{q_i\ge N+2}$, then the vector field $\mathbb {X}$ has a rational first integral.

As it was mentioned earlier our work here is based on the result of the paper [16] where the classification theorem according to the configurations of invariant straight lines for systems in ${\mathbb {CSL}}_9$ were proved (see further below). In what follows we recall some results of [16] which will be needed to state the mentioned theorem [16, Main Theorem]. Consider generic cubic systems of the form:

$$\begin{aligned} \frac{dx}{dt}= & {} p_0+ p_1(x,y)+\,p_2(x,y)+\,p_3(x,y) \equiv P(a,x,y), \nonumber \\ \frac{dy}{dt}= & {} q_0+ q_1(x,y)+\,q_2(x,y)+\,q_3(x,y)\equiv Q(a,x,y), \end{aligned}$$

(6)

with real homogeneous polynomials $p_i$ and $q_i$ $(i=0,1,2,3)$ of degree i in x, y. We introduce the following polynomials:

$$\begin{aligned} C_i = yp_i(x,y)-xq_i(x,y), \quad D_j = \frac{\partial p_j}{\partial x}+ \frac{\partial q_j}{\partial y}, \end{aligned}$$

for $i=0,1,2,3$ and $j=1,2,3$ which in fact are GL–comitants, see [30].

In order to state the classification theorem we need to construct some T-comitants and CT-comitants which will be responsible for the existence of the maximum number of invariant straight lines for system (6). They are constructed by using the polynomials $C_i$ and $D_i$ via the differential operator $(f,g)^{(k)}$ called transvectant of index k (see for instance [20]) which acts on $\mathbb {R}[{\varvec{a}},x,y]$ as follows:

$$\begin{aligned} (f,g)^{(k)}= \sum _{h=0}^k (-1)^h {k\atopwithdelims ()h} {\partial ^k f\over \partial x^{k-h}\partial y^h} {\partial ^k g\over \partial x^h\partial y^{k-h}}. \end{aligned}$$

Here f(x, y) and g(x, y) are polynomials in x and y of the degree r and s, respectively, and ${\varvec{a}}\in \mathbb {R}^{20}$ is the 20–tuple formed by all the coefficients of system (6).

In order to define the needed invariant polynomials it is necessary to construct the following comitants of second degree with respect to the coefficients of the initial system:

$$\begin{aligned} \begin{array}{llll} S_1=\left( C_0,C_1\right) ^{(1)},&{}\quad S_8=\left( C_1,C_2\right) ^{(2)},&{}\quad S_{15}=\left( C_2,D_2\right) ^{(1)},&{}\quad S_{22}\!=\!\left( D_2,D_3\right) ^{(1)},\\ S_2=\left( C_0,C_2\right) ^{(1)},&{}\quad S_9=\left( C_1,D_2\right) ^{(1)},&{}\quad S_{16}=\left( C_2,C_3\right) ^{(1)},&{}\quad S_{23}=\left( C_3,C_3\right) ^{(2)},\\ S_3=\left( C_0,D_2\right) ^{(1)},&{}\quad S_{10}=\left( C_1,C_3\right) ^{(1)},&{}\quad S_{17}=\left( C_2,C_3\right) ^{(2)},&{}\quad S_{24}=\left( C_3,C_3\right) ^{(4)},\\ S_4=\left( C_0,C_3\right) ^{(1)},&{}\quad S_{11}=\left( C_1,C_3\right) ^{(2)},&{}\quad S_{18}=\left( C_2,C_3\right) ^{(3)},&{}\quad S_{25}=\left( C_3,D_3\right) ^{(1)},\\ S_5=\left( C_0,D_3\right) ^{(1)},&{}\quad S_{12}=\left( C_1,D_3\right) ^{(1)},&{}\quad S_{19}=\left( C_2,D_3\right) ^{(1)},&{}\quad S_{26}=\left( C_3,D_3\right) ^{(2)},\\ S_6=\left( C_1,C_1\right) ^{(2)},&{}\quad S_{13}=\left( C_1,D_3\right) ^{(2)},&{}\quad S_{20}=\left( C_2,D_3\right) ^{(2)},&{}\quad S_{27}=\left( D_3,D_3\right) ^{(2)}.\\ S_7=\left( C_1,C_2\right) ^{(1)},&{}\quad S_{14}=\left( C_2,C_2\right) ^{(2)},&{}\quad S_{21}\!=\!\left( D_2,C_3\right) ^{(1)},&{}\quad \\ \end{array} \end{aligned}$$

We shall use here the following invariant polynomials constructed in [16] to characterize the system in ${\mathbb {CSL}}_9$:

$$\begin{aligned} {\mathcal {D}}_1(a)= & {} 6S_{24}^3-\left[ (C_3,S_{23})^{(4)}\right] ^2,\\ {\mathcal {D}}_2(a,x,y)= & {} -S_{23},\\ {\mathcal {D}}_3(a,x,y)= & {} (S_{23},\,S_{23})^{(2)} -6C_3(C_3,\,S_{23})^{(4)},\\ {\mathcal {D}}_4(a)= & {} (C_3,\, {\mathcal {D}}_2)^{(4)}, {\mathcal {V}}_1(a,x,y)= S_{23}+2D_3^2, {\mathcal {V}}_2(a,x,y)=S_{26},\\ {\mathcal {V}}_3(a,x,y)= & {} 6S_{25}-3S_{23}-2D_3^2, {\mathcal {V}}_4(a,x,y)= C_3\left[ \left( C_3,S_{23}\right) ^{(4)}\ +\ 36\left( D_3,S_{26}\right) ^{(2)}\right] ,\\ {\mathcal {L}}_1(a,x,y)= & {} 9C_2\left( S_{24}\ +\ 24S_{27}\right) \ 12D_3\left( S_{20}+8S_{22}\right) -12\left( S_{16},D_3\right) ^{(2)} -3\left( S_{23},C_2\right) ^{(2)}\\&-16\left( S_{19},C_3\right) ^{(2)} +12\left( 5S_{20}+24S_{22},C_3\right) ^{(1)},\\ {\mathcal {L}}_2(a,x,y)= & {} 32\left( 13\ S_{19}\ +\ 33\ S_{21},D_2\right) ^{(1)} \\&+84\left( 9\ S_{11}\ -\ 2\ S_{14},D_3\right) ^{(1)} \\&- 448\left( S_{18},C_2\right) ^{(1)}\ + 8D_2\left( 12S_{22}+35S_{18} - 73S_{20}\right) - 56\left( S_{17},C_2\right) ^{(2)}\\&- 63\left( S_{23},C_1\right) ^{(2)}+756D_3S_{13} - 1944D_1S_{26} + 112\left( S_{17},D_2\right) ^{(1)}\\&- 378\left( S_{26},C_1\right) ^{(1)}+9C_1\left( 48S_{27} - 35S_{24}\right) ,\\ {\mathcal {L}}_3(a,x,y)= & {} (S_{23}, D_3)^{(2)} [ (D_2, S_{22})^{(1)} - D_1 S_{27}],\ \ {\mathcal {L}}_4(a,x,y) = S_{25},\\ {\mathcal U}_1(a)= & {} S_{24} - 4 S_{27},\ \mathcal {U}_2(a,x,y) = 6 (S_{23} - 3 S_{25}, S_{26})^{(1)} - 3 S_{23} (S_{24} - 8 S_{27})\\&-24 S_{26}^2+ 2 C_3 (C_3, S_{23})^{(4)}+24 D_3 (D_3, S_{26})^{(1)}+24 D_3^2 S_{27},\\ {{\mathcal {N}}}_1(a,x,y)= & {} 4 C_2 (27 D_1 D_3 - 8 D_2^2) + 2 C_2 (20 S_{15} - 4 S_{14} + 39 S_{12}) + 18 C_1 (3 S_{21} - D_2 D_3)\\&+ 54 D_3 (3 S_4 - S_7) - 288 C_3 S_9 + 54 (S_7, C_3)^{(1)} - 567 (S_4, C_3)^{(1)} + 135 C_0 D_3^2,\\ {{\mathcal {N}}}_2(a,x,y)= & {} 2 C_2 D_3 - 3 C_3 D_2,\quad {\mathcal {N}}_3(a,x,y) = C_2 D_3 + 3 S_{16},\\ {\mathcal {N}}_4(a,x,y)= & {} D_2 D_3 + 9 S_{21} - 2 S_{17},\quad {\mathcal {N}}_5(a,x,y) = S_{17} + 2 S_{19},\\ {\mathcal {N}}_6(a,x,y)= & {} 6 C_3 (S_{12} + 6 S_{11}) - 9 C_1 (S_{23} + S_{25}) - 8 (S_{16}, C_2)^{(1)} - C_3 D_2^2,\\ {\mathcal {N}}_7(a,x,y)= & {} 6 C_3 (12 S_{11} - S_{12} - 6 D_1 D_3) - 21 C_1 S_{23} - 24 (S_{16}, C_2)^{(1)} + 3 C_1 S_{25} \ \\&+ 4 D_2 (S_{16} + 2 D_2 C_3 - C_2 D_3),\quad {\mathcal {N}}_8(a,x,y) = D_2^2 - 4 D_1 D_3,\\ {\mathcal {N}}_9(a,x,y)= & {} C_2^2 - 3 C_1 C_3,\quad {\mathcal {N}}_{10}(a,x,y) = 2 C_2 D_1 + 3 S_4,\quad {\mathcal {N}}_{11}(a) = S_{13},\\ {\mathcal {N}}_{12}(a,x,y)= & {} -32 D_3^2 S_2 - 108 D_1 D_3 S_{10} + 108 C_3 D_1 S_{11} - 18 C_1 D_3 S_{11} - 27 S_{10} S_{11} \\&+ 4 C_0 D_3 (9 D_2 D_3 + 4 S_{17}) + 108 S_4 S_{21},\\ {\mathcal {N}}_{13}(a,x,y)= & {} -S_{14}^2 - 2 D_2^2 (3 S_{14} - 8 S_{15}) - 12 D_3 (S_{14}, C_1)^{(1)} \\&+D_2 (-48 D_3 S_9 +16 (S_{17}, C_1)^{(1)}),\\ {\mathcal {N}}_{14}(a,x,y)= & {} 36 D_2 D_3 (S_8 - S_9) + D_1 (108 D_2^2 D_3 - 54 D_3 (S_{14} - 8 S_{15})) \\&+2 S_{14} (S_{14} - 22 S_{15}) - 8 D_2^2 (3 S_{14} + S_{15}) - 9 D_3 (S_{14}, C_1)^{(1)}-16 D_2^4. \end{aligned}$$

We apply a translation $x=x'+x_0$, $y=y'+y_0$ to the polynomials P(a, x, y) and Q(a, x, y) from the right-hand part of (6). Therefore we obtain ${\tilde{P}}(\tilde{a}(a,x_0,y_0),x',y')=P(a, x'+x_0, y'+y_0),$ $\quad {\tilde{Q}}(\tilde{a}(a,x_0,y_0),x',y')=Q(a, x'+x_0, y'+y_0).$ We construct the following polynomials:

$$\begin{aligned} \Omega _i(a,x_0,y_0)\equiv & {} {\mathrm{Res}}_{x'} \Big (C_i\big (\tilde{a}(a,x_0,y_0),x',y'\big ),C_0\big (\tilde{a}(a,x_0,y_0),x',y'\big )\Big )/(y')^{i+1},\\ \tilde{\mathcal {G}}_i(a,x,y)= & {} \left. \Omega _i(a,x_0,y_0)\right| _{\{x_0=x,\ y_0=y\}}\in {\mathbb R}[a,x,y] \ \ (i=1,2,3) \end{aligned}$$

where $\mathrm{Res}_{x'}$ is the resultant of the above polynomials with respect the variable $x'$.

Notation 6

Assume ${\mathcal {G}}_i(a,X,Y,Z)$ $(i=1,2,3)$ be the homogenization of $\tilde{\mathcal {G}}_i(a,x,y)$, i.e.

$$\begin{aligned} {\mathcal {G}}_1(a,X,Y,Z)= & {} Z^8\tilde{\mathcal {G}}_1(a,X/Z,Y/Z),\\ {\mathcal {G}}_2(a,X,Y,Z)= & {} Z^{10}\tilde{\mathcal {G}}_2(a,X/Z,Y/Z),\\ {\mathcal {G}}_3(a,X,Y,Z)= & {} Z^{12}\tilde{\mathcal {G}}_3(a,X/Z,Y/Z), \end{aligned}$$

and ${ H}(a,X,Y,Z)=\gcd \Big ({\mathcal {G}}_1(a,X,Y,Z), {\mathcal {G}}_2(a,X,Y,Z), {\mathcal {G}}_3(a,X,Y,Z) \Big )$ $\in$ ${\mathbb R}[a,X,Y,Z]$.

The geometrical meaning of the above defined affine comitants is given by the following two lemmas (see [16]):

Lemma 7

The straight line $L(x,y)\equiv ux+vy+w=0$, $u,v,w\in {\mathbb C}$, $(u,v)\ne (0,0)$ is an invariant straight line for a vector field $\mathbb {X}$ if and only if L(x, y) is a common factor of the polynomials $\tilde{\mathcal {G}}_1(a,x,y)$, $\tilde{\mathcal {G}}_2(a,x,y)$ and $\tilde{\mathcal {G}}_3(a,x,y)$ over ${\mathbb C}$, i.e. $\tilde{\mathcal {G}}_i(a,x,y)=(ux+vy+w)\widetilde{W}_i(x,y)\ (i=1,2,3),$ where $\widetilde{W}_i(x,y)\in {\mathbb C}[x,y].$

Lemma 8

Consider a cubic system (6) and let $a\in {\mathbb R}^{20}$ be its 20-tuple of coefficients.

• (a) If $L(x,y)\equiv ux+vy+w=0$, $u,v,w\in {\mathbb C}$, $(u,v)\ne (0,0)$ is an invariant straight line of multiplicity k for this system then $[L(x,y)]^k\mid \gcd (\tilde{\mathcal {G}}_1,\tilde{\mathcal {G}}_2,\tilde{\mathcal {G}}_3)$ in ${\mathbb C}[x,y]$, i.e. there exist $W_i(a,x,y)\in {\mathbb C}[x,y]$ $(i=1,2,3)$ such that

  $$\begin{aligned} \tilde{\mathcal {G}}_i(a,x,y)= (ux+vy+w)^k W_i(a,x,y),\quad i=1,2,3. \end{aligned}$$

  (7)

• (b) If the line $l_\infty :Z=0$ is of multiplicity $k>1$ then $Z^{k-1}\mid \gcd ({\mathcal {G}}_1, {\mathcal {G}}_2, {\mathcal {G}}_3)$, i.e. we have $Z^{k-1}\mid H(a,X,Y,Z)$.

We underline that by $P^{\star }(X,Y,Z), Q^{\star }(X,Y,Z)$ we denote the homogeneous polynomials associated to the polynomials P(a, x, y), Q(a, x, y), i.e.

$$\begin{aligned} P^{\star }(X, Y,Z) = Z^n P(X/Z, Y/Z),\quad Q^{\star }(X, Y,Z) = Z^n Q(X/Z, Y/Z) \end{aligned}$$

(8)

and $C^{\star }(X, Y,Z) = Y P^{\star }(X, Y,Z) - XQ^{\star }(X, Y,Z).$

In order to determine the degree of the common factor of the polynomials $\tilde{\mathcal {G}}_i(a,x,y)$ for $i=1,2,3,$ we shall use the notion of the $k^{th}$ subresultant of two polynomials with respect to a given indeterminate (see for instance, [20]).

We say that the k–th subresultant with respect to variable z of the two polynomials f(z) and g(z) is the $(m+n-2k)\times (m+n-2k)$ determinant

(9)

in which there are $m-k$ rows of a’s and $n-k$ rows of b’s, and $a_i=0$ for $i>n$, and $b_j=0$ for $j>m$.

For $k=0$ we obtain the standard resultant of two polynomials. In other words we can say that the k–th subresultant with respect to the variable z of the two polynomials f(z) and g(z) can be obtained by deleting the first and the last k rows and columns from its resultant written in the form (9) when $k=0$.

The geometrical meaning of the subresultants is based on the following lemma.

Lemma 9

(see [20]) Polynomials f(z) and g(z) have precisely k roots in common (considering their multiplicities) if and only if the following conditions hold:

$$\begin{aligned} R_z^{(0)}(f,g)=R_z^{(1)}(f,g)=R_z^{(2)}(f,g)= \cdots = R_z^{(k-1)}(f,g)= 0\ne R_z^{(k)}(f,g). \end{aligned}$$

For the polynomials in more than one variables it is easy to deduce from Lemma 9 the following result.

Lemma 10

Two polynomials $\tilde{f}(x_1,x_2,\ldots ,x_n)$ and $\tilde{g} (x_1,x_2,\ldots ,x_n)$ have a common factor of degree k with respect to the variable $x_j$ if and only if the following conditions are satisfied:

$$\begin{aligned} R_{x_j}^{(0)}(\tilde{f},\tilde{g})= R_{x_j}^{(1)}(\tilde{f},\tilde{g})= R_{x_j}^{(2)}(\tilde{f},\tilde{g})= \cdots = R_{x_j}^{(k-1)} (\tilde{f},\tilde{g})= 0\not = R_{x_j}^{(k)}(\tilde{f},\tilde{g}), \end{aligned}$$

where $R_{x_j}^{(i)}(\tilde{f},\tilde{g})=0$ in ${\mathbb R}[x_1,\ldots x_{j-1},x_{j+1},\ldots , x_n].$

Next we consider the differential operator ${\mathcal {L}}= x\cdot \mathbf{L}_2 -y\cdot \mathbf{L}_1$ constructed in [3] and acting on $\mathbb R[a,x,y]$, where

$$\begin{aligned} \mathbf{L}_1= & {} 3a_{00}\frac{\partial }{\partial a_{10}} + 2a_{10}\frac{\partial }{\partial a_{20}} + a_{01}\frac{\partial }{\partial a_{11}} + \frac{1}{3}a_{02}\frac{\partial }{\partial a_{12}} +\frac{2}{3}a_{11}\frac{\partial }{\partial a_{21}} + a_{20}\frac{\partial }{\partial a_{30}}\\&+ 3b_{00}\frac{\partial }{\partial b_{10}} + 2b_{10}\frac{\partial }{\partial b_{20}} + b_{01}\frac{\partial }{\partial b_{11}} + \frac{1}{3}b_{02}\frac{\partial }{\partial b_{12}} +\frac{2}{3}b_{11}\frac{\partial }{\partial b_{21}} + b_{20}\frac{\partial }{\partial b_{30}},\\ \mathbf{L}_2= & {} 3a_{00}\frac{\partial }{\partial a_{01}} + 2a_{01}\frac{\partial }{\partial a_{02}} + a_{10}\frac{\partial }{\partial a_{11}} + \frac{1}{3}a_{20}\frac{\partial }{\partial a_{21}} +\frac{2}{3}a_{11}\frac{\partial }{\partial a_{12}} + a_{02}\frac{\partial }{\partial a_{03}}\\&+ 3b_{00}\frac{\partial }{\partial b_{01}} + 2b_{01}\frac{\partial }{\partial b_{02}} + b_{10}\frac{\partial }{\partial b_{11}} + \frac{1}{3}b_{20}\frac{\partial }{\partial b_{21}} +\frac{2}{3}b_{11}\frac{\partial }{\partial b_{12}} + b_{02}\frac{\partial }{\partial b_{03}}. \end{aligned}$$

Using this operator and the affine invariant $\mu _0=\mathrm{Resultant}_x\big (p_3( a,x,y),q_3( a,x,y)\big )/y^9$ we construct the following polynomials: $\mu _i( a,x,y) =\dfrac{1}{i!} {\mathcal {L}}^{(i)}(\mu _0), \ i=1,\ldots ,9,$ where ${\mathcal {L}}^{(i)}(\mu _0)={\mathcal {L}}({\mathcal {L}}^{(i-1)}(\mu _0))$ and ${\mathcal {L}}^{(0)}(\mu _0)= \mu _0$.

The geometrical meaning of these polynomial is revealed in the next lemma.

Lemma 11

(see [2, 3]) Assume that a cubic system (S) with coefficients $\tilde{a}$ belongs to the family (6). Then:

• (a) The total multiplicity of all finite singularities of this system equals $9-k$ if and only if for every $i\in \{0,1,\ldots ,k-1\}$ we have $\mu _i(\tilde{a},x,y)=0$ in the ring ${\mathbb {R}}[x,y]$ and $\mu _k(\tilde{a},x,y)\ne 0$. In this case the factorization $\mu _{k}(\tilde{a},x,y)={\prod _{i=1}^{k}(u_ix-v_iy)\ne 0}$ over $\mathbb {C}$ indicates the coordinates $[v_i{:}u_i{:}0]$ of those finite singularities of the system (S) which “have gone” to infinity. Moreover the number of distinct factors in this factorization is less than or equal to four (the maximum number of infinite singularities of a cubic system) and the multiplicity of each one of the factors $u_ix-v_iy$ gives us the number of the finite singularities of the system (S) which have collapsed with the infinite singular point $[v_i{:}u_i{:}0]$.

• (b) The system (S) is degenerate (i.e. $\gcd (P,Q)\ne \mathrm{const}$) if and only if $\mu _i(\tilde{a},x,y)=0$ in ${\mathbb {R}}[x,y]$ for every $i=0,1,\ldots ,9$.

Let $L(x,y)= U x+V y+W=0$ be an invariant straight line of cubic systems (S). Then, according to the definition of an invariant line, we have $U P(x,y)+V Q(x,y)=(U x+V y+W)(Ax^2+2Bxy+Cy^2+Dx+Ey+F),$ and this identity provides the following 10 relations:

$$\begin{aligned} Eq_1= & {} (a_{30}-A)U+b_{30}V=0,\nonumber \\ Eq_2= & {} (3a_{21}-2B)U+(3b_{21}-A)V=0,\nonumber \\ Eq_3= & {} (3a_{12}-C)U+(3b_{12}-2B)V=0,\ Eq_4=a_{03}U+(b_{03}-C)V =0,\nonumber \\ Eq_5= & {} (a_{20}-D)U+b_{20}V-AW=0,\nonumber \\ Eq_6= & {} (2a_{11}-E)U+(2b_{11}-D)V-2BW=0,\nonumber \\ Eq_7= & {} a_{02}U+(b_{02}-E)V-CW=0,\ Eq_8=(a_{10}-F)U+b_{10}V-DW=0,\nonumber \\ Eq_9= & {} a_{01}U+(b_{01}-F)V-EW=0,\ Eq_{10}=a_{00}U+b_{00}V-FW=0. \end{aligned}$$

(10)

Fig. 1

Configurations of cubic systems in Poincaré disc

2 The Classification Theorem in Terms of Configurations of Invariant Straight Lines for the Family of Systems ${\mathbb {CSL}}_9$

Taking into account [4, 16] we prove the next result.

Theorem 12

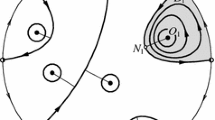
Any cubic system having invariant straight lines of total multiplicity 9 including the line at infinity and considering their multiplicities via an affine transformation and time rescaling can be written as one of the following 24 systems. In the figure associated to each system is presented the configuration of its invariant straight lines in the Poincaré disc (see Fig. 1). Moreover, every system has associated a set of affine invariant conditions which characterize it.

•    $\mathcal {D}_1>0,\ \mathcal {D}_2>0,\ \mathcal {D}_3>0,\ \mathcal {V}_1=\mathcal {V}_2=\mathcal {L}_1=\mathcal {L}_2={\mathcal {N}}_1=0$:

  • 1.    $\mathcal {L}_3<0\ \Leftrightarrow \$ $\dot{x}= x(x^2-1),\ \ \dot{y}=(y^2-1)y;$ $\ \Leftrightarrow \$ Fig. 1(1);

  • 2.    $\mathcal {L}_3>0\ \Leftrightarrow \$ $\dot{x}= x(x^2+1),\ \ \dot{y}=(y^2+1)y;$ $\ \Leftrightarrow \$ Fig. 1(2);

  • 3.    $\mathcal {L}_3=0\ \Leftrightarrow \$ $\dot{x}= x^3, \ \ \dot{y}= y^3;$ $\ \Leftrightarrow \$ Fig. 1(3);

•    $\mathcal {D}_1>0,\ \mathcal {D}_2>0,\ \mathcal {D}_3>0,\ \mathcal {V}_3=\mathcal {V}_4=\mathcal {L}_1=\mathcal {L}_2={\mathcal {N}}_1=0$:

  • 4.    $\mathcal {L}_3>0\ \Leftrightarrow \$ $\dot{x}= 2x(x^2-1), \ \ \dot{y}=(y^2-1)(3x-y);$ $\ \Leftrightarrow \$ Fig. 1(4);

  • 5.    $\mathcal {L}_3<0\ \Leftrightarrow \$ $\dot{x}= 2x(x^2+1),\ \ \dot{y}=(y^2+1)(3x-y);$ $\ \Leftrightarrow \$ Fig. 1(5);

  • 6.    $\mathcal {L}_3=0\ \Leftrightarrow \$ $\dot{x}= 2x^3, \ \ \dot{y}= y^2(3x-y);$ $\ \Leftrightarrow \$ Fig. 1(6);

•    $\mathcal {D}_1<0,\ \mathcal {V}_1=\mathcal {V}_2=\mathcal {L}_1=\mathcal {L}_2={\mathcal {N}}_1=0$:

  • 7.    $\mathcal {L}_3\ne 0,\ \mathcal {L}_4<0\ \Leftrightarrow \$ $\dot{x}= x(x^2+1), \ \ \dot{y}=(1-y^2)y;$ $\ \Leftrightarrow \$ Fig. 1(7);

  • 8.    $\mathcal {L}_3=0,\ \mathcal {L}_4<0\ \Leftrightarrow \$ $\dot{x}= x^3, \ \ \dot{y}=-y^3;$ $\ \Leftrightarrow \$ Fig. 1(8);

  • 9.    $\mathcal {L}_3\ne 0,\ \mathcal {L}_4>0\ \Leftrightarrow \$ $\dot{x}= x(1+x^2-3y^2), \ \ \dot{y}= y(1+3x^2-y^2);$ $\ \Leftrightarrow \$ Fig. 1(9);

  • 10.    $\mathcal {L}_3=0,\ \mathcal {L}_4>0\ \Leftrightarrow \$ $\dot{x}= x(x^2-3y^2), \ \ \dot{y}= y(3x^2-y^2);$ $\ \Leftrightarrow \$ Fig. 1(10);

  • 11.    $\mathcal {L}_3<0,\ \Leftrightarrow \$ $\dot{x}= 2x(x^2-1), \ \ \dot{y}= y(3x^2+y^2+1);$ $\ \Leftrightarrow \$ Fig. 1(11);

  • 12.    $\mathcal {L}_3>0,\ \Leftrightarrow \$ $\dot{x}= 2x(x^2+1), \ \ \dot{y}= y(3x^2+y^2-1);$ $\ \Leftrightarrow \$ Fig. 1(12);

  • 13.    $\mathcal {L}_3=0,\ \Leftrightarrow \$ $\dot{x}= 2x^3 , \ \ \dot{y}= y(3x^2+y^2);$ $\ \Leftrightarrow \$ Fig. 1(13);

•    $\mathcal {D}_1=\mathcal {D}_3=\mathcal {D}_4= \mathcal {V}_1={\mathcal {N}}_1={\mathcal {N}}_2={\mathcal {N}}_3=0,\ \mathcal {D}_2\ne 0:$

  • $\mathcal {L}_4<0$:

    • 14.    ${\mathcal {N}}_7=0,\ {\mathcal {N}}_8<0\ \Leftrightarrow \$ $\dot{x}= x(x^2-1), \ \ \dot{y}=2y;$ $\ \Leftrightarrow \$ Fig. 1(14);

    • 15.    ${\mathcal {N}}_7=0,\ {\mathcal {N}}_8>0\$ $\Leftrightarrow \$ $\dot{x}= x(x^2+1), \ \ \dot{y}=-2y;$ $\ \Leftrightarrow \$ Fig. 1(15);

    • 16.    ${\mathcal {N}}_6=0,\ {\mathcal {N}}_8>0\ \Leftrightarrow \$ $\dot{x}= x(x^2-1), \ \ \dot{y}=-y;$ $\ \Leftrightarrow \$ Fig. 1(16);

    • 17.    ${\mathcal {N}}_6=0,\ {\mathcal {N}}_8<0\ \Leftrightarrow \$ $\dot{x}= x(x^2+1), \ \ \dot{y}=y;$ $\ \Leftrightarrow \$ Fig. 1(17);

    • 18.    ${\mathcal {N}}_6=0,\ {\mathcal {N}}_8=0\ \Leftrightarrow \$ $\dot{x}= x^3, \ \ \dot{y}=1;$ $\ \Leftrightarrow \$ Fig. 1(18);

  • $\mathcal {L}_4>0$:

    • 19.    ${\mathcal {N}}_6=0,\ {\mathcal {N}}_8>0\ \Leftrightarrow \$ $\dot{x}= x(x^2-1), \ \ \dot{y}=y(3x^2-1);$ $\ \Leftrightarrow \$ Fig. 1(19);

    • 20.    ${\mathcal {N}}_6=0,\ {\mathcal {N}}_8<0\ \Leftrightarrow \$ $\dot{x}= x(x^2+1), \ \ \dot{y}=y(3x^2+1);$ $\ \Leftrightarrow \$ Fig. 1(20);

    • 21.    ${\mathcal {N}}_7=0,\ {\mathcal {N}}_8>0\ \Leftrightarrow$ $\dot{x}= 2x(x^2-1), \dot{y}=y(3x^2+1);$ $\ \Leftrightarrow$ Fig. 1(21);

    • 22.    ${\mathcal {N}}_7=0,\ {\mathcal {N}}_8<0\ \Leftrightarrow$ $\dot{x}= 2x(x^2+1), \dot{y}=y(3x^2-1);$ $\ \Leftrightarrow$ Fig. 1(22);

• $\mathcal {D}_1=\mathcal {D}_2=\mathcal {D}_3=\mathcal {V}_1={\mathcal {N}}_2= {\mathcal {N}}_3={\mathcal {N}}_9={\mathcal {N}}_{10}=0\ \Leftrightarrow$

  • 23. $\dot{x}= x, \dot{y}=y-x^3;$ $\ \Leftrightarrow \$ Fig. 1(23);

• $\mathcal {D}_1=\mathcal {D}_3=\mathcal {D}_4=\mathcal {V}_1={\mathcal {N}}_{1}={\mathcal {N}}_{11}= {\mathcal {N}}_{12}={\mathcal {N}}_{13}={\mathcal {N}}_{14}=0,\ \mathcal {D}_{2}{\mathcal {N}}_{2}\ne 0,\ \mathcal {L}_{4}<0 \Leftrightarrow$

  • 24. $\dot{x}= x(9x^2 - 4), \dot{y}=2y(9x - 2);$ $\ \Leftrightarrow \$ Fig. 1(24).

Remark 13

Real invariant straight lines are represented by continuous lines, whereas complex invariant straight lines are represented by dashed lines. If in a configuration an invariant straight line has multiplicity $k>1$, then the number k appears near the corresponding straight line and this line is in bold face. We indicate next to the real singular points of the system, located on the invariant lines, their corresponding multiplicities. By the notation (a, b) we point out the maximum number a (respectively b) of infinite (respectively finite) singularities which can be obtained by perturbation of the multiple point.

Proof of Theorem 12

We remark that the first 23 configurations of invariant lines as well as the corresponding affine invariant conditions where constructed in paper [16]. On the other hand in article [4] a new class of planar cubic systems possessing invariant lines of total multiplicity 9, which was omitted in [16] was presented. So it remains to find out the necessary and sufficient conditions for the realization of this new class.

First of all we mention that the omitted misstep in paper [16] was localized in Section 7 and namely, it is related with the case of systems (66), i.e. systems of the form

$$\begin{aligned} \dot{x} = a + c x + d y + 2hxy+ky^2+x^3,\quad \dot{y} = b + e x + f y + lx^2+2mxy+ ny^2.\nonumber \\ \end{aligned}$$

(11)

For this system we have $C_3(x,y)=x^3y$ and therefore, there exist two directions for the possible invariant straight lines: $x=0$ and $y=0$.

Direction $x=0$. From (10) for $U=1,\ V=0$ it was obtained $A=1,\, B=C=0,$ $D=-W,\, E=2h,\, F=W^2+c,\, Eq_7=k=0,\, Eq_9=-2hW+d=0$ and $Eq_{10}=-W^3-cW+a=0.$ The last equations imply the conditions $k=h=d=0$ (in order to have the maximum number of invariant straight lines).

Direction $y=0$. In this case $U=0,\ V=1$ and, from (10) we get $A=B=C=0,$ $D=2m,\ E=n,\ F=-nW+f$ and

$$\begin{aligned} Eq_5=l,\ Eq_8=-2mW+e,\ Eq_{10}=nW^2-fW+b. \end{aligned}$$

(12)

Evidently the condition $Eq_5=0$ is equivalent to $l=0$, whereas the condition $Eq_8 =0$ implies two possibilities: $(\alpha )$ $m=0$ (then $e=0$) and $(\beta )$ $m\ne 0$ (then $W=e/(2m)$). The first case was examined in [16], whereas the second case when $m\ne 0$ was omitted. Here further below we show that in the case $m\ne 0$ systems (11) also possess invariant lines of total multiplicity 9 and we present the corresponding configuration. Furthermore we construct necessary and sufficient conditions to get this configuration in terms of invariant polynomials.

It is worth to point out that if for perturbed systems some condition $U(x,y)=0$ holds, where U(x, y) is an invariant polynomial, then this condition must hold also for the initial (not-perturbed) systems. So considering Theorem 12 (more exactly its part related with the configurations Figs. 1–13 which was proved in [16]) we arrive at the next remark.

Remark 14

The condition $\mathcal {L}_1=\mathcal {L}_2=0$ is necessary for any cubic system possessing invariant lines of total multiplicity 9.

The case $\mathbf{m\ne 0.}$ Thus in what follows we consider $m\ne 0$. It was shown above that for a system (11) to possess at least 4 invariant lines in two directions ($x=0$ and $y=0$) the conditions $k=h=d=l=0$ are necessary. So considering Remark 14 we calculate $\mathcal {L}_1=0$ and $\mathcal {L}_2=20736 n x (m x - 3 n y)$. It is evident that the polynomial $\mathcal {L}_2$ vanishes if and only if $n=0$. In this case applying the rescaling $(x,y,t)\mapsto (m x, y,t/m^2)$ we can set $m=1$ and systems (11) become $\ \dot{x}= a + c x +x^3,\quad \dot{y}= b + ex+ f y + 2 x y. \$ Considering (12) we get $Eq_8=-2W+e=0,\ Eq_{10}=-fW+b=0$. These equations have a common solution if and only if the resultant $R_W(Eq_8,Eq_{10})= -2b+fe=0$, i.e. $b=e f/2$ (see Lemma 9). So, the conditions $k=h=d=l=n=0, m=1$ and $b=e f/2$ yield the following systems of equations

$$\begin{aligned} \dot{x}= a + c x +x^3\equiv P(x),\quad \dot{y}= (f + 2 x) (e + 2 y)/2\equiv (e + 2 y)Q(x). \end{aligned}$$

(13)

Remark 15

It is clear that systems (13) are degenerate if and only if the polynomials P(x) and Q(x) have a non-constant common factor (depending on x). So, the following condition must hold:

$$\begin{aligned} \Phi \equiv R_x^{(0)}( P(x), Q(x))\ne 0. \end{aligned}$$

(14)

For systems (13) we calculate $H(X,Z)=2^{-1}Z (2 Y + e Z) (X^3 + c X Z^2 + a Z^3)$ for which $\deg {H}=5$. On the other hand for a system in ${\mathbb {CSL}}_9$ the corresponding polynomial H must have the degree eight.

Considering Lemmas 7 and 8 we determine the conditions to get a common factor of degree three of the polynomials $\mathcal {G}_i/H,\ i=1,2,3$. For systems (13) we calculate

$$\begin{aligned} \mathcal {G}_1/H= & {} 4X^3 + (sf -4)X^2Z - 4fXZ^2 + (cf-2a - f^2)Z^3,\\ \mathcal {G}_2/H= & {} (3 X - 2 Z) )(2X + fZ)(X^3 + cXZ^2 + aZ^3). \end{aligned}$$

Since the polynomials $\mathcal {G}_i/H,\ (i = 1, 2)$ do not depend on Y we conclude that the common factor of degree 3 of these two polynomials must depend on X. So by Lemma 9 the following condition is necessary in order to have a such a factor:

$$\begin{aligned} R^{(0)}_X(\mathcal {G}_2/H,\mathcal {G}_1/H)=R^{(1)}_X(\mathcal {G}_2/H,\mathcal {G}_1/H)= R^{(2)}_X(\mathcal {G}_2/H,\mathcal {G}_1/H)=0. \end{aligned}$$

Calculations yield

$$\begin{aligned} R^{(2)}_X(\mathcal {G}_2/H,\mathcal {G}_1/H) = -2(64 + 288a + 64c + 48f -96cf + 12f^2 - 27f^3)Z^3 = 0 \end{aligned}$$

and this implies $a = (96cf -64 -64c -48f -12f2 + 27f3)/288$. Then we obtain

$$\begin{aligned}&\displaystyle R^{(1)}_X(\mathcal {G}_2/H,\mathcal {G}_1/H) =(4 + 3f)^2(4 + 9f)^2(16 + 16c + 3f^2)^2Z^8/576 = 0,\\&\displaystyle \quad \Phi = R_x^{(0)}( P(x), Q(x))=(4 + 3f)(16 + 16c + 3f^2)/288\ne 0 \end{aligned}$$

and clearly the above relations imply $4 + 9f = 0$, i.e. f = -4/9. Herein we calculate

$$\begin{aligned}&\displaystyle R^{(0)}_X(\mathcal {G}_2/H,\mathcal {G}_1/H) =2^{16}3^{-31}(4 + 9c)^3(28 + 27c)^3Z^{15} = 0,\\&\displaystyle \Phi = R_x^{(0)}( P(x), Q(x))=4(28 + 27c)/729\ne 0 \end{aligned}$$

and therefore we obtain $c =-4/9 = f$ which implies $a = 0$.

Thus for systems (11) with $m\ne 0$ (then we assume $m=1$) we get the set of conditions

$$\begin{aligned} k=h=d=l=n=a=0,\ \ f=c=-4/9,\ \ b=-2 e/9 \end{aligned}$$

(15)

which leads to a system belonging to ${\mathbb {CSL}}_9$. Moreover applying the transformation $(x,y,z)\mapsto (x,(2y-e)/2, 9t)$ this system could be brought to the form

$$\begin{aligned} \dot{x}=x (9 x^2-4),\ \ \dot{y}=2y(9 x-2). \end{aligned}$$

(16)

For this system we have $H(X,Y,Z)=-18 X^2 Y (3 X - 2 Z)^3 Z (3 X + 2 Z)$.

Considering Lemma 11 we calculate: $\mu _0=\cdots =\mu _5=0,\ \ \mu _6= 373248 x^6\ne 0.$ By the same lemma six finite singular points from 9 have gone to infinity and collapsed with the singular point [0, 1, 0] located on the “end” of the invariant line $x=0$. On the other hand system (16) possesses three finite singular points (0, 0) and $(\pm 2/3,0)$ and the invariant straight lines:

$$\begin{aligned} L_{1,2}:\ x=0,\ L_3: y=0,\ L_{4,5,6}: 3x-2=0,\ L_7: 3x+2=0,\ L_{7,8}: Z=0. \end{aligned}$$

In this case the configuration of invariant lines of the system (16) corresponds to Fig. 1(24).

Invariant conditions for the realization of the configuration given by Fig. 1(24)

Now we construct the necessary and sufficient conditions in terms of affine invariant polynomials using the theory of algebraic invariants developed by Sibirschi’s school (see for instance, [30]).

From [16, Proposition 28] we need the following result:

Proposition 16

If for a cubic system (6) the conditions $\mathcal {D}_1 = \mathcal {D}_3 = \mathcal {D}_4 = 0,\ \mathcal {D}_2\ne 0$ and $\mathcal {V}_1 = 0$ hold, then via a linear transformation and time rescaling the homogeneous cubic part of this system becomes into the form $\ p_3=x^3,\ q_3=0\$ for $\mathcal {L}_4 < 0$.

So, we get systems (11) (with $(p_3,q_3)=(x^3,0)$) and, as it was earlier showed, in the case $m\ne 0$ (then we may assume $m=1$ due to a rescaling) the conditions (15) (which are in terms of the coefficient of these systems) are necessary and sufficient for a system (11) to have 9 $\mathbb {IL}s$. We calculate

$$\begin{aligned} {\mathcal {N}}_3=-12 x^2 (l x^3 + (2 h -n)x y^2 + 2 k y^3) \end{aligned}$$

and taking into consideration Remark 14 and the fact that $\mathcal {L}_2=0\ \Leftrightarrow \ n=0$ from the page 13 we obtain that ${\mathcal {N}}_3=\mathcal {L}_2=0\ \Leftrightarrow \ l=k=n=h=0.$

In this case we calculate ${\mathcal {N}}_2=-18 mx^4y$ and therefore the condition $m\ne 0$ is governed by the invariant polynomial ${\mathcal {N}}_2$ and in what follows we assume ${\mathcal {N}}_2\ne 0$, i.e. $m=1$.

We continue with the calculation of ${\mathcal {N}}_{11}=12d=0$, i.e. $d=0$ and this implies ${\mathcal {N}}_{12}=1296 (e f-2 b ) x^6.$ It is evident that ${\mathcal {N}}_{12}=0\ \Leftrightarrow \ e f-2 b=0$, i.e. $b=ef/2$. In this case the calculations yield

$$\begin{aligned} {\mathcal {N}}_{13}=5184 (c - f) x^4,\quad {\mathcal {N}}_{14}=2592 (4 + 6 c + 3 f) x^4. \end{aligned}$$

It is not too hard to see that ${\mathcal {N}}_{13}={\mathcal {N}}_{14}=0$ is equivalent with $f=c=-4/9$ and these leads to ${\mathcal {N}}_1=-1944 a x^4 y$ and clearly the condition ${\mathcal {N}}_1=0$ gives $a=0$.

This completes the proof of Theorem 12. $\square$

Table 1 First integrals, integrating factors and phase portraits

Fig. 2

Topologically distinct phase portraits

3 Main Results: First Integrals and Phase Portraits of Cubic Systems with the Maximum Number of Invariant Straight Lines

Theorem 17

Consider systems (6) in ${\mathbb {CSL}}_9$. Then these systems with five exceptions have the polynomial inverse integrating factors as well as the rational first integrals corresponding to each one of the 24 canonical forms as it is indicated in Table 1. This table also lists all phase portraits P.1–P.24 corresponding to the configurations Fig. 1(1)–(24) of invariant straight lines of such systems. Moreover using the geometrical (numeric) invariants (see Remark 18) in the diagram from Fig. 2 it is shown that among these 24 phase portraits only 18 are topologically distinct.

Remark 18

In order to distinguish topologically the phase portraits of the systems we obtained, we use the following geometric invariants:

• The number $IS^{\mathbb R}$ of real infinite singularities.

• The number $FS^{\mathbb R}$ of real finite singularities.

• The number $Sep^{\,f}$ of separatrices associated to finite singularities.

• The number $Sep^{\,\infty }$ of separatrices associated to infinite singularities.

• The number FSep of separatrices connecting finite singularities.

• The number SC of separatrix connections.

Proof

Using Theorems 12 and 3 it follows after some easy calculations the expressions for the integrating factors and the first integrals of Table 1.

The phase portraits of polynomial differential equations are usually presented in the Poincaré disc using the so called Poincaré compactification, see for details Chapter 5 of [14]. The existence of the 9 invariant straight lines taking into account their multiplicities and the knowledge of the rational first integrals allows us to drown the 24 phase portraits of the systems given in Theorem 17. After we prove that only 18 of these phase portraits are topologically different using Remark 18. They are given in Fig. 2.

We note that the systems in Theorem 12 have no parameters and the study of their phase portraits also can be done using the algebraic program P4, see for details Chapters 9 and 10 of [14].

We also observe that the inverse integrating factors described in Table 1 are all polynomial except 5 of them. $\square$