Introduction

Currently, aerospace and automotive industries are developing new materials and new processes for decreasing the pollutant gas emissions from the engine, obtaining considerable weight reduction, and saving energy in order to meeting the environmental regulations for cars, buses and aircrafts. To achieve these objectives, light and efficient engine materials as well as structural light materials for manufacturing parts are the focus of current research topics. Carbon fiber composites, high-strength aluminium alloys, high-strength low alloy steels, TRIP steels and titanium alloys have been the main investigated materials in recent years for their superior properties, such as high strength-to-weight ratio, fatigue and corrosion resistance.

In particular, the Ti6Al4V titanium alloy also shows high temperature mechanical strength and excellent corrosion behaviour, superior to aluminium alloys, for applications demanding high performances under severe in-service conditions [1, 2]. However, Ti6Al4V alloy formability is poor at room temperature, as a result of its Hexagonal Closed Packed (HCP) lattice characterized by a limited number of slip planes, thus, forcing to carry out forming operations at elevated temperature to activate additional slip planes [3, 4]. Ti6Al4V Super Plastic Forming with Diffusion Bonding (SPF-DB) at high temperature is a well-known manufacturing process for producing aerospace structural components [1]. However, the typically very low production rates of the SPF-DB process as well the high costs of the initial sheets, which must be fine grained to present superplastic properties, limit a widespread industrial application. On the contrary, Ti6Al4V sheets of conventional microstructure can be heated to a temperature where they present a sufficient increase of formability and then deformed. In this way, besides the formability increase, a significant reduction of both the forming force and springback phenomenon can be achieved. A few papers are available in literature dealing with high temperature forming of Ti6Al4V sheets, which show the temperature and rolling direction sensitivity of material flow stress and strain at fracture [5], and the modelling of fracture onset for different temperature ranges [6].

In the design and manufacturing of parts by sheet metal forming, the Map of Principal Surface Limit Strains (MPLS) [7] is a well-established approach at both academic and industrial level [8] and is an essential aid to the successful design of parts by means of numerical simulations and experimental investigations of failure. Sheet metal formability data are commonly evaluated experimentally and the experimental Forming Limit Curves (FLCs) are plotted in the MPLS, which define the safe and unsafe regions for attaining maximum surface principal strains. Experimental FLCs are based on sheet formability tests and obtained by measuring the principal strains on the sheet surface, major true strain ε1 and minor true strain ε2, nearest to fracture site. Linear strain paths are usually employed by means of Nakajima and uniaxial tensile tests [9]. Principal or major and minor true strains on the sheet surface are measured during deformation by using Direct Image Correlation techniques applied to a printed grid of regular circles or stochastic patterns.

Theoretical predictions of FLCs at room temperature is state-of-the-art and several authors focused their efforts in the calibration and evaluation of the available theoretical models [10] applied for different materials such as steel alloys [11] or aluminum alloys [12, 13]. However, the theoretical FLCs prediction at warm and hot temperatures are still a pioneering research as the current approaches must be extended to consider the material behavior sensitivity to temperature and strain rate. In this case, some authors developed procedures to evaluate the FLCs at elevated temperature for high strength steel [14], or aluminum alloys [15] applied in hot stamping processes. However, the problem of predicting the FLCs in temperature assisted processes is most commonly addressed using FE models due to the increased complexity added by the temperature effects, tool and specimen geometries. Some examples can be found in literature for high strength steel [16], aluminum [17] and titanium alloys [18], but these require complex and time-consuming numerical approaches.

In this context, the aim of present work is to compare experimental FLC curves from Nakajima and in-plane tensile testing of sheet specimens with predictions from D-Bressan’s macroscopic modelling approaches for Ti6Al4V titanium alloy sheets deformed at room temperature and 600 °C. This is a limiting high temperature of die tool steels for acceptable service life. Moreover, it was expected enhanced formability of Ti6Al4V sheet at this warm temperature than at 400 °C [5, 6]. As temperature increases, the material rupture mechanisms leading to sheet failure may change as well as ductility and limit strains. Consequently, two different D-Bressan analytical modelling [7] were employed to predict the FLC: the critical fast shear stress and the critical strain gradient criteria. In order to calibrate the models, the plasticity parameters of normal anisotropy R, work hardening exponent n-value, strain rate sensitivity exponent M-value and initial pre-strain εo were obtained from standard tensile tests at room temperature and 600 °C. Additional parameters were determined experimentally to complete the required variables: a) the normalized critical shear stress ratio to the yield stress, rcr = τcr /σo at plane strain condition, for the critical fast shear stress criterion and b) the normalized critical strain gradient (λ/μ)* for localized necking in the critical strain gradient criterion. Shear stress fracture mechanism was also confirmed by experimental fractograph observations of thickness surface rupture by optical microscope.

Analytical modelling of limit strains

Stretch forming and deep drawing operations are considered failed when either shear stress fracture or surface localized necking occur on the sheet metal. Extensive experimental observations and literature survey have shown that sheet metal failure during forming operations are generally due to shear stress fracture mechanisms [19] or by highly localized necking and that these mechanisms are influenced by the process temperature [7]. Therefore, the localized rupture mechanisms may occur with visible surface localized necking which degenerates to posterior through-thickness shear stress fracture, but also by abrupt shear stress without any highly evident localized necking or grooving.

The MPLS map defines safe and unsafe regions of limiting surface strains in sheet metal forming processes and can be also divided in two main regions: the biaxial stretching region (minor true strain ε2 > 0) and the drawing quadrant (ε2 < 0) [7]. In the first one, the sample is deformed following a positive plastic strain path α (= dε2/dε1). For linear plastic strain path, α varies from 1 for a balanced biaxial stress state to zero for the plane strain condition which identifies the critical minimum point of FLC, named FLCo. In the negative quadrant, α varies from plane strain condition up to −0.5 for uniaxial tension and − 1 for pure shear strain, considering an isotropic sheet metal. However, it is well known that strain path may change significantly and affects the FLC curve [20], as do different amounts of pre-strain [21]. As a consequence of that, the effect of the strain-path changes on the FLCs has been studied quite extensively as in [22] and proposed alternative forming limit diagrams not dependent on the strain path have been proposed as in [23]. Furthermore, wrinkling represents an important formability issue and its limit strain curve can be plotted as well in the MPLS.

Hence, three FLCs are needed to design a safe sheet metal processing window in the MPLS map: (i) the visible localized necking limit strain curve (FLC-N), (ii) the limit strain curve for fast fracture by shear stress (FLC-S), and (iii) limit strain curve for wrinkling (FLC-W) [7]. The inner region limited by these three curves gives the safe combination of sheet surface strains, whereas the external region is unsafe or failure. Consequently, three different types of theoretical models are required to accurately predict the safe and unsafe regions. However, in the present work, no wrinkling phenomenon appeared during the Nakajima tests. Therefore, only the first two above mentioned failure mechanisms were considered for predicting Ti6Al4V sheet formability at room temperature and 600 °C.

Various theoretical models to predict the onset of localized necking and ductile fracture in sheet metal forming have been developed and presented in the scientific literature. In the first model, Hill (1952) proposed an approach to predict the onset of localized necking in sheet metal forming for a negative strain path [24]. In 1965, experimental observations of sheets deformed under positive strain paths conditions, reported by Keeler [25], showed the occurrence of visible mini-grooves on samples surface before failure. Thus, later in 1967, Marciniak and Kuczynski [26] proposed an analytical model (the so-called M-K model) to predict localized necking under the same conditions, during biaxial stretching tests. In this case, it was assumed that an initial defect of thickness fo should evolve to plane strain state and, thus leading to visible localized necking. While plane strain conditions were not reached, then the sheet material should continue to deform plastically without the inception of localized necking. However, it is possible that the material may fracture in the incipient neck before plane strain is reached. Also, the M-K model is very sensitive to the initial defect parameter and has shown poor predicting capabilities for some materials when compared to experimental FLCs, possibly due to the discrepancies between the material model parameters and the real material behaviour. Nevertheless, the M-K model is effective and one of the most employed models in literature for theoretical investigations of sheet forming limit strains [27].

Several other analytical models have been proposed to predict the FLC, which assume that ductile fracture develops after the shear-joining of voids [28], and use of Hill’s quadratic yield criterion with different material models [29] or the modified Mohr-Coulomb fracture criterion [30]. Additionally, other models were proposed using empirical stress or strain functions [31] and were based on bifurcation theory. Other researchers developed approaches based on evolution of microstructural imperfections inside the rupture site such as nucleation, growth and coalescence of micro-porosities [32], evaluating their results on different materials [33] and including the effect of the workpiece anisotropy and strain-rate [34]. Finally, other authors presented models computing the surface roughness evolution during the forming process, triggering the crack propagation along the workpiece thickness [35, 36].

FLC-S modelling by shear stress fracture criterion

As previously mentioned above, from experimental observations of sheet metal surface, failure in sheet forming is either by a process of fast shear stress fracture without visible necking or by inception of progressive local necking or grooving and subsequent final rupture by rapid shear stress mechanism inside the surface neck. Bressan and Williams model (B-W) presented in 1983 [37] assumed plane stress and an instability concept that was a maximum in the shear stress at onset of local necking. This maximum shear stress was in a specific plane, inclined through the thickness and of pure shear strain, where the shear stress attained a critical value which is a material parameter. Hence, the B-W concept was initially based on stress instability criterion for development of localized narrow straining band or local necking due to shear bands formation in the sheet thickness and not thought of as fast shear stress fracture mechanism. For strain-rate-independent materials (strain-rate sensitivity neglectable) but exhibiting strain hardening behaviour such as brass, aluminium and some steel alloys [19, 37] at room temperature, the B-W model have shown good correlation with the experimental results for the FLC in the positive and negative quadrant of MPLS. However, for strain-rate sensitive materials such as A-K steel, IF steel at room temperature and aluminium alloy and steel alloys at high temperatures, the failure mechanism has been by visible local necking, thus, the correlation of B-W model has been poor. Large post-uniform deformation up to rupture due to hardening material with large strain-rate sensitivity exponent provides delay on local necking development in tensile test. In addition, later observations of fracture surface through the sheet thickness of those strain-rate-independent materials have proved to be by shear stress mechanism. Consequently, the approach was modified recently by Bressan and Barlat [38] to modelling properly shear stress fracture without necking in sheet metal forming.

The Storen and Rice (S-R) modelling (1975) [39] also examined plane stress and instability but they proposed the occurrence of a vertex on the material subsequent yield locus in continued loading path for arising local necking in biaxial stretching. This would allow mathematical conditions for strain localization to develop a local neck on sheet surface. This grown and pointed vertex on the yield locus was considered a material instability in the constitutive law, which the incipient non-uniform flow across a narrow band in the sheet surface allows bifurcation of deformation rate and directions. Thus, a difference in strain velocities inside and outside the neck would be permitted, leading to sheet surface localized neck for strain path in the positive quadrant of MPLS. The S-R model presented reasonable agreement with some experimental results for FLC in the stretching quadrant of MPLS, but poor correlation in the negative quadrant [39].

D-Bressan modelling of fast shear stress fracture, without an evident localized necking at sheet surface or just at the inception of local necking by shear band formation, occurs in a particular plane inclined through the thickness, where the shear stress reaches a critical value, namely τcr. Its major advantages are the mathematical simplicity to describe the FLC-S, the possibility to compute both an upper and lower-bound limit values for a material FLC curve, and the capacity to account for non-linear strain paths [20, 40].

The governing equation for drawing the FLC-S in sheet metal forming processes is [7, 38],

$$ {\sigma}_1=\left|\frac{2+\alpha }{\sqrt{1+\alpha }}\right|\;{\tau}_{cr} $$
(1)

where σ1 is the maximum principal in-plane stress while τcr and α = dε2 / dε1 are respectively the critical shear stress at rupture and the strain path. The critical shear stress at rupture τcr is a material property which value can be obtained from tensile or plane strain tests and is a function of temperature, strain rate and pre-straining.

By assuming the anisotropic yield criterion proposed by Hill (1979) for plane stress conditions where σ1 and σ2 are the sheet in-plane principal stresses [41], and the normal anisotropy coefficient R-values can be lower than 1, the equivalent flow stress is defined as:

$$ \overline{\sigma}=\frac{1}{{\left[2\left(1+R\right)\right]}^{1/m}}\;{\left[\left(1+2R\right){\left|{\sigma}_1-{\sigma}_2\right|}^m+{\left|{\sigma}_1+{\sigma}_2\right|}^m\right]}^{1/m} $$
(2)

where m is an anisotropy-dependent parameter: m = 2.0 for R ≥ 1; m = 1.14 + 0.86R for R < 1 [37]. However, as present analysis is applied to thin sheet metals formed under in-plane uniaxial and biaxial stretching at constant temperature, the material exhibiting normal anisotropy and strain and strain rate hardening behavior, thus, the flow stress can be modelled according to the modified Swift law [42],

$$ \overline{\sigma}=K\;{\left({\varepsilon}_o+\overline{\varepsilon}\right)}^n=\tilde{K}\;{\left({\varepsilon}_o+\overline{\varepsilon}\right)}^n{\left(\dot{\overline{\varepsilon}}/{\dot{\varepsilon}}_o\right)}^M $$
(3)

where K is the material strength coefficient, \( \overline{\varepsilon} \) the equivalent strain, εo the pre-strain, n the material strain hardening exponent, \( \dot{\overline{\varepsilon}} \) the equivalent strain rate, \( {\dot{\varepsilon}}_o \) the reference strain rate, and M the strain rate sensitivity coefficient. All the plasticity parameters, namely K, n and M, depend on temperature and strain rate.

By defining the stress ratio X = σ2/σ1 and employing \( \overline{\varepsilon}=z\;\left(1+\alpha \right)\;{\varepsilon}_1 \) for linear strain paths [42], introducing Eqs. (1) and (2) into Eq. (3), then the major principal limit strain can be computed according to the equation:

$$ {\varepsilon}_1^{\ast }=\left\{\frac{{\left[\left(1+2R\right){\left|1-X\right|}^m+{\left|1+X\right|}^m\right]}^{1/n\;m}}{{\left[2\left(1+R\right)\right]}^{1/n\;m}\;}\;{\left|\frac{2+\alpha }{\sqrt{1+\alpha }}\right|}^{1/n}{\left(\frac{\tau_{cr}}{\sigma_o}\right)}^{1/n}-1\right\}\;\frac{\varepsilon_o}{z\;\left(1+\alpha \right)} $$
(4)

as a function of the strain path and material plasticity parameters. In order to calculate the stress ratio X it is possible to use the Hill flow rule [42] as a function of the strain path α according to [7], while the generalized subtangent z (general condition for localized necking in the drawing quadrant, \( d\overline{\sigma}/\overline{\sigma}=d\overline{\varepsilon}/z \)) [42] is determined from the definition of equivalent strain increment according to Eq. (5):

$$ z=\frac{{\left[2\left(1+R\right)\right]}^{1/m}}{2\left(1+\alpha \right)}\;{\left\{\frac{{\left|1-\alpha \right|}^{m/\left(m-1\right)}}{{\left(1+2R\right)}^{1/\left(m-1\right)}}+{\left|1+\alpha \right|}^{m/\left(m-1\right)}\right\}}^{\frac{m-1}{m}} $$
(5)

Therefore, the generalized subtangent z is constant for a constant strain path α . By using Eq. (4) it is possible to compute the limiting strain curve for shear stress rupture: varying the strain path values, substituting the plasticity parameters and normalized critical shear stress ratio to the yield stress, rcr = τcr /σo. For plane strain stretching test (FLCo), surely linear strain path for in-plane testing with appropriate specimen, the normalized critical shear stress is calculated by,

$$ {r}_{cr}=\frac{\left(1+R\right)}{2\sqrt{\left(1+2R\right)}}\;{\left[1+\frac{\left(1+R\right)}{\sqrt{\left(1+2R\right)}}\frac{FL{C}_o}{\varepsilon_o}\right]}^n $$
(6)

FLC-N modelling by strain gradient approach

To overcome the limitations of the fast shear stress fracture model in the case of visible localized necking before rupture, a strain gradient evolution model was proposed by Bressan and Williams in 1985 [42]. In the proposed approach, the computed local strain gradient asses the cumulated growth till the beginning of localized necking or groove and subsequent sheet fracture [7]. Particularly, in the proposed approach an imperfection parameter μ due to fluctuations in the initial sheet thickness leads to the localized necking.

The strain gradient \( \lambda =\partial \overline{\varepsilon}/\partial x \) at the groove site, located outside but at neck border, expresses the variation of the equivalent strain \( \overline{\varepsilon} \) along the coordinate x, perpendicular to the necking direction. It is possible to define a critical strain gradient value that trigger the emerging local neck when reached [7, 42]. Figure 1 shows a sketch of sheet metal element in biaxial stretching, showing a local neck or groove and the definition of local strain gradient λ.

Fig. 1
figure 1

Sketch of element of sheet metal in biaxial stretching, showing a local neck or groove and the definition of local strain gradient λ, located outside but at neck border

Full size image

As in previous approach, also in this modelling the sample of thin sheet metal exhibits strain hardening and strain rate hardening behavior according to the constitutive law of Eq. (3).

The prediction of localized necking in the two quadrants of MPLS, is given by [42]:

$$ \frac{\partial\;\left(\lambda /\mu \right)}{\partial\;\overline{\varepsilon}}=\frac{1}{M}+\frac{1}{M}\left\{\frac{1}{\;\left(\alpha +1\right)z}-\frac{n}{\left({\varepsilon}_o+\overline{\varepsilon}\right)}\right\}\;\frac{\lambda }{\mu} $$
(7)
$$ \frac{\partial\;\left(\lambda /\mu \right)}{\partial\;\overline{\varepsilon}}=\frac{1}{M}+\frac{1}{M}\left\{\frac{1}{z}-\frac{n}{\left({\varepsilon}_o+\overline{\varepsilon}\right)}\right\}\;\frac{\lambda }{\mu } $$
(8)

where μ = (−1/ho)(dho/dx) is the initial imperfection of thickness and ho is the sheet nominal thickness. In the negative quadrant of MPLS, Eq. (8) assumes that x-axis direction is perpendicular to the expected localized neck which is situated along the zero elongation direction on the sheet surface. By using the Hill’s 1979 anisotropic yield criterion [41] and the related flow rule in the case of plane stress, the equivalent true strain increment is defined as:

$$ d\overline{\varepsilon}=\frac{{\left[2\left(1+R\right)\right]}^{1/m}}{2}{\left\{\frac{{\left|1-\alpha \right|}^{m/\left(m-1\right)}}{{\left(1+2R\right)}^{1/\left(m-1\right)}}+{\left|1+\alpha \right|}^{m/\left(m-1\right)}\right\}}^{\frac{m-1}{m}}d{\varepsilon}_1 $$
(9)

Assuming a linear strain path and varying α, the FLC-N curve can be calculated by numerical integration of Eqs. (7) and (8) from initial λ = 0. However, a non-linear strain path can be also assumed to obtain a different FLC-N which depends on the adopted strain path; for example, pre-strain in biaxial stretching followed by plane strain deformation. The start of surface local necking occurs when one of the following conditions is reached: (i) the strain gradient λ attains a critical value λcrit = 0.20/mm or (ii) the normalized strain gradient attains a critical value (λ/μ )crit = (λ/μ)* = constant for the different strain path of FLC-N [42, 43].

For strain rate-independent material, which exhibit M = 0, Eqs. (7) and (8) reduce to the equations for principal limit strain, Eqs (10) and (11), respectively:

$$ {\varepsilon}_1^{\ast }=\frac{1}{\left(1+\alpha \right)}\left\{\frac{n}{\left[1/\left(1+\alpha \right)+z/{\left(\lambda /\mu \right)}_{crit}\right]}-\frac{\varepsilon_o}{z}\right\} $$
(10)
$$ {\varepsilon}_1^{\ast }=\frac{1}{\left(1+\alpha \right)}\left\{\frac{\;n}{\left[1+z/{\left(\lambda /\mu \right)}_{crit}\right]}-\frac{\varepsilon_o}{z}\right\} $$
(11)

It can be observed that, the initial thickness defect parameter μ , the plasticity parameters n, M, and the pre-strain have a large influence on the FLC-N values. Furthermore, by integrating Eqs. (7) and (8) from the value of diffuse equivalent strain \( \overline{\varepsilon}={\overline{\varepsilon}}_{diffuse} \) up to the limit strain \( \overline{\varepsilon} \)=\( \overline{\varepsilon} \)*, it is possible to calculate the inception of localized necking starting from the maximum load or instability or diffuse necking point, \( {\overline{\varepsilon}}_{diffuse}={z}_d{\varepsilon}_1^{diffuse}={z}_dn-{\varepsilon}_o \). For Hill’s local necking in the drawing quadrant, \( {\overline{\varepsilon}}_{neck}=z\left(1+\alpha \right)\;{\varepsilon}_1^{neck}=z\;n-{\varepsilon}_o \), thus, local necking major limit strain is \( {\varepsilon}_1^{neck}=n/\left(1+\alpha \right)-{\varepsilon}_o/\left(z\left(1+\alpha \right)\right) \). Where zd = (1 + α)z.

Material and experimental procedures

The metal alloy object of present investigation is the Ti6Al4V titanium alloy provided in form of annealed sheets of 1 mm thickness (chemical composition reported in Table 1).

Table 1 Chemical composition of the Ti6Al4V titanium alloy sheets (wt%)
Full size table

In-plane uniaxial tensile tests on smooth and notched specimens (Fig. 2a) and Nakajima tests on circular and notched specimens, expressly designed to attain different strain path and stress triaxiality values (Fig. 2b), were performed at 25 °C and 600 °C for obtaining the Ti6Al4V titanium sheet formability limits, according to the experimental plan seen in Table 2.

Fig. 2
figure 2

Ti6Al4V sheet specimens for: (a) in-plane uniaxial tensile and (b) Nakajima tests

Full size image
Table 2 Experimental plan for the tensile and Nakajima tests (R is the notch radius)
Full size table

An MTS™ universal testing machine was used to perform the tensile tests, while the thermal cycle has been applied by means of a frontal inductor. The specimen’s temperature was measured during the test using a k-type thermocouple spot-welded on its surface and the measured temperature was used to control the heating power with a closed loop control system. Two different high temperature resistant paints for application up to 1200 °C, one white and one black, were applied as stochastic pattern on each specimen in order to record its deformation during the entire test with a high speed camera; then, the acquired images were analyzed by means of the Aramis™ Digital Image Correlation (DIC) system to evaluate on-line the surface true strains from the beginning of the test till fracture. The uniaxial tensile tests were carried out at room temperature and at 600 °C, with three different strain rates from 0.01 to 1 s−1 and along three different rolling directions, namely 0°,45° and 90° (see Table 2). The tensile tests on smooth and notched samples were repeated 3 times, while the Nakajima tests were carried out with 5 repetitions, as these tests typically exhibit a higher dispersion of results due to a more complex image data processing procedure.

The flow stress curves obtained from the standardized uniaxial tensile tests were also used to compute the Lankford coefficients of plastic anisotropy, according to ASTM E517–18 standard, as well as the material strain and strain rate hardening coefficients. The choice of the testing temperature of 600 °C was made based on a previous research work [5, 6] where a wide range of temperatures from 25 to 900 °C was tested by means of tensile tests. The results showed that, within this range, the Ti6Al4V sheets exhibited a sufficient formability increase at 600 °C, while the surface oxidation was limited. Furthermore, a process temperature of 600 °C is considered the limiting one for steel dies in service [44]. Room temperature testing was carried out as well for sake of formability comparison.

As shown in Table 2, in-plane tensile tests were also carried out on notched specimens, with three different notch radii of 10, 5 and 2 mm (see Fig. 1a) to evaluate the sheet formability under different strain paths. These specimens were cut along the rolling direction and tested at 25 °C and 600 °C with a strain rate of 0.1 s−1. Furthermore, Nakajima tests were carried both at room temperature and at 600 °C with a hemispherical rigid punch of 100 mm diameter (for details, see references [5, 9]). The used equipment allows to heat up the sheets specimens till the testing temperature, using induction heating, while their temperature was measured by means of spot-welded k-thermocouples and used to control the heating system in a closed loop configuration. At the same time, the tools were heated at the same temperature by means of multiple cartridge heaters to perform the tests in isothermal condition till the fracture occurrence.

In order to use the Aramis™ system to measure the sheets surface strains values during the tests, the outer surface of each sample was painted with a stochastic pattern. An analysis window of 10 × 6 pixels for the tensile tests and 22 × 18 pixels for the Nakajima tests was used. Considering the resolution of employed cameras, the grid area to calculate strain corresponded to 1.3 × 0.8 mm2 for tensile tests and 1.12 × 0.92 mm2 for Nakajima tests. The specimen strains during the tensile tests were recorded using a high frequency CCD camera at a frame rate of 100 Hz, while during the Nakajima tests two CCD cameras with a frame rate of 50 Hz were used. The major and minor limiting true strains were calculated for points at surface very near to the middle of final crack after recording the strain path history by Aramis™ system.

A solid graphite foil, with thickness of 0.5 mm, was used as lubricant between the punch and specimen, to limit the friction forces and ensure the fracture occurrence near the pole. The Nakajima tests were carried out at 25 °C and 600 °C on specimens cut along the rolling direction. An average strain rate of 0.1 s−1 was chosen for all the tests, being consistent with the strain rate values typical of temperature-assisted forming processes. To obtain an average strain rate of 0.1 s−1 the punch speed of 15 mm/s was determined based on the results of the numerical modelling of the Nakajima tests.

Table 3 shows the anisotropy coefficients, elastic modulus and plasticity parameters at the tested temperatures as obtained from the tensile tests on smooth samples. The anisotropy coefficients proved a fairly planar isotropy that allowed employing the Hill 1979 yield criterion [41]. The values of elastic modulus, yield stress σo, strain hardening exponent n, pre-strain εo, strain rate sensitivity coefficient M at room temperature and 600 °C were calculated from tensile test data obtained from samples cut at 0° with respect to the rolling direction, at plastic strain of 0.25 and reference strain rate of 0.01 s−1. Additionally, surface roughness parameters were also measured to characterize Ti6Al4V specimens’ initial surface and calculate the thickness defect parameter μ. The 3D surface profiler Sensofar™ Plu Neox equipment was used to measure an average root mean square of roughness slope, Rda = 7.9o.

Table 3 Ti6Al4V sheet parameters at strain rate 0.1 s−1 and at temperatures 25 °C and 600 °C
Full size table

Results and discussion

Tensile testing and fitting the stress-strain curves

The Ti6Al4V strain hardening behaviour, required for calibrating the critical shear stress and strain gradient models and predicting the FLCs at the tested temperatures, was obtained by fitting the stress-strain curves from experimental tensile tests data with the Ramberg-Osgood-Swift elasto-plastic equation that shows a smooth elastic-plastic transition and is defined as:

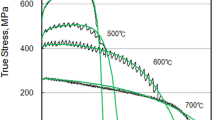
$$ {\varepsilon}_t={\varepsilon}_{el}+{\varepsilon}_p=\frac{\sigma }{E}+{\left(\frac{\sigma }{K}\right)}^{1/n}-{\varepsilon}_o $$
(12)

where εel is the elastic strain, εp the plastic strain, E is the elastic modulus, σ the current tensile true stress, εο the pre-strain, n the strain hardening exponent, \( K=\tilde{K}\;{\left(\dot{\varepsilon}/{\dot{\varepsilon}}_o\right)}^M \) the strength coefficient, \( \dot{\varepsilon} \) the uniaxial strain rate, \( {\dot{\varepsilon}}_o \) the reference strain rate and M the strain rate sensitivity coefficient. The experimental flow stress behavior along the three rolling directions and the Ramberg-Osgood-Swift fitting curves are shown in Figs. 3, 4 and 5. In particular, Figs. 3 and 4 show the flow stress behavior at room temperature and 600 °C, respectively, together with the related plastic equations at varying rolling direction and strain rate of 0.1 s−1. Figure 5 shows the curves obtained at 600 °C and 1 s−1, whereas curves at room temperature and 1 s−1 are not reported as, in cold condition, this material did not show any strain rate dependency [45]. It is worth noting that at 600 °C the material shows a certain strain rate hardening dependency along the three directions, as evidenced in Fig. 6 in the case of samples cut at 0° with respect to the rolling direction.

Fig. 3
figure 3

Fitting of Ti6Al4V tensile test data with Ramberg-Osgood-Swift equation at 25 °C, strain rate of 0.1 s−1, and correspondent plastic strain hardening equation

Full size image
Fig. 4
figure 4

Fitting of Ti6Al4V tensile test data with Ramberg-Osgood-Swift equation at 600 °C, strain rate of 0.1 s−1, and correspondent plastic strain hardening equation

Full size image
Fig. 5
figure 5

Fitting of Ti6Al4V tensile test data with Ramberg-Osgood-Swift equation at 600 °C, strain rate of 1 s−1, and correspondent plastic strain hardening equation

Full size image
Fig. 6
figure 6

Strain rate sensitivity of Ti6Al4V sheet at 600 °C

Full size image

Strain paths and strain distributions

As highlighted in the previous paragraph, each test specimen was strain monitored using DIC techniques (Aramis™ Gom) to evaluate the true strain distribution over the specimens during the entire test. Figures 7 and 8 show the strain paths for the different formability tests carried out at room temperature and at 600 °C.

Fig. 7
figure 7

Strain paths for Ti6Al4V tensile and Nakajima tests sheet at room temperature

Full size image
Fig. 8
figure 8

Strain paths for Ti6Al4V tensile and Nakajima tests sheet at 600 °C

Full size image

Furthermore, Fig.9 shows the thickness distributions over the tensile testing time for smooth specimens tested at strain rate 0.1 s−1 both at room temperature (Fig. 9a)) and at 600 °C (Fig. 9 b)) computed with DIC techniques [46]. The Aramis™ software computes the principal strain values along the specimen surface, major true strain ε1and minor true strain ε2, from the analysis of the images acquired by the camera during the test. Then, the strain along the thickness direction and the thickness values are calculated assuming the volume constancy. Five different points were chosen, from P1 where the fracture took place to P5 at the end of the gauge length; the data were sampled every 0.01 s. The initial distance from P1 to P2 was 1.5 mm while the others were equally-spaced till the end of the gauge length. Additionally, the correspondent points of major true strain evolution along the smooth specimens over time was plotted in Fig. 9c and d. Highly localized necking is observed only for point 1 at room temperature. Similarly, Fig. 10, shows the thickness and major true strain distribution over the testing time along biaxial stretching specimens for room temperature (Fig. 10a and c) and 600 °C (Fig. 10b and d). Also, in this case five measuring points were taken into analysis: P1 on the fracture zone, and P5 near the blank holder. Non-uniform thickness distributions along the principal axis, shown in Fig. 10 and perpendicular to the crack, reveals that rupture occurred after diffuse necking, but highly localized necking was observed only in tensile test. For 1 mm sheet specimens, the expected width of local necking would be about 2 to 3 mm, according to experimental investigations by Ghosh [47].

Fig. 9
figure 9

Thickness and major true strain evolution along the smooth specimens over the tensile testing time at room temperature a) and c); 600 °C b) and d)

Full size image
Fig. 10
figure 10

Thickness and major true strain evolution along the biaxial stretching specimens over the testing time at room temperature a) and c); 600 °C b) and d)

Full size image

Map of principal limit strains and shear rupture mechanism

For sake of comparison, experimental FLC curves at room temperature and at 600 °C and predicted theoretical limit strain curves by the D-Bressan shear stress criterion were plotted in the MPLS and are presented in Fig. 11. The tensile and Nakajima test specimens for each experimental strain path and surface limit strains are shown in Figs. 7 and 8. The parameter rcr, namely the normalized critical shear stress ratio to the yield stress, was chosen for best fitting of the FLC-S at the plane strain point, FLCo, whose strain path is certainly linear, seen in Fig. 11. By interpolating the experimental FLC-S points near plane strain, the normalized critical shear stress parameters, rcr = τcr /σo, calculated by Eq. (6) were 0.695 and 0.754 for room temperature and 600 °C, respectively. In the negative quadrant of MPLS, the dispersion of experimental points may be due to variations in material properties, thickness defects, non-linear strain paths, or strain measurement accuracies in the neck. Nevertheless, the fitting between predicted limit strains values, using the D-Bressan critical shear stress criterion and the experimental average results is reasonably good. This gives support to the assumption that the critical shear stress model can be applied to sheet metals which M is close to zero [5], as is the case of present Ti6Al4V sheets deformed at 25 °C, that exhibited M equal to 0.002.

Fig. 11
figure 11

Map of Principal Limit Strains of Ti6Al4V. Experimental and predicted FLC-S at 25 °C and 600 °C, using D-Bressan critical shear stress criterion

Full size image

However, Ti6Al4V sheets deformed at 600 °C showed M equal to 0.025, which would suggest the occurrence of some visible necking before rupture, but n was small and equal to 0.072. Experimental observations of the fracture locations in tensile specimens confirmed that the macroscopic mechanism of sheet rupture was by fast shear at both room temperature and 600 °C (see Fig. 12), but a sharp visible local necking is noted at the surface rupture region.

Fig. 12
figure 12

Surface view of the fracture by shear mechanism in tensile smooth specimens deformed at room temperature and 600 °C

Full size image

Furthermore, experimental observations of fracture locations in Nakajima specimens, deformed in the stretching quadrant, revealed a macroscopic mechanism of sheet rupture by fast shear at both room temperature and 600 °C (see Fig. 13) without visible necking, despite ductile micromechanism of rupture is by void coalescence, Valoppi at al. [6]. One possible explanation for the lack of experimental visible local necking in the stretching quadrant of present Ti6Al4V sheet is small M and small fracture strain in biaxial stretching. Small M-values indicates a strain-rate independent material behaviour [37, 47].

Fig. 13
figure 13

Thickness view of fracture by shear mechanism in Nakajima specimens deformed at room temperature and 600 °C. No visual local necking is observed

Full size image

Figure 14 shows the comparison among the experimental FLCs at room temperature and 600 °C, the predicted FLC-N curves using the D-Bressan strain gradient evolution model and additional diffuse necking curves for the maximum load criterion [7]. The predicted curves at room temperature and 600 °C have the same trend, with the one at room temperature setting at lower level. The localized necking limit was calculated using Eqs.(7) and (8) from the point of diffuse necking (assuming valid the maximum load criterion and λ ~0) and guessing the normalized critical strain gradient (λ/μ)* attaining a constant critical value to fit the experimental limit points. However, assuming that the local imperfections in thickness h(x) can be related to the roughness profile at diffuse necking point, μ = (1/hdiff)(dhdiff /dx) = (1/hdiff) tgθd, where tgθd is the roughness profile slope at diffuse necking (average root mean square of roughness slope, θd = Rdad) [43], then, the thickness defect at diffuse necking could be calculated by μ ≅ tg(Rdad)/ hdiff. On the other hand, the strain gradient λ at diffuse necking point and for constant strain path could be calculated by the analysis of experimental thickness strain distribution \( \lambda =\partial \overline{\varepsilon}/\partial x=\left(1/z\right)\left(\partial {\varepsilon}_3/\partial x\right) \).

Figure 14
figure 14

Experimental FLC and predicted FLC-N at 25 °C and 600 °C, using D-Bressan critical strain gradient criterion and comparison with Hill’s local necking

Full size image

Nevertheless, guessing the normalized critical strain gradient attaining a constant critical value (λ/μ)* = 45 to fit the experimental points at 600 °C and (λ/μ)* = 90 to fit the experimental points at room temperature, the FLC-N curve was calculated and plotted in Fig.14. But, such estimated values of the normalized critical strain gradient are very high, leading to a poor correlation, which suggests that the mechanism is not localized necking formation prior to fracture. This means that, both at room temperature and 600 °C, the Ti6Al4V sheet fracture better correlates with the shear stress fracture criterion, despite a relative high value of the strain rate sensitivity coefficient of 0.025 at 600 °C than 0.002 at 25 °C. Shear stress fracture mechanism without local necking for strain rate-independent material have been reported in literature through fractograph observations of thickness surface rupture of stainless steel sheet by Koronen et al. [48] and Xu et al. [19] and TRIP steel sheet by Li et al. [30]. Moreover, good correlation of predicted FLC-S by present shear stress fracture criterion for aluminium alloy have been also shown by Bressan et al. [7, 40] and for brass sheet [37].

Additionally, for comparison with present critical strain gradient approach, Hill’s local necking limit curve for 600 °C was plotted in the negative quadrant. Hill’s curve is situated well below the experimental points and follows the trend of present model curve.

Wang et al. [45] showed that Ti6Al4V tensile test specimens fractured after diffuse necking at room and 600 °C and that the thickness strain gradient near the rupture site was very small about 0.047/mm, which is corroborated by the thickness distribution of Fig. 9. Again, assuming that initial and local imperfections in thickness ho(x) can be related to the roughness profile [43], μ = (1/ho)(dho/dx) = (1/ho)tgθ, where ho = 1 mm, then, μ ≅ 0.139/ho (average root mean square of roughness slope, Rda = 7.9o experimentally measured for the Ti6Al4V sheet specimen at initial conditions, using the 3D surface profiler Sensofar™ Plu Neox). Thus, the predicted normalized critical strain gradient would be (λ/μ)* ≅ 7.19λcrit ≅ 71.9 (assuming λcrit ≅ 10/mm). On the other hand, the experimental thickness strain gradient at rupture site divided by the initial thickness defect μ ≅ 0.139/mm, results in (λ/μ) ≅ 0.059/0.139 ≅ 0.388, which is much smaller than the theoretical normalized critical strain gradient (λ/μ)* ≅ 71.9 for predicting localized necking curves.

Effect of temperature on formability parameters n and M

Generally, sheet metal forming carried out at warm and hot temperatures are expected to present reduced flow stress and enhanced formability caused by the increased metal ductility at high temperatures. However, the experimental FLC of Ti6Al4V at 600 °C did not reached values as high as expected, when compared to the one at room temperature. Formability parameters n and M of Ti6Al4V sheets similar to present work were investigated by means of tensile tests at room and high temperatures up to 800 °C by same research group, Wang et al. [5, 45]. In particular, the strain hardening and strain rate sensitivity exponents were evaluated, which it is well known to have an impact on the FLC level [42]. In Fig. 15, the experimental data of the strain hardening exponent and strain rate sensitivity coefficient values above 400 °C, as calculated by Wang et al. [45], are plotted and examined as a function of inverse temperature (temperature expressed in K) to correlate with an Arrhenius’ equation type: M = Aexp(−Q/RT). This graph shows the variation of plasticity parameters n and M as a function of inverse temperature. The strain hardening exponent presents a maximum value equal to 0.12 at 1.5 × 10−3 K−1 (~400 °C), but the strain rate sensitivity coefficient is very low, equal to 0.008. A significant increase of the strain rate sensitivity coefficient, up to 0.025, is observed only at 1.1 × 10−3 K−1 (~600 °C), but with a much lower strain hardening exponent equal to 0.08. Microstructure recrystallization is expected to occur at about 0.5Tm (~690 °C; Tm is melting temperature), which introduces new mechanisms of plastic deformation, reducing n but increasing exponentially M. Above forming temperature of about 400 °C (below 1.5 × 10−3 K−1), the parameter M is possibly governed by a good fit of Arrhenius’ equation type: M = 48.2exp(−Q/RT), where T is temperature in K, Q the mechanism activation energy, and -Q/R = -3.37. For temperatures lower than 400 °C, there are large dispersion of experimental points.

Fig. 15
figure 15

Strain rate sensitivity coefficient M and strain hardening exponent n versus inverse temperature at varying rolling direction [45]

Full size image

According to Kotkunde et al. [4], the Ti6Al4V FLC at 400 °C, which n = 0.08 and M = 0.013, has superior values in the stretching positive quadrant of MPLS map than the FLC at 600 °C. Thus, the FLC obtained from similar sheets deformed at 400 °C, with maximum n = 0.12, is expected to exhibit similar or higher level as present FLC-S at 600 °C. However, much superior level of FLC is predicted at 800 °C where M = 0.12.

Concluding remarks

The analysis of formability of Ti6Al4V thin sheet reported in this paper shows the comparison between experimental FLC curves outcomes, obtained at room temperature and 600 °C and at strain rate of 0.1 s−1, with the theoretical predictions of limit strains, using the D-Bressan analytical modelling: the critical shear stress rupture and the critical strain gradient criteria. The main conclusions accomplished can be summarized as follows:

  1. a)

    From experimental observations of specimen fracture surface, ductile rupture mechanism in Ti6Al4V sheets deformed both at room temperature and 600 °C is governed by a fast-critical shear stress fracture macroscopic mechanism through the sheet thickness without the presence of visible localized necking, except in tensile testing. Moreover, despite failure occurred after onset of diffuse necking and that microscopic mechanism of ductile rupture is by void coalescence, the failure mechanism revealed to be dominated by fast shear stress.

  2. b)

    The FLC-S predicted using the D-Bressan critical shear stress rupture criterion showed good correlation with the experimental FLC curves both at room temperature and 600 °C.

  3. c)

    The FLC-N predicted using D-Bressan critical strain gradient and Hill local necking criteria for highly localized necking showed poor correlation with the experimental FLC curves for both room temperature and 600 °C.

  4. d)

    The limiting major true strain of the predicted FLC-S is governed by the following parameters: normal anisotropy R, strain hardening exponent n, pre-strain and normalized critical shear stress parameter rcr = τcr /σo. The parameter rcr depend on n, R, pre-strain, and FLCo, according to Eq. (6), whereas n depends largely on temperature. The FLC-N predicted by strain gradient depend on both n and M.

  5. e)

    The best fit of the critical shear stress model with the experimental FLC-S points was given by the Nakajima specimen whose width was 100 mm (near plane strain or FLCo). This was the specimens used to calibrate the parameter rcr by interpolating the experimental point for plane strain FLCo.

  6. f)

    According to Ti6Al4V tensile test, the FLC-S at 400 °C is expected to present similar level of FLC-S at 600 °C due to a maximum n-value of 0.12 at 400 °C.

  7. g)

    Based on present good prediction of the Ti6Al4V alloy FLC-S curve, as well as corroborated by previous published works by the authors on validation of the critical shear stress fracture criterion, a common feature of various strain-rate independent metals with different crystal packing structures and different slip systems (FCC, BCC and HCP), annealed or cold rolled and for strain velocity lower than 0.1 s−1, is that the main fracture mechanism of thin sheet metals can be considered as fast shear stress through sheet thickness without visible localized necking, within the range of strain paths in biaxial stretching.