1 Introduction

In recent years, environmental preservation and energy conservation have been hot issues worldwide. In the automotive industry, many efforts have been made to save energy by reducing the fuel consumption of cars. One such attempt is the adoption of lightweight materials such as aluminum, magnesium, and titanium. For most of the second half of the twentieth century, Ti–6Al–4V accounted for about 45 % of the total weight of all titanium alloys shipped. Recently, many researchers [1–3] have applied a forming process for Ti–6Al–4V sheets to verify the effects of forming techniques on the mechanical properties and material characterization of products at room and elevated temperatures. Others have attempted to apply an incremental forming process to make automotive service panels [4]. In addition, electric hot incremental forming [5] and a high tool rotation speed in incremental forming [6], which can improve the formability of products by heating the sheet metal of Ti–6Al–4V, were studied to evaluate and investigate the effects of geometry and parameters governing mechanical properties of Ti–6Al–4V sheets. Finite element (FE) simulation in sheet metal forming [7–10] for the automobile industry is beneficial in reducing tool costs in the design stage and for optimizing the current process. With the growing use of lightweight materials, accurate numerical models are necessary for simulations of forming. In this study, the focus is on the yield function description.

Many yield functions have been defined to describe the yield behavior of different sheet materials [11–15]. The Hill’48 model [11] was successfully applied for steel sheets. The parameters were simply determined by an uni-axial tensile test at 0°, 45°, and 90° with respect to the rolling direction. Barlat et al. [12–14] developed another series of yield functions for aluminum. Model parameters for the yield function proposed in 1989 (Yld89) were determined based on uni-axial tensile tests, considering either the yield stress or the Lankford value at 0°, 45°, and 90° with respect to the rolling direction. For the yield function proposed in 1991 (Yld91), the equi-biaxial yield stress was considered. These models were typically used for sheet materials, and the parameters were determined from the uni-axial yield stress, the Lankford value, and the equi-biaxial yield stress. For the yield function proposed in 2000 (Yld2000), the strain ratio in equi-biaxial stress was also used.

All yield functions referenced above are global functions of the six or three stress components. There is a need to propose a new non-quadratic yield criterion for some materials having complex yield locus such as anisotropic and asymmetric behavior in tension/compression zones. However, most of the material parameters were determined from uni-axial tension and equi-biaxial tests.

As mentioned in previous studies [16, 17], titanium alloy sheets are classified as lightweight material with excellent specific strength and corrosion resistance as well as good performance at temperatures as high as 400 °C. Recently, titanium alloys are being widely employed not only in aerospace components, but also in bio prostheses and motorcycles. Titanium alloy sheets are usually formed by a slow forming technique in a high-temperature environment due to their low formability at room temperature and their hexagonal close packed (HCP) structure. The yield behavior of HCP structure material shows two types of deformation modes, slip (slip hardening) and/or twinning (twin hardening), which results in the anisotropic and asymmetric phenomenon [18]. Thus, to understand the difference between the yield behavior of tension and compression zones, in-plane tension/compression tests are performed. The plastic deformation mechanism of Ti–6Al–4V alloys at room temperature is mainly due to dislocations on the slip planes. Some twining is observed at room temperature and high strain rate (5000 s−1) [19]. Since dislocation mobility is low at these conditions, plastic deformation under high stress is caused by deformation twins. However, low strain rate and high temperatures does not show any twining for Ti–6Al–4V alloys, because dislocation mechanisms are expected to be the dominating components in the deformation mechanism of the alloys through planar slips, with almost negligible amounts of deformation twins [20]. As temperature increases, dynamic recovery and recrystallization actively occurs and these processes govern the global plastic deformation of Ti–6Al–4V alloy material.

In this paper, a new approach is suggested for planar anisotropic material and yielding asymmetry between the tension and compression of titanium alloy sheets by investigating the yield loci in the plane stress and principal stress space (σ 1, σ 2) based on an experiment using biaxial tension equipment. The material model proposed in this paper utilizes not only uni-axial tension and compression results, but also biaxial tension results. The purpose of this paper is to propose a yield function for titanium alloy sheets with a simple idea based on the interpolation of experimental data apart from uni-axial and biaxial test data. The approach that is adopted, is to develop the function of the radius for the yield locus. To determine the material parameters of the yield function, a fitting method is adopted using the least squares fitting method (lsqcurvefit) of the MATLAB tool. The proposed yield function shows good improvement in the yield locus prediction for Ti–6Al–4V titanium alloy sheets at elevated temperatures.

2 Experimental Procedure and Results

Previous research [17] conducted uni-axial tensile tests on (Ti–6Al–4V) titanium alloy sheets with a thickness of 1.0 mm at temperatures of 400–700 °C under a strain rate of 0.001 s−1. Here the tensile (JIS 13 B-type) specimens were cut from the sheet parallel to the rolling direction, whose main chemical composition is shown Table 1. Tensile tests of the specimens were carried out using an MTS 810. To achieve high-accuracy FE simulation results, the identification of material properties and deformation characteristics such as constitutive equations were essential. Constitutive equations should be able to represent the flow behavior of the material with adequate accuracy and reliability over a wider processing domain. With regard to forming at elevated temperatures, many studies were conducted in order to establish the flow stress relationships of materials based on experimental results, and significant progress was made [21–26]. Among the various equations, the combined hardening/softening behavior of flow stress equation (Eq. 1) based on Voce’s law [17] was proposed and material parameters were determined by utilizing the least squares fitting method, as shown in Table 2. The true stress–plastic strain curves determined from the experiments and calculations are depicted in Fig. 1. Flow stress equations, representing the deformation behavior of the material at high temperatures, have a significant influence on the accuracy of FE simulation results [24–26].

Table 1 Chemical composition of tested material [10]
Full size table
Table 2 Hardening and softening parameters at elevated temperatures determined by fitting curves [10]
Full size table
Fig. 1
figure 1

Stress–strain curves based on measured and calculated data at elevated temperatures [10]

Full size image
$$ \bar \sigma = {\sigma_Y} + P(1 - \exp ( - Q\varepsilon )) + B(1 - \exp (C\varepsilon )), $$
(1)

where \( \bar \sigma , \) σ Y and ε are the equivalent stress, tension yield stress, and yield strain, respectively. P, Q and B, C are the plastic coefficients of hardening and softening behaviors, respectively.

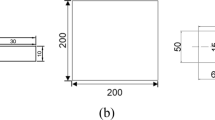
Figure 2 shows the biaxial tensile test specimen geometry and the experimental procedures used in this study to achieve the plastic deformation behavior of Ti–6Al–4V alloy sheets with a thickness of 1.0 mm at an elevated temperature. Here, the slit in the specimen was processed by laser-cutting. Biaxial tensile tests were performed at different stress ratios of X–Y axes, which were 1:2, 1:1, and 2:1, using an in-house developed biaxial testing device. The basic and detailed design concepts of the biaxial tester was referred from [27] and shown in Fig. 3. Opposing hydraulic cylinders were connected to a common hydraulic line so that they could be subjected to the same hydraulic pressure. The hydraulic pressure of each pair of opposing hydraulic cylinders was independently servo-controlled. Displacements of opposing hydraulic cylinders were equalized using the pantograph-type link mechanism.

Fig. 2
figure 2

Biaxial tensile test specimen geometry (a) and experimental procedures (b)

Full size image
Fig. 3
figure 3

An in-house developed experimental apparatus for biaxial tensile test

Full size image

Nominal strain components, ε x and ε y , were measured using four biaxial strain gages mounted on the center lines of the specimen at (x, y) = (7.5 mm, 0) and (0, 7.5 mm) respectively, but a CCD camera was required to measure the strain at elevated temperatures.

In addition, true stress components, σ x and σ y , in the gage section were determined by dividing the measured loads F x (rolling direction) and F y (transverse direction) by the current cross-sectional area of the gage section determined from the measured values of logarithmic plastic strain components ε xp and ε yp using the assumption of constant volume.

To obtain yield loci, the principle of equivalent plastic work was employed. First, uni-axial tensile tests in the rolling direction of the specimen were carried out, and the uni-axial true stresses, σ 0 corresponding to particular values of logarithmic plastic strains \( \varepsilon_0^p \) were determined. The corresponding plastic work (W) per unit volume was measured for each \( \varepsilon_0^p. \) In the same manner, the uni-axial true stresses, σ 90 in the transverse direction of the specimen were determined at the plastic work equal to (W). In the biaxial tensile tests, the true stress components (σ Yx and σ Yy ) were determined at the plastic work equal to (W). Moreover, in the uni-axial compression test, the true stress σ 0-com in the rolling direction and σ 90-com in the transverse direction of the specimen were determined at the plastic work equal to (W). Finally, the contours of plastic work were constructed in the stress space by connecting a family of stress points (σ 0, 0), (σ Yx , σ Yy ), (0, σ 90), and (σ 0-com, 0). Figure 4 shows the yield loci for Ti–6Al–4V alloy at 600 °C and logarithmic plastic strain \( \varepsilon_0^p \) = 0.01. As shown in Fig. 4, Ti–6Al–4V, alloy sheets exhibit strong asymmetric behavior under tension and compression.

Fig. 4
figure 4

Yield loci for Ti–6Al–4V alloy sheet at 600 °C

Full size image

Additionally, the effects of microstructural conditions on the mechanical properties at elevated temperatures with in-plane uni-axial tension and compression tests are significant. There are many studies on microstructure development and texture evolution following uni-axial tension tests at room temperature. Chan and Koss [28] investigated the influence of crystallographic texture on the deformation and fracture behaviors of strongly textured Ti alloy sheets. They showed that the crystallographic texture influenced yield strength, particularly the through-thickness deformation as measured by the plastic anisotropy parameter. Bridier et al. [29] studied the slip systems activated in a polycrystalline Ti–6Al–4V alloy. They showed the coexistence of basal, prismatic, and first-order pyramidal slip modes. The models that considered the microstructure of materials for deformation at high temperatures, involved changing the grain size, which was determined by grain growth and dynamic softening by dynamic recovery and dynamic recrystallization. Dynamic recrystallization involves unstable internal energy generated by deformation, making new grain boundaries and changing them to stable grains. Degree of recrystallization of deformed samples are determined by plastic deformation conditions, such as strain, strain rate, and temperature. Previous models [28–30] had considered dynamic recrystallization. In this study, the microstructural condition of the Ti–6Al–4V alloy sheets is determined using a scanning electron microscope. The microstructural directions and their observation of Ti–6Al–4V alloy sheets are depicted in Fig. 5, where, the photomicrographs of the initial microstructures reveal an alpha–beta type microstructure. To prepare soft Ti–6Al–4V alloy sheets, mill-annealing condition was employed, which had an alpha–beta structure. As shown in Fig. 6, the microstructure consists of globular alpha phase. The samples show that, at the temperature of 400 °C the amount of beta structure is small in the range of 10–20 % (Fig. 6a). However, as temperature increases up to 600 °C, the portion of beta structure increases (Fig. 6c).

Fig. 5
figure 5

The initial microstructures at various directions of Ti–6Al–4V alloy sheets

Full size image
Fig. 6
figure 6

The microstructure of mill-annealed alpha–beta Ti–6Al–4V alloy sheets in 400 °C (a), 500 °C (b) and 600 °C (c)

Full size image

3 Yield Criteria Description

In a two-dimensional principal stress space, a stress point is represented by the radius distance (r) and direction cosine (θ). For a polycrystalline metallic material, the yield locus is smooth, i.e., it does not contain corners and the yield function is continuously differentiable. The Von Mises yield function in a plane stress condition is written as:

$$ {\sigma_1}^2 + {\sigma_2}^2 - {\sigma_1}{\sigma_2} = {\bar \sigma^2}, $$
(2)
$$ {\sigma_1} = r\cos (\theta ),\quad {\sigma_2} = r\sin (\theta ). $$
(3)

Combining Eqs. (2) and (3):

$$ {r^2}{\cos^2}(\theta ) + {r^2}{\sin^2}(\theta ) - {r^2}\cos (\theta )\sin (\theta ) = {\bar \sigma^2}; $$

Therefore,

$$r = \bar \sigma \sqrt {\frac{1}{(1 - \cos (\theta )\sin (\theta ))}} . $$
(4)

Now, r is a function of θ. This concept is adopted for Ti–6Al–4V alloy sheets with equivalent stress, \( \bar \sigma \) = 403.1 MPa as shown in Fig. 7a in the (Von Mises) curve.

Fig. 7
figure 7

The relation between angle and radius for various yield criterions (a) and yield loci (b) when comparing with experimental data at 600 °C and logarithmic plastic strains \( \varepsilon_0^p \) of 0.01

Full size image

The other yield criterion considering anisotropic material behavior can be described with a different radius and phase shift. The Hill’48 yield criterion [11] and Logan and Hosford yield criterion [31] can be written as:

$$ r = \bar \sigma \sqrt {\frac{{{R_{90}}(1 + {R_0})}}{{({R_0}{{\sin }^2}(\theta ) + {R_{90}}{{\cos }^2}(\theta ) - 2{R_0}{R_{90}}\cos (\theta )\sin (\theta ) + {R_0}{R_{90}})}}} , $$
(5)
$$ r = \sqrt[a]{{\frac{{(1 + {R_m}){{\bar \sigma }^a}}}{{({{\cos }^a}(\theta ) + {{\sin }^a}(\theta ) + {R_m}|\cos (\theta ) - \sin (\theta ){|^a}}}}}, $$
(6)

where the anisotropic coefficients (R 0, R 45, R 90) are determined by measuring the strains in the width and thickness directions obtained in an experimental tensile test for three directions in the plane of the sheet metal (0°, 45°, 90°), respectively, and R m  = (R 0 + 2R 45 + R 90)/4. Figure 7a shows the relation between the radius and angle for Hill’48 and Logan and Hosford yield criteria in the Hill'48 and Logan & Hosford curves, respectively, with \( \bar \sigma \) = 403.1 MPa, R 0 = 1.1, R 90 = 1.5, R m  = 2, and a = 8.

As shown in Fig. 7a, usually the radius is quite different at 45°, a condition of equi-biaxial tension and at 225°, a condition of equi-biaxial compression for each others. For the Hill model, the radii are not equal at angles of 0°, 90°, and 270°. As shown in Eqs. (4)–(6), r is the periodic function of θ and regenerated by superposition of sine and cosine functions with the material constant. The radii at 45°, a condition of equi-biaxial tension, and at 225°, a condition of equi-biaxial compression, are similar to a period of 180°. Figure 7b presents the comparison between the experimental results and various yield criteria and shows the mismatch of predictions. This means that classical yield criteria can not describe the yielding asymmetry between tension and compression. HCP structure materials such as magnesium and titanium alloy shows the yielding asymmetry between tension and compression [32, 33].

4 Proposed Yield Function for Ti–6Al–4V Alloy Sheets at Elevated Temperatures

To describe both the yielding behavior of asymmetry between tension and compression and the anisotropy of a material, the proposed yield criterion should be the periodic function of 360°, and the radius should not necessarily be “1” at 90° and 270°. Here, we suggest the generalized yield criterion written below:

$$ r = \bar \sigma {\left( {\frac{A}{(B + C\sin (\theta ) + D\cos (\theta ) + E\sin (2\theta ))}} \right)^2}, $$
(7)

where A, B, C, D, and E are material constants. In this study, we have utilized the least squares fitting method (lsqcurvefit) of MATLAB to determine the material constants and obtained the values of A, B, C, D, and E as 12.203, 11.170, 0.488, 0.737, and −2.197 for the yield locus at 600 °C. As shown in Fig. 8a, the proposed yield criterion has a period of 360°, and the new yield function is a fully asymmetrical yield function with continuance. As shown in Fig. 8b, the new yield criterion has been compared with the experimental results and are found to be in good agreement; here the errors can be calculated as: Error (%) = (|r cal  – r exp|/r exp) × 100 for each cosine (θ) direction. The average error between the new yield criterion and the experimental results is estimated as, 4.325 %.

Fig. 8
figure 8

The relation between angle and radius for new yield function (a) and predicted yield loci (b) at 600 °C

Full size image

Even though the newly proposed yield function accurately predicted the yield locus at a temperature of 600 °C, it was necessary to represent the radius (r) of the yield criterion as a function of temperature (r(T, θ)) as well, in order to apply the proposed yield function in numerical analysis using FEM for a wider range of temperatures.

Based on the relationship between the yield stress (σ Y ) and temperatures, as shown in Table 2, we employed the curve fitting tool of MATLAB to express the yield as a function of temperature σ Y (T), meaning that the equivalent stress is also a function of temperature \( \bar \sigma (T). \) The relationship between yield stress and temperature is expressed in Eq. (8). Based on Eq. (8), Eq. (7) can be rewritten as Eq. (9)

$$ \bar \sigma (T) = {\sigma_Y}(T) = - 0.00145{T^2} + 0.6825T + 495.6, $$
(8)
$$ r = {\sigma_Y}(T){\left( {\frac{A}{{\left( {B + C\sin (\theta ) + D\cos (\theta ) + E\sin (2\theta )} \right)}}} \right)^2}. $$
(9)

The yield loci at elevated temperatures may be calculated from Eq. (9) with the temperature dependent yield stress obtained from Eq. (8). Figure 9a shows the relationship between the radii and angles at elevated temperatures of 400–700 °C. The calculated yield loci at elevated temperatures were also depicted and compared with the measured data in Fig. 9b. The predicted yield loci were in good agreement with the experimental data.

Fig. 9
figure 9

Prediction of proposed yield function at elevated temperatures with radius versus angle (a) and yield loci (b)

Full size image

The accuracy in calculating yield loci for anisotropic and asymmetrical behavior of (Ti–6Al–4V) titanium sheets at elevated temperatures was achieved by using the proposed equation. This model can be applied to HCP materials, e.g., Mg-alloys, Co–Re alloys, zinc alloys, etc. It can thus also be applied in simulation of high precision FEM results over a wider range of temperatures, both quantitatively and qualitatively.

5 Conclusion

In this study, biaxial tensile tests with a cruciform specimen were performed until the specimen was broken down to characterize the plastic deformation behavior of Ti–6Al–4V alloy sheets using biaxial tensile test equipment. The experimental results for yield loci were compared with several theoretical predictions such as Von Mises, Hill, and Logan–Hosford models. However, those yield criteria did not clearly explain the deformation behavior of Ti–6Al–4V. Thus, a new yield criterion was proposed based on the relation between angles and radii to describe not only the anisotropic behavior of material, but also the asymmetric behavior between tension and compression. To determine the material parameters, curve fitting was used. The predicted yield loci agreed well with the experimental results at a wider range of elevated temperatures. The proposed function could also be applied to simulate high-accuracy yield loci by a numerical method for other anisotropic and asymmetric materials at elevated temperatures.