Stress and strain based fracture forming limit curves for advanced high strength steel sheet

Abstract

In this work, strain based fracture forming limit curve (FFLC) of advanced high strength (AHS) steel grade 980 was determined by means of experimental Nakajima stretch-forming test and tensile tests of samples under shear deformation. During the tests, a digital image correlation (DIC) technique was applied to capture the developed strain histories of deformed samples up to failure. The gathered fracture strains from different stress states were used to construct the FFLC. Subsequently, the FFLC in the strain space was transformed to a principal stress space by using plasticity theories. As a result, the fracture forming limit stress curve (FFLSC) of examined steel was obtained. Furthermore, fracture locus (FL) as a relationship between stress triaxialities and critical plastic strains was determined. Hereby, two anisotropic yield functions, namely, the Hill’48 and Yld89 model were taken into account and their effects on the calculated curves were investigated. To verify the applicability of the obtained limit curves, rectangular cup drawing test and forming tests of so-called Diabolo and mini-tunnel samples were performed. Obviously, the FFLSCs and FLs more accurately described the failure occurrences of 980 steel sheets than the FFLCs. In addition, it was found that the drawing depths predicted by the FLs and the Yld89 yield criterion slightly better agreed with the experimental results than those from the FFLSCs and the Hill’48 model, respectively.

Introduction

Nowadays, the automotive industries have rapidly grown up and investments are greatly increased due to much larger technological competitions. For the manufacturing of automotive parts and components, sheet metal forming still belongs to one of the most important and frequently employed processes. The automotive industries are being intensely forced to design and produce vehicles under considerations of weight reduction, crash performance, energy saving and environmental aspect. To achieve lighter vehicles with reduced fuel consumption but improved safety performance advanced high strength (AHS) sheet steels have been progressively developed and applied. These AHS steel grades are such steel sheets with complex microstructures, for example, dual phase (DP) steel, transformation induced plasticity (TRIP) steel, complex (CP) steel and ultra–high strength (UHS) steels like press hardened boron alloy steel [1]. In spite of the great high strength to density ratios of AHS steels, low formability is their major drawback. Hence, a precise prediction of forming limit behavior for such novel steel grades is strongly necessary. The formability characteristics of AHS steels played an important role in designing an appropriate forming process [2]. Basically, both necking and fracture are the major failure mechanisms of sheet metals during forming. The occurrence of diffuse and subsequent local necking could be well described by empirical, analytical and numerical tools. However, the AHS steel sheets with reduced ductility brought up an issue concerning shear fracture due to the damage emergences in microstructure, which could not be properly predicted by the conventional forming limit curve (FLC). The failure of AHS steel sheets could thus take place before the state of localized necking. It was observed on the microstructure level that ductile damages of high strength dual phase steel sheets were caused by void development induced by the debonding of phase boundaries between ferrite and martensite, brittle cracking of hard martensite and by inclusions or small precipitates [3, 4]. Furthermore, Muenstermann et al. [5] and Lian et al. [6] emphasized that fractures on the macro-scale of these steels were found with the absence of strain localization. Hence, the failure of AHS steel sheets in any forming processes is governed by competing or combining mechanisms between local damage evolution and plastic instability. As a result, the methods for formability prediction of AHS steels need to be improved. On the one hand, various physically based fracture and damage models have been developed for ductile materials, for example, the Gurson-Tvergaard-Needleman (GTN) model [7, 8]. Hereby, void nucleation and growth were firstly proposed to be the main factor for failure in ductile materials. Afterwards, secondary voids occurred after a certain plastic strain and accelerated void coalescences were incorporated in the model. In several works, the GTN model has been successfully applied to predict damage evolution in steels. Besson et al. [9] introduced a GTN based damage model to describe crack growths in round bar and plane strain sample, in which no detailed procedure for identifying material parameters was given. Lemaitre [10] demonstrated that the ductile damage in metal strongly related to governing stress triaxiality. Dhar et al. [11] employed the Lemaitre’s model in FE simulations with large strain deformation, by which the critical load for crack initiation in material could be predicted. Nevertheless, applications of such physically based models are restricted in the industries, because a large number of materials parameters and extensive determination procedures are involved.

On the other hands, a common tool for formability prediction of sheet metals is the forming limit curve (FLC), which was introduced by Keeler and Backofen [12] and has been widely used to evaluate localized necking of formed parts. However, it was well reported that the strain-based FLC is not appropriate for real complex parts, since it is determined on the basis of linear strain paths. To enhance accuracy of such prediction tools new concepts and methods have been continuously developed. For example, the forming limit criterion was presented in a principal stress space by Uthaisangsuk et al. [13] which was found to be less sensitive to forming histories. Under shear loading, by which the value of stress triaxiality was low or close to zero, and compression, particular forming limit and ductile fracture behavior of aluminium alloy samples were investigated by Bao and Wierzbicki [14, 15]. In case of AHS steel sheets, fracture often occurred after a little amount of necking that was different from other conventional steel sheets. Thus, strain- and stress-based fracture forming limit curves (FFLC) have been introduced. Lou et al. [16] proposed a fracture model for sheet metals, in which void nucleation was described by the equivalent plastic strain, void growth depended on the stress triaxiality and void coalescence was controlled by the normalized maximum shear stress. Then, the fracture model was calibrated by experimental and numerical method of various types of specimens, namely, dog-bone, central hole, plane strain tensile, in-plane shear and notched specimens for the AHS steel grade 980 [17]. Hereby, the forming limits regarding shear fracture, which took place in the region between deep drawing and uniaxial tension, were determined and validated. In addition, the effects of material anisotropy of steel on the fracture predictions were studied by Park et al. [2, 18], in which the Hill’48 yield function was considered. The anisotropic strain-based FFLC and FFLC in the space of stress triaxiality and equivalent plastic strain and of maximum and minimum principal stresses were determined for a wide range of stress state from shear to biaxial state. The similar experimental procedure using the digital image correlation (DIC) method was carried out to calibrate the fracture curves. For the prediction under shear deformation domain, shear test needed to be developed in order to achieve larger strains without plastic instability. An overview of the most commonly used shear test configurations for sheet metal characterization was provided by Yin et al. [19]. In this work, resulting strain and stress distributions in the shear zones of Miyauchi sample, ASTM sample and in-plane torsion sample obtained by DIC technique and FE simulations were compared and discussed. Gorji et al. [20] developed a FFLC on the basis of strain localization and the results were validated by a 3-point bending test. Furthermore, the strain-based FFLCs were transformed to stress triaxialities and equivalent plastic strains by numerical calculations coupled with the Yld2000-2d yield criterion. In Panich et al. [21], the forming limit stress curves (FLSCs) of steel grade DP780 and TRIP780 were obtained by using the experimental FLC data of Nakajima test and M-K model in combination with different yield functions. It was shown that the calculated FLSCs regarding experimental FLC data were more accurate than those derived from the M-K model. Butuc et al. [22] determined FLSCs from experimental FLC for a bake hardened steel and an aluminum alloy grade AA6016-T4. Different yield criteria, for example, the Yld96 yield function were coupled with various hardening models in order to exhibit their influences on the calculated FLSCs. The influences of work hardening coefficient and strain rate sensitivity on the theoretical FLSCs were also evaluated. It was reported that the combination of strain-based and stress-based failure criterion could be a promising approach for multi-stage sheet metal forming, when a proper yield function was applied.

It is seen that a formability prediction tool with higher accuracy is required for AHS steel sheets. Therefore, in this work, the strain-based FFLC of AHS steel grade 980 was experimentally determined first. The Nakajima test and tensile tests of pure shear and combined loading samples were performed and local critical strains before fracture were then gathered by means of the DIC technique. Afterwards, the FFLCs in the principal stress space were computed on the basis of experimental FFLC data by using the Hill’48 and Yld89 yield criteria. Moreover, the FFLC was transformed to fracture loci (FL) representing a relationship between stress triaxiality and effective critical plastic strain. To verify the applicability of obtained fracture curves forming tests of various samples, namely, mini-tunnel, rectangular cup and Diabolo sample were carried out. The corresponding FE simulations were conducted in parallel and the resulted strain and stress paths up to the experimentally identified failure states were identified and compared with the FFLSCs and FLs.

Materials characterization

A commercial AHS steel sheet grade 980 with the initial thickness of 0.97 mm was used in this work. It was a complex phase (CP) steel, which exhibited a finely multiphase microstructure containing small martensitic islands and different bainitic phases dispersed in a ferritic matrix. The investigated steel grade 980 showed rather high phase fractions of martensite and bainite, which provided increased strength but lowered ductility characteristics, as depicted in Fig. 1.

Fig. 1

Micrograph of the investigated steel grade 980

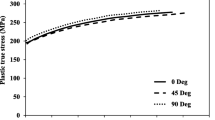
Tensile tests under various loading directions were conducted for determining material yield behaviors and stress-strain responses of the examined steel. The uniaxial tensile tests were performed on a universal testing machine using the specimen according to ASTM E8 standard. The steel sheet samples were prepared along the directions 0, 45 and 90° with regard to the rolling direction (RD). The stress-strain curves and r-values of tested steel samples were then determined. During the tests, an optical strain measurement system was employed to measure the longitudinal elongation and width reduction of samples. The strain rate of 0.001 s⁻¹ was given for all tests by controlling the crosshead speed. The yield strength (YS), tensile strength (UTS), uniform elongation, total elongation and r-values of sheet samples taken from different orientations were obtained and summarized in Table 1. Note that the r-values were calculated by a linear approximation of the true width and true thickness strains measured at about 14% of the total elongation. It was found that the samples at 0° (RD) showed the highest strengths as well as largest elongations which were obviously higher than other samples. The samples at 45 and 90° (TD) exhibited the similar achieved strengths and elongations. However, the determined r-value of samples at 0° was lowest and the r-values of samples from all directions were quite lower than 1. The plastic true stress-strain curves gathered from tensile test and its corresponding curve described by the Swift hardening law are illustrated in Fig. 2. Moreover, a hydraulic bulge test was conducted for determining the stress-strain response of examined steel under biaxial stress state. In the experiment, a non-Newtonian fluid was employed to transfer pressure from punch to sheet metal specimen instead of conventional oil. The testing setup was given in details in the former work [21]. The true stress-strain curves of steel grade 980 from the uniaxial tensile and bulge test and their representations using the Swift hardening law are compared in Fig. 2. It is seen that both stress-strain responses were comparable, but the biaxial flow stress curves clearly achieved higher strain. The strain hardening of uniaxial flow curve was somewhat higher than that of biaxial one at the beginning, while at higher strain the hardening rates of both curves became similar. Usually, the stress-strain behaviour obtained from the hydraulic bulge test is more suitable for representing the state of stress in most sheet metal forming processes, especially where large plastic deformation was expected. Therefore, in this work, the biaxial stress-strain curve was applied in further calculations for the investigated steel.

Table 1 Tensile properties of the investigated steel grade 980 (engineering value)

Fig. 2

Plastic true stress-strain curves of steel grade 980 determined by uniaxial tensile and hydraulic bulge tests including their representations using the Swift law

Afterwards, the anisotropy coefficients of the Hill’48 yield criterion were calculated with regard to the r-values of samples from the 0, 45 and 90° to the RD and the uniaxial yield stress at the RD, as provided in Table 2. For the Yld89 yield model, the material properties required for computing its anisotropic coefficients were the uniaxial yield stresses and r-values of samples from the 0 and 90° to the RD, which are demonstrated in Table 3. Note that the description of the Yld89 yield function and corresponding anisotropy parameters can be found in details in Barlat et al. [23]. The Swift hardening law, as expressed in Eq. (1), was used to describe the plastic stress–strain curve of the steel obtained from the biaxial hydraulic bulge test, as provided in Fig. 2.

$$ \overline{\sigma}=K{\left({\overline{\varepsilon}}_0+{\overline{\varepsilon}}_{\mathrm{p}}\right)}^n $$

(1)

Table 2 Determined anisotropic coefficients of the Hill’48 yield criterion (r-value based) for the examined steel

Table 3 Determined anisotropic coefficients of the Yld89 yield criterion (r-value based) for the examined steel

Where $\overline{\sigma}$ and ${\overline{\varepsilon}}_{\mathrm{p}}$ are the effective stress and plastic strain, respectively. K, n and ε _o are the material constants, which were determined from the experimental biaxial stress–strain curves by means of a regression method, as given in Table 4.

Table 4 Determined material constants of the Swift hardening model for the investigated steel

With regard to the gathered materials parameters, flow stresses and r-values were calculated by using the Hill’48 and Yld89 yield criteria. Then, the experimentally determined and numerically predicted yield loci as the function between normalized TD stress and normalized RD stress are presented in comparison in Fig. 3. It is observed that the Hill’48 yield model overestimated the experimental yield stress under uniaxial tension in the 90° direction, but underestimated the yield stress under biaxial condition. Nevertheless, the Yld89 yield criterion just slightly overestimated the experimental results of uniaxial tension in the TD and balanced biaxial state.

Fig. 3

Yield loci experimentally determined and numerically predicted by different yield criteria for the investigated steel

Determination of strain based fracture forming limit curve

To determine the FFLC for describing fracture states of the investigated steel grade 980, experimental Nakajima test and tensile tests of shear samples were carried out, in which an optical strain measurement with the DIC technique were employed .

Nakajima stretch-forming test

For the experimental determination of strain-based FFLC of the examined steel, the Nakajima stretch-forming test [5] was carried out by using the sample standard ISO 120004-2 [24]. Figure 4 depicts the schematic description of used tools and machine for the Nakajima test. The sheet samples with the same length of 200 mm and different widths between 55 and 200 mm were prepared. A black and white patterns for the optical strain measurement were applied on the surface of test samples. During the test, the samples were pressed until fracture by a hemispherical punch with a diameter of 100 mm. A punch speed of 10 mm/min and a blank holder force of 300 kN were employed. The frictions between samples and tooling were minimized by using latex foil sheets and lubricant oil.

Fig. 4

Schematic description of the used (a) tools and (b) machine setup for Nakajima test

By the test, the local strain histories of deformed samples were gathered by mean of the DIC technique, as shown in Fig. 4b. The local major and minor in-plane strains obtained during the entire tests were used to identify the necking and fracture state for each stress state. Note that the limiting plastic strains of a conventional FLC were basically determined from strain distributions at the stage of localized necking. This stage could be well evaluated by considering the intersection point of slope lines at stable and unstable thickness reduction rates, as illustrated in Fig. 5a and b for the 55 and 140 mm samples, respectively. In this work, the major and minor principal plastic strains at the maximum rate of thickness reduction were determined. Subsequently, these plastic strains from samples with varying dimensions were taken and used as the critical strains to fracture for constructing the FFLC of examined steel. It is seen that the critical strains at the fracture states were somewhat higher than those at the necking states in dependence on the governing state of stress.

Fig. 5

Determined major and minor strains and thickness reduction rate of (a) 55 mm and (b) 140 mm Nakajima sample for identifying the localized necking and fracture state

Shear fracture test

The tensile tests of pure shear and combined loading samples were performed for obtaining the failure threshold strains under shear fracture mode. Figure 6a and b depict the geometries of used pure shear and combined loading sample, respectively, which were similar to those reported in other previous works [4, 21]. Three repeated samples were tested for each case. Hereby, the DIC based optical strain measurement system was applied for experimentally evaluating local strain distributions developed in the critical area of both specimens. Figure 7a and b depict the measured strain distributions on pure shear and combined loading sample, respectively, at a stage before fracture. The strain paths until fracture of the middle section of pure shear samples, where plastic strains were highest as seen in Fig. 7a, were determined. It was found that they properly passed through the shear stress region and showed a linear behaviour until sample failure, as shown in Fig. 8. By the experiments, the fracture of AHS steel grade 980 samples occurred so early that sample rotation was still not significant. The final rapture exactly took place in the middle of samples where shear deformation was expected. Furthermore, the hydrostatic stresses or mean stresses σ _m in this area were calculated. They were very small in comparison to their accompanying effective stresses that led to a stress triaxiality value close to zero. Thus, it meant that the middle section of used pure shear sample certainly exhibited a nearly in-plane shear deformation state.

Fig. 6

a Pure shear sample and (b) combined loading sample [4, 21]

Fig. 7

Measured strain distributions of (a) pure shear sample and (b) combined loading sample at a state before fracture

Fig. 8

Determined strain based FFLC along with the measured strain paths of shear and combined loading sample and conventional FLC of the investigated steel grade 980

For the combined loading sample, the dimension of shear sample was slightly modified to generate a specific stress state induced by the combination of shear and tensile deformation, as reported in [14, 15]. In Fig. 7b, it can be observed that measured plastic strains were clearly high in the vicinity of both edges of the sample. For this sample, the determined strain paths of this area were also linear until fracture, but located between shear and uniaxial tension stress state, as presented in Fig. 8. On the other hand, the computed stress triaxiality values from this region of combined loading sample were slightly higher than those of pure shear sample. Both used shear samples exhibited a local shear deformation as described by the strain paths between the shear and uniaxial tension stress state with the strain ratio between −1 and 0.5. This range should be used to evaluate the shear fracture in a deep drawing process, as reported by Gorji et al. [25]. Similar to the Nakajima test, the maximum and minimum in-plane plastic strains of both samples were determined at the moment, by which the rate of thickness reduction was maximum. These critical strains represented the states shortly before crack appearance. Then, they were included as the limit fracture strains for the shear deformation domain in the FFLC.

Resulted strain based FFLC

From the overall results of Nakajima stretch-forming test and tensile tests of shear and combined loading sample, the strain based FFLC of investigated steel grade 980 was obtained, as illustrated in Fig. 8. Obviously, the FFLC coupled the strain domain of conventional FLC with additional strain range on the left hand side area, which generally attributed to shear fracture mode. It can be seen here that the strain based FFLC consisted of three strain branches. The first branch corresponded to the stress states between biaxial tension (φ ₁ = φ ₂)and plane strain(φ ₂ = 0). The second region was the range from plane strain(φ ₂ = 0)to uniaxial tension(φ ₁ =  ‐ 2φ ₂). The last branch represented the stress state from uniaxial tension(φ ₁ =  ‐ 2φ ₂)to pure shear(φ ₁ =  ‐ φ ₂). This additional domain showed the limit strains of examined steel sheet under shear deformation, which were directly determined from the experiments of two sample types. Thus, the determined FFLC covered all states of stress, which could occur in sheet metal forming, especially deep drawing process. The conventional FLC of steel determined by the experimental Nakajima test at localized necking state, which was taken from the previous work [21], was compared with the FFLC in Fig. 8. This FLC is commonly used for formability evaluation of sheet metals in part making industries. It is clearly seen that the FLC of steel grade 980 was slightly lower than the FFLC from the biaxial range to uniaxial tensile stress range. Within the shear and uniaxial tension domain, failure strains extrapolated from the conventional FLC would largely overestimate those from the proposed FFLC. Moreover, it was well reported that the Nakajima based FLC could not accurately describe material failure particularly due to a shear fracture, which was the typical failure mode of complex AHS steel part, as mentioned in [26,27,28]. Therefore, the introduced FFLC should better predict the limiting strains of sheet metal components under shear deformation, which will be verified by three further experimental forming tests of mini-tunnel, rectangular cup and Diabolo sample.

Determination of stress based fracture forming limit curve

In this work, the determined strain based FFLC was transformed to stress based FFLC in a principal stress space and fracture locus in a space of stress triaxiality and effective plastic strain. As the conventional FLC is determined under proportional loading conditions, it is thus limited to the situation, in which strain paths during forming processes is linear, in order to achieve a reliable prediction. In several experimental and theoretical analyses, it was shown that the maximum allowable limit strains strongly depended on various physical factors. Among which the most important ones were materials work-hardening, strain rate sensitivity, evolution of deformation mode or strain path history, and plastic anisotropic characteristic induced by rolling direction. Furthermore, it was well established that the FLC was sensitive to the pre-deformation of steel sheets occurred during forming process, especially under non − linear deformation paths. In industrial applications, most stamping parts are usually complex and produced in multi − step procedures. Such non-proportional strain histories strongly affected the level of FLC [1, 13]. Arrieux et al. [29, 30] proposed a concept for constructing stress based forming limit curve, which was found to be independent of strain path changes. In a recent study, Stoughton [30] reported that an application of stress based FLC extended the validity range of failure criterion for forming process concerning non − proportional loading. Additionally, stress based FFLC can be generated from the strain based FFLD. Hereby, the major and minor principal stress components at the onset of fracture could be calculated with regard to an adequate flow and hardening model. It was reported that the stress based fracture criterion was robust against any changes of strain path developing in a forming process [31, 32]. In this work, the stress based FFLC of investigated steel was determined on the basis of the critical strains from experimental FFLC data and plasticity theory coupled with two different yield criteria, namely, Hill’48 and Yld89 model. Note that the used computation method was similar to that proposed by Butuc et al. [22], Butuc et al. [33] and Panich et al. [1].

For the calculations of critical fracture stress values, it was assumed that the principal anisotropy axes of orthotropic symmetry were coincident with the principal stress axes. The strain path could be thus characterized by the strain ratio [22, 33], as expressed in the following equation.

$$ \rho =\frac{\varepsilon_2}{\varepsilon_1} $$

(2)

The stress ratio was then represented by Eq. (3).

$$ \alpha =\frac{\sigma_2}{\sigma_1} $$

(3)

Note that the linear strain ratio can be well used to describe the strain path of deformed conventional materials until the localized necking state as represented by FLC. After the necking, strain path can noticeably deviate from the initial strain path. However, such AHS steels as used in this work failed with a very little necking appearance, as discussed by Li et al. [26] and Beese et al. [27]. Park et al. [2] reported that in the case of AHS steel sheets, very small necking zone and thickness reduction were observed before the fracture initiation due to their poor ductility. No significant triaxiality stress state developed in their specimen. In [2, 18], it was demonstrated that a linear strain path until fracture state was obtained from pure shear sample. This strain ratio was also applied to a transformation into a stress spaces. Therefore, it could be assumed that the strain ratios of AHS steel sheets by Nakajima test and tensile test of shear samples were constant up to fracture.

For in–plane isotropic material and by the absence of shear stress in a coordinate system aligning with the anisotropy axes, the major and minor true stresses can be expressed as following.

$$ {\sigma}_1=\frac{\overline{\sigma}\left(\overline{\varepsilon}\right)}{\xi } $$

(4)

$$ {\sigma}_2={\alpha \sigma}_1 $$

(5)

Where $\overline{\sigma}\left(\overline{\varepsilon}\right)$ represents the effective stress computed through the Swift hardening model in Eq. (1). The parameter ξ was determined as the ratio of the effective stress and maximum principal stress, as demonstrated in Eq. (6).

$$ \xi =\frac{\overline{\sigma}}{\sigma_1}=\frac{\sqrt{1+2\overline{r}}}{\left(\left(1+\overline{r}\right)+\overline{r}\rho \right)}\times \sqrt{1+\left(\frac{2\overline{r}}{1+\overline{r}}\rho \right)+{\rho}^2} $$

(6)

The average normal anisotropy $\left(\overline{r}\right)$ is expressed in Eq. (7)

$$ \overline{r}=\left(\frac{r_0+2{r}_{45}+{r}_{90}}{4}\right) $$

(7)

Where r ₀ , r ₄₅and r ₉₀ are the r–values at 0, 45 and 90° to the rolling direction.

In case of the Yld89 yield model, which was developed by Barlat and Lian in 1989 [23], the yield potential was expressed as following.

$$ f=a{\left|{k}_1+{k}_2\right|}^M+a{\left|{k}_1-{k}_2\right|}^M+c{\left|2{k}_2\right|}^M=2{\overline{\sigma}}^M $$

(8)

Where a, c, h, p are material anisotropic parameters with regard to the r ₀, r ₉₀ and the yield stress at 0° (σ ₀), and 90° (σ ₉₀), to the rolling direction. M is defined according to the crystallographic structure of material, for example, M = 6 (BCC) and M = 8 (FCC).

The material parameters in Eq. (8) are described in Eqs. (9)–Eq. (10).

$$ {k}_1=\frac{\sigma_x+h{\sigma}_y}{2};{k}_2=\sqrt{\left[{\left(\frac{\sigma_x-h{\sigma}_y}{2}\right)}^2+{p}^2{\sigma}_{xy}^2\right]} $$

(9)

$$ a=2-c=2-2\sqrt{\frac{r_0}{1+{r}_0}\frac{r_{90}}{1+{r}_{90}}};h=\sqrt{\frac{r_0}{1+{r}_0}\frac{1+{r}_{90}}{r_{90}}} $$

(10)

In sheet metal forming, a plane stress anisotropic condition can be assumed so that the yield potential in Eq. (8) was simplified to Eq. (11), as shown in details in Basak et al. [34].

$$ f=a{\left|{\sigma}_1\right|}^M+a{\left|h{\sigma}_2\right|}^M+c{\left|{\sigma}_1-h{\sigma}_2\right|}^M=2{\overline{\sigma}}^M $$

(11)

As a result, the stress ratio parameter ξ for the Yld89 yield model was rearranged in the new form, as given in Eq. (12).

$$ \xi =\frac{\overline{\sigma}}{\sigma_1}={\left[\frac{1}{2}\left(a+a{\left| h\alpha \right|}^M+c{\left|1- h\alpha \right|}^M\right)\right]}^{\frac{1}{M}} $$

(12)

Here, the strain ratio ρ can be then written as a function of α as following.

$$ \rho =\frac{a{\left| h\alpha \right|}^{M-1}- ch{\left|1- h\alpha \right|}^{M-1}}{a+c{\left|1- h\alpha \right|}^{M-1}} $$

(13)

Therefore, the stress based FFLC could be determined from the experimental fracture strains of various stress states taking into account both yield criteria, as demonstrated in Fig. 9. It is recognized that the obtained FFLSC somewhat depended on the shape of yield surface and hardening law used to describe the plastic deformation of investigated steel. Note that these FFLSCs represented the maximum in–plane stresses at fracture of the steel grade 980 in the rolling direction. The fracture stress curves could describe the stress states ranging from the pure shear deformation until equi–biaxial tension, as indicated in Fig. 9. The additional stress domain on the left hand side of FFLSC could be used for describe failure in complex sheet metal forming of AHS steels.

Fig. 9

Stress based FFLCs determined on the basis of experimental strain based FFLC data and different yield criteria for the steel grade 980

Transformation of fracture FLSC to fracture loci

Furthermore, the obtained fracture limit strains were transformed into stress triaxiality and effective plastic strain space under consideration of the anisotropic Hill’48 yield function as described in Isik et al. [35] and the Yld89 anisotropic yield criterion as shown in Basak et al. [34]. Then, the triaxiality could be determined from the critical limit strains via a simple coordinate transformation. For the transformation, the strain ratio (ρ), stress ratio (α) and average normal anisotropy, as given in Eqs. (2), (3) and (7), respectively, were needed. These ratios could be correlated with each other. Regarding the Hill’48 model the stress ratio were described as a function of strain ratio and average normal anisotropy, as provided in Isik et al. [35] and Panich et al. [36]. The general relationship between the described strain ratio (ρ) and stress ratio (α) can be expressed in Eq. (14).

$$ \alpha =\frac{2\rho +1}{2+\rho } $$

(14)

The stress triaxiality (η) as the ratio between means stress or hydrostatic stress (σ _m) and equivalent stress could be calculated with respect to the stress ratio (α) in Eq. (14) and the stress ratio parameter (ξ). The general descriptions of stress triaxiality and effective strain are expressed in Eqs. (15) and Eq. (16), respectively. Finally, relationship between triaxiality and critical equivalent plastic strain at fracture was obtained by transforming the maximum and minimum principal strains from FLC data and then plotted as the fracture locus.

$$ \eta =\left(\frac{1+\alpha }{3}\right)\times \left(\frac{1}{\xi}\right) $$

(15)

$$ \overline{\varepsilon}=\frac{\varepsilon_1}{\xi}\left(1+\rho \alpha \right) $$

(16)

As a result, the fracture loci determined by using the Hill’48 and Yld89 yield function are demonstrated for the investigated steel in Fig. 10. Note that the fracture loci also presented three different stress domains, which corresponded to the same states of stress as shown in the strain based FFLC. Basically, the FLs consisted of three branches in the space of effective plastic strain and stress triaxiality. The first branch described the stress states between biaxial tension (η = 0.667) and plane strain tension (η = 0.577). The second branch covered the range from plane strain tension (η = 0.577) to uniaxial tension (η = 0.33). The third branch extended from uniaxial tension (η = 0.33) to pure shear (η = 0), as illustrated in Fig. 10. The FLs calculated by both yield criteria obviously showed some discrepancies at all states of stress, since at large plastic strains the yield function could strongly affect the resulting limit strains. In general, the Yld89 model predicted somewhat higher fracture strains than the Hill’48 model.

Fig. 10

Fracture loci determined on the basis of experimental strain based FFLC data and different yield criteria for the steel grade 980

Verification

Mini-tunnel forming test (biaxial state of stress)

In order to compare and verify the applicability of the strain, stress based FFLCs and FLs, the experimental stamping tests of mini-tunnel part were carried out. Figure 11 depicts the used experimental setup, dies and formed samples at failure. By this stamping test, it was found that the most critical area of deformed mini-tunnel samples, as shown in Fig. 11c was governed by the biaxial state of stress. The specimens were prepared so that the sample length was in parallel to the rolling direction. The experiment was performed on a servo hydraulic press machine. During the tests, the draw-in of outer periphery of sample into die was controlled by means of a constant blank holder force of 1400 kN. The friction between samples and dies was minimized by using oil lubricant. The samples were pressed until fracture occurred, in which the drawing depth of around 73 mm was achieved. This drawing depth was later used to validate the FE results. Subsequently, FE simulations of the stamping test of mini-tunnel part were conducted, for which the models are illustrated in Fig. 12. Hereby, four node shell elements were defined for the blank. The boundary conditions similar to the experiment were given for the model. The material anisotropic yield behaviour and strain hardening with regard to the biaxial bulge test were described by the Hill’48 and Yld89 yield criteria and the Swift law, respectively. The coulomb friction coefficient of 0.08 was given. The punch, die and blank holder were defined as rigid body. From FE simulations, stress and strain components were determined for the critical areas of formed samples until the experimental maximum drawing depth. In Fig. 13, it is observed that the predicted critical areas were related to the sites with large thickness reduction, which also fairly agreed with the location where crack occurred in the experiment, as seen in Fig. 11.

Fig. 11

Setup of stamping test of mini-tunnel sample: (a), (b) used die set and (c), (d) formed sample at failure

Fig. 12

FE model for the stamping test of mini-tunnel sample

Fig. 13

Calculated thickness reduction of stamped mini-tunnel part

Diabolo test

Another verification of the determined FFLCs, FFLSCs and FLs, a so-called Diabolo test was carried out for the investigated steel. The Diabolo test is a novel sheet forming test using a Diabolo punch, by which the edge crack sensitivity of trimmed parts could be evaluated. Generally, the AHS steels exhibited increased risk of edge cracking. A reduction of formability on shear cut edges was observed in deep drawing or flanging operations. It was found that such cracks could be not properly predicted by common failure criteria like FLC [3]. The Diabolo test was developed as an alternative of the hole expanding test according to the standard ISO 16630, as presented in Liewald and Gall [37, 38]. The introduced special punch geometry caused more pronounced strain localization at the edge of formed specimen, which finally led to crack initiation. The resulted formability was certainly depended on the edge quality and sample preparation. However, the effect of edge quality was not considered in this work. It was aimed to investigate the determined FFLC and FFLSC on failure prediction for such sample. The material around the critical areas of sample was subjected to the uniaxial state of stress approximately similar to that governed in the hole expanding test. Figure 14a illustrates the schematic experimental setup of the proposed Diabolo test. Note that the dies of Nakajima stretch-forming test were applied here, but the spherical punch was just replaced by the Diabolo punch, as depicted in Fig. 14b. The size of used sample was 40 × 200 mm². During the tests, sheet samples were pressed in the Nakajima die by the Diabolo punch until failure occurred, as shown in Fig. 14c. The blank holder force of 1000 kN was applied on the blank for preventing material draw-in to the die. Both latex foil and oil lubricant were used to minimize friction between blank and dies during the test. The DIC optical strain measurement was also applied for comparing the results with the simulations. Moreover, FE simulations using the shell element for blank and rigid body for punch, die and blank holder as in the case of stamping test of mini-tunnel sample were carried out for the steel grade 980. The described biaxial plastic flow behavior using Swift hardening law and anisotropic Hill’48 and Yld89 yield functions were considered in the simulations. The calculated major strain distribution on formed Diabolo samples at failure state and observed critical area are shown for example in Fig. 15.

Fig. 14

a Schematic setup of the Diabolo test, (b) used Diabolo punch and (c) deformed samples at failure

Fig. 15

Calculated major strain distribution on formed Diabolo sample at failure state of the examined steel

Rectangular cup drawing (shear stress state)

Eventually, the experimental rectangular cup drawing tests were performed for the examined steel until fracture, as seen in Fig. 16, in order to verify the obtained strain based FFLCs, stress based FFLCs and FLs. Fig. 16a illustrates the schematic description of the cup drawing test applied in this work. The investigated final part was a non-symmetric rectangular cup. During the tests, a constant blank holder force of 1200 kN was used and oil lubricant was employed to minimize friction between blank, dies and punch. The samples were pressed until failure, by which final rapture took place approximately at the drawing depth of 30 mm. This value was subsequently used to compare with the FE results. In the experiments, it was obvious that the fracture zone commonly occurred at the side wall close to the part corner, as demonstrated in Fig. 16b. Additionally, the FE simulations of cup drawing tests were carried out as other forming experiments. Both Hill’48 and Yld89 yield criteria were applied. The FE models of each part are depicted in Fig. 17, for which all boundary conditions were defined similar to those in the experiment. From the FE results, the principal stress and strain paths were gathered from the critical area of deformed part until the fracture state that was observed in the experiments. Figure 18 shows the calculated major strain distribution on deformed sample during the cup drawing test. It is seen that the predicted critical areas, which were described by the maximum major strains, were around the side wall corners. These results were well in accordance with those of the experiments.

Fig. 16

a Schematic description of rectangular cup drawing test and (b) drawn rectangular cup sample at failure

Fig. 17

FE model of the rectangular cup drawing test

Fig. 18

Calculated major strain distribution on deformed sample of rectangular cup drawing test for the examined steel

Results and discussion

Application of FFLC

First, the experimentally determined FFLC of the steel grade 980 was verified by the mini-tunnel stamping test, Diabolo test and rectangular cup drawing test. Initially, the experimental failure moments were identified and the achieved drawing depths or punch strokes from the experiments were evaluated. Subsequently, up to these corresponding points of time, the strain paths of major and middle principal strains were gathered for the fracture initiating areas on deformed samples in the simulations. These principal strain paths were calculated with regard to the Hill’48 and Yld89 yield criterion and plotted along with the strain based FFLC, as depicted in Fig. 19. Obviously, the strain paths up to experimental fracture from the Diabolo test ended far below the FFLC. On the other hand, the strain paths from the rectangular cup drawing test crossed over the FFLC. The strain paths from the mini-tunnel forming test terminated precisely close to the FFLC. It meant that the FFLC predicted too high critical deformation states for the Diabolo samples, while the FFLC slightly underestimated the failure of rectangular cup samples. Nevertheless, the FFLC could more precisely describe the fracture state of formed mini-tunnel samples. It can be seen that the critical areas of rectangular cup samples exhibited the strain paths, which located between the pure shear and uniaxial stress state, as shown in Fig. 19. By the experiment, the fracture occurred during the drawing process was observed on the side wall of sample, slightly below the corner, as illustrated in Fig. 16b. This result was well in accordance with that of corresponding FE simulations, as seen in Fig. 6b. Moreover, it was found that the thickness of this region was not considerably decreased and crack took place abruptly without localized necking appearance. Therefore, this fracture was nearly related to a shear fracture under in-plane shear deformation. In some previous works as in [26, 39], it was demonstrated that shear fracture in their experiments directly occurred in the region of shear stress state with the strain ratio of −1. On the other hand, Gorji et al. [25] reported that shear crack could occur in a cup drawing sample, in which bending stress was incorporated that caused an out of plane shear state. This out of plane shear deformation also led to a shear fracture mechanism under tension that principally took place due to a rather small die corner. By the out of plane shear or deformation through thickness condition, the sample corner or area of small die radius was elongated and its thickness was also decreased at the same time. It was also shown in [25] that most of the local strains from failed triangular cup sample were placed between the shear and uniaxial tension loadings on the left hand side of FLC. The fracture observed in [25] was rather governed by the stress state that was much closer to the uniaxial tension state when comparing with the fracture occurred in the rectangular cup sample in this work. All such shear stress states are not described in a conventional FLC so that the FLC would not accurately predict resulting failure or provides much larger limit strains.

Fig. 19

Strain paths of the critical elements in rectangular cup drawing, Diabolo and mini–tunnel forming test calculated by FE simulations coupled with different yield criteria until the experimental failures in comparison with the determined FFLCs of the investigated steel

The critical region of Diabolo samples exhibited the strain paths, which corresponded to a uniaxial tension state. However, the fracture of Diabolo samples took place in the experiments much earlier than that predicted by the strain based FFLC. It meant that the FFLC could not well predict failure emerged in the Diabolo test, since it was found that fracture of Diabolo samples was basically due to the edge cracking. Therefore, it is still not appropriate to use the FFLC to evaluate such edge fracture behaviour of blanked or punched steel sheets of the steel grade 980. The critical area of mini–tunnel sample was governed by the state of stress, which was approximately related to the biaxial stress state. For this stress region, the FFLC could better describe the critical deformation state of examined steel. Additionally, some discrepancies were observed between the strain histories from all performed forming tests calculated by the Hill’48 and Yld89 yield criterion. Both slopes and failure strains of the strain paths were slightly different. Nevertheless, it seemed that the plastic deformation of such complex parts could be more precisely predicted by the non–quadratic anisotropic Yld89 yield model.

Application of FFLSC based on experimental FFLC data

The stress based FFLCs, which were calculated on the basis of experimental strain based FFLC data coupled with the Hill’48 and Yld89 yield criterion, were plotted along with the stress paths obtained from the rectangular cup drawing, Diabolo and mini-tunnel stamping tests in Figs. 20 and 21, respectively for the investigated steel grade 980. Note that the stress paths were gathered from FE simulations until the experimental points of fracture of steel. Regarding the FFLSCs the critical stresses at failure of the forming histories in biaxial state from stamped mini-tunnel samples located very close to the threshold curves. In the same manner, the principal stress histories until fracture in shear stress region from drawn rectangular cup samples accurately ended on the FFLSCs. In contrast, the FFLSCs somewhat overestimated the calculated failure stresses in uniaxial tension state of Diabolo samples. Nevertheless, the discrepancies of the FFLSCs from the experimental results were considerably smaller than those of the strain based FFLC. In general, according to the investigated forming tests under varying states of stress the FFLSCs could more precisely describe the failure states of investigated steels than the FFLC. The stress based failure criterion FFLSC should thus reproduce local deformation conditions during cracking more realistically than the strain based failure criterion. Furthermore, the formability of steel grade 980 under shear stress zone could be well evaluated by the proposed FFLSCs. It is also seen that the mini-tunnel sample with more complex geometry exhibited noticeable deviation between the predictions by the Yld89 and Hill’48 yield model.

Fig. 20

Stress paths of the critical element of formed cup drawing, Diabolo and mini-tunnel samples calculated by FE simulations coupled with the Hill’48 yield criterion until the experimental failures in comparison with the correspondingly determined FFLSC of the investigated steel

Fig. 21

Stress paths of the critical element of formed cup drawing, Diabolo and mini-tunnel samples calculated by FE simulations coupled with the Yld89 yield criterion until the experimental failures in comparison with the correspondingly determined FFLSC of the investigated steel

Application of FLs based on experimental FFLC data

The FLs in the space of stress triaxiality and effective plastic strain transformed from the strain based FFLC data couples with the Hill’48 and Yld89 yield criterion were demonstrated in Figs. 22 and 23, respectively, for the examined steel grade 980 in comparison with the triaxiality vs. strain paths of rectangular cup, Diabolo and mini-tunnel samples obtained by FE simulations using the different yield criteria until observed experimental fractures. Also here, it can be seen that all triaxiality vs. strain paths under varying stress states terminated very close to the FLs. With the exception of Diabolo test, the triaxiality vs. strain histories noticeably ended rather below the FLs, because the Diabolo samples generally failed at the cutting edge of deformed blanks. To more accurately predict such edge crack occurrence incipient damage on the cutting edge due to blank preparation must be taken into account. Nevertheless, in this case the FLs still better described the fracture point than the strain based FFLC, but not as precise as the stress based FFLSC. Also, in general, the FLs could more accurately predict the failures of steel grade 980 than the strain based FFLC. Otherwise, the triaxiality vs. strain paths calculated by the Hill’48 and Yld89 yield criterion were similar and ended closed to each other. The measured and predicted drawing depths were later compared in order to evaluate the predictions provided by the proposed FFLSCs and FLs.

Fig. 22

Triaxiality vs. strain paths of the critical element of formed cup drawing, Diabolo and mini–tunnel samples calculated by FE simulations coupled with the Hill’48 yield criterion until the experimental failures in comparison with the correspondingly determined FL of the investigated steel

Fig. 23

Triaxiality vs. strain paths of the critical element of formed cup drawing, Diabolo and mini–tunnel samples calculated by FE simulations coupled with the Yld89 yield criterion until the experimental failures in comparison with the correspondingly determined FL of the investigated steel

Finally, the achieved drawing depths of deformed rectangular cup and mini-tunnel parts at fracture state were measured from the experiments. They were then compared with those predicted by the FFLCs and FLs coupled with different yield functions, as shown in Fig. 24, for the investigated steel grade 980. By this manner, accuracies of the predictions by the determined FFLSCs and FLs could be better evaluated. It is seen that the used yield models more significantly affected the calculated drawing depths of mini-tunnel samples, whereas the computed drawing depths of rectangular cup samples were just slightly influenced. This can be likely due to that the mini-tunnel sample exhibited complex geometries and consequently induced larger critical areas than the rectangular cup sample. The non-quadratic Yld89 yield criterion is more suitable for describing material under large strain deformation in a combined stress state than the Hill’48 yield function [23]. The errors of drawing depth predicted by the FFLSCs and FLs coupled with the Hill’48 and Yld98 yield criterion are summarized for the rectangular cup and mini-tunnel samples of steel grade 980 in Table 5. Obviously, the results of the Yld98 model better agreed with the experimental ones than the Hill’48 model in all cases. Additionally, the drawing depths predicted by the FLs in the space of stress triaxiality and effective plastic strain were somewhat closer to the measured results than the FFLSCs, in which smaller error values are provided in Table 5 for the FLs by both states of stress.

Fig. 24

Predicted and measured drawing depths of rectangular cup and mini–tunnel samples at the moments of fracture by the FFLSCs and FLs based on different yield criteria in comparison for the steel grade 980

Table 5 Experimentally determined and predicted drawing depths at fracture of the rectangular cup and mini-tunnel samples of investigated steel

Conclusions

The failure limit curves for evaluating fracture occurrence in forming of the AHS steel sheet grade 980 were determined and presented in the space of stress triaxiality, effective plastic strain and maximum, minimum principal stress. The Nakajima stretch-forming test and tensile tests of pure shear and combined loading samples were performed in combination with the DIC method. First, the strain based FLC at fracture was obtained. Then, the failure strains were transformed to maximum, minimum principal stresses and stress triaxialities, effective strains by means of the plasticity theory under consideration of the Hill’48 and Yld89 yield criteria. To verify the applicability of the determined failure curves the experimental forming tests of rectangular cup, Diabolo and mini-tunnel samples were carried out and corresponding FE simulations were conducted. Afterwards, the calculated strain and stress paths from the critical areas of each formed sample were compared with the FFLC, FFLSCs and FLs. The results of this work can be concluded as following.

• The experimentally determined strain based FFLC, stress based FFLSCs and FLs provided the fracture limits in a wide range of stress state from shear stress domain to biaxial stress state.

• In case of deformed non-symmetric rectangular cup samples, the critical stress and strain paths in a shear domain were induced, whereas for mini-tunnel samples stress and strain paths in a biaxial stress state developed. The conventional FLC predicted much too late failure in the shear stress region, while it was better described by the determined FFLC. The proposed FFLSCs and FLs could accurately predict the shear fracture occurrences at side wall corner of rectangular cup samples and the failure of mini-tunnel samples. Nevertheless, the shear fracture of rectangular cup sample was slightly underestimated by the FFLC.

• The Diabolo test provided the stress and strain paths corresponding to a uniaxial tension state. These paths until failure ended below all determined fracture limit curves. This was due to that the Diabolo samples basically failed by edge cracking, for which pre damage of the cutting edges should be taken into account. However, the FFLSCs and FLs could still more precisely describe such failure than the FFLC.

• The predictions by the FFLSCs coupled with the Hill’48 and Yld89 yield function showed noticeable deviations. The similar discrepancies were also observed in the case of FLs. It seemed that the fracture of samples with more complex shape like the mini-tunnel part should be described by the Yld89 model.

• The drawing depths at fracture state predicted by the FLs better agreed with the experimental results than those by the FFLSCs.