Semi-analytical models for flexure deformation in one-step simulation of sheet metal forming

Abstract

This paper presents the application of multi scale techniques to the simulation of sheet metal forming using the one-step method. When a blank flows over the die radius, it undergoes a complex cycle of bending and unbending. First, we describe an original model for the prediction of residual plastic deformation and stresses in the blank section. This model, working on a scale about one hundred times smaller than the element size, has been implemented in SIMEX, one-step sheet metal forming simulation code. The utilisation of this multi-scale modeling technique improves greatly the accuracy of the solution. Finally, we discuss the implications of this analysis on the prediction of springback in metal forming.

Introduction and state of the art

After the first industrial applications [1, 2], sheet metal forming simulation is nowadays part of industrial design processes. Most of the time, we use so called incremental codes for this task, where there is a Finite Element model of physical forming tools and a step-by-step simulation of their contact with the blank.

An alternative technique, one-step or inverse simulation [3], uses only the final geometry of the stamped part to predict metal deformation. This feature makes it easier to integrate this kind of simulation in the design cycle. For example, we can use the same Finite Element model for crash and metal forming simulations, making it much easier to couple the two processes and leading to much better accuracy in the prediction of performances.

This paper presents an original analytic approach to the study of the cycles of bending and unbending. This approach was developed in 2003, but it is receiving attention in this past months. Flexure bending and unbending is a process that takes place over a distance comparable to the thickness of the blank. Capturing the gradient of deformation would thus require a discretization of the order of the tenth of a millimeter, whereas typical mesh size for this kind of simulation is one hundred times larger. We have used multi scale techniques to integrate this analysis into our simulation.

Since the beginning of scientific study of metal forming [4] the attention has been drawn by the cycles of bending and unbending induced by tool geometrical features such as die radii or drawbeads to generate both a restraining force and a permanent plastic deformation.

Cycles of bending and unbending also create residual stresses, which, in turn generate springback deformations when the tools are released [5,6,7,8].

In this paper, we describe the formulations of the code SIMEX as an example of one-step sheet metal forming simulations. The first version of SIMEX was released in 1994, and since 2004 it is integrated in the solution package of ESI Group. Other commercial one-step simulation codes are marketed by ALTAIR, AUTOFORM, LSTC, etc. ...

This paper describes the theoretical foundation and the implementation in SIMEX of an equivalent model for the cycles of bending and unbending undergone by the blank over the die radius. This development greatly improved the accuracy of SIMEX simulation.

One step metal forming simulation

Formulation

The starting point of the inverse simulation is the finite element model of the stamped part. The algorithm of inverse simulation enables the user to find the position of the stamped part’s nodes on the blank’s initial geometry (Fig. 1). This search is carried out without taking into account the history of the deformation, hence the naming of “one-step”. The calculated displacements field ensures the equilibrium of the stamped part, through the calculations of the deformation (thinning, elongation) and of the constraints.

Fig. 1

One step sheet metal forming simulation

The characteristic feature of the inverse problem is that the unknowns are distributed between the flat blank (result of the computation) and the stamped part (starting point of the computation).

The problem can be posed in mathematical terms as finding the displacement u_x and u_y in the plane of the original blank, so that the stamped part is in equilibrium under the action of internal stresses, reaction forces, friction forces and restraining forces.

	known quantities	unknown quantities
initial geometry	Thickness t0, null stresses, strains	ux, uy displacement, blank contour
stamped part	Geometry uz, displacement, restraining forces, blank contour	Thickness t, stresses and strains, tool reactions

One-step simulation relies on two simplifying assumption:

The elastic component of the deformation can be ignored with respect to the plastic component.

The deformation paths are radial (Fig. 2), e.g. at each instant t > 0:

$$ \frac{\varepsilon_1(t)}{\varepsilon_2(t)}=\alpha \left( cons\tan t\right) $$

(1)

Fig. 2

Radial strain path vs. actual strain path

On the basis of these hypotheses, the equations of the material flow (associative plasticity of Von Mises and Hill, [9]) can be integrated to give rise to and explicit relation between the eigenvalues of the stress and the strain tensors (Eq. 2)

$$ {\displaystyle \begin{array}{c}\hfill {\sigma}_1\hfill \\ {}\hfill {\sigma}_2\hfill \end{array}}={E}_s{P}^{-1}{\displaystyle \begin{array}{c}\hfill {\varepsilon}_1\hfill \\ {}\hfill {\varepsilon}_2\hfill \end{array}} $$

(2)

Here, E_s is the secant modulus, i.e. the ratio between σ and ioε_p from Eq. (3.1)

$$ \sigma =k{\left({\varepsilon}_0+{\varepsilon}_p\right)}^n $$

(3.1)

P is a matrix, function of the chosen plasticity criterion. For the Henki-Mises criterion, the P matrix is given by Eq. (3.2), where R is the Lankford anisotropy coefficient.

$$ {P}^{-1}=\left[\begin{array}{cc}\hfill \frac{{\left(1+R\right)}^2}{\left(1+R\right)\left(1+2R\right)}\hfill & \hfill \frac{R\left(1+R\right)}{1+2R}\hfill \\ {}\hfill \frac{R\left(1+R\right)}{1+2R}\hfill & \hfill \frac{{\left(1+R\right)}^2}{\left(1+R\right)\left(1+2R\right)}\hfill \end{array}\right] $$

(3.2)

As for the friction, we Coulomb’s law is the usual choice. Two friction-contact models can be established:

• Unilateral contact between the metal sheet and the punch.

• Bilateral contact between metal sheet, die and blankholder.

Modeling issues

The most important simplification of the inverse method is therefore the search of the equilibrium in the final configuration of the process. There are two important factors which are not taken into account:

• The history of deformation.

• The history of the contact between the sheet metal and the tool.

Achieving accuracy with one-step simulation implies the design and development of equivalent models, which reconstruct the history of contact and/or deformation.

The development presented in this article allows for the reproduction of the effect of some deformation history features. Other equivalent models, already implemented in SIMEX, take into account the history of contact between the blank and the tools.

In order to understand how the equivalent contact models work in one-step sheet metal forming simulation, let us consider a simple, U-shaped forming operation.

The model represents the final shape of the part, it contains 1905 nodes and 1600 quadrilateral elements. In order to define equivalent models, it must be partitioned according to the role of the different areas in the forming operations (Fig. 3, which shows also the profile sections on which we shall take profiles of thinning strains).

Fig. 3

U-shape finite element model

We should point out that the Finite Element model presents sharp edges for the punch and die line, whereas in reality there will be fillets. This is consistent with the modeling procedures for stress analysis and crash simulation.

In an actual punch die forming process, the advancing punch would adhere to the surface of the blank and prevent this portion of material from deformation. As one-step simulation does not take into account the history of contact, this effect is not simulated and the blank at the bottom of the U shape shows significant deformation (see the “standard bottom” thinning profile in Fig. 4). Assigning a stick feature to the bottom of the punch triggers an approximate simulation of the history of contact. The deformation under the punch is negligible and the results are much more realistic.

Fig. 4

Approximate simulation of history of contact using the stick feature

Taking into account the history of contact is important but it is not sufficient to assure the accuracy of the simulation.

Figure 5 shows the thinning distribution (relative to the case where the bottom is modeled with stick feature). We can point out the following problems:

Fig. 5

Thinning distribution on U-shape part

The wall deformation (about 17% thinning) is caused essentially by the blankholder force through the friction coefficient. The force corresponding to this deformation is 200 tons, corresponding to 667 Mpa of pressure for a friction coefficient of 0.2. This is an extremely high value for the blankholder pressure with respect to industrial standards.

The thinning distribution on the wall shows significant reduction on the extremities. In reality we would have small gradient of thinning but by no means comparable with what we see in Fig. 5.

The reason for these problems is that, in the physical process, the process of bending/unbending over the die radius controls the wall deformation.

Blankholder restraining force plays a much less important role. Among other things, bending/unbending would induce a state of deformation close to a plane strain, greatly reducing the gradient of deformation along the y axis of our model.

In the following, we describe the theoretical foundation and the implementation of an equivalent model for the cycles of bending and unbending undergone by the blank over the die radius. We shall see that this improve the qualitative distribution of thinning on the U-shape part and allows for an excellent comparison between experimental and SIMEX results.

We should point out that bending/unbending cycles over the die radius, apart from inducing a permanent deformation and thinning on the blank material, lock a gradient of stress in the fibers thereof. In this analysis we neglect this phenomenon, which will be the object of further studies. However, this is the cause curved wall shapes that we find in deep drawn profiles after springback (Fig. 6).

Fig. 6

U-shape part after springback (courtesy of FIAT Research Center

Flexural deformation in metal forming

Description of the model

In order to understand the physical processes involving flexure in sheet metal forming, let us consider the very simple U-shape of Fig. 5. This simple shape can be obtained from two different processes: bending and forming with punch and die tooling.

In bending, the initially flat blank is bent on the four corners. Several sequences of bending are possible depending on the tooling setup. Generally speaking, the deformations of the different corners are independent on each other and the portion of materials between the bend are not affected by the deformation process. When we release the tools, each corner will undergo its own springback and recover part or the imposed deformation.

In punch and die tooling, the initially flat blank is set over a die. Prior to actual forming, a blankholder presses the blank against the die. The forming of the U-shape is obtained when a male tool (punch) pushes the blank into the die cavity. The material flowing into the die cavity undergoes a cycle of bending/unbending when it flows around the die entry radius. As a result, although the shape of the part wall may look at first sight identical to that obtained from a bending process, this material locks in both a plastic deformation and significant residual stresses. The shape of such a part after springback shows a typical curved wall.

For the case of bending and punch and die forming alike, the final shape presents four bends, i.e. areas of significant curvature. However, the deformation processes of the blank over these bends are very different.

In the case of a bending process, the deformation over the bends will be purely flexural, and can be written, as long as the radius of curvature is large with respect to the material thickness as in Eq. (4)

$$ {\varepsilon}_x=\frac{y}{R_D+\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} $$

(4)

The x and y axis belonging to the curvilinear reference frame defined in Fig. 7.

Fig. 7

History of deformation over the die radius

In the case of a punch and die forming, this distribution of deformation will essentially be correct for the two bends on the punch nose or punch line. However, over the die radius, the distribution of deformation will vary greatly along the curvilinear coordinate, as it will be shown in the following.

For the sake of simplicity, we assume that the effect of friction is negligible. We also assume that the blank is in the elastic phase before entering the die radius. The blank, goes through the following process (Fig. 7):

• A: Unloaded elastic state. A relatively small, uniform stress and strain across the thickness can be present. A resultant force per unit width, greater than or equal to T will be present, for equilibrium considerations, over all the sections of the die radius.

• B: After entering the die radius (classical theory of continuum mechanics suggests a distance approximately equal to the blank thickness) the section will have a curvature radius equal to r_D + h/2. The energy required for this deformation is provided by a traction force T_C applied at the end of the die radius by the punch via the formed material. This force must be balanced, so that the deformation state of the blank will be a combination of the flexural deformation (1) and of a membrane deformation ε_M^B (Eq. 5).

$$ {\varepsilon}_x=\frac{y}{R_D+\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+{\varepsilon}_M^B $$

(5)

• C: At the exit of the die radius, the blank will be flat again, or in any case the residual radius of curvature will be much higher than the die radius r_D. The deformation will be again constant across the thickness, equal to a new value ε_M^C.

Semi-analytical model of deformation

We study the deformation of a material segment (in the sense of [10]) of blank flowing over the die radius. This treatment gives us values for the permanent plastic deformation ε_M^C and for the traction T = T_C at the end of the die bend.

We should point out that the traction force T may be below yield level (i.e., the ration T/h may be less than the yield stress σ_y). However, plastic deformation is usually present across the whole thickness of the blank. Further, depending on the strain hardening characteristics, there is usually a gradient of stress across the thickness, leading to a springback deformation when the residual stresses are released.

Before implementation into SIMEX, we present the results of a semi-analytical analysis. In this connection, we make a few simplifying assumptions.

The first assumption is that plain sections remain plane, i.e. we can define a flexural component of the deformation (Eq. 6):

$$ {\varepsilon}_f=\frac{y}{R_D+\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} $$

(6)

Maximum flexural deformation will take place on the upper (sup) and lower (inf) skin of the blank (Eq. 7)

$$ {\varepsilon}_f^{\mathrm{sup}}=\frac{h}{2\left({R}_D+\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)},{\varepsilon}_f^{\mathrm{inf}}=-\frac{h}{2\left({R}_D+\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)} $$

(7)

The second assumption is that bending and unbending cause the same amount of membrane deformation across the thickness of the blank (Eq. 8).

The third assumption is that the material hardening behavior is isotropic, i.e. the yield surface expands without shifting when the Von Mises stress increases according to the Krupkowsky-Swift law (3.1). Analysis of the effect of different hardening behaviour will be presented in a future publication.

The last assumption is that we shall neglect the elastic component of the deformation.

The mechanical deformation of the material going over the die radius is described by Eq. (8).

$$ T\delta x=\underset{V}{\int }{\sigma}_{ij}{\delta \varepsilon}_{ij} dV $$

(8)

In Eq. (8), T = T_c is the traction force at the exit of the die radius, δx is the corresponding infinitesimal displacement, V is the volume of material over the die radius σ_ij and ε_ij are respectively the tensor field of stress and strain.

As all the fibers of the material move along the curvilinear coordinate x, Eq. (8) simplifies into Eq. (9).

$$ T{v}_x\delta t=\underset{V}{\int }{\sigma}_x{\delta \varepsilon}_x dV $$

(9)

The infinitesimal perturbation δε_x is a material perturbation [9], which can be written as in Eq. (10).

$$ {\delta \varepsilon}_x=\frac{\partial {\varepsilon}_x}{\partial t}\delta t+{v}_x\frac{\partial {\varepsilon}_x}{\partial x}\delta t $$

(10)

Equation 10 becomes Eq. (11) for a stationary material flow.

$$ {\delta \varepsilon}_x={v}_x\frac{\partial {\varepsilon}_x}{\partial x}\delta t $$

(11)

Substituting (11) into (8) we obtain Eqs. (12.1) and (12.2)

$$ T{v}_x\delta t={v}_x\delta t{\int}_{-h/2}^{h/2} dy\underset{0}{\overset{L}{\int }}{\sigma}_x\frac{\partial {\varepsilon}_x}{\partial x} dx $$

(12.1)

$$ T={\int}_{-h/2}^{h/2} dy\underset{0}{\overset{L}{\int }}{\sigma}_x\frac{\partial {\varepsilon}_x}{\partial x} dx $$

(12.2)

Equations (12.1) and (12.2) can be simplified, as stress and strain variation take place only in the proximity of points B and C. Substituting ${d\varepsilon}_x=\frac{\partial {\varepsilon}_x}{\partial x} dx$ we obtain:

$$ T={\int}_{-h/2}^{h/2} dy\left[{\int}_0^{\varepsilon_f+{\varepsilon}_M^B}{\sigma}_x\left(\varepsilon \right) d\varepsilon +{\int}_{\varepsilon_f+{\varepsilon}_M^B}^{\varepsilon_M^C}{\sigma}_x\left(\varepsilon \right) d\varepsilon \right] $$

(13)

The flexural deformation ε_f is given by Eq. (6). The actual integrals in Eq. (14) depend on the stress-strain paths of the material, in particular on the hardening characteristics. For an elastic-perfectly plastic material, the generic strain paths on the upper and lower surfaces are presented in Fig. 8.

Fig. 8

Stress/strain paths of upper and lower surface

As we can see, there is a profile of residual stresses in the material section at point C. The resultant of these stresses must be equal to the traction force T (Eq. 14).

$$ T={\int}_{-h/2}^{h/2}{\sigma}_x^C dy $$

(14)

Equations (13) and (14), along with assumption (9), lead to a system of two equations and two unknowns, enabling us to predict the values of stresses and strains for a material flowing over a die radius.

If we neglect the elastic deformation energy, the above treatment can be immediately extended to a situation where a traction force is present before the die entry radius (section A) as it would be the case in the presence of a blankholder restraining force.

$$ T-{T}_A={\int}_{-h/2}^{h/2} dy\left[{\int}_0^{\varepsilon_f+{\varepsilon}_M^B}{\sigma}_x\left(\varepsilon \right) d\varepsilon +{\int}_{\varepsilon_f+{\varepsilon}_M^B}^{\varepsilon_M^C}{\sigma}_x\left(\varepsilon \right) d\varepsilon \right] $$

(15)

Equation (14) stays unchanged.

Finally, we can point out that the stress distribution at the end of the die radius (point C) gives rise to a moment M_C, defined as in Eq. (16).

$$ {M}_C={\int}_{-h/2}^{h/2}y{\sigma}_x^C dy $$

(16)

In order to compute stress and deformation patterns, we have developed an interactive semi-analytical tool based on SimTech’s ENKIDOU package. The tool enables the user to enter the relevant parameters for the die radius geometry and material properties before solving Eqs. (13) and (14) for the equilibrium of the flowing blank material.

The first results presented are relative to a typical low grade steel blank of thickness h = 0.67, drawn over a die radius R = 5 mm. The hardening curve is given by Eq. (17).

$$ \sigma =491{\left(0.00725+{\varepsilon}_p\right)}^{0.182} $$

(17)

This expression (Fig. 9) corresponds to the following material characteristics:

• Yield strength σ_y = 200 Mpa

• Necking engineering deformation = 20%

• Ultimate strength (engineering) R_m = 302 Mpa

Fig. 9

Hardening curve for the material studied

No restraining force T_A is present at this time. Figure 10a, b show the deformation profiles across the thickness for section B (bending loading) and C (bending unloading).

Fig. 10

a Stress and strain after bending loading. b Stress and strain after bending unloading

After the bending loading (section B) the fibers of the material are in traction above the neutral fiber y₀, in compression below the neutral fiber. The value of y₀ is given by Eq. (18).

$$ {\displaystyle \begin{array}{l}{y}_0={\varepsilon}_M^B{R}_h=\frac{\varepsilon_M^B}{2}{R}_h\\ {}{R}_h=R+\frac{h}{2}\end{array}} $$

(18)

Fiber stress will be above σ_y in the extended fibers and below -σ_y in the compressed fibers.

During the unbending process, the deformation will be brought to a constant value ε_M, but the different fibers will follow different paths (Fig. 8)

• For y < −y₀ (lower fibers) the strain will increase to ε_M while the stress will revert above σ_y.

• For y > y₀ (upper fibers) the strain will decrease to ε_M while the stress will revert below -σ_y.

• Finally, for - y₀ < y < y₀, the strain will increase to ε_M while the stress keeps the constant value corresponding to this plastic deformation.

Our model predicts the restraining (traction) force T and the residual moment M. We present the results for this two quantities, normalized with respect to the values corresponding to a totally plastified section (Eqs. 19 and 20).

$$ {T}_{norm}=\frac{T}{\sigma_yh} $$

(19)

$$ {M}_{norm}=\frac{M}{\sigma_y\raisebox{1ex}{${h}^2$}\!\left/ \!\raisebox{-1ex}{$4$}\right.} $$

(20)

We can now analyze the behavior of the metal sheet going through the die radius. It will be determined by the die geometry, modeled via the flexural strain ε_f, defined as in Eq. (21).

$$ {\varepsilon}_f=\frac{h}{2{R}_h} $$

(21)

Effect of material properties

We analyze here the effect of the material properties, by comparing the behavior of a ductile material (low grade steel) with a perfectly plastic material.

Permanent deformation after die radius has a very similar pattern for different materials as a function of flexural strain (Fig. 11).

Fig. 11

Permanent deformation vs. flexural strain

Traction force, on the other hand, is significantly affected by material hardening. In both cases, value of traction force is very small for small flexural strains, but it increases much more rapidly in the presence of significant hardening, to a value of about 40% of T_norm (Fig. 12).

Fig. 12

Traction force vs. flexural strain

Material hardening affects greatly also the resultant moment of residual stresses (Fig. 13).

Fig. 13

a Residual moment vs. flexural strain. b Effect of restraining force on permanent deformation

Effect of restraining force

If we apply a force prior to point A of Fig. 6, both permanent deformation and traction force show a significant amount of variation. As expected, they increase, for a given value of flexural deformation, as the restraining force increases (Figs. 14, 15 and 16).

Fig. 14

Effect of restraining force on traction force

Fig. 15

Effect of restraining force on residual moment

Fig. 16

Effect of restraining force stress profile

It should be pointed out that the material prior to point A is well into the elastic phase, the restraining force being, in all the cases considered, well below yield values. However, due to the effect of flexure cycling, a significant amount of permanent deformation is gained.

Implementation in simulation code

The above described methodology has been imbedded in the “bending” boundary condition of SIMEX code. Even though the mesh size is roughly the order of magnitude of the die radius, this boundary condition models the bending/unbending cycle which takes place on a much lower scale.

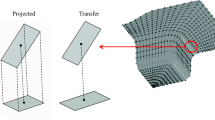
During the simulation iteration, for each element labelled “WALL” (cfr. Figure 3), the code computes an approximated trajectory. This is the projection of the total displacement vector on the extended final part geometry. The extension is obtained superposing the (computed) initial geometry to the final geometry, which is the original data of the one-step simulation (Fig. 17).

Fig. 17

construction of element trajectory

If an element is detected as crossing the flexure boundary condition line, the system composed of Eqs. (14) and (15) is solved to find the strain tensor induced by the flexural/bending and unbending. This tensor is added to the membrane strain to yield corrected stresses and internal forces.

The implementation of this model in SIMEX allows for the simulation of bending/unbending cycle over the die radius. Figure 18 shows the profiles of thinning for the U shaped part described in “One step metal forming simulation” section. For a blankholding pressure of 50 MPa, the figure presents the thinning profiles relative to three different die entry radii, 4, 6 and 12 mm respectively.

Fig. 18

Effect of different die radii on thinning profile

Application to industrial part

The French RNTL MACARENA project addressed the general issue of coupling crash computation with metal forming simulation. SimTech was a partner in MACARENA alongside, among others, PCA Peugeot Citroen and RENAULT.

One of the problems addressed within MACARENA was the accuracy of one-step sheet metal forming simulations. In order to validate the new features of SIMEX, we referred to the component shown in Fig. 19. RENAULT had designed, built, instrumented and measured this component to reproduce deformation patterns of actual industrial components, even though it not correspond to any actual vehicle component.

Fig. 19

RENAULT MACARENA rail

Formed material was a steel with the following characteristics:

• thickness = 1.97 mm

• yield strength = 315 Mpa

• ultimate strength = 425 Mpa

• necking elongation = 18%

• Lankford coefficient = 1.43

The relevant process data were:

• Blankholder force = 32 tons

• Friction coeff. = 0.15

• die entry radius = 3 mm

After forming, measurements of residual thickness have been carried out on 55 points on the part surface (5 replications). 17 points were situated along a section at part center, whereas the other 38 points were spread in significant positions over the part surface (Fig. 20).

Fig. 20

MACARENA rail with measurement points

The mesh chosen for simulation (Fig. 21) is representative of coupling with crash, fatigue or other engineering analyses. It consists of a total of 5321 elements (4034 trias, 1287 quads).

Fig. 21

SIMEX mesh for MACARENA rail

The mesh is divided in three parts, approximatively modeling the forming process:

• A bottom part, sticking to the punch

• A wall part, which flows over the die radius during the forming process

• A blankholder part, subjected to the 32 ton holding force

Flexure conditions are generated along the die entry radius to simulate the flexure cycle.

Figure 22 presents the comparison of the residual thickness along the central line. SIMEX results are shown with respect to experimental measurements. The qualitative comparison is excellent, The peaks of deformation are correctly reproduced as well as the region of low deformation. As for quantitative results, maximum difference between experimental measurement and simulation is 30 μm.

Fig. 22

SIMEX vs. measured thickness of central section

Figure 23 presents the comparison of results on measure points on the part wall. Here too the agreement between measurements and SIMEX prediction is very good, with an average difference of 12 μm and a maximum difference of 50 μm.

Fig. 23

SIMEX vs. measured thickness on part wall

We have also an excellent agreement on the bottom of the part (Fig. 24), thanks to the effective treatment of punch/blank contact with the stick model described above. Average and maximum difference between measurements and SIMEX prediction are respectively 5 and 8 μm.

Fig. 24

SIMEX vs. measured thickness on part bottom

Comparison is less satisfactory on the corner of the part (Figs. 25 and 26). However, we should point out that the average thinning (15%) is the same between measurement and SIMEX prediction. Also, we find a maximum thinning of 20% in both cases. Due to its radial strain hypothesis, SIMEX concentrates the deformation on the corner, whereas in reality the adjacent areas are most strained.

Fig. 25

SIMEX vs. measured thickness on part corner

Fig. 26

Position of measurement points and SIMEX thinning prediction

Conclusions

Material flow over a die radius and the associated cycles of bending and unbending happen on a relatively small scale, with respect to the average element size in one step simulation. We have developed a semi-analytical model for the prediction of the residual strains and stresses in the sections after the die radius and we have implemented it into SIMEX code.

The application of this model has greatly improved the prediction capabilities of the code. On the industrial parts studied, the agreement between numerical results and SIMEX prediction is excellent.