1 Introduction

In this article, we formulate a mathematical model to examine the power expended by a cyclist on a velodrome. The model includes several simplifying assumptions that permit the derivation of closed-form expressions, while nevertheless capturing the mechanical behavior in an empirically adequate manner. The assumptions pertain to both the bicycle-cyclist system and the design of the velodrome track.

For the former, we assume the cyclist to be already in a launched effort, which renders the model adequate for longer events, such as a 4000-metre pursuit or, in particular, the Hour Record. For our analysis, we focus on the average properties of a steady ride, which is tantamount a constant centre-of-mass speed. We distinguish between the centre-of-mass and wheel speeds to decompose the forces that act on various parts of bicycle-cyclist system throughout a given lap. We determine the lean angles by assuming the system is in instantaneous rotational equilibrium, which is tantamount to net zero torque about the axis parallel to the instantaneous velocity through the centre of mass.

For the latter, geometrically, we consider a velodrome with its straights, circular arcs and connecting transition curves, whose inclusion—as indicated by Fitzgerald et al. [8]—has been commonly neglected in previous studies. While this inclusion presents a mathematical challenge, it increases the empirical adequacy of the model. However, we consider that the geometric features of the black line, which is an offset curve at a fixed distance from the inner edge of the track, are adequately represented by a line confined to the horizontal plane. In addition, we assume an idealized wheel path such that the cyclist trajectory is coincident with the black line. By alleviating the computational and modelling requirements that would entail a general wheel-path trajectory on the velodrome, we focus on the phenomenological quantities that affect the bicycle-cyclist system.

Various power models and velodrome geometries have been presented in previous studies. Almost a quarter-of-a-century ago, Martin et al. [11] formulate and examine a road-cycling model. Proceeding with velodrome models, Underwood and Jermy [15, 16] formulate and examine a model for individual pursuits that includes leaning on the bends, but only use straights and bends without transition curves. Lukes et al. [10] model the power of a cyclist on a velodrome, including the tire scrubbing effects. Fitton and Symons [6] present a model that includes slip and steering angles for deviations of the bicycle wheels from the black line, and use velodrome models based on theodolite measurements. Stanoev [14] models a velodrome as a ruled surface and provides technical considerations of its design, but does not present a cyclist model.

Most recently, Fitzgerald et al. [8] quantify the effects of transition curves on a power model consistent with Lukes et al. [10] and Martin et al. [11]. They consider two types of transition curves, namely, a twice-differentiable linear increase in curvature, which is the Euler spiral, and a sinusoid, which exhibits a continuous derivative of curvature. The effects of these curves are estimated using least squares optimization of black-line measurements obtained with theodolite measurements.

We begin this article by expressing mathematically the geometry of both the black line and the inclination of the track. We provide a detailed derivation of the Euler spiral, which appeared in our earlier arXiv article [3] and was referred to by Fitzgerald et al. [8] as the most detailed to date. Also, we derive a Bloss-transition curve, whose curvature is thrice-differentiable. Our expressions are accurate representations of the common geometry of modern 250 -metre velodromes, whose design details were provided by Mehdi Kordi (pers. comm., 2020), who is currently the head coach for the Dutch track sprint team. We proceed to formulate an expression for power used against dissipative forces and power used to increase mechanical energy. In particular, while earlier work considers changes in potential energy as a function of vertical location on a banked velodrome (e.g., Benham et al. [1]) or of the lean angle and the vertical inclination of the trajectory (e.g., Fitton and Symons [6]), we consider—in accordance with the assumption of instantaneous rotational equilibrium—increases in potential energy due solely to straightening of the cyclist upon exiting the curves, with wheels remaining along the black line. We show that a significant amount of power is expended in that process. To present a numerical example and for a comparison with the model of Fitzgerald et al. [8], we examine the case of a constant centre-of-mass speed, which we consider the best mathematical analogy for steadiness of time trial efforts on a velodrome.

2 Track

2.1 Black-line parameterization

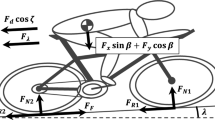
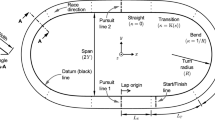
To model the required power of a cyclist who follows the black line, in a constant aerodynamic position, as illustrated in Fig. 1, we define this line by three parameters.

Fig. 1
figure 1

A constant aerodynamic position along the black line

Full size image

  • \(L_s\) : the half-length of the straight

  • \(L_t\) : the length of the transition curve between the straight and the circular arc

  • \(L_a\) : the length of the remainder of the quarter circular arc

The length of the track is \(S=4(L_s+L_t+L_a)\) . In Fig. 2, we show a quarter of a black line for \(L_s=19\) m, \(L_t=13.5\) m and \(L_a=30\) m, which results in \(S=250\) m. Therein, the transition curve is black and connects the straight and circular arc.

Fig. 2
figure 2

A quarter of the black line for a 250 -metre \(C^2\) track

Full size image

This curve has a continuous derivative up to order two; it is a \(C^2\) curve, whose curvature is continuous.

To formulate, in Cartesian coordinates, the curve shown in Fig. 2, we consider the following.

  • The straight,

    $$\begin{aligned} y_1=0,\qquad 0\leq x\leq a, \end{aligned}$$

    shown in gray, where \(a:=L_s\) .

  • The transition, shown in black—following a standard design practice—we take to be an Euler spiral, which can be parameterized by Fresnel integrals,

    $$x_2(\varsigma )= a+\sqrt{\frac{2}{A}}\int \limits _0^{\varsigma \sqrt{\!\frac{A}{2}}} \!\!\!\!\cos \!\left( x^2\right) \,\textrm{d}x \qquad \textrm{and} \qquad y_2(\varsigma )= \sqrt{\frac{2}{A}}\int \limits _0^{\varsigma \sqrt{\!\frac{A}{2}}} \!\!\!\!\sin \!\left( x^2\right) \,\textrm{d}x,$$

    with \(A>0\) to be determined; herein, \(\varsigma\) is the curve parameter. Since the arclength differential, \(\textrm{d}s,\)  is such that

    $$\begin{aligned} \textrm{d}s=\sqrt{x_2'(\varsigma )^2+y_2'(\varsigma )^2}\,\textrm{d}\varsigma =\sqrt{\cos ^2\left( \dfrac{A\varsigma ^2}{2}\right) +\sin ^2\left( \dfrac{A\varsigma ^2}{2}\right) }\,\textrm{d}\varsigma =\textrm{d}\varsigma , \end{aligned}$$

    we write the transition curve as

    $$\begin{aligned} (x_2(s),y_2(s)), \quad 0\leq s\leq b:=L_t. \end{aligned}$$

  • The circular arc, shown in gray, whose centre is \((c_1,c_2)\) and whose radius is R, with \(c_1,\)  \(c_2\) and R to be determined. Since its arclength is specified to be \(c:=L_a,\) we may parameterize the quarter circle by

    $$\begin{aligned} x_3(\theta )=c_1+R\cos (\theta ) \end{aligned}$$
    (1)

    and

    $$\begin{aligned} y_3(\theta )=c_2+R\sin (\theta ), \end{aligned}$$
    (2)

    where \(-\theta _0\leq \theta \leq 0\) , for \(\theta _0:=c/R\) . The centre of the circle is shown as a black dot in Fig. 2.

We wish to connect these three curve segments so that the resulting global curve is continuous along with its first and second derivatives. This ensures that the curvature of the track is also continuous.

To do so, let us consider the connection between the straight and the Euler spiral. Herein, \(x_2(0)=a\) and \(y_2(0)=0\) , so the spiral connects continuously to the end of the straight at (a, 0) . Also, at (a, 0) ,

$$\begin{aligned} \frac{\textrm{d}y}{\textrm{d}x}=\frac{y_2'(0)}{x_2'(0)}=\frac{0}{1}=0, \end{aligned}$$

which matches the derivative of the straight line. Furthermore, the second derivatives match, since

$$\begin{aligned} \frac{\textrm{d}^2y}{\textrm{d}x^2}=\frac{y''_2(0)x_2'(0)-y'_2(0)x_2''(0)}{(x_2'(0))^2}=0, \end{aligned}$$

which follows, for any \(A>0\) , from

$$x_2'(\varsigma )= \cos \left( \dfrac{A\,\varsigma ^2}{2}\right) ,\qquad y_2'(\varsigma )= \sin \left( \dfrac{A\,\varsigma ^2}{2}\right)$$
(3)

and

$$\begin{aligned} x_2''(\varsigma )=-A\,\varsigma \sin \left( \dfrac{A\,\varsigma ^2}{2}\right) , \quad y_2''(\varsigma )=A\,\varsigma \cos \left( \dfrac{A\,\varsigma ^2}{2}\right) . \end{aligned}$$

Let us consider the connection between the Euler spiral and the arc of the circle. In order that these connect continuously,

$$\begin{aligned} \big (x_2(b),y_2(b)\big )=\big (x_3(-\theta _0),y_3(-\theta _0)\big ), \end{aligned}$$

we require

$$\begin{aligned} x_2(b)=c_1+R\cos (\theta _0)\,\,\iff \,\,c_1=x_2(b)-R\cos \!\left( \dfrac{c}{R}\right) \end{aligned}$$
(4)

and

$$\begin{aligned} y_2(b)=c_2-R\sin (\theta _0)\,\,\iff \,\, c_2=y_2(b)+R\sin \!\left( \dfrac{c}{R}\right) . \end{aligned}$$
(5)

For the tangents to connect continuously, we invoke expression (3) to write

$$\begin{aligned} (x_2'(b),y_2'(b))=\left( \cos \left( \dfrac{A\,b^2}{2}\right) ,\,\sin \left( \dfrac{A\,b^2}{2}\right) \right) . \end{aligned}$$

Following expressions (1) and (2), we obtain

$$\begin{aligned} \big (x_3'(-\theta _0),y_3'(-\theta _0)\big )=\big (R\sin (\theta _0),R\cos (\theta _0)\big ), \end{aligned}$$

respectively. Matching the unit tangent vectors results in

$$\cos \left( \dfrac{A\,b^2}{2}\right)= \sin \!\left( \dfrac{c}{R}\right) ,\qquad \sin \left( \dfrac{A\,b^2}{2}\right)= \cos \!\left( \dfrac{c}{R}\right) .$$
(6)

For the second derivative, it is equivalent—and easier—to match the curvature. For the Euler spiral,

$$\kappa _2(s)=\dfrac{x_2'(s)y_2''(s)-y_2'(s)x_2''(s)}{\Big (\big (x_2'(s)\big )^2+\big (y_2'(s)\big )^2\Big )^{\frac{3}{2}}} = A\,s\cos ^2\left( \dfrac{A\,s^2}{2}\right) +A\,s\sin ^2\left( \dfrac{A\,s^2}{2}\right) = A\,s,$$

which is indeed the defining characteristic of an Euler spiral: the curvature grows linearly in the arclength. Hence, to match the curvature of the circle at the connection, we require

$$\begin{aligned} A\,b=\frac{1}{R} \,\,\iff \,\,A=\frac{1}{b\,R}. \end{aligned}$$

Substituting this value of A in Eqs. (6), we obtain

$$\begin{aligned} \cos \!\left( \dfrac{b}{2R}\right)&=\sin \!\left( \dfrac{c}{R}\right) \,,\quad \sin \!\left( \dfrac{b}{2R}\right) =\cos \!\left( \dfrac{c}{R}\right) \\&\iff \dfrac{b}{2R}=\dfrac{\pi }{2}-\dfrac{c}{R}\\&\iff R=\frac{b+2c}{\pi }. \end{aligned}$$

It follows that

$$\begin{aligned} A=\frac{1}{b\,R}=\frac{\pi }{b\,(b+2c)}; \end{aligned}$$

hence, the continuity condition stated in expressions (4) and (5) determines the centre of the circle, \((c_1,c_2)\) .

For the case shown in Fig. 2, the numerical values are \(A=3.1661\times 10^{-3}\) m\({}^{-2}\), \(R=23.3958\) m , \(c_1=25.7313\) m and \(c_2=23.7194\) m . The complete track—with its centre at the origin , (0, 0)—is shown in Fig. 3.

Fig. 3
figure 3

Black line of 250 -metre \(C^2\) track

Full size image

The corresponding track curvature is shown in Fig. 4. Note that the curvature transitions linearly from the constant value of straight, \(\kappa =0\) , to the constant value of the circular arc, \(\kappa =1/R\) .

Fig. 4
figure 4

Curvature of the black line, \(\kappa\) , as a function of distance, s , with a linear transition between the zero curvature of the straight and the 1/R curvature of the circular arc

Full size image

2.2 \(C^3\) transition curve

As stated by [8],

[t]here can be a trade-off between good spatial fit (low continuity for matching a built velodrome) and a good physical fit (high continuity for matching a cyclist’s path). If this model is used to calculate the motion of cyclists on a velodrome surface then a spatial fit can be prioritised. However, if it is used to directly model the path of a cyclist then higher continuity is required.

Should it be desired that the trajectory have continuous derivatives up to order \(r\geqslant 0\)—which makes it in class \(C^r\) , so that its curvature is of class \(C^{r-2}\)—it is possible to achieve this by a transition curve \(y=p(x)\) , where p(x) is a polynomial of degree \(2r-1\) and the solution of a \(4\times 4\) system of nonlinear equations, assuming a solution exists.

In case \(r=2\) , this would correspond to a transition by a polynomial of degree \(2r-1=3\) , often referred to as a cubic spiral. In case \(r=3\) , this would correspond to a transition by a polynomial of degree \(2r-1=5\) , often referred to as a Bloss transition.

The motivation for a \(C^3\) transition curve is to increase the smoothness of the black line, which we assume to coincide with the wheel-path trajectory. The increased continuity increases the smoothness of the calculated power values at discretized points along the black line, as discussed in Sect. 5. While the following derivation demonstrates the procedure to obtain the Bloss transition curve, the approach can be used more generally to obtain curves of even higher continuity, should it be warranted from a modelling perspective.

To see how to do this, for simplicity’s sake, let \(a=L_s\) . We use a Cartesian formulation, namely,

  • \(y=0,\) \(0\leqslant x\leqslant a\) : the half straight

  • \(y=p(x),\) \(a\leqslant x\leqslant X\) : the transition curve between the straight and circular arc

  • \(y=c_2-\sqrt{R^2-(x-c_1)^2}\) : the end circle, with centre at \((c_1,c_2)\) and radius R.

Here \(x=X\) is the point at which the polynomial transition connects to the circle \((x-c_1)^2+(y-c_2)^2=R^2\) .

X , \(c_1\) , \(c_2\) and R are a priori unknowns that need to be determined. These four values determine completely the transition zone, \(y=p(x),\) \(a\leqslant x\leqslant X\) .

Given X , \(c_1\) , \(c_2\) and R , we can compute p(x) as the Lagrange–Hermite interpolant of the data

$$\begin{aligned} p^{(j)}(a)=0,\quad 0\leqslant j\leqslant r,\,\,\hbox {and}\,\, p^{(j)}(X)=y^{(j)}(X),\quad 0\leqslant j\leqslant r, \end{aligned}$$

where \(y(x)=c_2-\sqrt{R^2-(x-c_1)^2}\) is the circle. Indeed, this is given in Newton form as

$$\begin{aligned} p(x)=\sum _{j=0}^{2r+1} p[x_0,\cdots ,x_j]\prod _{k=0}^{j-1}(x-x_k), \end{aligned}$$

with

$$\begin{aligned} x_0=x_1=\cdots =x_r=a\,\,\hbox {and},\,\, x_{r+1}=\cdots =x_{2r+1}=X \end{aligned}$$

and, for any values \(t_1,t_2,\cdots ,t_m\) , the divided difference ,

$$\begin{aligned} p[t_1,t_2,\cdots ,t_m], \end{aligned}$$

may be computed from the recurrence

$$\begin{aligned} p[t_1,\cdots ,t_m]=\frac{p[t_2,\cdots .t_m]-p[t_1,\cdots ,t_{m-1}]}{t_m-t_1}, \end{aligned}$$

with

$$\begin{aligned} p\underbrace{[a,\cdots ,a]}_{\textrm{multiplicity}\,\,j+1}:=0,\,\, 0\leqslant j\leqslant r \end{aligned}$$

and

$$\begin{aligned} p\underbrace{[X,\cdots ,X]}_{\textrm{multiplicity}\,\,j+1}:=\frac{y^{(j)}(X)}{j!},\,\, 0\leqslant j\leqslant r, \end{aligned}$$

where again \(y(x)=c_2-\sqrt{R^2-(x-c_1)^2}\) is the circle.

Note, however, that this defines p(x) as a polynomial of degree \(2r+1\) exceeding our claimed degree \(2r-1\) by 2. Hence, the first two of our equations are that p(x) is actually of degree \(2r-1\) , i.e., its two leading coefficients are zero. More specifically, from the Newton form,

$$\begin{aligned} p[\,\underbrace{a,a,\cdots ,a}_{r+1\,\,\textrm{copies}},\underbrace{X,X,\cdots ,X}_{r+1\,\,\textrm{copies}}\,]=0 \end{aligned}$$
(7)

and

$$\begin{aligned} p[\,\underbrace{a,a,\cdots ,a}_{r+1\,\,\textrm{copies}},\underbrace{X,X,\cdots ,X}_{r\,\,\textrm{copies}}\,]=0. \end{aligned}$$
(8)

The third equation is that the length of the transition is specified to be \(L_t\) , i.e.,

$$\begin{aligned} \int \limits _a^X \sqrt{1+\left( p'(x)\right) ^2}\,\textrm{d}x=L_t. \end{aligned}$$
(9)

Note that this integral has to be estimated numerically.

Finally, the fourth equation is that the remainder of the circular arc—from \(x=X\) to the apex \(x=c_1+R\)—have length \(L_a\) . This is equally accomplished. The two endpoints of the circular arc are (X, y(X)) and \((c_1+R,c_2)\) giving a circular segment of angle \(\theta\) , say, between the two vectors connecting these points to the centre, i.e., \(\langle X-c_1,y(X)-c_2\rangle\) and \(\langle R,0\rangle\) . Then,

$$\begin{aligned} \cos (\theta )=\frac{\langle X-c_1,y(X)-c_2\rangle \,\cdot \,\langle R,0\rangle }{\Vert \langle X-c_1,y(X)-c_2\rangle \Vert _2 \Vert \langle R,0\rangle \Vert _2}=\frac{X-c_1}{R}. \end{aligned}$$

Hence the fourth equation is

$$\begin{aligned} R\,\cos ^{-1}\left( \dfrac{X-c_1}{R}\right) =L_a. \end{aligned}$$
(10)

Together, Eqs. (7), (8), (9) and (10) form a system of four nonlinear equations in four unknowns, \(c_1\) , \(c_2\) , R and X , determining a \(C^r\) transition given by p(x) , a polynomial of degree \(2r-1\) , satisfying the design parameters.

Fig. 5
figure 5

Transition zone track curvature, \(\kappa\) , as a function of distance, s , which—in contrast to Fig. 4—exhibits a smooth (\(C^1\)) transition between the zero curvature of the straight and the 1/R curvature of the circular arc

Full size image

For the velodrome under consideration, and a Bloss \(C^3\) transition, with curvature \(C^1\) , we obtain \(c_1=25.7565\,\textrm{m}\) , \(c_2=23.5753\,\textrm{m}\) , \(R = 23.3863\,\textrm{m}\) and \(X =32.3988\, \textrm{m}\) , which—as expected—are similar to values obtained in Sect. 2.1. The corresponding trajectory curvature is shown in Fig. 5.

Returning to the quote given on page 7, at the beginning of Sect. 2.2, the requirement of differentiability of the trajectory traced by bicycle wheels, which is expressed in spatial coordinates, is a consequence of a dynamic behaviour, which is expressed in temporal coordinates, namely, the requirement of smoothness of the derivative of acceleration, which is commonly referred to as a jerk or jolt. In other words, a natural motion of the bicycle-cyclist system, which is laterally unconstrained, ensures that the third temporal derivative of position is smooth.

2.3 Track-inclination angle

Fig. 6
figure 6

Track inclination, \(\theta\) , as a function of the black-line distance, s

Full size image

There are many possibilities to model the track inclination angle. We choose a trigonometric formula in terms of arclength, which is a good analogy of an actual 250 -metre velodrome. The minimum inclination of \(13^\circ\) corresponds to the midpoint of the straight, and the maximum of \(44^\circ\) to the apex of the circular arc. For a track of length S ,

$$\begin{aligned} \theta (s)=28.5-15.5\cos \!\left( \frac{4\pi }{S}s\right) ; \end{aligned}$$
(11)

\(s=0\) refers to the midpoint of the lower straight, in Fig. 3, and the track is oriented in the counterclockwise direction. Figure 6 shows this inclination for \(S=250\,\textrm{m}\) .

It is not uncommon for tracks to be slightly asymmetric with respect to the inclination angle. In such a case, they exhibit a rotational symmetry by \(\pi\)  but not a reflection symmetry about the vertical or horizontal axis. This asymmetry can be modeled by including \(s_0\) in the argument of the cosine in expression (11).

$$\begin{aligned} \theta (s)=28.5-15.5\cos \!\left( \frac{4\pi }{S}(s-s_0)\right) ; \end{aligned}$$
(12)

\(s_0\approx 5\) provides a good model for several existing velodromes. Referring to discussions about the London Velodrome of the 2012 Olympics, Solarczyk [13] writes that

the slope of the track going into and out of the turns is not the same. This is simply because you always cycle the same way around the track, and you go shallower into the turn and steeper out of it.

The last statement is not obvious. For a constant centre-of-mass speed, under rotational equilibrium, the same transition curves along the black line imply the same lean angle.

3 Dissipative forces

A mathematical model to account for the power required to propel a bicycle against dissipative forces is based on

$$\begin{aligned} P_F=F\,V, \end{aligned}$$
(13)

where F stands for the magnitude of forces opposing the motion and V for speed. Herein, we model the bicycle-cyclist system as undergoing instantaneous circular motion in a horizontal plane, in rotational equilibrium about the instantaneous centre-of-mass velocity, \({\varvec{V}}\). While this model involves several simplifying assumptions, it nevertheless captures the mechanical behaviour of the system, while allowing us to derive closed-form expressions. Specifically, the assumption of instantaneous circular motion allows us to model motion along a black line of arbitrary geometry in terms of a radius of curvature that is varying from point to point. The assumption of this circular motion occurring in a horizontal plane, while clearly not strictly valid (since the centre of mass moves first down and then up as the cyclist enters and exits a turn, respectively), is nevertheless an excellent description of a motion whose horizontal displacements have much larger magnitudes than vertical displacements. Similarly, the assumption of rotational equilibrium about the instantaneous centre-of-mass velocity, \({\varvec{V}}\), is also not strictly valid, since as the cyclist enters and exits a turn, the lean angle first increases, reaches a maximum, and then decreases, respectively. However, this approximation successfully captures the mechanical behaviour of the system, specifically the changing lean of the cyclist, for lap-averaged considerations, while again allowing us to derive closed-form expressions. In view of Fig. 7, along the black line, in windless conditions,

$$\begin{aligned}&P_F\nonumber \\&\quad =\dfrac{1}{1-\lambda }\,\,\Bigg \{ \end{aligned}$$
(14a)
$$\begin{aligned}&\quad \Bigg ({\textrm{C}_{\textrm{rr}}}\underbrace{\overbrace{\,m\,g\,}^{F_g}(\sin \theta \tan \vartheta +\cos \theta )}_N\cos \theta +{\textrm{C}_{\textrm{sr}}}\Bigg |\underbrace{\overbrace{\,m\,g\,}^{F_g}\frac{\sin (\theta -\vartheta )}{\cos \vartheta }}_{F_f}\Bigg |\sin \theta \Bigg )\,v \end{aligned}$$
(14b)
$$\begin{aligned}&\quad +\,\,\tfrac{1}{2}\,{\textrm{C}_{\textrm{d}}\text {A}}\,\rho \,V^3\Bigg \}\,, \end{aligned}$$
(14c)

where m is the mass of the cyclist and the bicycle, g is the acceleration due to gravity, \(\theta\) is the track-inclination angle, \(\vartheta\) is the bicycle-cyclist lean angle, \(\textrm{C}_{\textrm{rr}}\) is the rolling-resistance coefficient, \(\textrm{C}_{\textrm{sr}}\) is the coefficient of the lateral friction, \(\textrm{C}_\mathrm{d}\mathrm{A}\) is the air-resistance coefficient, \(\rho\) is the air density, \(\lambda\) is the drivetrain-resistance coefficient. Herein, v is the speed at which the points on the track, where the rotating wheels contact it, move along the track. The speed v is assumed to coincide with the black-line speed. The wheels are assumed to roll without slipping, so that v is also the tangential speed of a point on the circumference of a wheel with respect to the axle. V is the centre-of-mass speed. Since lateral friction is a dissipative force, it does negative work, and the work done against it—as well as the power—are positive. For this reason, in expression (14b), we consider the magnitude, \(\big |{\,\,}\big |\) .

Fig. 7
figure 7

Force diagram for the bicycle-cyclist system in the plane perpendicular to the centre-of-mass velocity, \({\varvec{V}}\). Shown are the forces acting on the system in that plane and, as a dotted arrow, their resultant, the centripetal force, \(\textbf{F}_{cp}\)

Full size image

To formulate summand (14b), we use the relations among the magnitudes of vectors \(\textbf{N}\) , \(\textbf{F}_g\) , \(\textbf{F}_{cp}\) and \(\textbf{F}_f\) , illustrated in Fig. 7. In accordance with Newton’s second law, for a cyclist to maintain a horizontal trajectory, the resultant of all vertical forces must be zero,

$$\begin{aligned} \sum F_y=0=N\cos \theta +F_f\sin \theta -F_g . \end{aligned}$$
(15)

In other words, \(\textbf{F}_g\) must be balanced by the sum of the vertical components of normal force, \(\textbf{N}\) , and the friction force, \(\textbf{F}_f\) , which is parallel to the velodrome surface and perpendicular to the instantaneous velocity. Depending on the centre-of-mass speed and the radius of curvature for the centre-of-mass trajectory, if \(\vartheta <\theta\) , \(\textbf{F}_f\) points upwards, in Fig. 7, which corresponds to its pointing outwards, on the velodrome; if \(\vartheta >\theta\) , it points downwards and inwards. If \(\vartheta =\theta\) , \(\textbf{F}_f=\textbf{0}\) . Since we assume no lateral motion, \(\textbf{F}_f\) accounts for the force that prevents it. Heuristically, it can be conceptualized as the force exerted in a lateral deformation of the tires.

For a cyclist to follow the curved bank, the resultant of the horizontal forces,

$$\begin{aligned} \sum F_x=-N\sin \theta +F_f\cos \theta =-F_{cp} , \end{aligned}$$
(16)

is the centripetal force, \(\textbf{F}_{cp}\) , whose direction is perpendicular to the direction of motion and points towards the centre of the radius of curvature. According to the rotational equilibrium about the centre of mass,

$$\begin{aligned} \sum \tau _z=0=F_f\,h\,\cos \left( \theta -\vartheta \right) -N\,h\,\sin (\theta -\vartheta ), \end{aligned}$$
(17)

where \(\tau _z\) is the torque about the axis parallel to the instantaneous centre-of-mass velocity and h is the upright height of the centre of mass of the bicycle-cyclist system. This condition implies

$$\begin{aligned} F_f=N\tan (\theta -\vartheta ). \end{aligned}$$
(18)

Substituting expression (18) in expression (15), we obtain

$$\begin{aligned} N=\dfrac{m\,g}{\cos \theta + \tan (\theta -\vartheta )\sin \theta } =m\,g\,(\sin \theta \tan \vartheta +\cos \theta ) . \end{aligned}$$
(19)

Using this result in expression (18), we obtain

$$\begin{aligned} F_f=m\,g\,(\sin \theta \tan \vartheta +\cos \theta )\tan (\theta -\vartheta ) =m\,g\,\dfrac{\sin (\theta -\vartheta )}{\cos \vartheta }. \end{aligned}$$
(20)

We restrict our study to steady efforts, which—following the initial acceleration—are consistent with a pace of an individual pursuit or the Hour Record. Steadiness of effort is an important consideration in the context of measurements within a fixed-wheel drivetrain, as discussed by Danek et al. [4, Section 5.2]. For road-cycling models [e.g., [4], expression (1)]—where curves are neglected so that acceleration has no centripetal component and there is no need to distinguish between the wheel speed and the centre-of-mass speed—such a restriction would correspond to setting the acceleration, a , to zero. On a velodrome, where on the curves acceleration also has a centripetal component, this is tantamount to a constant centre-of-mass speed, \(\textrm{d}V/\textrm{d}t=0\) .

Let us return to expression (14). Therein, \(\theta\) is given by expression (11). The lean angle is

$$\begin{aligned} \vartheta =\arctan \dfrac{V^2}{g\,r_\mathrm{\scriptscriptstyle CoM}}, \end{aligned}$$
(21)

where \(r_\mathrm{\scriptscriptstyle CoM}\) is the centre-of-mass radius, and—along the curves, at any instant—the centre-of-mass speed is

$$\begin{aligned} V=v\,\dfrac{\overbrace{(R-h\sin \vartheta )}^{\displaystyle r_\mathrm{\scriptscriptstyle CoM}}}{R} =v\,\left( 1-\dfrac{h\,\sin \vartheta }{R}\right) , \end{aligned}$$
(22)

where R is the radius discussed in Sect. 2.1. Along the straights, the black-line speed is equal to the centre-of-mass speed, \(v=V\) . As expected, \(V=v\) if \(h=0\) , \(\vartheta =0\) or \(R=\infty\) . The lean angle , \(\vartheta\) , is determined by assuming that, at all times, the system is in rotational equilibrium about the line of contact of the tires with the ground; this assumption yields the implicit condition on \(\vartheta\) , stated in expression (21).

As illustrated in Fig. 7, expressions (21) and (22) assume instantaneous circular motion of the centre of mass to occur in a horizontal plane. Therefore, using this expression implies neglecting the vertical motion of the centre of mass. Accounting for the vertical motion of the centre of mass would mean allowing for a nonhorizontal centripetal force, and including the work done in raising the centre of mass.

In our model, we also neglect the effect of air resistance of rotating wheels (e.g., [4], Sect. 5.5). We consider only the air resistance due to the translational motion of the bicycle-cyclist system. Also, in view of a steady ride and the quantification of average properties per lap, we assume \(\mathrm {C_dA}\) is constant value, which differs from one cyclist to another but does not vary significantly from small variations from common pursuit speed or track position.

4 Conservative forces

4.1 Mechanical energy

Commonly, in road-cycling models (e.g., [4], expression (1)), we include \(m\,g\sin \varTheta\) , where \(\varTheta\) corresponds to a slope; this term represents force due to changes in potential energy associated with hills. This term is not included in expression (14). However—even though a black line of a velodrome is horizontal—we need to account for the power required to increase potential energy to raise the centre of mass upon exiting the curves.

In Sect. 3, we assume the cyclist’s centre of mass to travel in a horizontal plane—an approximation, since in actuality it follows a three-dimensional trajectory, lowering while entering a turn and rising while exiting it. However, the horizontal component of the centre-of-mass velocity, corresponding to the cyclist’s forward motion, is much larger than the vertical component, corresponding to the up and down motion of the centre of mass. Therefore, we can neglect the vertical motion when calculating the power expended against air resistance, which is proportional to the cube of the centre-of-mass speed, V . On the other hand, we cannot neglect the vertical motion of the centre of mass when calculating the changes in the cyclist’s potential energy along the transition curves. In Sect. 4.2, below, we calculate these changes using the changes in the lean angle, whose values are obtained from the assumption of instantaneous rotational equilibrium.

Since dissipative forces, discussed in Sect. 3, are nonconservative, the average power expended against them depends on the details of the path traveled by the cyclist, not just on its endpoints. For this reason, to calculate the average power expended against dissipative forces, we require a detailed model of the cyclist’s path to calculate the instantaneous power. Instantaneous power is averaged to obtain the average power expended against dissipative forces over a lap. This is not the case for calculating the average power needed to increase the cyclist’s mechanical energy. Provided this increase is monotonic, the change in mechanical energy—and therefore the average power—does not depend on the details of the path traveled by the cyclist, but only on its endpoints. In brief, the path dependence of work against dissipative forces requires us to examine instantaneous motion to calculate the associated average power, but the path independence of work to change mechanical energy makes the associated average power independent of such an examination.

4.2 Potential energy

Let us determine the work—and, hence, average power, per lap—performed by a cyclist to change the potential energy,

$$\begin{aligned} U = m\,g\,h\,\cos \vartheta . \end{aligned}$$

Since we assume a model in which the cyclist is instantaneously in rotational equilibrium about the black line, only the increase of the centre-of-mass height is relevant for calculating the increase in potential energy, and so for obtaining the average power required for the increase. Since the lean angle, \(\vartheta\) , depends on the centre-of-mass speed, V , as well as on the radius of curvature, R , of the black line, \(\vartheta\)—and therefore the height of the centre of mass—changes if either V or R changes. The work done is the increase in potential energy resulting from a monotonic decrease in the lean angle from \(\vartheta _1\) to \(\vartheta _2\) ,

$$\begin{aligned} \varDelta U = m\,g\,h\,\left( \cos \vartheta _2-\cos \vartheta _1\right) . \end{aligned}$$

In the case of a constant centre-of-mass speed, as well as of constant black-line speed,

$$\begin{aligned} \varDelta U = 2\,m\,g\,h\,\left( \cos \vartheta _2-\cos \vartheta _1\right) , \end{aligned}$$

since—in either case—the bicycle-cyclist system straightens twice per lap, upon exiting a curve. The average power required for this increase of potential energy is

$$\begin{aligned} P_U=\dfrac{1}{1-\lambda }\dfrac{\varDelta U}{t_\circlearrowleft }. \end{aligned}$$
(23)

As discussed in Sect. 4.1, we neglect the vertical motion of the centre of mass to calculate the power expended against dissipative forces. However, this approximation does not capture the changes in the cyclist’s potential energy along the transition curves. Instead, we calculate these changes starting from the assumption of instantaneous rotational equilibrium and the resulting decrease in the lean angle while exiting a turn. The work to increase potential energy is ultimately done by the cyclist through pedaling. Therefore, it is subject to the same drivetrain losses as the work done against dissipative forces (and, in cases involving a changing centre-of-mass speed, to increase kinetic energy); hence, the presence of \(\lambda\) in expression (23).

Returning to the first paragraph of Sect. 4.1, we note that the changes in potential energy discussed here are different from the changes associated with hills. When climbing a hill, a cyclist does work to increase potential energy. When descending, a portion of that energy may be converted into kinetic energy of forward motion. However, this is not the case for a cyclist straightening up when coming out of a turn. For example, in the case of constant centre-of-mass speed, as the cyclist straightens, potential energy increases while kinetic energy remains constant. (In the case of constant black-line speed, as the cyclist straightens, both potential and kinetic energies increase.) In neither case is there conversion of one form of energy into another. Instead, the rider performs work to increase mechanical energy.

Similarly, a cyclist leaning into a turn at a constant centre-of-mass speed, potential energy decreases while kinetic energy of forward motion remains constant, again meaning one cannot be converted into the other. In this case, there may be some conversion of potential energy into kinetic energy of rotation about the line of contact of the wheels with the ground. However, the fact that the lean angle remains constant on the circular arc portion of a turn means rotational kinetic energy is zero there, and is not available for conversion into potential energy when exiting the turn. In summary, the presence of dissipative forces means the bicycle-cyclist system is not conservative, and the mechanical energy of the system is not constant.

Finally, we neglect the rotational kinetic energy of the wheels. For a cyclist traveling with constant centre-of-mass speed, the black-line speed and therefore the wheel speed increase when entering a turn and decrease when exiting it. However, the resulting changes in rotational energy are much smaller than the changes in potential energy due to the lowering and raising of the centre of mass. Specifically, using the values of the relevant parameters assumed in Sect. 6 and assuming disk wheels with a mass of \(0.900\,\textrm{kg}\) each, the magnitudes of the changes in rotational and potential energy on the transitions curves are \(7.9\,\textrm{J}\) and \(337\,\textrm{J}\), respectively. The changes in rotational energy are nearly two orders of magnitude smaller than the changes in potential energy, justifying neglecting the former.

5 Constant centre-of-mass speed

In accordance with expression (14), let us find the values of P at discrete points of the black line , under the assumption of a constant centre-of-mass speed, V . Stating expression (22), as

$$\begin{aligned} v=V\dfrac{R}{R-h\sin \vartheta }, \end{aligned}$$

we write expression (14) as

$$\begin{aligned}&P_F=\nonumber \\&\quad \dfrac{V}{1-\lambda }\,\,\Bigg \{ \\&\quad\Bigg ({\textrm{C}_{\textrm{rr}}}\,m\,g\,(\sin \theta \tan \vartheta +\cos \theta )\cos \theta \nonumber +{\textrm{C}_{\textrm{sr}}}\Bigg |\,m\,g\,\frac{\sin (\theta -\vartheta )}{\cos \vartheta }\Bigg |\sin \theta \Bigg )\,\dfrac{R}{R-h\sin \vartheta } \nonumber \\&\quad +\,\,\tfrac{1}{2}\,{\textrm{C}_{\textrm{d}}\text {A}}\,\rho \,V^2\Bigg \}\,. \end{aligned}$$
(24)

Equation (21), namely,

$$\begin{aligned} \vartheta =\arctan \dfrac{V^2}{g\,(R-h\sin \vartheta )}, \end{aligned}$$

can be solved for \(\vartheta\)—to be used in expression (24)—given V , g , R , h ; along the straights, \(R=\infty\) and, hence, \(\vartheta =0\) ; along the circular arcs, R is constant, and so is \(\vartheta\) ; along transition curves, the radius of curvature changes monotonically, and so does \(\vartheta\) . Along these curves, the radii are given by solutions of equations discussed in Sect. 2.1 or in Sect. 2.2.

The values of \(\theta\) are given—at discrete points—from expression (11), namely,

$$\begin{aligned} \theta (s)=28.5-15.5\cos \!\left( \frac{4\pi }{S}s\right) . \end{aligned}$$

The values of the bicycle-cyclist system, h , m , \(\mathrm{C_{d}A}\), \(\mathrm{C_{rr}}\), \(\mathrm{C_{sr}}\) and \(\lambda\) , are provided, and so are the external conditions, g and \(\rho\) .

Under the assumption of a constant centre-of-mass speed, V , there is no power used to increase the kinetic energy, only the power, \(P_U\) , used to increase the potential energy. The latter is obtained by expression (23), where the pertinent values of \(\vartheta\) for that expression are taken from model (24).

6 Numerical example

To examine the model, including the effects of modifications in its input parameters, let us consider the following values. An Hour Record of \(57500\,\textrm{m}\) , which corresponds to an average laptime of \(15.6522\,\textrm{s}\) and the average black-line speed of \(v=15.9776\,\mathrm{m/s}\) . A bicycle-cyclist mass of \(m=90\,\textrm{kg}\), a surrounding temperature of \(T=27^\circ \textrm{C}\) , altitude of \(105\,\textrm{m}\) , which correspond to Montichiari, Brescia, Italy; hence, acceleration due to gravity of \(g=9.8063\,\mathrm{m/s}^2\), air density of \(\rho =1.1618\,\mathrm{kg/m}^3\) . Note that the latter two quantities are calculated using the normal-gravity formula with the free-air correction [9, Sects. 2.4.4 and 2.5.4.4] and the ideal gas law with atmospheric pressure as a function of altitude [2, Sect. 2.2]. Let us assume \(h=1.2\,\textrm{m}\) along with typical coefficient values of \({\textrm{C}_\textrm{d}\textrm{A}}=0.19\,\textrm{m}^2\) [7, Table 2], \({\textrm{C}_{\textrm{rr}}}=0.0015\) and \({\mathrm{\mathrm C}_{\textrm{sr}}}=0.0025\) [12, Table 1] , and \(\lambda =0.015\) [10, p. 147] .

The required average power—under the assumption of a constant centre-of-mass speed—is \(P=499.6979\,{\textrm{W}}\) , which is the sum of \(P_F=454.4068\,{\textrm{W}}\) and \(P_U=45.2911\,{\textrm{W}}\) ; \(90.9\%\) of power is used to overcome dissipative forces and \(9.1\%\) to increase potential energy by raising the centre of mass, as discussed in Sect. 4.2. The corresponding centre-of-mass speed is \(V=15.6269\,\mathrm{m/s}\) . During each lap, the power, P , varies by \(3.1\%\) and the black-line speed, v , by \(3.9\%\) , which agrees with empirical results for steady efforts.

Also, during each lap, the lean angle varies, \(\vartheta \in [\,0^\circ ,47.9067^\circ \,]\)  and hence, for each curve, the centre of mass is raised by \(1.2\,(\cos (0^\circ )-\cos (47.9067^\circ ))=0.3956\,\textrm{m}\) . For this Hour Record, which corresponds to 230 laps, the centre of mass is raised by \(2(230)(0.3956\,\textrm{m})=181.9760\,\textrm{m}\) in total.

To gain an insight into the stability of the model, let us consider slight variations in the input values, namely, \(m=90\pm 1\,\textrm{kg}\), \(T=27\pm 1^\circ \textrm{C}\), \(h=1.20\pm 0.05\,\textrm{m}\), \({\textrm{C}_\textrm{d}\textrm{A}}=0.19\pm 0.01\,{\textrm{m}^2}\), \({\textrm{C}_{\textrm{rr}}}=0.0015\pm 0.0005\), \({\textrm{C}_{\textrm{sr}}}=0.0025\pm 0.0005\) and \(\lambda =0.015\pm 0.005\) . For the limits that diminish the required power—which are all lower limits, except for T—we obtain \(P=463.6691\,{\textrm{W}}\) . For the limits that increase the required power—which are all upper limits, except for T—we obtain \(P=536.3512\,{\textrm{W}}\) . The greatest effect is due to \({\textrm{C}_\textrm{d}\textrm{A}}=0.19\pm 0.01\,{\textrm{m}^2}\). If we consider this variation only, we obtain \(P=477.1924\,{\textrm{W}}\) and \(P=522.2033\,{\textrm{W}}\) , respectively. In other words, a \(5.3\%\) change in \({\textrm{C}_\textrm{dA}}\) results in a \(4.5\%\) change in total power.

To gain an insight into the effect of different input values on the required power, let us consider several modifications to the Hour Record distance, environmental conditions—such as altitude and temperature, which are known to affect cycling performance [5, e.g.,]—and cyclist parameters. Such modifications allow us to evaluate the relative importance of various quantities in optimizing the performance for a desired result.


Hour Record: Let the only modification be the reduction of Hour Record to \(55100\,\textrm{m}\). The required average power reduces to \(P=440.9534\,{\textrm{W}}\). Thus, reducing the Hour Record by \(4.2\%\) reduces the required power by \(11.8\%\) . However, since the relation between power and speed is nonlinear, this ratio is not the same for other values, even though—in general—for a given an increase in speed, the proportional increase of the corresponding power is greater (e.g., [4], Section 4, Figure 11).


Altitude: Let the only modification be the increase of altitude to \(2600\,\textrm{m}\)  which corresponds to Cochabamba, Bolivia. The corresponding adjustments are \(g=9.7769\,\mathrm{m/s}^2\) and \(\rho =0.8754\,\mathrm{kg/m}^3\) ; hence, the required average power reduces to \(P=394.2511\,{\textrm{W}}\), which is a reduction by \(21.1\%\).


Temperature: Let the only modification be the reduction of temperature to \(T=20^\circ \textrm{C}\) . The corresponding adjustment is \(\rho =1.1892\,\mathrm{kg/m}^3\) ; hence, the required average power increases to \(P=509.7835\,{\textrm{W}}\) .


Mass: Let the only modification be the reduction of mass to \(m=85\,\textrm{kg}\) . The required average power reduces to \(P=495.6926\,{\textrm{W}}\) , which is the sum of \(P_F+P_U=452.9177\,{{\textrm{W}}} + 42.7749\,{{\textrm{W}}}\) . The reduction of m by \(5.6\%\) reduces the required power by \(0.8\%\), which is manifested in reductions of \(P_F\) and \(P_U\) by \(0.3\%\) and \(5.6\%\) , respectively. In accordance with a formulation in Sect. 4.2, the reductions of m and \(P_U\) are equal to one another.


Centre-of-mass height: Let the only modification be the reduction of the centre-of-mass height to \(h=1.1\,\textrm{m}\)Ṫhe corresponding adjustments are \(P_F=456.7678\,{\textrm{W}}\) , \(P_U=41.5346\,{\textrm{W}}\) and \(V=15.6556\,\mathrm{m/s}\) ; hence, the required average power decreases to \(P=498.3023\,{\textrm{W}}\) , which reduces the required power by 0.3% ; this reduction is a consequence of relations among \(P_F\), \(P_U\) , V and \(\vartheta\) .

\(\textrm{C}_\textrm{d}\textrm{A}\) : Let the only modification be the reduction of the air-resistance coefficient to \({\textrm{C}_\textrm{dA}}=0.17\,\textrm{m}^2\) . The required average power reduces to \(P=454.6870\,{\textrm{W}}\) , which is the sum of \(P_F+P_U=409.3959\,{{\textrm{W}}} + 45.2911\,{{\textrm{W}}}\) . The reduction of \(\textrm{C}_\textrm{d}\textrm{A}\) by \(10.5\%\) reduces the required power by \(9.0\%\), \(P_F\) by \(9.9\%\) and no reduction in \(P_U\) .


Mass and \(\textrm{C}_\textrm{d}\textrm{A}\) : Let the two modifications be \(m=85\,\textrm{kg}\) and \({\textrm{C}_\textrm{d}\textrm{A}} = 0.17\,\textrm{m}^2\). The required average power is \(P=450.6817\,{\textrm{W}}\), which is the sum of \(P_F+P_U=407.9068\,{{\textrm{W}}} + 42.7749\,{{\textrm{W}}}\). The reduction in required average power is the sum of reductions due to decreases of m and \({\textrm{C}_\textrm{d}\textrm{A}}\)  \(4.0\,{{\textrm{W}}}+45.0\,{{\textrm{W}}}=49.0\,{{\textrm{W}}}\) . In other words, The two modifications reduce the required power by \(9.8\%\)  wherein \(P_F\) and \(P_U\) are reduced by \(10.2\%\) and \(5.6\%\) , respectively.


Track-inclination asymmetry: Let the only modification be \(s_0=5\) , in expression (12). The required average power is \(P=499.7391\,{\textrm{W}}\) , which is a reduction of less than 0.01% .

Euler spiral: Let the only modification be the \(C^2\) , as opposed to \(C^3\) , transition curve. The required average power is \(P=499.7962\,{\textrm{W}}\) , which is a reduction of less than 0.01% .

7 Comparison to Fitzgerald et al. [8]

Let us compare model (14) to Fitzgerald et al. [8, expression (24)], which—expressed in our notation—is

$$\begin{aligned} P_F'&= \frac{1}{1-\lambda }\,\,\Bigg \{\tfrac{1}{2}\,{\textrm{C}_\textrm{d}\textrm{A}}\,\rho V^3\nonumber \\&\quad +\left( {\textrm{C}_{\textrm{rr}}}\,m\,g\,\frac{\cos (\vartheta -\theta )}{\cos \vartheta }+ {\textrm{C}_{\textrm{rr}}}\, \mu _\textrm{s}\,m\,g\,\frac{\cos (\vartheta -\theta )}{\cos \vartheta }\,|\vartheta -\theta |\right) v\Bigg \}; \end{aligned}$$
(25)

it omits changes in potential and kinetic energy, but encompasses the dominant resistive forces for steady riding. Model (25) differs from model (14) by using \(\mu _\textrm{s}\) , which is a scrubbing resistance (e.g., Lukes et al. [10]) associated with the assumption of a slight shifting of the handlebars to avoid lateral slipping along the banked track, as opposed to \(\textrm{C}_{\textrm{sr}}\) , the coefficient of lateral friction. Both models assume that the bicycle-cyclist system follows the black line. Notably, the same restriction is made by Fitton and Symons [6] to validate their model, even though their initial formulation includes deviations of the wheels from that line.

For the comparison, we use input parameters specified by Fitzgerald et al. [8, Sect. 3]. For the cyclist, \(h=1\) m, \(m=75\) kg, \({\textrm{C}_\textrm{d}\textrm{A}} = 0.2\,\textrm{m}^2\), \(\textrm{C}_{\textrm{rr}}=0.002\), \(\mu _\textrm{s} = 0.4125/\)rad, \(\lambda =0.02\). For the environmental conditions, \(g=9.81\,\mathrm{m/s}^2\), \(\rho = 1.2\,\mathrm{kg/m}^3\). For the velodrome, the length of the track is \(S=250\) m, the turn radius is \(R=23.1950\) m, the length of the transition is \(b=24.9\) m, and the bank angle [8, eq. (19)] is

$$\begin{aligned} \theta (s) = \left( \frac{\theta _\textrm{max}-\theta _\textrm{min}}{2}\right) \sin \left( \frac{4\pi }{S}\,s-\frac{\pi }{2}\right) + \frac{\theta _\textrm{max}+\theta _\textrm{min}}{2}, \end{aligned}$$

where \(\theta _\textrm{min}=13^\circ\) and \(\theta _\textrm{max}=43^\circ\). Using the expressions in Sect. 2.1, the respective values of the remainder of the quarter circular arc, the half-length of the straight, and the Euler spiral coefficient are

$$c= \frac{\pi \,R - b}{2} = 23.9846\,\textrm{m},\quad a = \frac{S}{4}-b-c = 13.6154\,\textrm{m},\quad A= \frac{1}{R\,b} = 0.001731\,\textrm{m}^{-2}.$$

In a manner consistent with our approach, Fitzgerald et al. [8] specify the instantaneous lean angle and centre-of-mass speed agreeing with expressions (21) and (22)—the numerical experiments assume a steady ride with \(V=16\) m/s, which corresponds to \(v=16.2890\,\mathrm{m/s}\) and, hence, \(t_\circlearrowleft =15.3511\,\textrm{s}\) . Using these values, together with \(\textrm{C}_{\textrm{sr}}=0.0025\) , we compare the models to obtain

$$\begin{aligned} P_F = 531.2604\,{{\textrm{W}}} \quad \text { and }\quad P_F' = 534.7769\,{{\textrm{W}}}. \end{aligned}$$
(26)

Hence, our power to overcome dissipative forces is consistent with Fitzgerald et al. [8] to within one percent: \(100\,(|P_F-P_F'|/P_F')=0.6576\%\) , in spite of a different formulation of lateral forces to avoid slipping along the banked track. Also, for either model, during a lap, the power varies by \(2.56\%\) and \(2.85\%\) , respectively, which agrees with the assumption of a steady ride.

However, as discussed in Sect. 4, a velodrome model requires considerations of not only dissipative but also conservative forces. Herein, for either model, \(P_U = 34.0442\) W; hence, we claim that—for our and the Fitzgerald et al. [8] model, and as opposed to values (26)—the required power is \(565.3046\,{\textrm{W}}\) and \(568.8212\,{\textrm{W}}\) , respectively.

8 Conclusions

The mathematical model presented in this article offers the basis for a quantitative study of individual time trials on a velodrome. For a given power, the model can be used to predict laptimes; also, it can be used to estimate the expended power from the recorded times. In the latter case, which is an inverse problem, the model can be used to infer values of parameters, in particular, \(\textrm{C}_\textrm{d}\textrm{A}\) , \(\textrm{C}_{\textrm{rr}}\) , \(\textrm{C}_{\textrm{sr}}\) and \(\lambda\) . Such an inference is of immediate use in strategizing the performance for individual pursuits and the Hour Record.

Let us emphasize that our model is phenomenological. It is consistent with—but not derived from—fundamental concepts. Its purpose is to provide quantitative relations between the model parameters and observables. Its key justification is the agreement between measurements and predictions. The relative simplicity of our model—as well as the model by Fitzgerald et al. [8] and in contrast to Fitton and Symons [6]—facilitates an empirical examination of specific assumptions. While the accuracy of measurements is insufficient to distinguish between predictions of \(P_F = 531.2604\,{{\textrm{W}}}\) versus \(P_F' = 534.7769\,{{\textrm{W}}}\)  discussed in Sect. 7, it is possible to obtain empirical evidence for an increase of \(P_U = 34.0442\,{\textrm{W}}\)  predicted by our model.

Furthermore, let us comment on the use of the \(C^3\) transition curve of Sect. 2.2. A track model with a discontinuity in a certain order of derivative of arc length with respect to time may result in a physical quantity (such as acceleration) not being well-defined at all points of the track. Besides the obvious theoretical difficulty that this presents, such discontinuities can often lead to unreliable numerical results. Our methods allow one to make the track as smooth as necessary to overcome these difficulties. For the purposes of average per-lap power calculations, our results in Sect. 6 indicate that, in practice, \(C^2\) continuity suffices. However, the fact that a particular form of a transition curve has a negligible effect on power considerations—even if a cyclist is to follow strictly the black line—gives certain freedom and flexibility in velodrome design and construction.