1 Introduction

In professional cycling, to win an individual time trial (ITT) stage, a combination of physiological characteristics, bicycle settings, pacing strategy, and riding skills is required. The physiological [1], biomechanical [2], and anthropometric [3] characteristics, and pacing strategies in professional ITTs [4] have been extensively studied and documented. For example, physiological determinants of the ITT performance include: high values of the power output at the onset of blood lactate accumulation (normalised per body weight with exponent 0.32) [5], high critical power values [6], and high power output values eliciting the first ventilatory threshold [7]. Regarding the pacing strategy, it has been theoretically and experimentally shown that varying the power output according to the slope or wind improves ITT performance [8, 9]. In brief, the best pacing strategy consists in increasing the power output in hard sections (uphills and headwinds) and restore energy sources by decreasing the power output in the favourable sections (downhills and tailwinds). Little is known about the riding skills required to race ITT at the highest levels, and how these characteristics might affect the pacing strategy.

During ITT stages, athletes race against the clock [10] and the contribution of external factors like team strategy and drafting is removed [11]. Mathematical models of cycling locomotion [12] have been widely adopted to quantify the influence of the aforementioned physiological characteristics on ITT performance [13, 14] or to inform about the best pacing strategy. The calculation of the pacing strategy requires the combination of a cycling model with a dynamic optimisation tools. For example, an optimal control problem can be formulated [15,16,17,18,19,20], where the objective is to minimise the arrival time by appropriate selection of the power output distribution. In these optimal control problems, the physiological constraints such as the anaerobic sources depletion are typically included by means of the critical power model [21, 22].

Usually, the models adopted to simulate ITT stages are monodimensional (1D) and they only equate expressions for power production and power demand in the longitudinal direction [23,24,25]. However, the overall speed at which athletes can ride does not only depend on longitudinal forces. On corners, the maximal speed is determined by the friction coefficient between tyres and road [26] and, therefore, by the maximal lateral (i.e., centripetal) forces. A few models (e.g., [18, 27, 28]) included the corners (or recognised their importance) in the calculation of the optimal pacing strategy. In corners, longitudinal and lateral forces influence each others, and set the limits to the accelerations in the two orthogonal directions [29] by creating the so-called friction ellipse. This phenomena, in conjunction with the rider’s attitude to push to the limits [30], can differentiate riders by skills. As a consequence, models that do not include accelerations phases due to the turns cannot inform about realistic power output and velocity profiles and take riding skills into consideration.

Borrowing upon principles of vehicle dynamics, the optimal trajectory [31] can be defined as the one that the cyclist has to follow to complete the track in the minimum time. The choice of the trajectory (i.e., the cornering strategy [32]) depends on the space available on the road and it is subject to dynamics and physical constraints, such as the maximum grip of the tyres and the available energy sources.

A rider can negotiate a turn in two ways [33]. In a first scenario, the rider tries to maintain a high speed throughout the corner and track a path with a large curvature radius. This is often the case of those riders who lack in power output delivery abilities. In a second scenario, the rider tries to deliver the power output as early as possible for a faster exit speed and tracks straight trajectories. This is often the case of the most powerful athletes and generally the best strategy for racing, with a lower entry speed but a faster exit speed. This strategy requires a late braking point, and, therefore, good braking abilities. The two scenarios lead to different velocity, power distributions, and to minimal time differences after the single turn. However, they can lead to meaningful time differences after long technical sections.

The selection of the best cornering strategy during an ITT race is indeed an optimisation problem with a clear goal (i.e., the minimisation of the race final time) subject to a number of physical/physiological constraints. However, optimal control problems applied on long and realistic ITT courses require considerable computational efforts, as they need to be solved for a high number of nodes. If additional variables and inputs are included, for example, by including lateral bicycle dynamics and anaerobic sources depletion, the optimal control problem becomes even more complex and challenging (a few examples are available in the literature [18, 27, 28]). This complexity and the related computational issues limit the applicability of these models in practice.

The goal of this manuscript was to present a numerically efficient tool to simulate realistic ITT stages in a reasonable amount of time. A cyclist-bicycle model that accounts for longitudinal–lateral vehicle dynamics and physiological characteristics was adopted. The simulation results were compared with experimental data collected during two ITT professional stages. Given that the experimental velocity and power distributions are stereotypical between different cyclists, the model simulations were compared with the mean of all the riders in the sample. Additionally, a 1D model was used to represent the current state-of-the-art in the literature [20] and web-based tools (e.g., https://www.bestbikesplit.com/bestbikesplit.com).

2 Methods

2.1 Rider/bicycle model

2.1.1 The 3D model

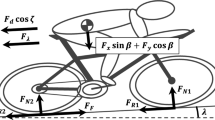
Dynamical models that include both longitudinal and lateral bicycle dynamics are well known in the field of two-wheeled vehicle dynamics [34, 35]. However, they have been rarely adopted [36] together with 3D road geometry and anaerobic source depletion models to simulate realistic professional ITT stages and to obtain detailed turn-by-turn predictions of power output and velocity profiles. The 3D model developed here was a sort of inverted pendulum moving along a curve. The turning rate was directly expressed by the steering angle \(\delta\) (rad) on the road surface [35]. The lateral velocity was considered negligible, and therefore, the bicycle tire could roll without longitudinal or lateral slippage. A schematic representation of the model is provided in Fig. 1 and the numerical values and units of the parameters are provided in the Appendix 6.2.

Cartesian position of the bicycle was described with curvilinear coordinates [37]. In particular: (1) the coordinate s (m) defines the longitudinal position along the road midline; (2) the coordinate n (m) defines the lateral displacement; and (3) the heading \(\alpha\) (rad) defines the orientation of the bicycle with reference to the heading of the road. The equations of motion were written in terms of space coordinate s [20, 37].

Equation 1 describes the dynamics of the heading of the bicycle \(\alpha (s)\):

$$\begin{aligned} \dfrac{\mathrm {d}\alpha (s)}{\mathrm {d} s}&= \dfrac{ \delta _\mathrm{n}(s) \delta _{\mathrm {max}}}{L \, s_{\mathrm {dot}}(s)}-\kappa (s), \end{aligned}$$
(1)

where \(\delta _\mathrm{n}\) (i.e., \(\delta _n=\delta /\delta _\mathrm{max}\)) is the normalised steering angle [the steering angle \(\delta\) (rad) can be expressed as function of the handle bar rotation (\(\delta _\mathrm{f}\)) via the steering axis inclination \(\epsilon\) (or front fork inclination) (i.e., \(\delta = \delta _\mathrm{f}/\sin (\epsilon )\))], \(s_{\mathrm {dot}}(s)\) (m/s) is the travelling speed along the midline, \(\kappa\) (1/m) is the road curvature, and L (m) is the bicycle length.

Equation 2 describes the dynamics of the lateral displacement of the bicycle n:

$$\begin{aligned} \dfrac{\mathrm {d}n(s)}{\mathrm {d} s}&= \dfrac{1}{s_{\mathrm {dot}}(s)} \left( v(s) \sin (\alpha (s)) \right) , \end{aligned}$$
(2)

where v (m/s) is the longitudinal velocity of the bicycle.

Equation 3 describes the dynamics of the longitudinal velocity of the bicycle v:

$$\begin{aligned} \dfrac{m\,v(s)}{W_{\mathrm {max}}}\,\dfrac{\mathrm {d}v(s)}{\mathrm {d} s}&= \dfrac{W_\mathrm{n}(s)}{s_{\mathrm {dot}}(s)} \nonumber \\&\quad - \dfrac{v(s)}{s_{\mathrm {dot}}(s)W_{\mathrm {max}}} \left( m\,g (c_\mathrm{rr}\,\cos (\beta (s))\right. \nonumber \left. + \sin (\beta (s))) \right) \nonumber \\&\quad - \dfrac{v(s)}{s_{\mathrm {dot}}(s)W_{\mathrm {max}}} k_v (v(s) - V_w(\alpha (s))^2, \end{aligned}$$
(3)

where \(W_\mathrm{n}\) is the normalised power (i.e., \(W_\mathrm{n}=W/W_\mathrm{max}\)), which is positive when the rider is pedalling and negative when the rider is braking. The power output (W) is given by \(W_\mathrm{n}^{+}(s) W_{\mathrm {max}}\), where \(W_{\mathrm {max}}\) is the maximum power output and the braking power (W) is given by \(W_\mathrm{n}^{-}(s)\mu _x\,g\,m\,v(s)\), where \(\mu _x\) is the peak longitudinal adherence (that, together with the peak lateral adherence \(\mu _y\), creates the friction ellipse reported in Fig. 1 [30, 38]). In 3, \(\beta\) (rad) is the slope of the road (in the present formulation, the banking angle of the road is not included [37]), kv (kg/m) is the air drag coefficient obtained as \(0.5 A_f C_D\rho\) (where \(\rho\) is the air density in \(\mathrm{kg}/\mathrm{m}^3\), \(A_\mathrm{f}\) is the cyclists’ frontal area in \(\mathrm{m}^2\), and where \(C_\mathrm{D}\) is the coefficient of drag [39]), m is the total mass m (kg) of the system, and \(c_\mathrm{rr}\) is the rolling friction coefficient [40]. Estimated wind data (intensity \(Vw_0\) and direction wD, Fig. 1) were retrieved from https://www.weatherspark.com and https://www.windfinder.com. Relative wind speed was computed as: \(Vw=Vw_0\cdot \cos ( \alpha (s){-}wD)\). Wind direction was expressed with reference to the true North, defined at \(\pi /2\) rad.

Equations in 4 and in 5 describe the dynamics of the roll angle \(\phi\) (rad) and its rate of change \(\phi _\mathrm{dot}\) (rad/s):

$$\begin{aligned} \dfrac{\mathrm {d}\phi (s)}{\mathrm {d} s}&= \frac{\phi _{\mathrm {dot}}(s)}{s_{\mathrm {dot}}(s)} \end{aligned}$$
(4)
$$\begin{aligned} \dfrac{I_{X0}}{h\,m\,g} \dfrac{\mathrm {d}\phi _{\mathrm {dot}}(s)}{\mathrm {d} s}&= \dfrac{1}{g\,L\, s_{\mathrm {dot}}(s)} (v(s)^2 \delta _{\mathrm {max}}\delta _n(s) + L\,g\,\phi (s)), \end{aligned}$$
(5)

where \(I_{X0} = h^2\,m +I_{X}\) (\(m^2kg\)) is the overall roll moment of inertia, h (m) is the height of the center of mass from ground, and g (\(\mathrm{m/s}^2\)) is the constant of gravity.

Equation 6 describes the dynamics of the normalised power output \(W_\mathrm{n}\):

$$\begin{aligned} \dfrac{\mathrm {d}W_\mathrm{n}(s)}{\mathrm {d} s}&= \dfrac{v_{W_\mathrm{n}}(s)}{s_{\mathrm {dot}}(s)}. \end{aligned}$$
(6)

The power output variation \(v_\mathrm{W}\) (W/s) is normalised on maximal power output variation (i.e., \(v_{W_\mathrm{n}} = v_W/v_{W_{\mathrm {max}}}\)).

Equation 7 describes the dynamics of the normalised steering angle \(\delta _\mathrm{n}\):

$$\begin{aligned} \dfrac{\mathrm {d}\delta _\mathrm{n}(s)}{\mathrm {d} s}&= \dfrac{v_{\delta _\mathrm{n}}(s)}{s_{\mathrm {dot}}(s)}, \end{aligned}$$
(7)

where the normalised steering angle rotational velocity \(v_{\delta _\mathrm{n}}\) (rad/s) was obtained from the maximal steering angle rotational velocity (i.e., \(v_{\delta _\mathrm{n}} = v_{\delta }/v_{\delta _{\mathrm {max}}}\)).

Equation 8 describes the dynamics of travelling speed \(s_{\mathrm {dot}}(s)\) along the reference line:

$$\begin{aligned} s_{\mathrm {dot}}(s)&= \dfrac{v(s)\cos (\alpha (s))}{1 - n(s)\kappa (s)}. \end{aligned}$$
(8)

With this notation, the time t (s) was obtained by simple integration of the variable \(s_{\mathrm {dot}}(s)\).

A modified critical power model [21, 41] was used to describe the rider’s ability to sustain the effort above the critical power threshold (W, \(W_\mathrm{C}\)). The corresponding dynamic equation 9 describes the evolution of the anaerobic sources \(E_\mathrm{A}\) (J, normalised with the maximal anaerobic sources, i.e., \(E_{{{\rm A}_{\rm n}}}=E_{{\rm A/E}_{ {\rm An0}}}\)):

$$\begin{aligned} \dfrac{{\rm d}E_{{{\rm A}_{\rm n}}}(s)}{{\rm d} s}&= - \dfrac{1}{E_{{\rm An0}}s_{{\rm dot}}(s)}\left( W_{\rm n}(s)^{+}W_{{\rm max}}-W_{\rm C} \right). \end{aligned}$$
(9)

The fact that energy expenditure and recovery are characterised by the same rate is an assumption that might limit the applicability of the model [42, 43]. The fact that the maximal power output \(W_{\mathrm {max}}\) is kept constant during the whole race duration is also a limitation, as the ability to deliver maximal power output levels decays after spending anaerobic energy sources [43].

Fig. 1
figure 1

Schematic representation of the model. x is the longitudinal axis and it points forward, y is the lateral axis and it points leftward, and z is the vertical axis and it points upward. Top view, Curvilinear coordinates are highlighted. s is the curvilinear abscissa, n is the lateral displacement from the midline of the road, and \(\alpha\) is the attitude angle. The road is characterised by the curvature radius k and the right \(R_\mathrm{width}\) and left width \(L_\mathrm{width}\). Friction ellipse is used to define the limits to the lateral and longitudinal accelerations. The semi-axes of the friction ellipse can be directly computed from the longitudinal \(\mu _x\) and lateral \(\mu _y\) friction coefficients. A schematic compass is used to indicate the true North, which gives the reference for the wind. The wind is characterised by a magnitude \(V_{w0}\) and direction wD. The steering angle of the bicycle \(\delta\) is also reported. Lateral view, the road is characterised by a slope angle \(\beta\). The bicycle is characterised by a length L. Together with the rider, the bicycle forms a rider–bicycle system that has a total mass m. The centre of mass of this lumped system is positioned at a distance h perpendicular to the road surface. The centre of mass of the system is where the resistive forces (i.e., wind resistance and rolling resistance) are applied. Frontal view, the contact point on the road is highlighted here. The contact point is where the contact forces (braking and traction forces) are applied. The roll angle of the rider–bicycle system \(\phi\) is also reported

Full size image

2.2 Optimal control problem

The problem of finding the pacing and cornering strategies was formulated as a constrained optimal control problem. The optimal control problem was solved for nodes at every 0.25 m of the course. The Maple package XOptima, as part of software PINS (i.e., a collection of libraries and numerical solvers for optimal control problems [44]), was used to formulate the optimal control problem and generate the equations and the Jacobians. PINS solves the optimal control problem with an indirect approach [45]: it symbolically derives the necessary condition of optimality and finds a numerical solution for the Pontryagin’s minimum principle. This approach allows to analytically formulate the optimisation problem [46], and to automatically derive the conditions of optimality and the Jacobians for the numerical solution.

The objective function \(J(\varvec{u})\) was defined as a weighted sum of three different goals subject to the system’s dynamics and path constraints:

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \limits _{u\in \mathcal {U}} \bigg \{ J(\varvec{u}):= {\displaystyle \int _{0}^{L_p}} \dfrac{1}{s_{{\rm dot}}(s)} \left( 1 +W_{{\rm J}_1}\left( \dfrac{v_{\delta }}{v_{\delta _{{\rm max}}}} \right) ^2 +W_{{\rm J}_2}\left( \dfrac{v_{W}}{v_{W_{ {\rm max}}}} \right) ^2 \right) \,{\rm d}s \bigg \} \\ \text {subject to}: \\ \varvec{b}(\varvec{x}(0),\varvec{x}(L_p)) = \varvec{0} \\ \varvec{c}(\varvec{x}(s),\varvec{u}(s)) \ge \varvec{0}, \end{array}\right. } \end{aligned}$$
(10)

where \(L_\mathrm{p}\) is the length of the stage, \(\varvec{x} = \left[ \alpha , n, \phi , \phi _{\mathrm {dot}}, E_{A_\mathrm{n}}, W_\mathrm{n}, \delta, v \right]\) is the vector of states, and \(\varvec{u} = \left[ v_{\delta }, v_{W_\mathrm{n}}\right]\) is the vector of controls. The objective function \(J(\varvec{u})\) minimises the race time and the rate of change of the steering angle \(v_{\delta }\) and of the power output \(v_{W}\). In 10, \(W_{{\rm J}_1}\) and \(W_{{\rm J}_2}\) are weighting factors that scale the penalisation of the input rate of change. These two elements minimise the rate of variation of the inputs together with other goals to: generate smooth movements, cope with the delays between neural signalling and movement actuation, and to reject the noise that increase the variability of the outcome [47,48,49,50,51,52]. The vector \(\varvec{b}\) lists the boundary conditions (i.e., the start and end values of the states \(\varvec{x}\)) that correspond to the case of a bicycle in vertical position. In particular, the initial speed was set to 0 and the final speed was free to change. Similarly, the initial value of the anaerobic energy (\(E_\mathrm{A}\)) was set to the maximum value and the final value was free to change. Finally, vector \(\varvec{c}\) represents a list of inequality constraints (i.e., path constraints), which limited the evolution of the states and controls:

$$\begin{aligned} L_\mathrm{W}(s) \le\,&n(s) \le R_\mathrm{W}(s) \end{aligned}$$
(11)
$$\begin{aligned} 0 \le\,&E_\mathrm{A}(s) \end{aligned}$$
(12)
$$\begin{aligned} -1 \le\,&W_\mathrm{n}(s) \le 1 \end{aligned}$$
(13)
$$\begin{aligned} -1 \le\,&\delta _\mathrm{n}(s) \le 1 \end{aligned}$$
(14)
$$\begin{aligned} W_{\mathrm {max}} =\,&0 \,\,\mathrm {if} \quad |\phi |\ge 20^\circ \end{aligned}$$
(15)
$$\begin{aligned} \left( \dfrac{a_x(s)}{\mu _x\,g}\right) ^2+\left( \dfrac{a_y(s)}{\mu _y\,g}\right) ^2 \le&1, \end{aligned}$$
(16)

where \(L_\mathrm{W}(s)\) and \(R_\mathrm{W}(s)\) are the left width and right width of the road borders which determine (with Eq. 11) the limits to the bicycle displacement n from the reference line of the road. Equation 12 requires the anaerobic sources \(E_\mathrm{A}\) to be positive. Equations 13 and 14 constraint the normalised steering angle \(\delta _\mathrm{n}\) and output power \(W_\mathrm{n}\) in the range \([-\,1,1]\). Equation 15 is a function that limits the maximum power output with the roll angle \(\phi\), which is different than 0 only if the roll angle is in the range \([-\,20^\circ , 20^\circ ]\). This is because cyclists do not pedal during sharp turns. Finally, the lateral and longitudinal accelerations are constrained in the friction ellipse (Eq. 16) (Fig. 1 [30, 38]). The friction ellipse represents the combined limits to the lateral and longitudinal accelerations that the bicycle–rider system can sustain and produces the so-called g–g diagram [38]. The semi-axes of the friction ellipse are given by the friction peak coefficients \(\mu _y\) and \(\mu _x\) for lateral and longitudinal directions, respectively. The values of \(\mu _y\) provide the maximal roll angles that the bicycle–rider system can sustain (i.e., \(\phi _{\mathrm {max}} = \arctan (\mu _y)\)) and they can be used to equally express a road with poor friction or a cyclists with a different attitude towards risk.

2.2.1 1D model

The 3D model was compared to a 1D model, which currently represents the gold standard in pacing strategy computation. The equation of motions were derived from those introduced in the previous section. The main simplification was that the lateral bicycle dynamics was neglected; therefore, the dimension of the system and the number of inputs were reduced. The state variables for this model were: v, \(W_\mathrm{n}\), \(EA_\mathrm{n}\), and t; the only input was \(vW_\mathrm{n}\). Riders’ characteristics and the other variables (e.g., the attitude angle \(\alpha\) and the slope \(\beta\)) and parameters (e.g., the wind magnitude and direction, and longitudinal friction coefficient \(\mu _{x}\)) were the same of the 3D model. The 1D model was also used to compute the pacing strategy with an optimal control approach, as it has been done for the 3D model. However, in the case of the 1D model, the objective function (e.g., Eq. 10) did not consider the term that penalises the rate of change of the steering angle (i.e., \(W_{\mathrm{J}_1}=0\)).

2.3 Rider–bicycle model parameter calibration and validation

Experimental data adopted in this study were collected by 28 professional cyclists at the Giro d’Italia during two different stages. Data were then donated by the head scientists of the professional teams and used retrospectively in this study. Riders gave informed written and verbal consent before providing the data. The study has been conducted in agreement with the declaration of Helsinki and the guidelines of the Ethical Committee of the University of Trento. The same data collection procedure is routinely performed by the riders during races and training sessions; therefore, it could not cause any harm to the riders nor to their safety and performance. Experimental longitudinal velocity and travelled distance were collected by an odometer connected to a global positioning system (GPS) (Garmin Edge 520, 720, 1030, or Sigma Rox 11, 12 at 1 Hz sampling frequency). The power output data were collected with power meters mounted in the central movement (Shimano R9100P, FSA Power2Max NG, SRAM RED AXS). The slope of the course was computed from altitude barometric data with simple trigonometry. The unknown parameters were adjusted manually by trial-and-error starting from values retrieved from the literature and using a residual analysis. Residuals were computed as the difference between experimental and simulated data. The mean absolute error (MAE, km/h or W) and the root-mean-square error (RMSE, km/h or W) were used to concisely express the goodness of the agreement. The portion (\(\%\)) of the course where the predicted values fell within the \(\mathrm{CI}_{95\%}\) of the experimental data was also computed. During the calibration of the model, values of the parameters were adjusted to minimise MAE and RMSE. The same values were used to validate the 1D and 3D models.

The points of the 16th stage of the Giro d’Italia 2018 (Rovereto, Trento, May 22nd) were tracked using Google Earth path tools and then interpolated with 379 clothoids using [46]. The length of the course was 34.2 km, with a positive altitude gain of 214 m. An overview of the course is presented in Fig. 2a. The data of 15 professional cyclists taking part in the race were used to calibrate the model, i.e., to adjust the parameters of the model (Appendix 6.2).

Fig. 2
figure 2

a The course of the 16th stage of the Giro d’Italia 2018 (Rovereto, Trento, May 22nd). b The course of the 21st stage of the Giro d’Italia 2019 (Verona, June 2nd). The blue shaded circle indicates the turn that is used to compare trajectories for different cornering strategies. For both courses, the schematic compass indicates the true North, the wind direction and intensity is specified, and the numbers identify the distance in metres from the starting line (i.e., the curvilinear abscissa). Different distance proportions were used in the two panels

Full size image

The points of the complete 21st stage of the Giro d’Italia 2019 (Verona, June 2nd) were extracted and interpolated with 388 clothoids. The length of the course was 16.8 km, with a positive altitude gain of 205 m. An overview of the course is presented in Fig. 2b. This course was used to validate the models and, hence, test their predictive ability. The data of 13 professional cyclists taking part in the race were used. The set of parameters obtained during the calibration process was used (Appendix 6.2).

2.4 Sensitivity to rider characteristics

To evaluate the effect of changes in the riders’ characteristics on pacing and cornering strategies, three virtual riders were created: a typical professional cyclist, an ITT specialist, and a weak climber [1]. The characteristics of the different riders have retrieved from the literature [1, 53] (assuming that the critical power corresponds to the onset of blood lactate accumulation, which constitutes an approximation [54]). The three virtual riders were characterised by different values of body weight, frontal area, and critical power (Table 2). The 3D model (1) was used to simulate the Verona ITT for the three virtual riders.

3 Results

Every simulation required less than 5 min to converge to a solution (MacBook Pro, 2.8 GHz Intel Core i7).

3.1 Comparison with experimental data

The mean and the standard deviation (SD) of power output and velocity (mean(SD)) registered by the riders were: 334(48) W and 46.4(1.3) km/h in Rovereto and 346(45) W and 42(1.4) km/h in Verona. In Table 1, the results of the comparison with the experimental data are reported (absolute values).

Table 1 Comparison between simulated and experimental data: mean average error (MAE), root-mean-square error (RMSE), and fraction of the simulated data that fell within the \(\mathrm{CI}_{95\%}\) of the experimental data
Full size table

The mean \(\mathrm{CI}_{95\%}\) of the experimental data was 2.0 and 1.9 km/h in terms of speed and 43 and 63 W in terms of power for Rovereto and Verona ITT, respectively. The predicted speed and power output laid outside the mean \(\mathrm{CI}_{95\%}\) of the experimental data in different portions of the course. In Figs. 3 and 4, the simulated and experimental data are compared. While the model was able to follow the general trend of the experimental data, clear differences can be observed.

Fig. 3
figure 3

Comparison between simulated (solid line) and mean experimental data and \(\mathrm{CI}_{95\%}\) (shaded) in the Rovereto stage. From top to bottom: power output profile, velocity profile, and elevation profile

Full size image
Fig. 4
figure 4

Comparison between simulated 3D model (solid line) and 1D model (dashed line) and mean experimental data and \(\mathrm{CI}_{95\%}\) (shaded) in the Verona stage. From top to bottom: power output profile, velocity profile, and elevation profile (with the limits of the descending section). The blue shaded circle indicates the turn that is used to compare trajectories

Full size image

3.2 interplay between rider’s characteristics and cornering strategies

Using all the space on the road, cyclists can ride along straight lines, and travel fast before reaching the limits of the tyre’s grip. However, the cornering strategy is highly individual (Fig. 5). Between the three virtual riders, the race time differences were due to the different power output values in the straight sections of the course and to the different cornering strategies (Fig. 5). Not surprisingly, all the virtual riders explored the limits of the grip of the tyres. This was confirmed by the similar maximal roll angle values. However, the differences in the velocity and power distributions were relevant, and they led to a time difference of 0.33 s after a turn (Fig. 5) or 32 s after the descending phase (4.7 km long and 13 turns). The effects of the different power distribution on the longitudinal speed were also apparent in the longitudinal acceleration results: after exiting the turn, the more powerful rider could promptly accelerate and restore high-speed values. All three virtual riders had the same braking ability and potential, but the ITT specialist could brake later before the turn, therefore reducing the velocity to low values. After the turn, the ITT specialist could deliver enough power to propel himself out of the corner with high speed. The time differences between riders are reported in Table 2.

Fig. 5
figure 5

In the top graph, the trajectories of three virtual cyclists with different physical/physiological characteristics have been obtained by simulation. The three riders represent: the typical professional rider (solid line), an individual time trial specialist (dashed line), and a weak climber (dash-dot line). Trajectories are compared for a hair pin turn during the downhill section of a an individual time trial (Verona, Giro d’Italia, 2018). From top to bottom, the longitudinal speeds (v, km/h) of the three virtual cyclists are compared to the experimental data. The shaded area represents the \(\mathrm{CI}_{95\%}\) of the experimental data. The lateral displacement from the midline of the road (n, m) of the three virtual cyclists is given and the roll angle (\(\varPhi\), \(^\circ\)) values are provided. The absolute power (W, W) and the longitudinal acceleration (\(a_x\), \(\mathrm{m/s}^2\)) are reported in the lower graphs

Full size image
Table 2 Final time and local turn times obtained by simulation
Full size table

4 Discussion

A 3D model for cycling locomotion was created. It included lateral and longitudinal bicycle dynamics and a critical power model for human bioenergetics. The model was used in an optimal control framework, where the pacing and cornering strategy problems were solved together. The optimal control problem consisted in four key mathematical elements: the equation of motions of the rider–bicycle system (i.e., Eqs. 1–9), the controls that can influence the behaviour of the system (i.e., the steering angle and the power output), the constraints that the solution must satisfy (i.e., Eqs. 11–15), and the performance criterion that should be minimised by appropriate selection of the control (i.e., Eq. 10). The results of the simulations were compared against experimental data and suggested that: (1) there was an interplay between pacing and cornering strategies, and (2) this framework could be used to assess new ITT performance indexes and to plan racing strategies on the race day.

The applicability of this model is hindered by limitations. (a) The 3D model conjugates both lateral and longitudinal dynamics in cycling locomotion, and the aim was to check if this model was sensitive to the turns and to the maximal lateral accelerations that the bicycle can sustain. The next step will be to change the parameters of the rider (e.g., body mass, air drag friction coefficient, critical power, etc.) and to check if the 3D model is able to predict individualised pacing and cornering strategies on an athlete-by-athlete basis. Anonymised data were used, so the characteristics of the individual cyclists were unknown. However, the sample was considered a good representation of the professional cyclist population and mean values of the parameters were retrieved from the literature [1]. (b) ITT stages may not always be raced at maximal level [53]: the role of an individual rider within a team often determines the intensity at which a time trial is raced [55]. However, power output and velocity distributions were stereotypical across the riders (as indicated by a relatively low \(\mathrm{CI}_{95\%}\)): the riders had to slow down and accelerate in the same sections of the course. Of course, absolute power output and velocity values were expected to be different, and to obtain personalised simulations, it would be important to know rider-specific parameters like frontal area, body mass, and critical power [6]. (c) The exact values of road width and banking were unknown. Furthermore, errors in slope and wind data estimation could have negatively affect the predictive ability of the models. (d) Experimental data were not available for all the variables. Therefore, it was impossible to evaluate the goodness of the predictions of the roll angles, lateral accelerations, and steering angles. Similarly, the choice of the bioenergetic model (i.e., the critical power model) might not have been the best possible choice [22] and this assumption cannot be tested against any experimental data. (e) In the adopted version of the critical power model, the time characteristics (\(\tau\)) for the discharge and the recharge of the anaerobic sources were considered equal. In the critical power model proposed by Skiba et al. [56], \(\tau\)-recharge was much slower than \(\tau\)-discharge and it was affected by the recovery conditions. As a consequence, using a value for \(\tau\) was an assumption that limited the accuracy of the models. (f) Different riding positions were not included. However, they could have had influence on the frontal area of the riders (and, therefore, the aerodynamic drag coefficient) [57], their ability to deliver maximal power outputs [58], and cycling efficiency [59]. (g) The drivetrain efficiency was not taken into account. Accordingly, in [25], the estimated power output needed to be divided by a chain efficiency factor. Therefore, power output could be underestimated. (h) The aforementioned limitations could only in part explain the discrepancies between simulated and experimental data in Figs. 3 and 4. Another source of error could lie within the optimal control approach. Optimal control is regarded as one of the best tools to simulate human movement, but the objective function should reflect what the riders are trying to achieve [48]. In this framework, the race time and the rate of change of the steering angle and power were minimised. However, in ITT raced on uneven terrains, the pacing strategy is regulated by highly complex interactions between the peripheral sensory feedback, the perceived effort, and the anticipated workload remaining [4]. It would be challenging to include all these complex interactions in this optimal control framework. (i) The problem was highly non-linear and there was no formal method to guarantee that the solution constituted a global optimum. An indirect method with penalty approximation of the constrain problem on control was used; therefore, the second derivative of the cost function with respect to the control was positive and the solution found was a minimum [60].

In spite of the limitations, this work represents a step-forward in the current literature: it follows and extends the work of Maroński [15], Swain [61], Gordon [16], and Wolf et al. [20], and takes the problem of pacing strategy calculation during ITT races to a next level of complexity and potential. This framework currently represents one of the few published tools (other examples are [43] or [62]) that can be used to evaluate the interplay between the physical/physiological characteristics, the 3D road geometry, the race-day conditions, the pacing/cornering strategies, and the overall ITT performance.

In 2014 [28] and 2015 [63], Sundrström and colleagues included the turns as constraints to the maximal velocity (computed from turning radii) in a 1D model of bicycle dynamics. Their simulation results confirmed what it was already anecdotally known, i.e., turns can affect the pacing strategy and impact on the performance time. However, their model cannot be used to study the optimal trajectory in different turns, because the lateral displacement from the midline and the 3D geometry of the road are not taken into account [33]. Furthermore, they imposed a speed constraint linked to the road curvature, and not based on the real trajectory of the riders. More recently, Fitton and Symons [64] presented an interesting multidimensional model for track cycling. Despite the elegant analytical solution for the forward dynamics, this model cannot be used in long ITT courses, mainly because it does not include the bioenergetics constraints and it is not presented together with a dynamic optimisation tool.

In the present work, the predictive power of the 3D model was compared to that of a 1D model. In Fig. 4 and in Table 2, the differences between the two estimations are presented. The 1D model could correctly predict maximal speed values, while the 3D model often underestimated the actual longitudinal speed of the rider. These differences could be due to the variations of the power output predicted by the 3D model, that could deplete the anaerobic energy sources faster than a constant power output value. This might indicate that turns could affect the power that can be delivered during the flat straight portions of the ITT, because the accelerations after the turns require an additional power output that depletes the anaerobic energy sources. From Table 2, it is also evident that a 1D model could not correctly estimate the speed on single turns and after long technical sections. For example, the 1D model predicts that the descending section (4.7 km, 13 turns) of the Verona ITT could be completed in 4 min and 32 sec (and 6.43 s to complete the single turn (120 m)): this was unrealistic, because a rider cannot complete a hair-pin turn at 67 km/h without crashing.

Indirect optimal control approaches have already shown their potential in locomotion [60], biomechanics [65], and pacing strategy in ITT [27]. However, De Jong et al. [18] only considered the longitudinal bicycle dynamics, and therefore only one input at time, i.e., the mechanical power.

Jeukendrup and Martin [14] used a mathematical model [25] to calculate the contribution of physiological, mechanical, and environmental factors on the 40 km ITT performance in elite cyclists. They estimated the contribution of a training programme which includes high intensity or altitude training, CHO-electrolyte solutions assumed during the race, caffeine ingestion prior the race, and a bicycle mass reduction. The contribution of the riding skills and the presence of a series of turn (i.e., a technical section) are yet to be estimated, as they depend on the ITT course and, in particular, on the extension of the technical sections. The results of this study suggest that physical/physiological characteristics and riding skills are linked together in the determination of the pacing and cornering strategies. For example, Fig. 5 shows that the most powerful athletes (e.g., the ITT specialist), to exploit their power output to the maximum, must be able to brake hard before the turns and to deliver high power output values after.

The 3D model presented here allows the calculation of new performance indexes (e.g., the friction ellipse) and the estimation of new variables (e.g., steering angle, roll angle, lateral accelerations, etc., Fig. 5) starting from odometer and GPS data. This model might be used to evaluate the time-differences between riders after completing a turn and to compare cyclists with different riding skills, different attitude to risk or to simulate dry/wet road conditions. For example, it can hypothesised that the closer the cyclists are going to the edge of the friction ellipse, the more they are risking. The framework presented here can be used to test such hypotheses.

5 Conclusions

A model that included both longitudinal and lateral bicycle dynamics, 3D road geometry, and rider’s anaerobic sources depletion was presented. This model, in an optimal control formulation, could simulate professional ITT stages. This framework, therefore, constitutes a tool for: computing the pacing strategy of ITT stages in advance and evaluating the contribution of riding skills and road conditions to the ITT performance. The same depth of analysis cannot be obtained with the existing 1D models. However, the model presented here relies on crucial assumptions and simplifications that need to be refined. Additionally, a powerful optimal control solver such as PINS and a considerable computational effort are needed to solve the optimal control problem.