Comparison of Various Angle-Tracking Algorithms to Balance Performance and Noise for a Steering-by-Wire System

Abstract

This paper compares various angle-tracking algorithms to balance the performance and noise for a steering-by-wire (SBW) system. Direct and quiet steering experiences can improve drivers’ acceptance of the SBW system. Linear quadratic regulator (LQR) control, robust control, and conventional cascade proportional–integral (PI) control have been developed and compared both theoretically and experimentally. To avoid the risky and time-consuming parameter-tuning process, a high-fidelity steering resistance model, which comprises a linear two-degree-of-freedom vehicle model and a dynamic LuGre friction model is established. Step and sine wave tests are simulated in a Matlab/Simulink environment to determine the reasonable parameter region for various methods. Then, the three types of algorithms are implemented on a prototype SBW vehicle and compared under the same scenarios. Finally, the simulated and experimental results are illustrated in detail. According to the indicators of control bandwidths, steady-state errors, cockpit sounds, and current waveforms, it is clear that LQR and robust control can achieve faster response and more acceptable noise, with uncertain and relatively larger tracking errors. Cascade PI control, in comparison, can realize smaller steady-state errors and gentler current waveforms, with slight noise and slower response.

1 Introduction

Steering-by-wire systems have received increasing research attention owing to the steering system’s internal advancements and potential for extensive connection with automated driving. Over the past few decades, steering systems have utilized hydraulic oil and electric motors to decrease driver effort and improve vehicle maneuverability. Electric power-assisted systems tend to completely replace hydraulic power-assisted systems in passenger cars of different sizes due to their compact structure, enhanced steering feel and return characteristics, and intelligent applications for driver-assisted systems. Motivated by X-by-wire technologies, SBW systems, which substitute mechanical linkage with electronic communication, are anticipated to become the norm in the future. Due to the removal of the steering column, steering feel can be designed according to individual driving styles, and the response from the drivers to the tires can be achieved more quickly. SBW systems can extend steering functions and cooperate with other by-wire chassis components from the perspective of Domain-based integrated control or shared steering control (Fang et al., 2023).

SBW systems have the advantages of customized tuning and naturally road disturbance-free steering feel. Significant research (Balachandran & Gerdes, 2015) has contributed toward realizing a realistic steering feel. In this work, we concentrate on high-quality angle-tracking algorithms that improve the overall driving experience by making drivers feel closely connected to vehicle motion. The main challenge faced by angle-tracking algorithms is maintaining a balance between performance and noise, particularly for electric vehicles, with quiet engines. Many algorithms are investigated for their system robustness against velocity-dependent road steering resistance moment, sensor delay, and parameter uncertainty. Sliding mode control (SMC) is a popular method used for practical angle tracking in SBW systems. However, the chattering phenomenon caused by discontinuous inputs has led to many challenges in SMC. Several strategies—such as using a special sliding surface (Wang et al., 2014), adopting high-order structures (Utkin, 2016), estimating parameters (Wu et al., 2018) or disturbances (Wu et al., 2019), and softening the input can prevent or eliminate the unexpected chattering effects. In engineering applications, proportional–integral–derivative (PID) controllers are widely used owing to their simplified structures and quick computation speeds. Recently, some researchers have removed the speed loop and adopted parameter optimization (He et al., 2022; Huang et al., 2020a, 2020b; Hwang & Nam, 2019) to refine the conventional cascade three-layer PID control structures. Further, some researchers have used fraction-order PID (Dumlu & Erenturk, 2014) and feedforward compensation structures to improve control performance. In addition, some others have proposed model predictive control (Huang et al., 2020a, 2020b) and intelligent control (Wang et al., 2023) to cope with system uncertainties and unknown bounds. However, these complex methods require excessive computation resources, making it challenging to meet real-time demands under a small sampling period.

A considerable portion of angle-tracking algorithms has been validated by software-in-loop and hardware-in-loop platforms, where cockpit acoustic noises are difficult to detect. In addition, automotive applications, some novel algorithms are limited by the cost-sensitive output capacity. Further, consumer-oriented comfort is equally important. Thus, a trade-off between eliminating noise and improving performance remains challenging.

In the angle-tracking system, the dynamics between motor force and steering angle are similar to a double integral unit. Conventional cascade PI structures use speed loops to attenuate the influence of unknown disturbances. However, the speed loop, as a backward channel for sensor noise, deteriorates the system input. Recently, time-domain optimal and frequency-domain optimal control algorithms have become good candidates for balancing performance, control input, and noise attenuation. Motivated by these issues, this paper introduces and compares cascade PI control, LQR control combined with Kalman filters, and $H_{\infty }$ synthesis control, which weights the influence of specialized tracking performance, sensor noise, control capacity, and external disturbances. To validate various algorithms, a high-fidelity steering resistance model is constructed first and compared with the data collected by vehicle-mounted rack force sensors. Various simulations are conducted to ascertain the reasonable region of control parameters. Then, a prototype vehicle equipped with the SBW system is constructed, and these algorithms are deployed into the steering controller. Finally, the simulation and experimental results are presented and discussed.

The remainder of this paper is organized as follows. Section 2 presents the architecture of the SBW system, the second-order steering model, steering resistance model, and permanent magnet synchronous motor (PMSM) model. Section 3 develops the cascade PI control, LQR control, and $H_{\infty }$ synthesis control in detail. In Sect. 4, these algorithms are verified by simulations and vehicle experiments; the comparative experimental results are then illustrated and analyzed. Finally, Sect. 5 concludes this paper and presents future work.

2 SBW Architecture and Modeling

2.1 Architecture

In general, the SBW system is divided into the hand wheel actuator (HWA) subsystem and front axle actuator (FAA) subsystem, as shown in Fig. 1. The HWA subsystem comprises a hand wheel, a power pack, a torque and angle sensor (TAS), and a reducer. The FAA subsystem consists of road wheels, a power pack, a steering angle sensor (SAS), and a reducer. The connection between the hand wheel and road wheels is established using a controlled area network (CAN). Steering feel is designed through a disturbance observer function and a torque control function. Correspondingly, tire angles follow the command from a variable steering ratio (VSR) module through an angle-tracking control function.

Fig. 1

Steer-by-wire architecture

2.2 Modeling

2.2.1 FAA Subsystem Model

According to previous research (Hwang & Nam, 2019), the dynamics of FAA subsystems are summarized into a second-order steering model, where the damping coefficient, friction, inertia, mass, motor torque, and steering resistance are equivalent to the steering shaft.

$$\begin{gathered} J\ddot{\delta } + B\dot{\delta } + T_{{\text{f}}} + T_{r} = i_{{\text{m}}} T_{{\text{m}}} \hfill \\ J = i_{{\text{m}}}^{2} J_{{\text{m}}} + i_{{\text{r}}}^{2} M_{{\text{r}}} ,B = i_{m}^{2} B_{{\text{m}}} + i_{{\text{r}}}^{2} B_{{\text{r}}} \hfill \\ T_{{\text{f}}} = i_{{\text{m}}} T_{{{\text{fm}}}} + i_{{\text{r}}} F_{{{\text{fr}}}} ,T_{{\text{r}}} = i_{{\text{r}}} F_{{\text{r}}} \hfill \\ \end{gathered}$$

(1)

where J and B are the equivalent inertia and damping coefficient, respectively. δ is the angle of the steering pinion. i_m is the general ratio between the pinion angle and motor angle. i_r is the gear ratio between the pinion angle and rack displacement. J_m is the motor inertia. M_r is the rack mass. B_m and B_r are the damping coefficients of the motor and rack, respectively. T_fm and F_fr are the motor friction torque and rack friction force, respectively. F_r is the rack resistance force originating from the tire-road contact and the suspension system. T_f and T_r are the equivalent friction torque and resistance torque from the tire, respectively.

2.2.2 Steering Resistance Model

In the SBW system, a comprehensive steering resistance model is vital to both creating a realistic steering feel and tracking driver command. In addition to system inertia and damping, the major components of steering resistance arise from self-centering torque, load-dependent friction torque, and jacking torque. Jacking torque can be equivalently modeled as a stiffness-varying spring model.

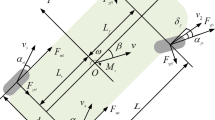
To obtain the self-centering torque, a linear two-degree-of-freedom (2-DOF) vehicle model is used to emulate front axle lateral forces. The SAS measured angle and vehicle velocity ${\text{v}}_{\text{x}}$ are used as model inputs, as follows:

$$\begin{aligned} \left[ {\begin{array}{*{20}l} {\dot{\beta }} \hfill \\ r \hfill \\ \end{array} } \right] = \, & \left[ {\begin{array}{*{20}c} {\frac{{C_{f} + C_{r} }}{{mv_{x} }}} & {\frac{{aC_{f} - bC_{r} }}{{mv_{x}^{2} }} - 1} \\ {\frac{{aC_{f} - bC_{r} }}{{I_{z} }}} & {\frac{{a^{2} C_{f} + b^{2} C_{r} }}{{I_{z} v_{x} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} \beta \hfill \\ r \hfill \\ \end{array} } \right] + \left[ {\begin{array}{*{20}r} \hfill { - \frac{{C_{f} }}{{mv_{x} }}} \\ \hfill { - \frac{{aC_{f} }}{m}} \\ \end{array} } \right]\delta_{f} \\ F_{y} = & \, - C_{f} \alpha_{f} ,\,{\kern 1pt} \,\,\alpha_{f} = \beta + \frac{ar}{{v_{x} }} - \delta_{f} \\ \end{aligned}$$

(2)

where β is the vehicle body slip angle. r is the vehicle yaw rate. a and b are the distances between the center of gravity and the centers of the front axle and rear axle, respectively. C_f and ${\text{C}}_{\text{r}}$ are the front and rear axle cornering stiffness, respectively. m and ${\text{I}}_{\text{z}}$ are the vehicle mass and yaw inertia, respectively. δ_f is the front tire steering angle. F_y is the tire lateral force. α_f is the front wheel slip angle.

The self-centering torque is calculated from the product of lateral forces and tire total trails via tie-rod steering linkages:

$$\begin{aligned} T_{{\text{a}}} = \, & - F_{{\text{y}}} \left( {\tau_{{\text{m}}} + \tau_{{\text{p}}} } \right) \\ \tau_{{\text{p}}} = & \,\tau_{{{\text{p}}0}} \left( {1 - {\text{sgn}} \left( {\alpha_{{\text{f}}} } \right)\frac{{C_{{\text{f}}} }}{{3\mu F_{{\text{z}}} }}\tan \left( {\alpha_{{\text{f}}} } \right)} \right) \\ \end{aligned}$$

(3)

where T_a is the self-centering torque. τ_m and τ_p are the mechanical trail and pneumatic trail, respectively. μ is the road adhesion coefficient. F_z is the tire vertical load.

Friction, which can stabilize steering systems, is inevitable. In this context, the LuGre dynamic friction model (Panagiotis et al., 2004) is applied for simulating the stick–slip feature, and the amplitude of friction depends on the total steering load. The advantages of the LuGre friction model are that the friction characteristics are lumped into several states and described by ordinary differential equations. The friction state z is introduced to interpret the mean deflection of the junctions between the two sliding surfaces. The instantaneous friction synthesizes the Coulomb friction F₀, static friction F_s, and Stribeck characteristic velocity v_s:

$$\begin{aligned} g(v) = & \,F_{0} + \left( {F_{{\text{s}}} - F_{0} } \right){\text{e}}^{{ - \left( {\frac{v}{{v_{{\text{s}}} }}} \right)^{2} }} \\ \frac{{{\text{d}}z}}{{ {\text{d}}t}} = & \,v - \frac{{\sigma_{0} }}{g(v)}z|v| \\ F_{{\text{f}}} = & \,\sigma_{0} z + \sigma_{1} \frac{{{\text{d}}z}}{{ {\text{d}}t}} + \sigma_{3} v \\ \end{aligned}$$

(4)

where v is the LuGre model input speed. σ₀, σ₁, and σ₃ represent the microcosmic bristle stiffness, damping coefficient, and macroscopic rotation damping coefficient, respectively.

2.2.3 PMSM Model

In this paper, a dual-windings PMSM is adopted as the steering actuator, owing to its high power density, low torque ripple, harmonics attenuation, natural redundancy, and fault-tolerant behavior compared with the traditional single-winding PMSM. The two sets of windings are spatially symmetrical with zero angle displacement to facilitate ease of control. In addition, a surface-mounted rotor is adopted without the reluctance torque. Considering the rotor synchronous coordinates, the dual-windings PMSM mathematical model is given as follows:

$$\begin{aligned} u_{{{\text{di}}}} = & \,L_{{{\text{di}}}} \frac{{di_{{{\text{di}}}} }}{dt} + Ri_{{{\text{di}}}} - \omega_{{\text{e}}} L_{{{\text{qi}}}} i_{{{\text{qi}}}} \\ u_{{{\text{qi}}}} = & \,L_{{{\text{qi}}}} \frac{{di_{{{\text{qi}}}} }}{dt} + Ri_{{{\text{qi}}}} + \omega_{{\text{e}}} \left( {L_{{{\text{di}}}} i_{{{\text{di}}}} + \psi_{{\text{m}}} } \right) \\ T_{{\text{m}}} = & \,\frac{3}{2}p\psi_{{\text{m}}} \left( {i_{{{\text{q}}1}} + i_{{{\text{q}}2}} } \right) \\ \end{aligned}$$

(5)

where u_di and u_qi are the direct-quadrature (d–q) axis voltages, respectively. L_di and L_qi are the d-q axis inductances, respectively. i_di and i_qi are the d-q axis stator currents, respectively. R is the stator resistance. ω_e is the rotor electrical angular speed. ψ_m is the d-axis flux linkage from the permanent magnet rotor. p is the pole pairs.

3 Controller Design and Analysis

3.1 Controller Design

3.1.1 LQR Control with Kalman Filters (KF)

In this section, three types of controllers are designed and compared theoretically. In the LQR control scheme (Lewis et al., 2012), $\dot{\delta }_{{{\text{aim}}}}$ is calculated from the derivative of $\delta_{{{\text{aim}}}}$. The speed, angle, and angle integral error between target signals and sensor-measured signals are selected as system states where the integral state is adopted to realize zero steady-state tracking errors:

$$\begin{gathered} \dot{x} = Ax + BT_{{\text{m}}} + d \hfill \\ \dot{\gamma }_{{{\text{aim}}}} - \dot{\gamma }_{{{\text{act}}}} = \delta_{{{\text{aim}}}} - \delta_{{{\text{act}}}} \hfill \\ A = \left[ {\begin{array}{*{20}c} {B/J} & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{array} } \right],B = \left[ {\begin{array}{*{20}c} {i_{{\text{m}}} /J} \\ 0 \\ 0 \\ \end{array} } \right],d = \left[ {\begin{array}{*{20}c} {\dot{V}_{{{\text{aim}}}} + \frac{{T_{{\text{d}}} }}{J}} \\ 0 \\ 0 \\ \end{array} } \right] \hfill \\ \end{gathered}$$

(6)

where $x = [\dot{\delta }_{{{\text{aim}}}} - \dot{\delta }_{{{\text{act}}}} { }\delta_{{{\text{aim}}}} - \delta_{{{\text{act}}}} \gamma_{{{\text{aim}}}} - \gamma_{{{\text{act}}}} ]$ reflects the system states. ${\text{T}}_{\text{d}}= -{{\text{T}}_{\text{f}}-{\text{T}}}_{\text{r}}-{\text{V}}_{\text{aim}}$ is assumed as a lumped disturbance. $\gamma_{{{\text{aim}}}} - \gamma_{{{\text{act}}}}$ is the angle integral error.

In the steering system, speed signals cannot be measured directly. The derivative of $\delta_{{{\text{act}}}}$ induces excessive noise and low pass filtering leads to severe phase delays. Owing to this, the Kalman filter is adopted owing to its balance between phase delay and noise, where $\ddot{\delta }$ is assumed as Gaussian white noise:

$$\begin{aligned} \left[ {\begin{array}{*{20}l} {\dot{\delta }} \hfill \\ {\ddot{\delta }} \hfill \\ \end{array} } \right] = & \,\left[ {\begin{array}{*{20}l} 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} \delta \hfill \\ {\dot{\delta }} \hfill \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {n_{1} } \hfill \\ {n_{2} } \hfill \\ \end{array} } \right] \\ \delta = & \,\delta_{{\text{s}}} + n_{3} \\ \end{aligned}$$

(7)

where n₁ and n₂ are the model update noises. n₃ is sensor measurement noise.

Proper Q₁ and R₁ values are chosen as the process noise covariance matrix and measurement covariance matrix, respectively. The asymptotically converging Kalman gain L₁ is calculated from the standard KF algorithm process (Kim & Sul, 1996). $\delta_{{{\text{act}}}} { }$ and $\dot{\delta }_{{{\text{act}}}}$ are given as follows:

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {\delta_{{{\text{act}},{\text{k - 1}}}} } \\ {\dot{\delta }_{k} } \\ \end{array} } \right] = \, & (1 + TA)\left[ {\begin{array}{*{20}c} {\delta_{{{\text{act}},{\text{k - 1}}}} } \\ {\dot{\delta }_{{{\text{act}},{\text{k - 1}}}} } \\ \end{array} } \right] \\ \left[ {\begin{array}{*{20}c} {\delta_{{{\text{act}},{\text{k}}}} } \\ {\dot{\delta }_{{{\text{act}},{\text{k}}}} } \\ \end{array} } \right] = & \,\left[ {\begin{array}{*{20}c} {\delta_{{\text{k}}} } \\ {\dot{\delta }_{{\text{k}}} } \\ \end{array} } \right] + L_{1} (\delta_{{{\text{s}},{\text{k}}}} - \delta_{{\text{k}}} ) \\ \end{aligned}$$

(8)

where $\delta_{{\text{k}}}$, $\delta_{{\text{act,k}}}$, and $\delta_{{\text{s,k}}}$ are the model update value, estimated value, and sensor-measured value at the k-th sample time, respectively.

In the LQR scheme, feedforward compensations from $T_{{\text{d}}}$ and $\ddot{\delta }_{{{\text{aim}}}}$ are canceled to avoid system oscillation due to inaccurate and rough feedforward reference signals. The cost function of LQR control is defined as follows:

$$J_{{{\text{cost}}}} = \int_{{t_{{\text{f}}} }}^{\infty } {(x(} t)^{{\text{T}}} Qx(t) + u(t)^{{\text{T}}} Ru(t))dt$$

(9)

where Q and R are the tracking performance weight matrix and control input limit weight matrix, respectively.

The control input is calculated using the algebraic Riccati equation (ARE). The system parameters are assumed as constant in this paper:

$$\begin{gathered} PA + A^{{\text{T}}} P - PBR^{ - 1} B^{{\text{T}}} P + Q = 0 \hfill \\ u = - R^{ - 1} B^{{\text{T}}} Px^{.} \hfill \\ \end{gathered}$$

(10)

where P is the positive definite solution of the ARE. u is the control input.

For LQR control, the controller gains depend on the pre-defined Q and R matrices. In this paper, we constrain the selection range of Q and R based on the physical properties of the steering angle and speed loop gains. Then, we adjust the magnitudes of Q and R within this range to balance tracking performance and the controlled output.

3.1.2 Robust Control

In the robust control structure diagram (Philippe, 2013), the tracking performance, noise attenuation, and actuator capacity are evaluated by mixed-sensitivity weight functions, as shown in Fig. 2. In the frequency domain, W₁ is applied to guarantee the tracking performance and large in the low-frequency part to reduce steady-state errors under external disturbances. W₂ is used to limit the control input in the high-frequency band related to motor capacity and system resonance. W₃ is used to attenuate noise beyond the system bandwidth. $\dot{\delta }$ and $\delta$ are selected as system states. Further, we use the sensor measured angle $\delta_{{\text{s}}}$ and Kalman filter observed speed $\dot{\delta }_{{{\text{act}}}}$ as system outputs:

$$\left[ {\begin{array}{*{20}c} {z_{1} } \\ {z_{2} } \\ {z_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {W_{1} } & { - W_{1} G} \\ 0 & {W_{2} } \\ 0 & {W_{3} G} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \omega \\ u \\ \end{array} } \right]$$

(11)

where $\omega = \left[ {\begin{array}{*{20}c} {\delta_{{{\text{aim}}}} } & {\dot{\delta }_{{{\text{aim}}}} } \\ \end{array} } \right]$. z₁, z₂, and z₃ are used to define the tracking performance, control input limit, and output noise attenuation, respectively.

Fig. 2

Robust control diagram

The weight functions W₁, W₂, and W₃ are shown in Eq. (12):

$$W_{1} = \frac{1}{s + 0.001}\frac{{T_{1} s + 1}}{{T_{2} s + 1}},W_{2} = \frac{{0.01\left( {T_{3} s + 1} \right)}}{{T_{4} s + 1}},W_{3} = \frac{{0.1\left( {T_{5} s + 1} \right)}}{{T_{6} s + 1}}$$

(12)

where T₁ = k₁T₂, (k₁ > 1). T₃ = k₂T₄, k₂ > 1). T₅ = k₃T₆, (k₃ < 1). s is the Laplace variable.

Combined with controller K, Eq. (11) is represented by the closed-loop state space equation. Open-loop states are extended to closed-loop states x_cl, and the system output z_∞ is defined as z_∞ = [z₁, z₂, z₃]^T:

$$\begin{gathered} \dot{x}_{cl} = \,A_{cl} x_{cl} + B_{cl} \omega \hfill \\ z_{\infty } = C_{cl} x_{cl} + D_{cl} \omega \hfill \\ \end{gathered}$$

(13)

where A_cl, B_cl, C_cl, and D_cl are the closed-loop coefficient matrices.

The state space controller K is solved using the linear matrix inequalities method:

$$\left[ {\begin{array}{*{20}c} {A_{{{\text{cl}}}}^{T} P + PA_{{{\text{cl}}}} } & {PB_{{{\text{cl}}}} } & {C_{{{\text{cl}}}}^{T} } \\ {B_{{{\text{cl}}}}^{T} P} & { - \gamma^{2} I} & {D_{{{\text{cl}}}}^{T} } \\ {C_{{{\text{cl}}}} } & {D_{{{\text{cl}}}} } & { - I} \\ \end{array} } \right] < 0$$

(14)

where P is a symmetric positive definite matrix and I is the identity matrix.

For robust control, the controller gains depend on pre-determined weight functions. Tracking performance at low, mid, and high frequencies are adjusted by T₁ and T₂ in the weight function W₁. Larger T₁ and smaller T₂ can enhance the system response. T₃ and T₄ in the weight function W₂ are used to suit different steering motor torque output performance. Smaller T₃ and larger T₄ represent better steering motor performance. T₅ and T₆ in the weight function W₃ are used to suppress high-frequency noise in the steering. Larger T₅ and smaller T₆ represent higher requirements for steering noise suppression.

3.1.3 Cascade PI Control

In conventional cascade PI control schemes, proportional control is used in the angle loop to obtain the aim speed. PI control is used in the speed loop to deal with external resistances:

$$\begin{aligned} \dot{\delta }_{{{\text{aim}}}} = & \,P_{{\text{a}}} (\delta_{{{\text{aim}}}} - \delta_{{{\text{act}}}} ) \\ T_{{{\text{aim}}}} = & \,(P_{{\text{v}}} + \frac{{I_{{\text{v}}} }}{s})(\dot{\delta }_{{{\text{aim}}}} - \dot{\delta }_{{{\text{act}}}} ) \\ \end{aligned}$$

(15)

where P_a, P_v, and I_v are the cascade PI angle loop proportional gain, speed loop proportional gain, and speed loop integral gain, respectively.

For cascade PI control, the angle loop gain determines the system’s bandwidth, while the gain of the speed loop determines the delay when changing the steering direction. However a higher gain in the steering angle loop leads to a higher system bandwidth but also results in system overshoot. A higher gain in the speed loop makes the system overcome friction more quickly, but it can also potentially reduce the system’s phase margin. In general, the magnitude of the speed loop gain depends on the characteristics of the speed signals. Low latency and low-noise speed signals can appropriately increase the speed gain.

3.2 Controller Analysis

In this paper, Bode plots are used to analyze the three types of controllers in the frequency domain. The robust controller is simplified by a zeros-poles cancellation method. Compensators C₁ and C₂ are used in the angle loop and speed loop, as shown in Eq. (16). In addition to the system bandwidth, we compare their performance at withstanding external disturbances and attenuating the speed signal noises, as illustrated in Fig. 3.

Fig. 3

Three types of controllers: a Cascade PI control; b LQR control; c robust control

The open-loop transfer functions of the three controllers are used to evaluate the system bandwidth and response, where sensor noises and external disturbances are ignored:

$$\begin{aligned} T_{{{\text{PI}}}} = \, & P_{{\text{a}}} (P_{{\text{v}}} + \frac{{I_{{\text{v}}} }}{s})G \\ T_{{{\text{LQR}}}} = \, & (P_{{{\text{q1}}}} + \frac{{I_{{{\text{q1}}}} }}{s} + sP_{{{\text{q1}}}} )G_{\nu } \\ T_{{\text{H}}} = & \,\left( {\left( {P_{{{\text{rl}}}} + \frac{{I_{{{\text{rl}}}} }}{s}} \right)C_{1} + sP_{{{\text{r2}}}} C_{2} } \right)G \\ \end{aligned}$$

(16)

Here T_PI, T_LQR, and T_H are the open-loop transfer functions of the cascade PI controller, LQR controller, and robust controller, respectively.

The Bode plots of these open-loop transfer functions are given in Fig. 4. The cutoff frequencies of the LQR and robust controllers are higher than those of the cascade PI controller due to the separation of the angle loop and speed loop, as shown in Fig. 3. However, in comparison to the cascade PI controller, LQR and robust controllers have a steeper curve slope at 0 dB, which tends to cause system overshoots. In comparison to LQR control, robust control has smaller gains in the high-frequency range and tends to reduce system noise.

Fig. 4

Open-loop transfer functions

In angle-tracking systems, the speed signal contributes to high-frequency noise. In this context, closed-loop transfer functions from speed noise to control inputs are used to assess the ability of the three controllers to attenuate control fluctuations. Figure 5 shows that the cascade PI controller tends to amplify high-frequency noise, which is likely to exist in the speed signal, in contrast to other controllers:

$$\begin{aligned} T_{{{\text{sPI}}}} = & \,\frac{{sP_{{\text{v}}} + I_{{\text{v}}} }}{{s + P_{{\text{a}}} {(}sP_{{\text{v}}} + I_{{\text{v}}} )G + s(sP_{{\text{v}}} + I_{{\text{v}}} )G}} \\ T_{{{\text{sLQR}}}} = & \,\frac{{s^{2} P_{{{\text{q2}}}} }}{{s + (sP_{{{\text{ql}}}} + I_{{{\text{q1}}}} + s^{2} P_{{{\text{q2}}}} )G}} \\ T_{{{\text{sH}}}} = \, & \frac{{s^{2} P_{{{\text{r2}}}} C_{2} }}{{s + \left( {(sP_{{{\text{rl}}}} + I_{{{\text{rl}}}} )C_{1} + s^{2} P_{{{\text{r2}}}} C_{2} } \right)G}} \\ \end{aligned}$$

(17)

where T_sPI, T_sLQR, and T_sH are closed-loop transfer functions from speed noises to the control input of the cascade PI controller, LQR controller, and robust controller, respectively.

Fig. 5

Comparison of speed noise transfer functions

In addition, the steering disturbances have a significant impact on the tracking error; the closed-loop transfer functions of disturbances with regard to angle-tracking errors can then be derived. The Bode plot results demonstrate that the cascade PI controller can effectively reduce the influence of disturbances on tracking error in the low-frequency region in comparison to other controllers, as shown in Fig. 6. As a result, Cascade PI controllers tend to have smaller steady-state errors due to external disturbances:

$$\begin{aligned} T_{{{\text{dPI}}}} = & \,\frac{sG}{{s + P_{{\text{a}}} \left( {sP_{{\text{v}}} + I_{{\text{v}}} } \right)G + s\left( {P_{{\text{v}}} s + I_{{\text{v}}} } \right)G}} \\ T_{{{\text{dLQR}}}} = & \,\frac{sG}{{s + (sP_{{{\text{ql}}}} + I_{{{\text{ql}}}} + s^{2} P_{{{\text{q2}}}} )G}} \\ T_{{{\text{dH}}}} = & \,\frac{sG}{{s + \left( {(sP_{{{\text{rl}}}} + I_{{{\text{rl}}}} )C_{1} + s^{2} P_{{{\text{r2}}}} C_{2} } \right)G}} \\ \end{aligned}$$

(18)

where T_dPI, T_dLQR, and T_dH are closed-loop transfer functions from external disturbances to the tracking errors of the cascade PI controller, LQR controller, and robust controller, respectively.

Fig. 6

Comparison of disturbance responses

In the frequency-domain analysis, different controllers exhibit distinct pros and cons. LQR and robust controllers tend to have a quicker response and higher bandwidth, with smoother control input. Cascade PI controllers tend to have smaller steady-state errors.

4 Simulation and Vehicle Experiments

To validate and compare the performance of three algorithms, we establish three controller models, the controlled plant, and the steering resistance model in the Matlab/Simulink platform. Step and sine tests are first conducted in the Simulink environment. Then, we adopt a joint simulation with Carsim vehicle dynamic model to ensure the effectiveness of the three algorithms before conducting real vehicle tests. In addition, double-lane changing tests are chosen in the Carsim/Simulink joint simulation. The overall block diagram of proposed control algorithms is illustrated in Fig. 7.

Fig. 7

Simulation block diagram of proposed control scheme

4.1 Simulations

4.1.1 Model Validation in the Simulink platform

To validate the model, step and sine wave tests were simulated in a Matlab/Simulink environment. System parameters are listed in Table 1.

Table 1 System parameters

Virtual simulations constrain control parameters within a reasonable range for practical applications, and the data collected by vehicle-mounted sensors improves the fidelity of the steering model. Particularly, we focused on the steering resistance model and compared the steering resistance data collected by tie-rod force sensors with the simulated data at different vehicle speeds. Figures 8 and 9 show a comparison of the rack forces between simulation results and sensor-measured results at 0 and 40 km/h, respectively. The results indicate that the friction characteristics of the tire-road contact at 0 km/h are perfectly matched by the LuGre friction model combined with the jacking torque. The 2-DOF vehicle model can effectively match the lateral characteristics of the tire-road contact at medium–high speeds. In addition, we add high-frequency white noise to match the practical speed signals in the Simulink platform.

Fig. 8

Comparison results of the rack forces at 0 km/h

Fig. 9

Comparison results of the rack forces at 40 km/h speed

4.1.2 Performance Validation in the Simulink Platform

The control performance of three controllers is validated first using step and various sine wave reference signals. Even though some reference signals are discontinuous or intense, we can adjust them using a rate-limiting function module and a low-pass filter. Considering the precision and inevitable noise of the sensors, we also employ some dead-zone functions. To deploy the same code using model-based design techniques, the algorithm’s sampling time is 1 ms, which is consistent with the vehicle hardware controller; Fig. 10 illustrates the step response results of three controllers. In this test case, a step target is established for classical driving scenarios such as emergency steering or obstacle avoidance maneuvers. Figure 11 illustrates the sine wave test results. In this case, sine wave steering maneuvers often occur during merging onto a ramp road or double-lane changing on highways.

Fig. 10

Step tests in the Simulink platform

Fig. 11

Sine wave tests in the Simulink platform

From Fig. 10, it can be seen that LQR and robust controllers have faster response speeds and larger steady-state errors than the cascade PI controller. Further, LQR controllers exhibit some overshoot. Figure 11 displays the responses of the three controllers at frequencies of 1 Hz, 2 Hz, and 4 Hz, with amplitudes of 20 degrees. LQR and robust controllers have smaller transient errors during fast steering processes. From Figs. 10 and 11, it can be seen that the faster responses of LQR and robust controllers result from more aggressive control inputs than the cascade PI controller. Furthermore, the cascade PI control inputs are not as effective in attenuating speed signal noise in comparison to other controllers.

Moreover, the specific and quantified indices—which include the steady-state error, overshoot, delay time, phase lag degrees(PLD), and mean absolute error (MAE)—are summarized in Table 2. The comparison results of quantitative metrics are consistent with the analysis above.

Table 2 Statistic data of tests in Simulink platform

4.1.3 Carsim/Simulink Joint Experiments

In the joint simulation, we configure the basic information of the Casim vehicle model based on the data in Table 1. This procedure demonstrates a common double-lane changing handling test at 80 km/h. The steering control module receives commands from the driver model. Carsim takes the actual steering wheel angle as input and feeds back the steering resistance torque to the Simulink module. The specific significance of joint simulation, as compared to the Simulink platform, is that the steering resistance is provided by the powerful Carsim software. Finally, we compare the results of three controllers in the joint simulations. Figure 12 shows that LQR and robust controllers exhibit similar performance and have smaller dynamic errors and faster response when changing direction compared to the cascade PI control, while cascade PI control can better match the peak of the reference command.

Fig. 12

Double lane change test

4.2 Vehicle Experiments

4.2.1 Design of the Vehicle Platform

The simulation platform in Sect. 4.1 can be used to verify the control performance of these controllers. However, the complex tire-road contact and suspension properties, sensitive sensor characteristics, field-oriented control strategies, and the inherent limitations of hardware have effects on practical operation. Furthermore, it is difficult to convey subjective feelings from the driver’s perspective in simulations. To compare these algorithms practically, a vehicle experimental platform is shown in Fig. 13. The prototype vehicle is a modified Sedan-PREFACE L provided by Geely with a non-load mass of 1.5 tons and a wheelbase of 1.8 m, which is consistent with the simulation model. Both FAA and HWA adopt a dual-winding PMSM motor and dual-redundant controllers. Two rack force sensors, which are installed at the left and right tie rod, are used to collect the resistant forces from the left and right tires, respectively. One Micro dSPACE II is used to connect the FAA and HWA subsystems through CAN communications and collect the analog signals from sensor amplifiers.

Fig. 13

Vehicle experimental platform

4.2.2 Pivot Steering Tests

In the pivot steering tests, TAS collects the steering command from the drivers and sends it to the steering controller through CAN. To evaluate the three controllers fairly, the driver performs approximate step and sine wave operations. The amplitudes of the step are approximately 100 degrees. The frequencies of the sine waves gradually increase from about 1 Hz to 2 Hz, and then to 4 Hz. The amplitudes of the sine waves decrease as the frequencies increase, which conforms to the physical law of human manipulation. It is worth noting that the resistance during a pivot turn is the highest while driving.

Furthermore, drivers also tend to complete parking maneuvers and similar actions by making rapid and sharp turns. Therefore, the pivot tests can help assess the controller’s performance under heavy loads.

Figures 14, 15 and 16 illustrate the step test and sine waves test results of the cascade PI controller, LQR controller, and robust controller, respectively. The target angle and actual angle curves of the step response are shown in the top-left subplot of these figures, while the motor current and tracking error curves are shown in the bottom-left subplot. Furthermore, the subplot in the top-right includes the target angle and actual angle curves of the sine wave response, while the subplot in the bottom-right includes the motor current and tracking error curves.

Fig. 14

Cascade PI controller pivot steering tests

Fig. 15

LQR controller pivot steering tests

Fig. 16

Robust controller pivot steering tests

From the test results, it can be seen that the LQR and robust controller have a faster response than the cascade PI controller, which is consistent with the simulation results. Furthermore, the current signals in the cascade PI controller exhibit greater fluctuations, corresponding to more noticeable mechanical vibrations and auditory noise. The steady-state errors of the LQR controller and robust controller are uncertain; however, on the whole, they are greater than that of the cascade PI controller. The reason for this phenomenon is that the friction in the actual system is passive and lies within a certain range. The remaining friction force during steering stops is uncertain. Since it is difficult to achieve complete waveform consistency in the actual manipulation process, the performance of the three controllers is compared by steady-state errors of the delay time, 1 Hz MAE, 2 Hz PLD, and 4 Hz PLD, which are summarized in Table 3.

Table 3 Statistical data of the pivot steering tests

In order to compare the performance of three controllers from a frequency-domain perspective, the CAN link between HWA and FAA systems is disconnected. The command is sent to the steering motor via dSPACE CAN module. In the real-time environment of dSPACE, the steering command frequency is set within the range of 0.1 to 10 Hz, with amplitudes of 10 degrees. Matlab system identification application is used to analyze the collected tests results. Figure 17 shows that at low frequencies, the magnitude of cascade PI control is slightly greater than LQR and robust control, which is consistent with the time-domain data. In addition, the bandwidth of LQR and robust controllers is higher than cascade PI controller.

Fig. 17

Comparison of closed-loop responses

4.2.3 Dynamic Steering Tests

The dynamic test was conducted at a parking lot exit. The vehicle first starts on a short straight line, then accelerates through a left turn ①, after which the driver is required to perform a sinusoidal steering maneuver ②. Finally, the driver completes a double-lane changing maneuver ③, as shown in Fig. 18.

Fig. 18

Map of the dynamic steering test site

In addition to signals during the static test, we also plot the vehicle velocity signal in Figs. 19, 20 and 21. In comparison to pivot steering, the motor current required for steering motion decreases sharply as the vehicle starts moving, indicating a reduction in steering load. From the test results of left turns, sinusoidal motions, and double lane changes, it can be seen that the LQR controller and robust controller exhibit smaller transient errors and faster responses. Furthermore, the performances of the three controllers in the dynamic test are summarized in Table 4.

Fig. 19

Cascade PI controller dynamic steering tests

Fig. 20

LQR controller dynamic steering tests

Fig. 21

Robust controller dynamic steering tests

Table 4 Statistic data of the dynamic steering tests

At the same time, LQR and robust controllers have smoother motor current curves, which indicates a reduction in mechanical vibrations and noise. For this, we conduct a fast Fourier analysis on the current in the ② zone for each set of controllers separately. Figure 22 shows that, compared to LQR and robust controllers, cascade PI controller has two peaks around 40 Hz and 80 Hz, resulting in higher noise. This conclusion aligns with the subjective perceptions during the vehicle experiments.

Fig. 22

Fourier analysis on the PMSM current

In both the pivot steering tests and dynamic tests, the time delay of the LQR and robust controllers is about 20 ms, while the traditional cascade PI controller has a delay of about 40 ms. From the frequency-domain results, the bandwidth of the PI controller is about 3–4 Hz, while the bandwidth of LQR and robust controllers is about 4–5 Hz.

In addition, LQR control and robust control can attenuate noise caused by rotational speed signals and decrease mechanical vibrations. On the other hand, the traditional cascade PI controller can effectively handle external disturbances and consistently maintain the steady-state error within 0.2 degrees. However, the steady-state error of the first two controllers varies from 0.2 to 1.5 degrees due to uncertainties caused by external disturbances.

5 Conclusion

In this paper, three types of controllers for angle tracking in the steering-by-wire system are designed and analyzed in detail. We use open-loop transfer functions, closed-loop transfer functions from speed noise to the control input, and closed-loop transfer functions from external disturbances to tracking errors to compare the system bandwidth and performance for speed noise attenuation and disturbance rejection. The results of frequency-domain analysis show that LQR and robust controllers have higher bandwidth, and can successfully reduce the influence of speed noise. Relatively, the cascade PI controller can reduce the effect of external disturbances to angle-tracking errors.

To verify the performance of the three controllers in the time domain, a high-fidelity model is established, where the results of the steering resistance simulation are consistent with the results collected by vehicle-mounted rack force sensors. Standard step and sinusoidal test results indicate that LQR and robust controllers have faster responses and smoother input waveforms, but have larger steady-state errors. The cascade PI controller can regulate steady-state errors within a narrow range, but its response is slower and the control input has high-frequency fluctuations.

To further validate the performance of the three algorithms considering limited motor output, limited computing resources, real sensor characteristics, and real tire-road contact, we conducted pivot steering and dynamic steering tests. The results of approximate step and sinusoidal tests in pivot steering maneuvers demonstrate that LQR and robust controllers have faster responses, smaller transient errors, and smoother current curves, but have uncertain and relatively large steady-state errors. The conventional cascade PI controller always exhibits a small steady-state error, but has a slower response speed and contains high-frequency noise in the current curves. The same conclusion can be drawn from the results of the dynamic tests, which include left-turn, sinusoidal, and double-lane changing maneuvres. Moreover, the pivot and dynamic tests reveal that the noise and vibrations sent to the cockpit in cascade PI controllers are more subjectively perceivable.

At low speeds, steering maneuvers tend to be fast. Drivers are sensitive to steering delay and steering noise. Therefore, LQR and robust controllers are recommended. At high speeds, steering maneuvers tend to be slower, and the steering load is lower, making it less likely to result in steering noise during normal situations. Drivers are more concerned about the precision of steering. Therefore, cascade PI control is recommended. Furthermore, it must be stated that the implementation of LQR and robust controllers relies on the unique architecture of the SBW system. The update time of the steering command signal is decreased from 10 ~ 20 ms to 1 ~ 2 ms, which makes the steering speed information in the steering command more meaningful.

The simulation and the actual vehicle test come to the same conclusions regarding controller performance, both in terms of the performance of a single controller or the comparison of controller performance. Further virtual simulation tests should be conducted to reduce the cost of actual vehicle calibrations and tests. Furthermore, it is necessary to introduce vehicle dynamics signals, such as the yaw rate and lateral acceleration signals, into the assessment of these three controllers in the future work.