Abstract
Let \(A\in M_2({\mathbb {Z}})\) be an expanding integer matrix and \(D=\{d_1={\textbf{0}},d_2,d_3\}\subset {\mathbb {Z}}^2\). It follows from Hutchinson (Indiana Univ Math J 30:713–747, 1981) that the generalized Sierpinski self-affine set \({\textbf{T}}(A,D)\) is the unique compact set determined by the pair (A, D) satisfing the set-valued equation \(A{\textbf{T}}(A,D)=\bigcup _{i=1}^3({\textbf{T}}(A,D)+d_i)\). In this paper, we show that Fuglede’s conjecture holds on\({\textbf{T}}(A,D)\), which states that \({\textbf{T}}(A,D)\) is a spectral set if and only if \({\textbf{T}}(A,D)\) is a translational tile. For the classical Sierpinski self-affine set \({\textbf{T}}(A,D_{c})\) with \(D_{\text {c}}=\{(0,0)^t,(1,0)^t, (0,1)^t\}\), a finer characterization of tiling set is given. As an application, we find that the classical Sierpinski self-affine tile \({\textbf{T}}(A,D_{\text {c}})\) is suitable for Kolountzakis’ conjecture on product domain. This enriches the results that are now known.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 A Review of the Fuglede Problem on Spectral Sets and Tiles
Definition 1.1
Let \(\mu \) be a Borel probability measure on \({\mathbb {R}}^n\) with compact support \(\Omega \), and let \(\langle \cdot ,\cdot \rangle \) denote the standard inner product on \({\mathbb {R}}^n\). We say that \(\mu \) is a spectral measure if there exists a countable set \(\Lambda \subset {\mathbb {R}}^n\) such that the exponential function system
forms an orthonormal basis for the Hilbert space \(L^2(\Omega ,\mu )\). In this case, we call \(\Lambda \) a spectrum of \(\mu \) and \((\mu ,\Lambda )\) a spectral pair. In particular, if \(\mu \) is the normalized Lebesgue measure supported on a Borel set \(\Omega \), then \(\Omega \) is called a spectral set.
The most classical example of spectral set is the cube \(\left[ -\frac{1}{2},\frac{1}{2}\right] ^n\), and its spectrum is the integer lattice \({\mathbb {Z}}^n\). Spectral sets have long fascinated mathematicians, which can date back to Fuglede [20], who conjectured a connection between the notation of spectrality and another geometrical notation of tiling.
Definition 1.2
We say \(\Omega \) is a translational tile with respect to a countable set \({\mathcal {T}}\subset {\mathbb {R}}^n\) if the set \(\Omega \) satisfies
or equivalently, \(\Omega \oplus {\mathcal {T}}={\mathbb {R}}^n\) and the translates \(\Omega +t,~t\in {\mathcal {T}}\), partition \({\mathbb {R}}^n\) up to null sets. In this case, \({\mathcal {T}}\) is called a translational tiling set of \(\Omega \) and the set \(\{\Omega +t\}_{t\in {\mathcal {T}}}\) is a tiling of \({\mathbb {R}}^n\).
In 1974, Fuglede [20] conjectured that the spectral sets could be characterized in geometric terms using the concept of translational tile in the following way.
Fuglede’s conjecture: \(\Omega \subset {\mathbb {R}}^n\) is a spectral set if and only if \(\Omega \) is a translational tile.
This conjecture (also called Spectral set conjecture in some literatures) inspired extensive research over the years, revealing a wealth of connections to functional analysis, combinatorics, commutative algebra, number theory and Fourier analysis. The following partial results of this conjecture are known.
-
Fuglede’s conjecture holds for lattice tiling [20].
-
Iosevich et al. [25] proved the conjecture holds for convex planar domains.
-
Lev and Matolcsi [48] completely settled this conjecture for convex domains in all dimensions.
-
The non-convex case is considerably more complicated, and is not understood even in dimension one.
 [35] established the conjecture for the union of two intervals on the real line. Fu et al. [18] proved that the conjecture holds for the self-similar set \({\textbf{T}}(4,D)=\sum _{k=1}^\infty 4^{-k}D\) with the digit set \(D=\{0,a,b,c\}\subset {\mathbb {Z}}\).
[35] established the conjecture for the union of two intervals on the real line. Fu et al. [18] proved that the conjecture holds for the self-similar set \({\textbf{T}}(4,D)=\sum _{k=1}^\infty 4^{-k}D\) with the digit set \(D=\{0,a,b,c\}\subset {\mathbb {Z}}\). -
In general setting for finite abelian groups, Fuglede’s conjecture is known to be true for cyclic groups \({\mathbb {Z}}_{p^{n} q^{k}}\), where \(n, k \in {\mathbb {N}} \) and \(k \le 6\) [50], for \({\mathbb {Z}}_{p^n}\) [36], for \({\mathbb {Z}}_{p^nq}\) [51], for \({\mathbb {Z}}_{p q r s}\) [31], for \({\mathbb {Z}}_{p^{n} q r}\) [54, 58], where p, q, r, s are different primes. For product of cyclic groups it is known that the conjecture holds for \({\mathbb {Z}}_{p^{n}} \times {\mathbb {Z}}\) [57], for \({\mathbb {Z}}_{p}\times {\mathbb {Z}}_{p}\) [26], for \({\mathbb {Z}}_{p}^{2} \times {\mathbb {Z}}_{q}^{2}\) [15] and for \( {\mathbb {Z}}_{p}^{3}\) for \( p=5,7\) [2, 16], and does not hold for \({\mathbb {Z}}_{p}^{4}\) [19, 52], where p is an odd prime. The conjecture is also true for p-adic field \({\mathbb {Q}}_p\) [17].
-
The first counterexample was given by Tao [56], which displayed a non-tiling spectral set of \({\mathbb {R}}^n\) (\(n\ge 5\)).
-
More results of non-tiling spectral sets and non-spectral tiles were also found by Matolcsi [49], Kolountzakis and Matolcsi [33, 34].
-
Fuglede’s conjecture remains open in dimensions one and two.
Although Fuglede’s conjecture in its original form was disproved for \(n\ge 3\), it plays a key role in bringing many branches of mathematics closer together. A significant contribution of Fuglede’s conjecture is creating a bridge between fractal theory and spectral theory. The primary aim of this paper is to establish a connection between tiling and spectrality of a class of fractal sets, and our main results will be presented in Sect. 2.
1.2 IFS and Fractal Measures
The problem of spectral measures is intriguing when we consider fractal measures such as self-similar/self-affine measures, and readers may refer to e.g. [14] for more general background of fractal theory.
Definition 1.3
([14, 24]) Let \(\{\phi _d(x)\}_{d\in D}\) be an iterated function system (IFS) defined by
where \(A\in M_n({\mathbb {R}})\) is an expanding real matrix (that is, all the eigenvalues of A are larger than one in module), and \(D\subset {\mathbb {R}}^n\) is a finite digit set. The self-affine measure is the unique probability measure \(\mu :=\mu _{A,D}\) satisfying
where \(\#D\) is the cardinality of the digit set D. Such a measure \(\mu _{A,D}\) is supported on the self-affine set (or attractor) \(\textbf{T}(A,D)\), which is the unique nonempty compact set that satisfies
Moreover, \({\textbf{T}}(A,D)\) can be expressed by the following radix expansion
In particular, if A is a multiple of an orthonormal matrix, \({\textbf{T}}(A,D)\) and \(\mu _{A,D}\) are often called self-similar set and self-similar measure, respectively.
It is somewhat surprising that He, Lai and Lau [23] proved that if a self-affine measure \(\mu \) is spectral, then it must be of pure type, i.e., \(\mu \) is discrete with finite support, singularly continuous or absolutely continuous with respect to Lebesgue measure. A general result was proved by Dutkay and Lai [12] that an absolutely continuous measure is a spectral one only if it is a normalized Lebesgue measure restricting on a domain \(\Omega \). In particular, if we take \(\Omega \) as some attractor \({\textbf{T}}(A,D)\), in terms of Fuglede’s conjecture, then one can consider its tiling and related properties. We say \({\textbf{T}}(A,D)\) a self-affine tile if it has positive Lebesgue measure and \(|\det (A)|=\#D\). In this case, the associated digit set D is called a tile digit set. Lagarias and Wang [38, 40] studied in detail the structure and tiling properties of self-affine tiles. On the other hand, there are few works on characterizing the digit sets yielding the self-affine tiles. Lagarias and Wang [39] and Odlyzko [53] investigated the related problem about some product-form tile digit sets on \({\mathbb {R}}\), which are extension of standard digit set. After that, Lai et al. [41, 42], Lau and Rao [43] extended product form to certain modulo product forms.
Definition 1.4
Let \(A\in M_n({\mathbb {Z}})\) be an expanding matrix and \(D\subset {\mathbb {Z}}^n\) be a digit set. We call D a standard digit set for A if D is a complete set of coset representatives of \({\mathbb {Z}}^n/A{\mathbb {Z}}^n\).
For the singularly continuous case, it can be traced back to 1998, Jorgensen and Pedersen [27] constructed the first example of singular, non-atomic spectral measure (sometimes we call this JP-spectral measure). They proved that the one-fourth Cantor measure is a spectral measure with the spectrum \(\Lambda _{\text {JP}}:=\{\sum _{k=0}^d4^k\ell _k:\ell _k\in \{0,1\},d\in {\mathbb {N}}\}\), but the standard one-third Cantor measure is non-spectral. Since then, the study of the spectrality of singular measures becomes an active research field, see [1, 5,6,7, 9, 11, 18, 23, 28, 37, 44, 55] and the references therein.
Given a self-affine measure \(\mu _{A,D}\), the most fundamental problem is to determine its spectrality or non-spectrality. In general research of spectrality, one needs to show the existence of infinite orthogonal sets and figure out which can be considered as Fourier bases in \(L^2(\mu _{A,D})\). Up to now, all these studying has closely related to the Fourier transform \({\hat{\mu }}_{A,D}\) of the measure \(\mu _{A,D}\) [see (3.1) for the definition of Fourier transform]. This observation follows from the well-known fact [27] that \(\mu _{A,D}\) is a spectral measure with a spectrum \(\Lambda \) if and only if \(\sum _{\lambda \in \Lambda }|{{\hat{\mu }}_{A,D}(\xi +\lambda )}|^2=1\) for all \(\xi \in {\mathbb {R}}^n\). Moreover, in the process of studying spectrality, following the terminology of Hadamard triple [55], leads the research to another approachable way.
Definition 1.5
Let \(A\in M_n({\mathbb {Z}})\) be an expanding matrix, and let \(D,S\subset {\mathbb {Z}}^n\) be two finite digit sets with the same cardinality. We say that (A, D, S) forms a Hadamard triple (or \((A^{-1}D, S)\) forms a compatible pair or (A, D) is admissible) if the matrix
is unitary, i.e., \(H^*H=I\), where \(H^*\) denotes the conjugate transposed matrix of H.
Jorgensen and Pedersen [27] proved that if (A, D, S) is a Hadamard triple, then \({\textbf{E}}_{\Lambda (A,S)}\) is an infinite orthogonal system in \(L^2(\mu _{A,D})\), where \( \Lambda (A,S)=\{\sum _{j=0}^{k-1} A^{*j}s_j:k\ge 1, s_j\in S \}. \) Moreover, Dutkay and Jorgensen [11, 13] believed that \(\mu _{A,D}\) is always a spectral measure if (A, D) is admissible. Łaba and Wang [37] first corroborated it on \({\mathbb {R}}\). The situation becomes more complicated when dimension \(n>1\). This problem has been considered actively under some additional assumptions [11, 55], and it was eventually addressed by Dutkay et al. [9].
Theorem 1.6
([9]) Suppose that (A, D) is admissible on \({\mathbb {R}}^n\), then \(\mu _{A,D}\) is a spectral measure.
It is natural to ask whether the converse is also true, namely, if a self-affine measure \(\mu _{A,D}\) is a spectral measure, is (A, D) admissible? This question is refuted by an example with \(A=4\) and \(D=\{0,1,8,9\}\). Fu et al. [18] show that \(\mu _{A,D}\) is a spectral measure, but (A, D) is not an admissible pair. Nevertheless, it holds in many instances, such as Dai, He, and Lau [6] proved that the Bernoulli convolution \(\mu _{\rho , D}\), where \(D=\{0,1,2,\ldots ,N-1\}\), is a spectral measure if and only if \(\rho =\frac{1}{q}\) for some integer \(q>1\) and N|q, which indicates the admissibility of \((\rho ^{-1},D)\). An et al. [1] proved that the classical Sierpinski self-affine measure \(\mu _{A,D_{c}}\) is a spectral measure if and only if \((A,D_{c})\) is admissible, where \(A\in M_2({\mathbb {Z}})\) and \(D_{c}=\{(0,0)^t,(1,0)^t,(0,1)^t\}\). These works provide valuable insights for researchers tackling spectral problems.
For the generalized Sierpinski self-affine measure \(\mu _{A,D}\), where \(A\in M_2({\mathbb {Z}})\) and the digit set \(D=\{d_1={\textbf{0}},d_2,d_3\}\subset {\mathbb {Z}}^2\), one may write
The first and second author proved that if \(\det (A)\notin 3{\mathbb {Z}}\) and \(\alpha _{1}\beta _{2}-\alpha _{2}\beta _{1}\ne 0\), then the mutually orthogonal exponential functions in \(L^2(\mu _{A,D})\) are finite [3]. Last but not least, Liu et al. [46, 47] further considered the remaining cases and gave the necessary and sufficient conditions for \(\mu _{A,D}\) to be a spectral measure. We summarize the spectrality of generalized Sierpinski self-affine measure \(\mu _{A,D}\) in Table 1.
Based on the known results mentioned above, it is not difficult to see that the spectrality of generalized Sierpinski self-affine measures has been almost completely solved. To the best of our knowledge, there are few literatures considering Fuglede’s conjecture among the spectrality of self-affine measures, the corresponding self-affine sets and their tiling properties. This is the research initial motivation of our paper. We first show that Fuglede’s conjecture holds on generalized Sierpinski self-affine sets, meanwhile, some key techniques shall be given. For the special case of the classical Sierpinski self-affine set \({\textbf{T}}(A,D_{c})\), where \(D_{c}=\{(0,0)^t,(1,0)^t,(0,1)^t\}\), we obtain a characterization of tiling set. Furthermore, inspired by Kolountzakis’ theorem [32], we find that the classical Sierpinski self-affine tile \({\textbf{T}}(A,D_{c})\) is suitable for Kolountzakis’ conjecture.
2 Main Results
The main results of this paper are summarized in this section. To study Fuglede’s conjecture on the generalized Sierpinski self-affine set \({\textbf{T}}(A,D)\), it is natural to require \(|\det (A)|=\#D=3\). Meanwhile, for the sake of convenience, in what follows, we refer to the spectral measure \(\mu _{A,D}\) as equivalent to saying that \({\textbf{T}}(A,D)\) is a spectral set.
Theorem 2.1
Let \({\textbf{T}}(A,D)\) be the generalized Sierpinski self-affine set defined by (1.2), where \(A\in M_2({\mathbb {Z}})\) with \(|\det (A)|=3\) and D is given by (1.3). Then \({\textbf{T}}(A,D)\) is a spectral set if and only if it is a translational tile.
It should be noted that Theorem 2.1 completely settles Fuglede’s conjecture on generalized Sierpinski self-affine sets. To do so, we divide the proof of Theorem 2.1 into the following two cases.
-
D is non-collinear, i.e., \(\alpha _1\beta _2-\alpha _2\beta _1\ne 0\). Our main techniques are based on a similarity transformation, which states that the tiling property of a self-affine set and its spectrality remain unchanged under some similar transformation (see Theorem 4.2). Using this fact, we prove that the spectrality of \({\textbf{T}}(M,{\mathcal {D}})\) instead of \({\textbf{T}}(A,D)\), where M and \({\mathcal {D}}\) are corresponding matrix and digit set after a similarity transformation [for more details, please refer to (4.1) and (4.2)]. Furthermore, we use some ingenious approaches to prove that \({\textbf{T}}(M,{\mathcal {D}})\) is a spectral set if and only if \({\textbf{T}}(M,{\mathcal {D}})\) is a tile when \(\eta =0\) and \(\eta >0\) in \({\mathcal {D}}\) respectively (see Theorems 4.3 and 4.5). In particular, we point out that our ideas and techniques are closely related to the entries in the matrix M.
-
D is collinear, i.e., \(\alpha _1\beta _2-\alpha _2\beta _1=0\). The key to solving this case is to give the equivalent characterization of \({\mathcal {Z}}(m_D)\ne \emptyset \), where \({\mathcal {Z}}(m_D)=\{\xi :m_{D}(\xi )=\frac{1}{\#D}\sum _{d\in D}{e^{2\pi i\langle d,\xi \rangle }}=0\}\). To be more precise, there exists an integer vector \(v\in {\mathbb {Z}}^2\setminus \{{\textbf {0}}\}\) such that \(D=\{0,n,m\}v\) with \(n,m\in {\mathbb {Z}}\) and \(\{n,m\}=\{1,2\}\pmod 3\) (see Lemma 4.12). Moreover, the proof is also based on the fact that the set of vectors \(\{v, Av\}\) is linearly independent.
Owing to the generic of the digit set D, the proof of Theorem 2.1 is not very well dealt with. However, for the special case that D is the classical digit
we have the following finer results.
Theorem 2.2
Let \({\textbf{T}}(A,D_{c})\) be the classical Sierpinski self-affine set defined by (1.2), where \(A\in M_2({\mathbb {Z}})\) with \(|\det (A)|=3\) and \(D_{c}\) is given by (2.1). Then the following four statements are equivalent:
-
(i)
\({\textbf{T}}(A,D_{c})\) is a spectral set;
-
(ii)
\(A=\begin{bmatrix} a &{} b\\ c&{} d \end{bmatrix}\) satisfies \(a-c\equiv b-d\equiv 0 \pmod 3\);
-
(iii)
\(D_{c}\) is a standard digit set for A;
-
(iv)
\({\textbf{T}}(A,D_{c})\) is a translational tile.
Furthermore, if \({\textbf{T}}(A,D_{c})\) is a spectral set, then \({\mathbb {Z}}^2\) is the unique spectrum containing \({\textbf{0}}\) and it is a tiling set for \({\textbf{T}}(A,D_{c})\).
As an application, we will show that the classical Sierpinski self-affine tile \({\textbf{T}}(A,D_{c})\) is suitable for Kolountzakis’ conjecture on the product domain.
Conjecture 2.3
(Kolountzakis’ conjecture, [32]) Let \(U\subset {\mathbb {R}}^n\) and \(V\subset {\mathbb {R}}^m\) be two bounded Lebesgue measurable sets. Then \(\Omega =U\times V\) is a spectral set if and only if U and V are both spectral sets.
It is known [28] that if \(U\subset {\mathbb {R}}^n\) and \(V\subset {\mathbb {R}}^m\) are both spectral sets, then their Cartesian product \(\Omega =U\times V\) is a spectral set in \({\mathbb {R}}^n\times {\mathbb {R}}^m\). However, the “only if" part of this conjecture is the non-trivial one. The difficulty lies in that we assume the product set \(\Omega \) to be spectral, but we do not make any assumption that the spectrum \(\Lambda _{\Omega }\) also has a product structure, so it is not obvious which sets \(\Lambda _U\) and \(\Lambda _V\) may serve as spectra for the factors U and V, respectively. To our knowledge, there are few results on this conjecture. Greenfeld and Lev [21] proved that in the case where one of the factors, say U, is an interval on real line, Conjecture 2.3 holds. In [32], it was established, using a different approach, that the conjecture is also true if the set U is the union of two intervals in \({\mathbb {R}}\). Recently, the conjecture was proved when the factor U is a convex polygon in \({\mathbb {R}}^2\) [22].
Interestingly enough, if we substitute the factor U for the classical Sierpinski self-affine tile \({\textbf{T}}(A,D_{c})\), where \(D_{c}\) is given by (2.1), we can obtain the following Theorem 2.4. Although it is only a class of simple examples, it provides a method to construct a number of sets which are non-convex, satisfying the spectrality equivalent over the product domain. In this sense, our result gives a supplement to this problem. For later statements, we use \({\mathcal {L}}(\Omega )\) to denote the Lebesgue measure of a subset \(\Omega \subset {\mathbb {R}}^n\).
Theorem 2.4
Let \({\textbf{T}}(A,D_{c})\) be the classical Sierpinski self-affine tile defined by (1.2), where \(A\in M_2({\mathbb {Z}})\) and \(D_{c}\) is given by (2.1), and let V be a bounded Lebesgue measurable set in \({\mathbb {R}}^n\) with \({\mathcal {L}}(V)=1\). Then the product domain \(\Omega ={\textbf{T}}(A,D_{c})\times V\) is a spectral set if and only if \({\textbf{T}}(A,D_{c})\) and V are both spectral sets.
This paper is organized as follows. In Sect. 3, we introduce some basic definitions and several lemmas needed to prove our main results. In Sect. 4, we are committed to proving Theorem 2.1. As applications, in Sect. 5, we prove Theorems 2.2 and 2.4. Finally, some further results and remarks are given in Sect. 6.
3 Preliminaries
In this section, we will introduce some standard notations and recall some basic definitions related to self-affine measures. We collect some known results on the properties of Hadamard triple that we will use in our proof, and others concerning self-affine tiles.
Let \(\mu _{A,D}\) be a self-affine measure defined by (1.1), the Fourier transform of it is defined as usual,
where \(A^*\) denotes the transpose of A and \(m_{D}(\cdot )=\frac{1}{\#D}\sum _{d\in D}{e^{2\pi i\langle d,\cdot \rangle }}\) is the mask polynomial of D. It is easy to see that \(m_D(\cdot )\) is a \({\mathbb {Z}}^n\)-periodic function if \(D\subset {\mathbb {Z}}^n\). Let \({\mathcal {Z}}(f)=\{x:f(x)=0\}\) be the zero set of a function f. It follows from (3.1) that
For any two distinct \(\lambda _1,\lambda _2\in {\mathbb {R}}^n\), the orthogonality condition means that
It is easy to see that for a countable set \(\Lambda \subset {\mathbb {R}}^n\), \({\textbf{E}}_\Lambda =\{e^{2\pi i\langle \lambda ,x\rangle }:\lambda \in \Lambda \}\) is an orthogonal family of \(L^2(\mu _{A,D})\) if and only if
As the properties of spectra are invariant under a translation, one may assume \({\textbf{0}}\in \Lambda \), and hence \(\Lambda \subset \Lambda -\Lambda \).
For a discrete set \(E\subset {\mathbb {R}}^n\), let \(\delta _E=\frac{1}{\#E}\sum _{e\in E}\delta _e\), where \(\delta _e\) is the Dirac measure at the point e. The following lemma gives an effective method to construct spectra of discrete-type measures.
Lemma 3.1
([9, 37]) Let \(A\in M_n({\mathbb {Z}})\) be an expanding matrix, and let \(D,S\subset {\mathbb {Z}}^n\) be two finite digit sets with the same cardinality. Then the following three affirmations are equivalent:
-
(i)
(A, D, S) is a Hadamard triple;
-
(ii)
\(m_{D}(A^{*-1}(s_1-s_2))=0\) for any distinct \(s_1, s_2\in S\);
-
(iii)
\((\delta _{A^{-1}D},S)\) is a spectral pair.
The following proposition relates the Hadamard triple to the self-affine tile. It provides an idea to prove direction of “spectral \(\Rightarrow \) tile" of Fuglede’s conjecture. Although it can be found in [8], for the sake of readability, we briefly give the proof here.
Proposition 3.2
Suppose that (A, D) is admissible, then the elements of D belong to different residual classes of \({\mathbb {Z}}^2/A{\mathbb {Z}}^2\). Moreover, if \(|\det (A)|=\# D\), then D is a standard digit set for A.
Proof
Since (A, D) is admissible, it follows that there exists \(S\subset {\mathbb {Z}}^n\) such that (A, D, S) is a Hadamard triple. This implies that the rank of the matrix
which is recorded as \(\text {R}(H)\), is equal to the cardinality of D. That is, \(\text {R}(H)=\#D\). However, if there exist \(d_1, d_2\in D\) such that \(d_2=d_1+A z\) for some \(z\in {\mathbb {Z}}^{2}\), then for any \(s \in S\),
This means that H has two identical columns, and thus \(\text {R}(H)<\#D\), a contradiction. So each element in D must be a distinct representative in \({\mathbb {Z}}^{2}/A{\mathbb {Z}}^{2}\). Moreover, if \(|\det (A)|=\# D\), it follows from Definition 1.4 that D is a standard digit set for A. This ends the proof. \(\square \)
Lagarias and Wang [40] gave the following characterization on standard digit set.
Theorem 3.3
([40]) Every integralFootnote 1 self-affine tile \({\textbf{T}}(A,D)\) coming from a standard digit set gives a lattice tiling of \({\mathbb {R}}^n\) with some lattice \({\mathcal {T}}\subset {\mathbb {Z}}^n\).
In [29], Kenyon provided an effective criterion to determine whether a self-similar set is a tile or not in dimension one. Inspired by this, Lagarias and Wang [39] derived the following equivalent conditions to verify when a self-affine set has positive Lebesgue measure.
Theorem 3.4
([39]) For any expanding matrix \(A\in M_n({\mathbb {Z}})\) and a finite digit set \(D\subset {\mathbb {Z}}^n\) with \({\#D}=|\det (A)|\), the following three conditions are equivalent:
-
(i)
\({\textbf{T}}(A,D)\) has positive Lebesgue measure;
-
(ii)
For each \(k\ge 1\), the set \(\sum _{j=0}^{k-1} A^jD\) contains \((\#D)^k\) distinct elements;
-
(iii)
For each \(s\in {\mathbb {Z}}^n\setminus \{{\textbf {0}}\}\), there exists a nonnegative integer \(k=k(s)\) such that s is the zero of the function \(h_k(x)=\frac{1}{{\#D}}\sum _{d\in D}e^{2\pi i\langle A^{-k}d,x\rangle }.\)
In order to present some lemmas conveniently, in what follows we define
The following lemma is a special case in [4, Lemma 4.1], which is useful for our further investigations.
Lemma 3.5
([4]) Let \(A\in M_2({\mathbb {Z}})\) be an expanding matrix and \({\mathcal {F}}\) be given by (3.4). Then \(A{\mathcal {F}}={\mathcal {F}} \pmod {{\mathbb {Z}}^2}\) if and only if \(\det (A)\notin 3{\mathbb {Z}}\).
In this paper, we will mainly use the equivalence conditions in Theorem 3.4 to investigate the tiling property of \({\textbf{T}}(A,D)\). In fact, by (3.2) and Theorem 3.4, it is not difficult to find that \({\textbf{T}}(A,D)\) is a tile if and only if
Based on the zero set \({\mathcal {Z}}(m_D)\) of generalized Sierpinski self-affine measure \(\mu _{A,D}\), we first establish four preparatory lemmas.
Lemma 3.6
Let \(A\in M_2({\mathbb {Z}})\) be an expanding matrix with \(|\det (A)|=3\) and \({\mathcal {F}}\) be given by (3.4). Suppose that \(A\xi \in {\mathbb {Z}}^2\) for some \(\xi \in {\mathcal {F}}\). Then the following statements hold.
-
(i)
\(\bigcup _{j=1}^\infty A^j \big (\pm \xi +{\mathbb {Z}}^2\big )={\mathbb {Z}}^2{\setminus }\{\textbf{0}\} \).
-
(ii)
For any \(v\in {\mathbb {Z}}^2\setminus \{\textbf{0}\}\), there exist unique \(\xi _0\in \{\pm \xi \}\), \(j\in {\mathbb {N}}\) and \(u\in {\mathbb {Z}}^2\) such that \(A^j(\xi _0+u)=v\).
Proof
(i) Firstly, \(\bigcup _{j=1}^\infty A^j \big (\pm \xi +{\mathbb {Z}}^2\big )\subset {\mathbb {Z}}^2\) is directly obtained due to \(A\in M_2({\mathbb {Z}})\) and \(A\xi \in {\mathbb {Z}}^2\). Furthermore, we have \( {\textbf {0}}\notin \bigcup _{j=1}^\infty A^j \big (\pm \xi +{\mathbb {Z}}^2\big ). \) Indeed, if there exist \(j_0\in {\mathbb {N}}\) and \(v_0\in {\mathbb {Z}}^2\) such that \({\textbf {0}}=A^{j_0}(\pm (\xi +v_0))\), then we obtain \(\pm (\xi +v_0)=A^{-j_0}{} {\textbf {0}}={\textbf {0}}\), which implies \(\xi =-v_0\in {\mathbb {Z}}^2\). This contradicts the fact \(\xi \notin {\mathbb {Z}}^2\), hence \( \bigcup _{j=1}^\infty A^j \big (\pm \xi +{\mathbb {Z}}^2\big )\subset {\mathbb {Z}}^2{\setminus }\{{\textbf {0}}\}. \)
Secondly, we devote to proving \( \bigcup _{j=1}^\infty A^j \big (\pm \xi +{\mathbb {Z}}^2\big )\supset {\mathbb {Z}}^2{\setminus }\{{\textbf {0}}\}. \) Let
By a direct calculation, one can easily get that
If there exists \(\xi \in {\mathcal {F}}\) such that \(A\xi \in {\mathbb {Z}}^2\), without loss of generality, we suppose \(\xi =(\frac{1}{3},\frac{2}{3})^t\). Then Lemma 3.1 implies that \((A,D_1)\) is admissible, and the elements of \(D_1\) belong to different residual classes of \({\mathbb {Z}}^2/A{\mathbb {Z}}^2\) by Proposition 3.2. Since \(|\det (A)|=3\), it follows that \(D_1\) is a standard digit set for A, and then \({\textbf{T}}(A,D_1)\) is a tile by Theorem 3.3. Therefore, Theorem 3.4 [also see (3.5)] shows that
Similarly, for other \(\xi \in {\mathcal {F}}\), one may also find a suitable digit set from \(D_1, D_2, D_3\) and \(D_4\) such that it is a standard digit set for A. Hence we also have \( \bigcup _{j=1}^\infty A^j \big (\pm \xi +{\mathbb {Z}}^2\big )={\mathbb {Z}}^2{\setminus }\{{\textbf {0}}\}. \)
(ii) Suppose, on the contrary, that there exist \(v\in {\mathbb {Z}}^2\setminus \{{\textbf {0}}\}\), \(j_1, j_2\in {\mathbb {N}}\), \(u_1,u_2\in {\mathbb {Z}}^2\) and \(\xi _1, \xi _2 \in \{\pm \xi \}\) such that
If \(j_1\ne j_2\), without loss of generality, suppose \(j_1< j_2\), then \(\xi _1+u_1=A^{j_2-j_1}(\xi _2+u_2)\). This is impossible since \(A^{j_2-j_1}(\xi _2+u_2)\in {\mathbb {Z}}^2\) and \(\xi _1+u_1\in {\mathcal {F}} +{\mathbb {Z}}^2\). Thus \(j_1=j_2\) and \(A^{j_1}(\xi _1+u_1)=v=A^{j_1}(\xi _2+u_2)\). Note that A is a nonsingular matrix, it is easy to deduce that \(\xi _1=\xi _2\) and \(u_1=u_2\). This completes the proof of Lemma 3.6. \(\square \)
Lemma 3.7
Let \(A\in M_2({\mathbb {Z}})\) be an expanding matrix with \(|\det (A)|=3\) and \({\mathcal {F}}\) be given by (3.4). If there exists an integer \(r>1\) such that \(A^r\xi \in {\mathbb {Z}}^2\) and \(A^{r-1}\xi \notin {\mathbb {Z}}^2\) for some \(\xi \in {\mathcal {F}}\), then
Proof
Since \(A\in M_2({\mathbb {Z}})\) and \(A^r\xi \in {\mathbb {Z}}^2\), using the same argument as in the proof of Lemma 3.6, we can easily carry out
Since \(A^{r-1}\xi \notin {\mathbb {Z}}^2\), it follows from \(A\in M_2({\mathbb {Z}})\) that \(A^i\xi \in {\mathcal {F}}\pmod {{\mathbb {Z}}^2}\) for all \(1\le i<r\). Let \(A^{i}(\pm \xi )=\pm \xi _{i}\pmod {{\mathbb {Z}}^2}\) for \(1\le i<r\), where \(\xi _{i}\in {\mathcal {F}}\). This together with \(A\in M_2({\mathbb {Z}})\) implies
where \(v_{r-1}\in {\mathbb {Z}}^2\). By \(A^r\xi \in {\mathbb {Z}}^2\) and the definition of \(\xi _{r-1}\), we can get \(A\xi _{r-1}\in {\mathbb {Z}}^2\). In view of Lemma 3.6, we obtain
Now we suppose \(\bigcup _{j=r}^\infty A^j \big (\pm \xi +{\mathbb {Z}}^2\big )={\mathbb {Z}}^2{\setminus }\{{\textbf {0}}\}. \) According to (3.6) and (3.7), one has
Since \(A\xi _{r-1}\in {\mathbb {Z}}^2\), it follows from Lemma 3.6 that for any \(v\in {\mathbb {Z}}^2\setminus \{{\textbf {0}}\}\), there exist unique \(j\in {\mathbb {N}}\), \(\xi _0\in \{\pm \xi _{r-1}\}\) and \(u\in {\mathbb {Z}}^2\) such that \(A^j(\xi _0+u)=v\). So the above equation holds only if \(A{\mathbb {Z}}^2={\mathbb {Z}}^2\), which implies \(|\det (A)|=1\). This contradicts the assumption \(|\det (A)|=3\). Therefore, \( \bigcup _{j=r}^\infty A^j \big (\pm \xi +{\mathbb {Z}}^2\big )\subsetneqq {\mathbb {Z}}^2{\setminus }\{{\textbf {0}}\}. \) \(\square \)
Lemma 3.8
Let \(A\in M_2({\mathbb {Z}})\) be an expanding matrix with \(|\det (A)|=3\) and \(\zeta =\left( \frac{l_1}{3^{k_1}\gamma _1},\frac{l_2}{3^{k_2}\gamma _2} \right) ^t\), where \(l_i\in {\mathbb {Z}}\), \(k_i \in {\mathbb {N}}\) and \(\gamma _i\in {\mathbb {Z}}\setminus 3{\mathbb {Z}}\) for \(i=1,2\). If \(A^j\zeta \in {\mathbb {Z}}^2\) for some \(j\in {\mathbb {N}}\), then \(\gamma _i\mid l_i\) for \(i=1,2\).
Proof
Since \(A^j\zeta \in {\mathbb {Z}}^2\) for some \(j\in {\mathbb {N}}\), there exists a vector \(v\in {\mathbb {Z}}^2\) such that
Thus we conclude from \(|\det (A)|=3\) that \(\left( \frac{l_1}{3^{k_1}\gamma _1},\frac{l_2}{3^{k_2}\gamma _2} \right) ^t=A^{-j}v=\frac{1}{3^j}A'v\) for an integer matrix \(A'\), which implies that \(\gamma _i\mid l_i\) for \(i=1,2\). \(\square \)
Lemma 3.9
Let \(A\in M_2({\mathbb {Z}})\) be an expanding matrix with \(|\det (A)|=3\) and \({\mathcal {F}}\) be given by (3.4). Then there exists a unique \(\pm \xi \in {\mathcal {F}}\) such that \(A(\pm \xi )\in {\mathbb {Z}}^2\).
Proof
We first prove the existence. Suppose otherwise, that \(A(\xi )\notin {\mathbb {Z}}^2\) for any \(\xi \in {\mathcal {F}}\). Then \(A\in M_2({\mathbb {Z}})\) implies that \(A{\mathcal {F}}\subset {\mathcal {F}}+{\mathbb {Z}}^2\). It follows from \(|\det (A)|=3\) and Lemma 3.5 that \(A{\mathcal {F}}\subsetneqq {\mathcal {F}}\pmod {{\mathbb {Z}}^2}\). This illustrates that there exist \(\xi _0,\xi _1,\xi _2\in {\mathcal {F}}\) such that \(A\xi _1=\xi _0=A\xi _2\pmod {{\mathbb {Z}}^2}\), and then \(A(\xi _1-\xi _2)\in {\mathbb {Z}}^2\). This contradicts the fact \(A(\xi _1-\xi _2)\in A({\mathcal {F}}+{\mathbb {Z}}^2)\subset {\mathcal {F}}+{\mathbb {Z}}^2\), and hence there must exist \(\xi \in {\mathcal {F}}\) such that \(A\xi \in {\mathbb {Z}}^2\).
Next we prove the uniqueness. Suppose there exist two elements \(\eta _1,\eta _2\in {\mathcal {F}}\) with \(\eta _1\ne \pm \eta _2\) such that \(A\eta _1,A\eta _2 \in {\mathbb {Z}}^2\), then \(A(\pm (\eta _1+\eta _2)), A(\pm (\eta _1-\eta _2))\in {\mathbb {Z}}^2\). It can be easily verified that \(\eta _1,\eta _2, \eta _1-\eta _2, \eta _1+\eta _2 \pmod {{\mathbb {Z}}^2}\) are four distinct elements. Thus \(A{\mathcal {F}}\subset {\mathbb {Z}}^2\). Combining this and \((1/3,0)^t, (0,1/3)^t\in {\mathcal {F}}\), it is easy to infer that the entries of the matrix A belong to \(3{\mathbb {Z}}\), i.e., \(A\in M_2(3{\mathbb {Z}})\). This gives \(9\mid \det (A)\), which contradicts the fact \(|\det (A)|=3\). The desired result follows. \(\square \)
4 Proof of Theorem 2.1
In this section, we focus on proving Theorem 2.1. Our proof is summarized by the diagram in Fig. 1.
Logical Diagram of Proof for Theorem 2.1
4.1 Non-collinear Digit
4.1.1 Techniques
We first introduce a key technique, which plays an important role in the proof of our main results.
Lemma 4.1
(Similarity transformation) Let \(A_1, A_2\in M_n({\mathbb {R}})\) be two expanding matrices, and let \(D_1, D_2\subset {\mathbb {R}}^n\) be two finite digit sets with the same cardinality. If there exists a matrix \(Q\in M_n({\mathbb {R}})\) such that \(A_2=QA_1Q^{-1}\) and \(D_2=QD_1\), then
-
(i)
\(\mu _{A_1,D_1}\) is a spectral measure with a spectrum \(\Lambda \) if and only if \(\mu _{A_2,D_2}\) is a spectral measure with a spectrum \(Q^{*-1}\Lambda \).
-
(ii)
\({\textbf{T}}(A_1,D_1)\) is a tile with a tiling set \({\mathcal {T}}\) if and only if \({\textbf{T}}(A_2,D_2)\) is a tile with a tiling set \(Q{\mathcal {T}}\).
Proof
The conclusion (i) can be get directly from Lemma 4.1 in [10]. For (ii), since
and
the assertion follows. \(\square \)
Lemma 4.1 tells us that the spectral and tiling properties maintain invariant under a similarity transformation. Based on this fact, we shall always assume that \(\gcd (\alpha _1,\alpha _2,\beta _1,\beta _2)=1\). Below we will give a specific similar matrix. In particular, it should be noticed that we have designed a similarity transformation so that we can convert the difficulties in the proof process into some simple cases to reach the desired result.
Let \(A\in M_2({\mathbb {Z}})\) with \(|\det (A)|=3\) and \(D=\{(0,0)^t,(\alpha _1,\alpha _2)^t,(\beta _1,\beta _2)^t\}\) with \(\alpha _1\beta _2-\alpha _2\beta _1\ne 0\). We can write
and \(\alpha _1\beta _2-\alpha _2\beta _1=3^{\eta }\gamma \) for some integers \(\eta \ge 0\) and \(3\not \mid \gamma \). Without loss of generality, assume \(\gcd (\alpha _1,\alpha _2)=\sigma \) with \(3\not \mid \sigma \) (otherwise, we can choose \(\sigma =\gcd (\beta _1,\beta _2)\) with \(3\not \mid \sigma \), since \(\gcd (\alpha _1,\alpha _2,\beta _1,\beta _2)=1\)). Let \(\alpha _1=\sigma t_1\) and \(\alpha _2=\sigma t_2\) with \(\gcd (t_1,t_2)=1\), then there exist two integers p and q such that \(pt_1+qt_2=1\). It is easy to check that \(\sigma =p\alpha _1+q\alpha _2\) and \(\sigma \mid \gamma \). For convenience, we denote \(\omega =p\beta _1+q\beta _2\) and \(\vartheta =\gamma /\sigma \notin 3{\mathbb {Z}} \). Take
Note that \(t_2\alpha _1=t_1\alpha _2\) and \(t_1\beta _2-t_2\beta _1=3^\eta \vartheta \), then
and
For the sake of simple symbols, we also write \(M=\begin{bmatrix} a&{}b \\ c&{}d \end{bmatrix}\) because it is easy to verify that M is still expanding and \(|\det (M)|=|\det (A)|=3\). By a direct calculation, we have
where
and
According to Lemma 4.1, our aim can be converted to considering the spectral and tiling properties of \({\textbf{T}}(M,{\mathcal {D}})\). So Theorem 2.1 is equivalent to say
Theorem 4.2
Let \({\textbf{T}}(M,{\mathcal {D}})\) be defined by (1.2), where M and \({\mathcal {D}}\) are given by (4.1) and (4.2) respectively. Then \({\textbf{T}}(M,{\mathcal {D}})\) is a spectral set if and only if it is a translational tile.
Notice that after a similarity transformation, the digit set D is converting to a new one \({\mathcal {D}}\) which is in form of upper triangle, and entry \(3^{\eta }\vartheta \) is closely related to powers of the variable 3 [see (4.2)]. This observation of \({\mathcal {D}}\) leads us to decompose the proof of Theorem 4.2 into two cases \(\eta =0\) and \(\eta >0\).
4.1.2 Case I, \(\eta =0\)
Theorem 4.3
Let \({\textbf{T}}(M,{\mathcal {D}})\) be defined by (1.2), where M and \({\mathcal {D}}\) are given by (4.1) and (4.2) respectively. If \(\eta =0\) in \({\mathcal {D}}\), then \({\textbf{T}}(M,{\mathcal {D}})\) is a spectral set if and only if it is a translational tile.
Proof
Suppose \({\textbf{T}}(M,{\mathcal {D}})\) is a translational tile. Applying Theorem 3.4, we know that for any \(z\in {\mathbb {Z}}^2{\setminus }\{{\textbf {0}}\}\), there exists an integer \(j\ge 1\) such that \(m_D((M^*)^{-j}z)=0\). This implies \({\mathbb {Z}}^2{\setminus }\{{\textbf {0}}\} \subset \bigcup _{j=1}^\infty M^{*j}{\mathcal {Z}}(m_{{\mathcal {D}}})\). As \(\eta =0\), it follows from (4.3) that \({\mathcal {Z}}(m_{\mathcal {D}})=Z'_{1} \cup Z'_2\) with
and
For any \(\xi \in {\mathcal {Z}}(m_{{\mathcal {D}}})\) satisfying \(M^{*j}\xi \in {\mathbb {Z}}^2\) for a positive integer j, it follows from (4.4), (4.5) and Lemma 3.8 that \(\xi \in \{(l_1/3, l_2/3)^t: l_1\in {\mathbb {Z}}{\setminus } 3{\mathbb {Z}}, l_2\in {\mathbb {Z}}\}\). Furthermore, it can be easily checked that \(\pm (\vartheta /3, (2\sigma -\omega )/3)^t \in {\mathcal {Z}}(m_{{\mathcal {D}}})\) and any \(\xi =(l_1/3, l_2/3)^t\in {\mathcal {Z}}(m_{{\mathcal {D}}})\) satisfies \(\xi =\pm (\vartheta /3, (2\sigma -\omega )/3)^t \pmod {{\mathbb {Z}}^2}\), where \(\vartheta =\gamma /\sigma \in {\mathbb {Z}}\setminus 3{\mathbb {Z}}\). Hence \({\mathbb {Z}}^2{\setminus }\{{\textbf {0}}\} \subset \bigcup _{j=1}^\infty M^{*j}{\mathcal {Z}}(m_{{\mathcal {D}}})\) and the \({\mathbb {Z}}^2\)-periodic of \(m_{{\mathcal {D}}}\) implies that
With Lemmas 3.6 and 3.7, we conclude that \(M^{*}(\vartheta /3, (2\sigma -\omega )/3)^t\in {\mathbb {Z}}^2.\) Let \(S=\{(0,0)^t,\pm M^{*}(\vartheta /3, (2\sigma -\omega )/3)^t\}\). In view of Lemma 3.1, one can easily get that \((M,{\mathcal {D}},S)\) is a Hadamard triple. Therefore, \({\textbf{T}}(M,{\mathcal {D}})\) is a spectral set by Theorem 1.6, which proves the sufficiency.
Next we prove the necessity. Suppose \({\textbf{T}}(M,{\mathcal {D}})\) is a spectral set, it follows from Table 1 that \((M,{\mathcal {D}})\) is admissible. Together with Proposition 3.2 and \(|\det (M)|=3=\#{\mathcal {D}}\), it shows that \({\mathcal {D}}\) is a standard digit set of M. Thus \({\textbf{T}}(M,{\mathcal {D}})\) is a translational tile by Theorem 3.3. We complete the proof. \(\square \)
4.1.3 Case II, \(\eta >0\)
For Case II, we need to use a different method from Case I to complete the proof. A key technique is to classify matrices and investigate the properties of corresponding self-affine sets. Recall that \(M\in M_2({\mathbb {Z}})\) is an expanding matrix with \(|\det (M)|=3\), we use the residue system of modulo 3 and rewrite the matrix M in the following form:
where \(s\ge 1\), \(a,b,d\in {\mathbb {Z}}\) and \(c\in ({\mathbb {Z}}\setminus 3{\mathbb {Z}})\cup \{0\}\), and the entries of the matrix \(M_k\) belong to the set \(\{0,1,2\}\). It is obvious that s can be any positive integer if \(c=0\). Without loss of generality, in the rest of this paper, we always assume \(s\ge \eta \) in this case. As \(|\det (M)|=3\), there are nine different classifications of matrices \(M_k\) as follows:
where \(p_1,p_2,p_3,p_4\in \{1,2\}\) and \(p_1p_4-p_2p_3\in 3{\mathbb {Z}}\).
Fix \(k\in \{1,2,\ldots ,9\}\), denote
Furthermore, denote
The following theorem gives some necessary and sufficient conditions for \(\mu _{M,{\mathcal {D}}}\) to be a spectral measure.
Theorem 4.4
([47]) With the above notations, the following statements hold.
-
(i)
\(\mu _{M,{\mathcal {D}}}\) is a spectral measure if and only if there exists a matrix \(Q\in M_2({\mathbb {R}})\) such that \(({\tilde{M}},{\tilde{D}})\) is admissible, where \({\tilde{M}}=QMQ^{-1}\) and \({\tilde{D}}=Q{\mathcal {D}}\).
-
(ii)
If \(\sigma -2\omega \in 3{\mathbb {Z}}\), then \(\mu _{M,{\mathcal {D}}}\) is a spectral measure if and only if \(M\in {\mathfrak {B}}_1\cup {\mathfrak {B}}_2\).
-
(iii)
If \(\sigma -2\omega \notin 3{\mathbb {Z}}\) and \(\mu _{M,{\mathcal {D}}}\) is a spectral measure, then \(M\in {\mathfrak {B}}_3\).
We now are in a position to present our main result in this subsection as follows.
Theorem 4.5
Let \({\textbf{T}}(M,{\mathcal {D}})\) be defined by (1.2), where M and \({\mathcal {D}}\) are given by (4.1) and (4.2) respectively. If \(\eta >0\) in \({\mathcal {D}}\), then \({\textbf{T}}(M,{\mathcal {D}})\) is a spectral set if and only if it is a translational tile.
Before stating the proof of Theorem 4.5, we need some technical preparations.
Proposition 4.6
Let \(M=\begin{bmatrix} 3a&{}3b\\ 3c+p&{}3d \end{bmatrix}\in M_2({\mathbb {Z}})\) be an expanding matrix with \(|\det (M)|=3\) and \(p\notin 3{\mathbb {Z}}\), and let \({\mathcal {D}}\) be given by (4.2). If \(\eta >0\) and \(\sigma -2\omega \notin 3{\mathbb {Z}}\) in \({\mathcal {D}}\), then \({\textbf{T}}(M,{\mathcal {D}})\) is not a tile.
Proof
In order to prove \({\textbf{T}}(M,{\mathcal {D}})\) is not a tile, by Theorem 3.4 and (4.3), we only need to show that
For this purpose, we first prove the following claim.
Claim Let \(\lambda _1,\lambda _2\in {\mathcal {Z}}(m_{{\mathcal {D}}})\). If \(j_1,j_2\in {\mathbb {N}}\) are the least positive integers such that \(M^{*j_{1}}\lambda _1,M^{*j_{2}}\lambda _2\in {\mathbb {Z}}^2\), then \(j_{1}=j_{2}:=j_0\ge 2\) and \(M^{*j_{0}-1}\lambda _i\in \{\pm (\frac{1}{3},0)^t\} \pmod {{\mathbb {Z}}^2}\) for \(i=1,2\). Moreover, if \(\lambda _1,\lambda _2\in Z_k\) for \(k=1\) or 2, then \(M^{*j_{0}-2}\lambda _1=M^{*j_{0}-2}\lambda _2\in {\mathcal {F}} \pmod {{\mathbb {Z}}^2}\).
Proof of Claim
We first prove \(j_{1}=j_{2}:=j_0\ge 2\). For any \(j\ge 1\), a simple calculation gives
where \(a_j, b_j\in {\mathbb {Z}}\), \(s_{1j},s_{2j}\in {\mathbb {N}}\) and \(c_j,d_j\notin 3{\mathbb {Z}}\). As \(\sigma , \gamma ,\sigma -2\omega \notin 3{\mathbb {Z}}\), it follows from (4.3) and Lemma 3.8 that \(\lambda _i=\left( \frac{l_{i1}}{3},\frac{l_{i2}}{3^{\eta +1}} \right) ^t\) with \(l_{i1},l_{i2}\in {\mathbb {Z}}{\setminus } 3{\mathbb {Z}}\), \(i=1,2\). Thus \(M^{*j}\lambda _i\in {\mathbb {Z}}^2\) if and only if \(\min \{s_{1j},s_{2j}\}\ge \eta +1\). Since \(j_{1}\) and \(j_{2}\) are the least positive integers such that \(\min \{s_{1j_{1}},s_{2j_{1}}\}, \min \{s_{1j_{2}},s_{2j_{2}}\}\ge \eta +1\), it follows that \(j_{1}=j_{2}:=j_0\). Moreover, using \(l_{i1},l_{i2}\in {\mathbb {Z}}\setminus 3{\mathbb {Z}}\), one may infer that \(M^{*}\lambda _i=\begin{bmatrix} 3a&{}3c+p\\ 3b&{}3d \end{bmatrix}\begin{pmatrix} \frac{l_{i1}}{3}\\ \frac{l_{i2}}{3^{\eta +1}}\end{pmatrix} \notin {\mathbb {Z}}^2\). Therefore, \(j_0\ge 2\).
Next, we prove \(M^{*j_{0}-1}\lambda _i\in \{\pm (\frac{1}{3},0)^t\} \pmod {{\mathbb {Z}}^2}\) for \(i=1,2\). In fact, \(M^{*j_{0}-1}\lambda _i\in {\mathcal {F}} \pmod {{\mathbb {Z}}^2}\). Suppose otherwise, that \(M^{*j_{0}-1}\lambda _i \notin {\mathcal {F}} +{\mathbb {Z}}^2\). Using \(M\in M_2({\mathbb {Z}})\) and \(M^{*j_{0}-1}\lambda _i\notin {\mathbb {Z}}^2\), we deduce \(M^{*j_{0}-1}\lambda _i=\left( \frac{l'_{i1}}{3^s},\frac{l'_{i2}}{3^s} \right) ^t\) with \(s\ge 2\) and at least one of \(l'_{i1}\) and \(l'_{i2}\) belongs to \({\mathbb {Z}}\setminus 3{\mathbb {Z}}\). Thus \(M^{*j_{0}}\lambda _i\in {\mathbb {Z}}^2\) implies that
for some integer vector \(v_i\in {\mathbb {Z}}^2.\) Since \(|\det (M)|=3\), it follows that there exists \(u_i\in {\mathbb {Z}}^2\) such that \(\left( \frac{l'_{i_1}}{3^s},\frac{l'_{i_2}}{3^s} \right) ^t=M^{*-1}v_i=\frac{1}{3}u_i\). This is a contradiction, and hence \(M^{*j_{0}-1}\lambda _i\in {\mathcal {F}} \pmod {{\mathbb {Z}}^2}\). By a simple calculation and Lemma 3.9, one may infer that \((\pm \frac{1}{3},0)^t\) are the only elements of \({\mathcal {F}}\) satisfying \(M^*(\pm \frac{1}{3},0)^t\in {\mathbb {Z}}^2\). This means that \(M^{*j_{0}-1}\lambda _i\in \{\pm (\frac{1}{3},0)^t\} \pmod {{\mathbb {Z}}^2}\), and the assertion follows.
Finally, we prove \(M^{*j_{0}-2}\lambda _1=M^{*j_{0}-2}\lambda _2\in {\mathcal {F}} \pmod {{\mathbb {Z}}^2}\) if \(\lambda _1,\lambda _2\in Z_k\) for \(k=1\) or 2. As \(|\det (M)|=3\), it follows \(b\notin 3{\mathbb {Z}}\). Then for \(s_1\notin 3{\mathbb {Z}}\) and \(s_2\in {\mathbb {Z}}\), we have
Combining this with \(M^{*j_{0}-1}\lambda _i\in \{\pm (\frac{1}{3},0)^t \}\pmod {{\mathbb {Z}}^2}\), one derives \(M^{*j_{0}-2}\lambda _1, M^{*j_{0}-2}\lambda _2\in {\mathcal {F}} \pmod {{\mathbb {Z}}^2}\). Observe that \(\lambda _i=\left( \frac{l_{i1}}{3},\frac{l_{i2}}{3^{\eta +1}} \right) ^t\) with \(l_{i1},l_{i2}\in {\mathbb {Z}}{\setminus } 3{\mathbb {Z}}\) and
we conclude that \(\min \{s_{1{j_0-2}},s_{2{j_0-2}}\}=\eta \). As \(\lambda _i=\left( \frac{l_{i1}}{3},\frac{l_{i2}}{3^{\eta +1}} \right) ^t\in Z_k\) for \(k=1\) or 2, one has \((l_{11}, l_{12})^t=(l_{21}, l_{22})^t \pmod {3{\mathbb {Z}}^2}\) and \(\lambda _1-\lambda _2=\left( l'_{1}, \frac{l'_{2}}{3^{s}}\right) ^t\) with \(s\le \eta \). Consequently,
This illustrates that \(M^{*j_{0}-2}\lambda _1=M^{*j_{0}-2}\lambda _2\in {\mathcal {F}} \pmod {{\mathbb {Z}}^2}\). \(\square \)
We now continue with the proof of Proposition 4.6. By Claim, we let \( \xi _k= {\mathcal {F}}\cap (M^{*j_{0}-2}Z_k\pmod {{\mathbb {Z}}^2})\) for \(k=1,2\). Then
Similar to the proof of Lemma 3.7, one may get \(\bigcup _{i=1}^\infty M^{*i} \big (\{M^*\xi _1,M^*\xi _2\}+M^*{\mathbb {Z}}^2\big )\subsetneqq {\mathbb {Z}}^2{\setminus }\{{\textbf {0}}\}\). Thus (4.8) shows that (4.7) holds, and hence \({\textbf{T}}(M,{\mathcal {D}})\) is not a tile by Theorem 3.4. \(\square \)
In order to complete the proof of Theorem 4.2 in Case II, we need to figure out which matrices M satisfy \({\mathcal {Z}}({\hat{\mu }}_{M, {\mathcal {D}}})\cap {\mathbb {Z}}^2=\emptyset \).
Lemma 4.7
Let \({\mu }_{M, {\mathcal {D}}}\) be defined by (1.1), where M and \({\mathcal {D}}\) are given by (4.1) and (4.2) respectively. If \(\eta >0\) in \({\mathcal {D}}\), then the following assertions hold.
-
(i)
If \(\sigma -2\omega \in 3{\mathbb {Z}}\) and \(M\in {\mathfrak {B}}_4\), then \({\mathcal {Z}}({\hat{\mu }}_{M, {\mathcal {D}}})\cap {\mathbb {Z}}^2=\emptyset \).
-
(ii)
If \(\sigma -2\omega \notin 3{\mathbb {Z}}\) and \(M\in {\mathfrak {M}}_5\), then \({\mathcal {Z}}({\hat{\mu }}_{M, {\mathcal {D}}})\cap {\mathbb {Z}}^2=\emptyset \).
Proof
The proof follows directly from the proofs of Lemma 3.2 and Proposition 4.3 in [47]. \(\square \)
Proposition 4.8
Let \({\textbf{T}}(M,{\mathcal {D}})\) be defined by (1.2), where M and \({\mathcal {D}}\) are given by (4.1) and (4.2) respectively. If \({\textbf{T}}(M,{\mathcal {D}})\) is a translational tile and \(\eta >0\) in \({\mathcal {D}}\), then the following assertions hold.
-
(i)
If \(\sigma -2\omega \in 3{\mathbb {Z}}\), then \(M\in {\mathfrak {B}}_1\cup {\mathfrak {B}}_2\).
-
(ii)
If \(\sigma -2\omega \notin 3{\mathbb {Z}}\), then \(M\in {\mathfrak {B}}_3\).
Proof
To complete the proof of this proposition, it suffices to prove that \({\textbf{T}}(M,{\mathcal {D}})\) is not a tile if \(M\in {\mathfrak {B}}_5\) or \(M\in {\mathfrak {B}}_6\cup {\mathfrak {B}}_7\) for \(\sigma -2\omega \in 3{\mathbb {Z}}\) or \(\sigma -2\omega \notin 3{\mathbb {Z}}\) respectively, where
It is clear that \({\mathfrak {B}}_5=\{{\mathfrak {M}}_k\}_{k=1}^9\setminus ({\mathfrak {B}}_1\cup {\mathfrak {B}}_2)\) and \({\mathfrak {B}}_6\cup {\mathfrak {B}}_7=\{{\mathfrak {M}}_k\}_{k=1}^9\setminus {\mathfrak {B}}_3\).
(i) If \(M\in {\mathfrak {B}}_5\cap {\mathfrak {M}}_1\), one may deduce from Lemma 4.7 that \({\mathcal {Z}}({\hat{\mu }}_{M, {\mathcal {D}}})\cap {\mathbb {Z}}^2=\emptyset \). In view of Theorem 3.4, \({\textbf{T}}(M,{\mathcal {D}})\) is not a tile.
If \(M\in {\mathfrak {B}}_5\cap {\mathfrak {M}}_6\), it follows from (4.6) that \( M=\begin{bmatrix} 3a+p_1&{}3b+p_2\\ 3^{s}c&{}3d \end{bmatrix}, \) where \(s\ge \eta \), \(a,b,d\in {\mathbb {Z}}\), \(c\in ({\mathbb {Z}}\setminus 3{\mathbb {Z}})\cup \{0\}\) and \(p_1,p_2\in \{1,2\}\). It is clear that there exists \(\tau \in \{1,2\}\) such that \(p_2-\tau p_1\in 3{\mathbb {Z}}\). Take \(Q_1=\begin{bmatrix} 1&{}\tau \\ 0&{}1 \end{bmatrix}\), thus one has
and
Using \(p_1\in \{1,2\}\) and \(p_2-\tau p_1\in 3{\mathbb {Z}}\), we see that \(M_1\in {\mathfrak {B}}_5\cap {\mathfrak {M}}_1\). Moreover, it follows from \(\sigma -2\omega \in 3{\mathbb {Z}}\) and \(\eta >0\) that \( \sigma -2(\omega +3^{\eta }\tau \vartheta ) \in 3{\mathbb {Z}}\), thus \({\mathcal {D}}_1\) has the same property as \({\mathcal {D}}\). Applying Lemma 4.7 and Theorem 3.4, one may infer that \({\textbf{T}}(M,{\mathcal {D}})\) is not a tile.
According to \({\mathfrak {B}}_5=\{{\mathfrak {M}}_k\}_{k=1}^9\setminus ({\mathfrak {B}}_1\cup {\mathfrak {B}}_2)\) and \({\textbf{T}}(M,{\mathcal {D}})\) is not a tile for \(M\in {\mathfrak {B}}_5\), we obtain \(M\in {\mathfrak {B}}_1\cup {\mathfrak {B}}_2\). This proves (i).
(ii) We first prove \({\textbf{T}}(M,{\mathcal {D}})\) is not a tile for \(M\in {\mathfrak {B}}_6=\left\{ {M}: {M}\in {\mathfrak {M}}_k, k\in \{3,5,7,9\}\right\} \).
\(\textcircled {1}\) If \(M\in {\mathfrak {M}}_3\), it yields from the facts \(\eta >0\), \(\sigma -2\omega \notin 3{\mathbb {Z}}\) and Proposition 4.6.
\(\textcircled {2}\) If \(M\in {\mathfrak {M}}_5\), using Lemma 4.7, we obtain \({\mathcal {Z}}({\hat{\mu }}_{M, {\mathcal {D}}})\cap {\mathbb {Z}}^2=\emptyset \). Hence Theorem 3.4 shows that \({\textbf{T}}(M,{\mathcal {D}})\) is not a tile.
\(\textcircled {3}\) If \(M\in {\mathfrak {M}}_7\cup {\mathfrak {M}}_9\), using (4.6), one can write M as
where \(s\ge 1\), \(a',b',d\in {\mathbb {Z}}\), \(c\in ({\mathbb {Z}}\setminus 3{\mathbb {Z}})\cup \{0\}\), \(p_3,p_4\in \{1,2\}\) and \(a' p_4-b' p_3\in 3{\mathbb {Z}}\). Then we can choose \(\tau \in \{1,2\}\) such that \( \tau p_3+p_4\in 3{\mathbb {Z}}\). This together with \(a' p_4-b' p_3\in 3{\mathbb {Z}}\) yields that
Notice that \(p_3\in \{1,2\}\), so (4.9) implies \(\tau a'+b'\in 3{\mathbb {Z}}\). Take \(Q_2=\begin{bmatrix} 1&{}-\tau \\ 0&{}1 \end{bmatrix}\). Then one has
and
As \(\tau ,p_3\in \{1,2\}\) and \( \tau a'+b', \tau p_3+p_4\in 3{\mathbb {Z}}\), it follows that
On the other hand, we deduce from \(\sigma -2\omega \notin 3{\mathbb {Z}}\) and \(\eta >0\) that \( \sigma -2(\omega -3^{\eta }\tau \vartheta ) \notin 3{\mathbb {Z}}\), which means that \({\mathcal {D}}_2\) has the same property as \({\mathcal {D}}\). By Theorem 3.4, Proposition 4.6 and Lemma 4.7, we infer that \({\textbf{T}}(M,{\mathcal {D}})\) is not a tile. Therefore, \({\textbf{T}}(M,{\mathcal {D}})\) is not a tile for \(M\in {\mathfrak {B}}_6\).
Next, we prove \({\textbf{T}}(M,{\mathcal {D}})\) is not a tile for \(M\in {\mathfrak {B}}_7\). If \(M\in {\mathfrak {B}}_7\), (4.6) implies that M can be expressed as
where \(1\le s<\eta \), \(a',b',d'\in {\mathbb {Z}}\), \(c\in {\mathbb {Z}}\setminus 3{\mathbb {Z}}\) and \(a'd'\in 3{\mathbb {Z}}\). Take \(Q_3=\begin{bmatrix} 1&{}0 \\ 0&{}\frac{1}{3^s} \end{bmatrix}\). Thus
Note that \(a'd'\in 3{\mathbb {Z}}\) and \(\eta -s\ge 1\), one can easily see that \(M_3\in {\mathfrak {B}}_6\), and \({\mathcal {D}}_3\) has the same property as \({\mathcal {D}}\). According to the previous proof, we conclude that \({\textbf{T}}(M,{\mathcal {D}})\) is not a tile. Hence we complete the proof of Proposition 4.8. \(\square \)
Having established the above preparations, now we can prove Theorem 4.5.
Proof of Theorem 4.5
Suppose \({\textbf{T}}(M,{\mathcal {D}})\) is a spectral set, it follows from Theorem 4.4 that there exists a matrix \(Q\in M_2({\mathbb {R}})\) such that \(({\widetilde{M}},{\widetilde{D}})\) is admissible, where \({\widetilde{M}}=QMQ^{-1}\) and \({\widetilde{D}}=Q{\mathcal {D}}\). In view of Proposition 3.2, \({\widetilde{D}}\) is a standard digit set for \({\widetilde{M}}\). By Theorem 3.3 and Lemma 4.1, we conclude that \({\textbf{T}}(M,{\mathcal {D}})\) is a translational tile.
Conversely, suppose \({\textbf{T}}(M,{\mathcal {D}})\) is a translational tile. If \(\sigma -2\omega \in 3{\mathbb {Z}}\) in \({\mathcal {D}}\), then Proposition 4.8 shows \(M\in {\mathfrak {B}}_1\cup {\mathfrak {B}}_2\). Hence \({\textbf{T}}(M,{\mathcal {D}})\) is a spectral set by Theorem 4.4. On the other hand, if \(\sigma -2\omega \notin 3{\mathbb {Z}}\) in \({\mathcal {D}}\), using Proposition 4.8 again, one has \(M\in {\mathfrak {B}}_3\). According to the definition of \({\mathfrak {B}}_3\) and (4.6), we can write the matrix \(M\in {\mathfrak {B}}_3\) as
where \(s\ge \eta \), \(a',b',d'\in {\mathbb {Z}}\), \(c\in ({\mathbb {Z}}\setminus 3{\mathbb {Z}})\cup \{0\}\) and \(a'd'\in 3{\mathbb {Z}}\). Let \(Q_4=\begin{bmatrix} 1&{}0 \\ 0&{}\frac{1}{3^\eta } \end{bmatrix}\), we get
Since \({\textbf{T}}(M,{\mathcal {D}})\) is a translational tile, we infer from Lemma 4.1 that \({\textbf{T}}(M_4,{\mathcal {D}}_4)\) is a translational tile. Together with \(\sigma \vartheta \notin 3{\mathbb {Z}}\) and Theorem 4.3, it gives that \({\textbf{T}}(M_4,{\mathcal {D}}_4)\) is a spectral set. By Lemma 4.1 again, \({\textbf{T}}(M,{\mathcal {D}})\) is also a spectral set. Thus the sufficiency follows. \(\square \)
4.2 Collinear Digit
In this subsection, we investigate the remaining case where the digit set D is collinear. That is, \(D=\{(0,0)^t,(\alpha _1,\alpha _2)^t,(\beta _1,\beta _2)^t\}\) satisfies \(\alpha _1\beta _2-\alpha _2\beta _1=0\). The following is our main result.
Theorem 4.9
Let \({\textbf{T}}(A,D)\) be the generalized Sierpinski self-affine set defined by (1.2), where \(A\in M_2({\mathbb {Z}})\) with \(|\det (A)|=3\) and D is given by (1.3). If \(\alpha _1\beta _2-\alpha _2\beta _1=0\) in D, then \({\textbf{T}}(A,D)\) is a spectral set if and only if it is a translational tile.
To complete the proof of Theorem 4.9, we first introduce the following lemma, which has been proved by the second author and Luo [45, Lemma 3.1] and plays an important role in the proof of direction “tile \(\Rightarrow \) spectral" of Fuglede’s conjecture.
Lemma 4.10
Let \(A \in M_{n}({\mathbb {Z}})\) be an integer matrix with characteristic polynomial \(f(x)=x^{n}+a_{1} x^{n-1}+\cdots +a_{n-1} x+a_{n}\) and \(v=\left( x_{1}, \ldots , x_{n}\right) ^{t} \in {\mathbb {Z}}^{n} \backslash \{{\textbf {0}}\}\). If \(\{v, A v, \ldots , A^{n-1} v\}\) is a linearly independent set, then there exists an integer matrix B such that
and \(B^{-1} v=(0, \ldots , 0,1)^{t}\).
For more general collinear digit set D, Kirat and Lau [30] gave a criterion for such a self-affine set \({\textbf{T}}(A,D)\) to be a tile.
Theorem 4.11
([30]) Suppose that \(A \in M_{n}({\mathbb {Z}})\) is an expanding matrix with \(|\det (A)|=q\), where \(q \ge 2\) is a prime. Let \(D=\{d_{1} v, \ldots , d_{q} v\}\) with \(v \in {\mathbb {R}}^{n} \backslash \{{\textbf {0}}\}\) and \(d_{i} \in {\mathbb {Z}}\). Then \({\textbf{T}}(A,D)\) is a self-affine tile if and only if \(\{v, A v, \ldots , A^{n-1} v\}\) is a linearly independent set and \(\{d_{1}, \ldots , d_{q}\}=q^{l}\{d_{1}^{\prime }, \ldots , d_{q}^{\prime }\}\), where l is a nonnegative integer with \(\{d_{1}^{\prime }, \ldots , d_{q}^{\prime }\}\), is a complete set of coset representatives of \({\mathbb {Z}}_{q}\).
In particular, if \(v \in {\mathbb {Z}}^{n} \backslash \{{\textbf {0}}\}\), then \(\{v, A v, \ldots , A^{n-1} v\}\) is automatically a linearly independent set. Hence \({\textbf{T}}(A,D)\) is a self-affine tile if and only if the above \(\{d_{1}^{\prime }, \ldots , d_{q}^{\prime }\}\) is a complete set of coset representatives of \({\mathbb {Z}}_{q}\).
The following lemma is a fundamental fact by a simple calculation.
Lemma 4.12
Let D be given by (1.3). If \(\alpha _1\beta _2-\alpha _2\beta _1=0\), then \({\mathcal {Z}}(m_D)\ne \emptyset \) if and only if there exists an integer vector \(v\in {\mathbb {Z}}^2\setminus \{{\textbf {0}}\}\) such that \(D=\{0,n,m\}v\) with \(n,m\in {\mathbb {Z}}\) and \(\{n,m\}=\{1,2\}\pmod 3\).
Proof
Since \(\alpha _1\beta _2-\alpha _2\beta _1=0\), we can always express D as \(D=\{0,n,m\}v\), where \(v\in {\mathbb {Z}}^2\setminus \{{\textbf {0}}\}\), \(n,m\in {\mathbb {Z}}\) and \(\gcd (n,m)=1\). Next, we prove \(\{n,m\}=\{1,2\}\pmod 3\). Let \(v=(v_1,v_2)^t\). According to \({\mathcal {Z}}(m_D)= 1+e^{2\pi in(v_1x_1+v_2x_2)}+e^{2\pi im(v_1x_1+v_2x_2)}=0 \) if and only if
where \(k_1,k_2,k_3,k_4\in {\mathbb {Z}}\), it is easy to see that (4.10) holds if and only if \(\{n,m\}=\{1,2\}\pmod 3\). This finishes the proof. \(\square \)
With the above preparations, now we can prove Theorem 4.9.
Proof of Theorem 4.9
Suppose \({\textbf{T}}(A,D)\) is a spectral set, then \(L^2(\mu _{A,D})\) admits an infinite orthogonal set. Together with (3.2) and (3.3), it gives \({\mathcal {Z}}(m_D)\ne \emptyset \). In view of Lemma 4.12, we have \(D=\{0,n,m\}v\), where \(\{n,m\}=\{1,2\}\pmod 3\) and \(v\in {\mathbb {Z}}^2\setminus \{{\textbf {0}}\}\). This implies that \(\{0,n,m\}\) is a complete set of coset representatives of \({\mathbb {Z}}_{3}\), thus \({\textbf{T}}(A,D)\) is a translational tile by Theorem 4.11. Hence the necessity follows.
Conversely, suppose \({\textbf{T}}(A,D)\) is a translational tile and let \(A=\begin{bmatrix} a&{}b \\ c&{}d \end{bmatrix}\). By \(|\det (A)|=3\) and a simple calculation, we get that the characteristic polynomial of A is \(f(x)=x^2-(a+d) x+ad-bc\), where \(|ad-bc|=3\). According to Theorem 3.4, it can be easily seen that \({\mathcal {Z}}(m_D)\ne \emptyset \). With Lemma 4.12, one has \(D=\{0,n,m\}v\), where \(\{n,m\}=\{1,2\}\pmod 3\) and \(v\in {\mathbb {Z}}^2{\setminus }\{{\textbf {0}}\}\). Using Theorem 4.11, we obtain that \(\{v, Av\}\) is a linearly independent set. Then by Lemma 4.10, there exists an integer matrix C such that
Using \(|ad-bc|=3\) and \(\{n,m\}=\{1,2\}\pmod 3\), it is easy to check that \(\pm (0,1/3)^t\in {\mathcal {Z}}(m_{{\tilde{D}}})\) and \({\tilde{A}}^*(0,1/3)^t\in {\mathbb {Z}}^2\). Thus \(({\tilde{A}},{\tilde{D}})\) is admissible. In view of Theorem 1.6 and Lemma 4.1, \({\textbf{T}}(A,D)\) is a spectral set. We complete the proof. \(\square \)
5 A Finer Characterization and Its Application
In this section, we will give some interesting applications on Theorem 2.1. We first restrict the digit set to the classical digit set, and in this case we obtain some more refined results. Also for such self-affine tiles, we further prove that they are suitable for Kolountzakis’ conjecture.
5.1 The Classical Sierpinski Self-Affine Set
Let \({\textbf{T}}(A,D_{c})\) be the classical Sierpinski self-affine set and \(\mu _{A,D_{c}}\) be the corresponding Sierpinski self-affine measure, where
A known fact is that the spectrality of \(\mu _{A,D_{c}}\) has been completely characterized by An et al. [1]. In this subsection, we further study its tiling property and characterize the tiling set of \({\textbf{T}}(A,D_{c})\). To achieve this goal, we need to introduce the definition of dual lattice.
Definition 5.1
Let \(\Lambda \) be a full rank lattice in \({\mathbb {R}}^n\), i.e., \(\Lambda =Q{\mathbb {Z}}^n\) for some \(Q\in M_n({\mathbb {R}})\). The dual lattice \(\Lambda ^{\star }\) of \(\Lambda \) is defined as
In [20], Fuglede proved that if \(\Omega \) is a tile (or a spectral set) with a lattice tiling set (or spectrum) \(\Lambda \subset {\mathbb {R}}^n\), then \(\Omega \) is a spectral set (or a tile), and the dual lattice \(\Lambda ^{\star }\) is a spectrum (or a tiling set) of it. For the classical Sierpinski self-affine set \({\textbf{T}}(A,D_{c})\), we get the following interesting result.
Theorem 5.2
Let \({\textbf{T}}(A,D_{c})\) be the classical Sierpinski self-affine set defined by (1.2), where \(A\in M_2({\mathbb {Z}})\) with \(|\det (A)|=3\) and \(D_{c}\) is given by (2.1). Then the following statements are equivalent:
-
(i)
\({\textbf{T}}(A,D_{c})\) is a spectral set;
-
(ii)
\(A=\begin{bmatrix} a &{} b\\ c&{} d \end{bmatrix}\) satisfies \(a-c\equiv b-d\equiv 0 \pmod 3\);
-
(iii)
\(D_{c}\) is a standard digit set for A;
-
(iv)
\({\textbf{T}}(A,D_{c})\) is a translational tile.
Furthermore, if \({\textbf{T}}(A,D_{c})\) is a spectral set, then \({\mathbb {Z}}^2\) is the unique spectrum containing \({\textbf{0}}\) and it is a tiling set for \({\textbf{T}}(A,D_{c})\).
Proof
Note that \(|\det (A)|=3\), then the assertions (i) \(\Rightarrow \) (ii), (iii) \(\Rightarrow \) (iv) and (iv) \(\Rightarrow \) (i) follow immediately from [1, Theorem 1.2], Theorems 3.3 and 2.1, respectively. It suffices to prove (ii) \(\Rightarrow \) (iii).
Suppose \(A=\begin{bmatrix} a &{} b\\ c&{} d \end{bmatrix}\) satisfies \(a-c\equiv b-d\equiv 0 \pmod 3\), and let
It is clear that \(S\subset {\mathbb {Z}}^2\). Since \(\pm (1/3,-1/3)^t\in {\mathcal {Z}}(m_{D_c})\) and \(A^*(1/3,-1/3)^t=((a-c)/3,(b-d)/3)^t\in {\mathbb {Z}}^2\), it follows from \(S\subset {\mathbb {Z}}^2\) and Lemma 3.1 that (A, D, S) is a Hadamard triple. Then Proposition 3.2 shows that \(D_{c}\) is a standard digit set for A, which proves (ii) \(\Rightarrow \) (iii).
Finally, if \({\textbf{T}}(A,D_{c})\) is a spectral set, we show that \({\mathbb {Z}}^2\) is the unique spectrum containing \({\textbf{0}}\) and it is a tiling set for \({\textbf{T}}(A,D_{c})\). By a simple calculation, we obtain
Since \({\textbf{T}}(A,D_{c})\) is a spectral set, it follows that \(A=\begin{bmatrix} a &{} b\\ c&{} d \end{bmatrix}\) satisfies \(a-c\equiv b-d\equiv 0 \pmod 3\). Then for \(\xi =(1/3,-1/3)^t\), a simple calculation gives \(A^*\xi \in {\mathbb {Z}}^2\). Applying (3.2) and Lemma 3.6, one may get
Let \(\Lambda \) be a spectrum of \(\mu _{A,D_{c}}\) with \({\textbf {0}}\in \Lambda \). From (3.3) and (5.2), we have \(\Lambda \subset {\mathbb {Z}}^2\). If \(\Lambda \ne {\mathbb {Z}}^2\), we have \(a\bot \Lambda \)Footnote 2 for any \(a\in {\mathbb {Z}}^2{\setminus }\Lambda \). This is a contradiction, and hence \({\mathbb {Z}}^2\) is the unique spectrum containing \({\textbf{0}}\). Moreover, \(\mu _{A,D_c}\) is a spectral measure implies that \({\textbf{T}}(A,D_{c})\) is a tile. Since \({\mathbb {Z}}^2\) is the unique spectrum of \({\textbf{T}}(A,D_{c})\), it follows from [20] that its dual lattice \(({\mathbb {Z}}^2)^{\star }={\mathbb {Z}}^2\) is a tiling set for \({\textbf{T}}(A,D_{c})\). We complete the proof. \(\square \)
5.2 Application to Kolountzakis’ Conjecture on Product Domain
Let \(\Omega =U \times V\) be the cartesian product of two bounded Lebesgue measurable set \(U\subset {\mathbb {R}}^n,V\subset {\mathbb {R}}^m\). We are interested in the spectral relationship among \(\Omega ,U\) and V. In dimension \(2+m\), Greenfeld and Lev [22] showed that where the factor U is a convex polygon in \({\mathbb {R}}^2\), \(\Omega \) is a spectral set if and only if U, V are all spectral sets. As an application, in this subsection, we consider the case that one of factor is the classical Sierpinski self-affine tile \({\textbf{T}}(A,D_{c})\), where \(A\in M_2({\mathbb {Z}})\) with \(|\det (A)|=3\) and \(D_{c}\) is given by (2.1). We prove
Theorem 5.3
Let \({\textbf{T}}(A,D_{c})\) be the classical Sierpinski self-affine tile, and V be a bounded Lebesgue measurable set in \({\mathbb {R}}^n\) with \({\mathcal {L}}(V)=1\). Then the product domain \(\Omega ={\textbf{T}}(A,D_{c})\times V\) is a spectral set if and only if \({\textbf{T}}(A,D_{c})\) and V are both spectral sets.
In order to prove Theorem 5.3, we begin with the notion of orthogonal packing region.
Definition 5.4
Let W and U be two bounded Lebesgue measurable sets in \({\mathbb {R}}^n\). We say that W is an orthogonal packing region for U if \((W-W)\cap {\mathcal {Z}}({{\hat{\chi }}}_{U})=\emptyset .\)
In the above definition, \({{\hat{\chi }}}_{U}\) denotes the Fourier transform of the characteristic function \({\chi }_{U}\). For an absolutely continuous measure \(\mu \), we have the following.
Lemma 5.5
Let \(\mu \) be a Borel probability measure on \({\mathbb {R}}^n\) and \(K\subset {\mathbb {R}}^n\) be a compact set. Suppose that \(\mu \) is absolutely continuous with respect to the Lebesgue measure and supported on K, then \({\mathcal {Z}}({\hat{\mu }})={\mathcal {Z}}({\hat{\chi }}_K)\).
Proof
From the definition of Fourier transform, we have
This implies \({\mathcal {Z}}({\hat{\mu }})={\mathcal {Z}}({\hat{\chi }}_K)\), the assertion follows. \(\square \)
The following result comes from Kolountzakis [32], which provides a method for proving in certain situations that the spectrality of a product set \(\Omega =A\times B\) yielding the spectrality of factors A and B. On the other hand, it gives a geometrically intuitive way to verify the spectrality.
Theorem 5.6
(Kolountzakis’ theorem, [32]) Suppose that \(\Omega =U\times V\subset {\mathbb {R}}^n\times {\mathbb {R}}^m\) has \({\mathcal {L}}(U)={\mathcal {L}}(V)=1\), and suppose the bounded Lebesgue measurable set \(W\subset {\mathbb {R}}^n\) is an orthogonal packing region for U. If \({\mathcal {L}}(W)=1\) and \(\Omega \) is a spectral set, then V is also a spectral set.
If \(\Omega ={\textbf{T}}(A,D_{c})\times V\) is a spectral set in \({\mathbb {R}}^{2+m}\), where \({\textbf{T}}(A,D_{c})\) is a classical Sierpinski self-affine set with positive Lebesgue measure and V is a bounded measurable set in \({\mathbb {R}}^m\) with \({\mathcal {L}}(V)=1\), by Theorem 5.6, we only need to find a suitable packing region W for \({\textbf{T}}(A,D_c)\).
Proof of Theorem 5.3
Let \({\textbf{T}}(A,D_{c})\) be the classical Sierpinski self-affine tile. According to Lemma 3.6, Theorem 5.2 and Lemma 5.5, one has
Using Theorem 2.2, and by the Poisson Summation formula, we have
Take \(W=(0,1)\times (0,1)\), then it is easy to check that W is a packing region for \({\textbf{T}}(A,D_{c})\) and \({\mathcal {L}}(W)=1\). Therefore, we derive that V is a spectral set. At the same time, Theorem 5.2 shows that the self-affine tile \({\textbf{T}}(A,D_{c})\) is a spectral set. This proves the necessity. The sufficiency is a trivial result. \(\square \)
6 Further Results and Remarks
For a given expanding matrix A, characterize all digit sets D such that \({\textbf{T}}(A,D)\) has positive Lebesgue measure appears to be a difficult question. If the determinant of matrix A is prime, Lagarias and Wang [39] gave a complete characterization for this problem under some additional conditions.
Theorem 6.1
([39]) Let \(A\in M_n({\mathbb {Z}})\) be an expanding matrix such that \(|\det {(A)}|=p\) is prime, and suppose that
If \(D\subset {\mathbb {Z}}^n\) is a digit set with \(\#D=p\), then \({\mathcal {L}}({\textbf{T}}(A,D))>0\) if and only if D is a standard digit set.
Remark 6.2
We focus on the following two aspects.
-
1.
Theorem 6.1 can be regarded as giving an equivalent characterization of tiles \({\textbf{T}}(A,D)\) under the assumption (6.1) when \(|\det (A)|=p\) is a prime. It is worth noting that the assumption (6.1) is always satisfied in dimension one by Kenyon [29]. For the high-dimensional case, Lagarias and Wang [39] thought that the conclusion of Theorem 6.1 may well be true without the assumption (6.1).
-
2.
We have to say that the definition of standard digit set in Theorem 6.1 is actually more widely. In other words, let \(A\in M_n({\mathbb {Z}})\) be an expanding matrix and \(D\subset {\mathbb {Z}}^n\) be a digit set. Suppose that there exists an invertible matrix Q such that
$$\begin{aligned} {\textbf{T}}(A,D)=Q{\textbf{T}}({\widetilde{A}},{\widetilde{D}}). \end{aligned}$$(6.2)D is called a standard digit for A if the pair \(({\widetilde{A}},{\widetilde{D}})\) given by (6.2) has \({\widetilde{D}}\) being a complete set of coset representatives of \({\mathbb {Z}}^n/{\widetilde{A}}{\mathbb {Z}}^n\). Coincidentally, by Theorems 4.2, 4.4 and 4.9, we can immediately obtain the following concise result, which illustrates that for prime \(p=3\), the assumption (6.1) in dimension two can be removed in the sense of this extensive definition.
Corollary 6.3
Let \({\textbf{T}}(A,D)\) be the generalized Sierpinski self-affine set defined by (1.2), where \(A\in M_2({\mathbb {Z}})\) with \(|\det (A)|=3\) and D is given by (1.3). Then \({\textbf{T}}(A,D)\) is a spectral set \(\Leftrightarrow {\textbf{T}}(A,D)\) is a translational tile \(\Leftrightarrow \) D is a standard digit set for A.
Much more can be said here, we give an example below to illustrate that Theorem 6.1 still holds without the assumption (6.1).
Example 6.4
Let \(A=\begin{bmatrix} 1&{}2 \\ 1&{}-1 \end{bmatrix}\) and \(D_{c}\) be given by (2.1). Theorem 2.2 tells us that the classical Sierpinski self-affine set \({\textbf{T}}(A,D_c)\) is a tile if and only if \(D_c\) is a standard digit for A. However, it is clear to see that \(p:=|\det {(A)}|=\#D=3\) and \(A^2=\begin{bmatrix} 3&{}0 \\ 0&{}3 \end{bmatrix}\), which implies \(p{\mathbb {Z}}^2=A^2{\mathbb {Z}}^2\). Thus (6.1) does not hold.
So far as we know, the majority of studies of Fuglede’s problem on higher dimension are under the assumption of convex sets. From Fig. 3, we can see that some Sierpinski self-affine sets which generated by non-collinear digits are non-convex and have a complex internal structure. However, the following result indicates that some Sierpinski self-affine tiles with collinear digits have a “good" geometrical property.
Proposition 6.5
Let \({\textbf{T}}(A,D)\) be the generalized Sierpinski self-affine set defined by (1.2), where \(A\in M_2({\mathbb {Z}})\) with the characteristic polynomial \(f(x)=x^2\pm 3\) and \(D=\{0,1,2\}v\) with \(v\in {\mathbb {Z}}^2\setminus \{{\textbf {0}}\}\). Then \({\textbf{T}}(A,D)\) is a parallelogram.
Proof
By Lemmas 4.1 and 4.10, there exists an integer matrix B such that
By a simple calculation, we obtain
Since the image of a parallelogram under a linear transformation is also a parallelogram, it is sufficient to prove that \({\textbf{T}}(A',D')\) is a parallelogram. The proof will be divided into the following two cases.
-
(i)
If \(A'=\begin{bmatrix} 0&{}1 \\ 3&{}0 \end{bmatrix}\), a simple calculation gives
$$\begin{aligned} {A'}^{-1}&=\frac{1}{3}\begin{bmatrix} 0&{}1 \\ 3&{}0 \end{bmatrix},\quad {A'}^{-2}=\frac{1}{3^2}\begin{bmatrix} 3&{}0 \\ 0&{}3 \end{bmatrix},\quad {A'}^{-3}=\frac{1}{3^3}\begin{bmatrix} 0&{}3 \\ 9&{}0 \end{bmatrix}, {A'}^{-4}=\frac{1}{3^4}\begin{bmatrix} 9&{}0 \\ 0&{}9 \end{bmatrix},\cdots . \end{aligned}$$Hence, using the definition of \({\textbf{T}}(A',D')\), one may get
$$\begin{aligned} {\textbf{T}}(A',D')&=\left\{ \sum _{j=1}^{\infty }{A'}^{-j}d_j:d_j\in \left\{ \begin{pmatrix} 0\\ 0\end{pmatrix},\begin{pmatrix} 0\\ 1 \end{pmatrix}, \begin{pmatrix} 0\\ 2 \end{pmatrix}\right\} \ \mathrm{for \ all} \ j\in {\mathbb {N}}\right\} \\&=\left\{ \begin{pmatrix} \sum \limits _{i\in {\mathbb {N}}}\frac{s_i}{3^i}\\ \sum \limits _{j\in {\mathbb {N}}}\frac{r_j}{3^j} \end{pmatrix}:s_i,r_j\in \left\{ 0,1,2\right\} \right\} =[0,1]\times [0,1]. \end{aligned}$$ -
(ii)
If \(A'=\begin{bmatrix} 0&{}1 \\ -3&{}0 \end{bmatrix}\), we can similarly get \({\textbf{T}}(A',D')=[-3/4,1/4]\times [-3/4,1/4]\).
From the above two cases, we conclude that \({\textbf{T}}(A,D)\) is a parallelogram. \(\square \)
The following example effectively illustrates Theorem 6.5.
Example 6.6
Let \(A=\begin{bmatrix} 1&{}2 \\ 1&{}-1 \end{bmatrix}\) and \(D_{\{{\textbf{0}},{\textbf{1}},{\textbf{2}}\}}=\left\{ \begin{pmatrix} 0\\ 0\end{pmatrix},\begin{pmatrix} 1\\ 1 \end{pmatrix}, \begin{pmatrix} 2\\ 2 \end{pmatrix}\right\} .\) By Theorem 6.5, we know that the corresponding self-affine set \({\textbf{T}}(A,D_{\{{\textbf{0}},{\textbf{1}},{\textbf{2}}\}})\) is a parallelogram, as shown in Fig. 2.
In the study of tiling, the periodicity, uniqueness (up to a translation) and other related properties of tiling sets have been of interest to scholars. Theorem 6.5 gives a class of self-affine sets generated by collinear digit sets, and we know that all parallelograms are tiles, and the tiling sets are not unique. However, the situation is quite different if the self-affine tile is generated by a non-collinear digit set. Even for the classical digit set \(D_c\), it is hard to find another tiling set for the classical Sierpinski self-affine tile besides \({\mathbb {Z}}^2\). The following two examples give a vision of tiling process of two classical Sierpinski self-affine tiles \({\textbf{T}}(A,D_{c})\).
Example 6.7
Let \(D_{c}\) be given by (2.1) and
Figure 3 presents two different classical Sierpinski self-affine tiles \({\textbf{T}}(A_1,D_{c})\) and \({\textbf{T}}(A_2,D_{c})\), see the first and third picture in Fig. 3 respectively. And the second and last picture in Fig. 3 correspond to the translation of the first and third picture via the set \(\{(1,0)^t,(0,1)^t,(-1,0)^t,(0,-1)^t\}\). By observation and using Theorem 2.2, it is evident that
and \({\mathbb {Z}}^2\) is their unique spectrum containing \({\textbf{0}}\).
Example 6.7 gives two classical Sierpinski self-affine tiles. It follows from the spectrality of \({\textbf{T}}(A,D_c)\) and duality criterion that for such classical Sierpinski self-affine tiles \({\textbf{T}}(A,D_c)\), we can take \({\mathbb {Z}}^2\) as their tiling sets. By plotting and analyzing, we think that the uniqueness of tiling sets is essentially related to the regularity of self-affine tiles (“regularity" we means that one of the edges of self-affine sets is a line segment). That is, the self-affine tiles generated by the non-collinear digit set \(D_c\) are “irregular”. The following question is naturally raised.
Question: Whether \({\mathbb {Z}}^2\) is the unique tiling set of the classical Sierpinski self-affine tile \({\textbf{T}}(A,D_{c})\) up to a translation?
At the end of this paper, we give a more concrete example to exhibit the different tiling properties between collinear and non-collinear digit sets for their corresponding Sierpinski self-affine sets.
Example 6.8
Let \(A=\begin{bmatrix} 0&{}-1 \\ 3&{}1 \end{bmatrix}\), \(D_{\{{\textbf{0}},{\textbf{1}},{\textbf{2}}\}}=\left\{ \begin{pmatrix} 0\\ 0\end{pmatrix},\begin{pmatrix} 1\\ 1 \end{pmatrix}, \begin{pmatrix} 2\\ 2 \end{pmatrix}\right\} \) and let \(D_{c}\) be given by (2.1). From Fig. 4, it is not difficult to see that two self-affine sets \({\textbf{T}}(A,D_{\{{\textbf{0}},{\textbf{1}},{\textbf{2}}\}})\) and \({\textbf{T}}(A,D_c)\) have completely different properties. By Theorems 2.2 and 4.9, we know that \({\textbf{T}}(A,D_{\{{\textbf{0}},{\textbf{1}},{\textbf{2}}\}})\) is spectral set (or a tile) but \({\textbf{T}}(A,D_c)\) is not.
Data availability
No data was used for the research described in the article.
Notes
The “integral” means that A is an integer matrix and D is an integer digit set.
The symbol “\(a\bot \Lambda \)” means \(<e_a,e_\lambda >=0\) for any \(\lambda \in \Lambda \), where \(e_{\xi }=e^{2 \pi i <\xi ,\cdot >}\).
References
An, L.X., He, X.G., Tao, L.: Spectrality of the planar Sierpinski family. J. Math. Anal. Appl. 432, 725–732 (2015)
Birklbauer, P.: The Fuglede conjecture holds in \({\mathbb{Z} }_{5}^{3}\). Exp. Math. 31, 456–460 (2022)
Chen, M.L., Liu, J.C.: The cardinality of orthogonal exponentials of planar self-affine measures with three-element digit sets. J. Funct. Anal. 277, 135–156 (2019)
Chen, M.L., Liu, J.C.: On spectra and spectral eigenmatrices of self-affine measures on \({\mathbb{R} }^n\). Bull. Malays. Math. Sci. Soc. 46, 162 (2023)
Chen, M.L., Liu, J.C., Wang, X.Y.: Spectrality of a class of self-affine measures on \({\mathbb{R} }^2\). Nonlinearity 34, 7446–7469 (2021)
Dai, X.R., He, X.G., Lau, K.S.: On spectral N-Bernoulli measures. Adv. Math. 259, 511–531 (2014)
Deng, Q.R., Lau, K.S.: Sierpinski-type spectral self-similar measures. J. Funct. Anal. 269, 1310–1326 (2015)
Dutkay, D.E., Emami, S., Lai, C.K.: Existence and exactness of exponential Riesz sequences and frames for fractal measures. J. Anal. Math. 143, 289–311 (2021)
Dutkay, D.E., Haussermann, J., Lai, C.K.: Hadamard triples generate self-affine spectral measures. Trans. Am. Math. Soc. 371, 1439–1481 (2019)
Dutkay, D.E., Jorgensen, P.E.T.: Analysis of orthogonality and of orbits in affine iterated function systems. Math. Z. 256, 801–823 (2007)
Dutkay, D.E., Jorgensen, P.E.T.: Fourier frequencies in affine iterated function systems. J. Funct. Anal. 247, 110–137 (2007)
Dutkay, D.E., Lai, C.K.: Uniformity of measures with Fourier frames. Adv. Math. 252, 684–707 (2014)
Dutkay, D.E., Jorgensen, P.E.T.: Probability and Fourier duality for affine iterated function systems. Acta Appl. Math. 107, 293–311 (2009)
Falconer, K.J.: Fractal geometry, mathematical foundations and applications. Wiley, New York (1990)
Fallon, T., Kiss, G., Somlai, G.: Spectral sets and tiles in \({\mathbb{Z} }_{p}^{2} \times {\mathbb{Z} }_{q}^{2} \). J. Funct. Anal. 282, 109472 (2022)
Fallon, T., Mayeli, A., Villano, D.: The Fuglede conjecture holds in \({\mathbb{F}}_{p}^{3}\) for \( p=5,7 \). Proc. Am. Math. Soc. (2019). https://doi.org/10.48550/arXiv.1902.02936
Fan, A.H., Fan, S.L., Liao, L.M., Shi, R.X.: Fuglede’s conjecture holds in \({\mathbb{Q} }_p\). Math. Ann. 375, 315–341 (2019)
Fu, X.Y., He, X.G., Lau, K.S.: Spectrality of self-similar tiles. Constr. Approx. 42, 519–541 (2015)
Ferguson, S.J., Sothanaphan, N.: Fuglede’s conjecture fails in \(4\) dimensions over odd prime fields. Discrete Math. 343, 111507 (2020)
Fuglede, B.: Commuting self-adjoint partial differential operators and a group theoretic problem. J. Funct. Anal. 16, 101–121 (1974)
Greenfeld, R., Lev, N.: Spectrality and tiling by cylindric domains. J. Funct. Anal. 271, 2808–2821 (2016)
Greenfeld, R., Lev, N.: Spectrality of product domains and Fuglede’s conjecture for convex polytopes. J. Anal. Math. 140, 409–441 (2020)
He, X.G., Lai, C.K., Lau, K.S.: Exponential spectra in \(L^2(\mu )\). Appl. Comput. Harmon. Anal. 34, 327–338 (2013)
Hutchinson, J.E.: Fractals and self-similarity. Indiana Univ. Math. J. 30, 713–747 (1981)
Iosevich, A., Katz, N., Tao, T.: The Fuglede spectral conjecture holds for convex planar domains. Math. Res. Lett. 10, 559–569 (2003)
Iosevich, A., Mayeli, A., Pakianathan, J.: The Fuglede conjecture holds in \({\mathbb{Z} }_{p}\times {\mathbb{Z} }_{p}\). Anal. PDE 10, 757–764 (2017)
Jorgensen, P.E.T., Pedersen, S.: Dense analytic subspaces in fractal \(L^2\)-spaces. J. Anal. Math. 75, 185–228 (1998)
Jorgensen, P.E.T., Pedersen, S.: Spectral pairs in Cartesian coordinates. J. Fourier Anal. Appl. 5, 285–302 (1999)
Kenyon, R.: Self-replicating tilings. Contemp. Math. 135, 239–263 (1992)
Kirat, I., Lau, K.S.: On the connectedness of self-affine tiles. J. Lond. Math. Soc. 62, 291–304 (2000)
Kiss, G., Malikiosis, R.D., Somlai, G., Vizer, M.: Fuglede’s conjecture holds for cyclic groups of order \(pqrs\). J. Fourier Anal. Appl. 28, 79 (2022)
Kolountzakis, M.N.: Packing near the tiling density and exponential bases for product domains. Bull. Hell. Math. Soc. 60, 97–109 (2016)
Kolountzakis, M.N., Matolcsi, M.: Tiles with no spectra. Forum Math. 18, 519–528 (2006)
Kolountzakis, M.N., Matolcsi, M.: Complex Hadamard matrices and the spectral set conjecture. Collect. Math. (2006). https://doi.org/10.48550/arXiv.math/0411512
Łaba, I.: Fuglede’s conjecture for a union of two intervals. Proc. Am. Math. Soc. 129, 2965–2972 (2001)
Łaba, I.: The spectral set conjecture and multiplicative properties of roots of polynomials. J. Lond. Math. Soc. 65, 661–671 (2002)
Łaba, I., Wang, Y.: On spectral Cantor measures. J. Funct. Anal. 193, 409–420 (2002)
Lagarias, J.C., Wang, Y.: Self-affine tiles in \({\mathbb{R} }^n\). Adv. Math. 121, 21–49 (1996)
Lagarias, J.C., Wang, Y.: Integral self-affine tiles in \({\mathbb{R} }^n\). I. Standard and nonstandard digit sets. J. Lond. Math. Soc. 54, 161–179 (1996)
Lagarias, J.C., Wang, Y.: Integral self-affine tiles in \(\mathbb{R} ^n\). II. Lattice tilings. J. Fourier Anal. Appl. 3, 83–102 (1997)
Lai, C.K., Lau, K.S., Rao, H.: Spectral structure of digit sets of self-similar tiles on \({\mathbb{R} }^1\). Trans. Am. Math. Soc. 365, 3831–3850 (2013)
Lai, C.K., Lau, K.S., Rao, H.: Classification of tile digit sets as product-forms. Trans. Am. Math. Soc. 369, 623–644 (2017)
Lau, K.S., Rao, H.: On one-dimensional self-similar tilings and the \(pq\)-tilings. Trans. Am. Math. Soc. 355, 1401–1414 (2003)
Li, J.L.: Spectral self-affine measures on the planar Sierpinski family. Sci. China Math. 56, 1619–1628 (2013)
Liu, J.C., Luo, J.J.: Spectral property of self-affine measures on \({\mathbb{R} }^n\). J. Funct. Anal. 272, 599–612 (2017)
Liu, J.C., Wang, Z.Y.: The spectrality of self-affine measure under the similar transformation of \(GL_n(p)\). Constr. Approx. (2023). https://doi.org/10.1007/s00365-023-09621-9
Liu, J.C., Zhang, Y., Wang, Z.Y., Chen, M.L.: Spectrality of generalized Sierpinski-type self-affine measures. Appl. Comput. Harmon. Anal. 55, 129–148 (2021)
Lev, N., Matolcsi, M.: The Fuglede conjecture for convex domains is true in all dimensions. Acta Math. 228, 385–420 (2022)
Matolcsi, M.: Fuglede’s conjecture fails in dimension 4. Proc. Am. Math. Soc. 133, 3021–3026 (2005)
Malikiosis, R.D.: On the structure of spectral and tiling subsets of cyclic groups. Forum Math. Sigma 10, e23 (2022)
Malikiosis, R.D., Kolountzakis, M.N.: Fuglede’s conjecture on cyclic groups of order \(p^nq\). Discrete Anal. 12, 16 pp (2017)
Mattheus, S.: A counterexample to Fuglede’s conjecture in \(({\mathbb{Z} } / p {\mathbb{Z} })^{4}\) for all odd primes. Bull. Belg. Math. Soc. Simon Stevin. 27, 481–488 (2020)
Odlyzko, A.M.: Nonnegative digit sets in positional number systems. Proc. Lond. Math. Soc. 37, 213–229 (1978)
Shi, R.X.: Fuglede’s conjecture holds on cyclic groups \({\mathbb{Z} }_{pqr}\). Discrete Anal. 14, 14 pp (2019)
Strichartz, R.: Mock Fourier series and transforms associated with certain Cantor measures. J. Anal. Math. 81, 209–238 (2000)
Tao, T.: Fuglede’s conjecture is false in 5 and higher dimensions. Math. Res. Lett. 11, 251–258 (2004)
Zhang, T.: Fuglede’s conjecture holds in \({\mathbb{Z} }_{p} \times {\mathbb{Z} }_{p^{n}} \). SIAM J. Discrete Math. 37, 1180–1197 (2023)
Zhang, T.: A group ring approach to Fuglede’s conjecture in cyclic groups (2023). Arxiv preprint https://doi.org/10.48550/arXiv.2210.15174
Acknowledgements
The authors would like to thank the anonymous referees for their valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The research is supported in part by the NNSF of China (Nos. 12071125, 11831007, 12301104 and 12271194), the Jiangxi Provincial Natural Science Foundation (No. 20232BAB211003), the Science and Technology Research Project of Jiangxi Provincial Department of Education (No. GJJ2201244).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Chen, ML., Liu, JC. & Zheng, J. Tiling and Spectrality for Generalized Sierpinski Self-Affine Sets. J Geom Anal 34, 5 (2024). https://doi.org/10.1007/s12220-023-01447-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12220-023-01447-y



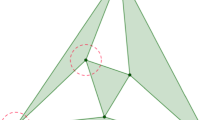
 [
[


