On the Anti-invariant Cohomology of Almost Complex Manifolds

Abstract

We study the space of closed anti-invariant forms on an almost complex manifold, possibly non-compact. We construct families of (non-integrable) almost complex structures on ${{\mathbb {R}}}^4$, such that the space of closed J-anti-invariant forms is infinite dimensional, and also 0- or 1-dimensional. In the compact case, we construct 6-dimensional almost complex manifolds with arbitrary large anti-invariant cohomology and a 2-parameter family of almost complex structures on the Kodaira–Thurston manifold whose anti-invariant cohomology group has maximum dimension.

1 Introduction

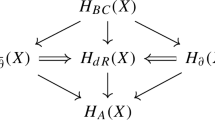
Cohomological properties provide a connection between analytical and topological features of complex manifolds. Indeed for a given complex manifold (M, J), natural complex cohomologies are defined, e.g., the Dolbeault, Bott–Chern and Aeppli cohomology groups, given by

$$\begin{aligned} H^{\bullet ,\bullet }_{{\overline{\partial }}}(M)=\frac{{{\,\mathrm{Ker}\,}}{\overline{\partial }}}{{{\,\mathrm{Im}\,}}{\overline{\partial }}}\,,\,\, H^{\bullet ,\bullet }_{BC}(M)=\frac{{{\,\mathrm{Ker}\,}}\partial \cap {{\,\mathrm{Ker}\,}}{\overline{\partial }}}{{{\,\mathrm{Im}\,}}\partial {\overline{\partial }}}\,,\,\, H^{\bullet ,\bullet }_{A}(M)=\frac{{{\,\mathrm{Ker}\,}}\partial {\overline{\partial }}}{{{\,\mathrm{Im}\,}}\partial +{{\,\mathrm{Im}\,}}{\overline{\partial }}}\,. \end{aligned}$$

Furthermore, if (M, J) is a compact complex manifold admitting a Kähler metric, that is a J-Hermitian metric whose fundamental form is closed, as a consequence of Hodge theory, the complex de Rham cohomology groups decompose as the direct sum of (p, q)-Dolbeault groups and strong topological restrictions on M are derived.For an almost complex manifold (M, J) the exterior differential d acting on the space of complex valued (p, q)-forms splits as

$$\begin{aligned} \mathrm{{d}}=\mu +\partial +{\overline{\partial }}+{\overline{\mu }}, \end{aligned}$$

where ${\overline{\partial }}$, respectively ${\overline{\mu }}$, are the $(p,q+1)$, respectively, the $(p-1,q+2)$ components of d. It turns out that the almost complex structure J is integrable if and only if ${\overline{\mu }}=0$. Consequently, in the non-integrable case, ${\overline{\partial }}$ is not a cohomological operator.In [13] Li and Zhang, motivated by the study of comparison of tamed and compatible symplectic cones on a compact almost complex manifold, introduced the J-anti-invariant and J-invariant cohomology groups as the (real) de Rham 2-classes represented by J-anti-invariant, respectively, J-invariant forms and the notion of ${\mathcal {C}}^\infty -\textit{pure-and-full}$ almost complex structures, namely those ones such that the second de Rham cohomology group decomposes as the direct sum of the J-anti-invariant and J-invariant cohomology groups. In [5], Drǎghici et al. proved that an almost complex structure on a compact 4-dimensional manifold is ${\mathcal {C}}^\infty$-pure-and-full.

In [6, 7], the same authors continue the study of the J-anti-invariant cohomology of an almost complex manifold (M, J). Let $h^-_J$ be the dimension of the real vector space of closed anti-invariant 2-forms on (M, J). Note that in the case when the manifold is 4-dimensional every closed anti-invariant form $\alpha$ is $\Delta _{g_J}$-harmonic, where $g_J$ is a Hermitian metric and $\Delta _{g_J}$ denotes the Hodge Lapacian, see Sect. 2. Thus in the compact 4 dimensional case $h^-_J$ is the dimension of the anti-invariant cohomology. The following conjectures appear in [6].

Conjecture 2.4

For generic almost complex structures J on a compact 4-manifold M, $h^-_J= 0$.

In the case when $b^+ =1$ this was proved as Theorem 3.1 the same paper. The conjecture in general was established by Tan et al. [15].

Conjecture 2.5

On a compact 4-manifold, if $h^-_J\ge 3$ , then J is integrable.

By starting with a (compact) Kähler surface with holomorphically trivial canonical bundle, Drǎghici, Li and Zhang obtain non-integrable almost complex structures with $h^-_J=2$. More precisely, for a given (compact) Kähler surface (M, J) with holomorphically trivial canonical bundle, they take a closed 2-form trivializing the canonical bundle. Then, fixing a conformal class of Hermitian metrics compatible with J, they consider the Gauduchon metric representing such a conformal class and they associate an almost complex structure $J_{f,s,l}$ depending on three smooth functions satisfying some suitable conditions. Then, generically, $h^-_{J_{f,s,l}}=0$, but cases when $h^-_{J_{f,s,l}}=1$ and $h^-_{J_{f,s,l}}=2$ also occur. Therefore, again in [6], as an extension of Conjecture 2.5, the authors asked the following natural

Question 3.23

Are there (compact, 4-dimensional) examples of non-integrable almost complex structures J with $h^{-}_J\ge 2$ other than the ones arising from [6], Proposition 3.21? In particular, are there any examples with $h^-_J \ge 3$?

For other results on ${\mathcal {C}}^\infty$-pure-and-full and J-anti-invariant closed forms see [2,3,4, 9, 11].

In this note, motivated by Conjecture 2.5 and Question 3.23, we study the anti-invariant cohomology and the space of anti-invariant harmonic forms of an almost complex manifold, possibly non-compact.

Starting with the non-compact case, we first note that the space of closed anti-invariant forms with respect to the standard integrable complex structure i on ${{\mathbb {R}}}^4 \equiv {{\mathbb {C}}}^2$ is infinite dimensional: indeed, for every given holomorphic function $h(z_1,z_2)$, the real and imaginary parts of $h(z_1, z_2)dz_1\wedge dz_2$ are closed and anti-invariant.

As Theorem 3.7, we show the same can also hold in the non-integrable case.

Theorem

There exists a (non-integrable) almost complex structure on ${{\mathbb {R}}}^4$, such that the space of closed J-anti-invariant forms is infinite dimensional.

As a consequence, we see that compactness is essential for Conjecture 2.5

In contrast we also show the following (see Theorem 3.8, and Lemma 3.4 for the integrability statement).

Theorem

There exists a family of almost complex structures $\{J_f\}$ on ${{\mathbb {C}}}^2$, parameterized by smooth functions $f: {{\mathbb {C}}}^2 \rightarrow {{\mathbb {R}}}$, with the following properties.

• $J_f$ coincides with the standard complex structure i exactly at points where $f=0$;

• $J_f$ is integrable if and only if the gradient of f in the $z_2$ direction is 0;

• if f has compact support and $f \not \equiv 0$ then $h^-_{J_f}=1$.

In particular, an arbitrarily small, compactly supported, perturbation of a complex structure having an infinite dimensional space of anti-invariant forms may admit only a single such form up to scale. This provides supporting evidence for Conjecture 2.5, showing that typically anti-invariant forms do not persist under non-integrable perturbations.

A similar argument gives the following, see Corollary 3.9.

Corollary

There exist almost complex structures on ${{\mathbb {C}}}^2$ which agree with i outside of a compact set and have $h^-_J =0$.

We note that integrable complex structures on ${{\mathbb {C}}}^2$ which agree with i outside of a compact set are biholomorphic to ${{\mathbb {C}}}^2$ itself, and so have $h^-_J = \infty$. This follows from Yau [17], Theorem 5, since such complex structures can be extended to give complex structures on ${{\mathbb {C}}}P^2$.

Given the original motivations for studying anti-invariant cohomology groups it is natural to ask about compatibility properties for our almost complex structures. We point out in Remark 3.10 that the almost complex structures described in both of the above theorems are indeed almost Kähler, that is, they are compatible with a symplectic form on ${{\mathbb {C}}}^2$.

In the compact case, we construct a 2-parameter family of (non-integrable) almost complex structures on the Kodaira–Thurston manifold, depending on two smooth functions, for which the anti-invariant cohomology group has maximum dimension equal to 2 (see Proposition 4.2). This provides an affirmative answer to Question 3.23. In the last section, we give a simple construction to obtain 6-dimensional compact almost complex manifolds with arbitrary large anti-invariant cohomology (see Proposition 5.1). Hence dimension 4 is also an essential part of Conjecture 2.5.

For almost-complex structure on a 4-manifold which are tamed by a symplectic form, Drǎghici et al. [5], Theorem 3.3, that $h^-_J \le b^+ -1$. Thus any counterexamples to Conjecture 2.5 cannot come from tame almost-complex structures on symplectic 4-manifolds with $b^+ \le 3$. Moreover Li [12], Theorem 1.1, shows that symplectic 4-manifolds of Kodaira dimension 0 all have $b^+ \le 3$. We thank Weiyi Zhang for pointing this out.

2 Anti-invariant Cohomology

In this Section we will fix some notation and recall the generalities on anti-invariant forms and some notion about the cohomology of almost complex manifolds. Let M be a smooth 2n-dimensional manifold. We will denote by J a smooth almost complex structure on M, that is a smooth (1, 1)-tensor J field satisfying $J^2=-\hbox {id}$. The almost complex structure J is said to be integrable if its Nijenhuis tensor, that is the (1, 2)-tensor given by

$$\begin{aligned} N_J(X,Y)=[JX,JY]-[X,Y]-J[JX,Y]-J[X,JY], \end{aligned}$$

According to Newlander–Nirenberg Theorem, J is integrable if and only if J is induced by a structure of complex manifold on M. Let J be a smooth almost-complex structure on a M and denote by $\Lambda ^r(M)$ the bundle of r-forms on M; let $\Omega ^r(M):=\Gamma (M,\Lambda ^r(M))$ be the space of smooth global sections of $\Lambda ^r(X)$ and let $\Lambda ^r(M;{{\mathbb {C}}})=\Lambda ^r(M)\otimes {{\mathbb {C}}}$. Then J acts in a natural way on the space $\Omega ^r(M;{{\mathbb {C}}})$ of smooth sections of $\Lambda ^r(M;{{\mathbb {C}}})$ giving rise to the following bundle decomposition

$$\begin{aligned} \Lambda ^r(M;{{\mathbb {C}}})=\bigoplus _{p+q=r}\Lambda ^{p,q}_J(M). \end{aligned}$$

Accordingly, $\Omega ^r(M;{{\mathbb {C}}})$ and $\Omega ^r(M)$ decompose, respectively, as

$$\begin{aligned} \Omega ^r(M;{{\mathbb {C}}})=\bigoplus _{p+q=r}\Omega ^{p,q}_J(M). \end{aligned}$$

and

$$\begin{aligned} \Omega ^r(M)=\bigoplus _{p+q=r,\,p\le q}\Omega ^{(p,q),(q,p)}(M)_{{\mathbb {R}}}, \end{aligned}$$

where, for $p <q$

$$\begin{aligned} \Omega ^{(p,q),(q,p)}(M)_{{\mathbb {R}}}=\{\alpha \in \Omega ^{p,q}_J(M)\oplus \Omega ^{q,p}_J(M)\,\,\,\vert \,\,\, \alpha ={\overline{\alpha }}\}, \end{aligned}$$

and

$$\begin{aligned} \Omega ^{(p,p)}(M)_{{\mathbb {R}}}=\{\beta \in \Omega ^{p,p}_J(M)\,\,\,\vert \,\,\, \beta ={\overline{\beta }}\}. \end{aligned}$$

In particular for $r=2$, J acts as involution on $\Omega ^2(M)$ by

$$\begin{aligned} J\alpha (X,Y)=\alpha (JX,JY), \end{aligned}$$

for every pair of vector fields X, Y on M. Then we denote as usual by $\Lambda ^-_J(M)$ (respectively, $\Lambda ^+_J(M)$) the $+1$ (resp. $-1$)-eigenbundle; then the space of corresponding sections $\Omega ^-_J(M)$ (respectively, $\Omega ^+_J(M)$) are defined to be the spaces of J-anti-invariant, (respectively, J-invariant) forms, i.e.,

$$\begin{aligned} \Omega _J^\pm (M)= & {} \{\alpha \in \Omega ^2(M)\,\,\,\vert \,\,\,J\alpha =\pm \alpha \}\\ \Omega ^{(2,0),(0,2)}(M)_{{\mathbb {R}}}= & {} \Omega ^-_J(M),\quad \Omega ^{1,1}(M)_{{\mathbb {R}}}=\Omega ^+_J(M). \end{aligned}$$

Let

$$\begin{aligned} {\mathcal {Z}}^\pm _J(M)={\mathcal {Z}}^2(M)\cap \Omega ^\pm _J(M)=\{\alpha \in \Omega ^\pm _J(M)\,\,\,\vert \,\,\,\mathrm{{d}}\alpha =0\}. \end{aligned}$$

If $\{\varphi ^1,\ldots ,\varphi ^n\}$ is a local coframe of (1, 0)-forms on (M, J), then $\Lambda ^-_J(M)$ is locally spanned by

$$\begin{aligned} \{ \hbox {Re}(\varphi ^r\wedge \varphi ^s), \quad \hbox { Im}(\varphi ^r\wedge \varphi ^s),\,\, 1\le r<s \le n \}. \end{aligned}$$

Then, according to the previous decomposition on forms, Li and Zhang [13] defined the following cohomology spaces

$$\begin{aligned} H^\pm _J (X)= \left\{ {\mathfrak {a}} \in H^2_{dR}(X;{{\mathbb {R}}}) \,\,\, \vert \, \,\,\exists \,\alpha \in {{\mathcal {Z}}}^{\pm }_J\,\,\vert \,\, {\mathfrak {a}}=[\alpha ]\right\} , \end{aligned}$$

and they gave the following (see [13, Definition 4.12])

Definition 2.1

An almost complex structure J on M is said to be

• ${\mathcal {C}}^\infty$-pure if

  $$\begin{aligned} H^{+}_J (M) \cap H^{-}_J (M)=\{0\}\,. \end{aligned}$$

• ${\mathcal {C}}^\infty$-full if

  $$\begin{aligned} H^{2}_{dR} (M;{{\mathbb {R}}}) =H^{+}_J (M) + H^{-}_J (M). \end{aligned}$$

• ${\mathcal {C}}^\infty$-pure-and-full if

  $$\begin{aligned} H^{2}_{dR} (M;{{\mathbb {R}}}) =H^{+}_J (M) \oplus H^{-}_J (M). \end{aligned}$$

Given an almost complex manifold (M, J), we denote by

$$\begin{aligned} h^-_J(M)=\dim _{{\mathbb {R}}}{\mathcal {Z}}^-_J(M). \end{aligned}$$

For a given Hermitian metric $g_J$ on the 2n-dimensional almost complex manifold (M, J), we will denote by ${\mathcal {H}}_J^-(M)$ the space of J-anti-invariant harmonic 2-forms, that is

$$\begin{aligned} {\mathcal {H}}_J^-(M):=\{\alpha \in \Omega ^-(M)\,\,\,\vert \,\,\,\Delta _{g_J}\alpha =0\}, \end{aligned}$$

where $\Delta _{g_J}$ denotes the Hodge Laplacian.

Following [6, 10, Prop.2.4], once a J-Hermitian metric $g_J$ is fixed, the space ${\mathcal {Z}}^-_J(M)$ is contained in the kernel of a second-order elliptic differential operator ${\mathbb {E}}$, that is ${\mathcal {Z}}^-_J(M) \subset \hbox {Ker}\,{\mathbb {E}}$. Explicitly,

$$\begin{aligned} E\alpha = \Delta _{g_J}\alpha +\frac{1}{(n-2)!}\mathrm{{d}}((\alpha \wedge \mathrm{{d}}(\omega ^{n-2}))), \end{aligned}$$

where $\omega$ is the fundamental form of $g_J$. Hence, if M is a compact 2n-dimensional almost complex manifold, then ${\mathcal {Z}}^-_J(M)$ has finite dimension. Also, in view of [1], assuming M is connected, if $\alpha$ is any closed anti-invariant form vanishing to infinite order at some point p, then $\alpha =0$.

In the case when $2n=4$, then any J-anti-invariant closed form $\alpha$ on (M, J) satisfies $\Delta _{g_J}\alpha = {\mathbb {E}}\alpha = 0$ and so ${\mathcal {Z}}^-_J(M) \subset {\mathcal {H}}_J^-(M)$. Thus if M is compact the natural map ${\mathcal {Z}}^-_J(M) \hookrightarrow H_J^-(M)$ is an isomorphism. This also holds for compact M in higher dimensions provided that J is compatible with a symplectic form, that is, (M, J) is an almost Kähler manifold, see for example, [6] or [10, Proposition 2.2, Corollary 2.3].

Finally, again in dimension $2n=4$, we can check that in fact ${\mathcal {Z}}^-_{J}(M)\subset {\mathcal {H}}^+_{g_J} \subset {\mathcal {H}}_J^-(M)$ where ${\mathcal {H}}^+_{g_J}$ is the space of self-dual harmonic forms. So in the compact case we have $h^-_J(M)\le b^+(M)$.

3 Closed J-Anti-invariant Forms and an Integrability Condition

Let J be an almost complex structure on a 4-dimensional manifold. Let $\omega \ne 0$ be a closed J-anti-invariant form on M. Then, according to [5, Lemma 2.6] (see also [10, Prop. 2.6]) the zero set $\omega ^{-1}(0)$ of $\omega$ has empty interior, so that $M\setminus \omega ^{-1}(0)$ is open and dense. Since $M\setminus \omega ^{-1}(0)$ coincides with the subset of M where $\omega$ is non-degenerate (see [5, Lemma 2.6] or [10, Lemma 1.1]), we have the following

Lemma 3.1

Let (M, J) be a 4-dimensional almost complex manifold and $0\ne \omega \in {\mathcal {Z}}^-_J$. Then $\omega$ is a symplectic form on the open dense set $M\setminus \omega ^{-1}(0)$.

Let $J_0$ be the standard complex structure on the vector space ${{\mathbb {C}}}^n\simeq {{\mathbb {R}}}^{2n}$ induced by the multiplication by i, that is,

$$\begin{aligned} J_0(z_1,\ldots ,z_n)=(e^{i\frac{\pi }{2}}z_1,\ldots ,e^{i\frac{\pi }{2}}z_n). \end{aligned}$$

Then, for every given real number r, define $J_0^r\in \hbox { End}({{\mathbb {C}}}^n)$, by setting

$$\begin{aligned} J^r_0(z_1,\ldots ,z_n)=(e^{i\frac{\pi }{2}r}z_1,\ldots ,e^{i\frac{\pi }{2}r}z_n). \end{aligned}$$

Let now J be any almost complex structure on the manifold ${{\mathbb {C}}}^n\simeq {{\mathbb {R}}}^{2n}$; then there exists $A:{{\mathbb {R}}}^{2n}\rightarrow \hbox { GL}(2n,{{\mathbb {R}}})$ such that J is conjugated to the standard complex structure $J_0$, i.e.,

$$\begin{aligned} J_x=A(x)J_0A^{-1}(x). \end{aligned}$$

For $r=r(x)\in {{\mathbb {R}}}$, define

$$\begin{aligned} J_x^r:=A(x)J_0^rA^{-1}(x). \end{aligned}$$

Let (M, J) be a 2n-dimensional almost complex manifold and let $\omega \in \Omega ^-_J(M)$. Let ${\mathcal {U}}$ be a coordinate neighborhood. We can find A(x) for $x \in {\mathcal {U}}$ conjugating $J_x$ to $J_0$. Given a smooth function $r : M \rightarrow {{\mathbb {R}}}$ equal to 0 outside of ${\mathcal {U}}$ we can define a bilinear form $\theta ^r$ on M which agrees with $\omega$ outside of ${\mathcal {U}}$ by setting, at any given $x\in {\mathcal {U}}$,

$$\begin{aligned} \theta ^r_x(v,w)=\omega _x(v,J^{r(x)}_xw), \end{aligned}$$

(1)

for every pair of tangent vectors v, w.

Lemma 3.2

The form $\theta ^r$ is skew-symmetric and J-anti-invariant, that is, $\theta ^r \in \Omega ^-_J(M)$.

Proof

For any given pair of tangent vectors v, w at x,

$$\begin{aligned} \begin{array}{l} J_x\theta ^r_x(v,w)=\theta ^r_x(J_xv,J_xw)=\omega _x(J_xv,J^{r+1}_xw) =-\omega _x(v,J^{r}_xw)=-\theta ^r_x(v,w), \end{array} \end{aligned}$$

that is $J\theta ^r=-\theta ^r$.

Note that when $r=0$ we have $\theta ^0 = \omega$ is skew. To check $\theta ^r$ is skew for all r, we fix x (and so can think of r as a real number) and working in $T_x M$ can choose a basis such that we can identify J with the standard complex structure $J_0$ on ${{\mathbb {C}}}^n$. Then

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}r}J^r = \frac{\pi }{2} J^{r+1}. \end{aligned}$$

Hence

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}r} \theta ^r(v,w) =\frac{\mathrm{{d}}}{\mathrm{{d}}r} \omega (v,J^r w)=\frac{\pi }{2}\omega (v,J^{r+1} w)= \frac{\pi }{2} \theta (v,Jw). \end{aligned}$$

For the same fixed v, w, we define a function

$$\begin{aligned} f(r) = ( \theta ^r(v,w) + \theta ^r(w,v) )^2 + ( \theta ^r(v, Jw) + \theta ^r(Jw,v) )^2. \end{aligned}$$

Then

$$\begin{aligned} \frac{\mathrm{{d}}f}{\mathrm{{d}}r}= & {} \frac{\pi }{2}( \theta ^r(v,w) + \theta ^r(w,v) ) ( \theta ^r(v,Jw) + \theta ^r(w,Jv) )\\&+ \frac{\pi }{2}( \theta ^r(v, Jw) + \theta ^r(Jw,v) )( - \theta (v, w) + \theta (Jw,Jv)) =0, \end{aligned}$$

using the fact that $J\theta ^r = -\theta ^r$. Hence $f'(r) = 0$ and since $f(0)=0$ we see that $f(r)=0$ for all r and $\theta ^r$ is skew for all r. $\square$

The last Lemma allows to produce anti-invariant forms starting from an anti-invariant one. For the sake of completeness we recall the proof of an integrability result in the 4-dimensional case obtained by Drǎghici et al. (see [5, Lemma 2.12]).

Proposition 3.3

Let (M, J) be a 4-dimensional almost complex manifold. Let $0 \ne \omega \in {\mathcal {Z}}^-_J(M)$. If the form $\theta _x(\cdot ,\cdot )=\omega _x(\cdot ,J_x\cdot )$ is closed, then J is integrable.

Proof

It suffices to check the Nijenhuis tensor $N_J=0$, at any point of the dense subset $M\setminus \omega ^{-1}(0)$. This implies $N_J=0$ on the whole M and J is integrable.

By Lemma 3.1 the 2-form $\omega$ is a symplectic structure on $M\setminus \omega ^{-1}(0)$. Let $x\in M\setminus \omega ^{-1}(0)$ and ${\mathcal {U}}$ be a coordinate neighborhood of x contained in $M\setminus \omega ^{-1}(0)$. Define a local complex 2-form on (M, J) by setting, for every $x\in {\mathcal {U}}$,

$$\begin{aligned} \Psi _x=\omega _x-i\theta _x. \end{aligned}$$

We show that $\Omega$ is of type (2, 0). Indeed, for every given v, w,

$$\begin{aligned} \begin{array}{ll} \Psi _x(v-iJv,w+iJw)&{}=(\omega _x-i\theta _x)(v-iJv,w+iJw)\\ &{}= \omega _x(v,w)+\omega _x(Jv,Jw)-i\big (\theta _x(v,w)+\theta _x(Jv,Jw)\big )\\ &{}\quad + i\big (\omega _x(v,Jw)-\omega _x(Jv,w)-i(\theta _x(v,Jw)-\theta _x(Jv,w))\big )\\ &{}= 0, \end{array} \end{aligned}$$

since $\omega$ and $\theta$ are J-anti-invariant. Therefore, $\Psi$ vanishes on any pair of complex vectors of type (1, 0), (0, 1), respectively, that is

$$\begin{aligned} \Psi \in \Omega ^{2,0}_J({\mathcal {U}})\oplus \Omega ^{0,2}_J({\mathcal {U}}). \end{aligned}$$

Similarly,

$$\begin{aligned} \begin{array}{ll} \Psi _x(v+iJv,w+iJw)&{}=(\omega _x-i\theta _x)(v+iJv,w+iJw)\\ &{}= \omega _x(v,w)-\omega _x(Jv,Jw)-i\big (\theta _x(v,w)-\theta _x(Jv,Jw)\big )\\ &{}\quad + i\big (\omega _x(v,Jw)+\omega _x(Jv,w)-i\big (\theta _x(v,Jw)+\theta _x(Jv,w)\big )\big )\\ &{}= 2\big (\omega _x(v,w)-i\theta _x(v,w)\big )+2i\big (\omega _x(v,Jw)-i\theta _x(v,Jw)\big )\\ &{}= 2\big (\omega _x(v,w)-i\theta _x(v,w)\big )+2i\big (\theta _x(v,w)+i\omega _x(v,w)\big )\\ &{}= 0. \end{array} \end{aligned}$$

Therefore, $\Psi \in \Omega ^{2,0}_J({\mathcal {U}})$ is nowhere vanishing and closed. Let $\alpha$ be any local complex (1, 0)-form. Then, by type reason, $\alpha \wedge \Psi =0$. Hence, at x,

$$\begin{aligned} 0=d(\alpha \wedge \Psi )=\mathrm{{d}}\alpha \wedge \Psi =(\mathrm{{d}}\alpha )^{0,2}\wedge \Psi , \end{aligned}$$

which implies that the (0, 2)-part $(\mathrm{{d}}\alpha )^{0,2}$ of $\mathrm{{d}}\alpha$ vanishes and $N_J(x)=0$. $\square$

Let $(x_1,x_2,y_1,y_2)$ be natural coordinates on ${{\mathbb {R}}}^4$ and $f=f(x_1,x_2,y_1,y_2)$ be a smooth ${{\mathbb {R}}}$-valued function on ${{\mathbb {R}}}^4$. Define $J_f\in \hbox {End}(T{{\mathbb {R}}}^4)$ by setting

$$\begin{aligned} J_f\frac{\partial }{\partial x_1}=f\frac{\partial }{\partial x_2}+\frac{\partial }{\partial y_1},\, J_f\frac{\partial }{\partial x_2}=\frac{\partial }{\partial y_2},\, J_f\frac{\partial }{\partial y_1}=-\frac{\partial }{\partial x_1}-f\frac{\partial }{\partial y_2},\, J_f\frac{\partial }{\partial y_2}=-\frac{\partial }{\partial x_2}\qquad \end{aligned}$$

(2)

and extend it ${\mathcal {C}}^\infty ({{\mathbb {R}}}^4)$-linearly. Then $J_f$ gives rise to an almost complex structure on ${{\mathbb {R}}}^4$.

Lemma 3.4

The almost complex structure $J=J_f$ is integrable if and only if

$$\begin{aligned} f_{x_2}=0,\quad f_{y_2}=0. \end{aligned}$$

Proof

It is enough to show that $N_J(\frac{\partial }{\partial x_1},\frac{\partial }{\partial x_2})=0$ if and only if

$$\begin{aligned} f_{x_2}=0,\quad f_{y_2}=0. \end{aligned}$$

We easily compute

$$\begin{aligned} \begin{array}{ll} N_J(\frac{\partial }{\partial x_1},\frac{\partial }{\partial x_2})&{}= [J\frac{\partial }{\partial x_1},J\frac{\partial }{\partial x_2}]-[\frac{\partial }{\partial x_1},\frac{\partial }{\partial x_2}]-J[J\frac{\partial }{\partial x_1},\frac{\partial }{\partial x_2}] -J[\frac{\partial }{\partial x_1},J\frac{\partial }{\partial x_2}]\\ &{}=[f\frac{\partial }{\partial x_2}+\frac{\partial }{\partial y_1},\frac{\partial }{\partial y_2}] -J[f\frac{\partial }{\partial x_2}+\frac{\partial }{\partial y_1},\frac{\partial }{\partial x_2}] -J[\frac{\partial }{\partial x_1},\frac{\partial }{\partial y_2}]\\ &{}=-f_{y_2}\frac{\partial }{\partial x_2}+f_{x_2}\frac{\partial }{\partial y_2} \end{array} \end{aligned}$$

Lemma is proved. $\square$

According to the definition of $J_f$, the induced almost complex structure $J_f$ on $T^*{{\mathbb {R}}}^4$ is given by

$$\begin{aligned} J_f\mathrm{{d}}x_1=-\mathrm{{d}}y_1,\quad J_f\mathrm{{d}}x_2=f\mathrm{{d}}x_1-\mathrm{{d}}y_2, \quad J_f\mathrm{{d}}y_1=\mathrm{{d}}x_1, \quad J_f\mathrm{{d}}y_2=-f\mathrm{{d}}y_1+\mathrm{{d}}x_2.\nonumber \\ \end{aligned}$$

(3)

Consequently, setting

$$\begin{aligned} \varphi ^1=\mathrm{{d}}x_1+id\mathrm{{d}}y_1,\quad \varphi ^2=\mathrm{{d}}x_2+i(-f\mathrm{{d}}x_1+\mathrm{{d}}y_2), \end{aligned}$$

then $\{\varphi ^1,\varphi ^2\}$ is a complex (1, 0)-coframe on the almost complex manifold $({{\mathbb {R}}}^4,J_f)$, so that

$$\begin{aligned} \beta =\hbox {Re}(\varphi ^1\wedge \varphi ^2), \quad \gamma =\hbox {Im}(\varphi ^1\wedge \varphi ^2), \end{aligned}$$

is a global frame of $\Lambda ^-_{J_f}({{\mathbb {R}}}^4)$. Explicitly,

$$\begin{aligned} \beta = \mathrm{{d}}x_1\wedge \mathrm{{d}}x_2-f\mathrm{{d}}x_1\wedge \mathrm{{d}}y_1- \mathrm{{d}}y_1\wedge \mathrm{{d}}y_2,\quad \gamma = \mathrm{{d}}x_1\wedge \mathrm{{d}}y_2-\mathrm{{d}}x_2\wedge \mathrm{{d}}y_1. \end{aligned}$$

(4)

Lemma 3.5

Let $\alpha$ be an arbitrary smooth section of $\Lambda ^-_{J_f}({{\mathbb {R}}}^4)$. Set

$$\begin{aligned} \alpha =a\beta +b\gamma , \end{aligned}$$

for a, b smooth ${{\mathbb {R}}}$-valued functions on ${{\mathbb {R}}}^4$. Then $d\alpha =0$ if and only if the following condition holds

$$\begin{aligned} \left\{ \begin{array}{lll} a_{y_1}-b_{x_1}+(fa)_{x_2}&{}=&{} 0 \\ a_{x_1}+b_{y_1}+(fa)_{y_2}&{}=&{} 0 \\ a_{y_2}-b_{x_2}&{}=&{} 0 \\ a_{x_2}+b_{y_2}&{}=&{} 0. \end{array} \right. \end{aligned}$$

(5)

Proof

Expanding $\mathrm{{d}}\alpha$ we get:

$$\begin{aligned} \begin{array}{ll} d\alpha &{}= \mathrm{{d}}a\wedge \beta - a \mathrm{{d}}f\wedge \mathrm{{d}}x_1\wedge \mathrm{{d}}y_1 +\mathrm{{d}}b\wedge \gamma \\ &{}= (a_{x_1}\mathrm{{d}}x_1+a_{x_2}\mathrm{{d}}x_2+a_{y_1}\mathrm{{d}}y_1+a_{y_2}\mathrm{{d}}y_2)\wedge (\mathrm{{d}}x_1\wedge \mathrm{{d}}x_2 -f\mathrm{{d}}x_1\wedge \mathrm{{d}}y_1- \mathrm{{d}}y_1\wedge \mathrm{{d}}y_2)\\ &{} -a(f_{x_1}\mathrm{{d}}x_1+f_{x_2}\mathrm{{d}}x_2+f_{y_1}\mathrm{{d}}y_1+f_{y_2}\mathrm{{d}}y_2)\wedge \mathrm{{d}}x_1\wedge \mathrm{{d}}y_1 +\\ &{} + (b_{x_1}\mathrm{{d}}x_1+b_{x_2}\mathrm{{d}}x_2+b_{y_1}\mathrm{{d}}y_1+b_{y_2}\mathrm{{d}}y_2)\wedge (\mathrm{{d}}x_1\wedge \mathrm{{d}}y_2 -\mathrm{{d}}x_2\wedge \mathrm{{d}}y_1)\\ &{}= -a_{x_1} \mathrm{{d}}x_1\wedge \mathrm{{d}}y_1\wedge \mathrm{{d}}y_2 + a_{x_2}f \mathrm{{d}}x_1\wedge \mathrm{{d}}x_2\wedge \mathrm{{d}}y_1 - a_{x_2} \mathrm{{d}}x_2\wedge \mathrm{{d}}y_1\wedge \mathrm{{d}}y_2+\\ &{} +a_{y_1} \mathrm{{d}}x_1\wedge \mathrm{{d}}x_2\wedge \mathrm{{d}}y_1 + a_{y_2} \mathrm{{d}}x_1\wedge \mathrm{{d}}x_2\wedge \mathrm{{d}}y_2 - a_{y_2}f \mathrm{{d}}x_1\wedge \mathrm{{d}}y_1\wedge \mathrm{{d}}y_2\\ &{} + af_{x_2} \mathrm{{d}}x_1\wedge \mathrm{{d}}x_2\wedge \mathrm{{d}}y_1-af_{y_2} \mathrm{{d}}x_1\wedge \mathrm{{d}}y_1\wedge \mathrm{{d}}y_2 - b_{x_1} \mathrm{{d}}x_1\wedge \mathrm{{d}}x_2\wedge \mathrm{{d}}y_1+ \\ &{} - b_{x_2} \mathrm{{d}}x_1\wedge \mathrm{{d}}x_2\wedge \mathrm{{d}}y_2 - b_{y_1} \mathrm{{d}}x_1\wedge \mathrm{{d}}y_1\wedge \mathrm{{d}}y_2 - b_{y_2} \mathrm{{d}}x_2\wedge \mathrm{{d}}y_1\wedge \mathrm{{d}}y_2\\ &{}=(a_{y_1}-b_{x_1}+ (af)_{x_2})\,\mathrm{{d}}x_1\wedge \mathrm{{d}}x_2\wedge \mathrm{{d}}y_1+(a_{y_2}-b_{x_2}) \,\mathrm{{d}}x_1\wedge \mathrm{{d}}x_2\wedge \mathrm{{d}}y_2+\\ &{}- (a_{x_1}+b_{y_1}+ (af)_{y_2})\,\mathrm{{d}}x_1\wedge \mathrm{{d}}y_1\wedge dy_2- (a_{x_2}+b_{y_2})\,\mathrm{{d}}x_2\wedge \mathrm{{d}}y_1\wedge \mathrm{{d}}y_2. \end{array} \end{aligned}$$

Therefore, $\mathrm{{d}}\alpha =0$ if and only if (5) holds. $\square$

Remark 3.6

Set $z_1=x_1+iy_1,$ $z_2=x_2+iy_2$ and

$$\begin{aligned} \begin{array}{ll} \partial _{z_1}=\frac{1}{2}(\partial _{x_1}-i\partial _{y_1}),&{} \partial _{z_2}=\frac{1}{2}(\partial _{x_2}-i\partial _{y_2})\\ \partial _{{\overline{z}}_1}=\frac{1}{2}(\partial _{x_1}+i\partial _{y_1}),&{} \partial _{{\overline{z}}_2}=\frac{1}{2}(\partial _{x_2}+i\partial _{y_2}). \end{array} \end{aligned}$$

Then a pair of real valued functions (a, b) on ${{\mathbb {R}}}^4$ is a solution of (5) if and only if the complex valued function $w=a-ib$ solves the following

$$\begin{aligned} \left\{ \begin{array}{l} \partial _{{\overline{z}}_1}w +\frac{i}{2}\partial _{z_2}(f(w+{\overline{w}}))= 0 \\ \partial _{{\overline{z}}_2}w = 0. \end{array} \right. \end{aligned}$$

(6)

The system above is a perturbed Cauchy–Riemann PDEs system. Furthermore, it is immediate to note that, condition (5) of Lemma 3.5 can be rewritten as

$$\begin{aligned} db=(a_{y_1}+(af)_{x_2})\mathrm{{d}}x_1+ a_{y_2}\mathrm{{d}}x_2- (a_{x_1}+(af)_{y_2})\mathrm{{d}}y_1-a_{x_2}\mathrm{{d}}y_2. \end{aligned}$$

Therefore, given a, there exists a b such that $\alpha = a \beta + b \gamma$ is a closed J-anti-invariant form on $({{\mathbb {R}}}^4,J)$ if and only if the differential form

$$\begin{aligned} (a_{y_1}+(af)_{x_2})\mathrm{{d}}x_1+ a_{y_2}\mathrm{{d}}x_2- (a_{x_1}+(af)_{y_2})\mathrm{{d}}y_1-a_{x_2}\mathrm{{d}}y_2, \end{aligned}$$

is closed. The latter condition is equivalent to the following PDEs system:

$$\begin{aligned} \left\{ \begin{array}{lll} a_{x_1y_2}-a_{x_2y_1}-(af)_{x_2x_2}&{}=&{} 0 \\ a_{x_1y_2}-a_{x_2y_1}+(af)_{y_2y_2}&{}=&{} 0\\ a_{x_1x_1}+a_{y_1y_1}+(af)_{x_2y_1}+(af)_{x_1y_2}&{}=&{} 0 \\ a_{x_1x_2}+a_{y_1y_2}+(af)_{x_2y_2}&{}=&{} 0. \\ a_{x_2x_2}+a_{y_2y_2}&{}=&{} 0. \end{array} \right. \end{aligned}$$

(7)

We are ready to state and prove the following

Theorem 3.7

Let $f(x_1,x_2,y_1,y_2)=x_2$, $J=J_{x_2}$ be defined as in (2) and $g_J$ be a J-Hermitian metric on ${{\mathbb {R}}}^4$. Let

$$\begin{aligned} \beta = \mathrm{{d}}x_1\wedge \mathrm{{d}}x_2-f\mathrm{{d}}x_1\wedge \mathrm{{d}}y_1- \mathrm{{d}}y_1\wedge \mathrm{{d}}y_2,\quad \gamma = \mathrm{{d}}x_1\wedge \mathrm{{d}}y_2-\mathrm{{d}}x_2\wedge \mathrm{{d}}y_1. \end{aligned}$$

Then

• (I) J is a non-integrable almost complex structure on ${{\mathbb {R}}}^4$.

• (II) For every given pair $(s,t)\in {{\mathbb {R}}}^2$, such that

  $$\begin{aligned} s^2+t^2+t=0, \end{aligned}$$

  the form

  $$\begin{aligned} \alpha _{s,t}=te^{sx_1+ty_1}\beta - se^{sx_1+ty_1}\gamma , \end{aligned}$$

is a J-anti-invariant and closed. Therefore, ${\mathcal {H}}^-_{J}({{\mathbb {R}}}^4)$ has infinite dimension.

Proof

• (I) In view of Lemma 3.4, J is integrable if an only if $f_{x_2}=f_{y_2}=0$. By assumption, we get $f_{x_2}=1$. Therefore J is not integrable.

• (II) Set $z_1=x_1+iy_1,$ $z_2=x_2+iy_2$. Then, for $f = x_2$, the complex PDEs system (6) becomes

  $$\begin{aligned} \left\{ \begin{array}{l} \partial _{{\overline{z}}_1}w +\frac{i}{4}(z_2+{\overline{z}}_2)\partial _{z_2}w +\frac{i}{4}(w+{\overline{w}})= 0 \\ \partial _{{\overline{z}}_2}w = 0. \end{array} \right. \end{aligned}$$

  (8)

A straightforward computation shows that, given any pair of real numbers (s, t) satisfying

$$\begin{aligned} s^2+t^2+t=0, \end{aligned}$$

the complex function

$$\begin{aligned} w = te^{s\frac{z_1-{\bar{z}}_1}{2}+t\frac{z_1-{\bar{z}}_1}{2i}}+ise^{s\frac{z_1-{\bar{z}}_1}{2}+t\frac{z_1-{\bar{z}}_1}{2i}}, \end{aligned}$$

solves (8). Take

$$\begin{aligned} s_n=\frac{\sqrt{n-1}}{n},\qquad t_n=-\frac{1}{n}, \end{aligned}$$

Then, for such a choice, $s_n^2+t_n^2+t_n=0$. In view of the computations above, for any given integer $n\ge 1$, the J-anti-invariant forms

$$\begin{aligned} \alpha _n:=t_ne^{s_nx_1+t_ny_1}\beta - s_ne^{s_nx_1+t_ny_1}\gamma , \end{aligned}$$

are closed, and consequently $g_J$-harmonic. Therefore, $\{\alpha _n\}_{n\ge 1}$ is a sequence of harmonic forms on $({{\mathbb {R}}}^4,J,g_J)$ and it is immediate to check that, for any given positive integer m, the forms $\{\alpha _1,\ldots , \alpha _m\}$ are linearly independent. This ends the proof. $\square$

Next we demonstrate the contrasting behavior when our almost complex structure is defined using functions with compact support.

Theorem 3.8

Let f have compact support and the almost complex structures $J_f$ on ${{\mathbb {C}}}^2$ be defined by (2).

Then if f is non-zero we have $h^-_{J_f}=1$.

Note that since f has compact support neither $f_{x_2}$ nor $f_{y_2}$ can vanish identically and so by Lemma 3.4 we see that $J_f$ is non-integrable. As mentioned in the introduction, Yau’s solution to the Calabi conjecture actually implies that no integrable complex structures J can be standard outside of a compact set and satisfy $h^-_{J}=1$.

Proof

We determine the anti-holomorphic forms by finding solutions to the system (7).

First note that the first two lines in Eq. (7) imply that af is a harmonic function of $x_2, y_2$, which is identically 0 outside of a compact set (since f is). Hence af is identically 0 everywhere.

Fix $x_1, y_1$, say $x_1=s, y_1=t$, so that f does not vanish identically on the corresponding $x_2, y_2$ plane. Working in this plane, as af is identically 0 it follows that a is identically 0 on the open set where f is nonzero. But the final line in Eq. (7) says that a is also harmonic in $x_2, y_2$, hence a vanishes identically on the whole plane, and similarly on all nearby $x_2, y_2$ planes.

Next we look at $x_1, y_1$ planes. As $af=0$ the third line in Eq. (7) says that a is harmonic. But as we know that a is 0 close to (s, t) we can conclude that $a=0$ everywhere.

Therefore the only closed anti-invariant forms $a \beta + b \gamma$ are of the form $a=0$ and b constant, showing that $h^-_{J_f}=1$ as required. $\square$

Similar almost complex structures give the following corollary.

Corollary 3.9

There exist almost complex structures on ${{\mathbb {C}}}^2$ which agree with i outside of a compact set and have $h^-_J =0$.

Proof

The proof of Theorem 3.8 implies that if $J = J_f$ on some region, say $\{ |z_1 -3| < 1\}$ and f is not identically 0 on the planes $\{z_1 =c\}$ when $|c-3|<1$ then any closed anti-invariant form on $\{ |z_1 -3| < 1\}$ is a multiple of $\gamma$. We fix such an f with support in a ball $B_2(3,0)$ about (3, 0) of radius 2.

Consider the mapping $T:{{\mathbb {C}}}^2 \rightarrow {{\mathbb {C}}}^2$, $(z_1, z_2) \mapsto (z_2, -iz_1)$, which takes $\{|z_2 - 3| <1\}$ to $\{ |z_1 -3| < 1\}$. Then $\rho = T^* \gamma = dx_1 \wedge dx_2 - dy_1 \wedge dy_2$ and $J' = T^* J_f$ coincides with i outside of a ball about $B_2(0,3)$. Also, any closed $J'$-anti-invariant form on $\{|z_2 - 3| <1\}$ is a multiple of $\rho$ on $\{|z_2 - 3| <1\}$.

Now, both J and $J'$ agree with i outside of the two balls, and so we can find an almost complex structure $J''$ agreeing with J on $B_2(3,0)$ and $J'$ on $B_2(0,3)$ and i away from the two balls. Any corresponding $J''$ anti-invariant form is a multiple of both $\gamma$ and $\rho$ on $\{ |z_1 -3|< 1, |z_2 - 3| <1\}$ and so is equal to 0 on this region. Hence by unique continuation, see Sect. 2, the form must be identically 0 everywhere. $\square$

We conclude this section with a remark about the compatibility of our almost complex structures with symplectic forms.

Remark 3.10

The almost complex structures referred to in Theorems 3.7 and 3.8 are almost Kähler, that is, they are compatible with symplectic forms on ${{\mathbb {C}}}^2$. In the case when $f = f(x_1, x_2)$ we can check directly that $J_f$ is compatible with the symplectic form

$$\begin{aligned} \omega _f = \mathrm{{d}}x_1 \wedge \mathrm{{d}}y_1 + \mathrm{{d}}x_2 \wedge \mathrm{{d}}y_2 + f \mathrm{{d}}x_1 \wedge \mathrm{{d}}x_2. \end{aligned}$$

In the case when f has compact support the almost complex structure $J_f$ is tamed by

$$\begin{aligned} \omega _K = K \mathrm{{d}}x_1 \wedge \mathrm{{d}}y_1 + \mathrm{{d}}x_2 \wedge \mathrm{{d}}y_2, \end{aligned}$$

for a sufficiently large constant K. This means that $\omega _K (v, J_f v) \ge 0$ with equality only if $v=0$. It then follows from Gromov’s theory of pseudoholomorphic curves, [8], see also [16] for this application, that $J_f$ is in fact compatible with a symplectic form $\omega _c$.

Standard methods in symplectic geometry, see [14], can be used to show that $\omega _f$ and $\omega _c$ are diffeomorphic to the standard symplectic form $\omega _0 = \mathrm{{d}}x_1 \wedge \mathrm{{d}}y_1 + \mathrm{{d}}x_2 \wedge \mathrm{{d}}y_2$, and in fact the diffeomorphisms can be chosen smoothly with f. Hence in both theorems we may assume without loss of generality that our almost complex structures are all compatible with $\omega _0$.

4 Families of Non-integrable Almost Complex Structures with $h^-_J=2$ on the Kodaira–Thurston Manifold

We recall the construction of the Kodaira–Thurston Manifold.

Let ${{\mathbb {R}}}^4$ be the Euclidean space with coordinate $(x_1,\ldots , x_4)$ endowed with the following product $*$: given any $a=(x_1,\ldots ,x_4),y=(y_1\ldots , y_4)\in {{\mathbb {R}}}^4$, define

$$\begin{aligned} x*y=(x_1+y_1,x_2+y_2, x_3+x_1y_2+y_3,x_4+y_4). \end{aligned}$$

Then $({{\mathbb {R}}}^4,*)$ is a nilpotent Lie group and

$$\begin{aligned} \Gamma =\{(\gamma _1,\ldots ,\gamma _4)\in {{\mathbb {R}}}^4\,\,\,\vert \,\,\, \gamma _j\in {{\mathbb {Z}}}, j=1,\ldots ,4\}, \end{aligned}$$

is a uniform discrete subgroup of $({{\mathbb {R}}}^4,*)$, so that $M=\Gamma \backslash {{\mathbb {R}}}^4$ is a 4-dimensional compact manifold. Setting,

$$\begin{aligned} E^1=\mathrm{{d}}x_1,\quad E^2=\mathrm{{d}}x_2,\quad E^3=\mathrm{{d}}x_3-x_1\mathrm{{d}}x_2,\quad E^4=\mathrm{{d}}x_4,\, \end{aligned}$$

then it is immediate to check that $E^1,E^2,E^3,E^4$ are $\Gamma$-invariant 1-forms on ${{\mathbb {R}}}^4$, and, consequently, they give rise to a global coframe on M. Then the following structure equations hold

$$\begin{aligned} \mathrm{{d}}E^1=0,\qquad \mathrm{{d}}E^2=0,\qquad \mathrm{{d}}E^3=-E^1\wedge E^2,\qquad \mathrm{{d}}E^4=0. \end{aligned}$$

Denoting by $\{E_1,\ldots ,E_4\}$ the dual global frame on M, then

$$\begin{aligned} {[}E_1,E_2]=E_3, \end{aligned}$$

the other brackets vanishing. Let $\lambda =\lambda (x_4)$, $\mu =\mu (x_4)$ be non-constant ${{\mathbb {R}}}$-valued smooth ${{\mathbb {Z}}}$-periodic functions. Define an almost complex structure $J=J_{\lambda ,\mu }$ on M by setting

$$\begin{aligned} JE_1=e^{\lambda (x_4)}E_2,\, JE_2=-e^{-\lambda (x_4)}E_1, JE_3=e^{\mu (x_4)}E_4, \, JE_4=-e^{-\mu (x_4)}E_3. \end{aligned}$$

(9)

Lemma 4.1

The almost complex structure J is non-integrable.

Proof

We compute

$$\begin{aligned} \begin{array}{ll} N_J(E_1,E_3)&{}= [JE_1,JE_3]-[E_1,E_3]-J[JE_1,E_3] -J[E_1,JE_3]\\ &{}=[e^{\lambda (x_4)}E_2,e^{\mu (x_4)}E_4] -J[e^{\lambda (x_4)}E_2,E_3] -J[E_1,e^{\mu (x_4)}E_4]\\ &{}=-E_4(e^{\lambda (x_4)})E_2=-e^{\lambda (x_4)}\lambda '(x_4)E_2\ne 0. \end{array} \end{aligned}$$

$\square$

Proposition 4.2

Let $J=J_{\lambda ,\mu }$ be the family of the (non-invariant) almost complex structures on the Kodaira–Thurston manifold defined as in (9). Then $h_J^-(M)=2$.

Proof

By the definition of J, the following

$$\begin{aligned} \psi ^1=E^1+ie^{-\lambda (x_4)}E^2,\quad \psi ^2=E^3+ie^{-\mu (x_4)}E^4, \end{aligned}$$

is a global (1, 0)-coframe on (M, J). Then

$$\begin{aligned} \theta ^1=E^1\wedge E^3- e^{-(\lambda (x_4)+\mu (x_4))} E^2\wedge E^4,\quad \theta ^2=e^{-\mu (x_4)} E^1\wedge E^4+ e^{-\lambda (x_4)} E^2\wedge E^3, \end{aligned}$$

globally span $\Lambda ^-_J(M)$. We immediately obtain

$$\begin{aligned} d\theta ^1=0,\quad d(e^{\lambda (x_4)}\theta ^2) =0, \end{aligned}$$

that is $\theta ^1$, $e^{\lambda (x_4)}\theta ^2$ are closed J-anti-invariant forms, hence harmonic, which span $\Lambda ^-_J(M)$. Since $b^+(M)=2$ and $h^-_J(M)\le b^+(M)$ for every compact almost complex manifold, we conclude that $h^-_J(M)=2$ and

$$\begin{aligned} H^-_{J}(M)\simeq \hbox { Span}_{{\mathbb {R}}}\langle \theta ^1,e^{\lambda (x_4)}\theta ^2 \rangle . \end{aligned}$$

$\square$

Remark 4.3

It should be noted that the two-parameter family of almost complex structures on the Kodaira surface as in Proposition 4.2 cannot be metric related to an integrable almost complex structure, as, on the contrary, in view of [6, Proposition 3.20], such almost complex structures have $h^{-}_{J_{\lambda ,\mu }}\le 1$.

5 6-Dimensional Compact Almost Complex Manifolds with Arbitrarily Large Anti-invariant Cohomology

In this Section we provide simple examples of compact 6-dimensional manifolds endowed with a non-integrable almost complex structure with arbitrary large anti-invariant cohomology. Let $\Sigma _g$ be a compact Riemann surface of genus $g\ge 2$. On the differentiable product $X=\Sigma _g\times \Sigma _g$, denote by J the complex product structure. Let ${{\mathbb {T}}}^2={{\mathbb {R}}}^2/{{\mathbb {Z}}}^2$ be the real 2-torus, where we indicate with $(t_1,t_2)$ global coordinates on ${{\mathbb {R}}}^2$ and let $f:X\rightarrow {{\mathbb {R}}}$ be a smooth positive non-constant function. Let $M=X\times {{\mathbb {T}}}^2$. Define ${\mathcal {J}}\in \hbox {End}(TM)$ by setting

$$\begin{aligned} {\mathcal {J}}\big (V,a\frac{\partial }{\partial t_1}+b\frac{\partial }{\partial t_2}\big ) =\big (JV,-\frac{b}{f}\frac{\partial }{\partial t_1}+ fa\frac{\partial }{\partial t_2}\big ). \end{aligned}$$

Then, we have the following

Proposition 5.1

${\mathcal {J}}$ is a non-integrable almost complex structure on $M=X\times {{\mathbb {T}}}^2$ such that

$$\begin{aligned} h_{{\mathcal {J}}}^-(M)\ge 2g^2. \end{aligned}$$

Proof

It is immediate to check that ${\mathcal {J}}^2=-\hbox {id}$. Let $p\in X$ such that $df(p)\ne 0$ and let $(z_1=x_1+iy_1,z_2=x_2+iy_2)$ be local holomorphic coordinates on X around p. We may assume that $\frac{\partial }{\partial z_1}f(p)\ne 0$. We have:

$$\begin{aligned} \begin{array}{ll} N_{{\mathcal {J}}}(\frac{\partial }{\partial x_1},\frac{\partial }{\partial t_1})&{}= [{{\mathcal {J}}}\frac{\partial }{\partial x_1},{{\mathcal {J}}}\frac{\partial }{\partial t_1}]-[\frac{\partial }{\partial x_1},\frac{\partial }{\partial t_1}]-{{\mathcal {J}}}[{{\mathcal {J}}}\frac{\partial }{\partial x_1},\frac{\partial }{\partial t_1}] -{{\mathcal {J}}}[\frac{\partial }{\partial x_1},{{\mathcal {J}}}\frac{\partial }{\partial t_1}]\\ &{}=[\frac{\partial }{\partial x_1},f\frac{\partial }{\partial t_1}]- {{\mathcal {J}}}[\frac{\partial }{\partial x_1},f\frac{\partial }{\partial t_2}]\\ &{}=f_{x_1}(p)\frac{\partial }{\partial t_t}+f_{y_1}(p)\frac{\partial }{\partial t_2} \ne 0. \end{array} \end{aligned}$$

Denote by $\{\gamma _1,\ldots ,\gamma _g\}$, $\{\gamma '_1,\ldots ,\gamma '_g\}$, respectively, be a basis of $H^{1,0}_{{\overline{\partial }}}$ on the first and on the second copy of $\Sigma _g$, respectively. Then

$$\begin{aligned} H^{(2,0)}_{{\overline{\partial }}}(X)\simeq \hbox {Span}_{{\mathbb {C}}}\langle \gamma _r\wedge \gamma '_s,\quad 1\le r,s\le g\rangle , \end{aligned}$$

and clearly $\mathrm{{d}}(\gamma _r\wedge \gamma '_s)=0$, for every $1\le r,s\le g$. Then $h_J^-(X)=2g^2$. Therefore,

$$\begin{aligned} h_{{\mathcal {J}}}^-(M)\ge 2g^2. \end{aligned}$$

$\square$

Remark 5.2

The previous Proposition gives a positive answer to the question raised in [3, Question 5.2] where it was asked for examples of non-integrable almost complex structures J on a compact 2n-dimensional manifold with $h^-_J(M)>n(n-1)$.