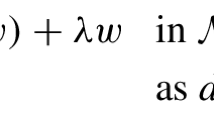The LIR Method. $L^{r}$ Solutions of Elliptic Equation in a Complete Riemannian Manifold

Abstract

We introduce the Local Increasing Regularity Method (LIRM) which allows us to get from local a priori estimates, on solutions u of a linear equation $\displaystyle Du=\omega ,$global ones. As an application we shall prove that if D is an elliptic linear differential operator of order m with ${\mathcal {C}}^{\infty }$ coefficients operating on the sections of a complex vector bundle $\displaystyle G:=(H,\pi ,M)$ over a compact Riemannian manifold M without boundary and $\omega \in L^{r}_{G}(M)\cap (\mathrm {k}\mathrm {e}\mathrm {r}D^{*})^{\perp },$ then there is a $u\in W^{m,r}_{G}(M)$ such that $Du=\omega$ on M. Next we investigate the case of a compact manifold with boundary by using the “Riemannian double manifold.” In the last sections we study the more delicate case of a complete but non-compact Riemannian manifold by the use of adapted weights.

1 Introduction

Let (M, g) be a complete Riemannian manifold and $\Delta :=dd^{*}+d^{*}d$ be the Hodge laplacian on it. Let $\displaystyle \Lambda ^{p}(M)$ be the set of p-forms ${\mathcal {C}}^{\infty }$ smooth on M,  then we have $\Delta :\ \Lambda ^{p}\rightarrow \Lambda ^{p}.$ The Poisson equation $\Delta u=\omega$ for $\omega \in \Lambda ^{p}(M)$ was extensively studied. Set $L_{p}^{r}$ the closure of $\displaystyle \Lambda ^{p}(M)$ in the space $L^{r}(M)$ for the volume measure of M. We define as usual the Sobolev spaces $W_{p}^{k,r}(M)$ to be the set of p-forms on M in $L^{r}_{p}(M)$ together with all its covariant derivatives up to order k.

Then $\displaystyle L_{p}^{r}$ estimates for the solutions of the Poisson equation are essentially equivalent to the $L_{p}^{r}$ Hodge decomposition:

$$\begin{aligned} \displaystyle L^{r}_{p}(M)={\mathcal {H}}^{r}_{p}\oplus dW^{1,r}_{p-1}(M)\oplus d^{*}W^{1,r}_{p+1}(M). \end{aligned}$$

Let us recall some results in the case M compact without boundary.

The basic work of CB Morrey [22] for $\omega \in L^{2}(M)$ has led to the $L^{2}$ Hodge decomposition:

$$\begin{aligned} \displaystyle L^{2}_{p}(M)={\mathcal {H}}^{2}_{p}\oplus dW^{1,2}_{p-1}(M)\oplus d^{*}W^{1,2}_{p+1}(M), \end{aligned}$$

which is useful in Algebraic Geometry, see C. Voisin [28].

In 1995 Scott [25] proved a strong $\displaystyle L^{r}$ Hodge decomposition:

$$\begin{aligned} \displaystyle \forall r>1,\ L^{r}_{p}(M)={\mathcal {H}}^{r}_{p}\oplus dW^{1,r}_{p-1}(M)\oplus d^{*}W^{1,r}_{p+1}(M). \end{aligned}$$

Schwarz [24] proved the same result but in a compact Riemannian manifold with boundary.

For the case of a complete non-compact Riemannian manifold, there are also classical results.

In 1949, Kodaira [20] proved that the $\displaystyle L^{2}$-space of p-forms on $\displaystyle (M,g)$ has the (weak) orthogonal decomposition:

$$\begin{aligned} L^{2}_{p}(M)={\mathcal {H}}^{2}_{p}\oplus {\overline{d{\mathcal {D}}_{p-1}(M)}}\oplus {\overline{d^{*}{\mathcal {D}}_{p+1}(M)}}, \end{aligned}$$

and in 1991 Gromov [15] proved a strong $\displaystyle L^{2}$ Hodge decomposition, under the hypothesis that $\Delta$ has a spectral gap in $\displaystyle L_{p}^{2}$:

$$\begin{aligned} \displaystyle L^{2}_{p}(M)={\mathcal {H}}^{2}_{p}\oplus dW^{1,2}_{p-1}(M)\oplus d^{*}W^{1,2}_{p+1}(M). \end{aligned}$$

There are also nice results by X-D. Li [21] who proved a strong $\displaystyle L^{r}$ Hodge decomposition on complete non-compact Riemannian manifold. See the references list on these questions therein.

Finally, by using the raising steps method, I proved in [5] that we have a non-classical weighted$L^{r}_{p}(M)$ Hodge decomposition in a complete non-compact Riemannian manifold.

The aim of this work is to extend these results to the general case of a linear elliptic operator D of order m in place of the Hodge Laplacian. If (M, g) is a compact boundary-less Riemannian manifold, this was done in the $L^{2}$ case, for instance, by Warner [29] and Donaldson [10]. See the references therein.

Here we shall study the equation $Du=\omega$ for a general linear elliptic operator D of order m acting on sections of $\displaystyle G:=(H,\pi ,M),$ a complex ${\mathcal {C}}^{m}$ vector bundle over M of rank N with fiber H in the Riemannian manifold M.

Let M be a complete n-dimensional ${\mathcal {C}}^{m}$ Riemannian manifold for some $m\in {\mathbb {N}},$ and let $G:=(H,\pi ,M)$ be a complex ${\mathcal {C}}^{m}$ vector bundle over M of rank N with fiber H. By a trivializing coordinate system $(U_{\varphi },\varphi ,\ \chi _{\varphi })$ for G we mean a chart $\varphi$ of M with domain $U_{\varphi }\subset M$ together with a trivializing map:

$$\begin{aligned} \pi ^{-1}(U_{\varphi })\rightarrow U_{\varphi }{\times }H,\ g\rightarrow (\pi (g),\chi _{\varphi }(g)), \end{aligned}$$

over $U_{\varphi }$ for G. Given a section u of G,  its local representation $u_{\varphi }$ with respect to $\displaystyle (U_{\varphi },\varphi ,\ \chi _{\varphi })$ is defined by $u_{\varphi }:=\chi _{\varphi }\circ u\circ \varphi ^{-1}.$

Then given $s\in [0,\ m]$ and $r\in (1,\infty ),$ we denote by $W^{s,r}_{G}(M)$ the vector space of all sections u of G such that $\psi u_{\varphi }\in W^{s,r}(\varphi (U_{\varphi }),H)$ for each ${\mathcal {C}}^{m}$ function $\psi$ with compact support in $\varphi (U_{\varphi })\subset {\mathbb {R}}^{n}$ and each trivializing coordinate system $(\varphi ,U_{\varphi },\chi _{\varphi })$ for G,  where sections coinciding almost everywhere have been identified and $\displaystyle W^{s,r}$ is the usual Sobolev space whose main properties are recalled in the Sect. 7.2 of Appendix. In particular we have $\displaystyle L^{r}_{G}(M)=W^{0,r}_{G}(M).$

By analogy with the bundle of p-forms on M,  we shall call G-forms the measurable sections of G.

The method we shall use is different from the previous ones. We shall provide a way to go from local results to global ones by using the Local Increasing Regularity, LIR for short, given by the fundamental elliptic estimates. We shall introduce a quite general method, the LIR method, which allows us to get the generalization to $L^{r}$ of the result of Warner [29] and Donaldson [10] done for $L^{2}.$

Theorem 1.1

Let (M, g) be a ${\mathcal {C}}^{\infty }$ smooth compact Riemannian manifold without boundary. Let $D:G\rightarrow G$ be an elliptic linear differential operator of order m with ${\mathcal {C}}^{\infty }$ coefficients acting on the complex ${\mathcal {C}}^{m}$ vector bundle G over M. Let $\omega \in L^{r}_{G}(M)\cap \mathrm {(}\mathrm {k}\mathrm {e}\mathrm {r}D^{*}\mathrm {)}^{\perp }$ with $r\ge 2.$ Then there is a bounded linear operator $S:L^{r}_{G}(M)\cap \mathrm {(}\mathrm {k}\mathrm {e}\mathrm {r}D^{*}\mathrm {)}^{\perp }\rightarrow W^{m,r}_{G}(M)$ such that $\displaystyle DS(\omega )=\omega$ on M. So, with $u:=S\omega$ we get $\displaystyle Du=\omega$ and $\displaystyle u\in W^{m,r}_{G}(M).$

By duality we get the range $r<2$ as we did in [3], using an avatar of the Serre duality [26].

To study the same problem when M has a smooth boundary $\partial M,$ we shall use the technique of the “Riemannian double.”

The “Riemannian double” $\Gamma :=\Gamma (M)$ of M,  obtained by gluing two copies of (a slight extension of) M along $\partial M,$ is a compact Riemannian manifold without boundary. Moreover, by its very construction, it is always possible to assume that $\displaystyle \Gamma$ contains an isometric copy M of the original domain M. See Guneysu and Pigola  [16, Appendix B].

We shall need:

Definition 1.2

We shall say that D has the weak maximum property, WMP, if, for any smooth DG-harmonic h,  i.e., a G-form such that $Dh=0$ in M,  smooth up to the boundary $\partial M,$ which is flat on $\partial M,$ i.e., zero on $\partial M$ with all its derivatives, then h is zero in M.

This definition has to be linked to Definition [19, Introduction, p. 948]:

Definition 1.3

We shall say that an operator D has the Unique Continuation Property, UCP, if $Du=0$ on $\Gamma$ and $u=0$ in an open set ${\mathcal {O}}\ne \emptyset$ of $\Gamma$ implies that $u\equiv 0$ in $\Gamma .$

WMP is weaker than the UCP, because if D has the UCP and if h is flat on $\partial M,$ then we can extend h by zero in $M^{c}$ in $\Gamma ,$ which makes h still DG-harmonic, and apply the UCP to get that h is zero in M.

The Hodge Laplacian in a Riemannian manifold has the UCP for p-forms by a difficult result by Aronszajn et al.  [6]. Then we get:

Theorem 1.4

Let M be a smooth compact Riemannian manifold with smooth boundary $\partial M.$ Let $\displaystyle \omega \in L^{r}_{G}(M).$ There is a form $u\in W^{m,r}_{G}(M),$ such that $Du=\omega$ and ${\left\| {u}\right\| }_{W^{m,r}_{G}(M)}\le c{\left\| {\omega }\right\| }_{L^{r}_{G}(M)},$ provided that the operator D has the WMP.

We shall use the same ideas as we did in [5] to go from the compact case to the non-compact one.

First we have to define a $m,\epsilon$-admissible ball centered at $x\in M.$ Its radius R(x) must be small enough to make that ball like its euclidean image. Precisely:

Definition 1.5

Let (M, g) be a Riemannian manifold and $\displaystyle x\in M.$ We shall say that the geodesic ball $\displaystyle B(x,R)$ is $m,\epsilon$admissible if there is a chart $\varphi \ :\ (y_{1},\ldots ,y_{n})\rightarrow {\mathbb {R}}^{n}$ defined on it with

• (1) $\displaystyle (1-\epsilon )\delta _{ij}\le g_{ij}\le (1+\epsilon )\delta _{ij}$ in $\displaystyle B(x,R)$ as bilinear forms,

• (2) $\displaystyle \ \sum _{\left| {\beta }\right| \le m-1}{\sup \ _{i,j=1,\ldots ,n,\ y\in B_{x}(R)}\left| {\partial ^{\beta }g_{ij}(y)}\right| }\le \epsilon .$

We naturally take $\epsilon <1$ in order to have that the Riemannian metric in the admissible ball be equivalent to the euclidean one in ${\mathbb {R}}^{n}.$

Of course, without any extra hypotheses on the Riemannian manifold M,  we have $\forall m\in {\mathbb {N}},\ m\ge 2,\ \forall \epsilon >0,\ \forall x\in M,$ taking $\displaystyle g_{ij}(x)=\delta _{ij}$ in a chart on $\displaystyle B(x,R)$ and the radius R small enough, the ball $\displaystyle B(x,R)$ is $m,\epsilon$ admissible.

Definition 1.6

Let $\displaystyle x\in M,$ we set $\displaystyle R^{\prime }(x)=\sup \ \lbrace R>0::B(x,R)\ is\ \epsilon \ admissible\rbrace .$ We shall say that $\displaystyle R_{\epsilon }(x):=\min \ (1,R^{\prime }(x))$ is the $m,\epsilon$admissible radius at $\displaystyle x.$

Our admissible radius is bigger than the harmonic radius $\displaystyle r_{H}(1+\epsilon ,\ m-1,\ 0)$ defined in the Hebey’s book  [17, p. 4], because we do not require the coordinates to be harmonic. I was strongly inspired by this book.

When comparing non-compact M to the compact case treated above, we have four important issues:

• (0) we have no longer, in general, a global solution $u\in L_{G}^{2}(M)$ of $Du=\omega$ for a G-form $\displaystyle \omega \in L_{G}^{2}(M)$ verifying $\displaystyle \omega \perp \mathrm {k}\mathrm {e}\mathrm {r}D^{*}.$ So we have to make this “threshold” hypothesis, which depends on G.

  In case the elliptic operator D is essentially self-adjoint, this amounts to ask that its spectrum has a gap near 0, i.e., $\exists \delta >0$ such that D has no spectrum in $]0,\delta [.$ We shall note this hypothesis (THL2G). Moreover, because $\displaystyle L^{2}_{G}(M)$ is a Hilbert space, we have that the $u\in L^{2}_{G}(M),\ Du=\omega$ with the smallest norm is given linearly with respect to $\omega .$ This means that the hypothesis (THL2G) gives a bounded linear operator $\displaystyle S:\ L^{2}_{G}(M)\rightarrow L^{2}_{G}(M)$ such that $D(S\omega )=\omega$ provided that $\displaystyle \omega \perp \mathrm {k}\mathrm {e}\mathrm {r}D^{*}.$

• (1) The “ellipticity constant” may go to zero at infinity and we prevent this by asking that D is uniformly elliptic in the sense of Definition 3.1.

  To be sure that the constants in the local elliptic inequalities are uniform, we make also the hypothesis that the coefficients of D are in ${\mathcal {C}}^{1}(M).$ These are the hypotheses (UEAB) in Definition 6.3.

• (i) The “admissible” radius may go to $\displaystyle 0$ at infinity, which is the case, for instance, if the canonical volume measure $\displaystyle dv_{g}$ of $\displaystyle (M,g)$ is finite and M is not compact.

• (ii) If $\displaystyle dv_{g}$ is not finite, which is the case, for instance, if the “admissible” radius is bounded below, then G-forms in $\displaystyle L^{t}_{G}(M)$ are generally not in $\displaystyle L^{r}_{G}(M)$ for $\displaystyle r<t.$

We address these two last problems by the use of adapted weights on $\displaystyle (M,g).$ These weights are relative to a Vitali type covering ${\mathcal {C}}_{\epsilon }$ of “admissible balls”: the weights are positive functions which vary slowly on the balls of the covering ${\mathcal {C}}_{\epsilon }.$

To state our result in the case of a complete non-compact Riemannian manifold M without boundary, we shall use the following definition:

Definition 1.7

We shall define the Sobolev exponents $\displaystyle S_{k}(r)$ by $\displaystyle \ \frac{1}{S_{k}(r)}:=\frac{1}{r}-\frac{k}{n}$ where n is the dimension of the manifold M.

Now we suppose we have an elliptic operator D with ${\mathcal {C}}^{1}(M)$ smooth coefficients, of order m,  operating on the vector bundle $\displaystyle G:=(H,\pi ,M)$ over M. We set $t_{l}:=S_{ml}(2).$ We suppose that $\displaystyle t_{l-1}\le r<t_{l},$ and $\displaystyle t_{l-1}<\infty .$

We set the weights, with R(x) the admissible radius at the point $x\in M:$

$$\begin{aligned} \displaystyle \ w_{l}(x)=R(x)^{lmt_{l-1}} \hbox { and } \displaystyle v_{r}(x):=R(x)^{\left( \frac{r}{t_{l}}-1\right) +(l+2)mr}. \end{aligned}$$

Now we can state the main result of this section, where we omit the subscript G to ease the notation.

Theorem 1.8

Under hypotheses (THL2G) and (UEAB), we have provided that:

$$\begin{aligned} \displaystyle \omega \in L^{2}(M)\cap L^{t_{l-1}}(M,w_{l}),\ \omega \perp \mathrm {k}\mathrm {e}\mathrm {r}D^{*}, \end{aligned}$$

that $\displaystyle u:=S\omega$ verifies $\displaystyle Du=\omega$ with the estimates:

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{L^{r}(M,v_{r})}\le \max \left( {\left\| {\omega }\right\| }_{L^{t_{l-1}}(M,w_{l})},{\left\| {\omega }\right\| }_{L^{2}(M)}\right) . \end{aligned}$$

We also have with the same u:

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{m,r}(M,v_{r})}\le c_{1}{\left\| {\omega }\right\| }_{L^{t_{l}}(M,v_{r})}+c_{2}\max \big ({\left\| {\omega }\right\| }_{L^{t_{l-1}}(M,w_{l})},{\left\| {\omega }\right\| }_{L^{2}(M)}\big ). \end{aligned}$$

Remark 1.9

If the admissible radius R(x) is uniformly bounded below, we can forget the weights and we get the existence of a solution u of $Du=\omega$ with:

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{L^{r}(M)}\le & {} \max \big ({\left\| {\omega }\right\| }_{L^{t_{l-1}}(M)},{\left\| {\omega }\right\| }_{L^{2}(M)}\big ).\\ \displaystyle {\left\| {u}\right\| }_{W^{m,r}(M)}\le & {} c_{1}{\left\| {\omega }\right\| }_{L^{t_{l}}(M)}+c_{2}\max \big ({\left\| {\omega }\right\| }_{L^{t_{l-1}}(M)},{\left\| {\omega }\right\| }_{L^{2}(M)}\big ). \end{aligned}$$

An advantage of this method is that it separates cleanly the geometry and the analysis:

• The geometry controls the behavior of the admissible radius R(x) as a function of x in M. For instance by Theorem 1.3 in Hebey [17], we have that the harmonic radius $\displaystyle r_{H}(1+\epsilon ,\ m,0)$ is bounded below if the Ricci curvature $\displaystyle Rc$ verifies $\displaystyle \ \forall j\le m,\ {\left\| {\nabla ^{j}Rc}\right\| }_{\infty }<\infty$ and the injectivity radius is bounded below. This implies that the $m,\epsilon$ admissible radius R(x) is also bounded below.

• The analysis gives the weights as function of R(x) to get the right estimates. For instance if the admissible radius R(x) is bounded below, then we can forget the weights and we get more “classical” estimates, as in Remark 1.9.

I am indebted to Bachelot, Helffer, Métivier, and Sjöstrand for clearing strongly my knowledge on the local existence of solutions to system of elliptic equations needed in the study of elliptic equations acting on vector bundles.

This work is presented in the following way.

• In the next section we state the LIR method in the general context of metric spaces.

• In Sect. 3 we apply it for the case of elliptic equations in a compact connected Riemannian manifold without boundary.

• In Sect. 4 we study the case of elliptic equations in a compact connected Riemannian manifold with a smooth boundary.

• In Sect. 5 we show that the LIR condition, which is a priori estimates, implies the existence of a local solution with good estimates.

• In Sect. 6 we study the more delicate case of elliptic equations in a complete non-compact connected Riemannian manifold without boundary.

• Finally in Appendix we have put technical results concerning the $\epsilon$ admissible balls, Vitali coverings, and Sobolev spaces.

If the general ideas under this work are quite simple and natural, unfortunately the computations to make them work are a little bit technical.

2 The Local Increasing Regularity Method (LIRM)

Let X be a complete metric space with a positive $\sigma$-finite measure $\mu .$ Let $\Omega$ be a relatively compact domain in X. We shall denote $E^{p}(\Omega )$ the set of ${\mathbb {C}}^{p}$ valued functions on $\Omega .$

This means that $\omega \in E^{p}(X)\iff \omega (x)=(\omega _{1}(x),\ldots ,\omega _{p}(x)).$ We put a punctual norm on $\omega$ in $\displaystyle E^{p}(\Omega )$ in the following way: for any $x\in \Omega ,\ \left| {\omega (x)}\right| ^{2}:=\sum _{j=1}^{p}{\left| {\omega _{j}(x)}\right| ^{2}}.$ We consider the Lebesgue space $L^{r}_{p}(\Omega ),$ i.e.,

$$\begin{aligned} \omega \in L^{r}_{p}(\Omega )\iff {\left\| {\omega }\right\| }^{r}_{L^{r}_{p}(\Omega )}:=\int _{\Omega }{\left| {\omega (x)}\right| ^{r}d\mu (x)}<\infty . \end{aligned}$$

The space $L^{2}_{p}(\Omega )$ is a Hilbert space with the scalar product ${\left\langle {\omega ,\omega ^{\prime }}\right\rangle }:=\int _{\Omega }{{\left( {\sum _{j=1}^{p}{\omega _{j}(x)\bar{\omega }^{\prime }_{j}(x)}}\right) }d\mu (x)}.$

We are interested in solutions of a linear equation $Du=\omega ,$ where $D=D_{p}$ is a linear operator acting on $E^{p}.$ This means that D is a matrix whose entries are linear operators on functions.

We shall make the following hypotheses.

Let $\Omega$ be a relatively compact connected domain in X. Let $B:=B(x,R)$ be a ball in X and $B^{1}:=B(x,R/2).$ There is a $\tau >0$ with $\displaystyle \frac{1}{t}=\frac{1}{r}-\tau$ such that:

• (i) Local Increasing Regularity (LIR), we have

  $$\begin{aligned}&\forall x\in \bar{\Omega },\ \exists R>0::\forall r\ge s,\ \exists c_{l}>0,\ \forall u\in L_{p}^{r}(B),\nonumber \\&{\left\| {u}\right\| }_{L_{p}^{t}(B^{1})} \le c_{l}({\left\| {Du}\right\| }_{L_{p}^{r}(B)}+{\left\| {u}\right\| }_{L_{p}^{r}(B)}). \end{aligned}$$

It may happen, in the case X is a manifold, that we have a better regularity locally:

• (i’) Local Increasing Regularity (LIR) with Sobolev estimates: there is $\alpha >0$ such that

  $$\begin{aligned}&\forall x\in \bar{\Omega },\ \exists R>0::\forall r\ge s,\ \exists c_{l}>0,\ \forall u\in L_{p}^{r}(B),\nonumber \\&{\left\| {u}\right\| }_{W_{p}^{\alpha ,r}(B^{1})} \le c_{l}({\left\| {Du}\right\| }_{L_{p}^{r}(B)}+{\left\| {u}\right\| }_{L_{p}^{r}(B)}). \end{aligned}$$

• (ii) Global resolvability. There exists a threshold $s\in (1,\infty )$ such that we can solve $Dw=\omega$ globally in $\Omega$ with $L^{s}-L^{s}$ estimates. It may happen that there is a constrain: let K be a subspace of $L_{p}^{s^{\prime }}(\Omega ),\ s^{\prime }$ the conjugate exponent of s,  then we can solve $Dw=\omega$ if $\displaystyle \omega \perp K.$ In case with no constrain, we set $K=\lbrace 0\rbrace .$ This means:

  $$\begin{aligned}&\exists c_{g}>0,\ \exists w\ s.t.\ Dw=\omega \hbox { in } \displaystyle \Omega \hbox { and } {\left\| {w}\right\| }_{L_{p}^{s}(\Omega )}\le c_{g}{\left\| {\omega }\right\| }_{L_{p}^{s}(\Omega )},\\&\quad \hbox { provided that } \omega \perp K. \end{aligned}$$

  It may happen, in the case X is a manifold, that we have a better regularity for the global existence:

• (ii’) Sobolev regularity: We can solve $Dw=\omega$ globally in $\Omega$ with $L^{s}-W^{\alpha ,s}$ estimates, i.e.,

  $$\begin{aligned}&\exists c_{g}>0,\ \exists w\ s.t.\ Dw=\omega \hbox { in } \displaystyle \Omega \hbox { and } {\left\| {w}\right\| }_{W_{p}^{\alpha ,s}(\Omega )}\le c_{g}{\left\| {\omega }\right\| }_{L_{p}^{s}(\Omega )},\\&\quad \hbox { provided that } \displaystyle \omega \perp K. \end{aligned}$$

  Then we have:

Theorem 2.1

Under the assumptions (i), (ii) above, there is a positive constant $\displaystyle c_{f}$ such that for $r\ge s,$ if $\omega \in L_{p}^{r}(\Omega ),\ \omega \perp K$ there is a$\ u\in L_{p}^{t}(\Omega )$ with $\displaystyle \frac{1}{t}=\frac{1}{r}-\tau ,$ such that $Du=\omega$ and ${\left\| {u}\right\| }_{L_{p}^{t}(\Omega )}\le c_{f}{\left\| {\omega }\right\| }_{L_{p}^{r}(\Omega )}.$

If moreover we have (i’) and (ii’) and the manifold X admits the Sobolev embedding theorems, then $u\in W_{p}^{\alpha ,r}(\Omega )$ with control of the norm.

Proof

Let $\omega \in L^{r}_{p}(\Omega ),\ r>s.$ Because $\Omega$ is relatively compact and $\mu$ is $\sigma$-finite, we have that $\displaystyle \omega \in L^{s}_{p}(\Omega ).$ The global resolvability, condition (ii), gives that there is a $u\in L^{s}_{p}(\Omega )$ such that $Du=\omega ,$ provided that $\displaystyle \omega \perp K.$

The LIR, condition (i), gives that for any $x\in \bar{\Omega }$ there is a ball $B:=B(x,R)$ and a smaller ball $\displaystyle B^{1}:=B(x,R/2)$ such that, with $\displaystyle \frac{1}{t_{1}}=\frac{1}{s}-\tau$ (we often forget the subscript p for simplicity),

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{L^{t_{1}}(B^{1})}\le & {} C({\left\| {Du}\right\| }_{L^{s}(B)}+{\left\| {u}\right\| }_{L^{s}(B)})\\= & {} C({\left\| {\omega }\right\| }_{L^{s}(B)}+{\left\| {u}\right\| }_{L^{s}(B)})\le C({\left\| {\omega }\right\| }_{L^{r}(B)}+{\left\| {u}\right\| }_{L^{s}(B)}), \end{aligned}$$

because ${\left\| {\omega }\right\| }_{L^{s}(B)}\lesssim {\left\| {\omega }\right\| }_{L^{r}(B)},$ since $r\ge s$ and $\bar{\Omega }$ is compact.

Then applying again the LIR we get, with the smaller ball $B^{2}:=B(x,R/4)$ and with $t_{2}:=\min (r,t_{1}),$

$$\begin{aligned} {\left\| {u}\right\| }_{L^{t_{2}}(B^{2})}\le C({\left\| {\omega }\right\| }_{L^{t_{1}}(B^{1})}+{\left\| {u}\right\| }_{L^{t_{1}}(B^{1})})\lesssim ({\left\| {\omega }\right\| }_{L^{r}(B)}+{\left\| {u}\right\| }_{L^{s}(B)}). \end{aligned}$$

• If $t_{1}\ge r\Rightarrow t_{2}=r,$ and ${\left\| {u}\right\| }_{L^{r}(B^{1})}\lesssim ({\left\| {Du}\right\| }_{L^{r}(B)}+{\left\| {u}\right\| }_{L^{s}(B)})$ and with $\displaystyle \frac{1}{t}=\frac{1}{r}-\tau$,

  $$\begin{aligned} {\left\| {u}\right\| }_{L^{t}(B^{2})}\lesssim ({\left\| {\omega }\right\| }_{L^{r}(B^{1})}+{\left\| {u}\right\| }_{L^{r}(B^{1})})\lesssim ({\left\| {\omega }\right\| }_{L^{r}(B)}+{\left\| {u}\right\| }_{L^{s}(B)}). \end{aligned}$$

  It remains to cover $\bar{\Omega }$ by a finite set of balls $B^{2}$ to be done, because

  $$\begin{aligned} \displaystyle \sum _{B^{2}}{{\left\| {u}\right\| }_{L^{t}(B)}}\lesssim {\left\| {u}\right\| }_{L^{t}(\Omega )} \hbox { and } \displaystyle {\left\| {u}\right\| }_{L^{s}(\Omega )}\lesssim {\left\| {\omega }\right\| }_{L^{s}(\Omega )} \hbox { by the threshold hypothesis}. \end{aligned}$$

• If $t_{1}<r,$ we still have:

  $$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{L^{t_{2}}(B^{2})}\lesssim ({\left\| {\omega }\right\| }_{L^{r}(B^{1})}+{\left\| {u}\right\| }_{L^{t_{1}}(B^{1})}). \end{aligned}$$

Then applying again the LIR we get, with the smaller ball $B^{3}:=B(x,R/8)$ and with $t_{3}:=\min (r,t_{2}),$

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{L^{t_{3}}(B^{3})}\lesssim & {} ({\left\| {\omega }\right\| }_{L^{r}(B^{2})}+{\left\| {u}\right\| }_{L^{t_{2}}(B^{2})})\lesssim ({\left\| {\omega }\right\| }_{L^{r}(B^{1})}+{\left\| {u}\right\| }_{L^{t_{1}}(B^{1})})\\\lesssim & {} ({\left\| {\omega }\right\| }_{L^{r}(B)}+{\left\| {u}\right\| }_{L^{s}(B)}). \end{aligned}$$

Hence if $t_{2}\ge r$ we are done as above, if not we repeat the process. Because $\frac{1}{t_{k}}=\frac{1}{s}-k\tau$ after a finite number $k\le 1+\frac{1}{\tau }(\frac{r-s}{2s})$ of steps, we have $t_{k}\ge r$ and we get, with $\displaystyle B^{k}:=B(x,R/2^{k})$ and another constant $C,\ {\left\| {u}\right\| }_{L^{t_{k}}(B^{k})}\le C({\left\| {\omega }\right\| }_{L^{r}(B)}+{\left\| {u}\right\| }_{L^{s}(B)}).$

It remains to cover $\bar{\Omega }$ with a finite number of balls $B^{k}(x)$ to prove the first part of the theorem.

For the second part, the global resolvability, condition (ii), gives that there is a global solution $u\in L^{s}(\Omega )$ such that $Du=\omega$ in $\Omega$ with ${\left\| {u}\right\| }_{L^{s}(\Omega )}\lesssim {\left\| {\omega }\right\| }_{L^{s}(\Omega )}.$ Now if we have the LIR with Sobolev estimates, condition (i’), then

$$\begin{aligned}&\forall x\in \bar{\Omega },\ \exists R>0::\forall r\ge s,\ \exists C>0,\ \forall v\in L^{r}(B(x,R)),\nonumber \\&{\left\| {v}\right\| }_{W^{\alpha ,r}(B^{1})} \le C({\left\| {Dv}\right\| }_{L^{r}(B)}+{\left\| {v}\right\| }_{L^{r}(B)}), \end{aligned}$$

with, as usual, $B:=B(x,R)$ and $B^{1}:=B(x,R/2).$

So, because $r\ge s,$ and $\bar{\Omega }$ is compact, $\displaystyle \omega \in L^{s}(\Omega )$ and we get

$$\begin{aligned} {\left\| {u}\right\| }_{W^{\alpha ,s}(B^{1})}\lesssim ({\left\| {Du}\right\| }_{L^{s}(B)}+{\left\| {u}\right\| }_{L^{s}(B)})\lesssim ({\left\| {\omega }\right\| }_{L^{r}(B)}+{\left\| {u}\right\| }_{L^{s}(B)}). \end{aligned}$$

The Sobolev embedding theorems, true by assumption here, give ${\left\| {u}\right\| }_{L^{\tau }(B^{1})}\le c{\left\| {u}\right\| }_{W^{\alpha ,s}(B^{1})}$ with $\frac{1}{\tau }=\frac{1}{s}-\frac{\alpha }{n}.$

So applying again the LIR condition in a ball $B^{2}:=B(x,R/4),$ we get, with $t_{1}:=\min (\tau ,r),$

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{\alpha ,t_{1}}(B^{2})}\lesssim ({\left\| {\omega }\right\| }_{L^{t_{1}}(B)}+{\left\| {u}\right\| }_{L^{t_{1}}(B^{1})})\lesssim ({\left\| {\omega }\right\| }_{L^{r}(B)}+{\left\| {u}\right\| }_{L^{s}(B)}). \end{aligned}$$

Now we proceed as above. If $\tau \ge r\Rightarrow t_{1}=r,$ then we apply again the LIR condition to a smaller ball $B^{3}:=B(x,R/8),$ we get

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{\alpha ,r}(B^{3})}\lesssim ({\left\| {\omega }\right\| }_{L^{r}(B)}+{\left\| {u}\right\| }_{L^{r}(B^{2})})\lesssim ({\left\| {\omega }\right\| }_{L^{r}(B)}+{\left\| {u}\right\| }_{L^{s}(B)}). \end{aligned}$$

and we are done by covering $\bar{\Omega }$ by a finite set of balls $B^{3}$ as above.

If $\tau <r,$ then we iterate the process as in the previous part, adding the use of the Sobolev embedding theorem to increase the exponent, up to the moment we reach r.

$\square$

Remark 2.2

We notice that in fact the solution u in Theorem 2.1 is the same as the one given by condition (ii). It is a case of “self improvement” of estimates.

3 Application to Elliptic PDE

Let (M, g) be a ${\mathcal {C}}^{\infty }$ smooth connected compact Riemannian manifold without boundary. We shall denote $\displaystyle G:=(H,\pi ,M)$ a complex ${\mathcal {C}}^{m}$ vector bundle over M of rank N with fiber H. The fiber $\pi ^{-1}(x)\simeq H$ is equipped with a scalar product varying smoothly with x in M.

We can define punctually, for $\omega ,\varphi \in {\mathcal {C}}^{\infty }_{G}(M),$ two smooth sections of G over M,  a scalar product $(\omega ,\varphi )(x):={\left\langle {\omega (x),\varphi (x)}\right\rangle }_{H_{x}}$ where $H_{x}:=\pi ^{-1}(x)$ is the fiber over $x\in M.$ This gives a modulus: for $x\in M,\ \left| {\omega }\right| (x):={\sqrt{(\omega ,\omega )(x)}}.$ By using the canonical volume $dv_{g}$ on M we get a scalar product:

$$\begin{aligned} \displaystyle {\left\langle {\omega ,\varphi }\right\rangle }:=\int _{M}{(\omega ,\varphi )(x)dv_{g}(x)}, \end{aligned}$$

for G-forms in $L^{2}_{G}(M)$, i.e., such that

$$\begin{aligned} \displaystyle {\left\| {\omega }\right\| }_{L^{2}_{G}(M)}^{2}:=\int _{M}{\left| {\omega }\right| ^{2}(x)dv_{g}(x)}<\infty . \end{aligned}$$

The same way we define the spaces $L^{r}_{G}(M)$ of G-forms $\omega$ such that

$$\begin{aligned} \displaystyle {\left\| {\omega }\right\| }_{L^{r}_{G}(M)}^{r}:=\int _{M}{\left| {\omega }\right| ^{r}(x)dv_{g}(x)}<\infty . \end{aligned}$$

Let $D:G\rightarrow G$ be a linear differential operator of order m with ${\mathcal {C}}^{\infty }$ coefficients. There is a formal adjoint $\displaystyle D^{*}:G\rightarrow G$ defined by the identity ${\left\langle {D^{*}f,g}\right\rangle }={\left\langle {f,Dg}\right\rangle }.$

We shall use the definition of ellipticity given by Warner [29, Definition 6.28, p. 240] or by Donaldson [10, p. 17].

Let $D:E\rightarrow F$ be a differential operator of order m operating from the sections of the vector bundle E to the ones of the vector bundle F over M. Then at each point $x\in M$ and for each cotangent vector $\xi \in T^{*}M$ there is a linear map $\sigma _{\xi }:E_{x}\rightarrow F_{x}$ which can be defined in the following way: choose a section s of E,  and a function f on M,  vanishing at x and with $df=\xi$ at x. Then we can define $\sigma _{\xi }(s(x))=D(f^{m}s)(x).$ We can check that this definition is independent of the choice of f, s. Now we can state:

Definition 3.1

An operator $D:E\rightarrow F$ is elliptic if for each non-zero $\xi \in TM_{x},$ the linear map $\sigma _{\xi }$ is an isomorphism from $E_{x}$ to $\displaystyle F_{x}.$ We shall say that D is uniformly elliptic if the isomorphism $\sigma _{\xi }$ and its inverse are bounded independently of the point $x\in M$ for $\left| {\xi }\right| =1.$

Then for $s=2,$ Warner [29, Exercise 21, p. 257] or also Donaldson [10, Theorem 4, p. 16] proved:

Theorem 3.2

Let D be an operator of order m acting on sections of $G:=(H,\pi ,M)$ in the connected compact Riemannian manifold M without boundary. Suppose that D is elliptic and with ${\mathcal {C}}^{\infty }$ smooth coefficients.

• 1. In $L^{2}_{G}(M),\ \mathrm {k}\mathrm {e}\mathrm {r}D,\ \mathrm {k}\mathrm {e}\mathrm {r}D^{*}$ are finite dimensional vector spaces.

• 2. We can solve the equation $Du=\omega$ in $\displaystyle L^{2}_{G}(M)$ if and only if $\omega$ is orthogonal to $\mathrm {k}\mathrm {e}\mathrm {r}D^{*}.$

Moreover, because $\displaystyle L^{2}_{G}(M)$ is a Hilbert space, we have that there is a bounded linear operator $\displaystyle S:\ L^{2}_{G}(M)\rightarrow L^{2}_{G}(M)$ such that $D(S\omega )=\omega$ provided that $\displaystyle \omega \perp \mathrm {k}\mathrm {e}\mathrm {r}D^{*}.$

On the other hand, we have local interior regularity by Hörmander [18, Theorem 17.1.3, p. 6], in the case of functions. We quote it in the weakened form we need:

Theorem 3.3

(LIR) Let D be an operator of order m on ${\mathcal {C}}^{\infty }(M)$ in the complete Riemannian manifold M. Suppose that D is elliptic and with ${\mathcal {C}}^{\infty }$ smooth coefficients. Then, for any $x\in M$ there is a ball $B_{x}:=B(x,R)$ and a smaller ball $\displaystyle B^{\prime }_{x}$ relatively compact in $B_{x},$ such that:

$$\begin{aligned} {\left\| {u}\right\| }_{W^{m,r}(B^{\prime }_{x})}\le C({\left\| {Du}\right\| }_{L^{r}(B_{x})}+{\left\| {u}\right\| }_{L^{r}(B_{x})}). \end{aligned}$$

For the case of G-forms, we need to use Agmon et al.  [2, Theorem 10.3]:

Theorem 3.4

Positive constants $r_{1}$ and $K_{1}$ exist such that, if $r\le r_{1}$ and the ${\left\| {u_{j}}\right\| }_{t_{j}},\ j=1,\ldots ,N,$ are finite, then $\displaystyle {\left\| {u_{j}}\right\| }_{l+t_{j}}$ also is finite for $\displaystyle j=1,\ldots ,N,$ and

$$\begin{aligned} \displaystyle {\left\| {u_{j}}\right\| }_{l+t_{j}}\le K_{1}{\left( {\sum _{j}{{\left\| {F_{j}}\right\| }_{l-s_{j}}}+\sum _{j}{{\left\| {u_{j}}\right\| }_{0}}}\right) }. \end{aligned}$$

The constants $r_{1},K_{1}$ depend on $n,N,t^{\prime },A,b,p,k,$, and l and also on the modulus of continuity of the leading coefficients in the $l_{ij}.$

From this theorem we get quite easily what we want (in the case $r=2$ and in its global version, F.W. Warner [29, Theorem 6.29, p. 240] quotes it as Fundamental Inequality):

Theorem 3.5

(LIR) Let D be an operator of order m on G in the complete Riemannian manifold M. Suppose that D is elliptic and with ${\mathcal {C}}^{1}(M)$ smooth coefficients. Then, for any $x\in M$ there is a ball $B:=B(x,R)$ and, with the ball $\displaystyle B^{1}:=B(x,R/2),$ we have

$$\begin{aligned} {\left\| {u}\right\| }_{W^{m,r}_{G}(B^{1})}\le c_{1}{\left\| {Du}\right\| }_{L^{r}_{G}(B)}+c_{2}R^{-m}{\left\| {u}\right\| }_{L^{r}_{G}(B)}). \end{aligned}$$

Moreover the constants are independent of the radius R of the ball B.

Proof

Let $\displaystyle x\in M$; we choose a chart $(V,\ \varphi (y))$ so that $g_{ij}(x)=\delta _{ij}$ and $\varphi (V)=B_{e}$ where $B_{e}=B_{e}(0,R_{e})$ is a Euclidean ball centered at $\varphi (x)=0$ and $g_{ij}$ are the components of the metric tensor w.r.t. $\varphi .$ We choose also the chart $\displaystyle (V,\ \varphi )$ to trivialize the bundle G. So read in $\displaystyle (V,\varphi )$ we have that the sections of G are just ${\mathbb {C}}^{N}$ valued functions.

We denote by $D_{\varphi }$ the operator D read in the map $(V,\varphi ).$ This is still an elliptic system operating on ${\mathbb {C}}^{N}$ valued functions in $B_{e}$ in ${\mathbb {R}}^{n}.$ Let $\chi \in {\mathcal {D}}(B_{e})$ such that $\chi =1$ in $B^{1}_{e}:=B_{e}(0,R_{e}/2)\Subset B_{e}.$ Let u be a G-form in $L^{r}_{G}(\varphi ^{-1}(B_{e}))$ such that Du is also in $\displaystyle L^{r}_{G}(\varphi ^{-1}(B_{e})).$ Denote by $u_{\varphi }$ the ${\mathbb {C}}^{N}$ valued functions u read in $(V,\varphi ).$ We can apply the Agmon et al. Theorem 3.4 to $\chi u_{\varphi }$ and we get, with the constant K independent of the radius $R_{e}$ of $B_{e},$

$$\begin{aligned} {\left\| { \chi u_{\varphi }}\right\| }_{W^{m,r}(B_{e})}\le K\left( {\left\| {D_{\varphi }(\chi u_{\varphi })}\right\| }_{L^{r}(B_{e})}+R_{e}^{-m}{\left\| {\chi u_{\varphi }}\right\| }_{L^{r}(B_{e})}\right) . \end{aligned}$$

(3.1)

We have that $D_{\varphi }(\chi u_{\varphi })=\chi D_{\varphi }(u_{\varphi })+u_{\varphi }D_{\varphi }\chi +\Delta _{\varphi },$ with $\Delta _{\varphi }:=D_{\varphi }(\chi u_{\varphi })-\chi D_{\varphi }(u_{\varphi })-u_{\varphi }D_{\varphi }\chi .$ The point is that $\Delta _{\varphi }$ contains only derivatives of the $j^{th}$ component of $u_{\varphi }$ of order strictly less than in the $j^{th}$ component of $u_{\varphi }$ in $D_{\varphi }u_{\varphi }.$ So we have

$$\begin{aligned} {\left\| {\Delta _{\varphi }}\right\| }_{L^{r}(B_{e})}\le {\left\| {\partial \chi }\right\| }_{\infty }{\left\| {\chi u_{\varphi }}\right\| }_{W^{m-1,r}(B_{e})}\le R_{e}^{-1}{\left\| {\chi u_{\varphi }}\right\| }_{W^{m-1,r}(B_{e})}. \end{aligned}$$

We can use the “Peter-Paul” inequality [14, Theorem 7.28, p.  173] (see also [29, Theorem 6.18, (g) p.  232] for the case $r=2.$)

$$\begin{aligned} \displaystyle \forall \epsilon>0,\ \exists C_{\epsilon }>0::{\left\| {\chi u_{\varphi }}\right\| }_{W^{m-1,r}(B_{e})}\le \epsilon {\left\| {\chi u_{\varphi }}\right\| }_{W^{m,r}(B_{e})}+C\epsilon ^{-m+1}{\left\| {\chi u_{\varphi }}\right\| }_{L^{r}(B_{e})}. \end{aligned}$$

We choose $\epsilon =R_{e}\eta$ and we get

$$\begin{aligned} \displaystyle R_{e}^{-1}{\left\| {\chi u_{\varphi }}\right\| }_{W^{m-1,r}(B_{e})}\le \eta {\left\| {\chi u_{\varphi }}\right\| }_{W^{m,r}(B_{e})}+C\eta ^{-m+1}R_{e}^{-m}{\left\| {\chi u_{\varphi }}\right\| }_{L^{r}(B_{e})}. \end{aligned}$$

Putting this in (3.1) we get

$$\begin{aligned} \displaystyle {\left\| {\chi u_{\varphi }}\right\| }_{W^{m,r}(B_{e})}\le & {} K\left( {\left\| {\chi D_{\varphi }u_{\varphi }}\right\| }_{L^{r}(B_{e})}+\eta {\left\| {\chi u_{\varphi }}\right\| }_{W^{m,r}(B_{e})}\right. \\&\left. +C\eta ^{-m+1}R_{e}^{-m}{\left\| {\chi u_{\varphi }}\right\| }_{L^{r}(B_{e})}+{\left\| {u_{\varphi }D_{\varphi }\chi }\right\| }_{L^{r}(B_{e})}\right) . \end{aligned}$$

But again ${\left\| {D_{\varphi }\chi }\right\| }_{\infty }\le R_{e}^{-m}$ so, choosing $\eta$ small enough to get $\eta K\le 1/2,$ we have with new constants still independent of $R_{e}$:

$$\begin{aligned} \frac{1}{2}{\left\| {\chi u_{\varphi }}\right\| }_{W^{m,r}(B_{e})}\le c_{1}{\left\| {\chi D_{\varphi }u_{\varphi }}\right\| }_{L^{r}(B_{e})}+c_{2}R_{e}^{-m}{\left\| {\chi u_{\varphi }}\right\| }_{L^{r}(B_{e})}. \end{aligned}$$

Now $\chi =1$ in $B^{1}_{e}$ and $\chi \le 1$ gives, changing the constants suitably,

$$\begin{aligned} {\left\| { u_{\varphi }}\right\| }_{W^{m,r}(B^{1}_{e})}\le c_{1}{\left\| {D_{\varphi }u_{\varphi }}\right\| }_{L^{r}(B_{e})}+c_{2}R_{e}^{-m}{\left\| {u_{\varphi }}\right\| }_{L^{r}(B_{e})}. \end{aligned}$$

(3.2)

It remains to go back to the manifold M to end the proof. $\square$

We deduce the local elliptic inequalities:

Corollary 3.6

Let D be an operator of order m on G in the complete Riemannian manifold M. Suppose that D is elliptic and with ${\mathcal {C}}^{1}(M)$ smooth coefficients. Then, for any $x\in M$ there is a ball $B:=B(x,R)$ and the smaller ball $\displaystyle B^{1}:=B(x,R/2),$ such that, $\forall k\in {\mathbb {N}},$ with D in ${\mathcal {C}}^{k+1}(M)$ here, we get for any G-form $\displaystyle u\in W^{m+k,r}_{G}(B^{1}):$

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{m+k,r}_{G}(B^{1})}\le \sum _{j=0}^{k}{c_{j}R^{-jm}{\left\| {Du}\right\| }}_{W^{k-j,r}_{G}(B)}+c_{k+1}R^{-(k+1)m}{\left\| {u}\right\| }_{L^{r}_{G}(B)}. \end{aligned}$$

Moreover the constants are independent of the radius R of the ball B.

Proof

As for Theorem 3.5, we choose a chart $(V,\ \varphi )$ trivializing the bundle G and so that $g_{ij}(x)=\delta _{ij}$ and $\varphi (V)=B$ where B is a Euclidean ball centered at $\varphi (x)=0$ and $g_{ij}$ are the components of the metric tensor w.r.t. $\varphi .$ We start with the Eq. (3.2) in ${\mathbb {R}}^{n}$ and we apply it to $\partial _{j}u_{\varphi }:=\frac{\partial u_{\varphi }}{\partial y_{j}}$ instead of $u_{\varphi }.$ We get

$$\begin{aligned} \displaystyle {\left\| {\partial _{j}u_{\varphi }}\right\| }_{W^{m,r}(B^{1})}\le c_{1}{\left\| {D_{\varphi }(\partial _{j}u_{\varphi })}\right\| }_{L^{r}(B)}+c_{2}R_{e}^{-m}{\left\| {\partial _{j}u_{\varphi }}\right\| }_{L^{r}(B)}. \end{aligned}$$

Now $\displaystyle D_{\varphi }(\partial _{j}u_{\varphi })=\partial _{j}D_{\varphi }(u_{\varphi })+[D_{\varphi },\partial _{j}]u_{\varphi },$ with as usual, $\displaystyle [D_{\varphi },\partial _{j}]u_{\varphi }:=D_{\varphi }(\partial _{j}u_{\varphi })-\partial _{j}D_{\varphi }(u_{\varphi }).$

So we get

$$\begin{aligned} \displaystyle {\left\| {\partial _{j}u_{\varphi }}\right\| }_{W^{m,r}(B^{1})}\le c_{1}{\left\| {\partial _{j}D_{\varphi }u_{\varphi }}\right\| }_{L^{r}(B)}+c_{1}{\left\| {[D_{\varphi },\partial _{j}]u_{\varphi }}\right\| }_{L^{r}(B)}+c_{2}R_{e}^{-m}{\left\| {\partial _{j}u_{\varphi }}\right\| }_{L^{r}(B)}. \end{aligned}$$

So, because $\displaystyle [D_{\varphi },\partial _{j}]$ is a differential operator of order m,  we get

$$\begin{aligned} \displaystyle {\left\| {\partial _{j}u_{\varphi }}\right\| }_{W^{m,r}(B^{1})}\le c_{1}{\left\| {D_{\varphi }u_{\varphi }}\right\| }_{W^{1,r}(B)}+c_{1}{\left\| {u_{\varphi }}\right\| }_{W^{m,r}(B)}+c_{2}R_{e}^{-m}{\left\| {u_{\varphi }}\right\| }_{W^{1,r}(B)}. \end{aligned}$$

This is true for any $j=1,\ldots ,n$ so

$$\begin{aligned} \displaystyle {\left\| {u_{\varphi }}\right\| }_{W^{m+1,r}(B^{1})}\le c_{1}{\left\| {D_{\varphi }u_{\varphi }}\right\| }_{W^{1,r}(B)}+c_{1}{\left\| {u_{\varphi }}\right\| }_{W^{m,r}(B)}+c_{2}R_{e}^{-m}{\left\| {u_{\varphi }}\right\| }_{W^{1,r}(B)}. \end{aligned}$$

We always have $\ {\left\| {u_{\varphi }}\right\| }_{W^{1,r}(B)}\le {\left\| {u_{\varphi }}\right\| }_{W^{m,r}(B)}$ hence, with other constants $c_{j},$

$$\begin{aligned} \displaystyle {\left\| {u_{\varphi }}\right\| }_{W^{m+1,r}(B^{1})}\le & {} c_{1}{\left\| {D_{\varphi }u_{\varphi }}\right\| }_{W^{1,r}(B)}+(c_{1}+c_{2}R^{-m}){\left\| {u_{\varphi }}\right\| }_{W^{m,r}(B)}\\\le & {} c_{1}{\left\| {D_{\varphi }u_{\varphi }}\right\| }_{W^{1,r}(B)}+c_{2}R^{-m}{\left\| {u_{\varphi }}\right\| }_{W^{m,r}(B)}, \end{aligned}$$

because $R\le 1.$

Now we use again Eq. (3.2) to get

$$\begin{aligned} \displaystyle {\left\| {u_{\varphi }}\right\| }_{W^{m,r}(B)}\le c_{1}{\left\| {D_{\varphi }u_{\varphi }}\right\| }_{L^{r}(B)}+c_{2}R_{e}^{-m}{\left\| {u_{\varphi }}\right\| }_{L^{r}(B)}, \end{aligned}$$

hence still with different constants from line to line

$$\begin{aligned} \displaystyle {\left\| {u_{\varphi }}\right\| }_{W^{m+1,r}(B^{1})}\le & {} c_{1}{\left\| {D_{\varphi }u_{\varphi }}\right\| }_{W^{1,r}(B)}+c_{2}R_{e}^{-m}({\left\| {D_{\varphi }u_{\varphi }}\right\| }_{L^{r}(B)}+c_{2}R_{e}^{-m}{\left\| {u_{\varphi }}\right\| }_{L^{r}(B)})\\ \displaystyle\le & {} c_{1}{\left\| {D_{\varphi }u_{\varphi }}\right\| }_{W^{1,r}(B)}+c_{2}R_{e}^{-m}{\left\| {D_{\varphi }u_{\varphi }}\right\| }_{L^{r}(B)}+c_{3}R_{e}^{-2m}{\left\| {u_{\varphi }}\right\| }_{L^{r}(B)}). \end{aligned}$$

Now, proceeding by induction along the same lines, we get

$$\begin{aligned} \displaystyle {\left\| {u_{\varphi }}\right\| }_{W^{m+k,r}(B^{1})}\le \sum _{j=0}^{k}{c_{j}R^{-jm}{\left\| {D_{\varphi }u_{\varphi }}\right\| }}_{W^{k-j,r}(B)}+c_{k+1}R_{e}^{-(k+1)m}{\left\| {u_{\varphi }}\right\| }_{L^{r}(B)}. \end{aligned}$$

It remains to go back to the manifold M to end the proof. $\square$

Remark 3.7

We stress here the dependence in R because we shall need it to study the case of non-compact Riemannian manifolds.

Now we can prove

Theorem 3.8

Let (M, g) be a ${\mathcal {C}}^{\infty }$ smooth compact Riemannian manifold without boundary. Let $D:G\rightarrow G$ be an elliptic linear differential operator of order m with ${\mathcal {C}}^{\infty }(M)$ coefficients. Let $\omega \in L^{r}_{G}(M)\cap \mathrm {(}\mathrm {k}\mathrm {e}\mathrm {r}D^{*}\mathrm {)}^{\perp }$ with $r\ge 2.$ Then there is a $u\in W^{m,r}_{G}(M)$ such that $Du=\omega$ on M. Moreover u is given linearly w.r.t. to $\omega .$

Proof

Let $\omega \in L^{r}_{G}(M)\cap \mathrm {(}\mathrm {k}\mathrm {e}\mathrm {r}D^{*}\mathrm {)}^{\perp }$ with $r\ge 2.$ Because M is compact, we have $\displaystyle \omega \in L^{2}_{G}(M).$ Theorem 3.2 gives us the Global Resolvability, condition (ii), with the threshold $s=2,$ and with $K:=\mathrm {k}\mathrm {e}\mathrm {r}D^{*},$ i.e., provided that $\omega \perp K$:

$$\begin{aligned} u:=S\omega \in L^{2}_{G}(M)::Du=\omega ,\ {\left\| {u}\right\| }_{2}\le C{\left\| {\omega }\right\| }_{2}. \end{aligned}$$

The Theorem 3.5 of Agmon et al. gives us the Local Interior Regularity with the Sobolev estimates for $\alpha =m.$

So we can apply Theorem 2.1 and we use Remark 2.2 to have that $u=S\omega$ so u is given linearly w.r.t. to $\omega .$ The proof is complete. $\square$

By duality we get the range $r<2.$ We shall proceed as we did in [3], using an avatar of the Serre duality [26].

Let $g\in L^{r^{\prime }}_{G}(M)\cap \mathrm {k}\mathrm {e}\mathrm {r}D^{\perp },$ because $D^{*}$ has the same elliptic properties than D,  we can solve $D^{*}v=g,$ with $r^{\prime }<2$ and $r^{\prime }$ conjugate to r in the following way.

We know by the previous part that

$$\begin{aligned} \forall \omega \in L^{r}_{G}(M)\cap \mathrm {(}\mathrm {k}\mathrm {e}\mathrm {r}D^{*}\mathrm {)}^{\perp },\ \exists u\in L^{r}_{G}(M),\ Du=\omega . \end{aligned}$$

(3.3)

Consider the linear form

$$\begin{aligned} \forall \omega \in L^{r}_{G}(M),\ {\mathcal {L}}(\omega ):={\left\langle {u,g}\right\rangle }, \end{aligned}$$

where u is a solution of (3.3); in order for ${\mathcal {L}}(\omega )$ to be well defined, we need that if $u^{\prime }$ is another solution of $Du^{\prime }=\omega ,$ then ${\left\langle {u-u^{\prime },g}\right\rangle }=0;$ hence we need that g must be “orthogonal” to G-forms $\varphi$ such that $D\varphi =0,$ which is precisely our assumption.

Hence we have that ${\mathcal {L}}(f)$ is well defined and linear; moreover

$$\begin{aligned} \displaystyle \ \left| {{\mathcal {L}}(f)}\right| \le {\left\| {u}\right\| }_{L^{r}(M)}{\left\| {g}\right\| }_{L^{r^{\prime }}(M)}\le c{\left\| {\omega }\right\| }_{L^{r}(M)}{\left\| {g}\right\| }_{L^{r^{\prime }}(M)}. \end{aligned}$$

So this linear form is continuous on $\omega \in L^{r}_{G}(M)\cap (\mathrm {k}\mathrm {e}\mathrm {r}D^{*})^{\perp }.$ By the Hahn Banach Theorem there is a form $v\in L^{r^{\prime }}_{G}(M)$ such that

$$\begin{aligned} \displaystyle \forall \omega \in L^{r}_{G}(M)\cap (\mathrm {k}\mathrm {e}\mathrm {r}D^{*})^{\perp },\ {\mathcal {L}}(\omega )={\left\langle {\omega ,v}\right\rangle }={\left\langle {u,g}\right\rangle }. \end{aligned}$$

But $\omega =Du,$ so we have ${\left\langle {\omega ,v}\right\rangle }={\left\langle {Du,v}\right\rangle }={\left\langle {u,D^{*}v}\right\rangle }={\left\langle {u,g}\right\rangle },$ for any $u\in {\mathcal {C}}^{\infty }_{G}(M).$ Hence we solved $D^{*}v=g$ in the sense of distributions with $v\in L^{r^{\prime }}_{G}(M).$ So we proved:

Theorem 3.9

For any $r,\ 1<r\le 2,$ if $g\in L_{G}^{r}(M)\cap (\mathrm {k}\mathrm {e}\mathrm {r}D)^{\perp }$ there is a $v\in L^{r}_{G}(M)$ such that $D^{*}v=g,\ {\left\| {v}\right\| }_{L^{r}_{G}(M)}\le c{\left\| {g}\right\| }_{L^{r}_{G}(M)}.$

Moreover the solution is in $W^{m,r}_{G}(M).$

It remains to prove the “moreover” and for this we use the LIR Theorem 3.5: for any $x\in M$ there is a ball $B:=B(x,R)$ and, with the ball $\displaystyle B^{1}:=B(x,R/2),$ we get

$$\begin{aligned} {\left\| {u}\right\| }_{W^{m,r}_{G}(B^{1})}\le C\big ({\left\| {Du}\right\| }_{L_{G}^{r}(B)}+{\left\| {u}\right\| }_{L_{G}^{r}(B)}\big ). \end{aligned}$$

We cover M with a finite number of balls $B^{1}$ to prove the theorem. $\square$

Set ${\mathcal {H}}_{G}^{2}:=\mathrm {k}\mathrm {e}\mathrm {r}D^{*}\cap L^{2}_{G}(M).$

Because D and $D^{*}$ have the same elliptic properties, we finally proved:

Theorem 3.10

Let (M, g) be a ${\mathcal {C}}^{\infty }$ smooth compact Riemannian manifold without boundary. Let $D:G\rightarrow G$ be an elliptic linear differential operator of order m with ${\mathcal {C}}^{1}$ coefficients. Let $\omega \in L^{r}_{G}(M)\cap ({\mathcal {H}}_{G}^{2})^{\perp }$ with $r>1.$ Then there is a $u\in L^{r}_{G}(M)$ such that $Du=\omega$ on M. Moreover the solution is in $W^{m,r}_{G}(M).$

Now we make the hypothesis that D has ${\mathcal {C}}^{\infty }$ smooth coefficients. Theorem 3.2 of Warner or Donaldson gives, on a compact manifold M without boundary, that $\mathrm {d}\mathrm {i}\mathrm {m}_{{\mathbb {R}}}{\mathcal {H}}_{G}^{2}<\infty .$

We shall generalize here a well-known result valid for the Hodge Laplacian.

Lemma 3.11

We have $\displaystyle {\mathcal {H}}_{G}^{2}\subset {\mathcal {C}}^{\infty }(M).$

Proof

Take $x\in M,\ h\in {\mathcal {H}}_{G}^{2}.$ The fundamental inequalities, Corollary 3.6, give, applied to $D^{*},$ that there is a ball $B:=B(x,R)$ with the ball $\displaystyle B^{1}:=B(x,R/2)$ such that

$$\begin{aligned} \forall k\in {\mathbb {N}},\ {\left\| {h}\right\| }_{W^{m+k,2}(B^{1})}\le c_{k+1}R^{-(k+1)m}{\left\| {h}\right\| }_{L^{2}(B)}. \end{aligned}$$

The Sobolev embedding theorems, valid in a these balls, give that, for any $l\in {\mathbb {N}},\ h\in {\mathcal {C}}^{l}(B^{1}).$ Then $\displaystyle h\in {\mathcal {C}}^{\infty }(B^{1}).$

Because the ${\mathcal {C}}^{\infty }$ regularity is a local property, we get that $\displaystyle h\in {\mathcal {C}}^{\infty }(M).$$\square$

Lemma 3.12

There is a linear projection from $L^{r}_{G}(M)$ to $\displaystyle {\mathcal {H}}_{G}^{2}.$

Proof

We set

$$\begin{aligned} \displaystyle \forall v\in L^{r}_{G}(M),\ H(v):=\sum _{j=1}^{N}{{\left\langle {v,e_{j}}\right\rangle }e_{j}}, \end{aligned}$$

where $\lbrace e_{j}\rbrace _{j=1,\ldots ,N}$ is an orthonormal basis for $\displaystyle {\mathcal {H}}_{G}^{2}.$ This is meaningful because $v\in L^{r}_{G}(M)$ can be integrated against $e_{j}\in {\mathcal {H}}_{G}^{2}\subset {\mathcal {C}}^{\infty }(M).$ Moreover we have $v-H(v)\in L^{r}_{G}(M)\cap {\mathcal {H}}_{G}^{\perp }$ in the sense that $\forall h\in {\mathcal {H}}_{G}^{2},\ {\left\langle {v-H(v),\ h}\right\rangle }=0;$ it suffices to test on $h:=e_{k}.$ We get

$$\begin{aligned} \displaystyle {\left\langle {v-H(v),\ e_{k}}\right\rangle }={\left\langle {v,e_{k}}\right\rangle }-{\left\langle {\sum _{j=1}^{N}{{\left\langle {v,e_{j}}\right\rangle }e_{j},e_{k}}}\right\rangle }={\left\langle {v,e_{k}}\right\rangle }-{\left\langle {v,e_{k}}\right\rangle }=0. \end{aligned}$$

This ends the proof. $\square$

Proposition 3.13

We have a direct decomposition:

$$\begin{aligned} \displaystyle L^{r}_{G}(M)={\mathcal {H}}_{G}^{2}\oplus \mathrm {I}\mathrm {m}D(W^{2,r}_{G}(M)). \end{aligned}$$

Proof

Let $v\in L^{r}_{G}(M).$ Set $h:=H(v)\in {\mathcal {H}}^{2}_{G},$ and $\omega :=v-h.$ We have that $\forall k\in {\mathcal {H}}^{2}_{G},\ {\left\langle {\omega ,k}\right\rangle }={\left\langle {v-H(v),\ k}\right\rangle }=0.$ Hence we can solve $Du=\omega$ with $u\in W^{2,r}_{G}(M)\cap L^{2}_{G}(M).$ So we get $v=h+Du$ which means

$$\begin{aligned} \displaystyle L^{r}_{G}(M)={\mathcal {H}}_{G}^{2}+\mathrm {I}\mathrm {m}D(W^{2,r}_{G}(M)). \end{aligned}$$

The decomposition is direct because if $\omega \in {\mathcal {H}}^{2}_{G}\cap \mathrm {I}\mathrm {m}D(W^{2,r}_{G}(M)),$ then $\omega \in {\mathcal {C}}^{\infty }(M)$ and

$$\begin{aligned} \omega =Du\Rightarrow \forall k\in {\mathcal {H}}^{2}_{G},\ \omega \perp k, \end{aligned}$$

so choosing $k=\omega \in {\mathcal {H}}^{2}_{G}$ we get $\displaystyle {\left\langle {\omega ,\omega }\right\rangle }=0$; hence $\omega =0.$ The proof is complete. $\square$

In the special case where D is the Hodge Laplacian, we already seen [4] that we recover this way the strong $L^{r}$ Hodge decomposition without using Gaffney’s inequalities.

4 Case of Compact Manifold with a Smooth Boundary

Let N be a ${\mathcal {C}}^{\infty }$ smooth connected Riemannian manifold compact with a ${\mathcal {C}}^{\infty }$ smooth boundary $\partial N.$ We want to show how the results in case of a compact boundary-less manifold apply to this case.

First we know that a neighborhood V of $\partial N$ in N can be seen as $\partial N{\times }[0,\delta ]$ by [23, Theorem 5.9 p. 56] or by  [9, Théorème (28) p. 1–21]. This allows us to “extend” slightly N :  we have $N=(N\backslash V)\cup V\simeq (N\backslash V)\cup (\partial N{\times }[0,\delta ]).$ So we set $M:=(N\backslash V)\cup (\partial N{\times }[0,\delta +\epsilon ]).$

Then M can be seen as a Riemannian manifold with boundary $\partial M\simeq \partial N$ and such that $\bar{N}\subset M.$

Now a classical way to get rid of a “annoying boundary” of a manifold is to use its “double.” For instance, Duff [12], Hörmander [18, p. 257]. Here we copy the following construction from Guneysu and Pigola [16, Appendix B].

The “Riemannian double” $\Gamma :=\Gamma (M)$ of M,  obtained by gluing two copies, M and $M_{2},$ of M along $\partial M,$ is a compact Riemannian manifold without boundary. Moreover, by its very construction, it is always possible to assume that $\displaystyle \Gamma$ contains an isometric copy of the original manifold N. We shall also write N for its isometric copy to ease notation.

We extend the operator D to M smoothly by extending smoothly its coefficients, and because D is strictly elliptic, choosing $\epsilon$ small enough, we get that the extension is still an elliptic operator on M. Then we take a ${\mathcal {C}}^{\infty }$ function $\chi$ with compact support on $M\subset \Gamma$ such that $0\le \chi \le 1;\ \chi \equiv 1$ on N;  and we consider $\tilde{D}:=\chi D+(1-\chi )D_{2}$ where $D_{2}$ is the operator D on the copy $M_{2}$ of M. Then $\tilde{D}\equiv D$ on N and is elliptic on $\Gamma .$

Now we shall use Definition 1.2 from the introduction; we recall it here for the reader convenience.

Definition 4.1

We shall say that D has the weak maximum property, WMP, if, for any smooth DG-harmonic h,  i.e., G-form such that $Dh=0$ in M,  smooth up to the boundary $\partial M,$ which is flat on $\partial M,$ i.e., zero on $\partial M$ with all its derivatives, then h is zero in M.

Of course if there is a maximum principle for D, then WMP is true. This is the case for smoothly bounded open sets in ${\mathbb {R}}^{n}$ by a Theorem of Agmon [1] for functions and by  [2, Theorem 4.2, p. 59] in the case $G=\Lambda ^{p}(M)$ of p-forms on M.

Because this maximum principle is not local, I do not know what happen on a compact Riemannian manifold with smooth boundary for general elliptic operator, even in the case $\displaystyle G=\Lambda ^{p}(M).$

Nevertheless the Hodge Laplacian in a Riemannian manifold has the UCP for p-forms by a difficult result by Aronszajn et al. [6]; hence it has the WMP too.

The main lemma of this section is:

Lemma 4.2

Let $\omega \in L^{r}_{G}(N),$ then we can extend it to $\omega ^{\prime }\in L^{r}_{G}(\Gamma )$ such that $\forall h\in {\mathcal {H}}_{G}(\Gamma ), {\left\langle {\omega ^{\prime },h}\right\rangle }_{\Gamma }=0$ provided that the operator D has the WMP for the D-harmonic G-forms.

Proof

Recall that ${\mathcal {H}}_{G}(\Gamma ):=\mathrm {k}\mathrm {e}\mathrm {r}D^{*}\cap L^{2}_{G}(\Gamma )$ is of finite dimension $K_{G}$ and ${\mathcal {H}}_{G}(\Gamma )\subset {\mathcal {C}}^{\infty }(\Gamma )$ by Lemma 3.11.

Make an orthonormal basis $\lbrace e_{1},\ldots ,e_{K_{G}}\rbrace$ of ${\mathcal {H}}_{G}(\Gamma )$ with respect to $L^{2}_{G}(\Gamma ),$ by the Gram-Schmidt procedure so ${\left\langle {e_{j},e_{k}}\right\rangle }_{\Gamma }:=\int _{\Gamma }{e_{j}e_{k}dv}=\delta _{jk}.$

Set ${\lambda _{j}:={\left\langle {\omega {\mathbb {1}}_{N},e_{j}}\right\rangle }={\left\langle {\omega ,e_{j}{\mathbb {1}}_{N}}\right\rangle },\ j=1,\ldots ,K_{G};}$ this makes sense since $e_{j}\in {\mathcal {C}}^{\infty }(\Gamma )\Rightarrow e_{j}\in L^{\infty }(\Gamma ),$ because $\Gamma$ is compact.

We shall see that the system ${\displaystyle \lbrace e_{k}{\mathbb {1}}_{\Gamma \backslash N}\rbrace _{k=1,\ldots ,K_{G}}}$ is a free one. Suppose this is not the case, then it will exist $\gamma _{1},\ldots ,\gamma _{K_{G}},$ not all zero, such that ${\sum _{k=1}^{K_{G}}{\gamma _{k}e_{k}{\mathbb {1}}_{\Gamma \backslash N}}=0}$ in $\Gamma \backslash N.$ But the function $h:=\sum _{k=1}^{K_{G}}{\gamma _{k}e_{k}}$ is in ${\mathcal {H}}_{G}(\Gamma )$ and h is zero in $\Gamma \backslash N$ which is non-void; hence h is flat on $\partial N.$ Then $h\equiv 0$ in $\Gamma$ by the WMP. But this is not possible because $e_{k}$ make a basis for ${\mathcal {H}}_{G}(\Gamma ).$ So the system ${\lbrace e_{k}{\mathbb {1}}_{\Gamma \backslash N}\rbrace _{k=1,\ldots ,K_{G}}}$ is a free one.

We set ${\gamma _{jk}:={\left\langle {e_{k}{\mathbb {1}}_{\Gamma \backslash N},e_{j}{\mathbb {1}}_{\Gamma \backslash N}}\right\rangle }}$ and hence we have that $\mathrm {d}\mathrm {e}\mathrm {t}\lbrace \gamma _{jk}\rbrace \ne 0.$ So we can solve the linear system to get $\lbrace \mu _{k}\rbrace$ such that

$$\begin{aligned} {\forall j=1,\ldots ,K_{G},\ \sum _{k=1}^{K_{G}}{\mu _{k}{\left\langle {e_{k}{\mathbb {1}}_{\Gamma \backslash N},e_{j}}\right\rangle }}=\lambda _{j}.} \end{aligned}$$

(4.1)

We put ${\omega ^{\prime \prime }:=\sum _{j=1}^{K_{G}}{\mu _{j}e_{j}{\mathbb {1}}_{\Gamma \backslash N}}}$ and ${\omega ^{\prime }:=\omega {\mathbb {1}}_{N}-\omega ^{\prime \prime }{\mathbb {1}}_{\Gamma \backslash N}=\omega -\omega ^{\prime \prime }}$. From (4.1) we get

$$\begin{aligned} {\displaystyle \forall j=1,\ldots ,K_{G},\ {\left\langle {\omega ^{\prime },e_{j}}\right\rangle }_{\Gamma }={\left\langle {\omega ,e_{j}}\right\rangle }-{\left\langle {\omega ^{\prime \prime },e_{j}}\right\rangle }=\lambda _{j}-\sum _{k=1}^{K_{G}}{\mu _{k}{\left\langle {e_{k}{\mathbb {1}}_{\Gamma \backslash N},e_{j}}\right\rangle }}=0.} \end{aligned}$$

So the G-form $\omega ^{\prime }$ is orthogonal to ${\mathcal {H}}_{G}.$ Moreover $\omega ^{\prime }_{\mid N}=\omega$ and clearly $\omega ^{\prime \prime }\in L^{r}_{G}(\Gamma )$ being a finite combination of ${\displaystyle e_{j}{\mathbb {1}}_{\Gamma \backslash N}}$, so $\omega ^{\prime }\in L^{r}_{G}(\Gamma )$ because $\omega$ itself is in $\displaystyle L^{r}_{G}(\Gamma ).$ The proof is complete. $\square$

Now let $\omega \in L^{r}_{G}(N)$ and see N as a subset of $\Gamma ;$ then extend $\omega$ as $\omega ^{\prime }$ to $\Gamma$ by Lemma 4.2.

By the results on the compact manifold $\Gamma ,$ because $\omega ^{\prime }\perp {\mathcal {H}}_{G}(\Gamma ),$ we get that there exists $u^{\prime }\in W^{m,r}_{G}(\Gamma ),$ such that $Du^{\prime }=\omega ^{\prime };$ hence if u is the restriction of $u^{\prime }$ to N we get $u\in W^{m,r}_{G}(N),\ Du=\omega$ in N.

Hence we proved

Theorem 4.3

Let N be a smooth compact Riemannian manifold with smooth boundary $\partial N.$ Let $\displaystyle \omega \in L^{r}_{G}(N).$ There is a G-form $u\in W^{m,r}_{G}(N),$ such that $Du=\omega$ and ${\left\| {u}\right\| }_{W^{m,r}_{G}(N)}\le c{\left\| {\omega }\right\| }_{L^{r}_{G}(N)},$ provided that the operator D has the WMP for the D-harmonic G-forms.

Remark 4.4

I had the hope that the WMP condition be also necessary, but this is not the case as the Theorem 5.2 shows.

5 Relations with the Local Existence of Solutions

Let (M, g) be a ${\mathcal {C}}^{\infty }$ smooth compact Riemannian manifold without boundary.

Let $D:G\rightarrow G$ be a linear differential operator of order m with ${\mathcal {C}}^{\infty }$ coefficients.

As above we suppose that D is elliptic in the sense of Definition 3.1.

Let $x\in M$ and take a ball $B:=B(x,R).$ We suppose that $\omega \in L_{G}^{2}(B)$ and we want to solve $Du=\omega .$ For this we shall extend $\omega$ as $\omega ^{\prime }\in L^{2}_{G}(M)$ in the whole of M with $\omega ^{\prime }\perp {\mathcal {H}}_{G}(M):=\mathrm {k}\mathrm {e}\mathrm {r}D^{*}$ in order to apply Theorem 3.2.

Consider ${\omega :=\omega {\mathbb {1}}_{B}}$ the trivial extension of $\omega$ to M. We have, with $P_{h}$ the orthogonal projection on ${\mathcal {H}}_{G}(M),\ h:=P_{h}\omega .$ Set $N:=K_{G}$ the finite dimension of $\displaystyle {\mathcal {H}}_{G}(M).$ Take an orthonormal basis $\lbrace e_{1},\ldots ,\ e_{N}\rbrace$ of ${\mathcal {H}}_{G}(M),$ and then we have

$$\begin{aligned} h:=\sum _{j=1}^{N}{h_{j}e_{j}}. \end{aligned}$$

If $h=0,$ we set $\omega ^{\prime }=\omega$ and we are done. If not let the radius R of the ball B be small enough to have

$$\begin{aligned} {\displaystyle {\left\| {e_{1}{\mathbb {1}}_{B}}\right\| }\le \frac{1}{4{\sqrt{N}}},\ ...,\ {\left\| {e_{N}{\mathbb {1}}_{B}}\right\| }\le \frac{1}{4{\sqrt{N}}}.} \end{aligned}$$

This is possible because $e_{j}$ are in ${\mathcal {C}}^{\infty }(M)$ so if B is small enough we have ${\displaystyle {\left\| {e_{j}{\mathbb {1}}_{B}}\right\| }\le \frac{1}{4{\sqrt{N}}}}$, and we have a finite number of such conditions.

We set ${\displaystyle \omega _{1}:={\mathbb {1}}_{B^{c}}\sum _{j=1}^{N}{h_{j}e_{j}}}$. Then

$$\begin{aligned} \displaystyle {\left\| {\omega _{1}}\right\| }^{2}:=\int _{B^{c}}{\left| {\sum _{j=1}^{N}{h_{j}e_{j}}}\right| ^{2}dv\le }\int _{M}{\left| {\sum _{j=1}^{N}{h_{j}e_{j}}}\right| ^{2}dv\le }{\left\| {h}\right\| }^{2} \end{aligned}$$

and

$$\begin{aligned} {\displaystyle {\left\| {h-\omega _{1}}\right\| }\le \sum _{j=1}^{N}{\left| {h_{j}}\right| {\left\| {{\mathbb {1}}_{B}e_{j}}\right\| }}\le \frac{1}{4}\sum _{j=1}^{N}{\left| {h_{j}}\right| }\le {\sqrt{N}}{\left\| {h}\right\| }\frac{1}{4{\sqrt{N}}}=\frac{1}{4}{\left\| {h}\right\| }.} \end{aligned}$$

Hence, because $P_{h}$ has norm one,

$$\begin{aligned} \displaystyle {\left\| {h-P_{h}\omega _{1}}\right\| }={\left\| {P_{h}h-P_{h}\omega _{1}}\right\| }\le {\left\| {h-\omega _{1}}\right\| }\le \frac{1}{4}{\left\| {h}\right\| }. \end{aligned}$$

Now we set $h_{1}:=h-P_{h}\omega _{1}.$ Then ${\left\| {h_{1}}\right\| }\le \frac{1}{4}{\left\| {h}\right\| }$ and we have $\displaystyle h_{1}:=\sum _{j=1}^{N}{h^{1}_{j}e_{j}}.$ So we set ${\omega _{2}:={\mathbb {1}}_{B^{c}}\sum _{j=1}^{N}{h^{1}_{j}e_{j}}}$. We have in the same way:

$$\begin{aligned} \displaystyle {\left\| {\omega _{2}}\right\| }\le {\left\| {h_{1}}\right\| }\le \frac{1}{4}{\left\| {h}\right\| } \hbox { and } \displaystyle {\left\| {h_{1}-P_{h}\omega _{2}}\right\| }\le \frac{1}{4}{\left\| {h_{1}}\right\| }\le \frac{1}{4^{2}}{\left\| {h}\right\| }. \end{aligned}$$

At the step k we get

$$\begin{aligned} \displaystyle {\left\| {h_{k}-P_{h}\omega _{k+1}}\right\| }\le \frac{1}{4}{\left\| {h_{k}}\right\| }\le \frac{1}{4^{k}}{\left\| {h}\right\| } \hbox { and } \displaystyle {\left\| {\omega _{k+1}}\right\| }\le \frac{1}{4^{k}}{\left\| {h}\right\| }. \end{aligned}$$

We set $\omega ^{\prime \prime }:=\sum _{j=1}^{\infty }{\omega _{j}}.$ We get that the series converges in norm $L^{2}(M)$ and $P_{h}\omega ^{\prime \prime }=h.$

Setting $\omega ^{\prime }:=\omega -\omega ^{\prime \prime },$ we get that $\omega ^{\prime }=\omega$ on B and $P_{h}(\omega ^{\prime })=0,$ which means that $\omega ^{\prime }\perp {\mathcal {H}}_{G}(M).$

We can apply Theorem 3.2 to get $Du^{\prime }=\omega ^{\prime }$ with $\displaystyle u^{\prime }\in L^{2}_{G}(M)$ because $\omega ^{\prime }\perp {\mathcal {H}}_{G}.$ We set $u:=u^{\prime }_{\mid B}$ in B to have $Du=\omega$ in B.

So we proved:

Theorem 5.1

Let x in M. There is a $R_{0}(x)>0$ such that for any $0<R\le R_{0}$ if $\displaystyle \omega \in L_{G}^{2}(B)$ with $B:=B(x,R)$ there is a $\displaystyle u\in L_{G}^{2}(B)$ such that $Du=\omega$ and ${\left\| {u}\right\| }_{L_{G}^{2}(B)}\lesssim {\left\| {\omega }\right\| }_{L_{G}^{2}(B)}.$

To get the $\displaystyle L_{G}^{r}(B)$ case for $r>2,$ we proceed as in the proof of Theorem 2.1.

Theorem 5.2

Under the assumptions above, for any $x\in M$ and $r\ge 2,$ there is a positive constant $\displaystyle c_{f}$ such that, if $\omega \in L^{r}(B),$ there is a$\ u\in L^{t}(B^{1})$ with $\displaystyle \frac{1}{t}=\frac{1}{r}-\tau ,$ such that $Du=\omega$ and ${\left\| {u}\right\| }_{L^{t}(B^{1})}\le c_{f}{\left\| {\omega }\right\| }_{L^{r}(B)}.$

Moreover we have $u\in W_{G}^{m,r}(B^{1})$ with control of the norm.

Proof

Let $r\ge 2$ and $\displaystyle \omega \in L^{r}_{G}(B).$ Because B is relatively compact and dv is $\sigma$-finite, we have that $\displaystyle \omega \in L^{2}_{G}(B).$ Theorem 5.1 gives that there is a $u\in L^{2}_{G}(B)$ such that $Du=\omega .$ Now we proceed exactly as in the proof of Theorem 2.1, using the same induction procedure. $\square$

So we proved the local existence of solutions with estimates; this is an already known theorem in ${\mathbb {R}}^{n},$ hence also locally in M (see for instance [11]). This means also that the LIR condition is stronger than the local existence of solutions with estimates. These solutions were the basis of Raising Steps Method, see [5].

6 The Non-compact Case

We shall use the same ideas as in [5] to go from the compact case to the non-compact one.

In order to deal with G-forms in the non-compact case, we have to warranty that the bundle G has trivializing charts defined on balls of the covering ${\mathcal {C}}_{\epsilon }.$

Definition 6.1

We say that the bundle $\displaystyle G:=(H,\pi ,M)$ is compatible with the covering ${\mathcal {C}}_{\epsilon }$ if there is a $\epsilon >0$ such that, for any ball $B\in {\mathcal {C}}_{\epsilon },$ the chart $(B,\varphi )$ is a trivializing map of the bundle G. Precisely this means that $G\simeq \varphi (B){\times }{\mathbb {R}}^{N}$ where N is the dimension of H and the equivalence has bounds independent of $\displaystyle B\in {\mathcal {C}}_{\epsilon }.$

Example 6.2

The bundle of p-forms in a Riemannian manifold (M, g) is compatible. To see this take a ball $B(x,R)\in {\mathcal {C}}_{\epsilon },$ and then we have that $\displaystyle (1-\epsilon )\delta _{ij}\le g_{ij}\le (1+\epsilon )\delta _{ij}$ in $\displaystyle B(x,R)$ as bilinear forms, so, because $\epsilon <1,$ the 1-forms $dx_{j},\ j=1,\ldots ,n$ are “almost” orthonormal and hence linearly independent. This gives that the cotangent bundle $T^{*}M$ is equivalent to $T^{*}{\mathbb {R}}^{n}$ over B,  the constants depending only on $\epsilon .$

By tensorization we get the same for the bundle of p-forms.

From now on we shall always suppose that the bundle $\displaystyle G:=(H,\pi ,M)$ is compatible with the covering ${\mathcal {C}}_{\epsilon }.$

In Sect. 7.1 we define a Vitali type covering ${\mathcal {C}}_{\epsilon }$ by balls suited to our “admissible balls” (see Definition 1.5). We use these notions now.

Definition 6.3

We shall say that the hypothesis (UEAB) is fulfilled for the operator D if D has smooth ${\mathcal {C}}^{1}(M)$ coefficients.

Moreover we ask that D be uniformly elliptic as in Definition 3.1.

We start with $\omega \text {in} L^{2}_{G}(M),$ by the (THL2p) hypothesis, provided that $\omega \perp \mathrm {k}\mathrm {e}\mathrm {r}D^{*},$ there is a G-form $u\in L^{2}_{G}(M)$ such that $Du=\omega .$ Moreover, because $\displaystyle L^{2}_{G}(M)$ is a Hilbert space, $u\in L^{2}_{G}(M),\ Du=\omega$ with the smallest norm, is given linearly with respect to $\omega .$ This means that we have a bounded linear operator $\displaystyle S:\ L^{2}_{G}(M)\rightarrow L^{2}_{G}(M)$ such that $D(S\omega )=\omega$ provided that $\displaystyle \omega \perp \mathrm {k}\mathrm {e}\mathrm {r}D^{*}.$

The local elliptic inequalities by Theorem 3.5 become uniform by the hypothesis (UEAB):

Corollary 6.4

Let D be an operator of order m acting on sections of G in the complete Riemannian manifold M. Suppose that D verifies (UEAB). Then, for any $B_{x}:=B(x,R)\in {\mathcal {C}}_{\epsilon }$ and $\displaystyle B^{1}_{x}:=B(x,R/2),$ we have, with D with ${\mathcal {C}}^{1}(M)$ coefficients:

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{m,r}_{G}(B^{1}_{x})}\le c_{1}{\left\| {Du}\right\| }_{L^{r}_{G}(B_{x})}+c_{2}R^{-m}{\left\| {u}\right\| }_{L^{r}_{G}(B_{x})}. \end{aligned}$$

The hypotheses (UEAB) are precisely done to warranty that the constants $c_{1},c_{2}$ depend only on $n=\mathrm {d}\mathrm {i}\mathrm {m}_{{\mathbb {R}}}M,\ r$ and $\epsilon .$

With $\displaystyle t=S_{m}(r),$ we get, by Lemma 7.7 from the Appendix,

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{L^{t}_{G}(B(x,R))}\le CR^{-m}\ {\left\| {u}\right\| }_{W^{m,r}_{G}(B(x,R))}. \end{aligned}$$

When there is no ambiguity we shall omit the subscript G,  i.e., $\displaystyle L^{2}_{G}(B)$ becomes $\displaystyle L^{2}(B),$ etc.

Lemma 6.5

We have, with $B^{l}:=B(x,2^{-l}R)$ and $t_{0}=2,\ B^{0}=B(x,R),$ the a priori estimates:

$$\begin{aligned} \displaystyle R^{(l+1)m}{\left\| {u}\right\| }_{L^{t_{l}}(B^{l})}\le \sum _{j=1}^{l}{c_{j}R^{(l-j+1)m}{\left\| {Du}\right\| }_{L^{l-j}(B^{l-j})}}+c_{l+1}{\left\| {u}\right\| }_{L^{2}(B)} \end{aligned}$$

and

$$\begin{aligned} \displaystyle R^{(l+2)m}{\left\| {u}\right\| }_{W^{m,t_{l}}(B^{l+1})}\le & {} c_{0}R^{(l+2)m}{\left\| {Du}\right\| }_{L^{t_{l}}(B^{l})}\\&+\sum _{j=1}^{l}{c_{j}R^{(l-j+1)m}{\left\| {Du}\right\| }_{L^{t_{l-j}}(B^{l-j})}}+c_{l+1}{\left\| {u}\right\| }_{L^{2}(B)}. \end{aligned}$$

Proof

From the LIR, Theorem 3.5, we have

$$\begin{aligned} \displaystyle \forall B\in {\mathcal {C}}_{\epsilon },\ {\left\| {u}\right\| }_{W^{m,2}(B^{1})}\le c_{1}{\left\| {D(u)}\right\| }_{L^{2}(B)}+c_{2}R^{-m}{\left\| {u}\right\| }_{L^{2}(B)}. \end{aligned}$$

Now we shall use the local Sobolev embedding theorem, Lemma 7.7, to get

$$\begin{aligned} \displaystyle \forall B\in {\mathcal {C}}_{\epsilon },\ {\left\| {u}\right\| }_{L^{t_{1}}(B^{1})}\le CR^{-m}{\left\| {u}\right\| }_{W^{m,2}(B)} \end{aligned}$$

so we get

$$\begin{aligned} \forall B\in {\mathcal {C}}_{\epsilon },\ {\left\| {u}\right\| }_{L^{t_{1}}(B^{1})}\le c_{1}R^{-m}{\left\| {Du}\right\| }_{L^{2}(B)}+c_{2}R^{-2m}{\left\| {u}\right\| }_{L^{2}(B)} \end{aligned}$$

with $\frac{1}{t_{1}}:=\frac{1}{2}-\frac{m}{n}\iff t_{1}:=S_{m}(2).$

• If $t_{1}\ge r,$ then we get still by the LIR, Theorem 3.5:

$$\begin{aligned} \forall B\in {\mathcal {C}}_{\epsilon },\ {\left\| {u}\right\| }_{W^{m,t_{1}}(B^{2})}\le c_{1}{\left\| {Du}\right\| }_{L^{t_{1}}(B^{1})}+c_{2}R^{-m}{\left\| {u}\right\| }_{L^{t_{1}}(B^{1})}. \end{aligned}$$

(6.1)

Putting the estimate of $\displaystyle {\left\| {u}\right\| }_{L^{t_{1}}(B^{1})}$ in (6.1) we get

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{m,t_{1}}(B^{2})}\le c_{1}{\left\| {Du}\right\| }_{L^{t_{1}}(B^{1})}+c_{2}R^{-m}{\left( {c_{1}{\left\| {Du}\right\| }_{L^{2}(B)}+c_{2}R^{-m}{\left\| {u}\right\| }_{L^{2}(B)}}\right) } \end{aligned}$$

so, with suitable constants

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{m,t_{1}}(B^{2})}\le c_{1}{\left\| {Du}\right\| }_{L^{t_{1}}(B^{1})}+c_{2}R^{-m}{\left\| {Du}\right\| }_{L^{2}(B)}+c_{3}R^{-2m}{\left\| {u}\right\| }_{L^{2}(B)}. \end{aligned}$$

Putting the powers of R on the other side to isolate $\displaystyle {\left\| {u}\right\| }_{L^{2}(B)},$ we get

$$\begin{aligned} \displaystyle R^{2m}{\left\| {u}\right\| }_{W^{m,t_{1}}(B^{2})}\le c_{1}R^{2m}{\left\| {Du}\right\| }_{L^{t_{1}}(B^{1})}+c_{2}R^{m}{\left\| {Du}\right\| }_{L^{2}(B)}+c_{3}{\left\| {u}\right\| }_{L^{2}(B)}. \end{aligned}$$

We iterate, using again the local Sobolev embedding theorem, Lemma 7.7,

$$\begin{aligned} \displaystyle u\in L^{t_{2}}(B^{2}),\ {\left\| {u}\right\| }_{L^{t_{2}}(B^{2})}\le cR^{-m}{\left\| {u}\right\| }_{W^{m,t_{1}}(B^{2})}, \end{aligned}$$

and hence

$$\begin{aligned} \displaystyle R^{3m}{\left\| {u}\right\| }_{L^{t_{2}}(B^{2})}\le c_{1}R^{2m}{\left\| {Du}\right\| }_{L^{t_{1}}(B^{1})}+c_{2}R^{m}{\left\| {Du}\right\| }_{L^{2}(B)}+c_{3}{\left\| {u}\right\| }_{L^{2}(B)}. \end{aligned}$$

with $\displaystyle \frac{1}{t_{2}}:=\frac{1}{t_{1}}-\frac{m}{n}=\frac{1}{2}-\frac{2m}{n}\iff t_{2}:=S_{2m}(2).$ The LIR gives again:

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{m,t_{2}}(B^{3})}\le c_{1}{\left\| {Du}\right\| }_{L^{t_{2}}(B^{2})}+c_{2}R^{-m}{\left\| {u}\right\| }_{L^{t_{2}}(B^{2})} \end{aligned}$$

so

$$\begin{aligned} \displaystyle R^{4m}{\left\| {u}\right\| }_{W^{m,t_{2}}(B^{3})}\le c_{1}R^{4m}{\left\| {Du}\right\| }_{L^{t_{2}}(B^{2})}+c_{2}R^{3m}{\left\| {u}\right\| }_{L^{t_{2}}(B^{2})}, \end{aligned}$$

and hence

$$\begin{aligned} \displaystyle R^{4m}{\left\| {u}\right\| }_{W^{m,t_{2}}(B^{3})}\le & {} c_{1}R^{4m}{\left\| {Du}\right\| }_{L^{t_{2}}(B^{2})}\\&+\,c_{2}R^{2m}{\left\| {Du}\right\| }_{L^{t_{1}}(B^{1})}+c_{3}R^{m}{\left\| {Du}\right\| }_{L^{2}(B)}+c_{4}{\left\| {u}\right\| }_{L^{2}(B)}. \end{aligned}$$

Iterating the same way we get

$$\begin{aligned} \displaystyle R^{(l+1)m}{\left\| {u}\right\| }_{L^{t_{l}}(B^{l})}\le & {} c_{1}R^{lm}{\left\| {Du}\right\| }_{L^{t_{l-1}}(B^{l-1})}+c_{2}R^{(l-1)m}{\left\| {Du}\right\| }_{L^{t_{(l-2)}}(B^{(l-2)})}+\cdot \cdot \cdot \\&\displaystyle +\,c_{l}R^{m}{\left\| {Du}\right\| }_{L^{2}(B)}+c_{l+1}{\left\| {u}\right\| }_{L^{2}(B)}, \end{aligned}$$

which gives, using the LIR,

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{m,t_{l}}(B^{l+1})}\le c_{1}{\left\| {Du}\right\| }_{L^{t_{l}}(B^{l})}+c_{2}R^{-m}{\left\| {u}\right\| }_{L^{t_{l}}(B^{l})} \end{aligned}$$

so

$$\begin{aligned} \displaystyle R^{(l+2)m}{\left\| {u}\right\| }_{W^{m,t_{l}}(B^{l+1})}\le c_{1}R^{(l+2)m}{\left\| {Du}\right\| }_{L^{t_{l}}(B^{l})}+c_{2}R^{(l+1)m}{\left\| {u}\right\| }_{L^{t_{l}}(B^{l})} \end{aligned}$$

and

$$\begin{aligned} \displaystyle R^{(l+2)m}{\left\| {u}\right\| }_{W^{m,t_{l}}(B^{l+1})}\le & {} c_{1}R^{(l+2)m}{\left\| {Du}\right\| }_{L^{t_{l}}(B^{l})}+c_{2}R^{lm}{\left\| {Du}\right\| }_{L^{t_{(l-1)}}(B^{(l-1)})}\\&\displaystyle +\,c_{3}R^{(l-1)m}{\left\| {Du}\right\| }_{L^{t_{(l-2)}}(B^{(l-2)})}+\cdot \cdot \cdot +c_{l}R^{m}{\left\| {Du}\right\| }_{L^{2}(B)}\\&+\,c_{l+1}{\left\| {u}\right\| }_{L^{2}(B)}, \end{aligned}$$

which proves the lemma. $\square$

Lemma 6.6

We have for $r<t,\ B:=B(x,R),$

$$\begin{aligned} \displaystyle \forall f\in L^{r}(B),\ {\left\| {f}\right\| }_{L^{r}(B)}\le R^{\frac{1}{r}-\frac{1}{t}}{\left\| {f}\right\| }_{L^{t}(B)}. \end{aligned}$$

Proof

Because the measure ${\displaystyle d\mu (x):=\frac{{\mathbb {1}}_{B}(x)}{\left| {B}\right| }dm(x)}$ is a probability measure, using that $r<t,$ we have ${\left\| {f}\right\| }_{L^{r}(\mu )}\le {\left\| {f}\right\| }_{L^{t}(\mu )}$ which implies readily the lemma. $\square$

Corollary 6.7

Let $\forall j\in {\mathbb {N}},\ \frac{1}{t_{j}}=\frac{1}{2}-\frac{jm}{n}.$ Fix $r\ge 2,$ we have, for $t_{l-1}<r<t_{l},$

$$\begin{aligned} \displaystyle R^{\left( \frac{1}{t_{l}}-\frac{1}{r}\right) +(l+1)m}{\left\| {u}\right\| }_{L^{r}(B^{l})}\le \sum _{j=1}^{l}{c_{j}R^{(l-j+1)m}{\left\| {Du}\right\| }_{L^{l-j}(B^{l-j})}}+c_{l+1}{\left\| {u}\right\| }_{L^{2}(B)}. \end{aligned}$$

Proof

By Lemma 6.6 we get $\displaystyle {\left\| {u}\right\| }_{L^{r}(B^{l})}\le R^{\frac{1}{r}-\frac{1}{t_{l}}}{\left\| {u}\right\| }_{L^{t}(B^{l})}$ so by Lemma 6.5 we have

$$\begin{aligned} \displaystyle R^{(l+1)m}{\left\| {u}\right\| }_{L^{r}(B^{l})}\le & {} R^{\frac{1}{r}-\frac{1}{t_{l}}}{\left\| {u}\right\| }_{L^{t}(B^{l})}\\\le & {} R^{\frac{1}{r}-\frac{1}{t_{l}}}\sum _{j=1}^{l}{c_{j}R^{(l-j+1)m}{\left\| {Du}\right\| }_{L^{l-j}(B^{l-j})}}+c_{l+1}R^{\frac{1}{r}-\frac{1}{t_{l}}}{\left\| {u}\right\| }_{L^{2}(B)}. \end{aligned}$$

Isolating $\displaystyle {\left\| {u}\right\| }_{L^{2}(B)}$ we get

$$\begin{aligned} \displaystyle R^{\left( \frac{1}{t_{l}}-\frac{1}{r}\right) +(l+1)m}{\left\| {u}\right\| }_{L^{r}(B^{l})}\le \sum _{j=1}^{l}{c_{j}R^{(l-j+1)m}{\left\| {Du}\right\| }_{L^{l-j}(B^{l-j})}}+c_{l+1}{\left\| {u}\right\| }_{L^{2}(B)}. \end{aligned}$$

Now we have a finite number of terms, so changing the values of the constants, we get

$$\begin{aligned} \displaystyle R^{\left( \frac{r}{t_{l}}-1\right) +(l+1)mr}{\left\| {u}\right\| }_{L^{r}(B^{l})}^{r}\le \sum _{j=1}^{l}{c_{j}R^{(l-j+1)mr}{\left\| {Du}\right\| }_{L^{l-j}(B^{l-j})}^{r}}+c_{l+1}{\left\| {u}\right\| }_{L^{2}(B)}^{r}. \end{aligned}$$

which ends the proof of the corollary. $\square$

We shall use the following weights, with $t_{j}:=S_{jm}(2)\, i.e.,\ \frac{1}{t_{j}}=\frac{1}{2}-\frac{jm}{n}:$

$$\begin{aligned} \displaystyle t_{l-1}<r<t_{l},\ v_{r}(x):=R(x)^{\left( \frac{1}{t_{l}}-\frac{1}{r}\right) +(l+1)m},\ w_{j}(x)=R^{(l+1-j)m} \end{aligned}$$

and we set

$$\begin{aligned} \displaystyle {\left\| {\omega }\right\| }_{L^{t_{l-j}}(M,w_{j}^{t_{l-j}})}^{t_{l-j}}:=\int _{M}{\left| {\omega (x)}\right| ^{t_{l-j}}w_{j}(x)^{t_{l-j}}dv(x)}. \end{aligned}$$

Theorem 6.8

Under hypotheses (THL2G) and (UEAB), with the weights defined above, we have, provided that $\displaystyle \omega \perp \mathrm {k}\mathrm {e}\mathrm {r}D^{*},$ that there is a $u:=S\omega$ linearly given from $\omega$ such that $\displaystyle Du=\omega$ and

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{L^{r}_{G}(M,v_{r}^{r})}\le \sum _{j=1}^{l}{c_{j}{\left\| {\omega }\right\| }_{L^{t_{l-j}}_{G}(M,w_{j}^{t_{l-j}})}}+c_{l+1}{\left\| {\omega }\right\| }_{L^{2}_{G}(M)}. \end{aligned}$$

Proof

By hypothesis (THL2G) for $\omega \in L^{2}_{G}(M)$ with $\displaystyle \omega \perp \mathrm {k}\mathrm {e}\mathrm {r}D^{*}$ we set $u:=S\omega \in L^{2}_{G}(M).$

We have, with hypothesis (UEAB) and using the covering of M by the $B^{l},$ hence a fortiori by the $B^{j},\ j<l,$

$$\begin{aligned} {\left\| { u}\right\| }_{L^{r}(M,v_{r}^{r})}^{r}\le \sum _{B\in {\mathcal {C}}_{\epsilon }}{R^{\left( \frac{1}{t_{l}}-\frac{1}{r}\right) +(l+1)mr}{\left\| {u}\right\| }_{L^{r}(B^{l})}^{r}}. \end{aligned}$$

(6.2)

Using that the overlap of the covering is bounded by T, 

$$\begin{aligned} \sum _{ B\in {\mathcal {C}}_{\epsilon }}{R^{(l+1-j)mt_{l-j}}{\left\| {\omega }\right\| }_{L^{t_{(l-j)}}(B^{l-j})}^{t_{l-j}}}\le T{\left\| {\omega }\right\| }_{L^{t_{l-j}}(M,w_{j}^{t_{l-j}})}^{t_{l-j}} \end{aligned}$$

(6.3)

with $\displaystyle w_{j}(x)=w_{j,l}(x)=R^{(l+1-j)m},$ and for any $\gamma ,\ {\left\| {\gamma }\right\| }_{L^{s}(M,w_{k}^{s})}^{s}:=\int _{M}{\left| {\gamma (x)w_{k}(x)}\right| ^{s}dv(x)}.$

Now if $r\ge t_{l-1}\ge t_{l-j},\ j\le l-1,$ we have $\sum _{j\in {\mathbb {N}}}{a_{j}^{r}}\le {\left( {\sum _{j\in {\mathbb {N}}}{a_{j}^{t_{l-j}}}}\right) }^{r/t_{l-j}},$ so

$$\begin{aligned} \displaystyle \sum _{B\in {\mathcal {C}}_{\epsilon }}{R^{(l+1-j)mr}{\left\| {\omega }\right\| }_{L^{t_{(l-j)}}(B^{l-j})}^{r}}\le {\left( {\sum _{B\in {\mathcal {C}}_{\epsilon }}{R^{(l+1-j)mt_{l-j}}{\left\| {\omega }\right\| }_{L^{t_{(l-j)}}(B^{l-j})}^{t_{l-j}}}}\right) }^{r/t_{l-j}}. \end{aligned}$$

Using (6.3) we get

$$\begin{aligned} \displaystyle \sum _{B\in {\mathcal {C}}_{\epsilon }}{R^{(l+1-j)mr}{\left\| {\omega }\right\| }_{L^{t_{(l-j)}}(B^{l-j})}^{r}}\le T^{r/t_{l-j}}{\left\| {\omega }\right\| }_{L^{t_{l-j}}(M,w_{j}^{t_{l-j}})}^{r}. \end{aligned}$$

Grouping with (6.2) we deduce

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{L^{r}(M,v_{r}^{r})}^{r}\le \sum _{j=1}^{l}{c_{j}T^{r/t_{l-j}}{\left\| {\omega }\right\| }_{L^{t_{l-j}}(M,w_{j}^{t_{l-j}})}^{r}}+c_{l+1}{\left\| {u}\right\| }_{L^{2}(M)}^{r}. \end{aligned}$$

Changing the constants, we take the r root to get, using the hypothesis (THL2G), which says also that $\displaystyle {\left\| {u}\right\| }_{L^{2}(M)}\le c{\left\| {\omega }\right\| }_{L^{2}(M)},$

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{L^{r}(M,v_{r}^{r})}\le \sum _{j=1}^{l}{c_{j}{\left\| {\omega }\right\| }_{L^{t_{l-j}}(M,w_{j}^{t_{l-j}})}}+c_{l+1}{\left\| {\omega }\right\| }_{L^{2}(M)}. \end{aligned}$$

The proof is complete. $\square$

Lemma 6.9

Provided that $\displaystyle \omega \in L^{2}(M)\cap L^{t_{k}}(M,R(x)^{\alpha _{k}}),$ with

$$\begin{aligned} \displaystyle \alpha _{j}:=\frac{k+1}{k}m{\times }jt_{j},\ \beta _{j}:=(j+1)m{\times }t_{j}, \end{aligned}$$

we have

$$\begin{aligned} \displaystyle \forall j\le k,\ \omega \in L^{t_{j}}(M,R^{\beta _{j}}),\ {\left\| {\omega }\right\| }_{L^{t_{j}}(M,R^{\beta _{j}})}\le C\max ({\left\| {\omega }\right\| }_{L^{t_{k}}(M,R^{\alpha _{k}})},\ {\left\| {\omega }\right\| }_{L^{2}(M)}). \end{aligned}$$

Proof

Recall the Stein-Weiss interpolation Theorem  [8, Theorem 5.5.1, p. 110]

$$\begin{aligned}&{\left( {L^{s_{0}}(v_{0}),L^{s_{1}}(v_{1})}\right) }_{\theta ,t}=L^{s}(v),\ 0<\theta <1 \hbox { where } v:=v_{0}^{s(1-\theta )/s_{0}}v_{1}^{s\theta /s_{1}}, \\&\qquad \frac{1}{s}=\frac{1-\theta }{s_{0}}+\frac{\theta }{s_{1}}. \end{aligned}$$

We choose $s_{0}=2,\ v_{0}=1\ ;\ s_{1}=t_{k}=S_{km}(2),\ s=t_{j}=S_{jm}(2),$ so $\frac{1}{t_{k}}=\frac{1}{2}-\frac{km}{n},\ \frac{1}{t_{j}}=\frac{1}{2}-\frac{jm}{n}.$ This fixes $\theta$:

$$\begin{aligned} \displaystyle \frac{1}{s}=\frac{1}{t_{j}}=\frac{1}{2}-\frac{jm}{n}=(1-\theta )\frac{1}{2}+\theta \left( \frac{1}{2}-\frac{km}{n}\right) \Rightarrow \theta =\frac{j}{k}. \end{aligned}$$

Replacing $v_{0}=w_{1}^{2}=1,\ v_{1}=w_{2}^{s_{1}}=R(x)^{(k+1)m{\times }t_{k}}$ and using $\displaystyle v:=v_{0}^{s(1-\theta )/s_{0}}v_{1}^{s\theta /s_{1}}$ we get

$$\begin{aligned} v=v_{1}^{\frac{s}{s_{1}}{\times }\frac{j}{k}}\Rightarrow \frac{s}{s_{1}}{\times }\frac{j}{k}=\frac{t_{j}}{t_{k}}{\times }\frac{j}{k}\Rightarrow v=R(x)^{(k+1)m{\times }t_{k}{\times }\frac{t_{j}}{t_{k}}{\times }\frac{j}{k}}=R(x)^{\frac{k+1}{k}m{\times }jt_{j}}. \end{aligned}$$

So, because the function $\frac{x+1}{x}$ is decreasing, we get $\frac{k+1}{k}\le \frac{j+1}{j}$ for $j\le k$ so, $R(x)\le 1\Rightarrow R(x)^{\alpha _{j}}\ge R(x)^{\beta _{j}}$ with $\alpha _{j}:=\frac{k+1}{k}m{\times }jt_{j},\ \beta _{j}:=(j+1)m{\times }t_{j}$ and $\alpha _{j}\le \beta _{j}.$

Using this we get

$$\begin{aligned} {\left\| { \omega }\right\| }_{L^{t_{j}}(M,R^{\beta _{j}})}\le {\left\| {\omega }\right\| }_{L^{t_{j}}(M,R^{\alpha _{j}})}. \end{aligned}$$

(6.4)

By interpolation we have that $\omega \in L^{2}(M)\cap L^{t_{k}}(M,R^{\alpha _{k}})\Rightarrow \omega \in L^{t_{j}}(M,R^{\alpha _{j}}),$ with

$$\begin{aligned} \displaystyle {\left\| {\omega }\right\| }_{L^{t_{j}}(M,R^{\alpha _{j}})}\le C\max ({\left\| {\omega }\right\| }_{L^{t_{k}}(M,R^{\alpha _{k}})},\ {\left\| {\omega }\right\| }_{L^{2}(M)}). \end{aligned}$$

Now using (6.4) we get

$$\begin{aligned} \displaystyle \forall j\le k,\ \omega \in L^{t_{j}}(M,R^{\beta _{j}}),\ {\left\| {\omega }\right\| }_{L^{t_{j}}(M,R^{\beta _{j}})}\le C\max ({\left\| {\omega }\right\| }_{L^{t_{k}}(M,R^{\alpha _{k}})},\ {\left\| {\omega }\right\| }_{L^{2}(M)}). \end{aligned}$$

This proves the lemma. $\square$

Corollary 6.10

Let $\forall j\in {\mathbb {N}},\ \frac{1}{t_{j}}=\frac{1}{2}-\frac{jm}{n}.$ With $\displaystyle w_{1}(x)=w_{1,l}(x)=R^{lm},$ fix $r\ge 2,$ we have, provided that $\displaystyle \omega \in L^{2}(M)\cap L^{t_{l-1}}(M,w_{1}^{t_{l-1}}),\ t_{l-1}\le r<t_{l},$ and that $\displaystyle \omega \perp \mathrm {k}\mathrm {e}\mathrm {r}D^{*},$ with $u:=S\omega \Rightarrow Du=\omega ,$

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{L^{r}(M,v_{r}^{r})}\le C\max ({\left\| {\omega }\right\| }_{L^{t_{l-1}}(M,w_{1}^{t_{l-1}})},{\left\| {\omega }\right\| }_{L^{2}(M)}). \end{aligned}$$

Proof

Clear. $\square$

To get an estimate for $\displaystyle {\left\| {u}\right\| }_{W^{m,r}(B)}$ we use again the LIR, Theorem 3.5:

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{m,t_{l}}(B^{l+1})}\le c_{1}{\left\| {Du}\right\| }_{L^{t_{l}}(B^{l})}+c_{2}R^{-m}{\left\| {u}\right\| }_{L^{t_{l}}(B^{l})}. \end{aligned}$$

Replacing $\displaystyle {\left\| {u}\right\| }_{L^{t_{l}}(B^{l})}$ by the use of Corollary 6.7, we get

$$\begin{aligned} \displaystyle R^{\left( \frac{1}{t_{l}}-\frac{1}{r}\right) +(l+2)m}{\left\| {u}\right\| }_{W^{m,r}(B^{l+1})}\le & {} c_{1}R^{\left( \frac{1}{t_{l}}-\frac{1}{r}\right) +(l+2)m}{\left\| {\omega }\right\| }_{L^{t_{l}}(B^{l})}\\&+\,c_{2}R^{\left( \frac{1}{t_{l}}-\frac{1}{r}\right) +(l+1)m}{\left\| {u}\right\| }_{L^{t_{l}}(B^{l})}, \end{aligned}$$

so

$$\begin{aligned} \displaystyle R^{\left( \frac{1}{t_{l}}-\frac{1}{r}\right) +(l+2)m}{\left\| {u}\right\| }_{W^{m,r}(B^{l+1})}\le & {} c_{1}R^{\left( \frac{1}{t_{l}}-\frac{1}{r}\right) +(l+2)m}{\left\| {\omega }\right\| }_{L^{t_{l}}(B^{l})}\\&\displaystyle +\sum _{j=1}^{l}{c_{j}R^{(l-j+1)m}{\left\| {\omega }\right\| }_{L^{l-j}(B^{l-j})}}+c_{l+1}{\left\| {u}\right\| }_{L^{2}(B)}. \end{aligned}$$

Now we cover the manifold M the same way as for the proof of Lemma 6.9 and we prove, with $\displaystyle v_{r}^{\prime }(x):=R(x)^{(\frac{r}{t_{l}}-\mathrm {1})+(l+2)mr}$ and $\displaystyle w_{j}(x)=w_{j,l}(x)=R^{(l+1-j)m},$

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{m,r}(M,v^{\prime }_{r})}\le c_{1}{\left\| {\omega }\right\| }_{L^{t_{l}}(M,v^{\prime }_{r})}+\sum _{j=1}^{l}{c_{j}{\left\| {\omega }\right\| }_{L^{t_{l-j}}(M,w_{j}^{t_{l-j}})}}+c_{l+1}{\left\| {\omega }\right\| }_{L^{2}(M)}. \end{aligned}$$

Using again Lemma 6.9, we end with

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{m,r}(M,v^{\prime }_{r})}\le c_{1}{\left\| {\omega }\right\| }_{L^{t_{l}}(M,v^{\prime }_{r})}+c_{2}\max ({\left\| {\omega }\right\| }_{L^{t_{l-1}}(M,w_{1}^{t_{l-1}})},{\left\| {\omega }\right\| }_{L^{2}(M)}). \end{aligned}$$

So we proved, using the weights: $\displaystyle v_{r}^{\prime }(x):=R(x)^{(\frac{r}{t_{l}}-1)+(l+2)mr},\ w_{1}^{\prime }(x)=R^{lmt_{l-1}},$ the following result:

Theorem 6.11

Under hypotheses (THL2G) and (UEAB), let $\forall j\in {\mathbb {N}},\ \frac{1}{t_{j}}=\frac{1}{2}-\frac{jm}{n}$ and fix $r\ge 2$ and l such that $\displaystyle t_{l-1}\le r<t_{l}.$ Provided that $\displaystyle \omega \perp \mathrm {k}\mathrm {e}\mathrm {r}D^{*}$ we get that $u:=S\omega \Rightarrow Du=\omega$ verifies

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{m,r}_{G}(M,v^{\prime }_{r})}\le c_{1}{\left\| {\omega }\right\| }_{L^{t_{l}}_{G}(M,v^{\prime }_{r})}+c_{2}\max ({\left\| {\omega }\right\| }_{L^{t_{l-1}}_{G}(M,w_{1}^{\prime })},{\left\| {\omega }\right\| }_{L^{2}_{G}(M)}). \end{aligned}$$

Remark 6.12

We always ask that $t_{l-1}<\infty$ to have $\displaystyle r<\infty ,$ because $t_{l-1}\le r<t_{l},$ and this implies that $2(l-1)m<n.$ This condition in turn implies that $\displaystyle (\frac{r}{t_{l}}-1)+(l+2)mr\ge 0.$ So, if the admissible radius R(x) is uniformly bounded below, we can forget the weights and we get, with the same hypotheses,

$$\begin{aligned} \displaystyle {\left\| {u}\right\| }_{W^{m,r}_{G}(M)}\le c_{1}{\left\| {\omega }\right\| }_{L^{t_{l}}_{G}(M)}+c_{2}\max ({\left\| {\omega }\right\| }_{L^{t_{l-1}}_{G}(M)},{\left\| {\omega }\right\| }_{L^{2}_{G}(M)}). \end{aligned}$$

Appendix

We shall use the following lemma.

Lemma 7.1

Let (M, g) be a Riemannian manifold; then with $\displaystyle R(x)=R_{\epsilon }(x)=$ the $\epsilon$ admissible radius at $\displaystyle x\in M$ and $\displaystyle d(x,y)$ the Riemannian distance on $\displaystyle (M,g)$ we get

$$\begin{aligned} \displaystyle d(x,y)\le \frac{1}{4}(R(x)+R(y))\Rightarrow R(x)\le 4R(y). \end{aligned}$$

Proof

Let $\displaystyle x,y\in M::d(x,y)\le \frac{1}{4}(R(x)+R(y))$ and suppose for instance that $\displaystyle R(x)\ge R(y).$ Then $\displaystyle y\in B(x,R(x)/2)$ and hence we have $\displaystyle B(y,R(x)/4)\subset B(x,\frac{3}{4}R(x)).$ But by the definition of $\displaystyle R(x),$ the ball $\displaystyle B(x,\frac{3}{4}R(x))$ is admissible and this implies that the ball $\displaystyle B(y,R(x)/4)$ is also admissible for exactly the same constants and the same chart; this implies that $\displaystyle R(y)\ge R(x)/4.$$\square$

1.1 Vitali Covering 

Lemma 7.2

Let ${\mathcal {F}}$ be a collection of balls $\lbrace B(x,r(x))\rbrace$ in a metric space, with $\forall B(x,r(x))\in {\mathcal {F}},\ 0<r(x)\le R.$ There exists a disjoint subcollection ${\mathcal {G}}$ of ${\mathcal {F}}$ with the following property: every ball B in ${\mathcal {F}}$ intersects a ball C in ${\mathcal {G}}$ and $\displaystyle B\subset 5C.$

This is a well-known lemma, see for instance  [13], Section 1.5.1.

Fix $\epsilon >0$ and let $\displaystyle \forall x\in M,\ r(x):=R_{\epsilon }(x)/120,\$where $\displaystyle R_{\epsilon }(x)$ is the admissible radius at $\displaystyle x,$ and we built a Vitali covering with the collection ${\mathcal {F}}:=\lbrace B(x,r(x))\rbrace _{x\in M}.$ The previous lemma gives a disjoint subcollection ${\mathcal {G}}$ such that every ball B in ${\mathcal {F}}$ intersects a ball C in ${\mathcal {G}}$ and we have $\displaystyle B\subset 5C.$ We set ${\mathcal {G}}^{\prime }:=\lbrace x_{j}\in M::B(x_{j},r(x_{j}))\in {\mathcal {G}}\rbrace$ and ${\mathcal {C}}_{\epsilon }:=\lbrace B(x,5r(x)),\ x\in {\mathcal {G}}^{\prime }\rbrace .$ We shall call ${\mathcal {C}}_{\epsilon }$ the $m,\epsilon$admissible covering of $\displaystyle (M,g).$

We shall fix $m\ge 2$ and we omit it in order to ease the notation.

Recall that $\epsilon <1,$ then we have:

Proposition 7.3

Let (M, g) be a Riemannian manifold. The overlap of the $\epsilon$ admissible covering ${\mathcal {C}}_{\epsilon }$ is less than $\displaystyle T=\frac{(1+\epsilon )^{n/2}}{(1-\epsilon )^{n/2}}(120)^{n},$ i.e.,

$$\begin{aligned} \forall x\in M,\ x\in B(y,5r(y)) \end{aligned}$$

for at most T such balls, where $B(y,r(y))\in {\mathcal {G}}.$

So we have

$$\begin{aligned} \forall f\in L^{1}(M),\ \sum _{j\in {\mathbb {N}}}{\int _{B_{j}}{\left| {f(x)}\right| dv_{g}(x)}}\le T{\left\| {f}\right\| }_{L^{1}(M)}. \end{aligned}$$

Proof

Let $B_{j}:=B(x_{j},r(x_{j}))\in {\mathcal {G}}$ and suppose that $\displaystyle x\in \bigcap _{j=1}^{k}{B(x_{j},5r(x_{j}))}.$ Then we have

$$\begin{aligned} \displaystyle \forall j=1,\ldots ,k,\ d(x,x_{j})\le 5r(x_{j}) \end{aligned}$$

and hence

$$\begin{aligned} \begin{aligned} \displaystyle d(x_{j},x_{l})&\le d(x_{j},x)+d(x,x_{l})\le 5(r(x_{j})+r(x_{l}))\le \frac{1}{4}(R(x_{j})+R(x_{l}))\\&\Rightarrow R(x_{j})\le 4R(x_{l}) \end{aligned} \end{aligned}$$

and by exchanging $\displaystyle x_{j}$ and $\displaystyle x_{l},\ R(x_{l})\le 4R(x_{j}).$

So we get

$$\begin{aligned} \displaystyle \forall j,l=1,\ldots ,k,\ r(x_{j})\le 4r(x_{l}),\ r(x_{l})\le 4r(x_{j}). \end{aligned}$$

Now the ball $\displaystyle B(x_{j},5r(x_{j})+5r(x_{l}))$ contains $\displaystyle x_{l}$ and hence the ball $\displaystyle B(x_{j},5r(x_{j})+6r(x_{l}))$ contains the ball $\displaystyle B(x_{l},r(x_{l})).$ But, because $\displaystyle r(x_{l})\le 4r(x_{j}),$ we get

$$\begin{aligned} \displaystyle B(x_{j},5r(x_{j})+6{\times }4r(x_{j}))=B(x_{j},r(x_{j})(5+24))\supset B(x_{l},r(x_{l})). \end{aligned}$$

The balls in ${\mathcal {G}}$ being disjoint, we get, setting $\displaystyle B_{l}:=B(x_{l},\ r(x_{l})),$

$$\begin{aligned} \displaystyle \ \sum _{j=1}^{k}{\mathrm {V}\mathrm {o}\mathrm {l}(B_{l})}\le \mathrm {V}\mathrm {o}\mathrm {l}(B(x_{j},29r(x_{j}))). \end{aligned}$$

The Lebesgue measure read in the chart $\varphi$ and the canonical measure $dv_{g}$ on $\displaystyle B(x,R_{\epsilon }(x))$ are equivalent; precisely because of condition (1) in the admissible ball definition, we get that

$$\begin{aligned} \displaystyle (1-\epsilon )^{n}\le \left| {\mathrm {d}\mathrm {e}\mathrm {t}g}\right| \le (1+\epsilon )^{n}, \end{aligned}$$

and the measure $dv_{g}$ read in the chart $\varphi$ is $dv_{g}={\sqrt{\left| {\mathrm {d}\mathrm {e}\mathrm {t}g_{ij}}\right| }}d\xi ,$ where $\displaystyle d\xi$ is the Lebesgue measure in ${\mathbb {R}}^{n}.$ In particular,

$$\begin{aligned} \displaystyle \forall x\in M,\ \mathrm {V}\mathrm {o}\mathrm {l}(B(x,\ R_{\epsilon }(x)))\le (1+\epsilon )^{n/2}\nu _{n}R^{n}, \end{aligned}$$

where $\nu _{n}$ is the euclidean volume of the unit ball in ${\mathbb {R}}^{n}.$

Now because $\displaystyle R(x_{j})$ is the admissible radius and $\displaystyle 4{\times }29r(x_{j})<R(x_{j}),$ we have

$$\begin{aligned} \displaystyle \mathrm {V}\mathrm {o}\mathrm {l}(B(x_{j},29r(x_{j})))\le 29^{n}(1+\epsilon )^{n/2}v_{n}r(x_{j})^{n}. \end{aligned}$$

On the other hand we also have

$$\begin{aligned} \displaystyle \mathrm {V}\mathrm {o}\mathrm {l}(B_{l})\ge v_{n}(1-\epsilon )^{n/2}r(x_{l})^{n}\ge v_{n}(1-\epsilon )^{n/2}4^{-n}r(x_{j})^{n}, \end{aligned}$$

and hence

$$\begin{aligned} \displaystyle \ \sum _{j=1}^{k}{(1-\epsilon )^{n/2}4^{-n}r(x_{j})^{n}}\le 29^{n}(1+\epsilon )^{n/2}r(x_{j})^{n}, \end{aligned}$$

so finally

$$\begin{aligned} \displaystyle k\le (29{\times }4)^{n}\frac{(1+\epsilon )^{n/2}}{(1-\epsilon )^{n/2}}, \end{aligned}$$

which means that $\displaystyle T\le \frac{(1+\epsilon )^{n/2}}{(1-\epsilon )^{n/2}}(120)^{n}.$

Saying that any $\displaystyle x\in M$ belongs to at most T balls of the covering $\displaystyle \lbrace B_{j}\rbrace$ means that ${\sum _{j\in {\mathbb {N}}}{{\mathbb {1}}_{B_{j}}(x)}\le T}$, and this implies easily that

$$\begin{aligned} \displaystyle \forall f\in L^{1}(M),\ \sum _{j\in {\mathbb {N}}}{\int _{B_{j}}{\left| {f(x)}\right| dv_{g}(x)}}\le T{\left\| {f}\right\| }_{L^{1}(M)}. \end{aligned}$$

$\square$

1.2 Sobolev Spaces

We have to define the Sobolev spaces in our setting, following Hebey [17], p. 10.

First define the covariant derivatives by $\displaystyle (\nabla u)_{j}:=\partial _{j}u$ in local coordinates, while the components of $\nabla ^{2}u$ are given by

$$\begin{aligned} (\nabla ^{2}u)_{ij}=\partial _{ij}u-\Gamma ^{k}_{ij}\partial _{k}u, \end{aligned}$$

(7.1)

with the convention that we sum over repeated index. The Christoffel $\displaystyle \Gamma ^{k}_{ij}$ verify [7]:

$$\begin{aligned} \Gamma ^{k}_{ij}=\frac{1}{2}g^{il}\left( \frac{\partial g_{kl}}{\partial x^{j}}+\frac{\partial g_{lj}}{\partial x^{k}}-\frac{\partial g_{jk}}{\partial x^{l}}\right) . \end{aligned}$$

(7.2)

If $\displaystyle k\in {\mathbb {N}}$ and $r\ge 1$ are given, we denote by ${\mathcal {C}}^{r}_{k}(M)$ the space of smooth functions $u\in {\mathcal {C}}^{\infty }(M)$ such that $\displaystyle \ \left| {\nabla ^{j}u}\right| \in L^{r}(M)$ for $\displaystyle j=0,\ldots ,k.$ Hence

$$\begin{aligned} \displaystyle {\mathcal {C}}^{r}_{k}(M):=\left\{ u\in {\mathcal {C}}^{\infty }(M),\ \forall j=0,\ldots ,k,\ \int _{M}{\left| {\nabla ^{j}u}\right| ^{r}dv_{g}}<\infty \right\} . \end{aligned}$$

Now we have [17].

Definition 7.4

The Sobolev space $\displaystyle W^{k,r}(M)$ is the completion of ${\mathcal {C}}^{r}_{k}(M)$ with respect to the norm:

$$\begin{aligned} {\left\| {u}\right\| }_{W^{k,r}(M)}=\sum _{j=0}^{k}{{\left( {\int _{M}{\left| {\nabla ^{j}u}\right| ^{r}dv_{g}}}\right) }^{1/r}}. \end{aligned}$$

We extend in a natural way this definition to the case of G-forms.

Let the Sobolev exponents $\displaystyle S_{k}(r)$ be as in Definition 1.7, then the k th Sobolev embedding is true if we have

$$\begin{aligned} \displaystyle \forall u\in W^{k,r}(M),\ u\in L^{S_{k}(r)}(M). \end{aligned}$$

This is the case in ${\mathbb {R}}^{n},$ or if M is compact, or if M has a Ricci curvature bounded from below and $\displaystyle \inf \ _{x\in M}v_{g}(B_{x}(1))\ge \delta >0,$ due to Varopoulos [27], see Theorem 3.14, p. 31 in [17].

Lemma 7.5

We have the Sobolev comparison estimates where $\displaystyle B(x,R)$ is a $\epsilon$ admissible ball in M and $\varphi \ ,\ B(x,R)\rightarrow {\mathbb {R}}^{n}$ is the admissible chart relative to $\displaystyle B(x,R),$

$$\begin{aligned} \displaystyle \forall u\in W^{m,r}(B(x,R)),\ {\left\| {u}\right\| }_{W^{m,r}(B(x,R))}\le (1+\epsilon C){\left\| {u\circ \varphi ^{-1}}\right\| }_{W^{m,r}(\varphi (B(x,R)))}, \end{aligned}$$

and, with $\displaystyle B_{e}(0,t)$ the euclidean ball in ${\mathbb {R}}^{n}$ centered at 0 and of radius $\displaystyle t,$

$$\begin{aligned} \displaystyle \ {\left\| {v}\right\| }_{W^{m,r}(B_{e}(0,(1-\epsilon )R))}\le (1+2C\epsilon ){\left\| {u}\right\| }_{W^{m,r}(B(x,R))}. \end{aligned}$$

Proof

We have to compare the norms of $\displaystyle u,\ \nabla u,...,\ \nabla ^{m}u$ with the corresponding ones for $\displaystyle v:=u\circ \varphi ^{-1}$ in ${\mathbb {R}}^{n}.$

First we have because $\displaystyle (1-\epsilon )\delta _{ij}\le g_{ij}\le (1+\epsilon )\delta _{ij}$ in $\displaystyle B(x,R)$:

$$\begin{aligned} \displaystyle B_{e}(0,(1-\epsilon )R)\subset \varphi (B(x,R))\subset B_{e}(0,(1+\epsilon )R). \end{aligned}$$

Because

$$\begin{aligned} \displaystyle \ \sum _{\left| {\beta }\right| \le m-1}{\sup \ _{i,j=1,\ldots ,n,\ y\in B_{x}(R)}\left| {\partial ^{\beta }g_{ij}(y)}\right| }\le \epsilon \hbox { in } \displaystyle B(x,R), \end{aligned}$$

we have the estimates, with $\displaystyle \forall y\in B(x,R),\ z:=\varphi (y),$

$$\begin{aligned} \displaystyle \forall y\in B(x,R),\ \left| {u(y)}\right| =\left| {v(z)}\right| ,\ \ \left| {\nabla u(y)}\right| \le (1+C\epsilon )\left| {\partial v(z)}\right| . \end{aligned}$$

Because of (7.2) and (7.1) we get

$$\begin{aligned} \displaystyle \forall y\in B(x,R),\ \left| {\nabla ^{2}u(y)}\right| \le \left| {\partial ^{2}v(z)}\right| +\epsilon C\left| {\partial v(z)}\right| . \end{aligned}$$

And taking more derivatives, because

$$\begin{aligned} \displaystyle \sum _{\left| {\beta }\right| \le m-1}{\sup \ _{i,j=1,\ldots ,n,\ y\in B_{x}(R)}\left| {\partial ^{\beta }g_{ij}(y)}\right| }\le \epsilon , \end{aligned}$$

we get, for $2\le k\le m,$

$$\begin{aligned} \displaystyle \forall y\in B(x,R),\ \left| {\nabla ^{k}u(y)}\right| \le \left| {\partial ^{k}v(z)}\right| +\epsilon (C_{1}\left| {\partial v(z)}\right| +\cdot \cdot \cdot +C_{k-1}\left| {\partial ^{k-1}v(z)}\right| ). \end{aligned}$$

Integrating this we get for $2\le k\le m,$

$$\begin{aligned} \displaystyle {\left\| {\nabla ^{k}u}\right\| }_{L^{r}(B(x,R))}\le & {} {\left\| {\left| {\partial ^{k}v}\right| +\epsilon (C_{1}\left| {\partial v(z)}\right| +\cdot \cdot \cdot +C_{k-1}\left| {\partial ^{k-1}v(z)}\right| )}\right\| }_{L^{r}(B_{e}(0,(1+\epsilon )R))}\\ \displaystyle\le & {} {\left\| {\partial ^{k}v}\right\| }_{L^{r}(B_{e}(0,(1+\epsilon )R))}+C_{1}\epsilon {\left\| {\partial v}\right\| }_{L^{r}(B_{e}(0,(1+\epsilon )R))}+\cdot \cdot \cdot \\&+\,C_{k-1}\epsilon {\left\| {\partial ^{k-1}v}\right\| }_{L^{r}(B_{e}(0,(1+\epsilon )R))}, \end{aligned}$$

and

$$\begin{aligned} \displaystyle \ {\left\| {\nabla u}\right\| }_{L^{r}(B(x,R))}\le (1+C\epsilon ){\left\| {\partial v}\right\| }_{L^{r}(B_{e}(0,(1+\epsilon )R))}. \end{aligned}$$

We also have the reverse estimates

$$\begin{aligned} \displaystyle \ {\left\| {\partial ^{k}v}\right\| }_{L^{r}(B_{e}(0,(1-\epsilon )R))}\le & {} {\left\| {\nabla ^{k}v}\right\| }_{L^{r}(B_{e}(0,(1+\epsilon )R))}+C_{1}\epsilon {\left\| {\nabla v}\right\| }_{L^{r}(B_{e}(0,(1+\epsilon )R))}+\cdot \cdot \cdot \\&\displaystyle +\,C_{k-1}\epsilon {\left\| {\nabla ^{k-1}v}\right\| }_{L^{r}(B_{e}(0,(1+\epsilon )R))}, \end{aligned}$$

and

$$\begin{aligned} \displaystyle \ {\left\| {\partial v}\right\| }_{L^{r}(B_{e}(0,(1-\epsilon )R))}\le (1+C\epsilon ){\left\| {\nabla u}\right\| }_{L^{r}(B(x,R))}. \end{aligned}$$

So, using that

$$\begin{aligned} \displaystyle \ {\left\| {u}\right\| }_{W^{k,r}(B(x,R))}={\left\| {\nabla ^{k}u}\right\| }_{L^{r}(B(x,R))}+\cdot \cdot \cdot +{\left\| {\nabla u}\right\| }_{L^{r}(B(x,R))}+{\left\| {u}\right\| }_{L^{r}(B(x,R))}, \end{aligned}$$

we get

$$\begin{aligned} \displaystyle \ {\left\| {u}\right\| }_{W^{k,r}(B(x,R))}^{r} &\!\le \!{\left\| {\partial ^{k}v}\right\| }_{L^{r}(B_{e}(0,(1+\epsilon )R))}+C_{2}\epsilon {\left\| {\partial ^{2}v}\right\| }_{L^{r}(B_{e}(0,(1+\epsilon )R))}+\cdot \cdot \cdot \\&\displaystyle +\quad C_{k-1}\epsilon {\left\| {\partial ^{k-1}v}\right\| }_{L^{r}(B_{e}(0,(1+\epsilon )R))}\!+\!(1+C\epsilon ){\left\| {\partial v}\right\| }_{L^{r}(B_{e}(0,(1+\epsilon )R))}\\&\displaystyle +\quad {\left\| {v}\right\| }_{L^{r}(B_{e}(0,(1+\epsilon )R))}\\ \displaystyle\le & {} (1+2\epsilon C){\left\| {v}\right\| }_{W^{k,r}(B_{e}(0,(1+\epsilon )R))}. \end{aligned}$$

Again all these estimates can be reversed so we also have

$$\begin{aligned} \displaystyle \ {\left\| {v}\right\| }_{W^{m,r}(B_{e}(0,(1-\epsilon )R))}\le (1+2C\epsilon ){\left\| {u}\right\| }_{W^{m,r}(B(x,R))}. \end{aligned}$$

This ends the proof of the lemma. $\square$

We have to study the behavior of the Sobolev embeddings w.r.t. the radius. Set $\displaystyle B_{R}:=B_{e}(0,R).$

Lemma 7.6

We have, with $\displaystyle t=S_{m}(r),$

$$\begin{aligned} \displaystyle \forall R,\ 0<R\le 1,\ \forall u\in W^{m,r}(B_{R}),\ {\left\| {u}\right\| }_{L^{t}(B_{R})}\le CR^{-m}\ {\left\| {u}\right\| }_{W^{m,r}(B_{R})} \end{aligned}$$

the constant C depending only on $\displaystyle n,\ r.$

Proof

Start with $\displaystyle R=1,$ and then we have by Sobolev embeddings with $\displaystyle t=S_{m}(r),$

$$\begin{aligned} \forall v\in W^{m,r}(B_{1}),\ {\left\| {v}\right\| }_{L^{t}(B_{1})}\le C{\left\| {v}\right\| }_{W^{m,r}(B_{1})}, \end{aligned}$$

(7.3)

where $\displaystyle C$ depends only on n and $\displaystyle r.$ For $\displaystyle u\in W^{m,r}(B_{R})$ we set

$$\begin{aligned} \displaystyle \forall x\in B_{1},\ y:=Rx\in B_{R},\ v(x):=u(y). \end{aligned}$$

Then we have

$$\begin{aligned} \displaystyle \partial v(x)= & {} \partial u(y){\times }\frac{\partial y}{\partial x}=R\partial u(y);\\ \displaystyle \partial ^{2}v(x)= & {} \partial ^{2}u(y){\times }\left( \frac{\partial y}{\partial x}\right) ^{2}=R^{2}\partial ^{2}u(y);\ ...\ ;\\ \displaystyle \partial ^{m}v(x)= & {} \partial ^{m}u(y){\times }\left( \frac{\partial y}{\partial x}\right) ^{m}=R^{m}\partial ^{m}u(y). \end{aligned}$$

So we get, because the Jacobian for this change of variables is $\displaystyle R^{-n},$

$$\begin{aligned} \displaystyle \ {\left\| {\partial v}\right\| }_{L^{r}(B_{1})}^{r}=\int _{B_{1}}{\left| {\partial v(x)}\right| ^{r}dm(x)}=\int _{B_{R}}{\left| {\partial u(y)}\right| ^{r}\frac{R^{r}}{R^{n}}dm(x)}=R^{r-n}{\left\| {\partial u}\right\| }_{L^{r}(B_{R})}^{r}. \end{aligned}$$

So

$$\begin{aligned} {\left\| {\partial u}\right\| }_{L^{r}(B_{R})}=R^{-1+n/r}{\left\| {\partial v}\right\| }_{L^{r}(B_{1})}. \end{aligned}$$

(7.4)

The same way we get

$$\begin{aligned} {\left\| {\partial ^{m}u}\right\| }_{L^{r}(B_{R})}=R^{-m+n/r}{\left\| {\partial ^{m}v}\right\| }_{L^{r}(B_{1})} \end{aligned}$$

(7.5)

and of course $\displaystyle \ {\left\| {u}\right\| }_{L^{r}(B_{R})}=R^{n/r}{\left\| {v}\right\| }_{L^{r}(B_{1})}.$

So with 7.3 we get

$$\begin{aligned} {\left\| {u}\right\| }_{L^{t}(B_{R})}=R^{n/t}{\left\| {v}\right\| }_{L^{t}(B_{1})}\le CR^{n/t}{\left\| {v}\right\| }_{W^{m,r}(B_{1})}. \end{aligned}$$

(7.6)

But

$$\begin{aligned} \displaystyle \ {\left\| {u}\right\| }_{W^{m,r}(B_{R})}:={\left\| {u}\right\| }_{L^{r}(B_{R})}+{\left\| {\partial u}\right\| }_{L^{r}(B_{R})}+\cdot \cdot \cdot +{\left\| {\partial ^{m}u}\right\| }_{L^{r}(B_{R})}, \end{aligned}$$

and

$$\begin{aligned} \displaystyle \ {\left\| {v}\right\| }_{W^{m,r}(B_{1})}:={\left\| {v}\right\| }_{L^{r}(B_{1})}+{\left\| {\partial v}\right\| }_{L^{r}(B_{1})}+\cdot \cdot \cdot +{\left\| {\partial ^{m}v}\right\| }_{L^{r}(B_{1})}, \end{aligned}$$

so

$$\begin{aligned} \displaystyle \ {\left\| {v}\right\| }_{W^{m,r}(B_{1})}:=R^{-n/r}{\left\| {u}\right\| }_{L^{r}(B_{R})}+R^{1-n/r}{\left\| {\partial u}\right\| }_{L^{r}(B_{R})}+\cdot \cdot \cdot +R^{m-n/r}{\left\| {\partial ^{m}u}\right\| }_{L^{r}(B_{R})}. \end{aligned}$$

Because we have $\displaystyle R\le 1,$ we get

$$\begin{aligned} \displaystyle \ {\left\| {v}\right\| }_{W^{m,r}(B_{1})}\le & {} R^{-n/r}\big ({\left\| {u}\right\| }_{L^{r}(B_{R})}+{\left\| {\partial u}\right\| }_{L^{r}(B_{R})}+\cdot \cdot \cdot +{\left\| {\partial ^{m}u}\right\| }_{L^{r}(B_{R})}\big )\\= & {} R^{-n/r}{\left\| {u}\right\| }_{W^{m,r}(B_{R})}. \end{aligned}$$

Putting it in (7.6) we get

$$\begin{aligned} \displaystyle \ {\left\| {u}\right\| }_{L^{t}(B_{R})}\le CR^{n/t}{\left\| {v}\right\| }_{W^{m,r}(B_{1})}\le CR^{-n\left( \frac{1}{r}-\frac{1}{t}\right) }{\left\| {u}\right\| }_{W^{m,r}(B_{R})}. \end{aligned}$$

But, because $\displaystyle t=S_{m}(r),$ we get $\displaystyle (\frac{1}{r}-\frac{1}{t})=\frac{m}{n}$ and

$$\begin{aligned} \displaystyle \ {\left\| {u}\right\| }_{L^{t}(B_{R})}\le CR^{-m}{\left\| {u}\right\| }_{W^{m,r}(B_{R})}. \end{aligned}$$

The constant C depends only on $\displaystyle n,r.$ The proof is complete. $\square$

Lemma 7.7

Let $x\in M$ and $\displaystyle B(x,R)$ be a $\epsilon$ admissible ball; we have, with $\displaystyle t=S_{m}(r),$

$$\begin{aligned} \displaystyle \forall u\in W^{m,r}(B(x,R)),\ {\left\| {u}\right\| }_{L^{t}(B(x,R))}\le CR^{-m}\ {\left\| {u}\right\| }_{W^{m,r}(B(x,R))}, \end{aligned}$$

the constant $\displaystyle C$ depending only on $\displaystyle n,\ r$, and $\displaystyle \epsilon .$

Proof

This is true in ${\mathbb {R}}^{n}$ by Lemma 7.6 so we can apply the comparison Lemma 7.5. $\square$