Abstract
Under the usual condition that the volume of a geodesic ball is close to the Euclidean one or the injectivity radii is bounded from below, we prove a lower bound of the \(C^{\alpha } \cap W^{1, q}\) harmonic radius for manifolds with bounded Bakry–Émery Ricci curvature when the gradient of the potential is bounded. Under these conditions, the regularity that can be imposed on the metrics under harmonic coordinates is only \(C^\alpha \cap W^{1,q}\), where \(q>2n\) and n is the dimension of the manifolds. This is almost 1-order lower than that in the classical \(C^{1,\alpha } \cap W^{2, p}\) harmonic coordinates under bounded Ricci curvature condition (Anderson in Invent Math 102:429–445, 1990). The loss of regularity induces some difference in the method of proof, which can also be used to address the detail of \(W^{2, p}\) convergence in the classical case. Based on this lower bound and the techniques in Cheeger and Naber (Ann Math 182:1093–1165, 2015) and Wang and Zhu (Crelle’s J, http://arxiv.org/abs/1304.4490), we extend Cheeger–Naber’s Codimension 4 Theorem in Cheeger and Naber (2015) to the case where the manifolds have bounded Bakry–Émery Ricci curvature when the gradient of the potential is bounded. This result covers Ricci solitons when the gradient of the potential is bounded. During the proof, we will use a Green’s function argument and adopt a linear algebra argument in Bamler (J Funct Anal 272(6):2504–2627, 2017). A new ingredient is to show that the diagonal entries of the matrices in the Transformation Theorem are bounded away from 0. Together these seem to simplify the proof of the Codimension 4 Theorem, even in the case where Ricci curvature is bounded.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we extend two important results from the case of bounded Ricci curvature to the case of bounded Bakry–Émery curvature with \(C^1\) potential. One of these is Anderson’s lower bound for harmonic radius [1] and the other is Cheeger–Naber’s codimension 4 theorem [10]. While many results in these two cases are parallel, extending these two results requires some new effort and entails new applications which we explain now.
In a series of works [4,5,6,7,8,9,10,11,12], Cheeger–Colding–Tian–Naber developed a very deep and powerful theory for studying the Gromov–Hausdorff limits of manifolds with bounded Ricci curvature. In particular, when the manifolds are in addition volume non-collapsed, according to their results, we know that the Gromov–Hausdorff limits decompose into the union of the regular set and singular set. The regular set is an open convex \(C^{1,\alpha }\) manifold, the singular set has codimension at least 4, and the tangent cone at any point must be a metric cone.
However, there are objects in geometry where the boundedness of the Ricci curvature is not available. One of these is a Ricci soliton under the typical condition that the gradient of the potential is bounded. More generally, these solitons belong to a class of manifolds where the Bakry–Émery Ricci curvature is bounded. The later has become a subject of study by numerous authors. Many of the classical geometric and analytic results such as volume comparison theorems and gradient bounds, valid under pointwise Ricci bound, have been extended to this case in the papers [15, 19, 23]. Recently Wang and Zhu [24] established analogous results for most of the Cheeger–Colding–Tian–Naber theory. One notable exception is the codimension 4 theorem for the singular part. A goal of this paper is to prove such a theorem.
Another case of interest is when the Ricci curvature in only in certain \(L^p\) spaces (see e.g., [25] or [13] for motivation). The first effort was made by Petersen–Wei [17, 18], where they assumed that \(|Ric^-|\in L^p\) for some \(p>n/2\) and obtained extended Laplacian and volume comparison theorems and continuity of volume under Gromov–Hausdorff limit. Recently, Tian and Zhang [22] successfully extended most of the Cheeger–Colding–Tian–Naber theory except for the codimension 4 theorem for the singular part. Bamler [3] proves a codimension 4 theorem for some Ricci flat singular spaces.
In proving these results under weaker Ricci curvature conditions, one needs to extend many key ingredients therein, such as Cheng–Yau gradient estimate, Segment inequality, Poincaré inequality, maximum principle, heat kernel estimates, Abresch–Gromoll estimate, and Anderson’s bound on harmonic radius. While many of the extensions are expected to be true and the proofs are analogous, there are notable exceptions. One of them is the bound on harmonic radius in the spirit of Anderson [1]. In that paper, Anderson proved the following result. Under suitable conditions on volume of balls or injectivity radius, if also the Ricci curvature is bounded, then \(C^{1, \alpha }\) harmonic radius has a positive lower bound and the metric is \(C^{1,\alpha } \cap W^{2, q}\) within such a radius. The lower bound of harmonic radius is very useful in many situations such that in establishing compactness of families of manifolds, e.g. However, one cannot expect such a result under Bakry–Émery Ricci curvature bound. Instead one can only expect \(C^{\alpha } \cap W^{1, q}\) property for harmonic radius and the metric. To see this, let us recall the equation connecting metric g and Ricci curvature under a harmonic coordinate chart:
Here Q is an expression involving quadratic quantity of \(\partial g\). Assuming the Bakry–Émery Ricci curvature is bounded, then the right-hand side of the equation is the sum of an \(L^\infty \) function and the Hessian of the function L. So if one wishes g is a \(W^{2, p}\) function, one needs to assume that the Hessian of L is \(L^p\). However, this is not available for us.
The first result of this paper is a lower bound for such harmonic radius under suitable conditions on volume of balls.
In order to state the result rigorously, following Anderson–Cheeger [2], let us define the \(W^{1,q}\) harmonic radius. Let \((\mathbf{M}^n,g)\) be an n-dimensional Riemannian manifold, and denote by \(B_r(x)\) the geodesic ball in \(\mathbf{M}\) centered at x with radius r.
Definition 1.1
For \(x\in \mathbf{M}\), the \(W^{1,q}\) harmonic radius \(r_h(x)\) at x is the largest \(r\ge 0\) such that there is a coordinate chart \(\Phi =(v_1,v_2,\ldots ,v_n):B_r(x)\rightarrow \mathbb {R}^n\) centered at x such that \(\Phi \) is a diffeomorphism onto its image, and
-
(1)
\(\Delta _g v_k=0\), \(1\le k\le n\);
-
(2)
let \(g_{ij}=g(\partial _{v_i},\partial _{v_j})\) be the component of the metric g considered as a function on \(B_r(x)\). We have
$$\begin{aligned} \Vert g_{ij}-Id_{ij}\Vert _{C^{0}(B_r(x))}+r^{1-\frac{n}{q}}||\partial _{v_k} g_{ij}||_{L^q(B_r(x))}\le \frac{1}{10}, \end{aligned}$$(1.2)where \(Id_{ij}\) is the standard Euclidean metric on \(\mathbb {R}^n\).
Our first main result is
Theorem 1.2
Let \((\mathbf{M}^n,g)\) be a Riemannian n-manifold and p be a point in \(\mathbf{M}^n\). For each \(q>2n\), there exist positive constants \(\delta =\delta (n,q)\) and \(\theta =\theta (n,q)\) with the following properties.
-
(a)
If \(|Ric+\nabla ^2 L|\le n-1\) with \(|\nabla L|\le 1\), and
$$\begin{aligned} {{\mathrm{Vol}}}(B_{\delta }(p))\ge (1-\delta ){{\mathrm{Vol}}}(B_{\delta }(0^n)), \end{aligned}$$(1.3)where \(0^n\) denotes the origin of \(\mathbb {R}^n\), then the \(W^{1,q}\) harmonic radius \(r_h(x)\) satisfies
$$\begin{aligned} r_h(x)\ge \theta d(x,\partial B_{\delta ^2}(p)), \end{aligned}$$for all \(x\in B_{\delta ^2}(p)\).
-
(b)
If \(|Ric+\nabla ^2 L|\le n-1\) with \(|\nabla L|\le 1\), and the injectivity radius satisfies
$$\begin{aligned} inj(x)\ge i_0>0 \end{aligned}$$in \(B_{10}(p)\), then the \(W^{1,q}\) harmonic radius \(r_h(x)\) satisfies
$$\begin{aligned} r_h(x)\ge \theta d(x,\partial B_{1}(p)), \end{aligned}$$for all \(x\in B_{1}(p)\).
Remark 1.3
Under the condition of the theorem, since \(q>2n>n\), one knows that \(W^{1, q}\) space embeds into \(C^\alpha \) for \(\alpha =1- \frac{n}{q}\). So we know that the metric is \(C^\alpha \) automatically.
Remark 1.4
Also indicated in the proof of Theorem 1.2 is the continuity of the \(W^{1,q}\) harmonic radius.
An immediate consequence of the theorem is the following:
Corollary 1.5
Let \(\lambda _1, \lambda _2, i_0, D\) be fixed positive numbers and L be any smooth function. The space of compact Riemannian n-manifolds such that
is compact in the \(C^\alpha \) topology.
The next theorem of the paper is
Theorem 1.6
Suppose a sequence of pointed manifolds \((\mathbf{M}^n_j, g_j, p_j)\) satisfies that
and
where \(L_j\in C^{\infty }(\mathbf{M}_j)\), and \(\rho >0\) is a constant.
If \((\mathbf{M}_j, d_j, p_j)\xrightarrow {d_{GH}}(X,d,p)\), then the singular set \(\mathcal {S}\) satisfies
Remark 1.7
The constants \(n-1\) and 1 in the assumptions on Bakry–Émery Ricci curvature in the above theorems are chosen for convenience. They can be replaced by any positive constants.
Remark 1.8
In the special case where \((\mathbf{M}_j, g_j)\) is a sequence of gradient shrinking Ricci solitons, i.e., \(Rc+\nabla ^2L=g\), with the additional assumption that the diameters of \(\mathbf{M}_j\) are uniformly bounded, the conclusion in Theorem 1.6 can be derived from the original arguments of Cheeger–Naber [10] by using a conformal transformation of the metrics as in [27] (See also [21] for a similar result for compact shrinking Kähler–Ricci solitons).
More generally, the method of conformal transformation in [27] can also be applied whenever \(|\nabla L|\) and \(|\Delta L|\) are bounded. However, in Theorem 1.6, the boundedness of \(|\Delta L|\) is not assumed.
The rest of the paper is organized as follows. In Sect. 2, we prove Theorem 1.2. The proof follows the strategy in [1] where a method of contradiction is used following a blow-up procedure. Since our Ricci condition is weaker, a deeper analysis of the metric equation within harmonic radius is needed. These include mixed second derivative bound of Greens function and a careful covering argument. The main issue is to prove \(W^{1, q}\) convergence of the metrics in a blow-up process. One technical difficulty is that bounded sets in \(W^{1, q}\) may not be compact in \(W^{1, q'}\) for \(q'<q\), which is different from the fact that bounded sets in \(C^\alpha \) is compact in \(C^{\alpha '}\) if \(\alpha '<\alpha \). An example is the sequence \(f_k = \frac{1}{k} \sin (kx), x \in [0, 2 \pi ]\) in \(W^{1, 2}([0, 2\pi ])\). During the blow-up process, it is easy to prove \(C^\alpha _{loc}\) convergence of the metrics. However, \(C^\alpha _{loc}\) convergence does not imply \(W^{1, q}\) convergence. So we cannot immediately deduce that the non-linear term Q in (1.1) converges. In the classical case, one can prove \(C^{1, \alpha }_{loc}\) convergence quickly and this already implies the \(C^{\alpha /2}_{loc}\) convergence of the non-linear term.
Theorem 1.6 will be proved in Sect. 3. The proof is based on the techniques in [10, 24]. A new ingredient is to show that the diagonal entries of the matrices in the Transformation Theorem are bounded away from 0. Some other short cuts to the proof are also found. Together these seem to simplify the proof of the Transformation Theorem in [10], even in the original case.
2 Bounds on Harmonic Radius and \(\epsilon \)-Regularity
Let us start with a simple observation. Recall the condition that
The theorem and proof are local in space. After blowing up of metrics, this condition on Ricci curvature is always satisfied and actually becomes better.
Let G(x, y) be the Green’s function on \(\mathbf{M}\). It is standard (using gradient bound on heat kernel, etc.) to show that (see e.g., [20])
Here and for the rest of this section, we use C to denote constants depending only on the dimension n and the parameters in the assumptions.
Suppose that \(\Phi :U\rightarrow \mathbb {R}^n\) is a local coordinate chart on some open subset U of \(\mathbf{M}\). Denote by \(\partial _{y_j}G(x,y)\) the jth component of \(\nabla _y G(x,y)\). Then it is a harmonic function off the diagonal as a function of x. Thus, by the gradient estimate under Bakry–Émery Ricci condition, it follows that (see e.g., [20])
Lemma 2.1
Under assumption (2.1), it holds
where \(\nabla _{x}\partial _{y_j}G(x,y)\) is the gradient of \(\partial _{y_j}G(x,y)\) as a function of x.
Here, gradient estimate works for (2.3) because only mixed derivative is involved in the proof, which only requires the control of the quantities in (2.1) but not the whole curvature tensor.
As a consequence of the Green’s function estimates (2.2) and (2.3), one can show
Lemma 2.2
Assume that (2.1) holds. Then for any \(r\le 1\), \(0<\alpha \le 1\), and \(y, x_1,x_2\in B_{2r}(p),\) we have
if \(B(y, 100) \subset U\).
Proof
We only prove the second estimate in (2.4). The proof of the first one is similar but easier.
If \(d(x_1,y)\le 2d(x_1,x_2)\), then (2.2) implies that
and
The estimates are similar when \(d(x_2,y)\le 2d(x_1,x_2)\).
Finally, if \(\min (d(x_1,y),d(x_2,y))>2d(x_1,x_2)\), then by (2.3), one gets
Notice that in this case
Thus,
\(\square \)
Proof of Theorem 1.2:
Proof of (a): We will use the blow-up argument in [1] together with an extensive use of the “intrinsic” Green’s function on the manifold \(\mathbf{M}\). Let us remark here that alternatively, one may also use the “extrinsic” Green’s function, namely, the Green’s function of the operator \(g^{ab} \frac{\partial ^2}{\partial v_a \partial v_b}\) in the Euclidean space, after extending \(g^{ab}\) suitably to the whole space.
Notice that by rescaling the metric g by a factor \(\delta ^{-4}\), it amounts to prove the following statement. If \(|Ric+\nabla ^2 L|\le (n-1)\delta ^4\) with \(|\nabla L|\le \delta ^2\), and
then the \(W^{1,q}\) harmonic radius \(r_h(x)\) satisfies
for all \(x\in B_{1}(p)\).
Under condition (2.5), by Theorem 1.2 in [23] (see also Corollary 2.5 in [26]), we have for any \(x\in B_{1}(p)\),
Thus, when \(\delta \) is small, it implies that
Then applying the volume comparison theorem (Theorem 1.2 in [23]) one more time yields
Again, if \(\delta \) is small enough, one gets
Now we argue by contradiction to show that the theorem holds for some small \(\delta \). Suppose that the theorem is not true. Then for any \(\delta _j\rightarrow 0\), there is a sequence of manifolds \((\mathbf{M}_j, g_j)\), points \(p_j\in \mathbf{M}_j\), and smooth functions \(L_j\) such that
and
but for some \(z_j\in B_{1}(p_j)\), we have
Without loss of generality, we may assume that \(z_j\) is chosen so that the ratio \(\frac{r_h(z)}{ d(z,\partial B_{1}(p_j))}\) reaches the minimum in \(\overline{B_{1}(p_j)}\). It then implies that in the ball \(B_{\frac{1}{2}d(z_j,\partial B_{1}(p_j))}(z_j)\), we have
In the following, we finish the proof in 5 steps.
Step 1 Blow-up and \(C^{\alpha }\) convergence
Denote by \(r_j=r_h(z_j)\). Note that (2.9) implies that \(r_j\rightarrow 0\). Let us rescale the metric \(g_j\) by the factor \(r_j^{-2}\), i.e., \(g_j\rightarrow r_j^{-2}g_j\). In the following, unless otherwise specified, all norms are taken with respect to the rescaled metric \(r_j^{-2}g_j\). Hence, the manifold \((\mathbf{M}_j, g_j)\) satisfies
and
Also, from (2.9), one has
Gromov’s precompact theorem implies that by passing to a subsequence, we have
\((B_{d(z_j,\partial B_{r_j^{-1}}(p_j))}(z_j), d_j, z_j) \xrightarrow {d_{GH}}(\mathbf{M}_{\infty }, d_{\infty }, z_{\infty })\), where \(d_j\) is the distance function related to the Riemannian metric \(g_j\). Then Corollary 4.8 and Remark 4.9 in [24] and (2.8) conclude that \((\mathbf{M}_{\infty }, d_{\infty })=(\mathbb {R}^n, |\cdot |)\), where \(|\cdot |\) denotes the standard Euclidean distance. Without loss of generality, we may assume that \(z_{\infty }=0^n\).
On the other hand, by (2.10), there is an open cover \(\{B_{1/2}(z_{j_k})\}\) of \(B_{\frac{1}{2}d(z_j,\partial B_{r_j^{-1}}(p_j))}(z_j)\) such that \(B_{1/4}(z_{j_k})\) are mutually disjoint and there is a \(W^{1,q}\) harmonic coordinate chart on all the balls. Since \(q>2n\), by Sobolev embedding and the virtue of Lemma 2.1 in [1] (See also [16]), it actually holds that \((B_{d(z_j,\partial B_{r_j^{-1}}(p_j))}(z_j), g_j, z_j)\xrightarrow {C^{\alpha '}}(\mathbb {R}^n, Id_{ij}, 0^n)\) for any \(\alpha '<1-\frac{n}{q}\) in Cheeger–Gromov sense, i.e., there exist exhausting open subsets \(U_j\) and \(V_j\) of \(\mathbb {R}^n\) and \(B_{d(z_j,\partial B_{r_j^{-1}}(p_j))}(z_j)\), respectively, and diffeomorphisms \(F_j: U_j\rightarrow V_j\) such that \(F_j^*g_j\) converges in \(C^{\alpha '}\) to Id on compact subsets of \(\mathbb {R}^n\). Moreover, we may assume that the index set \(\{k\}\) is the same for all \(B_{d(z_j,\partial B_{r_j^{-1}}(p_j))}(z_j)\), and \(B_{1/2}(z_{j_k})\xrightarrow {d_{GH}}B_{1/2}(z_{\infty ,k})\) for fixed k, as \(j\rightarrow \infty \).
Next, we want to show that the convergence actually takes place in \(C^{\alpha }\) and \(W^{1,s}\) topology for any \(\alpha \in (0,1)\) and \(1<s<\infty \).
The estimates below work for all \(\mathbf{M}_j\)’s, so the subscript j is dropped for convenience. In the remaining context of this step, denote by \(\partial _{v_a}\) the partial derivative operator \(\frac{\partial }{\partial v_a}\). In harmonic coordinates, the components of the Ricci curvature tensor can be expressed as
where \(Q(\partial g, g)\) is a quantity quadratic in the components of \(\partial g\). The above equation may be viewed as a semi-linear elliptic equation of \(g_{kl}\), namely,
from which we can derive the local \(W^{1,s}\) boundedness of \(g_{kl}\). Below, we present the rough idea of getting the \(W^{1,s}\) bound, see for example (2.40) and the discussions thereafter for more details. In fact, the worst term on the right-hand side of (2.14) is \(\nabla _k\nabla _l L\). To deal with it, one may first rewrite (2.14) as
where \(p_0\) is some fixed point, and \(\Gamma ^m_{kl}\) is the Christoffel symbol of g. Multiplying both sides by a cut-off function \(\phi \) (see the first paragraph of step 2 below) yields
where \(T(\partial \phi , \partial ^2\phi )\) is the quantity involving the partial derivatives of \(\phi \), and \(\cdots \) represents all the other mild terms. It then follows from Green’s formula that
where \(G_{p_0}(x,y)\) is the kernel of the operator \(g^{ab}(p_0)\partial _{ v_a}\partial _{v_b}\). Thus, inside the ball where \(\phi =1\), we have
Notice that by the definition of harmonic coordinates, \(\partial _x\partial _y G_{p_0}(x,y)\) is a Calderón–Zygmund kernel, and \(|\partial g|\in L^q\), \(g^{ab}\in C^{\alpha '}\), \(|Ric+\nabla ^2 L|\in L^{\infty },\) and \(|\nabla L|\in L^{\infty }\). Therefore, one can see from (2.18) that the \(W^{1,s}\) norm of \(g_{kl}\) is uniformly bounded locally for all \(1<s<\infty \).
Since we have got the uniform \(W^{1,s}\) bound of \(g_j\) on compact subsets, it then follows from Sobolev embedding and the Arzela–Ascoli lemma that \((B_{d(z_j,\partial B_{r_j^{-1}}(p_j))}(z_j), g_{j}, z_j)\xrightarrow {C^\alpha } (\mathrm {R}^n, Id, 0^n)\) for any \(\alpha \in (0,1)\). Here \(g_j=(g_{kl})_j,\) where j is the index in the sequence of metrics.
Step 2 control of the \(W^{1,s}\) norm on small scales
To show the \(W^{1,s}\) convergence of \(g_j\), for any \(z\in B_{1/2}(z_{j_k})\), let \(\eta >0\) be an arbitrary constant such that \(B_{2\eta }(z)\subseteq B_{1/2}(z_{j_k})\). Choose a cut-off function \(\phi \) supported in \(B_{2\eta }(z)\) such that \(\phi =1\) in \(B_{3\eta /2}(z)\) and \(|\Delta \phi |+|\nabla \phi |^2\le C/\eta ^2\). For the existence, see e.g., Lemma 1.5 in [24]. Also, for simplicity of presentation we temporarily drop the index j in the metrics, unless there is confusion. Then for
from (2.14), we have
It follows from Green’s formula that
and hence
in \(B_{\eta }(z)\).
For any \(q<s<\infty \), let \(s'=\frac{s}{s-1}\) and \(\psi \in C_0^{\infty }(B_{\eta }(z))\). In the following, the \(L^s\) and \(L^t\) norms are taken over \(B_{2\eta }(z)\). From (2.20), one has
Firstly, by (2.2) and (2.11), we have
Next, by writing \(h_{kl}=(g_{kl}-Id_{kl})-(g_{kl}-Id_{kl})(z)\) and using the \(C^{\alpha }\) boundedness of \(|g-Id|\), we have for any \(\alpha \in (1-\frac{n}{s}, 1)\) that
For \(I_4\), using integration by parts yields
From (2.23), we have
Similarly, by Lemma 2.1, we get
Since \(g^{ab}\in W^{1,q}\), it follows that
Here we have used \(q>2n\). Thus, putting (2.24), (2.25), and (2.26) together, one has
Moreover, since \(Q(\partial g,g)\in L^{q/2}\), applying Hölder inequality followed by Young’s inequality implies that
where \(\Vert \partial g\Vert _{L^s}\) means the sum of the \(L^s\) norms of all the components of \(\partial g\), and t satisfies
Noticing that \(q>2n\), it is easy to check that \((n-1)t<n\), and hence
Thus, we have
Finally,
For the second and third terms above, since \(\Gamma _{kl}^n\in L^q\), \(|\nabla \phi |\le C/\eta \) and \(|\nabla L|\le Cr_j\), as in (2.22) we get
For the first term, using Hölder inequality gives
where in the last step we have used the fact that
This is because G(x, y) is the kernel of the Laplace operator \(g^{ab}\frac{\partial ^2}{\partial v_a \partial v_b}\), and then we may rewrite equation \(g^{ab}\frac{\partial ^2 u}{\partial v_a \partial v_b}=\psi \) as \(g^{ab}(z)\frac{\partial ^2 u}{\partial v_a \partial v_b}= (g^{ab}(z)-g^{ab})\frac{\partial ^2 u}{\partial v_a \partial v_b}+\psi \) and use the fact that \(g^{ab}\in C^{\alpha }\) and \(\partial _x\partial _y G_z(x,y)\) is a Calderón–Zygmund kernel. Here \(G_z(x,y)\) denotes the kernel of the operator \(g^{ab}(z)\frac{\partial ^2 }{\partial v_a \partial v_b}\).
Thus, combining (2.29) and (2.30), we get
Putting (2.22), (2.23), (2.27), (2.28), and (2.31) together in (2.21), we obtain
where \(0<a<1\) is a constant.
Therefore, by taking supremum over \(\psi \) on the left-hand side and summing up all indices, we have, after recalling that \(g=g_j\) in the sequence of metrics, that
Step 3 covering argument and \(W^{1,s}\) convergence
Even though the second term on the right is approaching 0, estimate (2.32) above cannot be applied directly to derive the \(W^{1,s}\) convergence of the metrics due to the difference between the size of the balls centered at z. The idea is to make the sizes of the balls on both sides even. For this purpose, we take advantage of the Whitney covering, which allows us to cover a big ball with countable many small balls while none of the small balls will escape the big ball and the overlapping number can be uniformly controlled. Eventually, the \(L^s\) norm of \(\partial g_j\) on both sides will be on the same ball, and \(\delta \) can be replaced by the largest diameter of the balls in the covering. Hence, by making \(\delta \) small enough, one will get the \(\Vert \partial g_j\Vert _{L^s}\rightarrow 0\) as desired.
We choose the Whitney covering \(\mathcal {B}\) of \(B_{1/2}(z_{j_k})\) as follows: for some \(m_0\) chosen below, cover the ball \(B_{\frac{1}{2}-\frac{1}{2^{m_0}}}(z_{j_k})\) with finitely many balls \(B_{\frac{1}{2^{m_0+1}}}\) of fixed size, cover the sphere \(\partial B_{\frac{1}{2}-\frac{1}{2^{m}}}(z_{j_k})\), \(m\ge m_0\) with balls \(B_{\frac{1}{2^{m+1}}},\) and cover the remaining region in the annulus \(B_{\frac{1}{2}-\frac{1}{2^{m+1}}}(z_{j_k})\setminus B_{\frac{1}{2}-\frac{1}{2^{m}}}(z_{j_k})\) also by balls \(B_{\frac{1}{2^{m+2}}}\), where \(B_r\) denotes a ball with radius r. Hence, \(B_{1/2}(z_{j_k})\) is the union of all the balls in the covering. In addition, we may require all the balls with half of the radius to be disjoint.
Denote the number of balls with the radius \(\frac{1}{2^{m+1}}\) by \(K_m\). To estimate \(K_m\), first notice that \(K_{m_0}\) is a constant only depending on \(m_0\) and the parameters in the assumptions of the theorem. Then for each \(m\ge m_0+1\), since the balls \(B_{\frac{1}{2^{m+1}}}\) are contained in the annulus \(B_{\frac{1}{2}-\frac{1}{2^{m+1}}}\setminus B_{\frac{1}{2}-\frac{1}{2^{m-2}}}\), and these balls with half of the radius \(\frac{1}{2^{m+2}}\) are disjoint and volume non-collapsed, we have
which implies that
In the above, the right-hand side of (2.33) is derived by integrating the area of geodesic spheres between \(B_{\frac{1}{2}-\frac{1}{2^{m+1}}}\) and \(B_{\frac{1}{2}-\frac{1}{2^{m-2}}}\), and using the volume element comparison. See e.g., [23] (also [24] or [26]).
In (2.32), we replace \(B_{\eta }(z)\) on the left-hand side by the balls in the Whitney cover \(\mathcal {B}\) and sum up all the integrals. Note that balls \(\{B_{2\eta }(z)\}\) also form a Whitney cover of \(B_{1/2}(x_{j_k})\), denoted by \(2\mathcal {B}\), and the overlapping number N is uniformly bounded regardless the choice of \(m_0\). By using (2.34), one has
Therefore, one can see that for any \(s>q\), by choosing \(m_0\) and \(\alpha \) so that \(\frac{C}{2^{asm_0}}N<\frac{1}{2}\) and \(1-(1-\alpha )ns>0\), it follows that
which amounts to
since both \(r_j\rightarrow 0\) and \(\Vert g_j-Id\Vert _{C^{\alpha }}\rightarrow 0.\)
This implies the \(W^{1,s}\) convergence of \((B_{d(z_j,\partial B_{r_j^{-1}}(p_j))}(z_j), g_j, z_j)\). Indeed, for a fixed small radius \(\eta >0\) and any compact subset \(D \subset B_{d(z_j,\partial B_{r_j^{-1}}(p_j))}(z_j)\), by using volume comparison, one can get a uniform control (independent of j) of the number of points in the \(\eta /4\)-net of D. When \(\eta \) is chosen small enough, we can get a covering of D with balls with radius \(\eta /2\), such that on each ball there is a harmonic coordinate chart. Then by using a similar argument as in the proof of Whitney embedding theorem, we may construct an smooth embedding from D to \(\mathbb {R}^N\). Moreover, under this embedding, the local images are graphs. Since from (2.35), we have the \(W^{1,s}\) convergence of the metrics in harmonic coordinates to the Euclidean metric on \(\mathbb {R}^n\), the transition functions of the covering of D are converging in \(W^{2,s}\) to the transition functions of \(\mathbb {R}^n\). Also, for the same reason, the local graphs are converging in \(W^{2,s}\) norm. And hence, when j is large enough there exist diffeomorphisms between exhausting compact sets in \(\mathbb {R}^n\) and sets \(B_{d(z_j,\partial B_{r_j^{-1}}(p_j))}(z_j)\) such that the pull back metrics of \(g_j\) are converging in \(W^{1,s}\) norm to \(Id_{ij}\). See e.g., Proposition 12 in [14] for more details. One can also find similar arguments on \(W^{1, s}\) convergence in [2]. Note in that paper, one assumes the Ricci curvature is bounded from below. However, this assumption is only used to deduce volume comparison results which also holds in our situation. So the proof is valid in our case.
Therefore, we have shown that \((B_{d(z_j,\partial B_{r_j^{-1}}(p_j))}(z_j), g_j, z_j)\xrightarrow {C^{\alpha }\cap W^{1,s}}(\mathbb {R}^n,Id_{ij}, 0^n)\).
Step 4 Constructing harmonic coordinates on balls with radius larger than 1
From step 3 and the definition of Cheeger–Gromov convergence, we have that for j sufficiently large, there is a diffeomorphism \(F_j: U_j\rightarrow V_j\) such that \(F_j^{*}g_j\) converges to Id in \(W^{1,s}\) topology on compact subsets of \(\mathbb {R}^n\), where \(U_j\) and \(V_j\) are exhausting open subsets of \(\mathbb {R}^n\) and \(\mathbf{M}_j\), respectively. Thus, there is a covering of \(B_2(0^n)\), denoted by \(\{B_{i}\}\), with balls of radius 1 / 2, on each of which there is a harmonic coordinate chart \(\{v_1,\ldots , v_n\}\) uniformly bounded in \(C^{1,\alpha }\cap W^{2,s}\). In fact, the Laplace equation in Euclidean coordinates reads
Here \(\Delta _j\) is the Laplace operator of the metric \(h_j=F_j^*g_j\), and \(\{x_k\}\) are the standard Euclidean coordinates. Thus, the \(W^{2,s}\) bound of \(v_k\) follows from the \(W^{1,s}\) bound of \(h_j\) and standard elliptic regularity theory (see e.g., (2.40) and the discussion below it).
To construct larger harmonic coordinate chart with respect to \(h_j\), let \(y_k=y_k(j)\) be the solution of the Dirichlet problem
We first show that \(\{y_k\}\) gives a harmonic coordinate chart on \(B_{5/4}(0^n)\). Indeed, let \(w_k=x_k-y_k\), then
In Euclidean coordinates \(\Delta _j x_k= \frac{1}{\sqrt{det(h_j)}}\frac{\partial }{\partial x_a}(\sqrt{det(h_j)}h^{ab}\frac{\partial x_k}{\partial x_b})\). Since the metrics \(h_j\) converges in \(W_{loc}^{1,s}\) norm to the Euclidean metric, it implies that
Thus, by the maximal principle, one gets that
It then follows from the gradient estimate under Bakry–Émery Ricci condition that
Let \(\phi \) be a cut-off function supported in \(B_{3/2}(0^n)\) such that \(\phi =1\) in \(B_{11/8}(0^n)\) and \(|\Delta _j \phi |+|\nabla _j \phi |\le C\). From (2.36) and Green’s formula, we have
From Lemma 2.2, we have for \(x_1,x_2\in B_{5/4}(0^n)\) that
Then by Hölder inequality, (2.37), (2.38), and (2.39), it implies that for \(\alpha \in (0, 1-\frac{n}{s})\)
In particular, \(\{y_1,\ldots , y_n\}\) forms a coordinate system on \(B_{5/4}(0^n)\) when j is big enough.
Step 5 larger \(W^{1,q}\) harmonic radius and contradiction
It is left to show that (1.2) is satisfied under \(\{y_k\}\) with \(r=\frac{5}{4}\). For this, we need to show that \(y_k\) converges in \(W^{2,s}\) norm. In each \(B_i\), under the harmonic coordinates \(\{v_1,\ldots ,v_n\}\), (2.36) can be written as
For any point \(v_0\in B_i\), let \(\phi \) be a cut-off function supported in \(B_{2\eta }(v_0)\) such that \(\phi =1\) in \(B_{\eta }(v_0)\) and \(|\Delta \phi |+|\nabla \phi |^2\le C/\eta ^2\), where \(\eta \) is a small constant which will be determined later.
Then, we have
Since \(h_j^{mn}(v_0)\) is a constant satisfying \((1-c)Id\le h_j(v_0)\le (1+c)Id\), it follows that \(\partial _x\partial _y G_{v_0}(x,y)\) is a Calderón–Zygmund kernel, where \(G_{v_0}(x,y)\) is the kernel of the operator \(h_j^{ab}(v_0)\frac{\partial ^2 }{\partial v_a\partial v_b}\). Hence, it defines a Calderón–Zygmund operator bounded on \(L^s\) space, namely, we have
By the \(C^{\alpha }\) boundedness of \(h_j^{ab}\), one derives
By choosing \(\eta \) small enough, we can make \(C\eta ^{\alpha }<\frac{1}{2}\), and hence from (2.37), (2.38), (2.39), it follows that
Through a standard covering argument, it is easy to see that
This is sufficient to indicate that
Therefore, it follows that \(\{y_1,\ldots , y_n\}\) is a \(W^{1,q}\) harmonic coordinate chart on \(B_{5/4}(0^n)\) when j is large enough, which in term induces a \(W^{1,q}\) harmonic coordinate chart on a ball centered at \(z_j\) with radius larger than 1 in \(\mathbf{M}_j\), and contradicts to the hypothesis that the \(W^{1,q}\) harmonic radius \(r_h(z_j)=1\).
Proof of (b) The proof of part (b) is similar. One just needs to first notice that by modifying the proof of part (a) slightly, one can derive the following compactness result for manifolds under \(W^{1,s}\) convergence. \(\square \)
Theorem 2.3
Let \((\mathbf{M}^n_j, g_j, p_j)\) be a sequence of pointed Riemannian manifolds satisfying that \(|Ric_{\mathbf{M}_j}+\nabla ^2 L_j|\rightarrow 0\), \(|\nabla L_j|\rightarrow 0\), and \((\mathbf{M}^n_j, d_j, p_j)\xrightarrow {d_{GH}}(\mathbf{M}_{\infty }, d_{\infty }, p)\). Suppose also the \(W^{1, s}\) harmonic radius is bounded from below by a uniform positive constant for all \(s>2n\). Then there is a \(C^{\alpha }\cap W^{1,s}\) Riemannian metric \(g_{\infty }\) on \(\mathbf{M}_{\infty }\) such that \((\mathbf{M}^n_j, g_j, p_j)\xrightarrow {C^{\alpha }\cap W^{1,s}}(\mathbf{M}_{\infty }, g_{\infty }, p)\) in Cheeger–Gromov sense for any \(0<\alpha <1\) and \(1<s<\infty \).
Indeed, from the assumption and Arzela–Ascoli lemma, we immediately get \(C^{\alpha '}\) convergence of the sequence of manifolds for any \(0<\alpha '<1-\frac{n}{s}\). To show the \(W^{1,s}\) convergence, we just need to replace the Euclidean metric Id in step 2 and 3 in the proof of part (a) by \(g_{\infty }\), and estimate \(\Vert \partial g - \partial g_{\infty }\Vert _{L^s}\) instead of \(\Vert \partial g\Vert _{L^s}\). So instead of (2.35), one obtains
Here we have assumed, without loss of generality, the harmonic radii is bounded from below by 1. Also
Now the convergence in \(C^\alpha \) sense follow from Sobolev imbedding.
With Theorem 2.3 in hand, we can finish the proof of part (b). The difference from part (a) is that in this case, the fact that the limit space is \(\mathbb {R}^n\) will follow from Cheeger–Gromoll splitting theorem as argued in [1]. Indeed, by Theorem 2.3 and the equation for the Ricci curvature tensor in harmonic radius, the limit space is Ricci flat. On the other hand, the injectivity radius becomes infinity after blowing up. Hence, Cheeger–Gromoll splitting theorem can be applied. \(\square \)
Following the arguments in [5], one may also show that under condition (2.1), the codimension of the singular space of the Gromov–Hausdorff limit is still at least 2 (see Theorem 5.1 in [24]). Combining this result with Theorem 1.2, we have
Theorem 2.4
\((\epsilon \)-regularity) Given \(\rho >0\) and \(q>2n\), for each \(\epsilon >0\), there is a \(\delta =\delta (\epsilon ~|n,\rho ,q)\) such that if \((\mathbf{M}, g)\) is a Riemannian manifold with \(|Ric+\nabla ^2L|\le (n-1)\delta ^2\), \(|\nabla L|\le \delta \), and \({{\mathrm{Vol}}}(B_{10}(p))\ge \rho \), and
where \((0^{n-1},x^*)\in \mathbb {R}^{n-1}\times X\) for some metric space X, then the \(W^{1,q}\) harmonic radius \(r_h(p)\) satisfies
3 The Transformation Theorem
In this and next section, following the guidelines in [10], we prove the Transformation and Slicing Theorems, which allow us to derive the Codimension 4 Theorem by following the remaining arguments as in [10]. However, since our assumption is made on the Bakry–Émery Ricci curvature, to be able to overcome some technical difficulties, we need to add a weight to the concepts used in [10]. We start by restating the definition of \(\epsilon \)-splitting map introduced in [10].
Definition 3.1
A harmonic map \(u=(u^1, u^2,\ldots , u^k):\ B_r(x)\rightarrow \mathbb {R}^k\) is an \(\epsilon \)-splitting map, if
-
(1)
\(|\nabla u|\le 1+\epsilon \) in \(B_r(x)\);
-
(2)
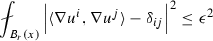 , \(\forall i,j\);
, \(\forall i,j\); -
(3)
 , \(\forall i\).
, \(\forall i\).
Denote by \(\Delta _L:=\Delta -\nabla L\cdot \nabla \) the drifted Laplacian by the vector field \(\nabla L\), \(dV_L:=e^{-L}dV\) the weighted volume form, \( {{\mathrm{Vol}}}_L(B_r(x)):=\int _{B_r(x)}dV_L\) the weighted volume of the geodesic ball \(B_r(x)\), and  the weighted average value over the ball \(B_r(x)\).
the weighted average value over the ball \(B_r(x)\).
In the definition above, using the drifted Laplacian and weighted average value instead of the regular ones, we define
Definition 3.2
A map \(f=(f^1,f^2,\ldots ,f^k): B_r(x)\rightarrow \mathbb {R}^k\) is called an L-harmonic map, if \(\Delta _L f^i=0\), for \(i=1,2,\ldots ,k\).
Moreover, an L-harmonic map \(f: B_r(x)\rightarrow \mathbb {R}^k\) is called an L-drifted \(\epsilon \)-splitting map if
-
(1’)
\(|\nabla f|\le 1+\epsilon \) in \(B_r(x)\);
-
(2’)
 , \(\forall i,j\);
, \(\forall i,j\); -
(3’)
 , \(\forall i\).
, \(\forall i\).
In the following, we first prove that the concepts of \(\epsilon \)-splitting and L-drifted \(\epsilon \)-splitting maps are equivalent. This equivalence will be used in the proof of Theorem 1.6.
Lemma 3.3
Given \(\rho >0\). For each \(\epsilon >0\) there exists an \(\delta =\delta (\epsilon ~|n,\rho )\) satisfying the following property. Suppose that a manifold \(\mathbf{M}^n\) satisfies \(Ric+\nabla ^2 L\ge -(n-1)\delta \), \(|\nabla L|\le \delta \), and \({{\mathrm{Vol}}}(B_{1}(x))\ge \rho \). Then for any \(r\le 1\), and an \(\epsilon \)-splitting map u on \(B_r(x)\), there is an L-drifted \(C\epsilon ^{1/2}\)-splitting map f on \(B_{\frac{1}{4}r}(x)\) for some constant \(C=C(n,\rho )\), and the converse is also true.
The notation \(\delta (\epsilon ~|n,\rho )\) means a constant depending on the parameters in the parenthesis and \(\delta \rightarrow 0\) as \(\epsilon \rightarrow 0\).
Proof
Suppose that u is an \(\epsilon \)-splitting map on \(B_r(x)\). Without loss of generality, we may assume that \(\epsilon \le 1\). Let \(h^i\), \(i=1,2,\ldots ,k\), be the solution of the Dirichlet problem
Since \(u^i\) is a harmonic function, the function \(h^i=f^i-u^i\) satisfies
Observe that \(\Delta _L=e^L\text {div}(e^{-L}\nabla )\) and we can assume L is locally bounded by replacing \(L(\cdot )\) by \(L(\cdot )-L(x)\); it is well known that the integral maximum principle (or mean value property) and gradient estimate still hold for equation (3.2) (see e.g., [24]).
From the assumption on u, we have \(|\nabla u|\le 1+\epsilon \). Combining this with \(|\nabla L|\le \delta \) and using the maximum principle, we get that for some \(q>n/2\),

Then it follows from the gradient estimate that

i.e.,
Also, from (3.3), (1), and (2) in Definition 3.1, and the boundedness of L, one has

Now, let \(\phi \) be a cut-off function supported in \(B_{\frac{1}{2}r}(x)\) with \(\phi =1\) in \(B_{\frac{1}{4}r}(x)\) and \(|\nabla \phi |^2+|\Delta \phi |\le \frac{C}{r^2}\) (See Lemma 1.5 in [24]). It is straightforward to check that for the drifted Laplacian we have the following Bochner’s formula.
Setting \(F=f^i\), it implies that (see e.g., p. 13 in [24])

Here, in the last step, we have used (3.5).
Combining (3.4), (3.5), and (3.6), we have shown that f is an L-drifted \(C\epsilon ^{1/2}\)-splitting map on \(B_{\frac{1}{4}r}(x)\) for sufficiently small constant \(\delta \). \(\square \)
Next, recall the concept of the singular scale in [10]:
Definition 3.4
Let \(u: B_2(p)\rightarrow \mathbb {R}^k\) be a harmonic map. For \(x\in B_1(p)\), \(\delta >0\), the singular scale \(s_x^{\delta }\ge 0\) is the infimum of radii s such that for all \(s\le r\le \frac{1}{4}\) and all \(1\le l\le k\), we have

where \(\tilde{w}^l=du^1\wedge du^2\wedge \cdots \wedge du^l\).
Replacing harmonic map and Laplacian \(\Delta \) above by L-harmonic map and the drifted Laplacian \(\Delta _L\), we define similarly
Definition 3.5
Let \(f: B_2(p)\rightarrow \mathbb {R}^k\) be an L-harmonic map. For \(x\in B_1(p)\), \(\delta >0\), the L-singular scale \(s_{L,x}^{\delta }\ge 0\) is the infimum of radii s such that for all \(s\le r\le \frac{1}{4}\) and all \(1\le l\le k\), we have

where \(w^l=df^1\wedge df^2\wedge \cdots \wedge df^l\).
In the proofs of the Transformation and Slicing Theorems, we will use L-singular scale, but return to \(\epsilon \)-splitting maps at the end. Now, we are ready to state the Transformation Theorem, whose proof essentially follows the idea of [10]. But for the purpose of deriving the higher-order estimates as in Theorem 1.26 in [10], we first need to work with the drifted Laplacian and L-drifted \(\epsilon \)-splitting maps, and prove certain transformation theorem under this weighted setting. Then come back to the regular Laplacian and \(\epsilon \)-splitting maps by using the equivalence between \(\epsilon \)-splitting maps and drifted \(\epsilon \)-splitting maps in Lemma 3.3.
It seems that by using a Green’s function argument instead of the heat kernel argument in [10] for Claim 3 below, and adapting an argument in [3], the original proof can be shortened. Moreover, a uniformly positive lower bound of the diagonal entries of the matrices in the conclusion is obtained. More precisely, we have
Theorem 3.6
(Transformation Theorem) Given \(\rho >0\); for every \(\epsilon >0\), there exists a \(\delta =\delta (\epsilon ~|n,\rho )>0\) with the following property. Suppose that a manifold \(\mathbf{M}^n\) satisfies \(Ric+\nabla ^2 L\ge -(n-1)\delta \) with \(|\nabla L|\le \delta \), and \({{\mathrm{Vol}}}(B_{10}(p))\ge \rho \), and let \(f: B_{2}(p)\rightarrow \mathbb {R}^k\) be an L-drifted \(\delta \)-splitting map. Then
-
(a)
for any \(x\in B_1(p)\) and \(r\in [s_{L,x}^{\delta },\frac{1}{4}]\), there exists a lower triangular matrix \(A=A(x,r)\) with positive diagonal entries so that \(A\circ f: B_r(x)\rightarrow \mathbb {R}^k\) is an L-drifted \(\epsilon \)-splitting map;
-
(b)
there is a constant \(c_0=c_0(n)>0\), such that for any matrix \(A(x,r)=(a_{ij})\) above, we have
$$\begin{aligned} a_{ii}\ge c_0, \ 1\le i\le k. \end{aligned}$$(3.9)
Proof
Following [10], we prove by induction on k. Unless otherwise specified, the letter C always denotes some constant depending on n, \(\lambda ,\) and \(\rho \). First of all, the proof of the theorem when \(k=1\) is analogous to the proof of Lemma 3.34 in [10]. By using the Bochner’s formula, we get
Notice that since \(\Delta f = <\nabla L, \nabla f>\), the improved Kato’s inequality becomes
Thus, it follows from (3.10) that
Then using (3.8) gives

and hence,

Thus, by setting  , we may proceed as in Lemma 3.34 in [10]. Here notice that the heat kernel Gaussian bounds was used in the proof of Lemma 3.34 in [10]. In our case, it is well known that the Gaussian bounds of the heat kernel and Green’s function estimates for the drifted Laplacian \(\Delta _L\) are still valid, since both \(|\nabla L|\) and |L| are bounded. Or instead, one can use the mean value property.
, we may proceed as in Lemma 3.34 in [10]. Here notice that the heat kernel Gaussian bounds was used in the proof of Lemma 3.34 in [10]. In our case, it is well known that the Gaussian bounds of the heat kernel and Green’s function estimates for the drifted Laplacian \(\Delta _L\) are still valid, since both \(|\nabla L|\) and |L| are bounded. Or instead, one can use the mean value property.
Now suppose that the theorem holds for \(k-1\) and fails for k. Then there exists an \(\epsilon >0\) such that for some \(\delta _j\rightarrow 0\), there is a sequence of pointed manifolds \((\mathbf{M}^n_j,g_j,p_j)\) and smooth functions \(\{L_j\}\) with
and \(L_j\)-drifted \(\delta _j\)-splitting maps \(f_j: B_2(p_j)\rightarrow \mathbb {R}^k\) together with points \(x_j\in B_1(p_j)\) and \(r_j\in [s_{L_j,x_j}^{\delta _j},\frac{1}{4}]\), such that there is no lower triangular matrix A with positive diagonal entries so that \(A\circ f_j: B_{r_j}(x_j)\rightarrow R^k\) is \(L_j\)-drifted \(\epsilon \)-splitting.
Notice that \(r_j\rightarrow 0\). Indeed, if \(r_j\ge c>0\), then since \(r_j\le 1/4\), we have \(B_{c}(x_j)\subseteq B_{r_j}(x_j)\subseteq B_{5/4}(p_j)\subseteq B_{3/2}(x_j)\subseteq B_2(p_j)\), which means the sizes of all these balls are comparable. Then the fact that \(f_j: B_2(p_j)\rightarrow \mathbb {R}^k\) is \(L_j\)-drifted \(\delta _j\) splitting and the volume doubling property immediately implies that \(f_j: B_{r_j}(x_j)\rightarrow \mathbb {R}^k\) is an \(L_j\)-drifted \(C\delta _j\)-splitting map, which in particular is an \(L_j\)-drifted \(\epsilon \)-splitting when j is big enough, and hence contradicts to the hypothesis above.
Thus, we may assume that \(r_j\) is the supremum of the radii for which \(A\circ f_j: B_{r_j}(x_j)\rightarrow R^k\) is not an \(L_j\)-drifted \(\epsilon \)-splitting map for any lower triangular matrix A. It then follows that there exists a lower triangular matrix \(A_j\) such that \(A_j\circ f_j: B_{2r_j}(x_j)\rightarrow \mathbb {R}^k\) is an \(L_j\)-drifted \(\epsilon \)-splitting map. Moreover, since \(|\nabla L_j|\) is bounded, by replacing \(L_j\) by \(L_j-L_j(x_j)\) whenever necessary, we may assume that \(|L_j|\) is bounded in \(B_{1}(x_j)\).
Let
and use the rescaled metric \(g'_j=r_j^{-2}g_j\) for the following arguments. Then \(v_j: B_2(x_j)\rightarrow \mathbb {R}^k\) is \(L_j\)-drifted \(\epsilon \)-splitting, and for any \(2\le r\le \frac{1}{4}r_j^{-1}\), there is a lower triangular matrix \(A_r\) with positive diagonal entries such that \(A_r\circ v_j: B_r(x_j)\rightarrow \mathbb {R}^k\) is \(L_j\)-drifted \(\epsilon \)-splitting. \(\square \)
The following Claims 1 and 2 are directly from [10] (see pp. 1118–1121 for proofs). The only change caused by the drifted situation is that the volume element dV becomes \(dV_{L_j}\).
Claim 1
For any \(2\le r\le \frac{1}{4}r_j^{-1}\), one has
which implies that for any \(1\le a,l\le k\),



Claim 2
There exists a lower triangular matrix A with positive diagonal entries such that \(|A-I|\le C\epsilon \), \(A\circ v_j: B_2(x_j)\rightarrow \mathbb {R}^k \) is \(L_j\)-drifted \(C\epsilon \)-splitting, and for each \(R>0\), after discarding the last component, the map \(A\circ v_j: B_R(x_j)\rightarrow \mathbb {R}^{k-1}\) is \(L_j\)-drifted \(\epsilon _j(R)\)-splitting. Here \(\epsilon _j(R)\rightarrow 0\) whenever R is fixed.
From now on, let \(v_j\) represents \(A\circ v_j\) in claim 2. Thus, as shown in (3.61) and (3.63) in [10], we have for any \(2\le r\le \frac{1}{4}r_j^{-1}\) and \(1\le l\le k\) that


where \(w_j^l=dv_j^1\wedge dv_j^2\wedge \cdots \wedge dv_j^l\).
From Claim 2, we know that \((v_j^1,\ldots ,v_j^{k-1})\) is \(L_j\)-drifted \(\epsilon _j\)-splitting on \(B_1(x_j)\). To get a contradiction, we also need to show that after transformation, the average of \(|dv_j^k|^2\) is approaching 1, and \(dv_j^k\) and \(dv_j^1,\ldots ,dv_j^{k-1}\) tend to be orthogonal.
To show this, we first show that the standard deviation of \(|dv_j^k|^2\) and \(<dv_j^a,dv_j^k>\) (\(1\le a\le k-1\)) are approaching 0 on scale larger than 1 (Claims 3 and 4 below) similar to [10]. However, we use another approach to prove these claims. For Claim 3 below, instead of using the heat kernel, the proof uses an argument involving Green’s function.
Claim 3
For any \(R\ge 1\), we have

and

Proof of Claim 3
Fix an \(R\ge 1\). For any \(x\in B_R(x_j)\) and \(1\le l\le k\), let

Then as in (3.65) in [10], since we have (3.16), by the maximal function arguments, there exists a subset \(U_j\subseteq B_R(x_j)\) satisfying
To get (3.17), it suffices to show that
because it will then follow that

Since \(|w_j^l|\le C(n)\), to show (3.21), we only need to show
First, choose a cut-off function \(\phi \) such that \(\phi =1\) in \(B_{\frac{1}{8}r_j^{-1}}(x_j)\), \(\phi =0\) in \(B^c_{\frac{1}{4}r_j^{-1}}(x_j)\), and
Denote by \(G_{L_j}(x,y)\) the Green’s function for the drifted Laplacian \(\Delta _{L_j}\) on \(\mathbf{M}_j\). Since \(|L_j|\) is bounded on \(B_{r_j^{-1}}(x_j)\), for the Green’s function for \(\Delta _{L_j}\), we still have that
Without loss of generality, we may assume that \(R\le \frac{1}{16}r_j^{-1}\). Thus, for \(x,y\in U_j\).
Using (3.13), (3.22), and (3.23), we have
Similarly, from (3.15), (3.22), and (3.23), one gets \(II\le \epsilon _j(R)\).
Finally, one has

while from (3.16), we have

Therefore, we get \(III\le \epsilon _j(R)\), and this finishes the proof of (3.17).
The proof of (3.18) is similar. Firstly, for the maximal function argument to work, by Claim 2, one needs the smallness of  , for any \(1\le a\le k-1\) and \(2\le r\le \frac{1}{8}r_j^{-1}\). To see this, let \(\phi \) be a cut-off function such that \(\phi =1\) in \(B_r(x_j)\), \(\phi =0\) outside \(B_{2r}(x_j)\), and \(|\nabla \phi |^2+|\Delta \phi |\le \frac{C}{r^2}\). Then,
, for any \(1\le a\le k-1\) and \(2\le r\le \frac{1}{8}r_j^{-1}\). To see this, let \(\phi \) be a cut-off function such that \(\phi =1\) in \(B_r(x_j)\), \(\phi =0\) outside \(B_{2r}(x_j)\), and \(|\nabla \phi |^2+|\Delta \phi |\le \frac{C}{r^2}\). Then,

Notice that \(Ric_{\mathbf{M}_j}+\nabla ^2 L_j+(n-1)\delta _j g_j\) is a non-negative bilinear form, and by Cauchy–Schwartz and Hölder inequalities, one gets

By Bochner’s formula, it is not hard to see that

and similarly

Plugging above estimates in (3.24), we reach

Thus, an analogue of the proof of (3.21) gives
For any \(x\in U_j\), by (3.19), (3.20), and (3.29), we have

Thus, it follows that

This finishes the proof of Claim 3. \(\square \)
Next, we follow a method in [3] to show Claim 4 below and derive the contradiction.
Claim 4
For any \(R\ge 1\), we have

The details of the proof of the Claim was not given in [3]. For readers’ convenience, we give a proof in Appendix A.
Now similar to the arguments on page 101 in [3], let

and

Then \((\hat{v}_j^1,\ldots ,\hat{v}_j^k): B_1(x_j)\rightarrow \mathbb {R}^k\) is an \(L_j\)-drifted \(\epsilon _j\)-splitting map, which contradicts to the inductive hypothesis when j is sufficiently large. The details can also be found in Appendix A.
Hence, this finishes the proof of part a).
To show b), denote by \(v=(v^1,\ldots ,v^k)=A\circ f\) the L-drifted \(\epsilon \)-splitting map from \(B_r(x)\) to \(\mathbb {R}^k\). From the definition, we have

which together with the fact that f is an L-drifted \(\delta \)-splitting map, implies that

i.e.,
Similarly, since
we have

Obviously, when \(\delta \) is chosen small enough so that \(C\delta <1\), then we get \(a_{22}\ge c_0\).
In general, notice that
where \(\eta _i\)’s are constants depending on the entries \(a_{ij}\), \(1\le i,j\le l\).
Since \(dv^1, \ldots , dv^{l-1}, dv^l\) are almost orthonormal under the inner product  , it is not hard to see that
, it is not hard to see that

regardless of the values of \(\eta _1,\ldots ,\eta _{l-1}\). Thus, we get
due to the fact that \(|df^l|^2\le 1+C\delta \).
The proof of the theorem is completed. \(\square \)
4 The Slicing Theorem and Proof of Theorem 1.6
Using the Transformation Theorem, we are able to prove the Slicing Theorem. But before that, we need two more lemmas. Assume that \(f:B_2(p)\rightarrow \mathbb {R}^k\) is an L-drifted \(\delta \)-splitting map. For any open set U and \(1\le l\le k\), define measure
where \(w^l=df^1\wedge df^2\wedge \cdots \wedge df^l\), and \(dV_L=e^{-L}dV\) is the weighted volume element.
Using similar arguments as in Lemma 4.1 in [10], we can show a doubling property for \(\mu _L^l\).
Lemma 4.1
For any \(x\in B_1(p)\), \(s_{L,x}^{\delta }\le r\le 1/4,\) and \(1\le l\le k\), we have
Moreover, by (3.9) Theorem 3.6 part (b), and following a similar proof, one can actually derive a slight more general result than Lemma 4.2 in [10], which is needed for completing the proof of the Slicing Theorem. More explicitly,
Lemma 4.2
For any \(x\in B_1(p)\), \(s_{L,x}^{\delta }\le r\le 1/4,\) and \(1\le l\le k\), we have
where \(|f(B_r(x))|\) denotes the Euclidean measure of \(f(B_r(x))\subseteq \mathbb {R}^k\).
Proof
By Theorem 3.6, there is a lower triangular matrix \(A=(a_{ij})\in GL(k)\) with positive diagonal entries such that
is an \(\epsilon \)-splitting, and hence

where \(\bar{w}^l=d\bar{f}^1\wedge \cdots \wedge d\bar{f}^l\).
Define
Since f is L-drifted \(\delta \)-splitting on \(B_2(p)\), by the volume comparison, it is L-drifted \(C\delta \)-splitting on \(B_{3/2}(p)\).
This together with (4.4) implies

On the other hand, since \(|\nabla \bar{f}|\le 1+\epsilon \) in \(B_{2r}(x)\), it is easy to check that
Thus,
Combining (4.5) and (4.6), we get
Notice that
and from (3.9) in Theorem 3.6 part b), one has
Plugging (4.8) and (4.9) into (4.7), the lemma follows immediately. \(\square \)
To prove the Slicing theorem, we also need the following higher- order integral estimates for a \(\delta \)-splitting map, the proof of which again is similar to Theorem 1.26 in [10].
Theorem 4.3
Given \(\rho >0\). For each \(\epsilon >0\), there exists a \(\delta _1=\delta _1(\epsilon ~|n,\rho )>0\) with the following property. Suppose that a manifold \(\mathbf{M}^n\) satisfies \(Ric+\nabla ^2 L\ge -(n-1)\delta _1\) with \(|\nabla L|\le \delta _1\), and \({{\mathrm{Vol}}}(B_{10}(p))\ge \rho \). Let \(f:B_2(p)\rightarrow \mathbb {R}^k\) be an L-drifted \(\delta \)-splitting map. Then we have:
-
(1)
There exists \(\gamma (n,\rho )>0\) such that for each \(1\le l\le k\),
 (4.10)
(4.10) -
(2)
For any \(1\le l\le k\), the normal mass of \(\Delta _L|w^l|\) satisfies
 (4.11)
(4.11)
The higher-order estimate (4.11) will be used in the proof of the Slicing Theorem below, whose proof follows from the Bochner’s formula for the drifted Laplacian \(\Delta _L\), similar to the proof of (3.24).
Now we are ready to prove the Slicing theorem
Theorem 4.4
(Slicing Theorem) Given \(\rho >0\). For each \(\epsilon >0\), there exists a \(\bar{\delta }=\bar{\delta }(\epsilon ~|n,\rho )>0\) such that the following is satisfied. Suppose that a manifold \(\mathbf{M}^n\) satisfies \(Ric+\nabla ^2 L\ge -(n-1)\bar{\delta }\), \(|\nabla L|\le \bar{\delta }\), and \({{\mathrm{Vol}}}(B_{10}(p))\ge \rho \). Let \(f: B_2(p)\rightarrow \mathbb {R}^{n-2}\) be an L-drifted \(\delta \)-splitting map. Then there is a subset \(G_{\epsilon }\subseteq B_1(0^{n-2})\) such that
-
(1)
\({{\mathrm{Vol}}}(G_{\epsilon })\ge {{\mathrm{Vol}}}(B_1(0^{n-2}))-\epsilon \),
-
(2)
\(f^{-1}(s)\ne \emptyset \) for each \(s\in G_{\epsilon }\),
-
(3)
for each \(x\in f^{-1}(G_{\epsilon })\) and \(r\le 1/4\), there is a lower triangular matrix A with positive diagonal entries so that \(A\circ f: B_r(x)\rightarrow \mathbb {R}^{n-2}\) is an L-drifted \(\epsilon \)-splitting map.
Proof
Firstly, by a generalization of the results in Sect. 2 in [8] (see e.g., Lemma 5.7 in [24]), we know that there exists a \(\delta _2>0\) such that when the assumptions of the theorem are satisfied, we have
Let \(\delta \) be the parameter in the Transformation Theorem 3.6. Set
Next, we show that for \(\bar{\delta }\) small enough, it holds that
Then, setting \(G_{\epsilon }=f(B_1(p))\setminus f(D_{\delta })\) will finish the proof of the theorem.
The collection of balls \(\left\{ B_{s_{L,x}^{\delta }}(x)\right\} ,\ x\in D_{\delta }\) forms a covering of \(D_{\delta }\). Therefore, there exists a subcollection of mutually disjoint balls \(\{B_{s_j}(x_j)\}\), where \(s_j=s_{L,x_j}^{\delta }\), such that
Since \(s_j\) is the L-singular scale, the inequality (3.7) reaches equality at \(w^{l_j}\) for some \(1\le l_j\le n-2\), i.e.,

Moreover, we may assume that \(\bar{\delta }\) is small enough so that \(s_{L,x}^{\delta }\le 1/32\). Then, by Lemma 4.1 (see (4.2)), Lemma 4.2 (see (4.3)), and (4.13), we have
From the fact that f is L-drifted \(\delta \)-splitting on \(B_2(p)\), we know that

Putting this and the fact that \(\{B_{s_j}(x_j)\}\) are disjoint into (4.14), we finally reach

The last step above holds since we may choose \(\delta _1=\delta _1(n, \frac{\epsilon }{2}C^{-1}\delta )\) in Theorem 4.3.
Therefore, setting \(\bar{\delta }<\min (\delta _1,\delta _2,\delta )\) completes the proof. \(\square \)
With the Slicing Theorem, we can finish the proof of Theorem 1.6.
Proof of Theorem 1.6
Firstly, we need the lemma below to play the role of Lemma 1.21 in [10], which generalized the corresponding result in [4] to the case where Bakry–Émery Ricci curvature has a lower bound. \(\square \)
Lemma 4.5
Given \(\rho >0\), for any \(\epsilon \), there exist \(\delta =\delta (\epsilon ~|n,\rho )>0\) such that the following holds. Assume that \({{\mathrm{Ric}}}+\nabla ^2 L \ge - \delta g\), \(|\nabla L|\le \delta \), and
-
(a)
If
$$\begin{aligned} d_{GH}(B_{\delta ^{-1}}(p), B_{\delta ^{-1}}((0^k,x^*))\le \epsilon , \end{aligned}$$where \((0^k,x^*)\in \mathbb {R}^k\times C(X)\) with \(x^*\) being the vertex of the metric cone C(X) over some metric space X, then for any \(R\le 1\), there exists an L-drifted \(\epsilon \)-splitting map \(f=(f_1, f_2, \ldots , f_k):\ B_R(p)\rightarrow \mathbb {R}^k\).
-
(b)
If \(f=(f_1, f_2, \ldots , f_k):\ B_{8R}(p)\rightarrow \mathbb {R}^k\) is an L-drifted \(\delta \)-splitting map for \(R\le 1\), then there is a map \(\Phi : B_R(x)\rightarrow f^{-1}(0)\) such that \((u,\Phi ): B_R(p)\rightarrow B_{R}((0^{k},x^*))\subset \mathbb {R}^k\times f^{-1}(0)\) is an \(\epsilon \)-Gromov Hausdorff approximation.
For a proof of part (a), see e.g., the proof of Lemma 4.11 in [24]. Part (b) holds because from Lemma 3.3 there is a \(C\delta ^{1/2}\)-splitting map u on \(B_{2R}(p)\), which implies that \(B_R(p)\) is \(\epsilon \) close in Gromov Hausdorff sense to a ball in \(\mathbb {R}^k\times u^{-1}(0)\) (see e.g., the proof of Proposition 11.1 in [3]). Then the conclusion in (b) follows from the fact that f and u are close as shown in Lemma 3.3.
Next, as in [10], to rule out the codimension 2 singularity, we only need to show that \(\mathbb {R}^{n-2}\times C(S^1_{\beta })\), \(\beta < 2 \pi \), is not the GH limit of sequences of manifolds under our assumptions. The reason is the following. When the Ricci curvature is bounded, from Theorem 5.2 in [5], if there is a codimension 2 singularity, then a tangent cone is a metric cone \(\mathbb {R}^{n-2}\times Y\) where Y is a cone over a one-dimensional compact metric space of diameter \(\le \pi \). Here the diameter means the maximum length of minimal geodesics. In our setting, the situation is the same by virtue of Theorem 4.3 in [24].
We argue by contradiction, and assume that there is a sequence of pointed Riemannian manifolds \((\mathbf{M}^n_j, g_j, p_j)\) and smooth functions \(L_j\in C^{\infty }(\mathbf{M}_j)\) with \(|Ric_{\mathbf{M}_j}+\nabla ^2 L_j|\le (n-1)\delta _j\rightarrow 0\) and \(|\nabla L_j|\le \delta _j\rightarrow 0\), and \({{\mathrm{Vol}}}(B_{10}(p_j))\ge \rho \) satisfying
where \(S^1_{\beta }\) is a circle of circumference \(\beta <2\pi \) and p is a vertex of the cone.
Let \(\epsilon _j\rightarrow 0\), and \(f_j: B_{\epsilon _j^{-1}}(p)\rightarrow B_{\epsilon ^{-1}_j}(p_j)\) the \(\epsilon _j\)-Gromov–Hausdorff approximation. Denote by \(\mathcal {S}_j=f_j(\mathcal {S})\). Since away from \(\mathcal {S}_j\) the balls in \(\mathbf{M}_j\) are close to balls in \(\mathbb {R}^n\) in Gromov–Hausdorff sense, as shown in the proof of Theorem 1.2, the \(W^{1,q}\) (\(q>2n\)) harmonic radius \(r_h(x)\) is continuous. In particular, we have \(r_h(x)\ge \frac{\tau }{2}\) for any \(x\in B_1(p_j)\setminus T_{\tau }(\mathcal {S}_j)\).
Then we can choose \(\delta _j\) small enough so that there is an \(L_j\)-drifted \(\delta _j\)-splitting map \(u_j: B_2(p_j)\rightarrow \mathbb {R}^{n-2}\) satisfying Theorem 4.4. Hence, it is possible to pick a \(s_j\in G_{\epsilon _j}\cap B_{1/10}(p_j)\) and choose the smallest \(W^{1,q}\) harmonic radius on the submanifold \(u_j^{-1}(s_j)\cap B_1(p_j)\), namely, let
Assume that \(r_j\) is achieved at some point \(x_j\), i.e., \(r_j=r_h(x_j)\). Then it is not hard to see that \(x_j\rightarrow \mathcal {S}_j\cap B_{1/10}(p_j)\) and \(r_j\rightarrow 0\).
By Theorem 3.6, there is a lower triangular matrix \(A_j\) with positive diagonal entries, such that \(v_j=A_j\circ (u_j-s_j): B_{2r_j}(x_j)\rightarrow \mathbb {R}^{n-2}\) is an \(L_j\)-drifted \(\epsilon _j\)-splitting map.
Proceeding as in [10], by passing to a subsequence, the blow-up sequence \((\mathbf{M}^n_j, r_j^{-1}d_j, x_j)\)\(\xrightarrow {d_{GH}}(X,d_X,x)\), where X splits off an \(\mathbb {R}^{n-2}\) factor. Moreover, \(\tilde{v}_j=r_j^{-1}v_j: B_{2}(x_j)\rightarrow \mathbb {R}^{n-2}\) is an \(L_j\)-drifted \(\epsilon _j\)-splitting map. By the proof of Claim 2 in Theorem 3.6, one can see that \(\tilde{v}_j: B_R(x_j)\rightarrow \mathbb {R}^{n-2}\) is an \(L_j\)-drifted \(C(n,\rho ,R)\epsilon _j\)-splitting map for any \(R>2\). In particular, it implies that \(\tilde{v}_j\rightarrow v\) for some \(v: X\rightarrow \mathbb {R}^{n-2}\). Then Lemma 4.5 implies that
Since for any \(y\in \tilde{v}_j^{-1}(0)\), the \(W^{1,q}\) radius \(r_h(y)\ge 1\), by Theorem 2.3, we know that X is \(C^{\alpha }\cap W^{1,s}\) in a neighborhood of \(v^{-1}(0)\). Hence X is a \(C^{\alpha }\cap W^{1,s}\) manifold with \(r_h\ge 1\), and \((\mathbf{M}_j, r_j^{-2}g_j, x_j)\xrightarrow {C^{\alpha }\cap W^{1,s}}(X,g_X,x)\) in Cheeger–Gromov sense. In particular, since the \(W^{1,q}\) harmonic radius is continuous, we have \(r_h(x)=1\).
On the other hand, the expression of the Ricci curvature tensor in harmonic coordinates is
where \(\{v_1, v_2,\ldots , v_n\}\) is a local harmonic coordinate chart. Since \(|Ric+\nabla ^2L|\le (n-1)r_j^2\rightarrow 0\) and \(|\nabla L|\le r_j\rightarrow 0\), and the sequence of metrics \(\{r_j^{-2}g_j\}\) is converging in \(W^{1,s}\) norm on compact sets, one can see that the limit metric \(g_{X}\) is a weak solution of the equation
Therefore, by the standard elliptic regularity theory, it follows that \(g_{X}\) is smooth and Ricci flat, and hence X is a flat manifold since the dimension of \(v^{-1}(0^{n-2})\) is 2. Moreover, by volume continuity under Gromov–Hausdorff convergence (see e.g., Theorem 4.10 in [24]), we have \({{\mathrm{Vol}}}(B_r(x))\ge C\rho r^n\) for any \(r>0\). Thus, it follows that \(X=\mathbb {R}^n\).
Especially, we have \(r_h(x)=\infty \) and contradicts to \(r_h(x)=1\). Therefore, the singular set has codimension at least 3.
Finally, to rule out the codimension 3 singularity, again we can use a similar argument as in [10]. One just needs to notice that by Lemmas 4.5 and 3.3, the \(\epsilon \)-splitting map \(u_j: B_2(p_j)\rightarrow \mathbb {R}^{n-3}\) still exists. Then since the metrics converge in \(C^{\alpha }\) norm and \(u_j\) are harmonic functions, we can still get the bounds on the gradient and hessian of \(u_j\). Also, the Poisson approximation \(h_j\) of the square of the distance function exists by Lemmas 2.3 and 2.4 in [24] (See also the proof of Theorem 6.3 in [26]). Since \(\Delta h_j=2n\) and the metrics \(g_j\) have uniform \(C^{\alpha }\) bound, the standard elliptic regularity theory implies that \(h_j\) have \(C^2\) bound.
Therefore, this completes the proof. \(\square \)
References
Anderson, M.: Convergence and rigidity of manifolds under Ricci curvature bounds. Invent. Math. 102, 429–445 (1990)
Anderson, M., Cheeger, J.: \(C^{\alpha }\)-compactness for manifolds with Ricci curvature and injectivity radius bounded below. J. Differ. Geom. 35, 265–281 (1992)
Bamler, R.: Structure theory of singular spaces. J. Funct. Anal. 272(6), 2504–2627 (2017)
Cheeger, J., Colding, T.H.: Lower bounds on Ricci curvature and the almost rigidity of warped products. Ann. Math. (2) 144(1), 189–237 (1996)
Cheeger, J., Colding, T.H.: On the structure of spaces with Ricci curvature bounded below. I. J. Differ. Geom. 46(3), 406–480 (1997)
Cheeger, J., Colding, T.H.: On the structure of spaces with Ricci curvature bounded below. II. J. Differ. Geom. 54(1), 13–35 (2000)
Cheeger, J., Colding, T.H.: On the structure of spaces with Ricci curvature bounded below. III. J. Differ. Geom. 54(1), 37–74 (2000)
Cheeger, J., Colding, T.H., Tian, G.: On the singularities of spaces with bounded Ricci curvature. Geom. Funct. Anal. 12(5), 873–914 (2002)
Cheeger, J., Naber, A.: Lower bounds on Ricci curvature and quantitative behavior of singular sets. Invent. Math. 191(2), 321–339 (2013)
Cheeger, J., Naber, A.: Regularity of Einstein Manifolds and the codimension 4 conjecture. Ann. Math. 182, 1093–1165 (2015)
Colding, T.H.: Ricci curvature and volume convergence. Ann. Math. (2) 145(3), 477–501 (1997)
Colding, T.H., Naber, A.: Sharp Hölder continuity of tangent cones for spaces with a lower Ricci curvature bound and applications. Ann. Math. (2) 176(2), 1173–1229 (2012)
Dai, X., Wei, G., Zhang, Z.: Local Sobolev constant estimate for integral Ricci curvature bounds. Adv. Math. 325, 1–33 (2018)
Hebey, E., Herzlich, M.: Harmonic coordinates, harmonic radius and convergence of Riemannian manifolds. Rend. Mat. Appl. (7) 17(4), 569–605 (1998)
Li, X.-D.: Liouville theorems for symmetric diffusion operators on complete Riemannian manifolds. J. Math. Pures Appl. (9) 84(10), 1295–1361 (2005)
Petersen, P.: Convergence theorems in Riemannian geometry, comparison geometry. Math. Sci. Res. Inst. Publ. 30, 167–202 (1997)
Petersen, P., Wei, G.: Relative volume comparison with integral curvature bounds. Geom. Funct. Anal. 7(6), 1031–1045 (1997)
Petersen, P., Wei, G.: Analysis and geometry on manifolds with integral Ricci curvature bounds. II. Trans. Am. Math. Soc. 353, 457–478 (2001)
Qian, Z.: Estimates for weighted volumes and applications. Q. J. Math. Oxford Ser. (2) 2(48), 235–242 (1997)
Tian, G., Zhang, Q.S.: A compactness result for Fano manifolds and Kähler Ricci flows. Math. Ann. 362(3–4), 965–999 (2015)
Tian, G., Zhang, Z.: Degeneration of Kähler-Ricci solitons. Int. Math. Res. Not. IMRN 5, 957–985 (2012)
Tian, G., Zhang, Z.: Regularity of Kähler-Ricci flows on Fano manifolds. Acta Math. 216(1), 127–176 (2016)
Wei, G., Wylie, W.: Comparison geometry for the Bakry-Émery Ricci tensor. J. Differ. Geom. 83(2), 377–405 (2009)
Wang, F., Zhu, X.: Structure of spaces with Bakry-Émery Ricci curvature bounded below. Crelle’s J. arXiv:1304.4490
Yang, D.: Convergence of Riemannian manifolds with integral bounds on curvature: I. Ann. Sci. École Norm. Sup. (4) 25(1), 77–105 (1992)
Zhang, Q.S., Zhu, M.: New volume comparison results and applications to degeneration of Riemannian metrics. Adv. Math. arXiv:1605.09420
Zhang, Z.: Degeneration of shrinking Ricci solitons. Int. Math. Res. Not. IMRN 21, 4137–4158 (2010)
Acknowledgements
Q.S.Z is grateful to the Simons foundation for its support. M. Z’s research is partially supported by National Natural Science Foundation of China Grant No. 11501206, Shanghai Pujiang Program No. 18PJ1403000, and Science and Technology Commission of Shanghai Municipality (No. 18dz2271000). M. Z would like to thank Prof. Huai-Dong Cao for constant support and his interest in this paper. Both authors wish to thank Professors M. Anderson, Hong Huang, A. Naber, L. H. Wang, G.F. Wei, Z.L. Zhang, and X.H. Zhu for helpful suggestions. We are very grateful to Dr. Kewei Zhang who pointed out a typo in the statement of Theorem 1.2 in an earlier version. Prof. Z.L. Zhang kindly informed us that he and Prof. W.S. Jiang are able to extend Cheeger and Naber’s result under the condition that the Ricci curvature is \(L^p\) with \(p>n/2\). In this case, the metric is \(W^{2, p}\) rather than \(W^{1, p}\) in the current paper. Finally, we also wish to thank the referee for helpful suggestions. Most of the paper was finished when M. Z. was a Visiting Assistant Professor at UC Riverside. He is grateful for the math department there for warm hospitality and for providing a great environment for collaborations.
Author information
Authors and Affiliations
Corresponding author
Appendix A
Appendix A
In this section, we prove Claim 4 and finish the proof of Theorem 3.6 part a).
Proof of Claim 4
We first show that

Here, as usual, define
Thus,
Since \((v_j^1, \ldots , v_j^{k-1})\) is an \(\epsilon _j(R)\)-splitting on \(B_R(x_j)\) by Claim 2, it is not hard to see that

Therefore, (A.1) follows from (3.18) and (A.2) immediately.
Notice that \(w_j^k=w_j^{k-1}\wedge dv_j^k\), and
From (3.17), we have

This, together with (A.1), implies that

Combining this with the fact that \((v_j^1,\ldots , v_j^{k-1})\) is an \(L_j\)-drifted \(\epsilon _j(R)\)-splitting map on \(B_R(x_j)\), we have

Therefore, it finishes the proof of Claim 4. \(\square \)
Recall that

and
Since \((v_j^1,\ldots ,v_j^k): B_2(x_j)\rightarrow \mathbb {R}^k\) is \(L_j\)-drifted \(C\epsilon \)-splitting, and \((v_j^1,\ldots ,v_j^{k-1}): B_2(x_j)\rightarrow \mathbb {R}^{k-1}\) is \(L_j\)-drifted \(\epsilon _j\)-splitting, it follows that

Hence,
The above facts and (3.18) imply that

and

Setting

one has

where we have used (3.31), (A.4), and the fact that \((v_j^1, \ldots , v_j^{k-1})\) is an \(L_j\)-drifted \(\epsilon _j\)-splitting map. Therefore, by using the similar technique as in Lemma 3.34 in [10] (or mean value inequality), one can get
and


It is obvious that (A.7), (A.8), and (A.9) together with the fact that \((v_j^1,\ldots ,v_j^{k-1})\) is \(L_j\)-drifted \(\epsilon _j\)-splitting imply that \((\hat{v}_j^1,\ldots ,\hat{v}_j^k): B_1(x_j)\rightarrow \mathbb {R}^k\) is an L-drifted \(\epsilon _j\)-splitting map. Since \(B_1(x_j)\) in the metric \(r_j^{-2}g_j\) is exactly the ball \(B_{r_j}(x_j)\) in the metric \(g_j\) and \(\epsilon _j\rightarrow 0\), this means that before rescaling \((\hat{v}_j^1,\ldots ,\hat{v}_j^k): B_{r_j}(x_j)\rightarrow \mathbb {R}^k\) is \(L_j\)-drifted \(\epsilon \)-splitting when j is sufficiently large, which contradicts to the inductive hypothesis that there is no matrix A such that \(A\circ u\) is \(L_j\)-drifted \(\epsilon \)-splitting on \(B_{r_j}(x_j)\).
Hence, this finishes the proof of Theorem 3.6 part a).
Rights and permissions
About this article
Cite this article
Zhang, Q.S., Zhu, M. Bounds on Harmonic Radius and Limits of Manifolds with Bounded Bakry–Émery Ricci Curvature. J Geom Anal 29, 2082–2123 (2019). https://doi.org/10.1007/s12220-018-0072-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12220-018-0072-9



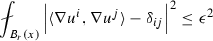 ,
,  ,
,  ,
,  ,
, 
