Pattern Formation in Miscible Rotating Hele-Shaw Flows Induced by a Neutralization Reaction

Abstract

We study the centrifugal buoyancy-driven chemoconvection in a Hele-Shaw cell that uniformly rotates around e perpendicular axis. The slot is considered thin enough to neglect the influence of the Coriolis force. The initial configuration of the system consists of two aqueous reacting solutions separated by a concentric boundary. The acid solution fills the center of the cavity, while the base solution is in the periphery. Bringing liquids into contact initiates a neutralization reaction to form a salt. We show that reaction-diffusion processes produce a potential well near the reaction front, which determines the pattern formation of the system. For some ratios of initial concentrations, there appears a periodic sequence of chemoconvective vortices in the well, while for others, when the well collapses, a shock-like density wave occurs. When the density of the acid solution is higher, the Rayleigh-Taylor instability develops in the system. We found that an increase in the rotation speed leads to a gradual disruption of the structure periodicity. It can even result in the ejection of some vortices from the potential well. We show that the density wave is extremely sensitive to the magnitude of the centrifugal force, occurring only at some critical value. Finally, we obtained a stability map of the system by performing direct numerical simulations for increasing the centrifugal Rayleigh number and the dimensionless distance of the initial contact surface between the solutions from the axis of rotation.

Introduction

Fig. 1

Schematic representation of the problem of a self-gravitating spherical fluid layer heated laterally, which rotates uniformly around a fixed axis (in the center). This complicated geophysical problem simulating the planet’s atmosphere is the starting point for two more simplified formulations, one of which includes a rotating cylindrical layer (shown on the left) and the other is a kind of Rayleigh-Bénard problem with uniform rotation around an orthogonal axis (shown on the right)

In recent decades, multiple studies have shown that an inertial field tuned from the outside can be a powerful tool for controlling heat and mass transfer processes in liquid media Gershuni and Lyubimov (1998); Allali et al. (2002); Lyubimov et al. (2006); Shevtsova et al. (2010); Bratsun et al. (2017). In this case, different types of inertial fields have distinct effects on the liquid. For example, linearly polarized high-frequency vibrations produce an averaged force field that acts uniformly in the medium Gershuni and Lyubimov (1998). In contrast to that, the rotation generates a spatially inhomogeneous effect due to centrifugal force and Coriolis force Chandrasekhar (1961). The first force affects the fluid element the more significantly, the further it is located from the axis of rotation. The second one acts stronger on those volume elements that move faster. Generally, the classification of problems with rotating systems depends on the Rossby number defined as the ratio between inertial forces (triggered by gravity, centrifugal force, or pressure gradient) and Coriolis force. The authors of the recent work Rouhi et al. (2021) made a complete review of the papers devoted to various types of centrifugation. They have noticed that the systems characterized by large values of the Rossby number received insufficient attention Busse and Carrigan (1974); Stevens et al. (2013); Read et al. (2008); Von Larcher et al. (2018).

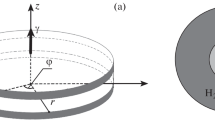
The mutual orientation of the rotation axis and the gradient of density is another important criterion for classifying the type of problem (see Fig. 1 for details). Rouhi et al. (2021) distinguished two main classes of problems: (a) centrifugal convection in a cylindrical gap, where the axis of rotation and the density gradient due to heating across the gap are perpendicular Busse and Carrigan (1974); Read et al. (2008); Von Larcher et al. (2018); Fowlis and Hide (1965); Hide and Mason (1970; b) rotating Rayleigh-Bénard convection in a plain layer, where the axis of rotation and the density gradient are collinear Chandrasekhar (1953); Veronis (1959, 1968); Shaidurov et al. (1969); Julien et al. (1996); De Wit et al. (2020). Figure 1 schematically shows these formulations as two simplifications of the geophysical problem of a uniformly rotating spherical fluid layer that radially gravitates and is subject to lateral heating (presented in the center of the figure). A rotating spherical layer gives an example of much more complicated configuration, in which the angle between the indicated vectors changes when an observer is moving along the sphere. It seems clear that problem formulations presented in the figure historically have been motivated by a research interest in geophysical applications and planetary explorations Cordero and Busse (1992); Busse et al. (1997). One can see from Fig. 1, all three configurations demand the study of three-dimensional fluid flows and require the Coriolis force to be taken into account.

Chandrasekhar (1961, 1953) and Veronis (1959, 1968) seem to be the first to study the effect of rotation in the Rayleigh-Bénard problem (Fig. 1, scheme on the right). In this formulation, the Coriolis force plays a principal role in the transfer processes. Based on the linear theory of hydrodynamic stability, the authors showed that rotation generally stabilizes the mechanical equilibrium of liquid and increases the threshold for the onset of convection. They found that the critical wave number also increases with increasing rotational intensity. The stability of an advective flow in a rotating horizontal layer was studied in Julien et al. (1996); Schwarz (2005); Aristov and Shvarts (2016); Aristov and Schwarz (2006); Novi et al. (2019).

As a rule, centrifugal convection is studied in a thin cylindrical layer Rouhi et al. (2021), where the centrifugal force has a quasi-constant value within the cavity (Fig. 1, scheme on the left). And again, in this case, the Coriolis force plays a principal role. At very high Rossby numbers (small Coriolis effect), such a configuration is essentially analogous to the Rayleigh-Bénard problem, in which the centrifugal force replaces the static gravity field. Here we should note that existing centrifugation setups can easily reach rotational speeds, at which centrifugal force can be one to two orders of magnitude greater than the acceleration due to gravity. Therefore, a thin cylindrical layer rotating around the axis of symmetry is a model system to study the effect of constant inertia. It is important to note that one can change this force field to both microgravity and hypergravity conditions.

Fig. 2

Schematic representation of the problem under the consideration. Two miscible reacting solutions fill the cylindrical Hele-Shaw cell rotating around a perpendicular axis. Since the cell gap h is small compared with the characteristic size of the disk $r_0$, the Coriolis force does not contribute to the dynamics of the system. In this case, the density gradient, which depends on the local values of the concentrations of the reactants, is always perpendicular to the axis of rotation

Another problem arises if we consider a plain layer of fluid where the density variations are directed along with the layer, and all system rotates around a perpendicular axis (see Fig. 2 and compare it with configurations presented in Fig. 1). If the layer gap width tends to zero $h/r_0\rightarrow 0$ reflecting the Hele-Shaw approximation, then the inverse Rossby number also tends to zero. In this case, the Coriolis force is small and can be neglected compared with the centrifugal force. On the one hand, this problem differs significantly from the Rayleigh-Bénard problem with rotation in that the density gradient is perpendicular to the axis of rotation (Fig. 1, scheme on the right). On the other hand, we cannot reduce this problem to canonical centrifugal convection discussed above. The Coriolis force does not matter here, and centrifugal force creates a spatially-inhomogeneous inertial field. Interest in such problems is not associated with geophysical or astrophysical applications but with a convenient configuration for studying the mixing process in the miscible solutions and problems of chemical technology Chen et al. (2006, 2011); Leandro et al. (2008).

As is known, the non-linear interaction of chemical reactions and convection expands the capabilities of a medium to organize the fluid flow. Here, both previously well-studied instabilities and completely new types of chemoconvective instabilities can arise Avnir and Kagan (1995); Eckert and Grahn (1999); Bees et al. (2001); Almarcha et al. (2010); Bratsun et al. (2015). Besides, this area of research has a lot of technological applications Reschetilowski (2013); Jensen (2001); Bratsun et al. (2018). In recent years, the above reasons have stimulated the interest of researchers to study the processes of mutual influence of chemical transformations and convective mass transfer. Even without macroscopic movement of reacting fluids, reaction-diffusion problems represent a separate research area with numerous publications. In this case, the kinetics of the reactions considered in reaction-diffusion problems can be very diverse. Therefore, to study the effect of chemical reactions on fluid motion in interdisciplinary problems, researchers usually limit themselves to considering reactions with simple albeit non-linear kinetics. The acid neutralization reaction with a base of the form $\text {A} + \text {B} \rightarrow \text {S}$ is an ideal candidate for such problems since this is a well-studied second-order reaction. It ensured the popularity of this reaction scheme among researchers.

The excitation of convective motion induced by a neutralization reaction between two solutions under a static gravity field was experimentally investigated in Zalts et al. (2008); Asad et al. (2010); Almarcha et al. (2011). The general classification of instabilities that can occur in miscible systems was given in Trevelyan et al. (2015). The authors found a self-similar solution of the reaction-diffusion equations in the large-time asymptotics and described the basic scenarios for the evolution of a two-layer system. Our recent studies Bratsun et al. (2015, 2016, 2017) have shown that the classification suggested in Trevelyan et al. (2015) should be supplemented with at least two more chemoconvection modes. One of them is a periodic system of vortices that develop inside a potential density well, which arises due to reaction-diffusion processes Bratsun et al. (2015). The second scenario includes the excitation of a shock-like density wave followed by intense convection in the cocurrent flow Bratsun et al. (2017). Besides, in Bratsun et al. (2017), we have formulated a new dimensionless parameter, the number of reaction-induced buoyancy, which defines the occurrence of new modes of chemoconvection. A complete description of the processes in a two-layer miscible system of two reacting fluids under static gravity was given in two recent works Mizev et al. (2021); Bratsun et al. (2021). This convective system under static gravity g are characterised by the set of solutal Rayleigh number $R_{i}$ defined as

$$\begin{aligned} Ra_i= & {} \frac{g \beta _i A^{*}h^3}{\nu D_{A0}} , \end{aligned}$$

(1)

where $\beta _{i}$ is the solutal expansion coefficient for i-species (i stands for any of three concentrations of acid A, base B, and salt C), $\nu$ is the kinematic viscosity of solvent (water), $D_{A0}$ is the tabular value of the diffusion coefficient of the leading reactant (acid), and $A^{*}$ is the characteristic concentration difference of acid. In reaction-diffusion problems, in contrast to non-isothermal problems with external heating, the characteristic difference in density is specified using the initial conditions for the concentrations. Once established at the very beginning of the experiment, the experimenter then cannot change it. Therefore, the solutal Rayleigh number (1), in fact, is not a governing parameter of the problem in the true sense of the word, yielding this right to the initial concentrations of reactants. In this paper, however, we consider the problem of uniform rotation with an angular velocity $\Omega$. It means that the Rayleigh parameter  (1) must be replaced by the centrifugal number defined as

$$\begin{aligned} Ra_i^{\Omega }= & {} \frac{\beta _i \Omega ^2 A^{*}h^4}{\nu D_{A0}} . \end{aligned}$$

(2)

In this case, the situation dramatically changes since we can control the processes inside the rotating system by tuning the rotation velocity $\Omega$.

Thus, in this paper, we investigate the development of chemoconvection in a system of reacting fluids filling a Hele-Show cell, which rotates uniformly around an axis perpendicular to the layer. Let us list again the principal differences of our problem formulation (Fig. 2) from configurations shown in Fig. 1: (i) the density gradient is determined by the concentrations of reacting species; (ii) the density gradient is orthogonal to the rotation axis; (iii) the density gradient varies along with the layer, which makes it possible to consider an ultra-narrow layer where the Coriolis force can be neglected and only two-dimensional flows can be considered; (iv) the inertial field defined by only centrifugal force is spatially inhomogeneous. Finally, we can tune this field by changing the magnitude of the angular velocity. We study the problem numerically and show how the system changing its behavior depending on the rotation speed, the location of the initial contact surface, and the initial concentrations of the solutions.

Mathematical Formulation

We consider a two-layer system of miscible liquids placed in a gap between two parallel solid plates and initially separated by a contact surface (Fig. 2). Let the plates be circular with a radius of $r_0$ each. The resulting cylindrical slot filled with an incompressible liquid uniformly rotates around the axis of symmetry of the cylinder with the angular velocity $\mathbf {\Omega }=\Omega \mathbf {\gamma }$, where $\mathbf {\gamma }$ stands for the unit vector perpendicular to the slot.

We assume that two miscible liquids are an aqueous solution of nitric acid A, which is located in the center of the cuvette, and an aqueous solution of sodium hydroxide B, which is located at the periphery (Fig. 2). Let us denote the distance from the axis of rotation to the contact surface of two mixtures as $l_0$. The initial concentrations of reactants are $A_0$ and $B_0$. The acid diffuses to react with the base to form their salt C under the production of water. Such a neutralization reaction can be described by the simplified equation:

$$\begin{aligned} \text {A} + \text {B} \rightarrow \text {C} + \text {Q} \end{aligned}$$

(3)

with the reaction rate characterized by the constant K. Thus, a second-order exothermic neutralization reaction defined by (3) has comparatively simple, albeit nonlinear, kinetics. It is worth noting that the wide plates are usually from glass, which transmits significant heat because the thermal conductivity coefficients of water and glass are nearly the same. Thus, in experiments, the thermal effects can be controlled to a greater extent compared with the concentration-dependent phenomena. In Bratsun et al. (2021), we evaluated the contribution of two effects to the buoyancy force and concluded that the thermal effect can be neglected. The simplified kinetics of the neutralization reaction given by Eq. (3) ignores water production. It can be a problem in some situations since the concentration of substances near the reaction front constantly decreases. The use of the model (3) is somewhat justified by the simultaneous decrease in the concentration of all substances, while the change in the balance of the reactants with respect to each other is more sensitive.

To describe the effect of rotation on the transfer processes in the cylindrical slot shown in Fig. 2, we move to the frame of reference, rotating with the plates in an anticlockwise direction about its cylindrical axis $\mathbf {\gamma }$. By taking into account the geometry of the cell, we represent the total velocity field $\mathbf {u}$ in the form of a two-component velocity ${\mathbf {u}}_{||}=(u_r, u_\phi )$ acting in the plane of the layer and an orthogonal component $u_z$. In this case, the set of reaction-diffusion-convection equations has the following form:

$$\begin{aligned} \nabla _{||} \cdot {\mathbf {u}}_{||} + \frac{\partial u_z}{\partial z} = 0, \end{aligned}$$

(4)

$$\begin{aligned} \rho \left( \frac{\partial {{\mathbf {u}}_{||}}}{\partial t} + ({{\mathbf {u}}_{||}}\cdot \nabla _{||}) {{\mathbf {u}}_{||}} + u_z\frac{\partial {\mathbf {u}}_{||}}{\partial z}\right) = - \nabla _{||} p + \eta \nabla ^2_{||}{{\mathbf {u}}_{||}} + \end{aligned}$$

$$\begin{aligned} \qquad + \eta \frac{\partial ^2{\mathbf {u}}_{||}}{\partial z^2} + 2\rho \Omega ({\mathbf {u}}_{||}\times {\mathbf {\gamma }}) + \rho \Omega ^2 ({\mathbf {\gamma }} \times {\mathbf {r}}) \times {\mathbf {\gamma }} , \end{aligned}$$

(5)

$$\begin{aligned}&\rho \left( \frac{\partial {u_z}}{\partial t} + ({\mathbf {u}}_{||}\cdot \nabla _{||}) {u_z} + u_z\frac{\partial {u_z}}{\partial z}\right) = - \frac{\partial p}{\partial z} + \eta \nabla ^2_{||}{u_z} + \nonumber\\&\qquad \qquad + \eta \frac{\partial ^2{u_z}}{\partial z^2} - \rho g, \end{aligned}$$

(6)

$$\begin{aligned} \frac{\partial A}{\partial t} + ({\mathbf {u}}_{||}\cdot \nabla _{||}) A + u_z\frac{\partial {A}}{\partial z} = \nabla \cdot (D_A \nabla A) - K A B, \end{aligned}$$

(7)

$$\begin{aligned} \frac{\partial B}{\partial t} + ({\mathbf {u}}_{||}\cdot \nabla _{||}) B + u_z\frac{\partial {B}}{\partial z} = \nabla \cdot (D_B \nabla B) - K A B, \end{aligned}$$

(8)

$$\begin{aligned} \frac{\partial C}{\partial t} + ({\mathbf {u}}_{||}\cdot \nabla _{||}) C + u_z\frac{\partial {C}}{\partial z} = \nabla \cdot (D_C \nabla C) + K A B, \end{aligned}$$

(9)

where Navier-Stokes Equation (5, 6) couples to evolution Equations (7, 8, 9) for the concentrations of species A, B, C, and the continuity Equation (4). Here, p is the pressure, $\rho$ is the density of the fluid, $\eta$ is the coefficient of dynamic viscosity, and g is the acceleration due to gravity.

This system is complemented by the boundary conditions in the form:

$$ r = r_0:\quad {\mathbf {u}}={} 0,\ \frac{\partial A}{\partial r} = 0,\ \frac{\partial B}{\partial r} = 0,\ \frac{\partial C}{\partial r} = 0 ,$$

(10)

$$z = \pm \frac{h}{2}: \quad {\mathbf {u}}= {} 0,\ \frac{\partial A}{\partial z} = 0,\ \frac{\partial B}{\partial z} = 0,\ \frac{\partial C}{\partial z} = 0 ,$$

(11)

where we assume that the cavity is closed and has solid boundaries.

In addition to boundary conditions (10, 11), we must require the boundedness of the values of all fields at the singular point of the problem $r=0$. Below we will show how this condition was fulfilled when finding a numerical solution to the problem.

By taking into account that $l_0$ is the distance from the axis of rotation to the initial contact surface of two mixtures (Fig. 2), the initial conditions are

$$\begin{aligned} t= & {} 0,\ 0\leqslant r \leqslant l_0:\quad {\mathbf {u}}=0,\ A = A_0,\ B = 0 , \end{aligned}$$

(12)

$$\begin{aligned} t= & {} 0,\ l_0 < r \leqslant r_0:\quad {\mathbf {u}} = 0,\ A=0,\ B = B_0 . \end{aligned}$$

(13)

Then we expand the medium density $\rho$ as a power series of concentrations retaining only linear terms:

$$\begin{aligned} \rho = \rho _0(1 +\beta _A A +\beta _B B +\beta _C C) , \end{aligned}$$

(14)

where $\rho _0$ is the density of the solvent (water), $\beta _{A,B,C}$ stand for the solutal expansion coefficients of species. In (14), we take into account the fact that all the dissolved substances are heavier than water. The Boussinesq approximation for the convection problems assumes that the variations (14) should be taken into account only in terms depending on the volumetric forces. The Boussinesq approach is justified for the problems in which “weak” convection exists in the cavity on the laboratory scale, and the density variations caused by thermal or concentration expansion are relatively small.

To render the equations dimensionless, we choose the following characteristic scales for variables:

$$\begin{aligned}&x^{*}, y^{*} \sim h,\quad t^{*} \sim \frac{h^2}{D_{a0}}, \quad u^{*} \sim \frac{D_{a0}}{h} , \nonumber \\&p^{*}\sim \frac{\rho _0\nu D_{a0}}{h^2},\quad A^{*}, B^{*}, C^{*}\sim A_{lim}. \end{aligned}$$

(15)

Here, $A_{lim}$ is the upper limit of the acid concentration range, in which diffusion coefficients of species linearly depend on their concentrations (see Bratsun et al. (2015, 2021) for more details), $D_{a0}$ is the tabular value of the diffusion coefficient of nitric acid. When evaluating the dimensionless parameters, we use the values $A_{lim}=3$ mol/l and $D_{a0}=3.15\times 10^{-5}$ cm$^2$/s. In what follows, we keep the same symbols for dimensionless variables as for dimensional ones. Then we obtain:

$$\begin{aligned} \nabla _{||} \cdot {\mathbf {u}}_{||} + \frac{\partial u_z}{\partial z} = 0, \end{aligned}$$

(16)

$$\begin{aligned} \frac{1}{Sc}\left( \frac{\partial {{\mathbf {u}}_{||}}}{\partial t} + ({{\mathbf {u}}_{||}}\cdot \nabla _{||}) {{\mathbf {u}}_{||}} + u_z\frac{\partial {\mathbf {u}}_{||}}{\partial z}\right) = - \nabla _{||} p + \end{aligned}$$

$$\begin{aligned} \qquad + \nabla ^2_{||}{{\mathbf {u}}_{||}} + \frac{\partial ^2{\mathbf {u}}_{||}}{\partial z^2} + \sqrt{Ta} ({\mathbf {u}}_{||}\times {\mathbf {\gamma }}) + \end{aligned}$$

$$\begin{aligned} \qquad + Ra_A^{\Omega } ( A + R_B B + R_C C) ({\mathbf {\gamma }} \times {\mathbf {r}}) \times {\mathbf {\gamma }} , \end{aligned}$$

(17)

$$\begin{aligned} \frac{1}{Sc}\left( \frac{\partial {u_z}}{\partial t} + ({\mathbf {u}}_{||}\cdot \nabla _{||}) {u_z} + u_z\frac{\partial {u_z}}{\partial z}\right) = - \frac{\partial p}{\partial z} + \nabla ^2_{||}{u_z} + \end{aligned}$$

$$\begin{aligned} \qquad \qquad + \frac{\partial ^2{u_z}}{\partial z^2} - Ra_A ( A + R_B B + R_C C), \end{aligned}$$

(18)

$$\begin{aligned} \frac{\partial A}{\partial t} + ({\mathbf {u}}_{||}\cdot \nabla _{||}) A + u_z\frac{\partial {A}}{\partial z} = \nabla \cdot (D_A \nabla A) - \end{aligned}$$

$$\begin{aligned} \qquad \qquad - Da A B, \end{aligned}$$

(19)

$$\begin{aligned} \frac{\partial B}{\partial t} + ({\mathbf {u}}_{||}\cdot \nabla _{||}) B + u_z\frac{\partial {B}}{\partial z} = \nabla \cdot (D_B \nabla B) - \end{aligned}$$

$$\begin{aligned} \qquad \qquad - Da A B, \end{aligned}$$

(20)

$$\begin{aligned} \frac{\partial C}{\partial t} + ({\mathbf {u}}_{||}\cdot \nabla _{||}) C + u_z\frac{\partial {C}}{\partial z} = \nabla \cdot (D_C \nabla C) + \end{aligned}$$

$$\begin{aligned} \qquad \qquad + Da A B, \end{aligned}$$

(21)

$$\begin{aligned} r = R:\quad {\mathbf {u}}= & {} 0,\ \frac{\partial A}{\partial r} = 0,\ \frac{\partial B}{\partial r} = 0,\ \frac{\partial C}{\partial r} = 0 , \end{aligned}$$

(22)

$$\begin{aligned} z = \pm \frac{1}{2}: \quad {\mathbf {u}}= & {} 0,\ \frac{\partial A}{\partial z} = 0,\ \frac{\partial B}{\partial z} = 0,\ \frac{\partial C}{\partial z} = 0 . \end{aligned}$$

(23)

$$\begin{aligned} t= & {} 0,\ 0\leqslant r \leqslant L:\quad {\mathbf {u}}=0,\ A = \gamma _A,\ B = 0 , \end{aligned}$$

(24)

$$\begin{aligned} t= & {} 0,\ L < r \leqslant R:\quad {\mathbf {u}} = 0,\ A=0,\ B = \gamma _B . \end{aligned}$$

(25)

Let us list all the dimensionless parameters, which appear in the problem (16)–(25). These are

$$\begin{aligned} Sc= & {} \frac{\nu }{D_{A0}} ,\ Da = \frac{K A_{lim} h^2}{D_{A0}},\ Ta =\left( \frac{2\Omega h^2}{\nu }\right) ^2,\nonumber \\ Ra_A= & {} \frac{g\beta _A A_{lim} h^3}{\nu D_{A0}},\ Ra_A^{\Omega } = \frac{\beta _A \Omega ^2 A_{lim} r_0 h^3}{\nu D_{A0}} ,\ \nonumber \\ R_B= & {} \frac{\beta _B}{\beta _A} , \ R_C = \frac{\beta _C}{\beta _A} , \\ \gamma _A= & {} \frac{A_0}{A_{lim}} ,\ \gamma _B = \frac{B_0}{A_{lim}},\ L = \frac{l_0}{h} ,\ R = \frac{r_0}{h} \nonumber \end{aligned}$$

(26)

the Schmidt number, the Damköhler number, the Taylor number, the gravity-based solutal Rayleigh number, the centrifugal Rayleigh number, the ratio of solutal expansion coefficients of base and acid, the ratio of solutal expansion coefficients of salt and acid, the initial concentration of acid, the initial concentration of base, the dimensionless position of the initial reaction front, and the dimensionless radius of the disk-shaped cavity, respectively. Based on experimental measurements, we can estimate some of parameters (26) for a given pair of acid and base: $Sc = 317$, $Da\approx 10^3$, $R_B=6/5$, $R_C = 8/5$.

We will further assume that the Froude number, which is a dimensionless number defined as the ratio of the flow inertia to gravity, is much greater than unity Aristov and Schwarz (2006):

$$\begin{aligned} Fr = \frac{Ra_A^{\Omega }}{Ra_A} = \frac{\Omega ^2 r_0}{g} \gg 1 . \end{aligned}$$

(27)

Modern experimental setup for centrifugation can create overload conditions in which the inertia is tens and even hundreds of times higher than the static gravity force. So, we can neglect the effect of gravity in Eqs. (17, 18). However, one should keep in mind that near the rotation axis, the inertial forces are negligible. Therefore, in this area, static gravity can have a significant effect. It implies that we must formulate the initial conditions so that the primary development of the chemoconvective instability occurs far enough from the rotation axis.

The right side of the equation of motion (17) contains two forces of inertia, the Coriolis force (the penultimate term) and centrifugal force (the last one). Let us estimate the contribution of these terms in the problem under consideration. This issue has been discussed for quite some time in various papers devoted to the rotation of the Hele-Shaw cell (see, for example, Carillo et al. (1996); Alvarez-Lacalle et al. (2004)). As is known, from the mathematical point of view, the fluid flow in a Hele-Shaw cell is similar to the filtration of fluid through a porous medium. The closely spaced wide walls of the HS cell generate a significant resistance force, which produces an effect similar to the resistance of a solid porous matrix to percolating fluid. The simplest mathematical model in both cases is the Darcy filtration, where the fluid velocity is directly determined by the force applied to it (so-called “Aristotle mechanics”). The velocity values during the filtration are always small. And since the magnitude of the fluid velocity is a fundamentally important component of the Coriolis force, the Hele-Shaw approximation significantly weakens this force. Let us estimate the Taylor and Rayleigh numbers, which determine the intensity of the Coriolis and centrifugal forces, respectively, for a typical Hele-Shaw cell, which we used in an experimental study presented in Mizev et al. (2021):

$$\begin{aligned} \sqrt{Ta}= & {} \frac{2 \Omega h^2}{\nu } \approx \Omega \ \text {s} ,\\ Ra_A^{\Omega }= & {} \frac{\Omega ^2 \beta _A A_{lim}r_0 h^3}{\nu D_{A0}} \approx 3 \cdot 10^3\Omega ^2\ \text {s}^2 , \end{aligned}$$

where we used the data for water and nitric acid. We can see from the estimates above that even near the axis of rotation (at a distance $\sim h$), the Coriolis force cannot compete with the centrifugal force at $\Omega \geqslant 1$ rps. Such competition could appear with super slow rotation $\Omega ~\ll ~1$ rps, but we do not consider this case in the present work.

Let us estimate the distance from the axis of rotation, at which the centrifugal force and the Coriolis force are of the same order of magnitude:

$$\begin{aligned} \Omega ^2 r \approx \Omega U^{*} , \end{aligned}$$

where $r\in [0,r_0]$ stands for the current radius, $U^{*}$ is the characteristic fluid velocity. Consider the case of a not too high rotation speed, which creates a centrifugal force about g at the edge of the disk: $\Omega ^2 r_0\approx 1g$ . By using the wave propagation speed $5\cdot 10^3$ cm/s as the characteristic convective velocity $U^{*}$ (see  Bratsun et al. (2017)), we immediately get an estimate:

$$\begin{aligned} r \approx 10^{-4} r_0 . \end{aligned}$$

Assume, further, that the gap width between the plates h is small enough that the emerging flows to be two-dimensional $h/r_0\rightarrow 0$ (see Fig. 2). Thus, the cylindrical cavity is, in fact, a Hele-Show cell, and the governing equations can be averaged across the gap using the following approximations:

$$\begin{aligned} {\mathbf {u}}_{||} (r,\phi ,z) = \frac{3}{2}\left( 1 - 4z^2\right) {\mathbf {U}} (r,\phi ) ,\quad u_z = 0, \nonumber \\ A = A(r,\phi ),\ B = B(r,\phi ),\ C = C(r,\phi ) , \end{aligned}$$

(28)

which satisfy the boundary conditions (22, 23). Here, ${\mathbf {U}} = (u_r, u_{\phi })$ is the two-component velocity field in the $(r,\phi )$-plane of the Hele-Shaw slot.

It is worth noting that the Poiseuille flow taken as an approximation for the fluid flow in the Hele-Shaw cell (28) works well when the influence of the Coriolis force is negligible. If this is not the case, then another type of flow can be used (for example, the Hartmann flow).

The approximations (28) should then be substituted into the Eqs. (16)–(21) and averaged across the gapwidth:

$$\begin{aligned} <...> = \int _{-1/2} ^{1/2} ... dz. \end{aligned}$$

(29)

By introducing a stream function $\Psi (r, \phi )$ defined by

$$\begin{aligned} u_r = \frac{1}{r}\frac{\partial \Psi }{\partial \phi } , \quad u_\phi = -\frac{\partial \Psi }{\partial r} \end{aligned}$$

(30)

we obtain the dimensionless system of reaction-diffusion-convection equations in the final form:

$$\begin{aligned} \nabla ^2 \Psi + \Phi = 0 , \end{aligned}$$

(31)

$$\begin{aligned} \frac{1}{Sc} \left( \frac{\partial \Phi }{\partial t} + \frac{6}{5r} \frac{\partial (\Phi , \Psi ) }{\partial (r, \phi ) } \right) = \nabla ^2 \Phi -12 \Phi - R_A \frac{\partial {\hat{\rho }}}{\partial \phi } , \end{aligned}$$

(32)

$$\begin{aligned} \frac{\partial A}{\partial t} + \frac{1}{r} \frac{\partial (A , \Psi ) }{\partial (r, \phi ) } = \nabla \cdot (D_A (A) \nabla A) - Da AB , \end{aligned}$$

(33)

$$\begin{aligned} \frac{\partial B}{\partial t} + \frac{1}{r} \frac{\partial (B , \Psi ) }{\partial (r, \phi ) } = \nabla \cdot (D_B (B) \nabla B) - Da AB , \end{aligned}$$

(34)

$$\begin{aligned} \frac{\partial C}{\partial t} + \frac{1}{r} \frac{\partial (C , \Psi ) }{\partial (r, \phi ) } = \nabla \cdot (D_C (C) \nabla C) + Da AB , \end{aligned}$$

(35)

$$\begin{aligned} \hat{\rho }= A + R_B B + R_C C , \end{aligned}$$

(36)

where $\Phi \equiv (\nabla \times \mathbf {v})_z$ stands for the vorticity. In (32)–(36), the Jacobian is defined as

$$\begin{aligned} \frac{\partial (a , b) }{\partial (r, \phi ) }\equiv \frac{\partial a}{\partial r}\frac{\partial b}{\partial \phi }-\frac{\partial a}{\partial \phi }\frac{\partial b}{\partial r}. \end{aligned}$$

(37)

The dimensionless variable $\hat{\rho }(t,\rho ,\phi )$ given by (36) is the deviation of the medium density from the density of the solvent, which occurs due to the dissolved reactants.

In addition to the correction factor 6/5  Aristov (1990); Ruyer-Quil (2001); Aristov and Schwartz (2011), Eq. (32) differs from the standard Navier-Stokes equation by the Darcy term proportional to the velocity. One can interpret this term as the average friction force due to the presence of the plates. We can learn from the experimental observations made in the static gravity field Mizev et al. (2021) that at the very beginning of evolution ($t<200$ s), the characteristic size of structures can be small enough and the velocity diffusion represented by the Brinkman term can play an important role in the system dynamics. At later times ($t>200$ s), Darcy’s law can be used to model the flow. Generally, the use of the averaged two-dimensional Navier-Stokes-Darcy Equation (32) allows us to unify both limiting cases. The Darcy model for the Hele-Shaw cell description is valid when the cell gap is small compared to this characteristic reaction-diffusion length, whereas fully three-dimensional flows governed by the Navier-Stokes equation are obtained in the opposite limit. The use of the Eq. (32) allows us to give a good approximation in the intermediate range of cell thicknesses Ruyer-Quil (2001); Martin et al. (2002).

The laws of concentration-dependent diffusion are based on a linear approximation of the results of experimental measurements and are valid in the concentration range from 0.1 to 3.0 mol/l. These laws have been first formulated in the dimensionless form in Bratsun et al. (2015) as follows

$$\begin{aligned} D_A (A)\approx & {} 0.881 + 0.158 A ,\nonumber \\ D_B (B)\approx & {} 0.594 - 0.087 B , \nonumber \\ D_C (C)\approx & {} 0.487 - 0.284 C . \end{aligned}$$

(38)

These relations cannot describe the diffusion of solutions at sufficiently low concentrations, where nonlinear effects dominate. However, the neutralization reaction proceeds quite intensively under the conditions of convective mixing. In this case, the reactants quickly burn out, and all nonlinear contributions to (38) can be neglected as quantities of the second order of smallness. Also, in what follows, we neglect the concentration-dependence of diffusion from other species and the effect of cross-diffusion.

We formulate the boundary conditions

$$\begin{aligned} r=R:\quad \Psi= & {} 0,\quad \frac{\partial \Psi }{\partial r} = 0,\nonumber \\ \frac{\partial A}{\partial r}= & {} 0,\quad \frac{\partial B}{\partial r} = 0,\quad \frac{\partial C}{\partial r} = 0 , \end{aligned}$$

(39)

and initial conditions

$$\begin{aligned} t= & {} 0,\quad 0\leqslant r \leqslant L:\quad \Psi = 0,\quad A=\gamma _A,\quad B = 0 , \end{aligned}$$

(40)

$$\begin{aligned} t= & {} 0,\quad L< r \leqslant R:\quad \Psi = 0, \quad A=0, \quad B = \gamma _B . \end{aligned}$$

(41)

Thus, we have formulated the complete mathematical problem, which includes the governing Equations (31)–(38), boundary conditions (39), and initial conditions (40, 41). The control parameters of the problem are $Ra_A^{\Omega }$, $\gamma _A$, $\gamma _B$, and L. In the experiment, the first parameter can be easily changed by adjusting the rotation speed. The rest of the parameters can be changed during preparation for each individual experiment, but remain unchanged if the experiment is already running.

Base State Solution

The problem (31)–(41) is not autonomous in the sense that reaction-diffusion-convection processes proceed irreversibly in a closed cavity. Let us focus on an unsteady solution, which describes the reaction-diffusion processes with the fluid remaining at mechanical equilibrium. We will refer to this solution as a base state solution. Specifically, we assume that the fluid velocity equals zero in Eqs. (31)–(35) and that the concentration fields are axisymmetric and depend only on the radius and time: $A^0(t,r)$, $B^0(t,r)$, $C^0(t,r)$. The resulting time-dependent nonlinear equations

$$\begin{aligned} \frac{\partial A^0}{\partial t}= & {} D_{A}(A^0)\frac{\partial ^2 A^0}{\partial r^2} + \frac{D_{A}(A^0)}{r}\frac{\partial A^0}{\partial r}+\nonumber \\&\quad + \frac{d D_{A}(A^0)}{d A^0}\left( \frac{\partial A^0}{\partial r}\right) ^2- Da A^0 B^0 , \end{aligned}$$

(42)

$$\begin{aligned} \frac{\partial B^0}{\partial t}= & {} D_{B}(B^0)\frac{\partial ^2 B^0}{\partial r^2} + \frac{D_{B}(B^0)}{r}\frac{\partial B^0}{\partial r}+\nonumber \\&\quad + \frac{d D_{B}(B^0)}{d B^0}\left( \frac{\partial B^0}{\partial r}\right) ^2- Da A^0 B^0 , \end{aligned}$$

(43)

$$\begin{aligned} \frac{\partial C^0}{\partial t}= & {} D_{C}(C^0)\frac{\partial ^2 C^0}{\partial r^2} + \frac{D_{C}(C^0)}{r}\frac{\partial C^0}{\partial r}+\nonumber \\&\quad + \frac{d D_{C}(C^0)}{d C^0}\left( \frac{\partial C^0}{\partial r}\right) ^2+ Da A^0 B^0 \end{aligned}$$

(44)

should be complemented with the boundary conditions

$$\begin{aligned} r=R:\quad \frac{\partial A^0}{\partial r} = 0 ,\quad \frac{\partial B^0}{\partial r} =0 ,\quad \frac{\partial C^0}{\partial r} = 0 , \end{aligned}$$

(45)

and initial conditions

$$\begin{aligned} t= & {} 0,\quad 0\leqslant r \leqslant L:\quad A^0=\gamma _A,\quad B^0 = 0 , \end{aligned}$$

(46)

$$\begin{aligned} t= & {} 0,\quad L< r \leqslant R:\quad A^0 = 0, \quad B^0 = \gamma _B , \end{aligned}$$

(47)

and the formulas for concentration - dependent diffusion (38). Generally, the problem (42)–(47) has no analytical solution and can only be solved numerically. The solution method is discussed in the next section.

The existence of a solution with an inhomogeneous density distribution and mechanical equilibrium of the fluid is determined by the fact that the density gradient in the base state is always collinear with the centrifugal force. If this would not the case, then the equilibrium of the fluid would be impossible. To satisfy the equilibrium condition, the reacting solutions must fill the cavity in such a way that the cylindrical symmetry of the problem would not be violated.

Fig. 3

Stability map constructed by in the ($\gamma _A$, $\gamma _B$) parameter space. Abbreviations DLC, SW, CDD, and RT denote the diffusive layer convection, shock wave, convection of concentration-dependent diffusion, Rayleigh-Taylor convection, respectively. In all calculations, it is assumed that $R=20$ and $L=R/\sqrt{2}$. The characteristic cross-section $\gamma _{A}=0.667$ of the stability map is marked by the red straight line, and four special cases of the density field indicated by the open circles are illustrated in Fig. 4. Points a, b, c, d correspond to the values of the initial concentration of base $\gamma _{B}=0.9$, 0.667, 0.57, and 0.35, respectively

Fig. 4

Instantaneous density fields $\hat{\rho }^0 (t,r)$ for the reaction-diffusion base state calculated for the fixed value of the initial acid concentration $\gamma _{A}=0.667$ and four different values of the initial concentration of base $\gamma _B$ marked on the stability map by the open circles (see Fig. 3). The position of the initial contact surface of the mixtures is determined by $L=R/\sqrt{2}$. All fields are shown for time $t=2$

After bringing the solutions of $\text {HNO}_3$ and $\text {NaOH}$ into contact, the reaction-diffusion processes transform the density field and may cause potentially unstable conditions for the system under the centrifugal force. As is known, the final answer to the question of which flows will be preferentially excited for the fixed set of parameter values is given by a linear stability analysis and a direct numerical simulation. Nevertheless, we can reveal the general structure of the stability map of the system under consideration using a simpler approach based on the analysis of the base state Trevelyan et al. (2015); Bratsun et al. (2021). It should be noted here that this approach only helps to identify a potential source of instability in the system. Moreover, there are situations where such an analysis may give the wrong answer, as, for example, in the case of double diffusion instability. Therefore, the base state analysis of inertia-dependent instabilities should be used with caution and must be accompanied either by a linear stability analysis of infinitesimal perturbations or by numerical simulation of the complete nonlinear problem.

We should note that a reaction-diffusion problem with a cylindrical shape of the initial contact surface (42)–(47) differs from a similar problem with a planar front previously studied in Bratsun et al. (2021) by an additional diffusion term (second terms on the right in Eqs. (42)–(44). The influence of this term is the stronger, the closer the front is to the axis of rotation. In limit $r\rightarrow \infty$, the influence of the term becomes negligible, and the indicated problems coincide.

The stability map on the parameter plane of the initial values for the concentrations of acid $\gamma _A$ and base $\gamma _B$, obtained in this way, is shown in Fig. 3. The sequence of transformations of the density field under different initial concentrations is shown in Fig. 4. This figure presents density fields that correspond to a vertical slice indicated in Fig. 3. As one can see from the stability map, there are four regions, where qualitatively different density fields are observed. The regions are separated from each other by three bifurcation curves.

The key bifurcation curve is defined by the relation:

$$\begin{aligned} \gamma _B = \frac{\beta _A}{\beta _B}\gamma _A = \frac{\gamma _A}{R_B} , \end{aligned}$$

(48)

which corresponds to a line of equal density for the central and peripheral layers, that is, an isopycnal line (thick solid line in Fig. 3). The relation (48) implies that the weight of an elementary volume of a liquid depends both on the structure of the solute’s molecule and on the amount of solute. If the parameters are taken above the isopycnal line, then the base solution at the periphery of a cylindrical cuvette is heavier than the acid solution near the rotation axis. It means that the system under centrifugal force is statically stable at the beginning of the evolution, and the instability can develop only after some time. Below the isopycnal line, the situation is reversed: a denser fluid is closer to the axis of rotation, which leads to the development of the Rayleigh-Taylor instability regardless of the ongoing reaction-diffusion processes.

Fig. 5

Stability map constructed in the ($\gamma _B$, L/R) parameter space. Abbreviations DLC, SW, CDD, and RT denote the diffusive layer convection, shock wave, convection of concentration-dependent diffusion, Rayleigh-Taylor convection, respectively. In all calculations, it is assumed that $\gamma _A=0.667$ and $R=20$. The characteristic cross-section $L/R=1/\sqrt{2}$ of the stability map is marked with the red straight line, and four special cases of the density field indicated by the open circles are illustrated in Fig. 4

We have shown in Mizev et al. (2021); Bratsun et al. (2021) that the neutralization reaction, coupled with the concentration-dependent diffusion, can result in a potential well and can maintain it for a long time in a quasi-steady state. Being under the influence of an external inertial field, a system with such a feature of the density field can demonstrate completely new pattern formation scenarios. The condition for the appearance of a local minimum in the density field is determined by the inflection point of the radial density profile calculated in the base state:

$$\begin{aligned} \frac{\partial ^2 \hat{\rho }^0 (t,r)}{\partial r^2} = 0 . \end{aligned}$$

(49)

This bifurcation curve is indicated in Fig. 3 by a thin solid line. Eq. (49) shows that the location of the curve is time-dependent. However, after the initial stage of rapid changes in the density field ($t<0.1$), the system quickly passes to a quasi-stationary regime, in that the concentration and density fields change relatively slowly. All bifurcation curves shown in Fig. 3 are calculated for time $t=2$.

It is worth noting that although the effect of con-centration-dependent diffusion has been rarely considered in the fluid mechanics, some analogy can be drawn, for example, with viscous fingering in miscible displacement flows in porous media Hickernell and Yortsos (1986); Manickam and Homsy (1995); Loggia et al. (1995). Both the concentra-tion-dependent viscosity and the heterogeneity in the permeability of the porous medium can produce the simple nonmonotonicity in the mobility profiles somewhat similar to those in the reactive case.

Moving down along the red line in Fig. 3, we cross one more bifurcation curve indicated by a dash-dotted line. It corresponds to the situation when the densities of the reaction zone and the central layer become equal:

$$\begin{aligned} \hat{\rho }^0 (t,0) = \hat{\rho }^0 (t,r_{max}) , \end{aligned}$$

(50)

where $r_{max}$ stands for the position of a local maximum of the density. The nature of this local maximum has been explained in Bratsun et al. (2015, 2021). On the one hand, the density maximum is formed due to the relatively heavy salt, which is the product of the neutralization reaction. On the other hand, the diffusion coefficient of salt decreases with increasing concentration (see formulas (38)). Thus, the more salt is produced by the reaction, the less it becomes mobile and more likely accumulates near the reaction front than diffuses from it.

Thus, analyzing Figs. 3 and 4, we can conclude that the list of potential instabilities that can occur in the system includes the instability of the diffusive layer (DLC), the concentration-dependent diffusion instability (CDD), the flow in the form of a density shock wave (SW), and Rayleigh-Taylor convection (RT). In what follows, we validate these predictions of the base state analysis by direct numerical simulations.

The initial position of the contact surface L/R between two mixtures is another dimensionless parameter influencing the onset of instability. Figure 5 presents a map of stability in the ($\gamma _B$, L/R) parameter plane at a fixed value $\gamma _A=0.667$. The map is calculated at time $t=2$. The vertical cross-section of the map marked with the red line is the same as in Fig. 3. At this position of the initial front, the volumes of two mixtures with reactants are approximately equal. When the contact surface is shifted to one side or the other, the amount of one of the reactants in the closed reactor begins to prevail. If the contact surface is moved to the axis of rotation, one of the potential wells narrows and eventually disappears in the range of $\gamma _B$, at which the system is statically stable at the very beginning (above the isopycnal line in Fig. 5). The analysis of the base state implies that if the initial front is closer to the rotation axis than $L/R=0.2$, local convection has no chance to develop at all. As the contact surface moves away from the axis of rotation, the region of existence of two potential wells gradually expands. If the surface is near the solid boundary of the Hele-Shaw cell, then the potential well disappears again. However, it should be borne in mind that, due to the small reserve of the base, the reaction-diffusion processes proceed here much faster and the potential well has time to appear and extinguish at earlier times of evolution.

From this analysis, we can conclude that chemoconvection, which can potentially develop locally in potential wells, is more convenient to observe by preparing the system with the initial contact surface further from the axis of rotation.

Numerical Solution Technique

The problem (31)–(41) has been solved numerically by the finite difference method using a two-field formulation technique. We consider a circular Hele-Shaw cell of the radius $R=20$. Spatial differential operators were approximated by central differences on a uniform mesh constructed in polar coordinates. We have used the series of meshes with different resolutions: $21\times 121$, $41\times 241$, $61\times 361$, $81\times 481$, $101\times 601$, $121\times 721$, and $141\times 841$. As an example, the first mesh in the series is shown in Fig. 6.

We have also performed a study of the convergence of the numerical results with the gradual refinement of the grid. A typical example of such a study is presented in Fig. 7. Since most of our calculations have been performed in the range of initial concentrations where the cellular CDD convection arises, the convergence example is presented for the fixed values of the governing parameters: $\gamma _A = 0.667$, $\gamma _B = 0.667$, $L/R =0.3$, and $Ra_A^{\Omega } = 6\times 10^4$. Most of the numerical results presented below are obtained on the grid $101\times 601$ (101 nodes in the radius and 601 nodes in the angle). We chose this resolution so that there are $6 \times 6$ nodes per unit area element in polar coordinates. The choice of this resolution is based on our previous experience in the numerical simulation of buoyancy-driven flows induced by the neutralization reaction Bratsun et al. (2015, 2017, 2021). We can see from Fig. 7 that the grid network $101\times 601$ used in this work gives a result within 3% of the relative error of the value to which the stream function converges when the grid is improved.

Fig. 6

The typical uniform polar mesh of the two-dimensional flow field containing 21$\times$ 121 nodes for the circular domain of the radius $R=20$

Fig. 7

Convergence of the maximum value of the stream function under mesh refinement. The convergence was studied for local cellular convection (see Section 5.1) at fixed values of the governing parameters: $\gamma _A = 0.667$, $\gamma _B=0.667$, $L/R~=~0.3$, $R=20$, $Ra_A^{\Omega } = 6\times 10^4$, and time $t=2$

We should notice that a significant part of the fluid flow dynamics is localized near the reaction front and, in some cases, propagates along with the computational domain. The wavelengths of various instabilities that can potentially develop in the system under consideration are discussed in Mizev et al. (2021); Bratsun et al. (2021) in detail. Near the axis of rotation, the liquid is in conditions close to weightlessness. The fluid flows that arise here are weak and quickly decay. Therefore, the singularity at $r = 0$ is not dangerous for the stability of the numerical scheme. All of this explains the use of a uniform polar mesh. For the time derivative, we used the Euler scheme with the order of $O(\tau + h_r^2 + h_{\phi }^2)$.

The nonlinear equations are solved using an explicit scheme.

Let us describe the numerical scheme in more detail. Let us denote the discrete analogue of the function $f(t,r,\phi )$ as $f_{i,k}^m$ , which gives the value of the function at the grid point i, k and at time $t_m = \sum \Delta t_m$. Let the indices i, k number the grid nodes in terms of radius and angle, respectively. Then the finite-difference equations obtained from Eqs. (31)–(36) have the form:

$$\begin{aligned} \Phi _{i,k}^{m+1} = - \nabla ^2 \Psi _{i,j}^{m+1} , \end{aligned}$$

(51)

$$\begin{aligned} \Phi _{i,k}^{m+1} = \Phi _{i,k}^{m} + \Delta t_m \left( \frac{}{} Sc \nabla ^2 \Phi _{i,k}^{m} - 12 Sc \Phi _{i,k}^{m} - \right. \end{aligned}$$

$$\begin{aligned} \qquad \quad \left. - Sc Ra_A^{\Omega } \frac{\partial \hat{\rho }_{i,k}^{m+1}}{\partial \phi } - \frac{6}{5r_i} \frac{\partial (\Phi _{i,k}^{m},\Psi _{i,k}^{m})}{\partial (r,\phi )} \right) , \end{aligned}$$

(52)

$$\begin{aligned} A_{i,k}^{m+1} = A_{i,k}^m + \Delta t_m \left( \nabla \cdot (D_A (A_{i,k}^m) \nabla A_{i,k}^m ) - \right. \end{aligned}$$

$$\begin{aligned} \qquad \quad \left. - Da A_{i,k}^m B_{i,k}^m - \frac{1}{r_i} \frac{\partial (A_{i,k}^{m}, \Psi _{i,k}^{m})}{\partial (r,\phi )}\right) , \end{aligned}$$

(53)

$$\begin{aligned} B_{i,k}^{m+1} = B_{i,k}^m + \Delta t_m \left( \nabla \cdot (D_B (B_{i,k}^m) \nabla B_{i,k}^m ) - \right. \end{aligned}$$

$$\begin{aligned} \qquad \quad \left. - Da A_{i,k}^m B_{i,k}^m - \frac{1}{r_i} \frac{\partial (B_{i,k}^{m}, \Psi _{i,k}^{m})}{\partial (r,\phi )} \right) , \end{aligned}$$

(54)

$$\begin{aligned} C_{i,k}^{m+1} = C_{i,k}^m + \Delta t_m \left( \nabla \cdot (D_C (A_{i,k}^m) \nabla A_{i,k}^m ) - \right. \end{aligned}$$

$$\begin{aligned} \qquad \quad \left. + Da A_{i,k}^m B_{i,k}^m - \frac{1}{r_i} \frac{\partial (C_{i,k}^{m}, \Psi _{i,k}^{m})}{\partial (r,\phi )} \right) , \end{aligned}$$

(55)

$$\begin{aligned} \hat{\rho }_{i,k}^{m+1} = A_{i,k}^{m+1} + R_B B_{i,k}^{m+1} + R_C C_{i,k}^{m+1} . \end{aligned}$$

(56)

In addition to the finite-difference Equations (51)–(56), we have to require the boundedness of variables at the center of the domain $r=0$. For example, the finite-difference equation for calculating the vorticity can be obtained by passing to the limit $r \rightarrow 0$. The uncertainties, which arise in this way, should be disclosed according to the L’Hôpital rule:

$$\begin{aligned} \Phi _0^{m+1} = \Phi _0^{m} + Sc \Delta t_m \left( \nabla ^2 \Phi _0^{m} - 12\Phi _0^{m} - Ra_A^{\Omega } \frac{\partial \hat{\rho }_0^{m+1}}{\partial \phi } + \right. \end{aligned}$$

$$\begin{aligned} \left. + \frac{3 (1/Sc)}{5 N \Delta h_r ^2 \Delta h_{\phi }} \sum _{k=0}^{N-1} (\Psi _{1,k+1}^m - \Psi _{1,k-1}^m)(\Phi _{1,k}^m - \Phi _0^m) \right) . \end{aligned}$$

(57)

Let us describe the sequence of events during the operation of the computational scheme. Let at moment $t_m$ we know all the fields: $\Phi _{i,k}^m$, $\Psi _{i,k}^m$, $A_{i,k}^m$, $B_{i,k}^m$, and $C_{i,k}^m$. Then, using explicit recurrent Equations (53)–(55), we can obtain values for concentrations of all species at a new time step: $A_{i,k}^{m+1}$, $B_{i,k}^{m+1}$, $C_{i,k}^{m+1}$. Then, substituting fresh values for concentrations in (52), we find new values of the vorticity: $\Phi _{i,k}^{m+1}$. In the end, the most important procedure is performed, which includes an iterative solution of Poisson’s Equation (51), the result of which is the determination of the stream function $\Psi _{i,k}^{m+1}$. Then the procedure is repeated for the next time step.

When using this scheme, one has to control the time step. To ensure the stability of the numerical scheme, we used Courant’s formula to calculate new time step at each iteration:

$$\begin{aligned} \Delta t_m = \frac{\Delta h_r ^2}{2(2+max( \vert \Psi \vert , \vert \Phi \vert ))}. \end{aligned}$$

(58)

The Poisson equation for the stream function (51) was solved by the iterative Liebman successive over- relaxation method at each time step: the accuracy of the solution was fixed to $10^{-4}$. A noisy stream function field $\Psi$ with amplitude less than $10^{-3}$ was used in the initial condition.

Fig. 8

Evolution of the fields of dimensionless density $\hat{\rho }(t,r,\phi )$ (the top row) and stream function $\Psi (t,r,\phi )$ (the bottom row) at times t: $0.05;\, 0.2;\, 0.5;\, 2.0$ showing the formation of the CDD convection cells. The centrifugal Rayleigh number is $Ra_A^{\Omega } = 5 \times 10^4$. The distance of the initial contact surface from axis is $L/R = 0.5$. The initial concentrations of the reactants are $\gamma _A=0.667$, $\gamma _B = 0.667$

Integral quantities play a principal role in the analysis of system dynamics. They are constructed based on fields obtained as part of the computational process, and their evolution is tracked throughout the entire simulation. We have already pointed out the existence of a close relationship between chemical transformations and convective instabilities. Chemical reactions contribute to the appearance of irregularities in the distribution of concentrations in the system. On the one hand, it can both contribute to the development of convection and suppress it. On the other hand, macroscopic motion affects the frequency of ion collisions, i. e. the rate at which the reaction proceeds. In this regard, the beneficial measurement is the mixing rate $\mu (t)$ computed as the number of points where the concentration of salt $C(t,r,\phi )$ is larger than an arbitrary threshold $C^*$. In other words, we compute a time-dependent integral quantity:

$$\begin{aligned} \mu (t) = \frac{1}{\pi R^2} \int _0^R\int _0^{2\pi } \zeta (t, r, \phi ) r dr d\phi , \end{aligned}$$

(59)

where

$$\begin{aligned} \zeta (t,r,\phi ) = H(C(t,r,\phi )-C^*)=\left\{ \begin{array}{ll} 0, \,\,\, C < C^* , \\ 1, \,\,\, C \ge C^* . \end{array} \right. \end{aligned}$$

Here, H stands for the Heaviside function with an argument in the form of the difference between the current salt concentration in a given volume element and some threshold value $C^*$. There is considerable arbitrariness in determining the quantity $C^*$, and, in this work, we have taken it equal $C^* = 10^{-3}$. In fact, this value characterizes the degree of mixing in the given miscible system since it shows how well the reaction product C has been redistributed over the volume. Since the diffusion coefficient of salt decreases with increasing concentration, the redistribution of its concentration occurs mainly due to convection. The integral (59) is normalized by the area of the Hele-Shaw cell.

Fig. 9

Stability map constructed in the parameter space of the cetrifugal Rayleigh number $Ra_A^{\Omega }$ and the dimensionless distance of the initial contact line from the axis of rotation L/R. The map is based on numerical simulations of the full non-linear problem (31-41). Abbreviations DLC and CDD denote the diffusive layer convection and convection of concentration-dependent diffusion, respectively. The cross-section a–d corresponds to $R_A=6\times 10^4$ and $L/R=0.9,0.6,0.3,0.2$, respectively. The cross-section e–h corresponds to $L/R=0.5$ and $Ra_A^{\Omega }= 10^4, 4\times 10^4, 9\times 10^4, 1.1\times 10^5$, respectively. In all calculations, it is assumed that $\gamma _A=0.667$, $\gamma _B = 0.667$, $R=20$, and $t=2$

Numerical Results

Concentration-Dependent Diffusion Instability

Let us focus our attention on the region of the stability map shown in Fig. 3 where cellular convection presumably occurs (point b). The CDD convection was previously studied in detail in the works of the authors Bratsun et al. (2015, 2021). As it was shown, a necessary condition for the appearance of a periodic system of chemoconvective cells is the presence of a potential well in the density field. This condition is fulfilled if the reaction zone is heavier than the upper layer throughout the entire evolution or, at least, for a sufficient time for instability to develop. The specificity of the problem under consideration lies in the fact that the inertial field is created here by a centrifugal force and not by a static gravity field. One of the important consequences of such a replacement is the shape of the potential well, which allows the instability to develop almost immediately, as an inflection point appears in the radial density profile. This is due to an additional term in the reaction-diffusion Equations (42)–(44) discussed above. Another feature of centrifugal inertia is its dependence on the distance from the axis of rotation. The force intensity increases when $r\rightarrow \infty$. Therefore, it is important to study the effect of one more parameter, the dimensionless distance of the initial contact surface from the axis of rotation L/R on the onset of instability.

Figure 8 shows the characteristic temporal evolution of the density field and the stream function at the initial concentrations of reactants $\gamma _A = 0.667$ and $\gamma _B = 0.667$ (the region of the CDD instability, see Fig. 3b). The frames illustrate the dynamics of the system at successive times. The centrifugal Rayleigh number is $Ra_A^{\Omega } = 5 \times 10^4$, which approximately corresponds to the value $\sim 0.5 g$. The position of the initial reaction front is chosen just in the middle of the distance from the axis to the outer wall of the disk: $L/R=0.5$. One can see from the figure that, at the beginning of evolution, only one potential well exists (Fig. 8, $t=0.05$). One more potential well develops later and can be seen already at $t=0.2$. This result is consistent with the result of the reaction-diffusion problem solution (Fig. 4b). Finally, we can observe the excitation of convective motions, which take on a distinct form by the time $t=0.5$.

Fig. 10

Time evolution of the spatial reaction rate $\mu (t)$ defined by (59) for points a–d (left) and e–h (right) marked on the stability map in Fig. 9

Fig. 11

Time evolution of the stream function maximum for points a–d (left) and e–h (right) marked on the stability map in Fig. 9

The DLC instability develops in the central potential well adjacent to the rotation axis. Large-scale DLC vortices form radial jets that deliver fresh acid from the center of the cavity to the reaction front. The instability is asymmetric because its propagation in the radial direction is limited by a potential barrier. This feature distinguishes DLC instability shown in Fig. 8 from its classical pattern observed in systems without a reaction. An interesting peculiarity of a system with centrifugal force is a region near the axis of rotation, which is a state close to weightlessness. The movement of the liquid here is an order of magnitude slower than near the reaction front. The main reason for the fluid movement here is the flow triggered by inertia from areas where the centrifugal force is acting in full.

On the other side of the potential barrier at $r~\approx ~L$, the mechanical equilibrium of the liquid also loses its stability. The second potential well, located farther from the axis of rotation, creates a closed cylindrical layer. The chemoconvective cells arising here can neither float to the center of the disk nor escape to the periphery of the rotating cell. The CDD instability earlier got its name because the second potential well is formed due to the effect of the concentration-dependence of the diffusion coefficients of reactants Bratsun et al. (2015).

The wavelength of both DLC and CDD perturbations depends on the width of the potential well, which in turn depends on the interaction of a nonlinear reaction with concentration-dependent diffusion. One can see from Fig. 4b that the width of the central potential well is wider, which results in the development of larger vortices of the DLC instability. Two instabilities, separated by a potential barrier near $r\approx L$, can interact using diffusive signals. This process was studied in Ref. Bratsun (2019) for a system under the action of a static gravity field. We have shown that diffusion waves have a modulating effect on CDD convection, which leads to the development of a quasiperiodic spatial pattern in the case of a flat potential barrier. In the case of a cylindrical barrier, there is a forced synchronization of structures occurring between two instabilities (Fig. 8).

We note an interesting feature of the CDD instability. The flow physics looks similar to the classical Rayleigh-Bénard convection. The instability is triggered by unstable stratification of heavy salt (product of reaction) that is deposited near the reaction front. Here, the conditions of the onset of the solutal Rayleigh-Benard convection are reproduced locally: the instability domain is limited by the motionless layers, the density variation in the base state is linear, and the onset of convection has a threshold character. That is why the disturbance wavelength correlates very well with the convective instability wavelength in a plain layer (see Ref. Mizev et al. (2021) for more details).

Fig. 12

Evolution of the fields of dimensionless density $\hat{\rho }(t,r,\phi )$ (the top row) and stream function $\Psi (t,r,\phi )$ (the bottom row) at times t: $0.05;\, 0.2;\, 0.5;\, 2.0$ showing the formation of the shock-wave pattern. The centrifugal Rayleigh number is $Ra_A^{\Omega } = 10^5$. The distance of the initial contact surface from axis is $L/R = 0.7$. The initial concentrations of the reactants are $\gamma _A=0.667$, $\gamma _B = 0.57$

Figure 9 presents a stability map on the plane of the control parameters $Ra_A^{\Omega }$ and L/R. As one can see from the figure, there is an area on the map where the inertial force cannot excite instability, and the fluid is in mechanical equilibrium. We illustrate this case by the characteristic density fields calculated for the points d and e marked on the map. This region is characterized either by a sufficiently small distance of the initial contact surface from the axis of rotation or by a relatively low speed of rotation. In both limiting cases, we can observe reaction-diffusion processes with the appearance of one or two potential wells proceeding in a non-convective manner. With an increase in the amplitude of the inertial field, we can observe the excitation of convection in one or another potential well. An interesting feature of the centrifugal system is the ability to split the DLC and CDD instabilities. For example, there is a range of parameters where only CDD instability is observed (Fig. 9c). This effect can be achieved by manipulating the position of the initial contact surface at a fixed rotational speed. As can be seen from the stability map, splitting occurs if the initial reaction front is sufficiently close to the axis of rotation, which leads to attenuation of the DLC disturbances developing closer to the axis of rotation. At the same time, the amplitude of the centrifugal field is quite sufficient for the development of CDD disturbances.

Finally, consider the range of parameters where the centrifugal force exceeds the amplitude of the static gravity field. In the case of hypergravity, the plumes of the DLC instability in the central potential well have an irregular shape almost from the very beginning of evolution (Fig. 9g, h). As for the second well, its depth is relatively small. It leads to the fact that some density fluctuations eventually can overcome the potential barrier. As a result, some chemoconvective vortices can leave the potential well under the action of a centrifugal force. In this case, the vortex propagates radially until the density of the surrounding liquid becomes equal to the density of the drop. On the whole, the cellular structure of CDD disturbances loses its periodicity regardless of the influence of DLC convection.

Figure 10 shows the temporal evolution of the spatial reaction rate $\mu (t)$ defined by (59) for all points highlighted on the stability map shown in Fig. 9. As one can see from the figures, the mixing rate of the fluids increases both with the distance of the initial contact surface from the axis of rotation and with an increase in the centrifugal Rayleigh number. It is curious that changing parameter L/R looks much more efficient than increasing the Rayleigh number. In fact, a change in parameter L/R also implicitly sets a change in the amplitude of the centrifugal force in the area of the contact surface. However, the gradual transfer of the initial reaction front to the periphery of the disk creates an additional effect of expanding the space of the central zone, which is available for vigorous DLC convection. The redistribution of density under the action of centrifugal force leads to the collision of vortices near the axis. DLC plumes, converging towards the center, compete with each other, which explains the nonstationary nature of the stream function evolution at large overloads (see Fig. 11).

Fig. 13

Stability map constructed in the parameter space of the cetrifugal Rayleigh number $Ra_A^{\Omega }$ and the dimensionless distance of the initial contact line from the axis of rotation L/R. The map is based on numerical simulations of the full non-linear problem (31-41). Abbreviations SW denote the shock-wave pattern. The cross-section a–d corresponds to $R_A=6\times 10^4$ and $L/R=0.9,0.6,0.3,0.1$, respectively. The cross-section e–h corresponds to $L/R=0.5$ and $Ra_A^{\Omega }=10^3, 4\times 10^4, 9\times 10^4, 1.1\times 10^5$, respectively. In all calculations, it is assumed that $\gamma _A=0.667$, $\gamma _B = 0.57$, $R=20$, and $t=2$

Shock-Wave Pattern

In this section, we will consider the scenario of pattern formation with a density wave. Let us fix the initial concentrations of solutions at values $\gamma _A=0.667$ and $\gamma _B = 0.57$ (point c in Fig. 3). Figure 3 shows that the density field in the base state formally still has two potential wells. An important difference from the previous case is the fact that the density of the acid solution is now greater than the density of the reaction zone but at the same time less than the density of the base solution at the disk periphery. In work Bratsun et al. (2021), we have shown that the study of the linear stability of such a profile to small local perturbations does not make much sense since a global restructuring of the entire system occurs. Figure 12 illustrates this process presenting the time variation of the density field and the stream function at a fixed value of the centrifugal Rayleigh number $R_a = 10^5$ (it approximately corresponds to g near the reaction front) and the dimensionless distance of the initial contact surface from the axis of rotation $L/R=0.7$. This value of the last parameter ensures the equality of the volumes of mixtures at the beginning of evolution. This condition guarantees the longest reaction time until both components of the mixture have reacted.

Since the density of the potential barrier becomes less than the density of the central zone, it simply disappears, floating up to the axis of rotation (Fig. 12, $t=0.05$). In this case, the potential barrier formed by the base solution survives, but the density of the entire central region is leveled out due to intense convection. In the cross-section, the density field becomes similar to a step function with a sharp density drop at the front of reaction (Fig. 12, $t=0.5$). This gap spreads rapidly away from the axis of rotation. We associated this pattern with a shock wave in Bratsun et al. (2017), meaning that the wave moves faster than any disturbance in the system. Therefore, the velocity discontinuity at the front $r_{wave}$ separates the region of vigorous convection ($r<r_{wave}$) and the region of motionless fluid ($r>r_{wave}$). It should keep in mind that the term “shock wave” means a generalized wave, which propagates fast, but not necessarily supersonic, compared with characteristic velocity in a given media (see Landau and Lifshitz (1987) for more details).

Fig. 14

Time evolution of the spatial reaction rate $\mu (t)$ (59) for points a–d (left) and e–h (right) marked on the stability map in Fig. 13

Fig. 15

Time evolution of the stream function maximum for points a–d (left) and e–h (right) marked on the stability map in Fig. 13

We found in Bratsun et al. (2017) that the theory based on classical shock wave equations is surprisingly in excellent agreement with the experimental measurements and observations. If the density wave moves faster than $\sqrt{Sc}$, we can hypothetically observe a subsonic analog of the shock wave in gas. Thus, the dimensionless value $\sqrt{Sc}$ plays the role of the speed of sound for a given medium. This velocity estimated for the two-layer reactive system under the static gravity field was found to equal $c^*\approx 17.8$ ($c^*\approx 0.056$ mm/s in dimensional units). We observed also that, as soon as the wave velocity fell below this value, the wave immediately stops and was replaced by a common fingering under either DLC or CDD mode. One can notice that the medium is assumed to be slightly compressible in that sense that the chemical reaction between components dissolved in water can locally change the density of the medium $\hat{\rho }$ defined by (36) even though the water itself is almost incompressible.

It is interesting to note that the structure of the cocurrent flow behind the shock wave is not homogeneous. A system of relatively dense jets appears formed in the central disk, which delivers fresh acid from the area adjacent to the axis of rotation to the reaction front (Fig. 12, $t=2$). We found that a network of such jets is a long-lived formation, and some of the jets retain their structure throughout the evolution of the system. Figure 12 illustrates well this property of the system under consideration (compare the frames at times 0.5 and 2). Ultimately, the development of convection in the wake flow leads to the rapid establishment of a turbulent regime. The reaction rate increases many times in comparison with the diffusion-controlled convective mode discussed in the previous Section. Therefore, the complete burnout of reactants in the shock wave mode occurs much faster than in the case of sluggish DLC convection and a local system of chemoconvective cells trapped in a potential well.

Fig. 16

Evolution of the fields of dimensionless density $\hat{\rho }(t,r,\phi )$ (the top row) and stream function $\Psi (t,r,\phi )$ (the bottom row) at times t: $0.05;\, 0.2;\, 0.5;\, 2.0$ showing the formation of the Rayleigh-Taylor pattern. The centrifugal Rayleigh number is $Ra_A^{\Omega } = 6\times 10^4$. The distance of the initial contact surface from axis is $L/R = 0.5$. The initial concentrations of the reactants are $\gamma _A=0.667$, $\gamma _B = 0.35$

The stability boundaries of the shock wave pattern calculated on the plane of the control parameters $R_A$ and L/R are shown in Fig. 13. As can be seen from the stability map, the mechanism of shock wave formation is triggered even in microgravity conditions. For example, at the initial location of the front $L/R=0.5$, the centrifugal field can reach a value of only $Ra_A^{\Omega }\approx 2\times 10^3\approx 0.02g$, which triggers the process of the appearance of a shock wave, i. e. the collapse of the density field formed by the reaction-diffusion processes began (compare the frames e and f in Fig. 13). A similar transition occurs at a fixed rotation speed and a simultaneous change in the initial front position. There is a critical distance from the axis of rotation, at which the density field does not overturn, and a shock wave does not arise. For example, at $Ra_A^{\Omega }= 6\times 10^4$, the critical radius is approximately $L/R\approx 0.1$ (compare the frames c and d in Fig. 13).

We also found that the effect of sudden stopping of the shock wave and the resorption of the density jump is more pronounced in the case of a system with cylindrical symmetry. When the wave moves from the axis of rotation, the wavefront gradually lengthens, and the area occupied by the acid increases according to the law $\sim r_{wave}^2$. It leads to the fact that the concentration of the acid solution in the center of the cuvette $0<r<r_{wave}$ gradually decreases. In this case, the concentration of the base solution, which is located on the periphery of the disc $r_{wave}<r<R$, remains the same since this area is in a state of mechanical equilibrium. Over time, it leads to the fact that the ratio of the concentrations $\gamma _A/\gamma _B$ changes in favor of the base, and the system leaves the range of parameters where a shock wave must arise (see Fig. 3).

Figure 14 shows the time evolution of the integral characteristic $\mu (t)$ defined by (59) for all points marked on the stability map presented in Fig. 13. One can see that, at the beginning of evolution, the system experiences an “explosion”, in which a significant part of it in the range $0<r<r_{wave}$ is intensively mixed, as a result of the rise of the reaction zone. For example, the system with the initial contact surface at $L/R=0.5$ (the cross-section e–h) demonstrates the following levels of mixing to time 0.5: 0.35 (h), 0.3 (g), 0.2 (f), 0.05 (e). We must account that the maximum available part of the mixing space at the initial moment is 1/3 of the total area of the disk. The points g and h correspond to cases of almost complete mixing in the area with the radius $r_{wave}$. After time $t=0.5$, the mixing is carried out only due to the expansion of the central region via the shock wave movement. By this time, the motion of the liquid at further moments takes the form of a sequence of large vortices, which form a branched structure in the density distribution discussed above. The essentially non-stationary nature of the vortex motion in the central region naturally entails oscillations of the stream function maximum (Fig. 15). The speed of movement of the shock wave to the periphery increases with an increase in the rotation parameter $Ra_A^{\Omega }$. The complete stop of the wave occurs only at the moment of complete burnout of reactants. In the limiting cases of a small volume occupied by an acid (point c in Fig. 13) or a base (point a), this happens rather quickly. If the volumes occupied by the solutions are approximately equal at the initial moment (Fig. 12), the shock front eventually reaches the edge of the cell. In this case, it is possible to completely mix the solutions in the volume due to the natural convection.

Rayleigh-Taylor Convection

Finally, we will briefly consider the development of the Rayleigh-Taylor instability. The region of this instability is below the isopycnal line, where the initial density of the acid solution exceeds the density of the base solution. Let us fix the values of the initial concentrations of species $\gamma _A=0.667$ and $\gamma _B = 0.35$ (the point d marked in Fig. 3). Figure 16 shows the time evolution of the density field and stream function for four consecutive times. As can be seen from the figure, the fluid motion occurs at an arbitrarily small value of the centrifugal field since the stratification of the medium is unstable from the very beginning. The potential barrier formed by the heavy salt released in the reaction can no longer retain liquid near the reactant contact line. The instability develops in the form of large fingers, which begin to move in different directions: light plumes float to the center, heavy structures move radially towards the edge of the disk (Fig. 16, $t=0.2$). By the time $t=0.5$, plumes with acid reach the edges of the cuvette, and the reaction covers its entire volume. The intensity of mixing increases significantly compared with the previously considered cases since the vortex motion covers the entire system at once. By the time $t=2$, any reaction-diffusion-convection processes cease, and the system becomes almost uniform in density. The described scenario looks quite standard and does not require further explanation.

Conclusions

This work is a numerical study of the effect of uniform rotation on the development of chemo-convective instability in a two-layer system of reacting miscible liquids. We show that, depending on the initial concentrations in the system, different scenarios of the instability development can occur. The dependence of the diffusion coefficients on concentration leads to the appearance of a potential well in the base-state density field. Under the influence of an inertial field, convective motion can develop in the form of a periodic sequence of vortices in a potential well (CDD convection). With a sufficient distance from the line of contact of solutions from the axis, the central area of the system becomes unstable via the DLC instability. It has a modulating effect on the cellular pattern. Therefore, the periodicity of the structure can be violated with an increase in both the angular velocity and the position of the initial contact surface. With a change in the initial concentrations, this regime is replaced by a density shock wave rapidly propagating in the direction of the inertial field. The effect of an increase in the wave speed with an increase in the overload is found. If the center region is heavier than all the others, then the standard Rayleigh-Taylor instability develops. The instability boundaries are found using direct numerical simulations.