1 Introduction

Data are generated in all branches of social, biological, physical and engineering sciences. They are modelled by means of probability distributions for better understanding. It is important and necessary that an appropriate probability distribution be fitted to empirical data, so that meaningful and correct conclusions can be drawn.

In this connection, characterization results have been used to test goodness of fit for probability distributions. Marchetti and Mudholkar [23] showed that characterization theorems can be natural, logical and effective starting points for constructing goodness-of-fit tests. Nikitin [27] observed that tests based on characterization results are usually more efficient than the other tests. Goodness-of-fit tests based on new characterizations results abound in the literature. Baringhaus and Henze [5] studied two new omnibus goodness of fit tests for exponentiality, each based on a characterization of the exponential distribution via the mean residual life function. Akbari [2] presented characterization results and new goodness-of-fit tests based on these new characterizations for the Pareto distribution. Earlier, Glänzel [10] derived characterization theorems for some families of both continuous and discrete distributions and used them as a basis for parameter estimation.

The main purpose of the present work is to present characterization results for the unit-Gompertz distribution introduced by Mazucheli et al. [25]. Essentially, this new distribution is derived from the Gompertz distribution. Recall that the density function of the Gompertz distribution is given by

$$\begin{aligned} g\left( y\mid \alpha , \beta \right) = \alpha \beta \exp \left( \alpha +\beta y - \alpha e^{\beta y}\right) , \end{aligned}$$

where \( y>0; \) and \( \alpha > 0 \) and \( \beta >0 \) are the shape and the scale parameters, respectively. Using the transformation

$$\begin{aligned} X= e^{-Y}, \end{aligned}$$

this new distribution with support on \( \left( 0, 1\right) , \) which is referred to as the unit-Gompertz distribution, is obtained. For brevity, we shall refer to it subsequently as the UG distribution. Its pdf and cdf are given by

$$\begin{aligned} f\left( x\mid \alpha , \beta \right) = \frac{\alpha \beta \exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] }{x^{1+\beta }}; \quad \alpha>0, \quad \beta >0, \quad x \in (0, 1) \end{aligned}$$
(1)

and

$$\begin{aligned} F\left( x\mid \alpha , \beta \right) =\exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] , \end{aligned}$$
(2)

respectively.

Mazucheli et al. [25] used this new distribution to model the maximum flood level (in millions of cubic feet per second) for Susquehanna River at Harrisburg, Pennsylvania (reported in Dumonceaux and Antle [9]) and tensile strength of polyester fibers as given in Quesenberry and Hales [29]. Jha et al. [14] considered the reliability estimation in a multicomponent stress-strength based on an unit-Gompertz distribution. As an application, Jha et al. [15] discussed the problem of estimating multicomponent stress-strength reliability under progressive Type II censoring when stress and strength variables follow UG distributions with a common scale parameter.

Inferential issues have also been studied. In this connection, mention may be made of Kumar et al. [20] who were concerned with the inference for the unit-Gompertz model based on record values and inter-record times. Arshad et al. [4] were interested in the estimation of the parameters under the framework of the dual generalized order statistics. Anis and De [3] not only corrected some of the subtle errors in the original paper of Mazucheli et al. [25], but also discussed some reliability properties and stochastic ordering among others. However, no characterization results of this new distribution have been studied.

This paper attempts to fill in this gap and is organized as follows. At first some more properties—which were not investigated earlier—are presented in Sect. 2. The characterizations of the distribution are studied in Sect. 3. Section 4 concludes the paper.

2 Properties

Most of the important properties of this distribution were considered in Mazucheli et al. [25] and the complementary paper by Anis and De [3]. For completeness, we consider the \( L\textrm{-moments}, \) two new measures of entropy, aging intensity and reversed aging intensity functions.

2.1 \( L\textrm{-Moments} \)

\( L\textrm{-Moments} \) are summary statistics for probability distributions and data samples. These \( L\textrm{-moments} \) are computed from linear combinations of the ordered data values (hence the prefix L). Hosking [13] showed that the \( L\textrm{-moments} \) possess some theoretical advantages over ordinary moments. Moreover, they are less sensitive to outliers compared to the conventional moments. Computation of the first few sample \( L\textrm{-moments} \) and \( L\textrm{-moment} \) ratios of a data set provides a useful summary of the location, dispersion, and shape of the distribution, from which the sample was drawn. They can be used to obtain reasonably efficient estimates of parameters when a distribution is fitted to the data. As noted in Hosking [13], the main advantage of \( L\textrm{-moments} \) over conventional moments is that \( L\textrm{-moments}, \) being linear functions of the data, suffer less from the effects of sampling variability; are more robust than conventional moments to outliers in the data and enable more secure inferences to be made from small samples about an underlying probability distribution. \( L\textrm{-moments} \) sometimes yield more efficient parameter estimates than the maximum likelihood estimates.

These \( L\textrm{-moments} \) can be defined in terms of probability weighted moments (PWMs) by a linear combination. The probability weighted moments \( M_{p, r, s} \) are defined by

$$\begin{aligned} M_{p, r, s}= \int _{-\infty }^{\infty }x^{p}\left[ F\left( x\right) \right] ^{r}\left\{ 1-F\left( x\right) \right\} ^{s} f\left( x\right) dx. \end{aligned}$$

Observe that \( M_{p, 0, 0} \) represents the conventional noncentral moments. We shall use the quantities \( M_{1, r, 0} \) when the random variable x enters linearly. In particular, we define \( \tau _{r} = M_{1, r, 0}\) as the probability weighted moments. The \( \tau _{r}\mathrm {'s} \) find application, for example, in evaluating the moments of order statistics (discussed in Anis and De [3]). Hosking [13] showed that the linear combination between the \( L\textrm{-moments} \) (denoted by \( \lambda _{i} \)) and the PWMs \( \tau _{r}, \) for the first four moments, are as given below:

$$\begin{aligned} \lambda _{1}= & {} \tau _{0};\\ \lambda _{2}= & {} 2\tau _{1}-\tau _{0};\\ \lambda _{3}= & {} 6\tau _{2}-6\tau _{1}+\tau _{0};\\ \lambda _{4}= & {} 20\tau _{3} - 30\tau _{2}+12\tau _{1}-\tau _{0}. \end{aligned}$$

In the particular case of the unit-Gompertz distribution, after routine calculation, we find that the \( r\mathrm {-th} \) PWM is given by

$$ \tau _{r}=\alpha ^{1/\beta }\left( r+1\right) ^{\frac{1}{\beta }-1} e^{\left( r+1\right) \alpha }\Gamma \left( 1-\frac{1}{\beta }; \left( r+1\right) \alpha \right) ,$$

where \( \Gamma \left( s;x\right) \) is the upper incomplete gamma function and is defined as

$$\begin{aligned} \Gamma \left( s; x\right) =\int _{x}^{\infty }t^{s-1}e^{-t} dt. \end{aligned}$$
(3)

Hence, the the \( L\textrm{-moments} \) can be obtained. It should be noted that the algebraic expressions are rather involved; but for given values of the parameters \( \alpha \) and \( \beta , \) these \( L\textrm{-moments} \) can be easily obtained numerically. As an example, we give in Table 1, the \( L\textrm{-moments} \) for some specific values of the parameters \( \alpha \) and \( \beta \) of the unit-Gompertz distribution. Here we have chosen the parameter values \(\alpha =0.25, 0.50,0.75\) and \(\beta =1.0, 1.5, 2.0, 2.5, 3.0\). From Table 1, we can observe that as the value of parameter \(\alpha \) increases, the value of \(L\textrm{-moments}\) significantly increase. This is apparent from the expression of \(\tau _r\) because \(\alpha \) appears as a power of exponential.

Table 1 \( L\textrm{-Moments} \) for some specific values of the parameters \( \alpha \) and \( \beta \) of the unit-Gompertz distribution
Full size table

2.2 Entropy

Entropy is used to measure the amount of information (or uncertainty) contained in a random observation regarding its parent distribution (population). A large value of entropy implies greater uncertainty in the data. Since its introduction by Shannon [31], it has witnessed many generalizations. Anis and De [3] discussed the popular Shannon and Rényi entropies for the unit-Gompertz distribution. For completeness, we list them below:

  • The Shannon entropy \( I_{S}: \)

    $$\begin{aligned} I_{S}= & {} 1- \ln \left( \alpha \beta \right) - \left( 1+\beta \right) \frac{e^{\alpha }}{\beta }\Gamma \left( 0;\alpha \right) , \quad \alpha>0, \quad \beta >0; \end{aligned}$$

  • The Rényi entropy \( I_{R}\left( \gamma \right) : \)

    $$\begin{aligned} I_{R}\left( \gamma \right)= & {} \frac{1}{1-\gamma }\left[ \alpha \gamma + \frac{\left( 1-\gamma \right) }{\beta } \ln \alpha - \left( 1-\gamma \right) \ln \beta +\frac{1}{\beta }\left\{ 1-\gamma \left( 1+\beta \right) \right\} \ln (\gamma )\right. \\{} & {} +\, \left. \ln \left( \Gamma \left( \gamma +\frac{1}{\beta }\left( \gamma -1\right) , \alpha \gamma \right) \right) \right] , \quad \alpha>0, \quad \beta>0; \quad \gamma >0. \end{aligned}$$

Next, we look at four other genralizations.

2.2.1 The Tsallis entropy

The Tsallis entropy was introduced by Tsallis [36] and is defined by

$$\begin{aligned} I_{T}\left( \gamma \right) =\frac{1}{\gamma -1}\left( 1-\int _{-\infty }^{\infty }\left[ f\left( x\right) \right] ^{\gamma }dx\right) , \quad 0<\gamma \ne 1. \end{aligned}$$

Clearly, the Tsallis entropy reduces to the classical Shannon entropy as \( \gamma \rightarrow 1.\) There are many applications of the Tsallis entropy. In physics, it is used to describe a number of non-extensive systems [12]. It has found application in image processing [43] and signal processing [34]. Zhang et al. [45] used a Tsallis entropy-based measure to reveal the presence and the extent of development of burst suppression activity following brain injury. Zhang and Wu [44] used the Tsallis entropy to propose a global multi-level thresholding method for image segmentation.

For the unit-Gompertz distribution, the Tsallis entropy is given by

$$\begin{aligned} I_{T}\left( \gamma \right) =\frac{1}{\gamma -1}\left[ 1 - \frac{\alpha ^{\frac{1-\gamma }{\beta }}\beta ^{\gamma -1}}{\gamma ^{\frac{\gamma +\beta \gamma -1}{\beta }}}e^{\alpha \gamma }\Gamma \left( \frac{\gamma +\beta \gamma -1}{\beta }; \alpha \gamma \right) \right] , 0<\gamma \ne 1, \alpha>0, \beta >0; \end{aligned}$$

where \( \Gamma \left( s; x\right) \) is defined in (3).

2.2.2 The Mathai–Haubold entropy

Mathai and Haubold [24] introduced a new measure of entropy. It is defined by

$$\begin{aligned} I_{MH}\left( \gamma \right) = \frac{1}{\gamma -1 }\left( \int _{-\infty }^{\infty }\left[ f\left( x\right) \right] ^{2- \gamma }dx -1\right) , \quad \gamma \ne 1,\quad \gamma <2. \end{aligned}$$

The entropy \( I_{MH}\left( \gamma \right) \) is an inaccuracy measure through disturbance or distortion of systems. As \( \gamma \rightarrow 1, \) the entropy \( I_{MH}\left( \gamma \right) \) reduces to the Shannon entropy. In case of the unit-Gompertz distribution, the Mathai-Haubold entropy is given by

$$\begin{aligned} I_{MH}\left( \gamma \right)&= \frac{1}{\gamma -1}\left[ \frac{\alpha ^{\frac{\left( \gamma -1\right) }{\beta }}\beta ^{1-\gamma }}{\left( 2-\gamma \right) ^{\left[ \frac{\left( 1+\beta \right) \left( 1-\gamma \right) }{\beta }+1\right] }}e^{\alpha \left( 2-\gamma \right) }\Gamma \left( \frac{\left( 1+\beta \right) \left( 1-\gamma \right) }{\beta }+1; \alpha \left( 2-\gamma \right) \right) \!\! -\!\! 1 \right] , \\&\quad \gamma \ne 1, \quad \gamma <2, \quad \alpha>0, \quad \beta >0; \end{aligned}$$

where \( \Gamma \left( s; x\right) \) is defined in (3).

2.2.3 The Varma entropy

Varma [38] introduced a new measure of entropy, indexed by two parameters, \( \gamma \) and \( \delta , \) which make this new measure of entropy much more flexible, thereby enabling several measurements of uncertainty within a given distribution. It plays a major role as a measure of complexity and uncertainty in different areas such as coding theory and electronics, engineering and physics to describe many chaotic systems. To understand the use of entropy in information theory, one can refer to Cover and Thomas [8]. The Varma entropy is defined as

$$\begin{aligned} I_{V}\left( \gamma , \delta \right) = \frac{1}{\delta -\gamma }\ln \left[ \int _{-\infty }^{\infty } f^{\gamma +\delta -1}\left( x\right) dx \right] , \quad \delta -1<\gamma <\delta , \quad \delta \geqslant 1, \quad \gamma \ne \delta . \end{aligned}$$

When \( \delta \rightarrow 1 \) and \( \gamma \rightarrow 1,\) then \(I_{V}\left( \gamma , \delta \right) \rightarrow I_{S}\left( \gamma \right) , \) the Shannon entropy. For the unit-Gompertz distribution, the Varma entropy is given by

$$\begin{aligned} I_{V}\left( \gamma , \delta \right)= & {} \frac{1}{\delta - \gamma }\left\{ \left[ \alpha \left( \gamma + \delta -1\right) \right] + \left[ \ln \left\{ \alpha ^{\frac{2-\delta -\gamma }{\beta }}\beta ^{\gamma + \delta -2}\left( \gamma + \delta -1\right) ^{\frac{2+\beta - \left( 1+\beta \right) \left( \gamma + \delta \right) }{\beta }}\right\} \right] \right\} \\{} & {} +{~} \frac{1}{\delta - \gamma }\left[ \ln \left\{ \Gamma \left( \frac{\left( 1+\beta \right) \left( \gamma + \delta -2\right) }{\beta }+1; \alpha \left( \gamma + \delta -1\right) \right) \right\} \right] , \quad \alpha , \beta >0; \end{aligned}$$

where \( \Gamma \left( s; x\right) \) is defined in (3).

2.2.4 The Kapur entropy

Kapur [18] proposed another measure of entropy. It is defined as

$$\begin{aligned} I_{K}\left( \gamma , \delta \right) = \frac{1}{\delta - \gamma }\ln \left\{ \frac{\int _{-\infty }^{\infty } f^{\gamma }\left( x\right) dx}{\int _{-\infty }^{\infty } f^{\delta }\left( x\right) dx}\right\} . \end{aligned}$$

Clearly, if \( \delta =1 \), then the Kapur entropy reduces to the Rényi entropy. Furthermore, if \( \delta =1 \) and \( \gamma \rightarrow 1, \) then the Kapur entropy converges to the Shannon entropy. It has varied uses. For example, Upadhyay and Chhabra [37] used Crow Search Algorithm based on the Kapur entropy to estimate optimal values of multilevel thresholds. Specifically, for the unit-Gompertz distribution, the Kapur entropy is given by

$$\begin{aligned} I_{K}\left( \gamma , \delta \right)= & {} \frac{1}{\delta - \gamma }\left\{ \left[ \alpha \left( \gamma - \delta \right) \right] + \left[ \ln \left\{ \alpha ^{\frac{\delta -\gamma }{\beta }}\beta ^{\gamma - \delta }\left( \delta \right) ^{\frac{\delta +\delta \beta - 1 }{\beta }}\Gamma \left( \frac{\left( \gamma + \beta \gamma -1\right) }{\beta }; \alpha \gamma \right) \right\} \right] \right\} \\{} & {} -\, \frac{1}{\delta - \gamma }\left[ \ln \left\{ \gamma ^{\frac{\gamma +\beta \gamma -1}{\beta }} \Gamma \left( \frac{\left( \delta + \beta \delta -1\right) }{\beta }; \alpha \delta \right) \right\} \right] , \end{aligned}$$

where \( \Gamma \left( s; x\right) \) is defined in (3).

2.3 Aging intensity and reversed aging intensity functions

The reliability related functions like the hazard rate function, mean residual life function, reversed hazard rate function and expected inactivity time of the unit-Gompertz distribution were discussed in Anis and De [3]. For completeness, we shall simply list down the final expressions of these functions for the unit-Gompertz distribution.

  • Hazard rate function:

    $$ h(x)= \frac{\alpha \beta \exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] }{x^{1+\beta }\left\{ 1-\exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] \right\} }; $$

  • Mean Residual Life function:

    $$e\left( t\right) = \frac{1}{\bar{F}\left( t\right) } \left\{ e^{\alpha }\alpha ^{1/\beta }\left[ \Gamma \left( 1-\frac{1}{\beta }; \alpha \right) - \Gamma \left( 1-\frac{1}{\beta }; \frac{\alpha }{t^{\beta }}\right) \right] \right\} -t,$$

    where \( \Gamma \left( s, x\right) \) is the upper incomplete gamma function defined in (3);

  • Reversed hazard rate function:

    $$\begin{aligned} r\left( x\right) =\frac{\alpha \beta }{x^{1+\beta }}; \end{aligned}$$

  • Expected inactivity time function:

    $$I\left( x\right) =\frac{e^{\alpha /x^{\beta }}\alpha ^{1/\beta }}{\beta }\Gamma \left( \frac{-1}{\beta };\frac{\alpha }{x^{\beta }}\right) ,$$

    where \( \Gamma \left( s, x\right) \) is the upper incomplete gamma function defined in (3).

Next, we shall discuss two relatively new but important functions.

Let f,  F and \( \bar{F}=1-F \) be the pdf, cdf and survival function of the random variable X. Jiang et al. [16] defined the aging intensity function (AIF), denoted by \( L\left( x\right) ,\) as

$$\begin{aligned} L\left( x\right) =\frac{xf\left( x\right) }{- \bar{F}\left( x\right) \ln \left[ \bar{F}\left( x\right) \right] }, \quad x>0. \end{aligned}$$

Though \( L\left( x\right) \) is related to the failure rate function, it does not determine the distribution uniquely. Numerically, \( L\left( x\right) >1, \) if the failure rate is increasing; \( L\left( x\right) =1, \) if the failure rate is constant and \( L\left( x\right) <1, \) if the failure rate is decreasing. The larger the value of \( L\left( x\right) , \) the stronger is the tendency of aging and vice versa. Thus, it describes the aging property quantitatively. It can also be interpreted as the percentage the cdf changes (decreases) when the lifetime x changes (decreases) by a small amount. Jiang et al. [17] used the AIF for parameter estimation when the data are heavily censored. For the UG distribution, we have

$$\begin{aligned} L\left( x\right) =\frac{-\alpha \beta H\left( \alpha , \beta \right) }{x^{\beta }\left[ 1 - H\left( \alpha , \beta \right) \right] \ln \left( 1-H\left( \alpha , \beta \right) \right) }, \quad \alpha>0,\quad \beta >0; \end{aligned}$$

where \( H\left( \alpha , \beta \right) =\exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] . \)

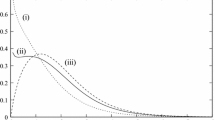
Figure 1 shows the plots of the AIF for different values of \(\alpha \) and \(\beta \). These plots clearly show that the AIF is bathtub-shaped.

Fig. 1
figure 1

Plots of aging intensity function for different values of \(\alpha \) and \(\beta \)

Full size image

The dual concept of reversed aging intensity function \( \widetilde{L} \left( x\right) \) is defined by

$$\begin{aligned} \widetilde{L}\left( x\right) =\frac{xf\left( x\right) }{- F\left( x\right) \ln \left[ F\left( x\right) \right] }, \quad x>0. \end{aligned}$$

The larger the numerical value of the reversed aging intensity function, the weaker is the tendency of aging. The aging intensity function L and the reversed aging intensity function \( \widetilde{L}\) do not characterize the family of distribution uniquely. See Szymkowiak [32] and Buono et al. [6] for details.

For the UG distribution, we get

$$\begin{aligned} \widetilde{L}\left( x\right) =\frac{\beta }{1-x^{\beta }}, {~~~} \beta >0. \end{aligned}$$

Observe that the first derivative of \(\widetilde{L}\left( x\right) \) is

$$\begin{aligned} \widetilde{L}^{'}\left( x\right) =\frac{\beta ^2x^{\beta -1}}{(1-x^{\beta })^2}, {~~~} \beta >0 . \end{aligned}$$

For \(x\in (0,1)\), \(\widetilde{L}^{'}\left( x\right) >0\) implies that the reversed aging intensity function is always non-decreasing and this can be visualised from Fig. 2. It can also be observed from Fig. 2 that the value of \(\widetilde{L}(x)\) increases as the value of \(\beta \) increases and is an asymptote at \(x=1\) for all values of \(\beta >0\).

Fig. 2
figure 2

Plot of reversed aging intensity function for different values of \(\beta \)

Full size image

3 Characterizations

We shall now give characterizations of the unit-Gompertz distribution based on (i) truncated first moment; (ii) hazard function; (iii) reversed hazard function; (iv) Mills ratio and (v) elasticity function.

3.1 Characterizations based on the truncated first moment

We shall begin with characterizations based on the truncated first moment. To prove the characterization results, we shall need two lemmas and an assumption, which are presented first.

Assumption

\(\mathcal {A}\): Assume that X is an absolutely continuous random variable with the pdf given in (1) and the corresponding cdf given in (2). Assume that \( E\left( X\right) \) exits and the density \( f\left( x\right) \) is differentiable. Define \( \eta = \sup \left\{ x: F\left( x\right) <1\right\} \) and \( \zeta = \inf \left\{ x: F\left( x\right) >0\right\} . \)

Lemma 3.1

Under Assumption \(\mathcal {A}\), if \(E\left( X\mid X \le x\right) = g\left( x\right) \tau \left( x\right) , \) where \( g\left( x\right) \) is a continuous differentiable function of x with the condition that \(\int _{\zeta }^{x}\frac{u-g^{\prime }(u)}{g(u)}du\) is finite for all \( x> \zeta , \) and \( \tau \left( x\right) =\frac{f\left( x\right) }{F\left( x\right) } \), then

$$\begin{aligned} f\left( x\right) =c\exp \left[ {\int \frac{x-g^{\prime }\left( x\right) }{g\left( x\right) }dx}\right] , \end{aligned}$$

where the constant c is determined by the condition \(\int _{\zeta }^{\eta }f\left( x\right) dx=1.\)

Lemma 3.2

Under Assumption \(\mathcal {A}\), if \(E\left( X\mid X \ge x\right) = h\left( x\right) r \left( x\right) , \) where \( h\left( x\right) \) is a continuous differentiable function of x with the condition that \(\int _{\zeta }^{x}\frac{u-h^{\prime }(u)}{h(u)}du\) is finite for all \( x>\zeta , \) and \( r\left( x\right) =\frac{f\left( x\right) }{1- F\left( x\right) } \), then

$$\begin{aligned} f\left( x\right) =c\exp \left[ - {\int \frac{x+h^{\prime }\left( x\right) }{h\left( x\right) }dx}\right] , \end{aligned}$$

where c is a constant determined by the condition \(\int _{\zeta }^{\eta }f\left( x\right) dx=1.\)

See Ahsanullah [1] for the details of proofs of Lemmas 3.1 and 3.2.

3.1.1 Characterization theorems

We shall now state and prove two characterization theorems based on the truncated first moment.

Theorem 3.3

Suppose that the random variable X satisfies Assumption \(\mathcal {A}\) with \(\zeta =0\) and \(\eta =1.\) Then, \(E\left( X\mid X \le x\right) = g\left( x\right) \tau \left( x\right) , \) where \(\tau (x)=\frac{f(x)}{F(x)}\) and

$$\begin{aligned} g\left( x\right) =\frac{\alpha ^{1/\beta }}{\alpha \beta }\exp \left( \frac{\alpha }{x^{\beta }}\right) x^{1+\beta }\Gamma \left( \left\{ 1-\frac{1}{\beta }\right\} ; \frac{\alpha }{x^{\beta }}\right) , \end{aligned}$$
(4)

where \( \Gamma \left( s; x\right) \) is defined in (3), if and only if

$$\begin{aligned} f\left( x\mid \alpha , \beta \right) = \frac{\alpha \beta \exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] }{x^{1+\beta }}; \quad \alpha>0, \quad \beta >0, \quad x \in (0, 1). \end{aligned}$$

Proof

Suppose

$$ f\left( x\mid \alpha , \beta \right) = \frac{\alpha \beta \exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] }{x^{1+\beta }}; \quad \alpha>0, \quad \beta >0, \quad x \in (0, 1). $$

We have

$$\begin{aligned} g\left( x\right) \tau \left( x\right) = E\left( X\mid X \le x\right) = \frac{1}{F\left( x\right) }\int _{0}^{x}t f\left( t\right) dt. \end{aligned}$$

Since \(\tau (x)=\frac{f(x)}{F(x)},\) it follows that

$$\begin{aligned} g\left( x\right) f\left( x\right)= & {} \int _{0}^{x}t f\left( t\right) dt\\= & {} \int _{0}^{x}t \frac{\alpha \beta \exp \left[ -\alpha \left( 1/t^{\beta }-1\right) \right] }{t^{1+\beta }}dt\\= & {} e^{\alpha }\alpha ^{1/\beta }\Gamma \left( \left\{ 1-\frac{1}{\beta }\right\} ; \frac{\alpha }{x^{\beta }}\right) , \end{aligned}$$

where \( \Gamma \left( s;x\right) \) is the upper incomplete gamma function defined in (3). Hence, after simplifying, we obtain

$$\begin{aligned} g\left( x\right) =\frac{\alpha ^{1/\beta }}{\alpha \beta }\exp \left( \frac{\alpha }{x^{\beta }}\right) x^{1+\beta }\Gamma \left( \left\{ 1-\frac{1}{\beta }\right\} ; \frac{\alpha }{x^{\beta }}\right) . \end{aligned}$$

Conversely, suppose that \( g\left( x\right) \) is given by (4). Differentiating \(g\left( x\right) \) with respect to x,  and simplifying, we obtain

$$\begin{aligned} g^{\prime }\left( x\right)= & {} x- g\left( x\right) \left[ \frac{\alpha \beta }{x^{\beta +1}} - \frac{\beta +1}{x}\right] . \end{aligned}$$

Hence,

$$\begin{aligned} \frac{x-g^{\prime }\left( x\right) }{g\left( x\right) }= \frac{\alpha \beta }{x^{\beta +1}} - \frac{\beta +1}{x}. \end{aligned}$$

By Lemma 3.1, we have

$$\begin{aligned} \frac{f^{\prime }\left( x\right) }{f\left( x\right) }= \frac{\alpha \beta }{x^{\beta +1}} - \frac{\beta +1}{x}. \end{aligned}$$
(5)

Integrating both sides of (5) with respect to x,  we obtain

$$\begin{aligned} f\left( x\right) =k\frac{\exp \left( -\alpha x^{-\beta }\right) }{x^{\beta +1}}, \end{aligned}$$

where k is a constant. Using the condition \( \int _{0}^{1} f\left( x\right) dx=1,\) we get

$$\begin{aligned} f\left( x\right) = \frac{\alpha \beta \exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] }{x^{1+\beta }}. \end{aligned}$$

This completes the proof. \(\square \)

Theorem 3.4

Suppose that the random variable X satisfies Assumption \(\mathcal {A}\) with \(\zeta =0\) and \(\eta =1.\) Then, \(E\left( X\mid X \ge x\right) = h\left( x\right) r \left( x\right) , \) where \(r(x)=\frac{f(x)}{1-F(x)}\) and

$$\begin{aligned} h\left( x\right) =\frac{\alpha ^{1/\beta }}{\alpha \beta }\exp \left( \frac{\alpha }{x^{\beta }}\right) x^{1+\beta }\left[ \Gamma \left( \left\{ 1-\frac{1}{\beta }\right\} ;\alpha \right) - \Gamma \left( \left\{ 1-\frac{1}{\beta }\right\} ; \frac{\alpha }{x^{\beta }}\right) \right] , \end{aligned}$$
(6)

where \( \Gamma \left( s;x\right) \) is the upper incomplete gamma function defined in (3), if and only if

$$\begin{aligned} f\left( x\mid \alpha , \beta \right) = \frac{\alpha \beta \exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] }{x^{1+\beta }}; \quad \alpha>0, \quad \beta >0, \quad x \in (0, 1). \end{aligned}$$

Proof

Suppose

$$ f\left( x\mid \alpha , \beta \right) = \frac{\alpha \beta \exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] }{x^{1+\beta }}; \quad \alpha>0,\quad \beta >0,\quad x \in (0, 1). $$

We have

$$\begin{aligned}h\left( x\right) r\left( x\right) = E\left( X\mid X \ge x\right) = \frac{1}{1-F\left( x\right) }\int _{x}^{1}t f\left( t\right) dt. \end{aligned}$$

Since \(r(x)=\frac{f(x)}{1-F(x)},\) it follows that

$$\begin{aligned} h\left( x\right) f\left( x\right)= & {} \int _{x}^{1}t f\left( t\right) dt\\= & {} E\left( X\right) - \int _{0}^{x}t f\left( t\right) dt\\= & {} E\left( X\right) -\int _{0}^{x}t \frac{\alpha \beta \exp \left[ -\alpha \left( 1/t^{\beta }-1\right) \right] }{t^{1+\beta }}dt\\= & {} e^{\alpha }\alpha ^{1/\beta }\left[ \Gamma \left( \left\{ 1-\frac{1}{\beta }\right\} ;\alpha \right) -\Gamma \left( \left\{ 1-\frac{1}{\beta }\right\} ; \frac{\alpha }{x^{\beta }}\right) \right] , \end{aligned}$$

where \( \Gamma \left( s;x\right) \) is the upper incomplete gamma function defined in (3). Hence,

$$\begin{aligned} h\left( x\right) =\frac{\alpha ^{1/\beta }}{\alpha \beta }\exp \left( \frac{\alpha }{x^{\beta }}\right) x^{1+\beta }\left[ \Gamma \left( \left\{ 1-\frac{1}{\beta }\right\} ;\alpha \right) - \Gamma \left( \left\{ 1-\frac{1}{\beta }\right\} ; \frac{\alpha }{x^{\beta }}\right) \right] . \end{aligned}$$

Conversely, suppose that \( h\left( x\right) \) is given by (6). Differentiating \(h\left( x\right) \) with respect to x,  and simplifying, we obtain

$$\begin{aligned} h^{\prime }\left( x\right)= & {} -x- h\left( x\right) \left[ \frac{\alpha \beta }{x^{\beta +1}} - \frac{\beta +1}{x}\right] . \end{aligned}$$

Hence,

$$\begin{aligned} -\frac{x+h^{\prime }\left( x\right) }{h\left( x\right) }= \frac{\alpha \beta }{x^{\beta +1}} - \frac{\beta +1}{x}. \end{aligned}$$

By Lemma 3.2, we have

$$\begin{aligned} \frac{f^{\prime }\left( x\right) }{f\left( x\right) }= \frac{\alpha \beta }{x^{\beta +1}} - \frac{\beta +1}{x}. \end{aligned}$$
(7)

Integrating both sides of (7) with respect to x,  we obtain

$$\begin{aligned} f\left( x\right) =k\frac{e^{-\alpha x^{-\beta }}}{x^{\beta +1}}, \end{aligned}$$

where k is a constant. Using the condition \( \int _{0}^{1} f\left( x\right) dx=1,\) we get

$$\begin{aligned} f\left( x\right) = \frac{\alpha \beta \exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] }{x^{1+\beta }}. \end{aligned}$$

This completes the proof. \(\square \)

3.2 Characterization based on the hazard function

Mazucheli et al. [25] obtained the hazard rate function of the UG distribution. Specifically, it is given by

$$\begin{aligned} h_{F}\left( x\right) =\frac{\alpha \beta \exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] }{x^{1+\beta }\left\{ 1-\exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] \right\} }. \end{aligned}$$

Anis and De [3] discussed the shape of the hazard function.

We shall now use it to provide a characterization result for this distribution. It is well known that the hazard function uniquely determines the distribution. More specifically, the hazard function, \( h_{F}, \) of a twice differentiable distribution function, F,  satisfies the first order differential equation

$$\begin{aligned} \frac{d}{dx}\left[ \ln f\left( x\right) \right] =\frac{h_{F}^{\prime }\left( x\right) }{h_{F}\left( x\right) }-h_{F}\left( x\right) , \end{aligned}$$

where \( f\left( x\right) = \frac{dF\left( x\right) }{dx}.\) The next theorem establishes a characterization of the UG distribution based on the hazard rate function.

Theorem 3.5

The pdf of X is given by (1) if and only if its hazard function, \( h_{F}, \) satisfies the first order differential equation

$$\begin{aligned}{} & {} h_{F}^{\prime }\left( x\right) \left\{ 1-\exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] \right\} - h_{F}\left( x\right) \frac{\alpha \beta \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] }{x^{1+\beta }} \nonumber \\{} & {} \quad = \frac{\alpha \beta }{x^{2\left( 1+\beta \right) }}\exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] \left[ \alpha \beta -\left( 1+\beta \right) x^{\beta }\right] . \end{aligned}$$
(8)

Proof

If the random variable X has the pdf (1), then it is easy to check that the differential equation (8) holds.

Conversely, suppose the differential equation in (8) is true. Then, it is easy to see that the left hand side of (8) can be rewritten as \( \frac{d}{dx}\left[ h_{F}\left( x\right) \left\{ 1-\exp \left[ - \alpha \left( \frac{1}{x^{\beta }} -1\right) \right] \right\} \right] ; \) while the right hand side is just \( \frac{d}{dx}\left[ \frac{\alpha \beta \exp \left[ -\alpha \left( \frac{1}{x^{\beta }} -1\right) \right] }{x^{1+\beta }} \right] . \) Hence, we have

$$\begin{aligned} \frac{d}{dx}\left[ h_{F}\left( x\right) \left\{ 1-\exp \left[ -\alpha \left( \frac{1}{x^{\beta }} -1\right) \right] \right\} \right] = \frac{d}{dx}\left[ \frac{\alpha \beta \exp \left[ - \alpha \left( \frac{1}{x^{\beta }} -1\right) \right] }{x^{1+\beta }} \right] . \end{aligned}$$

Thus, we have

$$\begin{aligned} h_{F}\left( x\right) =\frac{\alpha \beta \exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] }{x^{1+\beta }\left\{ 1-\exp \left[ -\alpha \left( 1/x^{\beta }-1\right) \right] \right\} }, \end{aligned}$$

which is the hazard function of the UG distribution. \(\square \)

3.3 Characterization based on the Mills ratio

The Mills ratio \( M\left( x\right) \) was introduced into the statistical literature by Mills [26]. Essentially, it is the reciprocal of the hazard function. The convexity of the Mills ratio of continuous distributions has important applications in monopoly theory, especially in static pricing problems. Xu and Hopp [42] used the convexity of Mills ratio to establish that the price is a sub-martingale. Like the hazard function, the Mills ratio \( M\left( x\right) , \) of a twice differentiable distribution function, F,  satisfies the first order differential equation

$$\begin{aligned} \frac{f^{\prime }\left( x\right) }{f\left( x\right) }+\frac{1}{M\left( x\right) }+\frac{M^{\prime }\left( x\right) }{M\left( x\right) }=0, \end{aligned}$$

where \( f\left( x\right) = \frac{dF\left( x\right) }{dx}.\) The next theorem establishes a characterization of the UG distribution based on the Mills ratio.

Theorem 3.6

The pdf of X is given by (1) if and only if its Mills ratio \( M\left( x\right) \) satisfies the first order differential equation

$$\begin{aligned}{} & {} M^{\prime }\left( x\right) \frac{\alpha \beta \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] }{x^{1+\beta }}+ M\left( x\right) \frac{\alpha \beta \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] }{x^{2\left( 1+\beta \right) } }\left[ \alpha \beta -\left( 1+\beta \right) x^{\beta }\right] \nonumber \\{} & {} \quad +\, \frac{\alpha \beta \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] }{x^{ 1+\beta } }=0. \end{aligned}$$
(9)

Proof

If the random variable X has the pdf (1), then routine but elaborate calculations show that the differential equation (9) holds.

Conversely, suppose the differential equation in (9) is true. Then, the above differential equation can be rewritten as

$$\begin{aligned} \frac{d}{dx}\left[ M\left( x\right) \frac{\alpha \beta \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] }{x^{1+\beta }}\right] + \frac{d}{dx}\left[ F\left( x\right) -1\right] =0; \end{aligned}$$

or equivalently,

$$\begin{aligned} \frac{d}{dx}\left[ M\left( x\right) \frac{\alpha \beta \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] }{x^{1+\beta }}\right] = \frac{d}{dx}\left[ 1- F\left( x\right) \right] ; \end{aligned}$$

and hence

$$\begin{aligned} M\left( x\right) =\left( \frac{1- F\left( x\right) }{\exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] }\right) \frac{x^{1+\beta }}{\alpha \beta }= \left( \frac{1-\exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] }{\exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] }\right) \frac{x^{1+\beta }}{\alpha \beta }, \end{aligned}$$

which represents the Mills ratio for the UG distribution. \(\square \)

3.4 Characterization based on the reversed hazard rate function

The reversed hazard rate function \( r_{F}\left( x\right) \) is an important characteristic of a random variable and has found many applications. Lagakos et al. [21] used the reversed hazard rate function to analyze right-truncated data. Cheng and Zhu [7] used the reverse hazard rate function to characterize the best strategy for allocating servers in a tandem system. Kijima [19] used the reversed hazard rate function to study continuous time Markov Chains. Gupta et al. [11] used the reversed hazard rate function to calculate the Fisher information. Townsend and Wenger [35] used the reversed hazard rate function to model information processing capacity. Razmkhah et al. [30] used the reversed hazard rate function to calculate the Shannon entropy.

Anis and De [3] showed that for the UG distribution, \(r_{F}\left( x\right) =\frac{\alpha \beta }{x^{1+\beta }}. \)

The reversed hazard rate function can be used to characterize a random variable. More precisely, the reversed hazard rate function, \( r_{F}, \) of a twice differentiable distribution function, F,  satisfies the first order differential equation

$$\begin{aligned} \frac{d}{dx}\left[ \ln f\left( x\right) \right] =\frac{r_{F}^{\prime }\left( x\right) }{r_{F}\left( x\right) }+ r_{F}\left( x\right) , \end{aligned}$$

where \( f\left( x\right) = \frac{dF\left( x\right) }{dx}.\) The next theorem establishes a characterization of the UG distribution based on the reversed hazard rate function.

Theorem 3.7

The pdf of X is given by (1) if and only if its reversed hazard function, \( r_{F}, \) satisfies the first order differential equation

$$\begin{aligned}{} & {} r_{F}^{\prime }\left( x\right) \left\{ \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] \right\} + r_{F}\left( x\right) \frac{\alpha \beta \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] }{x^{1+\beta }} \nonumber \\{} & {} \quad = \frac{\alpha \beta }{x^{2\left( 1+\beta \right) }}\left\{ \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] \right\} \left[ \alpha \beta -\left( 1+\beta \right) x^{\beta }\right] . \end{aligned}$$
(10)

Proof

If the random variable X has the pdf (1), then it is easy to check that the differential equation (10) holds.

Conversely, suppose the differential equation in (10) is true. Then, the above differential equation can be rewritten as

$$\begin{aligned} \frac{d}{dx}\left[ r_{F}\left( x\right) \left\{ \exp \left[ -\alpha \left( \frac{1}{x^{\beta }} -1\right) \right] \right\} \right] = \frac{d}{dx}\left[ \frac{\alpha \beta \exp \left[ -\alpha \left( \frac{1}{x^{\beta }} -1\right) \right] }{x^{1+\beta }}\right] . \end{aligned}$$

This implies \( r_{F}\left( x\right) =\frac{\alpha \beta }{x^{1+\beta }}, \) which is essentially the reversed hazard rate function of the UG distribution. \(\square \)

3.5 Characterization based on the elasticity function

The elasticity function of a random variable is a relatively new concept. Veres-Ferrer and Pavía [39,40,41] studied this function and its relationship with other stochastic functions. Essentially, the elasticity function \( e\left( x\right) \) of a random variable is defined by \( e\left( x\right) = \frac{x f\left( x\right) }{F\left( x\right) }. \) As an example of its application, mention may be made of Pavía et al. [28] who used these concepts to study risk management in business. Szymkowiak [33] used it to characterize a parent distribution uniquely. Lariviere and Porteus [22] adopted this concept and applied it to the supply chain management. For the UG distribution, the elastic function is given by \( e\left( x\right) = \frac{\alpha \beta }{x^{\beta }}. \) The elasticity function satisfies the first order equation

$$\begin{aligned} \frac{d}{dx}\left[ \ln f\left( x\right) \right] =\frac{e^{\prime }\left( x\right) }{e\left( x\right) }+\frac{e\left( x\right) }{x} - \frac{1}{x}. \end{aligned}$$

The following theorem establishes a characterization of the UG distribution based on the elasticity function.

Theorem 3.8

The pdf of X is given by (1) if and only if its elasticity function \( e\left( x\right) \) satisfies the first order differential equation

$$\begin{aligned}{} & {} e^{\prime }\left( x\right) \left\{ \frac{\alpha \beta }{x^{\beta }} \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] \right\} + e\left( x\right) \frac{\alpha \beta \left( \alpha \beta -\beta x^{\beta }\right) \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] }{x^{1+2\beta }} \nonumber \\{} & {} \quad = \frac{\left( \alpha \beta \right) ^{2}}{x^{ 1+3\beta }}\left\{ \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] \right\} \left( \alpha \beta - 2\beta x^{\beta }\right) . \end{aligned}$$
(11)

Proof

If the random variable X has the pdf (1), then routine, but elaborate calculation shows that the differential equation (11) holds.

Conversely, suppose the differential equation in (11) holds. Then, the above differential equation can be simplified as

$$\begin{aligned} \frac{d}{dx}\left[ e\left( x\right) \frac{\alpha \beta \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] }{x^{\beta }} \right] = \frac{d}{dx}\left[ \frac{\left( \alpha \beta \right) ^{2}}{x^{2\beta }} \exp \left[ -\alpha \left( \frac{1}{x^{\beta }}-1\right) \right] \right] , \end{aligned}$$

and hence \( e\left( x\right) = \frac{\alpha \beta }{x^{\beta }}, \) which is the elastic function of the UG distribution. \(\square \)

4 Conclusion

In this work, we have presented five characterizations of the recently-introduced unit-Gompertz distribution. To the best of our knowledge, this is the only work on the characterizations of this distribution available in the literature till date. We hope this will enable researchers to understand whether the given data at hand can be modeled by this distribution. We also looked at the L-moments, four measures of entropy, aging intensity and reversed aging intensity functions.