1 Introduction

Chemical kinetics of reacting chemical systems is generally governed by multi-dimensional systems that may contain embedded negative or positive feedback loops in addition to the concentration solutions of the chemical species. It is an arduous task to analyze these systems in the presence of nonlinear terms. Despite all difficulties, this nonlinearity enhances the chances of solutions to exhibit oscillatory or chaotic behaviors [7]. These ubiquitous mathematical behaviors can be found in many “far-from-equilibrium” chemical systems [25]. Recent efforts have been focused to study some related equations with fractional derivatives as in [1,2,3,4, 20, 24].

One of the most significant far-from-equilibrium chemical systems is the Belousov–Zhabotinsky (B–Z) reaction [6, 18, 22]. Due to its nonlinearity, Belousov-Zhabotinsky reaction can exhibit oscillatory behavior because of the second law of thermodynamics [17]. Additionally, this reaction exhibits many fractures including oscillations, deterministic chaos, multistability and excitability. A general way to describe the reaction is the following autonomous differential equation (see [23])

$$\begin{aligned} \dot{v}(t)\,=\,& \alpha \left( u\left( t\right) -\left( v\left( t\right) -\mu _{1}\right) \left( v\left( t\right) -\mu _{2}\right) \left( v\left( t\right) -\mu _{3}\right) +\mu _{4}\right) , \end{aligned}$$
(1)
$$\begin{aligned} \dot{u}(t)\,=\,& c_{1}-c_{2}p\left( t\right) -c_{3}v\left( t\right) -u\left( t\right) , \end{aligned}$$
(2)
$$\begin{aligned} \dot{p}(t)\,=\,& \gamma _{1}v\left( t\right) -\gamma _{2}p\left( t\right) , \end{aligned}$$
(3)

where \(t\ge t_{0}\), constants \(\alpha \), \(\mu _{1}\), \(\mu _{2}\), \(\mu _{3}\), \(\mu _{4}\), \(c_{1}\), \(c_{2}\), \(c_{3}\), \(\gamma _{1}\) and \(\gamma _{2}\), state v can be viewed as autocatalytic reagent, state u expresses a negative feedback response and state p is associated to the catalyst concentration. The coefficients of the prior system are related to concentrations imposed at the beginning of the experiment. They are time-invariant because they are assumed not to vary in a large range. However, this assumption is not guaranteed to occur in every case.

This paper generalizes Belousov–Zhabotinsky (B–Z) reaction differential-based system into the time-varying framework which is more realistic than the time-invariant one. The formulation of the new system is given in Sect. 2. In Sect. 3, it is shown that the new time-varying system is able to oscillate. Moreover, the origin attractivity is investigated which guarantees that vanishing of all states. On the other hand, the hysteretic behavior of the output v is studied in Sect. 4 in which a mathematical expression for the hysteresis loop is derived.

2 System under study

We generalize the Belousov–Zhabotinsky (B–Z) reaction (1)–(3) into the following time-varying system

$$\begin{aligned} \dot{v}(t)\,=\,& \alpha \left( t\right) \left( u\left( t\right) -\left( v\left( t\right) -\mu _{1}\left( t\right) \right) \left( v\left( t\right) -\mu _{2}\left( t\right) \right) \left( v\left( t\right) -\mu _{3}\left( t\right) \right) +\mu _{4}\left( t\right) \right) , \end{aligned}$$
(4)
$$\begin{aligned} \dot{u}(t)\,=\,& c_{1}\left( t\right) -c_{2}\left( t\right) p\left( t\right) -c_{3}\left( t\right) v\left( t\right) -u\left( t\right) , \end{aligned}$$
(5)
$$\begin{aligned} \dot{p}(t)\,=\,& \gamma _{1}\left( t\right) v\left( t\right) -\gamma _{2}\left( t\right) p\left( t\right) , \end{aligned}$$
(6)

where \(t\ge t_{0}\), states v, u, and p, continuous real functions \(\mu _{1}\), \(\mu _{2}\), \(\mu _{3}\), \(\mu _{4}\), \(c_1\), \(c_2\), \(c_3\), \(\gamma _1\) and \(\gamma _2\), and a Lebesgue measurable function \(\alpha :\mathbb {R}\rightarrow \mathbb {R}\). The right-hand sides of (4)–(6) are measurable in t, locally bounded and continuous with respect to the states. Therefore, the system admits an absolutely continuous Carathéodory solution that is defined on a maximal existence interval \([t_{0},\omega )\) where \(\omega \) can be infinity [5, Section 1.1].

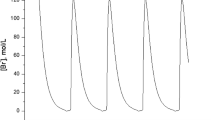
The system (4)–(6) is able to exhibit oscillations which occurs in the presence of limit cycles. To see this, let \(t_0=0\), \(v(t_0)=0.5\), \(u(t_0)=1\), \(p(t_0)=1\), \(\alpha \left( t\right) =0.065\), \(\mu _{1}\left( t\right) =\frac{1}{t+1}+1\), \(\mu _{2}\left( t\right) =\frac{1}{t+1}+2\), \(\mu _{3}\left( t\right) =\frac{1}{t+1}+3\), \(\mu _{4}\left( t\right) =-4\), \(c_{1}\left( t\right) =436.57731\), \(c_{2}\left( t\right) =3714.28317\times 10^{-3}\), \(c_{3}\left( t\right) =21.7\) and \(\gamma _{1}\left( t\right) =\gamma _{2}\left( t\right) =0.23\). As illustrated in Fig. 1, the states v(t), u(t) and p(t) reach steady states just beyond transient effects. Moreover, the figure shows the limit cycles exhibited by the system.

Fig. 1
figure 1

Upper left \(v\left( t\right) \) versus t. Upper right \(u\left( t\right) \) versus t. Middle left \(p\left( t\right) \) versus t. Middle right \(u\left( t\right) \) versus \(v\left( t\right) \). Lower left p(t) versus u(t). Lower right \(p\left( t\right) \) versus v(t)

Full size image

3 Boundedness and attractivity of solutions

In this section, we mainly aim to investigate conditions that make the concentrations decay to zero as t gets larger. In other words, we aim to study the attractivity of the system (4)–(6) in which all states converge to zero as t goes to infinity [11, 16, 19]. To clinch this goal, we recall some results from [10, 13].

Theorem 3.1

[10, Theorem 2.1] Consider the system

$$\begin{aligned} \dot{w}\left( t\right) =e\left( t\right) -q\left( t\right) \beta \left( w\left( t\right) \right) , \end{aligned}$$
(7)

for every \(t\ge t_0\), state \(w\in \mathbb {R}\), initial value \(w\left( t_{0}\right) \ge 0\), a strictly increasing function \(\beta \in C^{0}\left( \mathbb {R},\mathbb {R}\right) \) with \(\beta \left( 0\right) =0\), and continuous functions \(e,\, q\,\in C^{0}\left( \mathbb {R},\mathbb {R}_{+}\right) \). Assume that \(q\left( t\right) >0,\forall t\ge t_{0}\), \(\intop _{t_{0}}^{\infty }q\left( \tau \right) d\tau =\infty \), \(\lim _{t\rightarrow \infty }\frac{e\left( t\right) }{q\left( t\right) }=L\ge 0\) and \(L\in \text{ Range }\left\{ \beta \right\} \). Then for every initial value \(w(t_0)\ge 0\) and every solution w(t) with maximal existence interval \([t_{0},\omega )\); \(\omega \in (t_{0},\infty ]\), we have \(\omega =\infty \), \(\left\| w\right\| _{\infty }<\infty \) and \(\lim _{t\rightarrow \infty }w\left( t\right) =\beta ^{-1}\left( L\right) \).

Proposition 3.1

[13, Prop. 3.2] Consider a locally absolutely continuous function \(z:[t_{0},\omega )\rightarrow \mathbb {R}_{+}\), where \(\omega \in (t_{0},\infty ]\). Assume the existence of some continuous functions \(\psi _1\in C^{0}\left( [t_{0},\infty ),\mathbb {R}_{+}\right) \) and \(\psi _2\in C^{0}\left( [t_{0},\infty ),\mathbb {R}_{+}\right) \) such that \(z(t_{0})<\psi _{2}\left( t_{0}\right) \), \(\psi _{1}\left( t\right) <\psi _{2}\left( t\right) ,\;\forall t\ge t_{0}\) and

$$\begin{aligned} \dot{z}\left( t\right) \le \dot{\psi }_{2}\left( t\right) \text{ for } \text{ almost } \text{ all } t\in (t_{0},\omega ), \text{ that } \text{ satisfy } \psi _{1}\left( t\right)<z(t)<\psi _{2}\left( t\right) . \end{aligned}$$
(8)

Then we have \(z(t)<\psi _{2}\left( t\right) ,\;\forall t\in [t_{0},\omega )\).

Now we make the following assumptions.

Assumption 1

The function \(\alpha \) is continuous and for all \(t\ge t_0\), we have \(\gamma _2(t)>0\) and

$$\begin{aligned} \alpha \left( t\right) \left( \mu _{1}\left( t\right) \mu _{2}\left( t\right) +\mu _{1}\left( t\right) \mu _{3}\left( t\right) +\mu _{2}\left( t\right) \mu _{3}\left( t\right) \right) >0, \end{aligned}$$

with

$$\begin{aligned} \intop _{t_{0}}^{\infty }\alpha \left( t\right) \left( \mu _{1}\left( t\right) \mu _{2}\left( t\right) +\mu _{1}\left( t\right) \mu _{3}\left( t\right) +\mu _{2}\left( t\right) \mu _{3}\left( t\right) \right) dt=\intop _{t_{0}}^{\infty }\gamma _2\left( t\right) dt=\infty . \end{aligned}$$

Define \(Q\in C^{0}\left( [t_{0},\infty ),\mathbb {R}\right) \) and \(E\in C^{0}\left( [t_{0},\infty ),\mathbb {R}\right) \) as

$$\begin{aligned} Q\left( t\right)= & \min {\left( 1,\gamma _2\left( t\right) ,\alpha \left( t\right) \left( \mu _{1}\left( t\right) \mu _{2}\left( t\right) +\mu _{1}\left( t\right) \mu _{3}\left( t\right) +\mu _{2}\left( t\right) \mu _{3}\left( t\right) \right) \right) }. \\ E\left( t\right)= & \left| \alpha \left( t\right) \right| \left( 1+\left| \mu _{1}\left( t\right) +\mu _{2}\left( t\right) +\mu _{3}\left( t\right) \right| +\left| \mu _{1}\left( t\right) \mu _{2}\left( t\right) \mu _{3}\left( t\right) +\mu _{4}\left( t\right) \right| \right) \\&+\left| c_{1}\left( t\right) \right| +\left| c_{2}\left( t\right) \right| +\left| \gamma _{1}\left( t\right) \right| +\left| \alpha \left( t\right) -c_{3}\left( t\right) \right| ,\,\,\forall t\ge t_{0}. \end{aligned}$$

Obviously, we have \(Q\left( t\right) >0\) and \(E\left( t\right) \ge 0\) for all \(t\ge t_0\).

Assumption 2

\(\lim _{t\rightarrow \infty }\left( \frac{E\left( t\right) }{Q\left( t\right) }\right) =0\).

Observe that to make Assumption 2 satisfied, we need to have

$$\begin{aligned} \lim _{t\rightarrow \infty }{c_{1}\left( t\right) }=\lim _{t\rightarrow \infty }{c_{2}\left( t\right) }=\lim _{t\rightarrow \infty }{c_{3}\left( t\right) }=\lim _{t\rightarrow \infty }{\gamma _{1}\left( t\right) }=\lim _{t\rightarrow \infty }{\alpha \left( t\right) }=0. \end{aligned}$$

The next theorem proves the boundedness of solutions and the local attractivity of the origin.

Theorem 3.2

Under Assumptions \(1-2\), there exists some \(c>0\) such that the states v(t), u(t) and p(t) are bounded and continuable on \([t_0,\infty )\) and the origin is locally attractive, that is \(\lim _{t\rightarrow \infty }{v\left( t\right) }=\lim _{t\rightarrow \infty }{u\left( t\right) }=\lim _{t\rightarrow \infty }{p\left( t\right) }=0\), for each initial value \(\left( v\left( t_{0}\right) ,u\left( t_{0}\right) ,p\left( t_{0}\right) \right) \in \mathbb {R}^{3}\) with magnitude less than c.

Proof

Since the function \(\alpha \) is assumed to be continuous, the right-hand sides of the system (4)–(6) is continuous and locally Lipschitz with respect to states. Thus, the system (4)–(6) has a unique continuously differentiable solution that is defined on an interval of the form \([t_0,\omega )\); \(\omega \in (t_{0},\infty ]\) [21, p. 66]. Consider the Lyapunov function \(V:[t_{0},\omega )\rightarrow \mathbb {R}_{+}\) such that \(V\left( t\right) =v^{2}\left( t\right) +u^{2}\left( t\right) +p^{2}\left( t\right) ,\forall t\in [t_{0},\omega )\). Pick \(v(t_0)\in \mathbb {R}\), \(u(t_0)\in \mathbb {R}\) and \(p(t_0)\in \mathbb {R}\). For all \(t\in (t_{0},\omega )\), we have

$$\begin{aligned} \dot{V}\left( t\right)\,=\,& 2\alpha \left( t\right) v\left( t\right) \left( u\left( t\right) -\left( v\left( t\right) -\mu _{1}\left( t\right) \right) \left( v\left( t\right) -\mu _{2}\left( t\right) \right) \left( v\left( t\right) -\mu _{3}\left( t\right) \right) +\mu _{4}\left( t\right) \right) \\&+2u\left( t\right) \left( c_{1}\left( t\right) -c_{2}\left( t\right) p\left( t\right) -c_{3}\left( t\right) v\left( t\right) -u\left( t\right) \right) \\&+2p\left( t\right) \left( \gamma _{1}\left( t\right) v\left( t\right) -\gamma _{2}\left( t\right) p\left( t\right) \right) , \end{aligned}$$

so that

$$\begin{aligned} \dot{V}\left( t\right)= & 2\alpha \left( t\right) v\left( t\right) \Bigl [u\left( t\right) -v^{3}\left( t\right) +\left( \mu _{1}\left( t\right) +\mu _{2}\left( t\right) +\mu _{3}\left( t\right) \right) v^{2}\left( t\right) \\&-\left( \mu _{1}\left( t\right) \mu _{2}\left( t\right) +\mu _{1}\left( t\right) \mu _{3}\left( t\right) +\mu _{2}\left( t\right) \mu _{3}\left( t\right) \right) v\left( t\right) +\mu _{1}\left( t\right) \mu _{2}\left( t\right) \mu _{3}\left( t\right) +\mu _{4}\left( t\right) \Bigr ] \\&+2u\left( t\right) \left( c_{1}\left( t\right) -c_{2}\left( t\right) p\left( t\right) -c_{3}\left( t\right) v\left( t\right) -u\left( t\right) \right) \\&+2p\left( t\right) \left( \gamma _{1}\left( t\right) v\left( t\right) -\gamma _{2}\left( t\right) p\left( t\right) \right) . \end{aligned}$$

Thus, for a given \(\delta \ge 1\) and for all \(t\in (t_{0},\omega )\) that satisfy \(V(t)<\delta \), we have

$$\begin{aligned} \dot{V}\left( t\right)\le & -2\left( \alpha \left( t\right) \left( \mu _{1}\left( t\right) \mu _{2}\left( t\right) +\mu _{1}\left( t\right) \mu _{3}\left( t\right) +\mu _{2}\left( t\right) \mu _{3}\left( t\right) \right) v^{2}\left( t\right) +u^{2}\left( t\right) +\gamma _2\left( t\right) p^{2}\left( t\right) \right) \\&+2\left( \alpha \left( t\right) -c_{3}\left( t\right) \right) v\left( t\right) u\left( t\right) +2\left| \alpha \left( t\right) \right| \delta ^{2}+2\left| \alpha \left( t\right) \right| \left| \mu _{1}\left( t\right) +\mu _{2}\left( t\right) +\mu _{3}\left( t\right) \right| \delta ^{\frac{3}{2}} \\&2\left| \alpha \left( t\right) \right| \left| \mu _{1}\left( t\right) \mu _{2}\left( t\right) \mu _{3}\left( t\right) +\mu _{4}\left( t\right) \right| \sqrt{\delta }+2\left| c_{1}\left( t\right) \right| \sqrt{\delta }+2\left( \left| c_{2}\left( t\right) \right| +\left| \gamma _{1}\left( t\right) \right| \right) \delta . \end{aligned}$$

This implies that: for all \(t\in (t_{0},\omega )\) that satisfy \(V(t)<\delta \), we get

$$\begin{aligned} \dot{V}\left( t\right) \le -2Q\left( t\right) \left( v^{2}\left( t\right) +u^{2}\left( t\right) +p^{2}\left( t\right) \right) +2\delta ^{2}E\left( t\right) , \end{aligned}$$

or

$$\begin{aligned} \dot{V}\left( t\right) \le -q\left( t\right) V\left( t\right) +e\left( t\right) , \text{ for } \text{ all } t\in (t_{0},\omega ) \text{ that } \text{ satisfy } V(t)<\delta , \end{aligned}$$
(9)

where \(q\left( t\right) =2Q\left( t\right) \) and \(e\left( t\right) =2\delta ^{2}E\left( t\right) \) for all \(t\in [t_{0},\infty )\). Assumption 1 states that \(\lim _{t\rightarrow \infty }\left( \frac{E\left( t\right) }{Q\left( t\right) }\right) =0\) and hence there exists some \(T\ge t_0\) such that \(\frac{E\left( t\right) }{Q\left( t\right) }<\frac{1}{\delta },\forall t\ge T\). Thus, we have

$$\begin{aligned} \frac{e\left( t\right) }{q\left( t\right) }=\frac{2\delta ^{2}E\left( t\right) }{2Q\left( t\right) }<\frac{\delta ^{2}}{\delta }=\delta ,\forall t\ge T. \end{aligned}$$

Therefore, we deduce by (9) that

$$\begin{aligned} \dot{V}\left( t\right) \le 0, \text{ for } \text{ all } t\in \left( T,\omega \right) \text{ that } \text{ satisfy } \frac{e\left( t\right) }{q\left( t\right) }<V\left( t\right) <\delta . \end{aligned}$$
(10)

The continuity of the mapping \(t\rightarrow \frac{e\left( t\right) }{q\left( t\right) }\) ensures that it attains its infimum on the compact interval \(\left[ t_{0},T\right] \) and thus we can find a positive real number \(\delta _{*}\) such that

$$\begin{aligned} \delta _{*}<\min {\left( \inf _{t\in \left[ t_{0},T\right] }{\frac{e\left( t\right) }{q\left( t\right) }},\delta \right) }. \end{aligned}$$
(11)

Observe that \(\delta _{*}<\delta \). If \(V(t_0)<\delta _{*}\), we claim that \(V\left( t\right) \le \delta _{*},\forall t\in \left( t_{0},T\right) \). To prove this, assume the existence of some \(t_1\in \left( t_{0},T\right) \) such that \(V\left( t_{1}\right) >\delta _{*}\). Thus, by contradiction, we can easily see that there exists some \(t_2\in \left( t_{0},t_1\right) \) such that \(V(t_2)=\delta _{*}\) and that \(V<\delta _{*}<\delta \) on \([t_0,t_2]\) and hence (11) gives

$$\begin{aligned} V\left( t\right)<\delta _{*}<\frac{e\left( t\right) }{q\left( t\right) },\,\forall t\in [t_{0},t_{2}]. \end{aligned}$$

Therefore, we deduce by (9) that \(\dot{V}\left( t\right) <0,\forall t\in [t_{0},t_{2}]\) so that V is decreasing on \([t_{0},t_{2}]\) which contradicts the facts that \(V(t_0)<\delta _{*}\) and \(V(t_2)=\delta _{*}\). This proves our claim that states that \(V\left( t\right) \le \delta _{*},\forall t\in \left( t_{0},T\right) \). As a results, we get by (10) that

$$\begin{aligned} \dot{V}\left( t\right) \le 0, \text{ for } \text{ all } t\in \left( T,\omega \right) \text{ that } \text{ satisfy } \frac{e\left( t\right) }{q\left( t\right) }<V\left( t\right) <\delta . \end{aligned}$$
(12)

Thus, all conditions of Proposition 3.1 are satisfied with \(z(t)=V(t)\), \(\psi _{1}\left( t\right) =\frac{e\left( t\right) }{q\left( t\right) }\) and \(\psi _{2}\left( t\right) =\delta \) for all \(t\in (t_0,\omega )\). Therefore, for all \(V(t_0)<\delta _{*}\), one has \(V\left( t\right) <\delta =\psi _{2}\left( t\right) \) on \(t\in (t_{0},\omega )\). Hence \(\omega =\infty \); that is the Lyapunov function and the states of (4)–(6) are global. As a result, the inequality (9) is satisfied for all \(t>t_0\) whenever \(V(t_0)<\delta _{*}\).

Assumptions 1 and 2 give \(\intop _{t_{0}}^{\infty }q\left( t\right) dt=\infty \) and \(\lim _{t\rightarrow \infty }\left( \frac{e\left( t\right) }{q\left( t\right) }\right) =0\). Thus, the system

$$\begin{aligned} \dot{w}\left( t\right)\,=\,& e\left( t\right) -q\left( t\right) w\left( t\right) \\ w(t_0)\,=\,& V(t_0)\in [0,\delta _{*}), \end{aligned}$$

satisfies all conditions of Theorem 3.1 with \(L=0\) and \(\beta \) is the identity function and hence its global solution is bounded and goes to zero as \(t\rightarrow \infty \). Furthermore, a comparison principle [9, Theorem 3.1.1] gives \(V(t)\le w(t), \forall t\ge t_0\) so that \(\lim _{t\rightarrow \infty }V\left( t\right) =0\). By the definition of V, we deduce that the origin is attractivity, that is \(\lim _{t\rightarrow \infty }{v\left( t\right) }=\lim _{t\rightarrow \infty }{u\left( t\right) }=\lim _{t\rightarrow \infty }{p\left( t\right) }=0\), for any initial value \(\left( v\left( t_{0}\right) ,u\left( t_{0}\right) ,p\left( t_{0}\right) \right) \in \mathbb {R}^{3}\) with magnitude less than \(c=\sqrt{\delta _{*}}\). \(\square \)

Fig. 2
figure 2

v(t), u(t) and p(t) versus t. Observe that as time of reaction increases, the variation in concentrations of reactants go down until all reactant concentrations finish

Full size image

Simulations. Let \(t_0=1\), \(\left( \begin{array}{ccc} v(t_{0})&u(t_{0})&p(t_{0})\end{array}\right) =\left( \begin{array}{ccc} 1.5&2.5&2\end{array}\right) \). For all \(t\ge t_0\) let \(\alpha \left( t\right) =c_{3}\left( t\right) =-\frac{1}{t}\), \(\mu _{1}\left( t\right) =\mu _{4}\left( t\right) =t\), \(\mu _{2}\left( t\right) =-t\), \(\mu _{3}\left( t\right) =c_{1}\left( t\right) =c_{2}\left( t\right) =\gamma _1(t)=\frac{1}{t}\) and \(\gamma _2(t)=1\). We get

$$\begin{aligned} Q\left( t\right)= & \min {\left( 1,1,t\right) }=1,\,\forall t\ge t_{0}=1, \\ E\left( t\right)= & \frac{2}{t}-\frac{1}{t^{2}},\,\forall t\ge t_{0}=1. \end{aligned}$$

It can be easily verified that Assumptions 1 and 2 are satisfied. Therefore, Theorem 3.2 implies that the solution is global and the origin is attractive when the initial values \(v(t_{0})\), \(u(t_{0})\) and \(p(t_{0})\) belong to some neighborhood about the origin. This is illustrated in Fig. 2.

Remark 3.1

Suppose that all conditions of Theorem 3.2 are satisfied. Then one can easily see by (4) that if \(\left\| \mu _{i}\right\| _{\infty }<\infty \) for \(i=1,2,3\); then \(\lim _{t\rightarrow \infty }{\alpha \left( t\right) \mu _{4}\left( t\right) }=-\infty \) is a necessary and sufficient condition for the property \(\lim _{t\rightarrow \infty }{\dot{v}\left( t\right) }=\infty \) which means that the concentration rate \(\dot{v}\) diverges to infinity. This implies that concentration v vanishes rapidly as well. On the other hand, by (6) we conclude that \(\lim _{t\rightarrow \infty }{\gamma _{2}\left( t\right) }=\infty \) is a necessary condition for the property \(\lim _{t\rightarrow \infty }{\dot{p}\left( t\right) }=\infty \) so that the catalyst p vanishes rapidly. Finally, the equation (5) leads to \(\lim _{t\rightarrow \infty }{\dot{u}\left( t\right) }=0\) which means that the negative feedback u vanishes slowly.

4 Hysteresis behavior of the state v

Hysteresis is a physical phenomenon that is related to nonlinear input-output systems. A system is hysteretic if a looping behavior appears when plotting output versus input for different frequencies of a sinusoidal input. One way to characterize hysteresis is the consistency which can be formulated as follows [8]: Consider an input function \(\kappa :[t_0,\infty )\rightarrow \mathbb {R}\) belonging to the Sobolev space \(W^{1,\infty }\left( [t_0,\infty ),\mathbb {R}\right) \); that is \(\kappa \) is locally absolutely continuous with \(\left\| \dot{\kappa }\right\| _{\infty }<\infty \) and \(\left\| \kappa \right\| _{\infty }< \infty \). When considering the time-scaled input \(u\left( \frac{t}{\gamma }\right) ,\forall t\ge t_{0},\forall \gamma >0\), the output is expected; in general, to depend on both t and \(\gamma \); say \(\phi \left( t,\gamma \right) \). If \(t\rightarrow \Phi \left( t,\gamma \right) :=\phi \left( \gamma t,\gamma \right) \) is convergent in \(L^{\infty }\) as \(\gamma \rightarrow \infty \), then the system is said to be consistent. In the present of consistent hysteresis behavior, if \(\Phi \left( t,\gamma \right) \) depends of \(\gamma \), the hysteresis is called rate-dependent. When \(\gamma \rightarrow \infty \), the time dependent set \(\left\{ \left( \kappa \left( t\right) ,\Phi \left( t,\gamma \right) \right) :\;t\ge t_{0}\right\} \) converges; in the Hausdorff space, to the limiting set \(\left\{ \left( \kappa \left( t\right) ,\Phi ^{*}\left( t\right) \right) :\;t\ge t_{0}\right\} \) which represents the so called hysteresis loop including transient. Otherwise; i.e. when \(\Phi \left( \gamma t,\gamma \right) \) is independent of \(\gamma \), say \(\Phi \left( \gamma t,\gamma \right) =\Phi \left( t\right) \), the hysteresis is called rate-independent. In this case, the so-called hysteresis loop is represented by the set \(\left\{ \left( \kappa \left( t\right) ,\Phi \left( t\right) \right) :\;t\ge t_{0}\right\} \). More discussions about the consistency of Duhem models can be found in [12, 14, 15].

The present section aims to investigate hysteresis between the state v and some input signal \(\kappa \in W^{1,\infty }\left( [t_0,\infty ),\mathbb {R}\right) \) that depends on the parameters \(\alpha \) and \(\mu _4\). The prior function \(\kappa \) is also based on the feedback-stimulus which is represented by u(t). To this end, we make the following assumptions.

Assumption i. the functions \(c_2(t)\) and \(c_3(t)\) are uniformly zero; while the function \(c_1(t)\) is bounded.

Observe that the prior assumption implies that the differential equation (5) contains only one state which is u. Thus, for each initial value \(u(t_0)\in \mathbb {R}\), a unique global continuously differentiable solution U(t) for (4) exists. Since \(c_1(t)\) is bounded, the solution U(t) is bounded as well (this can be shown by a simple Lyapunov argument). As a result, the right-hand side of (4) is bounded and so is \(\dot{U}(t)\). Therefore, U(t) belongs to Sobolev space \(W^{1,\infty }\left( [t_0,\infty ),\mathbb {R}\right) \).

Assumption ii. \(\mu _{4}\in W^{1,\infty }\left( [t_0,\infty ),\mathbb {R}\right) \) and \(\mu _{i}\) are uniformly constant for \(i=1,2,3\); say \(\mu _{i}(t)=\mu _{i}^{*}, \forall t\ge t_0\).

Assumption iii. there exists \(G\in C^{0}\left( \mathbb {R},\mathbb {R}\right) \) such that \(\alpha \left( t\right) =G\left( \left| \dot{U}\left( t\right) +\dot{\mu }_{4}\left( t\right) \right| \right) \) for almost all \(t>t_0\). Note that \(\alpha \) may be discontinuous.

Consider the feedback-based input \(\kappa \left( t\right) =U\left( t\right) +\mu _{4}\left( t\right) ,\forall t\ge t_{0}\), then \(\kappa \in W^{1,\infty }\left( [t_0,\infty ),\mathbb {R}\right) \). Therefore, Assumption iii and the differential equation (4) yield the Duhem model

$$\begin{aligned} \dot{v}(t)\,=\,& G\left( \left| \dot{\kappa }\left( t\right) \right| \right) \left( -\left( v\left( t\right) -\mu _{1}^{*}\right) \left( v\left( t\right) -\mu _{2}^{*}\right) \left( v\left( t\right) -\mu _{3}^{*}\right) +\kappa \left( t\right) \right) , \end{aligned}$$
(13)
$$\begin{aligned} v(t_0)\,=\,& v_0, \end{aligned}$$
(14)

for almost all \(t\ge t_0\) and all \(\gamma >0\). If the input \(\kappa \circ s_{\gamma }\) is considered instead of \(\kappa \) where \(s_\gamma \left( t\right)\,=\,\frac{t}{\gamma }, \gamma >0, t\ge 0\), then the system (13)–(14) gives

$$\begin{aligned} \frac{\partial }{\partial t}v(t,\gamma )\,=\,& G\left( \left| \frac{1}{\gamma }\dot{\kappa }\left( \frac{t}{\gamma }\right) \right| \right) \biggl [-\left( v\left( t,\gamma \right) -\mu _{1}^{*}\right) \left( v\left( t,\gamma \right) -\mu _{2}^{*}\right) \left( v\left( t,\gamma \right) -\mu _{3}^{*}\right) +\kappa \left( \frac{t}{\gamma }\right) \nonumber \\&+\kappa \left( \frac{t}{\gamma }\right) \biggr ], \end{aligned}$$
(15)
$$\begin{aligned} v(t_{0},\gamma )\,=\,& v_0, \text{ for } \text{ almost } \text{ all } t\ge t_0 \text{ and } \text{ all } \gamma >0. \end{aligned}$$
(16)

Define \(\Phi :[t_{0},\infty )\times \mathbb {R}_{+}\rightarrow \mathbb {R}^{m}\) as \(\Phi \left( t,\gamma \right)\,=\,v\left( t\gamma ,\gamma \right) ,\forall t\ge t_{0},\forall \gamma >0\). We get by chain rule that \(\frac{\partial }{\partial t}\Phi \left( t,\gamma \right)\,=\,\gamma \frac{\partial v}{\partial t}\left( t\gamma ,\gamma \right) ,\forall t\ge t_{0},\forall \gamma >0\). Thus, we conclude by the system (15)–(16) that the function \(\Phi \) depends on \(\gamma \) and

$$\begin{aligned} \frac{\partial }{\partial t}\Phi \left( t,\gamma \right)= & \gamma G\left( \frac{\left| \dot{\kappa }\left( t\right) \right| }{\gamma }\right) \Bigl [-\left( \Phi \left( t,\gamma \right) -\mu _{1}^{*}\right) \left( \Phi \left( t,\gamma \right) -\mu _{2}^{*}\right) \left( \Phi \left( t,\gamma \right) -\mu _{3}^{*}\right) \nonumber \\&+\kappa \left( t\right) \Bigr ] \end{aligned}$$
(17)
$$\begin{aligned} \Phi \left( t_{0},\gamma \right)= & v_0, \end{aligned}$$
(18)

for almost all \(t\ge t_0\) and all \(\gamma >0\).

Simulations for a constant negative feedback case. Let \(t_0=0\), \(v(t_0)=0.2\), \(u(t_0)=1\), \(\mu _{i}^{*}=0\); for \(i=1,2,3\) and \(\mu _4(t)=1-\sin {(t)},\forall t\ge 0\), \(c_1(t)=1\) and \(c_2(t)=c_3(t)=0, \forall t\in [t_0,\infty )\). We conclude the only solution of the differential equation (2) is \(U(t)=1, \forall t\in [t_0,\infty )\). It is easy to see that Assumptions i-iv are satisfied. We have \(\kappa \left( t\right) =\sin {\left( t\right) },\forall t\ge t_{0}=0\) and hence the system (17)–(18) leads to

$$\begin{aligned} \frac{\partial }{\partial t}\Phi \left( t,\gamma \right)\,=\,& \gamma G\left( \frac{\left| \cos {\left( t\right) }\right| }{\gamma }\right) \left( -\Phi ^{3}\left( t,\gamma \right) +\sin {\left( t\right) }\right) ,\forall t\ge 0, \,\forall \gamma>0, \\ \nonumber \Phi \left( 0,\gamma \right)= & 0,\,\forall \gamma >0. \end{aligned}$$
(19)

The function G determines whether the hysteresis exhibited is rate-independent or rate-dependent. To see this, we consider two cases for the function \(\Phi \left( t,\gamma \right) \) as follows.

First: Let G be the identity function, then the solution of the system (19) does not depend on \(\gamma \), the consistency is trivially satisfied and

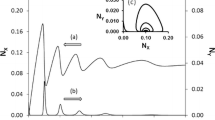
$$\begin{aligned} \dot{\Phi }\left( t\right)\,=\,\left| \cos {\left( t\right) }\right| \left( -\Phi ^{3}\left( t\right) +\sin {\left( t\right) }\right) ,\,\forall t\ge 0. \end{aligned}$$
(20)

Figure 3a shows the the function \(\Phi \) reaches the steady state somewhere after \(t=5\) which leads to a rate-independent hysteresis with limiting curve \(\left\{ \left( \kappa \left( t\right) ,\Phi \left( t\right) \right) :\;t\ge t_{0}\right\} \) as shown in Fig. 3b at which the hysteresis loop can be observed (including transient).

Fig. 3
figure 3

a \(\Phi (t)\) versus t for (20) b the limiting curve for (20) c \(\Phi ^{*}\left( t\right) -\Phi \left( t,\gamma \right) \) versus t for (21) when \(\gamma =1\), \(\gamma =3\), \(\gamma =5\) and \(\gamma =20\) hysteresis simulations

Full size image

Second: Let G be defined as \(G\left( \tau \right) =\frac{\tau }{1+e^{-\tau }},\forall \tau \in \mathbb {R}\). The system (20) becomes

$$\begin{aligned} \frac{\partial }{\partial t}\Phi \left( t,\gamma \right)\,=\,\frac{\left| \cos {\left( t\right) }\right| }{1+e^{-\frac{1}{\gamma }\left| \cos {\left( t\right) }\right| }}\left( -\Phi ^{3}\left( t,\gamma \right) +\sin {\left( t\right) }\right) ,\,\forall t\ge 0. \end{aligned}$$
(21)

The function \(\frac{\left| \cos {\left( \cdot \right) }\right| }{1+e^{-\frac{1}{\gamma }\left| \cos {\left( \cdot \right) }\right| }}\) converges in \(L^{\infty }\) to \(\frac{\left| \cos {\left( \cdot \right) }\right| }{2}\). Based on that fact, recent research [15] has proved that in the presence of a consistent hysteresis behavior, the limiting curve can be derived by the system

$$\begin{aligned} \frac{\partial }{\partial t}\Phi \left( t,\gamma \right) =\left( \frac{\left| \cos {\left( t\right) }\right| }{2}\right) \left( -\Phi ^{3}\left( t\right) +\sin {\left( t\right) }\right), \,\, \forall t\ge 0. \end{aligned}$$

Thus, \(\Phi \) is independent of \(\gamma \) with

$$\begin{aligned} \frac{d}{dt}\Phi ^{*}\left( t\right)\,=\,\frac{1}{2}\left| \cos {\left( t\right) }\right| \left( -\left( \Phi ^{*}\left( t\right) \right) ^{3}+\sin {\left( t\right) }\right) ,\,\,\forall t\ge 0. \end{aligned}$$
(22)

In other words, the solution function \(\Phi (t,\gamma )\) of (21) converges uniformly to the solution function \(\Phi ^{*}(t)\) of (22) as \(\gamma \rightarrow \infty \). This is illustrated in Fig. 3c. Observe that when \(\gamma \) diverges to infinity, the function \(\Phi \left( \cdot ,\gamma \right) -\Phi ^{*}\left( \cdot \right) \) goes to \(t-\)axis which emphasizes the consistency. For this case, the limiting curve is very similar to the one in 3(b) which has been plotted when G is the identity function.

5 Conclusions

The classical Belousov–Zhabotinsky reaction has been generalized into the nonautonomous framework in which all parameters are allowed to depend on time. Simulations ensure the existence of oscillatory behavior for the system. Sufficient conditions have been derived in Theorem 3.2 to ensure the “local” attractivity of the origin which implies that all concentration states are continuable on \([t_0,\infty )\) and converge to zero as t goes to infinity. Furthermore, the hysteresis behavior of the state v and some sinusoidal input has been investigated in Sect. 4 depending on the notion of consistency which has enabled us to find an explicit expression for the hysteresis loop including transient effects. Numerical simulations have been carried out to clarify that the hysteresis behavior exhibited by the system can be either rate-dependent or rate-independent.