Abstract
We recall and prove some basic properties of both the Schouten and Wagner curvature tensors. We consider—in some detail—the construction of the Wagner tensor, and then discuss how the vanishing of this tensor characterizes the flat structures, i.e., those for which the parallel translation is path-independent. (As a special case, we revisit the flatness of three-dimensional nonholonomic Riemannian manifolds.) In order to facilitate our presentation, we employ an extension of the notion of a connection to a “restricted connection.” Such connections are equivalently viewed as horizontal lifts (or horizontal distributions); hence we revisit the Schouten and Wagner tensors from this perspective. In particular, it turns out that the construction of the Wagner tensor may be equivalently formulated as a flag of horizontal distributions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A nonholonomic Riemannian structure is a quadruple \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\), consisting of a manifold \({\textsf {M}}\) equipped with a nonintegrable distribution \({\mathcal {D}}\), a complementary distribution \({\mathcal {D}}^{\perp }\), and a (positive definite) fibre metric \({\textbf {g}}\) on \({\mathcal {D}}\). Similar to a Riemannian structure, a nonholonomic Riemannian structure has a unique connection associated to it, referred to as the “nonholonomic connection.” The admissible curves are those tangent to \({\mathcal {D}}\); among these are the so-called nonholonomic geodesics, which are the geodesics of the nonholonomic connection. It turns out that these geodesics are precisely the solutions of the Chetaev equations for a nonholonomic mechanical system with constraints linear-in-velocities and a kinetic energy Lagrangian; accordingly, the chief motivation for the study of nonholonomic Riemannian structures comes from mechanics. From a mathematical perspective, nonholonomic Riemannian geometry is a natural generalization of Riemannian geometry; in this sense, it may be viewed as a counterpart to sub-Riemannian geometry. (A sub-Riemannian structure is simply a triple \(({\textsf {M}},{\mathcal {D}},{\textbf {g}})\), i.e., a nonholonomic Riemannian structure sans the choice of a complementary distribution.) Sub-Riemannian geometry generalizes the “metric” aspect of Riemannian geometry (the central object in sub-Riemannian geometry is the Carnot–Carathéodory distance), whereas nonholonomic Riemannian geometry generalizes the “connection” aspect (the nonholonomic connection is the central object). Along these lines, it was Hertz [16] (see also [28]) who essentially recognized that sub-Riemannian geometry studies the “shortest” curves, while nonholonomic Riemannian geometry studies the “straightest” curves. In general, \(\text {``shortest''} \ne \text {``straightest''}\), although the two classes of curves coincide for a Riemannian structure. (We note that, in the past, the term nonholonomic Riemannian geometry was used to refer to both of the above generalizations of Riemannian geometry. However, we shall use it to refer exclusively to the first; the term sub-Riemannian geometry has now also become fairly standard.) For more information on nonholonomic Riemannian geometry and sub-Riemannian geometry, see, e.g., [6, 9, 20, 28, 29].
Curvature plays a central rôle in Riemannian geometry, and as such has been extensively studied: presently many aspects of it are very well understood. In sharp contrast, the curvature of nonholonomic Riemannian structures has received very little attention. Although some elements of the curvature of nonholonomic Riemannian structures can be found in Synge [26], it was Schouten [25] who first explicitly considered curvature in the nonholonomic Riemannian context. In particular, Schouten introduced a curvature tensor associated to every nonholonomic Riemannian structure; this tensor is now referred to as the “Schouten curvature tensor” [10]. Nevertheless, the main development in the study of curvature of nonholonomic Riemannian structures was due to Wagner, who observed that (the vanishing of) the Schouten tensor does not characterise the flat nonholonomic Riemannian structures, i.e., those structures for which the parallel translation (induced by the nonholonomic connection) is path-independent. In a series of papers [30, 33, 34], Wagner extended Schouten’s work, defining a curvature tensor (now called the “Wagner curvature tensor”), the vanishing of which does characterise the flat structures (see also [31, 32, 35]). (This resulted in Wagner being awarded Kazan University’s 1937 Lobachevskii prize for young Soviet mathematicians.) Nevertheless, Wagner’s construction has its limitations; in particular, it does not depend only on the data \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\), but also on some additional assumptions. As a result, it is not generally intrinsic, and so only provides a partial solution to the problem of flatness.
We briefly mention some more recent papers of interest that discuss and/or make use of the Schouten or Wagner curvature tensors. The two papers [1] and [3] are concerned with nonholonomic Riemannian structures in three dimensions, particularly left-invariant structures on Lie groups. The former paper classifies all such structures, and the latter considers the flat structures. Both papers make use of scalar invariants extracted from the Schouten curvature tensor. (Later in this paper we discuss some of the results of [3] in the context of the present paper.) Berestovskii [5] reviews various notions of curvature in sub-Riemannian geometry (which also apply to nonholonomic Riemannian structures), including the special case of sub-Riemannian structures with “rigged” distributions, i.e, those with a complementary distribution—the same data as for a nonholonomic Riemannian structure. (See also references in [5].) Galaev and coauthors have studied curvature (in particular, the Schouten and Wagner curvature tensors) in the context of (almost) contact metric structures [7, 11, 12] (see also references therein); as well as the metrizability of nonholonomic connections in three dimensions [13] (making use of the Schouten tensor). Zhao and Jiao [36] study conformal transformations (of sub-Riemannian structures with “rigged” distribution), and from the Schouten tensor calculate the “nonholonomic” Weyl tensor. Leites [19] (see also [15]) calculates a nonholonomic analogue of the Riemann tensor, using algebraic techniques. However, the notion of flatness that Leites introduces is different from that which we consider here. Indeed, for Leites, every contact manifold is flat; however, every three-dimensional nonholonomic Riemannian manifold is contact, yet there are many such structures whose parallel transport is path-dependent (see [3]). Lastly, we mention the paper of Dragović and Gajić [10] and that of Gorbatenko [14], both of which discuss the motivation for, and construction of, Wagner’s curvature tensor. (For the construction of Wagner’s tensor in this paper, see Sect. 4.1.)
In this paper we consider in some more detail the two curvature tensors mentioned above, with a view to understanding better the curvature of nonholonomic Riemannian structures. The paper is organized as follows. In Sect. 3 we introduce the Schouten curvature tensor, which is canonically associated to every nonholonomic Riemannian structure. We prove some symmetries of this tensor, and attempt to relate it (at least on an algebraic level) to a Riemannian-type curvature tensor. We do this by decomposing the Schouten tensor (in fact, the associated tensor obtained by using the metric to “lower an index”) into two components: a “Riemannian” component—which satisfies all the symmetries of a Riemannian curvature tensor—and a “remainder” that can be viewed as a deviation of the Schouten tensor from a Riemannian curvature tensor. Using the “Riemannian” component of the Schouten tensor, we are able to introduce notions of sectional curvature, a Ricci tensor, and a scalar curvature, analogous to the corresponding concepts in Riemannian geometry.
In Sect. 4 we consider the Wagner curvature tensor. The construction of this tensor is quite sophisticated, and relies on the flag of the distribution; however, the construction is not intrinsic, in that it relies on some additional assumptions. (Having said that, if the distribution is strongly nonholonomic, then these assumptions are automatically satisfied.) We define the Wagner tensor in Sect. 4.1, and prove some basic properties: in particular, how the vanishing of the Wagner tensor characterizes the flat structures, i.e., those whose parallel translation is path-independent. In Sect.4.2 we consider an “algebraic” interpretation of a collection of curvature tensors that arise in the construction of the Wagner tensor. (Briefly, these curvature tensors measure the extent to which certain maps fail to be homomorphisms.) Lastly, Sect. 4.3 considers the Wagner curvature tensor in the case of three-dimensional nonholonomic Riemannian structures. The flatness of such structures was recently treated in [3]; in particular, we find a new characterization of flatness in three dimensions, and relate it to that in [3].
Finally, in Sect. 5 we revisit both the Schouten and Wagner curvature tensors from an alternative viewpoint. The nonholonomic connection, as well as a collection of connections arising in the construction of Wagner’s curvature tensor, are equivalently viewed as horizontal lifts (or horizontal distributions). We express the Schouten tensor and the Wagner tensor in terms of horizontal lifts of vector fields. (The vanishing of these tensors then translates to involutivity conditions on the associated horizontal distributions.) A significant contribution of this section is also to show that Wagner’s construction is equivalently formulated as a flag of horizontal distributions.
2 Preliminaries
In this section we revisit some basic concepts and constructions in tensor analysis and the theory of connections; these are slightly extended (or rather, adapted) to a particular class of objects pertaining to our line of inquiry into nonholonomic Riemannian geometry. Specifically, we first consider derivations of tensors on a distribution. If there exists a projection onto the distribution, then there exists a natural generalization of the Lie derivative (essentially a “projected Lie derivative”); this will lead on to a natural notion of a “restricted” tensor derivation. Next, we consider a class of affine connections whose associated parallel translation is restricted to a subclass of curves. We consider two approaches to these “restricted” connections: as a covariant derivative operator, and as a horizontal lift. Following this we present some necessary elements of nonholonomic Riemannian geometry. Apart from some definitions, we recall the fundamental existence and uniqueness result for the nonholonomic connection (a restricted connection) and introduce its associated exterior covariant derivative.
Let \({\textsf {M}}\) be a (real, n-dimensional) manifold and let \({\mathcal {D}}\) and \({\mathcal {E}}\) be distributions on \({\textsf {M}}\), where \({\mathcal {D}}\) has rank r. Throughout, we assume that all manifolds, functions, vector fields, etc. are smooth (i.e., of class \({\mathcal {C}}^{\infty }\)) and that all distributions under consideration are regular (i.e., the dimension of each fiber does not depend on the base point). Furthermore, we shall follow the summation convention on repeated indices. Unless stated otherwise, the following ranges on indices are used: \(i,j,k = 1,\ldots ,n\) and \(a,b,c = 1,\ldots ,r\).
2.1 Restricted tensor derivations
Let \(T^k_{\ell }({\mathcal {D}})\) be the bundle of \((k,\ell )\)-tensors on \({\mathcal {D}}\), i.e., \(T^k_{\ell }({\mathcal {D}}) = \bigsqcup _{q \in {\textsf {M}}} \left[ {\textstyle \bigotimes ^k{\mathcal {D}}_q \otimes \bigotimes ^{\ell }{\mathcal {D}}^*_q}\right] \), and let \({\mathcal {T}}\,^k_{\ell }\,({\mathcal {D}}) = \varGamma (T^k_{\ell }({\mathcal {D}}))\) be the space of tensor fields on \({\mathcal {D}}\). A derivation of \({\mathcal {T}}\,^k_{\ell }({\mathcal {D}})\) (cf. [27]) is a collection of \(\mathbb {R}\)-linear maps \(\delta ^k_{\ell } : {\mathcal {T}}\,^k_{\ell }\,({\mathcal {D}}) \rightarrow {\mathcal {T}}\,^k_{\ell}\,({\mathcal {D}})\) (for every \(k,\ell \ge 0\)), all denoted by \(\delta \) when convenient, such that
for all tensor fields S and T. Here \({{\,\textrm{tr}\,}}^i_j\) denotes the contraction (trace) on the \(i{\text {th}}\) contravariant and \(j{\text {th}}\) covariant index. The space  of all derivations of \({\mathcal {T}}\,^k_{\ell }\,({\mathcal {D}})\) is a Lie algebra.
of all derivations of \({\mathcal {T}}\,^k_{\ell }\,({\mathcal {D}})\) is a Lie algebra.
If \(\delta \) is a derivation and T is a \((k,\ell )\)-tensor field on \({\mathcal {D}}\), then
for \(\omega ^1,\ldots ,\omega ^k \in \varGamma ({\mathcal {D}}^*)\) and \(X_1,\ldots ,X_{\ell } \in \varGamma ({\mathcal {D}})\). In particular, if \(\omega \in \varGamma ({\mathcal {D}}^*)\), then \(\delta (\omega )(X) = \delta (\omega (X)) - \omega (\delta (X))\) for \(X \in \varGamma ({\mathcal {D}})\). Derivations of \(T^k_{\ell }({\mathcal {D}})\) are completely specified by their action on \({\mathcal {T}}\,^\theta _0\,({\mathcal {D}})= {\mathcal {C}}^{\infty }({\textsf {M}})\) and on \({\mathcal {T}}\,^1 _0\,({\mathcal {D}})= \varGamma ({\mathcal {D}})\). Accordingly, given a map that acts as a derivation of \({\mathcal {C}}^{\infty }({\textsf {M}})\) and \(\varGamma ({\mathcal {D}})\), it may be uniquely extended to a derivation of \({\mathcal {T}}\,^k _{\ell}\,({\mathcal {D}}\).
Let \({\mathscr {P}} : T{\textsf {M}} \rightarrow {\mathcal {D}}\) be a projection and let \(\llbracket \cdot ,\cdot \rrbracket = {\mathscr {P}}([\cdot ,\cdot ]) : \varGamma (T{\textsf {M}}) \times \varGamma (T{\textsf {M}}) \rightarrow \varGamma ({\mathcal {D}})\). If \(Z \in \varGamma (T{\textsf {M}})\), then we define a derivation by the requirement that
by the requirement that
for \(f \in {\mathcal {C}}^{\infty }({\textsf {M}})\) and \(X \in \varGamma ({\mathcal {D}})\). We refer to \(\mathscr {L}\,^{\mathscr {P}}_Z\) as the \({\mathscr {P}}\)-Lie derivative along Z. It turns out that every element of  decomposes uniquely as the sum of a \({\mathscr {P}}\)-Lie derivative and a derivation that vanishes on functions.
decomposes uniquely as the sum of a \({\mathscr {P}}\)-Lie derivative and a derivation that vanishes on functions.
Proposition 1
Let  ; then:
; then:
-
(i)
\(\delta ^0_0 = 0\) if and only if \(\delta ^1_0\) is \({\mathcal {C}}^{\infty }({\textsf {M}})\)-linear, i.e., \(\delta ^1_0 \in {\mathcal {T}}\,^1_0\,({\mathcal {D}})\).
-
(ii)
There exists a unique vector field \(Z \in \varGamma (T{\textsf {M}})\) and a unique
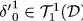 such that \(\delta = \mathscr {L}\,^{\mathscr {P}}_Z + \delta '\), where \({\delta '}^0_0 = 0\) and \({\delta '}^1_0 \in {\mathcal {T}}\,^1_0\,({\mathcal {D}})\).
such that \(\delta = \mathscr {L}\,^{\mathscr {P}}_Z + \delta '\), where \({\delta '}^0_0 = 0\) and \({\delta '}^1_0 \in {\mathcal {T}}\,^1_0\,({\mathcal {D}})\).
Let  and \(\mathscr {L}\,^{\mathscr {P}}_{T{\textsf {M}}} = \{\mathscr {L}\,^{\mathscr {P}}_Z : Z \in \varGamma (T{\textsf {M}})\}\). We have the (vector space) decomposition
and \(\mathscr {L}\,^{\mathscr {P}}_{T{\textsf {M}}} = \{\mathscr {L}\,^{\mathscr {P}}_Z : Z \in \varGamma (T{\textsf {M}})\}\). We have the (vector space) decomposition  ; furthermore,
; furthermore,  . We say that a derivation
. We say that a derivation  is an \({\mathcal {E}}\)-restricted derivation (or simply \({\mathcal {E}}\)-derivation) if
is an \({\mathcal {E}}\)-restricted derivation (or simply \({\mathcal {E}}\)-derivation) if  , where \(\mathscr {L}\,^{\mathscr {P}}_{{\mathcal {E}}} = \{\mathscr {L}\,^{\mathscr {P}}_X : X \in \varGamma ({\mathcal {E}})\}\). Let
, where \(\mathscr {L}\,^{\mathscr {P}}_{{\mathcal {E}}} = \{\mathscr {L}\,^{\mathscr {P}}_X : X \in \varGamma ({\mathcal {E}})\}\). Let  denote the space of all \({\mathcal {E}}\)-derivations.
denote the space of all \({\mathcal {E}}\)-derivations.
Remark 1
Dual to the \({\mathscr {P}}\)-Lie derivative is the \({\mathscr {P}}\)-exterior derivative \(d_{{\mathscr {P}}} : \Omega ^k({\mathcal {D}}) \rightarrow \Omega ^{k+1}({\mathcal {D}})\), defined as follows: if \(f \in {\mathcal {C}}^{\infty }({\textsf {M}})\), then \(d_{{\mathscr {P}}}f(X) = X[f]\) for every \(X \in \varGamma ({\mathcal {D}})\); if \(\omega \in \Omega ^k({\mathcal {D}})\), \(k \ge 1\), then
for \(X_0,\ldots ,X_k \in \varGamma ({\mathcal {D}})\) (where \({\widehat{X}}_i\) indicates the omission of that element). Many properties of the usual exterior derivative extend to \(d_{{\mathscr {P}}}\); however, we do not generally have \(d_{{\mathscr {P}}}^2 = 0\). Indeed, if \(f \in {\mathcal {C}}^{\infty }({\textsf {M}})\), then \(d^2_{{\mathscr {P}}}f(X,Y) = [X,Y][f] - {\mathscr {P}}([X,Y])[f]\) for \(X,Y \in \varGamma ({\mathcal {D}})\). Hence \(d^2_{{\mathscr {P}}}f = 0\) if and only if \({\mathcal {D}}\) is integrable.
2.2 Restricted connections
In this section we consider so-called “restricted connections,” i.e., connections whose associated parallel translation is restricted to precisely those curves that are tangent to a given distribution. Firstly, we consider a restricted connection as a covariant derivative. In this vein, we then discuss the associated parallel translation map, parallel tensor fields, and parallel frames. Secondly, we consider a restricted connection as a horizontal lift, or equivalently, as a horizontal distribution. (Typically, the horizontal distribution will not form a full complement to the vertical distribution.) As expected, such a horizontal lift induces a unique covariant derivative, and conversely. Restricted connections (in the language of covariant derivatives) were first introduced in [17]; the notion of a restricted connection (particularly, as a horizontal lift) is also essentially covered in [8].
We assume that any two points of \({\textsf {M}}\) can be joined by an \({\mathcal {E}}\)-curve, i.e., a curve \(\gamma : [0,1] \rightarrow {\textsf {M}}\) such that \({\dot{\gamma }}(t) \in {\mathcal {E}}_{\gamma (t)}\) for every \(t \in [0,1]\). (This holds, for instance, when \({\mathcal {E}}\) is completely nonholonomic.) An \({\mathcal {E}}\)-restricted covariant derivative \(\nabla \) on \({\mathcal {D}}\) (or covariant \({\mathcal {E}}\)-derivative on \({\mathcal {D}}\)) is an \(\mathbb {R}\)-linear mapping \(\nabla : \varGamma ({\mathcal {E}}) \times \varGamma ({\mathcal {D}}) \rightarrow \varGamma ({\mathcal {D}})\), \((X,W) \mapsto \nabla _XW\) such that
for every \(f \in {\mathcal {C}}^{\infty }({\textsf {M}})\), \(X \in \varGamma ({\mathcal {E}})\) and \(W \in \varGamma ({\mathcal {D}})\). The usual basic properties of covariant differentiation extend to the case of a restricted covariant derivative. In particular, the expression \(\nabla _XW(q)\), \(q \in {\textsf {M}}\) depends only on the value of X at q, and the value of W along any \({\mathcal {E}}\)-curve tangent to X(q). Covariant differentiation may also be uniquely extended to arbitrary tensor fields in \({\mathcal {T}}\,\,^k_{\ell }\,({\mathcal {D}})\), in the usual fashion: let \(X \in \varGamma ({\mathcal {E}})\) and define \(\nabla _Xf = X[f]\) for \(f \in {\mathcal {C}}^{\infty }({\textsf {M}})\); then \(\nabla _X\) is a derivation of \({\mathcal {C}}^{\infty }({\textsf {M}})\) and \(\varGamma ({\mathcal {D}})\), and hence may be extended to a (unique) derivation of \({\mathcal {T}}\,\,^k_{\ell }\,({\mathcal {D}})\).
A covariant \({\mathcal {E}}\)-derivative \(\nabla \) on \({\mathcal {D}}\) induces a parallel translation along \({\mathcal {E}}\)-curves. A section V of \({\mathcal {D}}\) along an \({\mathcal {E}}\)-curve \(\gamma : [0,1] \rightarrow {\textsf {M}}\) is parallel along \(\gamma \) if \(\nabla _{{\dot{\gamma }}}V = 0\). Let \(W \in \varGamma ({\mathcal {D}})\); if \(W \circ \gamma \) is parallel along \(\gamma \) for every \({\mathcal {E}}\)-curve \(\gamma \), then W is simply called parallel. Clearly, a necessary and sufficient condition for W to be parallel is that \(\nabla W \equiv 0\).
Proposition 2
Let \(\gamma : [0,1] \rightarrow {\textsf {M}}\) be an \({\mathcal {E}}\)-curve and let \(V_0 \in {\mathcal {D}}_{\gamma (0)}\). There exists a unique parallel section V of \({\mathcal {D}}\) along \(\gamma \) such that \(V(0) = V_0\). (V is called the parallel translate of \(V_0\) along \(\gamma \).)
Let \(\gamma : [0,1] \rightarrow {\textsf {M}}\) be an \({\mathcal {E}}\)-curve. The parallel translation \(\Pi ^t_{\gamma } : {\mathcal {D}}_{\gamma (0)} \rightarrow {\mathcal {D}}_{\gamma (t)}\), \(t \in [0,1]\) is specified by setting \(\Pi ^t_{\gamma }(V_0) = V(t)\), where V is the parallel translate of \(V_0 \in {\mathcal {D}}_{\gamma (0)}\) along \(\gamma \). A (local) frame \((U_a)\) for \({\mathcal {D}}\) is called parallel if each element \(U_a\) is parallel. The existence of a parallel frame for \({\mathcal {D}}\) is not guaranteed; in fact, it places quite severe restrictions on the connection.
Proposition 3
There exists a parallel frame for \({\mathcal {D}}\) on an open set \({\mathcal {U}} \subseteq {\textsf {M}}\) if and only if for any two points \(p,q \in {\mathcal {U}}\) and for any \({\mathcal {E}}\)-curve \(\gamma : [0,1] \rightarrow {\mathcal {U}}\) joining p to q, the parallel translation \(\Pi _{\gamma }^1 : {\mathcal {D}}_p \rightarrow {\mathcal {D}}_q\) does not depend on \(\gamma \).
The notion of a parallel vector field is easily extended to arbitrary tensor fields. Indeed, a section A of \(T^k_{\ell }({\mathcal {D}})\) along an \({\mathcal {E}}\)-curve \(\gamma \) is called parallel along \(\gamma \) if \(\nabla _{{\dot{\gamma }}}A = 0\). A tensor field \(T \in {\mathcal {T}}\,^k_{\ell }\,({\mathcal {D}})\) is parallel if \(T\circ \gamma \) is parallel along \(\gamma \) for every \({\mathcal {E}}\)-curve \(\gamma \). Evidently, T is parallel if and only if \(\nabla T \equiv 0\).
Let \(\tau _{{\textsf {M}}} : T{\textsf {M}} \rightarrow {\textsf {M}}\) and \(\tau _{{\mathcal {D}}} : T{\mathcal {D}} \rightarrow {\mathcal {D}}\) denote the canonical projections of a tangent vector onto its base point. Let \(\pi = \tau _{{\textsf {M}}}|_{{\mathcal {D}}} : {\mathcal {D}} \rightarrow {\textsf {M}}\). The pullback bundle \(\pi ^*{\mathcal {E}}\) may be viewed as a vector bundle over \({\mathcal {D}}\) and over \({\mathcal {E}}\), with projections \({\widetilde{\pi }}_1 : \pi ^*{\mathcal {E}} \ni (U_q,X_q) \mapsto U_q \in {\mathcal {D}}\) and \({\widetilde{\pi }}_2 : \pi ^*{\mathcal {E}} \ni (U_q,X_q) \mapsto X_q \in {\mathcal {E}}\), respectively. An \({\mathcal {E}}\)-restricted connection on \({\mathcal {D}}\) (or \({\mathcal {E}}\)-connection on \({\mathcal {D}}\)) is a map \(h : \pi ^*{\mathcal {E}} \rightarrow T{\mathcal {D}}\) that is
-
(i)
a linear bundle map from \({\widetilde{\pi }}_1\) to \(\tau _{{\mathcal {D}}}\) covering the identity, i.e., \(\tau _{{\mathcal {D}}}\circ h = {\widetilde{\pi }}_1\);
-
(ii)
a bundle map from \({\widetilde{\pi }}_2\) to \(T\pi \) covering the inclusion \(\iota : {\mathcal {E}} \rightarrow T{\textsf {M}}\), i.e., \(T\pi \cdot h = \iota \circ {\widetilde{\pi }}_2\).
Such a connection h is called linear if \(T_{U_q}\phi _t\cdot h(U_q,X_q) = h(\phi _t(U_q),X_q)\) for every \((U_q,X_q) \in \pi ^*{\mathcal {E}}\), where \(\phi _t : {\mathcal {D}} \rightarrow {\mathcal {D}}\) denotes the canonical dilation \(\phi _t(U_q) = e^tU_q\). Let \({\mathcal {V}} = \ker T\pi \) be the vertical distribution and \({\mathcal {H}} = {{\,\textrm{im}\,}}h\) the horizontal distribution. The map \(v: \pi ^*{\mathcal {D}} \rightarrow {\mathcal {V}}\) given by
is a vector bundle isomorphism. If \(U_q \in {\mathcal {D}}\), then the linear isomorphism \(v_{U_q} = v(U_q,\,\cdot \,) : {\mathcal {D}}_q \rightarrow {\mathcal {V}}_{U_q}\) is called the vertical lift over \(U_q\). If \(X \in \varGamma ({\mathcal {D}})\), then we define the vertical lift of X to be the vertical vector field \(X^v \in \varGamma ({\mathcal {V}})\) given by
Similarly, the mapping \(h_{U_q} = h(U_q,\,\cdot \,) : {\mathcal {D}}_q \rightarrow {\mathcal {H}}_{U_q}\) is called the horizontal lift over \(U_q\) (or explicitly, the h-lift over \(U_q\)). The horizontal lift (or h-lift) of \(X \in \varGamma ({\mathcal {E}})\) is the vector field \(X^h \in \varGamma ({\mathcal {H}})\) given by
Projectable horizontal vector fields (i.e., vector fields \(Z \in \varGamma ({\mathcal {H}})\) for which there exists \(X \in \varGamma (T{\textsf {M}})\) such that \(T\pi \cdot Z = X\circ \pi \)) are exactly the horizontal lifts of vector fields in \(\varGamma ({\mathcal {E}})\). The following proposition collects some basic results about restricted connections.
Proposition 4
(cf. [8]) We have:
-
(i)
\(\pi _*{\mathcal {H}} = {\mathcal {E}}\), i.e., \(T_{U_q}\pi \cdot {\mathcal {H}}_{U_q} = {\mathcal {E}}_q\) for every \(U_q \in {\mathcal {D}}\).
-
(ii)
h linear if and only if \((\phi _t)_*{\mathcal {H}} = {\mathcal {H}}\).
-
(iii)
\({\mathcal {V}} \cap {\mathcal {H}} = \{0\}\), and \({\mathcal {V}} + {\mathcal {H}} \subseteq T{\mathcal {D}}\) with equality if and only if \({\mathcal {E}} = T{\textsf {M}}\).
Furthermore, we have that h is uniquely specified by its associated horizontal distribution \({\mathcal {H}}\):
Proposition 5
(cf. [8]) Let \({\mathcal {E}}\) and \({\mathcal {D}}\) be distributions on \({\textsf {M}}\) and \(\pi = \left. \tau _{{\textsf {M}}}\right| _{{\mathcal {D}}} : {\mathcal {D}} \rightarrow {\textsf {M}}\). If \({\mathcal {H}}\) is a distribution on \({\mathcal {D}}\) such that
then there exists a unique (not necessarily linear) \({\mathcal {E}}\)-connection h on \({\mathcal {D}}\) such that \({\mathcal {H}} = {{\,\textrm{im}\,}}h\).
We briefly address the relation between (linear) restricted connections and restricted covariant derivatives. Suppose that h is a linear \({\mathcal {E}}\)-connection on \({\mathcal {D}}\). Let \(X_q \in {\mathcal {E}}\) and \(Y_{U_q} \in T_{U_q}{\mathcal {D}}\), where \(U_q \in {\mathcal {D}}_q\) and \(Y_{U_q}\) satisfies \(T_{U_q}\pi \cdot Y_{U_q} = X_q\). Then it is easy to see that \(Y_{U_q} - h(U_q,X_q)\) is vertical, and hence we can define \(\nabla : \varGamma ({\mathcal {E}}) \times \varGamma ({\mathcal {D}}) \rightarrow \varGamma ({\mathcal {D}})\) by
\(\nabla \) is precisely a covariant \({\mathcal {E}}\)-derivative on \({\mathcal {D}}\). Conversely, given an covariant \({\mathcal {E}}\)-derivative \(\nabla \) on \({\mathcal {D}}\), there exists a unique linear \({\mathcal {E}}\)-connection h on \({\mathcal {D}}\) whose associated covariant derivative is exactly \(\nabla \).
Proposition 6
(cf. [8]) Let \(\nabla \) be a covariant \({\mathcal {E}}\)-derivative on \({\mathcal {D}}\); then \(\nabla \) is the covariant derivative associated to the unique \({\mathcal {E}}\)-connection h on \({\mathcal {D}}\) given by
Here \(U \in \varGamma ({\mathcal {D}})\) satisfies \(U(q) = U_q\). (The definition of h does not depend on the choice of U.)
Lastly, we state two technical results (to be used later in the paper). If \(\omega \in \varGamma ({\mathcal {D}}^*)\), then we shall denote by \({\overline{\omega }} \in {\mathcal {C}}^{\infty }({\mathcal {D}})\) the function given by \({\overline{\omega }}(U_q) = \omega _q(U_q)\).
Lemma 1
If \(W \in \varGamma ({\mathcal {V}})\) and \(\omega \in \varGamma ({\mathcal {D}}^*)\), then
for every \(U_q \in {\mathcal {D}}\).
Lemma 2
If \(X,Y \in \varGamma ({\mathcal {E}})\) and \(\omega \in \varGamma ({\mathcal {D}}^*)\), then:
-
(i)
\(X^h[{\overline{\omega }}] = \overline{\nabla _X\omega }\).
-
(ii)
\([X^h,Y^h][{\overline{\omega }}] = \overline{[\nabla _X,\nabla _Y]\omega }\).
2.3 Nonholonomic Riemannian structures
Given a distribution \({\mathcal {D}}\), its flag is the filtration \({\mathcal {D}}^1 \subseteq {\mathcal {D}}^2 \subseteq \cdots \) given by
We shall always assume that each component of the flag is regular. Evidently, the flag of \({\mathcal {D}}\) will stabilise after finitely many steps. If there exists \(N \ge 2\) such that \({\mathcal {D}}^{N-1} \subsetneq T{\textsf {M}}\) and \({\mathcal {D}}^N = T{\textsf {M}}\), then \({\mathcal {D}}\) is said to be completely nonholonomic, in which case N is the degree of nonholonomy of \({\mathcal {D}}\). When \(N = 2\), \({\mathcal {D}}\) is called strongly nonholonomic. Complete nonholonomy of \({\mathcal {D}}\) is a sufficient condition for any two points of \({\textsf {M}}\) to be joined by a \({\mathcal {D}}\)-curve (Chow–Rashevskii; see, e.g., [20]). A nonholonomic Riemannian manifold is a quadruple \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\), where \({\textsf {M}}\) is an n-dimensional manifold, \({\mathcal {D}}\) is a rank \(r < n\) completely nonholonomic distribution on \({\textsf {M}}\), \({\mathcal {D}}^{\perp }\) is a rank \(n-r\) distribution on \({\textsf {M}}\) complementary to \({\mathcal {D}}\) (i.e., \(T{\textsf {M}} = {\mathcal {D}}\oplus {\mathcal {D}}^{\perp }\)) and \({\textbf {g}}\) is a positive definite fiber metric on \({\mathcal {D}}\). For convenience, we also refer to a nonholonomic Riemannian manifold as a nonholonomic Riemannian structure. Let \({\mathscr {P}} : T{\textsf {M}} \rightarrow {\mathcal {D}}\) and \({\mathscr {Q}} : T{\textsf {M}} \rightarrow {\mathcal {D}}^{\perp }\) be the projectors corresponding to the decomposition \(T{\textsf {M}} = {\mathcal {D}}\oplus {\mathcal {D}}^{\perp }\). As before, we denote the projected Lie bracket \({\mathscr {P}}([\cdot ,\cdot ]) : \varGamma (T{\textsf {M}}) \times \varGamma (T{\textsf {M}}) \rightarrow \varGamma ({\mathcal {D}})\) by \(\llbracket \cdot ,\cdot \rrbracket \).
Remarkably, the existence and uniqueness result for the Levi-Civita connection (in the Riemannian case) generalizes to nonholonomic Riemannian geometry; more specifically, associated to every nonholonomic Riemannian structure \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) is a unique metric and torsion-free \({\mathcal {D}}\)-connection \(\nabla \) on \({\mathcal {D}}\). Here the torsion T of \(\nabla \) is given by
\(\nabla \) is referred to as the nonholonomic connection of \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\). Formally, we have the following statement.
Proposition 7
(see, e.g., [18]) Let \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) be a nonholonomic Riemannian structure. There exists a unique \({\mathcal {D}}\)-connection \(\nabla \) on \({\mathcal {D}}\) such that \(\nabla {\textbf {g}} \equiv 0\) and \(T \equiv 0\), i.e.,
for every \(X,Y,Z \in \varGamma ({\mathcal {D}})\). Furthermore, \(\nabla \) is characterized by Koszul’s formula:
A nonholonomic Riemannian structure \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) is said to be flat on \({\mathcal {U}}\) (where \({\mathcal {U}} \subseteq {\textsf {M}}\) is open) if there exists a parallel frame for \({\mathcal {D}}\) (with respect to the nonholonomic connection) defined on \({\mathcal {U}}\). If \({\mathcal {U}} = {\textsf {M}}\), then we simply say that \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) is flat; on the other hand, if \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) is flat on an open neighbourhood about every point in \({\textsf {M}}\), then we say that it is locally flat.
The \({\mathscr {P}}\)-exterior covariant derivative associated to \(\nabla \), denoted \(d^{\nabla }_{{\mathscr {P}}} : \Omega ^k({\mathcal {D}},{\mathcal {D}}) \rightarrow \Omega ^{k+1}({\mathcal {D}},{\mathcal {D}})\), is defined as follows:
-
(i)
If \(U \in \Omega ^0({\mathcal {D}},{\mathcal {D}}) = \varGamma ({\mathcal {D}})\), then \(d^{\nabla }_{{\mathscr {P}}}U(X) = \nabla _XU\) for every \( X \in \varGamma (\mathcal{D}) \).
-
(ii)
If \(\varphi \in \Omega ^k({\mathcal {D}},{\mathcal {D}})\), \(k \ge 1\), then
$$\begin{aligned}&d^{\nabla }_{{\mathscr {P}}}\varphi (X_0,\ldots ,X_k) = \sum _{i=0}^k(-1)^i\nabla _{X_i}\varphi (X_0,\ldots ,{\widehat{X}}_i,\ldots ,X_k)\\&\qquad + \sum _{0 \le i < j \le k} (-1)^{i+j}\varphi (\llbracket X_i,X_j \rrbracket ,X_0,\ldots ,{\widehat{X}}_i,\ldots ,{\widehat{X}}_j,\ldots ,X_k) \end{aligned}$$for \(X_0,\ldots ,X_k \in \varGamma ({\mathcal {D}})\). (Here \({\widehat{X}}_i\) indicates the omission of that element.)
In particular, for a \({\mathcal {D}}\)-valued 1-form \(\varphi \), we have
where \(X,Y \in \varGamma ({\mathcal {D}})\). (Note that the torsion of \(\nabla \) is exactly the \({\mathscr {P}}\)-exterior covariant derivative of the identity map \({{\,\textrm{id}\,}}_{{\mathcal {D}}} : {\mathcal {D}} \rightarrow {\mathcal {D}}\).)
3 The Schouten curvature tensor
Let \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) be a nonholonomic Riemannian manifold, with associated nonholonomic connection \(\nabla \). As \({\mathcal {D}}\) is nonintegrable, the standard curvature tensor \((X,Y,Z) \mapsto [\nabla _X,\nabla _Y]Z - \nabla _{[X,Y]}Z\) is no longer defined. Instead, we have the Schouten curvature tensor \(K \in {\mathcal {T}}\,^1_3\,({\mathcal {D}})\) [10]:
K is clearly skew-symmetric in its first two arguments; hence we may also view it as the mapping \(\varGamma (\textstyle \bigwedge ^2{\mathcal {D}}) \rightarrow {\mathcal {T}}\,^1_1\,({\mathcal {D}})\), \(K(X \wedge Y)Z = K(X,Y)Z\). The associated (0, 4)-tensor, which we denote \({\widehat{K}}\), is given by \({\widehat{K}}(W,X,Y,Z) = {\textbf {g}}(K(W,X)Y,Z)\).
The symmetries of the Riemannian curvature tensor are well known (see, e.g., [22]). In contrast, not all of those symmetries hold for the Schouten curvature tensor. A straightforward computation yields the following result.
Lemma 3
Let \(X,Y,Z \in \varGamma ({\mathcal {D}})\); then:
-
(i)
\((d^{\nabla }_{{\mathscr {P}}})^2Z(X,Y) = K(X,Y)Z + \llbracket {\mathscr {Q}}([X,Y]),Z\rrbracket \).
-
(ii)
\((d^{\nabla }_{{\mathscr {P}}})^2{{\,\textrm{id}\,}}_{{\mathcal {D}}}(X,Y,Z) = K(X,Y)Z + K(Y,Z)X + K(Z,X)Y\).
Since \(\nabla \) is torsion free, the first Bianchi identity holds; i.e., \((d^{\nabla }_{{\mathscr {P}}})^2{{\,\textrm{id}\,}}_{{\mathcal {D}}} \equiv 0\), or equivalently,
Remark 2
The second Bianchi identity does not generally hold for the Schouten tensor. Indeed, we may view K as an element of \(\Omega ^2({\mathcal {D}},T^1_1({\mathcal {D}}))\). Furthermore, the nonholonomic connection extends to a connection \(\nabla ^* : \varGamma ({\mathcal {D}}) \times {\mathcal {T}}\,^1_1\,({\mathcal {D}}) \rightarrow {\mathcal {T}}\,^1_1\,({\mathcal {D}})\), which has an associated \({\mathscr {P}}\)-exterior covariant derivative \(d^{\nabla ^*}_{{\mathscr {P}}} : \Omega ^k({\mathcal {D}},{\mathcal {T}}\,^1_1\,({\mathcal {D}})) \rightarrow \Omega ^{k+1}({\mathcal {D}},{\mathcal {T}}\,^1_1\,({\mathcal {D}}))\). The classical identity is \(d^{\nabla ^*}_{{\mathscr {P}}}K \equiv 0\) (see, e.g., [23]); however, in this case we have
Here \(\sum _{\circlearrowleft (X,Y,Z)}\) indicates the sum over the cyclic permutations of (X, Y, Z) and \({\mathcal {J}}_{{\mathscr {P}}}\) and \({\mathcal {J}}_{{\mathscr {Q}}}\) are the Jacobiators of \(\llbracket \cdot ,\cdot \rrbracket \) and \({\mathscr {Q}}([\cdot ,\cdot ])\), respectively (i.e., \({\mathcal {J}}_{{\mathscr {P}}}(X,Y,Z) = \sum _{\circlearrowleft (X,Y,Z)} \llbracket \llbracket X,Y \rrbracket ,Z \rrbracket \) and similarly for \({\mathcal {J}}_{{\mathscr {Q}}}\)).
The (0, 4)-tensor \({\widehat{K}}\) satisfies the following symmetries:
-
(S1)
\({\widehat{K}}(W,X,Y,Z) + {\widehat{K}}(X,W,Y,Z) = 0\).
-
(S2)
\({\widehat{K}}(W,X,Y,Z) + {\widehat{K}}(W,X,Y,Z) + {\widehat{K}}(W,X,Y,Z) = 0\).
However, in contrast to the Riemannian (0, 4)-tensor, \({\widehat{K}}\) is generally not skew-symmetric in the final two arguments, nor is it symmetric if one swaps the first two arguments with the last two. We decompose \({\widehat{K}}\) into two tensors \({\widehat{R}}\) and \({\widehat{C}}\), where \({\widehat{R}}\) is the component of \({\widehat{K}}\) that is skew-symmetric in the last two arguments and \({\widehat{C}}\) is the component that is symmetric in the last two arguments. Specifically, we define \({\widehat{R}},{\widehat{C}} \in {\mathcal {T}}\,^0_4\,({\mathcal {D}})\) as
\({\widehat{R}}\) and \({\widehat{C}}\) both satisfy the same two symmetries as \({\widehat{K}}\) (i.e., (S1) and (S2)); furthermore, we have
-
(S3)
\({\widehat{R}}(W,X,Y,Z) + {\widehat{R}}(W,X,Z,Y) = 0\).
-
(S4)
\({\widehat{R}}(W,X,Y,Z) = {\widehat{R}}(Y,Z,W,X)\). (This follows from the first three symmetries.)
-
(S5)
\({\widehat{C}}(W,X,Y,Z) = {\widehat{C}}(W,X,Z,Y)\).
Proposition 8
Let \(W,Y,X,Z \in \varGamma ({\mathcal {D}})\). Then
Proof
From the definition of \({\widehat{C}}\), we have
The first two terms are
Consequently,
Similarly, we have \(-{\textbf {g}}(\nabla _{\llbracket W,X \rrbracket }Y,Z) - {\textbf {g}}(Y,\nabla _{\llbracket W,X \rrbracket }Z) = -\llbracket W,X \rrbracket [{\textbf {g}}(Y,Z)]\) and
Substituting back into the expression for \(2\,{\widehat{C}}(W,X,Y,Z)\) yields the result. \(\square \)
It turns out–at least, when \({\mathcal {D}}\) is strongly nonholonomic–that the curvature tensor \({\widehat{C}}\) may be interpreted to measure the “geodesic invariance” of \({\mathcal {D}}\), i.e., the invariance (in a specific sense) of \({\mathcal {D}}\) under the geodesic flow. For further details (both on geodesic invariance and the aforementioned interpretation of \({\widehat{C}}\)), refer to [2].
Since \({\widehat{R}}\) satisfies all of the symmetries of the Riemannian (0, 4)-tensor, it has analogous algebraic properties. (Heuristically, we may thus view the Schouten tensor \({\widehat{K}}\) as consisting of a “Riemannian” component \({\widehat{R}}\) and a “remainder” \({\widehat{C}}\).) Hence we shall define a sectional curvature, a Ricci tensor, and a scalar curvature analogous to the corresponding tensors in Riemannian geometry.
Let \({\mathcal {S}}_q\), \(q \in {\textsf {M}}\) be a two-dimensional subspace of \({\mathcal {D}}_q\) and let \((X_q,Y_q)\) be a basis for \({\mathcal {S}}_q\). We define the sectional curvature of \({\mathcal {S}}_q\), denoted \({\widetilde{R}}({\mathcal {S}}_q)\), as
Here \({\widehat{R}}\) is viewed as the tensor \((W\wedge X,Y\wedge Z) \mapsto {\widehat{R}}(W,X,Z,Y)\) and \(\widehat{{\textbf {g}}}\) is the metric induced on \(\bigwedge ^2{\mathcal {D}}\) by \({\textbf {g}}\), i.e., \(\widehat{{\textbf {g}}}(W\wedge X,Y\wedge Z) = {\textbf {g}}(W,Y){\textbf {g}}(X,Z) - {\textbf {g}}(W,Z){\textbf {g}}(X,Y)\). We shall also write \({\widetilde{R}}({\mathcal {S}}_q)\) as \({\widetilde{R}}(X_q \wedge Y_q)\). As in the Riemannian case (see, e.g., [21]), one can show that \({\widetilde{R}}\) is well defined (i.e., does not depend on the choice of \(X_q \wedge Y_q\)). Furthermore, \({\widetilde{R}}\) determines \({\widehat{R}}\), in the following sense: suppose \(F \in {\mathcal {T}}\,^0_4\,({\mathcal {D}})\) satisfies the symmetries (S1)–(S4); in particular, F can be viewed as the tensor \(F : (W \wedge X,Y \wedge Z) \mapsto F(W,X,Z,Y)\). If
for every nonzero \(X_q \wedge Y_q \in \bigwedge ^2{\mathcal {D}}\), then \({\widehat{R}} = F\).
The Ricci tensor \({{\,\textrm{Ric}\,}}\in {\mathcal {T}}\,^0_2\,({\mathcal {D}})\) is defined as \({{\,\textrm{Ric}\,}}= {{\,\textrm{tr}\,}}^1_1 R\), i.e.,
where \((X_a)\) is an orthonormal frame for \({\mathcal {D}}\). The Ricci tensor is clearly symmetric. The trace of the endomorphism \({\textbf {g}}^{\sharp }\circ {{\,\textrm{Ric}\,}}^{\flat } : \varGamma ({\mathcal {D}}) \rightarrow \varGamma ({\mathcal {D}})\) is called the scalar curvature, denoted \(\textrm {Scal}\). (Here \(S^{\flat }\) denotes the map \(X \mapsto S(X,\cdot )\), while \(S^{\sharp }\) denotes the map \((S^{\flat })^{-1}\) whenever the tensor S is nondegenerate.) In terms of the orthonormal frame \((X_a)\), we have
In a similar fashion to the Ricci tensor, let \(A \in {\mathcal {T}}\,^0_2\,({\mathcal {D}})\) be defined as \(A = {{\,\textrm{tr}\,}}^1_1 C\), i.e.,
where \((X_a)\) is an orthonormal frame for \({\mathcal {D}}\). In general, A is not symmetric; thus we define two tensors \(A_{sym}\) and \(A_{skew}\) to be the symmetric and skew-symmetric parts of A, respectively. In terms of \((X_a)\), we then have
(Note that \(A_{skew} = -\frac{1}{2}{{\,\textrm{tr}\,}}^1_3C\).) It is not difficult to see that both \(A_{sym}\) and \(A_{skew}\) are trace-free.
4 The Wagner curvature tensor
We briefly describe Wagner’s approach to the construction of his curvature tensor. Although Wagner originally expressed his construction using the language of the Ricci calculus, there have also been some more modern expositions of his results, most notably [10]. Our approach largely follows the latter paper, presenting Wagner’s ideas in the language of modern differential geometry. (In Sect. 4.1 we discuss in more detail the differences between [10] and this paper.) Let \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) be a nonholonomic Riemannian structure and let \({\mathcal {D}} = {\mathcal {D}}^1 \subsetneq \cdots \subsetneq {\mathcal {D}}^N = T{\textsf {M}}\) be the flag of \({\mathcal {D}}\). The nonholonomic connection \(\nabla ^1 = \nabla \) induces a parallel translation along \({\mathcal {D}}^1\)-curves. For each component \({\mathcal {D}}^{i+1}\) of the flag, one constructs a \({\mathcal {D}}^{i+1}\)-connection \(\nabla ^{i+1}\) on \({\mathcal {D}}\). Such a connection induces a parallel translation along \({\mathcal {D}}^{i+1}\)-curves; furthermore, \(\nabla ^{i+1}\) is defined in such a way that it extends \(\nabla ^i\) and the set of parallel tensors of \(\nabla ^{i+1}\) coincides with that of \(\nabla ^i\). Finally, one gets a vector bundle connection \(\nabla ^N\) on \({\mathcal {D}}\) (whose corresponding parallel translation is along any curve in \({\textsf {M}}\)), with an associated curvature tensor \(K^N\); this is the Wagner curvature tensor. The vanishing of \(K^N\) characterizes the flatness of \(\nabla ^N\), and hence (by construction of \(\nabla ^2,\ldots ,\nabla ^{N-1}\)), the flatness of \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\).
4.1 Definition and basic properties
Let \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) be a nonholonomic Riemannian manifold, where \({\mathcal {D}}\) has degree of nonholonomy N, and let \({\mathcal {D}}^1 \subsetneq \cdots \subsetneq {\mathcal {D}}^N = T{\textsf {M}}\) be the flag of \({\mathcal {D}}\). In addition, let \({\mathcal {E}}^1,\ldots ,{\mathcal {E}}^{N-1}\) be distributions on \({\textsf {M}}\) such that
Let \({\mathscr {Q}}_i : T{\textsf {M}} \rightarrow {\mathcal {E}}^i\) denote the projection onto \({\mathcal {E}}^i\) and let \({\mathscr {P}}_i : T{\textsf {M}} \rightarrow {\mathcal {D}}^i\) be the projection onto \({\mathcal {D}}^i = {\mathcal {D}}\oplus {\mathcal {E}}^1\oplus \cdots \oplus {\mathcal {E}}^{i-1}\) defined as \({\mathscr {P}}_1 = {\mathscr {P}}\) and \({\mathscr {P}}_{i+1} = {\mathscr {P}} \oplus {\mathscr {Q}}_1 \oplus \cdots \oplus {\mathscr {Q}}_i\) for \(i \ge 1\). The distributions \({\mathcal {E}}^1,\ldots ,{\mathcal {E}}^{N-1}\) play a crucial rôle in the definition of the Wagner curvature tensor, yet in general there is no canonical choice for these distributions. Consequently, the Wagner curvature tensor is not intrinsically defined. (Wagner essentially proposed redefining a nonholonomic Riemannian structure to include \({\mathcal {E}}^1,\ldots ,{\mathcal {E}}^{N-1}\).) For the purposes of this paper, by a Wagner structure we shall mean a nonholonomic Riemannian structure \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\), with degree of nonholonomy \(N \ge 2\), together with distributions \({\mathcal {E}}^1,\ldots ,{\mathcal {E}}^{N-1}\) such that the Eq. (2) are satisfied. If \({\mathcal {D}}\) is strongly nonholonomic, then \({\mathcal {D}}^2 = T{\textsf {M}} = {\mathcal {D}}\oplus {\mathcal {D}}^{\perp }\), i.e., the choice of \({\mathcal {E}}^1\) is canonical. Thus we have the following result.
Proposition 9
Every nonholonomic Riemannian structure \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) with \({\mathcal {D}}\) strongly nonholonomic is a Wagner structure.
(Hence, when \({\mathcal {D}}\) is strongly nonholonomic, the Wagner curvature tensor will be intrinsic.) Similarly, if \({\textbf {g}}\) is the restriction \(\widetilde{{\textbf {g}}}|_{{\mathcal {D}}}\) to \({\mathcal {D}}\) of a Riemannian metric \(\widetilde{{\textbf {g}}}\) on \({\textsf {M}}\) (as in the case, for instance, of a nonholonomic mechanical system with kinetic energy Lagrangian and constraints linear-in-velocities), then there are canonical choices of the distributions \({\mathcal {E}}^1,\ldots ,{\mathcal {E}}^{N-1}\).
Proposition 10
Let \(({\textsf {M}},\widetilde{{\textbf {g}}})\) be a Riemannian manifold, \({\mathcal {D}}\) a completely nonholonomic distribution on \({\textsf {M}}\) and \({\mathcal {D}}^{\perp }\) the orthogonal complement of \({\mathcal {D}}\). Let \({\mathcal {D}} = {\mathcal {D}}^1 \subsetneq \cdots \subsetneq {\mathcal {D}}^N = T{\textsf {M}}\) be the flag of \({\mathcal {D}}\) and let \({\mathcal {E}}^i\) be the \(\left. \widetilde{{\textbf {g}}}\right| _{{\mathcal {D}}^{i+1}}\)-orthogonal complement of \({\mathcal {D}}^i\) in \({\mathcal {D}}^{i+1}\), \(i = 1,\ldots ,N-1\). Then \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },\left. \widetilde{{\textbf {g}}}\right| _{{\mathcal {D}}})\), together with the distributions \({\mathcal {E}}^1,\ldots ,{\mathcal {E}}^{N-1}\), is a Wagner structure.
Proof
The second part of (2) holds by construction of \({\mathcal {E}}^1,\ldots ,{\mathcal {E}}^{N-1}\). For the first part, since \({\mathcal {D}}^i = {\mathcal {D}} \oplus {\mathcal {E}}^1 \oplus \cdots \oplus {\mathcal {E}}^{i-1}\) and \({\mathcal {D}}^i \perp _{\widetilde{{\textbf {g}}}} {\mathcal {E}}^i\), we have \({\mathcal {D}} \perp _{\widetilde{{\textbf {g}}}} {\mathcal {E}}^i\). That is, \({\mathcal {D}}\) is orthogonal to each of \({\mathcal {E}}^1,\ldots ,{\mathcal {E}}^{N-1}\), and hence is orthogonal to \({\mathcal {E}}^1 \oplus \cdots \oplus {\mathcal {E}}^{N-1}\). Then \({\mathcal {E}}^1 \oplus \cdots \oplus {\mathcal {E}}^{N-1}\) is the orthogonal complement of \({\mathcal {D}}\), whence \({\mathcal {D}}^{\perp } = {\mathcal {E}}^1 \oplus \cdots \oplus {\mathcal {E}}^{N-1}\). \(\square \)
Let \(\Lambda _i : \varGamma (\bigwedge ^2{\mathcal {D}}^i) \rightarrow \varGamma ({\mathcal {E}}^i)\), \(i = 1,\ldots ,N-1\) be the tensors given by \(\Lambda _i(X \wedge Y) = {\mathscr {Q}}_i([X,Y])\) for \(X,Y \in \varGamma ({\mathcal {D}}^i)\). Since \({\mathcal {D}}\) is completely nonholonomic, each map \(\Lambda _i\) is surjective; hence (for a Wagner structure) one can canonically extend \({\textbf {g}}\) to a Riemannian metric.
Theorem 1
(cf. [10]) There exists a unique Riemannian metric \(\widetilde{{\textbf {g}}}\) on \({\textsf {M}}\) satisfying the following conditions:
-
(i)
The decomposition \(T{\textsf {M}} = {\mathcal {D}} \oplus {\mathcal {E}}^1 \oplus \cdots \oplus {\mathcal {E}}^{N-1}\) is orthogonal and \(\widetilde{{\textbf {g}}} = {\textbf {g}} \oplus {\textbf {h}}^1 \oplus \cdots \oplus {\textbf {h}}^{N-1}\), where \({\textbf {h}}^i = \left. \widetilde{{\textbf {g}}}\right| _{{\mathcal {E}}^i}\), \(i = 1,\ldots ,N-1\).
-
(ii)
Each map \(\left. \Lambda _i\right| _{(\ker \Lambda _i)^{\perp }} : (\ker \Lambda _i)^{\perp } \rightarrow {\mathcal {E}}^i\), \(i = 1,\ldots ,N-1\) satisfies
$$\begin{aligned} {\textbf {h}}^i(\Lambda _i(W \wedge X),\Lambda _i(Y \wedge Z)) = \widehat{{\textbf {g}}}^i(W \wedge X,Y \wedge Z) \end{aligned}$$for \(W \wedge X,Y \wedge Z \in (\ker \Lambda _i)^{\perp }\), where \(\widehat{{\textbf {g}}}^i\) is the metric induced on \(\bigwedge ^2{\mathcal {D}}^i\) by the metric \({\textbf {g}}^i = {\textbf {g}}\oplus {\textbf {h}}^1\oplus \cdots \oplus {\textbf {h}}^{i-1}\) on \({\mathcal {D}}^i\), i.e., \(\widehat{{\textbf {g}}}^i(W\wedge X,Y\wedge Z) = {\textbf {g}}^i(W,Y){\textbf {g}}^i(X,Z) - {\textbf {g}}^i(W,Z){\textbf {g}}^i(X,Y)\).
Proof
Let \({\textbf {g}}^1 = {\textbf {g}}\) and let \(\widehat{{\textbf {g}}}^1\) be the corresponding metric on \(\bigwedge ^2{\mathcal {D}}^1\). Let \((\ker \varDelta _1)^{\perp }\) be the orthogonal complement of \(\ker \varDelta _1 \subseteq \bigwedge ^2{\mathcal {D}}^1\) with respect to \(\widehat{{\textbf {g}}}^1\). As \(\varDelta _1\) is surjective, we can define a metric \({\textbf {h}}^1\) on \({\mathcal {E}}^1\) by the requirement that the isomorphism \(\left. \varDelta _1\right| _{(\ker \varDelta _1)^{\perp }} : (\ker \varDelta _1)^{\perp } \rightarrow {\mathcal {E}}^1\) is an isometry. Hence we have the metric \({\textbf {g}}^2 = {\textbf {g}}^1 \oplus {\textbf {h}}^1\) on \({\mathcal {D}}^2 = {\mathcal {D}} \oplus {\mathcal {E}}^1\), which induces a metric \(\widehat{{\textbf {g}}}^2\) on \(\bigwedge ^2{\mathcal {D}}^2\). Let \({\textbf {h}}^2\) be the metric on \({\mathcal {E}}^2\) induced by \(\left. \varDelta _2\right| _{(\ker \varDelta _2)^{\perp }}\). Continuing in this fashion, we get the Riemannian metric \(\widetilde{{\textbf {g}}} = {\textbf {g}} \oplus {\textbf {h}}^1 \oplus \cdots \oplus {\textbf {h}}^{N-1}\) on \(T{\textsf {M}} = {\mathcal {D}} \oplus {\mathcal {E}}^1 \oplus \cdots \oplus {\mathcal {E}}^{N-1}\). \(\square \)
Fix \(1 \le i \le N-1\). Let \(\nabla ^1 = \nabla \) and let \(\nabla ^{i+1} : \varGamma ({\mathcal {D}}^{i+1}) \times \varGamma ({\mathcal {D}}) \rightarrow \varGamma ({\mathcal {D}})\) be the \({\mathcal {D}}^{i+1}\)-connection on \({\mathcal {D}}\) specified as follows: if \(Z \in \varGamma ({\mathcal {D}}^{i+1})\) with \(X = {\mathscr {P}}_i(Z)\) and \(A = {\mathscr {Q}}_i(Z)\), then
Here \(\Theta _i = \left. \Lambda _i\right| _{(\ker \Lambda _i)^{\perp }}^{-1}\) and \(K^i : \varGamma (\bigwedge ^2{\mathcal {D}}^i) \times \varGamma ({\mathcal {D}}) \rightarrow \varGamma ({\mathcal {D}})\) is the curvature tensor of \(\nabla ^i\) defined as
(Note that, as \({\mathscr {Q}}([{\mathcal {D}},{\mathcal {D}}]) = {\mathscr {Q}}_1([{\mathcal {D}},{\mathcal {D}}])\), we have \(K^1 = K\).) In particular, for \(i = N-1\), we have a vector bundle connection \(\nabla ^N : \varGamma (T{\textsf {M}}) \times \varGamma ({\mathcal {D}}) \rightarrow \varGamma ({\mathcal {D}})\) on \({\mathcal {D}}\). Let \(K^N\) be the curvature tensor of this connection:
\(K^N\) is called the Wagner curvature tensor of \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\).
Theorem 2
(cf. [10]) Given \(T \in {\mathcal {T}}\,\,^k_{\ell }\,({\mathcal {D}})\), we have \(\nabla ^iT \equiv 0\) if and only if \(\nabla ^{i+1}T \equiv 0\).
Proof
Let \(T \in {\mathcal {T}}\,^k_{\ell}\,({\mathcal {D}})\); we have
where \(K^i(\Theta _i(A))\) is viewed as a derivation in  . Suppose that \(\nabla ^iT \equiv 0\); then
. Suppose that \(\nabla ^iT \equiv 0\); then
for every \(X,Y \in \varGamma ({\mathcal {D}}^i)\). We claim that \(K^i(\Theta _i(A))T + \mathscr {L}^{\mathscr {P}}_AT = 0\) for \(A \in \varGamma ({\mathcal {E}}^i)\). Indeed, suppose that \(\Theta _i(A) = X\wedge Y\) for \(X,Y \in \varGamma ({\mathcal {D}}^i)\); then
The case when \(\Theta _i(A)\) is a \({\mathcal {C}}^{\infty }({\textsf {M}})\)-combination of bivector fields follows from the tensoriality of \(K^i\). Hence, if \(Z \in \varGamma ({\mathcal {D}}^{i+1})\) with \(X = {\mathscr {P}}_i(Z)\) and \(A = {\mathscr {Q}}_i(Z)\), then
Conversely, suppose \(\nabla ^{i+1}T \equiv 0\); then \(\nabla ^i_XT = \nabla ^{i+1}_XT = 0\) for \(X \in \varGamma ({\mathcal {D}}^i)\), whence \(\nabla ^iT \equiv 0\). \(\square \)
Corollary 1
\(\nabla ^i\) is metric, i.e., \(\nabla ^i{\textbf {g}} \equiv 0\) (\(i = 1,\ldots ,N\)).
We have N restricted connections \(\nabla ^1,\ldots ,\nabla ^N\) on \({\mathcal {D}}\). The first connection (a nonholonomic, or \({\mathcal {D}}\)-connection on \({\mathcal {D}}\)) permits parallel translation only along \({\mathcal {D}}\)-curves, whereas the last (a vector bundle connection on \({\mathcal {D}}\)) permits parallel translation along any curve in \({\textsf {M}}\). In between we have the \({\mathcal {D}}^i\)-restricted connections \(\nabla ^i\) (for each \(i = 2,\ldots ,N-1\)) which permit parallel translation along \({\mathcal {D}}^i\)-curves. By Corollary 1, parallel translation (with respect to any of the connections \(\nabla ^1,\ldots ,\nabla ^N\)) is a linear isometry. For a \({\mathcal {D}}^i\)-curve \(\gamma : [0,1] \rightarrow {\textsf {M}}\), let \(\Pi ^{i,t}_{\gamma }\) denote the parallel translation along \(\gamma \) with respect to \(\nabla ^i\).
Proposition 11
If \(\gamma : [0,1] \rightarrow {\textsf {M}}\) is a \({\mathcal {D}}^i\)-curve, then \(\Pi ^{i,t}_{\gamma } = \Pi ^{i+1,t}_{\gamma }\) (\(i = 1,\ldots ,N-1\)).
Proof
Let \(\gamma : [0,1] \rightarrow {\textsf {M}}\) be a \({\mathcal {D}}^i\)-curve, \(U_0 \in {\mathcal {D}}_{\gamma (0)}\) and \(V(t) = \Pi ^{i,t}_{\gamma }(U_0)\), \(W(t) = \Pi ^{i+1,t}_{\gamma }(U_0)\). Let \((X^0_{a_0})\) be an orthonormal frame for \({\mathcal {D}}\) and \((X^i_{a_i})\) a frame for \({\mathcal {E}}^i\), where \(1 \le a_0 \le r\) and \(1 \le a_i \le {{\,\textrm{rank}\,}}({\mathcal {E}}^i)\). It follows that \((X^0_{a_0},X^1_{a_1},\ldots ,X^i_{a_i})\) is a frame for \({\mathcal {D}}^{i+1} = {\mathcal {D}} \oplus {\mathcal {E}}^1 \oplus \cdots \oplus {\mathcal {E}}^i\). There exist functions \(v^{a_0},w^{a_0} \in {\mathcal {C}}^{\infty }([0,1])\) such that \(V = v^{a_0}(X^0_{a_0}\circ \gamma )\) and \(W = w^{a_0}(X^0_{a_0}\circ \gamma )\). Furthermore, these functions satisfy the ODEs
where \(\varGamma ^{a_0}_{b_ic_0},\Omega ^{a_0}_{b_ic_0} \in {\mathcal {C}}^{\infty }({\textsf {M}})\) are defined by \(\nabla ^i_{X^j_{b_j}}X^0_{c_0} = \varGamma ^{a_0}_{b_jc_0}X^0_{a_0}\) (where \(0 \le j \le i\)) and \(\nabla ^{i+1}_{X^k_{b_k}}X^0_{c_0} = \Omega ^{a_0}_{b_kc_0}X^0_{a_0}\) (where \(0 \le k \le i+1\)). Since \(\nabla ^i_XU = \nabla ^{i+1}_XU\) for \(X \in \varGamma ({\mathcal {D}}^i)\) and \(U \in \varGamma ({\mathcal {D}})\), we have \(\varGamma ^{a_0}_{b_jc_0} = \Omega ^{a_0}_{b_jc_0}\) for \(j = 0,\ldots ,i\). Hence \(V = W\), and so \(\Pi ^{i,t}_{\gamma } = \Pi ^{i+1,t}_{\gamma }\). \(\square \)
Lastly, we state the main result of this section: the vanishing of the Wagner curvature tensor characterizes the flat Wagner structures.
Theorem 3
(cf. [10]) A Wagner structure \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) is locally flat if and only if \(K^N \equiv 0\).
Proof
The Wagner curvature tensor \(K^N\) is precisely the curvature tensor of the vector bundle connection \(\nabla ^N\), and so there exists a parallel frame for \({\mathcal {D}}\) on an open set in \({\textsf {M}}\) if and only if \(K^N\) vanishes identically on that set. Since every parallel vector field with respect to \(\nabla ^N\) is also parallel with respect to \(\nabla \), it follows that \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) is locally flat exactly when \(K^N\) vanishes identically. \(\square \)
Remark 3
As for the Schouten tensor, one can use \({\textbf {g}}\) to lower an index of \(K^i\), obtaining the tensor \({\widehat{K}}^i\) given by \({\widehat{K}}^i(X,Y,U,V) = {\textbf {g}}({\widehat{K}}^i(X \wedge Y)U,V)\) for \(X,Y \in \varGamma ({\mathcal {D}}^i)\) and \(U,V \in \varGamma ({\mathcal {D}})\). Each tensor \({\widehat{K}}^i\) then decomposes into two tensors \({\widehat{R}}^i\) and \({\widehat{C}}^i\):
We then have the following expression for \({\widehat{C}}^i\) (cf. Proposition 8):
Remark 4
Just as \({\widehat{C}}\) may be interpreted in terms of geodesic invariance of \({\mathcal {D}}\) (in the strongly nonholonomic case), so too may the tensors \({\widehat{C}}^i\) be interpreted in terms of the geodesic invariance of the distributions \({\mathcal {D}}^i\) (in the case of a Wagner structure) [2].
Remark 5
Regarding the construction of Wagner’s curvature tensor, we have departed slightly from the presentation in [10]; we have also filled in a number of missing details. For instance, we have made explicit the dependence of Wagner’s construction on the complementary distributions \({\mathcal {E}}^i\) (and show that a strongly nonholonomic structure, and a structure arising from a nonholonomic mechanical system, always satisfies the additional requirements in order to define Wagner’s tensor). We have also presented the construction in a more direct fashion (e.g., skipping the quotients of distributions in favour of using the projection mappings directly). This serves to simplify the presentation, and makes the construction more natural (particularly of the induced Riemannian metric in Theorem 1). Furthermore, the definition of the connections \(\nabla ^2,\ldots ,\nabla ^N\) in this paper is different from that in [10] (also in [30]). In [10], \(\nabla ^{i+1}\) is defined as
where \(\Lambda _i^{\dagger }\) is the adjoint of \(\Lambda _i\), i.e., \(\Lambda _i^{\dagger } = (\widehat{{\textbf {g}}}^i)^{\sharp } \circ \Lambda _i^* \circ ({\textbf {h}}^i)^{\flat }\). In fact, it turns out that the \(\Lambda _i^{\dagger }\) can be replaced with any right inverse of \(\Lambda _i\), and the crucial property of the \(\nabla ^i\)’s (viz., Theorem 2) will still hold. The approach we employ avoids a particular choice of right inverse to \(\Lambda _i\), and simplifies the construction. Nevertheless, this means that the definition of Wagner’s tensor \(K^N\) in this paper differs from that in [10, 30]. (See also [5, 14], who also present another alternative approach to constructing Wagner’s tensor. In particular, the connections \(\nabla ^{i+1}\) are instead defined as mappings \(\varGamma ({\mathcal {D}}^{i+1}) \times \varGamma ({\mathcal {D}}^i) \rightarrow \varGamma ({\mathcal {D}}^i)\), and the tensors \(K^{i+1}\) as \(\varGamma (\bigwedge ^2{\mathcal {D}}^{i+1}) \times \varGamma ({\mathcal {D}}^i) \rightarrow \varGamma ({\mathcal {D}}^i)\).) A key result of this section is that \(\nabla ^{i+1}\) “extends” \(\nabla ^i\) (Theorem 2). Hence, regarding the existence of a parallel vector field \(U \in \varGamma ({\mathcal {D}})\), rather than consider the equation \(\nabla U = 0\), we can consider the simpler, equivalent equation \(\nabla ^NU = 0\). In [10] one starts from the equation \(\nabla U = \varphi \), where \(\varphi \in {\mathcal {T}}\,^1_1\,({\mathcal {D}})\), and then one takes \(\varphi = 0\) as required. On the other hand, Theorem 2 in fact allows one to consider the existence of a parallel tensor field, i.e., the equation \(\nabla T = 0\), where \(T \in {\mathcal {T}}\,^k_{\ell }\,({\mathcal {D}})\) (a consequence of this is that each connection \(\nabla ^i\) is metric). We also consider the relation between the parallel transport of \(\nabla ^{i+1}\) and \(\nabla ^i\), which was not addressed in [10].
4.2 Algebraic interpretation of curvature tensors
For a vector bundle connection \({\widetilde{\nabla }}\) on \({\mathcal {D}}\), the curvature tensor \((X,Y) \mapsto [{\widetilde{\nabla }}_X,{\widetilde{\nabla }}_Y] - {\widetilde{\nabla }}_{[X,Y]}\) can be viewed as measuring the extent to which the mapping  , \(X \mapsto {\widetilde{\nabla }}_X\) fails to be a homomorphism (of Lie algebras). A similar interpretation holds for the curvature tensors \(K^i\).
, \(X \mapsto {\widetilde{\nabla }}_X\) fails to be a homomorphism (of Lie algebras). A similar interpretation holds for the curvature tensors \(K^i\).
Since the tangent bundle of \({\textsf {M}}\) decomposes as \(T{\textsf {M}} = {\mathcal {D}} \oplus {\mathcal {E}}^1 \oplus \cdots \oplus {\mathcal {E}}^{N-1}\), we have a corresponding decomposition \(\mathscr {L}^{\mathscr {P}}_{T{\textsf {M}}} = \mathscr {L}^{\mathscr {P}}_{{\mathcal {D}}} \oplus \mathscr {L}^{\mathscr {P}}_{{\mathcal {E}}^1} \oplus \cdots \oplus \mathscr {L}^{\mathscr {P}}_{{\mathcal {E}}^{N-1}}\). Moreover, as \({\mathcal {D}}^{i+1} = {\mathcal {D}}^i \oplus {\mathcal {E}}^i = {\mathcal {D}} \oplus {\mathcal {E}}^1 \oplus \cdots \oplus {\mathcal {E}}^i\), we get

(Consequently,
 is completely nonholonomic: if we define the flag \({\mathcal {S}}^1 \subsetneq {\mathcal {S}}^2 \subsetneq \cdots \) by
is completely nonholonomic: if we define the flag \({\mathcal {S}}^1 \subsetneq {\mathcal {S}}^2 \subsetneq \cdots \) by  and \({\mathcal {S}}^{i+1} = {\mathcal {S}}^i + [{\mathcal {S}}^i,{\mathcal {S}}^i]\), \(i \ge 1\), then
and \({\mathcal {S}}^{i+1} = {\mathcal {S}}^i + [{\mathcal {S}}^i,{\mathcal {S}}^i]\), \(i \ge 1\), then  and
and  We shall also use \({\mathscr {P}}_i\) to denote the projection
We shall also use \({\mathscr {P}}_i\) to denote the projection  ; likewise, let \({\mathscr {Q}}_i\) be the projection
; likewise, let \({\mathscr {Q}}_i\) be the projection  .
.
Lemma 4
Fix \(1 \le i \le N\) and let  , where \(\delta _1 = \mathscr {L}^{\mathscr {P}}_X + \delta _1'\) and \(\delta _2 = \mathscr {L}^{\mathscr {P}}_Y + \delta _2'\) for \(X,Y \in \varGamma ({\mathcal {D}}^i)\) and
, where \(\delta _1 = \mathscr {L}^{\mathscr {P}}_X + \delta _1'\) and \(\delta _2 = \mathscr {L}^{\mathscr {P}}_Y + \delta _2'\) for \(X,Y \in \varGamma ({\mathcal {D}}^i)\) and  . Then
. Then
Proof
We have \([\delta _1,\delta _2] = [\mathscr {L}^{\mathscr {P}}_X,\mathscr {L}^{\mathscr {P}}_Y] + [\mathscr {L}^{\mathscr {P}}_X,\delta _2'] + [\delta _1',\mathscr {L}^{\mathscr {P}}_Y] + [\delta _1',\delta _2']\). Moreover, since  , it follows that
, it follows that  . Consider the term \([\mathscr {L}^{\mathscr {P}}_X,\mathscr {L}^{\mathscr {P}}_Y]\); we have \([\mathscr {L}^{\mathscr {P}}_X,\mathscr {L}^{\mathscr {P}}_Y](f) = [X,Y][f]\) for every \(f \in {\mathcal {C}}^{\infty }({\textsf {M}})\), and so
. Consider the term \([\mathscr {L}^{\mathscr {P}}_X,\mathscr {L}^{\mathscr {P}}_Y]\); we have \([\mathscr {L}^{\mathscr {P}}_X,\mathscr {L}^{\mathscr {P}}_Y](f) = [X,Y][f]\) for every \(f \in {\mathcal {C}}^{\infty }({\textsf {M}})\), and so
for some  . Moreover, as \(X,Y \in \varGamma ({\mathcal {D}}^i)\), we have \([X,Y] \in \varGamma ({\mathcal {D}}^{i+1})\). Thus \([\mathscr {L}^{\mathscr {P}}_X,\mathscr {L}^{\mathscr {P}}_Y] = \mathscr {L}^{\mathscr {P}}_{{\mathscr {P}}_i([X,Y])} + \mathscr {L}^{\mathscr {P}}_{{\mathscr {Q}}_i([X,Y])} + \delta '\), and so
. Moreover, as \(X,Y \in \varGamma ({\mathcal {D}}^i)\), we have \([X,Y] \in \varGamma ({\mathcal {D}}^{i+1})\). Thus \([\mathscr {L}^{\mathscr {P}}_X,\mathscr {L}^{\mathscr {P}}_Y] = \mathscr {L}^{\mathscr {P}}_{{\mathscr {P}}_i([X,Y])} + \mathscr {L}^{\mathscr {P}}_{{\mathscr {Q}}_i([X,Y])} + \delta '\), and so
Consequently, we have
\(\square \)
Clearly, \(\nabla ^i_X\) for \(X \in \varGamma ({\mathcal {D}}^i)\) is a \({\mathcal {D}}^i\)-derivation. The following result asserts that the curvature tensor \(K^i\) measures the extent to which \( \Gamma \left( {{\mathcal {D}}^{i} } \right) \to {\text{Der}}_{{{\mathcal{D}}_{{\text{i}}} }} \left( {\mathcal D} \right) \), \(X \mapsto \nabla ^i_X\) fails to be a homomorphism from \((\varGamma ({\mathcal {D}}^i),{\mathscr {P}}_i([\cdot ,\cdot ]))\) to  . (Note that these structures are not Lie algebras, as \({\mathscr {P}}_i([\cdot ,\cdot ])\) does not generally satisfy the Jacobi identity. Instead they are so-called almost Lie structures [24], and so “homomorphism” refers to a homomorphism of almost Lie structures.)
. (Note that these structures are not Lie algebras, as \({\mathscr {P}}_i([\cdot ,\cdot ])\) does not generally satisfy the Jacobi identity. Instead they are so-called almost Lie structures [24], and so “homomorphism” refers to a homomorphism of almost Lie structures.)
Theorem 4
We have
Proof
Let \(X,Y \in \varGamma ({\mathcal {D}}^i)\) and \(U \in \varGamma ({\mathcal {D}})\). There exist derivations  such that \(\nabla ^i_X = \mathscr {L}^{\mathscr {P}}_X + \delta _1\) and \(\nabla ^i_Y = \mathscr {L}^{\mathscr {P}}_Y + \delta _2\). Hence, by Lemma 4, we have \({\mathscr {P}}_i([\nabla ^i_X,\nabla ^i_Y]) = [\nabla ^i_X,\nabla ^i_Y] - \mathscr {L}^{\mathscr {P}}_{{\mathscr {Q}}_i([X,Y])}\). It follows that
such that \(\nabla ^i_X = \mathscr {L}^{\mathscr {P}}_X + \delta _1\) and \(\nabla ^i_Y = \mathscr {L}^{\mathscr {P}}_Y + \delta _2\). Hence, by Lemma 4, we have \({\mathscr {P}}_i([\nabla ^i_X,\nabla ^i_Y]) = [\nabla ^i_X,\nabla ^i_Y] - \mathscr {L}^{\mathscr {P}}_{{\mathscr {Q}}_i([X,Y])}\). It follows that
\(\square \)
4.3 Three-dimensional nonholonomic Riemannian structures
Flat nonholonomic Riemannian structures in three dimensions were considered in [3]; in particular, a characterization of flatness (in three dimensions) was given. This characterization (in fact, characterizing equation) was obtained in a rather direct way by using an intrinsic contact form, as well as the \({\mathscr {P}}\)-exterior covariant derivative and contractions of the Schouten curvature tensor. (Moreover, it turns out that the vanishing of the Schouten tensor is sufficient for flatness in three dimensions.) We shall relate the foregoing characterization with the Wagner curvature tensor.
Let \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) be a nonholonomic Riemannian structure, where \({\textsf {M}}\) is three-dimensional (and \({\mathcal {D}}\) is a rank two strongly nonholonomic distribution on \({\textsf {M}}\)). There exists a 1-form \(\omega \) on \({\textsf {M}}\) (a contact form) such that \({\mathcal {D}} = \ker \omega \); this 1-form is fixed up to sign by imposing the condition \(|d\omega (X_1,X_2)| = 1\), where \((X_1,X_2)\) is an orthonormal frame for \({\mathcal {D}}\). The connection \(\nabla ^2 : \varGamma (T{\textsf {M}}) \times \varGamma ({\mathcal {D}}) \rightarrow \varGamma ({\mathcal {D}})\) is given by
for \(Z \in \varGamma (T{\textsf {M}})\), where \(X = {\mathscr {P}}(Z)\) and \(A = {\mathscr {Q}}(Z)\). Here \(\Theta = \left. \Lambda \right| ^{-1}_{(\ker \Lambda )^{\perp }}\), where \(\Lambda : \varGamma (\bigwedge ^2{\mathcal {D}}) \rightarrow \varGamma ({\mathcal {D}}^{\perp })\), \(X \wedge Y \mapsto {\mathscr {Q}}([X,Y])\); in fact, we have \(\ker \Lambda = \{0\}\). For convenience, we shall denote \({\widetilde{\nabla }} = \nabla ^2\). The Wagner curvature tensor \({\widetilde{K}} = K^2\) is given by
for \(X,Y \in \varGamma (T{\textsf {M}})\) and \(U \in \varGamma ({\mathcal {D}})\). Define a tensor \({\widetilde{{{\,\textrm{Ric}\,}}}} : \varGamma (T{\textsf {M}}) \times \varGamma ({\mathcal {D}}) \rightarrow {\mathcal {C}}^{\infty }({\textsf {M}})\) as follows:
where \(X \in \varGamma (T{\textsf {M}})\), \(U \in \varGamma ({\mathcal {D}})\) and \((X_1,X_2)\) is an orthonormal frame for \({\mathcal {D}}\). (Note that \({\widetilde{{{\,\textrm{Ric}\,}}}}\) does not depend on the choice of \(X_1\) and \(X_2\).)
Theorem 5
Let \({\mathcal {U}} \subseteq {\textsf {M}}\) be open. \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) is locally flat on \({\mathcal {U}}\) if and only if \({\widetilde{{{\,\textrm{Ric}\,}}}}\) vanishes identically on \({\mathcal {U}}\).
Proof
Let \((X_0,X_1,X_2)\) be a frame on \({\mathcal {U}}\) such that \(X_0\) is a frame for \({\mathcal {D}}^{\perp }\) and \((X_1,X_2)\) is an orthonormal frame for \({\mathcal {D}}\). We have \([X_i,X_j] = c^k_{ij}X_k\) for structure constants \(c_{ij}^k \in {\mathcal {C}}^{\infty }({\mathcal {U}})\) (where i, j and k take the values 0, 1, 2); moreover, we may assume that \(c_{21}^0 = 1\). Let \(f_{01},f_{02} \in {\mathcal {C}}^{\infty }({\mathcal {U}})\) be defined as follows:
Here \(\kappa = \frac{1}{2}\textrm {Scal}= \frac{1}{2}(c^2_{10} - c^1_{20}) - (c^1_{21})^2 - (c^2_{21})^2 - X_1[c^2_{21}] + X_2[c^1_{21}]\). The expressions for \(f_{01}\) and \(f_{02}\) can be found in [3], where it is shown that \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) is flat on \({\mathcal {U}}\) if and only if \(f_{01} = f_{02} = 0\). It turns out that \(f_{01}\) and \(f_{02}\) are, up to sign, the only components of \({\widetilde{K}}\). Indeed, a straightforward (but tedious) calculation yields
Accordingly, we have \({\widetilde{{{\,\textrm{Ric}\,}}}}(X_0,X_1) = {\textbf {g}}(-f_{01}X_2,X_1) + {\textbf {g}}(-f_{02}X_2,X_2) = -f_{02}\). A similar calculation gives \({\widetilde{{{\,\textrm{Ric}\,}}}}(X_0,X_2) = f_{01}\), and so
where \((\nu ^0,\nu ^1,\nu ^2)\) is the coframe dual to \((X_0,X_1,X_2)\). (Notice that \({\widetilde{{{\,\textrm{Ric}\,}}}}^{\flat }\circ \Lambda \) is completely determined by its evaluation on \(X_2 \wedge X_1\).) Lastly, if \(X,Y \in \varGamma ({\mathcal {D}})\), then \({\widetilde{{{\,\textrm{Ric}\,}}}}(X,Y) = 0\). It follows that \({\widetilde{{{\,\textrm{Ric}\,}}}}\) vanishes if and only if \({\widetilde{{{\,\textrm{Ric}\,}}}}^{\flat }\circ \Lambda \) vanishes; the result follows. \(\square \)
Remark 6
We know that \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) is flat if and only if \(d^{\nabla }_{{\mathscr {P}}}F = F\circ \rho \) [3], where
and \(\rho (X_1 \wedge X_2) = d\omega (X_1,X_2){\mathscr {P}}(Z)\). Here \((X_1,X_2)\) is an orthonormal frame for \({\mathcal {D}}\) and \(Z \in \varGamma (T{\textsf {M}})\) is the Reeb vector field of \(\omega \) (i.e., the unique—up to sign—vector field on \({\textsf {M}}\) such that \(i_Z\omega = 1\) and \(i_Zd\omega = 0\)). It turns out that \({\textbf {g}}^{\sharp }\circ {\widetilde{{{\,\textrm{Ric}\,}}}}^{\flat }\circ \Lambda = d^{\nabla }_{{\mathscr {P}}}F - F\circ \rho \).
5 An alternative approach
The nonholonomic connection, as well as the connections \(\nabla ^2,\ldots ,\nabla ^N\) in the case of a Wagner structure, can be equivalently viewed as horizontal lifts/distributions. Accordingly, we shall consider curvature from this alternative perspective. In particular, we shall express the Schouten curvature tensor K, as well as the curvature tensors \(K^1,\ldots ,K^N\), in terms of horizontal lifts of vector fields. (As a corollary, we then characterize the vanishing of the curvature tensors in terms of involutivity conditions for the associated horizontal distributions.) We shall also show that the connections \(\nabla ^1,\ldots ,\nabla ^N\) are equivalently formulated as a flag of horizontal distributions on \({\mathcal {D}}\).
5.1 The Schouten tensor
Let \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) be a nonholonomic Riemannian manifold with associated nonholonomic connection \(\nabla \). We can extend \(\nabla \) to a vector bundle connection \(\mathring{\nabla }\) on \({\mathcal {D}}\) as follows (cf. [4]):
(Note that \(\mathring{\nabla }\) depends only on \({\mathcal {D}}\), \({\mathcal {D}}^{\perp }\) and \({\textbf {g}}\), hence it is intrinsic to the nonholonomic Riemannian structure.) The curvature tensor of \(\mathring{\nabla }\) is the (1, 3)-tensor field \(\mathring{R} : \varGamma (T{\textsf {M}}) \times \varGamma (T{\textsf {M}}) \times \varGamma ({\mathcal {D}}) \rightarrow \varGamma ({\mathcal {D}})\) given by \(\mathring{R}(X,Y)U = [\mathring{\nabla }_X,\mathring{\nabla }_Y]U - \mathring{\nabla }_{[X,Y]}U\). Clearly, we have \(\mathring{R}(X,Y) = K(X,Y)\) whenever \(X,Y \in \varGamma ({\mathcal {D}})\).
Proposition 12
Let \({\mathcal {U}} \subseteq {\textsf {M}}\) be open. If \(\mathring{R} \equiv 0\) on \({\mathcal {U}}\), then \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) is locally flat on \({\mathcal {U}}\). Conversely, if \((U_a)\) is a parallel frame for \({\mathcal {D}}\) defined on \({\mathcal {U}}\) such that \([U_a,\varGamma ({\mathcal {D}}^{\perp })] \subseteq \varGamma ({\mathcal {D}}^{\perp })\), then \(\mathring{R} \equiv 0\) on \({\mathcal {U}}\).
Proof
Suppose \(\mathring{R} \equiv 0\) on \({\mathcal {U}}\). Since \(\mathring{\nabla }\) is a vector bundle connection on \({\mathcal {D}}\), the vanishing of its curvature tensor \(\mathring{R}\) implies the existence of a parallel frame \((U_a)\) for \({\mathcal {D}}\) on \({\mathcal {U}}\). (Here “parallel” means “parallel with respect to \(\mathring{\nabla }\).”) That is, \(\mathring{\nabla }_ZU_a = 0\) for every \(Z \in \varGamma _{{\mathcal {U}}}(T{\textsf {M}})\). In particular, taking \(Z \in \varGamma _{{\mathcal {U}}}({\mathcal {D}})\), it follows that \(\nabla U_a \equiv 0\), and so \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) is locally flat on \({\mathcal {U}}\).
Conversely, suppose there exists a parallel (with respect to \(\nabla \)) frame \((U_a)\) for \({\mathcal {D}}\) defined on \({\mathcal {U}}\); then \(\mathring{\nabla }_XU_a = 0\) for every \(X \in \varGamma _{{\mathcal {U}}}({\mathcal {D}})\). On the other hand, we have \(\mathring{\nabla }_AU_a = \llbracket A,U_a \rrbracket \) for every \(A \in \varGamma _{{\mathcal {U}}}({\mathcal {D}}^{\perp })\). Accordingly, if \([U_a,\varGamma ({\mathcal {D}}^{\perp })] \subseteq \varGamma ({\mathcal {D}}^{\perp })\), then \(\mathring{\nabla }_AU_a = 0\), i.e., \((U_a)\) is also parallel with respect to \(\mathring{\nabla }\). It follows that the curvature tensor of \(\mathring{\nabla }\) vanishes on \({\mathcal {U}}\). \(\square \)
Let \(\pi : {\mathcal {D}} \rightarrow {\textsf {M}}\) be the natural projection. Associated to the nonholonomic connection \(\nabla \) and its extension \(\mathring{\nabla }\) are the restricted connections
and
respectively. Notice that \(f\big |_{\pi ^*{\mathcal {D}}} = h\); in particular, if \(X \in \varGamma ({\mathcal {D}})\), then \(X^f = X^h\) (where \(X^f\) is the f-lift of X, and \(X^h\) is the h-lift of X). Let \({\mathcal {V}} = \ker T\pi \) be the vertical distribution, \({\mathcal {H}} = {{\,\textrm{im}\,}}h\) the horizontal distribution of h and \({\mathcal {F}} = {{\,\textrm{im}\,}}f\) the horizontal distribution of f. We have \({\mathcal {H}} \subsetneq {\mathcal {F}}\); moreover, by Proposition 4, it follows that \({\mathcal {V}} \cap {\mathcal {H}} = {\mathcal {V}} \cap {\mathcal {F}} = \{0\}\), \({\mathcal {V}} + {\mathcal {H}} \subsetneq T{\mathcal {D}}\) and \({\mathcal {V}} + {\mathcal {F}} = T{\mathcal {D}}\). That is,
Let \({\mathcal {H}}^{\perp }\) denote the distribution on \({\mathcal {D}}\) given by \({\mathcal {H}}^{\perp } = {{\,\textrm{im}\,}}(f|_{\pi ^*{\mathcal {D}}^{\perp }})\), i.e., \({\mathcal {H}}^{\perp }_{U_q} = {{\,\textrm{span}\,}}\{f(U_q,X_q) : X_q \in {\mathcal {D}}^{\perp }_q\}\) for each \(U_q \in {\mathcal {D}}\). We have \(\pi _*{\mathcal {H}}^{\perp } = {\mathcal {D}}^{\perp }\) and \({\mathcal {F}} = {\mathcal {H}}\oplus {\mathcal {H}}^{\perp }\).
Remark 7
We have
As noted in, e.g., [11], a nonholonomic connection on \({\mathcal {D}}\) is precisely the specification of a \(\phi _t\)-invariant complement \({\mathcal {H}}\) to \({\mathcal {V}}\) in \((T\pi )^{-1}({\mathcal {D}})\), where \(\phi _t : {\mathcal {D}} \rightarrow {\mathcal {D}}\) is the dilation \(\phi _t(U_q) = e^t\,U_q\). Indeed, given such a complement, we have \(\pi _*{\mathcal {H}} = {\mathcal {D}}\), \({\mathcal {V}} \cap {\mathcal {H}} = \{0\}\) and \((\phi _t)_*{\mathcal {H}} = {\mathcal {H}}\). Hence, by Proposition 4 and Proposition 5, there exists a unique linear \({\mathcal {D}}\)-connection h on \({\mathcal {D}}\) with \({{\,\textrm{im}\,}}h = {\mathcal {H}}\).
Let \({\mathscr {V}} : T{\mathcal {D}} \rightarrow {\mathcal {V}}\), \({\mathscr {P}} : T{\mathcal {D}} \rightarrow {\mathcal {V}} \oplus {\mathcal {H}}\) and \({\mathscr {Q}} : T{\mathcal {D}} \rightarrow {\mathcal {H}}^{\perp }\) denote the projections corresponding to the decomposition \(T{\mathcal {D}} = {\mathcal {V}} \oplus {\mathcal {H}} \oplus {\mathcal {H}}^{\perp }\). Let \(\llbracket \cdot ,\cdot \rrbracket : \varGamma (T{\mathcal {D}}) \times \varGamma (T{\mathcal {D}}) \rightarrow \varGamma ({\mathcal {V}}\oplus {\mathcal {H}})\) be the projected Lie bracket \({\mathscr {P}}([\cdot ,\cdot ])\). If \(X \in \varGamma ({\mathcal {F}})\) is projectable, then \({\mathscr {P}}(X) = {\mathscr {P}}(\pi _*X)^h\) and \({\mathscr {Q}}(X) = {\mathscr {Q}}(\pi _*X)^f\).
Theorem 6
We have
for \(X,Y \in \varGamma ({\mathcal {D}})\) and \(U_q \in {\mathcal {D}}\).
Proof
Let \(X,Y \in \varGamma ({\mathcal {D}})\) and \(\omega \in \varGamma ({\mathcal {D}}^*)\). We may interpret the (1, 1)-tensor field K(X, Y) as an element of of  . In particular, \(K(X,Y)\omega \in \varGamma ({\mathcal {D}}^*)\) is given by
. In particular, \(K(X,Y)\omega \in \varGamma ({\mathcal {D}}^*)\) is given by
for \(U \in \varGamma ({\mathcal {D}})\). By Lemma 2, we have \(Z^{f}[{\overline{\omega }}] = \overline{\mathring{\nabla }_Z\omega }\) for \(Z \in \varGamma (T{\textsf {M}})\); hence
Since \(\pi _*\big ([X^h,Y^h]-[X,Y]^{f}\big ) = [\pi _*X^h,\pi _*Y^h]-[X,Y] = 0\), we have that \([X^{h},Y^{h}] - [X,Y]^{f}\) is vertical. Hence
and so \(\overline{K(X,Y)\omega } = {\mathscr {V}}\;(\llbracket X^{h},Y^{h}\rrbracket )[{\overline{\omega }}]\). Let \(U_q \in {\mathcal {D}}\); then
By Lemma 1, we thus have
Since \(\omega \) is arbitrary, the result follows. \(\square \)
Corollary 2
\(K \equiv 0\) if and only if \(\llbracket{\mathcal {H}}, \,{\mathcal {H}}\rrbracket \subseteq {\mathcal {H}}\).
5.2 The Wagner tensor
Suppose that \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) is a Wagner structure (with degree of nonholonomy N). Associated to each \(\nabla ^i\) is the restricted connection
We have \(h^1 = h\) and \(h^{i+1}\big |_{\pi ^*{\mathcal {D}}^i} = h^i\); let \({\mathcal {H}}^i = {{\,\textrm{im}\,}}h^i\), \({\mathcal {Q}}^i = {{\,\textrm{im}\,}}(h^{i+1}|_{\pi ^*{\mathcal {E}}^i})\) and let \({\mathcal {V}}\) be the vertical distribution; then \({\mathcal {H}}^{i+1} = {\mathcal {H}}^i \oplus {\mathcal {Q}}^i\), and hence
Let \({\mathscr {V}} : T{\mathcal {D}} \rightarrow {\mathcal {V}}\), \({\mathscr {P}} : T{\mathcal {D}} \rightarrow {\mathcal {V}}\oplus {\mathcal {H}}\) and \({\mathscr {Q}}_i : T{\mathcal {D}} \rightarrow {\mathcal {Q}}^i\) be the projections corresponding to the decomposition (3); similarly, let \({\mathscr {P}}_i = {\mathscr {P}}\oplus {\mathscr {Q}}_i\oplus \cdots \oplus {\mathscr {Q}}_{i-1}\) be the projection onto \({\mathcal {V}}\oplus {\mathcal {H}}^i\) (by convention, we take \({\mathscr {P}}_1 = {\mathscr {P}}\)). If \(X \in \varGamma ({\mathcal {H}}^N)\) is projectable, then
A result similar to Theorem 6 holds for each of the curvature tensors \(K^1,\ldots ,K^N\). Let \(\mathring{\nabla }^i\) be the \({\mathcal {D}}^{i+1}\)-connection on \({\mathcal {D}}\) given by
Let \(f^i : \pi ^*{\mathcal {D}}^{i+1} \rightarrow T{\mathcal {D}}\) be the associated horizontal lift, i.e.,
Theorem 7
We have
for \(X,Y \in \varGamma ({\mathcal {D}}^i)\) and \(U_q \in {\mathcal {D}}\) (\(i = 1,\ldots ,N\)).
Proof
(The proof is similar to that of Theorem 6, thus we shall omit some details.) Let \(X,Y \in \varGamma ({\mathcal {D}}^i)\) and \(\omega \in \varGamma ({\mathcal {D}}^*)\); then \([X,Y] \in \varGamma ({\mathcal {D}}^{i+1})\), and hence \(\overline{K^i(X,Y)\omega } = \overline{[\nabla ^i_X,\nabla ^i_Y]\omega } - \overline{\mathring{\nabla }^i_{[X,Y]}\omega }\). In fact, by Lemma 2, we have
Clearly, we have that \([X^{h^i},Y^{h^i}] - [X,Y]^{f^i}\) is vertical; thus \([X^{h^i},Y^{h^i}] - [X,Y]^{f^i} = {\mathscr {V}}({\mathscr {P}}_i([X^{h^i},Y^{h^i}]))\), and so \(\overline{K^i(X,Y)\omega } = {\mathscr {V}}({\mathscr {P}}_i([X^{h^i},Y^{h^i}]))[{\overline{\omega }}]\). If \(U_q \in {\mathcal {D}}\), then
whence \(K^i(X,Y)U_q = -v_{U_q}^{-1}\cdot \,{\mathscr {V}}({\mathscr {P}}_i([X^{h^i},Y^{h^i}]))(U_q)\). \(\square \)
Corollary 3
We have \(K^i \equiv 0\) if and only if \({\mathscr {P}}_i([{\mathcal {H}}^i,{\mathcal {H}}^i]) \subseteq {\mathcal {H}}^i\). In particular, \(({\textsf {M}},{\mathcal {D}},{\mathcal {D}}^{\perp },{\textbf {g}})\) is locally flat (i.e., \(K^N \equiv 0\)) if and only if \({\mathcal {H}}^N\) is integrable.
The restricted connections \(\nabla ^1,\ldots ,\nabla ^N\) are equivalently specified by the horizontal lifts \(h^1,\ldots ,h^N\), which are in turn equivalently specified by the horizontal distributions \({\mathcal {H}}^1,\ldots ,{\mathcal {H}}^N\). It follows that Wagner’s construction of \(\nabla ^1,\ldots ,\nabla ^N\) is equivalently formulated as the flag of horizontal distributions on \({\mathcal {D}}\)
This flag can be constructed iteratively, starting with \({\mathcal {H}}^1 = {\mathcal {H}}\).
Theorem 8
We have
Proof
Let \({\mathcal {S}}\,^1 = {\mathcal {H}}\) and \({\mathcal {S}}\,^{i+1} = {\mathcal {S}}^i + {{\,\textrm{span}\,}}\{[X^{h^i},Y^{h^i}] : X \wedge Y \in (\ker \varDelta _i)^{\perp }\}\) for \(i \ge 1\). We use induction on i to prove that \({\mathcal {S}}^i = {\mathcal {H}}^i\); by definition, we have \({\mathcal {S}}^1 = {\mathcal {H}}^1\). Suppose that \({\mathcal {S}}^i = {\mathcal {H}}^i\) for some \(1 \le i \le N-1\). We claim that \(\pi _*{\mathcal {S}}\,^{i+1} = {\mathcal {D}}^{i+1}\) and \({\mathcal {V}} \cap {\mathcal {S}}\,^{i+1} = \{0\}\). Let \(W_{U_q} + [X^{h^i},Y^{h^i}](U_q) \in {\mathcal {S}}^{i+1}_{U_q}\), where \(U_q \in {\mathcal {D}}\); then
and so \(\pi _*{\mathcal {H}}\,^{i+1} \subseteq {\mathcal {D}}^{i+1}\). Conversely, let \(W_q \in {\mathcal {D}}^i_q\) and \(X_q \in {\mathcal {E}}^i_q\); then \(W_q + X_q\) is an arbitrary element of \({\mathcal {D}}^{i+1}_q = {\mathcal {D}}^i_q\oplus {\mathcal {E}}^i_q\). Since \({\mathcal {S}}^i = {\mathcal {H}}^i\) by the inductive hypothesis, we have \(\pi _*{\mathcal {S}}^i = {\mathcal {D}}^i\). Accordingly, there exists \(V_{U_q} + [Y,Z](U_q) \in {\mathcal {S}}^i_{U_q}\) such that \(T_{U_q}\pi \cdot (V_{U_q} + [Y,Z](U_q)) = W_q\). Let \(A \wedge B = \Theta _i(X) \in (\ker \varDelta _i)^{\perp }\), where \(X \in \varGamma ({\mathcal {E}}^i)\) is a smooth extension of \(X_q\). (The case when \(\Theta _i(X)\) is a \({\mathcal {C}}^{\infty }({\textsf {M}})\)-combination of bivector fields from \(\varGamma ({\mathcal {D}}^i)\) can be treated in a similar fashion.) Then
Hence \(\pi _*{\mathcal {S}}^{i+1} = {\mathcal {D}}^{i+1}\). Let \(W_{U_q} + [X^{h^i},Y^{h^i}](U_q) \in {\mathcal {V}}_{U_q} \cap {\mathcal {S}}^{i+1}_{U_q}\), \(U_q \in {\mathcal {D}}\). We have
Both non-vertical components must vanish; in particular, \({\mathscr {Q}}_i([X,Y])(q) = 0\), i.e., \((X \wedge Y)(q) \in \ker \varDelta _{i,q}\). Since \(X \wedge Y \in (\ker \varDelta _i)^{\perp }\), it follows that \((X \wedge Y)(q) = 0\); then
whence \({\mathcal {V}} \cap {\mathcal {S}}^{i+1} = \{0\}\). By uniqueness of the connection associated to \({\mathcal {H}}^{i+1}\) (Proposition 5), it follows that \({\mathcal {S}}^{i+1} = {\mathcal {H}}^{i+1}\). This completes the proof of the inductive case. \(\square \)
6 Concluding remark
Further investigation (in the vein of [2]) into geometric interpretations of the Schouten and Wagner curvature tensors (including the tensors \(K^2,\ldots , K^{N-1}\) involved in Wagner’s construction) would be a worthwhile undertaking. A natural next step would be to consider how curvature affects nonholonomic geodesics; for instance, to generalize the notion of a Jacobi field to nonholonomic Riemannian geometry. A thorough study of curvature in lower dimensions would also be a topic of interest.
Data availibility
The authors declare that data availability is not applicable
References
Barrett, D.I., Biggs, R., Remsing, C.C., Rossi, O.: Invariant nonholonomic Riemannian structures on three-dimensional Lie groups. J. Geom. Mech. 8, 139–167 (2016)
Barrett, D.I., Remsing, C.C.: On geodesic invariance and curvature in nonholonomic Riemannian geometry. Publ. Math. Debr. 94, 197–213 (2019)
Barrett, D.I., Remsing, C.C.: A note on flat nonholonomic Riemannian structures on three-dimensional Lie groups. Beitr. Algebra Geom. 60, 419–436 (2019)
Bejancu, A.: On the geometry of nonholonomic mechanical systems with vertical distribution. J. Math. Phys. 48, 052903 (2007)
Berestovskii, V.N.: Curvatures of homogeneous sub-Riemannian manifolds. Eur. J. Math. 3, 788–807 (2017)
Bloch, A.M.: Nonholonomic Mechanics and Control, 2nd edn. Springer, New York (2003)
Bukusheva, A.V., Galaev, S.V.: Connections on distributions and geodesic sprays. Russ. Math. 57, 7–13 (2013)
Cantrijn, F., Langerock, B.: Generalised connections over a vector bundle map. Diff. Geom. Appl. 18, 295–317 (2003)
Cortés Monforte, J.: Geometric Control and Numerical Aspects of Nonholonomic Systems. Springer, New York (2002)
Dragović, V., Gajić, B.: The Wagner curvature tensor in nonholonomic mechanics. Regul. Chaot. Dyn. 8, 105–123 (2003)
Galaev, S.V.: The intrinsic geometry of almost contact metric manifolds. Izv. Saratov Univ. (N.S.) Ser. Math. Mech. Inform. 12, 16–22 (2012)
Galaev, S.V.: Geometric interpretation of the Wagner curvature tensor in the case of a manifold with contact metric structure. Sib. Math. J. 57, 498–504 (2016)
Galaev, S.V., Gokhman, A.V.: A metrizability condition for an affine connection on a nonholonomic manifold \(X^2_3\) (in Russian). In: Collection of Scientific Works. Mathematics. Mechanics, pp. 28–32, Izv. Saratov University Press, Saratov (2005)
Gorbatenko, E.M.: Differential geometry of nonholonomic manifolds (after V.V. Wagner) (in Russian), Geom. Sbornik, 31–43 (1985)
Grozman, P.Y., Leites, D.A.: The Riemann tensor for nonholonomic manifolds. Theor. Math. Phys. 153, 1511–1538 (2007)
Hertz, H.: The Principles of Mechanics Presented in a New Form (in German), Leipzig (1894). MacMillan, English translation, Basingstoke (1899)
Koiller, J., Rodrigues, P.R., Pitanga, P.: Non-holonomic connections following Élie Cartan. An. Acad. Bras. Cienc. 73, 165–190 (2001)
Langerock, B.: Nonholonomic mechanics and connections over a bundle map. J. Phys. A Math. Gen. 34, L609–L615 (2001)
Leites, D.A.: The Riemann tensor for nonholonomic manifolds. Homol. Homotopy Appl. 4, 397–407 (2002)
Montgomery, R.: A Tour of Subriemannian Geometries. In: American Mathematical Society, Providence, RI, Their Geodesics and Applications (2002)
O’Neill, B.: Semi-Riemannian Geometry. Academic Press, New York (1983)
Petersen, P.: Riemannian Geometry, 2nd edn. Springer, Berlin (2006)
Poor, W.A.: Differential Geometric Structures. McGraw-Hill, New York (1981)
Popescu, P.: Almost Lie structures, derivations and R-curvature on relative tangent spaces. Rev. Roum. Math. Pures Appl. 37, 779–789 (1992)
Schouten, J.A.: On nonholonomic connections. In: Proceedings of Sciences, Vol. 31, Kon. Akad. Wetensch., Amsterdam (1928)
Synge, J.L.: Geodesics in nonholonomic geometry. Math. Ann. 99, 738–751 (1928)
Szilasi, J., Lovas, R.L., Kertész, D.C.: Connections, Sprays and Finsler Structures. World Scientific, Singapore (2014)
Vershik, A.M., Gershkovich, V.Y.: Nonholonomic problems and the theory of distributions. Acta Appl. Math. 12, 181–209 (1988)
Vershik, A.M., Gershkovich, V.: Ya.: nonholonomic dynamical systems, geometry of distributions and variational problems. In: Arnol’d, V.I., Novikov, S.P. (eds.) Dynamical Systems VII. Springer, New York (1994)
Wagner, V.V.: On the differential geometry of nonholonomic manifolds (in French). In: Mémoires du Séminaire Pour L’Analyse Vectorielle et Tensorielle, Livres II–III, pp. 267–318 (1935)
Wagner, V.V.: On the geometrical interpretation of the curvature vector of a non-holonomic \(V_3\) in the three-dimensional Euclidean space. Rec. Math. 4, 339–356 (1938)
Wagner, V.V.: On \(V^2_3\) in \(R_3\) with zero curvature (in German). Rec. Math. 4, 333–338 (1938)
Wagner, V.V.: Differential geometry of nonholonomic manifolds (in Russian). In: Report on The VIII-th International Competition for the N.I. Lobachevskii Prize (1937), Kazan Physico-Mathematical Society (1940)
Wagner, V.V.: Geometric interpretation of the motion of nonholonomic dynamical systems (in Russian). Tr. Semin. Vectorn. Tenzorn. Anal. 5, 301–327 (1941)
Wagner, V.V.: The inner geometry of non-linear non-holonomic manifolds. Rec. Math. 13, 135–167 (1943)
Zhao, P., Jiao, L.: Conformal transformations on Carnot-Carathéodory spaces. Nihonkai Math. J. 17, 167–185 (2006)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Barrett, D.I., Remsing, C.C. On the Schouten and Wagner curvature tensors. Rend. Circ. Mat. Palermo, II. Ser 72, 1–26 (2023). https://doi.org/10.1007/s12215-021-00654-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12215-021-00654-2



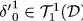 such that
such that