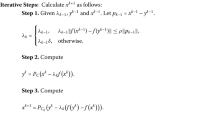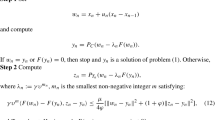Extension of the subgradient extragradient algorithm for solving variational inequalities without monotonicity

Abstract

Two improved subgradient extragradient algorithms are proposed for solving nonmonotone variational inequalities under the nonempty assumption of the solution set of the dual variational inequalities. First, when the mapping is Lipschitz continuous, we propose an improved subgradient extragradient algorithm with self-adaptive step-size (ISEGS for short). In ISEGS, the next iteration point is obtained by projecting sequentially the current iteration point onto two different half-spaces, and only one projection onto the feasible set is required in the process of constructing the half-spaces per iteration. The self-adaptive technique allows us to determine the step-size without using the Lipschitz constant. Second, we extend our algorithm into the case where the mapping is merely continuous. The Armijo line search approach is used to handle the non-Lipschitz continuity of the mapping. The global convergence of both algorithms is established without monotonicity assumption of the mapping. The computational complexity of the two proposed algorithms is analyzed. Some numerical examples are given to show the efficiency of the new algorithms.

1 Introduction

Let ${\mathbb {R}}^n$ be an n-dimensional Euclidean space, $C\subset {\mathbb {R}}^n$ be a nonempty closed convex set and $F:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ be a continuous mapping. We consider the variational inequalities ($\text{ VI }(F,C)$ for short), which is to find a vector $x^*\in C$ such that

$$\begin{aligned} \langle {F(x^*)},{x-x^*}\rangle \ge 0,~\forall x\in C, \end{aligned}$$

(1.1)

where $\langle {\cdot },{\cdot }\rangle$ denotes the inner product in ${\mathbb {R}}^n$. The dual variational inequalities of (1.1), is to find a vector $x^*\in C$ such that

$$\begin{aligned} \langle {F(x)},{x-x^*}\rangle \ge 0,~\forall x\in C. \end{aligned}$$

(1.2)

Denote by S the solution set of (1.1), i.e.,

$$\begin{aligned} S:=\{x^*\in C:\langle F(x^*),x-x^*\rangle \ge 0,~\forall x\in C\}, \end{aligned}$$

(1.3)

and denote by $S_D$ the solution set of (1.2), i.e.,

$$\begin{aligned} S_D:=\{x^*\in C:\langle F(x),x-x^*\rangle \ge 0,~\forall x\in C\}. \end{aligned}$$

(1.4)

When the mapping F is continuous and the set C is convex, we have $S_D\subset S$.

For solving $\text{ VI }(F,C)$, different types of projection algorithms have been proposed in the past few decades, see, for example, Goldstein–Levitin–Polyak projection algorithms [1, 2], proximal point algorithms [3, 4], extragradient algorithms [5, 6], projection and contraction algorithm [7], double projection algorithms [8, 9], subgradient extragradient algorithm [10], projected reflected gradient algorithm [11] and golden ratio algorithm [12], etc. The convergence of all the above algorithms is based on the common condition that $S= S_D$, which is a direct consequence of pseudomonotonicity of F on C when F is continuous. Note that the relationship $S= S_D$ may fail if the mapping F is continuous and quasimonotone on C, see, for example, [13, Example 4.2].

In order to solve quasimonotone variational inequalities, interior proximal algorithms [14, 15] have been proposed. However, the global convergence of those algorithms was obtained under more assumptions than $S_D\ne \emptyset$. Recently, the gradient algorithms with the new step-sizes [16] and two relaxed inertial subgradient extragradient algorithms [17] were proposed for quasimonotone variational inequalities. The global convergence was proved under the assumptions $S_D\ne \emptyset$ and

$$\begin{aligned} \{z\in C:F(z)=0\}\backslash S_D~\text{ is } \text{ a } \text{ finite } \text{ set }. \end{aligned}$$

(1.5)

However, the assumption (1.5) may not suit for solving quasimonotone variational inequalities, see, for example, [18, Example 4.4]. Therefore, it is important to propose some algorithms for quasimonotone variational inequalities or the general nonmonotone variational inequalities without the condition (1.5).

Under the assumption of $S_D\ne \emptyset$, Konnov [19] proposed the first extrapolation algorithm with Armijo-type line search and proved the sequence generated by that algorithm has a subsequence converging to a solution. To obtain the global convergence of the generated sequence, Ye and He [13] proposed a double projection algorithm for solving variational inequalities without monotonicity. The global convergence was proved under the mapping F is continuous and $S_D\ne \emptyset$. Note that the next iteration point in [13] is generated by projecting the current iteration point onto the intersection of the feasible set C and $k+1$ half-spaces, where k represents the current number of iteration steps. Therefore, in order to calculate the next iteration point, the computational cost will increase as the number of iteration steps increasing. To overcome the difficulty, Lei and He [20] proposed an extragradient algorithm for variational inequalities without monotonicity, in which the next iteration point is generated by projecting the current iteration point onto the feasible set C. In 2022, a modified Solodov–Svaiter algorithm was introduced by Van, Manh and Thanh [21], in which the next iteration point is obtained by projecting the current iteration point onto the intersection of the feasible set C and one half-space. The global convergence of these algorithms in [20] and [21] is proved under the mapping F is continuous and $S_D\ne \emptyset$. Note that in order to obtain the next iteration point of these algorithms, in [13, 20, 21], one projection onto the feasible set C or the intersection of the feasible C and one (or more) half-space(s) is required.

Very recently, some new projection algorithms have been proposed for nonmonotone variational inequalities to reduce the projection onto the feasible set C or the intersection of C and half-space(s). First, based on the modified projection-type algorithm [22], an infeasible projection algorithm was proposed by Ye [18] and the global convergence was proved under the mapping F is continuous and $S_D\ne \emptyset$. In the algorithm, the next iteration point is generated by projecting the current iteration point onto only one half-space. Then, based on the projection and contraction algorithm [7] and Tseng-type extragradient algorithm [23], Huang, Zhang and He [24] proposed a class modified projection algorithms for solving variational inequalities without monotonicity. In this algorithm, the generation of the next iteration point is obtained by projecting the current iteration point onto the intersection of multiple half-spaces. The global convergence is established under the mapping F is continuous and $S_D\ne \emptyset$. More algorithms for nonmonotone variational inequalities can be seen [25,26,27].

Inspired by the above related works, in this paper, we propose two improved subgradient extragradient algorithms for solving $\text{ VI }(F,C)$ without monotonicity. First, an improved subgradient extragradient algorithm with self-adaptive step-size ($\text{ ISEGS }$ for short) is proposed. The generation of the next iteration point in the algorithm is obtained by projecting sequentially the current iteration point onto two different half-spaces, and only one projection onto the feasible set C is needed in the process of constructing the half-spaces per iteration. Under the mapping F is Lipschitz continuous and $S_D\ne \emptyset$, the global convergence of $\text{ ISEGS }$ is established without the prior knowledge of Lipschitz constant of the mapping. Then, to weaken the Lipschitz continuity of the mapping F, an improved subgradient extragradient algorithm with Armijo line search ($\text{ ISEGA }$ for short) is proposed. Under the mapping F is continuous and $S_D\ne \emptyset$, the global convergence of $\text{ ISEGA }$ is proved.

Our algorithms can be regarded as an extension of the subgradient extragradient algorithm in [10], the infeasible projection algorithm in [18] and the class modified projection algorithms in [24]. Compared with the classical subgradient extragradient algorithm [10], in our two algorithms, the next iteration point is generated by introducing a new half-space and then projecting the point generated by [10] onto the new half-space. In this way, by improving the generation method of the next iteration point, we generalize the classical subgradient extragradient algorithm [10] from a class of monotone (or pseudomonotone) $\text{ VI }(F,C)$ to a class of nonmonone $\text{ VI }(F,C)$. Compared with the infeasible projection algorithm [18], although our two algorithms need to project sequentially onto two different half-spaces, the projection onto the half-space has an explicit expression, so it is as easy to implement as the algorithm in [18]. Finally, compared with the class modified projection algorithms in [24], our two algorithms do not need to project the current iteration point onto the intersection of multiple half-spaces, but onto two different half-spaces in sequence. Some numerical experiments show that our two algorithms are much more efficient than the existing algorithms from the view point of the number of iterations and $\text{ CPU }$ time.

The paper is organized as follows. In Sect. 2, some basic definitions and preliminary materials are introduced. In Sect. 3, we analyze the global convergence and the computational complexity of the proposed algorithms. Finally, we perform some numerical experiments to illustrate the behavior of our proposed algorithms and compare their performance with other algorithms in Sect. 4.

2 Preliminaries

In this section, we recall some basic definitions and well-known lemmas, which are helpful for convergence analysis in Sect. 3. Let $\Vert \cdot \Vert$ and $\langle \cdot ,\cdot \rangle$ denote the norm and inner product of ${\mathbb {R}}^n$, respectively.

Definition 2.1

Let $F:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ be a mapping. Then, the mapping

• (i) F is Lipschitz continuous on ${\mathbb {R}}^n$ with constant $L>0$, if

  $$\begin{aligned} \Vert {F(x)-F(y)}\Vert \le L\Vert {x-y}\Vert ,~~\forall x,y\in {\mathbb {R}}^n. \end{aligned}$$

  Specifically, if $L=1$ then F is said nonexpansive mapping.

• (ii) F is monotone on ${\mathbb {R}}^n$, if

  $$\begin{aligned} \langle {F(y)-F(x)},{y-x}\rangle \ge 0,~~\forall x,y\in {\mathbb {R}}^n. \end{aligned}$$

• (iii) F is pseudomonotone on ${\mathbb {R}}^n$, if

  $$\begin{aligned} \langle {F(x)},{y-x}\rangle \ge 0\Rightarrow \langle {F(y)},{y-x}\rangle \ge 0,~~\forall x,y\in {\mathbb {R}}^n. \end{aligned}$$

• (iv) F is quasimonotone on ${\mathbb {R}}^n$, if

  $$\begin{aligned} \langle {F(x)},{y-x}\rangle > 0\Rightarrow \langle {F(y)},{y-x}\rangle \ge 0,~~\forall x,y\in {\mathbb {R}}^n. \end{aligned}$$

From the above definitions, we see that $(\text{ ii})\Rightarrow (\text{ iii})\Rightarrow (\text{ iv})$. But the reverse is not true.

In the following, we give the definition and some properties of metric projection.

The metric projection of $x\in {\mathbb {R}}^n$ onto C is denoted by

$$\begin{aligned} \Pi _C(x):={\arg \min }\{\Vert x-y\Vert :y\in C\}. \end{aligned}$$

The distance function from $x\in {\mathbb {R}}^n$ to C is denoted by

$$\begin{aligned} \textrm{dist}(x,C):=\inf \{\Vert x-y\Vert :y\in C\}. \end{aligned}$$

Since C is a closed convex set and $\Pi _C$ is a single-valued mapping, we can obtain that $\textrm{dist}(x,C)=\Vert x-\Pi _C(x)\Vert$.

Lemma 2.1

[28, 29] Let $C\subset {\mathbb {R}}^n$ be a nonempty closed convex set and $x\in {\mathbb {R}}^n$ be any fixed point. Then, the following inequalities hold:

• (i) $\langle {\Pi _C(x)-x},{\Pi _C(x)-y}\rangle \le 0,~\forall y\in C$;

• (ii) $\Vert \Pi _C(x)-y\Vert ^2\le \Vert x-y\Vert ^2-\Vert x-\Pi _C(x)\Vert ^2,~\forall y\in C$;

• (iii) $\frac{\Vert {x-\Pi _C(x-\alpha F(x))}\Vert }{\alpha }\le \frac{\Vert {x-\Pi _C(x-\beta F(x))}\Vert }{\beta },~\forall \alpha \ge \beta >0$.

Lemma 2.2

[28] Let $a\in {\mathbb {R}}$ be a fixed vector and $H:=\{x\in {\mathbb {R}}^n:\langle {w},{x}\rangle \le a\}$ be a half-space. Then, for any $u\in {\mathbb {R}}^n$, we have

$$\begin{aligned} \Pi _H(u)=u-\max \bigg \{\frac{\langle {w},{u}\rangle -a}{\Vert {w}\Vert ^2},0\bigg \}w. \end{aligned}$$

Moreover, if in addition $u\notin H$, it follows that

$$\begin{aligned} \Pi _H(u)=u-\frac{\langle {w},{u}\rangle -a}{\Vert {w}\Vert ^2}w. \end{aligned}$$

Lemma 2.3

[28] Let $\{a_k\}$ and $\{b_k\}$ be two nonnegative real number sequences satisfying

$$\begin{aligned} a_{k+1}\le a_k+b_k,~\Sigma _{k=1}^\infty b_k<+\infty ,~\forall k\ge 0. \end{aligned}$$

Then, the sequence $\{a_k\}$ is convergent.

3 Main results

In this section, in order to solve $\text{ VI }(F,C)$ with the mapping F is Lipschitz continuous or continuous (without any generalized monotonicity), two improved subgradient extragradient algorithms are proposed. The generation of the next iteration point of these algorithms does not need to project the current point onto the feasible set C. In order to obtain the convergence proof of those two algorithms, we always assume that the following condition holds:

Condition 3.1

The solution set of the dual variational inequalities is nonempty, i.e., $S_D\ne \emptyset$.

Remark 3.1

Some sufficient conditions for $S_D\ne \emptyset$ were given in [13, Proposition 2.1] and [30, Proposition 1].

3.1 ISEGS for nonmonotone VI(F,C) with Lipschitz continuous

In this subsection, based on the subgradient extragradient algorithm [10], we introduce a new half-space and self-adaptive method to propose an improved subgradient extragradient algorithm with self-adaptive step-size ($\text{ ISEGS }$) for solving nonmonotone variational inequalities. To obtain the global convergence of $\text{ ISEGS }$, we assume the following condition holds:

Condition 3.2

The mapping $F:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ is Lipschitz continuous.

Now, we give the iterative format of $\text{ ISEGS }$ as follows:

Algorithm 3.1

Step 1.:

Let $x^0\in {\mathbb {R}}^n$ be chosen arbitrarily. Choose parameters $\tau \in (0,1)$, $\lambda _0>0$ and a nonnegative real sequence $\{\varepsilon _k\}$ satisfies $\mathop {\sum }\limits _{k=0}^\infty {\varepsilon _k}<+\infty .$ Set $k:=0.$

Step 2.:

Given the current iterations $x^k$ and $\lambda _k$, compute

$$\begin{aligned} y^k=\Pi _C(x^k-\lambda _kF(x^k)). \end{aligned}$$

If $x^k=y^k$ or $F(y^k)=0$, then stop and $y^k$ is a solution of $\text{ VI }(F,C)$. Otherwise, go to Step 3.

Step 3.:

Compute

$$\begin{aligned} z^k=\Pi _{T_k}(x^k-\lambda _k F(y^k)), \end{aligned}$$

where

$$\begin{aligned} T_k:=\{x\in {\mathbb {R}}^n:\langle {x^k-y^k-\lambda _k F(x^k)},{x-y^k}\rangle \le 0\}. \end{aligned}$$

(3.1)

Step 4.:

Let $H_k:=\{x\in {\mathbb {R}}^n:\langle {F(y^k)},{x-y^k}\rangle \le 0\}$ and choose

$$\begin{aligned} i_k:=\mathrm{arg\max _{0\le j\le k}}\frac{\langle {F(y^j)},{z^k-y^j}\rangle }{\Vert {F(y^j)}\Vert }. \end{aligned}$$

(3.2)

Compute

$$\begin{aligned} x^{k+1}=\Pi _{{\widetilde{H}}_k}(z^k)~\text {with}~{\widetilde{H}}_k:=H_{i_k} \end{aligned}$$

(3.3)

and

$$\begin{aligned} \lambda _{k+1} = {\left\{ \begin{array}{ll} ~\textrm{min}\{\lambda _k+\varepsilon _k,~\tau \frac{\Vert {x^k-y^k}\Vert }{\Vert {F(x^k)-F(y^k)}\Vert }\}, & \text {if}~F(x^k)\ne F(y^k), \\ ~\lambda _k+\varepsilon _k, & \text {otherwise}. \end{array}\right. } \end{aligned}$$

(3.4)

Let $k:=k+1$ and return to Step 2.

Remark 3.2

In [10], the next iteration point is defined by $x^{k+1}=\Pi _{T_k}(x^k-\lambda _k F(y^k))$. In Algorithm 3.1, the generation of the next iteration point is based on the subgradient extragradient algorithm in [10], by introducing a new half-space $H_k$, the point $\Pi _{T_k}(x^k-\lambda _k F(y^k))$ generated by [10] is projected onto one half-space ${\widetilde{H}}_k$, i.e.,

$$\begin{aligned} x^{k+1}=\Pi _{{\widetilde{H}}_k}(\Pi _{T_k}(x^k-\lambda _k F(y^k))). \end{aligned}$$

In this manner, it is unnecessary to assume the generalized monotonicity of the mapping F when proving the global convergence of the Algorithm 3.1.

According to Lemma 2.2, the projection onto the half-space has an explicit expression. Therefore, the calculation of the iteration points $z^{k}$ and $x^{k+1}$ is easy to implement.

Lemma 3.1

Assume that the Condition 3.2 holds. Let $\{\lambda _k\}$ be the sequence generated by Algorithm 3.1. Then, there exists a constant $\lambda >0$ such that $\lim \limits _{k\rightarrow \infty }\lambda _k=\lambda$.

Proof

Since the mapping F is Lipschitz continuous (Assume that the Lipschitz constant is $L>0$). In this case that $F(x^k)\ne F(y^k)$, we have

$$\begin{aligned} \tau \frac{\Vert {x^k-y^k}\Vert }{\Vert {F(x^k)-F(y^k)}\Vert }\ge \tau \frac{\Vert {x^k-y^k}\Vert }{L\Vert {x^k-y^k}\Vert }=\frac{\tau }{L}. \end{aligned}$$

(3.5)

According to the definition of $\lambda _k$ in (3.4) and mathematical induction, it follows that the sequence $\{\lambda _k\}$ has a lower bound $\min \{\frac{\tau }{L},\lambda _0\}.$ Hence, $\lambda _k>0$ holds for all k.

Next, we prove that the sequence $\{\lambda _k\}$ is convergent. By the definition of $\lambda _k$ in (3.4), we know that

$$\begin{aligned} \lambda _{k+1}\le \lambda _k+\varepsilon _k,~\forall k\ge 0. \end{aligned}$$

(3.6)

Since the sequence $\{\varepsilon _k\}$ satisfies $\mathop {\sum }\limits _{k=0}^\infty {\varepsilon _k}<+\infty$, use (3.6) and Lemma 2.3, we deduce that the sequence $\{\lambda _k\}$ is convergent, i.e., there exists a number $\lambda >0$ such that $\lim \limits _{k\rightarrow \infty }{\lambda _k}=\lambda .$ This completes the proof. $\square$

In the following, we shall present three lemmas utilized in the global convergence proof of Algorithm 3.1.

Lemma 3.2

Let $\{z^k\}$ be a sequence and $H_{k}$ be a half-space generated by Algorithm 3.1 and ${\widetilde{H}}_k$ be a half-space defined in (3.3). Then, for all $k\ge 0$, we deduce that $\textrm{dist}(z^k,H_j)\le \textrm{dist}(z^k,{\widetilde{H}}_k)$ holds for any $j\in \{0,1,\ldots ,k\}$.

Proof

Without loss of generality, let

$$\begin{aligned} I:= & \{j:z^k\in H_j,~j\in \{0,1,\ldots ,k\}\},\\ J:= & \{j:z^k\notin H_j,~j\in \{0,1,\ldots ,k\}\}. \end{aligned}$$

Therefore, for all $j\in \{0,1,\ldots ,k\}$, the above equations can be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} ~z^k\in H_j, & j\in I, \\ ~z^k\notin H_j, & j\in J. \end{array}\right. } \end{aligned}$$

(3.7)

For any fixed $\varsigma \in I$, according to (3.7), we have $z^k\in H_\varsigma$, then $\textrm{dist}(z^k,H_\varsigma )=0$. For any fixed $l\in J$, according to (3.7) and the definition of $H_j$, we know that $\langle F(y^l),z^k-y^l\rangle >0$. Further, by Lemma 2.2, we obtain that

$$\begin{aligned} \Pi _{H_l}(z^k)=z^k-\frac{\langle F(y^l),z^k-y^l\rangle }{\Vert F(y^l)\Vert ^2}F(y^l). \end{aligned}$$

(3.8)

Thus,

$$\begin{aligned} \begin{aligned} \textrm{dist}(z^k,H_l)&= ~ \Vert z^k-\Pi _{H_l}(z^k)\Vert \\&= ~\Vert z^k-z^k+\frac{\langle F(y^l),z^k-y^l\rangle }{\Vert F(y^l)\Vert ^2}F(y^l)\Vert \\&= ~\frac{\langle F(y^l),z^k-y^l\rangle }{\Vert F(y^l)\Vert }>0. \end{aligned} \end{aligned}$$

(3.9)

Hence, for all $j\in \{0,1,\ldots ,k\}$, we have

$$\begin{aligned} \textrm{dist}(z^k,H_j)= {\left\{ \begin{array}{ll} 0, & j\in I, \\ \frac{\langle F(y^j),z^k-y^j\rangle }{\Vert F(y^j)\Vert }>0, & j\in J. \end{array}\right. } \end{aligned}$$

(3.10)

By the definition of $i_k$ in (3.2), we know that $i_k\in \{0,1,\ldots ,k\}$ and

$$\begin{aligned} \frac{\langle {F(y^{i_k})},{z^k-y^{i_k}}\rangle }{\Vert {F(y^{i_k})}\Vert }\ge \frac{\langle {F(y^j)},{z^k-y^j}\rangle }{\Vert {F(y^j)}\Vert },~\forall j\in \{0,1,\ldots ,k\}. \end{aligned}$$

(3.11)

Combining (3.10) and (3.11), it follows from the definition of ${\widetilde{H}}_k$ in (3.3) that

$$\begin{aligned} 0\le \textrm{dist}(z^k,H_j)\le \textrm{dist}(z^k,{\widetilde{H}}_k),~\forall j\in \{0,1,\ldots ,k\} \end{aligned}$$

holds for all k. This completes the proof. $\square$

Lemma 3.3

Assume that Condition 3.1 holds. Let $H_k$, ${\widetilde{H}}_k$ and $T_k$ be the half-spaces generated by the Algorithm 3.1. Then, for all k, we have

$$\begin{aligned} S_D\subseteq C\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k\subseteq C\cap {{\widetilde{H}}_k}\subseteq T_k\cap {{\widetilde{H}}_k}. \end{aligned}$$

Proof

For any fixed $u\in S_D$, by the definition of $S_D$ in (1.4) and the fact $y^k\in C$, we have $\langle {F(y^k)},{u-y^k}\rangle \le 0.$ It follows from the definition of $H_k$, we deduce that $u\in H_k$ for all k, which means

$$\begin{aligned} u\in S_D\subseteq \bigcap _{k=0}^\infty H_k\subseteq {\widetilde{H}}_k. \end{aligned}$$

(3.12)

By the definition of $y^k$ and Lemma 2.1 (i), we have

$$\begin{aligned} \langle {x^k-\lambda _k F(x^k)-y^k},{y-y^k}\rangle \le 0,~\forall y\in C. \end{aligned}$$

Therefore, by the definition of $T_k$ in (3.1), we know that $C\subseteq T_k$ holds for all k. Hence, by the definition of $S_D$ and (3.12), we see that

$$\begin{aligned} S_D\subseteq C\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k\subseteq C\cap {{\widetilde{H}}_k}\subseteq T_k\cap {{\widetilde{H}}_k}. \end{aligned}$$

(3.13)

This completes the proof. $\square$

Lemma 3.4

Assume that Conditions 3.1 and 3.2 hold. Let $\{x^k\}, \{y^k\}, \{z^k\}$ be the sequences and $H_k$ be the half-space generated by Algorithm 3.1. Then, the following statements hold:

• (i) For any fixed $x\in C\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k$, we have

  $$\begin{aligned} \Vert z^k-x\Vert ^2\le \Vert x^k-x\Vert ^2-(1-\tau \frac{\lambda _k}{\lambda _{k+1}})(\Vert {x^k-y^k}\Vert ^2+\Vert y^k-z^k\Vert ^2). \end{aligned}$$

  (3.14)

• (ii) There exists $k_0\in {\mathbb {N}}^+$ such that $1-\tau {\lambda _k}/{\lambda _{k+1}}>0$ holds for all $k\ge k_0$.

• (iii) $\mathop {\lim }\limits _{k\rightarrow \infty }{\Vert x^k-y^k\Vert }=0,~\mathop {\lim }\limits _{k\rightarrow \infty }{\Vert y^k-z^k\Vert }=0~~\text{ and }~\mathop {\lim }\limits _{k\rightarrow \infty }{\Vert x^k-z^k\Vert }=0$.

Proof

• (i)   By Lemma 3.3, we know that $C\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k\ne \emptyset$. For any fixed $x\in C\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k\subseteq T_k\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k\subseteq T_k\cap {\widetilde{H}}_k$, by the definition of $z^{k}$ and Lemma 2.1 (ii), we have

  $$\begin{aligned} \Vert z^k-x\Vert ^2&\le ~\Vert x^k-\lambda _k F(y^k)-x\Vert ^2-\Vert x^k-\lambda _kF(y^k)-z^k\Vert ^2 \nonumber \\&= ~ \Vert x^k-x\Vert ^2-\Vert x^k-z^k\Vert ^2+2\lambda _k\langle {F(y^k)},{x-z^k}\rangle \nonumber \\&= ~ \Vert x^k-x\Vert ^2-\Vert x^k-z^k\Vert ^2+2\lambda _k\langle {F(y^k)},{x-y^k}\rangle +2\lambda _k\langle {F(y^k)},{y^k-z^k}\rangle \nonumber \\&\overset{(a)}{\le }\ ~ \Vert x^k-x\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2-2\langle {x^k-y^k},{y^k-z^k}\rangle \nonumber \\&\qquad + 2\lambda _k\langle {F(y^k)},{y^k-z^k}\rangle \\&= \Vert x^k-x\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2-2\langle {x^k-y^k-\lambda _kF(x^k)},{y^k-z^k}\rangle \nonumber \\&\qquad +2\lambda _k\langle {F(y^k)-F(x^k)},{y^k-z^k}\rangle \nonumber \\&\overset{(b)}{\le }\ ~ \Vert x^k-x\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2+2\lambda _k\langle {F(y^k)-F(x^k)},{y^k-z^k}\rangle \nonumber \\&\le \Vert x^k-x\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2+2\lambda _k\Vert F(y^k)-F(x^k)\Vert \Vert y^k-z^k\Vert , \nonumber \end{aligned}$$

  (3.15)

  where (a) holds from the facts that $\lambda _{k}>0$ for all k, $x\in H_k$ and the definition of $H_k$, and (b) uses the facts that $z^k\in T_k$ and the definition of $T_k$ in (3.1). In addition, we claim that

  $$\begin{aligned} \lambda _k\Vert F(y^k)-F(x^k)\Vert \le \tau \frac{\lambda _k}{\lambda _{k+1}}\Vert {x^k-y^k}\Vert . \end{aligned}$$

  (3.16)

  Indeed, if $\Vert F(x^k)-F(y^k)\Vert =0$, then (3.16) holds. Otherwise, by the definition of $\lambda _k$ in (3.4), we have

  $$\begin{aligned} \lambda _{k+1}=\textrm{min}\{\lambda _k+\varepsilon _k,~\tau \frac{\Vert {x^k-y^k}\Vert }{\Vert {F(x^k)-F(y^k)}\Vert }\}\le \tau \frac{\Vert {x^k-y^k}\Vert }{\Vert {F(x^k)-F(y^k)}\Vert }. \end{aligned}$$

  It implies that

  $$\begin{aligned} {\lambda _k}\Vert {F(x^k)-F(y^k)}\Vert \le \tau \frac{\lambda _k}{\lambda _{k+1}}\Vert {x^k-y^k}\Vert . \end{aligned}$$

  Therefore, we have (3.16) holds. Substituting (3.16) into (3.15), we have

  $$\begin{aligned} \begin{aligned} \Vert z^k-x\Vert ^2 \le&~ \Vert x^k-x\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2+2\tau \frac{\lambda _k}{\lambda _{k+1}}\Vert {x^k-y^k}\Vert \Vert y^k-z^k\Vert \\ \le&~ \Vert x^k-x\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2+\tau \frac{\lambda _k}{\lambda _{k+1}}(\Vert {x^k-y^k}\Vert ^2+\Vert y^k-z^k\Vert ^2)\\ \le&~ \Vert x^k-x\Vert ^2-(1-\tau \frac{\lambda _k}{\lambda _{k+1}})(\Vert {x^k-y^k}\Vert ^2+\Vert y^k-z^k\Vert ^2). \end{aligned} \end{aligned}$$

  (3.17)

• (ii)   By the facts that $\mathop {\lim }\limits _{k\rightarrow \infty }{\lambda _k}=\lambda >0$ and $\tau \in (0,1)$, we consider the limit

  $$\begin{aligned} \lim _{k\rightarrow \infty }(1-\tau \frac{\lambda _k}{\lambda _{k+1}})=1-\tau >0. \end{aligned}$$

  Thus, there exists $k_0\in {\mathbb {N}}^+$ such that $1-\tau {\lambda _k}/{\lambda _{k+1}}>0$ holds for all $k\ge k_0$.

• (iii)   By the definition of $x^{k+1}$ and the nonexpansive property of the projection, we obtain that

  $$\begin{aligned} \begin{aligned} \Vert x^{k+1}-x\Vert ^2 =&~\Vert \Pi _{{\widetilde{H}}_k}(z^k)-\Pi _{{\widetilde{H}}_k}(x)\Vert ^2\\ \le&~\Vert z^k-x\Vert ^2\\ \overset{(a)}{\le }\&~ \Vert x^k-x\Vert ^2-(1-\tau \frac{\lambda _k}{\lambda _{k+1}})(\Vert {x^k-y^k}\Vert ^2+\Vert y^k-z^k\Vert ^2), \end{aligned} \end{aligned}$$

  (3.18)

  where (a) holds from (3.17). Combine the fact that $1-\tau {\lambda _k}/{\lambda _{k+1}}>0$ for all $k\ge k_0$, we deduce that

  $$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x^k-y^k\Vert =0~~\text{ and }~\lim _{k\rightarrow \infty }\Vert y^k-z^k\Vert =0. \end{aligned}$$

  (3.19)

  Moreover, together with the fact that $\Vert x^k-z^k\Vert \le \Vert x^k-y^k\Vert +\Vert y^k-z^k\Vert$, we have

  $$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x^k-z^k\Vert =0. \end{aligned}$$

  (3.20)

This completes the proof. $\square$

Next, we give the global convergence analysis of Algorithm 3.1.

Theorem 3.1

Assume that Conditions 3.1 and 3.2 hold. Let $\{x^k\}, \{y^k\}, \{z^k\}$ be the sequences and $T_{k}$, $H_k$, ${\widetilde{H}}_k$ be the half-spaces generated by Algorithm 3.1. Then, the infinite sequence $\{x^k\}$ converges globally to a solution of $\text{ VI }(F,C)$.

Proof

For any fixed $x\in C\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k\subseteq {{\widetilde{H}}_k}$, by the definition of $x^{k+1}$ and Lemma 2.1 (ii), for all $k\ge k_0$, we have

$$\begin{aligned} \begin{aligned} \Vert {x^{k+1}-x}\Vert ^2&\le ~\Vert {z^k-x}\Vert ^2-\Vert {x^{k+1}-z^k}\Vert ^2\\&= ~\Vert {z^k-x}\Vert ^2-\textrm{dist}^2(z^k,{\widetilde{H}}_k)\\&\overset{(a)}{\le } \Vert x^k-x\Vert ^2-(1-\tau \frac{\lambda _k}{\lambda _{k+1}})(\Vert {x^k-y^k}\Vert ^2+\Vert y^k-z^k\Vert ^2)-\textrm{dist}^2(z^k,{\widetilde{H}}_k)\\&\overset{(b)}{\le }\ ~ \Vert x^k-x\Vert ^2-\textrm{dist}^2(z^k,{\widetilde{H}}_k), \end{aligned} \end{aligned}$$

(3.21)

where (a) follows from Lemma 3.4 (i) and (b) follows from Lemma 3.4 (ii). From the above inequality, we deduce that the sequence $\{\Vert x^k-x\Vert \}$ converges and

$$\begin{aligned} \lim _{k\rightarrow \infty }\textrm{dist}(z^k,{\widetilde{H}}_k)=0. \end{aligned}$$

(3.22)

Hence, it implies that the sequence $\{x^k\}$ is bounded. Then, there exists a subsequence $\{x^{k_l}\}$ of $\{x^k\}$ and a vector ${\overline{x}}\in {\mathbb {R}}^n$ such that $\{x^{k_l}\}$ converges to ${\overline{x}}$. By the facts that $\mathop {\lim }\limits _{k\rightarrow \infty }{\Vert x^k-y^k\Vert }=0$ and $\mathop {\lim }\limits _{k\rightarrow \infty }{\Vert x^k-z^k\Vert }=0$ in Lemma 3.4 (iii), we obtain that

$$\begin{aligned} \mathop {\lim }\limits _{{l}\rightarrow \infty }y^{k_l}={\overline{x}}~~\text{ and }~~\mathop {\lim }\limits _{{l}\rightarrow \infty }z^{k_l}={\overline{x}}. \end{aligned}$$

Moreover, by the definition of $y^k$, we know $y^{k_l}\in C$, combine the fact that C is a closed set, we have ${\overline{x}}\in C$.

Now, we prove that ${\overline{x}}\in \mathop {\bigcap }\limits _{k=0}^\infty H_k$. By the definition of ${\widetilde{H}}_k$ and Lemma 3.2, we know that

$$\begin{aligned} 0\le \textrm{dist}(z^k,H_j)\le \textrm{dist}(z^k,{\widetilde{H}}_k),~\forall j\in \{0,1,\ldots ,k\}. \end{aligned}$$

(3.23)

Taking the limit as $k\rightarrow \infty$ in (3.23) and combining (3.22), for any fixed nonnegative integer j, we have

$$\begin{aligned} \lim _{k\rightarrow \infty }\textrm{dist}(z^k,H_j)=0. \end{aligned}$$

Hence,

$$\begin{aligned} \lim _{l\rightarrow \infty }\textrm{dist}(z^{k_l},H_j)=0. \end{aligned}$$

Let $v^{k_l}:=\Pi _{H_j}(z^{k_l})$, it is clear that

$$\begin{aligned} \lim _{l\rightarrow \infty }\Vert v^{k_l}-z^{k_l}\Vert =0. \end{aligned}$$

By the fact that $\mathop {\lim }\limits _{l\rightarrow \infty }z^{k_l}={\overline{x}}$, we have $\mathop {\lim }\limits _{l\rightarrow \infty }v^{k_l}={\overline{x}}$. From the facts that $\{v^{k_l}\}\subset H_j$ and $H_j$ is closed set, we deduce that ${\overline{x}}\in H_j$ holds. By the arbitrariness of j, we obtain that ${\overline{x}}\in \mathop {\bigcap }\limits _{k=0}^\infty H_k$.

Next, we prove that ${\overline{x}}\in S$. According to $y^{k_l}=\Pi _C(x^{k_l}-\lambda _{k_l}F(x^{k_l}))$ and Lemma 2.1 (i), we obtain that

$$\begin{aligned} \langle {y^{k_l}-x^{k_l}+\lambda _{k_l}F(x^{k_l})},{y-y^{k_l}}\rangle \ge ~0,~\forall y\in C, \end{aligned}$$

which implies that

$$\begin{aligned} \frac{\langle {y^{k_l}-x^{k_l}},{y-y^{k_l}}\rangle }{\lambda _{k_l}}+\langle {F(x^{k_l})},{y-y^{k_l}}\rangle \ge 0,~\forall y\in C. \end{aligned}$$

(3.24)

Taking the limit as ${l}\rightarrow \infty$ in (3.24), combine with the facts that $\lim \limits _{{l}\rightarrow \infty }\lambda _{k_l}=\lambda >0$ (see Lemma 3.1), $\lim \limits _{{l}\rightarrow \infty }\Vert {x^{k_l}-y^{k_l}}\Vert =0$ (see Lemma 3.4 (iii)), the continuity of the mapping F and $\lim \limits _{{l}\rightarrow \infty }y^{k_l}={\overline{x}}$, we obtain that

$$\begin{aligned} \langle {F({\overline{x}})},{y-{\overline{x}}}\rangle \ge 0,~\forall y\in C, \end{aligned}$$

which implies ${\overline{x}}\in S$.

Finally, we prove that the entire sequence $\{x^k\}$ converges globally to ${\overline{x}}$. Since the fact

$$\begin{aligned} {\overline{x}}\in S\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k\subseteq C\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k. \end{aligned}$$

By replacing x by ${\overline{x}}$ in (3.21), we see that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x^k-{\overline{x}}\Vert =\lim _{{l}\rightarrow \infty }\Vert x^{k_l}-{\overline{x}}\Vert =0. \end{aligned}$$

This completes the proof. $\square$

Remark 3.3

According to Theorem 3.1, we know that the global convergence of Algorithm 3.1 is proved only need under conditions that the mapping F is Lipschitz continuous on ${\mathbb {R}}^n$ and $S_D\ne \emptyset$. This removes the condition that $S\backslash S_D$ is a finite set in [16].

Before ending this subsection, we give the computational complexity analysis of Algorithm 3.1.

Theorem 3.2

Assume that Conditions 3.1 and 3.2 hold. For any $k\ge 0$, let $x^k$, $y^k$, $z^k$, $T_{k}$, $H_k$ and ${\widetilde{H}}_k$ be generated by Algorithm 3.1. Denote ${\bar{\lambda }}=\lambda _{0}+{\bar{\varepsilon }}$, where ${\bar{\varepsilon }}=\mathop {\sum }\limits _{k=0}^\infty {\varepsilon _k}< +\infty$ and $\{\varepsilon _k\}$ is selected in Algorithm 3.1. If ${\bar{\lambda }}\in (0,\frac{1}{L})$ (where L is the Lipschitz constant of F), then for any $x^{*}\in S_{D}$ and for any $k\ge 0$,

$$\begin{aligned} \min \limits _{0\le i\le k}\Vert x^{i}-y^{i}\Vert ^{2}\le \frac{1}{k} \frac{\Vert x^{0}-x^{*}\Vert ^{2}}{1-{\bar{\lambda }}L}. \end{aligned}$$

Proof

By the definition of $\lambda _{k+1}$ in (3.4) and mathematical induction, we deduce that the sequence $\{\lambda _{k}\}$ has upper bound ${\bar{\lambda }}=\lambda _{0}+{\bar{\varepsilon }}$. Then, we know that

$$\begin{aligned} \lambda _{k}\le {\bar{\lambda }},~\forall k\ge 0. \end{aligned}$$

(3.25)

For any fixed $x^{*}\in S_{D}$, combine Lemma 3.3, we have $x^{*}\in T_{k}\cap {{\widetilde{H}}_k}\subseteq T_{k}$. By the definition of $z^{k}$ and Lemma 2.1 (ii), for any $k\ge 0$, we have

$$\begin{aligned} \Vert z^k-x^{*}\Vert ^2&\le ~\Vert x^k-\lambda _k F(y^k)-x^{*}\Vert ^2-\Vert x^k-\lambda _kF(y^k)-z^k\Vert ^2 \nonumber \\&\overset{(a)}{\le }\ ~ \Vert x^k-x^{*}\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2+2\lambda _k\Vert F(y^k)-F(x^k)\Vert \Vert y^k-z^k\Vert \nonumber \\&\overset{(b)}{\le }\ ~ \Vert x^k-x^{*}\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2+2{\bar{\lambda }}\Vert F(y^k)-F(x^k)\Vert \Vert y^k-z^k\Vert \nonumber \\&\le ~ \Vert x^k-x^{*}\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2+2{\bar{\lambda }}L\Vert y^k-x^k\Vert \Vert y^k-z^k\Vert \nonumber \\&\le ~ \Vert x^k-x^{*}\Vert ^2-(1-{\bar{\lambda }}L)(\Vert x^k-y^k\Vert ^2+\Vert y^k-z^k\Vert ^2), \end{aligned}$$

(3.26)

where (a) follows from (3.15) and (b) follows from (3.25).

By the fact $x^{*}\in T_{k}\cap {\widetilde{H}}_{k}\subseteq {\widetilde{H}}_{k}$, combine the definition of $x^{k+1}$ and the nonexpansive property of the projection, for all $k\ge 0$, we deduce that

$$\begin{aligned} \Vert x^{k+1}-x^{*}\Vert ^2&= ~\Vert \Pi _{{\widetilde{H}}_k}(z^k)-\Pi _{{\widetilde{H}}_k}(x^{*})\Vert ^2 \\&\le ~\Vert z^k-x^{*}\Vert ^2 \\&\overset{(a)}{\le }\ ~ \Vert x^k-x^{*}\Vert ^2-(1-{\bar{\lambda }}L)(\Vert {x^k-y^k}\Vert ^2+\Vert y^k-z^k\Vert ^2) \\&\overset{(b)}{\le }\ ~ \Vert x^k-x^{*}\Vert ^2-(1-{\bar{\lambda }}L)\Vert {x^k-y^k}\Vert ^2, \end{aligned}$$

where (a) follows from (3.26) and (b) follows from the fact ${\bar{\lambda }}\in (0,\frac{1}{L})$. Then, rearranging the above formula, we have

$$\begin{aligned} \Vert {x^k-y^k}\Vert ^2\le \frac{\Vert x^k-x^{*}\Vert ^2-\Vert x^{k+1}-x^{*}\Vert ^2}{1-{\bar{\lambda }}L},~ \forall k\ge 0. \end{aligned}$$

Summing the above display on both sides from $i = 0$ to k, we obtain that

$$\begin{aligned} \mathop {\sum }\limits _{i=0}^{k}\Vert {x^i-y^i}\Vert ^2 \le \frac{\Vert x^0-x^{*}\Vert ^2-\Vert x^{k+1}-x^{*}\Vert ^2}{1-{\bar{\lambda }}L} \le \frac{\Vert x^0-x^{*}\Vert ^2}{1-{\bar{\lambda }}L}. \end{aligned}$$

Then, we deduce that

$$\begin{aligned} \min \limits _{0\le i\le k}\Vert x^{i}-y^{i}\Vert ^{2}\le \frac{1}{k}\mathop {\sum }\limits _{i=0}^{k}\Vert {x^i-y^i}\Vert ^2 \le \frac{1}{k}\frac{\Vert x^0-x^{*}\Vert ^2}{1-{\bar{\lambda }}L}. \end{aligned}$$

This completes the proof. $\square$

3.2 ISEGA for nonmonotone VI(F,C) with continuous

In this subsection, in order to further weaken the Lipschitz continuity of the mapping F, we introduce a line search method to search for the step-size and propose an improved subgradient extragradient algorithm with Armijo line search ($\text{ ISEGA }$). To obtain the global convergence of $\text{ ISEGA }$, we assume the following condition holds:

Condition 3.3

The mapping $F:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ is continuous.

Now, we give the iterative format of $\text{ ISEGA }$ as follows:

Algorithm 3.2

Step 1.:

Let $x^0\in {\mathbb {R}}^n$ be chosen arbitrarily. Choose parameters $\eta ,\sigma \in (0,1)$ and $\mu >0$. Set $k:=0$.

Step 2.:

Given the current iteration point $x^k$, compute

$$\begin{aligned} y^k=\Pi _C(x^k-\lambda _kF(x^k)), \end{aligned}$$

where $\lambda _k:=\mu {\eta }^{m_k}$ and $m_k$ is the smallest nonnegative integer m satisfies

$$\begin{aligned} \mu \eta ^{m}\Vert F(x^k)-F(\Pi _C(x^k-\mu \eta ^{m}F(x^k)))\Vert \le \sigma \Vert x^k-\Pi _C(x^k-\mu \eta ^{m}F(x^k))\Vert .\nonumber \\ \end{aligned}$$

(3.27)

If $x^k=y^k$ or $F(y^k)=0$, then stop and $y^k$ is a solution of $\text{ VI }(F,C)$. Otherwise, go to Step 3.

Step 3.:

Compute

$$\begin{aligned} z^k=\Pi _{T_k}(x^k-\lambda _k F(y^k)), \end{aligned}$$

where

$$\begin{aligned} T_k:=\{x\in {\mathbb {R}}^n:\langle {x^k-y^k-\lambda _k F(x^k)},{x-y^k}\rangle \le 0\}. \end{aligned}$$

(3.28)

Step 4.:

Let $H_k:=\{x\in {\mathbb {R}}^n:\langle {F(y^k)},{x-y^k}\rangle \le 0\}$ and choose

$$\begin{aligned} i_k:=\mathrm{arg\max _{0\le j\le k}}\frac{\langle {F(y^j)},{z^k-y^j}\rangle }{\Vert {F(y^j)}\Vert }. \end{aligned}$$

(3.29)

Compute

$$\begin{aligned} x^{k+1}=\Pi _{{\widetilde{H}}_k}(z^k)~\text {with}~{\widetilde{H}}_k:=H_{i_k}. \end{aligned}$$

(3.30)

Let $k:=k+1$ and go to Step 2.

In the following lemma, we show that the Armijo line search rule (3.27) in Algorithm 3.2 is well defined.

Lemma 3.5

Assume that Condition 3.3 holds. Let $x^k$ be generated at the beginning of the k-th iteration of Algorithm 3.2 for any $k\ge 0$. Then, there exists a nonnegative integer m such that (3.27) holds.

Proof

If $x^k\in S$, then $x^k=\Pi _C(x^k-\mu F(x^k))$. Hence, (3.27) holds with $m=0$.

If $x^k\notin S$, suppose to the contrary that for all m, we have

$$\begin{aligned} \mu \eta ^{m}\Vert F(x^k)-F(\Pi _C(x^k-\mu \eta ^{m}F(x^k)))\Vert >\sigma \Vert x^k-\Pi _C(x^k-\mu \eta ^{m}F(x^k))\Vert .\nonumber \\ \end{aligned}$$

(3.31)

Then,

$$\begin{aligned} \Vert F(x^k)-F(\Pi _C(x^k-\mu \eta ^{m}F(x^k)))\Vert >\sigma \frac{\Vert x^k-\Pi _C(x^k-\mu \eta ^{m}F(x^k))\Vert }{\mu \eta ^{m}}.\nonumber \\ \end{aligned}$$

(3.32)

Now, we consider the following two possibilities of $x^k$:

i)  If $x^k\in C$, by the continuity of the metric projection $\Pi _C$, we have

$$\begin{aligned} \lim _{m\rightarrow \infty }\Vert {x^k-\Pi _C(x^k-\mu \eta ^{m}F(x^k))}\Vert =0. \end{aligned}$$

(3.33)

The continuity of the mapping F implies that

$$\begin{aligned} \lim _{m\rightarrow \infty }\Vert {F(x^k)-F(\Pi _C(x^k-\mu \eta ^{m}F(x^k)))}\Vert =0. \end{aligned}$$

Combining this with (3.32), we have

$$\begin{aligned} \lim _{m\rightarrow \infty }\frac{\Vert x^k-\Pi _C(x^k-\mu \eta ^{m}F(x^k))\Vert }{\mu \eta ^m}=0. \end{aligned}$$

(3.34)

Let $y_m^k:=\Pi _C(x^k-\mu \eta ^mF(x^k))$. By the Lemma 2.1 (i), we deduce that

$$\begin{aligned} \langle y_m^k-x^k+\mu \eta ^mF(x^k),y-y_m^k\rangle \ge 0,~\forall y\in C, \end{aligned}$$

or equivalently,

$$\begin{aligned} \langle \frac{y_m^k-x^k}{\mu \eta ^m},y-y_m^k\rangle +\langle F(x^k),y-y_m^k\rangle \ge 0,~\forall y\in C. \end{aligned}$$

(3.35)

Taking the limit as $m\rightarrow \infty$ in (3.35), combining (3.33) with (3.34), we obtain that

$$\begin{aligned} \langle F(x^k),y-x^k\rangle \ge 0,~\forall y\in C, \end{aligned}$$

which implies that it contradicts $x^k\notin S$.

ii)  If $x^k\notin C$, then

$$\begin{aligned} \lim _{m\rightarrow \infty }{\Vert x^k-\Pi _C(x^k-\mu \eta ^{m}F(x^k))\Vert }=\Vert x^k-\Pi _C(x^k)\Vert >0 \end{aligned}$$

(3.36)

and

$$\begin{aligned} \lim _{m\rightarrow \infty }\mu \eta ^m\Vert {F(x^k)-F(\Pi _C(x^k-\mu \eta ^{m}F(x^k)))}\Vert =0. \end{aligned}$$

(3.37)

Combining (3.31), (3.36) and (3.37), we obtain a contradiction. Therefore, there exists a nonnegative integer m such that (3.27) holds. This completes the proof. $\square$

Lemma 3.6

Assume that Conditions 3.1 and 3.3 hold. Let $\{x^k\},~\{y^k\}$, $\{z^k\}$ be the sequences and $T_{k}$, $H_{k}$, ${\widetilde{H}}_k$ be the half-spaces generated by Algorithm 3.2. Then, the following statements hold:

• (i) For any fixed $x\in C\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k$, we have

  $$\begin{aligned} \Vert {z^k-x}\Vert ^2\le \Vert x^k-x\Vert ^2-(1-\sigma )(\Vert x^k-y^k\Vert ^2+\Vert y^k-z^k\Vert ^2),~\forall k\ge 0.\nonumber \\ \end{aligned}$$

  (3.38)

• (ii) $\mathop {\lim }\limits _{k\rightarrow \infty }{\Vert x^k-y^k\Vert }=0,~\mathop {\lim }\limits _{k\rightarrow \infty }{\Vert y^k-z^k\Vert }=0~~and~ \mathop {\lim }\limits _{k\rightarrow \infty }{\Vert x^k-z^k\Vert }=0$.

Proof

• (i)   For any fixed $x\in C\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k\subseteq C\cap {{\widetilde{H}}_k}\subseteq T_k\cap {{\widetilde{H}}_k}$, by the definition of $z^{k}$ and Lemma 2.1 (ii), we have

  $$\begin{aligned} \Vert z^k-x\Vert ^2&\le ~\Vert x^k-\lambda _k F(y^k)-x\Vert ^2-\Vert x^k-\lambda _kF(y^k)-z^k\Vert ^2 \nonumber \\&= ~ \Vert x^k-x\Vert ^2-\Vert x^k-z^k\Vert ^2+2\lambda _k\langle {F(y^k)},{x-y^k}\rangle +2\lambda _k\langle {F(y^k)},{y^k-z^k}\rangle \nonumber \\&\le ~ \Vert x^k-x\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2-2\langle {x^k-y^k},{y^k-z^k}\rangle \nonumber \\&\quad ~ +2\lambda _k\langle {F(y^k)},{y^k-z^k}\rangle \nonumber \\&= ~ \Vert x^k-x\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2-2\langle {x^k-y^k-\lambda _kF(x^k)},{y^k-z^k}\rangle \nonumber \\&\quad ~ +2\lambda _k\langle {F(y^k)-F(x^k)},{y^k-z^k}\rangle \nonumber \\&\overset{(a)}{\le }~ \Vert x^k-x\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2+2\lambda _k\langle {F(y^k)-F(x^k)},{y^k-z^k}\rangle \nonumber \\&\overset{(b)}{\le }\ ~ \Vert x^k-x\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2+2\lambda _k\Vert F(y^k)-F(x^k)\Vert \Vert y^k-z^k\Vert \nonumber \\&\overset{(c)}{\le }\ ~ \Vert x^k-x\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2+2\sigma \Vert y^k-x^k\Vert \Vert y^k-z^k\Vert \nonumber \\&\le ~ \Vert x^k-x\Vert ^2-\Vert x^k-y^k\Vert ^2-\Vert y^k-z^k\Vert ^2+\sigma (\Vert x^k-y^k\Vert ^2+\Vert y^k-z^k\Vert ^2) \nonumber \\&= ~ \Vert x^k-x\Vert ^2-(1-\sigma )(\Vert x^k-y^k\Vert ^2+\Vert y^k-z^k\Vert ^2), \end{aligned}$$

  (3.39)

  where (a) follows from the fact $z^k\in T_k$ and the definition of $T_k$ in (3.28), (b) follows from the fact that $\lambda _k>0$ for all k and Cauchy–Schwarz inequality, and (c) follows from (3.27).

• (ii)   By the definition of $x^{k+1}$, the nonexpansive property of the projection and (3.39), we obtain that

  $$\begin{aligned} \begin{aligned} \Vert x^{k+1}-x\Vert ^2 =&~\Vert \Pi _{{\widetilde{H}}_k}(z^k)-\Pi _{{\widetilde{H}}_k}(x)\Vert ^2\\ \le&~\Vert z^k-x\Vert ^2\\ \le&~ \Vert x^k-x\Vert ^2-(1-\sigma )(\Vert x^k-y^k\Vert ^2+\Vert y^k-z^k\Vert ^2). \end{aligned} \end{aligned}$$

  (3.40)

  Since the fact $\sigma \in (0,1)$, we deduce that

  $$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x^k-y^k\Vert =0~~\text{ and }~~\lim _{k\rightarrow \infty }\Vert y^k-z^k\Vert =0. \end{aligned}$$

  (3.41)

  Furthermore, together with the fact $\Vert x^k-z^k\Vert \le \Vert x^k-y^k\Vert +\Vert y^k-z^k\Vert$, we have

  $$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x^k-z^k\Vert =0. \end{aligned}$$

This completes the proof. $\square$

In the following, we give the global convergence analysis of Algorithm 3.2.

Theorem 3.3

Assume that Conditions 3.1 and 3.3 hold. Let $\{x^k\},~\{y^k\}$, $\{z^k\}$ be the sequences and $T_{k}$, $H_{k}$, ${\widetilde{H}}_k$ be the half-spaces generated by Algorithm 3.2. Then, the infinite sequence $\{x^k\}$ converges globally to a solution of $\text{ VI }(F,C)$.

Proof

For any fixed $x\in C\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k\subseteq {{\widetilde{H}}_k}$, by the definition of $x^{k+1}$ and Lemma 2.1 (ii), we have

$$\begin{aligned} \begin{aligned} \Vert {x^{k+1}-x}\Vert ^2&\le ~\Vert {z^k-x}\Vert ^2-\Vert {x^{k+1}-z^k}\Vert ^2\\&= ~\Vert {z^k-x}\Vert ^2-\textrm{dist}^2(z^k,{\widetilde{H}}_k)\\&\overset{(a)}{\le }\ ~\Vert x^k-x\Vert ^2-(1-\sigma )(\Vert x^k-y^k\Vert ^2+\Vert y^k-z^k\Vert ^2)-\textrm{dist}^2(z^k,{\widetilde{H}}_k)\\&\overset{(b)}{\le }\ ~ \Vert x^k-x\Vert ^2-\textrm{dist}^2(z^k,{\widetilde{H}}_k), \end{aligned} \end{aligned}$$

(3.42)

where (a) follows from Lemma 3.6 (i), (b) follows from $\sigma \in (0,1)$. From the above inequality, we deduce that the sequence $\{\Vert x^k-x\Vert \}$ converges and

$$\begin{aligned} \lim _{k\rightarrow \infty }\textrm{dist}(z^k,{\widetilde{H}}_k)=0. \end{aligned}$$

(3.43)

Hence, it implies that the sequence $\{x^k\}$ is bounded. Then, there exists a subsequence $\{x^{k_n}\}$ of $\{x^k\}$ and ${\widetilde{x}}\in {\mathbb {R}}^n$ such that the subsequence $\{x^{k_n}\}$ converges to ${\widetilde{x}}$. By the facts that $\lim \limits _{k\rightarrow \infty }{\Vert x^k-y^k\Vert }=0$ and $\lim \limits _{k\rightarrow \infty }{\Vert x^k-z^k\Vert }=0$ in Lemma 3.6 (ii), we know that

$$\begin{aligned} \mathop {\lim }\limits _{{n}\rightarrow \infty }y^{k_n}={\widetilde{x}}~~\text{ and }~\mathop {\lim }\limits _{{n}\rightarrow \infty }z^{k_n}={\widetilde{x}}. \end{aligned}$$

Moreover, by the definition of $y^k$, we know $y^{k_n}\in C$, combine the fact that C is a closed set, we have ${\widetilde{x}}\in C$.

Now, we prove that ${\widetilde{x}}\in \mathop {\bigcap }\limits _{k=0}^\infty H_k$. We omit this part of the proof and refer to the corresponding part of the proof in Theorem 3.1.

Next, we prove that ${\widetilde{x}}\in S$. According to $y^{k_n}=\Pi _C(x^{k_n}-\lambda _{k_n}F(x^{k_n}))$ and Lemma 2.1 (i), we have

$$\begin{aligned} \langle {y^{k_n}-x^{k_n}+\lambda _{k_n}F(x^{k_n})},{y-y^{k_n}}\rangle \ge 0,~\forall y\in C, \end{aligned}$$

or equivalently,

$$\begin{aligned} \frac{\langle {y^{k_n}-x^{k_n}},{y-y^{k_n}}\rangle }{\lambda _{k_n}}+\langle {F(x^{k_n})},{y-y^{k_n}}\rangle \ge 0,~\forall y\in C. \end{aligned}$$

(3.44)

We consider the following two cases:

i)  If $\lim \limits _{n\rightarrow \infty }{\lambda _{k_n}}>0$. Taking the limit as $n\rightarrow \infty$ in (3.44), by the fact $\mathop {\lim }\limits _{n\rightarrow \infty }\Vert x^{k_n}-y^{k_n}\Vert =0$ in Lemma 3.6 (ii), the continuity of the mapping F and $\mathop {\lim }\limits _{n\rightarrow \infty }y^{k_n}={\widetilde{x}}$, we obtain that

$$\begin{aligned} \langle {F({\widetilde{x}})},{y-{\widetilde{x}}}\rangle \ge 0,~\forall y\in C, \end{aligned}$$

which means ${\widetilde{x}}\in S$.

ii)  If $\lim \limits _{n\rightarrow \infty }{\lambda _{k_n}}=0$. Assume $w^{k_n}:=\Pi _C(x^{k_n}-\lambda _{k_n}{\eta }^{-1}F(x^{k_n})).$ By the definition of $\lambda _k$, we know that $\lambda _{k_n}>0$ for all n. Hence, $\lambda _{k_n}{\eta }^{-1}>\lambda _{k_n}$ (since $\eta \in (0,1)$). Applying Lemma 2.1 (iii), we obtain that

$$\begin{aligned} \Vert x^{k_n}-w^{k_n}\Vert \le \frac{1}{\eta }\Vert x^{k_n}-y^{k_n}\Vert . \end{aligned}$$

By the fact that $\lim \limits _{n\rightarrow \infty }\Vert x^{k_n}-y^{k_n}\Vert =0$ in Lemma 3.6 (ii), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x^{k_n}-w^{k_n}\Vert =0, \end{aligned}$$

which implies that $\lim \limits _{n\rightarrow \infty }{w^{k_n}}={\widetilde{x}}$. Since the mapping F is continuous, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert F(x^{k_n})-F(w^{k_n})\Vert =0. \end{aligned}$$

(3.45)

By the definition of $\lambda _k$ in Step 2 of Algorithm 3.2 and (3.27), we have

$$\begin{aligned} \lambda _{k_n}{\eta }^{-1}\Vert F(x^{k_n})-F(\Pi _C(x^{k_n}-\lambda _{k_n}{\eta }^{-1}F(x^{k_n})))\Vert >\sigma \Vert x^{k_n}-\Pi _C(x^{k_n}-\lambda _{k_n}{\eta }^{-1}F(x^{k_n}))\Vert . \end{aligned}$$

Reformulating the above inequality, we obtain that

$$\begin{aligned} \frac{1}{\sigma }\Vert F(x^{k_n})-F(w^{k_n})\Vert >\frac{\Vert x^{k_n}-w^{k_n}\Vert }{\lambda _{k_n}{\eta }^{-1}}. \end{aligned}$$

(3.46)

Combining (3.45) and (3.46), we deduce that

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{\Vert x^{k_n}-w^{k_n}\Vert }{\lambda _{k_n}{\eta }^{-1}}=0. \end{aligned}$$

(3.47)

Furthermore, by the definition of $w^{k_n}$ and Lemma 2.1 (i), we have

$$\begin{aligned} \langle {w^{k_n}-x^{k_n}+\lambda _{k_n}{\eta }^{-1}F(x^{k_n})},{y-w^{k_n}}\rangle \ge 0,~\forall y\in C. \end{aligned}$$

The above inequality can be rewritten as

$$\begin{aligned} \frac{\langle {w^{k_n}-x^{k_n}},{y-w^{k_n}}\rangle }{\lambda _{k_n}{\eta }^{-1}}+\langle {F(x^{k_n})},{y-w^{k_n}}\rangle \ge 0,~\forall y\in C. \end{aligned}$$

(3.48)

Taking the limit as $n\rightarrow \infty$ in (3.48), according to (3.47), the mapping F is continuous and $\mathop {\lim }\limits _{n\rightarrow \infty }w^{k_n}={\widetilde{x}}$, we have

$$\begin{aligned} \langle {F({\widetilde{x}})},{y-{\widetilde{x}}}\rangle \ge 0,~\forall y\in C, \end{aligned}$$

which means ${\widetilde{x}}\in S$.

Finally, we prove that the entire sequence $\{x^k\}$ converges globally to ${\widetilde{x}}$. Since the fact that

$$\begin{aligned} {\widetilde{x}}\in S\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k\subseteq C\cap \mathop {\bigcap }\limits _{k=0}^\infty H_k. \end{aligned}$$

By replacing x by ${\widetilde{x}}$ in (3.42), we have

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x^k-{\widetilde{x}}\Vert =\lim _{{n}\rightarrow \infty }\Vert x^{k_n}-{\widetilde{x}}\Vert =0. \end{aligned}$$

This completes the proof. $\square$

Before ending this subsection, we give the computational complexity analysis of Algorithm 3.2.

Theorem 3.4

Assume that Conditions 3.1 and 3.3 hold. For any $k\ge 0$, let $x^k$, $y^k$, $z^k$ $T_{k}$, $H_k$ and${\widetilde{H}}_k$ be generated by Algorithm 3.2. If $\sigma \in (0,1)$, then, for any $x^{*}\in S_{D}$ and $k\ge 0$, we have

$$\begin{aligned} \min \limits _{0\le i\le k}\Vert x^{i}-y^{i}\Vert ^{2}\le \frac{1}{k} \frac{\Vert x^{0}-x^{*}\Vert ^{2}}{1-\sigma }. \end{aligned}$$

Proof

For any fixed $x^{*}\in S_{D}$, combine Lemma 3.3, we have $x^{*}\in T_{k}\cap {{\widetilde{H}}_k}\subseteq {\widetilde{H}}_k$. By the definition of $x^{k+1}$ and the nonexpansive property of the projection, for any $k\ge 0$, we have

$$\begin{aligned} \Vert x^{k+1}-x^{*}\Vert ^2&= ~\Vert \Pi _{{\widetilde{H}}_k}(z^k)-\Pi _{{\widetilde{H}}_k}(x^{*})\Vert ^2 \nonumber \\&\le ~\Vert z^k-x^{*}\Vert ^2 \nonumber \\&\overset{(a)}{\le }~ \Vert x^k-x^{*}\Vert ^2-(1-\sigma )(\Vert x^k-y^k\Vert ^2+\Vert y^k-z^k\Vert ^2) \\&\overset{(b)}{\le }~ \Vert x^k-x^{*}\Vert ^2-(1-\sigma )\Vert x^k-y^k\Vert ^2, \nonumber \end{aligned}$$

where (a) follows from Lemma 3.6 (i) and (b) follows from $\sigma \in (0,1)$. Then, rearranging the above formula, we deduce that

$$\begin{aligned} \Vert x^k-y^k\Vert ^2\le \frac{\Vert x^k-x^{*}\Vert ^2-\Vert x^{k+1}-x^{*}\Vert ^2}{1-\sigma },~\forall k\ge 0. \end{aligned}$$

By adding up the two sides of the above inequality, we obtain that

$$\begin{aligned} \mathop {\sum }\limits _{i=0}^{k}\Vert {x^i-y^i}\Vert ^2 \le \frac{\Vert x^0-x^{*}\Vert ^2-\Vert x^{k+1}-x^{*}\Vert ^2}{1-\sigma } \le \frac{\Vert x^0-x^{*}\Vert ^2}{1-\sigma }. \end{aligned}$$

Then, we deduce that

$$\begin{aligned} \min \limits _{0\le i\le k}\Vert x^{i}-y^{i}\Vert ^{2}\le \frac{1}{k}\mathop {\sum }\limits _{i=0}^{k}\Vert {x^i-y^i}\Vert ^2 \le \frac{1}{k}\frac{\Vert x^0-x^{*}\Vert ^2}{1-\sigma }. \end{aligned}$$

This completes the proof. $\square$

4 Numerical experiments

In this section, the effectiveness of our Algorithm 3.1 (Algorithm 3.1 for short) and Algorithm 3.2 (Algorithm 3.2 for short) will be illustrated through numerical experiments and compared with the existing algorithms. All programs are written in Matlab R2017a and executed on an Intel(R) Core(TM) i5-5350U CPU @ 1.80GHz 1.80GHz.

Let $\Vert {x^k-y^k}\Vert \le Err$ be the stopping criterion of these algorithms. We report that Iter. represents the number of iterations, np represents the number of projections onto the feasible set C and CPU(s) represents the time the program runs (in seconds).

Example 4.1

Considering the following variational inequality problem $\text{ VI }(F,C)$ with

$$\begin{aligned} F:(x_1,x_2,\ldots ,x_n)\mapsto (\sin x_{1},\sin x_{2},\ldots ,\sin x_{n})~~\text{ and }~~C=[0,\pi ]^{n}. \end{aligned}$$

One can see that the mapping F is not quasimonotone on the feasible set C. Indeed, taking ${\bar{x}}=(\frac{\pi }{6},\pi ,\pi ,\ldots ,\pi )$ and ${\bar{y}}=(\frac{\pi }{4},\frac{5\pi }{6},\pi ,\ldots ,\pi )$, we have

$$\begin{aligned} \langle F({\bar{x}}),{\bar{y}}-{\bar{x}}\rangle =\frac{\pi }{24}>0~~\text{ and }~~\langle F({\bar{y}}),{\bar{y}}-{\bar{x}}\rangle =\frac{\sqrt{2}-2}{24}\pi <0. \end{aligned}$$

In addition, it is clear that the mapping F is Lipschitz continuous on ${\mathbb {R}}^{n}$. Moreover, we have

$$\begin{aligned} S=\{(x_1,x_2,\ldots ,x_n):~x_i\in \{0,\pi \}\}~~\text{ and }~~S_D=\{(0,0,\ldots ,0)\}. \end{aligned}$$

Let $x^0:=(\frac{\pi }{2},\frac{\pi }{2},\ldots ,\frac{\pi }{2})$ be the initial point. In this example, we compare [18, Alg.1], Algorithms 3.1 and 3.2 by changing the dimension n and the value of Err. We use the same parameter settings as in [18]. That is, we choose $\eta =0.5,~\sigma =0.99$ for [18, Alg.1]. For Algorithm 3.1, we choose $\lambda _0 = 1.5,~\mu =0.6$, $\varepsilon _{k}=\frac{100}{(k+1)^2}$. For Algorithm 3.2, we choose $\mu =1.55,~\eta =0.4,~\sigma =0.99$. The computational results are reported in Table 1.

Table 1 Results for Example 4.1

Remark 4.1

From Table 1, one can see that Algorithm 3.1 needs only to calculate one projection onto the feasible set C per iteration. Moreover, from the view point of the number of iterations and computational time, we have Algorithm 3.1 is more efficient than [18, Alg.1] and Algorithm 3.2 for nonmonotone $\text{ VI }(F,C)$ with Lipschitz continuous on ${\mathbb {R}}^{n}$.

In the following three examples, it is easy to verify that the Lipschitz continuity of the mapping F on ${\mathbb {R}}^{n}$ is not true, therefore it does not satisfy the Condition 3.2 of Algorithm 3.1. Then, we only test the effectiveness of Algorithm 3.2 for these three examples.

Example 4.2

The well-known asymmetric transportation network equilibrium example was proposed in [31, Example 7.5]. The network has 25 nodes and 37 directed links (the set of directed links is denoted by L), and the network topology is shown in Fig. 1.

Fig. 1

A transportation network topology

Let W be a set of the origin/destination (O/D) pairs of this network, $P_w$ be a set of all paths corresponding to the O/D pair $\omega \in W$, and P be a set of all paths in the network. Then, we have the path set $P=\bigcup \limits _{\omega \in W}P_\omega .$ The O/D pairs and the number of paths of each O/D pair for this example are given in Table 2.

Table 2 The O/D pairs and the number of paths of each O/D pair

Denote by A the path-link incidence matrix, i.e.,

$$\begin{aligned} A=(\delta _{pl})_{55\times 37},~~\text {where}~\delta _{pl}= {\left\{ \begin{array}{ll} ~1, & \text {if}~\text {the link}~l\in p~(\text {where}~l\in L,~p\in P), \\ ~0, & \text {otherwise}. \end{array}\right. } \end{aligned}$$

Denote by B the path-O/D pair incidence matrix, i.e.,

$$\begin{aligned} B=(v_{p\omega })_{55\times 6},~~\text {where}~v_{p\omega }= {\left\{ \begin{array}{ll} ~1, & \text {if}~\text {the path}~p\in P_\omega ~(\text {where}~p\in P,~\omega \in W), \\ ~0, & \text {otherwise}. \end{array}\right. } \end{aligned}$$

We will use the symbol $x_p$ to represent the traffic flow on path p, then $x=(x_p)_{p\in P}\in {\mathbb {R}}^{55\times 1}$. Hence, the traffic flow f on link is $A^Tx$ and the traffic flow d between the O/D pair w is $B^Tx$.

For the link flow, there is a link travel cost function t(u) and a travel disutility function $\lambda (v)$, which are given in [32, Example 5.1]. Because both the travel cost and the travel disutility are functions of the path flow x, we can describe the traffic equilibrium example with link capacity bounds as the $\text{ VI }(F,C)$, i.e.,

$$\begin{aligned} F(x) = At(A^Tx) - B\lambda (B^Tx),~~C:=\{x\in {\mathbb {R}}_+^{55}: A^Tx\le b\}, \end{aligned}$$

and $b=q\cdot (1,1,\ldots ,1)^T\in {\mathbb {R}}^{37\times 1}$ is the vector indicating the capacity on links with $q\in {\mathbb {R}}^n_+$.

Since the mapping F is monotone, the relationship $S_D=S\ne \emptyset$ clearly holds. In this example, we compare [18, Alg.1], [24, Alg.3.2] and Algorithm 3.2 by changing the values of Err and q. We use the same parameter settings as in [18, 24]. That is, we choose $\eta =0.5,~\sigma =0.99$ for [18, Alg.1] and $\mu =0.5,~\eta =0.4,~\sigma =0.99$ for [24, Alg.3.2]. For Algorithm 3.2, we choose $\mu =0.14,~\eta =0.13,~\sigma =0.99$. We take the initial point $x^0=(1,1,\ldots ,1)^T$. The results are reported in Table 3.

Table 3 Results for Example 4.2

Remark 4.2

From Table 3, one can see that Algorithm 3.2 is more efficient than [18, Alg.1] in these aspects of the number of iterations and computational time. Moreover, it can be found from Table 3 that the computational time of Algorithm 3.2 is less than that of [24, Alg.3.2] even though the number of iterations of Algorithm 3.2 is more than [24, Alg.3.2].

Example 4.3

The following quasiconvex example was presented in [33, Exercise 4.7],

$$\begin{aligned} \text{ min }\Big \{g(x)=\frac{f_{0}(x)}{cx+d}:~x\in C\Big \} \end{aligned}$$

with $c\in {\mathbb {R}}^n$, $d\in {\mathbb {R}}$ and $C=\{x\in {\mathbb {R}}^n:f_{i}(x)\le 0,~i=1,2,\ldots ,m,~Ax=b\}$, where $f_{0},f_{1},\ldots ,f_{m}$ are convex functions, A is a matrix of order $m\times n$, $b\in {\mathbb {R}}^m$. This is a quasiconvex optimization problem.

Table 4 Results for Example 4.3

In this example, we choose

$$\begin{aligned} g(x) = \frac{\frac{1}{2}x^THx+q^Tx+r}{\Sigma _{i=1}^nx_i}, \end{aligned}$$

where $q=(-1,-1,\ldots ,-1)^T\in {\mathbb {R}}^n$, $r=1\in {\mathbb {R}}$, the positive diagonal matrix $H=hI$ with $h\in (0.1,1.6)$ and I is a identity matrix. The feasible set defined by

$$\begin{aligned} C:=\{x\in {\mathbb {R}}^n:x_i\ge 0,~i=1,2,\ldots ,n,~\Sigma _{i=1}^nx_i=a\},~a>0. \end{aligned}$$

It is clear that g is a smooth quasiconvex and can attain its minimum value on C (see [33, Exercise 4.7]), Hence, its derivative $F(x)= (F_1(x),F_2(x),\ldots ,F_n(x))^T$ with

$$\begin{aligned} F_i(x)=\frac{hx_i\Sigma _{i=1}^nx_i-\frac{1}{2}h\Sigma _{i=1}^n{x_i}^2-1}{(\Sigma _{i=1}^nx_i)^2} \end{aligned}$$

is quasimonotone on C. Moreover, it is routine to check that $S_D=\{(\frac{1}{n}a,\frac{1}{n}a,\ldots ,\frac{1}{n}a)^T\}$. Hence, solving this quasiconvex problem can be converted to solve quasimonotone $\text{ VI }(F,C)$.

Since this example was solved in [13, 21]. In this example, we test [13, Alg.2.1], [21, Alg.1] and Algorithm 3.2 by changing the value of Err and the dimension n. Let $h = 1.2$. We use the same parameter settings as in [13, 21]. That is, we choose $\gamma =0.4,~\sigma =0.99$ for [13, Alg.2.1] and $\eta =0.99,~\sigma =0.4$ for [21, Alg.1]. For Algorithm 3.2, we choose $\mu =2.8,~\eta =0.4,~\sigma =0.99$.

We take $a=n$ and the initial point

$$\begin{aligned} x^0:=\frac{a*rand(n,1)}{sum(rand(n,1))}, \end{aligned}$$

where $rand(n,1)\in {\mathbb {R}}^{n\times 1}$ is a random vector with each component selected from (0, 1). We generate 5 random initial points as described above. We present the computational results in Table 4, averaged over the 5 random initial points.

Remark 4.3

From Table 4, one can see that Algorithm 3.2 performs better than [13, Alg.2.1] and [21, Alg.1] in the number of iterations and computational time, and Algorithm 3.2 is less affected by changing the dimension n at the same stopping criterion accuracy.

Example 4.4

The nonmonotone variational inequality problem is considered in [13, Example 4.2], where the mapping F is defined by

$$\begin{aligned} F:(x_1,x_2,\ldots ,x_n)\mapsto (x_1^2,x_2^2,\ldots ,x_n^2), \end{aligned}$$

and the feasible set C is defined by $C=[-1,1]^n$. It is easy to verify that the mapping F is quasimonotone on the feasible set C whenever $n=1$ and the mapping F is not quasimonotone on the feasible set C whenever $n\ge 2$. Moreover, $S=\{(x_1,x_2,\ldots ,x_n)^T:x_i\in \{-1,0\},\forall i\},~S_D=\{(-1,-1,\ldots ,-1)^T\}$.

Since this example was solved in [13, 20, 21]. In this example, we compare [13, Alg.2.1], [20, Alg.1], [21, Alg.1] and Algorithm 3.2 by changing the value of Err and the dimension n. Let $x^0:=(1, 1, \ldots , 1)^T$ be the initial point. We use the same parameter settings as in [13, 20, 21]. That is, we choose $\gamma =0.4,~\sigma =0.99$ for [13, Alg.2.1], $\gamma =0.4,~\sigma =0.99,~\alpha _k=\alpha _k^0$ for [20, Alg.1] and $\eta =0.99,~\sigma =0.4$ for [21, Alg.1]. For Algorithm 3.2, we choose $\mu =1.5,~\eta =0.9,~\sigma =0.7$. We present the computational results in Table 5.

Table 5 Results for Example 4.4

Remark 4.4

From Table 5, one can see that the number of iterations and computational time of Algorithm 3.2 performs better than [20, Alg.1] and [21, Alg.1]. Moreover, it can be found from Table 5 that the computational time and the number of projections onto C of Algorithm 3.2 are less than that of [13, Alg.2.1] even though the number of iterations of Algorithm 3.2 is more than [13, Alg.2.1] when $Err=10^{-5}$.

5 Conclusion

In this paper, two improved subgradient extragradient algorithms are proposed for solving variational inequalities without monotonicity in a finite dimensional space ${\mathbb {R}}^n$. In the global convergence proof of the two new algorithms, we do not need to assume the generalized monotonicity of the mapping F. Under the mapping F is Lipschitz continuous (without the prior knowledge of Lipschitz constant) or continuous and $S_D\ne \emptyset$, the infinite sequences generated by Algorithms 3.1 and 3.2 converge globally to a solution of $\text{ VI }(F,C)$. Under some appropriate assumptions, we give the computational complexity analysis of the two algorithms. Finally, some numerical experiments are given to illustrate the efficiency of the two algorithms.