1 Introduction

Fractional integral and derivative can be used in characterizing hereditary properties of dynamical systems. Lately, a novel concept for the fractional–order operator with two orders has been introduced. The first-order is corresponding to the fractional derivative and the second-order is corresponding to the fractal differentiation. Fractal–fractional (FF) equations are receiving considerable attention and interest and been proven to model of many phenomena such as:

  • Electrical engineering (chaotic behavior of memory resistor to control the flow of electrical current in a circuit and recollecting the amount of charge that has previously flowed through it [1]).

  • Heat transfer and fluid flow (chaotic behavior of convective fluid movement inside the ellipsoid with heterogeneous external heating [2]).

  • Finance (dynamics of competition among rural and commercial banks [3, 4]).

  • Biology (epidemiological model of the Ebola virus [5]).

  • Dynamical systems (modeling attractors of chaotic dynamical systems [6]).

  • Drilling and petroleum engineering (dynamics of drilling system activated by electric induction motor [7]).

  • Disease (malaria disease mathematical model [8]).

  • Energy ( mathematical model for emissions of carbon dioxide (CO 2) [9]).

  • Complex dynamics (chemostat model [10]).

  • Smoking models [11].

The wide range applications of fractional calculus in modeling and analysis of many phenomena, together with the difficulty of computing analytical solutions of FF order differential equations, have attracted substantial attention to study these equations. In [12], a meshless scheme was introduced to solution of the FF advection–diffusion equation. The authors in [13] have applied ChPs for solving the FF Emden Fowler equation. The Mott polynomials in conjunction with the Legendre-Gauss quadrature rule (LGQR) have been employed for solving FF Fredholm-Volterra integro-differential equations in [14]. In [15], the Pell-Lucas polynomials and the LGQR have been used to solve FF optimal control and variational problems. Authors in [16, 17] derived sufficient criteria for the existence and uniqueness of the solution to nonlinear FF differential equations. Heydari [18, 19] explored the approximate solution of nonlinear FF optimal control problems. Araz [20] introduced a computational approach for solving FF Volterra integro-differential equations. The authors in [5] suggested a numerical simulation for the FF Ebola virus. Authors in [21] used Müntz-Legendre polynomials for solving FF 2D optimal control problems. In [22], the fractional shifted Morgan-Voyce neural network is applied to solve FF pantograph differential equations.

Fractional integro-differential equations find application in the modeling of diverse physical phenomena, such as mechanics and plasma physics [23], and biological models [24, 25]. There have been proposed different numerical methods to solution this class of equations. For example, Rahimkhani et al. [26] have utilized fractional-order Bernoulli functions to solve integro-differential equations (IDEs) involving fractional derivative. Also, they [27] applied the Hahn wavelets collocation method combined with Laplace transform method for solving these problems. Khader and Sweilam [28] proposed the pseudo-spectral scheme to solve system of fractional Volterra IDEs. Saadatmandi and Dehghan [29] have employed the Legendre collocation method together with the Gaussian integration method, Nemati et al. [30] have considered the second kind Chebyshev spectral method, Nemati et al. [31] have developed Legendre wavelet collocation method, Rahimkhani and Ordokhani [32] have applied fractional alternative Legendre functions, Doha et al. [33] have considered the shifted Legendre-Gauss-Lobatto collocation scheme for solving fractional IDEs.

In this article, we aim at designing a computational method based on Chelyshkov collocation scheme and OMs for solving FFIDEs in Atangana-Riemann-Liouville (A-R-L) sense. The orthogonal Chelyshkov polynomials are introduced in [34]. These polynomials have the analogous properties to those of the classical orthogonal polynomials. In fact, ChPs are an example of such alternative orthogonal ones, which are not solutions of the hypergeometric type equations, but can be expressed in terms of the Jacobi ones. These polynomials have been used for solving many different kinds of problems [35,36,37,38]. By utilizing OMs of integration, integer-order derivative and fractal-fractional-order derivative with the collocation points, the problem under consideration can be simplified to solving a system of nonlinear algebraic equations. Some of the main features of this scheme are listed as:

  • The solution obtained by the proposed method is continuous and differentiable.

  • A few terms of ChPs is required to obtain the high accuracy solutions.

  • The established algorithm transforms solving the main problem into solving a system of algebraic equations, which can be solved using a suitable numerical technique.

  • Approximation with the ChPs has short CPU time.

  • Implementing this scheme is very convenient and effective for other kinds of FF partial differential equations.

This paper is structured as follows: in Sect. 2, some preliminaries required in FF calculus are given. In section 3, the OMs of integration, integer-order derivative and fractal-fractional-order derivative based on ChPs are derived. In Sect. 4, sufficient conditions for the existence and uniqueness of solutions for the FFIDEs are provided. Also, it is devoted to applying a numerical technique to solve the FFIDEs. We investigate the convergence analysis of our approximate technique in Sect. 5. Section 6 is dedicated to multiple numerical simulations to show the precision of the presented approach. The final section allocates to the concluding remarks of this investigations.

2 Preliminary notes

In this section, we will introduce valuable definitions and significant properties of FF calculus, taken from [7, 18, 39].

Definition 1

We define the one and two–parameter Mittag–Leffler (M–L) functions respectively by the following relations [39]:

$$\begin{aligned} E_{\vartheta }(t)=\sum _{r=0}^{\infty }\frac{t^{r}}{\Gamma (r\vartheta +1)}, \hspace{1cm}\vartheta \in R^{+}, t\in R, \end{aligned}$$
(1)

and

$$\begin{aligned} E_{\vartheta , \iota }(t)=\sum _{r=0}^{\infty }\frac{t^{r}}{\Gamma (r\vartheta +\iota )}, \hspace{1cm}\vartheta , \iota \in R^{+}, t\in R. \end{aligned}$$
(2)

Definition 2

Let \( \alpha ,~\beta \in (0,1)\) and the real valued function N(x, t) is continuous. We define the following FF derivative of order \((\alpha ,\beta )\) in the A-R-L sense with M-L kernel as [7]

$$\begin{aligned} {}_0^{FFM}D_t^{\alpha ,\beta }N(x,t)= \frac{\Delta (\alpha )}{1-\alpha }\frac{d}{dt^{\beta }}\int _{0}^{t}E_{\alpha }\bigg ( \frac{-\alpha (t-s)^{\alpha }}{1-\alpha }\bigg ) N(x, s)ds, \end{aligned}$$
(3)

where \( \Delta (\alpha )= 1- \alpha + \frac{\alpha }{\Gamma (\alpha )}\).

Definition 3

The FF integral \({}_0^{FFM}I_{t}^{\alpha , \beta }\) of order \((\alpha ,\beta )\) in the A-R-L sense is obtained as [7]

$$\begin{aligned} {}_0^{FFM}I_{t}^{\alpha , \beta }N(x, t)= \frac{\alpha \beta }{\Delta (\alpha )\Gamma (\alpha )}\int _{0}^{t}s^{\beta -1}N(x, s)(t-s)^{\alpha -1}ds+ \frac{\beta (1-\alpha )t^{\beta -1}N(x, t)}{\Delta (\alpha )}. \end{aligned}$$
(4)

Lemma 1

Suppose that \( \alpha ,~\beta \in (0,1)\) and \(r \in N \cup \{0\}\). So, we obtain the following relation [18]

$$\begin{aligned} {}_{0}^{FFM}D_{t}^{\alpha , \beta }t^{r}= \frac{\Delta (\alpha ) r! t^{r-\beta +1}}{\beta (1- \alpha )}E_{\alpha , r+1}\bigg (\frac{-\alpha t^{\alpha }}{1-\alpha } \bigg ). \end{aligned}$$
(5)

Corollary

By using Lemma 1, we can extract the following results [12]

$$\begin{aligned}{} & {} {}_{0}^{FFM}D_{t}^{\alpha , \beta } e^{t}= \frac{\Delta (\alpha )t^{1-\beta }}{\beta (1-\alpha )} \sum _{r=0}^{\infty }t^{r}E_{\alpha , r+1}(\frac{-\alpha t^{\alpha }}{1-\alpha }),\nonumber \\{} & {} {}_{0}^{FFM}D_{t}^{\alpha , \beta } e^{-t}= \frac{\Delta (\alpha )t^{1-\beta }}{\beta (1-\alpha )} \sum _{r=0}^{\infty }(-1)^{r}t^{r}E_{\alpha , r+1}(\frac{-\alpha t^{\alpha }}{1-\alpha }),\nonumber \\{} & {} {}_{0}^{FFM}D_{t}^{\alpha , \beta } \sin (t)= \frac{\Delta (\alpha )t^{2-\beta }}{\beta (1-\alpha )} \sum _{r=0}^{\infty }(-1)^{r}t^{2r}E_{\alpha ,2 r+2}(\frac{-\alpha t^{\alpha }}{1-\alpha }),\nonumber \\{} & {} {}_{0}^{FFM}D_{t}^{\alpha , \beta } \cos (t)= \frac{\Delta (\alpha )t^{1-\beta }}{\beta (1-\alpha )} \sum _{r=0}^{\infty }(-1)^{r}t^{2r}E_{\alpha ,2 r+1}(\frac{-\alpha t^{\alpha }}{1-\alpha }). \end{aligned}$$
(6)

3 Properties of ChPs

In this section, we recall the definition and some properties of ChPs, OMs of FF derivative, integer-order integration, and derivative of them.

3.1 Chelyshkov polynomials (ChPs)

Let \(\Phi (t) = \left\{ {{\phi _{j,{\hat{r}}}}(t)} \right\} _{j =0}^{{\hat{r}}}\) be a set of the ChPs, where \({{\phi _{j,{\hat{r}}}}(t)}\) can be introduced on \(t \in [0, T] \) by the following formula [38]:

$$\begin{aligned} \phi _{j, \hat{r}}(t)=\sum _{i=j}^{\hat{r}}(-1)^{i-j}\left( {\begin{array}{*{5}c} \hat{r} -j \\ i - j \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +i+1 \\ \hat{r}- j \\ \end{array}} \right) \frac{t^{i}}{T^{i}},\hspace{1cm}j=0, 1, \ldots , M-1, \end{aligned}$$
(7)

where \(\hat{r}=M-1.\) These polynomials are orthogonal functions and their orthogonality condition is formulated as [38]

$$\begin{aligned} \int _{0}^{T} \phi _{j, \hat{r}}(t) \phi _{i, \hat{r}}(t) dt =\frac{T\delta _{j,i}}{j+i+1}, \end{aligned}$$
(8)

here \(\delta _{j,i}\) is Kronecker delta.

Any arbitrary function \(N(t) \in L^2[0, T ]\) can be approximated in terms of ChPs as

$$\begin{aligned}N(t) \simeq \sum \limits _{i = 0}^{{\hat{r}}} {{n_i}} {\phi _{i,{\hat{r}}}}(t) = {\mathcal {N}^T}\Psi (t),\end{aligned}$$

with

$$\begin{aligned} \Psi (t)= [\phi _{0, \hat{r}}(t), \phi _{1, \hat{r}}(t), \ldots , \phi _{\hat{r}, \hat{r}}(t) ]^{T}, \end{aligned}$$
(9)

and

$$\begin{aligned}\mathcal {N} = {\left[ {{n_0},{n_1},...,{n_{{\hat{r}}}}} \right] ^T},\end{aligned}$$

here we have

$$\begin{aligned} n_{i}=\frac{2i+1}{T}\int _{0}^{T}N(t)dt, \hspace{1cm}n=0, 1, \ldots , \hat{r}. \end{aligned}$$

Similarly, we shall approximate any bivariate function N(x, t) defined on \(L^2([0,T]) \times ([0,T])\) with the ChPs as follows

$$\begin{aligned}N(x,t) \simeq \sum \limits _{i = 0}^{{\hat{r}}} {\sum \limits _{j = 0}^{\tilde{r}} {{n_{ij}}} {\phi _{i,{\hat{r}}}}(x){\phi _{j,\tilde{r} }}(t)} = {\psi ^T}(x)\mathcal {N}\psi (t),\end{aligned}$$

where \(\tilde{r}=M'-1\) and \(\mathcal {N}=[n_{ij}]\) is a \({\hat{r}} \times \tilde{r} \) matrix.

3.2 FF derivative OM of ChPs

Theorem 1

Assume that \(\Psi (t)\) be the ChPs vector given by (9), then

$$\begin{aligned} {}^{FFM}_0 D_t^{\alpha ,\beta } \Psi (t) \simeq \Omega (\alpha , \beta )\Psi (t), \end{aligned}$$
(10)

in which \( \alpha ,~\beta \in (0,1)\) and \(\Omega (\alpha , \beta )\) is the \(\hat{r} \times \hat{r}\) OM of FF derivative.

Proof

From Eq. (9) we have

$$\begin{aligned} {}^{FFM}_0 D_t^{\alpha ,\beta }\Psi (t) =\bigg [{}^{FFM}_0 D_t^{\alpha ,\beta } \phi _{0, \hat{r}}(t), {}^{FFM}_0 D_t^{\alpha ,\beta } \phi _{1, \hat{r}}(t), \ldots , {}^{FFM}_0 D_t^{\alpha ,\beta }\phi _{\hat{r}, \hat{r}}(t) \bigg ]. \end{aligned}$$
(11)

Using Eq. (7), Lemma 1 and approximating the obtained elements in terms of the ChPs, we get

$$\begin{aligned} {}^{FFM}_0 D_t^{\alpha ,\beta }\phi _{i, \hat{r}}(t)= & {} \sum _{\kappa =i}^{\hat{r}}(-1)^{\kappa -i}\left( {\begin{array}{*{5}c} \hat{r} -i \\ \kappa - i \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +\kappa +1 \\ \hat{r}- i \\ \end{array}} \right) \frac{{}^{FFM}_0 D_t^{\alpha ,\beta }(t^{\kappa })}{T^{\kappa }}\nonumber \\ {}= & {} \sum _{\kappa =i}^{\hat{r}}(-1)^{\kappa -i}\left( {\begin{array}{*{5}c} \hat{r} -i \\ \kappa - i \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +\kappa +1 \\ \hat{r}- i \\ \end{array}} \right) \frac{\Delta (\alpha )\Gamma (\kappa +1)t^{\kappa -\beta +1}}{T^{\kappa }\beta (1- \alpha )}\nonumber \\{} & {} \quad \times E_{\alpha , \kappa +1} \bigg (\frac{-\alpha t^{\alpha }}{1-\alpha } \bigg )\simeq \sum _{j=0}^{\hat{r}}q_{i,j}^{\alpha , \beta }\phi _{j, \hat{r}}(t), \end{aligned}$$
(12)

in which

$$\begin{aligned} q_{i,j}^{\alpha , \beta }= & {} \frac{(2j+1)}{T} \sum _{\kappa =i}^{\hat{r}}(-1)^{\kappa -i}\left( {\begin{array}{*{5}c} \hat{r} -i \\ \kappa - i \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +\kappa +1 \\ \hat{r}- i \\ \end{array}} \right) \frac{\Delta (\alpha )\Gamma (\kappa +1)}{T^{\kappa }\beta (1- \alpha )}\nonumber \\{} & {} \quad \times \int _{0}^{T} t^{\kappa -\beta +1} E_{\alpha , \kappa +1}\bigg (\frac{-\alpha t^{\alpha }}{1-\alpha } \bigg ) \phi _{j, \hat{r}}(t) dt. \end{aligned}$$
(13)

From Eqs. (7) and (13), we have

$$\begin{aligned} \int _{0}^{T} t^{\kappa -\beta +1} E_{\alpha , \kappa +1}\bigg (\frac{-\alpha t^{\alpha }}{1-\alpha } \bigg ) \phi _{j, \hat{r}}(t)dt= & {} \int _{0}^{T} t^{\kappa -\beta +1} E_{\alpha , \kappa +1}\bigg (\frac{-\alpha t^{\alpha }}{1-\alpha } \bigg )\nonumber \\ {}{} & {} \times \sum _{r=j}^{\hat{r}}(-1)^{r-j}\left( {\begin{array}{*{5}c} \hat{r} -j \\ r - j \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +r+1 \\ \hat{r}- j \\ \end{array}} \right) \frac{t^{r}}{T^{r}}dt \nonumber \\= & {} \sum _{r=j}^{\hat{r}}(-1)^{r-j}\left( {\begin{array}{*{5}c} \hat{r} -j \\ r - j \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +r+1 \\ \hat{r}- j \\ \end{array}} \right) \frac{1}{T^{r}}\nonumber \\{} & {} \times \int _{0}^{T}t^{\kappa -\beta +r+1}E_{\alpha ,\kappa +1}\bigg (\frac{-\alpha t^{\alpha }}{1-\alpha } \bigg ) dt, \end{aligned}$$
(14)

substituting (14) into (13) and utilizing (12), we obtain that

$$\begin{aligned}{}_0^{FFM}D_t^{\alpha ,\beta }{\phi _{i,{\hat{r}}}}(t) \simeq \sum \limits _{j = 0}^{{\hat{r}}}{q_{i,j}^{\alpha ,\beta }{\phi _{j,{\hat{r}}}}(t)},\end{aligned}$$

where

$$\begin{aligned} q_{i,j}^{\alpha , \beta }= & {} \frac{(2j+1)\Delta (\alpha )}{T \beta (1-\alpha )}\sum _{\kappa =i}^{\hat{r}} \sum _{r=j}^{\hat{r}}(-1)^{\kappa +r-i-j}\left( {\begin{array}{*{5}c} \hat{r} -i \\ \kappa - i \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +\kappa +1 \\ \hat{r}- i \\ \end{array}} \right) \nonumber \\{} & {} \times \left( {\begin{array}{*{5}c} \hat{r} -j \\ r - j \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +r+1 \\ \hat{r}- j \\ \end{array}} \right) \frac{\Gamma (\kappa +1)}{T^{\kappa +r}}\Theta (\kappa , r, \alpha , \beta ), \end{aligned}$$
(15)

and

$$\begin{aligned} \Theta (\kappa , r, \alpha , \beta )= & {} \int _{0}^{T}t^{\kappa -\beta +r+1}E_{\alpha , \kappa +1}\bigg (\frac{-\alpha t^{\alpha }}{1-\alpha } \bigg ) dt. \end{aligned}$$

By applying finite terms of the M-L series presented in Eq. (2), we can compute \(\Theta (\kappa , r, \alpha , \beta )\) from the following relation

$$\begin{aligned} \Theta (k, r, \alpha , \beta )= & {} \int _{0}^{T}t^{\kappa -\beta +r+1} E_{\alpha , \kappa +1}\bigg (\frac{-\alpha t^{\alpha }}{1-\alpha } \bigg ) dt \nonumber \\= & {} \int _{0}^{T} t^{\kappa - \beta +r +1} \sum _{\ell =0}^{\tilde{n}}\frac{(-1)^{\ell }\alpha ^{\ell }t^{ \alpha \ell }}{(1-\alpha )^{\ell }\Gamma (\ell \alpha +\kappa +1)}dt \nonumber \\= & {} \sum _{\ell =0}^{\tilde{n}} \frac{(-1)^{\ell } (\alpha )^{\ell } T^{\alpha \ell +\kappa -\beta +r+2}}{(1-\alpha )^{\ell }\Gamma (\ell \alpha +\kappa +1) (\alpha \ell +\kappa -\beta +r+2) }. \end{aligned}$$
(16)

To show the calculation procedure we choose \(\hat{r}= \tilde{r}=5\), then we get

$$\begin{aligned}\Omega ^{(0.9, 0.3)} = \left[ \begin{array}{ccccc} -1.36971&{} 5.06126 &{}-20.8451 &{}39.0343 &{} -74.5652\\ -0.995655&{} 7.24907 &{} -14.3655 &{} 11.8974 &{}-16.0845 \\ -0.043172&{} -0.124456 &{} 6.49917 &{} -11.5771 &{} 4.30085\\ 0.00358712 &{}-0.00775258 &{}-0.170063 &{} 8.08527 &{}-13.3197 \\ -0.000659327&{} 0.00280109 &{} -0.00722902 &{} -0.0704058 &{}9.16045 \end{array}\right] , \end{aligned}$$

and

$$\begin{aligned}\Omega ^{(0.6, 0.8)} = \left[ \begin{array}{ccccc} 1.0458 &{}-0.695908 &{} -0.00172311 &{} -0.365416 &{} -0.0830235\\ -0.0294354&{} 1.33872 &{} -0.72447 &{} -0.0598104 &{} -0.298234\\ -0.000994249 &{} -0.0128173 &{} 1.45268 &{} -0.751993 &{} -0.103314\\ 0.000725649 &{} -0.00273143 &{} -0.00155093 &{}1.52118 &{} -0.770821\\ -0.000078943 &{} 0.000351969 &{}-0.00123675 &{}0.0014097 &{}1.57056 \end{array}\right] .\end{aligned}$$

\(\square \)

3.3 Integration OM of ChPs

Theorem 2

The integration OM of ChPs can be obtained as

$$\begin{aligned} \int _{0}^{t} \Psi (t) dt \simeq \Sigma \Psi (t), \end{aligned}$$
(17)

where \( \Sigma \) is the \(\hat{r} \times \hat{r}\) OM of integration.

Proof

From Eq. (9) we have

$$\begin{aligned} \int _{0}^{t} \Psi (t) dt =\bigg [\int _{0}^{t} \phi _{0, \hat{r}}(t) dt, \int _{0}^{t} \phi _{1, \hat{r}}(t) dt, \ldots , \int _{0}^{t}\phi _{\hat{r}, \hat{r}}(t) dt \bigg ]. \end{aligned}$$
(18)

Using Eq. (7), for \(i=0, 1, \ldots , \hat{r},\) we get

$$\begin{aligned} \int _0^t {{\phi _{i,{\hat{r}}}}(t)dt = \sum \limits _{\kappa =i}^{{\hat{r}}} {{{( - 1)}^{\kappa - i}}\left( {\begin{array}{*{20}{c}} {{\hat{r}} - i}\\ {\kappa - i} \end{array}} \right) } \left( {\begin{array}{*{20}{c}} {{\hat{r}} + \kappa + 1}\\ {{\hat{r}} - i} \end{array}} \right) } \frac{{\int _0^t {{t^\kappa }dt} }}{{{T^\kappa }}}\nonumber \\ =\sum \limits _{\kappa =i}^{{\hat{r}}} {{{( - 1)}^{\kappa - i}}\left( {\begin{array}{*{20}{c}} {{\hat{r}} - i}\\ {\kappa - i} \end{array}} \right) } \left( {\begin{array}{*{20}{c}} {{\hat{r}} + \kappa + 1}\\ {{\hat{r}} - i} \end{array}} \right) \frac{{{t^{\kappa + 1}}}}{{{T^\kappa }(\kappa + 1)}}. \end{aligned}$$
(19)

Now, approximating the elements of Eq. (19) using the ChPs yields

$$\begin{aligned}\int _0^t {{\phi _{i,{\hat{r}}}}(t)dt \simeq \sum \limits _{j = 0}^{{\hat{r}}} {{g_{i,j}}{\phi _{j,{\hat{r}}}}(t)} } =\Sigma \Psi (t),\end{aligned}$$

where

$$\begin{aligned} g_{i, j}= & {} \frac{2j+1}{T}\sum _{\kappa =i}^{\hat{r}}(-1)^{\kappa -i}\left( {\begin{array}{*{5}c} \hat{r} -i \\ \kappa - i \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} + \kappa +1 \\ \hat{r}- i \\ \end{array}} \right) \frac{1}{T^{\kappa }(\kappa +1)} \int _{0}^{T}t^{\kappa +1}\phi _{j, \hat{r}}(t) dt \nonumber \\= & {} (2j+1)T~\sum _{\kappa =i}^{\hat{r}} \sum _{r=j}^{\hat{r}}\frac{(-1)^{\kappa +r-i-j}}{(\kappa +1)(\kappa +r+2)}\left( {\begin{array}{*{5}c} \hat{r} -i \\ \kappa - i \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +\kappa +1 \\ \hat{r}- i \\ \end{array}} \right) \nonumber \\{} & {} \quad \times \left( {\begin{array}{*{5}c} \hat{r} -j \\ r - j \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +r+1 \\ \hat{r}- j \\ \end{array}} \right) . \end{aligned}$$
(20)

As an illustrate example, we choose \(\hat{r}=5\), thus we have

$$\begin{aligned} \Sigma = \left[ \begin{array}{ccccc} \frac{1}{50}&{}\frac{4}{25} &{} \frac{6}{35} &{} \frac{29}{100} &{} \frac{251}{700}\\ \\ -\frac{1}{75}&{}\frac{3}{50} &{} \frac{17}{70} &{} \frac{53}{200} &{} \frac{507}{1400}\\ \\ \frac{1}{175}&{}-\frac{9}{350} &{} \frac{1}{10} &{} \frac{63}{200} &{} \frac{71}{200}\\ \\ -\frac{1}{700}&{}\frac{9}{1400} &{} -\frac{1}{40} &{} \frac{7}{50} &{} \frac{19}{50}\\ \\ \frac{1}{6300}&{}-\frac{1}{1400} &{} \frac{1}{360} &{}- \frac{7}{450} &{} \frac{9}{50} \end{array}\right] .\end{aligned}$$

\(\square \)

3.4 Derivative OM of ChPs

Theorem 3

The derivative OM of ChPs can be obtained as

$$\begin{aligned} D\Psi (t) \simeq \Lambda \Psi (t), \end{aligned}$$
(21)

where \(\Lambda \) is the \(\hat{r} \times \hat{r}\) OM of derivative.

Proof

From Eq. (9) we have

$$\begin{aligned} D\Psi (t) = [D\phi _{0, \hat{r}}(t), D\phi _{1, \hat{r}}(t), \ldots , D\phi _{\hat{r}, \hat{r}}(t)]. \end{aligned}$$
(22)

Using Eq. (7), for \(i=0, 1, \ldots , \hat{r}, \) we find

$$\begin{aligned} D\phi _{i, \hat{r}}(t)= & {} \sum _{\kappa =i}^{\hat{r}}(-1)^{\kappa -i}\left( {\begin{array}{*{5}c} \hat{r} -i \\ \kappa - i \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +\kappa +1 \\ \hat{r}- i \\ \end{array}} \right) \frac{\kappa t^{\kappa -1}}{T^{\kappa }}\nonumber \\\simeq & {} \sum _{j=0}^{\hat{r}}\mathcal {S}_{i, j}\phi _{j, \hat{r}}(t)=\Lambda \Psi (t), \end{aligned}$$
(23)

where by approximating the elements of Eq. (23) in terms of the ChPs, we can calculate \(\mathcal {S}_{i,j}\) as

$$\begin{aligned} \mathcal {S}_{i,j}= & {} \frac{2j+1}{T}\sum _{\kappa =i}^{\hat{r}}(-1)^{\kappa -i}\left( {\begin{array}{*{5}c} \hat{r} -i \\ \kappa - i \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +\kappa +1 \\ \hat{r}- i \\ \end{array}} \right) \frac{\kappa }{T^{\kappa }} \int _{0}^{T}t^{\kappa -1}\phi _{j, \hat{r}}(t) dt \nonumber \\= & {} \frac{2j+1}{T}\sum _{\kappa =i}^{\hat{r}} \sum _{r=j}^{\hat{r}}(-1)^{\kappa +r-i-j}\left( {\begin{array}{*{5}c} \hat{r} -i\\ \kappa - i \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +\kappa +1 \\ \hat{r}- i \\ \end{array}} \right) \nonumber \\{} & {} \quad \times \left( {\begin{array}{*{5}c} \hat{r} -j \\ r - j \\ \end{array}} \right) \left( {\begin{array}{*{5}c} \hat{r} +r+1 \\ \hat{r}- j \\ \end{array}} \right) \frac{\kappa }{(r+\kappa )}. \end{aligned}$$
(24)

As an illustrate example, we choose \(\hat{r}=5\), thus we get

$$\begin{aligned} \Lambda = \left[ \begin{array}{ccccc} -12 &{}-15 &{} 5 &{} -7 &{} 9\\ \\ 4&{} \frac{3}{2}&{}- \frac{17}{2}&{}7&{} -9\\ \\ 0&{}\frac{21 }{10}&{}\frac{ 5}{2}&{}-\frac{43 }{5}&{}9\\ \\ 0&{}0&{}\frac{ 8}{7}&{}\frac{7 }{2}&{}-\frac{135 }{14}\\ \\ 0&{}0&{}0&{}\frac{1 }{2}&{}\frac{ 9}{2} \end{array}\right] .\end{aligned}$$

\(\square \)

4 A-R-L FFIDEs

In this section, first, we provide sufficient conditions for the existence and uniqueness of solutions of the A-R-L FFIDEs. Then we develop the new numerical technique for the A-R-L FFIDEs as

$$\begin{aligned} {}^{FFM}D_{t}^{\alpha ,\beta }N(x, t)= & {} \Theta (x, t, N(x, t), \frac{\partial N (x, t)}{\partial x}, \frac{\partial ^{2}N(x, t)}{\partial x^{2}})\nonumber \\{} & {} \quad + \gamma _{1} \int _{0}^{1}\int _{0}^{1}\mathcal {K}_{1}(x, t, \Im , \wp , \frac{\partial ^{i}N(\Im , \wp )}{\partial \Im ^{i}})d\Im d\wp \nonumber \\{} & {} \quad + \gamma _{2} \int _{0}^{x}\int _{0}^{t}\mathcal {K}_{2}(x, t, \Im , \wp , \frac{\partial ^{j}N(\Im , \wp )}{\partial \Im ^{j}} ) d\Im d\wp , \end{aligned}$$
(25)

with the initial and boundary conditions

$$\begin{aligned} N(x,0) = \zeta (x), \end{aligned}$$
(26)

and

$$\begin{aligned} N(0,t) = {\rho _0}(t),\,\,\,\,N(1,t) = {\rho _1}(t), \end{aligned}$$
(27)

where \(\Theta \), \(\mathcal {K}_{1}\) and \(\mathcal {K}_{2}\) are continuous linear or nonlinear functions, \(\alpha ,~ \beta \in (0,1)\), \((x,t) \in I=[0,1]\times [0,1]\) and \(i,j=0,1,2\).

4.1 Existence and uniqueness of the solutions

In this section, we show the existence and uniqueness of the solutions for Eq. (25). For ease of exposition, we will analyze the existence and uniqueness of the solutions and the error analysis for the case \(M=M'=\hat{r}+1\). Furthermore, we suppose that there exist Lipschitz constant \(\lambda _1,~\lambda _2, \lambda _3,~ {\lambda _{{\kappa _1}}},\) and \({\lambda _{{\kappa _2}}}\) such that

$$\begin{aligned} \begin{array}{l} {\left\| {\Theta (x,t,{u_1},{v_1},{w_1}) - \Theta (x,t,{u_2},{v_2},{w_2})} \right\| _{{L^\infty }(I)}} \le \\ \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\lambda _1}{\left\| {{u_1} - {u_2}} \right\| _{{L^\infty }(I)}} + {\lambda _2}{\left\| {{v_1} - {v_2}} \right\| _{{L^\infty }(I)}} + {\lambda _3}{\left\| {{w_1} - {w_2}} \right\| _{{L^\infty }(I)}}, \end{array} \end{aligned}$$
(28)
$$\begin{aligned} \left\| {{\mathcal {K} _1}(x,t,u,v,{w_1}) - {\mathcal {K} _1}(x,t,u,v,{w_2})} \right\| _{L^\infty (I)} \le {\lambda _{{\mathcal {K} _1}}}\left\| {{w_1} - {w_2}} \right\| _{L^\infty (I)}, \end{aligned}$$
(29)
$$\begin{aligned} \left\| {{\mathcal {K} _2}(x,t,u,v,{w_1}) - {\mathcal {K} _2}(x,t,u,v,{w_2})} \right\| _{L^\infty (I)} \le {\lambda _{{\mathcal {K} _2}}}\left\| {{w_1} - {w_2}} \right\| _{L^\infty (I)}. \end{aligned}$$
(30)

Applying the fractal–fractional integral on both sides of Eq. (25), we can write:

$$\begin{aligned} \begin{array}{l} N(x,t) = N(x,0) + {}_0^{FFM}I_t^{\alpha ,\beta }\Theta (x,t,N(x,t),\frac{{\partial N(x,t)}}{{\partial x}}, \frac{{{\partial ^2}N(x,t)}}{{\partial x^2}})\\ \\ \quad \qquad \quad + {\gamma _1}{}_0^{FFM}I_t^{\alpha ,\beta }({\Xi _1}N(x,t)) + {\gamma _2}{}_0^{FFM}I_t^{\alpha ,\beta }({\Xi _2}N(x,t)), \end{array} \end{aligned}$$
(31)

where

$$\begin{aligned} \begin{array}{l} {\Xi _1}N(x,t) = \int _0^1 {\int _0^1 {{\mathcal {K} _1}(x,t,\Im ,\wp ,\frac{{{\partial ^i}N(\Im ,\wp )}}{{\partial {\Im ^i}}})} } d\Im d\wp ,\\ \\ {\Xi _2}N(x,t) = \int _0^x {\int _0^t {{\mathcal {K} _2}(x,t,\Im ,\wp ,\frac{{{\partial ^j}N(\Im ,\wp )}}{{\partial {\Im ^j}}})} } d\Im d\wp .\\ \\ \end{array} \end{aligned}$$
(32)

We define an operator \(\mathcal {T}\) as follows:

$$\begin{aligned} \begin{array}{l} (\mathcal {T}N)(x,t) = N(x,0) + {}_0^{FFM}I_t^{\alpha ,\beta }\Theta (x,t,N(x,t), \frac{{\partial N(x,t)}}{{\partial x}},\frac{{{\partial ^2}N(x,t)}}{{\partial x^2}})\\ \\ \quad \qquad \qquad + {\gamma _1}{}_0^{FFM}I_t^{\alpha ,\beta }({\Xi _1}N(x,t)) + {\gamma _2}{}_0^{FFM}I_t^{\alpha ,\beta }({\Xi _2}N(x,t)). \end{array} \end{aligned}$$
(33)

Using this operator, Eq. (31) can be rewritten as \(\mathcal {T}N= N\), in order to prove our desired uniqueness result, we have to show that \(\mathcal {T}\) has a unique fixed point. Let us investigate the properties of the operator \(\mathcal {T}\).

To illustrate our main results, we need the next theorem.

Theorem 4

(Banach’s contraction theorem [40]) Assume E be a Banach space with a nonempty closed subset \(Q_{r^*}\). Then any contraction mapping \(\mathcal {T}~:~Q_{r^*}\rightarrow Q_{r^*}\) has a unique fixed point.

In the next theorem, we prove the existence of the solutions for A-R-L FFIDEs using Banach’s contraction theorem.

Theorem 5

Suppose that \(N,~\Theta ,~\mathcal {K}_{1}\) and \(\mathcal {K}_{2}\) are continuous and bounded. Also we assume that

$$\begin{aligned} {{{\left\| {\frac{{{\partial ^r}N(x,t)}}{{\partial {x^r}}} - \frac{{{\partial ^r}\bar{N}(x,t)}}{{\partial {x^r}}}} \right\| }_{{L^\infty }(I)}}} \le {\bar{\lambda }_r} \left\| {N(x,t) - {\bar{N}}(x,t)} \right\| _{{L^\infty }(I)} ,\,r = 0,1,2. \end{aligned}$$
(34)

where \(\bar{\lambda }_r\) is a constant and depends on r. Then, the A-R-L FFIDEs Eq. (25) has a unique solution on \({Q_{{r^*}}} = \left\{ {N(x,t) \in {C^2}(I):{{\left\| {N(x,t)} \right\| }_{{L^\infty }(I)}} \le {r^*}} \right\} \).

Proof

To begin, we demonstrate that the operator \(\mathcal {T}(Q_{r^*})\) is a subset of \(Q_{r^*}\). Let N(x, t) be an element of \(Q_{r^*}\). Clearly, the set \(Q_{r^*}\) is bounded, closed, and convex. Our goal is to prove that \({\left\| {(TN)(x,t)} \right\| _{{L^\infty }(I)}} \le {r^*}\). Assume that

$$\begin{aligned} \begin{array}{l} {\left\| {N(x,0)} \right\| _{{L^\infty }(I)}} \le {\aleph _1},\\ {\left\| {\Theta (x,t,N,\frac{{\partial N}}{{\partial x}},\frac{{{\partial ^2}N}}{{\partial {x^2}}})} \right\| _{{L^\infty }(I)}} \le {\aleph _2},\\ {\left\| {{\mathcal {K} _1}(x,t,\Im ,\wp ,\frac{{{\partial ^i}N}}{{\partial {x^i}}})} \right\| _{{L^\infty }(I)}} \le {\aleph _3},\\ {\left\| {{\mathcal {K} _2}(x,t,\Im ,\wp ,\frac{{{\partial ^i}N}}{{\partial {x^i}}})} \right\| _{{L^\infty }(I)}} \le {\aleph _4}. \end{array} \end{aligned}$$
(35)

Taking norm on both side of Eq. (33) and using Eqs. (35), we have the following relation:

$$\begin{aligned} \begin{array}{l} {\left\| {(TN)(x,t)} \right\| _{{L^\infty }(I)}} \le {\left\| {N(x,0)} \right\| _{{L^\infty }(I)}} + \,{\left\| {{}_0^{FFM}I_t^{\alpha ,\beta }\Theta (x,t,N(x,t),\frac{{\partial N(x,t)}}{{\partial x}}, \frac{{{\partial ^2}N(x,t)}}{{\partial x}})} \right\| _{{L^\infty }(I)}}\\ \\ +\, {\left\| {{\gamma _1}{}_0^{FFM}I_t^{\alpha ,\beta }({\Xi _1}N(x,t))} \right\| _{{L^\infty }(I)}} + {\left\| {{\gamma _2}{}_0^{FFM}I_t^{\alpha ,\beta }({\Xi _2}N(x,t))} \right\| _{{L^\infty }(I)}}\, \le {\left\| {N(x,0)} \right\| _{{L^\infty }(I)}}\\ \\ \quad + \,\left( {\frac{{\alpha \beta \,\Gamma (\beta ){{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha ) \Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha )\,\Gamma (\beta ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) \left( {{{\left\| {\Theta (x,t,N,\frac{{\partial N}}{{\partial x}},\frac{{{\partial ^2}N}}{{\partial {x^2}}})} \right\| }_{{L^\infty }(I)}}} \right. \\ \\ +\, \left. {{{\left\| {{\mathcal {K} _1}(x,t,\Im ,\wp ,\frac{{{\partial ^i}N}}{{\partial {x^i}}})} \right\| }_{{L^\infty }(I)}} + {{\left\| {{\mathcal {K} _2}(x,t,\Im ,\wp ,\frac{{{\partial ^i}N}}{{\partial {x^i}}})} \right\| }_{{L^\infty }(I)}}} \right) \\ \\ \le {\aleph _1} + \left( {\frac{{\alpha \beta \,\Gamma (\beta ){{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha )\,\Gamma (\beta ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) ({\aleph _2} + \gamma _1 {\aleph _3} +\gamma _2 {\aleph _4}) \le {r^*}. \end{array}\nonumber \\ \end{aligned}$$
(36)

Choosing

$$\begin{aligned} {r^*}{} & {} \ge {\aleph _1} + \left( {\frac{{\alpha \beta \,\Gamma (\beta ){{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha )\,\Gamma (\beta ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) \\{} & {} \quad \ ({\aleph _2} + \gamma _1{\aleph _3} + \gamma _2{\aleph _4}), \end{aligned}$$

is enough to imply that \(\mathcal {T}(Q_{r^*}) \subset Q_{r^*}\). In the next step, we will demonstrate that \(\mathcal {T}\) is a contraction as an operator. For every N and \({\bar{N}}\) in \(Q_{r^*}\), we have:

$$\begin{aligned}{} & {} {\left\| {(\mathcal {T}N)(x,t) - (\mathcal {T}{\bar{N}})(x,t)} \right\| _{{L^\infty }(I)}} \le {\left\| {N(x,0) - {\bar{N}}(x,0)} \right\| _{{L^\infty }(I)}}\nonumber \\{} & {} \quad + \,{\left\| {{}_0^{FFM}I_t^{\alpha ,\beta }\Theta (x,t,N(x,t),\frac{{\partial N(x,t)}}{{\partial x}},\frac{{{\partial ^2}N(x,t)}}{{\partial ^2 x}}) - {}_0^{FFM}I_t^{\alpha ,\beta }\Theta (x,t,{\bar{N}}(x,t), \frac{{\partial {\bar{N}}(x,t)}}{{\partial x}}, \frac{{{\partial ^2}{\bar{N}}(x,t)}}{{\partial ^2 x}})} \right\| _{{L^\infty }(I)}}\nonumber \\{} & {} \quad + {\left\| {{\gamma _1}{}_0^{FFM}I_t^{\alpha ,\beta }({{ \Xi }_1} N(x,t)) - {\gamma _1}{}_0^{FFM}I_t^{\alpha ,\beta } ({\Xi _1}{\bar{N}}(x,t)}) \right\| _{{L^\infty }(I)}}\nonumber \\{} & {} \quad + {\left\| {{\gamma _2}{}_0^{FFM}I_t^{\alpha ,\beta } ({{ \Xi }_2} N(x,t)) - {\gamma _2}{}_0^{FFM}I_t^{\alpha ,\beta }({\Xi _2}{\bar{N}}(x,t)}) \right\| _{{L^\infty }(I)}}\nonumber \\{} & {} \quad \le \left( 1+ \tilde{\lambda } \left( {\frac{{\alpha \beta \,\Gamma (\beta ){{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha )\,\Gamma (\beta ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) \right) {\left\| {N - {\bar{N}}} \right\| _{{L^\infty }(I)}}, \end{aligned}$$
(37)

where \(\tilde{\lambda }=({\lambda _1} + {\lambda _2}{\bar{\lambda }_1} + {\lambda _3}{\bar{\lambda }_2}+{\gamma _1}{\lambda _{{\kappa _1}}}{\bar{\lambda }_i}+{\gamma _2}{\lambda _{{\kappa _2}}}{\bar{\lambda }_j}).\) So we have

$$\begin{aligned}{\left\| {(\mathcal {T}N)(x,t) - (\mathcal {T}{\bar{N}})(x,t)} \right\| _{{L^\infty }(I)}} \le L\,{\left\| {N - {\bar{N}}} \right\| _{{L^\infty }(I)}}.\,\,\,\end{aligned}$$

For \(L < 1\), the contraction is obtained. Therefore, A-R-L FFIDEs Eq. (25) has a unique solution. \(\square \)

4.2 Computational strategy

This section is dedicated to introducing a numerical formulation for solving the model given in Eq. (25). For this purpose we approximate the highest order of derivative in Eq. (25) by ChPs as

$$\begin{aligned} \frac{\partial ^{3}N(x, t)}{\partial x^{2}\partial t}\simeq \Psi ^{T}(x)\mathcal {N}\Psi (t). \end{aligned}$$
(38)

Upon integrating Eq. (38) with respect to variable t, we obtain

$$\begin{aligned} \frac{\partial ^{2}N(x, t)}{\partial x^{2}}\simeq \Psi ^{T}(x) \mathcal {N} \Sigma \Psi (t) + \zeta ''(x)=\frac{\partial ^{2}N^{*}(x, t)}{\partial x^{2}}. \end{aligned}$$
(39)

Now, by integrating Eq. (38) twice with respect to variable x and by employing the initial condition, we derive

$$\begin{aligned} \frac{\partial N(x, t)}{\partial t}\simeq \Psi ^{T}(x) \Sigma ^{T^{2}}\mathcal {N} \Psi (t)+\frac{\partial \rho _{0}(t)}{\partial t}+x\frac{\partial }{\partial x}\bigg ( \frac{\partial N(x, t)}{\partial t}\bigg )\bigg \vert _{x=0}. \end{aligned}$$
(40)

To continue the process, we substitute \(x=1\) in Eq. (40) to obtain the unknown function \(\frac{\partial }{\partial x}\bigg ( \frac{\partial N(x, t)}{\partial t}\bigg )\bigg \vert _{x=0}\). Thus, we can rewrite Eq. (40) as

$$\begin{aligned} \frac{\partial N(x, t)}{\partial t}{} & {} \simeq \Psi ^{T}(x) \Sigma ^{T^{2}}\mathcal {N} \Psi (t)- x\Psi ^{T}(1) \Sigma ^{T^{2}}\mathcal {N} \Psi (t)+(1-x)\rho _{0}'(t)+x\rho '_{1}(t)\nonumber \\{} & {} =\frac{\partial N^{*}(x, t)}{\partial t}. \end{aligned}$$
(41)

Next, integrating Eq. (39) with respect to variable x leads to the following relation

$$\begin{aligned} N(x, t)\simeq \Psi ^{T}(x) \Sigma ^{T^{2}}\mathcal {N}\Sigma \Psi (t)+ \zeta (x)- \zeta (0)-x\zeta '(0)+ \rho _{0}(t)+x\frac{\partial N(x, t)}{\partial x}\bigg \vert _{x=0}, \end{aligned}$$
(42)

where \(\frac{\partial N(x, t)}{\partial x}\bigg \vert _{x=0}\) can be evaluated by replacing \(x=1\) in Eq. (42). Therefore, we can rewrite Eq. (42) as

$$\begin{aligned} N(x, t)\simeq \Psi ^{T}(x) \Sigma ^{T^{2}}\mathcal {N}\Sigma \Psi (t)- x\Psi ^{T}(1) \Sigma ^{T^{2}}\mathcal {N}\Sigma \Psi (t) + \varpi (x, t)= N^{*}(x, t), \end{aligned}$$
(43)

in which

$$\begin{aligned} \varpi (x, t)=\rho _{0}(t)+\zeta (x)-\zeta (0)-x\zeta '(0)+x(\rho _{1}(t)- \rho _{0}(t))+x(-\zeta (1)+\zeta (0)+ \zeta '(0)). \end{aligned}$$

By differentiating of Eq. (43) with respect to variable x, we deduce

$$\begin{aligned} \frac{\partial N(x, t)}{\partial x}\simeq \Psi ^{T}(x) \Lambda ^{T}\Sigma ^{T^{2}}\mathcal {N}\Sigma \Psi (t) - \Psi ^{T}(1) \Sigma ^{T^{2}}\mathcal {N}\Sigma \Psi (t) + \frac{\partial \varpi (x, t)}{\partial x}= \frac{\partial N^{*}(x, t)}{\partial x}. \end{aligned}$$
(44)

Moreover, it is necessary to derive an approximation for FF–derivative of N(x, t). By applying the properties and OM of FF derivative and Eq. (43), we derive

$$\begin{aligned} {}^{FFM}D_{t}^{\alpha , \beta }N(x, t)\simeq & {} \Psi ^{T}(x) \Sigma ^{T^{2}}\mathcal {N}\Sigma \Omega (\alpha , \beta ) \Psi (t)-x \Psi ^{T}(1) \Sigma ^{T^{2}} \mathcal {N}\Sigma \Omega (\alpha , \beta )\Psi (t)\nonumber \\ {}+ & {} {}^{FFM}D_{t}^{\alpha , \beta }\varpi (x, t)={}^{FFM}D_{t}^{\alpha , \beta }N^{*}(x, t). \end{aligned}$$
(45)

Substituting Eqs. (38)–(45) in Eq. (25), we gain

$$\begin{aligned} {}^{FFM}D_{t}^{\alpha ,\beta }N^{*}(x, t)= & {} \Theta (x, t, N^{*}(x, t), \frac{\partial N^{*} (x, t)}{\partial x}, \frac{\partial ^{2}N^{*}(x, t)}{\partial x^{2}})\nonumber \\{} & {} \quad + \gamma _{1} \int _{0}^{1}\int _{0}^{1}\mathcal {K}_{1}(x, t, \Im , \wp , \frac{\partial ^{i}N^{*}(\Im , \wp )}{\partial \Im ^{i}})d\Im d\wp \nonumber \\{} & {} \quad \gamma _{2} \int _{0}^{x}\int _{0}^{t}\mathcal {K}_{2}(x, t, \Im , \wp , \frac{\partial ^{j}N^{*}(\Im , \wp )}{\partial \Im ^{j}} ) d\Im d\wp . \end{aligned}$$
(46)

To evaluate the double Fredholm and Volterra integral in Eq. [41]. Thus, we get

$$\begin{aligned}{} & {} \int _{0}^{1}\int _{0}^{1}\mathcal {K}_{1}(x, t, \Im , \wp , \frac{\partial ^{i}N^{*}(\Im , \wp )}{\partial \Im ^{i}})d\Im d\wp \nonumber \\{} & {} \simeq \frac{1}{4}\sum _{i=1}^{n}\sum _{j=1}^{n^{*}}\omega _{i}\omega '_{j}\mathcal {K}_{1}(x, t, \frac{\eta _{i}+1}{2}, \frac{\eta '_{j}+1}{2}, \frac{\partial ^{i}N^{*}(\frac{\eta _{i}+1}{2}, \frac{\eta '_{j}+1}{2})}{\partial \Im ^{i}}), \end{aligned}$$
(47)

and

$$\begin{aligned}{} & {} \int _{0}^{x}\int _{0}^{t}\mathcal {K}_{2}(x, t, \Im , \wp , \frac{\partial ^{j}N^{*}(\Im , \wp )}{\partial \Im ^{j}} ) d\Im d\wp \nonumber \\{} & {} \quad \simeq \frac{xt}{4} \sum _{i=1}^{n}\sum _{j=1}^{n^{*}}\omega _{i}\omega '_{j}\mathcal {K}_{2}(x, t, \frac{x\eta _{i}+x}{2}, \frac{t\eta '_{j}+t}{2}, \frac{\partial ^{j}N^{*}(\Im , \wp )}{\partial \Im ^{j}} ). \end{aligned}$$
(48)

Taking into consideration Eqs. (47) and (48) in Eq. (46) yields

$$\begin{aligned} \Re (x, t)= & {} {}^{FFM}D_{t}^{\alpha ,\beta }N^{*}(x, t)-\Theta (x, t, N^{*}(x, t), \frac{\partial N^{*} (x, t)}{\partial x}, \frac{\partial ^{2}N^{*}(x, t)}{\partial x^{2}})\nonumber \\- & {} \frac{1}{4}\sum _{i=1}^{n}\sum _{j=1}^{n^{*}}\omega _{i}\omega '_{j}\mathcal {K}_{1}(x, t, \frac{\eta _{i}+1}{2}, \frac{\eta '_{j}+1}{2}, \frac{\partial ^{i}N^{*}(\frac{\eta _{i}+1}{2}, \frac{\eta '_{j}+1}{2})}{\partial \Im ^{i}})\nonumber \\- & {} \frac{xt}{4} \sum _{i=1}^{n}\sum _{j=1}^{n^{*}}\omega _{i}\omega '_{j}\mathcal {K}_{2}(x, t, \frac{x\eta _{i}+x}{2}, \frac{t\eta '_{j}+t}{2}, \frac{\partial ^{j}N^{*}(\Im , \wp )}{\partial \Im ^{j}} ). \end{aligned}$$
(49)

Finally, by utilizing the Legendre nodes in Eq. (49) the essential system of algebraic equations is derived as

$$\begin{aligned} \Re (x_{i}, t_{j}), \hspace{1cm}i=0,1, \ldots M-1; \hspace{1cm}j=0, 1, \ldots , M'-1. \end{aligned}$$
(50)

By employing Newton’s iterative method to solve the obtained system, one obtains an approximate solution N(x, t).

5 Convergence and error analysis

This section is dedicated to assessing the error norm associated with the numerical scheme introduced in Sect. 4. For the coming discussions, we assume that

$$\begin{aligned} \left\| {N(x,t) - {N^*}(x,t)} \right\| _{{L^\infty }(I)}^* = \max \left\{ {{{\left\| {\frac{{{\partial ^r}N(x,t)}}{{\partial {x^r}}} - \frac{{{\partial ^r}N^*(x,t)}}{{\partial {x^r}}}} \right\| }_{{L^\infty }(I)}}}, r = 0,1,2 \right\} . \nonumber \\ \end{aligned}$$
(51)

The following theorem will be useful in our analysis.

Theorem 6

Suppose that N(x, t) belongs to the Sobolev space \(H^{\mu ;{\hat{r}}}(I)\) associated with the \(\mu \ge 0\), and \(\sum \limits _{i = 0}^{{\hat{r}}}{\sum \limits _{j = 0}^{{\hat{r}}} {{n_{i,j}}{L_{i,{\hat{r}}}}(x)} } {L_{j,{\hat{r}}}}(t)\) is the the best approximation of N(x, t) using the set of the shifted Legendre polynomials. Then, we have [42]

$$\begin{aligned} \left\| {N(x,t) - \sum \limits _{i = 0}^{{\hat{r}}} {\sum \limits _{j = 0}^{{\hat{r}}} {{n_{i,j}}{L_{i,{\hat{r}}}}(x)} } {L_{j,{\hat{r}}}}(t)} \right\| _{L^\infty (I)} \le c{{{\hat{r}}}^{\frac{3}{4} - \mu }}{\left| N \right| _{{H^{\mu ;{\hat{r}}}}(I)}}, \end{aligned}$$
(52)

where \(c>0\) is a constant which is independent of function N and \({\hat{r}}\).

Since the best approximation of a given function \(N \in H^\mu (I)\) is unique [43], by Theorem 6, we get

$$\begin{aligned} \begin{array}{l} \left\| {N(x,t) - \sum \limits _{i = 0}^{{\hat{r}}} {\sum \limits _{j = 0}^{{\hat{r}}} {{n_{i,j}}{\phi _{i,{\hat{r}}}}(x)} } {\phi _{j,{\hat{r}}}}(t)} \right\| _{L^\infty (I)}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left\| {N(x,t) - \sum \limits _{i = 0}^{{\hat{r}}} {\sum \limits _{j = 0}^{{\hat{r}}} {{n_{i,j}}{L_{i, \hat{r}}}(x)} } {L_{j,{\hat{r}}}}(t)} \right\| _{L^\infty (I)} \le c{{{\hat{r}}}^{ \frac{3}{4}- \mu }}{\left| N \right| _{{H^{\mu ;{\hat{r}}}}(I)}}.\, \end{array} \end{aligned}$$
(53)

Definition 4

The beta function is defined by the integral as [44]

$$\begin{aligned} B(n,m) = \int _0^1 {{s^{n - 1}}{{(1 - s)}^{m - 1}}} ds,\, \end{aligned}$$
(54)

additionally, the definition of the beta function in terms of the gamma function is provided as follows:

$$\begin{aligned} B(n, m) = \frac{\Gamma (n)\Gamma (m)}{\Gamma (n + m)}. \end{aligned}$$
(55)

Lemma 2

Suppose that \(n,~m \in (0,1)\). Subsequently, the following relation holds:

$$\begin{aligned} \int _0^t {{s^{n - 1}}{{(t - s)}^{m - 1}}} ds = {t^{n + m - 1}}\,B(n, m) = {t^{n +m - 1}}\frac{{\Gamma (n)\Gamma (m)}}{{\Gamma (n + m)}}. \end{aligned}$$
(56)

Proof

It can be proved easily by using a simple change of variable and applying Eqs. (54) and (55).

Now, we will carry the convergence analysis of the suggested approach when applied to A-R-L FFIDEs. \(\square \)

Theorem 7

Consider the A-R-L FFIDEs presented in Eq. (25), where \(N(x,t) \in {H^\mu }(I)\) represents the exact solution of the problem and \(N^*(x,t)\) be the approximate solution of the problem which is acquired through the proposed approach. Then, we have

$$\begin{aligned} {\left\| {N(x,t)-N^*(x,t)} \right\| _{{L^\infty }(I)}} \le \,c{\lambda ^*}{{{\tilde{r}}}^{\frac{{11}}{4} - \mu }}{\left| N \right| _{{H^{\mu ,{\tilde{r}}}}(I)}}, \end{aligned}$$
(57)

where

$$\begin{aligned} {\lambda ^*} = 1 + \lambda \left( {\frac{{\alpha \beta \,\Gamma (\beta ){{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) , \end{aligned}$$
$$\begin{aligned} \lambda = \left( {{\lambda _1} + {\lambda _2} + {\lambda _3} + {\gamma _1}{\lambda _{{\mathcal {K} _1}}} + {\gamma _2}{\lambda _{{\mathcal {K} _2}}}}\right) , \end{aligned}$$

provided that \({{\hat{r}}}\) is sufficiently large.

Proof

Let \(e(x,t)=N(x,t)-N^*(x,t)\) denote the error function. By subtracting Eq. (46) from Eq. (25), fractal-fractional integration, and applying a norm to both sides, yields

$$\begin{aligned} \begin{array}{l} {\left\| {e(x,t)} \right\| _{{L^\infty }(I)}} \le {\left\| {N(x,0) - {N^*}(x,0)} \right\| _{{L^\infty }(I)}}\\ +\, {\left\| {{}_0^{FFM}I_t^{\alpha ,\beta }\Theta (x,t,N(x,t),\frac{{\partial N}}{{\partial x}}, \frac{{{\partial ^2}N}}{{\partial {x^2}}}) - {}_0^{FFM}I_t^{\alpha ,\beta }\Theta (x,t,{N^*}(x,t), \frac{{\partial {N^*}}}{{\partial x}},\frac{{{\partial ^2}{N^*}}}{{\partial {x^2}}})} \right\| _{{L^\infty }(I)}}\\ +\, {\gamma _1}{\left\| {{}_0^{FFM}I_t^{\alpha ,\beta }({\Xi _1}N(x,t)) - {}_0^{FFM}I_t^{\alpha ,\beta }(\Xi _1 N^*(x,t))} \right\| _{{L^\infty }(I)}}\\ + \,{\gamma _2}{\left\| {{}_0^{FFM}I_t^{\alpha ,\beta }({\Xi _2}N(x,t)) - {}_0^{FFM}I_t^{\alpha ,\beta }(\Xi _2 N^*(x,t))} \right\| _{{L^\infty }(I)}}, \end{array} \end{aligned}$$
(58)

in which \({\Xi _1}\) and \({\Xi _2}\) are given in Eq. (32). From Eqs. (28) and (51), we find

$$\begin{aligned} \begin{array}{l} {\left\| {\Theta (x,t,N(x,t),\frac{{\partial N(x,t)}}{{\partial x}},\frac{{{\partial ^2}N(x,t)}}{{\partial {x^2}}}) - \Theta (x,t,{N^*}(x,t),\frac{{\partial {N^*}(x,t)}}{{\partial x}},\frac{{{\partial ^2}{N^*}(x,t)}}{{\partial {x^2}}})} \right\| _{{L^\infty }(I)}}\,\,\,\\ \,\,\\ \le \,\, {\lambda _1}{\left\| {N(x,t) - {N^*}(x,t)} \right\| _{{L^\infty }(I)}} + {\lambda _2}{\left\| {\frac{{\partial N(x,t)}}{{\partial x}} - \frac{{{N^*}(x,t)}}{{\partial x}}} \right\| _{{L^\infty }(I)}} \\ \\ \quad +\,\, {\lambda _3}{\left\| {\frac{{{\partial ^2}N(x,t)}}{{\partial {x^2}}} - \frac{{{\partial ^2}{N^*}(x,t)}}{{\partial {x^2}}}} \right\| _{{L^\infty }(I)}} \le \left( {{\lambda _1} + {\lambda _2} + {\lambda _3}} \right) \left\| {N(x,t) - {N^*}(x,t)} \right\| _{{L^\infty }(I)}^*. \end{array} \end{aligned}$$
(59)

By using the definition of the fractional integral and Eq. (59) we obtain

$$\begin{aligned}\begin{array}{l} \left| {{}_0^{FFM}I_{t}^{\alpha ,\beta }\Theta (x,t,N(x,t),\frac{{\partial N}}{{\partial x}}, \frac{{{\partial ^2}N}}{{\partial {x^2}}}) - {}_0^{FFM}I_{t}^{\alpha ,\beta }\Theta (x,t,{N^*}(x,t), \frac{{\partial {N^*}}}{{\partial x}},\frac{{{\partial ^2}{N^*}}}{{\partial {x^2}}})} \right| \\ \\ \le \,\, \frac{{\alpha \beta }}{{\Delta (\alpha )\Gamma (\alpha )}}\int _0^t {\left| {{s^{\beta - 1}} {{(t - s)}^{\alpha - 1}}} \right| \left| {\Theta (x,s,N,\frac{{\partial N }}{{\partial x}},\frac{{{\partial ^2}N}}{{\partial {x^2}}}) - \Theta (x,s,{N^*},\frac{{\partial {N^*}}}{{\partial x}},\frac{{{\partial ^2}{N^*}}}{{\partial {x^2}}})} \right| } \,ds\\ \\ \quad +\,\, \frac{{\beta (1 - \alpha )}}{{\Delta (\alpha )}}\left| {{t^{\beta - 1}}} \right| \left| {\Theta (x,t,N(x,t),\frac{{\partial N}}{{\partial x}},\frac{{{\partial ^2}N}}{{\partial {x^2}}}) - \Theta (x,t,{N^*}(x,t),\frac{{\partial {N^*}}}{{\partial x}},\frac{{{\partial ^2}{N^*}}}{{\partial {x^2}}})} \right| \le \\ \\ \quad \,\, \frac{{\alpha \beta }}{{\Delta (\alpha )\Gamma (\alpha )}}\int _0^t {\left| {{s^{\beta - 1}} {{(t - s)}^{\alpha - 1}}} \right| {{\left\| {\Theta (x,s,N,\frac{{\partial N}}{{\partial x}}, \frac{{{\partial ^2}N}}{{\partial {x^2}}}) - \Theta (x,s,{N^*},\frac{{\partial {N^*}}}{{\partial x}},\frac{{{\partial ^2}{N^*}}}{{\partial {x^2}}})} \right\| }_{L^\infty (I)} }} \,ds\\ \\ \quad \,\, +\frac{{\beta (1 - \alpha )}}{{\Delta (\alpha )}}\left| {{t^{\beta - 1}}} \right| {\left\| {\Theta (x,t,N(x,t), \frac{{\partial N}}{{\partial x}},\frac{{{\partial ^2}N}}{{\partial {x^2}}}) - \Theta (x,t,{N^*}(x,t), \frac{{\partial {N^*}}}{{\partial x}},\frac{{{\partial ^2}{N^*}}}{{\partial {x^2}}})} \right\| _{L^\infty (I)} }\\ \\ \le \left( {\frac{{\alpha \beta }}{{\Delta (\alpha )\Gamma (\alpha )}}\int _0^t {\left| {{s^{\beta - 1}} {{(t - s)}^{\alpha - 1}}} \right| } \,ds + \frac{{\beta (1 - \alpha )\left| {{t^{\beta - 1}}} \right| }}{{\Delta (\alpha )}}} \right) \left( \lambda _1 + \lambda _2 + \lambda _3 \right) \left\| {N - {N^*}} \right\| ^* _{L^\infty (I)}, \end{array}\end{aligned}$$

using \(0<s<t<1\) and Lemma 2 leads to

$$\begin{aligned}&\left| {{}_0^{FFM}I_t^{\alpha ,\beta }\Theta (x,t,N(x,t),\frac{{\partial N}}{{\partial x}},\frac{{{\partial ^2}N}}{{\partial {x^2}}}) - {}_0^{FFM}I_t^{\alpha ,\beta }\Theta (x,t,{N^*}(x,t),\frac{{\partial {N^*}}}{{\partial x}},\frac{{{\partial ^2}{N^*}}}{{\partial {x^2}}})} \right| \\ {}&\quad \le \left( {\frac{{\alpha \beta }}{{\Delta (\alpha )\Gamma (\alpha )}}\int _0^t {{s^{\beta - 1}}{{(t - s)}^{\alpha - 1}}} \,ds + \frac{{\beta (1 - \alpha ){t^{\beta - 1}}}}{{\Delta (\alpha )}}} \right) \left( {{\lambda _1} + {\lambda _2} + {\lambda _3}} \right) \left\| {N - {N^*}} \right\| _{{L^\infty }(I)}^*\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\&\quad \le \left( {\frac{{\alpha \beta \,\Gamma (\beta )\mathop {\max }\limits _{t \in (0,1)} \left| {{t^{\alpha + \beta - 1}}} \right| }}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha )\mathop {\max }\limits _{t \in (0,1)} \left| {{t^{\beta - 1}}} \right| }}{{\Delta (\alpha )}}} \right) \left( {{\lambda _1} + {\lambda _2} + {\lambda _3}} \right) \left\| {N - {N^*}} \right\| _{{L^\infty }(I)}^*\\&\quad \le \left( {\frac{{\alpha \beta \,\Gamma (\beta ){{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) \left( {{\lambda _1} + {\lambda _2} + {\lambda _3}} \right) \left\| {N - {N^*}} \right\| _{{L^\infty }(I)}^*, \end{aligned}$$

so, we have

$$\begin{aligned} \begin{array}{l} {\left\| {{}_0^{FFM}I_t^{\alpha ,\beta }\Theta (x,t,N(x,t),\frac{{\partial N}}{{\partial x}}, \frac{{{\partial ^2}N}}{{\partial {x^2}}}) - {}_0^{FFM}I_t^{\alpha ,\beta }\Theta (x,t,{N^*}(x,t),\frac{{\partial {N^*}}}{{\partial x}},\frac{{{\partial ^2}{N^*}}}{{\partial {x^2}}})} \right\| _{{L^\infty }(I)}}\\ \\ \le \left( {\frac{{\alpha \beta \,\Gamma (\beta ){{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) \left( {{\lambda _1} + {\lambda _2} + {\lambda _3}} \right) \left\| {N - {N^*}} \right\| _{{L^\infty }(I)}^*. \end{array} \end{aligned}$$
(60)

It requires one to estimate \(\left\| {{}_0^{FFM}I_t^{\alpha ,\beta }\,({\Xi _1}N(x,t)) - {}_0^{FFM}I_t^{\alpha ,\beta }\,(\Xi _1 N^*(x,t))} \right\| _{L^\infty (I)}\). It follows from Eqs. (29) and (32) that

$$\begin{aligned} \begin{array}{l} \left| {\,{\Xi _1}N(x,t) - \,\Xi _1 N^*(x,t)} \right| \\ \\ \le \int _0^1 {\int _0^1 {\left| {{\mathcal {K} _1} (x,t,\Im ,\wp ,\frac{{{\partial ^i}N(\Im ,\wp )}}{{\partial {\Im ^i}}}) - {\mathcal {K} _1} (x,t,\Im ,\wp ,\frac{{{\partial ^i}{N^*}(\Im ,\wp )}}{{\partial {\Im ^i}}})} \right| d\Im d\wp } } \\ \\ \le \int _0^1 {\int _0^1 {{{\left\| {{\mathcal {K} _1}(x,t,\Im ,\wp ,\frac{{{\partial ^i}N(\Im ,\wp )}}{{\partial {\Im ^i}}}) - {\mathcal {K} _1}(x,t,\Im ,\wp ,\frac{{{\partial ^i}{N^*}(\Im ,\wp )}}{{\partial {\Im ^i}}})} \right\| }_{{L^\infty }(I)}}d\Im d\wp } } \\ \\ \le \int _0^1 {\int _0^1 {{\lambda _{{\mathcal {K} _1}}}{{\left\| {\frac{{{\partial ^i}N(\Im ,\wp )}}{{\partial {\Im ^i}}}-\frac{{{\partial ^i}{N^*}(\Im ,\wp )}}{{\partial {\Im ^i}}}} \right\| }_{{L^\infty }(I)}}d\Im d\wp } } \le {\lambda _{{\mathcal {K} _1}}}{\left\| {\frac{{{\partial ^i}N(\Im ,\wp )}}{{\partial {\Im ^i}}}-\frac{{{\partial ^i}{N^*} (\Im ,\wp )}}{{\partial {\Im ^i}}}} \right\| _{{L^\infty }(I)}}, \end{array} \end{aligned}$$
(61)

consequently, from Definition 3, Lemma 2 and Eq. (61) we obtain

$$\begin{aligned} \begin{array}{l} \left| {{}_0^{FFM}I_t^{\alpha ,\beta }\,({\Xi _1}N(x,t)) - {}_0^{FFM}I_t^{\alpha ,\beta }\,(\Xi _1 N^*(x,t))} \right| \\ \\ \le \,\, \frac{{\alpha \beta }}{{\Delta (\alpha )\Gamma (\alpha )}}\int _0^t {{s^{\beta - 1}}{{(t - s)}^{\alpha - 1}}\left| {{\Xi _1}N (x,s) - \Xi _1 N^*(x,s)} \right| } \,ds\\ \\ \quad + \,\,\frac{{\beta (1 - \alpha ){t^{\beta - 1}}}}{{\Delta (\alpha )}}\left| {{\Xi _1}N(x,t) - \Xi _1 N^*(x,t)} \right| \\ \\ \le \,\, \frac{{\alpha \beta {\lambda _{{\mathcal {K} _1}}}}}{{\Delta (\alpha )\Gamma (\alpha )}}\int _0^t {{s^{\beta - 1}}{{(t - s)}^{\alpha - 1}}{{\left\| {\frac{{{\partial ^i}N(\Im ,\wp )}}{{\partial {\Im ^i}}} - \frac{{{\partial ^i}{N^*}(\Im ,\wp )}}{{\partial {\Im ^i}}}} \right\| }_{{L^\infty }(I)}}} ds \\ \\ \quad +\,\, \frac{{\beta (1 - \alpha ){t^{\beta - 1}}{\lambda _{{\mathcal {K} _1}}}}}{{\Delta (\alpha )}} {\left\| {\frac{{{\partial ^i}N(\Im ,\wp )}}{{\partial {\Im ^i}}} - \frac{{{\partial ^i}{N^*}(\Im ,\wp )}}{{\partial {\Im ^i}}}} \right\| _{{L^\infty }(I)}}\\ \\ \le \,\, \left( {\frac{{\alpha \beta \,\Gamma (\beta )\mathop {\max }\limits _{t \in (0,1)} \left| {{t^{\alpha + \beta - 1}}} \right| }}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha )\mathop {\max }\limits _{t \in (0,1)} \left| {{t^{\beta - 1}}} \right| }}{{\Delta (\alpha )}}} \right) \,{\lambda _{{\mathcal {K} _1}}}\,{\left\| {\frac{{{\partial ^i}N(\Im ,\wp )}}{{\partial {\Im ^i}}} - \frac{{{\partial ^i}{N^*}(\Im ,\wp )}}{{\partial {\Im ^i}}}} \right\| _{{L^\infty }(I)}}\\ \\ \le \,\, \left( {\frac{{\alpha \beta \,\Gamma (\beta ){{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) \,{\lambda _{{\mathcal {K} _1}}}\,\left\| {N - {N^*}} \right\| _{{L^\infty }(I)}^*. \end{array} \end{aligned}$$
(62)

Moreover, we need to estimate \(\left\| {{}_0^{FFM}I_t^{\alpha ,\beta }({\Xi _2}N(x,t)) - {}_0^{FFM}I_t^{\alpha ,\beta }(\Xi _2 N^*(x,t))} \right\| _{L^\infty (I)}\). By using Eqs. (30) and (32) we get

$$\begin{aligned} \begin{array}{l} \left| {\,{\Xi _2}N(x,t) - \,\Xi _2 N^*(x,t)} \right| \\ \\ \le \int _0^x {\int _0^t {\left| {{\mathcal {K} _2}(x,t,\Im ,\wp ,\frac{{{\partial ^j}N(\Im ,\wp )}}{{\partial {\Im ^j}}}) - {\mathcal {K} _2}(x,t,\Im ,\wp ,\frac{{{\partial ^j}{N^*}(\Im ,\wp )}}{{\partial {\Im ^j}}})} \right| d\Im d\wp } } \\ \,\,\,\,\,\,\,\,\\ \le \int _0^x {\int _0^t {{{\left\| {{\mathcal {K} _2}(x,t,\Im ,\wp ,\frac{{{\partial ^j}N(\Im ,\wp )}}{{\partial {\Im ^j}}}) - {\mathcal {K} _2}(x,t,\Im ,\wp ,\frac{{{\partial ^j}{N^*}(\Im ,\wp )}}{{\partial {\Im ^j}}})} \right\| }_{{L^\infty }(I)}}d\Im d\wp } } \\ \\ \le \int _0^x {\int _0^t {{\lambda _{{\mathcal {K} _2}}}{{\left\| {\frac{{{\partial ^j}N(\Im ,\wp )}}{{\partial {\Im ^j}}} - \frac{{{\partial ^j}{N^*}(\Im ,\wp )}}{{\partial {\Im ^j}}}} \right\| }_{{L^\infty }(I)}}d\Im d\wp } } \le {\lambda _{{\mathcal {K} _2}}}{\left\| {\frac{{{\partial ^j}N(\Im ,\wp )}}{{\partial {\Im ^j}}} - \frac{{{\partial ^j}{N^*}(\Im ,\wp )}}{{\partial {\Im ^j}}}} \right\| _{{L^\infty }(I)}}, \end{array} \end{aligned}$$
(63)

thus we conclude with the assistance of definition of the fractal–fractional integral, Lemma 2 and Eq. (63) that

$$\begin{aligned} \begin{array}{l} \left| {{}_0^{FFM}I_t^{\alpha ,\beta }\,({\Xi _2}N(x,t)) - {}_0^{FFM}I_t^{\alpha ,\beta }\,(\Xi _2 N^*(x,t))} \right| \,\\ \\ \le \frac{{\alpha \beta }}{{\Delta (\alpha )\Gamma (\alpha )}}\int _0^t {{s^{\beta - 1}}{{(t - s)}^{\alpha - 1}} \left| {{\Xi _2}N(x,s) - \Xi _2 N^*(x,s)} \right| } \,ds \\ \\ + \frac{{\beta (1 - \alpha ){t^{\beta - 1}}}}{{\Delta (\alpha )}} \left| {{\Xi _2}N(x,t) - \Xi _2 N^*(x,t)} \right| \\ \\ \,\,\, \le \frac{{\alpha \beta {\lambda _{{\mathcal {K} _2}}}}}{{\Delta (\alpha )\Gamma (\alpha )}}{\int _0^t {{s^{\beta - 1}} {{(t - s)}^{\alpha - 1}}\left\| {\frac{{{\partial ^j}N(\Im ,\wp )}}{{\partial {\Im ^j}}} - \frac{{{\partial ^j}{N^*}(\Im ,\wp )}}{{\partial {\Im ^j}}}} \right\| } _{{L^\infty }(I)}}ds \\ \\ \quad + \frac{{\beta (1 - \alpha ){t^{\beta - 1}}{\lambda _{{\mathcal {K} _2}}}}}{{\Delta (\alpha )}}{\left\| {\frac{{{\partial ^j}N(\Im ,\wp )}}{{\partial {\Im ^j}}} - \frac{{{\partial ^j}{N^*}(\Im ,\wp )}}{{\partial {\Im ^j}}}} \right\| _{{L^\infty }(I)}}\\ \\ \,\,\, \le \left( {\frac{{\alpha \beta \,\Gamma (\alpha + \beta )\mathop {\max }\limits _{t \in (0,1)} \left| {{t^{\alpha + \beta - 1}}} \right| }}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha )\mathop {\max }\limits _{t \in (0,1)} \left| {{t^{\beta - 1}}} \right| }}{{\Delta (\alpha )}}} \right) \,{\lambda _{{\mathcal {K} _2}}}\,{\left\| {\frac{{{\partial ^j}N}}{{\partial {\Im ^j}}} - \frac{{{\partial ^j}{N^*}}}{{\partial {\Im ^j}}}} \right\| _{{L^\infty }(I)}}\\ \\ \,\,\, \le \left( {\frac{{\alpha \beta \,\Gamma (\beta ) {{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) \,{\lambda _{{\mathcal {K} _2}}}\,\left\| {N - {N^*}} \right\| _\infty ^*.\,\,\,\, \end{array} \end{aligned}$$
(64)

Now, by using Eqs. (58)–(64) we obtain

$$\begin{aligned}{} & {} {\left\| {e(x,t)} \right\| _{{L^\infty }(I)}} \le {\left\| {N(x,0) - {N^*}(x,0)} \right\| _{{L^\infty }(I)}}\nonumber \\{} & {} \quad + \left( {\frac{{\alpha \beta \,\Gamma (\beta ){{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) \left( {{\lambda _1} + {\lambda _2} + {\lambda _3}} \right) \left\| {N - {N^*}} \right\| _{{L^\infty }(I)}^*\nonumber \\{} & {} \quad + \left( {\frac{{\alpha \beta \,\Gamma (\beta ){{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) \,({\gamma _1}{\lambda _{{\mathcal {K} _1}}} + {\gamma _2}{\lambda _{{\mathcal {K} _2}}})\,\left\| {N - {N^*}} \right\| _\infty ^* \nonumber \\{} & {} \quad \le \left\| {N - {N^*}} \right\| _\infty ^* + \lambda \left( {\frac{{\alpha \beta \,\Gamma (\beta ){{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) \,\left\| {N - {N^*}} \right\| _{{L^\infty }(I)}^*\nonumber \\{} & {} \quad \, = \left( {1 + \lambda \left( {\frac{{\alpha \beta \,\Gamma (\beta ){{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) } \right) \left\| {N - {N^*}} \right\| _{{L^\infty }(I)}^*, \end{aligned}$$
(65)

where

$$\begin{aligned}\lambda = \left( {{\lambda _1} + {\lambda _2} + {\lambda _3} + {\gamma _1}{\lambda _{{\mathcal {K} _1}}} + {\gamma _2}{\lambda _{{\mathcal {K} _2}}}} \right) .\,\,\end{aligned}$$

By employing Theorem 6 for \(N(x,t) \in H^{\mu ;{\hat{r}}}(I)\), we can derive that

$$\begin{aligned} {\left\| {\frac{{{\partial ^r}N(x,t)}}{{\partial {x^r}}} - \frac{{{\partial ^r}{N^*}(x,t)}}{{\partial {x^r}}}} \right\| _{{L^\infty }(I)}} \le c{{{\tilde{r}}}^{\frac{3}{4} - (\mu - r)}}{\left| N \right| _{{H^{\mu ,{\tilde{r}}}}(I)}},\,\,\,r = 0,1,2. \end{aligned}$$
(66)

Finally, from Eqs. (51), (65) and (66), we find the upper bound for \(\left\| e(x,t) \right\| _{L^\infty (I)}\) as following

$$\begin{aligned}{\left\| {e(x,t)} \right\| _{{L^\infty }(I)}} \le \,c{\lambda ^*}{{\tilde{r}}^{\frac{{11}}{4} - \mu }}{\left| N \right| _{{H^{\mu ,\tilde{r}}}(I)}},\end{aligned}$$

where

$$\begin{aligned}{\lambda ^*} = 1 + \lambda \left( {\frac{{\alpha \beta \,\Gamma (\beta ) {{\left\| {{t^{\alpha + \beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )\Gamma (\alpha + \beta )}} + \frac{{\beta (1 - \alpha ){{\left\| {{t^{\beta - 1}}} \right\| }_{{L^\infty }(I)}}}}{{\Delta (\alpha )}}} \right) ,\end{aligned}$$

and this completes the proof. \(\square \)

6 Illustrative examples

We now present several numerical tests in order to investigate the applicability and accuracy of the mentioned approach.

Example 1

Take into account the following FFIDEs [14]:

$$\begin{aligned} {}^{FFM}D^{\alpha , \beta }_{t}N(x, t)-\frac{\partial ^{2}N(x, t)}{\partial x^{2}}+N(x, t)+\int _{0}^{x}\int _{0}^{t}\sin (t -\wp ) N^{2}(\Im , \wp ) d\wp d\Im = \mathcal {F}(x, t), \end{aligned}$$
(67)

where

$$\begin{aligned} \mathcal {F}(x, t)=xt+\frac{x^{3}}{3}(2\cos (t) + t^{2}-2)+\frac{\Delta (\alpha )t^{2-\beta }}{\beta (1-\alpha )} E_{\alpha , 2}(\frac{-\alpha t^{\alpha }}{1-\alpha }), \end{aligned}$$

incorporating the initial and boundary conditions

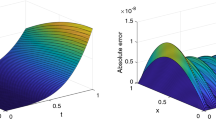
$$\begin{aligned} N(x, 0)=0, \hspace{1cm} N(0, t)=0, \hspace{1cm}N(1, t)=t. \end{aligned}$$

The precise solution to this issue is \(N(x, t)=xt.\) In this example, we have employed the proposed strategy in this paper. The absolute errors (AEs) and CPU time used (in seconds) for \(M = M'=2\) and various options of \(\alpha ,~\beta \) are outlined in Table 1. The findings indicate that when \(\alpha \) is near 1, the numerical solution is close to the precise solution. Numerical results (NRs), contour plot (CP) of NRs and absolute error with \(M = M'= 2\) and \(\alpha =~\beta =0.99\) are shown in Fig. 1. Plot of the NRs and AEs together with the CP for \(M = M'= 2\) and \(\alpha =~\beta =0.95\) are displayed in Fig. 2. Furthermore, the numerical outcomes obtained through the current approach for \(M = M'= 1\) and diverse values of \(\alpha ,~\beta ,~x\) are given in Fig. 3. The results show that the approximate solution has a high agreement with the exact solution.

Table 1 The AE values of ChPs method for \(M=M'=2\) and different choices of \(\alpha , \beta \) (Example 1)
Full size table
Fig. 1
figure 1

(a): NRs, (b): CP and (c): AE values for \(M=M'=2 \) and \(\alpha = \beta =0.99\) (Example 1)

Full size image
Fig. 2
figure 2

(a): NRs, (b): CP of NR, (c): AE and (d): CP of AE values for \(M=M'=2 \) and \(\alpha = \beta =0.95\) (Example 1)

Full size image
Fig. 3
figure 3

The NRs for (a): \(\beta = 0.5, x=0.1,\) (b): \(\beta = 0.5, x=0.5,\) (c): \(\beta = 0.5, x=0.9,\) (d): \(\alpha =0.5, x=0.1\), (e): \(\alpha =0.5, x=0.5\) and (f): \(\alpha =0.5, x=0.9\) and \(M=M'=1\) (Example 1)

Full size image

Example 2

Examine the subsequent FFIDEs [14]

$$\begin{aligned} \begin{array}{l} N(x, t)- {}^{FFM}D^{\alpha , \beta }_{t}N(x, t)+\frac{\partial N(x, t)}{\partial x}+\frac{\partial ^{2}N(x, t)}{\partial x^{2}}\\ \\ -\int _{0}^{1}\int _{0}^{1}x\cos (\Im - \wp ) \bigg (\frac{\partial N(\Im , \wp )}{\partial \Im }\bigg )^{2} d\wp d\Im = \mathcal {F}(x, t), \end{array} \end{aligned}$$
(68)

where

$$\begin{aligned}{} & {} \mathcal {F}(x, t)=-\frac{\Delta (\alpha )t^{2-\beta }}{\beta (1- \alpha )}\sum _{i=0}^{\infty }(-1)^{i}t^{2i}E_{\alpha , 2i+1}(\frac{-\alpha t^{\alpha }}{1-\alpha })x- \frac{\Delta (\alpha ) t^{2-\beta }}{\beta (1-\alpha )}\\{} & {} \quad E_{\alpha , 2}(\frac{-\alpha t^{\alpha }}{1- \alpha })+t +\sin (t)+x\sin (t)+\frac{8}{3}(x\sin (\frac{1}{2})^{4})(\sin (\frac{1}{2})^{2}-2), \end{aligned}$$

with the initial and boundary conditions as

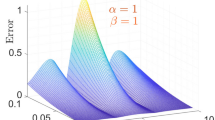
$$\begin{aligned} N(x, 0)=0, \hspace{1cm} N(0, t)=t, \hspace{1cm}N(1, t)=\sin (t)+ t. \end{aligned}$$

The analytic solution is \(N(x, t)=x\sin (t)+t.\) The numerical outcomes for this instance are documented in Table 2, and Figures 4-5. The AE values of ChPs method for \(M=M'=1\) and different choices of \(\alpha , \beta \) are presented in Table 2. Figure 4 displays the NRs and AE values for \(M=M'=1\) and \(\alpha = 0.99, \beta =0.60\). Also, plot of the NRs for \(\beta =0.1\) with \(M=M'=1 \) and varied values of x and \(\alpha \) are displayed in Fig. 5. The result shows that the approximate solution has a high agreement with the exact solution.

Example 3

Take into account the FFIDEs presented below [14]

$$\begin{aligned} {}^{FFM}D^{\alpha , \beta }_{t}N(x, t){} & {} +N(x, t)-\int _{0}^{x}\int _{0}^{t} (\Im + \cos (\wp ))N(\Im , \wp )d\wp d\Im \nonumber \\{} & {} +\int _{0}^{1}\int _{0}^{1} N(\Im , \wp )d\wp d\Im = \mathcal {F}(x, t), \end{aligned}$$
(69)

where

$$\begin{aligned} \mathcal {F}(x, t){} & {} =x\sin (t)-\frac{x^{2}}{4}+\frac{x^{2}\cos ^{2}(t)}{4}+\frac{x^{3}\cos (t)}{3}-\frac{x^{3}}{3}+\sin ^{2}(\frac{1}{2})\\{} & {} +\frac{\Delta (\alpha ) t^{2-\beta }}{\beta (1- \alpha )} \sum _{i=0}^{\infty } (-1)^{i}t^{2i}E_{\alpha , 2i+1}(\frac{-\alpha t^{\alpha }}{1- \alpha }), \end{aligned}$$

incorporating the initial and boundary conditions as

$$\begin{aligned} N(x, 0)=0, \hspace{1cm} N(0, t)=0, \hspace{1cm}N(1, t)=\sin (t). \end{aligned}$$

The analytic solution is \(N(x, t)=x\sin (t).\) The numerical outcomes for this instance are documented in Table 3, Fig. 6 and Fig. 7. In Table 3, we compare the absolute errors acquired through the suggested method, considering various selections of \(\alpha ,\beta , M\) and \(M'\) with the results given in [14]. Based on these findings, it is evident that the numerical solutions approach the exact one with \(M=M'=2,3\) and different choices of \(\alpha ,\beta \). Figure 6 displays NRs and CP of NRs with \(M =M'= 2\) and \(\alpha =0.4,~\beta =0.1\). In Fig. 7, the NRs given for \(M =M'=1\) and varied values of \(\alpha ,~\beta \) and x.

Table 2 The AE values of ChPs method for \(M=M'=1\) and different choices of \(\alpha , \beta \) (Example 2)
Full size table
Fig. 4
figure 4

(a): NRs and (b): AE values for \(M=M'=1 \) and \(\alpha = 0.99, \beta =0.60\) (Example 2)

Full size image
Fig. 5
figure 5

The NRs for \(\beta =0.1\) (a): \( x=0.1,\) (b): \(x=0.5,\) (c): \(x=0.9\) with \(M=M'=1\) and different values of \(\alpha \) (Example2)

Full size image
Fig. 6
figure 6

(a): NRs, (b): CP for \(M=M'=2 \) and \(\alpha = 0.4, \beta =0.1\) (Example 3)

Full size image
Fig. 7
figure 7

The NRs for (a): \(\beta = 0.3, x=0.1,\) (b): \(\beta = 0.3, x=0.5,\) (c): \(\beta = 0.3, x=0.9,\) (d): \(\alpha =0.3, x=0.1\), (e): \(\alpha =0.3, x=0.5\), and (f): \(\alpha =0.3, x=0.9\), and \(M=M'=1\) (Example 3)

Full size image

7 Conclusion

We develop novel computational approach for solving fractal-fractional integro-differential equations in A-R-L sense. To reach this goal, we have used Chelyshkov collocation scheme based on OMs, we achieve these matrices with high accuracy, for first time. By this method, the FFIDE is converted into a set of algebraic equations, solvable through conventional numerical methods and due to the computational complexity, it requires few computational efforts. We have derived sufficient conditions for the existence and uniqueness of the solution by using the Banach’s contraction theorem. An error analysis of this new scheme is given. Finally, we have examined and resolved three test problems to demonstrate the effectiveness and accuracy of the proposed technique. We offer the following works in the future:

Table 3 The comparison of the AE values and CPU time (Example 3)
Full size table

  • This method can be used to solve different problems such as fractal-fractional partial differential equations, fractal-fractional pantograph differential equations, fractal-fractional stochastic equations and so forth.

  • We can use the wavelets base instead of the polynomials base.

  • We can apply neural network and least squares-support vector regression for solving the proposed problem.

  • Stability analysis of the suggested schemes for the numerical approximation of the problem under study is an interesting problem for future works.