Controllability of fractional dynamical systems with $(k,\psi )$-Hilfer fractional derivative

Abstract

In this article, we study the controllability of dynamical systems with $(k,\psi )$-Hilfer fractional derivative. The Gramian matrix is used to get a necessary and sufficient controllability requirement for linear systems, which are characterized by the Mittag–Leffler (M–L) functions, while the fixed point approach is used to arrive at adequate controllability criteria for nonlinear systems. The novel feature of this study is to inquire into the controllability notion by using $(k,\psi )$-Hilfer fractional derivative, the most generalized variant of the Hilfer derivative. The advantage of this type of fractional derivative is that it recovers the majority of earlier studies on fractional differential equations (FDEs). Finally, we provide numerical examples to illustrate our main results.

1 Introduction

Nowadays, differential equations involving fractional order derivatives are receiving increasing interest in the scientific community due to numerous applications in widespread areas of sciences and engineerings such as signal processing, wave propagation, robotics and models of medicines, etc. [1]. The research publications [2,3,4,5] can be reviewed by the readers on the theory of fractional differential systems. The Hilfer fractional derivative [6] has the technical property that makes it significantly more relevant than other fractional derivatives since it unifies the Riemann–Liouville (R–L) and Caputo fractional derivatives. Due to this reason, Hilfer fractional derivatives are stronger mathematical tools for studying real-world occurrences and the resulting technical advancements [7]. Sousa and Oliveira introduced a new fractional derivative [8] called “$\psi$-Hilfer fractional derivative”, which generalizes several earlier fractional derivatives. The advantage of this type of fractional derivative is the flexibility to choose the kernel $\psi$, which enables the unification and recovery of most earlier studies of FDEs. The importance of $\psi$-Hilfer FDEs has made studying these kinds of equations essential.

The concept of k-gamma function was introduced in 2007 by Díaz and Pariguan [9]. They generalized the Euler gamma function $\Gamma (.)$ as

$$\begin{aligned} \Gamma _{k}(z)=\int \limits _{0}^{\infty }r^{z-1}e^{\frac{-r^{k}}{k}}dr,~z\in \mathbb {C,}~\text {Re}(z)>0,k>0~(k\in {\mathbb {R}}). \end{aligned}$$

For $k\rightarrow 1$, we obtain $\Gamma _{k}(z)\rightarrow \Gamma (z)$. Many definitions of fractional derivatives and integrals depend on the Euler gamma function. Using the definition of k-gamma function, Kucche and Mali [10] proposed a most generalized version of the Hilfer derivative so-called $(k,\psi )$-Hilfer fractional derivative. One can obtain the $(k,\psi )$-R–L and $(k,\psi )$-Caputo fractional derivatives as a particular case of $(k,\psi )$-Hilfer fractional derivative. We listed the various fractional derivatives [8, 10,11,12,13] that are particular cases of $(k,\psi )$-Hilfer fractional derivative in Table 1.

Controllability is one of the fundamental concepts in mathematical control theory. The controllability of a dynamical system means it steers a dynamical system from an arbitrary initial state to a desired final state by using a set of admissible controls. The controllability of nonlinear systems in finite dimensional spaces has been studied extensively using fixed point theorems [14,15,16,17]. Many authors [18,19,20] have established controllability results for linear and nonlinear fractional dynamical systems in finite dimensional spaces using Gramian matrix and rank condition. More recently, Selvam et al. [21] studied the controllability of fractional dynamical systems with $\psi$-Caputo fractional derivative. Yet, to our knowledge, no research on the controllability of nonlinear fractional dynamical systems with $(k,\psi )$-Hilfer fractional derivative has been published. Therefore, in this paper, we study the controllability of nonlinear fractional dynamical systems with $(k,\psi )$-Hilfer fractional derivative using the Gramian matrix and Schauder fixed point theorem.

Consider the nonlinear FDEs involving $(k,\psi )$-Hilfer fractional derivative

$$\begin{aligned} {\left\{ \begin{array}{ll} ^{k,H}\textrm{D}_{\beta _{1}^{+}}^{\delta ,\gamma ;\psi }w(s)=Aw(s)+Bu(s)+g(s,w(s),u(s)),\quad s\in (\beta _{1},\beta _{2}],\quad k\in (0,\infty ),\\ ^{k}\textrm{I}_{\beta _{1}^{+}}^{k-\mu _{k};\psi }w(\beta _{1})=w_{\beta _{1}},\quad \mu _{k}=\delta +\gamma (k-\delta ), \end{array}\right. } \end{aligned}$$

(1.1)

where $^{k,H}\textrm{D}_{a^{+}}^{\delta ,\gamma ;\psi }(\cdot )$ is the $(k,\psi )$-Hilfer fractional derivative of order $\delta$ and type $\gamma$ with $\delta \in (0,k)$, $0\le \gamma \le 1$, and $^{k}\textrm{I}_{a^{+}}^{k-\mu _{k};\psi }(\cdot )$ is the $(k,\psi )$-R–L fractional integral of order $k-\mu _{k}$. The vectors $w\in {\mathbb {R}}^{n}$ and $u\in {\mathbb {R}}^{m}$ are the state variable and control function respectively, $\textrm{A}$ is an $n\times n$ matrix, and $\textrm{B}$ is $n\times m$ matrix. The continuous function g is the ${\mathbb {R}}^{n}$ valued function from $[\beta _{1},\beta _{2}]\times {\mathbb {R}}^{n}\times {\mathbb {R}}^{m}$.

2 Preliminaries

In this section, we describe the notations, definitions, lemmas, and introductory information that are necessary to establish our main results.

Definition 2.1

[11] Let $d\in {\mathbb {R}},~1\le p\le \infty$ and $0<\beta _{1}<\beta _{2}<\infty .$ The space $\textrm{Y}^{p}_{d}[\beta _{1},\beta _{2}]$ is collection of complex-valued Lebesgue measurable functions on $[\beta _{1},\beta _{2}]$ for which $\parallel h\parallel _{\textrm{Y}^{p}_{d}}<\infty$, with

$$\begin{aligned} \parallel h\parallel _{\textrm{Y}^{p}_{d}}=\left( \int \limits _{\beta _{1}}^{\beta _{2}}\frac{|s^{d}h(s)|^{p}}{s}ds\right) ^{\frac{1}{p}},~ (1\le p<\infty ,~ d\in {\mathbb {R}}) \end{aligned}$$

(2.1)

and

$$\begin{aligned} \parallel h\parallel _{\textrm{Y}^{p}_{d}}=ess \underset{s\in [\beta _{1},\beta _{2}]}{\sup }\{s^{d}|h(s)|\},~ ( p=\infty ). \end{aligned}$$

(2.2)

The space $\textrm{Y}^{p}_{d}[\beta _{1},\beta _{2}]$ coincides with the space $\textrm{L}_{p}[\beta _{1},\beta _{2}]$ when $d=\frac{1}{p},$ and

$$\begin{aligned} \parallel h\parallel _{\textrm{Y}^{p}_{d}}=\left( \int \limits _{\beta _{1}}^{\beta _{2}}|h(s)|^{p}ds\right) ^{\frac{1}{p}},~ (1\le p<\infty , d\in {\mathbb {R}}) \end{aligned}$$

(2.3)

and

$$\begin{aligned} \parallel h\parallel _{\textrm{Y}^{p}_{d}}=ess \underset{s\in [\beta _{1},\beta _{2}]}{\sup }\{|h(s)|\},~ ( p=\infty ). \end{aligned}$$

(2.4)

Let $\textrm{J}=[\beta _{1},\beta _{2}]$ be an interval and $\psi :\textrm{J}\rightarrow {\mathbb {R}}^{+}$ be an increasing and positive function for all $s\in \textrm{J}$. The space $\textrm{C}_{\rho :\psi }(\textrm{J},{\mathbb {R}})$ denotes the weighted functions g defined on $\textrm{J}$, i.e.

$$\begin{aligned} \textrm{C}_{\rho :\psi }(\textrm{J},{\mathbb {R}})=\left\{ g:\textrm{J}\rightarrow {\mathbb {R}}|(\psi (.)-\psi (\beta _{1}))^{\rho }g(.)\in \textrm{C}(\textrm{J},{\mathbb {R}})\right\} ,~0\le \rho <1, \end{aligned}$$

with norm

$$\begin{aligned} \parallel g\parallel _{\textrm{C}_{\rho :\psi }(\textrm{J},{\mathbb {R}})}=\underset{s\in \textrm{J}}{\max }\left| (\psi (s)-\psi (\beta _{1})^{\rho }g(s)\right| . \end{aligned}$$

Definition 2.2

[11] Let $\psi (x)\in \textrm{C}^{1}(\textrm{J})$ with $\psi '(x)>0,\forall x\in (\beta _{1},\beta _{2})$. For $\delta >0$, the $\psi$-R–L fractional integral of a function w of order $\delta$ is defined by

$$\begin{aligned} I_{\beta _{1}^{+}}^{\delta ;\psi }w(s)=\dfrac{1}{\Gamma (\delta )}\int \limits _{\beta _{1}}^{s}\psi '(r)(\psi (s)-\psi (r))^{\delta -1}w(r)dr,\quad s>\beta _{1}, ~\delta >0. \end{aligned}$$

Definition 2.3

[11] Let $\psi (x)\in \textrm{C}^{1}(\textrm{J})$ with $\psi '(x)>0,\forall x\in (\beta _{1},\beta _{2})$. For $\delta >0$, the $\psi$-R–L fractional derivative of a function w of order $\delta$ is defined by

$$\begin{aligned}&^{RL}\textrm{D}_{\beta _{1}^{+}}^{\delta ;\psi }w(s)=\left( \dfrac{1}{\psi '(s)}\frac{d}{ds}\right) ^{m}I_{\beta _{1}^{+}}^{m-\delta ;\psi }w(s)\\&=\dfrac{1}{\Gamma (m-\delta )}\left( \dfrac{1}{\psi '(s)}\frac{d}{ds}\right) ^{m}\int \limits _{\beta _{1}}^{s}\psi '(r)(\psi (s)-\psi (r))^{m-\delta -1}w(r)dr, \quad s>\beta _{1},~\delta >0, \end{aligned}$$

where $m-1=[\delta ]$.

Definition 2.4

[11] Let $\psi (x)\in \textrm{C}^{1}(\textrm{J})$ with $\psi '(x)>0,\forall x\in (\beta _{1},\beta _{2})$. For $\delta >0$, the $\psi$-Caputo fractional derivative of a function w of order $\delta$ is defined by

$$\begin{aligned} ^{\textrm{C}}\textrm{D}_{\beta _{1}^{+}}^{\delta ;\psi }w(s)&=I_{\beta _{1}^{+}}^{m-\delta ;\psi }\left( \dfrac{1}{\psi '(s)}\frac{d}{ds}\right) ^{m}w(s), \end{aligned}$$

where $m-1=[\delta ].$

Definition 2.5

[11] Let $\psi \in \textrm{C}^{m}(\textrm{J})$ be positive function on $(\beta _{1},\beta _{2}]$ such that $\psi '(x)$ is continuous and $\psi '(x)>0,\forall x\in (\beta _{1},\beta _{2})$. Let $w\in \textrm{C}^{m}(\textrm{J})$ then the left $\psi$-Hilfer fractional derivative of w of order $\delta$ and type $\gamma$ is defined by

$$\begin{aligned} \textrm{D}_{\beta _{1}^{+}}^{\delta ,\gamma ;\psi }w(s)=I_{\beta _{1}^{+}}^{\gamma (m-\delta );\psi }\left( \dfrac{1}{\psi '(s)}\frac{d}{ds}\right) ^{m}I_{\beta _{1}^{+}}^{(1-\gamma )(m-\delta );\psi }w(s), \end{aligned}$$

(2.5)

where $m-1=[\delta ].$

Definition 2.6

[13] Let $\psi (x)\in \textrm{C}^{1}(\textrm{J})$ with $\psi '(x)>0,\forall x\in (\beta _{1},\beta _{2})$ and $w\in \textrm{Y}^{p}_{d}[\beta _{1},\beta _{2}]$. Then, the $(k,\psi )$-Riemann–Liouville fractional integral of a function w of order $\delta$ is defined by

$$\begin{aligned} ^{k}I_{\beta _{1}^{+}}^{\delta ;\psi }w(s)=\frac{1}{k \Gamma _{k}(\delta )}\int _{\beta _{1}}^{s}\psi '(r)(\psi (s)-\psi (r))^{\frac{\delta }{k} -1}w(r)dr,\quad s>\beta _{1}, ~\delta >0. \end{aligned}$$

(2.6)

Definition 2.7

[10] Let $\delta ,k\in {\mathbb {R}}_{+}=(0,\infty ),~\gamma \in [0,1],~\psi \in \textrm{C}^{m}(\textrm{J})(m\in {\mathbb {N}}),\psi '(s)\not =0, s\in \textrm{J}$ and $w\in \textrm{C}^{m}(\textrm{J})$. Then, the $(k,\psi )$-Hilfer fractional derivative of a function w of order $\delta$ and type $\gamma$ is defined by

$$\begin{aligned} ^{k,H}\textrm{D}_{\beta _{1}^{+}}^{\delta ,\gamma ;\psi }w(s){=}~^{k}I_{\beta _{1}^{+}}^{\gamma (mk-\delta );\psi }\left( \frac{k}{\psi '(s)}{\frac{d}{ds}}\right) ^{m}~^{k}I_{\beta _{1}^{+}}^{(1-\gamma )(mk-\delta );\psi }w(s),~m {=} \begin{bmatrix} \frac{\delta }{k} \end{bmatrix}.\quad \end{aligned}$$

(2.7)

Table 1 List of particular cases of $(k,\psi )$-Hilfer fractional derivatives

Definition 2.8

[23] Let $f,\psi :[\beta _{1},\infty )\rightarrow {\mathbb {R}}$ be functions such that $\psi$ is continuous and $\psi '(s)>0$ on $(\beta _{1},\beta _{2})$. Also, let $\rho ,k>0$. The $(k,\psi )$ generalized Laplace transform of f is defined as the following:

$$\begin{aligned} {\mathcal {L}}^{\rho ,\psi }_{k,\beta _{1}}\{f(s)\}(\lambda )=\int \limits _{\beta _{1}}^{\infty }e^{-\lambda k^{1-\frac{\rho }{k}}(\psi (s)-\psi (\beta _{1}))}f(s)\psi '(s)ds,~\forall \lambda \in {\mathbb {R}}. \end{aligned}$$

(2.8)

Definition 2.9

[22] Let f and h be two functions which are piecewise continuous at each interval $[\beta _{1},s]$ and of exponential order. We define the generalized convolution of f and h by

$$\begin{aligned} (f*_{\psi }h)(s)=\int \limits _{\beta _{1}}^{s}f(r)h\left( \psi ^{-1}(\psi (s)+\psi (\beta _{1})-\psi (r))\right) \psi '(r)dr,~s\in J. \end{aligned}$$

The generalized convolution of two functions is commutative.

Lemma 2.10

[23] Let f and h be two functions which are piecewise continuous at each interval $[\beta _{1},s]$ and of exponential order. Then

$$\begin{aligned} {\mathcal {L}}^{\rho ,\psi }_{k,\beta _{1}}\{f*_{\psi }h\}={\mathcal {L}}^{\rho ,\psi }_{k,\beta _{1}}\{f\}{\mathcal {L}}^{\rho ,\psi }_{k,\beta _{1}}\{h\}. \end{aligned}$$

Lemma 2.11

[23] Let $f(t)\in \textrm{C}^{m-1}_{\rho :\psi }(\textrm{J},{\mathbb {R}})$ such that $f^{[j]} (j= 0, 1,\cdots , m-1)$ are $\psi$-exponential order. Also, let $f^{[j]}$ be a piecewise continuous over every finite interval J. Then the $(k,\psi )$-generalized Laplace transform of $f^{[m]}$ exists and

$$\begin{aligned} {\mathcal {L}}^{\rho ,\psi }_{k,\beta _{1}}\left\{ f^{[m]}(s)\right\} (\lambda )=k^{m}\left[ \left( \lambda k^{1-\frac{\rho }{k}}\right) ^{m}{\mathcal {L}}^{\rho ,\psi }_{k,\beta _{1}}\left\{ f(s)\right\} -\sum _{j=0}^{m-1}\left( \lambda k^{1-\frac{\rho }{k}}\right) ^{m-j-1}f^{[j]}(\beta _{1})\right] .\nonumber \\ \end{aligned}$$

(2.9)

Lemma 2.12

[23] Let w(t) be a piecewise continuous over every finite interval $[\beta _{1},s]$ and of $\psi (t)$-exponential order. Also, let $\delta >0$ and $\psi '(t)>0.$ Then

$$\begin{aligned} {\mathcal {L}}^{\rho ,\psi }_{k,\beta _{1}}\left\{ ^{k}I_{\beta _{1}^{+}}^{\delta ;\psi }w(s)\right\} (\lambda )=\frac{ {\mathcal {L}}^{\rho ,\psi }_{k,\beta _{1}}\left\{ w(s)\right\} }{\left( \lambda k^{1-\frac{\rho }{k}}\right) ^{\frac{\delta }{k}}k^{\frac{\delta }{k}}}. \end{aligned}$$

(2.10)

Lemma 2.13

Let $w(t)\in \textrm{C}^{1}(\textrm{J})$ be a piecewise continuous and of $\psi (t)$-exponential order. Then the generalized Laplace transform of the $(k,\psi )$-Hilfer fractional derivative is given by

$$\begin{aligned} \begin{aligned}&{\mathcal {L}}^{k,\psi }_{k,\beta _{1}}\left\{ ^{k,H}\textrm{D}_{\beta _{1}^{+}}^{\delta ,\gamma ;\psi }w(s)\right\} (\lambda ) \\&= (k\lambda )^{\frac{\delta }{k}}{\mathcal {L}}^{k,\psi }_{k,\beta _{1}}\left\{ w(s)\right\} (\lambda )-(k)^{1-\frac{\gamma (k-\delta )}{k}}(\lambda )^{\frac{\gamma (\delta -k)}{k}}\left( ^{k}I_{\beta _{1}^{+}}^{(1-\gamma )(k-\delta );\psi }w\right) (\beta _{1}). \end{aligned} \end{aligned}$$

(2.11)

Proof

Using (2.7), we get

$$\begin{aligned} {\mathcal {L}}^{k,\psi }_{k,\beta _{1}}\left\{ ^{k,H}\textrm{D}_{\beta _{1}^{+}}^{\delta ,\gamma ;\psi }w(s)\right\} (\lambda )={\mathcal {L}}^{k,\psi }_{k,\beta _{1}}\left\{ ^{k}I_{\beta _{1}^{+}}^{\gamma (k-\delta );\psi }\left( \frac{k}{\psi '(s)}{\frac{d}{ds}}\right) ~^{k}I_{\beta _{1}^{+}}^{(1-\gamma )(k-\delta );\psi }w(s)\right\} (\lambda ) \end{aligned}$$

(2.12)

Also, using Lemma 2.11 and Lemma 2.12 for $\rho =k$ in (2.12), we obtain

$$\begin{aligned}{} & {} {\mathcal {L}}^{k,\psi }_{k,\beta _{1}}\left\{ ^{k,H}\textrm{D}_{\beta _{1}^{+}}^{\delta ,\gamma ;\psi }w(s)\right\} (\lambda )\\{} & {} = k(k\lambda )^{\frac{-\gamma (k-\delta )}{k}}{\mathcal {L}}^{k,\psi }_{k,\beta _{1}}\left\{ \left( ^{k}I_{\beta _{1}^{+}}^{(1-\gamma )(k-\delta );\psi }\right) ^{[1]}w(s)\right\} (\lambda )\\{} & {} = k(k\lambda )^{\frac{-\gamma (k-\delta )}{k}}\left[ \lambda {\mathcal {L}}^{k,\psi }_{k,\beta _{1}}\left\{ ^{k}I_{\beta _{1}^{+}}^{(1-\gamma )(k-\delta );\psi }w(s)\right\} - \left( ^{k}I_{\beta _{1}^{+}}^{(1-\gamma )(k-\delta );\psi }w\right) (\beta _{1})\right] \\{} & {} = (k\lambda )(k\lambda )^{\frac{-\gamma (k-\delta )}{k}}\left[ {\mathcal {L}}^{k,\psi }_{k,\beta _{1}}\left\{ ^{k}I_{\beta _{1}^{+}}^{(1-\gamma )(k-\delta );\psi }w(s)\right\} \right] \\{} & {} \quad - k(k\lambda )^{\frac{-\gamma (k-\delta )}{k}}\left( ^{k}I_{\beta _{1}^{+}}^{(1-\gamma )(k-\delta );\psi }w\right) (\beta _{1})\\{} & {} = (k\lambda )(k\lambda )^{\frac{-\gamma (k-\delta )}{k}}(k\lambda )^{\frac{(1-\gamma )(\delta -k)}{k}} {\mathcal {L}}^{k,\psi }_{k,\beta _{1}}\left\{ w(s)\right\} (\lambda )\\{} & {} \quad - k(k\lambda )^{\frac{-\gamma (k-\delta )}{k}}\left( ^{k}I_{\beta _{1}^{+}}^{(1-\gamma )(k-\delta );\psi }w\right) (\beta _{1})\\{} & {} = (k\lambda )^{\frac{\delta }{k}}{\mathcal {L}}^{k,\psi }_{k,\beta _{1}}\left\{ w(s)\right\} (\lambda )\\{} & {} \quad -(k)^{1-\frac{\gamma (k-\delta )}{k}}(\lambda )^{\frac{\gamma (\delta -k)}{k}}\left( ^{k}I_{\beta _{1}^{+}}^{(1-\gamma )(k-\delta );\psi }w\right) (\beta _{1}). \end{aligned}$$

$\square$

Definition 2.14

[5, 11] The two parameters Mittag-Leffler function is defined as

$$\begin{aligned} \textrm{E}_{\mu ,\sigma }(w)=\sum \limits _{n=0}^{\infty }\frac{w^{n}}{\Gamma (n\mu +\sigma )} \end{aligned}$$

(2.13)

for all $Re(\mu ),Re(\sigma )>0,w\in {\mathbb {C}}.$ The Mittag-Leffler function for a matrix $A_{m\times m}$ is given by

$$\begin{aligned} \textrm{E}_{\mu ,\sigma }(A)=\sum \limits _{n=0}^{\infty }\frac{A^{n}}{\Gamma (n\mu +\sigma )}. \end{aligned}$$

(2.14)

Lemma 2.15

[23] Let $Re(\mu )>0$ and $\left| \frac{K}{\lambda ^{\mu }}\right| <1.$ Then

$$\begin{aligned} {\mathcal {L}}^{k,\psi }_{k,\beta _{1}}\left[ \textrm{E}_{\mu }\left( K(\psi (s)-\psi (\beta _{1})\right) ^{\mu }\right] =\frac{\lambda ^{\mu -1}}{\lambda ^{\mu }-K} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {L}}^{k,\psi }_{k,\beta _{1}}\left[ \left( \psi (s)-\psi (\beta _{1})\right) ^{\sigma -1}\textrm{E}_{\mu ,\sigma }\left( K(\psi (s)-\psi (\beta _{1})\right) ^{\mu }\right] =\frac{\lambda ^{\mu -\sigma }}{\lambda ^{\mu }-K}. \end{aligned}$$

3 Controllability of linear systems

Now we consider the linear FDEs involving $(k,\psi )$-Hilfer fractional derivative

$$\begin{aligned} {\left\{ \begin{array}{ll} ^{k,H}\textrm{D}_{\beta _{1}^{+}}^{\delta ,\gamma ;\psi }w(s)=Aw(s)+Bu(s),~s\in (\beta _{1},\beta _{2}],~0<\delta <k,~0\le \gamma \le 1,\\ ^{k}\textrm{I}_{\beta _{1}^{+}}^{k-\mu _{k};\psi }w(\beta _{1})=w_{\beta _{1}},~\mu _{k}=\delta +\gamma (k-\delta ), \end{array}\right. } \end{aligned}$$

(3.1)

where $^{k,H}\textrm{D}_{\beta _{1}^{+}}^{\delta ,\gamma ;\psi }(.)$ is the $(k,\psi )$-Hilfer fractional derivative of order $\delta$ and type $\gamma$ and $^{k}\textrm{I}_{\beta _{1}^{+}}^{k-\mu _{k};\psi }(.)$ is the $(k,\psi )$-Riemann–Liouville fractional integral of order $k-\mu _{k}$. The vectors $w\in {\mathbb {R}}^{n}$ and $u\in {\mathbb {R}}^{m}$ are the state variable and control function respectively, $\textrm{A}$ is an $n\times n$ matrix and $\textrm{B}$ is $n\times m$ matrix.

Lemma 3.1

The solution of (3.1) is given by

$$\begin{aligned}{} & {} w(s) = k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (s)-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}} \nonumber \\{} & {} \quad +k^{\frac{-\delta }{k}} \int \limits _{\beta _{1}}^{s}\psi '(r)\left( \psi (s)-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (r))^{\frac{\delta }{k}}\right) \textrm{B}u(r)dr~ \forall s\in (\beta _{1},\beta _{2}].\nonumber \\ \end{aligned}$$

(3.2)

Proof

Applying the generalized Laplace transform to both sides of the equation (3.1) and then using Lemma 2.13, we get

$$\begin{aligned} (k\lambda )^{\frac{\delta }{k}}{\mathcal {L}}^{k,\psi }_{k,\beta _{1}}\left\{ w(s)\right\} (\lambda )-&(k)^{1-\frac{\gamma (k-\delta )}{k}}(\lambda )^{\frac{\gamma (\delta -k)}{k}}\left( ^{k}I_{\beta _{1}^{+}}^{\gamma (k-\delta );\psi }w\right) (\beta _{1})\nonumber \\ {}&= \textrm{A}{\mathcal {L}}^{k,\psi }_{k,\beta _{1}}[w(s)] + \textrm{B}{\mathcal {L}}^{k,\psi }_{k,\beta _{1}}[u(s)], \lambda >|A|^{\frac{k}{\delta }},\nonumber \\ {\mathcal {L}}^{k,\psi }_{k,\beta _{1}}[w(s)]&= \frac{k^{\left( 1-\frac{\mu _{k}}{k}\right) }\lambda ^{(\frac{\delta -\mu _{k}}{k})}}{\left( \lambda ^{\frac{\delta }{k}}I-k^{-\frac{\delta }{k}}\textrm{A}\right) }w_{\beta _{1}} + \frac{k^{-\frac{\delta }{k}}\textrm{B}}{\left( \lambda ^{\frac{\delta }{k}}I-k^{-\frac{\delta }{k}}\textrm{A}\right) }{\mathcal {L}}^{k,\psi }_{k,\beta _{1}}[u(s)]. \end{aligned}$$

(3.3)

Now taking the inverse generalized Laplace transform of equation (3.3) and using Lemma 2.15

$$\begin{aligned} w(s)&= k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (s)-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}} \\&\quad + k^{-\frac{\delta }{k}} ({\mathcal {L}}^{k,\psi }_{k,\beta _{1}})^{-1}[\textrm{B}\left( \lambda ^{\frac{\delta }{k}}I-k^{-\frac{\delta }{k}}\textrm{A}\right) ^{-1}]*_{\psi }({\mathcal {L}}^{k,\psi }_{k,\beta _{1}})^{-1}{\mathcal {L}}^{k,\psi }_{k,\beta _{1}}[u(s)] \\&= k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (s)-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}} \nonumber \\&\quad +k^{-\frac{\delta }{k}} \int \limits _{\beta _{1}}^{s}\psi '(r)\left( \psi (s)-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (r))^{\frac{\delta }{k}}\right) \textrm{B}u(r)dr. \end{aligned}$$

$\square$

Definition 3.2

The system (3.1) is said to be controllable on $\textrm{J}$, if for arbitrary $w_{\beta _{1}},w_{\beta _{2}}\in {\mathbb {R}}^{n}$, there exists a control function $u(.)\in \textrm{L}^{2}(\textrm{J},{\mathbb {R}}^{m})$ such that the solution of (3.1) satisfies $^{k}\textrm{I}_{\beta _{1}^{+}}^{k-\mu _{k};\psi }w(\beta _{1})=w_{\beta _{1}}$ and $w(\beta _{2})=w_{\beta _{2}}$.

Theorem 3.3

The system (3.1) is controllable on $\textrm{J}$ if and only if the $n\times n$ Gramian matrix

$$\begin{aligned} {\mathcal {G}}&=\int \limits _{\beta _{1}}^{\beta _{2}}\psi '(r)\left( \psi (\beta _{2})-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) \nonumber \\&\quad \times \textrm{B}\textrm{B}^{*}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}^{*}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) dr \end{aligned}$$

(3.4)

is positive definite, here $*$ denotes the matrix transpose.

Proof

Suppose that ${\mathcal {G}}$ is positive definite, then it is non-singular and therefore its inverse is well-defined. Then defining the control function

$$\begin{aligned} u(r)&=k^{-\frac{k}{\delta }}\textrm{B}^{*}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}^{*}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) {\mathcal {G}}^{-1}\nonumber \\&\times \left[ w_{\beta _{2}}{-}k^{\left( 1{-}\frac{\mu _{k}}{k}\right) }(\psi (\beta _{2}){-}\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2}){-}\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}}\right] \end{aligned}$$

(3.5)

is well defined and using the equations (3.4) and (3.5) into (3.2) at $s=\beta _{2}$, we get

$$\begin{aligned} w(\beta _{2})&=k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}}\\ {}&\quad +\int \limits _{\beta _{1}}^{\beta _{2}}\psi '(r)\left( \psi (\beta _{2})-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) \\&\quad \times \textrm{B}\textrm{B}^{*}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}^{*}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) {\mathcal {G}}^{-1}\\&\quad \times \left[ w_{\beta _{2}}-k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}}\right] \\&=k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}}+{\mathcal {G}}{\mathcal {G}}^{-1}\\&\quad \times \left[ w_{\beta _{2}}-k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}}\right] \\&=w_{\beta _{2}}. \end{aligned}$$

Hence, the system (3.1) is controllable on $\textrm{J}.$On the other hand, if ${\mathcal {G}}$ is not positive definite, then there exists a $z\not =0$ satisfies

$$\begin{aligned} z^{*}{\mathcal {G}}z=0, \end{aligned}$$

that is,

$$\begin{aligned} z^{*}\int \limits _{\beta _{1}}^{\beta _{2}}\psi '(r)\left( \psi (\beta _{2})-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) \\ \times \textrm{B}\textrm{B}^{*}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}^{*}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) drz=0. \end{aligned}$$

This implies, on $\textrm{J},$

$$\begin{aligned} z^{*}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) \textrm{B}=0. \end{aligned}$$

Let $w_{\beta _{1}}=\left[ k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) \right] ^{-1}z$. Since the system (3.1) is controllable on $\textrm{J}$, there exists a control function u(r) such that the solution of (3.1) satisfies $^{k}\textrm{I}_{\beta _{1}^{+}}^{k-\mu _{k};\psi }w(\beta _{1})=w_{\beta _{1}}$ and $w(\beta _{2})=0$. It follows that

$$\begin{aligned} w(\beta _{2})&=k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}}\nonumber \\&\quad +k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{\beta _{2}}\psi '(r)\left( \psi (s)-\psi (r)\right) ^{\frac{\delta }{k}-1}\times \textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (r))^{\frac{\delta }{k}}\right) \textrm{B}u(r)dr\\ 0&=z+k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{\beta _{2}}\psi '(r)\left( \psi (\beta _{2})-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) \textrm{B}u(r)dr\\ 0&=z^{*}z+k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{\beta _{2}}\psi '(r)\left( \psi (\beta _{2})-\psi (r)\right) ^{\frac{\delta }{k}-1}z^{*}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) \textrm{B}u(r)dr. \end{aligned}$$

So, we have $z^{*}z=0$, which is contradiction for $z\not =0$. Thus ${\mathcal {G}}$ is positive definite. $\square$

4 Controllability of nonlinear systems

Let $\textrm{Y}=\textrm{C}_{n}(\textrm{J})\times \textrm{C}_{m}(\textrm{J})$, where $\textrm{C}_{n}(\textrm{J})$ is the Banach space of continuous ${\mathbb {R}}^{n}$ valued functions defined on $\textrm{J}$. So, $\textrm{Y}$ is a Banach space with the norm $\Vert (w,u)\Vert =\Vert w\Vert +\Vert u\Vert ,$ where $\Vert w\Vert =\sup \{w(s):s\in \textrm{J}\}$ and $\Vert u\Vert =\sup \{u(s):s\in \textrm{J}\}$. For given any $(x,v)\in \textrm{Y}$, the system (1.1) is

$$\begin{aligned} {\left\{ \begin{array}{ll} ^{k,H}\textrm{D}_{a^{+}}^{\delta ,\gamma ;\psi }w(s)=Aw(s)+Bu(s)+g(s,x(s),v(s)),~s\in (\beta _{1},\beta _{2}]\\ ^{k}\textrm{I}_{a^{+}}^{k-\mu _{k};\psi }w(\beta _{1})=w_{\beta _{1}},~\mu _{k}=\delta +\gamma (k-\delta ). \end{array}\right. } \end{aligned}$$

(4.1)

Lemma 4.1

For a given control $u(s)\in \textrm{L}^{2}\left( \textrm{J},{\mathbb {R}}^{m}\right)$, the solution of dynamical system (4.1) is

$$\begin{aligned} w(s)&=k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (s)-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}}\nonumber \\&\quad +k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{s}\psi '(r)\left( \psi (s)-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (r))^{\frac{\delta }{k}}\right) \textrm{B}u(r)dr \nonumber \\&\quad +k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{s}\psi '(r)\left( \psi (s)-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (r))^{\frac{\delta }{k}}\right) \nonumber \\&\quad \times g(r,x(r),v(r))dr~\forall s\in (\beta _{1},\beta _{2}]. \end{aligned}$$

(4.2)

Proof

Proof is similar to Lemma 3.1. $\square$

Theorem 4.2

The nonlinear system (1.1) is controllable on $\textrm{J}$ if g satisfies the condition, for $|p=(x,v)|=|x|+|v|$, $\lim \limits _{|p|\rightarrow \infty }\frac{|g(s,p)|}{|p|}=0$ uniformly in $s\in \textrm{J}$, and its corresponding linear system (3.1) is also controllable on $\textrm{J}$.

Proof

Define ${\mathcal {L}}:\textrm{Y}\rightarrow \textrm{Y}$ by ${\mathcal {L}}(x,v)=(w,u)$, where

$$\begin{aligned} u(s)&= k^{-\frac{k}{\delta }}\textrm{B}^{*}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}^{*}(\psi (\beta _{2})-\psi (s))^{\frac{\delta }{k}}\right) {\mathcal {G}}^{-1}\\&\quad \times \bigg [w_{\beta _{2}} - k^{1-\frac{\mu _{k}}{k}}(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}} \\&\quad - k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{\beta _{2}}\psi '(r)(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) g(r,x(r),v(r))\,dr\bigg ] \end{aligned}$$

and

$$\begin{aligned} w(s)&=k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (s)-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}}\nonumber \\&\quad +k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{s}\psi '(r)\left( \psi (s)-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (r))^{\frac{\delta }{k}}\right) \textrm{B}u(r)dr \\&\quad +k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{s}\psi '(r)\left( \psi (s)-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (r))^{\frac{\delta }{k}}\right) g(r,x(r),v(r))dr. \end{aligned}$$

For our convenience, we denote the constants

$\tilde{a_{1}}=\parallel k^{-\frac{\delta }{k}}\psi '(r)\left( \psi (\beta _{2})-\psi (r)\right) ^{\frac{\delta }{k}-1}\parallel$,

$\tilde{a_{2}}=\parallel \textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) \parallel$,

${\tilde{a}}=\sup \{1,\tilde{a_{1}}\tilde{a_{2}}\Vert \textrm{B}^{*}\Vert |\beta _{2}-\beta _{1}\Vert \}$,

$\tilde{b_{1}}=\Vert k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}}\Vert ,$

$\tilde{c_{1}}=4\left[ \tilde{a_{2}}^{2}\Vert \textrm{B}^{*}\Vert {\mathcal {G}}^{-1}(\beta _{2}-\beta _{1})\right] ,$

$\tilde{c_{2}}=4\left[ \tilde{a_{1}}\tilde{a_{2}}|\beta _{2}-\beta _{1}|\right] ,$

$\tilde{d_{1}}=4\left[ \frac{1}{\tilde{a_{1}}}\Vert \textrm{B}^{*}\Vert \tilde{a_{2}}{\mathcal {G}}^{-1}[|w_{\beta _{2}}+\tilde{b_{1}}|]\right] ,$

$\tilde{d_{2}}=4[\tilde{b_{1}}],$

${\tilde{d}}=\max \{\tilde{d_{1}},\tilde{d_{2}}\}$,

$\sup |g|=\sup \{g(r,x(r),v(r));r\in \textrm{J}\}.$

Now,

$$\begin{aligned} |w(s)|&\le \frac{\tilde{d_{2}}}{4}+{\tilde{a}}\left( \frac{{\tilde{d}}}{4{\tilde{a}}}+\frac{{\tilde{c}}}{4{\tilde{a}}}\sup |g|\right) +\frac{\tilde{c_{2}}}{4}\sup |g|\\&\le \frac{{\tilde{d}}}{4}+\frac{{\tilde{d}}}{4}+\frac{{\tilde{c}}}{4}\sup |g|+\frac{{\tilde{c}}}{4}\sup |g|\\&\le \frac{{\tilde{d}}}{2}+\frac{{\tilde{c}}}{2}\sup |g| \end{aligned}$$

and

$$\begin{aligned} |u(s)|&\le \frac{\tilde{d_{1}}}{4}\sup |g|+\frac{\tilde{c_{1}}}{4{\tilde{a}}}\\&\le \frac{{\tilde{d}}}{4}\sup |g|+\frac{{\tilde{c}}}{4{\tilde{a}}}. \end{aligned}$$

Let ${\tilde{c}}>0$ and ${\tilde{d}}>0$, choose ${\tilde{r}}>0$ such that $\Vert q\Vert \le {\tilde{r}},$ by Theorem [24], we have ${\tilde{c}}|g(s,q)|+{\tilde{d}}\le {\tilde{r}}$. Let $\textrm{X}({\tilde{r}})=\left\{ (z,u):\Vert z\Vert \le \frac{{\tilde{r}}}{2},~\Vert u\Vert \le \frac{{\tilde{r}}}{2}\right\}$ be a convex subset of $\textrm{Y}$ which is also bounded by $\frac{{\tilde{r}}}{2}$ and closed. If $(x,v)\in \textrm{X}({\tilde{r}})$ then $|x(s)+v(s)|\le {\tilde{r}}$ which implies ${\tilde{c}}|g(s,q)|+{\tilde{d}}\le {\tilde{r}}$. Therefore, for every $s\in \textrm{J}$, $|u(s)|\le \frac{{\tilde{r}}}{4{\tilde{a}}}$ implies $\Vert u\Vert \le \frac{{\tilde{r}}}{4{\tilde{a}}}$ implies $\Vert z\Vert \le \frac{{\tilde{r}}}{2}.$ From the Arzela-Ascoli theorem, ${\mathcal {L}}:\textrm{X}({\tilde{r}})\rightarrow \textrm{X}({\tilde{r}})$ is continuous and compact. By Schauder fixed point theorem, there exists a $(x,v)\in \textrm{X}({\tilde{r}})$ such that ${\mathcal {L}}(x,v)=(x,v)=(w,u)$, where

$$\begin{aligned} w(s)&=k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (s)-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}}\\&\quad +k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{s}\psi '(r)\left( \psi (s)-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (r))^{\frac{\delta }{k}}\right) \textrm{B}u(r)dr\\&\quad +k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{s}\psi '(r)\left( \psi (s)-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (r))^{\frac{\delta }{k}}\right) g(r,x(r),v(r))dr. \end{aligned}$$

Then w(s) is the solution of the system (1.1) and

$$\begin{aligned} w(\beta _{2})&= k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}} \\&\quad + \int \limits _{\beta _{1}}^{\beta _{2}}\psi '(r)\left( \psi (\beta _{2})-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) \\&\quad \times \textrm{B}\textrm{B}^{*}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}^{*}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) {\mathcal {G}}^{-1} \\&\quad \times \bigg [w_{\beta _{2}}-k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}} \\&\quad -k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{\beta _{2}}\psi '(r)\left( \psi (\beta _{2})-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) g(r,x(r),v(r))dr\bigg ] \\&\quad + k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{s}\psi '(r)\left( \psi (s)-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (s)-\psi (r))^{\frac{\delta }{k}}\right) g(r,x(r),v(r))dr. \\&= k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}} \\&\quad + {\mathcal {G}} {\mathcal {G}}^{-1}\bigg [w_{\beta _{2}}-k^{\left( 1-\frac{\mu _{k}}{k}\right) }(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\mu _{k}}{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\mu _{k}}{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (\beta _{1}))^{\frac{\delta }{k}}\right) w_{\beta _{1}} \\&\quad -k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{\beta _{2}}\psi '(r)\left( \psi (\beta _{2})-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) g(r,x(r),v(r))dr\bigg ] \\&\quad + k^{-\frac{\delta }{k}}\int \limits _{\beta _{1}}^{\beta _{2}}\psi '(r)\left( \psi (\beta _{2})-\psi (r)\right) ^{\frac{\delta }{k}-1}\textrm{E}_{\frac{\delta }{k},\frac{\delta }{k}}\left( k^{-\frac{\delta }{k}}\textrm{A}(\psi (\beta _{2})-\psi (r))^{\frac{\delta }{k}}\right) g(r,x(r),v(r))dr \\&= w_{\beta _{2}}. \end{aligned}$$

$w(\beta _{2})=w_{\beta _{2}}$. Hence system (1.1) is controllable on $\textrm{J}.$ $\square$

5 Numerical examples

Example 5.1

Let us take the following nonlinear $(k,\psi )$-Hilfer fractional differential control system:

$$\begin{aligned} {\left\{ \begin{array}{ll} ^{1.5,H}\textrm{D}_{0^{+}}^{0.75,\frac{1}{2};s^{2}}w(s)=\left[ {\begin{array}{cc} -1 &{} 1 \\ 0 &{} 1 \\ \end{array} } \right] w(s)+\left[ {\begin{array}{cc} 2 \\ 1 \\ \end{array} } \right] u(s)+\left[ {\begin{array}{cc} \frac{1}{1+w^{2}_{2}(s)} \\ 0 \\ \end{array} } \right] ,~s\in (0,1],\\ ^{1.5}\textrm{I}_{0^{+}}^{0.375;s^{2}}w(0)=w_{0}=\left[ {\begin{array}{cc} 0 \\ 0 \\ \end{array} } \right] . \end{array}\right. } \end{aligned}$$

(5.1)

Comparing (5.1) with (1.1), we get $k=1.5,~\delta =0.75,\gamma =\frac{1}{2},\psi (s)=s^{2},~A=\left[ {\begin{array}{cc} -1 &{} 1 \\ 0 &{} 1 \\ \end{array} } \right] ,$ $B=\left[ {\begin{array}{cc} 2 \\ 1 \\ \end{array} } \right] ,\beta _{1}=0,\beta _{2}=1,w_{0}=\left[ {\begin{array}{cc} 0 \\ 0 \\ \end{array} } \right] ,~g(s,w(s),v(s))=\left[ {\begin{array}{cc} \frac{1}{1+w^{2}_{2}(s)} \\ 0\\ \end{array} } \right]$ and $w(s)=\left[ {\begin{array}{cc} w_{1}(s) \\ w_{2}(s) \\ \end{array} } \right]$. Let us take $w(1)=\left[ {\begin{array}{cc} w_{1}(s) \\ w_{2}(s) \\ \end{array} } \right] =\left[ {\begin{array}{cc} 1 \\ -1 \\ \end{array} } \right] .$ The Mittag-Leffler matrix function for the given matrix A is

$$\begin{aligned} \textrm{E}_{0.5,0.5}(As)=\left[ {\begin{array}{cc} \textrm{E}_{0.5,0.5}(-s) &{} \frac{1}{2}(\textrm{E}_{0.5,0.5}(s)-\textrm{E}_{0.5,0.5}(-s)) \\ 0 &{} \textrm{E}_{0.5,0.5}(s) \\ \end{array} } \right] . \end{aligned}$$

The controllability Gramian matrix

$$\begin{aligned} {\mathcal {G}}&=\int \limits _{0}^{1}2r(1-r^{2})^{(-0.5)}\textrm{E}_{0.5, 0.5}\left( (0.8165)\textrm{A}(1-r^{2})^{0.5}\right) \textrm{B}\textrm{B}^{*}\textrm{E}_{0.5,0.5}\left( (0.8165)\textrm{A}^{*}(1-r^{2})^{0.5}\right) dr\\&=\left[ {\begin{array}{cc} 15.3665 &{} 8.1931\\ 8.1931 &{} 9.4863\\ \end{array} } \right] , \end{aligned}$$

is positive definite. Therefore, the linear system corresponding to (5.1) is controllable on [0, 1]. Further, $\lim \limits _{|p|\rightarrow \infty }\frac{|g(s,p)|}{|p|}=0$ uniformly on [0, 1]. The system (5.1) is controllable on [0, 1] by Theorem 4.2. The controlled trajectories of the system (5.1) steering from the initial state $w(0)=\left[ {\begin{array}{cc} 0 \\ 0 \\ \end{array} } \right]$ to a desired state $w(1)=\left[ {\begin{array}{cc} 1 \\ -1 \\ \end{array} } \right]$ during [0, 1] can be approximated from the following algorithm

$$\begin{aligned} u^{n}(s)&{=}(0.44)\textrm{B}^{*}\textrm{E}_{0.5,0.5}\left( (0.8165)\textrm{A}^{*}(1{-}s^{2})^{0.5}\right) G^{-1}[0,1] [w(1){-}\int \limits _{0}^{1}(2r)\left( 1{-}r^{2}\right) ^{-0.5}\\&\quad \times \textrm{E}_{0.5,0.5}\left( (0.8165)\textrm{A}(1-r^{2})^{0.5}\right) g(r,w^{n}(r),v(r))dr] \\ w^{n+1}(s)&= (0.8165)\int \limits _{0}^{s}(2r)\left( s^{2}-r^{2}\right) ^{-0.5}\textrm{E}_{0.5,0.5}\left( (0.8165)\textrm{A}(s^{2}-r^{2})^{0.5}\right) \\&\quad \times \left( \textrm{B}u^{n}(r)+g(r,w^{n}(r),v(r))\right) dr, \end{aligned}$$

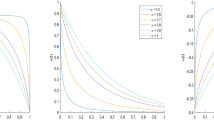
with $w^{0}(s)=w_{0}$, where $n=0,1,2,\cdots .$ Using MATLAB, the controlled trajectories and steering control u(s) are computed and are depicted in Figs. 1 and 2.

Fig. 1

The trajectory of u(s) of the system (5.1) on [0, 1]

Fig. 2

The trajectory of the system (5.1) steers from $\left[ {\begin{matrix}0\\ 0\end{matrix}}\right]$ to the final state $\left[ {\begin{matrix}1\\ -1\end{matrix}}\right]$ during the interval [0, 1]

Example 5.2

Let us take the following nonlinear $(k,\psi )$-Hilfer fractional differential control system:

$$\begin{aligned} {\left\{ \begin{array}{ll} ^{1,H}\textrm{D}_{0^{+}}^{\frac{1}{2},1;s}w(s)=\left[ {\begin{array}{cc} 0 &{} 1 \\ 1 &{} 0 \\ \end{array} } \right] w(s)+\left[ {\begin{array}{cc} 0 \\ 1 \\ \end{array} } \right] u(s)+\left[ {\begin{array}{cc} \sqrt{w^{2}_{1}(s)+2} \\ 0 \\ \end{array} } \right] ,~s\in (0,2],\\ w(0)=\left[ {\begin{array}{cc} 0 \\ 0 \\ \end{array} } \right] . \end{array}\right. } \end{aligned}$$

(5.2)

Fig. 3

The trajectory of u(s) of the system (5.2) on [0, 2]

Fig. 4

The trajectory of the system (5.2) steers from $\left[ {\begin{matrix}0\\ 0\end{matrix}}\right]$ to the final state $\left[ {\begin{matrix}1\\ 2\end{matrix}}\right]$ during the interval [0, 2]

Comparing (5.2) with (1.1), we get $k=1,~\delta =\frac{1}{2},\gamma =1,\psi (s)=s,~A=\left[ {\begin{array}{cc} 0 &{} 1 \\ 1 &{} 0 \\ \end{array} } \right] ,$

$B=\left[ {\begin{array}{cc} 0 \\ 1 \\ \end{array} } \right] ,\beta _{1}=0,\beta _{2}=2,w_{0}=\left[ {\begin{array}{cc} 0 \\ 0 \\ \end{array} } \right] ,~g(s,w(s),v(s))=\left[ {\begin{array}{cc} \sqrt{w^{2}_{1}(s)+2} \\ 0 \\ \end{array} } \right]$ and $w(s)=\left[ {\begin{array}{cc} w_{1}(s) \\ w_{2}(s) \\ \end{array} } \right]$. Let us take $w(2)=\left[ {\begin{array}{cc} w_{1}(2) \\ w_{2}(2) \\ \end{array} } \right] =\left[ {\begin{array}{cc} 1 \\ 2 \\ \end{array} } \right] .$ The Mittag-Leffler matrix function for the given matrix A is

$$\begin{aligned} s^{\frac{-1}{4}}\textrm{E}_{\frac{1}{2},\frac{1}{2}}(As)=\left[ {\begin{array}{cc} \mathrm {N_{1}(s)} &{} \mathrm {N_{2}(s)} \\ \mathrm {N_{2}(s)} &{} \mathrm {N_{1}(s)} \\ \end{array} } \right] , \end{aligned}$$

where $\mathrm {N_{1}(s)}=\frac{s^{\frac{-1}{4}}}{2}[\textrm{E}_{\frac{1}{2},\frac{1}{2}}(s)+\textrm{E}_{\frac{1}{2},\frac{1}{2}}(-s)]$ and $\mathrm {N_{2}(s)}=\frac{s^{\frac{-1}{4}}}{2}[\textrm{E}_{\frac{1}{2},\frac{1}{2}}(s)-\textrm{E}_{\frac{1}{2},\frac{1}{2}}(-s)].$ The controllability Gramian matrix

$$\begin{aligned} G[1,2]&=\int \limits _{1}^{2}\frac{1}{\sqrt{\left( 2-r\right) }}\textrm{E}_{\frac{1}{2},\frac{1}{2}}\left( k^{-\frac{\delta }{k}}\textrm{A}(2-r)^{\frac{1}{2}}\right) \textrm{B}\textrm{B}^{*}\textrm{E}_{\frac{1}{2},\frac{1}{2}}\left( k^{-\frac{\delta }{k}}\textrm{A}^{*}(2-r)^{\frac{1}{2}}\right) dr\\&=\int \limits _{0}^{2}\left[ {\begin{array}{cc} \mathrm {N^{2}_{2}(\sqrt{(2-r)})} &{} \mathrm {N_{1}(\sqrt{(2-r)})}\mathrm {N_{2}(\sqrt{(2-r)})} \\ \mathrm {N_{1}(\sqrt{(2-r)})}\mathrm {N_{2}(\sqrt{(2-r)})} &{} \mathrm {N^{2}_{1}(\sqrt{(2-r)})} \\ \end{array} } \right] dr\\&=\left[ {\begin{array}{cc} 32.7898 &{} 33.6254 \\ 33.6254 &{} 34.6631 \\ \end{array} } \right] , \end{aligned}$$

is positive definite. Therefore, the linear system corresponding to (5.2) is controllable on [0, 2]. Further, $\lim \limits _{|p|\rightarrow \infty }\frac{|g(s,p)|}{|p|}=0$ uniformly on [0, 2]. The system (5.2) is controllable on [0, 2] by Theorem 4.2. The controlled trajectories of the system (5.2) steering from the initial state $w(0)=\left[ {\begin{array}{cc} 0 \\ 0 \\ \end{array} } \right]$ to a desired state $w(2)=\left[ {\begin{array}{cc} 1 \\ 2 \\ \end{array} } \right]$ during [0, 2] can be approximated from the following algorithm

$$\begin{aligned} u^{n}(s)&=\textrm{B}^{*}\textrm{E}_{\frac{1}{2},\frac{1}{2}}\left( k^{-\frac{\delta }{k}}\textrm{A}^{*}(2-s)^{\delta }\right) G^{-1}[0,2] \\&\times \left[ w(2)-\int \limits _{0}^{2}\left( 2-r\right) ^{-\frac{1}{2}}\textrm{E}_{\frac{1}{2},\frac{1}{2}}\left( k^{-\frac{\delta }{k}}\textrm{A}(2-r)^{\frac{1}{2}}\right) g(r,w^{n}(r),v(r))dr\right] \\&w^{n+1}(s)=\int \limits _{0}^{s}\left( s-r\right) ^{-\frac{1}{2}}\textrm{E}_{\frac{1}{2},\frac{1}{2}}\left( k^{-\frac{\delta }{k}}\textrm{A}(s-r)^{\frac{1}{2}}\right) \left( \textrm{B}u^{n}(r)+g(r,w^{n}(r),v(r))\right) dr \end{aligned}$$

with $w^{0}(s)=w_{0}$, where $n=0,1,2,\cdots$. Using MATLAB, the controlled trajectories and steering control u(s) are computed and are depicted in Figs. 3 and 4.

6 Conclusion

In this article, we studied the controllability of fractional dynamical systems involving $(k,\psi )$-Hilfer fractional derivative. This study of controllability of $(k,\psi )$-Hilfer fractional derivative gives the controllability results for many other distinct fractional derivatives stated in Table 1. Here, we have used the controllability Gramian matrix and Schauder fixed point technique to establish sufficient conditions for the controllability of fractional dynamical systems. Numerical examples are provided to illustrate the main results.