New iterative methods for finding solutions of Hammerstein equations

Abstract

Let $G:H\rightarrow H$ and $K: H\rightarrow H$ be monotone mappings that are either sequentially weakly continuous or continuous, where H is a real Hilbert space. In this work, we introduce two new iterative methods for approximating solutions of the Hammerstein equation $u+GKu=0$, if they exist. The first iterative method is shown to always converge weakly to an element in the solution set of the Hammerstein equation if this solution set is nonempty. The second iterative method is a modification of the first method to upgrade weak convergence to strong convergence. Convergence results are obtained without requiring the maps to be bounded. Numerical examples are provided to demonstrate the convergence of one of these methods. Comparisons with some existing methods show that the method is cost effective in terms of the number of iterations required to obtain a solution and the computational time.

1 Introduction

The subject of discussion in this paper is iterative methods for solving the Hammerstein equation

$$\begin{aligned} u+GKu=0, \end{aligned}$$

(1)

where K and G are monotone mappings defined on a real Hilbert space H and u is a vector in H. A detailed discussion and formulation of nonlinear integral equations of Hammerstein type into (1) can be found in [11]. Results on the existence and uniqueness of solutions of Eq. (1) are also available in the literature, see for example Appell and Benavides [2], Brézis and Browder [6, 7], Browder [9,10,11], Browder et al. [13], Browder and Gupta [12], Chepanovich [14] and De Figueiredo and Gupta [32], Kazemi [36], Kazemi [37] and Kazemi and Ezzati [38]. Interest in the study of Hammerstein equations lies in their broad domain of application which include differential equations [46], automation and network theory as well as in optimal control systems [34].

It is known that nonlinear integral equations of Hammerstein type have in general no closed-form solution. For this reason, the theory of iterative methods plays a crucial role in approximating solutions of these types of equations. To the best of our recollection, Brézis and Browder [6] were the first to construct an iterative method that converges to the solution of the Hammerstein type integral equation in the case where one of the operators was assumed to be angle bounded (see also Brézis and Browder [8]). Since then, many researchers have constructed iterative methods that converge to the solution set of Eq. (1), if it is nonempty. These researchers include, Bello et al. [3], Chidume and Bello [15], Chidume et al. [28,29,30], Chidume and Djitte [16,17,18], Chidume and Idu [19], Chidume and Ofoedu [20], Chidume and Shehu [22,23,24], Chidume and Zegeye [25,26,27], Daman et al. [31], Djitte and Sene [33], Minjibir and Mohammed [42], Ofoedu and Onyi [44], Shehu [47], Tufa et al. [48], Uba et al. [49], Zegeye and Malonza [52]. Recent results in this direction have been proved for the case when both K and G are bounded, see Zegeye and Malonza [52] and Bello et al. [3]. In addition, the results in [3] rely on the existence of a certain constant $\gamma _0$ which is not clear how it is calculated. Numerical methods regarding the solution of Hammerstein integral equations can be found in Kürkçü [39], Neamprem et al. [43], Micula and Cattani [41], Allouch et al. [1] and Wang [50].

In this work, we introduce two iterative methods for solving Hammerstein equations for mappings that are not necessarily bounded. The main objective of introducing these methods is in three folds: (a) to get rid of the constant $\gamma _0$ used by Bello et al. [3] in their recent work; (b) get rid of the boundedness condition imposed on both G and K by Zegeye and Malonza [52] and Bello et al. [3]; and (c) introduce the over-relaxed parameter that has been used in the literature to improve the speed of convergence in other algorithms (for example, [5]) but has never been used in algorithms that approximate solutions of Hammerstein equations. The requirement imposed on our maps is that they are either monotone and sequentially weakly continuous or monotone and continuous. The first iterative method is shown to always converge weakly to an element in the solution set of the Hammerstein Eq. (1), if this solution set is nonempty, while the second iterative method is a modification of the first method to upgrade weak convergence to strong convergence. Numerical examples are provided to demonstrate the convergence of one of these methods. Comparisons with some existing methods show that the method is cost effective in terms of the number of iterations required to obtain a solution and the computational time taken for the generated sequence to converge to the solution.

The rest of the paper is organized as follows: In Sect. 2, preliminary results that help to establish and prove our main results are given. Section 3 presents the algorithms introduced in this paper and their associated convergence results, while Sect. 4 is dedicated to numerical examples for one of the algorithms. Finally, concluding remarks are given in Sect. 5. The acknowledgement, some declarations and the list of reference are found at the end of the paper.

2 Preliminaries

Throughout this paper, H will denote a real Hilbert space with inner product $\langle \cdot ,\cdot \rangle$ and induced norm $\left\| \,\cdot \,\right\|$. A mapping $A:H\rightarrow H$ is monotone if

$$\begin{aligned} \langle Ax-Ay,x-y\rangle \ge 0\quad \forall \quad x, y\in H. \end{aligned}$$

For any mapping $T:H\rightarrow H$, the set $\{z\in H: Tz=z\}$, called the set of fixed points of T will be denoted by F(T). Recall that $T:H\rightarrow H$ is said to be nonexpansive if for any $x,y\in H$,

$$\begin{aligned} \left\| Tx-Ty\right\| \le \left\| x-y\right\| , \end{aligned}$$

and a mapping $T:H\rightarrow H$ is called firmly nonexpansive if for any $x,y\in H$,

$$\begin{aligned} \left\| Tx-Ty\right\| ^2\le \langle Tx-Ty,x-y\rangle . \end{aligned}$$

Equivalently, T is firmly nonexpansive if for any $x,y\in H$,

$$\begin{aligned} \left\| Tx-Ty\right\| ^2\le \left\| x-y\right\| ^2-\left\| (x-Tx)-(y-Ty)\right\| ^2. \end{aligned}$$

It is obvious from the definition that a firmly nonexpansive mapping is both monotone and nonexpansive. The following lemma is well known in Hilbert spaces.

Lemma 1

Let $x,y\in H$ and $c\in (0,1)$. Then the following holds:

• (a) $\left\| cx+(1-c)y\right\| ^2= c\left\| x\right\| ^2+(1-c)\left\| y\right\| ^2-c(1-c)\left\| x-y\right\| ^2$;

• (b) $\left\| x+y\right\| ^2\le \left\| x\right\| ^2+2\langle y,x+y\rangle$.

Let C be a nonempty, closed and convex subset of H. The metric projection (nearest point mapping) $P_C: H\rightarrow C$ is defined as follows: Given $x\in H$, $P_C x$ is the unique point in C having the property

$$\begin{aligned} \left\| x-P_C x\right\| =\inf _{y\in C}\left\| x-y\right\| . \end{aligned}$$

The following two lemmas give characterizations of projections and nonexpansive mappings that will be key in proving our main result.

Lemma 2

Assume that C is a nonempty, closed and convex subset of H. Let $x\in H$ and $y\in C$ be given. Then $y=P_C x$ if and only if the inequality

$$\begin{aligned} \langle x-y,z-y\rangle \le 0,\quad \text{ for } \text{ all }\quad z\in C, \end{aligned}$$

holds true.

Lemma 3

(Goebel and Kirk [35]) A map $S: H \rightarrow H$ is firmly nonexpansive if and only if $2S - I$ (where I is the identity map) is nonexpansive.

Lemma 4

(Xu [51]) Let $(a_{n})$ be a sequence of nonnegative real numbers satisfying the following relation:

$$\begin{aligned} a_{n+1} \le (1-\beta _n)a_{n} + \beta _n\delta _n, n\ge n_0, \end{aligned}$$

where $(\beta _n) \subset (0,1)$ and $(\delta _n)\subset R$ satisfying the following conditions: $\sum _{n=1}^{\infty } \beta _n=\infty$, and $\limsup _{n\rightarrow \infty }\delta _n\le 0$. Then, $\lim _{n\rightarrow \infty }a_{n}=0$.

Lemma 5

(Maingé [40]) Let $(c_{n})$ be a sequence of real numbers such that there exists a subsequence $(n_i)$ of (n) such that $c_{n_i}<c_{{n_i}+1}$ for all $i\in \mathbb {N}$. Then there exists a nondecreasing sequence $(m_k)\subset \mathbb {N}$ such that $m_k\rightarrow \infty$ and the following properties are satisfied by all (sufficiently large) numbers $k\in \mathbb {N}$:

$$\begin{aligned} c_{m_k}\le c_{{m_k}+1}\quad \text{ and }\quad c_k\le c_{{m_k}+1}. \end{aligned}$$

In fact, $m_k=\max \{j\le k:c_j<c_{j+1}\}$.

Recall that a sequence $(x_n)$ in a Hilbert space H converges strongly (respectively, weakly) to $x\in H$ if $\left\| x_n-x\right\| \rightarrow 0$ (respectively, $\langle x_n,y\rangle \rightarrow \langle x,y\rangle$ for all $y\in H$). Strong (respectively, weak) convergence of $(x_n)$ to x is denoted by $x_n\rightarrow x$ (respectively, $x\rightharpoonup x$).

Given a mapping T from H into itself, $I-T$ is said to be demiclosed at zero if for any sequence $\{z_n\}$ in H satisfying the conditions

• (i) $\{z_n\}$ converges weakly to z;

• (ii) ${\lim _{n\rightarrow \infty }\left\| z_n-Tz_n\right\| }=0$, we have $z-Tz=0$.

The following lemma, which was proved in the setting of real Banach spaces, will be used to motivate our main results.

Lemma 6

(Blum and Oettli [4]) Let C be a nonempty, closed and convex subset of a real Hilbert space H and let f be a bifunction from $C\times C$ to $\mathbb {R}$ satisfying

• (A1) $f(x,x)=0$ for all $x\in C$;

• (A2) f is monotone, i.e., $f(x,y)+f(y,x)\le 0$ for all $x,y\in C$;

• (A3) for all $x,y,z\in C$,

  $$\begin{aligned} \limsup _{t\downarrow 0}f(tz+(1-t)x,y)\le f(x,y); \end{aligned}$$

• (A4) for all $x\in C$, $f(x,\cdot )$ is convex and lower semicontinuous. Let $r>0$ and $x\in H$. Then, there exists $z\in C$ such that

  $$\begin{aligned} f(z,y)+\frac{1}{r}\langle y-z, z-x\rangle \ge 0\quad \text{ for } \text{ all }\quad y\in C. \end{aligned}$$

Recall that a mapping $T:H\rightarrow H$ is called sequentially weakly continuous if for any sequence $\{z_n\}$ in H converging weakly to z, the sequence $\{Tz_n\}$ converges weakly to Tz.

Lemma 7

Let H be a real Hilbert space, $K:H\rightarrow H$ and $G:H\rightarrow H$ be monotone mappings that are either sequentially weakly continuous or continuous. Then for any $[x,y]\in X=H\times H$ and $r>0$, there exists $[w,z]\in X$ such that

$$\begin{aligned} \langle Kw-z, u-w\rangle +\langle Gz+w,v-z\rangle +\frac{1}{r}\langle w-x,u-w\rangle +\frac{1}{r}\langle z-y,v-z\rangle \ge 0 \end{aligned}$$

for all $[u,v]\in X$.

Proof

We prove the lemma for the case when both K and G are sequentially weakly continuous. The other case(s) can be proved in a similar way.

Define a mapping $T:X\times X\rightarrow \mathbb {R}$ by

$$\begin{aligned} T([w,z],[u,v])=\langle Kw-z, u-w\rangle +\langle Gz+w,v-z\rangle . \end{aligned}$$

Then $T([u,v],[u,v])=0$ for all $[u,v]\in X$, and from the monotonicity of K and G, we have

$$\begin{aligned} T([w,z],[u,v]) + T([u,v],[w,z])= & {} \langle Kw-z, u-w\rangle +\langle Gz+w,v-z\rangle \\&+ \langle Ku-v, w-u\rangle +\langle Gv+u,z-v\rangle \\= & {} \langle Kw-Ku, u-w\rangle +\langle v-z, u-w\rangle \\&+ \langle Gz-Gv,v-z\rangle +\langle w-u,v-z\rangle \\\le & {} 0. \end{aligned}$$

Moreover, if $t\in (0,1)$ and $[x,y], [u,v], [w,z]\in X$, then

$$\begin{aligned} T([t[w,z]+(1-t)[x,y]],[u,v])=T([tw+(1-t)x,tz+(1-t)y],[u,v]). \end{aligned}$$

Denote $b=tw+(1-t)x$ and $d=tz+(1-t)y$. Then $b\rightarrow x$ and $d\rightarrow y$ as $t\rightarrow 0$. This implies that $b\rightharpoonup x$ and $d\rightharpoonup y$ as $t\rightarrow 0$. Since K and G are sequentially weakly continuous, we have $K(b)-d\rightharpoonup Kx -y$ and $G(d)+b\rightharpoonup Gy+x$ as $t\rightarrow 0$. Therefore,

$$\begin{aligned}&T([t[w,z]+(1-t)[x,y]],[u,v])\\&\quad = \langle K(b)-d, u-b\rangle +\langle G(d)+b,v-d\rangle \\&\quad = \langle K(b)-d, t(u-w)+(1-t)(u-x)\rangle \\&\qquad +\langle G(d)+b,t(v-z)+(1-t)(v-y)\rangle \\&\quad = t\langle K(b)-d, u-w\rangle +(1-t)\langle K(b)-d, u-x\rangle \\&\qquad + t\langle G(d)+b,v-z\rangle +(1-t)\langle G(d)+b,v-y\rangle . \end{aligned}$$

This implies that

$$\begin{aligned} \limsup _{t\downarrow 0} T([t[w,z]+(1-t)[x,y]],[u,v])\le & {} \limsup _{t\downarrow 0}\langle K(b)-d, u-x\rangle \\&+\limsup _{t\downarrow 0}\langle G(d)+b,v-y\rangle \\= & {} \langle Kx-y, u-x\rangle +\langle Gy+x,v-y\rangle \\= & {} T([x,y],[u,v]). \end{aligned}$$

Furthermore, for all $[u,v]\in X$,

$$\begin{aligned} \lim _{[x,y]\rightarrow [x_0,y_0]} T([u,v],[x,y])= & {} \lim _{x\rightarrow x_0}\langle Ku-v,x-u\rangle +\lim _{y\rightarrow y_0}\langle Gv+u,y-v\rangle \\= & {} \langle Ku-v,x_0-u\rangle +\langle Gv+u,y_0-v\rangle \\= & {} T([u,v],[x_0,y_0]). \end{aligned}$$

This shows that for all $[u,v]\in X$, $T([u,v], \cdot )$ is continuous, and hence lower semicontinuous.

Next, we show that for all $[x,y]\in X$, $T([x,y], \cdot )$ is convex. Indeed, let $[x,y]\in X$ be arbitrary but fixed, and let $[u,v],[w,z]\in X$ and $c\in [0,1]$. Then

$$\begin{aligned} T([x,y],c[u,v]+(1-c)[w,z])= & {} T([x,y],[cu+(1-c)w,cv+(1-c)z]) \\= & {} \langle Kx-y, cu+(1-c)w-x\rangle \\&+ \langle Gy+x,cv+(1-c)z-y\rangle \\= & {} c\langle Kx-y, u-x\rangle +(1-c)\langle Kx-y, w-x\rangle \\&+ c\langle Gy+x,v-y\rangle +(1-c)\langle Gy+x,z-y\rangle \\= & {} cT([x,y],[u,v])+(1-c)T([x,y],[w,z]). \end{aligned}$$

We have shown that the bifunction T from $X\times X$ into $\mathbb {R}$ satisfies conditions (A1)–(A4). By Lemma 6, for any $[x,y]\in X$ and $r>0$, there exists $[w,z]\in X$ such that

$$\begin{aligned} T([w,z],[u,v])+\frac{1}{r}\langle [u,v] -[w,z], [w,z]-[x,y]\rangle \ge 0 \end{aligned}$$

for all $[u,v]\in X$. That is, for any $[x,y]\in X$ and $r>0$, there exists $[w,z]\in X$ such that

$$\begin{aligned} \langle Kw-z, u-w\rangle +\langle Gz+w,v-z\rangle +\frac{1}{r}\langle w-x,u-w\rangle +\frac{1}{r}\langle z-y,v-z\rangle \ge 0 \end{aligned}$$

for all $[u,v]\in X$. $\square$

Throughout this paper, A will denote a mapping from the set $X=H\times H$ into itself given by $A[x,y]=[Kx-y,Gy+x]$ for all $[x,y]\in X$, where K and G are monotone mappings from H into H. This mapping was first introduced and studied by Chidume and Zegeye [27] (see also Chidume and Zegeye [25, 26]), who showed that solving the Hammerstein Eq. (1) is equivalent to computing zeros of the mapping A. As usual, the set of zeros of A will be denoted by $A^{-1}[0,0]$.

Lemma 8

Fix $r>0$, and let H be a real Hilbert space, $K:H\rightarrow H$ and $G:H\rightarrow H$ be monotone mappings that are either sequentially weakly continuous or continuous such that $A^{-1}[0,0]\ne \emptyset$. Define a mapping $S_r:X\rightarrow X$ by

$$\begin{aligned} S_r[x,y]= & {} \left\{ [w,z]\in X: \langle Kw-z, u-w\rangle +\langle Gz+w,v-z\rangle +\frac{1}{r}\langle w-x,u-w\rangle \right. \nonumber \\&\left. +\frac{1}{r}\langle z-y,v-z\rangle \ge 0 \quad \forall \, [u,v]\in X\right\} \end{aligned}$$

(2)

for all $[x,y]\in X$. Then

• (a) $S_r$ is single valued;

• (b) $S_r$ is firmly nonexpansive on X, i.e., for all $[x,y], [w,z]\in X$,

  $$\begin{aligned} \left\| S_r[x,y]-S_r[w,z]\right\| ^2\le \left\langle S_r[x,y]-S_r[w,z],[x,y]-[w,z]\right\rangle ; \end{aligned}$$

• (c) $F(S_r)=A^{-1}[0,0]$;

• (d) $I-S_r$ is demiclosed at zero.

• (e) for all $[x,y]\in X$ and $[p,q]\in A^{-1}[0,0]$,

  $$\begin{aligned} \left\| S_r[x,y]-[p,q]\right\| ^2+\left\| [x,y]-S_r[x,y]\right\| ^2\le \left\| [x,y]-[p,q]\right\| ^2; \end{aligned}$$

• (f) $F(S_r)$ is closed and convex.

Proof

We prove the lemma for the case when both K and G are sequentially weakly continuous. The other case(s) can be proved in a similar way.

• (a) For any $[x,y]\in X$ and $r>0$, let $[x_1,y_1], [x_2,y_2]\in S_r[x,y]$. Then from the definition of $S_r$, we have

  $$\begin{aligned} T([x_1,y_1],[x_2,y_2])+\frac{1}{r}\langle [x_2,y_2]-[x_1,y_1], [x_1,y_1]-[x,y] \rangle \ge 0, \end{aligned}$$

  (where T is the mapping given in Lemma 7) and

  $$\begin{aligned} T([x_2,y_2],[x_1,y_1])+\frac{1}{r}\langle [x_1,y_1] - [x_2,y_2],[x_2,y_2] -[x,y]\rangle \ge 0. \end{aligned}$$

  Adding these two inequalities and using condition (A2), we obtain

  $$\begin{aligned}&\langle [x_2,y_2]-[x_1,y_1], [x_1,y_1]-[x,y] \rangle + \langle [x_1,y_1] - [x_2,y_2],[x_2,y_2] -[x,y]\rangle \\&\quad \ge 0, \end{aligned}$$

  which implies that

  $$\begin{aligned} \langle [x_2,y_2]-[x_1,y_1], [x_1,y_1]-[x_2,y_2]\rangle \ge 0. \end{aligned}$$

  It follows from this last inequality that

  $$\begin{aligned} \left\| [x_2,y_2]-[x_1,y_1]\right\| ^2\le 0, \end{aligned}$$

  which implies that $x_2=x_1$ and $y_2=y_1$.

• (b) Let $[x,y], [w,z]\in X$. Then

  $$\begin{aligned} T(S_r[x,y], S_r[w,z])+\frac{1}{r}\langle S_r[w,z] -S_r[x,y], S_r[x,y]- [x,y]\rangle \ge 0, \end{aligned}$$

  and

  $$\begin{aligned} T(S_r[w,z], S_r[x,y])+\frac{1}{r}\langle S_r[x,y]-S_r[w,z], S_r[w,z]- [w,z]\rangle \ge 0 \end{aligned}$$

  Adding these two inequalities and making use of (A2), we get

  $$\begin{aligned} \langle S_r[w,z]-S_r[x,y], S_r[x,y] - [x,y]+ [w,z]- S_r[w,z]\rangle \ge 0. \end{aligned}$$

  Rearranging terms, we obtain

  $$\begin{aligned} \langle S_r[w,z]-S_r[x,y], [w,z] - [x,y] \rangle \ge \left\| S_r[w,z]-S_r[x,y]\right\| ^2. \end{aligned}$$

• (c) We now show that $F(S_r)=A^{-1}[0,0]$. To this end, using the definition of $S_r$, we have

  $$\begin{aligned}{}[p,q]\in F(S_r)\Longleftrightarrow & {} S_r[p,q]=[p,q] \\\Longleftrightarrow & {} \langle Kp-q,u-p\rangle +\langle Gq+p,v-q\rangle +\frac{1}{r}\langle p-p,u-p\rangle \\&\; + \frac{1}{r}\langle q-q,v-q\rangle \ge 0\quad \forall \, [u,v]\in X \\\Longleftrightarrow & {} \langle Kp-q,u-p\rangle +\langle Gq+p,v-q\rangle \ge 0\quad \forall \, [u,v]\in X \\\Longleftrightarrow & {} \langle [Kp-q,Gq+p],[u-p,v-q]\rangle \ge 0\quad \forall \, [u,v]\in X\\\Longleftrightarrow & {} \langle A[p,q],[u,v]-[p,q]\rangle \ge 0\quad \forall \, [u,v]\in X\\\Longleftrightarrow & {} [p,q]\in A^{-1}[0,0], \end{aligned}$$

  where the last equivalence follows from Lemma 2.

• (d) Let $\{[x_n,y_n]\}$ be a sequence in X such that $[x_n,y_n] \rightharpoonup [p,q]$ and $[x_n,y_n]-S_r[x_n,y_n]\rightarrow 0$ as $n\rightarrow \infty$. It then follows that $x_n\rightharpoonup p$, $y_n\rightharpoonup q$ and $S_r[x_n,y_n] \rightharpoonup [p,q]$ as $n\rightarrow \infty$. Denote $[w_n,z_n]=:S_r[x_n,y_n]$. Then $[x_n,y_n]-[w_n,z_n]\rightarrow 0$ as $n\rightarrow \infty$ which implies that $x_n-w_n\rightarrow 0$ and $y_n-z_n\rightarrow 0$ as $n\rightarrow \infty$. Also, we have $w_n\rightharpoonup p$ and $z_n\rightharpoonup q$ as $n\rightarrow \infty$. From the definition of $S_r$, we have

  $$\begin{aligned}&\langle Kw_n-z_n,u-w_n\rangle +\langle Gz_n+w_n,v-z_n\rangle \\&\quad +\frac{1}{r}\langle w_n-x_n,u-w_n\rangle +\frac{1}{r}\langle z_n-y_n,v-z_n\rangle \ge 0 \end{aligned}$$

  for all $[u,v]\in X$. From the monotonicity of K and G, we have

  $$\begin{aligned}&\langle Ku-z_n,u-w_n\rangle +\langle Gv+w_n,v-z_n\rangle \\&\quad +\frac{1}{r}\langle w_n-x_n,u-w_n\rangle +\frac{1}{r}\langle z_n-y_n,v-z_n\rangle \ge 0 \end{aligned}$$

  for all $[u,v]\in X$. This last inequality is the same as

  $$\begin{aligned} 0\le & {} \langle Ku-v,u-w_n\rangle +\langle v-z_n,u-w_n\rangle +\langle Gv+u,v-z_n\rangle \\&+\langle w_n-u,v-z_n\rangle + \frac{1}{r}\langle w_n-x_n,u-w_n\rangle +\frac{1}{r}\langle z_n-y_n,v-z_n\rangle , \end{aligned}$$

  which is equivalent to

  $$\begin{aligned}&\langle Ku-v,u-w_n\rangle +\langle Gv+u,v-z_n\rangle +\frac{1}{r}\langle w_n-x_n,u-w_n\rangle \\&\quad +\frac{1}{r}\langle z_n-y_n,v-z_n\rangle \ge 0 \end{aligned}$$

  for all $[u,v]\in X$. Taking the limit as $n\rightarrow \infty$, we get

  $$\begin{aligned} \langle Ku-v,u-p\rangle +\langle Gv+u,v-q\rangle \ge 0 \quad \forall \; [u,v]\in X. \end{aligned}$$

  (3)

  Let $t\in (0,1)$ and set

  $$\begin{aligned}{}[\widehat{u}_t, \widehat{v}_t]=t[u,v]+(1-t)[p,q]=[tu+(1-t)p,tv+(1-t)q]\in X. \end{aligned}$$

  Obviously, $[\widehat{u}_t, \widehat{v}_t] \rightarrow [p,q]$ as $t\rightarrow 0$, which implies that $\widehat{u}_t \rightarrow p$ and $\widehat{v}_t \rightarrow q$ as $t\rightarrow 0$. This in turn implies that $\widehat{u}_t \rightharpoonup p$ and $\widehat{v}_t \rightharpoonup q$ as $t\rightarrow 0$. But both K and G are sequentially weakly continuous, and so $K(\widehat{u}_t)- \widehat{v}_t\rightharpoonup Kp-q$ and $G(\widehat{v}_t)+\widehat{u}_t \rightharpoonup Gq+p$ as $t\rightarrow 0$, respectively. Moreover, from (3), we have

  $$\begin{aligned} \langle K(\widehat{u}_t)- \widehat{v}_t, \widehat{u}_t-p\rangle +\langle G(\widehat{v}_t)+\widehat{u}_t, \widehat{v}_t-q\rangle \ge 0 \end{aligned}$$

  which implies that

  $$\begin{aligned} t\langle K(\widehat{u}_t)- \widehat{v}_t, u-p\rangle + t\langle G(\widehat{v}_t)+\widehat{u}_t, v-q\rangle \ge 0. \end{aligned}$$

  Since $t>0$, we have

  $$\begin{aligned} \langle K(\widehat{u}_t)- \widehat{v}_t, u-p\rangle +\langle G(\widehat{v}_t)+\widehat{u}_t, v-q\rangle \ge 0. \end{aligned}$$

  Taking the limit as $t\rightarrow 0$, we obtain

  $$\begin{aligned} \langle Kp-q,u-p\rangle +\langle Gq+p,v-q\rangle \ge 0\quad \forall \,\, [u,v]\in X. \end{aligned}$$

  Hence $[p,q]\in A^{-1}[0,0]=F(S_r)$, where equality of sets follows from part (c) above.

• (e) Note that the inequality in part (b) above is equivalent to

  $$\begin{aligned} \left\| S_r[x,y] -S_r[w,z]\right\| ^2\le & {} \left\| [x,y]-[w,z]\right\| ^2\\&-\left\| [x,y]-S_r[x,y]-([w,z]-S_r[w,z])\right\| ^2. \end{aligned}$$

  In particular, for $[w,z]=[p,q]\in A^{-1}[0,0]=F(S_r)$, we have

  $$\begin{aligned} \left\| S_r[x,y] -[p,q]\right\| ^2\le \left\| [x,y]-[p,q]\right\| ^2-\left\| [x,y]-S_r[x,y]\right\| ^2. \end{aligned}$$

• (f) We first show that $F(S_r)$ is closed. Let $\{[x_n,y_n]\}$ be a sequence in $F(S_r)$ such that $[x_n,y_n]\rightarrow [p,q]\in X$ as $n\rightarrow \infty$. Then from part (e) above,

  $$\begin{aligned} \left\| [x_n,y_n]-S_r[p,q]\right\| ^2+\left\| [p,q]-S_r[p,q]\right\| ^2\le \left\| [x_n,y_n]-[p,q]\right\| ^2, \end{aligned}$$

  which implies that

  $$\begin{aligned} \left\| [p,q]-S_r[p,q]\right\| \le \left\| [x_n,y_n]-[p,q]\right\| \rightarrow 0\quad \text{ as }\quad n\rightarrow \infty . \end{aligned}$$

  It means that $[p,q]\in F(S_r)$, showing that $F(S_r)$ is closed.

Finally, we show that $F(S_r)$ is convex. From part (e) above, we have

$$\begin{aligned} \left\| S_r[x,y] -[p,q]\right\| \le \left\| [x,y]-[p,q]\right\| \quad \forall \; [x,y]\in X\,\,\text{ and }\,\,\forall \,\, [p,q]\in F(S_r). \end{aligned}$$

(4)

Let $[p_1,q_1],[p_2,q_2]\in F(S_r)$ and $t\in [0,1]$. Denote $[x,y]=t[p_1,q_1]+(1-t)[p_2,q_2]$. Then from Lemma 1,

$$\begin{aligned} \left\| S_r[x,y]-[x,y]\right\| ^2= & {} \left\| t\left\{ S_r[x,y]-[p_1,q_1]\right\} +(1-t)\left\{ S_r[x,y]-[p_2,q_2]\right\} \right\| ^2 \\= & {} t\left\| S_r[x,y]-[p_1,q_1]\right\| ^2+(1-t)\left\| S_r[x,y]-[p_2,q_2]\right\| ^2\\&- t(1-t)\left\| [p_2,q_2]-[p_1,q_1]\right\| ^2. \end{aligned}$$

Now, using (4), we have

$$\begin{aligned} \left\| S_r[x,y]-[x,y]\right\| ^2\le & {} t\left\| [x,y]-[p_1,q_1]\right\| ^2+(1-t)\left\| [x,y]-[p_2,q_2]\right\| ^2\\&- t(1-t)\left\| [p_2,q_2]-[p_1,q_1]\right\| ^2 \\= & {} t(1-t)^2\left\| [p_2,q_2]-[p_1,q_1]\right\| ^2\\&+(1-t)t^2\left\| [p_1,q_1]-[p_2,q_2]\right\| ^2\\&- t(1-t)\left\| [p_2,q_2]-[p_1,q_1]\right\| ^2. \end{aligned}$$

Since $t(1-t)^2+(1-t)t^2-t(1-t)=0$, we conclude that $S_r[x,y]=[x,y]$. Therefore, $F(S_r)$ is convex. $\square$

3 Main results

To construct our algorithms, first assume that the solution set of the Hammerstein Eq. (1) is nonempty. Let $\lambda _n\in (0,2)$ for all $n\in \mathbb {N}$ and $r>0$. If the initial starting points $x_0$ and $y_0$ are given, then generate the $(n+1)$th iterate by

$$\begin{aligned}{}[x_{n+1},y_{n+1}]= (1-\lambda _n)[x_n,y_n] +\lambda _nS_r[x_n,y_n], \end{aligned}$$

(5)

where $S_r$ is as defined in Lemma 8.

Theorem 9

Let H be a real Hilbert space. Fix $r>0$, and the initial starting points $x_0\in H$ and $y_0\in H$. Assume that $\lambda _n\in [a,b]\subset (0,2)$ for all $n\in \mathbb {N}$. Let $K:H\rightarrow H$ and $G:H\rightarrow H$ be monotone mappings that are either sequentially weakly continuous or continuous such that the solution set of the Hammerstein Eq. (1) is nonempty. Assume that $\{[x_n,y_n]\}$ is a sequence generated by (5). Then $\{x_n\}$ converges weakly to some $x^*$, the solution of the Hammerstein Eq. (1), and $\{y_n\}$ converges weakly to $y^*$, where $y^*=Kx^*$.

Proof

We prove the theorem for the case when both K and G are sequentially weakly continuous. The other case(s) can be proved in a similar way.

Let p be the solution of the Hammerstein Eq. (1). Then $p+Gq=0$, where $q=Kp$. Therefore, $[p,q]\in A^{-1}[0,0]$. Denote $H_r=2S_r-I$, where I is the identity mapping on $H\times H$. Since $S_r$ is firmly nonexpansive by Lemma 8, we conclude by Lemma 3 that $H_r$ is nonexpansive. It then follows from (5) that

$$\begin{aligned}&\left\| [x_{n+1},y_{n+1}]-[p,q]\right\| ^2\nonumber \\&\quad = \left\| (1-\lambda _n)\{[x_n,y_n]-[p,q]\} +\lambda _n\{S_r[x_n,y_n]-[p,q]\}\right\| ^2 \nonumber \\&\quad = \left\| \left( 1-\frac{\lambda _n}{2}\right) \{[x_n,y_n]-[p,q]\} + \frac{\lambda _n}{2}\{H_r[x_n,y_n]-[p,q]\}\right\| ^2 \nonumber \\&\quad = \left( 1-\frac{\lambda _n}{2}\right) \left\| [x_{n},y_{n}]-[p,q]\right\| ^2+\frac{\lambda _n}{2}\left\| H_r[x_n,y_n]-H_r[p,q]\right\| ^2\nonumber \\&\qquad - \frac{\lambda _n}{2}\left( 1-\frac{\lambda _n}{2}\right) \left\| 2\{S_r[x_n,y_n]-[x_n,y_n]\}\right\| ^2\nonumber \\&\quad \le \left( 1-\frac{\lambda _n}{2}\right) \left\| [x_{n},y_{n}]-[p,q]\right\| ^2+\frac{\lambda _n}{2}\left\| [x_{n},y_{n}]-[p,q]\right\| ^2\nonumber \\&\qquad - \frac{\lambda _n(2-\lambda _n)}{4}\left\| 2\{S_r[x_n,y_n]-[x_n,y_n]\}\right\| ^2\nonumber \\&\quad =\left\| [x_{n},y_{n}]-[p,q]\right\| ^2-\lambda _n(2-\lambda _n)\left\| [x_{n},y_{n}]-S_r[x_{n},y_{n}]\right\| ^2. \end{aligned}$$

(6)

Using the assumptions on $\{\lambda _n\}$, we obtain from (6),

$$\begin{aligned} \left\| [x_{n+1},y_{n+1}]-[p,q]\right\| ^2\le & {} \left\| [x_{n},y_{n}]-[p,q]\right\| ^2\nonumber \\&-a(2-b)\left\| [x_{n},y_{n}]-S_r[x_{n},y_{n}]\right\| ^2, \end{aligned}$$

(7)

which implies that the sequence $\{[x_{n},y_{n}]-[p,q]\}$ is decreasing, hence it is convergent. That is, there exists a nonnegative real number $\gamma [p,q]$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\left\| [x_{n},y_{n}]-[p,q]\right\| =\gamma [p,q]. \end{aligned}$$

(8)

Taking the limit in (7), we deduce that

$$\begin{aligned} \lim _{n\rightarrow \infty }\left\| [x_{n},y_{n}]-S_r[x_{n},y_{n}]\right\| =0. \end{aligned}$$

(9)

In view of (8), $\{[x_{n},y_{n}]\}$ is bounded. Let $\{[x_{n_k},y_{n_k}]\}$ be a subsequence of $\{[x_{n},y_{n}]\}$ that converges weakly to $[x^*,y^*]\in H\times H$. Then (9) and Lemma 8(d) imply that $[x^*,y^*]\in F(S_r)$. By Lemma 8(c), $[x^*,y^*]\in A^{-1}[0,0]$. Therefore, (8) and Opial’s lemma [45] imply that $\{[x_{n},y_{n}]\}$ converges weakly to $[x^*,y^*]\in A^{-1}[0,0]$. That is, $\{x_n\}$ converges weakly to $x^*$, the solution of the Hammerstein Eq. (1), and $\{y_n\}$ converges weakly to $y^*$, where $y^*=Kx^*$. $\square$

In general, strong convergence is desired for effective approximation of solutions of a given equation. To generate sequences that always converge strongly to some solution of the Hammerstein Eq. (1) (assuming that the solution set of (1) is nonempty), we modify algorithm (5) to obtain the following viscosity type algorithm: Fix $r>0$ and let the initial starting points $x_0\in H$ and $y_0\in H$ be given. Then the $(n+1)$th iterate is given by

$$\begin{aligned}{}[x_{n+1},y_{n+1}]=a_n[f(x_n),g(y_n)]+(1-a_n)\left\{ (1-\lambda _n)[x_n,y_n] +\lambda _nS_r[x_n,y_n]\right\} , \end{aligned}$$

(10)

where $a_n\in (0,1)$ and $\lambda _n\in (0,2)$ for all $n\in \mathbb {N}$, $f:H\rightarrow H$ and $g:H\rightarrow H$ are contractions, and $S_r$ is as defined in Lemma 8.

Theorem 10

Let H be a real Hilbert space, $f:H\rightarrow H$ be a $\tau$-contraction and $g:H\rightarrow H$ be a $\eta$-contraction such that $\tau ,\eta <\frac{1}{2}$. Fix $r>0$ and choose the initial starting points $x_0\in H$ and $y_0\in H$ arbitrarily. Let $K:H\rightarrow H$ and $G:H\rightarrow H$ be monotone mappings that are either sequentially weakly continuous or continuous such that the solution set of the Hammerstein Eq. (1) is nonempty. Assume that $\{[x_n,y_n]\}$ is a sequence generated by (10), where $\lambda _n\in [a,b]\subset (0,2)$ and $a_n\in (0,1)$ for all $n\ge 0$ with $\lim _{n\rightarrow \infty }a_n=0$ and ${\sum _{n=0}^{\infty }a_n=\infty }$. Then $\{x_n\}$ converges strongly to some p, the solution of the Hammerstein Eq. (1), and $\{y_n\}$ converges strongly to q, where $q=Kp$.

Proof

We prove the theorem for the case when both K and G are sequentially weakly continuous. The other case(s) can be proved in a similar way.

Let $[u_n,v_n] = (1-\lambda _n)[x_n,y_n] +\lambda _nS_r[x_n,y_n]$ and let z be any solution of the Hammerstein Eq. (1). Then $z+Gw=0$, where $w=Kz$. Therefore, $[z,w]\in A^{-1}[0,0]$. Let [p, q] be the unique fixed point of $P_{A^{-1}[0,0]}B$, where $B:H\times H\rightarrow H\times H$ is given by $B[u,v]=[f(u),g(v)]$. That is, $[p,q]=P_{A^{-1}[0,0]}[f(p),g(q)]$. It is easy to check that B is a $\gamma$-contraction, where $\gamma =\max \{\tau ,\eta \}$. Then from (10) and (6), we have

$$\begin{aligned}&\left\| [x_{n+1},y_{n+1}]-[p,q]\right\| \nonumber \\&\quad = \left\| a_n\{[f(x_n),g(y_n)]-[p,q]\}+(1-a_n)\{[u_n,v_n]-[p,q]\}\right\| \nonumber \\&\quad \le a_n\left\| [f(x_n),g(y_n)]-[p,q]\right\| + (1-a_n)\left\| [u_n,v_n]-[p,q]\right\| \nonumber \\&\quad = a_n\left\| B[x_n,y_n]-[p,q]\right\| + (1-a_n)\left\| [u_n,v_n]-[p,q]\right\| \nonumber \\&\quad \le a_n\left\| B[x_n,y_n]-B[p,q]\right\| + a_n\left\| B[p,q]-[p,q]\right\| \nonumber \\&\qquad + (1-a_n)\left\| [x_n,y_n]-[p,q]\right\| \nonumber \\&\quad \le a_n\gamma \left\| [x_n,y_n]-[p,q]\right\| + a_n\left\| B[p,q]-[p,q]\right\| \nonumber \\&\qquad + (1-a_n)\left\| [x_n,y_n]-[p,q]\right\| \nonumber \\&\quad \le (1-\mu _n)\left\| [x_n,y_n]-[p,q]\right\| + \mu _n\frac{\left\| B[p,q]-[p,q]\right\| }{(1-2\gamma )}, \end{aligned}$$

(11)

where $\mu _n=a_n(1-2\gamma )$. Note that $\mu _n\in (0,1)$ for all $n\in \mathbb {N}$ with $\mu _n\rightarrow 0$ as $n\rightarrow \infty$ and $\sum _{k=1}^{\infty }\mu _k=\infty$. It then follows from (11) that

$$\begin{aligned} \left\| [x_{n+1},y_{n+1}]-[p,q]\right\|\le & {} \left[ 1-\prod _{k=0}^{n}(1-\mu _k)\right] \frac{\left\| B[p,q]-[p,q]\right\| }{(1-2\gamma )}\nonumber \\&+ \prod _{k=0}^{n}(1-\mu _k)\left\| [x_0,y_0]-[p,q]\right\| \nonumber \\\le & {} \max \left\{ \frac{\left\| B[p,q]-[p,q]\right\| }{(1-2\gamma )},\left\| [x_0,y_0]-[p,q]\right\| \right\} \nonumber \\= & {} M. \end{aligned}$$

(12)

This inequality shows that $\{[x_n,y_n]\}$ is bounded, and so there exists a subsequence $\{[x_{n_k},y_{n_k}]\}$ of $\{[x_n,y_n]\}$ such that

$$\begin{aligned}&\limsup _{n\rightarrow \infty }\langle [f(p),g(q)]-[p,q],[x_n,y_n]-[p,q]\rangle \\&\quad =\lim _{k\rightarrow \infty } \langle [f(p),g(q)]-[p,q],[x_{n_k},y_{n_k}]-[p,q]\rangle . \end{aligned}$$

Since $\{[x_n,y_n]\}$ is bounded, $\{[x_{n_k},y_{n_k}]\}$ has a subsequence, again denoted by $\{[x_{n_k},y_{n_k}]\}$, that converges weakly to $[\widehat{x},\widehat{y}]$ as $k\rightarrow \infty$. It then follows that

$$\begin{aligned}&\limsup _{n\rightarrow \infty }\langle [f(p),g(q)]-[p,q],[x_n,y_n]-[p,q]\rangle \nonumber \\&\quad = \langle [f(p),g(q)]-[p,q],[\widehat{x},\widehat{y}]-[p,q]\rangle . \end{aligned}$$

(13)

Next, we observe from Lemma 1 and (6) that

$$\begin{aligned}&\left\| [x_{n+1},y_{n+1}]-[p,q]\right\| ^2\nonumber \\&\quad \le (1-a_n)\left\| [u_n,v_n]-[p,q]\right\| ^2\nonumber \\&\qquad + 2a_n\langle [f(x_n),g(y_n)]-[p,q],[x_{n+1},y_{n+1}]-[p,q]\rangle \nonumber \\&\quad \le (1-a_n)\left\| [x_n,y_n]-[p,q]\right\| ^2 \nonumber \\&\qquad -\lambda _n(2-\lambda _n)(1-a_n)\left\| [x_n,y_n]-S_r[x_n,y_n]\right\| ^2\nonumber \\&\qquad + 2a_n\langle [f(x_n),g(y_n)]-[p,q],[x_{n+1},y_{n+1}]-[p,q]\rangle \nonumber \\&\quad \le (1-a_n)\left\| [x_n,y_n]-[p,q]\right\| ^2\nonumber \\&\qquad -a(2-b)(1-a_n)\left\| [x_n,y_n]-S_r[x_n,y_n]\right\| ^2\nonumber \\&\qquad + 2a_n\langle [f(x_n),g(y_n)]-[f(p),g(q)],[x_{n+1},y_{n+1}]-[p,q]\rangle \nonumber \\&\qquad + 2a_n\langle [f(p),g(q)]-[p,q],[x_{n+1},y_{n+1}]-[p,q]\rangle . \end{aligned}$$

(14)

From (11), (12) and the Cauchy–Schwarz inequality, we have

$$\begin{aligned}&\langle [f(x_n),g(y_n)]-[f(p),g(q)], [x_{n+1},y_{n+1}]-[p,q]\rangle \nonumber \\&\quad = \langle B[x_n,y_n]-B[p,q],[x_{n+1},y_{n+1}]-[p,q]\rangle \nonumber \\&\quad \le \left\| B[x_n,y_n]-B[p,q]\right\| \left\| [x_{n+1},y_{n+1}]-[p,q]\right\| \nonumber \\&\quad \le \gamma \left\| [x_n,y_n]-[p,q]\right\| \left\{ \mu _nM\right. \nonumber \\&\qquad + \left. (1-\mu _n)\left\| [x_n,y_n]-[p,q]\right\| \right\} \nonumber \\&\quad \le \gamma \left\| [x_n,y_n]-[p,q]\right\| ^2+\gamma M^2\mu _n. \end{aligned}$$

(15)

Again from the Cauchy–Schwarz inequality,

$$\begin{aligned}&\langle [f(p),g(q)]-[p,q],[x_{n+1},y_{n+1}]-[p,q]\rangle \nonumber \\&\quad = \langle [f(p),g(q)]-[p,q],[x_{n},y_{n}]-[p,q]\rangle \nonumber \\&\qquad + \langle [f(p),g(q)]-[p,q],[x_{n+1},y_{n+1}]-[x_n,y_n]\rangle \nonumber \\&\quad \le \langle [f(p),g(q)]-[p,q],[x_{n},y_{n}]-[p,q]\rangle \nonumber \\&\qquad + (1-2\gamma )\left\| [x_{n+1},y_{n+1}]-[x_n,y_n]\right\| M. \end{aligned}$$

(16)

Substituting (15) and (16) into (14), we obtain

$$\begin{aligned} \left\| [x_{n+1},y_{n+1}]-[p,q]\right\| ^2\le & {} (1-a_n(1-2\gamma ))\left\| [x_n,y_n]-[p,q]\right\| ^2 +2\gamma M^2a_n\mu _n \nonumber \\&+\,2\mu _n\left\| [x_{n+1},y_{n+1}]-[x_n,y_n]\right\| M\nonumber \\&+\,2a_n\langle [f(p),g(q)]-[p,q],[x_{n},y_{n}]-[p,q]\rangle \nonumber \\&-\,a\,(2-b)(1-a_n)\left\| [x_n,y_n]-S_r[x_n,y_n]\right\| ^2 \nonumber \\= & {} (1-\mu _n)\left\| [x_n,y_n]-[p,q]\right\| ^2+\mu _nb_n\nonumber \\&-\,a\,(2-b)(1-a_n)\left\| [x_n,y_n]-S_r[x_n,y_n]\right\| ^2, \end{aligned}$$

(17)

where

$$\begin{aligned} b_n= & {} 2\gamma M^2a_n+2M\left\| [x_{n+1},y_{n+1}]-[x_n,y_n]\right\| \\&+\frac{2}{1-2\gamma }\langle [f(p),g(q)]-[p,q],[x_{n},y_{n}]-[p,q]\rangle . \end{aligned}$$

To show that $\{[x_n,y_n]\}$ converges strongly to [p, q], we consider two possible cases on the sequence $\{[x_n,y_n]-[p,q]\}$.

Case I. Assume that $\{ \left\| [x_n,y_n]-[p,q]\right\| \}$ is decreasing. Then this sequence is convergent. From (17), and taking note that $\{[x_n,y_n]\}$ is bounded, we have

$$\begin{aligned} a(2-b)\left\| [x_n,y_n]-S_r[x_n,y_n]\right\| ^2\le & {} \left\| [x_n,y_n]-[p,q]\right\| ^2 - \left\| [x_{n+1},y_{n+1}]-[p,q]\right\| ^2\\&+ \mu _n\widetilde{M} \end{aligned}$$

for some $\widetilde{M}>0$. Using the condition $\mu _n\rightarrow 0$ as $n\rightarrow \infty$, we get

$$\begin{aligned} \lim _{n\rightarrow \infty }\left\| [x_n,y_n]-S_r[x_n,y_n]\right\| =0. \end{aligned}$$

(18)

But $[x_{n_k},y_{n_k}] \rightharpoonup [\widehat{x},\widehat{y}]$ as $k\rightarrow \infty$, and so $S_r[x_{n_k},y_{n_k}] \rightharpoonup [\widehat{x},\widehat{y}]$ as $k\rightarrow \infty$. Following similar steps as in the proof of Lemma 8, we obtain $[\widehat{x},\widehat{y}]\in A^{-1}[0,0]$. Therefore, from (13) and Lemma 2, we get

$$\begin{aligned}&\limsup _{n\rightarrow \infty }\langle [f(p),g(q)]-[p,q],[x_n,y_n]-[p,q]\rangle \nonumber \\&\quad =\langle [f(p),g(q)]-[p,q],[\widehat{x},\widehat{y}]-[p,q]\rangle \le 0. \end{aligned}$$

(19)

Also, from (10) and (18), we have

$$\begin{aligned} \left\| [x_{n+1},y_{n+1}]-[x_n,y_n]\right\|\le & {} a_n\left\| [f(x_n),g(y_n)]-[x_n,y_n]\right\| \nonumber \\&+\,\lambda _n(1-a_n)\left\| S_r[x_n,y_n]-[x_n,y_n]\right\| . \end{aligned}$$

Taking the limit on both sides as $n\rightarrow \infty$, we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\left\| [x_{n+1},y_{n+1}]-[x_n,y_n]\right\| =0. \end{aligned}$$

(20)

Therefore, we conclude that

$$\begin{aligned} \limsup _{n\rightarrow \infty } b_n\le 0. \end{aligned}$$

(21)

On the other hand, inequality (17) reduces to

$$\begin{aligned} \left\| [x_{n+1},y_{n+1}]-[p,q]\right\| ^2\le (1-\mu _n)\left\| [x_{n},y_{n}]-[p,q]\right\| ^2+\mu _nb_n. \end{aligned}$$

From this last inequality, (21) and Lemma 4, we conclude that $\{[x_n,y_n]\}$ converges strongly to [p, q]. That is, $\{x_n\}$ converges strongly to p and $\{y_n\}$ converges strongly to q, where $p+Gq=0$ and $q=Kp$. In particular, $\{x_n\}$ converges strongly to p, the solution of the Hammerstein Eq. (1).

Case II. Assume that there exists a subsequence $\{{n_i}\}$ of $\{{n}\}$ such that

$$\begin{aligned} \left\| [x_{n_i},y_{n_i}]-[p,q]\right\| <\left\| [x_{n_i+1},y_{n_i+1}]-[p,q]\right\| \end{aligned}$$

for all $i\in \mathbb {N}$. Then by Lemma 5, there exists a nondecreasing sequence $(m_{k})\subset \mathbb {N}$ such that $m_{k}\rightarrow \infty$ as $k\rightarrow \infty$ and

$$\begin{aligned} \max \{\left\| [x_{m_k},y_{m_k}]-[p,q]\right\| , \left\| [x_{k},y_{k}]-[p,q]\right\| \}\le \left\| [x_{m_k+1},y_{m_k+1}]-[p,q]\right\| \end{aligned}$$

(22)

for all $i\in \mathbb {N}$. In this case, we have from (17) and (22)

$$\begin{aligned} \left\| [x_{m_k+1},y_{m_k+1}]-[p,q]\right\| ^2\le & {} (1-\mu _{m_k})\left\| [x_{m_k},y_{m_k}]-[p,q]\right\| ^2+\mu _{m_k}b_{m_k}\\&-\, a(2-b)(1-\mu _{m_k})\left\| [x_{m_k},y_{m_k}]-S_r[x_{m_k},y_{m_k}]\right\| ^2\\\le & {} (1-\mu _{m_k})\left\| [x_{m_k+1},y_{m_k+1}]-[p,q]\right\| ^2+\mu _{m_k}b_{m_k}\\&-\,a(2-b)(1-\mu _{m_k})\left\| [x_{m_k},y_{m_k}]-S_r[x_{m_k},y_{m_k}]\right\| ^2. \end{aligned}$$

Rearranging, we obtain

$$\begin{aligned} \mu _{m_k}b_{m_k}\ge & {} \mu _{m_k}\left\| [x_{m_k+1},y_{m_k+1}]-[p,q]\right\| ^2\nonumber \\&+\, a(2-b)(1-\mu _{m_k})\left\| [x_{m_k},y_{m_k}]-S_r[x_{m_k},y_{m_k}]\right\| ^2. \end{aligned}$$

(23)

Taking the limit as $k\rightarrow \infty$ and remembering that the sequence $\{[x_{m_k},y_{m_k}]\}$ is bounded, we obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }\left\| [x_{m_k},y_{m_k}]-S_r[x_{m_k},y_{m_k}]\right\| =0. \end{aligned}$$

As in the proof of Case I, we easily derive the limit

$$\begin{aligned} \lim _{k\rightarrow \infty }\left\| [x_{m_k+1},y_{m_k+1}]-[x_{m_k},y_{m_k}]\right\| =0. \end{aligned}$$

Now, we can find a subsequence $\{[x_{m_k(l)},y_{m_k(l)}]\}$ of $\{[x_{m_k},y_{m_k}]\}$ such that

$$\begin{aligned}&\limsup _{k\rightarrow \infty } \langle [f(p),g(q)]-[p,q], [x_{m_k},y_{m_k}]-[p,q]\rangle \\&\quad = \lim _{l\rightarrow \infty }\langle [f(p),g(q)]-[p,q], [x_{m_k(l)},y_{m_k(l)}]-[p,q]\rangle . \end{aligned}$$

Following similar arguments as in the proof of Case I, we arrive at

$$\begin{aligned} \limsup _{k\rightarrow \infty } b_{m_k} \le 0. \end{aligned}$$

(24)

Finally, rearranging (23), we obtain

$$\begin{aligned} \left\| [x_{m_k+1},y_{m_k+1}]-[p,q]\right\| ^2 \le b_{m_k}, \end{aligned}$$

which together with (24) imply that

$$\begin{aligned} \lim _{k\rightarrow \infty } \left\| [x_{m_k+1},y_{m_k+1}]-[p,q]\right\| =0. \end{aligned}$$

Using (22), we deduce that

$$\begin{aligned} \lim _{k\rightarrow \infty } \left\| [x_{k},y_{k}]-[p,q]\right\| =0, \end{aligned}$$

showing that $\{[x_n,y_n]\}$ converges strongly to [p, q]. In particular, $\{x_n\}$ converges strongly to p, the solution of the Hammerstein Eq. (1). $\square$

Remark 1

Our results improve the results of Bello et al. [3] in the sense that the boundedness of both K and G have been dispensed with, and our results do not rely on the existence of the constant $\gamma _0$ used in [3] which is not clear how it can be found. For the Hilbert space setting the assumption that both K and G are bounded that was used by Zegeye and Malonza [52] have also been dispensed with. Our results also cover the case when K and G are sequentially weakly continuous which was not discussed in [52]. In addition, the presence of the viscosity approximation term and the over-relaxed parameter $\lambda _n\in (0,2)$ in our algorithm generalize the algorithm due to Zegeye and Malonza [52].

4 Numerical example

In this section, we give some examples to illustrate the convergence of one of our algorithm to solutions of the Hammerstein Eq. (1), when they exists. We also compare algorithm with the existing ones and present these comparisons using graphs and tables. All numerical experiments were performed on MATLAB R2022a version. The specifications of the laptop used to run the programs are: Intel(R) Core(TM) i7-7700HQ CPU @ 2.80 Ghz 2.81 GHz with 16 GB.

Example 1

Let $H=\mathbb {R}$, and define $K:H\rightarrow H$ by $Kx=3x$ and $G:H\rightarrow H$ by $Gx=x-4$. Then both K and G are monotone and continuous. The solution of the Hammerstein Eq. (1) is $x^*=1$ with $y^*=3$. Hence the only root of A is $z^*=[x^*,y^*]=[1,3]$, where as before $A:H\times H\rightarrow H\times H$ is given by $A[x,y]=[Kx-y,Gy+x]$. Moreover, for any $r>0$, one can check that

$$\begin{aligned} S_r[x,y]=\left[ \frac{(1+r)x+ry+4r^2}{4r^2+4r+1},\frac{(1+3r)y-rx+4r(1+3r)}{4r^2+4r+1}\right] . \end{aligned}$$

Define $f:H\rightarrow H$ by $f(x)=\frac{x}{4}$ and $g:H\rightarrow H$ by $g(x)=\frac{x}{3}$. Then both f and g are contractions that satisfy the condition of Theorem 10. Equation (10) can now be written as

$$\begin{aligned} \left. \begin{aligned} x_{n+1}&=a_n\frac{x_n}{4}+(1-a_n)\left( (1-\lambda _n)x_n+\lambda _n\left[ \frac{(1+r)x_n+ry_n+4r^2}{4r^2+4r+1}\right] \right) \\ y_{n+1}&=a_n\frac{y_n}{3}+(1-a_n)\left( (1-\lambda _n)y_n+\lambda _n\left[ \frac{(1+3r)y_n-rx_n+4r(1+3r)}{4r^2+4r+1}\right] \right) \end{aligned}\right\} \end{aligned}$$

(25)

To implement algorithm (25), we chose $a_n=(n+10000)^{-1}$ and $\lambda _n=\frac{n+3}{n+2}$ for all $n\ge 0$. Choosing $r=2$, we can see from Fig. 1a and b that the sequence $\{x_n\}$ converges to $x^*=1$, the solution of the Hammerstein Eq. (1) and the sequence $\{y_n\}$ converges to $y^*=3$, respectively, for different initial starting points $z_0=[x_0,y_0]$.

Fig. 1

Convergence of $\{x_n\}$ to $x^*$ and $\{y_n\}$ to $y^*$

If we now fix $z_0=[1.7,0]$, then it can be seen from Fig. 2a and b that the sequence $\{x_n\}$ converges to $x^*=1$, the solution of the Hammerstein Eq. (1), and the sequence $\{y_n\}$ converges to $y^*=3$, respectively, for different values of r.

Fig. 2

Convergence of $\{x_n\}$ to $x^*$ and $\{y_n\}$ to $y^*$

Figure 2a and b suggests that the sequence $\{x_n\}$ and $\{y_n\}$, respectively, requires fewer iterations to converge when the value of r is large compared to when r is small.

Now if we fix $z_0=[0.6,2.5]$ and $r=1$, then it can be seen from Fig. 3a and b that the sequence $\{x_n\}$ converges to $x^*=1$, the solution of the Hammerstein Eq. (1) and the sequence $\{y_n\}$ converges to $y^*=3$, respectively, for different values of $\lambda _n\in (0,2)$.

Fig. 3

Convergence of $\{x_n\}$ to $x^*$ and $\{y_n\}$ to $y^*$

Figure 3a and b suggests that the sequence $\{x_n\}$ and $\{y_n\}$, respectively, requires fewer iterations to converge when the value of $\lambda _n$ is large compared to when $\lambda _n$ is small.

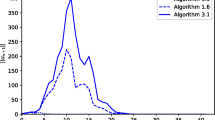
By means of numerical experiments, Bello et al. [3] showed that their algorithm

$$\begin{aligned} \left. \begin{aligned} w_n&= x_n-\theta _n(x_n-x_{n-1})\\ z_n&= y_n-\theta _n(y_n-y_{n-1})\\ x_{n+1}&= w_n-b_n(Kw_n-z_n)-b_nc_nw_n \\ y_{n+1}&= z_n-b_n(Gz_n+w_n)-b_nc_nz_n \end{aligned} \right\} \end{aligned}$$

(26)

converges much faster, in terms of the number of iterations than the convergence obtained with existing algorithms by Chidume and Shehu [23], Chidume and Shehu [21], Minjibir and Mohammad [42] and Shehu [47]. In Table 1, Figs. 4 and 5, we compare the convergence of (26) and (25). In this case, we choose the initial starting points $x_0=-1$ and $y_0=1$ for algorithm (25), and $x_0= -1.5$, $x_1=-1$, $y_0=0.5$ and $y_1=1$ for algorithm (26), $r=1$, $a_n=(n+10,000)^{-1}$, $\lambda _n=\frac{n+3}{n+2}$, $\theta _n=\frac{1}{(n+1)^2}$, $b_n=\frac{1}{(n+1)^{\frac{1}{4}}}$ and $c_n=\frac{1}{(n+1)^{\frac{1}{5}}}$. Results of this example are reported in Table 1 below.

Table 1 Numerical results for Example 1

Figure 4a and b give a comparison of algorithms (25) and (26) in terms of the number of iteration taken to reach the solution of the Hammerstein Eq. (1). Figure 5a and b gives a comparison of algorithm (25) and algorithm (26) in terms of the time taken to reach the solution of the Hammerstein Eq. (1).

Fig. 4

Convergence of $\{z_n\}$ to $z^*$

Figure 4a and b show that algorithm (25) takes fewer iterations to converge to the desired solution than algorithm (26). Figure 5a and b show that algorithm (25) takes less time to converge to the desired solution than algorithm (26).

Fig. 5

Convergence of $\{z_n\}$ to $z^*$

Example 2

Let $H=L_{2}^{\mathbb {R}}([0, 1])$ with the norm $\left\| x\right\| _{L_{2}}=\left( \int _{0}^{1}\left| x(t)\right| ^{2}dt\right) ^{\dfrac{1}{2}}$. Let K, G: $H\rightarrow H$ be defined by $K(x(t))=\frac{3}{4}x(t)+1$ and $G(y(t))=\frac{y(t)}{3} -3$. Let $f,g:H\rightarrow H$ be defined by $f(x(t))=\frac{x(t)}{3}$ and $g(x(t))=\frac{y(t)}{3}$. One can show that K and G are continuous monotone, and f and g are contraction mappings. In addition we observe that $S_r(x_n(t),y_n(t))=\Big (\frac{2x_n(t)}{5} + \frac{3y_n(t)}{10}+\frac{1}{2}, \frac{21 y_n(t)}{40}-\frac{3x_n(t)}{10}+\frac{15}{8}\Big )$ and the solutions of the equations $x(t)+GKx(t)=0$ is $x^{*}(t)=\dfrac{32}{15}$. Thus, the algorithm in (10) reduces to the following scheme: $x_{0}(t),y_0(t)\in H$, are chosen arbitrarily;

$$\begin{aligned} \left. \begin{aligned} x_{n+1}(t)&=a_n\frac{x_n(t)}{3} + (1-a_n)\left[ (1-\lambda _n)x_n(t)+\lambda _n w_n(t)\right] , \\ y_{n+1}(t)&=a_n\frac{y_n(t)}{3} + (1-a_n)\left[ (1-\lambda _n)y_n(t)+\lambda _n z_n(t)\right] . \end{aligned} \right\} \end{aligned}$$

(27)

Now, if we choose the initial starting point $(x_0(t),y_0(t))=(t, t)$, and $\lambda _n=\frac{n+1}{n+2}+0.002$, then the conditions of Theorem 10 are satisfied. Figure 6 gives the graph of the error term $E_n=\left\| x_n(t)-x^*(t)\right\| _{L_{2}}$ versus the number of iterations n for different values of the parameter $\{a_n\}$.

Fig. 6

Convergence of the sequence $\left\{ x_n(t)\right\}$ for different parameter $\{a_n\}$

Table 2 Numerical results for Example 2

Fig. 7

Convergence of $\{x_n(t)\}$ to $x^*(t)$ in terms of number of iterations

Fig. 8

Convergence of $\{x_n(t)\}$ to $x^*(t)$ in terms of elapsed time

From Fig. 6, we observe that the sequence $\{x_n(t)\}$ converges strongly to $x^*(t)=\frac{32}{15}$, which is the solution of the Hammerstein Eq. (1), and the convergence is faster when the coefficient of “n”in the denominator of the control parameter $\{a_n\}$ is large while the initial point and $\{\lambda _n\}$ are kept fixed.

In Table 2 and Fig. 6, we compare the convergence of (26) and (27). In this case, we choose $a_n= 1/(1000*n+1000)$, $\lambda _n=((n+1)/(n+2))+0.002$, and the initial starting point $x_1=t, y_1=t^2$, for algorithm (27). The parameters used for algorithm (26) are $\theta _n=1/((1*n+1)^2)$, $b_n=1/((n+1)^{(1/4)})$ and $c_n=1/((n+1)^{(1/5)})$, while the initial points chosen are $x0=-1.5$, $y0=0.5$, $x_1=t$ and $y_1=t^2$. Results of this example are reported in Table 2.

Figures 7 and 8 indicate that algorithm (27) converges faster than algorithm (26) in terms of both the number of iterations and the time taken to converge.

5 Conclusion

In this paper, we have introduced two iterative methods for approximating solutions of the Hammerstein Eq. (1), if they exist. It is then shown that under suitable assumptions, sequences generated by the first and second iterative methods always converge weakly and strongly, respectively, to an element in the solution set of the Hammerstein Eq. (1), if this solution set is nonempty. The common feature of our algorithms is the presence of the over-relaxed parameter $\lambda _n$ that has been used in the literature to speed up the rate of convergence of iterative methods. Numerical experiments show that our methods produce sequences that converges faster to the solution of the Hammerstein Eq. (1), assuming existence of solutions, compared with some of the iterative methods studied in the literature. Also, our results extend, improve and generalize some existing results in the literature.