Numerical schemes for the time-fractional mobile/immobile transport equation based on convolution quadrature

Abstract

In this work, the numerical approximation of the time-fractional mobile/immobile transport equation is considered. We investigate the solution regularity for two types of the initial data regularities. By applying the continuous piecewise linear finite elements in space, we obtain the spatial semidiscrete Galerkin scheme and derive its error estimates. We then propose two finite element schemes for the equation by employing convolution quadrature based on the backward Euler and the second-order backward difference methods. The corresponding error estimates for the two schemes are also given. Numerical examples of the two-dimensional problems are shown to confirm the convergence theory results.

1 Introduction

In this work, we study the numerical method for the time-fractional mobile/immobile transport Eq.

$$\begin{aligned} (\kappa _1\partial _t +\kappa _2{}_{RL}D_{0,t}^{\alpha })(u(x, t)-v)= & {} \mu \Delta u(x, t)+f(x, t), \ \text {in}\ \Omega \times (0, T],\nonumber \\ u(x, t)= & {} 0,\ \text {on}\ \partial \Omega \times (0, T],\nonumber \\ u(x,0)= & {} v(x),\ \text { in} \ {\overline{\Omega }}. \end{aligned}$$

(1)

Here, $\Omega \subset {\mathbb {R}}^{2}$ is a bounded convex domain with the boundary $\partial \Omega$. The parameters $\kappa _1, \kappa _2$, and $\mu$ are positive constants. The f and v are both prescribed functions. The fractional order $\alpha \in (0,1)$ and the Riemann-Liouville derivative ${}_{RL}D_{0,t}^{\alpha }$ is defined by

$$\begin{aligned} {}_{RL}D_{0,t}^{\alpha } u(\cdot , t)=\frac{\partial }{\partial t}\Big ({}_{RL}D_{0,t}^{-(1-\alpha )} u(\cdot ,t)\Big ), \end{aligned}$$

in which the Riemann-Liouville integral ${}_{RL}D_{0,t}^{-\nu }$ is given by

$$\begin{aligned} {}_{RL}D_{0,t}^{-\nu }u(\cdot ,t) = \frac{1}{\Gamma (\nu )} \int _{0}^{t}(t-s)^{\nu -1} u(\cdot ,s) d s, \end{aligned}$$

with $\nu >0$.

The Eq. (1) has attracted more and more interests in the last two decades. By introducing the power law memory function, the equation can be derived from the classic mobile/immobile transport theory, and can be regarded as the limiting equation that govern continuous time random walk with heavy tailed random waiting time [19]. There are many important applications in various fields for the fractional model (1), especially in groundwater solute modeling. For related discussions, please refer to [7, 24].

For the numerical study of the model (1) or its variants, there have been some research results so far, see [8, 13, 14] and the references therein. In [13], the authors considered a meshless method based on radial basis functions to derive the numerical scheme for solving the time-fractional mobile/immobile transport equation with different spatial domains. One can also refer to [17, 18] for further investigation on the radial basis functions technology in solving other fractional models. In [14], Liu et al. proposed the compact difference scheme for the one-dimensional case of (1) with a convection term. Jiang et al. presented the alternating direction implicit compact difference scheme for the two-dimensional time-fractional mobile/immobile equation with nonlinear terms based on the classical L1 method [8]. It can be seen that most of the convergence analysis in these studies are based on the solution being sufficiently smooth, which may be unrealistic in practice. Recently, Yin et al. employed a generalized BDF2-$\theta$ method with starting parts to the fractional mobile/immobile transport equations involving Riemann–Liouville derivative in time [21]. The starting term is designed to capture the singularities and this method has been widely used in dealing with the problem of non-smooth solutions in fractional models [6, 12, 22, 23]. However, one needs to impose certain compatibility condition on the source f since this method relies on expanding the solution into power series with respect to t [10].

In this paper, we are interested in the numerical methods for the fractional model with nonsmooth problem data in the sense that $v\in L^2(\Omega )$ and f is not compatible with the data. The nonsmooth data analysis has received great attention due to the important roles in various applications, such as inverse problems, one can refer to the review paper [10] for more details. It is known that the convolution quadrature developed by Lubich and further investigated by Jin et al., can provide the flexible framework for developing robust numerical schemes, one may refer to [10] for further discussion. In [9], by combining the finite element method with convolution quadrature, Jin et al. proposed two fully discrete schemes for the sudiffusion and diffusion-wave equations, and established error estimates optimal in the sense of data regularity. Very recently, by applying convolution quadrature, Chen and Nong developed the numerical schemes for time-fractional Cattaneo equation. They also given the error estimates of their schemes when the problem data is smooth or not smooth [3]. For the application of convolution quadrature in other fractional models, readers can refer to the references [1, 11, 25], just to name a few. However, to the best of our knowledge, there is no report about the convolution quadrature to solve the time-fractional mobile/immobile transport Eq. (1) with respect to data regularity, and this motivates our research for this paper.

The main contributions of this paper are as follows. First, we establish the regularity results of the solution by using the Laplace transform tools and operator approach. Second, by using the convolution quadrature time discretization with backward Euler (BE) and second-order backward difference (SBD) methods, we propose two efficient finite element schemes for numerically solving Eq. (1), cf. (14) and (17). Especially, when applying the SBD method, in order to maintain the temporal second-order convergence, we add some appropriate corrections to the first time layer. Third, by exploiting the operator trick, we further develop the error estimates of the proposed schemes with respect to different data regularity, cf. Theorems 4–7.

The rest of the paper is organized as follows. In Sect. 2, we introduce some useful notations and derive the properties of the solution operator. In Sect. 3, we propose the semidiscrete finite element scheme with the error estimates. Two fully discrete schemes based on convolution quadratures and the corresponding error analyses are presented in Sect. 4. In Sect. 5, the extensive numerical examples are conducted to verify the theoretical results. The conclusions of this paper are drawn in Sect. 6. We denote c as a constant which is independent of the temporal stepsize $\tau$ and spatial grid size h in this paper.

2 Preliminary

In this part, we present some useful notations and derive the integral representation of the solution in Eq. (1).

Note that the Laplace transform of ${}_{RL}D_{0,t}^\alpha g(t)$ is given by

$$\begin{aligned} {\mathcal {L}}\{{}_{RL}D_{0,t}^\alpha g(t); z\} = z^\alpha {\widehat{g}}(z), \end{aligned}$$

with the notation ${\widehat{g}}(z)=\int _0^\infty e^{-zt}g(t)dt$. Letting $A:=-\Delta$ and applying the Laplace transform to (1), we obtain

$$\begin{aligned} (\kappa _1 z + \kappa _2 z^\alpha )({\widehat{u}}(z) - z^{-1}v) + \mu A{\widehat{u}}(z)= {\widehat{f}}(z). \end{aligned}$$

(2)

Formally, we have

$$\begin{aligned} {\widehat{u}}(z)= {\widehat{E}}(z)\Big (v + \frac{1}{\kappa _1 + \kappa _2 z^{\alpha -1}}{\widehat{f}}(z)\Big ), \end{aligned}$$

(3)

with ${\widehat{E}}(z) = \frac{\hbar (z)}{z}(\hbar (z)I+A)^{-1}$. Here, $\hbar (z) = \frac{\kappa _1 z + \kappa _2 z^\alpha }{\mu }$.

The basic properties of the function $\hbar (z)$ are given by the following lemma. We omit the proof here, one can refer to [3] for similar discussion.

Lemma 1

For any $z\in \Sigma _\theta$ with the fixed $\theta \in (\pi /(2\alpha ),\pi )$, we have $\hbar (z)\in \Sigma _{{\tilde{\theta }}}$ and

$$\begin{aligned} |\hbar (z)|\le c(\kappa _1|z|+\kappa _2 |z|^{\alpha }). \end{aligned}$$

Here, ${\tilde{\theta }}=\alpha \theta >\pi /2$ and $\Sigma _\theta = \{z\in {\mathbb {C}}, z\ne 0, |\arg z|<\theta \}$.

Using the resolvent estimate $\Vert (zI+A)^{-1}\Vert \le c |z|^{-1}, \forall z\in \Sigma _\theta$ for the selfadjoint and positive definite operator A, we have

$$\begin{aligned} \Vert {\widehat{E}}(z)\Vert \le c |\frac{\hbar (z)}{z}|\cdot |\hbar (z)|^{-1} \le c |z|^{-1}. \end{aligned}$$

(4)

It follows that the solution operator of Eq. (1) can be expressed by inverse Laplace transform, that is,

$$\begin{aligned} E(t) = \frac{1}{2\pi i} \int _{\Gamma _{\theta , \delta }} e^{zt}{\widehat{E}}(z)dz, \end{aligned}$$

(5)

in which $\Gamma _{\theta , \delta } = \{re^{\pm i\theta }:r\ge \delta \}\cup \{\delta e^{i\phi }: |\phi |\le \theta \}$ with $\delta >0$ and $\theta \in (\pi /2, \pi )$.

Therefore, in view of the boundedness of ${\widehat{E}}(z)$ in (4) and Theorem 2.1 in [2], we conclude that the solution u of (1) is unique, and belongs to the space: $C([0,T]; L^2(\Omega )) \cap C((0,T]; {H}^2(\Omega )\cap H_0^1(\Omega ))$.

Next, we present the stability properties of the solution operator E(t). To this end, we let the Hilbert space ${\dot{H}}^r(\Omega )$ be the subspace of $L^2(\Omega )$ with the norm $\Vert v\Vert _{{\dot{H}}^r(\Omega )}^2 = \sum _{k=1}^{\infty }\lambda _k^r (v,\varphi _k)^2$. Here, $\lambda _k$ and $\varphi _k$ are the Dirichlet eigenvalues and eigenfunctions of A [20].

From here on, we always choose $\delta =1/t$ in $\Gamma _{\theta ,\delta }$ when deriving inequalities, unless otherwise stated. We present the stability results of solution operator E(t) as follows.

Theorem 1

Let m be a nonnegative integer and $k=0,1$. Then for $t>0$, we have:

• (a) If $v\in L^2(\Omega )$, then $\Vert A^k E^{(m)}(t)v\Vert \le c t^{-m-k\alpha }\Vert v\Vert .$

• (b) If $v\in {\dot{H}}^2(\Omega )$ and $k+m\ge 1$, then $\Vert A^k E^{(m)}(t)v\Vert \le ct^{-m+(1-k)\alpha }\Vert Av\Vert$.

Proof

We first consider the case (a) with $k=0$ and $m\ge 0$. By the Eq. (5) and the estimate (4), one gets

$$\begin{aligned} \Vert E^{(m)}(t)\Vert \le \Vert \frac{1}{2\pi i} \int _{\Gamma _{\theta , \delta }} z^m e^{zt}{\widehat{E}}(z)dz\Vert \le c \int _{\Gamma _{\theta , \delta }} |z|^m e^{\mathfrak {R}{(z)}t}\Vert {\widehat{E}}(z)\Vert |dz|\le ct^{-m}. \end{aligned}$$

So by operating the operator A and using the identity $A{\widehat{E}}(z) = \frac{\hbar (z)}{z}(I-\hbar (z)(\hbar (z)I+A)^{-1})$, we derive that

$$\begin{aligned} \Vert AE^{(m)}(t)\Vert \le c \int _{\Gamma _{\theta , \delta }} |z|^{m-1}|\hbar (z)| e^{\mathfrak {R}{(z)}t} |dz|. \end{aligned}$$

Combining the Lemma 1 with the inequality $t^{-m-1}\le T^{1-\alpha }t^{-m-\alpha }$, we further obtain

$$\begin{aligned} \Vert AE^{(m)}(t)\Vert\le & {} c \int _{\Gamma _{\theta , \delta }} (\kappa _1|z|^m + \kappa _2|z|^{m+\alpha -1})e^{\mathfrak {R}{(z)}t} |dz| \le c (\kappa _1 t^{-m-1} + \kappa _2 t^{-m-\alpha })\\\le & {} c t^{-m-\alpha }. \end{aligned}$$

For the case (b) with $k=0$ and $m\ge 0$, we apply the identity ${\widehat{E}}(z) = z^{-1}(I-(\hbar (z)I+A)^{-1}A)$ to get

$$\begin{aligned} E^{(m)}(t)v = \frac{1}{2\pi i} \int _{\Gamma _{\theta , \delta }} z^{m-1} e^{zt}(I-(\hbar (z)I+A)^{-1}A)v dz. \end{aligned}$$

Since $\int _{\Gamma _{\theta , 1/t}} z^{m-1} e^{zt}dz = 0$ for $m\ge 1$ and

$$\begin{aligned} \Vert (\hbar (z)I+A)^{-1}\Vert \le c |\hbar (z)|^{-1} \le c\min \left\{ \frac{1}{\kappa _1}|z|^{-1}, \frac{1}{\kappa _2}|z|^{-\alpha }\right\} , \end{aligned}$$

by observing the inequality $t^{\alpha -m}\le T^{1-\alpha }t^{1-m}$ for $m\ge 1$, we have

$$\begin{aligned} \Vert E^{(m)}(t)v\Vert\le & {} c\int _{\Gamma _{\theta , \delta }} |z|^{m-1} e^{\mathfrak {R}{(z)}t} \min \left\{ \frac{1}{\kappa _1}|z|^{-1}, \frac{1}{\kappa _2}|z|^{-\alpha }\right\} \Vert Av\Vert |dz|\\\le & {} c \min \left\{ \frac{1}{\kappa _1}t^{1-m}, \frac{1}{\kappa _2}t^{\alpha -m}\right\} \Vert Av\Vert \le c t^{\alpha -m}\Vert Av\Vert . \end{aligned}$$

Finally, the case $k=1$ in (b) can be readily derived from the special case $k=0$ in (a). $\square$

3 Semidiscrete scheme in space

In this section, we develop the semidiscrete scheme by using the finite element method in space and derive the corresponding error estimates.

Let ${\mathcal {T}}_{h}$ be a partition of the domain $\Omega$ with $h=\max _{K\in {\mathcal {T}}_h}h_K$, where $h_K$ denotes the diameter of the triangles K [20]. The continuous piecewise linear finite element space $V_h$ over the triangulation ${\mathcal {T}}_{h}$ is given by

$$\begin{aligned} V_{h}=\left\{ v_{h} \in H_{0}^{1}(\Omega ): v_{h}|_{K} \text { is the linear function and } \forall K \in {\mathcal {T}}_{h}\right\} . \end{aligned}$$

The $L^2(\Omega )$ orthogonal projection $P_h: L^2(\Omega )\rightarrow V_h$ is defined by

$$\begin{aligned} (P_h \varphi , \chi ) = (\varphi , \chi ), \quad \forall \chi \in V_h, \end{aligned}$$

and the Ritz projection $R_h: H_0^1(\Omega )\rightarrow V_h$ is given by

$$\begin{aligned} (R_h \varphi , \chi ) = (\nabla \varphi , \nabla \chi ), \quad \forall \chi \in V_h. \end{aligned}$$

The semidiscrete scheme for (1) is described as: Find $u_h(t)=u_h(\cdot ,t)\in V_h$ such that

$$\begin{aligned} ((\kappa _1\partial _t + \kappa _2{}_{RL}D_{0,t}^{\alpha }) (u_{h}-v_h), \chi ) +\mu (\nabla u_h,\nabla \chi )=(f, \chi ), \quad \forall \chi \in V_{h}, \end{aligned}$$

with the initial value condition $u_{h}(0)=v_h\in V_h$. Here $v_h$ is the proper approximation to the function v. By using the discrete Laplacian $A_h : V_{h} \rightarrow V_{h}$ defined by:

$$\begin{aligned} \left( A_{h} \varphi , \chi \right) =(\nabla \varphi , \nabla \chi ), \quad \forall \varphi , \chi \in V_{h}, \end{aligned}$$

one further has

$$\begin{aligned} (\kappa _1\partial _t + \kappa _2{}_{RL}D_{0,t}^{\alpha }) (u_{h}(t)-v_h)+\mu A_{h} u_{h}(t)=f_h(t), \quad t>0, \end{aligned}$$

(6)

where $f_h(t) = P_hf(t)$.

Next, we consider the error estimates for the semidiscrete scheme (6).

The semidiscrete solution $u_h(t)$ to (6) has the form:

$$\begin{aligned} u_h(t) = \frac{1}{2\pi i}\int _{\Gamma _{\theta , \delta }} e^{zt}{\widehat{E}}_h(z)v_hdz, \end{aligned}$$

(7)

where ${\widehat{E}}_h(z)$ is the form of ${\widehat{E}}(z)$ by replacing A with $A_h$. For the convenience of discussion, we denote $F(z)=(\hbar (z)I+A)^{-1}$ and $F_h(z)=(\hbar (z)I+A_h)^{-1}$. We need the following error estimate of $(F(z)-F_h(z)P_h)$ which is useful in the error analysis [2].

Lemma 2

Let $v\in L^2(\Omega )$ and $z\in \Sigma _\theta$. Then we have the following estimate:

$$\begin{aligned} \Vert (F(z)-F_h(z)P_h)v\Vert \le ch^2\Vert v\Vert . \end{aligned}$$

Let the error $e_h(t):=u(t)-u_h(t)$. Now the error estimates for the semidiscrete scheme (6) with $f=0$ is presented as follows.

Theorem 2

Let $f=0$ and $v\ne 0$ in (1). Then for the semidiscrete scheme (6), we have

• (a) If $v\in L^2(\Omega )$ and $v_h=P_hv$, then $\Vert e_h(t)\Vert \le ch^2 t^{-\alpha }\Vert v\Vert .$

• (b) If $v\in {\dot{H}}^2(\Omega )$ and $v_h=R_hv$, then $\Vert e_h(t)\Vert \le ch^2\Vert Av\Vert .$

Proof

For $v_h = P_hv$, we have

$$\begin{aligned} e_h(t) = \frac{1}{2\pi i}\int _{\Gamma _{\theta , \delta }} e^{zt}\frac{\hbar (z)}{z}(F(z)-F_h(z)P_h)vdz. \end{aligned}$$

It follows from Lemmas 1 and 2 that

$$\begin{aligned} \Vert e_h(t)\Vert\le & {} c\int _{\Gamma _{\theta , \delta }} e^{\mathfrak {R}{(z)}t}\frac{|\hbar (z)|}{|z|}\Vert (F(z)-F_h(z)P_h)v\Vert |dz|\\\le & {} ch^2 \Vert v\Vert \int _{\Gamma _{\theta , \delta }} e^{\mathfrak {R}{(z)}t}\frac{1}{\mu }\left( \kappa _1+\kappa _2|z|^{\alpha -1}\right) |dz|\\\le & {} ch^2 \left( \kappa _1t^{-1}+\kappa _2t^{-\alpha }\right) \Vert v\Vert \le ch^2 t^{-\alpha }\Vert v\Vert , \end{aligned}$$

where the inequality $t^{-1}\le T^{1-\alpha }t^{-\alpha }$ is used. Hence the proof of case (a) is finished. For case (b), using the identities $\hbar (z)F(z) = I - F(z)A$ and $\hbar (z)F_h(z) = I - F_h(z)A_h$, we have

$$\begin{aligned} e_h(t) = \frac{1}{2\pi i}\int _{\Gamma _{\theta , \delta }} e^{zt}(-F(z)A+F_h(z)A_hR_h)vdz. \end{aligned}$$

So combining the identity $A_hR_h = P_hA$ with Lemma 2, we obtain the desired results in case (b). $\square$

In the following, we denote the space ${\mathbf {S}}:=L^\infty (0,T;L^2(\Omega ))$ for notation simplification.

Theorem 3

Let $v=0$ and $f\in {\mathbf {S}}$ in (1). Then the error estimate of the semidiscrete scheme (6) is given by

$$\begin{aligned} \Vert e_h(t)\Vert \le ch^2|\ln (t^\alpha / h^2)|\Vert f\Vert _{\mathbf {S}}. \end{aligned}$$

Proof

From (3), we observe that the solution can be represented by means of inverse Laplace transform:

$$\begin{aligned} u(t) = \frac{1}{2\pi i}\int _{\Gamma _{\theta ,\delta }} e^{zt}\mu ^{-1}F(z){\widehat{f}}(z)dz = \int _0^t {\tilde{F}}(t-s)f(s)ds, \end{aligned}$$

(8)

where

$$\begin{aligned} {\tilde{F}}(t) = \frac{\mu ^{-1}}{2\pi i}\int _{\Gamma _{\theta ,\delta }} e^{zt}F(z)dz. \end{aligned}$$

(9)

Similarly, the semidiscrete solution of (6) can be represented by

$$\begin{aligned} u_h(t) = \int _0^t {\tilde{F}}_h(t-s)P_hf(s)ds, \end{aligned}$$

(10)

where ${\tilde{F}}_h(t)$ is the form of ${\tilde{F}}(t)$ in (9) with replacing A with $A_h$.

From (8) and (10), we have the following error equation:

$$\begin{aligned} e_h(t) = \int _0^t \left( {\tilde{F}}(t-s) - {\tilde{F}}_h(t-s)P_h\right) f(s)ds. \end{aligned}$$

We then divide the discussion into two cases: $t\le h^{2/\alpha }$ and $t>h^{2/\alpha }$. For the first case $t\le h^{2/\alpha }$, one gets

$$\begin{aligned} \Vert e_h(t)\Vert\le & {} c\int _0^t \left( \Vert ({\tilde{F}}(t-s) f(s)\Vert + \Vert {\tilde{F}}_h(t-s)P_h f(s)\Vert \right) ds \\\le & {} c\Vert f\Vert _{{\mathbf {S}}}\int _0^{h^{2/\alpha }}\Vert {\tilde{F}}(t-s)\Vert ds\\\le & {} c\Vert f\Vert _{{\mathbf {S}}}\int _0^{h^{2/\alpha }}(t-s)^{\alpha -1}ds \le c h^2\Vert f\Vert _{{\mathbf {S}}}, \end{aligned}$$

where we have used the estimate $\Vert {\tilde{F}}(t)\Vert \le ct^{\alpha -1}$ (or, see Theorem 4.2 in [3]). For the second case $t>h^{2/\alpha }$, by applying Lemma 2, we derive that

$$\begin{aligned} \Vert {\tilde{F}}(t) - {\tilde{F}}_h(t)P_h\Vert\le & {} c\int _{\Gamma _{\theta ,\delta }} e^{\mathfrak {R}{(z)}t}\Vert F(z)-F_h(z)P_h\Vert |dz| \le ch^2 \int _{\Gamma _{\theta ,\delta }} e^{\mathfrak {R}{(z)}t}|dz| \\\le & {} ch^2 t^{-1}. \end{aligned}$$

So

$$\begin{aligned} \Vert e_h(t)\Vert\le & {} \left( \int _0^{t-h^{2/\alpha }} + \int _{t-h^{2/\alpha }}^{t}\right) \Vert \big ({\tilde{F}}(t-s) - {\tilde{F}}_h(t-s)P_h\big )\Vert \Vert f(s)\Vert ds\\\le & {} ch^2\Vert f\Vert _{\mathbf {}}\int _0^{t-h^{2/\alpha }} (t-s)^{-1}ds \le ch^2\ln \big (t^\alpha / h^2\big )\Vert f\Vert _{{\mathbf {S}}}. \end{aligned}$$

Thus, the proof is completed. $\square$

4 Two fully discrete schemes

Let K(z) be analytic and bounded in the sector $\Sigma _\theta$ with $\theta \in (\frac{\pi }{2},\pi )$. Then K(z) is the Laplace transform of the distribution k(t), see [5] for further discussion. Denote $K(\partial _t)g=k*g$ with the time differentiation $\partial _t$ and kernel k. For a given positive integer N, we divide the time interval [0, T] into uniform grids $\{t_n = n\tau \}_{n=0}^N$ with $\tau =T/N$. The numerical approximation of $K(\partial _t)g$ at $t=t_n$ is described by

$$\begin{aligned} K({\partial }_{\tau }) g(t_n)=\sum _{k=0}^n w_{k}(\tau ) g(t_{n-k}), \end{aligned}$$

in which the weights $w_{k}(\tau )$ are provided by

$$\begin{aligned} \sum _{k=0}^{\infty } w_{k}(\tau ) s^{k}=K\Big (\frac{\varphi (s) }{\tau }\Big ). \end{aligned}$$

(11)

Here $\varphi (s) = 1-s$ for BE and $\varphi (s) = 1-s + (1-s^2)/2$ for the SBD. For other types of the generating function $\varphi$, see [15]. We shall need the following error estimates for convolution quadrature [16].

Lemma 3

Let K(z) be analytic in $\Sigma _\theta$ and the boundedness $\Vert K(z)\Vert \le M|z|^{-\lambda } (\forall z \in \Sigma _{\theta })$ holds. Here, $\lambda$ and M are some real numbers. Then for $g(t)=c t^{\sigma -1}$, we have

$$\begin{aligned} \Vert \left( K\left( \partial _{t}\right) -K({\partial }_{\tau })\right) g(t)\Vert \le \left\{ \begin{array}{ll}{c t^{\lambda -1} \tau ^{\sigma },} &{} {0<\sigma \le p,} \\ {c t^{\lambda -1+\sigma -p} \tau ^p,} &{} {\sigma \ge p,}\end{array}\right. \end{aligned}$$

where $p=1$ for BE and $p=2$ for SBD.

4.1 The BE method and its error estimates

We integrate the semidiscrete scheme (6) from 0 to t to get

$$\begin{aligned} \kappa _1(u_h - v_h) + \kappa _2{}_{RL}D_{0,t}^{\alpha -1}(u_h-v_h) +\mu {}_{RL}D_{0,t}^{-1}A_h u_{h}(t) ={}_{RL}D_{0,t}^{-1}f_{h}(t). \end{aligned}$$

This is

$$\begin{aligned} \kappa _1 u_h + \kappa _2{}_{RL}D_{0,t}^{\alpha -1}u_h +\mu {}_{RL}D_{0,t}^{-1}A_h u_{h}(t) =(\kappa _1+\kappa _2{}_{RL}D_{0,t}^{\alpha -1}))v_h+{}_{RL}D_{0,t}^{-1}f_{h}(t).\nonumber \\ \end{aligned}$$

(12)

Then applying the convolution quadratures based on the BE method to approximate the convolution terms, we have the approximation of $u_h(t)$ at $t_n$ with $U_h^n$ by

$$\begin{aligned} \kappa _1 U_h^n + \kappa _2\partial _\tau ^{\alpha -1}U_h^{n} +\mu \partial _\tau ^{-1}A_h U_h^{n} =\left( \kappa _1+\kappa _2\partial _\tau ^{\alpha -1}\right) v_h+\partial _\tau ^{-1}F_h^n, \end{aligned}$$

(13)

where $n=1,2,\cdots ,N, U_h^0 = v_h$, and $F_h^n = f_h(t_n)$. Operating $\partial _\tau$ on (13), we get the following BE scheme: Find $U_h^n$ for $n\ge 1$ such that

$$\begin{aligned} \left( \kappa _1{\partial }_{\tau } + \kappa _2{\partial }_{\tau }^{\alpha }\right) U_{h}^n +\mu A_{h} U_{h}^n =\left( \kappa _1{\partial }_{\tau } + \kappa _2{\partial }_{\tau }^{\alpha }\right) v_h + F_{h}^n. \end{aligned}$$

(14)

In the following, we give the error estimates for the BE scheme (14).

Theorem 4

For $f=0$, $v\ne 0$, and denote $U_h^n$ and u as the solutions of (14) and (1), respectively. Then we have

• (a) If $v\in L^2(\Omega )$ and $v_h=P_hv$, then

  $$\begin{aligned} \Vert U_h^n - u(t_n)\Vert \le c\big (h^2 t_n^{-\alpha } + \tau t_n^{-1}\big )\Vert v\Vert . \end{aligned}$$

• (b) If $v\in {\dot{H}}^2(\Omega )$ and $v_h=R_hv$, then

  $$\begin{aligned} \Vert U_h^n - u(t_n)\Vert \le c\big (h^2 + \tau t_n^{\alpha -1}\big )\Vert Av\Vert . \end{aligned}$$

Proof

We only need to consider the error estimates of $U_h^n-u_h(t_n)$. Let $\ell (z) = \hbar (z)(\hbar (z)I+A_h)^{-1}$. By (12) and (13), we have

$$\begin{aligned} U_h^n - u_h(t_n) = \big (\ell (\partial _\tau ) - \ell (\partial _t)\big )v_h. \end{aligned}$$

Since $\Vert \ell (z)\Vert \le c, \forall z\in \Sigma _\theta$, by letting $\lambda = 0, \sigma =1$ and $p=1$ in Lemma 3, we can derive that

$$\begin{aligned} \Vert U_h^n - u_h(t_n) \Vert \le c\tau t_n^{-1}\Vert v_h\Vert . \end{aligned}$$

This together the $L^2$-stability of $P_h$ yields the desired result of case (a). For the case (b), we observe that the identity $\ell (z) = I-(\hbar (z)I+A_h)^{-1}A_h$ holds. So we have

$$\begin{aligned} U_h^n - u_h(t_n) = (\tilde{\ell }(\partial _\tau ) - \tilde{\ell }(\partial _t))A_hv_h, \end{aligned}$$

with $\tilde{\ell }(z) = (\hbar (z)I+A_h)^{-1}$. Combining the inequality $\Vert \tilde{\ell }(z)\Vert \le c\min \{\frac{1}{\kappa _1}|z|^{-1}, \frac{1}{\kappa _2}|z|^{-\alpha }\}$ with Lemma 3 (i.e., $p=1, \sigma =1, \lambda = 1, \alpha$), we obtain

$$\begin{aligned} \Vert U_h^n - u_h(t_n) \Vert \le c\tau \min \left\{ \frac{1}{\kappa _1}, \frac{1}{\kappa _2}t_n^{\alpha -1}\right\} \Vert A_hR_hv\Vert \le c\tau t_n^{\alpha -1}\Vert P_hAv\Vert , \end{aligned}$$

where we have used $t_n^{\alpha -1}\le T^{1-\alpha }$ and $A_hR_h = P_hA$. The estimate in case (b) then follows from the $L^2$-stability of $P_h$. $\square$

The error estimate for the inhomogeneous problem is stated as below.

Theorem 5

Let $U_h^n$ and u be the solutions of (14) and (1) with $v=0$, respectively. Then we have

$$\begin{aligned} \Vert U_h^n - u(t_n)\Vert&\le c\Big (h^2|\ln (t_n^\alpha / h^2)|\Vert f\Vert _{{\mathbf {S}}} + \tau t_n^{\alpha -1}\Vert f(0)\Vert \\&\quad + \tau \int _0^{t_n} (t_n-s)^{\alpha -1}\Vert f'(s)\Vert ds\Big ). \end{aligned}$$

Proof

Let $\ell (z) = (\hbar (z)I+A_h)^{-1}$. It follows from (12) and (13) that

$$\begin{aligned} U_h^n - u_h(t_n) = (\ell (\partial _\tau ) - \ell (\partial _t)) f_h(0) + ((\ell (\partial _\tau ) - \ell (\partial _t))1) *f_h'(t)=I+II, \end{aligned}$$

where the Taylor expansion $f_h(t) = f_h(0) + (1*f_h')(t)$ and the associativity property of convolution quadrature are applied. Using Lemma 3 with $p=1, \sigma = 1, \lambda =1, \alpha$, we obtain

$$\begin{aligned} \Vert U_h^n - u_h(t_n)\Vert \le \Vert I\Vert + \Vert II\Vert \le c\Big (\tau t_n^{\alpha -1}\Vert f(0)\Vert + \tau \int _0^{t_n} (t_n-s)^{\alpha -1}\Vert f'(s)\Vert ds\Big ), \end{aligned}$$

in which the last inequality holds for $t_n^{\alpha -1}\le T^{1-\alpha }$. $\square$

4.2 The SBD method and its error estimates

In this part, we consider the SBD method to approximate the convolution terms in (12). We employ the following idea to guarantee the second-order accuracy in time. In view of (12), we have the semidiscrete solution $u_h(t)$ given by

$$\begin{aligned} u_h(t) = K(\partial _t)\left( v_h + \frac{1}{\mu }\hbar (z)^{-1}f_{h}(t)\right) , \end{aligned}$$

where $K(z) = \hbar (z)(\hbar (z)I+A_h)^{-1}$. Since $K(z) = I - (\hbar (z)I+A_h)^{-1}A_h$, the semidiscrete solution $u_h$ can be further recast as

$$\begin{aligned} u_h(t) = v_h+(\hbar (\partial _t)I+A_h)^{-1}\Big (-A_h\partial _t{}_{RL}D_{0,t}^{-1}v_h + \frac{1}{\mu }(\partial _t\partial _t^{-1}f_h(0) + {\widetilde{f}}_h(t))\Big ),\nonumber \\ \end{aligned}$$

(15)

where $t>0$ and ${\widetilde{f}}_h(t) = f_h(t) - f_h(0)$. Using the convolution quadratures generated by the SBD method, we have

$$\begin{aligned} U_h^n = v_h+(\hbar (\partial _t)I+A_h)^{-1}\Big (-A_h\partial _\tau {}_{RL}D_{0,t}^{-1}v_h + \frac{1}{\mu }(\partial _\tau {}_{RL}D_{0,t}^{-1}f_h(0) + {\widetilde{f}}_h(t))\Big ).\nonumber \\ \end{aligned}$$

(16)

Applying the identity $1_\tau ={\partial }_\tau {}_{RL}D_{0,t}^{-1}$ with the notation $1_\tau =(0, 3/2, 1, 1, \cdots )$, we get the following SBD scheme: Find $U_h^n$ for $n\ge 1$ such that

$$\begin{aligned} \big ( {\partial }_{\tau }+\kappa {\partial }_{\tau }^{\alpha } + \mu A_{h}\big )(U_h^n-v_h) = - \mu A_h 1_\tau v_h + 1_\tau f_h(0) + {\widetilde{F}}_h^n. \end{aligned}$$

(17)

That is,

$$\begin{aligned} \big ({\partial }_{\tau }+\kappa {\partial }_{\tau }^{\alpha }\big )U_h^n + \mu A_hU_h^n =\big ({\partial }_{\tau }+\kappa {\partial }_{\tau }^{\alpha }\big )v_h +{\overline{F}}_h^n, \end{aligned}$$

with ${\overline{F}}_h^1 = -\frac{1}{2} (\mu A_h)v_h+ \frac{1}{2}F_h^0+F_h^1$ for $n=1$, and ${\overline{F}}_h^n = F_h^n$ when $n\ge 2$.

Similar to the discussion in the BE scheme (14), we present the error estimates of the SBD scheme (17) for homogeneous and inhomogeneous problems in turn.

Theorem 6

Let $U_h^n$ and u be the solutions of (17) and (1) with $f=0$, respectively. Then we have

• (a) If $v\in L^2(\Omega )$ and $v_h=P_hv$, then

  $$\begin{aligned} \Vert U_h^n - u(t_n)\Vert \le c\big (h^2 t_n^{-\alpha }+\tau ^2t_n^{-2}\big )\Vert v\Vert . \end{aligned}$$

• (b) If $v\in {\dot{H}}^2(\Omega )$ and $v_h=R_hv$, then

  $$\begin{aligned} \Vert U_h^n - u(t_n)\Vert \le c\big (h^2 + \tau ^2 t_n^{\alpha -2}\big )\Vert Av\Vert . \end{aligned}$$

Proof

From (15) and (16), we have the following error equation:

$$\begin{aligned} U_h^n - u_h(t_n) = (\ell (\partial _\tau ) - \ell (\partial _t)){}_{RL}D_{0,t}^{-1}(A_hv_h), \end{aligned}$$

with $\ell (z) = -z(\hbar (z)I + A_h)^{-1}$. Since

$$\begin{aligned} \Vert \ell (z)\Vert \le c|z||\hbar (z)|^{-1}\le c\min \left\{ \frac{1}{\kappa _1}, \frac{1}{\kappa _2}|z|^{1-\alpha }\right\} , \end{aligned}$$

applying the Lemma 3 (i.e., $p=2, \sigma = 2, \lambda =0, \alpha -1$) and the identity $A_hR_h = P_hA$, we derive that

$$\begin{aligned} \Vert U_h^n - u_h(t_n)\Vert \le c\tau ^2\min \left\{ \frac{1}{\kappa _1}t_n^{-1}, \frac{1}{\kappa _2}t_n^{\alpha -2}\right\} \Vert P_hAv\Vert \le c\tau ^2t_n^{\alpha -2}\Vert Av\Vert , \end{aligned}$$

where the inequality $t_n^{-1}\ge T^{\alpha -1}t_n^{\alpha -2}$ is used. So the proof of case (b) is completed. For case (a), one may observe that the identity $\ell (z)A_h = -(z-z\hbar (z)(\hbar (z)I+A_h)^{-1})$ holds. It follows that $\Vert \ell (z)A_h\Vert \le c|z|$. By Lemma 3 (i.e., $p=2, \sigma = 2$ and $\lambda =-1$), we have the desired result of case (a). Thus we complete the proof. $\square$

Theorem 7

Let $U_h^n$ and u be the solutions of (17) and (1) with $v=0$, respectively. Then we have

$$\begin{aligned} \Vert U_h^n - u(t_n)\Vert\le & {} c\Big (h^2|\ln (t_n^\alpha / h^2)|\Vert f\Vert _{{\mathbf {S}}} + \tau ^2t_n^{\alpha -2}\Vert f(0)\Vert \\&+\, \tau ^2t_n^{\alpha -1}\Vert f'(0)\Vert +\tau ^2\int _0^{t_n}(t_n-s)^{\alpha -1}\Vert f''(s)\Vert ds\Big ). \end{aligned}$$

Proof

Let $\ell _1(z) = \frac{z}{\mu }(\hbar (z)I+A_h)^{-1}$ and $\ell _2(z) = \frac{1}{\mu }(\hbar (z)I+A_h)^{-1}$. By (12) and (13), we have $U_h^n - u_h(t_n) = I+II$ with

$$\begin{aligned} I= & {} (\ell _1(\partial _\tau ) - \ell _1(\partial _t)) tf_h(0), \quad \text {and}\quad II = (\ell _2(\partial _\tau ) \\&- \ell _2(\partial _t))tf_h'(0) + ((\ell _2(\partial _\tau ) - \ell _2(\partial _t))t)*f_h''. \end{aligned}$$

Here we have used the Taylor expansion $f_h(t) = f_h(0) + f_h'(0) + (t*f_h'')(t)$ and the associativity property of convolution quadrature. We observe that $\Vert \ell _1(z)\Vert \le c\min \{\frac{1}{\kappa _1}, \frac{1}{\kappa _2}|z|^{1-\alpha }\}$ and $\Vert \ell _2(z)\Vert \le c\min \left\{ \frac{1}{\kappa _1}|z|^{-1}, \frac{1}{\kappa _2}|z|^{-\alpha }\right\}$. By Lemma 3 (i.e., $p=2, \sigma = 2, \lambda =0, \alpha -1$ for the first term I; $\lambda =1, \alpha$ for the second term II), one has

$$\begin{aligned} \Vert I\Vert \le c\tau ^2\min \left\{ \frac{1}{\kappa _1}t_n^{-1}, \frac{1}{\kappa _2}t_n^{\alpha -2}\right\} \Vert f_h(0)\Vert , \end{aligned}$$

and

$$\begin{aligned} \Vert II\Vert\le & {} c\tau ^2\min \left\{ \frac{1}{\kappa _1}, \frac{1}{\kappa _2}t_n^{\alpha -1}\right\} \Vert f_h'(0)\Vert +c\tau ^2\int _0^t\min \left\{ \frac{1}{\kappa _1}, \frac{1}{\kappa _2}(t_n-s)^{\alpha -1}\right\} \Vert f_h''(s)\Vert ds\\\le & {} c\tau ^2\Big (t_n^{\alpha -1}\Vert f_h'(0)\Vert +\int _0^{t_n}(t_n-s)^{\alpha -1}\Vert f_h''(s)\Vert ds\Big ). \end{aligned}$$

Combining the $L^2$ stability of $P_h$, we obtain the desired result. $\square$

5 Numerical examples

Let $\Omega = (0, 1)^2$, and the parameter $\kappa _1=\kappa _2=\mu =1$. All the tests are executed by using the continuous piecewise linear finite elements in space and the iFEM software package presented in [4]. We denote $\chi _S$ as the characteristic function of the set S. For the model problem (1), we consider the data:

• (a) $v(x,y)=x(1-x)y(1-y)$ and $f=0$,

• (b) $v(x,y)=\chi _{(0,1/2]\times (0,1)}(x,y)$ and $f=0$,

• (c) $v = 0$ and $f=(1+t^{2.1})\chi _{(0,1/2]\times (0,1)}(x,y)$.

It can be seen that the three types of data listed above cover the cases discussed in the error estimates in Sect. 4, so it suffices to use them to verify that the BE and SBD schemes have the theoretical convergent order, which is the focus of interest in this paper.

Since the analytical solution of the equation is difficult to obtain, the reference solution is used instead. The temporal errors for the schemes (14) and (17) with fixed $h=1/10$ are tested at $T=0.1$. The reference solution $u_h(t_n)$ is computed by SBD scheme by fixed $N=4096$ and $h=1/10$. We present the numerical results in Tables 1, 2 and 3.

Table 1 The temporal errors and convergence orders for case (a)

Table 2 The temporal errors and convergence orders for case (b)

Table 3 The temporal errors and convergence orders for case (c)

Here, the $L^2$-norm errors are denoted by $e(N,h)=\Vert U_h^N-u(t_N)\Vert$ and the temporal convergence orders are computed by $\log (e(N,h)/e(2N,h))$. As can be seen from Table 1, for smooth initial data, the $L^2$-norm errors at the three different fractional orders $\alpha$ become smaller as the time stepsize $\tau$ is continuously halved for a fixed h, and the SBD scheme (17) is more accurate than the BE one (14). Furthermore, the temporal accuracy of the BE and SBD schemes are $O(\tau )$ and $O(\tau ^2)$, respectively, which are in good agreement with the theoretical analysis. Similar results are observed in Tables 2 and 3 for the other two cases (b) and (c). Thus, the numerical results illustrate the effectiveness of the schemes and the accuracy of the error estimates.

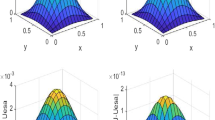
Finally, in order to better understand the dynamical behaviors of Eq. (1), we perform numerical simulations using non-smooth initial data, i.e., the case (b) in the above example. We give the numerical results in Fig. 1 by applying the SBD scheme (17) with fixed $h = 0.05$ and $N=64$.

Fig. 1

Comparison behavior of numerical solutions for Eq. (1)

From Fig. 1, we can observe that the solution profiles of the equation all tend to decay with time when the fractional order is fixed. Comparing the solutions at different fractional orders, i.e., $\alpha = 0.1$ and $\alpha =0.9$, we find that for the case of larger fractional order, it decays more slowly than that of smaller fractional order for a short time, while this phenomenon is becoming reversed as time evolves continuously, see $T=1$. This may illustrate the flexibility of the fractional model (1) in depicting anomalous diffusion, which needs further study for its physical interpretation in practical applications [19].

6 Conclusions

In this paper, the properties of the corresponding solution operator are given for the homogeneous problem in fractional model (1), and then the semidiscrete scheme is obtained by using the finite element method in space. Two finite element schemes are derived by convolution quadrature based on the BE and the SBD methods. We fully exploit the operator trick and prove the error estimates of the semidiscrete and fully discrete schemes under the data regularity. Numerical examples including smooth and nonsmooth data verify the accuracy of the convergence theory.

It is worth noting that although we consider only Laplacian in Eq. (1), our results in this paper can be extended to some general sector operators, such as the second-order coercive and symmetric elliptic differential operator with spatially variable coefficients [10]. However, the generalization to the one with temporal variable coefficients is not easy and requires further study.