Borodin–Kostochka’s conjecture on $(P_5,C_4)$-free graphs

Abstract

Brooks’ theorem states that for a graph G, if $\varDelta (G)\ge 3$, then $\chi (G)\le \max \{\varDelta (G),\omega (G)\}$. Borodin and Kostochka conjectured a result strengthening Brooks’ theorem, stated as, if $\varDelta (G)\ge 9$, then $\chi (G)\le \max \{\varDelta (G)-1,\omega (G)\}$. This conjecture is still open for general graphs. In this paper, we show that the conjecture is true for graphs having no induced path on five vertices and no induced cycle on four vertices.

1 Introduction

All the graphs considered are finite, simple, and undirected. In a graph, two vertices are said to be adjacent if there is an edge between them. A clique in a graph G is a set of pairwise adjacent vertices of G and the clique number of G is the maximum cardinality of a clique in G. Let $P_r$ and $C_s$ denote the path on r vertices and the cycle on s vertices, respectively. The complete graph on n vertices is denoted by $K_n$. The degree of a vertex in a graph G is the number of vertices adjacent to it and the maximum (resp. minimum) degree of the graph G is the maximum (resp. minimum) of the degrees of the vertices of G.

By proper coloring of a graph, we mean, assigning colors to the vertices of the graph in such a way that no two adjacent vertices receive the same color. A graph is k-colorable, if it has a proper coloring using at most k colors. The smallest k, for which a graph is k-colorable, is known as the chromatic number of the graph. It has always been a matter of interest with practical applications to bound the chromatic number of graphs by functions of different parameters such as clique number and maximum degree of the graphs. Extensive research has taken place to this end (see [11, 13, 15, 16]). For a graph $G=(V,E)$, we use $\chi (G)$, $\omega (G)$, $\varDelta (G)$, and $\delta (G)$ to denote the chromatic number, the clique number, the maximum degree, and the minimum degree of G, respectively. By greedy coloring approach, it is easy to see that $\chi (G)\le \varDelta (G)+1$. Brooks observed that odd cycles and complete graphs are the only graphs to achieve this bound and strengthened this bound by proving the following result.

Theorem 1

(Brooks’ theorem [1]) For a graph G, if $\varDelta (G)\ge 3$, then $\chi (G)\le \max \{\varDelta (G), \omega (G)\}$.

Borodin and Kostochka conjectured that Brooks’ bound can be further improved if $\varDelta (G)\ge 9$.

Conjecture 1

(Borodin–Kostochka [2]) For a graph G, if $\varDelta (G)\ge 9$, then $\chi (G)\le \max \{\varDelta (G)-1, \omega (G)\}$.

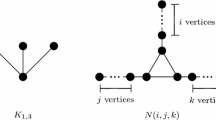
Note that if $\omega (G)\ge \varDelta (G)$, then by Brooks’ theorem, G satisfies the Borodin–Kostochka’s conjecture. Therefore, to prove the conjecture, it is sufficient to prove that for a graph G, if $\varDelta (G)\ge 9$ and $\omega (G)\le \varDelta (G)-1$, then $\chi (G)\le \varDelta (G)-1$. Cranston et al. [4] mentioned that Conjecture 1 cannot be strengthened by making $\varDelta (G)\ge 8$ or $\omega (G)\le \varDelta (G)-2$. For example if $\varDelta (G)=8$, then we get a counterexample (see the graph $G_1$ of Fig. 1) to Conjecture 1. Notice that $\varDelta (G_1)=8$ and $\omega (G_1)=6<7=\varDelta (G_1)-1$, whereas $\chi (G_1)=8>7=\varDelta (G_1)-1$. Moreover, if $\omega (G)\le \varDelta (G)-2$, then notice that for the graph $G_2$ (see Fig. 1), we have $\varDelta (G_2)=t\ge 9$ and $\omega (G_2)=\varDelta (G_2)-2$, whereas $\chi (G_2)=\varDelta (G_2)-1$. This implies that if the hypothesis $\omega (G)\le \varDelta (G)-1$ is strengthened to $\omega (G)\le \varDelta (G)-2$, then the bound $\chi (G)\le \varDelta (G)-1$ cannot be strengthened to $\chi (G)\le \varDelta (G)-2$.

Fig. 1

Some special graphs. In (i) and (ii), bolder edges represents that the sets at the ends are complete to each other

For a given positive integer k, we use the standard notation [k] to denote the set $\{1,2,\ldots ,k\}$. We say a graph G contains H if there is an induced subgraph of G isomorphic to H. A graph G is called H-free if G does not contain H. For a family of graphs ${\mathcal {H}}$, G is called ${\mathcal {H}}$-free if G is H-free for every $H\in {\mathcal {H}}$. A graph class ${\mathcal {G}}$ is said to be hereditary, if for every graph G in ${\mathcal {G}}$, all the induced subgraphs of G belong to ${\mathcal {G}}$. Note that the class of ${\mathcal {H}}$-free graphs is a hereditary graph class. If ${\mathcal {H}}=\{H\}$ (resp. ${\mathcal {H}}=\{H_1,H_2\}$), then ${\mathcal {H}}$-free graphs are simply written as H-free ($(H_1,H_2)$-free) graphs. In 1981, Dhurandhar [8], verified the Borodin–Kostochka’s conjecture for ${\mathcal {H}}$-free graphs, where ${\mathcal {H}}=\{claw, K_5-e,co-twin-house\}$. Kierstead and Schmerl [10] proved the validity of the conjecture in the class of $(claw, K_5-e)$-free graphs. In 2013, Cranston and Rabern [6] removed the need to exclude $K_5-e$ from the graph and verified the conjecture for claw-free graphs. Cranston and Rabern [5] showed that, if for a graph G, $\chi (G)\ge \varDelta (G)\ge 13$, then G contains a clique of size $\varDelta (G)-3$. Note that the Borodin–Kostochka’s conjecture can be restated as, if a graph G satisfies $\chi (G)\ge \varDelta (G)\ge 9$, then G contains a clique of size $\varDelta (G)$. In 1999, Reed [14] presented the strongest partial result towards the Borodin–Kostochka’s conjecture by showing that the conjecture is true for all graphs having maximum degree at least $10^{14}$. In a recent paper by Cranston et al. [4], the Borodin–Kostochka’s conjecture is verified for $(P_5,gem)$-free graphs.

In this note, we validate the Borodin–Kostochka’s conjecture for $(P_5,C_4)$-free graphs using their structural properties. The result is stated in the following theorem.

Theorem 2

Let G be a $(P_5,C_4)$-free graph. If $\varDelta (G)\ge 9$, then $\chi (G)\le \max \{\varDelta (G)-1,~\omega (G)\}$.

2 Terminology, notations, and preliminary results

Let G be a graph. The sets $N_G(v)=\{u:uv\in E(G)\}$ and $N_G[v]=N_G(v)\cup \{v\}$ are called the open neighborhood and the closed neighborhood of the vertex v in G. If $xy\in E(G)$ for $x,y\in V(G)$, then x and y are called the endpoints of the edge xy. The degree of a vertex v in G is denoted by $d_G(v)$. If the context of the graph is clear, we simply use N(v), N[v], and d(v) instead of $N_G(v), N_G[v]$, $d_G(v)$. For sets $A,B\subseteq V(G)$, [A] denotes the subgraph of G induced by vertices of A and [A, B] is the subset of E(G) consisting those edges which have one endpoint in A and other in B. We say A is complete to B, or simply [A, B] is complete, if every vertex of A is adjacent to every vertex of B. We say A is anticomplete to B or simply [A,  B] is anticomplete if $[A,B]=\emptyset$. Specifically, a vertex $v\in V(G){\setminus } A$ is said to be complete to A if $[\{v\}, A]$ is complete. For a set $A\subseteq V(G)$, $G-A$ is the graph obtained by removing the vertices belonging to A and all the edges incident on every vertex of A from G. If $A=\{v\}$, then we simply use $G-v$ instead of $G-\{v\}$.

The distance between two vertices u and v in G, denoted by $d_G(u,v)$ (or simply d(u, v) if context of the graph is clear) is the length of a shortest path between u and v. If H is a subgraph of G and $v\in V(G)$, we define d(v, H) as $\min \{d(v,x):x\in V(H)\}$. For $A\subseteq V(G)$, we simply use d(v, A) to denote d(v, [A]). For the notations not defined here, we refer to [9].

A graph G is called k-critical (resp. k-vertex critical), if $\chi (G)=k$ and any proper subgraph (induced subgraph) of G can be properly colored using $k-1$ colors. A graph G is called critical (resp. vertex critical), if it is k-critical (resp. k-vertex critical) for some positive integer k. The following lemma given by Dirac, states a useful property of vertex critical graphs. For completeness, we present a short proof of it.

Lemma 1

([7]) If a graph G is vertex critical, then $\delta (G)\ge \chi (G)-1$.

Proof

If possible, let v be a vertex of G with $d(v)\le \chi (G)-2$. Since G is vertex critical, $G-v$ is $(\chi (G)-1)$-colorable. So all $\chi (G)-1$ colors used in $G-v$ will not be used to color the vertices adjacent to v in G. Hence one of the colors among $(\chi (G)-1)$ colors can be given to v to produce a $(\chi (G)-1)$-coloring of G. This contradicts the fact that $\chi (G)$ is the chromatic number of G. So $\delta (G)\ge \chi (G)-1$. $\square$

A buoy is a graph G, whose vertex set can be partitioned into five nonempty sets, $H_1,H_2,H_3,H_4,$ and $H_5$ such that $[H_i,H_{i+1}]$ is complete and $[H_i,H_{i+2}]=[H_i,H_{i+3}]=\emptyset$ for every $i\in [5]$, where addition in indices are done in modulo 5 arithmetic. A buoy is said to be a complete-buoy if $H_i$ is a clique for every $i\in [5]$. In [4], it is proved that if G is a complete-bouy, then $\chi (G)\le \max \{\varDelta (G)-1,\omega (G)\}$ implying that a complete-bouy satisfies the Borodin–Kostochka’s conjecture. We record this in the following lemma to use later.

Lemma 2

([4]) A complete-buoy satisfies the Borodin–Kostochka’s conjecture.

Kostochka and Catlin independently presented a useful result, by which one can choose a counterexample for the Borodin–Kostochka’s conjecture in a hereditary graph class ${\mathcal {G}}$, if exists, to have maximum degree 9.

Theorem 3

([3, 12]) If ${\mathcal {G}}$ is a hereditary graph class and if the Borodin–Kostochka’s conjecture is true for all graphs $G\in {\mathcal {G}}$ having $\varDelta (G)=9$, then the conjecture is true for all graphs in ${\mathcal {G}}$.

3 Proof of Theorem 2

We first present a lemma that guarantees the existence of a vertex critical counterexample of Conjecture 1 if a counterexample exists for the conjecture.

Lemma 3

If G is a smallest counterexample (smallest in terms of the number of vertices) for the Borodin–Kostochka’s conjecture with $\varDelta (G)=9$, then G must be vertex critical.

Proof

Since G is a counterexample for the Borodin–Kostochka’s conjecture, we have $\omega (G)\le \varDelta (G)-1=8$ and $\chi (G)=\varDelta (G)=9$. Let $u\in V(G)$ be arbitrary. If $\varDelta (G-u)=\varDelta (G)=9$, then $\chi (G-u)\le 8$ since G is a smallest such graph. If $\varDelta (G-u)\le 8$, then by Brooks’ theorem, $\chi (G-u)\le \max \{\omega (G-u),\varDelta (G-u)\} \le 8$. So $\chi (G-u)\le 8<\chi (G)$ implying that G is vertex critical. $\square$

By Theorem 3 and Lemma 3, we can conclude that, if some hereditary graph class ${\mathcal {G}}$ contains a counterexample for the Borodin–Kostochka’s conjecture, then it must contain a vertex critical counterexample having maximum degree 9.

To prove Theorem 2, we proceed by analyzing the $(P_5,C_4)$-free graphs having an induced $C_5$ and not having an induced $C_5$. Let G be a $(P_5,C_4)$-free graph. If G does not contain an induced $C_5$, then G is perfect implying that $\chi (G)=\omega (G)$ and hence G satisfies the Borodin- Kostochka’s conjecture. If G contains an induced $C_5$, then we use the structural properties of G around an induced $C_5$ to show the validity of the Borodin- Kostochka’s conjecture. We now present the structural properties of a $(P_5,C_4)$-free graphs around an induced $C_5$.

Let G be a $(P_5,C_4)$-free graph and $C=v_1v_2v_3v_4v_5$ be an induced $C_5$ of G. All the indices that will be used are with respect to modulo 5 arithmetic. Define the following sets.

$$\begin{aligned} \begin{array}{lcl} {\mathcal {N}}_1=\{v\in V(G){\setminus }V( C):N(v)\cap V(C)\ne \emptyset \}, \\ {\mathcal {N}}_2=V(G){\setminus } ({\mathcal {N}}_1\cup V(C)), \\ \end{array} \end{aligned}$$

It is clear that if the sets V(C), ${\mathcal {N}}_1$ and ${\mathcal {N}}_2$ is a partition of V(G).

Claim 1

Each vertex in ${\mathcal {N}}_1$ is either adjacent to exactly three consecutive vertices in C or complete to C.

Proof of Claim 1:

Let $v\in {\mathcal {N}}_1$. If $|N(v)\cap V(C)|=5$, then we are done. So we may assume that $|N(v)\cap V(C)|\le 4$. If $|N(v)\cap V(C)|=1$, then without loss of generality, let $N(v)\cap V(C)=\{v_1\}$. Now $\{v,v_1,v_2,v_3,v_4\}$ induces a $P_5$, a contradiction. So $|N(v)\cap V(C)|\ge 2$. If $|N(v)\cap V(C)|=2$, then let $u,w\in N(v)\cap V(C)$. If u and w are consecutive in C, then let $u=v_i$ and $w=v_{i+1}$ for some $i\in [5]$. Now $\{v,v_{i+1},v_{i+2},v_{i+3},v_{i+4}\}$ induces a $P_5$, a contradiction. If u and w are non consecutive, then let $u=v_i$ and $w=v_{i+2}$ for some $i\in [5]$. Now $\{v,v_i,v_{i+1},v_{i+2}\}$ induces a $C_4$, a contradiction. So $|N(v)\cap V(C)|\ge 3$. If $|N(v)\cap V(C)|=4$, then let $v_i\notin N(v)$ for some $i\in [5]$. Now $\{v,v_{i-1},v_i,v_{i+1}\}$ induces a $C_4$, a contradiction. Thus $|N(v)\cap V(C)|=3$. If all three vertices are not consecutive, then there exists $i\in [5]$ such that $v_{i-1},v_{i+1}\in N(v)$ and $v_i\notin N(v)$. This is true since $d(u,w)\le 2$ for any pair of vertices u and w of C. Now $\{v,v_{i-1},v_i,v_{i+1}\}$ induces a $C_4$, a contradiction. Therefore, all vertices of $N(v)\cap V(C)$ must be consecutive. This completes the proof of the claim. $\square$

Fig. 2

Schematic representation of G. Here grey circular regions represent cliques and, bolder lines and curves represent that their corresponding ends are complete to each other

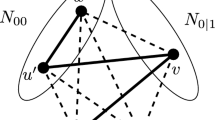
Using Claim 1, we now partition the set ${\mathcal {N}}_1$ into six sets $U\cup U_1\cup U_2 \cup U_3\cup U_4\cup U_5$, where U is complete to C and $U_i$ is complete to $\{v_{i-1},v_i,v_{i+1}\}$ and anticomplete to $\{v_{i+2},v_{i+3}\}$ for every $i\in [5]$. Now, we observe following properties (see Fig.  2).

• (3.1) U and $U_i$ are cliques for every $i\in [5]$.

  If $uu^*\notin E(G)$ for $u,u^* \in U$, then $\{u,v_1,u^*,v_3\}$ induces a $C_4$. Again if such u and $u^*$ are considered from $U_i$ for $i\in [5]$, then $\{u,v_{i+1},u^*,v_{i-1}\}$ induces a $C_4$.

• (3.2) $[U,\cup _{i=1}^5 U_i]$ is complete.

  If there exists $x\in U_i$ for some $i\in [5]$ and $u\in U$, such that u and x are not adjacent, then $\{u,v_{i-1},x,v_{i+1}\}$ induces a $C_4$ in G.

• (3.3) $[U_i,U_{i+1}]$ is complete and $[U_i,U_{i+2}]=[U_i,U_{i+3}]=\emptyset$ for all $i\in [5]$.

  If $[U_i,U_{i+1}]$ is not complete for some $i\in [5]$, then there exist $x\in U_i$ and $y\in U_{i+1}$ such that $xy\notin E(G)$. Then $\{y,v_{i+2},v_{i+3},v_{i+4},x\}$ induces a $P_5$. If $[U_i,U_{i+2}]\ne \emptyset$ for some $i\in [5]$, then there exist $x\in U_{i}$ and $y\in U_{i+2}$ such that $xy\in E(G)$. Now $\{x,v_{i+4},v_{i+3},y\}$ induces a $C_4$. Similarly if $[U_i,U_{i+3}]\ne \emptyset$ for some $i\in [5]$, then there exist $x\in U_{i}$ and $y\in U_{i+3}$ such that $xy\in E(G)$. Now $\{x,v_{i+1},v_{i+2},y\}$ induces a $C_4$.

• (3.4) $[{\mathcal {N}}_2,\cup _{i=1}^5 U_i]=\emptyset$.

  If $[{\mathcal {N}}_2,\cup _{i=1}^5 U_i]\ne \emptyset$, then there exist $x\in {\mathcal {N}}_2$ and $y\in U_{i}$ for some $i\in [5]$ such that $xy\in E(G)$. Now $\{x,y,v_{i+1},v_{i+2},v_{i+3}\}$ induces a $P_5$ in G.

Theorem 2

If G is a $(P_5,C_4)$-free graph with $\varDelta (G)\ge 9$, then $\chi (G)\le \max \{\varDelta (G)-1, \omega (G)\}$.

Proof

Let ${\mathcal {G}}$ be the class of all $(P_5,C_4)$-free graphs. It is sufficient to prove the theorem for connected graphs only. If possible, then let G be a smallest counterexample for the Borodin–Kostochka’s conjecture in ${\mathcal {G}}$ that minimizes $\varDelta (G)$. Since $\varDelta (G)\ge 9$, by Theorem 3, $\varDelta (G)=9$ and by Lemma 3, G is vertex critical. If $\omega (G)\ge 9$, then the result holds due to Brooks’ theorem. So we may assume that $\chi (G)=9$ and $\omega (G)\le 8$. By Lemma 1, each vertex in G has degree either 8 or 9. If G has no induced $C_5$, then, since G is $C_4$-free and every induced cycle of length more than 5 contains an induced $P_5$, G must be chordal implying that G is perfect. So $\chi (G)=\omega (G)\le \max \{\omega (G),\varDelta (G)-1\}$. This is a contradiction to the fact that G is a counterexample of Conjecture 1. Hence G must contain an induced $C_5$. Let $C=v_1v_2v_3v_4v_5$ be an induced $C_5$ in G. Define the sets ${\mathcal {N}}_1,~{\mathcal {N}}_2,~U$, and $U_i$ for each $i\in [5]$ as defined earlier. Now we proceed by considering the following two cases. In each case, we show a contradiction to the fact that G is a counterexample to Borodin-Kotoschka’s conjecture.

Case 1: $\cup _{i=1}^5 U_i=\emptyset$.

Recall that by Lemma 3, each vertex in G has degree 8 or 9; thus $d(v_1)\ge 8$. So $|N(v_1)\cap U|\ge 6$ implying that $|U|\ge 6$. By (3.1), U is a clique and by definition of U, U is complete to C. Thus $d(u)\ge 10$ for every $u\in U$. This is a contradiction to the fact that $\varDelta (G)=9$.

Case 2: $\cup _{i=1}^5 U_i\ne \emptyset$.

If $U=\emptyset$, then, since $[{\mathcal {N}}_2, \cup _{i=1}^5 U_i]=\emptyset$ by (3.4), we have ${\mathcal {N}}_2=\emptyset$. Now observe that G is isomorphic to $[C\cup (\cup _{i=1}^5 U_i)]$, which is a complete-buoy. By Lemma 2, G satisfies the Borodin–Kostochka’s conjecture. This is a contradiction to the fact that G is a counterexample for the Borodin–Kostochka’s conjecture. So we may assume that $U\ne \emptyset$.

If $U_i\ne \emptyset$ for every $i\in [5]$, then, since $[U, \cup _{i=1}^5 U_i]$ is complete by (3.2), we have $d(u)\ge 10$ for every $u\in U$. This is a contradiction to the fact that $\varDelta (G)=9$. So we may assume that $U_i=\emptyset$ for some $i\in [5]$. Let $j\in [5]$ be the index, such that $U_j=\emptyset$. Now if $U_i\ne \emptyset$ for every $i\in [5]$ and $i\ne j$, then, since $d(u)\in \{8,9\}$ for every $u\in U$ (in fact for every $u\in V(G)$), by (3.2), we have $|U|=1$ and $|U_i|=1$ for every $i\in [5]{\setminus }\{j\}$. Notice that $d(v_j)=5$. This is a contradiction to the fact that $\delta (G)\ge 8$. Hence we conclude that at least two among those sets must be empty. Let $j'\in [5]$ be the index other than j, such that $U_{j'}=\emptyset$. If j and $j'$ are consecutive, thus due to symmetry, we assume that $j'=j+1$, i.e. $U_j=U_{j+1}=\emptyset$. Now if $U_{j+2}, U_{j+3}$ and $U_{j+4}$ are non-empty, then by (3.1) and (3.2) and the fact that $\varDelta (G)=9$, we have $1\le |U|\le 2$ and $1\le |U_i|\le 2$ for every $i\in \{j+2,j+3,j+4\}$. Hence $d(v_j)\le 5$, which is again a contradiction to the fact that $\delta (G)\ge 8$. If j and $j'$ are non-consecutive, then, without loss of generality, we can assume $j'=j+2$, i.e. $U_j=U_{j+2}=\emptyset$. Now if $U_i\ne \emptyset$ for every $i\in [5]{\setminus } \{j,j+2\}$, then using the same arguments as above, we see that $d(v_j)\le 6$ which is a contradiction to the fact that $\delta (G)\ge 8$. Hence we conclude that at least three sets among $U_i$’s are empty, i.e. at most two sets are non-empty. Now we assume that exactly two sets among $U_i$’s are non-empty. Let $k, k'\in [5]$ with $k\ne k'$ such that $U_k$ and $U_{k'}$ are non-empty and $U_i=\emptyset$ for every $i\in [5]{\setminus } \{k,k'\}$. If k and $k'$ are consecutive, then due to symmetry, we can take $k'=k+1$. By definition of U and by (3.1)-(3.2), we have $|U|\le 3$. Now we can see that $d(v_{k+3})\le 5$ which is a contradiction to the fact that $\delta (G)\ge 8$. So we may assume that k and $k'$ to are nonconsecutive. Without loss of generality, we can take $k'=k+2$. Again using the definition of U, (3.1), and (3.2), we see that $1\le |U|\le 3$ and $1\le |U_i|\le 3$ for $i\in \{k,k'\}$. This gives $d(v_{k+3})\le 7$, once again a contradiction to the fact that $\delta (G)\ge 8$. So we can conclude that at most one set among $U_i$’s can be non-empty. Let $U_k\ne \emptyset$ and $U_i=\emptyset$ for every $i\in [5]{\setminus } \{k\}$. By (3.1) and (3.2), we have $|U|\le 4$. This gives $d(v_{k+2}) \le 6$, once again a contradiction to the fact that $\delta (G)\ge 8$. Hence we may assume that $U_i=\emptyset$ for every $i\in [5]$. But this contradicts the hypothesis taken in this case. So we can say that G cannot be a counterexample to the Borodin–Kostochka’s conjecture. $\square$