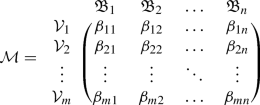Multiple attribute decision making based on immediate probabilities aggregation operators for single-valued and interval neutrosophic sets

Abstract

The objective of this paper is to present novel algorithms for solving the multiple attribute decision-making problems under the neutrosophic set environment. Single-valued and interval neutrosophic sets are the important mechanisms for directing the decision-making queries with unknown and indeterminant data by employing a degree of “acceptance”, “indeterminacy”, and “non-acceptance” in quantitative terms. Also, to describe the behavior of the decision-maker objectively (in terms of probability) and subjectively (in terms of weights), a concept of probabilistic information plays a dominant role in the investigation. Keeping these features in mind, this paper presents several probabilistic and immediate probability-based averaging and geometric aggregation operators for the collection of the single-valued and interval neutrosophic sets. The advantage of these proposed operators is that it simultaneously combines the objective and subjective behavior of the decision-maker during the process. The various salient features of the proposed operators are studied. Later, we develop two new algorithms based on the aggregation operators to solve multiple attribute decision-making problems with single-valued and interval neutrosophic sets features. A numerical example related to the demonetization is given to demonstrate the presented approaches, and the advantages, as well as comparative analysis, are given to shows its influence over existing approaches.

1 Introduction

Multiple attribute decision making (MADM) refers to the process of finding optimal alternatives in complex scenarios via synthetically evaluating the values of multiple criteria of all alternatives provided by a group of domain experts [1, 2]. In this process, there are two critical tasks. The first one is to describe the environment where the values of different criteria are measured effectively, while the second task is to aggregate the described information. However, in any case, because of the absence of learning and other factors, it is extremely troublesome- if not difficult express the data absolutely. To express the uncertainties in the data, a theory of fuzzy set (FS) [3] and its extension such as intuitionistic fuzzy set (IFS) [4], cubic intuitionistic fuzzy set [5], interval-valued IFS [6], linguistic interval-valued IFS [1], are used by the researchers. In all these theories, an object is evaluated in terms of their membership grade $\varsigma$ and non-membership grade $\upsilon$ such that $\varsigma +\upsilon \le 1$ for $\varsigma ,\upsilon \in [0,1]$. After their existence, several researchers have defined the basic operational laws [7, 8], distance or similarity measures [9, 10], aggregation operators [11, 12] to solve MADM problems. In modern life, the complex system requires the uncertainties in views of indeterminacy and hence the present sets, FS or IFS, are incapable to deal with the information correctly. To consider it, in 1998, Smarandache [13] presented neutrosophic set (NS) by involving the three independent functions namely “acceptance”, “indeterminacy” and “non-acceptance” which are the standard or non-standard real subsets of $]^-0, 1^+[$. However, for software engineering proposals and in a practical decision-making problems, the classical unit interval [0, 1] is used. Thus, Wang et al. [14] enriches the NS to single-valued NS (SVNS) while Wang et al. [15] enriches NS to interval neutrosophic set (INS) in which ranges of the independent degrees are taken as [0, 1] instead of $]^-0,1^+[$.

After the appearance of SVNS and INS, researchers have investigated the various kinds of applications which are categorized into two major aspects. The first and the important aspect is the basic operational laws. To address it, Ye [16] defined the subtraction and division operations between the two or more single-valued neutrosophic numbers (SVNNs). Rani and Garg [17] presented their modified operational laws for SVNNs. However, to order the given SVNSs, Peng et al. [18] defined the score function, while Nancy and Garg [19] presented its improved score function. The second task is to aggregate the described criterion information, by using suitable aggregation operators, to generate a ranking of all alternatives. For example, Ye [20] developed some weighted average and geometric aggregation operators for SVNNs. Zhang et al. [21] developed some weighted aggregation operators for interval neutrosophic numbers (INNs). Aiwu et al. [22] presented the generalized weighted aggregation operator for INNs. Nancy and Garg [23] developed weighted operators by using Frank t-norm operations for solving the MADM problems with SVNS information. Garg and Nancy [24] defined logarithm operational laws and its based weighted aggregation operators for SVNS to solve the MADM problems. Peng et al. [18] presented the simplified neutrosophic sets and several weighted and ordered weighted aggregation operators. Garg and Nancy [25] presented a TOPSIS (“Technique for Order Preference by Similarity to Ideal Solution”) strategy by formulating a nonlinear model to solve the MADM problem under the INS environment. Liu et al. [26] presented generalized neutrosophic Hamacher aggregation operators to solve the group decision-making problems. Peng and Liu [27] presented a similarity measure and an algorithm for neutrosophic soft decision making by using EDAS (“Evaluation Based on Distance from Average Solution”) method. Garg and Nancy [28, 29] presented a group decision-making problem approaches based on the prioritized Muirhead mean and hybrid weighted aggregation operators. Ye [30] presented a MADM method with credibility information under the INS features. Peng and Dai [31] presented a single-valued neutrosophic MADM method based on MABAC (“Multi-Attributive Border Approximation area Comparison”) and TOPSIS approach to solving the decision-making problems. Garg and Nancy [32] developed the hybrid Heronian mean AOs by considering the concept of Choquet and frank norm operational laws for SVNSs. An extensive review of the different approaches to solving the MADM problem under the SVNS and INS was presented by Peng and Dai [33].

The above-mentioned approaches are widely applicable in different fields. However, the approaches defined above are limited in access, as all the stated aggregation operators had constructed by assuming that the arguments are independent of each other. Also, to handle the subjective and objective information more clearly, a concept of probabilistic information plays a dominant role in the investigation. To address it, Merigo and its co-authors [34, 35] initiated the concept of the probability into the aggregation operators to solve the decision-making problems. In their work, they proposed the probabilistic weighted average and ordered weighted average operators to solve the MADM problems. Yager et al. [36] presented the concept of immediate probabilities (IP). Engemann et al. [37] incorporated the concept of IP into the decision making modeling, while Merigo [38] extends the idea of IP to the fuzzy decision-making process. Garg [39] and Wei and Merigo [40] presented the probabilistic weighted average and geometric operators for the Pythagorean and intuitionistic fuzzy sets environment. Peng et al. [41] presented the idea of a probability multi-valued neutrosophic set to solve the group MADM problems. Since probabilistic information along with the uncertain and vague information is more valuable to solve the real-life problems. Thus, there is a need to present some generalized aggregation operators to aggregate the given information using the concept of probabilities and immediate probability under the SVNS and INS environment.

Considering the versatility of the extensions of neutrosophic sets and the importance of the aggregation operators, this paper aims to present two novel MADM approaches to manage the information related to the SVNS and INS with some new aggregation operators. To address it completely, we embedded the concept of probabilistic information into the weighted average and geometric operators and hence defined the various form of the operators namely, “probabilistic single-valued neutrosophic weighted average” (P-SVNWA), “immediate probability single-valued neutrosophic ordered weighted average” (IP-SVNOWA), “probabilistic single-valued neutrosophic ordered weighted average” (P-SVNOWA), “probabilistic single-valued neutrosophic weighted geometric” (P-SVNWG), “immediate probability single-valued neutrosophic ordered weighted geometric” (IP-SVNOWG) and “probabilistic single-valued neutrosophic ordered weighted geometric” (P-SVNOWG). Further, these operators are extended to INS features. In all these operators, the importance of each number has complied with the probability and the attribute weights. The advantage of the developed operators is that it simultaneously combines the behavior of the decision-makers, objectively (in terms of probability) and subjectively (in terms of weights vector), into the single process. The various salient features of these operators are also explored to show its consistency. Holding all the above tips in mind, the main objective of the present work is listed as

• (1) to define some new probabilistic information based aggregation operators for given numbers under SVNS and INS environment.

• (2) to develop two new algorithms to determine the MADM problems based on the proposed operators.

• (3) to demonstrate the approach with a numerical example to explore the study.

• (4) to analyze the impact of different parameters on the decision-making process.

The rest of the text is summarized as. Section 2 gives brief review on neutrosophic set. In Sect. 3, we present several aggregation operators for SVNSs and INSs by utilizing probabilistic and immediate probabilistic information. In Sect. 4, we offer two algorithms based on proposed measures to solve the MADM problems. The utility of the presented algorithms is demonstrated with a numerical example in Sect. 5 and compare their results with several existing approaches. Finally, Sect. 6 ends up with concluding remarks.

2 Preliminaries

In it, we discuss some basic terms associated with SVNS and INS in universal set ${\mathcal {X}}$.

Definition 1

[13] A neutrosophic set ${\mathcal {N}}$ is given as

$$\begin{aligned} {\mathcal {N}} =\{(x,\varsigma _{{\mathcal {N}}}(x),\tau _{{\mathcal {N}}}(x), \upsilon _{{\mathcal {N}}}(x)) \mid x \in {\mathcal {X}} \} \end{aligned}$$

(1)

where $\varsigma _{{\mathcal {N}}}(x),\tau _{{\mathcal {N}}}(x), \upsilon _{{\mathcal {N}}}(x): {\mathcal {X}} \rightarrow ]^-0, 1^{+}[$ are the degrees of “acceptance”, “indeterminacy” and “non-acceptance” such that $^-0 \le \sup \varsigma _{{\mathcal {N}}}(x) + \sup \tau _{{\mathcal {N}}}(x) + \sup \upsilon _{{\mathcal {N}}}(x) \le 3^{+}$.

Definition 2

[14] A SVNS ${\mathcal {N}}$ in ${\mathcal {X}}$ is stated as

$$\begin{aligned} {\mathcal {N}}=\big \{( x,\varsigma _{{\mathcal {N}}}(x),\tau _{{\mathcal {N}}}(x), \upsilon _{{\mathcal {N}}}(x) )\mid x \in {\mathcal {X}} \big \} \end{aligned}$$

(2)

where $\varsigma _{{\mathcal {N}}},\tau _{{\mathcal {N}}},\upsilon _{{\mathcal {N}}} \in [0,1]$ and $0 \le \varsigma _{{\mathcal {N}}}+\tau _{{\mathcal {N}}}+\upsilon _{{\mathcal {N}}} \le 3$ for each $x\in {\mathcal {X}}$. We call a pair ${\mathcal {N}}=(\varsigma _{{\mathcal {N}}}, \tau _{{\mathcal {N}}}, \upsilon _{{\mathcal {N}}})$, throughout this article, and known as single-valued neutrosophic number.

Definition 3

[14] For two SVNNs ${\mathcal {N}}_1=(\varsigma _1, \tau _1, \upsilon _1)$ and ${\mathcal {N}}_2=(\varsigma _2, \tau _2,\upsilon _2)$, some basic operations are defined as

• (1) ${\mathcal {N}}_1\subseteq {\mathcal {N}}_2$ if $\varsigma _{1}\le \varsigma _{2}, \tau _{1} \ge \tau _{2}, \upsilon _{1}\ge \upsilon _{2}$.

• (2) ${\mathcal {N}}_1\cap {\mathcal {N}}_2=(\min (\varsigma _{1},\varsigma _{2}), \max (\tau _{1},\tau _{2}), \max (\upsilon _{1},\upsilon _{2}))$.

• (3) ${\mathcal {N}}_1\cup {\mathcal {N}}_2=(\max (\varsigma _{1}, \varsigma _{2}), \min (\tau _{1}, \tau _{2}), \min (\upsilon _{1}, \upsilon _{2}))$.

• (4) ${\mathcal {N}}_1={\mathcal {N}}_2$ if and only if ${\mathcal {N}}_1\subseteq {\mathcal {N}}_2$ and ${\mathcal {N}}_2\subseteq {\mathcal {N}}_1$.

• (5) Complement: ${\mathcal {N}}_1^c = (\upsilon _{1}, \tau _{1},\varsigma _{1})$.

Definition 4

[18] Let ${\mathcal {N}}=(\varsigma , \tau , \upsilon )$ be a SVNN, then its score function S is defined as $S({\mathcal {N}}) = \varsigma - \tau - \upsilon$, and an accuracy function H is defined as $H({\mathcal {N}}) = \varsigma + \tau + \upsilon$. Based on it, an order relation between two SVNNs ${\mathcal {N}}$ and ${\mathcal {M}}$ denoted by ${\mathcal {N}} \succ {\mathcal {M}}$ holds if either $S({\mathcal {N}}) > S({\mathcal {M}})$ or $S({\mathcal {N}}) = S({\mathcal {M}})$ and $H({\mathcal {N}})>H({\mathcal {M}})$ holds. Here, “$\succ$” means “preferred to”.

Definition 5

[18] For two SVNNs ${\mathcal {N}}_1=(\varsigma _{1},\tau _{1},\upsilon _{1})$ and ${\mathcal {N}}_2=(\varsigma _{2},\tau _{2},\upsilon _{2})$, the operation laws between them are defined as

• (1) ${\mathcal {N}}_1\oplus {\mathcal {N}}_2= \big ( \varsigma _{1} + \varsigma _{2} -\varsigma _{1}\varsigma _{2}, \tau _{1}\tau _{2}, \upsilon _{1}\upsilon _{2}\big )$.

• (2) ${\mathcal {N}}_1\otimes {\mathcal {N}}_2 = \big ( \varsigma _{1}\varsigma _{2}, \tau _{1} + \tau _{2} -\tau _{1}\tau _{2}, \upsilon _{1} + \upsilon _{2} -\upsilon _{1}\upsilon _{2} \big )$.

• (3) $\lambda {\mathcal {N}}_1= \left( 1-\left( 1-\varsigma _{1}\right) ^\lambda , \tau _{1}^\lambda , \upsilon _{1}^\lambda \right) ; \quad \lambda > 0$.

• (4) ${\mathcal {N}}_1^\lambda =\left( \varsigma _{1}^\lambda , 1-\left( 1-\tau _1\right) ^\lambda , 1-\left( 1-\upsilon _1\right) ^\lambda \right) ; \quad \lambda > 0$.

Definition 6

[18] Let ${\mathcal {N}}_j = (\varsigma _j, \tau _j, \upsilon _j)$ be “n” SVNNs and $\omega _j>0$ with $\sum _{j=1}^n \omega _j=1$ be the weight vector of ${\mathcal {N}}_j$. Then, weighted averaging and geometric operators are defined as

• (1) Single-valued neutrosophic weighted average (SVNWA) operator

  $$\begin{aligned} \text {SVNWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n)= \left( 1-\prod \limits _{j=1}^n \left( 1-\varsigma _j\right) ^{\omega _j}, \prod \limits _{j=1}^n \left( \tau _j\right) ^{\omega _j}, \prod \limits _{j=1}^n \left( \upsilon _j\right) ^{\omega _j}\right) \nonumber \\ \end{aligned}$$

  (3)

• (2) Single-valued neutrosophic weighted geometric (SVNWG) operator

  $$\begin{aligned}&\text {SVNWG}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n)\nonumber \\&\quad = \left( \prod \limits _{j=1}^n \left( \varsigma _j\right) ^{\omega _j}, 1-\prod \limits _{j=1}^n \left( 1-\tau _j\right) ^{\omega _j}, 1-\prod \limits _{j=1}^n \left( 1-\upsilon _j\right) ^{\omega _j}\right) \end{aligned}$$

  (4)

• (3) Single-valued neutrosophic ordered weighted average (SVNOWA) operator

  $$\begin{aligned}&\text {SVNOWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n)\nonumber \\&\quad = \left( 1-\prod \limits _{j=1}^n \left( 1-\varsigma _{\sigma (j)}\right) ^{\omega _j}, \prod \limits _{j=1}^n \left( \tau _{\sigma (j)}\right) ^{\omega _j}, \prod \limits _{j=1}^n \left( \upsilon _{\sigma (j)}\right) ^{\omega _j}\right) \end{aligned}$$

  (5)

• (4) Single-valued neutrosophic ordered weighted geometric (SVNOWG) operator

  $$\begin{aligned}&\text {SVNOWG}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n)\nonumber \\&\quad = \left( \prod \limits _{j=1}^n \left( \varsigma _{\sigma (j)}\right) ^{\omega _j},1-\prod \limits _{j=1}^n \left( 1-\tau _{\sigma (j)}\right) ^{\omega _j}, 1-\prod \limits _{j=1}^n \left( 1-\upsilon _{\sigma (j)}\right) ^{\omega _j} \right) \end{aligned}$$

  (6)

  where $\sigma$ permutes $(1,2,\ldots ,n)$ with ${\mathcal {N}}_{\sigma (j-1)} \ge {\mathcal {N}}_{\sigma (j)}$ for $j=2,\ldots ,n$.

Definition 7

[15] An INS ${\mathcal {N}}$ over ${\mathcal {X}}$ is given as

$$\begin{aligned} {\mathcal {N}} = \left\{ \left( x, \left[ \varsigma _{\mathcal {N}}^L(x), \varsigma _{\mathcal {N}}^U(x)\right] , \left[ \tau _{\mathcal {N}}^L(x), \tau _{\mathcal {N}}^U(x)\right] , \left[ \upsilon _{\mathcal {N}}^L(x), \upsilon _{\mathcal {N}}^U(x)\right] \right) \mid x\in {\mathcal {X}}\right\} \end{aligned}$$

where $\left[ \varsigma _{\mathcal {N}}^L, \varsigma _{\mathcal {N}}^U\right] , \left[ \tau _{\mathcal {N}}^L, \tau _{\mathcal {N}}^U\right]$, $\left[ \upsilon _{\mathcal {N}}^L, \upsilon _{\mathcal {N}}^U\right] \subseteq [0,1]$ with $\varsigma _{\mathcal {N}}^U+\tau _{\mathcal {N}}^U+\upsilon _{\mathcal {N}}^U\le 3$ for all $x \in {\mathcal {X}}$. For convenience, the pair ${\mathcal {N}} = \left( \left[ \varsigma ^L,\varsigma ^U\right] , \left[ \tau ^L,\tau ^U\right] , \left[ \upsilon ^L,\upsilon ^U\right] \right)$ is called as an interval neutrosophic number.

Definition 8

[15] For an INN ${\mathcal {N}} = ([\varsigma ^L,\varsigma ^U],[\tau ^L,\tau ^U],[\upsilon ^L,\upsilon ^U])$, a score function is defined as $S({\mathcal {N}}) = \dfrac{\varsigma ^L+\varsigma ^U-\tau ^L-\tau ^U-\upsilon ^L-\upsilon ^U}{2}$, while an accuracy function H is $H({\mathcal {N}}) = \dfrac{\varsigma ^L+ \varsigma ^U + \tau ^L + \tau ^U + \upsilon ^L+\upsilon ^U}{2}$. Based on it, an order relation between two INNs ${\mathcal {N}}_1$ and ${\mathcal {N}}_2$, denoted by ${\mathcal {N}}_1 \succ {\mathcal {N}}_2$ if either $S({\mathcal {N}}_1) > S({\mathcal {N}}_2)$ or $S({\mathcal {N}}_1) = S({\mathcal {N}}_2)$, $H({\mathcal {N}}_1)> H({\mathcal {N}}_2)$ holds.

Definition 9

[21] Let ${\mathcal {N}}_j = ([\varsigma _j^L,\varsigma _j^U],[\tau _j^L,\tau _j^U],[\upsilon _j^L,\upsilon _j^U])$ be “n” INNs and $\omega _j>0$ with $\sum _{j=1}^n \omega _j=1$ be the weight vector of ${\mathcal {N}}_j$. Then, weighted averaging and geometric operators are defined as

• (1) Interval neutrosophic weighted average (INWA) operator

  $$\begin{aligned}&\text {INWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n)\\&\quad = \left( \begin{aligned}&\left[ 1-\prod \limits _{j=1}^{n}\left( 1-\varsigma ^L_j\right) ^{\omega _j}, 1-\prod \limits _{j=1}^{n}\left( 1-\varsigma ^U_j\right) ^{\omega _j}\right] ,\\&\quad \left[ \prod \limits _{j=1}^{n}\left( \tau ^L_j\right) ^{\omega _j}, \prod \limits _{j=1}^{n} \left( \tau ^U_j\right) ^{\omega _j}\right] ,\\&\quad \left[ \prod \limits _{j=1}^{n} \left( \upsilon ^L_j\right) ^{\omega _j}, \prod \limits _{j=1}^{n} \left( \upsilon ^U_j\right) ^{\omega _j}\right] \end{aligned} \right) \end{aligned}$$

• (2) Interval neutrosophic weighted geometric (INWG) operator

  $$\begin{aligned}&\text {INWG}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) \\&\quad = \left( \begin{aligned}&\left[ \prod \limits _{j=1}^{n}\left( \varsigma ^L_j\right) ^{\omega _{j}}, \prod \limits _{j=1}^{n} \left( \varsigma ^U_j\right) ^{\omega _{j}}\right] ,\\&\quad \left[ 1-\prod \limits _{j=1}^{n}\left( 1-\tau ^L_j\right) ^{\omega _{j}}, 1-\prod \limits _{j=1}^{n}\left( 1-\tau ^U_j\right) ^{\omega _{j}}\right] ,\\&\quad \left[ 1-\prod \limits _{j=1}^{n}\left( 1-\upsilon ^L_j\right) ^{\omega _{j}}, 1-\prod \limits _{j=1}^{n}\left( 1-\upsilon ^U_j\right) ^{\omega _{j}}\right] \end{aligned} \right) \end{aligned}$$

3 New probabilistic operators with neutrosophic information

In this section, we present some new kinds of aggregation operators for the collections of SVNNs and INSs by introducing the concept of probabilistic and immediate probabilities into the analysis.

3.1 Aggregation operators for SVNS

Let $\varOmega$ be the collection of “n” SVNNs ${\mathcal {N}}_j=(\varsigma _j, \tau _j, \upsilon _j)$ whose subjective and objectively weights are denoted by $\omega _j$ and $p_j$, respectively such that $\omega _j > 0$, $\sum \nolimits _{j=1}^n \omega _j=1$ and $p_j > 0$, $\sum \nolimits _{j=1}^n p_j = 1$.

3.1.1 Probabilistic single-valued neutrosophic weighted average operator

Definition 10

Let ${\mathcal {N}}_j$ be the collections of n SVNNs, and let $\text {P-SVNWA}:\varOmega ^n \longrightarrow \varOmega$ is a map defined as

$$\begin{aligned} \text {P-SVNWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \bigoplus _{j=1}^n v_j {\mathcal {N}}_j \end{aligned}$$

(7)

then P-SVNWA is called the probabilistic single-valued neurotrophic weighted average operator, where $v_j =(1-\beta ) p_j + \beta \omega _j$ be the weight vector with $\beta \in [0,1]$ such that $\sum \nolimits _{j=1}^n v_j=1$.

Theorem 1

For “n” SVNNs ${\mathcal {N}}_j = (\varsigma _j, \tau _j, \upsilon _j)$, the aggregated value by P-SVNWA operator is also SVNN and is given by

$$\begin{aligned} \text {P-SVNWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n)=\left( 1-\prod \limits _{j=1}^n (1-\varsigma _j)^{v_j}, \prod \limits _{j=1}^n \tau _j^{v_j}, \prod \limits _{j=1}^n \upsilon _j^{v_j} \right) \end{aligned}$$

(8)

Proof

We will prove the Eq. (8) by applying induction on n. The following steps are summarized as

• Step 1: For $n=2$, we have ${\mathcal {N}}_1 =( \varsigma _1, \tau _1, \upsilon _1)$ and ${\mathcal {N}}_2= ( \varsigma _2, \tau _2, \upsilon _2 )$. Thus, by the operation of SVNNs, we have $v_1{\mathcal {N}}_1 = \big ( 1-(1-\varsigma _1)^{v_1}, (\tau _1)^{v_1}, (\upsilon _1)^{v_1} \big )$ and $v_2{\mathcal {N}}_2 = \big ( 1-(1-\varsigma _2)^{v_2}, (\tau _2)^{v_2}, (\upsilon _2)^{v_2} \big )$. Thus,

  $$\begin{aligned}&\text {P-SVNWA}({\mathcal {N}}_1,{\mathcal {N}}_2) = v_1{\mathcal {N}}_1 \oplus v_2{\mathcal {N}}_2 \\&\quad = \bigg ( 1-(1-\varsigma _1)^{v_1}, (\tau _1)^{v_1}, (\upsilon _1)^{v_1} \bigg ) \oplus \bigg ( 1-(1-\varsigma _2)^{v_2}, (\tau _2)^{v_2}, (\upsilon _2)^{v_2} \bigg ) \\&\quad = \bigg ( 1-(1-\varsigma _1)^{v_1}(1-\varsigma _2)^{v_2}, (\tau _1)^{v_1}(\tau _2)^{v_2}, (\upsilon _1)^{v_1}(\upsilon _2)^{v_2}\bigg ) \\&\quad = \Bigg ( 1-\prod \limits _{j=1}^2 (1-\varsigma _j)^{v_j}, \prod \limits _{j=1}^2 \tau _j^{v_j}, \prod \limits _{j=1}^2 \upsilon _j^{v_j} \Bigg ) \end{aligned}$$

  Hence, Eq. (8) true for $n=2$.

• Step 2: Assume Eq. (8) true for $n=k$, then for $n=k+1$, we have

  $$\begin{aligned}&\text {P-SVNWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_{k+1}) \\&\quad = \bigoplus _{j=1}^k v_j{\mathcal {N}}_j \oplus v_{k+1}{\mathcal {N}}_{k+1} \\&\quad = \left( 1-\prod \limits _{j=1}^k (1-\varsigma _j)^{v_j},\prod \limits _{j=1}^k \tau _j^{v_j}, \prod \limits _{j=1}^k \upsilon _j^{v_j} \right) \\&\qquad \oplus \bigg ( 1-(1-\varsigma _{k+1})^{v_{k+1}}, (\tau _{k+1})^{v_{k+1}}, (\upsilon _{k+1})^{v_{k+1}} \bigg ) \\&\quad = \Bigg ( 1-\prod \limits _{j=1}^{k+1} (1-\varsigma _j)^{v_j}, \prod \limits _{j=1}^{k+1} \tau _j^{v_j}, \prod \limits _{j=1}^{k+1} \upsilon _j^{v_j} \Bigg ) \end{aligned}$$

  which is true.

Finally, take $\text {P-SVNWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n)=(\varsigma _N, \tau _N, \upsilon _N)$ where $\varsigma _N = 1-\prod \nolimits _{j=1}^{n} (1-\varsigma _j)^{v_j}$, $\upsilon _N=\prod \nolimits _{j=1}^{n} \tau _j^{v_j}$ and $\upsilon _N=\prod \nolimits _{j=1}^{n} \upsilon _j^{v_j}$ then it is enough to prove

• (1) $0\le \varsigma _N, \tau _N, \upsilon _N \le 1$ ;

• (2) $\varsigma _N + \tau _N + \upsilon _N \le 3$.

As ${\mathcal {N}}_j = ( \varsigma _j,\tau _j,\upsilon _j)$ is SVNN for each j which means that $0\le \varsigma _j, \tau _j, \upsilon _j \le 1$ and $\varsigma _j + \tau _j + \upsilon _j \le 3$. Therefore, $0\le 1-\varsigma _j\le 1$ and for weight vector $v_j\in [0,1]$, we have $0\le (1-\varsigma _j)^{v_j}\le 1$ which implies that $0\le 1-\prod \nolimits _{j=1}^{n} (1-\varsigma _j)^{v_j} \le 1$. Similarly, $0\le \prod \nolimits _{j=1}^{n} \tau _j^{v_j}\le 1$ and $0\le \prod \nolimits _{j=1}^{n} \upsilon _j^{v_j}\le 1$. Further, $0\le \varsigma _N + \tau _N + \upsilon _N\le 3$ since all are independent.

Hence, the aggregated value by using P-SVNWA operator is again SVNN, which completes the proof. $\square$

Remark 1

From the proposed operator, it is deduce that

• (1) If $\beta =1$ then P-SVNWA operator becomes SVNWA operator [18];

• (2) If $\beta =0$ then P-SVNWA operator becomes the neutrosophic probabilistic aggregation operator.

To demonstrate the working of the proposed P-SVNWA operator, we present a numerical example as follows.

Example 1

Let ${\mathcal {N}}_1 = (0.4, 0.3, 0.6)$, ${\mathcal {N}}_2 = ( 0.2, 0.5, 0.5)$, ${\mathcal {N}}_3 = ( 0.6, 0.4, 0.2)$ and ${\mathcal {N}}_4 = ( 0.8, 0.1, 0.4)$ be four SVNNs and their associated probabilities and weight vector are taken as $p=(0.3,0.1,0.4,0.2)^T$ and $\omega =(0.2, 0.3, 0.1, 0.4)^T$ respectively. Without loss of generality, we take $\beta =0.60$, and hence $v_j = (1-\beta ) p_j + \beta \omega _j$ becomes $v_j=(0.24, 0.22, 0.22, 0.32)^T$. Now, based on these information, $1-\prod \nolimits _{j=1}^4 (1-\varsigma _j)^{v_j} = 1-(1-0.4)^{0.24}\times (1-0.2)^{0.22}\times (1-0.6)^{0.22}\times (1-0.8)^{0.32} = 0.5886$, $\prod \nolimits _{j=1}^4 \tau _j^{v_j} = (0.3)^{0.24}\times (0.5)^{0.22}\times (0.4)^{0.22}\times (0.1)^{0.32} = 0.2516$ and $\prod \nolimits _{j=1}^4 \upsilon _j^{v_j} = (0.6)^{0.24}\times (0.5)^{0.22}\times (0.2)^{0.22}\times (0.4)^{0.32} = 0.3976$ and hence by Eq. (8), we have $\text {P-SVNWA}({\mathcal {N}}_1,{\mathcal {N}}_2,{\mathcal {N}}_3,{\mathcal {N}}_4) = \big ( 0.5886, 0.2516, 0.3976\big )$.

The operator P-SVNWA satisfies boundedness, idempotent and monotonicity properties which are stated below.

Property 1

(Idempotency) If SVNNs ${\mathcal {N}}_j = {\mathcal {N}}_0$$\forall j$, then we have

$$\begin{aligned} \text {P-SVNWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n)={\mathcal {N}}_0 \end{aligned}$$

Proof

As ${\mathcal {N}}_j = {\mathcal {N}}_0$$\forall j$, therefore we get

$$\begin{aligned} \text {P-SVNWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \bigoplus _{j=1}^n v_j {\mathcal {N}}_j = \bigoplus _{j=1}^n v_j {\mathcal {N}}_0 = {\mathcal {N}}_0 \sum \limits _{j=1}^n v_j \end{aligned}$$

Since $\sum \nolimits _{j=1}^n v_j=\sum \nolimits _{j=1}^n \{(1-\beta ) p_j + \beta \omega _j\} = (1-\beta )\sum \nolimits _{j=1}^n p_j + \beta \sum \nolimits _{j=1}^n \omega _j = 1$, and hence we get

$$\begin{aligned} \text {P-SVNWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n)={\mathcal {N}}_0 \end{aligned}$$

$\square$

Property 2

(Boundedness) For P-SVNWA operator f, we have:

$$\begin{aligned} \min \limits _j\{{\mathcal {N}}_j\} \le f({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) \le \max \limits _j\{{\mathcal {N}}_j\} \end{aligned}$$

Proof

Take $\min \nolimits _j\{{\mathcal {N}}_j\} = a$ and $\max \nolimits _j\{{\mathcal {N}}_j\} = b$, therefore,

$$\begin{aligned}&f({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \bigoplus _{j=1}^n v_j {\mathcal {N}}_j \le \bigoplus _{j=1}^n v_j b = b\sum \limits _{j=1}^n v_j \\&\quad \text {and }~~f({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \bigoplus _{j=1}^n v_j {\mathcal {N}}_j \ge \bigoplus _{j=1}^n v_j a = a\sum \limits _{j=1}^n v_j \end{aligned}$$

As, $\sum \nolimits _{j=1}^n v_j = 1$ therefore $f({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) \le b$ and $f({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) \ge a$. Thus, $a \le f({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) \le b$ implies that

$$\begin{aligned} \min \limits _j\{{\mathcal {N}}_j\} \le f({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) \le \max \limits _j\{{\mathcal {N}}_j\} \end{aligned}$$

$\square$

Property 3

(Monotonicity) For a P-SVNWA operator f and two collections of SVNNs ${\mathcal {N}}_j=(\varsigma _{{\mathcal {N}}_j}, \tau _{{\mathcal {N}}_j}, \upsilon _{{\mathcal {N}}_j})$ and ${\mathcal {M}}_j=(\varsigma _{{\mathcal {M}}_j}, \tau _{{\mathcal {M}}_j}, \upsilon _{{\mathcal {M}}_j})$ satisfies $\varsigma _{{\mathcal {N}}_j} \le \varsigma _{{\mathcal {M}}_j}$, $\tau _{{\mathcal {N}}_j}\ge \tau _{{\mathcal {M}}_j}$ and $\upsilon _{{\mathcal {N}}_j}\ge \upsilon _{{\mathcal {M}}_j}$$\forall j$, then we have:

$$\begin{aligned} f({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) \le f({\mathcal {M}}_1,{\mathcal {M}}_2,\ldots ,{\mathcal {M}}_n) \end{aligned}$$

Proof

Follows from above. $\square$

3.1.2 Immediate probability single-valued neutrosophic ordered weighted operator

Due to the uncertain nature of probabilistic information, we cannot rely on the collected information. So, with a specific end goal to include the expert’s opinion into the probabilistic decision-making problems, a concept of immediate probability (IP) is studied by the researchers [36, 38]. For accomplishing this in the present investigation, we have characterized the IP based operators for SVNNs which join together the ordered weighted operator [42], signified by $\xi$, and the probabilistic data, signified by p.

Definition 11

For a collection of “n” SVNNs ${\mathcal {N}}_j$, a map $\text {IP-SVNOWA}: \varOmega ^n \longrightarrow \varOmega$, associated with weight $\xi _j >0$ such that $\sum \nolimits _{j=1}^n \xi _j = 1$, defined by

$$\begin{aligned} \text {IP-SVNOWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \bigoplus _{j=1}^n {\widehat{p}}_j {\mathcal {N}}_{\sigma (j)} \end{aligned}$$

(9)

then IP-SVNOWA is called the immediate probability single-valued neutrosophic ordered weighted average operator, where $\sigma$ permutes $(1,2,\ldots ,n)$ with ${\mathcal {N}}_{\sigma (j-1)} \ge {\mathcal {N}}_{\sigma (j)}$, for $j=2,3,\ldots ,n$, and ${\widehat{p}}_j = \dfrac{\xi _j p_j}{\sum \nolimits _{j=1}^n \xi _j p_j}$ is known as the “immediate probability” assign to the SVNN ${\mathcal {N}}_j$. We could also use ${\widehat{p}} = \frac{\xi _j + p_j}{\sum \nolimits _{j=1}^n (\xi _j +p_j)}$ or other similar approaches.

Theorem 2

For a collection of SVNNs ${\mathcal {N}}_j=( \varsigma _j, \tau _j, \upsilon _j)$, $\forall j$, the collective value given by IP-SVNOWA is a SVNN and given by

$$\begin{aligned}&\text {IP-SVNOWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n)\nonumber \\&\quad =\left( 1-\prod \limits _{j=1}^n \left( 1-\varsigma _{\sigma (j)}\right) ^{{\widehat{p}}_j}, \prod \limits _{j=1}^n \left( \tau _{\sigma (j)}\right) ^{{\widehat{p}}_j}, \prod \limits _{j=1}^n \left( \upsilon _{\sigma (j)}\right) ^{{\widehat{p}}_j} \right) \end{aligned}$$

(10)

Proof

Follows from Theorem 1, so we omit their proof here. $\square$

Like P-SVNWA, the IP-SVNOWA also satisfies the properties of boundedness, idempotency, and monotonicity. Next, we present a numerical example to demonstrate the concept of the IP-SVNOWA operator.

Example 2

Let ${\mathcal {N}}_1$ = (0.4, 0.2, 0.6), ${\mathcal {N}}_2$=(0.6, 0.1, 0.3), ${\mathcal {N}}_3$ = (0.8, 0.1, 0.2), ${\mathcal {N}}_4$ = (0.3, 0.2, 0.6) and ${\mathcal {N}}_5$ = (0.3, 0.2, 0.8) be five SVNNs with probabilistic data $p=(0.3, 0.3, 0.2, 0.1, 0.1)$ and the importance of each SVNN as $\omega =(0.20, 0.25, 0.15, 0.30, 0.10)$. In view of the scores of SVNNs, we calculate that $S({\mathcal {N}}_1)=-0.40$, $S({\mathcal {N}}_2)=0.20$, $S({\mathcal {N}}_3)=0.50$, $S({\mathcal {N}}_4)=-0.5$ and $S({\mathcal {N}}_5)=-0.7$. Since $S({\mathcal {N}}_3)>S({\mathcal {N}}_2)>S({\mathcal {N}}_1)>S({\mathcal {N}}_4)>S({\mathcal {N}}_5)$ and hence the permuted numbers becomes ${\mathcal {N}}_{\sigma (1)}={\mathcal {N}}_3$, ${\mathcal {N}}_{\sigma (2)}={\mathcal {N}}_2$, ${\mathcal {N}}_{\sigma (3)}={\mathcal {N}}_1$, ${\mathcal {N}}_{\sigma (4)}={\mathcal {N}}_4$ and ${\mathcal {N}}_{\sigma (5)}={\mathcal {N}}_5$. Furthermore, in order to create the choice more secure, the decision makers are interested in manipulating the probability by allotting the OWA weights $\xi =(0.1,0.2,0.2,0.2,0.3)$ which is clearly a pessimistic because it gives higher importance to the lowest result used in the last weights $\omega$. Now, based on such information, immediate probabilities are calculated by ${\widehat{p}}_j = \frac{\xi _j p_j}{\sum \nolimits _{j=1}^n \xi _j p_j}$ and get ${\widehat{p}}_j= (0.15, 0.10, 0.10, 0.20, 0.45)$. Therefore, $1-\prod \nolimits _{j=1}^n (1-\varsigma _{\sigma (j)}^2)^{{\hat{p}}_j} = 1-(1-0.8)^{0.15}\cdot (1-0.6)^{0.10}\cdot (1-0.4)^{0.10}\cdot (1-0.3)^{0.20}\cdot (1-0.3)^{0.45} = 0.4599$, $\prod \nolimits _{j=1}^n \tau _{\sigma (j)}^{{\hat{p}}_j} = (0.1)^{0.15}\cdot (0.1)^{0.10}\cdot (0.2)^{0.10}\cdot (0.2)^{0.20}\cdot (0.2)^{0.45} = 0.1682$ and $\prod \nolimits _{j=1}^n \upsilon _{\sigma (j)}^{{\hat{p}}_j} = (0.2)^{0.15}\cdot (0.3)^{0.10}\cdot (0.6)^{0.10}\cdot (0.6)^{0.20}\cdot (0.8)^{0.45} = 0.5404$ and hence Eq. (10) becomes $\text {IP-SVNOWA}({\mathcal {N}}_1,\ldots ,{\mathcal {N}}_5) = \big ( 0.4599, 0.1682, 0.5404 \big )$.

3.1.3 Probabilistic single-valued neutrosophic ordered weighted average operator

In this section, by taking the advantages of both P-SVNWA and IP-SVNOWA operators, we present a probabilistic single-valued neutrosophic ordered weighted average operator for a collection of SVNNs.

Definition 12

For a collection of “n” SVNNs ${\mathcal {N}}_j$, a map $\text {P-SVNOWA}:\varOmega ^n \longrightarrow \varOmega$ defined by is a map with associated weight $\xi _j>0$ such that $\sum \nolimits _{j=1}^n\xi _j =1$ defined as

$$\begin{aligned} \text {P-SVNOWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \bigoplus _{j=1}^n v_j {\mathcal {N}}_{\sigma (j)} \end{aligned}$$

(11)

is called as probabilistic single-valued neutrosophic ordered weighted average (P-SVNOWA) operator, where $\sigma$ permutes $(1,2,\ldots ,n)$ with ${\mathcal {N}}_{\sigma (j-1)} \ge {\mathcal {N}}_{\sigma (j)}$ for $j=2,3,\ldots ,n$; $p_j$ is the associated probability of ${\mathcal {N}}_{\sigma (j)}$, $\xi _j>0$ is the weight vector of ${\mathcal {N}}_j$ and $v_j = \beta \xi _j + (1-\beta ) p_j$ with $\beta \in [0,1]$ such that $\sum _j p_j = 1$ and $\sum _j \xi _j=1$.

Theorem 3

For a collection of “n” SVNNs ${\mathcal {N}}_j=( \varsigma _j, \tau _j, \upsilon _j)$, the collective value obtained through P-SVNOWA is again a SVNN and given by

$$\begin{aligned}&\text {P-SVNOWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n)\nonumber \\&\quad =\left( 1-\prod \limits _{j=1}^n \left( 1-\varsigma _{\sigma (j)}\right) ^{v_j}, \prod \limits _{j=1}^n \left( \tau _{\sigma (j)}\right) ^{v_j}, \prod \limits _{j=1}^n \left( \upsilon _{\sigma (j)}\right) ^{v_j} \right) \end{aligned}$$

(12)

Proof

As similar to Theorem 1. $\square$

Remark 2

From the definition of P-SVNOWA operator, we can deduce the following features:

• (1) When $\beta =1$, the P-SVNOWA operator becomes SVNOWA operator [18] as given in Eq. (5)

• (2) When $\beta =0$, the P-SVNOWA operator becomes SVN probabilistic aggregation operator.

Also, it has been noticed that the P-SVNOWA operator has characteristics of boundedness, idempotency, and monotonicity.

Example 3

Consider the data as given in Example 2 and assume that the importance to the subjective (probability) and objective (weightage) information is taken as 40% and 60%, respectively, so $v_j = \beta \xi _j + (1-\beta ) p_j$ is calculated as $v =(0.18, 0.24, 0.20, 0.16, 0.22)$. Based on such information, we have $1-\prod \nolimits _{j=1}^n (1-\varsigma _{\sigma (j)})^{v_j} = 1-(1-0.8)^{0.18}\cdot (1-0.6)^{0.24}\cdot (1-0.4)^{0.20}\cdot (1-0.3)^{0.16}\cdot (1-0.3)^{0.22} = 0.5264$, $\prod \nolimits _{j=1}^n \tau _{\sigma (j)}^{v_j} = (0.1)^{0.18}\cdot (0.1)^{0.24}\cdot (0.2)^{0.20}\cdot (0.2)^{0.16}\cdot (0.2)^{0.22} = 0.1495$, $\prod \nolimits _{j=1}^n \upsilon _{\sigma (j)}^{v_j} =(0.2)^{0.18}\cdot (0.3)^{0.24}\cdot (0.6)^{0.20}\cdot (0.6)^{0.16}\cdot (0.8)^{0.22} = 0.4441$. Thus, Eq. (12) becomes $\text {P-SVNOWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \big ( 0.5264, 0.1495, 0.4441\big )$.

3.1.4 Probabilistic single-valued neutrosophic weighted geometric operator

In this section, we present some probabilistic geometric aggregation operators named as probability single-valued neutrosophic weighted geometric (P-SVNWG), immediate probability single-valued neutrosophic ordered weighted geometric (IP-SVNOWG) and probability single-valued neutrosophic ordered weighted geometric (P-SVNOWG) for a collection of SVNNs.

Definition 13

A map $\text {P-SVNWG}:\varOmega ^n \rightarrow \varOmega$ on a collection of “n” SVNNs ${\mathcal {N}}_j = (\varsigma _j, \tau _j, \upsilon _j)$ is defined as

$$\begin{aligned}&\text {P-SVNWG}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \bigotimes _{j=1}^n \left( {\mathcal {N}}_j\right) ^{v_j} \nonumber \\&\quad = \left( \prod \limits _{j=1}^n \left( \varsigma _j\right) ^{v_j}, 1-\prod \limits _{j=1}^n \left( 1-\tau _j\right) ^{v_j}, 1-\prod \limits _{j=1}^n \left( 1-\upsilon _j\right) ^{v_j}\right) \end{aligned}$$

(13)

where $v_j = \beta \omega _j + (1-\beta )p_j$ is the weight vector with $\beta \in [0,1]$ such that $v_j>0$ and $\sum \nolimits _{j=1}^n v_j=1$. Then, P-SVNWG is called as probabilistic single-valued neutrosophic weighted geometric operator.

Remark 3

From the definition of P-SVNWG operator, we conclude that

• (1) When $\beta =1$, P-SVNWG operator becomes SVNWG [18].

• (2) When $\beta =0$, P-SVNWG operator becomes single-valued neutrosophic probabilistic geometric operator.

Definition 14

An immediate probability single-valued neutrosophic OWG (IP-SVNOWG) operator is a map $\text {IP-SVNOWG}:\varOmega ^n \longrightarrow \varOmega$ associated with weight $\xi =(\xi _1,\ldots ,\xi _n)^T$ such that $\xi _j >0$ and $\sum \nolimits _{j=1}^n \xi _j= 1$, defined as

$$\begin{aligned}&\text {IP-SVNOWG}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \bigotimes _{j=1}^n \left( {\mathcal {N}}_{\sigma (j)}\right) ^{{\widehat{p}}_j} \nonumber \\&\quad = \left( \prod \limits _{j=1}^n \left( \varsigma _{\sigma (j)}\right) ^{{\widehat{p}}_j}, 1-\prod \limits _{j=1}^n \left( 1-\tau _{\sigma (j)}\right) ^{{\widehat{p}}_j}, 1-\prod \limits _{j=1}^n \left( 1-\upsilon _{\sigma (j)}\right) ^{{\widehat{p}}_j} \right) \end{aligned}$$

(14)

where $\sigma$ permutes $(1,2,\ldots ,n)$ with ${\mathcal {N}}_{\sigma (j-1)} \ge {\mathcal {N}}_{\sigma (j)}$, $\forall j=2,3,\ldots ,n$, each ${\mathcal {N}}_{\sigma (j)}$ has associated a probability $p_j$, and ${\widehat{p}}_j = \frac{\xi _jp_j}{\sum \nolimits _{j=1}^n \xi _j p_j}$.

Definition 15

A probabilistic single-valued neutrosophic OWG (P-SVNOWG) operator is a map, $\text {P-SVNOWG}:\varOmega ^n \longrightarrow \varOmega$ defined as

$$\begin{aligned}&\text {P-SVNOWG}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \bigotimes _{j=1}^n \left( {\mathcal {N}}_{\sigma (j)}\right) ^{v_j}\nonumber \\&\quad = \left( \prod \limits _{j=1}^n \left( \varsigma _{\sigma (j)}\right) ^{v_j}, 1-\prod \limits _{j=1}^n \left( 1-\tau _{\sigma (j)}\right) ^{v_j}, 1-\prod \limits _{j=1}^n \left( 1-\upsilon _{\sigma (j)}\right) ^{v_j} \right) \end{aligned}$$

(15)

where $\sigma$ permutes $(1,2,\ldots ,n)$ with ${\mathcal {N}}_{\sigma (j)}$ is the largest SVNN, $p_j$ is the associated probability of ${\mathcal {N}}_{\sigma (j)}$, $\xi _j>0$ be the normalized weight vector of ${\mathcal {N}}_j$ and $v_j = \beta \xi _j + (1-\beta ) p_j$ with $\beta \in [0,1]$.

3.1.5 Generalized probabilistic ordered weighted operators

From the definition of P-SVNOWA operator, it is seen that the operator can be written as a linear combination of the SVNOWA operator and the probabilities operators, as

$$\begin{aligned} \text {P-SVNOWA}({{\mathcal {N}}_1}, {{\mathcal {N}}_2},\ldots ,{{\mathcal {N}}_n}) = \beta \bigoplus _{j=1}^{n}\omega _j{{\mathcal {N}}_{\sigma _{(j)}}} + (1-\beta )\bigoplus _{j=1}^{n}p_j{{\mathcal {N}}_j} \end{aligned}$$

(16)

In the below, we generalized the above-defined P-SVNOWA operator to its more generalized form, named as probabilistic generalized single-valued neutrosophic ordered weighted averaging (P-GSVNOWA) operator, by adding parameters $\lambda$ and $\delta$ which represents the behavior of the decision-makers.

Definition 16

For SVNNs ${\mathcal {N}}_j$, a P-GSVNOWA operator is a map $\text {P-GSVNOWA}: \varOmega ^n \rightarrow \varOmega$ associated with weights $\xi _j>0$, $\sum \nolimits _{j=1}^{n}\xi _j=1$, and a probabilities $p_j>0$, $\sum \nolimits _{j=1}^{n}p_j=1$, such that:

$$\begin{aligned} \text {P-GSVNOWA}({{\mathcal {N}}_1}, {{\mathcal {N}}_2},\ldots ,{{\mathcal {N}}_n}) = \beta \left( \bigoplus _{j=1}^{n}w_j{{\mathcal {N}}_{\sigma {(j)}}^\lambda }\right) ^{\frac{1}{\lambda }} +(1-\beta )\left( \bigoplus _{j=1}^{n}p_j{{\mathcal {N}}_j^\delta }\right) ^{\frac{1}{\delta }} \end{aligned}$$

(17)

where $\beta \in [0,1]$, $\lambda , \delta$ are real parameters.

From Eq. (17), it has been concluded that by varying values of $\beta$, $\lambda$ and $\delta$, we get their corresponding families of the operators, which are discussed below:

• (1) If $\beta =1$, then P-GSVNOWA becomes generalized SVNOWA operator [18].

• (2) If $\beta =0$, then P-GSVNOWA becomes generalized SVNPA operator.

• (3) If $\lambda =\delta =1$, then P-GSVNOWA converted to P-SVNOWA as defined in the Eq. (16).

• (4) If $\lambda \rightarrow 0$ and $\delta \rightarrow 0$, then P-GSVNOWA takes form of P-SVNOWG operator.

  $$\begin{aligned} \text {P-SVNOWG}({\mathcal {N}}_1, {\mathcal {N}}_2, \ldots ,{\mathcal {N}}_n)= \beta \prod \limits _{j=1}^{n}\left( {\mathcal {N}}_{\sigma {(j)}}\right) ^{w_j} + (1-\beta )\prod \limits _{j=1}^{n}\left( {\mathcal {N}}_j\right) ^{\widehat{p_j}} \end{aligned}$$

• (5) If $\lambda =\delta =-1$, then P-GSVNOWA operator becomes the probabilistic single-valued neutrosophic harmonic OWA (P-SVNHOWA) operator.

  $$\begin{aligned} \text {P-SVNHOWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) =\beta \frac{1}{\bigoplus \limits _{j=1}^{n} \left( \dfrac{w_j}{{\mathcal {N}}_{\sigma {(j)}}}\right) }+ (1-\beta )\frac{1}{\bigoplus \limits _{j=1}^{n} \left( \dfrac{p_j}{{\mathcal {N}}_j}\right) } \end{aligned}$$

• (6) If $\lambda =\delta =2$, then P-GSVNOWA operator reduced to the probabilistic single-valued neutrosophic quadratic OWA (P-SVNQOWA) operator.

  $$\begin{aligned} \text {P-SVNQOWA}({{\mathcal {N}}_1}, {{\mathcal {N}}_2},\ldots ,{{\mathcal {N}}_n})&= \beta \left( \bigoplus _{j=1}^{n}w_j{{\mathcal {N}}_{\sigma (j)}^2}\right) ^{\frac{1}{2}}\nonumber \\&\quad + (1-\beta )\left( \bigoplus _{j=1}^{n}p_j{{\mathcal {N}}_j^2}\right) ^{\frac{1}{2}} \end{aligned}$$

• (7) If $\lambda =\delta =3$, then P-GSVNOWA operator reduced to the probabilistic single-valued neutrosophic cubic ordered weighted averaging (P-SVNCOWA) operator.

  $$\begin{aligned} \text {P-SVNCOWA}({{\mathcal {N}}_1}, {{\mathcal {N}}_2},\ldots ,{{\mathcal {N}}_n})&= \beta \left( \bigoplus _{j=1}^{n}w_j{{\mathcal {N}}_{\sigma {(j)}}^3}\right) ^{\frac{1}{3}}\nonumber \\&\quad + (1-\beta )\left( \bigoplus _{j=1}^{n}p_j{{\mathcal {N}}_j^3}\right) ^{\frac{1}{3}} \end{aligned}$$

• (8) If $\lambda =2$ and $\delta =1$, we get the probabilistic SVN ordered weighted quadratic average (P-SVNOWQA).

  $$\begin{aligned} \text {P-SVNOWQA}({{\mathcal {N}}_1}, {{\mathcal {N}}_2},\ldots ,{{\mathcal {N}}_n})&=\beta \left( \bigoplus _{j=1}^{n}w_j{{\mathcal {N}}_{\sigma {(j)}}^2}\right) ^{\frac{1}{2}}\nonumber \\&\quad + (1-\beta )\left( \bigoplus _{j=1}^{n}p_j{{\mathcal {N}}_j}\right) \end{aligned}$$

• (9) If $\lambda =1$ and $\delta =2$, we get the probabilistic single-valued neutrosophic quadratic OWA (P-SVNQOWA).

  $$\begin{aligned} \text {P-SVNQOWA}({{\mathcal {N}}_1}, {{\mathcal {N}}_2},\ldots ,{{\mathcal {N}}_n})&= \beta \left( \bigoplus _{j=1}^{n}w_j{{\mathcal {N}}_{\sigma {(j)}}}\right) \nonumber \\&\quad + (1-\beta )\left( \bigoplus _{j=1}^{n}p_i{{\mathcal {N}}_j^2}\right) ^{\frac{1}{2}} \end{aligned}$$

• (10) If $\lambda =3$ and $\delta =1$, we get the probabilistic single-valued neutrosophic ordered weighted cubic average (P-SVNOWCA).

  $$\begin{aligned} \text {P-SVNOWCA}({{\mathcal {N}}_1}, {{\mathcal {N}}_2},\ldots ,{{\mathcal {N}}_n})&=\beta \left( \bigoplus _{j=1}^{n}w_j{{\mathcal {N}}_{\sigma {(j)}}^3}\right) ^{\frac{1}{3}}\nonumber \\&\quad + (1-\beta )\left( \bigoplus _{j=1}^{n}p_j{{\mathcal {N}}_j}\right) \end{aligned}$$

• (11) If $\lambda =1$ and $\delta =3$, we get the probabilistic single-valued neutrosophic cubic OWA (P-SVNCOWA) operator.

  $$\begin{aligned} \text {P-SVNCOWA}({{\mathcal {N}}_1}, {{\mathcal {N}}_2},\ldots ,{{\mathcal {N}}_n})&= \beta \left( \bigoplus _{j=1}^{n}w_j{{\mathcal {N}}_{\sigma {(j)}}}\right) \nonumber \\&\quad + (1-\beta )\left( \bigoplus _{j=1}^{n}p_j{{\mathcal {N}}_j^3}\right) ^{\frac{1}{3}} \end{aligned}$$

• (12) If $\lambda =2$ and $\delta =3$, we get the probabilistic single-valued neutrosophic cubic ordered weighted quadratic average (P-SVNCOWQA).

  $$\begin{aligned} \text {P-SVNCOWQA}({{\mathcal {N}}_1}, {{\mathcal {N}}_2},\ldots ,{{\mathcal {N}}_n})&=\beta \left( \bigoplus _{j=1}^{n}w_j{{\mathcal {N}}_{\sigma {(j)}}^2}\right) ^{\frac{1}{2}}\nonumber \\&\quad + (1-\beta )\left( \bigoplus _{j=1}^{n}p_j{{\mathcal {N}}_j^3}\right) ^{\frac{1}{3}} \end{aligned}$$

3.2 Aggregation operators for INS

In this section, we have extended the above defined aggregation operators from SVNNs to the interval neutrosophic numbers (INNs). Let $\varGamma$ be the collection of all INNs ${\mathcal {N}}_j=([\varsigma _j^L, \varsigma _j^U],[\tau _j^L, \tau _j^U]$, $[\upsilon _j^L, \upsilon _j^U])$, having weights $\omega = (\omega _1,\omega _2,\ldots ,\omega _n)^T$, $\omega _j >0$, $\sum \nolimits _{j=1}^n \omega _j =1$ and the probabilistic weight $p_j >0$, $\sum \nolimits _{j=1}^n p_j = 1$.

Definition 17

For a collection of “n” INNs ${\mathcal {N}}_j=([\varsigma _j^L, \varsigma _j^U],[\tau _j^L, \tau _j^U]$, $[\upsilon _j^L, \upsilon _j^U])$, a map $\text {P-INWA}:\varGamma ^n \longrightarrow \varGamma$ defined by

$$\begin{aligned}&\text {P-INWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \bigoplus _{j=1}^n v_j {\mathcal {N}}_j \nonumber \\&\quad = \left( \begin{aligned}&\left[ 1-\prod \limits _{j=1}^n \left( 1-\varsigma ^L_j\right) ^{v_j}, 1-\prod \limits _{j=1}^n \left( 1-\varsigma ^U_j\right) ^{v_j}\right] ,\\&\quad \left[ \prod \limits _{j=1}^n \left( \tau ^L_j\right) ^{v_j}, \prod \limits _{j=1}^n \left( \tau ^U_j\right) ^{v_j}\right] ,\\&\quad \left[ \prod \limits _{j=1}^n \left( \upsilon ^L_j\right) ^{v_j}, \prod \limits _{j=1}^n \left( \upsilon ^U_j\right) ^{v_j}\right] \end{aligned} \right) \end{aligned}$$

(18)

then P-INWA is called as probabilistic interval neutrosophic weighted average operator where $v_j = (1-\beta )p_j + \beta \omega _j$ with $\beta \in [0,1]$.

Remark 4

If $\beta = 1$ then P-INWA acted as INWA and if $\beta =0$ then it acts as interval neutrosophic probabilistic aggregation operator.

Definition 18

An immediate probability interval neutrosophic ordered weighted average (IP-INOWA) operator is a map $\text {IP-INOWA}:\varGamma ^n \rightarrow \varGamma$, with associated normalized weight vector $\xi =(\xi _1,\xi _2,\ldots ,\xi _n)^T$, defined as

$$\begin{aligned}&\text {IP-INOWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \bigoplus _{j=1}^n {\widehat{p}}_j {\mathcal {N}}_{\sigma (j)} \nonumber \\&\quad = \left( \begin{aligned}&\left[ 1-\prod \limits _{j=1}^n \left( 1-\varsigma ^L_{\sigma (j)}\right) ^{{\widehat{p}}_j}, 1-\prod \limits _{j=1}^n \left( 1-\varsigma ^U_{\sigma (j)}\right) ^{{\widehat{p}}_j} \right] ,\\&\quad \left[ \prod \limits _{j=1}^n \left( \tau ^L_{\sigma (j)}\right) ^{{\widehat{p}}_j}, \prod \limits _{j=1}^n \left( \tau ^U_{\sigma (j)}\right) ^{{\widehat{p}}_j}\right] ,\\&\quad \left[ \prod \limits _{j=1}^n \left( \upsilon ^L_{\sigma (j)}\right) ^{{\widehat{p}}_j}, \prod \limits _{j=1}^n \left( \upsilon ^U_{\sigma (j)}\right) ^{{\widehat{p}}_j}\right] \end{aligned} \right) \end{aligned}$$

(19)

where $\sigma$ permutes $(1,2,\ldots ,n)$ such that ${\mathcal {N}}_{\sigma (j-1)} \ge {\mathcal {N}}_{\sigma (j)}$ and ${\widehat{p}}_j = \frac{\xi _jp_j}{\sum \nolimits _{j=1}^n \xi _j p_j}$. We could also use ${\widehat{p}} = \frac{\xi _j + p_j}{\sum \nolimits _{j=1}^n (\xi _j +p_j)}$ or other similar approaches.

Definition 19

A probabilistic interval neutrosophic ordered weighted average (P-INOWA) operator is a map $\text {P-INOWA}:\varGamma ^n \rightarrow \varGamma$, with associated weight vector $\xi =(\xi _1,\xi _2,\ldots ,\xi _n)^T$, such that $\xi _j>0$ and $\sum \nolimits _{j=1}^n \xi _j =1$, and is defined as

$$\begin{aligned}&\text {P-INOWA}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \bigoplus _{j=1}^n v_j {\mathcal {N}}_{\sigma (j)} \nonumber \\&\quad = \left( \begin{aligned}&\left[ 1-\prod \limits _{j=1}^n \left( 1-\varsigma ^L_{\sigma (j)}\right) ^{v_j}, 1-\prod \limits _{j=1}^n \left( 1-\varsigma ^U_{\sigma (j)}\right) ^{v_j}\right] ,\\&\quad \left[ \prod \limits _{j=1}^n \left( \tau ^L_{\sigma (j)}\right) ^{v_j}, \prod \limits _{j=1}^n \left( \tau ^U_{\sigma (j)}\right) ^{v_j} \right] ,\\&\quad \left[ \prod \limits _{j=1}^n \left( \upsilon ^L_{\sigma (j)}\right) ^{v_j}, \prod \limits _{j=1}^n \left( \upsilon ^U_{\sigma (j)}\right) ^{v_j} \right] \end{aligned} \right) \end{aligned}$$

(20)

where $p_j$ is the associated probability of ${\mathcal {N}}_{\sigma (j)}$ and $v_j = (1-\beta ) p_j + \beta \xi _j$ with $\beta \in [0,1]$.

Remark 5

If $\beta =1$ then the P-INOWA takes form of INOWA and if $\beta =0$ then it converts to interval neutrosophic probabilistic aggregation.

Definition 20

A probability interval neutrosophic weighted geometric (P-INWG) operator is a map $\text {P-INWG}:\varGamma ^n \rightarrow \varGamma$ defined as

$$\begin{aligned}&\text {P-INWG}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) = \bigotimes _{j=1}^n \left( {\mathcal {N}}_j\right) ^{v_j} \nonumber \\&\quad = \left( \begin{aligned}&\left[ \prod \limits _{j=1}^n \left( \varsigma ^L_j\right) ^{v_j}, \prod \limits _{j=1}^n \left( \varsigma ^U_j\right) ^{v_j} \right] ,\\&\quad \left[ 1-\prod \limits _{j=1}^n \left( 1-\tau ^L_j\right) ^{v_j}, 1-\prod \limits _{j=1}^n \left( 1-\tau ^U_j\right) ^{v_j} \right] ,\\&\quad \left[ 1-\prod \limits _{j=1}^n \left( 1-\upsilon ^L_j\right) ^{v_j}, 1-\prod \limits _{j=1}^n \left( 1-\upsilon ^U_j\right) ^{v_j}\right] \end{aligned} \right) \end{aligned}$$

(21)

where $\omega _j >0$, $\sum \nolimits _{j=1}^n \omega _j = 1$ is the weight vector of ${\mathcal {N}}_j$, $v_j = (1-\beta )p_j + \beta \omega _j$ with $\beta \in [0,1]$ is the weight that binds the probabilities with the INWG in the similar data.

Remark 6

If $\beta =1$ then P-INWG takes form of INWG while if $\beta =0$ then it becomes the interval neutrosophic probabilistic geometric aggregation.

Definition 21

An immediate probability interval neutrosophic ordered weighted geometric (IP-INOWG) is a map $\text {IP-INOWG}:\varGamma ^n \rightarrow \varGamma$, with associated weight vector $\xi =(\xi _1,\xi _2,\ldots ,\xi _n)^T$, such that $\xi _j >0$, $\sum \nolimits _{j=1}^n \xi _j = 1$, defined as

$$\begin{aligned}&\text {IP-INOWG}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n) =\bigotimes _{j=1}^n \left( {\mathcal {N}}_{\sigma (j)}\right) ^{{\widehat{p}}_j} \nonumber \\&\quad = \left( \begin{aligned}&\left[ \prod \limits _{j=1}^n \left( \varsigma ^L_{\sigma (j)}\right) ^{{\widehat{p}}_j}, \prod \limits _{j=1}^n \left( \varsigma ^U_{\sigma (j)}\right) ^{{\widehat{p}}_j} \right] ,\\&\quad \left[ 1-\prod \limits _{j=1}^n \left( 1-\tau ^L_{\sigma (j)}\right) ^{{\widehat{p}}_j}, 1-\prod \limits _{j=1}^n \left( 1-\tau ^U_{\sigma (j)}\right) ^{{\widehat{p}}_j} \right] ,\\&\quad \left[ 1-\prod \limits _{j=1}^n \left( 1-\upsilon ^L_{\sigma (j)}\right) ^{{\widehat{p}}_j}, 1-\prod \limits _{j=1}^n \left( 1-\upsilon ^U_{\sigma (j)}\right) ^{{\widehat{p}}_j}\right] \end{aligned} \right) \end{aligned}$$

(22)

where $\sigma$ permutes $(1,2,\ldots ,n)$ with ${\mathcal {N}}_{\sigma (j-1)} \ge {\mathcal {N}}_{\sigma (j)}$$\forall$$j=2,3,\ldots ,n$, $p_j$ is the associated probability of ${\mathcal {N}}_{\sigma (j)}$ and ${\widehat{p}}_j = \frac{\xi _jp_j}{\sum \nolimits _{j=1}^n \xi _j p_j}$.

Definition 22

A probability interval neutrosophic ordered weighted geometric (P-INOWG) for INNs is a map $\text {P-INOWG}:\varGamma ^n \longrightarrow \varGamma$ defined by

$$\begin{aligned}&\text {P-INOWG}({\mathcal {N}}_1,{\mathcal {N}}_2,\ldots ,{\mathcal {N}}_n)=\prod \limits _{j=1}^n \left( {\mathcal {N}}_{\sigma (j)}\right) ^{v_j} \nonumber \\&\quad = \left( \begin{aligned}&\left[ \prod \limits _{j=1}^n \left( \varsigma ^L_{\sigma (j)}\right) ^{v_j}, \prod \limits _{j=1}^n \left( \varsigma ^U_{\sigma (j)}\right) ^{v_j} \right] ,\\&\quad \left[ 1-\prod \limits _{j=1}^n \left( 1-\tau ^L_{\sigma (j)}\right) ^{v_j}, 1-\prod \limits _{j=1}^n \left( 1-\tau ^U_{\sigma (j)}\right) ^{v_j} \right] ,\\&\quad \left[ 1-\prod \limits _{j=1}^n \left( 1-\upsilon ^L_{\sigma (j)}\right) ^{v_j}, 1-\prod \limits _{j=1}^n \left( 1-\upsilon ^U_{\sigma (j)}\right) ^{v_j}\right] \end{aligned} \right) \end{aligned}$$

(23)

where $v_j = (1-\beta )p_j + \beta \omega _j$ with $\beta \in [0,1]$ such that $v_j>0$ and $\sum \nolimits _{j=1}^n v_j=1$.

Remark 7

If $\beta =1$ then the P-INOWG converts to INOWG and if $\beta =0$ then it becomes the interval neutrosophic probabilistic OWG (INPOWG) operator.

The proposed operators P-INWA, IP-INOWA, P-INOWA, P-INWG, IP-INOWG, P-INOWG also have properties like boundedness, idempotency, and monotonicity.

4 Proposed algorithm

In this section, we present a decision-making algorithm for solving the MADM problems under the neutrosophic set environment. Consider a set of alternatives ${\mathcal {V}}_1, {\mathcal {V}}_2,\ldots , {\mathcal {V}}_m$ which are evaluated by an expert under the different attributes ${\mathfrak {B}}_1,{\mathfrak {B}}_2, \ldots , {\mathfrak {B}}_n$ and gives their preferences either in terms of SVNNs or INNs. Let $\omega =(\omega _1, \omega _2, \ldots , \omega _n)$ be the weight vector assigned to the given attributes ${\mathfrak {B}}_j$ such that $\omega _j>0$ and $\sum \nolimits _{j=1}^n \omega _j=1$. Then, the procedure for choosing the finest alternative(s) by utilizing the proposed operators are summarized in the following algorithms.

4.1 Algorithm 1: when ratings are given under SVNS environment

When an expert evaluate the given alternatives ${\mathcal {V}}_i$ under different attributes ${\mathfrak {B}}_j$ and represent their values in terms of SVNNs $\beta _{ij}=\left( \varsigma _{ij}, \tau _{ij}, \upsilon _{ij}\right)$ such that $\varsigma _{ij}, \tau _{ij}, \upsilon _{ij}\in [0,1]$ and $\varsigma _{ij}+\tau _{ij}+\upsilon _{ij}\le 3$. Then, the following are the steps summarized to find the best alternative(s).

• Step 1: Arrange the collective information of the expert in the neutrosophic decision matrix ${\mathcal {M}}=(\beta _{ij})_{m\times n}$ as

  

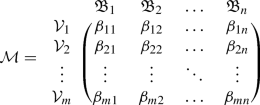
• Step 2: Set the probabilistic information p, weight vector w, ordered weights $\xi$ and the importance factor $\beta$. Based on such information, calculate the immediate probability ${\widehat{p}}=\frac{\xi _j p_j}{\sum \nolimits _{j=1}^n \xi _j p_j}$.

• Step 3: Aggregate the collection information of the alternative ${\mathcal {V}}_i$ with expert evaluation $\beta _{ij}, j=1,2,\ldots ,n$ into $\beta _i, i=1,2,\ldots ,m$ by using either of the proposed averaging operator such as P-SVNWA, P-SVNOWA, IP-SVNOWA, or by geometric operator such as P-SVNWG, P-SVNOWG, IP-SVNOWG operator.

• Step 4: Compute the score value of the obtained aggregated number $\beta _i=(\varsigma _i, \tau _i, \upsilon _i), i=1,2,\ldots ,m$ as

  $$\begin{aligned} S(\beta _i) = \varsigma _i - \tau _i - \upsilon _i \end{aligned}$$

  (24)

  If score values are equal for any two indices then compute the accuracy values for them by using Eq. (25).

  $$\begin{aligned} H(\beta _i) = \varsigma _i + \tau _i + \upsilon _i \end{aligned}$$

  (25)

• Step 5: Rank the given alternatives based on the descending values of score values of $\beta _i$ and hence select the best one(s).

4.2 Algorithm 2: when ratings are given under INS environment

When an expert evaluate the given alternatives ${\mathcal {V}}_i$ under different attributes ${\mathfrak {B}}_j$ and represent their values in terms of INNs $\gamma _{ij}=\left( \left[ \varsigma _{ij}^L, \varsigma _{ij}^U\right] , \left[ \tau _{ij}^L, \tau _{ij}^U\right] , \left[ \upsilon _{ij}^L, \upsilon _{ij}^U\right] \right)$ such that $\varsigma _{ij}^L, \varsigma _{ij}^U$, $\tau _{ij}^L$, $\tau _{ij}^U$, $\upsilon _{ij}^L$, $\upsilon _{ij}^U \in [0,1]$ and $\varsigma _{ij}^U+\tau _{ij}^U+\upsilon _{ij}^U\le 3$. Then, the following are the steps summarized to find the best alternative(s).

• Step 1: Arrange the collective information of the expert in the neutrosophic decision matrix ${\mathcal {M}}=(\gamma _{ij})_{m\times n}$ as

  

• Step 2: Set the probabilistic information p, weight vector w, ordered weights $\xi$ and the importance factor $\beta$. Based on such information, calculate the immediate probability ${\widehat{p}}=\frac{\xi _j p_j}{\sum \nolimits _{j=1}^n \xi _j p_j}$.

• Step 3: Aggregate the collection information of the alternative ${\mathcal {V}}_i$ with expert evaluation $\gamma _{ij}, j=1,2,\ldots ,n$ into $\gamma _i, i=1,2,\ldots ,m$ by using either of the proposed averaging operator such as P-INWA, P-INOWA, IP-INOWA, or by geometric operator such as P-INWG, P-INOWG, IP-INOWG operator.

• Step 4: Compute the score value of the obtained aggregated number $\gamma _i=([\varsigma _i^L, \varsigma _i^U]$, $[\tau _i^L, \tau _i^U]$, $[\upsilon _i^L, \upsilon _i^U]), i=1,2,\ldots ,m$ as

  $$\begin{aligned} S(\gamma _i) = \frac{\varsigma _i^L + \varsigma _i^U - \tau _i^L - \tau _i^U - \upsilon _i^L - \upsilon _i^U}{2} \end{aligned}$$

  (26)

  If score values are equal for any two indices then compute the accuracy values for them by using Eq. (27).

  $$\begin{aligned} H(\gamma _i) = \frac{\varsigma _i^L + \varsigma _i^U + \tau _i^L + \tau _i^U + \upsilon _i^L + \upsilon _i^U}{2} \end{aligned}$$

  (27)

• Step 5: Rank the given alternatives based on the descending values of score values of $\beta _i$ and hence select the best one(s).

5 Numerical example

To demonstrate the working of the above-defined algorithms, we illustrate them with a case study that can be read as follows.

“Demonetization is the withdrawal of a particular form of currency from circulation. On 8 November 2016, the Government of India announced in a broadcast to the nation that Rs. 500 and Rs. 1000 currency notes would no longer be recognized legally as currency. This step was taken to crack down the use of illicit and counterfeit cash to fund illegal activity and terrorism. The government knew that demonetization will affect the Indian economy and may also drop the country’s Gross domestic product (GDP) growth. So before the announcement of the demonetization, the Government wanted to conduct a survey of the effect of this bold move on various sectors of the Indian economy to take further decisions. For doing this, the Indian government hired an economist or decision-maker who is able to handle this kind of situation and able to crack that which sector (alternative) of the Indian economy will be affected by demonetization. For this, decision-maker assume the five important sectors on which our Indian economy depends and were given as: ${\mathcal {V}}_1$(Agriculture Sector), ${\mathcal {V}}_2$(Real-Estate Sector), ${\mathcal {V}}_3$(Information Technology Sector), ${\mathcal {V}}_4$(Educational Sector), ${\mathcal {V}}_5$(Industrial Sector). For evaluation, decision-maker considered criterion in the terms ‘how much effect of demonetization on particular sector in linguistic terms’ which are summarized as: ${\mathfrak {B}}_1$(Very low effect), ${\mathfrak {B}}_2$(Low effect), ${\mathfrak {B}}_3$(Regular effect), ${\mathfrak {B}}_4$( High effect) and ${\mathfrak {B}}_5$(Very high effect)”. The evaluation of these strategies is in terms of neutrosophic numbers taken by the evaluators/experts under the criteria defined above.

Table 1 Decision matrix in terms of SVNNs

5.1 When evaluations are taken in SVNNs

The access the best alternatives among the given ones, we implemented the steps of the proposed Algorithm 1 here.

• Step 1: Assume the given alternatives are evaluated by an expert and gives their rating in terms of SVNNs. Such values are represented in Table 1.

• Step 2: As decided by the experts according to the problem, the probability information and weight vector are set as $p=(0.3, 0.3$, 0.2, 0.1, $0.1)^T$ and $\omega =(0.2$, 0.25, 0.15, 0.3, $0.1)^T$. Further, take weighage to the probability information and the weightage average as 60% and 40%, respectively. The decision-maker wants to arrange the government when the situation becomes exceptionally critical for future objectives, so at that point, they control the probabilities by OWA weights $\xi =(0.1, 0.2$, 0.2, 0.2, $0.3)^T$. Finally, IPs are computed and are summarized in Table 2.

• Step 3a: By utilizing the P-SVNWA operator to aggregate the given information, we get the collective values of each alternative ${\mathcal {V}}_i$ as $\beta _1$=(0.4021, 0.2314, 0.3970), $\beta _2$= (0.6673, 0.1899, 0.2490), $\beta _3$=(0.5587, 0.1856, 0.3258), $\beta _4$=(0.6007, 0.2872, 0.2144) and $\beta _5$=(0.4210, 0.1306, 0.3423). On the other hand, if we utilize IP-SVNOWA operator to aggregate the numbers then we get $\beta _1$=(0.3774, 0.2372, 0.4345), $\beta _2$= (0.6682, 0.1888, 0.2551), $\beta _3$= (0.5504, 0.2228, 0.3545), $\beta _4$= (0.5842, 0.3270, 0.2245), and $\beta _5$= (0.4079, 0.1297, 0.3640).

• Step 3b: By utilizing the weighted geometric operator such as P-SVNWG to aggregate the information, we get the numbers are $\beta _1$=(0.3675, 0.2375, 0.4176), $\beta _2$=(0.6622, 0.2263, 0.2557), $\beta _3$=(0.5537, 0.2167, 0.3402), $\beta _4$=(0.5633, 0.3226, 0.2227), and $\beta _5$=(0.4137, 0.1499, 0.3910). However, if we utilize IP-SVNOWG operator for the given numbers then we get $\beta _1$=(0.3362, 0.2437, 0.4591), $\beta _2$=(0.6632, 0.2226, 0.2616), $\beta _3$=(0.5454, 0.2482, 0.3650), $\beta _4$=(0.5424, 0.3626, 0.2375), and $\beta _5$= (0.4021, 0.1481, 0.4052).

• Step 4: By Eq. (24), the score values of collective number obtained through P-SVNWA operator are computed as $S(\beta _1)=-0.2263$, $S(\beta _2)=0.2284$, $S(\beta _3)=0.0474$, $S(\beta _4)=0.0991$ and $S(\beta _5)=-0.0519$ while these values for the numbers obtained through P-SVNWG operator are $S(\beta _1)=-0.2877$, $S(\beta _2)=0.1803$, $S(\beta _3)=-0.0032$, $S(\beta _4)=0.0180$ and $S(\beta _5)=-0.1272$.

• Step 5: Based on the score value, the raking order of the alternatives is taken as ${\mathcal {V}}_2 \succ {\mathcal {V}}_4 \succ {\mathcal {V}}_3 \succ {\mathcal {V}}_5 \succ {\mathcal {V}}_1$, where $\succ$ means “preferred to”. From this ordering, we compute the ${\mathcal {V}}_2$ is the best alternative for the desired task.

Table 2 Immediate probabilities of the problem

5.2 Comparative analysis

To compare the performance of the proposed approach with the several existing approaches, we implement the existing averaging operators such as NWA [20], SVNWA [18], SVNOWA [18], SVNHWA [26] and SVNFWA [23] to aggregate the given information. The aggregated results corresponding to these existing approaches along with the proposed operators namely P-SVNWA, P-SVNOWA and IP-SVNOWA are summarized in Table 3.

Table 3 Neutrosophic aggregated results by averaging operators ($\beta =0.40$)

On the other hand, by utilizing the existing geometric operators such as NWG [20], SVNWG [18], SVNOWG [18], SVNHWG [26], and SVNFWG [23] to aggregate the given information along with the proposed ones namely P-SVNWG, P-SVNOWG and IP-SVNOWG operators, the results corresponding to them are listed in Table 4.

Table 4 Neutrosophic aggregated results by geometric operators ($\beta =0.40$)

Based on the score function as given in Eq. (24), the ranking order of the alternatives is represented in Table 5, where $\succ$ means “preferred to”. From this conclusion, we conclude that the ranking of alternatives slightly differs for different operators but the final outcome of the finest alternative is ${\mathcal {V}}_2$ under all operators. From this analysis, it has been concluded that a decision-maker can select the best alternatives as per their needs and desire. For example, to make an optimal decision according to the optimism nature then an expert can select the averaging operator while selecting a geometric operator for pessimism nature. Similarly, by considering the importance of probabilistic and immediate probabilistic, in terms of the subjective and objective information, a decision-maker can choose the appropriate one during the aggregation phase and the final ranking phase.

Table 5 Ordering of the alternatives

Table 6 Decision matrix in terms of INNs

Table 7 Immediate probabilities of the problem in case of interval-valued data

5.3 When evaluations are taken in INNs

Assume that the expert rates the given alternatives in terms of INNs. Then to access the best alternatives among them, we implemented the steps of the proposed Algorithm 2 here.

• Step 1: The rating values of the expert are summarized in Table 6.

• Step 2: The immediate probability values for the given problem are calculated and summarized in Table 7.

• Step 3a: Utilize P-INWA operator to aggregate the rating of Table 6 and the collective values of each alternative ${\mathcal {V}}_i$ are obtained as

  $$\begin{aligned} \gamma _1= & {} ([0.3316, 0.4878], [0.1514, 0.2562], [0.3498, 0.4882]), \\ \gamma _2= & {} ([0.6278, 0.7590], [0.1765, 0.2960], [0.2490, 0.3953]), \\ \gamma _3= & {} ([0.5095, 0.6103], [0.1856, 0.3163], [0.3005, 0.4025]), \\ \gamma _4= & {} ([0.5357, 0.6550], [0.2088, 0.3452], [0.1558, 0.2824]), \\ \text {and } \gamma _5= & {} ([0.3797, 0.4813], [0.1214, 0.2306], [0.3387, 0.4270]). \end{aligned}$$

  On the other hand, by taking IP-INOWA operator during the aggregation phase, we get the collective values for each alternative as

  $$\begin{aligned} \gamma _1= & {} ([0.3172, 0.4830], [0.1634, 0.2688], [0.3671, 0.5221]), \\ \gamma _2= & {} ([0.6168, 0.7551], [0.1852, 0.3053], [0.2449, 0.3873]), \\ \gamma _3= & {} ([0.5245, 0.6173], [0.2228, 0.3428], [0.3265, 0.4282]), \\ \gamma _4= & {} ([0.5126, 0.6268], [0.2697, 0.4161], [0.1714, 0.3071]), \\ \text { and } \gamma _5= & {} ([0.3572, 0.4585], [0.1212, 0.2348], [0.3620, 0.4364]). \end{aligned}$$

• Step 3b: Aggregate the given information by using P-INWG operator and get the collective values of each alternative ${\mathcal {V}}_i$ are

  $$\begin{aligned} \gamma _1= & {} ([0.3005, 0.4614], [0.1667, 0.2670], [0.3768, 0.5150]), \\ \gamma _2= & {} ([0.6181, 0.7523], [0.2075, 0.3179], [0.2557, 0.4163]), \\ \gamma _3= & {} ([0.4945, 0.6030], [0.2167, 0.3339], [0.3111, 0.4117]), \\ \gamma _4= & {} ([0.4796, 0.6087], [0.2849, 0.4169], [0.1794, 0.3086]), \\ \text {and } \gamma _5= & {} ([0.3582, 0.4614], [0.1292, 0.2411], [0.3775, 0.4586]) \end{aligned}$$

  while by IP-INOWG operator, these values are

  $$\begin{aligned} \gamma _1= & {} ([0.2884, 0.4529], [0.1809, 0.2814], [0.3975, 0.5476]), \\ \gamma _2= & {} ([0.6072, 0.7483], [0.2121, 0.3233], [0.2517, 0.4084]), \\ \gamma _3= & {} ([0.5137, 0.6122], [0.2482, 0.3573], [0.3364, 0.4369]), \\ \gamma _4= & {} ([0.4640, 0.5828], [0.3415, 0.4776], [0.2017, 0.3378]), \\ \text { and } \gamma _5= & {} ([0.3360, 0.4394], [0.1290, 0.2487], [0.3951, 0.4622]). \end{aligned}$$

• Step 4: By Eq. (26), we compute the score values of the numbers obtained by P-INWA operator as $S(\gamma _1) = -0.2131$, $S(\gamma _2) = 0.1350$, $S(\gamma _3) = -0.0426$, $S(\gamma _4) = 0.0992$ and $S(\gamma _5) = -0.1284$. On the other hand, these score values corresponding to the INNs obtained through IP-INOWG operator are $S(\gamma _1) = -0.3330$, $S(\gamma _2) = 0.0800$, $S(\gamma _3) = -0.1264$, $S(\gamma _4) = -0.1559$ and $S(\gamma _5) = -0.2297$.

• Step 5: Based on these score values, we obtain the ranking order of the given alternatives as ${\mathcal {V}}_2\succ {\mathcal {V}}_4\succ {\mathcal {V}}_3\succ {\mathcal {V}}_5\succ {\mathcal {V}}_1$ through P-INWA operator while ${\mathcal {V}}_2\succ {\mathcal {V}}_3\succ {\mathcal {V}}_4\succ {\mathcal {V}}_5\succ {\mathcal {V}}_1$ when IP-INOWG operator used. Clearly seen that there is change in the alternative ordering, while the best one remains same i.e., ${\mathcal {V}}_2$.

5.4 Comparative analysis

To compare the performance of the stated Algorithm 2 by using proposed P-INWA, P-INOWA, and IP-INOWA operators with the several existing operators such as INWA [21], INOWA [21], INFWA [23] and INHWA [26], we execute these operators to aggregate the given information. The resultant values of the alternatives obtained through each operator are listed in Table 8.

Table 8 Neutrosophic aggregated results by averaging operators ($\beta =0.40$)

On the other hand, we utilize the geometric operators namely P-INWG, P-INOWG, and IP-INOWG operators to aggregate the given information and compare their performance with the existing geometric operators namely INWG [21], INOWG [21], INFWG [23] and INHWG [26] with INS environment. The aggregative values obtained through each operator are summarized in Table 9.

Table 9 Neutrosophic aggregated results by geometric operators ($\beta =0.40$)

Based on the score values of the resultant numbers as summarized in Tables 8 and 9, the final ranking order of the given alternatives is listed in Table 10. From the table, it can easily be seen that the most effective sector is ${\mathcal {V}}_2$, although there is a change in their ranking order.

Table 10 Ordering of the alternative

5.5 Impact of the parameters $\lambda$, $\delta$ and $\beta$ on alternatives

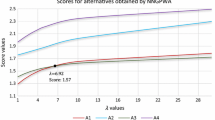
To study the impact of the parameters $\lambda$, $\delta$ and $\beta$ on to the ranks of the alternatives, an investigation has been done, in which the attitudinal characteristic of the decision-maker towards the alternative is varied, by using the proposed approach. The effects of these parametric values are summarized in Table 11 and the following observations have been noticed out:

• (1) By incorporating the feature of the probabilistic information along with the weight information during the analysis, the factor $\beta$ is varied from 0 to 1 and hence their corresponding impact on the final ranking of the alternatives have been analyzed for different pairs of the parameters $(\lambda ,\delta )$. For instance, if this pair is taken to be as $(\lambda ,\delta )=(1,1)$, then we see that overall evaluation value of each alternative, in terms of their score values, decreases with the increase of $\beta$. Similar observations have been noticed from the other pairs also.

• (2) Also, with a specific end objective to see the impact of parameters $\lambda$ and $\delta$ on to the individual alternatives as well as complete ranking of the alternatives, we have seen from this table that for a fix $\beta$, say 0.4, the overall value of each choice is to increase with the increase of $\lambda$ and $\delta$ simultaneously. On the other hand, if we fix $\lambda$ and $\beta$ say to 1 and 0.4 respectively, then by varying the value of $\delta$ from 1 to 2 and further to 3, we conclude that relative value of each alternative increases. For instance for alternative ${\mathcal {V}}_1$, its relative value is increases from $-0.2207$ to $-0.2017$ and further to $-0.1840$. Thus, different choices of the parameters will give the decision-maker more opportunities regarding the selection process and hence gives more valuable and reliable results during uncertainty.

Table 11 Ranking of alternatives for different values of parameters

6 Conclusion

The key contribution of the work can be summarized below.

• (1) The examined study employs the three independent degrees namely membership degree, non-membership degree and degree of indeterminacy to check the vagueness in the data.

• (2) To aggregate the different collection of SVNNs and INNs, we proposed some series of probabilistic and immediate probabilistic averaging and geometric operators and investigated their properties. The advantage of such operators is that they give the total perspective of indeterminate decision issues by thinking about the probabilistic data and the attitudinal character of the decision-makers’ choice. Also, from these stated operators, it can be concluded that by assigning the specific value to the factor $\beta$, several existing operators [18, 20, 21, 23, 26] under the SVNS and INS can be deduced.

• (3) In the stated operators, the importance of each number has complied with the probability and the attribute weights. The advantage of the developed operators is that it simultaneously combines the behavior of the decision-makers, objectively (in terms of probability) and subjectively (in terms of weights vector), into the one process.

• (4) The proposed aggregation operators have been extended to its more generalized form by adding the parameters $\lambda$, $\delta$ and $\beta$ into the analysis. By assigning the specific values to these parameters, we get a wide range of the generalized operators for the SVNS information.

• (5) Two new MADM algorithms, under SVNS and INS, based on the stated operators are explained, which is more generalized and flexible with the parameter $\lambda$, $\delta$ and $\beta$ to the decision-maker. The significance of these parameters is shown in detail (Table 11). Also, the presented method is based on the parameters which will make a decision maker flexible to choose their alternatives based on their preferences or goals.

• (6) To demonstrate the performance of the stated algorithms, a numerical example is given and compare their results with the existing studies [18, 20, 21, 23, 26]. It is concluded from this study that the proposed work gives more reasonable ways to handle the fuzzy information to solve the practical problems.

In the future, we shall lengthen the application of the proposed measures to the diverse fuzzy environment as well as different fields of application such as supply chain management, emerging decision problems, brain hemorrhage, risk evaluation, etc [43,44,45,46,47].