Certain types of irregular m-polar fuzzy graphs

Abstract

The notion of an m-polar fuzzy set is a generalization of a bipolar fuzzy set. We apply the concept of m-polar fuzzy sets to graphs. We introduce certain types of irregular m-polar fuzzy graphs and investigate some of their properties. We describe the concepts of types of irregular m-polar fuzzy graphs with several examples. We also present applications of m-polar fuzzy graphs in decision making and social network as examples.

1 Introduction

In 1965, Zadeh [14] introduced the concept of a fuzzy subset of a set. Since then, the fuzzy set theory has become a robust branch of research in different fields including graph theory, decision making, social science, medical field, management, artificial intelligence, engineering. In 1994, Zhang [16] proposed the concept of bipolar fuzzy sets as a generalization of fuzzy sets. The range of the membership degree of a bipolar fuzzy set is [$-$1,1]. In 2014, Chen et al. [7] proposed the concept of m-polar fuzzy set as a generalization of bipolar fuzzy set. He showed that bipolar fuzzy sets and 2-polar fuzzy sets are cryptomorphic mathematical notions and that we can obtain concisely one from the corresponding one [7]. The idea behind this is that “multipolar information” (not just bipolar information which correspond to two-valued logic) exists because the data for the real world problems is sometimes taken from n agents $(n \ge 2)$. For example, the exact degree of telecommunication safety of mankind is a point in $[0,1]^n$ $(n = 7 \times 10^9)$ because different persons have been monitored different times. There are many other examples such as truth degrees of a logic formula which are based on n logic implication operators $(n \ge 2)$, similarity degrees of two logic formulas which are based on n logic implication operators $(n \ge 2)$, ordering results of a magazine, ordering results of a university, and inclusion degrees (accuracy measures, rough measures, approximation qualities, fuzziness measures, decision preformation evaluations) of a rough set.

In 1973, Kaufmann [8] gave the basic concept of fuzzy graphs. In 1975, Rosenfeld [11] discussed the concept of fuzzy graphs. Rosenfeld [11] also considered the fuzzy relations between fuzzy sets and he obtained some results on fuzzy graphs. Bhattacharya [6] gave some remarks on fuzzy graphs. Mordeson and Nair [9] studied several concepts of fuzzy graphs. Nagoorgani and Latha [10] discussed irregular fuzzy graphs. Akram et al. [1–5] introduced many new concepts, including bipolar fuzzy graphs, irregular bipolar fuzzy graphs, bipolar fuzzy digraphs in decision support system, m-polar fuzzy graphs and m-polar fuzzy line graphs, certain metrices in m-polar fuzzy graphs. In this paper, we introduce certain types of irregular m-polar fuzzy graphs and investigate some of their properties. We describe the concepts of types of irregular m-polar fuzzy graphs with several examples. We also present applications of m-polar fuzzy graphs in decision making and social network as examples. We have used standard definitions and terminologies in this paper. For other notations, terminologies and applications not mentioned in the paper, the readers are referred to [9, 12, 13, 15, 17].

2 Preliminaries

We review some known definitions that are necessary for the work presented in this paper.

Definition 2.1

[11] By a fuzzy graph of a graph $G^* = (V,E)$, we mean a pair $G = (\mu ,\nu )$, where $\mu$ is a fuzzy set on V and $\nu$ is a fuzzy set on E such that

$$\begin{aligned} \nu (xy) \le \min \{\mu (x), \mu (y)\} \end{aligned}$$

for all $xy\in E$. Note that $\nu (xy) = 0$ for all $xy\in V \times V-E$.

Definition 2.2

[16] Let X be a nonempty set. A bipolar fuzzy set B in X is an object having the form $B = \{(x,\mu _{B}^{P}(x),\mu _{B}^{N}(x))|x\in X\}$, where $\mu _{B}^{P}:X \rightarrow [0,1]$ and $\mu _{B}^{N}:X \rightarrow [-1,0]$ are mappings. We use the positive membership degree $\mu _{B}^{P}(x)$ to denote the satisfaction degree of an element x to the property corresponding to a bipolar fuzzy set B, and the negative membership degree $\mu _{B}^{N}(x))$ to denote the satisfaction degree of an element x to some implicit counter-property corresponding to a bipolar fuzzy set B.

Definition 2.3

[16] Let X be a nonempty set. Then a mapping $A = (\mu _{A}^{P},\mu _{A}^{N}): X \times X \rightarrow [0,1] \times [-1,0]$ is called a bipolar fuzzy relation on X such that $\mu _{A}^{P}(x,y)\in [0,1]$ and $\mu _{A}^{N}(x,y)\in [-1,0]$.

Definition 2.4

[1] A bipolar fuzzy graph of a graph $G^* = (V,E)$ is a pair $G = (A,B)$, where $A = (\mu _{A}^{P},\mu _{A}^{N})$ is a bipolar fuzzy set on V and $B = (\mu _{B}^{P},\mu _{B}^{N})$ is a bipolar fuzzy relation on V such that

$$\begin{aligned} \mu _{B}^{P}(xy) \le \min \{\mu _{A}^{P}(x), \mu _{A}^{P}(y)\}\hbox { and } \mu _{B}^{N}(xy) \ge \max \{\mu _{A}^{N}(x), \mu _{A}^{N}(y)\} \end{aligned}$$

for all $xy\in E$. Note that $0<\mu _{B}^{P}(xy)\le 1, -1\le \mu _{B}^{N}(xy)<0$ and $\mu _{B}^{P}(xy) = 0$, $\mu _{B}^{N}(xy) = 0$ for all $xy\in V \times V-E$.

Definition 2.5

[7] An m -polar fuzzy set (or a ${[0,1]}^m$ -set) on X is a mapping $A: X \rightarrow {[0,1]}^m$. The set of all m-polar fuzzy sets on X is denoted by m(X). Note that $\mathbf{0} = (0,0,\ldots ,0)$ is the smallest element in ${[0,1]}^m$ and $\mathbf{1} = (1,1,\ldots ,1)$ is the largest element in ${[0,1]}^m$.

3 Certain types of irregular m-polar fuzzy graphs

An m-polar fuzzy relation is a generalization of a bipolar fuzzy relation. Akram and Neha [4] defined it as follow:

Definition 3.1

Let C be an m-polar fuzzy subset of a non-empty set V. An m-polar fuzzy relation on C is an m-polar fuzzy subset D of $V\times V$ defined by the mapping $D: V\times V\rightarrow [0,1]^m$ such that for all $x,y \in V$, $p_{i}\circ D(xy)\le \inf \{p_{i}\circ C(x),p_{i}\circ C(y)\}$, $i=1,2,3,\ldots ,m$, where $p_i\circ C(x)$ denotes the ith degree of membership of the vertex x and $p_i\circ D(xy)$ denotes the ith degree of membership of the edge xy.

Chen et al. [7] defined the concept of an m-polar fuzzy graph as follow.

Definition 3.2

An m-polar fuzzy graph of a graph $G^*$ = (V,E) is a pair G = (C,D),

where $C: V \rightarrow {[0,1]}^m$ is an m-polar fuzzy set in V and $D: E \rightarrow {[0,1]}^m$ is an m-polar fuzzy relation on V such that

$$\begin{aligned} p_{i} \circ D(xy) \le \inf \{p_{i} \circ C(x),p_{i} \circ C(y)\}, \end{aligned}$$

for all $x,y \in V$.

We note that $p_{i} \circ D(xy) = 0$ for all $xy\in V \times V-E$ for all $i = 1,2,3,\ldots ,m$. C is called the m-polar fuzzy vertex set of G and D is called the m -polar fuzzy edge set of G, respectively. An m-polar fuzzy relation D on X is called symmetric if  $p_{i} \circ D(xy) = p_{i} \circ D(yx)$ for all $x,y\in V$.

Example 3.3

Consider a crisp graph $G^{*}=(V,E)$ such that $V = \{c_{1},c_{2},c_{3},c_{4}\}$ and $E = \{c_{1}c_{2},c_{2}c_{3},c_{3}c_{4},c_{4}c_{1},c_{3}c_{1}\}$. Let C and D be 3-polar fuzzy sets on V and E, respectively, defined by

$$\begin{aligned} \begin{array}{|c|cccc|} \hline &{} c_{1} &{} c_{2} &{} c_{3} &{} c_{4} \\ \hline p_{1} \circ C &{} 0.3 &{} 0.5 &{} 0.2 &{} 0.3 \\ p_{2} \circ C &{} 0.4 &{} 0.3 &{} 0.6 &{} 0.5 \\ p_{3} \circ C &{} 0.5 &{} 0.6 &{} 0.7 &{} 0.8 \\ \hline \end{array} \qquad \qquad \qquad \quad \begin{array}{|c|ccccc|} \hline &{} c_{1}c_{2} &{} c_{2}c_{3} &{} c_{3}c_{4} &{} c_{4}c_{1} &{} c_{3}c_{1} \\ \hline p_{1} \circ D &{} 0.3 &{} 0.2 &{} 0.1 &{} 0.2 &{} 0.1 \\ p_{2} \circ D &{} 0.2 &{} 0.3 &{} 0.3 &{} 0.3 &{} 0.4 \\ p_{3} \circ D &{} 0.4 &{} 0.5 &{} 0.4 &{} 0.4 &{} 0.3 \\ \hline \end{array} \end{aligned}$$

Fig. 1

3-Polar fuzzy undirected graph

By direct calculations, it is easy to see from Fig. 1 that G is a 3-polar fuzzy graph.

Definition 3.4

An m polar fuzzy path P is a sequence of distinct vertices $u=v_1,v_2,\ldots ,v_n=v$ such that for all j there exists at least one i, $p_i\circ B(v_jv_{j+1})>0$. An m-polar fuzzy path is called an m-polar fuzzy cycle if $u=v$. An m-polar fuzzy graph $G = (A,B)$ is said to be connected, if there is a path between each pair of distinct vertices.

Definition 3.5

Let $G = (C,D)$ be an m-polar fuzzy graph of a graph $G^* = (V,E)$. Then we define the neighbourhood of a vertex x in graph G as

$$\begin{aligned} N(x)= \{ y\in V : p_{i} \circ D(xy)\le \inf (p_{i} \circ C(x), p_{i} \circ C(y)) \}, \end{aligned}$$

where $i=1,2,3,\ldots ,m$.

Definition 3.6

Let $G = (C,D)$ be an m-polar fuzzy graph of a graph $G^* = (V,E)$. Then we define the neighbourhood degree of a vertex x in graph G as

$$\begin{aligned} d_{G}(x)= & {} \Sigma _{y\in N(x)}p_{i} \circ C(y)\\= & {} (\Sigma _{y\in N(x)}p_{1} \circ C(y), \Sigma _{y\in N(x)}p_{2} \circ C(y), \Sigma _{y\in N(x)}p_{3} \circ C(y),\\&\ldots , \Sigma _{y\in N(x)}p_{m} \circ C(y)), \end{aligned}$$

$i = 1,2,3,\ldots ,m$.

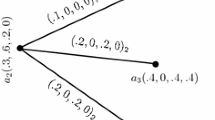
Example 3.7

Consider a 3-polar fuzzy graph $G = (C,D)$ of a crisp graph $G^* = (V,E)$, where $V = \{c_{1},c_{2},c_{3}\}$, $E = \{c_{1}c_{2},c_{2}c_{3},c_{3}c_{1}\}$.

Fig. 2

3-Polar fuzzy graph

By direct calculations, we have neighbourhood degree of each vertex from Fig. 2:

$$\begin{aligned} d_{G}(c_{1})= & {} (0.1 + 0.2,0.4 + 0.5,0.3 + 0.1) = (0.3,0.9,0.4),\\ d_{G}(c_{2})= & {} (0.2 + 0.2,0.4 +0.3,0.4 + 0.1) = (0.4,0.7,0.5),\\ d_{G}(c_{3})= & {} (0.1 + 0.2,0.3 + 0.5,0.3 + 0.4) = (0.3,0.8,0.7). \end{aligned}$$

Definition 3.8

Let $G = (C,D)$ be an m-polar fuzzy graph of a graph $G^* = (V,E)$. Then the graph G is called an irregular m-polar fuzzy graph if there exist a vertex whose adjacent vertices have distinct neighbourhood degrees. That is, $d_{G}(x) \ne n$ for all $x \in V$.

Example 3.9

Consider a 4-polar fuzzy graph G of a crisp graph $G^*=(V, E)$, where $V = \{c_{1},c_{2},c_{3},c_{4}\}$ and $E = \{c_{1}c_{2},c_{2}c_{3},c_{3}c_{4},c_{4}c_{1}\}$.

By direct calculations, we have

$$\begin{aligned} d_{G}(c_{1})= & {} (0.3 + 0.2,0.4 + 0.1,0.7 + 0.3,0.5 + 0.6) = (0.5,0.5,1.0,1.1),\\ d_{G}(c_{2})= & {} (0.3 + 0.2,0.6 + 0.7,0.1 + 0.4,0.3 + 0.2) = (0.5,1.3,0.5,0.5),\\ d_{G}(c_{3})= & {} (0.3 + 0.2,0.4 + 0.1,0.7 + 0.3,0.5 + 0.6) = (0.5,0.5,1.0,1.1),\\ d_{G}(c_{4})= & {} (0.3 + 0.2,0.6 + 0.7,0.1 + 0.4,0.3 + 0.2) = (0.5,1.3,0.5,0.5).\\ \end{aligned}$$

It is easy to see from Fig. 3 that G is an irregular 4-polar fuzzy graph.

Fig. 3

Irregular 4-Polar fuzzy graph

Definition 3.10

Let $G = (C,D)$ be an m-polar fuzzy graph of a graph $G^* = (V,E)$. Then we define the closed neighbourhood degree of a vertex x in graph G as

$$\begin{aligned} d_{G}[x]= & {} \Sigma _{y\in N(x)}p_{i} \circ C(y) + (p_{1} \circ C(x),p_{2} \circ C(x),p_{3} \circ C(x),\ldots ,p_{m} \circ C(x))\\= & {} d_{G}(x)+ (p_{1} \circ C(x),p_{2} \circ C(x),p_{3} \circ C(x),\ldots ,p_{m} \circ C(x)), \end{aligned}$$

$i = 1,2,3,\ldots ,m$.

Example 3.11

Consider a 3-polar fuzzy graph $G=(C, D)$ such that C and D are defined on $V = \{c_{1},c_{2},c_{3}\}$ and $E = \{c_{1}c_{2},c_{2}c_{3},c_{3}c_{1}\}$ by the following tables (Fig. 4).

$$\begin{aligned} \begin{array}{|c|cccc|} \hline &{} c_{1} &{} c_{2} &{} c_{3} &{} c_{4} \\ \hline p_{1} \circ C &{} 0.2 &{} 0.5 &{} 0.1 &{} 0.3 \\ p_{2} \circ C &{} 0.5 &{} 0.3 &{} 0.4 &{} 0.5 \\ p_{3} \circ C &{} 0.1 &{} 0.4 &{} 0.6 &{} 0.2 \\ \hline \end{array} \qquad \qquad \qquad \qquad \begin{array}{|c|cccc|} \hline &{} c_{1}c_{2} &{} c_{1}c_{3} &{} c_{3}c_{4} &{} c_{4}c_{1} \\ \hline p_{1} \circ D &{} 0.1 &{} 0.1 &{} 0.1 &{} 0.2 \\ p_{2} \circ D &{} 0.2 &{} 0.3 &{} 0.3 &{} 0.4 \\ p_{3} \circ D &{} 0.1 &{} 0.1 &{} 0.2 &{} 0.1 \\ \hline \end{array} \end{aligned}$$

Fig. 4

3-Polar fuzzy graph

By direct calculations, we see that:

$$\begin{aligned} d_{G}[c_{1}]= & {} (0.2 + 0.5 + 0.1 + 0.3,0.5 + 0.3 + 0.4 +0.5,0.1 + 0.4 + 0.6 + 0.2) \\= & {} (1.1,1.7,1.3),\\ d_{G}[c_{2}]= & {} (0.5 + 0.2,0.3 + 0.5,0.4 + 0.1) = (0.7,0.8,0.5),\\ d_{G}[c_{3}]= & {} (0.3 + 0.2 + 0.1,0.5 + 0.4 + 0.5,0.6 + 0.1 + 0.2) = (0.6,1.4,0.9),\\ d_{G}[c_{4}]= & {} (0.3 + 0.2 + 0.1,0.5 + 0.4 + 0.5,0.6 + 0.1 + 0.2) = (0.6,1.4,0.9). \end{aligned}$$

Definition 3.12

Let $G = (C,D)$ be an m-polar fuzzy graph of a graph $G^* = (V,E)$. The graph G is called a totally irregular m-polar fuzzy graph if there exist a vertex whose adjacent vertices have distinct closed neighbourhood degrees.

Example 3.13

Consider a 4-polar fuzzy graph G as shown in Fig. 5.

Fig. 5

Totally irregular 4-Polar fuzzy graph

By routine computations, we have

$$\begin{aligned} d_{G}[c_{1}]= & {} (0.7,1.1,1.4,1.4),\\ d_{G}[c_{2}]= & {} (0.8,1.7,1.2,1.0),\\ d_{G}[c_{3}]= & {} (0.8,1.2,1.1,1.3),\\ d_{G}[c_{4}]= & {} (0.7,1.4,0.8,1.1). \end{aligned}$$

It can be easily seen from Fig. 5 that G is a totally irregular 4-polar fuzzy graph.

Definition 3.14

Let $G = (C,D)$ be a connected m-polar fuzzy graph. Then G is called a neighbourly irregular m-polar fuzzy graph if every two adjacent vertices of G have distinct open neighbouhood degrees.

Example 3.15

Consider a 3-polar fuzzy graph G as shown in Fig. 6.

Fig. 6

Neighbourly irregular 3-Polar fuzzy graph

Then,

$$\begin{aligned} d_{G}(c_{1})= & {} (1.2,1.7,0.9),\\ d_{G}(c_{2})= & {} (1.1,1.6,1.2),\\ d_{G}(c_{3})= & {} (0.9,1.9,1.0),\\ d_{G}(c_{4})= & {} (1.2,1.8,1.2),\\ d_{G}(c_{5})= & {} (0.4,0.6,0.5). \end{aligned}$$

It is clear from calculations of Fig. 6 that G is a neighbourly irregular 3-polar fuzzy graph.

Definition 3.16

Let $G = (C,D)$ be a connected m-polar fuzzy graph.Then G is called a neighbourly totally irregular m-polar fuzzy graph if every two adjacent vertices of G have distinct closed neighbouhood degrees.

Example 3.17

Consider a 3-polar fuzzy graph G as shown in Fig. 7.

Fig. 7

Neighbourly totally irregular 3-Polar fuzzy graph

By routine calculations, we have

$$\begin{aligned} d_{G}[c_{1}]= & {} (1.3,2.0,0.6),\\ d_{G}[c_{2}]= & {} (1.0,1.9,0.9),\\ d_{G}[c_{3}]= & {} (1.6,2.0,0.6),\\ d_{G}[c_{4}]= & {} (1.0,1.9,0.9). \end{aligned}$$

It can be easily seen from Fig. 7 that G is neighbourly totally irregular 3-polar fuzzy graph.

Definition 3.18

A connected m-polar fuzzy graph $G = (C,D)$ is called a highly irregular m-polar fuzzy graph if every vertex of graph G is adjacent to vertices with distinct neighbourhood degrees.

Example 3.19

Consider a 3-polar fuzzy graph G as shown in Fig. 8.

Fig. 8

Highly irregular 3-Polar fuzzy graph

By routine calculations, we have

$$\begin{aligned} d_{G}(c_{1})= & {} (0.7,0.9,1.4),\\ d_{G}(c_{2})= & {} (1.1,1.3,1.3),\\ d_{G}(c_{3})= & {} (0.4,0.8,1.0),\\ d_{G}(c_{4})= & {} (0.7,0.9,1.4),\\ d_{G}(c_{5})= & {} (0.2,0.3,0.6). \end{aligned}$$

It is easy to see from Fig. 8 that G is highly irregular 3-polar fuzzy graph.

Remark 1

A highly irregular m-polar fuzzy graph may not be a neighbourly irregular m-polar fuzzy graph.

There is no relation between highly irregular m-polar fuzzy graphs and neighbourly irregular m-polar fuzzy graphs. We explain this concept with the following examples.

Example 3.20

Consider a 4-polar fuzzy graph G as shown in Fig. 9.

Fig. 9

Not neighbourly irregular 4-Polar fuzzy graph

By routine computations, we have

$$\begin{aligned} d_{G}(c_{1})= & {} (1.0,0.7,0.5,1.0),\\ d_{G}(c_{2})= & {} (0.4,0.1,0.2,0.5),\\ d_{G}(c_{3})= & {} (1.4,1.4,0.9,1.3),\\ d_{G}(c_{4})= & {} (0.7,0.5,0.5,1.1),\\ d_{G}(c_{5})= & {} (1.2,1.0,0.9,1.3),\\ d_{G}(c_{6})= & {} (1.2,1.0,0.9,1.3). \end{aligned}$$

We consider a vertex $c_{6}\in V$ whose adjacent vertices are $c_{2},c_{4}$ and $c_{5}$ which have distinct neighbourhood degrees. But $d_{G}(c_{6}) = d_{G}(c_{5})$. So, G is not a neighbourly irregular 4-polar fuzzy graph but it is a highly irregular 4-polar fuzzy graph.

Remark 2

A neighbourly irregular m-polar fuzzy graph may not be a highly irregular m-polar fuzzy graph.

Example 3.21

Consider a 3-polar fuzzy graph G as shown in Fig. 10.

Fig. 10

Not highly irregular 3-Polar fuzzy graph

By calculations, we have

$$\begin{aligned} d_{G}(c_{1})= & {} (0.8,1.1,0.5),\\ d_{G}(c_{2})= & {} (0.7,0.9,0.3),\\ d_{G}(c_{3})= & {} (0.8,1.1,0.5),\\ d_{G}(c_{4})= & {} (0.7,0.9,0.3). \end{aligned}$$

It is clear that every two adjacent vertices of graph G have distinct neighbourhood degrees. But take a vertex $c_{3}$ whose adjacent vertices are $c_{2}$ and $c_{4}$ which have same neighbourhood degrees, that is $d_{G}(c_{2}) = d_{G}(c_{4})$. So, G is not a highly irregular 3-polar fuzzy graph but G is a neighbourly irregular 3-polar fuzzy graph.

Theorem 3.22

Let $G = (C,D)$ be an m-polar fuzzy graph. Then G is highly irregular m-polar fuzzy graph and neighbourly irregular m-polar fuzzy graph if and only if the neighbourhood degrees of all the vertices of G are distinct.

Proof

Let G be an m-polar fuzzy graph with r vertices $c_{1},c_{2},\ldots ,c_{r}$. Suppose that G is highly irregular m-polar fuzzy graph and neighbourly irregular m-polar fuzzy graph.

We claim that the neighbourhood degrees of all the vertices of G are distinct. Let $d_{G}(c_{1}) = (l_{1},l_{2},\ldots ,l_{m})$, $d_{_{G}}(c_{2}) = (t_{1},t_{2},\ldots ,t_{m})$, $d_{G}(c_{3}) = (q_{1},q_{2},\ldots ,q_{m})$,$\ldots$, $d_{G}(c_{r}) = (s_{1},s_{2},\ldots ,s_{m})$. Suppose that the adjacent vertices of $c_{1}$ are $c_{2},c_{3},\ldots ,c_{r}$ with neighbourhood degrees $(t_{1},t_{2},\ldots ,t_{m})$, $(q_{1},q_{2},\cdots ,q_{m})$,$\ldots$, $(s_{1},s_{2},\ldots ,s_{m})$ respectively. Then we have, $t_{1} \ne q_{1} \ne \cdots \ne s_{1}$, $t_{2} \ne q_{2} \ne \cdots \ne s_{2}$,$\ldots$, $t_{m} \ne q_{m} \ne \cdots \ne s_{m}$, since G is highly irregular. Also $l_{1} \ne t_{1} \ne q_{1} \ne \cdots \ne s_{1}$, $l_{2} \ne t_{2} \ne q_{2} \ne \cdots \ne s_{2}$,$\ldots$, $l_{m} \ne t_{m} \ne q_{m} \ne \cdots \ne s_{m}$, since G is neighbourly irregular. Hence, the neighbourhood degrees of all the vertices of G are distinct.

Conversely, suppose that neighbourhood degrees of all the vertices of G are distinct.

We claim that G is highly irregular and neighbourly irregular m-polar fuzzy graph.

Let $d_{G}(c_{1}) = (l_{1},l_{2},\ldots ,l_{m})$, $d_{G}(c_{2}) = (t_{1},t_{2},\ldots ,t_{m})$, $d_{G}(c_{3}) = (q_{1},q_{2},\ldots ,q_{m})$,$\ldots$, $d_{G}(c_{r}) = (s_{1},s_{2},\ldots ,s_{m})$. Then by our supposition $l_{1} \ne t_{1} \ne q_{1} \ne \cdots \ne s_{1}$, $l_{2} \ne t_{2} \ne q_{2} \ne \cdots \ne s_{2}$,$\ldots$, $l_{m} \ne t_{m} \ne q_{m} \ne \cdots \ne s_{m}$, which implies that every two adjacent vertices have distinct neighbourhood degrees and every vertex is adjacent to vertices with distinct neighbourhood degrees. Hence, G is neighbourly irregular m-polar fuzzy graph and also highly irregular m-polar fuzzy graph. $\square$

Proposition 3.23

A neighbourly irregular m-polar fuzzy graph may not be a neighbourly totally irregular m-polar fuzzy graph.

Example 3.24

Consider a 4-polar fuzzy graph G as shown in Fig. 11.

Fig. 11

Simple 4-Polar fuzzy graph

By calculations, we have

$$\begin{aligned} d_{G}(c_{1})= & {} (0.8,1.1,0.5,1.2),\\ d_{G}(c_{2})= & {} (0.7,0.9,0.3,1.3),\\ d_{G}(c_{3})= & {} (0.8,1.1,0.5,1.2),\\ d_{G}(c_{4})= & {} (0.7,0.9,0.3,1.3). \end{aligned}$$

and

$$\begin{aligned} d_{G}[c_{1}]= & {} (1.2,1.6,0.7,1.9),\\ d_{G}[c_{2}]= & {} (1.1,1.4,0.5,2.0),\\ d_{G}[c_{3}]= & {} (1.1,1.5,0.6,1.8),\\ d_{G}[c_{4}]= & {} (1.1,1.5,0.6.1.8). \end{aligned}$$

It is clear that $d_{G}[c_{3}] = d_{G}[c_{4}]$. Hence, G is not a neighbourly totally irregular 4-polar fuzzy graph but a neighbourly irregular 4-polar fuzzy graph.

Remark 3

A neighbourly totally irregular m-polar fuzzy graph may not be a neighbourly irregular m-polar fuzzy graph.

Example 3.25

Consider a 3-polar fuzzy graph G as shown in Fig. 12.

Fig. 12

3-Polar fuzzy graph

By calculations of Fig. 12, we have

$$\begin{aligned} d_{G}[c_{1}]= & {} (0.8,1.8,0.7),\\ d_{G}[c_{2}]= & {} (0.9,1.8,0.6),\\ d_{G}[c_{3}]= & {} (0.7,1.8,0.8),\\ d_{G}[c_{4}]= & {} (0.6,1.8,0.9). \end{aligned}$$

But on the other hand

$$\begin{aligned} d_{G}(c_{1}) = d_{G}(c_{2}) = d_{G}(c_{3}) = d_{G}(c_{4}) \end{aligned}$$

Hence G is not a neighbourly irregular 3-polar fuzzy graph but G is a neighbourly totally irregular 3-polar fuzzy graph.

Proposition 3.26

Let G be an m-polar fuzzy graph. If G is neighbourly irregular m-polar fuzzy graph and $(p_{1} \circ C(x), p_{2} \circ C(x),\ldots , p_{m} \circ C(x)) = (c_{1},c_{2},\ldots ,c_{m})$ is a constant function, then G is a neighbourly totally irregular m-polar fuzzy graph.

Proof

Suppose that G is a neighbourly irregular m-polar fuzzy graph, i.e. every two adjacent vertices have distinct neighbourhood degrees. Let $v_{j}, v_{k}\in V$, where $v_{j}$ and $v_{k}$ are adjacent vertices with distinct neighbourhood degrees, $(l_{1},l_{2},\ldots ,l_{m})$ and $(t_{1},t_{2},\ldots ,t_{m})$ respectively. That is $d_{G}(v_{j}) = (l_{1},l_{2},\ldots ,l_{m})$ and $d_{G}(v_{k}) = (t_{1},t_{2},\ldots ,t_{m})$, where $l_{1} \ne t_{1}, l_{2} \ne t_{2},\ldots , l_{m} \ne t_{m}$.

Let us assume that,

$$\begin{aligned}&(p_{1} \circ C(x)(v_{j}), p_{2} \circ C(x)(v_{j}),\ldots , p_{m} \circ C(x)(v_{j})) = (p_{1} \circ C(x)(v_{k}),\\&\quad p_{2} \circ C(x)(v_{k}),\ldots , p_{m} \circ C(x)(v_{k})) = (c_{1},c_{2},\ldots ,c_{m}), \end{aligned}$$

where $c_{1},c_{2},\ldots ,c_{m}$ are constants and $c_{1},c_{2},\ldots ,c_{m}\in [0,1]$.

Therefore,

$$\begin{aligned} d_{G}[v_{j}]= & {} d_{G}(v_{j}) + (p_{1} \circ C(x)(v_{j}), p_{2} \circ C(x)(v_{j}),\ldots , p_{m} \circ C(x)(v_{j}))\\= & {} (l_{1},l_{2},\ldots ,l_{m}) + (c_{1},c_{2},\ldots ,c_{m})\\ d_{G}[v_{k}]= & {} d_{G}(v_{k}) + (p_{1} \circ C(x)(v_{k}), p_{2} \circ C(x)(v_{k}),\ldots , p_{m} \circ C(x)(v_{k}))\\= & {} (t_{1},t_{2},\ldots ,t_{m}) + (c_{1},c_{2},\ldots ,c_{m}) \end{aligned}$$

We claim that, $d_{G}[v_{j}] \ne d_{G}[v_{k}]$

Suppose on contrary that,  $d_{G}[v_{j}] = d_{G}[v_{k}]$  ,i.e.,

$$\begin{aligned}&(l_{1},l_{2},\ldots ,l_{m}) + (c_{1},c_{2},\ldots ,c_{m}) = (t_{1},t_{2},\ldots ,t_{m}) + (c_{1},c_{2},\ldots ,c_{m})\\&\quad \Rightarrow (l_{1},l_{2},\ldots ,l_{m}) = (t_{1},t_{2},\ldots ,t_{m})\,,\hbox {i.e.}, \end{aligned}$$

$l_{1} = t_{1}, l_{2} = t_{2},\ldots , l_{m} = t_{m}$, which is a contradiction to the fact that $l_{1} \ne t_{1}, l_{2} \ne t_{2},\ldots , l_{m} \ne t_{m}$

Therefore, $d_{G}[v_{j}] \ne d_{G}[v_{k}]$. Hence, G is a neighbourly totally irregular m-polar fuzzy graph. $\square$

Theorem 3.27

Let G be an m-polar fuzzy graph. If G is a neighbourly totally irregular and $(p_{1} \circ C(x), p_{2} \circ C(x),\ldots , p_{m} \circ C(x)) = (c_{1},c_{2},\ldots ,c_{m})$ is a constant function, then G is neighbourly irregular m-polar fuzzy graph.

Proof

Suppose that G is a neighbourly totally irregular m-polar fuzzy graph, i.e, every two adjacent vertices have distinct closed neighbourhood degrees. Let $v_{j},v_{k}\in V$ and $d_{G}[v_{j}] = (l_{1},l_{2},\ldots ,l_{m})$, $d_{G}[v_{k}] = (t_{1},t_{2},\ldots ,t_{m})$, where $l_{1} \ne t_{1}, l_{2} \ne t_{2},\ldots , l_{m} \ne t_{m}$

Assume that,

$$\begin{aligned}&(p_{1} \circ C(x)(v_{j}), p_{2} \circ C(x)(v_{j}),\ldots , p_{m} \circ C(x)(v_{j})) = (p_{1} \circ C(x)(v_{k}), \\&\quad p_{2} \circ C(x)(v_{k}),\ldots , p_{m} \circ C(x)(v_{k}))\\&\quad = (c_{1},c_{2},\ldots ,c_{m}),\\&\hbox {where}\,c_{1},c_{2},\ldots ,c_{m}\hbox { are constants and }c_{1},c_{2},\ldots ,c_{m}\\&\quad \in [0,1]\hbox { and} d_{G}[v_{j}] \ne d_{G}[v_{k}]. \end{aligned}$$

We claim that $d_{G}(v_{j}) \ne d_{G}(v_{k})$

By our supposition,

$$\begin{aligned} d_{G}[v_{j}]\ne & {} d_{G}[v_{k}]\\\Rightarrow & {} (l_{1},l_{2},\ldots ,l_{m}) + (c_{1},c_{2},\ldots ,c_{m}) \ne (t_{1},t_{2},\ldots ,t_{m}) + (c_{1},c_{2},\ldots ,c_{m})\\\Rightarrow & {} l_{1} \ne t_{1}, l_{2} \ne t_{2},\cdots , l_{m} \ne t_{m} \end{aligned}$$

i.e. the neighbourhood degrees of adjacent vertices of G are distinct. Hence, every two adjacent vertices have distinct neighbourhood degrees in G. Hence, G is neighbourly irregular m-polar fuzzy graph. $\square$

Remark 4

If G is neighbourly irregular m-polar fuzzy graph, then m-polar fuzzy subgraph $H=(C^{'},D^{'})$ of G may not be neighbourly irregular m-polar fuzzy graph.

Example 3.28

Consider a 3-polar fuzzy graph G as shown in the following Figure

• (1) For G: by calculations, we have

  $$\begin{aligned} d_{G}(c_{1})= & {} (1.2,0.5,0.5),\\ d_{G}(c_{2})= & {} (1.3,0.4,0.7),\\ d_{G}(c_{3})= & {} (1.8,0.9,0.8),\\ d_{G}(c_{4})= & {} (1.9,0.8,1.0),\\ d_{G}(c_{5})= & {} (1.3,0.6,0.7). \end{aligned}$$

• (2) For H: by calculations, we have

  $$\begin{aligned} d_{G}(c_{3})= & {} (1.2,0.8,0.6),\\ d_{G}(c_{4})= & {} (1.3,0.6,0.7),\\ d_{G}(c_{5})= & {} (1.3,0.6,0.7). \end{aligned}$$

  It is clear that $c_{4}$ and $c_{5}$ are adjacent vertices with same neighbourhood degrees in H. Hence H is not a neighbourly irregular 3-polar fuzzy graph but G is neighbourly irregular 3-polar fuzzy graph.

Remark 5

If G is totally irregular m-polar fuzzy graph, then m-polar fuzzy subgraph

$H=(C^{'},D^{'})$ of G needed not be totally irregular m-polar fuzzy graph.

Example 3.29

Consider a 5-polar fuzzy graph G as shown in the following Figure

• (1) For G: By calculations, we have

  $$\begin{aligned} d_{G}[c_{1}]= & {} (2.0,1.8,1.6,1.6,1.9),\\ d_{G}[c_{2}]= & {} (1.6,1.2,1.3,1.1,1.2),\\ d_{G}[c_{3}]= & {} (2.0,1.8,,1.6,1.6,1.9),\\ d_{G}[c_{4}]= & {} (1.4,1.6,0.9,1.5,1.6). \end{aligned}$$

  Here is a vertex $c_{3}$ which is adjacent to the vertices $c_{1},c_{2}$ and $c_{4}$, where $d_{G}[c_{1}] \ne d_{G}[c_{2}] \ne d_{G}[c_{4}]$.

• (2) For H: By calculations, we have

  $$\begin{aligned} d_{G}[c_{1}]= & {} (1.6,1.2,1.3,1.1,1.2),\\ d_{G}[c_{2}]= & {} (1.6,1.2,1.3,1.1,1.2),\\ d_{G}[c_{3}]= & {} (1.6,1.2,1.3,1.1,1.2). \end{aligned}$$

  Here is a vertex $c_{1}$ whose adjacent vertices are $c_{2}$ and $c_{3}$ with same closed neighbourhood degrees. A vertex $c_{2}$ whose adjacent vertices are $c_{1}$ and $c_{3}$ with same closed neighbourhood degrees and a vertex $c_{3}$ whose adjacent vertices are $c_{1}$ and $c_{2}$ with same closed neighbourhood degrees. Hence, G is totally irregular 5-polar fuzzy graph but H is not a totally irregular 5-polar fuzzy graph.

4 Applications of m-polar fuzzy graphs

4.1 m-Polar fuzzy graphs in decision making

m-polar fuzzy sets play an important role in decision making problems, when it is necessary to gather information. This happens when a group of friends decides which place to visit, when a company decides which product design to manufacture, when a democratic company elects its leader, when a company selects its employe, in cooperative games, in weighted games etc.

We discuss here an example of a company who want to select a manager.

Let $A = \{ \mathrm{Ali, Usman, Umar, Amir, Musa}\}$ be the set of candidates who have applied for the post of manager and $B = \{v_{1},v_{2},v_{3},v_{4},v_{5}\}$ be the set of members of HR department of a company. The members have to decide a candidate on the basis of their qualities that are $\{ \text {intelligence, communication, leadership, adaptability,} \mathrm{relationship building}\}$. For each candidate a member from set B can send a value in [0, 1] to $a\in A$, such as, $C(c_{1}) = (0.2,0.3,0.5,0.1,0.6)$, $C(c_{2}) = (0.8,0.4,0.6,0.5,0.2)$, $C(c_{3}) = (0.3,0.6,0.2,0.4,0.7)$, $C(c_{4}) = (0.2,0.5,0.6,0.5,0.2)$, $C(c_{5}) = (0.5,0.4,0.3,0.2,0.1)$. Then we obtain a 5-polar fuzzy graph, in which each member gives his preference degree to $a\in A$ on the basis of his qualities. So, $C(c_{1}), C(c_{2}), C(c_{3}), C(c_{4})$ and $C(c_{5})$ show the degree of intelligence, communication, leadership, adaptability and relationship building of each candidate given by the set of members of HR department and edges represent the common qualities of two candidates (Fig. 13).

Fig. 13

5-Polar fuzzy graph for decision making

The membership degree of edge $c_{1}c_{2}$ shows that the members $c_{1}$ and $c_{2}$ decide that Ali is 20% eligible, Usman is 30% eligible, Umar is 50% eligible, Amir is 10% eligible and Musa is 20% eligible. So, according to $c_{1}c_{2}$ Umar is an eligible candidate for the post of manager. Similarly, $c_{2}c_{3}$ selects Usman, $c_{3}c_{4}$ selects Usman, $c_{4}c_{5}$ also selects Usman, $c_{5}c_{2}$ selects Ali and $c_{5}c_{1}$ selects Usman. Hence, according to all members Usman has more degree of preference as compared to others.

4.2 m-Polar fuzzy graphs in social network

Graph models find broad applications in many disciplines of mathematics, social sciences, natural sciences and computer sciences. In studies of group behavior, it is inspected that many people can influence thinking of others. A digraph can be used to model such behavior and this graph is called an influence graph.

Definition 4.1

An m-polar fuzzy digraph of a digraph $G^* = (V,E)$ is a pair $G=(C,D)$, where $C: V \rightarrow {[0,1]}^m$ is an m-polar fuzzy set in V and $D: E \rightarrow {[0,1]}^m$ is an m-polar fuzzy relation on V such that $p_{i} \circ D(xy) \le \inf \{p_{i} \circ C(x),p_{i} \circ C(y)\}$ for all $x,y \in V$ and $i = 1,2,3,\cdots ,m$. We note that D need not to be symmetric, i.e. $p_{i} \circ D(xy) \ne p_{i} \circ D(yx)$.

We discuss the influence of a person in a social group on skype.

Let $G = \{\mathrm{Mike, ~Helly, ~David, ~Bisma, ~Ali, ~Umair, ~Zahra}\}$ be the set of seven persons in a social group. The influence degree depends on logical persuading, exchanging, alliance building, legitimizing and appealing to values. Then, we get a 5-polar fuzzy influence graph $D = (G,I)$, in which, vertices representing the persons of a social group and edges representing the influence of a person on other (Fig. 14).

Fig. 14

5-Polar fuzzy digraph

Here, G is the set of vertices defined as

$\{$(Mike,0.5,0.3,0.4,0.2,0.3), (Helly,0.3,0.6,0.5,0.4,0.2), (David,0.2,0.4,0.5,0.3,0.6), (Bisma,0.5,0.2,0.6,0.7,0.4), (Ali,0.4,0.2,0.5,0.6,0.3), (Umair,0.7,0.6,0.8,0.9,0.5), (Zahra,0.6,0.2,0.1,0.3,0.2)}.

I is the set of edges. The membership degree of edges can be calculated as

$$\begin{aligned} p_{i} \circ I(xy) \le \inf \{p_{i} \circ G(x), p_{i} \circ G(y)\} \end{aligned}$$

A graph shows that Umair influence Mike, Helly, Bisma and Zahra. We can see that Umair’s 50 % impact on Mike is due to logical persuading, 30 % is due to exchanging, 40 % is due to alliance building, 20 % is due to legitimizing and 30 % impact is due to appealing to values. Similarly, we can see for Bisma and Zahra. Mike influence Helly, Helly influence David, Bisma influence David and Ali, Ali influence Zahra, Zahra influence Mike. So, observations show that Umair is a most influential person in the group.

5 Conclusion and future work

Fuzzy graph theory is highly utilized in research fields of computer science along with the theory of control, mining of data, expert systems and theory of database. An m-polar fuzzy model is a generalization of the fuzzy model. In this paper, we have discussed certain types of irregular m-polar fuzzy graphs. We have also presented applications of m-polar fuzzy graphs. We are extending our research work to (1) m-polar fuzzy planar graphs, (2) m-polar fuzzy competition graphs, (3) m-polar fuzzy hypergraphs.