1 Introduction

Consider

$$\begin{aligned} \min _{x \in \mathfrak {R}^n} f(x), \end{aligned}$$
(1.1)

where \(f:\mathfrak {R}^n\rightarrow \mathfrak {R}\) is a possibly nonsmooth convex function. The problem (1.1) is equivalent to the following problem

$$\begin{aligned} \min _{x\in \mathfrak {R}^n} F(x), \end{aligned}$$
(1.2)

where \(F:\mathfrak {R}^n\rightarrow \mathfrak {R}\) is the so-called Moreau-Yosida regularization of f and defined by

$$\begin{aligned} F(x)=\min _{z\in \mathfrak {R}^n}\left\{ f(z)+\frac{1}{2\lambda }\Vert z-x\Vert ^2\right\} , \end{aligned}$$
(1.3)

where \(\lambda >0\) is a parameter and \(\Vert \cdot \Vert \) denotes the Euclidean norm. A remarkable feature of problem (1.2) is that the objective function F is a differentiable convex function, even when the function f is nondifferentiable. Furthermore, F has a Lipschitz continuous gradient. But, in general, F is not twice differentiable [23]. However, it is shown that, under some reasonable conditions, the gradient function of F can be proved to be semismooth [9, 32]. Based on these features, many algorithms have been proposed for (1.2) (see [3, 9, 32] etc.). The proximal methods have been proved to be effective in dealing with the difficulty of evaluating the function value of F(x) and its gradient \(\nabla F(x)\) at a given point x (see [5, 7, 19]). Lemaréchal [21] and Wolfe [39] initiated a giant stride forward in nonsmooth optimization by the bundle concept, which can handle convex and nonconvex f. All bundle methods carry two distinctive features: (i) They make use at the iterate \(x_k\) of the bundle of information \((f(x_k),\, g(x_k)),\,\, (f(x_{k-1}),g(x_{k-1})),\ldots \) collected so far to build up a model of f; (ii) If, due to the kinky structure of f, this model is not yet an adequate one, then they mobilize even more subgradient information close to \(x_k\) (or see Lemaréchal [22] and Zowe [48] in detail), where \(x_k\) the kth iteration and \(g(x_k)\in \partial f(x_k)\) (\(\partial f(x)\) is the subdifferential of f at x). Some further results can be found (see [18, 20, 33, 34] etc.). Recently, Yuan et al. [43] gave the conjugate gradient algorithm for large-scale nonsmooth problems and get some good results. In this paper, we will provide a new way to solve (1.2). The idea is motivated by the differentiability of F. We all know that there are many efficient methods for smooth optimization problems, where the nonlinear CG method is one of them. However the CG method for nonsmooth problems has not been studied. Considering the differentiability of F(x) and the same solution set of (1.1) and (1.2), we present a CG method for (1.2) instead of solving f(x).

The nonlinear conjugate gradient method is one of the most effective line search methods for smooth unconstrained optimization problem

$$\begin{aligned} \min _{v\in \mathfrak {R}^n} h(v), \end{aligned}$$
(1.4)

where \(h:\mathfrak {R}^n\rightarrow \mathfrak {R}\) is continuously differentiable. The CG method has simplicity, low storage, practical computation efficiency and nice convergence properties. The PRP (\(\beta ^{\textit{PRP}},\) see [27, 28]) method is one of the most efficient CG methods. It has been further studied by many authors (see [8, 10, 12, 29, 30] etc.). The sufficiently descent condition is often used to analyze the global convergence of the nonlinear conjugate gradient method. Many authors hinted that the sufficiently descent condition may be crucial for conjugate gradient methods [1, 2]. There are many modified nonlinear conjugate gradient formulas which possesses the sufficiently descent property without any line search (see [14, 15, 36, 41, 46] etc.). At present, the CG methods are only used to solve smooth optimization problems. Whether can the CG method be extent to solve nonsmooth problem (1.2)? We answer this question positively. Another effective method for unconstrained optimization (1.4) is quasi-Newton secant methods which obey the recursive formula

$$\begin{aligned} v_{k+1}=v_k-B_k^{-1}\nabla h(v_k), \end{aligned}$$

where \(B_k\) is an approximation Hessian of h at \(v_k\). The sequence of matrix \(\{B_k\}\) satisfies the secant equation

$$\begin{aligned} B_{k+1}S_k=\delta _k, \end{aligned}$$
(1.5)

where \(S_k=v_{k+1}-v_k\) and \(\delta _k=\nabla h(v_{k+1})-\nabla h(v_k).\) Obviously, only two gradients are exploited in the secant equation (1.5), while the function values available are neglected. Hence, techniques using gradients values as well as function values have been studied by several authors. An efficient attempt is due to Zhang et al. [44]. They developed a new secant equation which used both gradient values and function values. This equation is defined by

$$\begin{aligned} B_{k+1}S_k=\delta _k^1, \end{aligned}$$
(1.6)

where \(\delta _k^1=\delta _k+\gamma _k^1S_k\) and \(\gamma _k^1=\frac{3(\nabla h(v_{k+1})+\nabla h(v_k))^TS_k+6(h(v_k)-h(v_{k+1}))}{\Vert S_k\Vert ^2}.\) The new secant equation is superior to the usual one (1.5) in the sense \(\delta _k^1\) better approximates \(\nabla ^2 h(v_{k+1})S_k\) than \(\delta _k\). Consequently, the matrix which is obtained from the modified quasi-Newton update better approximates the Hessian matrix (see [44] in detail). Another significant attempt is due to Wei et al. (see [37]) and the equation is defined by

$$\begin{aligned} B_{k+1}S_k=\delta _k^2, \end{aligned}$$
(1.7)

where \(\delta _k^2=\delta _k+\gamma _k^2S_k\) and \(\gamma _k^2=\frac{(\nabla h(v_{k+1})+\nabla h(v_k))^TS_k+3(h(v_k)-h(v_{k+1}))}{\Vert S_k\Vert ^2}.\) A remarkable property of this secant equation (1.7) is that, if h is twice continuously differentiable and \(B_{k+1}\) is updated by the BFGS method, then the equality

$$\begin{aligned} h(v_k)=h(v_{k+1})+\nabla h(v_{k+1})^TS_k+\frac{1}{2}S_k^TB_{k+1}S_k \end{aligned}$$

holds for all k. Moreover this property is independent of any convexity assumption on the objective function. Furthermore, this equality does not hold for any update formula which is based on the usual secant condition (1.5), even for the new one (1.6). Additionally, comparing with the secant equation (1.6), one concludes that \(\gamma _k^2=\frac{1}{3}\gamma _k^1\). This is a very interesting fact. The superlinear convergence theorem of the corresponding BFGS method was established in [38]. Moreover, the work of [38] was extended to deal with large-scale problems in a limited memory scheme in [40]. The reported numerical results show that this extension is beneficial to the performance of the algorithm. However, the method based on (1.6) does not possess the global convergence and the superlinear convergence for general convex functions. In order to overcome this drawback, Yuan and Wei [42] presented the following secant equation

$$\begin{aligned} B_{k+1}S_k=\delta _k^3, \end{aligned}$$
(1.8)

where \(\delta _k^3=\delta _k+\gamma _k^3S_k\) and \(\gamma _k^3=\max \left\{ 0,\frac{(\nabla h(v_{k+1})+\nabla h(v_k))^TS_k+3(h(v_k)-h(v_{k+1}))}{\Vert S_k\Vert ^2}\right\} .\) Numerical results show that this method is competitive to other quasi-Newton methods (see [42]). Can these modified quasi-Newton methods be used in CG methods and extent to nonsmooth problems? One directive way is to replace the normal \(\delta _k\) by modified \(\delta _k^1\) (\(\delta _k^2\) or \(\delta _k^3\)) in CG formulas. Considering this view, we will present a modified CG method for nonsmooth problem (1.2), where the CG formula possesses not only the gradient values but also the function values.

The line search framework is often used in smooth and nonsmooth fields, where the earliest nonmonotone line search technique was developed by Grippo, Lampariello, and Lucidi in [11] for Newton’s methods. Many subsequent papers have exploited nonmonotone line search techniques of this nature (see [4, 16, 24, 47] etc.). Although these nonmonotone technique work well in many cases, there are some drawbacks. First, a good function value generated in any iteration is essentially discarded due to the max in the nonmonotone line search technique. Second, in some cases, the numerical performance is very dependent of the choice of M (see [11, 35]). In order to overcome these two drawbacks, Zhang and Hager [45] presented a new nonmonotone line search technique. Numerical results show that this technique is better than the normal nonmonotone technique and the monotone technique.

Motivated by the above observations, we will present a modified PRP conjugate gradient method which combines with a nonmonotone line search technique for (1.2). The main characteristics of this method are as follows.

  • A conjugate gradient method is introduced for nonsmooth problem (1.1) and (1.2).

  • All search directions are sufficient descent, which shows that the function values are decreasing.

  • All search directions are in a trust region, which hints that this method has good convergent results.

  • The global convergence is established under suitable conditions.

  • Numerical results show that this method is competitive to other three methods.

This paper is organized as follows. In the next section, we briefly review some known results of convex analysis and nonsmooth analysis. In Sect. 3, we deduce motivation of the search direction and the given algorithm. In Sect. 4, we prove the global convergence of the proposed method. Numerical results are reported in Sect. 5 and one conclusion is given in the last section. Throughout this paper, without specification, \(\Vert \cdot \Vert \) denotes the Euclidean norm of vectors or matrices.

2 Results of convex analysis and nonsmooth analysis

Some basic results in convex analysis and nonsmooth analysis, which will be used later, are reviewed in this section. Let

$$\begin{aligned} \theta (z)=f(z)+\frac{1}{2\lambda }\Vert z-x\Vert ^2 \end{aligned}$$

and denote \(p(x)=\text {argmin} \theta (z),\) where \(\lambda >0\) is a scalar. Then p(x) is well-defined and unique since \(\theta (z)\) is strongly convex. By (1.3), F(x) can be expressed by

$$\begin{aligned} F(x)=f(p(x))+\frac{1}{2\lambda }\Vert p(x)-x\Vert ^2. \end{aligned}$$

In what follows, we denote the gradient of F by g. Some features about F(x) can be seen in [5, 7, 17]. The generalized Jacobian of F(x) and the property of BD-regular can be found in [6, 31] respectively. Some properties are given as follows.

(i) The function F is finite-valued, convex, and everywhere differentiable with

$$\begin{aligned} g(x)=\nabla F(x)=\frac{x-p(x)}{\lambda }. \end{aligned}$$
(2.1)

Moreover, the gradient mapping \(g:\mathfrak {R}^n\rightarrow \mathfrak {R}^n\) is globally Lipschitz continuous with modulus \(\lambda ,\) i.e.,

$$\begin{aligned} \Vert g(x)-g(y)\Vert \le \frac{1}{\lambda }\Vert x-y\Vert ,\,\,\forall \,\,x,y\in \mathfrak {R}^n. \end{aligned}$$
(2.2)

(ii) x is an optimal solution to (1.1) if and only if \(\nabla F(x)=0,\) namely, \(p(x)=x.\)

(iii) By the Rademacher theorem and the Lipschitzian property of \(\nabla F,\) the set of generalized Jacobian matrices (see [17])

$$\begin{aligned} \partial _Bg(x)=\{V\in \mathfrak {R}^{n\times n}:V=\lim _{x_k\rightarrow x}\nabla g(x_k),x_k\in D_g\} \end{aligned}$$

is nonempty and compact for each \(x\in \mathfrak {R}^n,\) where \(D_g=\{x\in \mathfrak {R}^n: \hbox {g is } \hbox {differentiable} \hbox {at x}\}.\) Since g is a gradient mapping of the convex function F,  then every \(V\in \partial _Bg(x)\) is a symmetric positive semidefinite matrix for each \(x\in \mathfrak {R}^n.\)

(iv) If g is BD-regular at x,  namely all matrices \(V\in \partial _Bg(x)\) are nonsingular. Then, for all \(y\in \Omega ,\) there exist constants \(\mu _1>0,\,\mu _2>0\) and a neighborhood \(\Omega \) of x such that

$$\begin{aligned} d^TVd\ge \mu _1\Vert d\Vert ^2,\,\Vert V^{-1}\Vert \le \mu _2,\,\forall \,\,d\in \mathfrak {R}^n,\,V\in \partial _Bg(x). \end{aligned}$$

It is obviously that F(x) and g(x) can be obtained through the optimal solution of \(\text {argmin}_{z\in \mathfrak {R}^n}\theta (z).\) However, p(x),  the minimizer of \(\theta (z),\) is difficult or even impossible to exactly solve. Such makes that we can not apply the exact value of p(x) to define F(x) and g(x). Fortunately, for each \(x\in \mathfrak {R}^n\) and any \(\varepsilon >0,\) there exists a vector \(p^\alpha (x,\varepsilon )\in \mathfrak {R}^n\) such that

$$\begin{aligned} f(p^\alpha (x,\varepsilon ))+\frac{1}{2\lambda }\Vert p^\alpha (x,\varepsilon )-x\Vert ^2\le F(x)+\varepsilon . \end{aligned}$$
(2.3)

Thus, we can use \(p^\alpha (x,\varepsilon )\) to define approximations of F(x) and g(x) by

$$\begin{aligned} F^\alpha (x,\varepsilon )=f(p^\alpha (x,\varepsilon ))+\frac{1}{2\lambda }\Vert p^\alpha (x,\varepsilon )-x\Vert ^2 \end{aligned}$$
(2.4)

and

$$\begin{aligned} g^\alpha (x,\varepsilon )=\frac{x-p^\alpha (x,\varepsilon )}{\lambda }, \end{aligned}$$
(2.5)

respectively. A remarkable feature of \(F^\alpha (x,\varepsilon )\) and \(g^\alpha (x,\varepsilon )\) is given as follows (see [9]).

Proposition 2.1

Let \(p^\alpha (x,\varepsilon )\) be a vector satisfying (2.3), \(F^\alpha (x,\varepsilon )\) and \(g^\alpha (x,\varepsilon )\) are defined by (2.4) and (2.5), respectively. Then we get

$$\begin{aligned}&\displaystyle F(x)\le F^\alpha (x,\varepsilon )\le F(x)+\varepsilon ,\end{aligned}$$
(2.6)
$$\begin{aligned}&\displaystyle \Vert p^\alpha (x,\varepsilon )-p(x)\Vert \le \sqrt{2\lambda \varepsilon }, \end{aligned}$$
(2.7)

and

$$\begin{aligned} \Vert g^\alpha (x,\varepsilon )-g(x)\Vert \le \sqrt{2\varepsilon /\lambda }. \end{aligned}$$
(2.8)

The above proposition says that we can approximately compute \(F^\alpha (x,\varepsilon )\) and \(g^\alpha (x,\varepsilon ).\) By choosing parameter \(\varepsilon \) small enough, \(F^\alpha (x,\varepsilon )\) and \(g^\alpha (x,\varepsilon )\) may be made arbitrarily close to F(x) and g(x),  respectively.

3 Motivation and algorithm

The following iterative formula is often used by CG method for (1.4)

$$\begin{aligned} v_{k+1}=v_k+\alpha _k q_k,\,\,k=1,\,2,\ldots \end{aligned}$$
(3.1)

where \(v_k\) is the current iterate point, \(\alpha _k > 0\) is a steplength, and \(q_k\) is the search direction defined by

$$\begin{aligned} q_{k+1}=\left\{ \begin{array}{ll} -\nabla h_{k+1}+\beta _kq_{k}, &{} \quad \text{ if } k\ge 1\\ -\nabla h_{k+1},&{} \quad \text{ if } \,\,\,\,k=0, \end{array} \right. \end{aligned}$$
(3.2)

where \(\nabla h_{k+1}=\nabla h(v_{k+1})\) and \(\beta _k \in \mathfrak {R}\) is a scalar which determines different conjugate gradient methods. In order to ensure that search direction is sufficiently descent, Zhang et al. [46] presented a modified PRP method with

$$\begin{aligned} q_{k+1}=\left\{ \begin{array}{ll} -\nabla h_{k+1}+\beta _k^{PRP}q_{k}-\vartheta _k\delta _{k}, &{} \quad \text{ if } k\ge 1\\ -\nabla h_{k+1},&{} \quad \text{ if } k=0, \end{array} \right. \end{aligned}$$
(3.3)

where \(\vartheta _k=\frac{\nabla h_{k+1}^Tq_{k}}{\Vert \nabla h_{k}\Vert ^2},\) \(\beta _k^{\textit{PRP}}=\frac{\nabla h_{k+1}^T\delta _k}{\Vert \nabla h_k\Vert ^2},\) and \(\delta _k=\nabla h_{k+1}-\nabla h_{k}.\) It is not difficult to get \(q_k^T\nabla h_k=-\Vert \nabla h_k\Vert ^2.\) This method can be reduced to a standard PRP method if exact line search is used. Its global convergence with Armijo-type line search is obtained, but fails to weak wolfe-Powell line search. Even though this method has descent property, the direction search may not be a descent direction when \(v_k\) is far from the solution. In order to ensure the convergence of the given algorithm, the search direction should belong to a trust region. Motivated by this consideration, the method (3.3), and the observations in Sects. 1 and 2, we propose a modified PRP conjugate gradient formula for (1.2)

$$\begin{aligned} d_{k+1}=\left\{ \begin{array}{ll} -g^\alpha (x_{k+1},\varepsilon _{k+1})+\frac{g^\alpha (x_{k+1},\varepsilon _{k+1})^T y_k^*d_{k}-d_k^Tg^\alpha (x_{k+1},\varepsilon _{k+1})y_k^*}{\max \{2\Vert d_k\Vert \Vert y_k^*\Vert ,\Vert g^\alpha (x_{k},\varepsilon _{k})\Vert ^2\}}, &{} \quad \text{ if } k\ge 1\\ -g^\alpha (x_{k+1},\varepsilon _{k+1}),&{} \quad \text{ if } k=0, \end{array} \right. \end{aligned}$$
(3.4)

where \(y_k^*=y_k+A_ks_k,\,\,y_k=g^\alpha (x_{k+1},\varepsilon _{k+1})-g^\alpha (x_{k},\varepsilon _{k}),\,\,s_k=x_{k+1}-x_k,\) and

$$\begin{aligned}A_k=\max \left\{ 0, \frac{(g^\alpha (x_{k+1},\varepsilon _{k+1})+g^\alpha (x_{k},\varepsilon _{k}))^Ts_k+ 3(F^\alpha (x_{k},\varepsilon _{k})-F^\alpha (x_{k+1},\varepsilon _{k+1}))}{\Vert s_k\Vert ^2}\right\} . \end{aligned}$$

It is easy to see that the given method can be reduced to a standard PRP method if exact line search is used. For all k,  we can easily get \(d_{k+1}^Tg^\alpha (x_{k+1},\varepsilon _{k+1})= -\Vert g^\alpha (x_{k+1},\varepsilon _{k+1})\Vert ^2,\) which means that the proposed direction satisfies the sufficiently descent properties. Many authors hinted that the sufficiently descent condition may be crucial for conjugate gradient methods [1, 2]. This property can ensure that the function values is decreasing. Combining with a nonmonotone line search technique, we list the steps of our algorithm as follows.

Algorithm 3.1

Nonmonotone Conjugate Gradient Algorithm.

Step 0. Initialization. Given \(x_0 \in \mathfrak {R}^n, \,\,E_0\in \mathfrak {R},\) \(\sigma \in (0,1),\,\,s>0,\,\,\lambda >0,\,\rho \in [0,1],\,E_0=1,\,\,J_0=F^\alpha (x_0,\varepsilon _0),\,\,d_0=-g^\alpha (x_0,\varepsilon _0)\) and \(\epsilon \in (0,1).\) Let \(k=0.\)

Step 1. Termination Criterion. Stop if \(x_k\) satisfies termination condition \(\Vert g^\alpha (x_k,\varepsilon _k)\Vert < \epsilon \) of problem (1.2).

Step 2: Choose a scalar \(\varepsilon _{k+1}\) such that \(0<\varepsilon _{k+1}<\varepsilon _{k}\) and compute step size \(\alpha _k\) by the following Armijo-type line search rule

$$\begin{aligned} F^\alpha (x_{k}+\alpha _k d_{k},\varepsilon _{k+1})-J_k\le \sigma \alpha _k g^\alpha (x_{k},\varepsilon _k)^Td_{k}, \end{aligned}$$
(3.5)

where \(\alpha _k=s\times 2^{-i_k},\,\,i_k\in \{0,1,2,\ldots \}.\)

Step 3: Let \(x_{k+1}=x_k+\alpha _kd_k.\) If \(\Vert g^\alpha (x_{k+1},\varepsilon _{k+1})\Vert <\epsilon ,\) then stop.

Step 4: Update \(J_k\) by

$$\begin{aligned} E_{k+1}=\rho E_k+1,\,\,J_{k+1}=\frac{\rho E_kJ_k+F^\alpha (x_{k}+\alpha _k d_{k},\varepsilon _{k+1})}{E_{k+1}}. \end{aligned}$$
(3.6)

Step 5: Calculate the search direction by (3.4).

Step 6: Set \(k:=k+1\) and go to Step 2.

Remark

It is not difficult to see that \(J_{k+1}\) is a convex combination of \(J_k\) and \(F^\alpha (x_{k+1},\varepsilon _{k+1}).\) Since \(J_0=F^\alpha (x_0,\varepsilon _0),\) it follows that \(J_k\) is a convex combination of the function values \(F^\alpha (x_0,\varepsilon _0), F^\alpha (x_1,\varepsilon _1),\,\ldots , F^\alpha (x_k,\varepsilon _k).\) The choice of \(\rho \) controls the degree of nonmonotonicity. If \(\rho =0\), then the line search is the usual monotone Armijo line search. If \(\rho =1\), then \(J_k=C_k,\) where

$$\begin{aligned} C_k=\frac{1}{k+1}\sum _{i=0}^k F^\alpha (x_i,\varepsilon _i) \end{aligned}$$

is the average function value.

4 Properties and global convergence

In the section, we turn to the behavior of Algorithm 3.1 when it is applied to problem (1.1). In order to get the global convergence of Algorithm 3.1, the following assumptions are needed.

Assumption A

(i) The sequence \(\{V_k\}\) is bounded, i.e., there exists a positive constant M such that

$$\begin{aligned} \Vert V_k\Vert \le M,\,\,\forall \,\,k. \end{aligned}$$
(4.1)

(ii) F is bounded from below.

(iii) For sufficiently large \(k,\,\,\varepsilon _k\) converges to zero.

The following lemma shows that the conjugate gradient direction possesses the sufficiently descent property and belongs to a trust region.

Lemma 4.1

For all \(k\ge 0,\) we have

$$\begin{aligned} g^\alpha (x_k,\varepsilon _k)^T d_{k}=-\Vert g^\alpha (x_k,\varepsilon _k)\Vert ^2 \end{aligned}$$
(4.2)

and

$$\begin{aligned} \Vert d_{k}\Vert \le 2\Vert g^\alpha (x_k,\varepsilon _k)\Vert . \end{aligned}$$
(4.3)

Proof

For \(k=0,\) \(d_0=-g^\alpha (x_0,\varepsilon _0),\) we get (4.2) and (4.3). For \(k\ge 1,\) from the definition of \(d_k\), we obtain

$$\begin{aligned}&d_{k+1}^Tg^\alpha (x_{k+1},\varepsilon _{k+1})=-\Vert g^\alpha (x_{k+1},\varepsilon _{k+1})\Vert ^2\nonumber \\&+\left[ \frac{g^\alpha (x_{k+1},\varepsilon _{k+1})^Ty_k^*d_{k}-d_k^Tg^\alpha (x_{k+1},\varepsilon _{k+1})y_k^*}{\max \{2\Vert d_k\Vert \Vert y_k^*\Vert ,\Vert g^\alpha (x_{k},\varepsilon _{k})\Vert ^2\}}\right] ^Tg^\alpha (x_{k+1},\varepsilon _{k+1})\nonumber \\&=-\Vert g^\alpha (x_{k+1},\varepsilon _{k+1})\Vert ^2.\nonumber \end{aligned}$$

Then the relation (4.2) holds. Now we turn to prove that (4.3) holds too. By the definition of \(d_k\) again, we get

$$\begin{aligned} \Vert d_{k+1}\Vert= & {} \Vert -g^\alpha (x_{k+1},\varepsilon _{k+1})+ \frac{g^\alpha (x_{k+1},\varepsilon _{k+1})^Ty_k^*d_{k}-d_k^Tg^\alpha (x_{k+1},\varepsilon _{k+1})y_k^*}{\max \{2\Vert d_k\Vert \Vert y_k^*\Vert ,\Vert g^\alpha (x_{k},\varepsilon _{k})\Vert ^2\}}\Vert \nonumber \\\le & {} \Vert g^\alpha (x_{k+1},\varepsilon _{k+1})\Vert \\&+\frac{\Vert g^\alpha (x_{k+1},\varepsilon _{k+1})\Vert \Vert y_k^*\Vert \Vert d_{k}\Vert +\Vert d_k\Vert \Vert g^\alpha (x_{k+1},\varepsilon _{k+1})\Vert \Vert y_k^*\Vert }{\max \{2\Vert d_k\Vert \Vert y_k^*\Vert ,\Vert g^\alpha (x_{k},\varepsilon _{k})\Vert ^2\}}\nonumber \\\le & {} 2\Vert g^\alpha (x_{k+1},\varepsilon _{k+1})\Vert ,\nonumber \end{aligned}$$

where the last inequality follows

$$\begin{aligned}\max \{2\Vert d_k\Vert \Vert y_k^*\Vert ,\Vert g^\alpha (x_{k},\varepsilon _{k})\Vert ^2\}\ge 2\Vert d_k\Vert \Vert y_k^*\Vert .\end{aligned}$$

Then this completes the proof. \(\square \)

Based on the above lemma, similar to Lemma 1.1 in [45], it is not difficult to get the following lemma. So we only state as follows but omit the proof.

Lemma 4.2

Let Assumption A hold and the sequence \(\{x_k\}\) be generated by Algorithm 3.1. Then for each k, we have \(F^\alpha (x_{k},\varepsilon _k)\le J_k\le C_k.\) Moreover, there exists an \(\alpha _k\) satisfying Armijo conditions of the line search update.

The above lemma shows that Algorithm 3.1 is well-defined.

Lemma 4.3

Let Assumption A hold and the sequence \(\{x_k\}\) be generated by Algorithm 3.1. Suppose that \(\varepsilon _k=o(\alpha _k^2\Vert d_k\Vert ^2)\) holds. Then, for sufficiently large k,  there exists a positive constant \(m_0\) such that

$$\begin{aligned} \alpha _k\ge m_0. \end{aligned}$$
(4.4)

Proof

Let \(\alpha _k\) satisfy the line search (3.5). If \(\alpha _k\ge 1,\) the proof is complete. Otherwise we have \(\alpha _k'=\frac{\alpha _k}{2}\) satisfying

$$\begin{aligned}F^\alpha (x_{k}+\alpha _k' d_{k},\varepsilon _{k+1})-J_k> \sigma \alpha _k'g^\alpha (x_{k},\varepsilon _k)^Td_{k}. \end{aligned}$$

By Lemma 4.2, we have \(F^\alpha (x_{k},\varepsilon _k)\le J_k\le C_k\), then

$$\begin{aligned} F^\alpha (x_{k}+\alpha _k' d_{k},\varepsilon _{k+1})-F^\alpha (x_{k},\varepsilon _{k})\ge F^\alpha (x_{k}+\alpha _k' d_{k},\varepsilon _{k+1})-J_k> \sigma \alpha _k'g^\alpha (x_{k},\varepsilon _k)^Td_{k}\nonumber \\ \end{aligned}$$
(4.5)

holds. Using (4.5), (2.6), and Taylor’s formula, we get

$$\begin{aligned} \sigma \alpha _k'g^\alpha (x_{k},\varepsilon _k)^Td_{k}< & {} F^\alpha (x_{k}+\alpha _k' d_{k},\varepsilon _{k+1})-F^\alpha (x_{k},\varepsilon _k)\nonumber \\\le & {} F(x_{k}+\alpha _k' d_{k})-F(x_{k})+\varepsilon _{k+1}\nonumber \\= & {} \alpha _k' d_{k}^Tg(x_k)+\frac{1}{2}(\alpha _k')^2d_k^TV(\xi _k)d_k+\varepsilon _{k+1}\nonumber \\\le & {} \alpha _k' d_{k}^Tg(x_k)+\frac{M}{2}(\alpha _k')^2\Vert d_k\Vert ^2+\varepsilon _{k+1}, \end{aligned}$$
(4.6)

where \(V(\xi _k)\in \partial _B g(\xi _k),\,\,\xi _k=x_k+\theta \alpha _k' d_{k},\,\,\theta \in (0,1),\) and the last inequality follows (4.1). It follows that from (4.6)

$$\begin{aligned} \alpha _k'> & {} \Biggl [\frac{(g^\alpha (x_{k},\varepsilon _k) -g(x_k))^Td_k-(1-\sigma )g^\alpha (x_{k},\varepsilon _k)^Td_{k} -\varepsilon _{k+1}/(\alpha _k')^2}{\Vert d_k\Vert ^2}\Biggr ]\frac{2}{M}\nonumber \\\ge & {} \Biggl [\frac{(1-\sigma )\Vert g^\alpha (x_{k},\varepsilon _k)\Vert ^2-\sqrt{2\varepsilon _k/\lambda }\Vert d_k\Vert -\varepsilon _k}{\Vert d_k\Vert ^2}\Biggr ] \frac{2}{M}\nonumber \\= & {} \Biggl [\frac{(1-\sigma )\Vert g^\alpha (x_{k},\varepsilon _k)\Vert ^2}{\Vert d_k\Vert ^2}-o(\alpha _k)/\sqrt{\lambda }-o(1)\Biggr ]\frac{2}{M}\nonumber \\\ge & {} \frac{(1-\sigma )}{2M}, \end{aligned}$$
(4.7)

where the second inequality follows (2.8), (4.2), and \(\varepsilon _{k+1}\le \varepsilon _k,\) the equality follows \(\varepsilon _k=o(\alpha _k^2\Vert d_k\Vert ^2),\) and the last inequality follows (4.3). Thus, we have

$$\begin{aligned} \alpha _k\ge \frac{1-\sigma }{M}. \end{aligned}$$

Let \(m_0\in \Big (0,\frac{1-\sigma }{M}\Big ],\) we complete the proof. \(\square \)

Now we prove the global convergence of Algorithm 3.1.

Theorem 4.1

Let the conditions in Lemma 4.3 hold. Then, \(\lim _{k\rightarrow \infty } \Vert g(x_k)\Vert =0\) and any accumulation point of \(x_k\) is an optimal solution of (1.1).

Proof

We first show that

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert g^\alpha (x_k,\varepsilon _k)\Vert =0. \end{aligned}$$
(4.8)

Suppose that (4.8) is not true. Then there exist \(\epsilon _0>0\) and \(k_0>0\) satisfying

$$\begin{aligned} \Vert g^\alpha (x_k,\varepsilon _k)\Vert \ge \epsilon _0,\,\,\forall \,k>k_0. \end{aligned}$$
(4.9)

By (3.5), (4.2), (4.4), and (4.9), we get

$$\begin{aligned}&F^\alpha (x_{k+1},\varepsilon _{k+1})-J_k\le \sigma \alpha _k g^\alpha (x_k,\varepsilon _k)^Td_k\\&\quad =-\sigma \alpha _k\Vert g^\alpha (x_k,\varepsilon _k)\Vert ^2\le -\sigma m_0 \epsilon _0,\,\,\forall \,\,k>k_0. \end{aligned}$$

By the definition of \(J_{k+1},\) we have

$$\begin{aligned} J_{k+1}= & {} \frac{\rho E_kJ_k+F^\alpha (x_{k}+\alpha _k d_{k},\varepsilon _{k+1})}{E_{k+1}}\nonumber \\\le & {} \frac{\rho E_k J_k+J_k -\sigma m_0 \epsilon _0}{E_{k+1}}\nonumber \\= & {} J_k-\frac{\sigma m_0 \epsilon _0}{E_{k+1}}. \end{aligned}$$
(4.10)

Since \(F^\alpha (x,\varepsilon )\) is bounded from below and \(F^\alpha (x_{k},\varepsilon _{k})\le J_k\) holds for all k,  we conclude that \(J_k\) is bounded from below. It follows that from (4.10) that

$$\begin{aligned} \sum _{k=k_0}^{\infty }\frac{\sigma m_0 \epsilon _0}{E_{k+1}}<\infty . \end{aligned}$$
(4.11)

By the definition of \(E_{k+1},\) we get \(E_{k+1}\le k+2,\) then (4.8) holds. By (2.8), we have

$$\begin{aligned} \Vert g^\alpha (x_k,\varepsilon _k)-g(x_k)\Vert \le \sqrt{\frac{2\varepsilon _k}{\lambda }}. \end{aligned}$$

Together with Assumption A(iii), this means that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert g(x_k)\Vert =0 \end{aligned}$$
(4.12)

holds. Let \(x^*\) be an accumulation point of \(\{x_k\},\) without loss of generality, there exists a subsequence \(\{x_k\}_K\) satisfying

$$\begin{aligned} \lim _{k\in K,\,k\rightarrow \infty } x_k=x^*. \end{aligned}$$
(4.13)

From properties of F(x),  we have \(g(x_k)=(x_k-p(x_k))/\lambda .\) Then by (4.12) and (4.13), \(x^*=p(x^*)\) holds. Therefore \(x^*\) is an optimal solution of (1.1). \(\square \)

5 Numerical results

5.1 Small-scale problems

The nonsmooth problems of Table 1 can be found in [26]. Table 1 contains problem dimensions and optimum function values.

The algorithm is implemented by Matlab 7.6, experiments are run on a PC with CPU Intel Pentium Dual E7500 2.93GHz, 2G bytes of SDRAM memory, and Windows XP operating system. The parameters were chosen as \(s=\lambda =1,\,\,\rho =0.5,\,\,\sigma =0.8,\) and \(\varepsilon _k=1/(NI+2)^2\) (NI is the iteration number). For problem \(\min \,\theta (x),\) we use the function fminsearch of Matlab to get the solution p(x). We stopped the iteration when the condition \(\Vert g^\alpha (x,\varepsilon )\Vert \le 10^{-10}\) was satisfied. In order to show the performance of the given algorithm, we also list the results of paper [25] (proximal bundle method, PBL) and the paper [34] (trust region concept, BT). The numerical results of PBL and BT can be found in [25]. The columns of Table 2 have the following meanings:

Problem: the name of the test problem.

NI: the total number of iterations.

NF: the iteration number of the function evaluations.

f(x): the function evaluations at the final iteration.

\(f_{ops}(x)\): the optimization function evaluation.

Table 1 Small-scale nonsmooth problems
Full size table
Table 2 Test results
Full size table

From the numerical results in Table 2, for most of the test problems, it is not difficult to see that Algorithm 3.1 performs best among these three methods. The function value of the PBL and the BT more approximate to the optimization evaluation than Algorithm 3.1 does. Overall we think that the method provide a valid approach for solving nonsmooth problems.

5.2 Large-scale problems

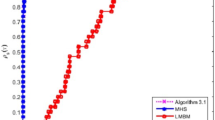
The following problems of Table 3 can be found in [13]. The numbers of variables used were 1000. The values of parameters were similar to the small-scale problems. The following experiments were implemented in Fortran 90. In order to show the performance of the given algorithm, we compared it with the method (LMBM) of paper [13]. The stop rule and parameters are the same as [13].

Table 3 Large-scale nonsmooth problems
Full size table

LMBM [13]. New limited memory bundle method for large-scale nonsmooth optimization. The fortran codes are contributed by Haarala, Miettinen, and Mäkelä, which are available at

http://napsu.karmitsa.fi/lmbm/.

Table 4 Test results
Full size table

For these six large-scale problems, the iteration number of Algorithm 3.1 is competitive to those of the LMBM method. The final gradient value of the LMBM is better than those of the given algorithm. Taking everything together, the preliminary numerical results indicate the proposed method is efficient (Table 4).

6 Conclusion

In this paper, we propose a conjugate gradient method for nonsmooth convex minimization. The global convergence is established under suitable conditions. Numerical results show that this method is interesting. The CG method has simplicity and low memory requirement, the PRP method is one of the most effective CG methods, the nonmonotone line search technique of [45] is competitive to other line search techniques, and the secant equation of [42] possesses better properties for general convex functions. Based on the above four cases, we present a modified PRP CG algorithm with a nonmonotone line search technique for nonsmooth optimization problems. This method has sufficiently descent property and the search direction belongs to a trust region. Moreover this method possesses the gradients information but also the functions information. The main work of this paper is to extend the CG method to solve nonsmooth problems.