Introduction

Water is the most widely distributed substance on earth, about 70% of the surface area is covered by water, and it plays an essential role in the environment and human life, the most important for humans is freshwater, but sustainable water resources available for human use are very limited (Shiklomanov 1991), humans have been consuming freshwater and using it for various purposes, the arbitrary use of freshwater has left most countries in a water scarcity situation (Kummu et al. 2016; Haddout et al. 2020). Moreover, with the growth of population and industrialization, human demand for water resources is increasing in different areas such as drinking water supply, flood control, agricultural irrigation, and industrial production. In addition, global warming, water environment pollution, and improper human use of water resources also pose a threat to water security (He et al. 2018; Ma et al. 2020), leading to the phenomenon of water shortage. China is no exception, as a water-poor country, with a per capita water possession rate of only 1/4 of the world average. In the past decades, as China emerges a major role in various fields and its idea of serving every people, we have vigorously developed the secondary and tertiary industries, focusing on poverty eradication, major science, infrastructure, and other fields, and the speed of industrialization and urbanization keeps accelerating, making China also experience a shortage of water resources, which poses a great threat to most areas of China (Zou and Kang 2022; Zhou et al. 2021). Therefore, the conservation and rational use of water resources is an important issue for human beings, and we need to take active measures to protect them (Li et al. 2021).

Optimal water allocation is an important solution to the reuse, sustainable use, and recycling of water resources, and it plays an important role in achieving a green and sustainable society by allocating water to the major categories of industrial, domestic, agricultural, and ecological water. For the purpose of stable development, many scholars (Singh 2022) have started to use the idea of optimal water allocation for water resources, Zou and Kang (2022) reduced the productivity gap of irrigation water to alleviate water shortage and ensure food security; Zhang and Shen (2019) analyzed the past, present, and future of wastewater in agricultural irrigation, concluding that wastewater irrigation can partially alleviate the water scarcity crisis in some parts of the world and that these activities have a positive impact in facing the problems of water pollution and water scarcity. However, they focus only on the social impacts of water resource allocation (i.e., meeting water demand), with little consideration of the economic and ecological impacts of these activities, let alone the impact of the combined benefits of linking the three aspects to each other. Therefore, this research proposes an integrated approach to water allocation optimization that examines their impacts in terms of social, economic, and ecological aspects (Wu and Wang 2022).

To describe and deal with water resources problems in a more intuitive and visual way, many scholars began to formally devote themselves to the study of water resources allocation, proposing specific model frameworks for water resources problems and exploring optimal solutions through various methods. Maass et al. (1962), based on Maglin’s theoretical analysis, first used a Pareto optimization framework and later proposed an example of the application of simulation techniques in the evaluation of economic indicators for watershed development, which was the beginning of water allocation models.

Since the 1970s, scholars in each era have used different approaches to water allocation because of the complexity of the multi-objective function, multi-variable parameters and multiple constraints of water allocation. In the past, scholars used traditional planning methods or combined them with multiple objectives for planning, such as Stephenson (1969) who incorporated mathematical planning into the allocation of water resources using traffic planning and decomposition principles for water resources allocation, Hagihara et al. (1981) who proposed the maximum principle approach incorporating iterative objective planning as a solution algorithm, Jønch-Clausen (1979) formulated and solved the allocation problem in an input-output framework, using iterative quadratic programming that minimized a concave objective function on a linear constraint set. However, because some mathematical optimization methods are cumbersome and the processing is very complicated and variable, it is definitely not satisfactory in the real application to reality. For example, the result of the solution strongly depends on the initial value; the minimum value, etc., or the inappropriate result that the lower bound is larger than the upper bound; the solution is outside of the feasible region, etc. (Huang and Dan Moore 1993; Chen et al. 2023; Wu et al. 2023; Yao et al. 2024; Wang et al. 2024).

With the development of science and technology, many scholars began to pay attention to intelligent optimization algorithms. Intelligent optimization algorithms are a kind of stochastic search algorithms inspired by human intelligence, the social nature of biological groups, or laws of natural phenomena, which do not rely on precise mathematical models and can handle both continuous and discrete variables. Early proposed algorithms include ant colony algorithm (ACA) (Dorigo et al. 1996), particle swarm optimization (PSO) (Kennedy and Eberhart 1995), genetic algorithm (GA) (Holland 1992), etc., as well as the recent emergence of slime mould algorithm (SMA) (Li et al. 2020), butterfly optimization algorithm (BOA) (Arora and Singh 2019), whale optimization algorithm (WOA) (Mirjalili and Lewis 2016), etc. Because of the advantages of intelligent optimization, they have been widely used in various fields (Ahmadianfar et al. 2017, 2022a, b, c). Tian et al. (2010) used ACA to classify wavelet coefficients in order to determine uniform local neighborhood coefficients and achieved better image denoising results. Samadi-Koucheksaraee et al. (2018) classified reservoirs into single-level and multi-level categories. They employed the gradient evolution algorithm to schedule each type separately, comparing the results with several algorithms. In each case, they achieved favorable outcomes. Alam et al. (2014) applied PSO to data clustering to improve various relevant indicators in the study of clustering analysis. Li et al. (2022) explored a hybrid search strategy of feasible and infeasible solutions using a forbidden search approach, guided by a reinforcement learning mechanism, and reported an improved best solution for a benchmark instance of the boarding gate assignment problem.

Due to the existence of deficiencies in mathematical optimization methods on water resources allocation, scholars in the water resources direction turned their attention to intelligent optimization algorithms, combining them with multiple objectives. At the beginning stage, Yang et al. (2005) used a genetic algorithm improved by node-order encoded to divide the water capacity into smaller parts, allowing successive operations to overlap, and successfully solved two cases of optimal water allocation by applying them in two nonlinear cases. In the development stage, Hou et al. (2014) used the multi-objective function and multiple constraints of the Pareto ACA to seek the optimal spatial results when allocating water resources (such as surface, ground, and transfer water) in the improvement phase, the pheromone range was first restricted and then the pheromone formula was improved so that it could be dynamically updated, so PACA can obtain the optimal results rapidly. At this stage, Lei et al. (2022) combined a neural network model with a wolf pack algorithm for long-term prediction of rainfall near mines, and then applied it to a mine water model to improve the stability of mine water allocation, allowing the water resources to be more inclined to the industrial side and to obtain higher benefits. More scholars have also solved water resources frameworks based on different models using meta-heuristic algorithms such as PSO, SMA, and other distinct algorithms (Rezaei and Safavi 2022; Zhang and Zhang 2020; Sharma et al. 2022; Yue et al. 2022). In addition to the focus on a single algorithm, some scholars have recently turned to integrating the advantages of different algorithms when allocating water resources (Liu et al. 2010; Yao et al. 2023a, b; Sangaiah and Khanduzi 2022), which can search the optimal solution faster and more accurate in part.

The marine predator algorithm (MPA) (Faramarzi et al. 2020) was introduced to optimize the regional water resources. The advantages of MPA are that (a) populations can be recorded through marine memory and updated by comparison at the next iteration; (b) predators and prey are relative, with elite matrices representing top predators, and location updates through the difference in speed between the two, allowing for good exploration and exploitation; (c) for different stages, different proportions of levy flight and Brownian motion are assigned to increase exploration and exploitation and expand the diversity of the population; (d) after each iteration, eddy formation and FADs effects are performed to avoid stagnation in the local optimum. These advantages have led to its use in different fields. Kaur et al. (2022) used MPA to optimize the performance of designed fin-shaped field-effect transistor structures. Houssein et al. (2022) combined reinforcement learning with MPA and applied it to design hybrid renewable energy microgrid systems to reduce energy costs. Hu et al. (2021) performed shape optimization of scalable surfaces by combining quasi-opposition strategies and differential evolutionary algorithms into MPA and get better result.

However, like other intelligent algorithms, MPA may encounter pitfalls such as uneven population distribution, search stagnation, and insufficient exploration of the global space in some iterations. The study uses the improved marine predator algorithm (IMPA), which is based on the original MPA, with chaotic initialization to avoid insufficient population diversity, golden sine algorithm to avoid search stagnation, and quadratic interpolation method to avoid insufficient search capability. IMPA is applied to the optimal allocation of water resources, and a global planning of integrated benefits based on the harmonization of ecological, economic and societal benefits is carried out for Huaying City. The straightforward transformation of multi-objectives into a single objective, whether in terms of effectiveness or reliability, has shortcomings. Therefore, this study adopts a Pareto-based optimization approach. Firstly, the Pareto solution set under the IMPA algorithm is established, analyzing the competitive relationships among the three objective functions. Subsequently, comprehensive comparisons are made among the solution sets of IMPA, MPA, and PSO. Weight proportions are determined through normalization and entropy-weight method, identifying the preferred method. Finally, the superiority and inferiority of scheduling schemes are analyzed from the perspectives of society, economy, and ecology. This provides data references for water resource allocation in the region in recent years.

Second section first introduces the multi-objective model, followed by the research methodology and improvements, and finally, specific plans and measures are proposed for multi-objective planning. In third section, the conditions of the studied area are described and the data used are listed. The experimental results under the IMPA are elaborated in fourth section. Thereafter, fifth section compares the original scheme with the different experimental results under MPA, IMPA, and SMA for a comprehensive analysis and discussion, and proposes suggestions for improving the water allocation in the study area. In sixth section, the process of research is summarized and reflections are offered.

Methodology

Mathematical model

A good planning scheme for water resources has a significant impact on social development (Shirvani-Hosseini et al. 2022), macroeconomic development, and sustainable development, and if the three are planned and handled in a reasonable and synergistic way, a better comprehensive benefit can be achieved. The model has three objectives and four constraints (see in Supplementary Note 1). Table 1 shows the parameters required to deal with the three objectives and the meaning of different variables.

Table 1 Parameters of objective functions
Full size table

Social objective

Nowadays, an important indicator of social development is the degree of urbanization. In the process of urbanization, the number of people in each city is increasing, and the water resources consumption is also increasing. Like civilization, the advancement of cities is also based on a certain amount of water resources. Adequate water resources are the most important natural resource for urban development, and only with water can the economy prosper and people live in peace and prosperity. In the development of cities, the lack of an effective supply of water resources is the most fundamental factor that restricts the development of the city scale.

Therefore, it is more reliable to use water shortage as a measure of the merit of social benefits. The minimum value of water shortage is expressed in Eq. (1), the unit is million \({m^3}\). The smaller the water shortage, the more the water demand of different cities can be ensured and the more the society can develop at a high speed.

$${Min}\; {f_1}(x)=\sum\limits_{{k=1}}^{K} {\sum\limits_{{j=1}}^{{J(K)}} {\left[ {D_{j}^{k} - \sum\limits_{{i=1}}^{{I(k)}} {x_{{ij}}^{k}} } \right]} }$$
(1)

Economic objective

The use of water resources can generate good economic benefits in different fields, such as aquaculture in agricultural production as well as manufacturing and cooling in industrial production, etc., all need water resources for participation, and a good planning arrangement can integrate various industries for maximizing economic benefits.

Therefore, Eq. (2) is used as a function of economic benefits, which indicates the maximum value of economic benefits in yuan after integrated planning. The greater the economic benefit, the faster each sector can also move forward.

$${Max}\; {f_2}(x)=\sum\limits_{{k=1}}^{K} {\sum\limits_{{j=1}}^{{J(k)}} {\sum\limits_{{i=1}}^{{I(k)}} {\left( {b_{{ij}}^{k} - c_{{ij}}^{k}} \right)} } } x_{{ij}}^{k}\alpha _{i}^{k}\beta _{j}^{k}{\omega _k}$$
(2)

\(\alpha _{i}^{k}\) is the order of water supply coefficient, which represents the order of water source i in partition k. The higher the coefficient, the higher the order. It is calculated as shown in Eq. (3).

$$\alpha _{i}^{k}=\frac{{1+I(k) - n_{i}^{k}}}{{\sum\limits_{{i=1}}^{{I(k)}} {\left( {1+I(k) - n_{i}^{k}} \right)} }}$$
(3)

\(n_{i}^{k}\) indicates the order of water supply from water source i to users in different areas k, the range is between 0 and 1, if the number is 1, it means that water source i has the highest priority for water supply.

\(\beta _{j}^{k}\) is the water equity coefficient, representing the degree of demand for water from user j in k subareas. The greater the degree of user demand, the greater the value. Its calculation method is shown in Eq. (4).

$$\beta _{j}^{k}=\frac{{1+J(k) - n_{j}^{k}}}{{\sum\limits_{{j=1}}^{{J(k)}} {\left( {1+J(k) - n_{j}^{k}} \right)} }}$$
(4)

\(n_{j}^{k}\) reflects the order of water use by user j of water source i in different area k. The range is between 0 and 1, if the number is 1, it means that user j has the highest priority for water use.

Ecological objective

With the development of urbanization, industrial wastewater discharge, domestic sewage discharge or agricultural drainage, etc., have caused pollution to water bodies as well as ecology. Ecological benefit precisely means that people’s damage to the natural ecosystem in the production process is reduced to a minimum, and it is related to the sustainable development of society, cities, and civilization.

Therefore, Eq. (5) is used as a function to judge the ecological benefit, which indicates the minimum value of pollutants discharged during the production process in mg. The less the discharge, the better the ecological environment, the more benefits we can achieve in our production and life, and the greater the benefits, the more we can invest in maintaining the ecological environment, and the two form a virtuous and efficient cycle.

$${Min}\; {f_3}(x)=\sum\limits_{{k=1}}^{K} {\sum\limits_{{j=1}}^{{J(K)}} {d_{j}^{k}} } \rho _{j}^{k}\sum\limits_{{i=1}}^{{I(k)}} {x_{{ij}}^{k}}$$
(5)
Fig. 1
figure 1

The whole process of water resource allocation

Full size image

The overall water resource allocation is shown in Fig. 1. The water source satisfies the water demand proposed to the users under each subarea, forming social benefits; the difference between the benefits and costs of water supplied to users in each subarea forms economic benefits; the sewage discharge produced by the users in each subarea, forming ecological benefits.

Improved marine predators algorithm

Improved marine predators algorithm

Although MPA (see in Supplementary Note 2) has numerous merits, it faces challenge such as uneven population distribution, search stagnation, and insufficient exploration. To address these issues for specific problems, this research draws inspiration from various improved ideas and approaches (Fang et al. 2021). Eventually, three different methods for improvement were employed, Table 2 delineates the associated parameters and respective significance.

Table 2 Parameters of IMPA
Full size table
  1. (1)

    Logistic chaos optimization initial population

Logistic chaos optimization is a typical representative of chaotic mapping, which is more widely used due to its simple mathematical form (Aggarwal et al. 2018; Benaissi et al. 2023). After this optimization, the coverage area of the initial solution distribution will be sufficiently broad. During the population update phase, a better initial population will contribute to more efficient subsequent prey and parameter updates. Its mathematical expression is shown in Eq. (6):

$${Y_{n+1}}=a{Y_n}\left( {1{\text{ }} - {\text{ }}{Y_n}} \right)$$
(6)

In Eq. (6), \({Y_n} \in [0,1]\), a is a logistic parameter with values from 0 to 4.

When a is taken to be 4, the area of initial value distribution will be more uniform. Logistic chaos mapping in MPA, it makes the area of an initial solution distribution cover widely enough in the population creation phase; in the population update phase, a better initial population will also make later prey and parameter updates more effective. This means that this application method improves the population search ability of MPA in the initial and process, and lays the foundation for the later iterations.

  1. (2)

    Sine cosine algorithm

The second stage of MPA is exploration and exploitation, but because Brownian motion and Levy motion are random swimming motion, the randomness is relatively large, so this research incorporates the idea of golden sine algorithm (Tanyildizi and Demir 2017) to update the prey’s location information in the second stage. The golden sine algorithm introduces the golden partition coefficients and in the process of position updating, so that the global exploration and local opening can reach a good balance, these coefficients reduce the search space and make the individual converge towards the optimum. The improved discoverer position update formula is Eq. (7).

$$X_{i}^{{t+1}}=X_{i}^{t}\left| {\sin \left( {r_{1}^{\prime }} \right)} \right|{\text{ }} - {\text{ }}r_{2}^{\prime }\sin \left( {r_{1}^{\prime }} \right)\left| {{t_1}D_{i}^{t} - {t_2}X_{i}^{t}} \right|$$
(7)
  1. (3)

    Quadratic interpolation method

In the iterative process, the initial exploration range is relatively large, and finding the optimal predator position is challenging, and the later development range is relatively small, leading to the presence of local optima. To avoid these phenomena as much as possible, so, the quadratic interpolation is utilized for improving the search and development capability, it utilizes curve fitting the shape of a quadratic function to obtain the optimal solution of the curve extreme value point approximation function. The obtained reference value is then compared with the current optimal value for comparison and replacement.

In Eq. (8), \(X=\left( {{x_1},{x_2}, \ldots ,{x_D}} \right),{\text{ }}Y=\left( {{y_1},{y_2}, \ldots ,{y_D}} \right),\) and the current global optimal position is \(Z=\left( {{z_1},{z_2}, \ldots ,{z_D}} \right)\), then the quadratic interpolation method forms a new individual \(\bar {X}=\left( {\overline {{{x_1}}} ,\overline {{{x_2}}} , \ldots ,\overline {{{x_D}}} } \right)\)according to the following formula:

$$\begin{array}{*{20}{l}} {\overline {{{x_q}}} =\frac{{\left( {z_{q}^{2} - y_{q}^{2}} \right) \times F(X)+\left( {x_{q}^{2} - z_{q}^{2}} \right) \times F(Y)+\left( {y_{q}^{2} - x_{q}^{2}} \right) \times F(Z)}}{{2\left[ {\left( {{z_q} - {y_q}} \right) \times F(X)+\left( {{x_q} - {z_q}} \right) \times F(Y)+\left( {{y_q} - {x_q}} \right) \times F(Z)} \right.}}} \end{array}$$
(8)

The fitness of the inserted \(\bar {X}\) is compared with the optimal fitness, and if F\((\bar {X})\) is better than F(Z) after the insertion, the optimal predator position and elite matrix are updated.

The flow chart of IMPA (Fig. 2), and the pseudo code (Algorithm 1), are shown below:

Algorithm 1
figure a

Pseudo-code of the IMPA

Full size image
Fig. 2
figure 2

Flowchart of IMPA

Full size image

Simulation experiment

To show the efficiency of IMPA compared to other algorithms better, it selected nine test functions for a series of performance comparisons. nine functions can be specifically divided into single-peak function (\({F_1}\), \({F_2}\) and \({F_3}\)), multi-peak function (\({F_4}\), \({F_5}\) and \({F_6}\)) and multi-peak function fixed dimension (\({F_7}\), \({F_8}\) and \({F_9}\)) three categories, such classification can be more show IMPA in a variety of types can show good ability. Functions are illustrated in Table 3 and functions images in Fig. S2 (Supplementary Note 3).

Table 3 Benchmark test functions
Full size table

For IMPA, the four most crucial parameters are p, FADs, t1, and t2. Among them, p plays a vital role in position updates. After multiple experiments, it was observed that the optimal performance is achieved when p is in the range of 0.3 to 0.7. Considering the original author’s parameter settings, we set this value to 0.5. The parameter FADs is dependent on the activity patterns of sharks. Following this principle, FADs is set to 0.2. Parameters t1 and t2 are two constants obtained through the golden section ratio calculation formula.

For the algorithms, BOA, seagull optimization algorithm (SOA) (Dhiman and Kumar 2019), WOA, artificial bee colony algorithm (ABC) (Karaboga and Akay 2009), MPA and IMPA are selected for testing, the population of each test function is 50, the number of algorithm iterations are 500, and the number of function runs are 30. The performance of the six algorithms is evaluated by comparing the optimal value, standard deviation and mean value. The parameter settings of the six algorithms are shown in Table 4, the adaptation curves are drawn as shown in Fig. 3, and the related results such as the optimal value, standard deviation and mean value are included in Table 5.

Table 4 Algorithm parameter configuration
Full size table
Fig. 3
figure 3

Summary diagram of simulation curves

Full size image

From the Table 5 analysis, it can be seen that the statistical results of IMPA for nine different test functions under the same test constraints are significantly better than the other five comparison algorithms. For the single-peak test function, only IMPA can find the theoretical optimal value on \({F_1}\) and \({F_2}\) test functions, and the stability and numerical magnitude of IMPA on the mean and standard deviation are better than the other algorithms, and the effect of finding the optimal value is much better than ABC and BOA; on \({F_3}\) test function, although IMPA is slightly inferior to SOA in finding the optimal value, it is much better than other algorithms; for the multi-peak benchmark test functions \({F_4}\), \({F_5}\) and \({F_6}\), MPA and IMPA are basically close to the theoretical optimum, but IMPA performs better in the calculation of the mean and standard deviation, and the two evaluation indexes are superior to other algorithms, and even exceed some algorithms by several orders of magnitude; for the multi-peak fixed dimensional test functions \({F_7}\), \({F_8}\) and \({F_9}\), ABC, MPA and IMPA can reach the theoretical optimal value, and the average value is close, but in terms of standard deviation, IMPA shows its stability better.

The results show that the stability and robustness of IMPA is significantly better than the other algorithms, both for single-peaked and multi-peaked functions, and in the process of finding the optimal value, IMPA finds the theoretical optimal value for all functions except \({F_3}\) in the process of finding the optimal value several times; IMPA also achieves better numerical performance in terms of standard deviation and mean value. In addition, it is also shown that IMPA can explore the search space sufficiently and efficiently compared with MPA, and ensure a strong global search capability and local exploration capability.

Table 5 Simulation results of benchmark test functions
Full size table

Comprehensive benefits

Multi-target process

Since the multi-objective model is more complex to solve and has more constraints, the desired results are not obtained by finding the optimum separately. Therefore, the utilization of the Pareto solution set is employed to address this issue. Initially, a series of non-dominated solution sets are obtained through algorithmic solving. Then, the entropy-weight method is applied to calculate the weight proportions of the generated solution sets. At last, the linear weighting method is employed to select the optimal solution as the allocation scheme for this region. The formula for the linear weighting method is as follows:

$$F(x)=\sum\limits_{{m=1}}^{M} {{\omega _m}} {f_m}(x)$$
(9)

In Eq. (9), F(x) is the comprehensive benefit function, and \({\omega _m}\) is the weight coefficient of the \({m^{th}}\) objective, which \({f_m}(x)\) is the value of the \({m^{th}}\) objective function.

Since the entropy weighting method (Yang et al. 2023) can profoundly reflect the distinguishing ability of indicators, determine better weights, assign more objective weights, have theoretical basis and higher credibility, and the algorithm is simple and practical, it uses the entropy weighting method for the determination of weight coefficients.

First, the values of the three objective functions are obtained separately, but because the units of the three objective function values are different, in order to avoid the influence of the original data dimension when seeking the comprehensive evaluation value, so it is necessary to first dimensionless processing of the three.

For solving the positive indicators, i.e., the larger the better.

$$f_{m}^{\prime }(x)=\frac{{{f_m}(x){\text{ }} - {\text{ }}{f_{m,\hbox{min} }}(x)}}{{{f_{m,\hbox{max} }}(x){\text{ }} - {\text{ }}{f_{m,\hbox{min} }}(x)}}$$
(10)

In Eq. (10), m takes the values of 1, 2, and 3, \({f_{m,\hbox{min} }}(x)\) denoted as the minimum value in the \({m^{th}}\) objective function and \({f_{m,\hbox{max} }}(x)\) denoted as the maximum value in the \({m^{th}}\) objective function.

For solving the negative indicator, i.e., the smaller the better.

$$f_{m}^{\prime }(x)=\frac{{{f_{m,\hbox{max} }}(x){\text{ }} - {\text{ }}{f_m}(x)}}{{{f_{m,\hbox{max} }}(x){\text{ }} - {\text{ }}{f_{m,\hbox{min} }}(x)}}$$
(11)

In Eq. (11), m takes the values of 1, 2, and 3, \({f_{m,\hbox{min} }}(x)\) denoted as the minimum value in the \({m^{th}}\) objective function and \({f_{m,\hbox{max} }}(x)\) denoted as the maximum value in the \({m^{th}}\) objective function.

Next, the ratio of indicator values for the nth evaluated object on the \({m^{th}}\) evaluation indicator is calculated:

$${p_{nm}}=f_{{nm}}^{\prime }(x)/\sum\limits_{{n=1}}^{N} {f_{{nm}}^{\prime }} (x)$$
(12)

In Eq. (12), n = 1, 2, …, N, N is the total number of evaluated objects, m = 1, 2, 3.

After that, the entropy value of the \({m^{th}}\) evaluation index is calculated.

$${e_m}= - \frac{1}{{\ln N}}\sum\limits_{{n=1}}^{N} {{p_{nm}}} \ln \left( {{p_{nm}}} \right)$$
(13)

In Eq. (13), \(0\;\leq e_m\leq1\).

Then, the coefficients of variability of the evaluation indicators were calculated.

$${g_m}=1 - {e_m}$$
(14)

In Eq. (14), The larger the value of \({g_m}\), the more importance should be attached to the role of this indicator in the comprehensive evaluation index system.

Finally, the determination of weighting coefficients is carried out.

$${\omega _m}={g_m}/\sum\limits_{{m=1}}^{M} {{g_m}}$$
(15)

In Eq. (15), \({\omega _m}\) is the final weight coefficient of each indicator, M = 3.

Constraint process

For the constraint treatment of water resources optimal allocation model, the main methods are rejection of infeasible solutions, penalty function method, Lagrange multiplier (LM) method, etc. For the infeasible solution method, it is very difficult to always reject infeasible solutions in the iterative process, especially when the feasible domain is very small, repeated trials will affect the solution speed; for the LM method, when seeking multi-objective solutions, it has a large computational complexity, and the processing problem will be slow. In view of these, this research selects the penalty function method to deal with the constraints.

$$f_{m}^{\prime }(x)={f_m}(x){\text{ }}+{\text{ }}\delta G(x)$$
(16)

In Eq. (16), G(x) is the set of constraints. Due to the possibility of encountering large numerical values like 10e10 in the computation of various benefits, not setting a sufficiently large penalty coefficient could lead to situations where the solution does not satisfy the constraints, yet the objective function remains greater than 0—an abnormal condition that is unacceptable. Therefore, the penalty factor \({\updelta }\) is set to 10e20 in this case.

In the optimization process, if the constraints are not satisfied, the objective function value after penalty will be extremely large, and then through the step-by-step iteration of IMPA, the range slowly approaches the constraints, and the function value slowly becomes smaller and approaches the optimal solution.

Overall process

The overall process is shown in Fig. 4.

Fig. 4
figure 4

Framework for optimal allocation of water resources using IMPA

Full size image
  1. (a)

    Obtain data on water resources in relevant areas and determine parameters such as water supply, water demand and equity coefficient.

  2. (b)

    Combine the relevant data and parameters and calculate the values of social, economic and ecological benefits using Eqs. (1), (2) and (5). Its primary role is to assess the accuracy of parameter inputs, verify the correctness of computational processes, ensure compliance with constraint conditions, and ascertain the orderly progression of objective function optimization during the process.

  3. (c)

    After computing the three types of benefits for each solution, they are incorporated into the Pareto solution set using a grid method. Then, at the end of each iteration, the solution set is updated until the maximum iteration count is reached. Next, the non-dominated solution sets are integrated, and 1000 data points are selected to obtain the weight coefficients based on Eqs. (10)–(15). This enables the three objectives to be compared on the same scale, facilitating the calculation of weights for a comprehensive benefit comparison.

  4. (d)

    Combine the constraints set by Eqs. (S1) - (S4) and add them to the set of constraints in Eq. (16).

  5. (e)

    Solve using the optimized ocean predator algorithm to obtain the optimal integrated benefit values, and output the optimal planning scheme and the corresponding values of the three benefits.

Study area and data

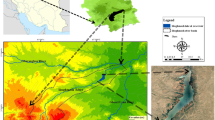
Huaying City (see in Supplementary Note 4), a county-level city under the jurisdiction of Sichuan Province, is administered by Guang’an City. It is located in the eastern part of the Sichuan Basin, between the western edge of the middle part of the Huaying Mountains in the parallel ridge valley of eastern Sichuan and the middle and upper part of the Drainage River, with a length of 40.75 km from north to south and a width of 28 km from east to west, and a total area of 464 \({ km}^{2}\). The geographical coordinates are between 30°07’~30°28’N latitude and 106°40’~106°54’E longitude.

Huaying City has a humid inland subtropical climate with a mild climate, abundant rainfall, four distinct seasons, rain and heat in the same season, dry and wet seasons, not hot in summer, no severe cold in winter, less frost and snow, early spring, but more cold waves and low temperatures, more continuous rain, fast cooling, and four seasons are suitable for farming. There are many rivers in Huaying City, except for the Qu River and small streams, the watershed areas of Huaying River, Qingxi River, Luxi River, Linxi River are larger. In 2021, the gross national product of Huaying City is 18.598 billion yuan, an increase of 7.6%. With the development of industrial and agricultural economy and the improvement of people’s living standards, water consumption is growing year by year, making the phenomenon that supply falls short of demand more pronounced in terms of water resources. And according to the actual conditions, some parameters (see in Supplementary Note 5) of the model can be valued.

Results and discussion

After the model and parameters were determined, the allocation of water resources for 2021 was performed using IMPA. Figure 5 illustrates the generated Pareto solution set and the trends in the curves of the social-economic, economic-ecological, and social-ecological aspects.

Fig. 5
figure 5

Pareto solution set of IMPA based on 2021 data

Full size image

The constraint method for handling the model is the penalty function method, which means that a great penalty factor (taken as 10e20) is added to the original objective function. Because the initial solution settings are random and do not meet the constraints, the function values are large. In the later stages of iteration, the majority of solutions can satisfy the constraint conditions. This demonstrates the beneficial impact of using penalty functions, laying a solid foundation for the formation of optimal solutions.

Among three objectives, the social and ecological objectives take the minimum value as negative indicators, i.e., the smaller the better, the economic objective takes the maximum value as positive indicators, i.e., the larger the better. By observing Fig. 5, we can discern that the curves of social-economic, economic-ecological, and social-ecological aspects depict the competitive relationships among the three. Specifically, an increase in one objective comes at the expense of a decrease in another objective. This situation highlights the necessity and significance of water resource scheduling.

To further analyze the IMPA’s effectiveness and its influence on the whole model, firstly, compare the distribution of objectives in each solution set. Then, contrast each objective’s maximum and minimum values, showcasing the superiority of the Pareto solution set generated by IMPA.

Fig. 6
figure 6

The distribution of objective functions in the solution sets obtained by IMPA, MPA, and PSO

Full size image

Figure 6 illustrates the distribution of objective functions for the solution sets generated by IMPA, MPA, and PSO. In this figure, a larger contour indicates greater concentration of data at that point, while a smaller contour suggests less data at that location. An analysis of the solution set for IMPA reveals that, for social benefits, the maximum value can reach 327.55 million \({m}^{3}\), the minimum can drop to 0.07 million\({m}^{3}\), and it is primarily concentrated around 40 million \({ m}^{3}\). Meanwhile, MPA is concentrated around 330 million \({ m}^{3}\), and PSO is concentrated between 160 and 180 million \({ m}^{3}\). For negative indicators of social benefits, IMPA’s solution set holds a significant advantage. Regarding economic benefits, IMPA exhibits a maximum value of 1193028.92 yuan, a minimum of 1165620.24 yuan, and is mainly concentrated around 1,191,000 yuan. In comparison, MPA is concentrated around 1,150,000 yuan, and PSO is centered around 1,180,000 yuan. For positive indicators of economic benefits, IMPA’s solution set is more stable and prominent than the others. For ecological benefits, IMPA shows a maximum value of 15587.76 mg, a minimum of 14158.47 mg, and is primarily concentrated between 15,000 and 15,500 mg. In contrast, MPA is concentrated around 14,300 mg, and PSO’s concentration is unclear, fluctuating in multiple areas. While IMPA’s solution set may not have a clear advantage in negative indicators of ecological benefits, it has a broader range, providing better selectivity in solution choices. For instance, opting for solutions around 14,200, which are fewer in number, could yield better results compared to MPA and PSO on the other two objectives. In summary, IMPA’s non-dominated solution set has improved compared to the original, demonstrating increased accuracy and reliability. It can effectively address water resource scheduling problems.

In the aforementioned solution sets, each solution within a set represents a non-dominated solution of its scheduling model, serving as a Pareto-optimal solution for the multi-objective scheduling model. To find the scheduling plan with the maximum comprehensive benefits, it is necessary to optimize and compare the scheduling plans within each solution set. The goal is to identify the best scheduling plan among the three. Using the 1000 solutions from each of the three sets as the data basis, the established evaluation index system needs to be uniformly quantified. The entropy weight method (Eqs. (10)–(15)) is employed to optimize the scheduling plans, resulting in recommended plans for IMPA, MPA, and PSO. After computation, the weights corresponding to social benefits, economic benefits, and ecological benefits are found to be 0.236, 0.229, and 0.535, respectively. Table 6 shows the allocation results for the three cases.

Table 6 Result of optimal allocation by different methods (Unit: million \({ m}^{3}\))
Full size table

Table 7 shows the three objective function values obtained from the three different allocation results by Eqs. (1)–(3) in second section.

Table 7 Adaptability values by different optimal allocation
Full size table
Fig. 7
figure 7

Comparison of different methods for optimal allocation

Full size image

Comparing the objective functions of different optimal allocation methods are shown in Fig. 7. In terms of social benefits, Compared to MPA and PSO, where the water shortage is 105.63 million \({ m}^{3}\) and 107.08 million \({ m}^{3}\), respectively, IMPA has achieved almost complete satisfaction of residents’ water needs in this crucial sector. The water shortage for IMPA is only 0.07 million \({ m}^{3}\). In terms of economic benefits, IMPA is significantly better than MPA as well as PSO, where IMPA gains about 5110.23 yuan more than MPA and supply 105.56 million \({ m}^{3}\) more water, gains about 4018.65 yuan more than PSO and supply 106.01 million \({m}^{3}\) more water, which is slightly better than others in these two aspects. In terms of economic benefits, MPA and PSO generate pollution levels that are quite close, measuring 15010.5 and 15000.31 mg, respectively, while IMPA slightly surpasses them with a value of 15587.76 mg. The quantity of water supply determines the quality of people’s lives, and economic benefits affect government revenue. The impacts of these two factors are profound for the entire society. Although the amount of pollutant emissions can influence the ecosystem, the government can take effective measures to address and protect against them. Therefore, in terms of overall benefits, IMPA is the optimal scenario for the three different allocation results.

In summary, the combined results obtained using IMPA outperformed MPA and PSO results in terms of the degree of adaptation, indicating that IMPA can, firstly, effectively give the optimal water allocation solution that meets the constraints in the face of the complex water resources system optimization allocation problem, and secondly, the optimal solution given shows a significant advantage over the results obtained by other algorithms, which has a positive effect on the overall water resources allocation model.

A reasonable allocation of water resources can alleviate the increasing tension between supply and demand and improve the efficiency of limited water resources utilization. The allocation scheme of IMPA alleviates the tension of water resources in Huaying City to a certain extent, provides a valuable reference for the efficient utilization and allocation. In addition, this study has a beneficial influence on promoting Huaying City to continue to maintain the status of national ecological protection and construction demonstration city, national soil and water conservation ecological civilization city.

In light of the present situation in Huaying City, the recommendations are proposed: The government should promote water conservation and reuse technology, and strengthen water resources management and protection. Meanwhile, Individuals should also develop good habits of water conservation to reduce water waste.

Conclusion

The study area is Huaying City, Sichuan Province, and the social, economic and ecological benefits and the coordinated and integrated benefits of the three are used as the model for optimal water resources allocation, and IMPA is applied to the model solving process. The relevant data for 2021 are used as the basis for parameter modification to form an overall water resource allocation scheme.

First, based on the original MPA, chaotic initialization was performed to avoid insufficient population diversity, the golden sine algorithm was added to avoid search stagnation, and the quadratic interpolation method was selected to avoid insufficient search capability, which effectively improved the rate of convergence and optimal solution accuracy. After that, using multiple single-peak, multi-peak, and multi-peak fixed-dimensional benchmark functions, IMPA is compared with five other algorithms for optimal values, standard deviations, and averages, demonstrating that IMPA’s performance is overwhelmingly superior to several algorithms.

Then, using IMPA for optimal allocation of water resources in the city, the rapid and stable rise of different objective function curves shows its better convergence ability.

Finally, according to the status of local water sources in Huaying City, categorizing the city’s water sources into three types: surface, ground (shallow and deep) and recycled water (sewage and rainwater). Since deep water and rainwater have zero sources in that year, they are not taken into consideration.

The water use sector is divided into three major categories of water use statistics for production, domestic and ecological, based on users’ characteristics, where water use for production is further divided into water use for primary industry, secondary industry and tertiary industry, in this article, the former two, i.e. industrial and agricultural water use, are mainly considered. Compare the Pareto solution sets optimized by IMPA with those optimized by MPA and PSO, as well as the optimal solutions selected after entropy-weight optimization, and the best water allocation scheme found by IMPA for all three is derived, followed by comprehensive analysis and discussion, and relevant suggestions for water resources treatment are proposed.

Through the above study, it can be shown that IMPA is effective and reasonable for water resource allocation in Huaying City, which can give the optimal solution without jumping out of the range of constraints while satisfying the needs of each user. From the analysis of the local results and the results obtained from IMPA, Huaying City is currently in a more serious shortage of water resources, but under the existing conditions, it can only basically meet the needs of users, but cannot strive for maximum benefits in other aspects. This research gives a better planning solution considering many aspects on this basis, and this work can be used as a reference to incorporate into a local water allocation scheme to better serve the people.

However, there are still some issues that are not considered in this study, such as: the consideration in this study focused solely on the single-block scheduling of water resources. In the future, there is potential for further refinement by integrating reservoir scheduling, expanding the scope of the problem (Ahmadianfar et al. 2022c, 2023); only one year is considered, and no specific reference scheme is given for planning water resources in future years; only three major objectives of domesticity, economy and industry are considered, and some necessary and important indicators, such as people’s happiness index and sewage treatment cost, are not considered. For these situations, the next study will consider and study them carefully, and strive to solve the problems to the best.