1 Introduction

Population growth in developing countries has increased the water demand to improve health, social welfare, economic development and food production, and to protect ecosystems. Reservoir operation is central to achieving sustainable development. The application of optimization algorithms is necessary in reservoir operation to achieve best management solutions. Evolutionary and meta-heuristic algorithms are applied to find the near-optimal solutions of complex problems efficiently (Bozorg-Haddad et al., 2017). The genetic algorithm (GA) (see, e.g., Goldberg & Holland, 1988, Holland, 1992), for instance, is a pioneering evolutionary algorithm that has been applied to solve reservoir operation problems that could not be solved with classic linear (LP) or nonlinear programing (NLP) (Louati et al., 2011; Jothiprakash & Shanthi, 2006). Hincal et al. (2011) investigated the efficiency of the GA in determining the optimal operation of multiple reservoirs. Three reservoirs were optimized in the Colorado River project to maximize energy production. Results were compared with data of actual operation, and the GAs results proved superior relative to traditional optimization methods.

Akbari-Alashti et al. (2014) implemented nonlinear programming (NLP), fixed length gene genetic programming (FLGGP) and GA to operate a three-reservoir system in Iran in real time to predict the hydroelectric power generated. The results showed that FLGGP provided the most flexible and efficient performance for extracting operating rules. Bashiri-Atrabi et al. (2015) developed the algorithm of harmony search (HS) to optimize reservoir operation to minimize water supply shortages and flood damage in the reservoir downstream. The HS results were compared with other methods with a single-reservoir operation problem. The HS featured superior performance based on convergence speed and accuracy to an optimal value compared to other methods [such as the honeybee mating optimization (HBMO) and nonlinear programming]. Bozorg-Haddad et al. (2015a) introduced the bat algorithm (BA) applied to the reservoir operation. It was applied to the Karun four-reservoir system (Iran) and a hypothetical four-reservoir system. Results showed that BA’s performance was superior compared to LP, NLP and the GA from the perspective of convergence to a global optimal. Bozorg-Haddad et al. (2015b) applied the water cycle (WC) algorithm to obtain the operation optimal policies of the Karun four-reservoir system (Iran) and a four-reservoir system. Results showed high efficiency of WC in reservoir operation. Azizipour et al. (2016) applied the invasive weed optimization (IWO) algorithm to optimally operate hydropower plant for single-reservoir and multi-reservoir systems during short-term, medium-term and long-term periods. Results were compared with particle swarm optimization (PSO) and the GA, and demonstrated that IWO was more reliable than PSO and GA for single- and multi-reservoir power plants. Akbarifard et al. (2020) conducted the moth swarm algorithm (MS) to optimize the hydropower operation (Karun four-reservoir system) (in Iran). Results revealed that MS was preferable relative to PSO and the GA in calculating optimal hydropower reservoir policies. Rani et al. (2020) proposed an integrated dynamic programing-particle swarm optimization (DP-PSO) algorithm, to detect the optimal policies of release from the Mola Reservoir in India. The results were compared from the point of view of objective function values and the central processing unit (CPU) time. Liu et al. (2020) used the NSGA-II and lion pride (LP) algorithm to optimize reservoir operation. Results indicated that the LP was preferable relative to the NSGA II. Donyaii et al. (2021) implemented the whale algorithm (WA), the gray wolf algorithm (GWA) and the crow search algorithm (CSA) to the Golestan single-reservoir optimal operation (Iran) to supply the water needs of downstream agriculture. The results demonstrated that GWA presented the better performance than the other two-algorithm. Bozorg-Haddad et al. (2021) applied the flower pollination (FP) algorithm to single-reservoir and multi-reservoir optimal operation. The results showed the FP results were close to those of NLP, and it was better than PSO from the point of view of reducing the optimization run-time and accuracy. Niu et al. (2021) proposed the hybrid gray wolf optimizer (HGWO) for enhancement of the efficiency and resolve the gray wolf optimizer’s (GWO) deficiencies. The HGWO formulated water reservoir operation policies with objective function of maximizing total revenue. Results indicated that HGWO calculated accurate multi-objective reservoir operation policies with rapid convergence. Nematollahi and Zarif Sanayei (2023) developed a groundwater operation model based on Harris hawk optimization (HHO) algorithm for conjunctive use of surface water and groundwater resources. The HHO provided the appropriate allocation of surface water and groundwater resources. Choi et al. (2023) developed an optimal hydropower reservoir rule by applying the improved gray wolf optimizer (IGWO). The results demonstrated that IGWO was a robust tool for reservoir operation.

There have been many studies related to the optimization of river–reservoir–irrigation network system based on meta-heuristic algorithms. The problem of integrated water resource management is inherently complex and nonlinear, and the complexity increases under climate change conditions. Therefore, this research develops a method or algorithm that has high accuracy and is cost-effective in terms of its computational burden. Specifically, the marine predators algorithm (MPA) is developed for river–reservoir–irrigation network system optimization. The developed algorithm’s performance is compared with GA, which is a widely used benchmark algorithm. Previous research shows that evolutionary algorithms perform better in solving complex problems dealing with the operation of water systems than DP, LP, NLP and dynamic programing (DP). The MPA is a meta-heuristic algorithm that has not been applied in hydro-systems. This work evaluates the MPA with mathematical functions and reservoir operation optimization.

2 Methodology

This section describes the MPA. This is followed by a description of the mathematical functions used in this study. The reservoir operation model is then defined. Lastly, the performance indexes of the reservoir are presented. This paper’s methodology is displayed in Fig. 1.

Fig. 1
figure 1

Flowchart of the methodology

Full size image

2.1 The MPA

MPA as an evolutionary algorithm is inspired by the random walk strategy of marine predators applied when trapping their prey in the ocean (Faramarzi et al., 2020). The MPA, in the same fashion as other population-based evolutionary algorithms, begins by generating a population of possible solutions. The generating equation of MPA is given by Eq. (1):

$$ X = X_{\min } + + {\text{rand}} \cdot \left( {X_{\max } - X_{\min } } \right) $$
(1)

where \(X\) = vector of generated possible solutions; \(X_{\max }\) and \(X_{\min }\) = the upper and the lower boundary in the search space, respectively, and rand = uniform random vector in the range 0–1.

The stronger hunters have a greater chance to secure food. Therefore, they are chosen as the best solution to build an elite matrix. The matrix elements quantify the process of searching for prey according to prey position:

$$ {\text{Elite}} = \left[ {\begin{array}{*{20}l} {X_{1,1}^{I} } \hfill & \cdots \hfill & {X_{1,d}^{I} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {X_{1,N}^{I} } \hfill & \cdots \hfill & {X_{N,d}^{I} } \hfill \\ \end{array} } \right] $$
(2)

where \({{X}^{I}}_{i,j}, j=1, 2, \dots , d=\) ith vector of solutions (predators), N = number of solutions and d = number of dimensions of the search space.

A second matrix called the elite prey is constructed on the basis of which hunters update their positions. The initialization creates the primary prey associated with the most suitable predator elite. Once a superior hunter is replaced by a better hunter at the end of each iteration, the elite matrix is updated to produce the elite prey matrix shown in Eq. (3):

$$ {\text{Prey}} = \left[ {\begin{array}{*{20}l} {X_{1,1} } \hfill & \cdots \hfill & {X_{1,d} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {X_{1,N} } \hfill & \cdots \hfill & {X_{N,d} } \hfill \\ \end{array} } \right] $$
(3)

where \(X_{i,j}\) = the i, jth element of the elite prey matrix.

The exploration and exploitation processes in the search for the best predator set is divided into three main optimization phases according to the speeds of predator and prey, which are described below. These phases are defined according to the rules governing the movements of the predator and prey in nature. A specific iteration period is specified for each iteration step. The predator and the prey are regarded as search variables. The prey searches for food and the predators search for prey.

2.1.1 First phase: ratio of high velocity

When there is a ratio of high velocity, the prey moves faster than the predator, and this happens in the first third of the total number of generations (i.e., tmax/3). In this case, the prey features Brownie motion. This scenario occurs in the early iterations of optimization where exploration is important. The best strategy for a predator is not to move at all. If prey is more successful in its search for food than a predator, it can be considered a predator. This means that the degree of fitness of prey is calculated, and, if better, it replaces the previous predator. Therefore, the updated prey matrix is obtained with Eqs. (4) and (5):

$$ S_{i} = R_{B} \otimes \left( {{\text{Elite}}_{i} - R_{B} \otimes {\text{Prey}}_{i} } \right), i = 1,2, \ldots ,N $$
(4)
$$ {\text{Prey}}_{i} = {\text{Prey}}_{i} + \left( {P \cdot R \otimes S_{i} } \right),\,\,1,2, \ldots ,N $$
(5)

where \(R_{B}\) = a vector including random numbers that represents Brownian motion; \({{\text{Prey}}}_{i}\)= the ith row of the updated prey matrix; \({S}_{i}\)= the ith row of the first update of the prey matrix; \({{\text{Elite}}}_{i}\) = the ith row of the elite matrix; \(\otimes\) = symbol for the element-by-element multiplication of vectors or matrices; \({R}_{B}\otimes {{\text{Prey}}}_{i}\) = simulation of the movement of prey; P = a constant number (equal to 0.5); R = a vector including random numbers in the range [0, 1]; and N = number of solutions.

2.1.2 Second phase: ratio of unit velocity

The predator and prey in this phase move at nearly the same velocity. To make a good transition from exploration to exploitation, first phase is designed. Half the population is for exploration and the rest for exploitation. The exploitation is for prey, and exploration is for predator. Therefore, predator–prey search for their food. The predator begins to search for his prey as a Brownian motion, while prey turns to Levy motion to search for an immediate neighbor and, if not found, the prey takes a long jump.

As hunters become closer to each other the jump length becomes shorter than in the previous stage. Environmental factors such as formation effects or fish aggregating devices (FADs) and the Levy strategy prevent the MPA from being trapped at local optima, thus achieving successful and rapid convergence to a near-optimal global solution. Equations (6)–(10) describe this stage of optimization:

$$ \frac{1}{3}t\max < t < \frac{2}{3}t\max $$
(6)

For the first half of population:

$$ S_{i} = R_{{\text{L}}} \otimes \left( {{\text{Elite}}_{i} - R_{{\text{L}}} \otimes {\text{Prey}}_{i} } \right),{\text{ i}} = 1,{ }2,{ } \ldots {\text{, N}}/2 $$
(7)
$$ {\text{Prey}}_{i} = {\text{Prey}}_{i} + \left( {P \cdot R \otimes S_{i} } \right), \,\,i = 1, 2, \ldots , N/2 $$
(8)

For the second half of population:

$$ S_{i} = R_{B} \otimes \left( {R_{B} \otimes {\text{Elite}}_{i} - {\text{Prey}}_{i} } \right),\,\,i = 1, 2, \ldots , N/2 $$
(9)
$$ {\text{Prey}}_{i} = {\text{Elite}}_{i} + \left( {P \cdot CF \otimes S_{i} } \right), \,\,i = 1, 2, \ldots , N/2 $$
(10)

where \(R_{{\text{L}}}\) = a vector containing random numbers, which represents the Levy motion \({R}_{{\text{L}}}\otimes {{\text{Prey}}}_{i}\) = simulation of the prey movement in a Levy pattern while increasing the step size toward the prey position; CF = an adaptive parameter (coefficient of convergence). \(R_{{\text{L}}} \otimes {\text{Elite}}_{i}\) = simulation of the motion of predators in the Brownian mode when prey changes position based on the Brownian motion of predators.

The convergence coefficient (CF) is calculated with Eq. (11):

$$ {\text{CF}} = \left( {1 - \frac{{{\text{Iter}}}}{{{\text{Max}} - {\text{Iter}}}}} \right)^{{2\frac{{{\text{Iter}}}}{{{\text{Max}} - {\text{Iter}}}}}} $$
(11)

where \({\text{Iter}}\) = the current iteration and \({\text{Max}} - {\text{Iter}}\) = the maximum iteration.

There are many environmental issues, including the FADs, that affect the behavior of marine predators. The effect of the FADs is calculated with Eqs. (12) and (13):

$$ {\text{Prey}}_{i} = {\text{Prey}}_{i} + {\text{CF}} \cdot \left[ {X_{\min } + r_{3} \cdot \left( {X_{\min } - X_{\max } } \right)} \right] \otimes U\,\,{\text{if}} r < {\text{FADs}} $$
(12)
$$ {\text{Prey}}_{i} = {\text{Prey}}_{i} + \left[ {{\text{FADs}} \cdot \left( {1 - r} \right) + r} \right]\left( {{\text{Prey}}_{{r_{1} }} - {\text{Prey}}_{{r_{2} }} } \right)\,\,{\text{if}} \,\,r \ge {\text{FADs}} $$
(13)

when FADs is equal to 0.2 there is a possibility of FADs affecting the simulation process; U = a binary vector consisting of zeros and ones; \(X_{\min }\) and \(X_{\max }\) = respectively the smallest and largest values of \(X\); \(r_{1}\) and \(r_{2}\) = the random indexes of the predator matrix, respectively.

2.1.3 Third phase: ratio of low-velocity

The predator in this stage is traveling faster than prey. This scenario is related to the last stage of optimization when there is high capture of prey. The predator changes his behavior from Brownian motion to Levy motion for a more efficient search of a particular area. The CF helps the predator to limit the search areas in a particular area for exploitation. Equations (14) through (16) govern this stage of optimization:

$$ t > \frac{2}{3}t\max $$
(14)
$$ S_{i} = R_{{\text{L}}} \otimes \left( {R_{{\text{L}}} \otimes {\text{Elite}}_{i} - {\text{Prey}}_{i} } \right), \,\,i = 1, 2, \ldots , n $$
(15)
$$ {\text{Prey}}_{i} = {\text{Elite}}_{i} + P \cdot {\text{CF}} \otimes S_{i} ,\,\, i = 1, 2, \ldots , n $$
(16)

where \(R_{{\text{L}}} \otimes {\text{Elite}}_{i}\) = simulation of the predator’s movement with the Levy strategy by adding step size to the Elite position and to aid in the upgrade of prey tracking process.

The MPA is summarized in Fig. 2, where the three stages of optimization are displayed graphically.

Fig. 2
figure 2

Flowchart of the MPA

Full size image

2.1.4 Benchmark functions

Several mathematical functions are used to evaluate the convergence properties of MPA. The mathematical functions are the Sphere, Ackley, Rosenbrock, Rastrigin and Zakharov functions. There is a number of benchmark mathematical functions available for the initial evaluation of evolutionary and meta-heuristic algorithms, in both constrained and unconstrained optimization. The absolute optimal value, equations and constraints are known in the case of constrained functions. Therefore, these functions are suitable to test the performance of algorithms and they solution accuracy. This work implements five common benchmark functions to evaluate algorithmic performance. These benchmark functions have been used in previous studies successfully (Garousi-Nejad et al., 2016; Bozorg-Haddad et al. 2016; Bahrami et al. 2018; Rahmati et al. 2021). The equations and graphs of these functions are given in Table 1.

Table 1 Description of the mathematical functions,
Full size table

2.1.5 Reservoir operation model

Objective function of the study is to minimize the relative deficit of water supply with optimal operation of reservoir over a period of time according to Eq. (17). Decision variable of the optimized model is the amount of water volume released from reservoir:

$$ {\text{Minimize}}\,\,{\text{Def}} = \mathop \sum \limits_{t = 1}^{T} \left( {\frac{{D_{t} - R_{t} }}{{D_{\max } }}} \right)^{2} $$
(17)

where \(R_{t}\) = water release volume from reservoir during period t; \(D_{t}\) = water demand volume downstream of reservoir at during period t; \({D}_{{\text{max}}}\) = the maximum water demand downstream from reservoir; and \({\text{Def}}\) = the volume of water deficit.

The equation of the continuity governing the reservoir and the imposed constraints are presented in Eqs. (18) through (23):

Continuity or conservation of water volume:

$$ S_{t + 1} = S_{t} + Q_{t} - SP_{t} - E_{t} - R_{t} \,\,t = 1,2, \ldots ,T $$
(18)

Evaporation losses:

$$ E_{t} = (e_{t} \cdot A_{t} /1000)\begin{array}{*{20}c} {} & {} \\ \end{array} \begin{array}{*{20}c} {} & {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} t = 1,2, \cdots ,T $$
(19)

Storage area function:

$$ A_{t} = aS_{t} + b\,\,\,a = 0.03,\,\,b = 0.8 $$
(20)
$$ D_{\min } \le R_{t} \le D_{\max } $$
(21)

Constraint on reservoir storage:

$$ S_{\min } \le S_{t} \le S_{\max } \,\,t\, = \,1, \, 2, \, \ldots , \, T $$
(22)

Constraint on reservoir spill:

$$ {\text{SP}}_{t} = \left\{ {\begin{array}{*{20}l} {S_{t} + Q_{t} - E_{t} - R_{t} - S_{\max } } \hfill & {{\text{if}} S_{t} + Q_{t} - E_{t} - R_{t} > S_{\max } } \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. $$
(23)

where \(S_{t + 1}\) = reservoir storage at time t + 1; \({\text{SP}}_{t}\) = reservoir spill volume at during period t; T = time interval of operation period; \(E_{t}\) = evaporation volume from the reservoir lake surface at during period t; \(e_{t}\) = evaporation rate (mm) from the reservoir lake surface at during period t; \(Q_{t}\) = reservoir inflow at during period t; Smin = minimum reservoir water storage; \(S_{\max }\) = maximum reservoir water storage; and \(A_{t}\) = reservoir lake area at time t.

Penalty functions that are introduced in Eqs. (24) and (25) are added to the objective function to avoid violating the set constraints on reservoir storage and the release volume from the reservoir lake surface:

$$ {\text{Penalty}}\,\,1 = \left\{ {\begin{array}{*{20}l} {\sum\limits_{t = 1}^{T} {\left( {\frac{{S_{t} - S_{\min } }}{{S_{\min } }}} \right)^{2} } } \hfill & {{\text{if}}\,\,S_{t} < S_{\min } } \hfill \\ {\sum\limits_{t = 1}^{T} {\left( {\frac{{S_{t} - S_{\max } }}{{S_{\max } }}} \right)^{2} } } \hfill & {{\text{if}}\,\,S_{t} > S_{\max } } \hfill \\ 0 \hfill & {{\text{if}}\,\,S_{\min } \le S_{t} \le S_{\max } } \hfill \\ \end{array} } \right. $$
(24)
$$ {\text{Penalty}}\,\,2 = \left\{ {\begin{array}{*{20}l} {\mathop \sum \limits_{t = 1}^{T} \left( {\frac{{R_{t} - D_{\min ,t} }}{{D_{\min ,t} }}} \right)^{2} } \hfill & {{\text{if}}\,\,R_{t} < D_{\min } } \hfill \\ {\mathop \sum \limits_{t = 1}^{T} \left( {\frac{{R_{t} - D_{\max ,t} }}{{D_{\max ,} }}} \right)^{2} } \hfill & {{\text{if}}\,\,R_{t} > D_{\max } } \hfill \\ 0 \hfill & {{\text{if}}\,\,D_{\min ,} \le R_{t} \le D_{\max } } \hfill \\ \end{array} } \right. $$
(25)

where \({D}_{{\text{min}}t}\) = the minimum downstream water demand volume at time t and \({D}_{{\text{max}},t}\) = the maximum demand at time t.

Objective function of problem herein presented is the minimization of the relative deficit amount during the time period. Decision variable is water release volume from reservoir. State variable is reservoir storage and it depends on decision variable. The constraints of reservoir operation are imposed on the volume of water storage and released water from reservoir. Decision space is defined as the constraints set. All the reservoir operation problem components are incorporated in the solution algorithm to yield an optimal solution.

2.1.6 Comparison of the MPA and the GA performances

The MPA’s and GA’s performances in solving the reservoir operation problem are compared. The reader is referred to Goldberg and Holland (1988), Holland (1975), Holland (1992) and Bozorg-Haddad et al. (2017) for a review of the GA.

2.1.7 Indexes of reservoir efficiency

Indexes of reliability–resiliency–vulnerability are employed to evaluate reservoirs operation in the study. Reliability [Eq. (26)] measures the fraction of time that water demand is met during operation. Resiliency [Eq. (27)] calculates the probability of meeting the demand of downstream water (satisfaction mode) after a deficit in supply (failure mode). Vulnerability [Eq. (28)] defines the ratio of deficit of water supply to the total water demand (Ashofteh et al., 2013a). The better the reservoir performance in meeting the downstream water demand, the higher the reliability. The higher the resiliency, the more likely it is that water demand will be met after a shortage. The vulnerability measures the degree to which the reservoir might not meet the water demand.

Reliability:

$$ \alpha = [N_{t = 1}^{T} (D_{t} \le R_{t} )]/T $$
(26)

Resiliency:

$$ \beta = {\text{PROB}}\,\left[ {{\text{SY}}_{t + 1} \in S\left| {{\text{SY}}_{t} \in F} \right.} \right] $$
(27)

Vulnerability:

$$ \upsilon = \left[ {\sum\nolimits_{t = 1}^{T} {(D_{t} - R_{t} \left| {D_{t} > R_{t} } \right.)} } \right]/\left[ {\sum\nolimits_{t = 1}^{T} {D_{t} } } \right] $$
(28)

where \(\alpha \) = reliability index; \(N_{t = 1}^{T} (D_{t} \le R_{t} )\) = number of water supply periods in which water demand is less than water release; \({\sum }_{t=1}^{T}\left({D}_{t}-{R}_{t}|{D}_{t}>{R}_{t}\right)\)= number of periods in which water demand exceeds water supply; \(\beta\) = resiliency index; S = satisfactory operation; F = failure in operation; PROB = probability function; SYt = state of the system of water supply in period t; SYt+1 = state of the system of water supply in period t + 1; and \(\upsilon \) = vulnerability index.

2.1.8 Goodness-of-fit criteria

The criteria of the mean absolute error (MAE), root mean square error (RMSE), Nash–Sutcliffe efficiency (NSE) and correlation coefficient (r) are applied to evaluate the goodness of fit between the reservoir releases and the downstream water demand. The equations related to these criteria are listed in Table 2.

Table 2 Equations of the mathematical goodness-of-fit criteria
Full size table

2.1.9 Case study

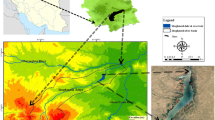
The studied basin is the Aydogmush river basin with an area of about 1802 km2, which is located in East Azerbaijan province. This river, 80 km long, originates in Ghurgard in Hashtroud highlands and flows to Qezal Ozen River (Ashofteh et al., 2013b) (Fig. 3a). The dam under study in this research is the Aydogmush Dam on the Aydogmush River, which has two water intake towers and an outlet valve, in the water intake tower there are four inlet valves at elevations of 1305.88, 1317.74, 1326.49 and 1332.5 m (above sea level) (Azadi et al., 2021a). Also, the outlet valve is located at a level of 1319.55 m (above sea level). Figure 3b) shows a view of the reservoir water intake tower. Some characteristics of the studied dam are shown in Fig. 4.

Fig. 3
figure 3

a Geographical location of the Aydogmush dam study area, b a view of the intake tower of the Aydogmush reservoir

Full size image
Fig. 4
figure 4

Specifications of the study dam

Full size image

The Aydogmush dam has several structures with the following characteristics: (1) Dam body: the Aydogmush dam body is of gravel type with an impermeable clay core. The height of the body from the foundation is 87 m. The depth of to bedrock under the river bed is about 20 m. The dam crest length is 297 m, its width is 12 m and its elevation is 1350 m above the sea level; (2) Spillway: the free spillway has a capacity of 2450 m3/s with a threshold length of 65 m; (3) Water diversion system: It consists of 2 tunnels (circular cross section) with a diameter of 4.5 m and a total length of 648 m. The capacity of the water diversion is 310 m3/s; and (4) water intake and outlet valve system. Water intake for agricultural purposes is through a water intake tower with a discharge capacity of 14.7 m3/s, which consists of four valves located at different elevations, and the outlet valve is also installed with a discharge capacity of 55 m3/s. Figure 5 shows the storage volume–water level diagram for Aydogmush reservoir.

Fig. 5
figure 5

Reservoir water storage volume–water level diagram

Full size image

Figure 6a–d displays the reservoir inflow, the water demand, changes in rainfall and temperature for the 14-year base period (1987–2000).

Fig. 6
figure 6

Graphs of the volume of a reservoir inflow, b water demand, c rainfall, dtemperature for the baseline 14-year period (1987–2000)

Full size image

The periods of reservoir operation herein considered are the baseline time series (1987–2000) and the 14-year period of climate change (2026–2039), which simulates the inflow and demand of agricultural water under climate change conditions. The climate change projections for the study area have been previously calculated by Ashofteh et al. (2013b) and Azadi et al. (2021b), and are applied in this work. The HadCM3 model and the A2 emission scenario were employed to generate the climate scenarios. Input data to the optimization model include reservoir specifications [such as maximum reservoir storage volume (145.7 × 106 m3) and minimum reservoir storage volume (8.7 × 106 m3)], monthly reservoir inflow time series, evaporation rates of reservoir lake surface and water demand time series downstream of the reservoir.

2.1.10 Results and discussion

The results of the MPA evaluation using the Sphere, Ackley, Rosenbrock, Rastrigin and Zakharov mathematical functions are indicated in Fig. 7. Figure 7 shows that the MPA achieved fast convergence to the minima of the benchmark functions. The function of Rosenbrock converged to zero, and the other functions converged to zero with a close approximation.

Fig. 7
figure 7

MPA convergence diagrams for the a Sphere, b Ackley, c Rosenbrock, d Rastrigin, e Zakharov functions

Full size image

After evaluating the successful performance of MPA with five mathematical functions, the MPA was applied to solve a reservoir operation problem. Results from the MPA the GA in five runs under the baseline and climate change periods are presented in Table 3 and Fig. 8. Table 3 lists results indicating that the MPA provided superior performance that the GA, and its results are closer to the absolute optimal solution than the GAs. The difference between the values of the best MPA and GA solutions is significant. Moreover, the run-time of the MPA is one twenty-sixth of the GAs. The graphs in Fig. 8 graphs establish that the MPA convergence curves for the baseline and future periods for the five runs were close to each other and reached the solution quickly, while the convergence curves of the GA did not feature good convergence. Evidently, the MPA performed better than the GA.

Table 3 Comparison of the value of the objective function obtained with the MPA and the GA in the baseline and climate change periods corresponding to five runs
Full size table
Fig. 8
figure 8

MPA convergence diagram in five runs corresponding to the a baseline and b climate change periods; GA convergence diagram corresponding to the c baseline and d climate change periods

Full size image

The volumes water release, reservoir storage, spill, water supply deficit and reservoir inflow were calculated with the MPA and are displayed in Fig. 9a–e, respectively. The GA-calculated results for optimal reservoir operation rules are shown in terms of the volumes of reservoir storage, water release, spill, water supply deficit and reservoir in Fig. 10a–e, respectively.

Fig. 9
figure 9

Volumes of a water release, b storage, c spill, d deficit and e reservoir inflow, under the baseline and climate change periods based on the MPA-calculated reservoir operation rule

Full size image
Fig. 10
figure 10

Volumes of a water release, b storage, c spill, d deficit and e reservoir inflow, under the baseline and climate change periods based on the GA-calculated reservoir operation rule

Full size image

Figure 9a shows that due to increase in water demand in future period compared to baseline in the previous study (Ashofteh et al., 2013a) the water releases in future period would be higher than in the baseline period. Meanwhile, reservoir storage in future would be smaller than in baseline (Fig. 9b), which is due to increase in future water release. Also, the spill volume in future period would decrease compared to baseline period (Fig. 9c) because the reservoir inflow declines in future period (Ashofteh et al., 2013a) (Fig. 9e), and this decrease occurs in the wet months (April and May). Therefore, according to Fig. 9d the reservoir performance in regulating the discharge in the future would be more successful than in the baseline. A comparison of Figs. 9 and 10 reveals that the MPA yields better reservoir operation rules than the GA, and the MPA results meet downstream water demand more successfully than the GAs.

The efficiency indexes for reservoir operation corresponding to the MPA and the GA under the baseline and climate change periods are listed in Table 4. According to Table 4 the vulnerability, reliability and resiliency under the baseline and climate change periods calculated with the MPA are significantly different and of superior quality that the GAs, indicating the better performance of the MPA in meeting downstream water demand. The higher vulnerability calculated with the GA indicates that the system is less likely to meet downstream water needs.

Table 4 Comparison of efficiency indexes for optimal reservoir operation calculated with the MPA and the GA under the baseline and climate change periods
Full size table

The goodness-of-fit criteria used to evaluate the monthly water allocation under the baseline and climate change periods corresponding to the MPA and GA are listed in Table 5. Table 5 clearly shows the MPA results have smaller errors than the GAs. Moreover, the MPA and the GA-calculated reservoir operation rules meet the downstream agricultural water demand well under the baseline and future periods.

Table 5 Comparison of the goodness-of-fit criteria between reservoir releases and water demand for optimal reservoir operation based on the MPA and GA in the baseline and climate change periods
Full size table

3 Concluding remarks

This work developed a new algorithm to optimize the reservoir operation rules with high accuracy and low run-time. This work’s results indicate that the MPA model determined the optimal policies of reservoir operation accurately with fast convergence to the optimum solution. The obtained results indicated that the MPA produced a better performance in optimization of the Aydogmush reservoir operation. Comparison of reservoir release obtained with the MPA and GA in five runs under baseline and climate change periods indicates better performance of MPA in meeting downstream water demand as well as minimizing the objective function. Comparison of MPA and GA performances with respect to optimal reservoir operation demonstrated that the MPA-calculated reliability under the baseline and climate change periods is 65 and 58% higher, respectively, that the GAs, the MPA-calculated vulnerability is 75 and 83% lower, respectively, than the GAs, and the MPA-calculated resiliency is by 35% lower under baseline and climate change periods than the GAs.