The editorial guidelines and methodological recommendations of several prominent educational and psychological journals have extensively recommended effect size reporting and interpreting practices for all primary outcomes of empirical studies. Accordingly, numerous practical suggestions for selecting, calculating, and interpreting effect size indices for various types of statistical analyses have been provided in the literature (see Alhija and Levy 2009; Breaugh 2003; Durlak 2009; Ferguson 2009; Fern and Monroe 1996; Grissom and Kim 2012; Huberty 2002; Kirk 1996; Kline 2004; Olejnik and Algina 2000; Richardson 1996; Rosenthal et al. 2000; Rosnow and Rosenthal 2003; Vacha-Haase and Thompson 2004). Overall, group difference and strength of association are two of the major classes of effect sizes in practical applications. It is essential to note that the standardized mean difference is a widely adopted effect size measure when comparing treatment means of two independent groups. On the other hand, in univariate research that compares more than two treatment effects, the correlation ratio, eta squared, measures the proportion of total variance accounted for by any of the treatment effects.

Eta squared is an appropriate generalization of the coefficient of determination and reflects the extent to which knowledge of group membership improves prediction of outcomes, two different extensions of standardized mean difference have also been proposed to represent the degree of difference among several treatment groups (Cohen 1969, 1988, Chapter 8). One index relies on the standard deviation of the standardized means and the second index is the range of the standardized means. To test the null hypothesis of no difference or zero effect, the analysis of variance (ANOVA) F test and the studentized range test are the two prominent procedures associated with the effect measures of the standard deviation of the standardized means and the range of the standardized means, respectively. Although there are more sophisticated statistical methods, ANOVA F test remains one of the most frequently used approaches to detecting group differences in the behavioral, educational and social sciences (Skidmore and Thompson 2010; Warne et al. 2012). To facilitate the application of F test for power and sample size calculations in planning research designs, Cohen (1988) provided comprehensive illustrations and extensive tables for the standard deviation of the standardized means.

The studentized range is an intuitively appealing extension of the standardized mean difference under a multiple treatments scenario. However, there are no corresponding demonstrations and explications for the studentized range test in Cohen (1988). It is conceivable that the distributional property of the studentized range statistic is more involved than that of the sample standardized mean difference. The quantiles of the studentized range statistic are commonly available in most statistical textbooks for conducting multiple comparisons between group means. Due to computational demands, the power behavior of a studentized range test is not as widely addressed as the F test for the alternative measure of the standard deviation of the standardized means. Specifically, David et al. (1972) and Hayter and Hurn (1992) conducted various power assessments of the studentized range test and the F test for the equality of several normal means. Hayter and Hurn (1992) found that in most situations the power performance of the F test and the studentized range test is very close to that of an optimal test procedure considered in Hayter and Liu (1992). However, the optimal test procedure is substantially more complicated to use than the F test and the studentized range test. More importantly, the empirical comparisons of David et al. (1972) showed that the studentized range test provides higher power than the F test at some configurations of the treatment means.

It is noteworthy that the prescribed appraisals of the F method and the studentized range procedure were confined to a test of the traditional null hypothesis of no difference in treatment means. However, researchers are often more concerned about whether the treatment effects are large enough to have a practical importance. Essentially, it is more appropriate to test the null hypothesis that the effects of treatments are trivial or negligible as advocated in Cohen (1994), Murphy (1990), and Serlin and Lapsley (1993). The tests of minimal effect null hypotheses require an operational definition of the target minimal reasonable value that corresponds to the threshold for identifying substantial research findings. Moreover, unlike the conventional approaches that test a simple null hypothesis of zero effect, the test statistics of minimum-effect are employed to conclude whether the observed effect sizes would be likely to occur for a range of population values in a composite null hypothesis. Therefore, the notion of least favorable configurations of treatment means is vital to determine the critical values for conducting tests of minimal effect. Such information is generally not available to applied researchers and it is impossible to implement the test procedures without an extensive set of tables or an efficient software package.

More general discussions of the fundamental concept and rationale of the F tests of minimal effect can be found in Murphy and Myors (1999) and Steiger (2004). Alternatively, Bau et al. (1993) and Chen et al. (2011) described the technical development and property for the studentized range test of minimum-effect hypotheses. Although these results justify the execution of the F test and the studentized range test of minimum effect, their formulations are markedly different and demand varying computational efforts. No investigation has systematically compared their distinct characteristics in terms of theoretical principles, power performance, and sample size requirement. Thus it is prudent to examine their unique features and fundamental discrepancies in order to better understand the selection of an appropriate procedure. Equivalence testing is recommended as a better alternative to the traditional difference-based methods for demonstrating the comparability of two or more treatment effects. The related features of both the ANOVA F and the studentized range tests for evaluating the comparability of several standardized effects can be found in Wellek (2010, Chapter 7), Giani and Finner (1991), Cribbie et al. (2010), Chen et al. (2009), and the references therein.

This article seeks to contribute to the literature on detecting a minimal important difference among standardized mean effects in three ways. First, the fundamental distinctions of the standard F test and the studentized range test are reviewed here to provide a clear and concise exposition of their inherent formulations and properties. This report adds to the general understanding of the utilities of effect size measures and enhances the practical importance of the tests of minimal effect hypotheses. Second, comprehensive empirical investigations are conducted to demonstrate the power performance and sample size requirements between the standard F test and the studentized range test under a wide variety of mean structures. The assessments discern not only which method is most suitable under what circumstances but also the actual differences between the contending test procedures. Third, to facilitate the application of the presented procedures, the corresponding computer codes are provided to compute the critical values, observed significance levels, attained power levels, and required sample sizes. Note that the computations of these procedures involve specialized programs not currently available in prevailing statistical packages. This article and the supplemental files present a unified set of algorithms for design planning and data analysis of the two tests of minimum-effect.

Effect Measures and Test Procedures

Consider the one-way fixed-effects ANOVA model

$$ {Y}_{ij}={\mu}_i+{\varepsilon}_{ij} $$
(1)

where Y ij is the value of the response variable in the jth trial for the ith factor level, μi are treatment means, ε ij are independent N(0, σ2) errors with i = 1, ..., G (≥ 2) and j = 1, …, N. To characterize the degree of departure from no treatment effect, two distinctive measures were proposed in Cohen (1969, 1988). The first index is the standard deviation of the standardized means

$$ f=\frac{\sigma \mu }{\upsigma}, $$
(2)

where \( \sigma ={\left({\sigma}^2\right)}^{1/2},{\sigma}_{\mu }={\left({\sigma}_{\mu}^2\right)}^{1/2},{\sigma}_{\mu}^2=\sum_{i=1}^G{\left({\mu}_{\mathrm{i}}-\overline{\mu}\right)}^2/G \) is the average dispersion between the treatment means, and \( \overline{\mu}=\sum_{i=1}^G{\mu}_i/G \) is the mean of the treatment effects.

It is useful to note that \( \sum_{i=1}^G\sum_{l=1}^G{\left({\mu}_i-{\mu}_l\right)}^2=2G\sum_{i=1}^G{\left({\mu}_i-\overline{\mu}\right)}^2 \) or \( {\sigma}_{\mu}^2=\sum_{i=1}^G\sum_{l=1}^G{\left({\mu}_i-{\mu}_l\right)}^2/\left(2{G}^2\right) \). Hence, \( f={\left\{\sum_{i=1}^G\sum_{l=1}^G{\delta}_{il}^2/\left(2{G}^2\right)\right\}}^{1/2} \) is also a function of the sum of all G(G − 1) square standardized mean differences δ il  = (μ i  − μ l )/σ , i and l = 1, …, G. The second index is based on the range of the standardized means

$$ {\delta}_R=\frac{\upmu_{max}-{\upmu}_{min}}{\upsigma}, $$
(3)

where μ max and μ min are the maximum and the minimum of the G treatment means, respectively. When G = 2, it can be shown that f = δ R /2 = |δ|/2, where δ = (μ 1 − μ 2)/σ is the well-known standardized mean difference. In general, the two effect sizes f and δ R have no direct functional relationship except for some special cases of the treatment means. Accordingly, the corresponding inferential procedures are also substantially different.

The common F* is the most widely used test statistic for the null hypothesis that all treatment means are equal:

$$ F*=\frac{SSR/\left(G-1\right)}{SSE/\left({N}_T-G\right)}, $$
(4)

where \( SSR=N\sum_{i=1}^G{\left({\overline{Y}}_i-\overline{Y}\right)}^2 \) is the treatment sum of squares, \( SSE=\sum_{i=1}^G\sum_{j=1}^N{\left({Y}_{ij}-{\overline{Y}}_i\right)}^2 \) is the error sum of squares, \( {N}_T=GN,{\overline{Y}}_i=\sum_{j=1}^N{Y}_{ij}/N \), and \( \overline{Y}=\sum_{i=1}^G\sum_{j=1}^N{Y}_{ij}/{N}_T \) . Here, the focus is on the minimal effect test of

$$ {H}_0:f\le {f}_0\mathrm{versus}{H}_1:f>{f}_0 $$
(5)

where f 0 (> 0) is a specified value and denotes a minimal significant difference among the treatment means. It follows from the model formulation in Eq. 1 that

$$ F\ast \sim F\left(G-1,{N}_T-G,\Lambda \right), $$
(6)

where F(G − 1, N T  − G, Λ) is the noncentral F distribution with (G – 1) and (N T – G) degrees of freedom, and noncentrality parameter Λ = N T f 2 and \( {f}^2={\sigma}_{\mu}^2/{\sigma}^2 \) is the signal to noise ratio (Fleishman 1980). Another useful effect size measure in ANOVA is the strength of association η2 that reflects the proportion of total variance that is attributable to treatment effects. Essentially, the index η2 is a function of f 2 and can be expressed as η 2 = f 2/(1 + f 2). In addition, the root-mean-square standardized effect Ψ described in Steiger (2004) is a scaled counterpart of f : \( \Psi ={\left\{\left[\sum_{i=1}^G{\left({\mu}_i-\overline{\mu}\right)}^2/{\sigma}^2\Big]/\Big(G-1\right)\right\}}^{1/2}={\left\{G/\left(G-1\right)\right\}}^{1/2}f \). Under the null hypothesis H 0: f ≤ f 0, the statistic F* has the distribution

$$ F\ast \sim F\left(G-1,{N}_T-G,{\Lambda}_0\right), $$
(7)

where \( {\Lambda}_0={N}_T{f}_0^2 \). It follows from the monotone property of a noncentral F distribution that P{F(G − 1, N T  − G, Λ0) > c} > P{F(G − 1, N T  − G, Λ) > c} for Λ0 > Λ ≥ 0 and a positive constant c (Ghosh 1973). Thus, the least favorable configuration of μ = (μ1, …, μ G ) is μ 0 = (μ10, …, μ G0) with the standard deviation of the standardized means f = f 0. Hence, H 0 is rejected at the significance level α if F *  > F α (G − 1, N T  − G, Λ0), where F α (G − 1, N T  − G, Λ0) is the upper (100⋅α)th percentile of the noncentral F distribution F(G − 1, N T  − G, Λ0). Then the corresponding power function of the F* test is of the form

$$ {\pi}_{F\ast}\left(\Lambda \right)=P\left\{F\left(G-1,{N}_T-G,\Lambda \right)>{F}_{\upalpha}\left(G-1,{N}_T-G,{\Lambda}_0\right)\right\}. $$
(8)

Alternatively, a minimum effect of the standardized means may be assessed with the studentized range test in terms of the range of the standardized means:

$$ {H}_0:{\delta}_R\le {\delta}_{R0}\mathrm{versus}\;{H}_1:{\delta}_R>{\delta}_{R0} $$
(9)

where δ R0 (> 0) is a designated constant and indicates a minimal significant difference among the treatment means. The studentized range is defined as

$$ Q\ast =\frac{N^{1/2}\left({\overline{Y}}_{max}-{\overline{Y}}_{min}\right)}{S}, $$
(10)

where \( {\overline{Y}}_{max} \) and \( {\overline{Y}}_{min} \) are the maximum and minimum of the G sample means, respectively, S = (S 2)1/2, and S 2 = SSE/(N T  − G) is the sample variance. The distribution of the studentized range statistic Q* depends on all pairwise mean differences μi – μ l , not just a function of the maximum mean difference μ max – μ min . Following the model formulation in Eq. 1, the distribution of Q* does not have a closed-form expression and a convenient unified notation. For ease of illustration, it is denoted here by

$$ Q*\sim Q\left(G,N,\boldsymbol{\uptau} \right), $$
(11)

where τ = (μ1, …, μ G )/σ. However, the cumulative distribution function Θ(q) of Q* can be expressed as follows:

$$ \Theta (q)=P\left\{Q\ast \le q\right\}={E}_K\left\{\underset{i=1}{\overset{G}{\Sigma}}{E}_{Zi}\left[\kern1em \begin{array}{c}G\kern1em \\ {}\kern1em \Pi \kern1em \\ {}\kern1em l=1\kern1em \\ {}\kern1em l\ne 1\end{array}\kern1em \left(\Phi \left\{{Z}_i+{N}^{1/2}{\delta}_{il}\right\}-\Phi \left\{{Z}_i+{N}^{1/2}{\delta}_{il}-q{\left[K/\left({N}_T-G\right)\right]}^{1/2}\right\}\right)\right]\right\}, $$
(12)

where K ∼ χ 2(N T  − G) is a chi-square random variable with degrees of freedom N T – G, Φ(·) is the cumulative distribution function of a standard normal distribution, Z i  ~ N(0, 1) are independent standard normal random variables, and E K {·} and E Zi {·} are taken with respect to the distribution of K and Z i , respectively. Under the assumption that all treatment means are equal, the property of Q* has been discussed in many statistics textbooks, and the cumulative probability and quantile can be readily computed with popular software systems. However, the general distribution of Q* is relatively more complex and a special purpose algorithm is required to perform the associated calculations.

Unlike the prescribed F* test, the hypothesis testing of H 0: δ R  ≤ δ R0 with the Q* statistic is more involved. As noted earlier, the distribution of Q* is not a simple function of δ R alone and thus, the critical value cannot be determined for arbitrary treatment means satisfying δ R  = δ R0. It follows from Bau et al. (1993) that the least favorable configuration of μ = (μ1, …, μ G ) with δ R  = δ R0 is μ 0 = (μ10, …, μ G0) where μ i0 = −σδ R0/2, for i = 1, …, [G/2], and μ i0 = σδ R0/2, for i = [G/2] + 1, …, G, and [G/2] is the greatest integer being less than or equal to G/2. In other words, P{Q(G, N, τ 0) > c} > P{Q(G, N, τ) > c} for τ 0 = μ 0/σ, any τ has the range of the standardized means δ R0, and a positive constant c. Hence, the null hypothesis H 0: δ R  ≤ δ R0 is rejected at the significance level α if Q *  > Q α (G, N, τ 0), where Q α (G, N, τ 0) is the upper (100⋅α)th percentile of the distribution of Q* when the treatment means have the least favorable configuration μ = μ 0 and τ 0 = μ 0/σ. Also, the power function of the Q* test is obtained as

$$ {\pi}_{Q*}\left(\boldsymbol{\uptau} \right)=P\left\{Q\left(G,N,\boldsymbol{\uptau} \right)>{Q}_{\upalpha}\left(G,N,{\boldsymbol{\uptau}}_0\right)\right\} $$
(13)

for all sets of standardized treatment means τ satisfying δ R  > δ R0.

To illustrate the application of the suggested procedures, the numerical demonstration of Olejnik and Algina (2000) is reexamined here for the detection of the minimal effect in terms of f and δ R . Their focus was on the computations and interpretations of standardized linear contrast of mean differences and the corresponding proportion of variance effect size. The data was obtained from a randomized groups pretest–posttest study reported in Baumann et al. (1992) and they were interested in comparing the relative effectiveness of three types of interventions (Talk-Aloud, Directed Reading-Thinking Activity, and Directed Reading Activity) designed to affect reading comprehension skills of fourth-grade students. Using the 66 outcomes of the posttest error detection task with the number of groups G = 3 and group sample size N = 22, the ANOVA F and the studentized range statistics are F* = 5.3119 and Q* = 4.5443, respectively. At the significance level α = 0.05 and the magnitude f 0 = 0.10, the critical value of the minimal effect F test is F 0.05 = 4.1011 and the corresponding p-value is 0.0209. For the studentized range test with a specific effect size δ R0 = 0.2 and the least favorable configuration τ 0 = {−0.1, 0.1, 0.1}, the computed critical value and p-value are 3.8307 and 0.0154, respectively. As suggested in Cohen (1969, 1988), the particular minimum effect sizes f 0 = 0.10 and δ R0 = 0.2 represent a small magnitude of the standard deviation of the standardized means f and the difference of the standardized means δ, respectively. Accordingly, the two minimum effect tests of H 0: f ≤ 0.10 and H 0: δ R  ≤ 0.2 are rejected and there exist some essential differences between the three types of intervention programs. The SAS/IML (SAS Institute 2014) and R (R Development Core Team 2014) programs employed to perform the exact critical value and p-value calculations of both tests are presented in supplementary files.

Power Calculations and Sample Size Determinations

The theoretical implications and computational feasibility are important aspects of a test procedure for making statistical inferences. In practice, a research study requires adequate statistical power and sufficient sample size to detect scientifically credible effects. It is sensible that the corresponding power calculations and sample size determinations must also be considered for a viable procedure to extend the applicability in planning research designs. Consequently, the presented power functions for the F* and Q* tests can be useful in conducting power analysis and sample size computation for detecting the differences among standardized mean effects. The following numerical assessment exemplifies a typical research scenario most frequently encountered in the planning stage of a study.

Due to the prospective nature of advance research planning, the general guidelines suggest that typical sources like published findings or expert opinions can offer plausible and reasonable planning values for the model characteristics of mean effects and variance components. To explicate the essential features, the abovementioned posttest error detection task data of the three interventions is employed to provide planning values of the model parameters and effect sizes for a future intervention study. Specifically, the mean effects and variance component are designated as μ = {7.77, 9.77, 6.68} and σ2 = 10.17, respectively. With the additional specifications of G = 3, N = 22, f 0 = 0.1, and δ R0 = 0.2, the resulting powers for the two tests are π F* = 0.7109 and π Q* = 0.7216, respectively, when the significance level is α = 0.05. The achieved power is slightly less than the fairly common and somehow minimal level of 0.80. Therefore, the power calculation suggests that the designated configurations may not warrant a decent chance of detecting the minimal difference between intervention effects.

With the power formulas and associated algorithms, the sample size N needed to attain the nominal power (1 – β) can be found by a simple iterative search for the chosen significance level α and parameter values. Further computations show that a target power of 0.80 necessitates a balanced group size of 28 and 27 for the F* and Q* tests, respectively. Due to the underlying metric of integer sample sizes, the corresponding actual powers are 0.8127 and 0.8088, and they are marginally greater than the nominal power level 0.80. Hence, the required sample size is nearly 25% more than is needed for the original design. These configurations are incorporated in the user specifications of the SAS/IML and R programs presented in the supplemental files. Ultimately, users can easily identify the statements containing the key values in the computer code and then modify the program to accommodate their own model specifications.

Although the power performance and sample size requirement between the two procedures are almost identical, the particular results are confined to the specified minimal effect sizes f 0 = 0.1 and δ R0 = 0.2. It is of theoretical importance and practical interest to evaluate the relative performance between the F* and Q* test procedures across a variety of comparable design configurations. However, the distinct formulation of statistical hypotheses and the distributional complexity of test statistics do not permit a complete analytic examination and technical justification. Instead, a comprehensive empirical appraisal is conducted to assess and compare the power and sample size behavior of the two methods.

Numerical Study

In order to provide a systematic investigation for the power behavior of the F* and Q* test procedures, the effect sizes f 0 and f 1 under the null and alternative hypotheses are chosen a priori to facilitate meaningful comparisons. Although δ R is not a function of f, there exists an intrinsic property for the lower and upper bounds of the range of the standardized means δ R when the standard deviation of the standardized means f is fixed (Pearson and Hartley 1951). It can be easily shown that, for all sets of standardized treatment means τ with a fixed value f, the maximum range is δ Rmax = (2G)1/2 f for τ = τ max where τ max  = {−(G/2)1/2 f, 0,  ... , 0, (G/2)1/2 f}. In contrast, when G is even, the minimum range is δ Rmin  = 2f for τ = τ Emin where τ Emin  = {τ1, …, τ G }, τ i  = −f, i = 1, …, G/2; and τ i  = f, i = G/2 + 1, …, G. On the other hand, when G is odd, the minimum range is δ Rmin = 2Gf/(G 2 − 1)1/2 for τ = τ Omin where τ Omin  = {τ1, …, τ G }, τ i  =  − Gf/(G 2 − 1)1/2, i = 1, …, (G – 1)/2; and τ i  = Gf/(G 2 − 1)1/2, i = (G – 1)/2 + 1, …, G. Although similar results were given in David et al. (1972), their formulation of τ Omin differs from the presented expression of the standardized mean structure with a simple location shift. Note that the definition of τ Omin conforms to the least favorable configuration τ 0 for determining the critical value of the Q* test of minimal effect null hypothesis. Essentially, such standardized mean configurations need to be identified and incorporated in the power evaluation of the Q* test.

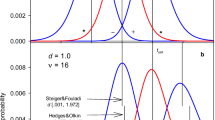
To delineate the underlying features of the two test procedures crossing different model characteristics, the numerical assessments are performed for (G, N) = (3, 16), (4, 12), and (6, 8). Accordingly, the total sample size is fixed as N T  = 48 for ease of comparison. Throughout this empirical study, the significance level and the minimum effect size are set as α = 0.05 and f 0 = 0.1, respectively. Thus, the associated critical values are F 0.05 = 3.9308, 3.2494, and 2.6663 for G = 3, 4, and 6, respectively. The corresponding least favorable standardized mean configurations of the Q* test are τ min  = {−0.1061, 0.1061, 0.1061}, {−0.1, −0.1, 0.1, 0.1}, and {−0.1, −0.1, −0.1, 0.1, 0.1, 0.1}. Moreover, the actual minimum effect sizes and critical values of the Q* test are δ R0 = 0.2121, 0.2, and 0.2, and Q 0.05 = 3.7964, 4.0524, and 4.4125 for G = 3, 4, and 6, respectively. Under the designated null hypothesis H 0: f ≤ 0.10 with the significance level α = 0.05, the power π F* of the F* test of the alternative hypothesis H 1: f > 0.10 are computed for the alternative effect size f = f 1 with f 1 = 0.1 to 0.9 with an increment of 0.1. For each f 1, the power π Q* of the Q* test of H 0: δ R  ≤ δ R0 versus H 1: δ R  > δ R0 are calculated for the two standardized mean extremes {τ max , τ Qmin } and {τ max , τ Emin } when G is odd and even, respectively. For ease of illustration, the attained powers π Q* of the Q* test evaluated at the two extremes are denoted by π Q*min and π Q*max , respectively. Accordingly, the designated effect sizes (f 1, δ Rmin , δ Rmax ) and resulting powers (π F*, π Q*min , π Q*max ) are summarized in Table 1 for the three model settings (G, N) = (3, 16), (4, 12), and (6, 8).

Table 1 Computed power of the F* and Q* tests for f 0 = 0.1 and α = 0.05
Full size table

It can be seen from the extensive numerical results that the achieved powers have a clear pattern π Q*max  > π F* > π Q*min for all f 1 > 0.1. The only exceptions occurred with the two cases of f 1 = 0.2 and 0.3 when G = 3. Specifically, the order between the three power levels is π F* > π Q*max  > π Q*min . On the other hand, the achieved powers of π F*, π Q*min , and π Q*max are decreasing in the number of groups G when all other factors remain constant including the total sample size. Thus, it requires a larger total sample size to achieve the designated power for the two tests when all other configurations are fixed. Instead of fixing the total sample size, the sample sizes required to achieve the nominal power 0.90 are also calculated for the selected group structures and effect settings. The computed sample sizes are presented in Table 2 and they are denoted by N F*, N Q*min , and N Q*max for the power functions π F*, π Q*min , and π Q*max , respectively. As expected, the necessary sample sizes decrease with increasing difference between f 1 and f 0 for all three scenarios. More importantly, the estimated sample sizes demonstrate a general phenomenon that N Q*min  ≥ N F* ≥ N Q*max . Also, the discrepancy between the three sample sizes (N Q*min , N F*, N Q*max ) substantially reduced as f 1 becomes larger than f 0. These findings extend those reported in David et al. (1972) for the traditional tests of zero effect. Hence, although the F test is a well-recognized method, the studentized range test may outperform the F test when the standardized mean structures are close to the extreme pattern of τ max . Therefore it is advisable that researchers need to conduct appropriate power analysis and employ suitable techniques based on the best knowledge of the vital model characteristics, especially the plausible and reasonable planning values for the mean effect configurations.

Table 2 Computed sample size of the F* and Q* tests for f 0 = 0.1, α = 0.05, and 1 – β = 0.90
Full size table

Conclusion

The two effect size measures of the standard deviation of the standardized means and the range of the standardized means among several treatments are direct extensions of the standardized mean difference between two groups. The existing literature on statistical hypothesis testing for comparisons among treatment means often assumes a null hypothesis of no difference. Consequently, the associated procedures and algorithms for data analysis and design planning are confined to the rejection of zero effect instead of the detection of treatment differences that are larger enough to have a practical impact. This study explicates and evaluates the features of the ANOVA F and the studentized range procedures for testing the null hypothesis that the treatment effects have a minimal important difference based on the standard deviation of the standardized means and the range of the standardized means, respectively. The notion of minimal important difference is vital to determine the critical values and power behavior of the ANOVA F and the studentized range procedures. The general guidance of Cohen (1969, 1988) suggests that the small, medium, and large effects in terms of f and δ could be defined as f = 0.10, 0.25, and 0.40, and δ = 0.2, 0.5, and 0.8, respectively. It is prudent to emphasize that the particular research question within a concentrated research field determines whether a specific effect size is practically or scientifically important. But in general, it should be based on substantive or empirical grounds, such as results from a prior effect size appraisal. Results in the current report showed that the relative power performance of the two approaches depends on the variability patterns of the mean effects. The studentized range method can be more or less powerful than the ANOVA F test if the mean structure has a maximum range or minimum range when the standard deviation of the standardized means remains constant. Numerical examples and computer algorithms were presented to illustrate the uses of the suggested methods for data analysis and design planning. The formulation and assessment described in this article gave a unified and rigorous explication of the two major procedures for detecting a minimal important difference among standardized means. The findings update and extend previous studies on the analysis of treatment effects among several groups.