Introduction

Simple mental arithmetic (e.g., 4 × 9) is an important skill and is required in many situations. It is widely accepted that educated adults use different strategies in mental arithmetic (e.g., Campbell and Xue 2001; Groen and Parkman 1972; LeFevre et al. 1996b): they retrieve the answer directly from their long-term memory or they calculate the answer by means of procedural strategies (e.g., decomposition of a problem into smaller facts). Simple arithmetic problems, such as 4 + 3 or 4 × 3, are conceptualized as arithmetic facts which are stored in long-term memory and which can be directly retrieved without any actual computational process. Typically, this applies to simple addition and multiplication problems with operands from 2 to 9 (LeFevre et al. 1996a; LeFevre et al. 1996b; Dehaene and Cohen 1997). In classical models of mental arithmetic, arithmetic facts are stored in and retrieved from a network of associations in declarative memory (e.g., Ashcraft 1987, 1992; Butterworth et al. 2001; Campbell 1994; Siegler 1988; Verguts and Fias 2005). A problem node stores information regarding the operands and the appropriate solution, and thus, the strength of associations between problems and possible answers determines the probability of the answers to be produced. When a problem is presented, activation spreads through the network, activating multiple nodes that share features with the presented problems. In a retrieval process, these multiple representations become active and compete until one reaches a sufficient level of activation and is finally selected and produced as an answer. For instance, when a priming task is performed, it has been observed that less time is required to name a numerical target which is primed by a single-digit arithmetic problem like 14 and 6 + 8, reflecting a facilitation effect, in both addition and multiplication problems (e.g., Jackson and Coney 2005).

Proof for the reliability of the associative cognitive models derives from performances in several tasks, such as number-matching task (LeFevre et al. 1988). In this task the participants are shown two numerical stimuli in sequence. The first stimulus (hereafter, the “cue”: e.g., 4 + 3) is a short-lasting pair of single- or double-digit numbers. The second stimulus consists of a single- or double-digit number (hereafter, the “target”: e.g., 5). Participants have to decide, as fast as possible, whether the target is one of the previously presented numbers or not, and, thus, mental arithmetic is completely irrelevant to the task. LeFevre et al. (1988) showed that response times (RTs) for rejecting non-matching targets were reliably higher when the target was the sum (7) of the numbers in the cue pair (e.g., 4 + 3) compared to when the target was neutral (or unrelated) as far as the cue numbers were concerned (9). The RT difference between sum and unrelated targets reflects an arithmetic fact interference effect, given that the sum node is automatically activated for the associated addition problem. This interference effect has been obtained with or without an arithmetic plus (+) symbol interposed between the numbers in the cue (Fabbri 2011; Fabbri et al. 2008; LeFevre et al. 1988). In a similar way, Thibodeau et al. (1996)showed that an interference effect could be obtained by presenting the product (e.g. 12 for the cues 4 and 3) of the numbers in the cue, interposing the multiplication symbol (“x”) between the cue digits. The product interference effect was found even when no multiplication symbol was presented (Galfano et al. 2009; Rusconi et al. 2004) and this interference was extended to the neighboring multiples in the multiplication network (Galfano et al. 2003). It can easily be assumed that sum and product interference effects are similar, reflecting a direct and automatic retrieval strategy of arithmetic facts from long-term memory. In other words, the interference effect is interpreted as evidence that the mere presentation of two single-digit numbers results in stimulus–driven activation of product or sum nodes via associative links in the network representing arithmetic facts.

Several models for addition (Butterworth et al. 2001) and multiplication (Verguts and Fias 2005) are proposed, suggesting that addition and multiplication facts might be stored in different semantic memory networks (Zhou 2011). However, those networks are not completely separate in memory. Indeed, the arithmetic problems share common operands, and it is likely that the mental representations of arithmetic facts contain overlapping features. For instance, in a verification task a cross-operation confusion effect has been found, suggesting longer reaction times in determining the correctness or incorrectness of an equation when the result is linked to another operation, such as 3 + 4 = 12 (e.g., Stazyk et al. 1982; Winkelman and Schmidt 1974; Zbrodoff and Logan 1986). Winkelman and Schmidt (1974) found this cross-operation confusion effect both when addition and multiplication problems were randomly presented in the same test (i.e., mixed condition), and when either addition or multiplication problems were presented in one test (i.e., pure condition). These results suggested that competing associations between addition and multiplication facts existed in long-term memory and these competing associations were activated, pushing the participants to inhibit the inappropriate responses. However, Zbrodoff and Logan (1986) noted that in Winkelman and Schmidt’s (1974) study a restricted set of stimuli was used and a within-subjects comparison was performed between mixed and pure conditions. Using all pairs of digits from 1 to 9 and considering the mixed and pure presentations as between-subjects factor, Zbrodoff and Logan found higher confusion effect in mixed condition than in pure condition, and this confusion effect was higher with multiplication problems than with addition problems. Thus, the authors ruled out the possibility that the arithmetic operations were interrelated each other.

However, there are several concerns which could question the interdependency between arithmetic networks, as showed by confusion problem effect. First, Stazyk et al. (1982) proposed that the confusion effect did not appear due to a competition of memory associations but it appeared due to a perceptual or encoding confusions. In other words, the individuals simply misperceived the arithmetic operator sign on these confusion problems. Second, the verification task differs from number-matching task. The first difference regards the activation of the arithmetic network which is automatic in number-matching task (e.g., LeFevre et al. 1988) while it is partially automatic in verification task (Zbrodoff and Logan 1986). The second difference regards the inhibition efficiency of arithmetic network. Indeed, the inhibition of arithmetic fact retrieval is necessary in the number-matching task to achieve the best performance, while the verification task requires at least a partial activation of the network as useful strategy in verification. Related to this point, the verification task assesses the arithmetic fact retrieval in an explicit way while the number-matching task does it in an indirect way. For instance, Zamarian and colleagues (Zamarian et al. 2007) showed that mild cognitive impairment patients did not differ from healthy controls in the arithmetic fact retrieval (in verification task), but they differed in their ability to suppress automatically accessed information (in number-matching task). Thus, the number-matching task could be considered as a suitable tool to address whether the addition and multiplication networks are or not interrelated.

The present study aimed to explore the interdependency between both operations using a number-matching task (LeFevre et al. 1988; Thibodeau et al. 1996). In other words, the aim was to study whether the interdependency between addition and multiplication problems also remained in a number-matching task, which is a powerful task for controlling the concerns questioning the interdependency (as indicated by cross-operation confusion effect) between arithmetic operation using a verification task. Specifically, in the present study the operation sign was not presented in the cue pair (and the misperception of operation signs was controlled) of the number-matching task and no calculation was requested to perform the task. At the same time, the arithmetic interference effect, usually found in this type of task even without any operation sign, could be considered as index of an arithmetic fact retrieval from arithmetic networks. To the goal of the study, pure and mixed conditions were created, as function of arithmetic problem embedded in the task. Moreover, the same task was performed three times. This experimental procedure related to the three testing sessions was relevant to study the presence of an interdependency between arithmetic operation problems because in each session (and every time the number-matching task was performed) only one arithmetic operation was embedded in the task. Thus, in the pure condition, the same arithmetic problem was embedded in the task along the three task sessions, while in the mixed condition, the arithmetic problem presented in the last session was different from that presented in the previous two sessions. Taking into account that the inhibition efficiency in this task increases when different sessions of the same task are performed (Fabbri et al. 2008) and that inhibition may be affected by practice (e.g., Harnishfeger 1995), it was expected that the pure and mixed conditions would not differ in the interference effect through sessions, if the addition and multiplication networks were interrelated. In other words, if the inhibition efficiency would increase in practicing with the task (and thus a decrease of arithmetic interference effect would expect) and the same operands would activate both addition and multiplication networks, when they were presented, then it did not matter to perform the task in pure and mixed conditions. Specifically, the interdependency between operations should be noted by similar interference effect pattern in the last session, given that this was the crucial session which differentiated pure from mixed conditions. The interdependency between addition and multiplication networks claims that the same operands (cue pair) active the retrieve of both sum and product related to presented operands, and thus, this activation pattern should be also expected in the present number-matching task during all three times with the activation of both arithmetic associative networks. This was the reason why the interdependency between addition and multiplication operations should show similar interference effect in the last session of pure and mixed conditions. By contrast, a significant difference between both conditions in the arithmetic interference effect of the last session probably argued for an independency between networks. In other words, in the pure condition only addition or multiplication network should be activated, reflecting a decrease of arithmetic interference effect, probably due to an increase of inhibition efficiency (Fabbri et al. 2008; Harnishfeger 1995). On the contrary, the mixed condition should induce a “switch” of activation from one operation network (in the first and second sessions) to other network in the last session, reflecting a greater arithmetic interference effect in the final testing session. This expectation could be in line with the Identical Elements (IE) model. According to this model, Rickard and colleagues (Rickard 2005; Rickard et al. 1994) suggested that problems facilitate each other with the use of a mediation strategy if their nodes contain exactly the same elements. Thus, facilitation effects are expected between multiplication and division, and between addition and subtraction, given that they are conceptually related to each other. Consequently, the interference effect found in the last session of the mixed condition (re-) appeared because a “different” arithmetic fact was presented respect to that of previous sessions, and a “different” network was activated.

Method

Participants

Eighty university students of the Department of Psychology participated in this study as volunteers. The students were enrolled both in basic (3 years of graduation) and in high (2 years of graduation) psychology course levels. The 83.75 % were females. The mean age was 25.08 years (SD = 6.01 years). The participants were all right-handed and had normal or corrected-to-normal vision. All participants provided written consent and the study was conducted following university ethical guidelines. According to the experimental design of 2 conditions × 2 arithmetic problems, the participants were randomly divided into four groups, in which the product and/or sum interference effect was implemented. In the pure conditions, two different groups were created: Group A (N = 20; mean age 24.65 ± 3.05 years; 15 females) performed the task in which product targets appeared, whereas Group B (N = 20; mean age 26.00 ± 5.50 years; 16 females) performed the task in which sum targets appeared. In a similar way, for the mixed conditions, two groups were created: Group C (N = 20; mean age 23.45 ± 5.49; 19 females) performed the task in which product targets appeared in the first and second sessions but a sum target appeared in the third session, whereas Group D (N = 20; mean age 26.20 ± 8.67 years; 17 females) performed the task with the opposite presentation of sum and product targets.

The four groups did not differ for age (F < 1.00) or gender (χ 2 < 3.50). Informed consent was obtained from all individual participants included in the study.

Materials

The materials for the number-matching task were the same as those described by Fabbri (2011) for addition and Galfano et al. (2003) for multiplication. Regardless of group condition, there was an initial cue of two digits followed by a target number according to which a “yes-no” decision was to be made, and one of two different keys (“q” and “p”) pressed on the computer keyboard. Participants were required to respond “NO” if the target did not match either of the numbers in the cue (non-matching stimuli) and “YES” if the target was one of the two numbers of the initial pair (matching stimuli). Matching trials made up half of the stimuli, whereas the other half formed non-matching trials. Within each group, half of the participants responded “yes” by pressing the “p” key with their right index finger and “no” by pressing the “q” key with their left index finger. The other half received the opposite instructions.

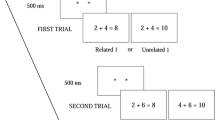
Three lists of 60 stimuli were created for each group. Each participant performed the task three times with the presentation of only one list for each testing session (Fig. 1). The order of the lists was counterbalanced across participants and testing sessions.

Fig. 1
figure 1

The left side of the Figure displays the experimental procedure of four Groups (and their relative operation embedded in the task for each session) during the three testing sessions. On the right side, the trial order of the number-matching task for a) product and b) sum interference effects

Full size image

For the multiplication problems, each trial included an initial cue of two different digits and a subsequent target. Stimuli were in Arabic format (Fig. 1). Combinations of digit cues and targets that might have evoked activation on the basis of some relationship between the items other than multiplication (e.g., addition, cues 8 and 3; target 11) were discarded from the stimulus set, in order to avoid generating associative confusion (Winkelman and Schmidt 1974). Ties (e.g., 2 and 2) were excluded, primarily because they appear to provoke access to the memory store more easily than other problems do (tie effect; Blankenberger 2001). Digit cues and targets composed of 0 and 1 were also excluded because they seem to elicit the retrieval of rules (e.g., Nx0 or Nx1; e.g., Baroody 1983; Sokol et al. 1991), instead of the retrieval of results (e.g., 9 × 4 = 36; Baroody 1983; Sokol et al. 1991). Each list contained six types of stimuli: three belonging to the non-matching category and three belonging to the matching category. In the non-matching category, the problem types were defined on the basis of the relationship between cues and target. Therefore, product, unrelated, and non-matching filler problems were defined. In product problems, the cues were two single-digit operands (e.g., 9 and 4) and the correct product was presented as target (e.g., 36) as shown by Fig. 1. In the unrelated problems, the cues were the same presented in the previous condition (e.g., 9 and 4), but the target was unrelated to either of the digits in the cue and it did not correspond to any neighboring multiples in the multiplication table (e.g., 38; Galfano et al. 2003). Finally, non-matching filler problems had a double-digit number in the cue (and the other cue was a single-digit number; e.g., 39 and 4) and a double-digit number in the target (e.g., 67), even if non-matching was present. Within the matching category, the problem types were target-balancing, cue-balancing, and matching filler stimuli. In target-balancing problems the correct product used in product problems was one of two digit cues (e.g., 36 and 7) and the following target (e.g., 36). In the cue-balancing problems, the same cues used in product trials were presented (e.g., 9 and 4), and one of the numbers in the pair was the target (e.g., 9). Finally, in matching filler problems, the cue pair was formed by a double- and a single-digit numbers, and the target always matched the double-digit number in the digit pair (e.g., cues 18 and 7; target 18). The three lists contained 10 stimuli for each problem type.

Also, for addition problems, cues and subsequent targets in Arabic format were presented (Fig. 1). Trials that could elicit activation based on multiplication (e.g., cues 2 and 4; target 8) were excluded, as well as ties and numbers 0 and 1 (e.g., N + 0 or N + 1; e.g., Baroody 1983; Pesenti et al. 2000) in the cue pair or in the target. The characteristics of stimuli for non-matching and matching categories were similar to those explained above. Thus, in the sum problems, the cues were two single-digit numbers (e.g., 5 and 7) and the subsequent target corresponded to their correct sum (e.g., 12), as shown by Fig. 1. In the unrelated problems, the same cue pair was presented (e.g., 5 and 7), but the target was unrelated to either of the digits in the cue and it did not correspond to any multiplication table (e.g., 22; Fabbri 2011). Finally, the non-matching filler problems were constructed using the same rules explained above (e.g., 5 and 32 as cues and 68 as target). Within the matching categories, in the target-balancing problems the correct sum used in sum problems and a single-digit number were presented as cue pair (e.g., 5 and 12), while the target matched with the correct sum (e.g., 12). In the cue-balancing problems, the same cues used in sum trials were presented (e.g., 5 and 7), and one of the numbers in the pair was the target (e.g., 5). As before, the matching filler problems contained double- and single-digit cues (e.g., 89 and 7) and the target matched with the double-digit number (e.g., 89). The three lists contained 10 stimuli for each problem type (6 types of problems × 10 stimuli for each problem type =60 stimuli for each list). For the three lists in which product or sum interference effect was embedded, the 60 (cue-target pairs) stimuli were different, according to the criteria of problem type. Presentation order was randomized for each subject, with the constraints that no more than three matching or non-matching stimuli appeared consecutively..

In each session, all digit cues were presented horizontally in white forecolor 40 Courier New bold font (5.73° × 2.87° of visual angle for each number) on a black background. All stimuli were presented in the center of the display. The numbers in each pair were not divided by any multiplication or addition sign, and they were separated by three spaces. The stimulus onset asynchrony (SOA) was fixed at 120 ms in both group conditions. This choice was grounded on the fact that Thibodeau et al. (1996) and LeFevre et al. (1988) found a product and sum interference effect, respectively, within the brief delays between cue and target presentation.

Design and Procedure

The experimental design foresaw 2 conditions (pure and mixed) and 2 different types of arithmetic interference effect (product and sum) presented in the number-matching task, determining 4 different groups (Fig. 1). Specifically, Group A (x, x, x) was presented with a product interference effect, and Group B (+, +, +) was presented with a sum interference effect in all three testing sessions. In Group C (x, x, +) a product interference effect was presented in the first and second sessions while a sum interference effect was presented in the last session. The reverse situation was encountered by Group D (+, +, x). The three testing sessions were scheduled for the same day with an interval of two hours between each other.

For each group, subjects were positioned 50 cm from the computer screen. The participants were instructed to respond accurately, but as quickly as possible. The order of trials in the task was displayed in Fig. 1, reporting examples of product and sum interference effect. At the center of the black screen a white hash symbol (#) appeared as a fixation point. The hash symbol was chosen in order to avoid generating any mathematical calculation. After 400 ms the digit cues appeared on the screen for 80 ms, and then they were masked for 20 ms by seven hash marks (#######). After this masking, an inter stimulus interval (ISI) of 20 ms was presented by way of a black screen. Finally, a target number appeared at the center of the screen. The digit target remained on the screen until the subjects responded “yes” or “no” or until 2500 ms had elapsed. In each testing session, participants underwent 18 training trials, with each problem type presented three times, before the test..

Data Analysis

The mean response time (RT) for correct responses and the percentage of errors were calculated for each group (Table 1).

Table 1 The mean RTs (and their SD) as well as mean percentage of errors (PE; and their SD) were reported for all problems in all groups
Full size table

In order to compare product and sum interference effects (i.e., longer RTs and more errors for product/sum than for corresponding unrelated problems), data analysis was focused only on non-matching product/sum and corresponding unrelated problems. Consequently, the arithmetic interference effect was defined as the difference between the mean RT for product/sum problems minus the mean RT for corresponding unrelated problems (dRT = RT product problems – RT unrelated problems or dRT = RT sum problems – RT unrelated problems). A positive difference indicated the presence of an arithmetic interference effect on RTs. The same difference was calculated for the percentage of errors (dPE = PE product problems – PE unrelated problems of dPE = PE sum problems – PE unrelated problems). This difference was calculated only after arcsine transformation of percentage of errors (Howell 1997). However, in the text the original percentages were reported. A positive difference indicated an arithmetic interference effect.

A two-way mixed ANOVA with Group (4 levels: A, B, C, and D), as between-subjects factor, and Session (three testing sessions) as a within-subject factor was performed on dRT and dPE, separately. Given that the third session was crucial for the hypothesis of the study, a further two-way ANOVA with Condition (pure vs. mixed) and Operation (multiplication vs. addition) as between-subject factors was performed on dRT and dPE separately. The Bonferroni post-hoc test was run when significant results were found. In all analyses, the p value was set at 0.05.

Results

When the analysis of RTs was performed, only correct responses were taken into consideration. Within these responses, RTs lower or higher than 3 SD were discarded from analysis (about 2.17 %). According to these criteria for detecting outliers, eight participants (two participants in each group) were discarded from the analysis. The four groups did not differ for the overall RTs (p = 0.40): A = 758 ms (SD = 133 ms), B = 809 ms (SD = 135 ms), C = 769 ms (SD = 111 ms) and D = 812 ms (SD = 87 ms).

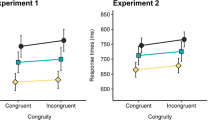
The Group x Session ANOVA on dRT showed significant Session effect (F(2136) = 25.87, p < 0.0001, η 2 p  = 0.28), but not a Group effect (p >. 10). For the Session effect, the post-hoc test showed that the dRT value was higher in the first session (dRT = +74.48 ms; SD = 39.65 ms) than the other two sessions (p < 0.0001 for both comparisons), as well as the comparison between second (dRT = +23.11 ms; SD = 55.61 ms) and third (dRT = +40.48 ms; SD = 31.39 ms) sessions (p < 0.0001). Crucially, a significant interaction between Group and Session factors was found (F(6136) = 3.56, p < 0.005, η 2 p  = 0.14), as shown in Fig. 2a. The post-hoc test showed that only in the third session, the four groups differed from each other. Specifically, the Group C (dRT = +55.25 ms; SD = 24.69 ms) and the Group D (dRT = +78.91 ms; SD = 11.00 ms) showed higher interference effect than that of Group A (dRT = +14.08 ms; SD = 32.41 ms) and Group B (dRT = +13.68 ms; SD = 57.44 ms), with p < 0.05 for all comparisons. No other significant comparisons were found.

Fig. 2
figure 2

a dRTs* (and their SD): pattern of product and sum interference effect for all groups through three testing sessions; b dPEs° (and their SD): pattern of product and sum interference effect for all groups through three testing sessions. *dRT = the mean RTs of sum/product problems minus the mean RTs of unrelated problems in ms. °dPE = the mean PEs of sum/product problems minus the mean PEs of unrelated problems

Full size image

The four groups did not differ for overall percentage of errors (p = 0.75): A = 4.69 % (SD = 5.23 %), B = 4.60 % (SD = 4.66 %), C = 3.46 % (SD = 3.88 %), and D = 4.97 % (SD = 3.89 %).

The same Group x Session ANOVA on dPE failed to show any main effect (ps > 0.06). In addition the Group x Session interaction was not significant (p > 0.10), as shown in Fig. 2b.

In order to deeply assess the arithmetic interference effect in the third session, the Condition x Operation ANOVA on dRT showed a significant Condition (F(1,68) = 40.10, p < 0.0001, η 2 p  = 0.37) effect, while Operation effect and Condition x Operation interaction did not reach statistical significance (ps > 0.15). The post-hoc revealed that in the last session the mixed condition induced an higher interference effect (dRT = +67.08 ms; SD = 22.33 ms) than that in the pure condition (dRT = +13.88 ms; SD = 45.97 ms).

The Condition x Operation ANOVA on dPE of the last session confirmed the Condition (F(1,68) = 11.00, p < 0.001, η 2 p  = 0.14) effect and the lack of significant Operation effect as well as its interaction with Condition factor (ps > 0.40). As before, the mixed condition of the last session had higher interference effect (dPE = +3.33 %; SD = 6.32 %) than that of the pure condition (dPE = −3.33 %; SD = 10.14 %)..

Discussion

In the present study, the interdependency of associative networks for addition and multiplication problems was tested in a number-matching task performed three times. In pure and mixed conditions, the changes in the arithmetic interference effect were observed through three sessions.

The results of analyses clearly indicated a specific pattern: there was a significant difference in the arithmetic interference effect in the last session. Specifically, the groups in the mixed condition (i.e., when a different operation from that of the previous sessions was embedded in the task) showed an higher interference effect than that found in the groups in the pure condition (i.e., when the same operation was embedded in the task through all sessions). Even when the last session was only considered, there was a difference between two conditions, with higher interference effect in the mixed condition than that in the pure condition.

According to an interdependency account between arithmetic networks, the interference effect pattern, found here, reflects that the addition and multiplication networks are interrelated, in a similar way to the confusion problem effect (Stazyk et al. 1982; Winkelman and Schmidt 1974; Zbrodoff and Logan 1986). According to the concept of the interdependency, the presentation of the cue pair (e.g., 3 and 4) should activate the corresponding nodes in both addition and multiplication networks. This activation should determine the activation of the related sum (e.g., 7) and product (e.g., 12) nodes, and this should be expected in all testing sessions. For instance, the associative network for multiplication problems has been “trained” in Sessions 1 and 2 and, thus, the addition network is (already) activated to retrieve the (correct) sum of addition problems presented in the third session (e.g., Group D) due to the interdependency between operations. Thus, during the first two sessions, the stimuli, such as 3 and 4, activated both addition and multiplication networks, but only one was active due to the type of operation (e.g., +) embedded in the task, implicitly. This network training could induce the activation of the other network, as soon as an operation (e.g., x) was involved in the task, allowing the automatic retrieval of related arithmetic fact.

Nevertheless, the findings of the present study seem to state more for an independency than interdependency between arithmetic networks. In fact, the interpretation of data according an interdependency account is less likely considering the significant session effect found. In pure condition, the interference effect decreased quite linearly through the sessions. In the mixed condition, this decrease was observed from the first to the second session, while in the last session the interference effect reached values similar to those found in the first session. Considering that inhibition functions normally suppress interference from distracting information (e.g., Bjorklund and Harnishfeger 1995), the interference effect not only reflects the automatic access to arithmetic facts stored in the networks, but also the efficiency of inhibition processes. Even if the interference effect was found in all sessions (e.g., positive dRT values), in the pure condition the participants “learned” to inhibit the (automatic) arithmetic fact retrieval through the sessions (Fabbri et al. 2008), suggesting that the inhibition could be affected by practice (Harnishfeger 1995). If the participants increased their efficiency in inhibiting the automatic retrieval, as shown in the pure condition (and in the first two sessions of mixed condition), then it was expected to also observe this efficiency for the last session of the mixed condition. In other words, if the idea of a network training reflected an instance of interdependency between networks, then this training effect should induce higher inhibition processes. The reappearing of the interference effect in the last session, when a “new” arithmetic problem was presented, could challenge the account of interdependency (i.e., network training) between networks, but indicate that the networks were separate or independent. This independency between networks could reflect the differences between number-matching and verification tasks, in terms of automatic activation of the arithmetic networks and of the involvement of inhibition processes (Fabbri 2011; Fabbri et al. 2008; LeFevre et al. 1988; Thibodeau et al. 1996; Zamarian et al. 2007). The proof of the interdependency of addition and multiplication as shown by the cross-operation confusion effect could be induced by the type of task used and, thus, by the type of processes involved in the task.

The pattern of the interference effect seems to be in line with the IE model (Rickard 2005; Rickard et al. 1994), and, as expected, the arithmetic interference effect of the last session in the mixed condition (re-) appeared because a “different” arithmetic fact was presented respect to that of previous sessions, and a “different” network was activated. This consideration could be also based on the fact that no operation sign was presented on the screen (no misperception of sign operations; Stazyk et al. 1982), and a number-matching task (i.e., no explicit calculation was required) was used, with the involvement of automatic (implicit) retrieval from semantic memory of arithmetic facts (Fabbri 2011; Fabbri et al. 2008; Galfano et al. 2003, 2009; LeFevre et al. 1988; Thibodeau et al. 1996).

Finally, the pattern of the interference effect was similar between multiplication and addition (i.e., no operation effect was found), confirming that simple arithmetic facts generated with numbers from 2 to 9 are stored in and retrieved from an associative network, with a similar retrieval strength for addition and multiplication problems (Ashcraft 1987, 1992; Butterworth et al. 2001; Campbell 1994; Siegler 1988; Verguts and Fias 2005). This aspect could add more evidence to the fact that these arithmetic operations are stored in different semantic networks (Zhou 2011).

However, the present data could be limited by the fact that the distribution of males and females was skewed toward females, probably reducing the generalizability of the results. In addition, the sample was composed by Psychology students, while the present study could be replicated, for example, in a sample of Mathematical students, with an high associative networks of arithmetic facts due to their expertise with arithmetic problems. Future studies should take into account these limits to address in a deep way the interdependency/independency between arithmetic fact networks, considering that, in many real situations, different operations are required to be performed in rapid succession in order to solve arithmetic problems (complex arithmetic problems often require multiple operations).

Using a verification task, a cross-operation confusion effect is general found, suggesting that addition and multiplication networks are interrelated. However, the experimental procedure used here with a number-matching task argues for an independency between arithmetic fact networks, even if this is an exploratory study. Thus, understanding the interaction between different arithmetic operations could be helpful to give a more detailed picture of current cognitive models of mental arithmetic and to propose therapeutic treatment, considering that, for instance, people with dyscalculia face persistent difficulties in retrieving arithmetic facts (e.g., De Visscher and Noël 2013).