Every Proposition is a Counterfactual

Abstract

I present and discuss two logical results. The first shows that a non-trivial counterfactual analysis exists for any contingent proposition that is false in at least two possible worlds. The second result identifies a set of conditions that are individually necessary and jointly sufficient for the success of a counterfactual analysis. I use these results to shed light on the question whether disposition ascribing propositions can be analyzed as Stalnaker-Lewis conditional propositions. The answer is that they can, but, in order for a counterfactual analysis to work, the antecedent and consequent must be related in a particular way, and David Lewis’s Time’s Arrow constraints on comparative world similarity must be relaxed. The upshot is that counterfactual analyses are easy to come by, in principle, even if not in practice. In that sense, it’s easy to be iffy.

1 Introduction

Counterfactual analyses, whether of causation, dispositions, belief, desire, or anything else, seem promising at first, yet they always seem to fail in the face of compelling counterexamples. Are counterfactual analyses just a bad idea? If not, what would suffice to make a counterfactual analysis successful? In this essay, I will answer these questions in the context of two logical results about counterfactual propositions. It turns out that a non-trivial counterfactual analysis exists for any robustly contingent proposition.

2 A Test Case: Dispositions

The difficulty of giving a conditional analysis of dispositions has received a great deal of attention. For example, David Lewis writes as follows:

All of us used to think, and many of us still think, that statements about how a thing is disposed to respond to stimuli can be analysed straightforwardly in terms of counterfactual conditionals. A fragile thing is one that would break if struck; an irascible man is one who would become angry if provoked; and so on. In general, we can state the simple conditional analysis thus:

Something x is disposed at time t to give response r to stimulus s iff, if x were to undergo stimulus s at time t, x would give response r.

Simple indeed—but false. (Lewis 1997, p. 143)

Several categories of counterexamples to the simple conditional analysis of dispositions are on record, including finks and reverse-cycle finks (Martin 1994) as well as mimicks and masks (Johnston 1992).

Consider the disposition to transmit electricity when touched by a conductor, which can also be referred to as the property of being live. A simple conditional analysis of a proposition ascribing this disposition would go as follows:

(LIVE):

The wire is live iff it would transmit electricity if it were touched by a conductor.

Martin (1994, pp. 2–3) notes the possibility of a dead (i.e., non-live) wire connected to an electro-fink, which is a device that would reliably detect that the wire is about to touch a conductor and would cause the wire to transmit electricity whenever it did touch a conductor. In such a case, (LIVE) fails from right to left: the wire is not disposed to transmit electricity, but, because of the action of the electro-fink, it would transmit electricity if were to touch a conductor. In short, a dead wire that is connected to an electro-fink is not live but would become live if touched by a conductor. Martin (1994, p. 3) also notes the possibility of a live wire connected to a reverse cycle electro-fink, which would reliably detect that the wire is about to touch a conductor and would prevent the wire from transmitting electricity if it were to touch a conductor. In short, a live wire that is connected to a reverse-cycle electro-fink is not dead but would be dead if it were touched by a conductor. In reverse-cycle electro-fink cases, the simple conditional analysis fails from left to right: the wire is disposed to transmit electricity, but the reverse-cycle electro-fink would prevent it from doing so if it were to touch a conductor.

Where finks and reverse finks involve externally caused counterfactual changes to a thing’s dispositional properties that thwart the simple conditional analysis, cases of mimicking (alternatively, masking) involve external factors that produce (prevent) the outcomes that count as manifestations of dispositions.¹ Consider a counterfactual analysis of a proposition ascribing fragility to a certain gold chalice:

(FRAGILE1):

The gold chalice is fragile iff it would shatter if it were dropped.

Johnston describes a case of mimicking that provides a counterexample to the right-to-left part of (FRAGILE1):

A gold chalice is not fragile but an angel has taken a dislike to it because its garishness borders on sacrilege and so has decided to shatter it when it is dropped. Even though the gold chalice would shatter when dropped, this does not make it fragile because while this dispositional conditional is not bare, i.e., the breaking when struck has a causal explanation, something extrinsic to the chalice is the cause of the breaking. (Johnston 1992, p. 232)

The chalice breaks when dropped, but, in disanalogy with the electro-fink case, it does not become fragile when dropped; the angel breaks it without making it fragile.

Consider, next, a counterfactual analysis of fragility for a certain glass cup:

(FRAGILE2):

The glass cup is fragile iff it would shatter if it were dropped.

Johnston (1992) describes the following case of masking,² a counterexample to the left-to-right part of (FRAGILE2):

Consider a fragile glass cup with internal packing to stabilize it against hard knocks. Packing companies know that the breaking of fragile glass cups involves three stages: first a few bonds break, then the cup deforms and then many bonds break, thereby shattering the cup. They find a support which when placed inside the glass cup prevents deformation so that the glass would not break when struck. Even though the cup would not break if struck the cup is still fragile. (Johnston 1992, p. 233)

The glass cup would not break if dropped, but, in disanalogy with the reverse-cycle electro-fink case, it would not cease being fragile when dropped; the packing material would prevent breakage without making the glass non-fragile.

These and many other counterexamples add up to such a compelling body of evidence against the viability of various conditional analyses of dispositions that many have decided to give up on the possibility of a conditional analysis. Shope (1978) is an early advocate of this position. More recent advocates include Lewis (1997), as we have seen, but also Fara, who writes:

The lesson that should be drawn from the preceding discussion is that conditionals are simply not suited to the task of stating the truth conditions of disposition ascriptions. (Fara 2005, p. 61)

Bonevac et al. (2006; 2011) have criticized this diagnosis and suggested (Bonevac et al. 2006, p. 314) that controversial rules of inference for the conditional (specifically, those associated with the semantic condition of Strong Centering) play a role in counterexamples to conditional analyses of dispositions. They write:

[F]ar from serving as a general recipe for the refutation of conditional analyses, “finking” cases can serve to expose presuppositions of some of our conditional modal thought. The relevant examples can be used as a tool for conditional archaeology: intuitive responses to the finking examples support investigation of the possibility of a new sort of conditional, a “neighborhood” conditional that does not satisfy some of the traditional presuppositions about conditionals. Bonevac et al. (2006, p. 315)

Though Bonevac et al. and Fara disagree about some things, the former seem willing to concede to Fara and other critics of conditional analyses of dispositions at least that the standard sort of Stalnaker-Lewis conditional is not suited to “the task of stating the truth conditions of disposition ascriptions.”

There is no need to concede even that much.

In what follows, I will show that one need not give up Strong Centering in order to maintain simple conditional analyses of disposition ascribing propositions. Any proposition can be given a conditional analysis using a strongly centered Stalnaker-Lewis counterfactual conditional. And if the analysandum proposition is robustly contingent, in the sense of being true in at least one possible world and false in at least two possible worlds, then a non-trivial counterfactual can be chosen as the analysans.

3 How to Make any Proposition a Counterfactual

Define a Lewis frame to be a triple 〈W, R, ≤ 〉 such that W is a nonempty set and R is a binary relation on W (the accessibility relation) and ≤ is a function mapping each i ∈ W to a binary comparative similarity relation ≤ _i such that R and ≤ _i satisfy Lewis’s conditions:³

• (1) ≤ _i is transitive;

• (2) ≤ _i is strongly connected: for each j, k ∈ W, either j ≤ _i k or k ≤ _i j;

• (3) R is reflexive;

• (4) ≤ _i is strongly centered, i.e., i is strictly minimal in ≤ _i : for any j ∈ W, if j ≤ _i i, then j = i;

• (5) inaccessible worlds are ≤ _i maximal: if j, k ∈ W and 〈i, k〉 ∉ R, then j ≤ _i k; and

• (6) accessible worlds are more similar to i than inaccessible worlds: if j, k ∈ W and 〈i, j〉 ∈ R and 〈i, k〉 ∉ R, then j < _i k.

Define a proposition ⁴ to be any subset of W, and for any proposition A and i ∈ W, define i to be an A-world iff i ∈ A. For any propositions A, B, define AB to be A ∩ B and define $\overline {A}$ to be W ∼ A (the complement of A in W).⁵ Since ≤ _i is strongly connected, we can define a strict subrelation < _i of ≤ _i as follows: j < _i k iff j ≤ _i k and k ≰ _i j. A is defined to be a contingent proposition iff A ⊆ W and W ≠ A ≠ ∅. Propositions A ₁, …, A _n are said to be compossible iff A ₁ ∩ A ₂ ∩ … ∩ A _n ≠ ∅. Propositions A and B are independent iff $A\cap \overline {B}\neq \emptyset \neq B\cap \overline {A}$. A entails B iff A ⊆ B. We let i R stand for the set of worlds accessible to i, i.e., {j ∈ W: 〈i, j〉 ∈ R}.

Next, define the counterfactual operator to be the binary function > mapping any pair A, B of propositions to the counterfactual proposition A > B as follows:

$$A>B=\{i\in W:\:iR\cap A=\emptyset\}\cup\{i\in W:\:\exists j\in AB\cap iR,\,\forall k\in A\overline{B},\, j<_{i} k\}$$

That is, A > B is true at world i iff either no world is accessible to i at which A is true, or else at least one AB-world accessible to i is more similar to i than any $A\overline {B}$-world. A > B is thus defined via the Lewis (1973) truth conditions for counterfactuals. Given these definitions, we prove the following:

First Conditional Analysis Theorem:

For any nonempty set W and any X ⊆ W, there exist R and ≤ such that W, R, ≤ is a Lewis frame and for some propositions A and B, X = (A > B). If X is a contingent proposition and there are at least two possible worlds at which X is false, then A and B can be chosen so that A ≠ W and B ⊈ X.

Proof

Let W be a nonempty set, and let X ⊆ W. Let R = W × W (so that every world is accessible to every world). There are three cases: either X = W or X = ∅ or W ≠ X ≠ ∅.

Case 1

Suppose X = W. Let A = ∅ and B = W, and, for each i ∈ W, let ≤ _i be any comparative world similarity relation on W satisfying Lewis’s conditions (1)–(6) relative to W and R. It follows that 〈W, R, ≤ 〉 is a Lewis frame and X = (A > B).

Case 2

Suppose X = ∅. Let A = W and B = ∅, and, for each i ∈ W, let ≤ _i be any comparative world similarity relation on W satisfying Lewis’s conditions (1)–(6) relative to W and R. It follows that 〈W, R, ≤ 〉 is a Lewis frame and X = (A > B).

Case 3

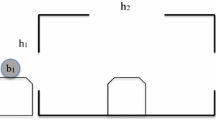
Suppose W ≠ X ≠ ∅. It follows that for some j, k ∈ W, j ∈ X, and k ∉ X. Let A be a proposition containing both j and k, and let B be a proposition such that ∅ ≠ A B ⊆ X and A X ⊆ B. If there is a k′ ∈ W such that k ≠ k′ ∉ X, then we can choose A and B so that j, k ∈ A and k′ ∉ A and j, k′ ∈ B and k ∉ B, in which case A ≠ W and B ⊈ X, as in Fig. 1.

Fig. 1

Choice of A and B relative to X, j, k, and $k^{\prime }$

It will always suffice to choose A = {j, k}, and, if k′ exists, it will suffice to choose B = {j, k′}; otherwise, it suffices to choose B = {j}.

Next, we show that ≤ can be chosen so that X = (A > B). The diagrams will include k′, but the same choice procedure works even if k′ does not exist and B is chosen so that j ∈ B ⊆ X.

First, consider any world i belonging to X. Since A X ⊆ B, $i\not \in A\overline {B}$. Hence, either i ∈ A B or $i\in \overline {A}\,\overline {B}$ or $i\in \overline {A}B$, as in Fig. 2. If i ∈ A B, choose ≤ _i arbitrarily, subject to Lewis’s constraints (1)–(6). Since i an AB-world, and since i is strictly minimal in ≤ _i , there is an AB-world (namely i) that is more similar to i than any $A\overline {B}$-world. Accordingly, i ∈ A > B.

Fig. 2

Cases in which i belongs to X

If $i\in \overline {A}\,\overline {B}$ or $i\in \overline {A}B$, choose ≤ _i so that Lewis’s conditions (1)–(6) are satisfied and so that j is the most similar world to i other than i itself. Then, once again, there is an AB-world (namely j) that is more similar to i than any $A\overline {B}$-world, since neither i nor j is an $A\overline {B}$-world. Hence, i ∈ A > B.

Having constructed ≤ _i so that i ∈ A > B if i ∈ X, consider now any world i not belonging to X. Since A B ⊆ X, we have i ∉ A B, hence either $i\in A\overline {B}$ or $i\in \overline {A}\,\overline {B}$ or $i\in \overline {A}B$, as in Fig. 3. If i is an $A\overline {B}$-world, then choose any ≤ _i such that Lewis’s conditions (1)–(6) are satisfied. Since i is an $A\overline {B}$-world and i is minimal in ≤ _i , no AB-world is more similar to i than every $A\overline {B}$-world; hence, i ∉ A > B.

Fig. 3

Cases in which i does not belong to X

If $i\in \overline {A}\,\overline {B}$ or $i\in \overline {A}B$, then choose ≤ _i so that Lewis’s conditions (1)–(6) are satisfied and so that k is the most similar world to i different from i. Since k is an $A\overline {B}$-world and i is not an AB-world, no AB-world is more similar to i than every $A\overline {B}$-world. Accordingly, i ∉ A > B.

Generalizing on i, we have in Case 3 that X = (A > B), and, if k′ exists, A ≠ W and B ⊈ X. Since for each i, ≤ _i was chosen as satisfying Lewis’s (1)–(6), it follows in Case 3 as in Cases 1 and 2 that 〈W, R, ≤ 〉 is a Lewis frame. □

What the First Conditional Analysis Theorem shows is that for any proposition X, there are propositions A and B such that X is the proposition A > B for a suitably chosen comparative similarity measure ≤ and accessibility relation R. Now, given Strong Centering, every proposition is trivially a counterfactual, since X = (W > X) always holds, but the theorem goes beyond this trivial point. If X is a robustly contingent proposition (in that X is true in at least one possible world and false in at least two possible worlds), then A and B can be chosen so that A ≠ W and B ≠ X and so that A and B are independent and A, B, and X are compossible. So, every proposition is a counterfactual, and every robustly contingent proposition is a non-trivial counterfactual.

4 Remarks on the First Conditional Analysis Theorem

The First Conditional Analysis Theorem sheds new light on the project of giving counterfactual analyses. For various properties and propositions, it is a matter of great controversy whether the property or proposition is “iffy” or whether it has some other status, such as the status of being “categorical”. The First Conditional Analysis Theorem shows that any attempt to make a distinction between those propositions that are “iffy”, and those that are not, simply fails, since any proposition can be described as a counterfactual proposition. “Iffy-ness” is easy to come by.

4.1 By Analyzing one Proposition one Analyzes all

One might object that the First Conditional Analysis Theorem does not really show that all propositions are iffy, since it operates by finding a counterfactual operator that is designed to yield a counterfactual analysis for a single target proposition rather than by finding a single counterfactual operator that yields iffy analyses of all propositions at once.⁶ This objection misses the mark, however. The counterfactual operator constructed by a single application of the First Conditional Analysis Theorem does always generate counterfactual analyses of all propositions, since the entire space of propositions is spanned by each counterfactual operator. That is, the set of propositions resulting from applying any single counterfactual operator to all pairs of propositions just is the set of all propositions.⁷ What the First Conditional Analysis Theorem does not do is guarantee a non-trivial analysis of all propositions at once. Instead, it allows us to guarantee a non-trivial analysis for a robustly contingent target proposition that we find of interest. But once the target proposition is analyzed, we will also have non-trivial counterfactual analyses of many other propositions, including some that have important logical relationships to the target proposition.

Consider the case of a disposition-ascribing target proposition and the counterfactual into which it is analyzed. Many of the propositions to which the disposition ascription is logically related will turn up as non-trivial counterfactuals having the same antecedent as the disposition ascription’s counterfactual analysis, and these other propositions will be of great interest in the context of the given disposition ascription. If we have analyzed a disposition ascription as saying that a certain manifestation condition would be true if a certain test condition were true, we will naturally be interested in what else would be the case if the test condition were true. Indeed, given a counterfactual analysis X = (A > B), the greatest interest will generally attach to propositions A > Y, for propositions Y that are logically or causally related to B.

But if counterfactual analyses are so easy to come by and if every counterfactual operator spans the whole space of propositions anyway, then what is there to learn from the First Conditional Analysis Theorem? Counterfactual analyses are notoriously unsuccessful. The First Conditional Analysis Theorem provides a recipe for devising counterfactual analyses that actually work. Time for an example.

4.2 An Example

The First Conditional Analysis Theorem seems to cast doubt on the lesson drawn by Lewis, Fara, and others that a simple conditional analysis of dispositions cannot work. Let us begin with a proposition that has nothing to do with dispositions and see how the First Conditional Analysis Theorem applies to it. We will return at a later point to the topic of dispositions.

Let W be the set of all possible worlds and consider the following robustly contingent proposition:

H::

Harvard has fewer than 20,000 students.

The First Conditional Analysis Theorem shows that there is a way of measuring comparative world similarity, and there are propositions A _H ≠ W and B _H ⊈ H such that A _H > B _H is the proposition H that Harvard has fewer than 20,000 students. Can we go further and identify suitable choices of A _H and B _H ? The proof uses a highly abstract and non-constructive procedure for finding A and B, but, even overlooking that obstacle, it would be fair to say that there is no reason to expect that English will happen to provide sentences that express suitable propositions A and B. In this case, however, we are in luck. English does provide suitable sentences.

First, recall that we must choose an antecedent that is compossible with H and also compossible with $\overline {H}$. The following choice of antecedent will work:

A _H ::

Harvard has exactly 100 nonstudent employees.

A consequent B _H must now be chosen so that A _H B _H entails H and so that H is not compossible with $A_{H}\overline {B_{H}}$, i.e., $A_{H}\overline {B_{H}}$ entails $\overline {H}$. It will work to choose B _H as follows:

B _H ::

The total number of Harvard’s students and nonstudent employees is less than 20,100.

Clearly, A _H ≠ W and B _H ⊈ H. Also, A _H B _H entails H, since given that Harvard has exactly 100 nonstudent employees but fewer than 20,100 students and nonstudent employees, it follows that Harvard has fewer than 20,000 students. In addition, $A_{H}\overline {B_{H}}$ is not compossible with H. Given that Harvard has exactly 100 nonstudent employees but at least 20,100 students and nonstudent employees, it cannot be true that Harvard has fewer than 20,000 students. The proof of our Theorem tells us that a comparative world similarity relation can be chosen so that H and A _H > B _H are identical.

A _H > B _H ::

If Harvard had exactly 100 nonstudent employees, the total number of Harvard students and nonstudent employees would be less than 20,100.

The idea that “H” and “A _H > B _H ” could refer to the same proposition may seem surprising, but notice that A _H > B _H already counts as a (slightly annoying) way to answer a question that would be most straightforwardly answered by H. Consider this exchange:

Watson::

Tell me this, Holmes. How many students are there at Harvard? Is it as many as 20,000?

Holmes::

Let’s put it this way: if there were exactly 100 non-student employees at Harvard, the total number of students and non-student employees would be less than 20,100.

Watson::

For pity’s sake, Holmes, why don’t you just say, “Harvard has fewer than 20,000 students”?

The First Conditional Analysis Theorem confirms Watson’s judgment that Holmes could have given the same answer to Watson’s question by asserting H as it is standardly worded.

Of course, the counterfactual operator can be interpreted in such a way that “H” and “A _H > B _H ” do not pick out the same proposition. Consider a world w ₀ in which Harvard has 6000 students but adopts a policy according to which whenever its non-student employee count drops below 125, a massive cohort of 100,000 previously unofficial online students become officially enrolled. Given whatever standard of comparative world similarity is implicit in our everyday judgments about counterfactuals, w ₀ will not be a world in which “A _H > B _H ” expresses a proposition that is true. The proposition expressed by the following sentence will be true at w ₀ instead:

If Harvard had exactly 100 non-student employees, the total number of Harvard’s students and non-student employees would be at least 100,100.

Thus, w ₀ is a counterexample to the identity H = (A _H > B _H ) under what Lewis called “a standard resolution of the vagueness of counterfactuals.” Nonetheless, by the First Conditional Analysis Theorem, there is an (evidently non-standard) resolution of the vagueness of counterfactuals on which “H” and “A _H > B _H ” do pick out the same proposition, and on that standard of comparative world similarity the following counterfactual is true at w ₀:

If Harvard had exactly 100 non-student employees, it would not observe a policy according to which whenever its non-student employee count drops below 125, a massive cohort of 100,000 students become officially enrolled.

Switching to a non-standard resolution of vagueness on which “H” and “A _H > B _H ” pick out the same proposition does not mean that there has been any change in which propositions are true at w ₀. Since w ₀ belongs to the same sets of worlds it always did, the same propositions are true at w ₀ as always were. What is different is the way in which certain of those propositions can be specified.

But is the non-standard resolution of vagueness that allows “H” and “A _H > B _H ” to refer to the same proposition legitimate? It is important to distinguish a non-standard resolution of vagueness from an illegitimate comparative world similarity relation. Any comparative world similarity relation that satisfies the six conditions of (Lewis 1973, p. 48) is formally legitimate, even if it does not satisfy the non-formal conditions on comparative world similarity developed in (Lewis 1979). We will return to this issue later.

4.3 Choosing the Antecedent and Consequent

In general, if B is chosen first in the counterfactual analysis of X described in Case 3 of the proof of the First Conditional Analysis Theorem, there is considerable latitude in the choice of A. As noted in the proof, one can always choose A to be the very specific proposition {j, k}. Another option is the very weak proposition X ≡ B,⁸ which turns out to be the weakest proposition that can serve as A. X ≡ B is the union of XB and $\overline {X}\;\overline {B}$; i.e., the set of all worlds in which X and B are (like j in the proof) both true or (like k) both false. The range of propositions eligible to serve as A consists of every proposition “between” {j, k} and X ≡ B, i.e., {j, k} ⊆ A ⊆ (X ≡ B). Equivalently, once j and k are chosen, A is the union of any subset of XB containing j with any subset of $\overline {X}\;\overline {B}$ containing k.

Applying the above to the Harvard example, suppose Harvard has exactly 100 non-student employees. Then either Harvard has at least 20,000 students and the total of its students and non-student employees is at least 20,100, or else Harvard has fewer than 20,000 students and the total of its students and non-student employees is fewer than 20,100. So, in the Harvard example, as expected, A _H ⊆ (H ≡ B _H ). The converse inclusion does not hold, however. In particular, there are worlds at which Harvard has at least 20,000 students and at least 20,100 students and non-student employees but without having exactly 100 non-student employees (say, because there are 125 non-student employees). Similarly, there are worlds at which Harvard has fewer than 20,000 students and fewer than 20,100 students and non-student employees but (again) without having exactly 100 non-student employees (say, because there are only 30 non-student employees). So, in the Harvard case, we have not chosen the weakest possible antecedent to go with consequent B _H .

5 Counterexamples Diagnosed

Now, what happens when we attempt to choose antecedents and consequents for a counterfactual analysis of a disposition-ascribing proposition? The usual approach, exemplified by (LIVE), (FRAGILE1), and (FRAGILE2), is to let the antecedent be an intuitively plausible test condition for the disposition and let the consequent be a description of the standard manifestation of the disposition. But, as we saw in Section 2, this approach leads to counterexamples involving finks, reverse finks, masks, and mimicks. We are now in a position to identify, for each kind of counterexample, which specific defect in a counterfactual analysis gives rise to that kind of counterexample.

Recall Martin’s example of a fink, in which a dead wire is connected to a device that detects whether the wire is touching a conductor. The device would cause the wire to transmit electricity if it were touching a conductor, hence this is a case in which (LIVE) fails because the disposition is absent, yet the corresponding counterfactual is true. In Martin’s example of a reverse fink, a live wire is connected to a device that detects whether the wire is touching a conductor. The device would prevent the wire from transmitting electricity if it were touching a conductor, hence we have a case in which (LIVE) fails because the disposition is present, but the corresponding counterfactual is false. Both fink and reverse fink cases involve counterfactual changes to a thing’s dispositional properties.

Now, recall Johnston’s mimicking example, in which an angel has taken a dislike to a garish gold chalice. The chalice is not fragile, but the angel has decided to shatter it if it should be dropped. In this example, (FRAGILE1) fails from right to left as (LIVE) does in the finkish case, but in disanalogy with the finkish case, the chalice does not become fragile when dropped. Instead, the angel breaks it without making it fragile. In Johnston’s masking example, a fragile glass cup is fitted with internal packing that would prevent the cup from breaking if it were dropped or struck. In this case, (FRAGILE2) fails from left to right as (LIVE) does in the reverse fink case, but in disanalogy with the reverse fink case, the cup does not cease being fragile at any point. The packing prevents breakage, yet the cup remains fragile.

What the masking and mimicking cases show about (FRAGILE1) and (FRAGILE2) is that the antecedent-consequent pairs and the disposition ascriptions that these pairs are used to analyze do not stand in the right entailment relations. In the counterfactual analysis, X = (A > B) found by the First Conditional Analysis Theorem, A and B are chosen so that AX entails B and AB entails X. The problem in mimicking cases is that AB does not entail X: the gold chalice’s being dropped and shattering does not entail its being fragile. In masking cases, the problem is that AX does not entail B: the glass cup’s being dropped while fragile does not entail its shattering. Analogous entailment failures hold in the fink and reverse fink cases, but in those cases the entailment failures are not the whole story. In fink and reverse fink cases something more is going on.

What finks and reverse finks show (that masking and mimicking cases do not) is that one must choose a comparative similarity relation such that X = (A > X).⁹ A comparative world similarity relation that does not make X and A > X the same proposition simply cannot make X and A > B the same proposition.¹⁰ In finking cases, X and A > X are distinct because A > X does not entail X: the wire is not live, but if a conductor were touching it, it would be live. In the proof of the First Conditional Analysis Theorem, we blocked this sort of case when, for i ∉ X but where either $i\in \overline {A}\;\overline {B}$ or $i\in \overline {A}B$, we chose k to be the most similar world to i different from i itself. In reverse finking cases, X and A > X are distinct because X does not entail A > X: the wire is live, but it’s not true that if it were touching a conductor, it would still be live. In the proof of the First Conditional Analysis Theorem, we blocked this sort of case when, for i ∈ X but where either $i\in \overline {A}\;\overline {B}$ or $i\in \overline {A}B$, we chose j to be most similar world to i different from i itself.

One might object as follows: isn’t it just false that X ever entails A > X and false that A > X ever entails X? Isn’t that precisely what the fink and reverse fink examples show? No, what those examples show is that X and A > X are distinct propositions under a standard resolution of the vagueness of counterfactuals. The right conclusion is that no standard resolution of vagueness is suited for a counterfactual analysis of a disposition ascribing proposition.¹¹

6 A Recipe for Success: the Second Conditional Analysis Theorem

In light of the preceding, we have precise diagnoses of what is wrong with counterfactual analyses in mask, mimick, fink, and reverse-fink examples. We have seen that a counterfactual analysis X = (A > B) will avoid masks and mimicks if A and B are chosen so that AX entails B and AB entails X. Given that A and B are so chosen, the analysis will avoid finks and reverse finks if the comparative world similarity measure for the counterfactual operator is chosen such that X = (A > X). But we can say even more than this. AX’s entailing B, AB’s entailing X, and X’s being identical to (A > X) do more than merely rule out specific classes of counterexamples to a counterfactual analysis. They are individually necessary and jointly sufficient for a successful counterfactual analysis. That is, we have the following:

Second Conditional Analysis Theorem

For any Lewis frame and any propositions A, B, and X defined thereon, X = (A > B) if and only if AX entails B, and AB entails X, and X = (A > X).

Proof

Let 〈W, R, ≤ 〉 be a Lewis frame, and suppose X, A, B ⊆ W.

Left to right: Where > is the counterfactual operator on this frame, suppose that X = (A > B).

First, we show that AX entails B. Let i ∈ A X; then i ∈ A and i ∈ (A > B). By the reflexivity of accessibility (Lewis 1973, p 48, (3)), at least one A-world, namely i, is accessible to i; so there is an AB-world j that is accessible to i and more similar to i than any $A\overline {B}$-world. Since i is an A-world, it follows by Strong Centering (Lewis 1973, p. 48, (4)) that j = i, so i is a B-world. Generalizing on i, we have that A X ⊆ B, i.e., AX entails B.

Next, we show that AB entails X. Let i ∈ A B; by the reflexivity of accessibility (Lewis 1973, p. 48, (3)), i is accessible to i; let j be any $A\overline {B}$-world. Then j ≠ i, so by Strong Centering j≰ _i i. By Strong Connectedness (Lewis 1973, p. 48, (2)), i ≤ _i j. So, i is more similar to i than j is. Generalizing on j, we have that i is an AB-world that is accessible to i and more similar to i than any $A\overline {B}$ world. Hence, i ∈ (A > B), i.e., i ∈ X. Generalizing on i, we have that A B ⊆ X, i.e., AB entails X.

Finally, we show that X = (A > X). Let i ∈ X, i.e., i ∈ (A > B). If no A-world is accessible to i, then i ∈ (A > X), so suppose without loss of generality that at least one A-world is accessible to i. Then there is an AB-world j that is accessible to i and more similar to i than any $A\overline {B}$-world. Since A B ⊆ X = (A > B), j is an A > B-world and therefore an A(A > B)-world. Let k be any $A\overline {(A>B)}$-world. Since A B ⊆ (A > B), k must be an $A\overline {B}$-world. Hence, j is more similar to i than k is. Generalizing on k, we have that j is an A(A > B)-world accessible to i and more similar to i than any $A\overline {(A>B)}$-world. So, i ∈ (A > (A > B)), i.e., i is an A > X-world. Generalizing on i, we have that X ⊆ (A > X). Conversely, suppose i ∈ (A > X); i.e., i ∈ (A > (A > B)). If no A-world is accessible to i, then i ∈ (A > B)=X, so suppose without loss of generality that at least one A-world is accessible to i. Then at least one A(A > B)-world j is accessible to i and more similar to i than any $A\overline {(A>B)}$-world. Since A X ⊆ B, j is an AB-world. Let k be any $A\overline {B}$-world; then, since A X ⊆ B, k must be an $A\overline {(A>B)}$-world, so j is more similar to i than k is. Generalizing on k, we have that j is an AB-world accessible to i and more similar to i than any $A\overline {B}$-world. Hence, i ∈ (A > B)=X. Generalizing on i, we have (A > X) ⊆ X, and thus X = (A > X).

Right to left: Suppose that A X ⊆ B and A B ⊆ X, and X = (A > X).

First, we show X ⊆ (A > B). Suppose i ∈ X; if no A-world is accessible to i, then i ∈ A > B by definition, so assume without loss of generality that at least one A-world is accessible to i. Since X = (A > X), at least one accessible AX-world m is more similar to i than any $A\overline {X}$-world. Since AX entails B, m is an AB-world. Let n be any $A\overline {B}$-world. Since AX entails B, n is an $A\overline {X}$-world, so m is more similar to i than n is. Generalizing on n, it follows that m is an AB-world accessible to i that is more similar to i than any $A\overline {B}$-world. Accordingly, i ∈ A > B. Generalizing on i, we have that X ⊆ (A > B).

We show (A > B) ⊆ X by contraposition. Suppose i ∉ X; then i ∉ A > X, so at least one A-world is accessible to i, and for every AX-world accessible to i, at least one $A\overline {X}$ world is at least as similar to i as the given AX-world is. Let m be an AB-world accessible to i. Since AB entails X, m is an AX-world. Hence, there is an $A\overline {X}$-world n _m such that n _m is at least as similar to i as m is. Since AB entails X, n _m is an $A\overline {B}$-world. So, given an AB-world m accessible to i, there is an $A\overline {B}$-world n _m such that n _m is at least as similar to i as m is. Generalizing on m, we have that i ∉ A > B. Generalizing on i, it follows that (A > B) ⊆ X, and thus X = (A > B). □

The Second Conditional Analysis Theorem specifies conditions necessary and sufficient for a counterfactual analysis to succeed. The significance of the First Conditional Analysis Theorem is that it establishes that these conditions can indeed be satisfied. And if the comparative world similarity relation constructed in the First Conditional Analysis Theorem seems artificial, the Second Conditional Analysis Theorem tells us what it is about the constructed comparative similarity relation that matters, namely the fact that it results in X = (A > X). The success of a counterfactual analysis does not require precisely the comparative similarity relation constructed in the First Conditional Analysis Theorem; any relation that supports X = (A > X) will do, provided that AX entails B and AB entails X.

7 The Conditional Fallacy Arguments

One matter that I alluded to earlier that deserves additional attention is the relationship between the Conditional Analysis Theorems and the discussion of Conditional Fallacy Arguments in (Bonevac et al. 2006). If the First and Second Conditional Analysis Theorems provide conditional analyses that are successful, then how do these results avoid the Conditional Fallacy Arguments?

Bonevac et al. (2006) describe the general form of one kind of Conditional Fallacy Argument as follows:

Suppose there is some set Σ of claims such that the following two conditions are met [where COND is the thesis that every disposition ascription d is necessarily equivalent to some conditional c > m]:

• 1. Σ in conjunction with COND entails some conclusion ϕ that makes some assertion about the disposition-possessing object (so, for us, paradigmatically ϕ is either d or ¬d). This is the inferential condition.

• 2. Σ together with ¬ϕ form an independently plausible scenario. This is the possibility condition.

If both the inferential and the possibility conditions are met, we have reason to reject COND—the compossibility of Σ and ¬ϕ is incompatible with the argument Σ, C O N D ⊩ ϕ. Bonevac et al. (2006, p. 279)

Consider, again, the case of a fragile glass cup. Let C be the proposition that the cup is fragile, and suppose that test condition A _C and manifestation condition B _C are as described in the hypothesis of the Second Conditional Analysis Theorem. We can suppose that B _C is the proposition that the cup breaks, but I offer no linguistic formulation of A _C and do not assume that one exists. By the Second Conditional Analysis Theorem, it follows that C = (A _C > B _C ). Now, let’s gather the ingredients of the Conditional Fallacy Argument as it applies to this analysis:

Σ _C ::

(1) If A _C were true, the cup’s internal packing would prevent it from breaking; (2) the truth of A _C is possible.

ϕ _C ::

¬C (The cup is not fragile.)

COND _C ::

Necessarily, the cup is fragile iff it would break if A _C were true, i.e., C = (A _C > B _C ).

In Lewi’s (1973) and Stalnake’s (1968) preferred systems of conditional logic, Σ _C and COND _C jointly entail ϕ _C , i.e., ¬C. Assume Σ _C and COND _C and suppose for reductio that the cup is fragile, i.e., C (equivalently, ¬ϕ _C ). Then by COND _C , the cup would break if A _C were true, and by Stalnaker-Lewis conditional logic, it follows that if A _C were true, it would still be the case that the cup would break if A _C were true, i.e., (A _C > (A _C > B _C )). So, by COND _C , the cup would still be fragile if A _C were true, i.e., (A _C > C). But by Σ _C (1), if A _C were true, the cup would fail to break despite the truth of A _C , i.e., (A _C > (A _C ∧ ¬B _C )). Applying strong centering inside the consequent of the latter, it follows that if A _C were true, the cup would fail to break if A _C were true, i.e., (A _C > (A _C > ¬B _C )). But necessity is alethic in Stalnaker-Lewis conditional logic,¹² so, by Stalnaker-Lewis conditional logic, A _C would be possible if A _C were true, i.e., (A _C > ◇A _C ). Hence, applying the principle of conditional non-contradiction inside the consequent of (A _C > (A _C > ¬B _C )),¹³ it follows that if A _C were true, it would not be the case that the cup would break if A _C were true, i.e., (A _C > ¬(A _C > B _C )). Applying COND _C to the negated consequent of this conditional, it follows that if A _C were true, the cup would not be fragile, i.e., (A _C > ¬C). Applying conditional non-contradiction to Σ _C (2) and the latter, it follows that it is not the case that if the cup were dropped, it would be fragile, i.e., ¬(A _C > C), which contradicts (A _C > C). By reductio we have ϕ _C : the cup is not fragile.¹⁴

So, Bonevac et al.’s inferential condition is satisfied in our example. What fails in our example is the possibility condition. Σ _C and ¬ϕ _C may appear at first to form an independently plausible scenario, but, upon closer scrutiny, this appearance dissolves.

Let’s examine the intuition that Σ _C and ¬ϕ _C do form an independently plausible scenario. Depending on how we imagine the rest of the details of the scenario, this intuition trades on either a confusion or an equivocation. Since the scenario is supposed to be one in which the cup is fragile but in which (A _C > B _C ) is false, either the cup’s fragility is being masked, in which case A _C C does not entail B _C , or its fragility is being reverse finked, in which case C does not entail (A _C > C). If we make the intuition more specific by imagining that A _C C does not entail B _C , then we imagine, confusedly, that A _C is like the antecedent of the counterfactual in FRAGILE2. It isn’t. Unlike its counterpart in FRAGILE2, A _C is assumed to have been chosen to that A _C C does entail B _C . Alternatively, if we make the intuition of an independently plausible scenario more specific by imagining that C does not entail (A _C > C), then we equivocate on the identity of the counterfactual operator by assuming for the counterfactual in Σ _C a different comparative world similarity relation than the one at work in COND _C , on which C does entail (A _C > C). That is, since we started by assuming that the conditions of the Second Conditional Analysis Theorem were satisfied, we equivocate if we then also imagine that C does not entail (A _C > C). So, neither way of further specifying the intuition that Σ _C and ¬ϕ _C form an independently plausible scenario pans out.

8 Lessons

We have seen that the problems faced by counterfactual analyses of disposition ascriptions can be traced to two sources. Masks and mimicks derive from a failure to identify antecedents and consequents that satisfy the entailment requirements of the Second Conditional Analysis Theorem, namely that AX entail B and that AB entail X. Finks and reverse finks can be traced to a failure to measure comparative world similarity so that X = (A > X). We can derive two main lessons about counterfactuals and counterfactual analyses from our discussion.

First, although we now know that AX must entail B and AB must entail X in order for the counterfactual analysis X = (A > B) to succeed, I know of no proposed counterfactual analysis (other than our Harvard example) that satisfies either entailment condition. Are suitable antecedent-consequent pairs really so difficult to come by? In the case of disposition ascriptions, a suitable consequent B is not usually difficult to find. For example, it seems uncontroversial that an object’s fragility is manifested by its breaking; the difficulty is finding the right fragility “test condition” to serve as the antecedent in the counterfactual analysis. As we saw above, once a suitable consequent B is chosen, we know that there is at least one antecedent that will yield a successful counterfactual analysis of X, namely the weakest antecedent option X ≡ B. From the point of view of giving an informative analysis, of course, X ≡ B will not do, since it refers explicitly to the analysandum X. But any proposition that is both compossible with XB and compossible with $\overline {X}\;\overline {B}$ and that entails X ≡ B will suffice as an antecedent. Natural language may or may not provide an informative way of expressing such an antecedent in any particular case, and its not doing so may explain why successful counterfactual analyses are so difficult to formulate. But at least we know where in the space of propositions to search for a suitable antecedent.

The second lesson is this: it is time to acknowledge that there are limits to the applicability of the standard resolution of the vagueness of counterfactuals. As we saw above, the avoidance of finks and reverse finks in a counterfactual analysis X = (A > B) requires adopting a comparative world similarity relation on which X = (A > X), and we should expect this relation to be a non-standard resolution of vagueness. What is such a relation like? It is a measure of comparative world similarity on which the closest A-worlds are free of any “funny business”, even funny business that may be actually present, such as Johnston’s internal packing. Choosing a measure of this sort is always possible if we assume that any comparative world similarity relation that satisfies Lewis’s conditions (1)–(6) is a possible basis for the counterfactual conditional in some context or other. Are we entitled to that assumption? We turn to this next.

Early critics of Lewis’s semantics, such as Fine (1975), are thought to have shown that some comparative world similarity relations that are admissible according to the formal model theory of Lewis (1973) must be rejected. Lewis (1979) agreed and provided a detailed account of comparative world similarity that excludes certain comparative world similarity relations that otherwise satisfy formal requirements (1)–(6). There is not sufficient space to discuss the issue fully here, but the crucial question to ask is this: What wasLewis (1979 ) trying to get right, in response to Fine? The answer is that Lewis was seeking an account of comparative world similarity for a certain range of ordinary contexts, like the context of a discussion among journalists and historians about would have happened if, instead of visiting China, Nixon had launched a nuclear strike against China in 1972.¹⁵ When people reason about dispositions, what is called for is a context that suits the discussion of dispositions and of testing for the presence of dispositions. Suppose that we are talking about the dispositions of Johnston’s glass cup. The cup might be sitting safely in the cupboard, but it might instead be being watched over by a disapproving angel. What the First Conditional Analysis Theorem shows is that we can choose for this context of discussion a measure of comparative world similarity that supports a conditional analysis of the fragility of the goblet while compensating for the funny business in worlds like the world of Johnston’s disapproving angel. It is clear that circumstances like the disapproving angel, and even more mundane circumstances like being protected by internal packing, make no difference to whether the glass cup is fragile. This indifference to external circumstances is a feature of contexts in which dispositions are under discussion, and we should expect this indifference to be built into measures of comparative world similarity that apply when dispositions are under discussion. Historically, in discussions of conditional analyses of dispositions, authors assumed the existence of a comparative world similarity relation that applied regardless of the topic of discussion—a comparative world similarity relation (or a class of them) that applies whether we are talking about Nixon pushing the button or the fragility of a glass cup. Having made this assumption, philosophers who thought about conditional analyses of disposition ascriptions searched in vain for the right sort of antecendent. The search was doomed because everyone assumed that a context for discussing dispositions would measure comparative world similarity in the same way as a context for discussing what would have happened if Nixon had pushed the button. The difference, or at least part of it, is that in a context for discussing the fragility of a particular cup we want a comparative world similarity relation that holds fixed the actual internal structure of the cup, while holding at bay any actual or counterfactual external circumstances that would contaminate a counterfactual test of the cup’s fragility. For example, for a world where our fragile cup is wrapped in styrofoam and a context in which fragility is under discussion, comparative world similarity must be measured so that if the cup’s fragility test condition were true, the cup would have its same molecular structure, but the styrofoam would no longer be protecting it. If asked in that context why my glass cup is wrapped in styrofoam I might say, “It’s wrapped in styrofoam because it would break if it were dropped.”¹⁶ Structure is held fixed, but stryofoam, anti-gravity fields, and disapproving angels are held at bay. This holding-fixed and holding-at-bay are accomplished via the choice of the comparative world similarity relation for the context, but Lewis’s Time’s Arrow criteria will not explain this choice, since, among matters of “particular fact” Lewis’s criteria cannot distinguish the internal structure of the cup from external circumstances like the styrofoam, the anti-gravity field, and Johnston’s disapproving angel.

The upshot of what I am suggesting is that there are legitimate contexts in which Lewis’s Time’s Arrow requirements on comparative world similarity do not apply. The account in (Lewis 1979) was designed as a theory of the standard resolution of vagueness, i.e., it was designed to yield intuitively correct truth values in the context of determinism for counterfactuals that come up in a certain range of examples. Whether it does so successfully has been widely discussed, but, in any case, Lewis’s Time’s Arrow account allows for contexts in which the vagueness of counterfactuals is non-standardly resolved, and I have argued that disposition ascribing propositions give rise to just that sort of context.

9 A new Conditional Operator or a Familiar one Liberated?

Bonevac et al. (2006, p. 315) recommend using masking and mimicking cases as data for investigating new conditional connectives, especially connectives that relax Lewis’s (1973, p. 48, (4)) requirement of Strong Centering, which ensures that i is the uniquely closest world to i, and which guarantees both modus ponens (MP) for the counterfactual and a converse of modus ponens:

(MP):

A, A > B⊧B.

(CMP):

A, B⊧A > B.

Far from rejecting (MP) and (CMP), our construction in Case 3 of the proof of the First Conditional Analysis Theorem relies on (MP) and (CMP) to ensure that the counterfactual found in Case 3 works as an analysis of X even in worlds where A and B are both true, and even in worlds where A is true and B is false. That is, since AB entails X, it had better turn out that AB entails A > B, too, as in (CMP), since a world in which AB is true and A > B is false would falsify X = (A > B). Similarly, since $A\overline {B}$ is not compossible with X, i.e., $A\overline {B}$ entails $\overline {X}$, it had better turn out that $A\overline {B}$ entails $\overline {A>B}$, too, which follows from (MP), since a world in which $A\overline {B}$ and A > B are both true would falsify X = (A > B). Strong Centering is thus central to the First Conditional Analysis Theorem, and to the Second one, too.

Still, one might argue that the conditional of the two Conditional Analysis Theorems ought to count as a new connective, albeit a connective of a different sort than that envisioned by Bonevac et al. The conditional of the Conditional Analysis Theorems seems new not because it has a different logic than a Stalnaker-Lewis conditional but because the range of its interpretation includes comparative world similarity relations that do not conform to the standard resolution of vagueness. I disagree. Since all we are doing is widening the class of admissible comparative world similarity relations and not revising the logic of the counterfactual conditional, it is fair to say that the identity of the conditional connective has not changed. Instead of introducing a new connective, we are liberating a familiar connective from semantic constraints that, as it happens, make no logical difference. That is, the counterfactual logic of Lewis (1973) is in fact the same with or without the constraints on comparative world similarity developed in Lewis (1979).¹⁷ The payoff of liberating Lewis’s semantics in this way is that doing so provides a strategy for using counterfactuals to analyze propositions about which we are concerned.

10 Conclusion

What do the Conditional Analysis Theorems mean for the project of giving counterfactual analyses? If a proposition’s having a counterfactual analysis is nothing special, then what is the value of the analysis?

On the negative side, it seems clear that since every proposition has a counterfactual analysis, having a counterfactual analysis has no reductive or explanatory significance, indeed no metaphysical significance at all. Counterfactual analyses do, however, have epistemological significance. A successful counterfactual analysis provides a formulation of the truth conditions of a proposition in terms of other propositions (the antecedent and consequent of the analysans) in a way that might facilitate an inquiry into the truth value of the analyzed proposition. If the proposition C, that my glass cup is fragile, is analyzed as the proposition that the cup would break (B _C ) if test condition A _C were true, and if I then actually bring about the truth of A _C , the question whether the cup was fragile will be definitively answered once we know whether the cup broke, since, if C = (A _C > B _C ), then A _C B _C entails C, and $A_{C}\overline {B}$ entails $\overline {C}$.¹⁸ Note that these entailments are not affected by the non-standardness of the resolution of vagueness at work in C = (A _C > B _C ). If there is even one comparative world similarity relation on which C = (A _C > B _C ), then, once the truth of A _C is brought about, the truth value of B _C equals the truth value of C. One could put it by saying that once A _C is true, Strong Centering takes over and the other details of the comparative world similarity relation don’t matter.

The expressive limitations of natural languages will, of course, limit the epistemological value of the Conditional Analysis Theorems. These theorems show that every proposition has a counterfactual analysis, but this does not mean that one will be able to find an informative counterfactual analysis in any given case. We were successful in the Harvard enrollment example, but the expressive limitations of particular languages may make it impossible to find antecedents that make the counterfactual analyses of certain propositions informative. This limitation seems to be a problem for disposition ascriptions, in particular. We have always known that finding counterfactual analyses of disposition ascriptions was difficult; now, I suggest, we know why.