The multiplicative complexity of 6-variable Boolean functions

Abstract

The multiplicative complexity of a Boolean function is the minimum number of two-input AND gates that are necessary and sufficient to implement the function over the basis (AND, XOR, NOT). Finding the multiplicative complexity of a given function is computationally intractable, even for functions with small number of inputs. Turan et al. [1] showed that n-variable Boolean functions can be implemented with at most $n-1$ AND gates for $n\leq 5$. A counting argument can be used to show that, for n ≥ 7, there exist n-variable Boolean functions with multiplicative complexity of at least n. In this work, we propose a method to find the multiplicative complexity of Boolean functions by analyzing circuits with a particular number of AND gates and utilizing the affine equivalence of functions. We use this method to study the multiplicative complexity of 6-variable Boolean functions, and calculate the multiplicative complexities of all 150 357 affine equivalence classes. We show that any 6-variable Boolean function can be implemented using at most 6 AND gates. Additionally, we exhibit specific 6-variable Boolean functions which have multiplicative complexity 6.

1 Introduction

Multiplicative complexity is a complexity measure defined as the minimum number of multiplications (AND gates) that are necessary and sufficient to implement a function with a circuit over the basis (AND, XOR, NOT). In many protocols for multi-party computation (e.g., [2]), fully homomorphic encryption (e.g., [3]), and zero-knowledge proofs (e.g., [4]), processing AND gates is more expensive than processing XOR gates. Moreover, the cost of some of the countermeasures against side channel attacks is related to the number of two-input AND gates in the implementation. For example, the complexity of higher-order masking schemes for S-boxes mainly depends on the masking complexity, which is defined as the minimum number of nonlinear field multiplications required to evaluate a polynomial representation of an (n,m)-bit S-box over ${\mathbb {F}}_{2^{n}}$ [5].

Determining the multiplicative complexity of a given function is computationally intractable, even for small number of variables. It is known that if one-way functions exist, then given a truth table for a Boolean function of n bits, it is not possible to compute the multiplicative complexity in polynomial time in the size of the truth table [6]. Turan and Peralta [1] showed that n-variable Boolean functions can be implemented with at most $n-1$ AND gates for $n\leq 5$.

Using a counting argument, Codish et al. [7] showed that there exist n-variable Boolean functions with multiplicative complexity at least n, for $n \geq 7$. It is also known that the multiplicative complexity of functions having algebraic degree d is at least $d-1$. This is called the degree bound. There are very few classes of functions for which lower bounds better than the degree bound are known (see [8]). Although the multiplicative complexity of a random n-variable Boolean function is at least $2^{n/2}-O(n)$ with high probability [9], prior to our present work, no specific n-variable function had been proven to have multiplicative complexity larger than $n-1$.

We propose a method to find the multiplicative complexity of Boolean functions. We use this method to study the multiplicative complexity of 6-variable Boolean functions. The method used by Turan and Peralta in [1] uses heuristics that do not provide optimal solutions for 6-variable Boolean functions. Here, the problem of finding the multiplicative complexity distribution of 6-variable Boolean functions is reduced to finding the multiplicative complexities of the 150 357 affine equivalence classes constructed in [10]. The multiplicative complexity of each class is determined by processing all circuits with a particular number of AND gates and then identifying the classes that could be generated by those circuits. We give a complete distribution of the multiplicative complexities of 6-variable Boolean functions and show that they can be implemented with at most 6 AND gates. Our techniques also enable us to exhibit specific 6-variable functions which have multiplicative complexity 6.

The organization of the paper is as follows. Section 2 gives definitions and preliminary information about Boolean functions and affine equivalence relations. Section 3 provides algorithms to construct and evaluate circuits. Section 4 focuses on the multiplicative complexity of 6-bit Boolean functions. Section 5 concludes the paper.

2 Preliminaries on Boolean functions

Let ${\mathbb {F}}_{2}$ be the finite field with two elements and let ${{\mathbb {F}}_{2}^{n}}$ denote the n-dimensional vector space over ${\mathbb {F}}_{2}$. An n-variable Boolean function f is a mapping from ${{\mathbb {F}}_{2}^{n}}$ to ${\mathbb {F}}_{2}$. Let $B_{n}$ be the set of n-variable Boolean functions, clearly $|B_{n}|= 2^{2^{n}}$. A Boolean function $f\in B_{n}$ can be represented uniquely by the multivariate polynomial defined by

$$ f(x_{1},\ldots,x_{n})=\bigoplus\limits_{u\in {{\mathbb{F}}_{2}^{n}}}{a_{u}x^{u}} $$

(1)

where $a_{u}\in {\mathbb {F}}_{2}$ and $x^{u} = x_{1}^{u_{1}}x_{2}^{u_{2}}{\cdots } x_{n}^{u_{n}}$ is a monomial composed of the variables for which $u_{i}= 1$. This polynomial is called the algebraic normal form (ANF) of f. The degree of a Boolean function is the highest number of variables in a monomial for which $a_{u}= 1$ in its ANF representation. The Boolean functions of the form $f(x)= a_{1}x_{1}+\ldots + a_{n}x_{n} + a_{0}$, where $a_{i} \in {\mathbb {F}}_{2}$, are called affine functions. If $a_{0}= 0$, f is called a linear function.

The Walsh transform of an n-variable Boolean Function f at point $w{\in {\mathbb {F}}_{2}^{n}}$ is defined as

$$ W_{f}(w)=\sum\limits_{x{\in{\mathbb{F}}_{2}^{n}}} {(-1)^{f(x)\oplus w\cdot x} }, $$

(2)

where $w\cdot x$ is the inner product $w_{1}x_{1}+\ldots +w_{n}x_{n}$. The vector

$$[W_{f}(\overline{0}),\ldots, W_{f}(\overline{2^{n}-1})]$$

is called the Walsh spectrum of f.

The autocorrelation of an n-variable Boolean Function f at point $w{\in {\mathbb {F}}_{2}^{n}}$ is defined as

$$ R_{f}(w)=\sum\limits_{x{\in{\mathbb{F}}_{2}^{n}}}{(-1)^{f(x)\oplus f(x\oplus w)}}. $$

(3)

The vector $[R_{f}(\overline {0}),\ldots , R_{f}(\overline {2^{n}-1})]$ is called the autocorrelation spectrum of f.

Definition 1

An affine transformation $(A,a,b,c)$ from f to g in $B_{n}$ is a mapping of the form $g(x) = f(Ax + a) + b \cdot x + c$, where A is a non-singular $n\times n$ matrix over $\mathbb {F}_{2}$, and $a,b\in {\mathbb {F}_{2}^{n}}$ and $c\in \mathbb {F}_{2}$. We call $(A,a)$ the inner transformation and $(b,c)$ the outer transformation.

Two functions $f,g$ are affine equivalent if there exist affine transformations between them. Affine equivalence is an equivalence relation. An algorithm to check whether two functions are equivalent is given in [10]. This algorithm also outputs an affine transformation between the input functions, if one exists. Constructing all equivalence classes is feasible for $n \leq 6$. In 1972, Berlekamp and Welch [11] described the 48 classes on 5-variable Boolean functions. In 1991, Maiorana [12] classified the 150 537 classes on 6-variable Boolean functions. This result was independently verified by Fuller [10] and Braeken et al. [13]. For $n = 7$, Hou [14] determined the number of equivalence classes to be $\approx$2^65.78.

Properties of Boolean functions such as multiplicative complexity, algebraic degree, the set of absolute values in the Walsh spectrum, and the set of absolute values in the autocorrelation spectrum remain unchanged after applying an affine transformation. These properties are said to be affine invariant [15] and they provide a useful tool for showing whether two functions are affine equivalent or not.

3 Boolean circuits and topologies

Definition 2

A Boolean circuit C with n inputs and 1 output is a directed acyclic graph where the inputs and the gates are the nodes, and the edges correspond to the Boolean-valued wires. The fan-in and fan-out of a node is the number of wires going in and out of the node, respectively. The nodes with fan-in zero are called the input nodes and are labeled with an input variable from X_n = {x₁,…,x_n}. The circuits we consider here have exactly one node with fan-out zero, which is called the output node.

Each Boolean circuit C with n input nodes computes a Boolean function $f \in B_{n}$. When a Boolean vector $\bar {x} \in \{0,1\}^{n}$ is fed to the input nodes, the logic gates compute the function where the output node gets the value $f(\bar {x})$. Any Boolean function can be evaluated using the basis ${\Omega }=\{$AND (∧), XOR (⊕), NOT (¬) }. Since $\neg x = x \oplus 1$, it is also possible to replace the NOT gates with XOR gates, when the constant 1 is allowed to be used as an input node. AND gates have fan-in two. XOR gates have fan-in one or more.

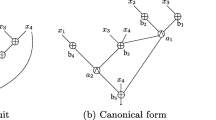
It is not hard to verify that a circuit computing the function f can be put in the following canonical form without changing the number of AND gates (see Fig. 3b for an example).

Unless otherwise specified, we will be assuming that circuits are in canonical form. Let $S_{i}$ be the set of AND gates that are inputs to the i th XOR gate ${\texttt {b}}_{i}$. Let $L_{i}$ be the set of inputs to ${\texttt {b}}_{i}$ not in $S_{i}$. Note that the elements of $L_{i}$ are either input nodes or the constant 1. Note also that $S_{i}$’s need not be disjoint. This notation is depicted in Figs. 1 and 2 and will be useful in the rest of this paper.

Fig. 1

Canonical form for a circuit computing the function f

Fig. 2

The L and S sets

Notation

Given a set V of nodes, let $\mathcal {X}_{V}$ denote the Boolean function computed as $\bigoplus _{v \in V} v$.¹ The output of the i-th XOR gate is $F_{{\texttt {b}}_{i}}=\mathcal {X}_{L_{i}} \oplus \mathcal {X}_{S_{i}}$, and the output of the i-th AND gate is

$$\begin{array}{@{}rcl@{}} F_{{\texttt{a}}_{i}} & = & (\mathcal{X}_{L_{2i-1}} \oplus \mathcal{X}_{S_{2i-1}}) \wedge (\mathcal{X}_{L_{2i}} \oplus \mathcal{X}_{S_{2i}}). \end{array} $$

(4)

Definition 3

Given a circuit, the ordered list $(L_{1},\ldots ,L_{2k + 1},S_{1},\ldots ,S_{2k + 1})$ is called the trace of the circuit. The ordered list $[(S_{1}, S_{2}),(S_{3}, S_{4}) \ldots ,(S_{2k-1}, S_{2k})]$ shows the relations between the AND gates, and is called the topology of the circuit. The ordered list (L₁,…,L_2k+ 1) shows the linear inputs to the XOR gates, and is called the input to the topology. $S_{2k + 1}$ is called the output mask.

Note that the trace of a circuit does not contain all the information about the circuit. So it is not possible to reconstruct a circuit from its trace.

By using the gate numbering given in Fig. 1, the topology of the circuit can be expressed in graphical form. We use the procedure of Algorithm 1.

Our depictions of topologies will not show the direction of edges (they point down) or the labels of gates (we are only interested in the structure of each graph). Table 1 contains topologies with 3 AND gates, along with their graphical representation.

Table 1 List of topologies with up to 3 AND gates

Example 1

The function $f=x_{1}x_{2}x_{3}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{4}$ has multiplicative complexity 2, as is clear from f = x₁(x₂x₃ + x₃ + x₄) + x₂x₃ + x₄. A circuit in canonical form that computes f is depicted in Fig. 3b. The trace for that circuit is

$$(\{x_{3}\},\{x_{2}\},\{x_{3},x_{4}\},\{x_{1}\},\{x_{4}\},\emptyset,\emptyset, \{a_{1}\},\emptyset, \{a_{1},a_{2}\}). $$

Fig. 3

Circuit and topology computing f

The topology of the circuit is $[(\emptyset ,\emptyset ),(\{a_{1}\},\emptyset )]$. The input to the topology is $(\{x_{3}\},\{x_{2}\},\{x_{3},x_{4}\},\{x_{1}\},\{x_{4}\})$, and the output mask is $\{a_{1},a_{2}\}$. The graphical representations of the circuit and its topology are given in Fig. 3.

Definition 4

Given a circuit in canonical form, a numbering of the AND gates is a proper numbering, if no gate is an ancestor of a lower-numbered gate (i.e. if the numbering does not violate topological ordering).

Definition 5

Two topologies are said to be isomorphic if one results from a proper re-numbering of the AND gates of the other.

Definition 6

A Boolean function f is computable by a topology T if it is computable by a circuit whose topology is T. The set of Boolean functions that are computable by a topology T is denoted $B(T)$.

Clearly, if two topologies are isomorphic, then the sets of functions computable by each are the same. We state this as a proposition.

Proposition 1

If topologies T and $T^{\prime }$ are isomorphic, then $B(T)=B(T^{\prime })$.

3.1 Evaluating topologies

Without loss of generality, the remainder of this paper only considers functions f for which $f(0) = 0$. These functions have negation-free circuits that are optimum with respect to multiplicative complexity. Any function for which $f(0) = 1$ is of the form $f(\bar {x}) = g(\bar {x}) + 1$ where $g(0) = 0$.

The aim of this section is to construct the set of Boolean functions that are computable by a topology $T=[(S_{1}, S_{2}),\ldots ,(S_{2k-1}, S_{2k})]$. The set $B(T)$ can be obtained by exhaustively evaluating the following family of circuit traces

$$(L_{1}^{*},\ldots,L_{2k + 1}^{*},S_{1},\ldots,S_{k}, S_{2k + 1}^{*}), $$

where $L_{i}^{*}$ is any subset of $\{{\texttt {x}}_{1},\ldots , {\texttt {x}}_{n}\}$ and $S_{2k + 1}^{*}$ is any subset of $\{{\texttt {a}}_{1},\ldots , {\texttt {a}}_{k}\}$. However, going over all possible $L_{i}^{*}$’s for $i = 1,\ldots , 2k + 1$ and $S_{2k + 1}^{*}$ quickly becomes inefficient, since there are $(2^{n})^{2k + 1} \times 2^{k} = 2^{2kn+k+n}$ possible choices for these sets (e.g., there are $2^{71}$ choices for a topology with 5 AND gates when $n = 6$).

Theorem 1

Let $f\in B_{n}$ be computable by a topology T. If $f^{\prime }$ is affine equivalent to f, then $f^{\prime }$ is also computable by T.

Proof

Let $C=(L_{1},\ldots ,L_{2k + 1},S_{1},\ldots ,S_{2k + 1})$ be the trace of a circuit with topology T that computes f. If $f^{\prime }$ is affine equivalent to f, then there exists an affine transformation $(A,a,b,c)$ satisfying f^′(x) = f(Ax + a) + bx + c. The circuit generated by applying the inner transformation $Ax+a$ to the inputs $\{{\texttt {x}}_{1},\ldots , {\texttt {x}}_{n}\}$, and adding outer transformation $bx+c$ to $L_{2k + 1}$ constructs $f^{\prime }$. Since the topology of the circuit is not affected by the affine transformation, $f^{\prime }$ is computable by T. □

Theorem 1 implies that either all or none of the functions in an equivalence class are computable by a topology T. We say that the equivalence class of f ∈ B_n is computable by a topologyT, if f is computable by T. Hence, in order to construct $B(T)$, we may construct the list of equivalence classes that are computable by T.

Corollary 1

Consider two circuits with traces

$$(L_{1},\ldots,L_{2k + 1},S_{1},\ldots,S_{k}, S_{2k + 1})\text{ and}$$

$$(L^{\prime}_{1},\ldots,L^{\prime}_{2k + 1},S_{1},\ldots,S_{k}, S_{2k + 1}).$$

If there exists an inner transformation $(A,a)$ that transforms $\mathcal {X}_{L_{i}} \rightarrow \mathcal {X}_{L^{\prime }_{i}}$ for $i = 1,\ldots , 2k$, then the circuits compute affine equivalent functions.

To see why the corollary holds, note that the outer transformation $(b,c)$ affecting $\mathcal {X}_{L^{\prime }_{2k + 1}}$ is a specific case of an affine transformation and hence does not change the equivalence class of a function.

Call two tuples $(L_{1}, \ldots , L_{2k})$ and $(L^{\prime }_{1}, \ldots , L^{\prime }_{2k})$ affine equivalent if there exists an invertible matrix A such that multiplication of the input vector by A maps one tuple to the other. This is an equivalence relation and, by Corollary 1, we need only test one tuple from each equivalence class. Thus, we would like to enumerate a maximal set of tuples no two of which belong to the same equivalence class. This problem corresponds to enumerating all m-dimensional subspaces in a $2k$-dimensional vector space, where m is the number of variables of the functions under consideration (see Table 3).

The number of subspaces of dimension m in a vector space of dimension $2k$ over a finite field of 2 elements is equal to the Gaussian binomial coefficient²$\binom {2k}{m}_{2}$ [16]. This is approximately $2^{26}$ inputs for $m = 6$, $k = 5$. The algorithm to construct the subspaces is given in [17]. In its simplest form, to generate a sufficient set of inputs of dimension m, for each component in an input we either introduce a new variable, or choose a linear combination of the previously used variables, by taking into account that the exact number of variables to be used is m.

Example 2

Consider the vector space consisting of all linear functions on variables $x_{1},x_{2},x_{3},x_{4}$. Denote by $(a_{1},a_{2},a_{3},a_{4})$ the subspace generated by all linear functions ${\sum }_{i = 1}^{4} a_{i} x_{i}$ where a_i ∈ {0, 1}. A maximal set of 3-dimensional subspaces in a 4-dimensional vector space (m = 3, $2k = 4$) is as follows:

$$\begin{array}{lll} (a_{1},a_{2},a_{3},0), &\quad(a_{1},a_{2},a_{3},a_{1}), &\quad(a_{1},a_{2},a_{3},a_{2}),\\ (a_{1},a_{2},a_{3},a_{1}+a_{2}), &\quad(a_{1},a_{2},a_{3},a_{3}), &\quad(a_{1},a_{2},a_{3},a_{1}+a_{3}),\\ (a_{1},a_{2},a_{3},a_{2}+a_{3}), &\quad(a_{1},a_{2},a_{3},a_{1}+a_{2}+a_{3}), &\quad(a_{1},a_{2},0,a_{3}),\\ (a_{1},a_{2},a_{1},a_{3}), &\quad(a_{1},a_{2},a_{2},a_{3}), &\quad(a_{1},a_{2},a_{1}+a_{2},a_{3}),\\ (a_{1},0,a_{2},a_{3}), &\quad(a_{1},a_{1},a_{2},a_{3}), &\quad(0,a_{1},a_{2},a_{3}) \end{array} $$

Notation

I_n,k denotes the set of subspaces of $\{0,1\}^{2k}$ of dimension at most $min\{n,2k\}$

3.2 Constructing topologies

All topologies with k AND gates have the form $[(S_{1},S_{2}) ,\ldots , (S_{2k-1}, S_{2k})],$where $S_{2i-1}, S_{2i} \subseteq \{{\texttt {a}}_{1},\ldots ,{\texttt {a}}_{i-1}\}$. The sets $S_{2i-1}$ and $S_{2i}$ can take $2^{i-1}$ different values, so the total number of topologies with k AND gates is

$$\prod\limits_{i = 1}^{k} (2^{i-1})^{2} = 2^{{\sum}_{i = 1}^{k} 2(i-1)} = 2^{k^{2}-k}.$$

However, this formula counts many topologies redundantly in the sense that there are many topologies computing the same set of Boolean functions. In addition to isomorphic topologies, redundant topologies can result from some transformations on pairs $(S_{2k-1}, S_{2k})$ corresponding to the AND gates that define the output of AND gate $a_{i}$ (see Eq. 4). Next, we derive some of these transformations.

Notation

Given two sets S_i, S_j ⊆{a₁,…,a_k} of AND gates, we denote by $S_{i}\oplus S_{j}$ the symmetric difference of S_i and $S_{j}$, i.e., the set of elements that are contained in $S_{i}$ or $S_{j}$ but not in both.

Remark 1

Let $h=(f+l_{1})(g+l_{2})$ with $f,g,l_{1},l_{2}\in \mathcal {B}_{n}$. Let $l_{3}= 1+l_{1}+l_{2}$. Then it follows that

$$\begin{array}{@{}rcl@{}} h &=& (f+l_{1})(f+g+l_{3})\\ h &=& (f+g+l_{3})(g+l_{2}) \end{array} $$

Proposition 2

Let $T=[(S_{1},S_{2}) ,\ldots , (S_{2k-1}, S_{2k})]$ be a topology. Let $T^{\prime }$ be the topology formed by replacing $(S_{2i-1},S_{2i})$ by $(S_{2i-1}, S_{2i-1} \oplus S_{2i}),$ and let $T^{\prime \prime }$ be the topology formed by replacing $(S_{2i-1},S_{2i})$ by $(S_{2i-1} \oplus S_{2i}, S_{2i})$. Then $B(T)=B(T^{\prime })=B(T^{\prime \prime })$.

Proof

Let $F_{{\texttt {a}}_{i}}=(\mathcal {X}_{L_{2i-1}} \oplus \mathcal {X}_{S_{2i-1}})\wedge (\mathcal {X}_{L_{2i}} \oplus \mathcal {X}_{S_{2i}})$ be a function generated by AND gate $a_{i}$. Then,

$$F_{{\texttt{a}}_{i}^{\prime}}=(\mathcal{X}_{L_{2i-1}} \oplus \mathcal{X}_{S_{2i-1}}) \wedge (1\oplus \mathcal{X}_{L_{2i}} \oplus \mathcal{X}_{L_{2i-1}}\oplus \mathcal{X}_{S_{2i}}\oplus \mathcal{X}_{S_{2i-1}})$$

and

$$F_{{\texttt{a}}_{i}^{\prime\prime}}=(1\oplus \mathcal{X}_{L_{2i}} \oplus \mathcal{X}_{L_{2i-1}}\oplus \mathcal{X}_{S_{2i}}\oplus \mathcal{X}_{S_{2i-1}}) \wedge (\mathcal{X}_{L_{2i}} \oplus \mathcal{X}_{S_{2i}})$$

are the same functions by Remark 1. □

Proposition 2 implies that for any pair $(S_{2i-1},S_{2i})$ in a topology, any choice of two input pairs from the set $\{S_{2i-1}, S_{2i}, S_{2i-1}\oplus S_{2i}\}$ for AND gate $a_{i}$ will not change the set of functions computable by the topology. This motivates the following definition.

Definition 7

The following six pairs are said to be equivalent.

$$\begin{array}{@{}rcl@{}} && (S_{2i-1},S_{2i}) \\ && (S_{2i}, S_{2i-1}) \\ && (S_{2i-1},S_{2i-1}\oplus S_{2i}) \\ && (S_{2i-1}\oplus S_{2i},S_{2i-1}) \\ && (S_{2i-1}\oplus S_{2i},S_{2i}) \\ && (S_{2i}, S_{2i-1}\oplus S_{2i}) \end{array} $$

From now on we will identify the pair $(S_{2i-1},S_{2i})$ with AND gate $a_{i}$ where doing so will not cause confusion.

We represent a set $S\subseteq \{{\texttt {a}}_{1},\ldots ,{\texttt {a}}_{k}\}$ by a k-bit mask $(v_{1},\ldots ,v_{k})$, each $v_{i}$ denoting the existence of $a_{i}$ in S. Since each gate has two sets of inputs, $(S_{2i-1},S_{2i})$ is represented by a $2k$-bit vector.

Definition 8

The minimal representation of an AND gate $a_{i}=(S_{2i-1},S_{2i})$ in a topology is the lexicographically smallest among the set of equivalent gates listed in Definition 7.

We use Algorithm 2 to construct the set of topologies with k AND gates. The exhaustive list of topologies having up to 3 AND gates after removing the redundant ones is shown in Table 2.

Table 2 The number of topologies up to 6 AND gates

3.3 Finding the multiplicative complexity of a Boolean function

In this section, we propose an algorithm to find the multiplicative complexity of a given Boolean function. Let $f \in B_{n}$ be a Boolean function with degree d. It is known that the multiplicative complexity of f is at least $d-1$. The first step of the algorithm is to use Algorithm 2 to construct the topologies with $k=d-1$ AND gates. Then, the set of $\binom {2k}{m}_{2}$ inputs for the topologies are constructed as explained in Section 3.1. If f is computable by any of the topologies, the algorithm outputs k, else k is incremented by one, and a new set of topologies is evaluated, until f is computable by one of the topologies, as given in Algorithm 3.

The algorithm is practical when the number k of AND gates is small. The algorithm can also be used for providing lower bounds on the multiplicative complexity of a given function, when it does not find a solution up to a particular value of k, establishing a lower bound of $k + 1$.

4 Multiplicative complexity of 6-variable Boolean functions

In this section, our aim is to find the multiplicative complexities of all Boolean functions in 6-variables. The number of affine equivalence classes in $\mathcal {B}_{6}$ is known to be $150\,357$. In this work, we use the representative functions computed in [10].

Our method can be summarized as follows: We iteratively construct and evaluate topologies until at least one function from each affine equivalence class is computed (See Algorithm 4). The algorithm identifies the set of affine equivalence classes generated by a topology, by going over all linear inputs and the output masks. Given a topology, a function is computed by providing a set of linear function inputs to this topology and combining the outputs of the AND gates with an output mask. For each function that is computed from a topology, the algorithm checks whether the function is affine equivalent to a Boolean function from the input set. If so, it means that this is the first time a function from this equivalence class is computed and the multiplicative complexity of this class is assigned the value k, and the function is removed from the set of input functions. The construction of topologies, described in Section 3.2, is independent of the number of variables the topology will be evaluated for. The input generation and determining the affine equivalence classes of functions is described in Sections 4.2 and 4.1, respectively.

It should be noted that an equivalence class may be generated by distinct topologies having a different number of AND gates. An equivalence class is assigned a multiplicative complexity value k, if it was generated by a topology having k AND gates and was not previously generated with a topology that had less than k AND gates. This is guaranteed by processing the topologies in order with respect to the number of AND gates.

4.1 Determining the equivalence classes of functions

An important step in finding the set of equivalence classes that is computable by a topology is determining the equivalence class of a specific function that is generated from that topology. It is crucial that this process be performed efficiently, since it will be repeated for each set of inputs supplied to a topology. An equivalence class is represented by a representative function from that class whose selection can be arbitrary.

Deciding on whether or not two given functions are affine equivalent is done by making use of the affine transformation invariant properties of functions, i.e., algebraic degree, absolute Walsh spectrum distribution, and absolute auto-correlation spectrum distribution. We call the values these three metrics take the signature of a function. For n ≤ 5, the signature of a function is sufficient to determine its class because the signatures of functions in different classes are different. However, for $n = 6$ there are a total number of 30 883 distinct signatures, which is less than the number of equivalence classes, implying that some equivalence classes have the same signature. Indeed, $17\ 234$ of the signatures belong to a unique class, whereas the remaining $13\ 649$ signatures are shared by two or more classes, with the maximum number of classes having the same signature being 564.

Suppose we want to determine the equivalence class of a function f. That is, we want to know which of the 150 357 representatives is affine equivalent to f. If the signature of f is among the $17\ 234$ signatures that uniquely identifies its class, then the representative is the one associated with the signature. Otherwise, it is the case that f is affine equivalent to one of the representatives, say $f_{1},...,\ldots ,f_{m}$, $m \geq 2$, whose signatures are equal to that of f ’s. Then, we use the methods described in [10], namely the local connectivity and indicator functions to eliminate the representatives that could not be affine equivalent to f until we’re left with a single candidate, which will be the representative that f is affine equivalent to.

4.2 Evaluating topologies

As described in Section 3.1, for a given n, the inputs to a topology with k AND gates are the functions that correspond to the subspaces of dimension m in a vector space of dimension $2k$, where $1\leq m \leq \min (2k,n)$. In [1], it was shown that any Boolean function on n-variables has multiplicative complexity at most $n-1$ for n ≤ 5. This implies that if we want to evaluate a topology with $k \leq 5$ AND gates, we can start from $m=k + 1$ by skipping the dimensions up to k because all functions on k or less number of variables should have to be generated with $k-1$ AND gates. This observation lets us reduce the number of dimensions m that must be considered when generating the inputs. Table 3 provides the list of dimensions m in a vector space of dimension $2k$ for $n = 6$.

Table 3 Size of the input combinations for evaluating topologies

4.3 Results

The algorithms for constructing and evaluating the topologies have been implemented in the C+ + programming language. The construction of topologies up to 5 AND gates took less than a minute on a standard desktop PC, whereas topologies with 6 AND gates could be generated in approximately one day. The task of identifying the equivalence classes generated by the topologies demanded more computation due to the large number of input combinations to be evaluated. We exploited the inherent parallelism of this process by running it on a cluster, with each node processing a certain subset of the topologies. The nodes in the cluster had dual Intel Xeon E5-2630 v3 processors³ (3.20 GHz, 8 cores) and 64 GB memory. The total computation took $38\ 422$ core hours.

Table 4 shows the results of the computation. The number of functions having a particular multiplicative complexity was calculated by adding the total number of functions in each equivalence class. After running Algorithm 4 up to 5 AND gates, there were still 931 equivalence classes on 6-variables that could not be generated, implying that their multiplicative complexity should be at least 6. The task of evaluating all topologies having 6 AND gates with all possible inputs was not feasible due to the large number of topologies and input combinations. However, it suffices to generate one function from each of the remaining 931 equivalence classes to conclude that these classes have multiplicative complexity 6. Therefore, a computation was carried out by picking a subset of 10,000 topologies with 6 AND gates and evaluating those topologies, which took a few hours to observe a function from each of the 931 classes.

Table 4 Multiplicative complexity distribution of the equivalence classes and functions for $n = 6$

The results can be accessed online at [18], which contains one representative from each affine equivalence class, along with a circuit for that function with a minimum number of multiplications.

Among the set of functions having multiplicative complexity 6, we list below all representatives with degree 4:

$$\begin{array}{@{}rcl@{}} f_{1}&=&x_{3}x_{5}+x_{3}x_{4}+x_{2}x_{4}+x_{2}x_{3}x_{6}+x_{2}x_{3}x_{4}x_{5}+x_{1}x_{6}+x_{1}x_{5}+x_{1}x_{4}x_{5}+x_{1}x_{3}+x_{1}x_{3}x_{4}\\ &&+x_{1}x_{3}x_{4}x_{6}+x_{1}x_{2}x_{5}x_{6}\\ f_{2}&=&x_{4}x_{5}+x_{3}x_{4}x_{5}+x_{2}x_{5}+x_{2}x_{4}+x_{2}x_{4}x_{6}+x_{1}x_{5}x_{6}+x_{1}x_{4}+x_{1}x_{3}+x_{1}x_{2}x_{4}x_{5}\\ &&+x_{1}x_{2}x_{3}x_{6}\\ f_{3}&=&x_{3}x_{5}+x_{3}x_{4}+x_{2}x_{4}+x_{2}x_{3}x_{6}+x_{2}x_{3}x_{4}x_{5}+x_{1}x_{4}+x_{1}x_{4}x_{5}+x_{1}x_{3}+x_{1}x_{3}x_{4}\\ && +x_{1}x_{3}x_{4}x_{6}+x_{1}x_{2}x_{5}x_{6}\\ f_{4}&=&x_{3}x_{5}+x_{3}x_{4}+x_{2}x_{4}+x_{2}x_{3}+x_{2}x_{3}x_{6}+x_{2}x_{3}x_{4}x_{5}+x_{1}x_{6}+x_{1}x_{5}+x_{1}x_{4}x_{5}\\ && +x_{1}x_{3}x_{4}+x_{1}x_{3}x_{4}x_{6}+x_{1}x_{2}+x_{1}x_{2}x_{5}x_{6}\\ f_{5}&=&x_{4}x_{6}+x_{4}x_{5}+x_{3}x_{5}+x_{2}x_{3}x_{6}+x_{2}x_{3}x_{4}x_{5}+x_{1}x_{5}+x_{1}x_{3}+x_{1}x_{3}x_{5}+x_{1}x_{3}x_{4}\\ && +x_{1}x_{3}x_{4}x_{6}+x_{1}x_{2}+x_{1}x_{2}x_{5}x_{6}+x_{1}x_{2}x_{4}\\ \end{array} $$

5 Conclusion

We explored the multiplicative complexity of 6-variable Boolean functions and showed that they can be implemented using at most 6 AND gates. More specifically, we computed the multiplicative complexity distribution of affine equivalence classes and the number of Boolean functions with multiplicative complexity k for $k = 0, \ldots , 6$. We were able to exhibit specific 6-variable functions which have multiplicative complexity 6.

The number of affine equivalence classes for $n = 7$ is $\approx$2^65.78. Thus, it is not practical to find the multiplicative complexity distribution of 7-variable Boolean functions using the proposed enumerative method. Non-enumerative methods, on the other hand, are very hard. For example, for a 6-variable function f having multiplicative complexity 6, we do not yet have a proof of the (seemingly obvious) statement that the multiplicative complexity of $g = x_{7} \cdot f$ is 7.

On the positive side, the methods in this paper can often be used for finding the multiplicative complexity of – or providing lower bounds for – specific Boolean functions even when n > 6. If a function has multiplicative complexity at most 6, then there exists a circuit for it with one of the topologies enumerated here.