1 Introduction

Deep learning has emerged as an extension and development of machine learning for providing appropriate solutions to challenging tasks. Deep learning algorithms have provided innovative solutions in many fields, including computer vision, industrial and financial engineering, biomedical engineering, healthcare, security, etc [22, 23, 28, 52, 56, 63,64,65]. Nowadays, Convolutional Neural Network (CNN) is among the most common deep learning models, especially in pattern recognition and image classification fields due to its compatibility with image architecture. CNN has shown outstanding results, especially in large image classification datasets (Image Net) [2, 43, 51, 59].

1.1 Problem statement

CNN remains limited because it can only provide point estimates of parameters and outcomes. This constraint leads to decisions being taken with a high degree of certainty, which can lead to undesirable results, particularly in situations where decisions require a high degree of caution and credibility. The drawback arises from the fact that a CNN is unable to capture model uncertainty; it consistently produces a result but fails to indicate the reliability or correctness of that result [34].

1.2 Current status

The Bayesian approach in deep learning algorithms can be used as an alternative to the deterministic approach to address this problem. [37]. The Bayesian approach provides a probabilistic interpretation for deep learning models that allows the determination of model uncertainty, which increases the credibility of neural network outcomes [1, 14, 32, 45].

A Bayesian Convolutional Neural Network (BCNN) is a form of artificial neural network in which the CNN parameters are represented as stochastic components of the network.

The BCNN is characterized not only by its capacity to quantify uncertainty in the network but also by its ability to discriminate between its two forms, which are epistemic and aleatoric uncertainty [14, 71]. Nevertheless, applying the Bayesian method to CNN remains challenging since it requires the computation of an integral over all possible values of CNN parameters to determine the posterior distribution of these models. To overcome this problem, we can infer this distribution using statistical estimates known as "approximate inferences" [19, 27, 27, 48, 60, 62]. In this context, there are many inferential estimation techniques used in deep learning algorithms, the most notable of which are Monte Carlo techniques and Variational Inference.

Monte Carlo methods are stochastic estimations that approximate expectations numerically by randomly generating samples from probability distributions.

Variational inference is an optimization technique that provides analytical estimates of the posterior distribution using another simple distribution [7, 60, 69].

1.3 Research hypothesis

In practical applications [3, 41, 46], posterior distributions are often complex and require more flexible models for accurate estimation. Therefore, this paper aims to approximate the posterior distribution using the Bayes by Backprop method by employing a multimodal distribution, specifically a mixture of factorized Gaussian distributions, as the variational distribution. This involves sampling the convolutional parameters from a mixture of K fully factorized Gaussian distributions at each iteration, where K represents the number of mixture components.

Multimodal distributions perform better than unimodal distributions in capturing complex patterns and variations in the posterior distribution.

1.4 The main contributions

The contributions of this paper are summarized as follows:

  • We employ the Bayes-Backprop method to train convolutional neural networks (CNNs) by employing a mixture of factorized Gaussian distributions as the variational distribution.

  • We show that the reparametrization of a GMM involves reparametrizing each Gaussian component independently. This process includes introducing a standard normal random variable and using it to reparameterize each component of the GMM.

  • We apply our proposed method to train CNNs on various datasets. Subsequently, we conduct a comparative analysis between our approach and previous methods to evaluate the obtained results.

  • We study the estimation of both aleatoric and epistemic uncertainties using a Gaussian mixture model (GMM) as the variational distribution. Through the experimental results, we demonstrate that as training accuracy increases, uncertainty decreases, resulting in more reliable decision-making by the network.

The remaining sections of this paper were ordered as follows: the second section provided an overview of most of the research related to this work, while Sect. 3 provided the background and tools that we will need in this research, including a description of the BCNN and the most important approaches used in it. Section 4 describes our contribution, which is represented by the application of the Bayes by backprop technique to train CNNs using mixture models. Then, in Sect. 5, we show the experimental results of this method and attempt to compare it to previous works. Finally, Sect. 6 summarizes this paper.

2 Related works

As previously stated, there are two ways to approximate the posterior distribution: stochastic estimations and variational inference methods (Table 1).

Markov chain Monte Carlo (MCMC) methods are one of the most important stochastic approaches. MCMC methods provide an approximate unbiased estimator of the true estimator by sampling the posterior distribution according to the Markov process. MCMC methods can guarantee convergence to the true estimator with increasing sample size from the posterior, which can be computationally expensive, especially in BCNN [5, 11, 12, 24, 49]. On the other hand, many approaches have contributed to developing analytical approximations to the posterior distribution, especially in deep learning models. In this context, MacKay (1992) successfully applied the Laplace approximation to neural networks [42]. The Laplace approach attempts to estimate the posterior using a Gaussian distribution whose mean achieves the maximum a posteriori (MAP) and whose covariance matrix is the inverse of the Hessian matrix of the cost function used in the MAP estimate around this mean [54]. This approach focuses only on the properties of a single-mode MAP. In the case of multiple modes, they will produce different distributions, which often fail to approximate the posterior distribution, particularly in BCNN. Subsequently, many researchers have developed these approaches in deep learning models, using mainly variational inference methods (Hinton and Van Camp (1993) [26], Barber and Bishop (1998) [4], Graves (2011) [20], Blundell and al (Bayes by Backprop 2015) [8]. Again, in 2016, Graves attempted to approximate the gradient estimators for mixture models by employing the quantile functions as an alternate transform to the reparameterization trick [21]. In 2019, Kumar Shridhar applied the Bayes-by-backprop method using a unimodal distribution to model convolutional kernels [58].

Table 1 Summary of related works
Full size table

Expectation Propagation (EP) is another method that estimates the true posterior by a simpler parametric factorized distribution from the exponential family. EP is based on minimizing the inverse form of the Kullback–Leibler (KL) divergence, KL(p//q), rather than the direct form of KL(q//p) used in variational inference (P.Minka [44]), (Hernandez-Lobato and P. Adams [25]). Sun et al. recently proposed "Generalized Expectation Propagation" (GEP) as an improved form of Expectation Propagation that can approximate multimodal posterior distributions, particularly in BCNN, by employing a mixture of exponential family distributions [61, 70]. Despite the scalability of the EP approach, the convergence using this method is not always assured, especially when using mixture models [13, 67]. On the other hand, Gal proved that training neural networks with dropout is similar to using a variational inference method with a Bernoulli distribution by transforming the dropout noise from the input space to the parameter space in neural networks (MC Dropout [16, 18]). While the MC Dropout method is suitable for deep learning models since it reduces overfitting and does not require as much modeling as other methods, it is also inflexible and cannot always fully express model uncertainty [10].

3 Background and preliminaries

3.1 Convolution neural network architecture

Assume we have N input images \(x=\{(x_{1}, x_{2},....,x_{N})\}\), and their labels \(y=\{(y_{1}, y_{2},....,y_{N})\}\), a standard CNN is a deep neural network that defines the output layer as a composition of convolution layers that extract the most significant features from the images, represented by, \(c^{\tiny {(i)}}\), \(i=1,...,N_{c}\), each \(c^{\tiny {(i)}}\) is a convolution operation between the input \(p^{\tiny {(i-1)}}\) and the filter matrix \(k^{\tiny {(i)}}\) shifted by the bias \(b_{c}^{\tiny {(i)}}\), followed by an activation function, \(s_{c}^{\tiny {(i)}}\), \(i=1,...,N_{c}\), and pooling layers, \(p^{\tiny {(i)}}\), \(i=1,...,N_{c}\), (\(N_{c}\) is the number of convolutional layers), each \(p^{\tiny {(i)}}\) is a pooling function (which may be average-pooling or maximum-pooling). Finally, the fully connected layers, which are represented, after flattening (or vectorization), as a succession of hidden layers, \(h^{\tiny {(j)}}\), \(j=1,...,N_{l}\), (\(N_{l}\) is the number of hidden layers), each \(h^{\tiny {(j)}}\) is a linear transformation,, accompanied by an activation function, \(s_{l}^{\tiny {(j)}}\), \(j=1,...,N_{l}\). The output \({\hat{y}}\) of CNN is represented as the last layer in the fully connected layers using Softmax probability as an activation function.

The parameter models of the CNN are \(\theta = \{K, b_{c}, \omega , b_{l}\}\), where K, \(b_{c}\) are the kernels and the biases of the convolution layers, and \(\omega\), \(b_{l}\) are the weights and the biases of the fully connected hidden layers.

The standard CNN works to find a point estimate of the probable function f that relates the input x to the output y using the parameters models, in other words, it works to obtain a point approximation of the model parameters \(\theta\) that fits the data-set \(D = \{(x,y)\}\) well.

To achieve this point estimate, the model employs the backpropagation algorithm to minimize the cost function [9, 38, 57], which is proportional to maximizing the log-likelihood (ML), and occasionally with a regularization component included if the maximum a posteriori estimation (MAP) is used (See Algorithm 1).

Algorithm 1
figure a

Convolutional Neural Networks: Training Procedure

Full size image

Finally, this algorithm returns a single optimum parameter \(\hat{\theta }\) that minimizes the cost function. For unseen input \(x^{*}\), CNN uses the optimum parameter \(\hat{\theta }\), to estimate their prediction.

$$\begin{aligned}{} & {} \hat{\theta } = argmin\hspace{0.1cm} Loss(y, {\hat{y}}) \end{aligned}$$
(1)
$$\begin{aligned}{} & {} {\hat{y}}^{*} = f(x^{*},\hat{\theta }) = cnn(x^{*},\hat{\theta }) \end{aligned}$$
(2)

Where \(\hat{\theta } = \{\hat{K}, \hat{b_{c}}, \hat{\omega }, \hat{b_{l}}\}\).

As we have shown, a standard CNN only gives a point estimate of the parameters, which works well on a large data set, but in some issues, larger quantities of data are not available. The problem with CNNs is that they quickly overfit with small data sets [17], which often results in overconfident predictions.

3.2 Variational inference

The Bayesian Convolutional Neural Network (BCNN) is a CNN trained by using Bayesian statistics, in which all parameters of the CNN are treated as stochastic components [17, 58].

The initial step in creating a BCNN is to determine the feedforward architecture of the CNN. We then apply the prior distribution \(p(\theta )\) of the CNN weights \(\theta\), indicating our previous beliefs about the parameters. Next, we define the likelihood \(p(y| x, \theta )\) as the independent conditional probability of the observed data given specific parameters. Generally, the likelihood for CNN models is defined as a categorical distribution of the softmax probabilities, as shown below:

$$\begin{aligned} \begin{aligned} p(y| x, \theta )&= \prod _{n=1}^{N}p(y_{n}| x_{n}, \theta ) = \prod _{n=1}^{N}p(y_{n}| f(x_{n}, \theta )) \\ {}&= \prod _{n=1}^{N}Categorical(f^{1}(x_{n}, \theta ),...,f^{C}(x_{n}, \theta )) \end{aligned} \end{aligned}$$
(3)

Where \(f^{c}(x_{n}, \theta ) = Softmax\Big (\omega ^{\tiny {(n_{l})}^{T}}_{c}h^{\tiny {(n_{l}-1)}} + b_{l_{c}}^{\tiny {(n_{l}})}\Big ) = \frac{exp\Big (\omega ^{\tiny {(n_{l})}^{T}}_{c}h^{\tiny {(n_{l}-1)}} + b_{l_{c}}^{\tiny {(n_{l}})}\Big )}{\sum _{c^{'}}^{C}exp\Big (\omega ^{\tiny {(n_{l})}^{T}}_{c^{'}}h^{\tiny {(n_{l}-1)}} + b_{l_{c^{'}}}^{\tiny {(n_{l}})}\Big )}\),

and C is the number of output classes.

We can then obtain the posterior distribution of CNN parameters given the observed data \(p(\theta | x, y)\) using the Bayes theorem as follows:

$$\begin{aligned} \begin{aligned} p(\theta | x, y) = \frac{p(y| x, \theta )p(\theta )}{p(D)}&= \frac{p(y| x, \theta )p(\theta )}{\int _{\theta } p(y| x, \theta ^{'})p(\theta ^{'}) d\theta ^{'}}\\ {}&\propto p(y| x, \theta )p(\theta ) \end{aligned} \end{aligned}$$
(4)

Deep learning models are made of a huge number of parameters, which makes determining the posterior distribution \(p(\theta | x, y)\) tricky since computing the evidence term

\(\int _{\theta } p(y| x, \theta ^{'})p(\theta ^{'}) d\theta ^{'}\) is hard.

The Variational Inference (VI) method was developed for solving an optimization problem to approximate the posterior distribution \(p(\theta | x, y)\) with a simple parametric distribution \(q_{\phi }(\theta )\) to overcome this problem [7, 69].

VI looks for an optimal variational parameter \({\hat{\phi }}\) such that the variational distribution \(q_{{\hat{\phi }}}(\theta )\) is as close as possible to the true posterior \(p(\theta | x, y)\) based on the Kullback–Leibler divergence [35], which is expressed as follows:

$$\begin{aligned} KL(q_{\phi }(\theta )||p(\theta | x, y)) = \int _{\theta }q_{\phi }(\theta ) \log \Big ( \frac{q_{\phi }(\theta )}{p(\theta | x, y)}\Big )d\theta \end{aligned}$$
(5)

To compute the KL(q||p), you must first compute the posterior distribution. As a result, the problem still exists. To get around this, we use the Evidence Lower BOund (ELBO) function \({\mathscr {L}}\), which can be obtained from KL(q||p) and the Bayes Formula as follows:

$$\begin{aligned} KL(q_{\phi }(\theta )||p(\theta | x, y)) = \log p(D) - {\mathscr {L}}(\phi ) \end{aligned}$$
(6)

Where

$$\begin{aligned} \begin{aligned} {\mathscr {L}}(\phi )&= \int _{\theta }q_{\phi }(\theta )\log p(y|x, \theta )d\theta \\ {}&- \int _{\theta }q_{\phi }(\theta )\log \Big (\frac{q_{\phi }(\theta )}{p(\theta )}\Big )d\theta \\ \\&= E_{q_{\phi }(\theta )}[\log p(y|x, \theta )] - KL(q_{\phi }(\theta )||p(\theta )) \end{aligned} \end{aligned}$$
(7)

Minimizing the KL divergence is now equivalent to maximizing the ELBO function \({\mathscr {L}}\) since the \(\log p(D)\) is constant over the variational parameters.

ELBO maximization needs to maximize the first term of the last equation, which denotes the expected log-likelihood and minimize the second term, indicating the KL divergence between \(q_{\phi }(\theta )\) and \(p(\theta )\). Generally, the second term serves as a regularizer [16].

The prediction in BCNN of a new input \(x^{*}\) is a probability distribution \(p(y^{*}|x^{*},D)\), called the predictive distribution [66]. It is defined by the expectation over the posterior distribution of the model’s output, as shown below:

$$\begin{aligned} \begin{aligned} p(y^{*}|x^{*},x,y)&= \int _{\theta }p(y^{*}|x^{*},\theta )p(\theta |x,y)d\theta \\ {}&= E_{p(\theta |x,y)}[p(y^{*}|x^{*},\theta )] \end{aligned} \end{aligned}$$
(8)

Using the variational inference method, the predictive distribution can be approximated as follows:

$$\begin{aligned} \begin{aligned} p(y^{*}|x^{*},x,y)&\approx \int _{\theta }p(y^{*}|x^{*},\theta )q_{{\hat{\phi }}}(\theta )d\theta \\ {}&= E_{q_{{\hat{\phi }}}(\theta )}[p(y^{*}|x^{*},\theta )] \\ {}&= q(y^{*}|x^{*}) \end{aligned} \end{aligned}$$
(9)

Where \({\hat{\phi }}\) are the optimal variational parameters.

3.3 Bayes by backprop

Variational inference is a powerful statistical estimate for Bayesian inference. However, the stochasticity of the parameters prevents back-propagation from working in deep learning models. To overcome this issue, Blundell et al. proposed the Bayes-by-backprop algorithm [8]. Bayes by Backprop is indeed a variational inference technique that looks for the variational parameters \({\hat{\phi }}\) that minimize the KL divergence between the posterior distribution \(p(\theta |x,y)\) and the variational distribution \(q_{\phi }(\theta )\).

$$\begin{aligned} \begin{aligned} {\hat{\phi }}&= \arg \min _{\phi } KL(q_{\phi }(\theta )||p(\theta | x, y))\\ \\&= \arg \min _{\phi } KL(q_{\phi }(\theta )||p(\theta )) - E_{q_{\phi }(\theta )}[\log p(y|x, \theta )]\\ \\&= \arg \min _{\phi } \underbrace{\hspace{-0.1cm}\int _{\theta }\hspace{-0.1cm}q_{\phi }(\theta )\underbrace{\hspace{-0.1cm}\Big (\log q_{\phi }(\theta ) \hspace{-0.1cm}- \log p(\theta )\hspace{-0.1cm} - \log p(y|x, \theta ) \Big )}_{l(\theta ,\phi )}d\theta }_{\mathscr {L}}({\mathscr {D}},\phi ) \end{aligned} \end{aligned}$$
(10)

Where \({\mathscr {L}}({\mathscr {D}},\phi )\) is the negative ELBO function.

The new aspect of the Bayes-by-backprop algorithm is to apply the reparametrization trick technique to the model parameters [30, 31]. The idea is to transform the randomness of the model parameters, \(\theta\), which is simulated from a parametric distribution \(q_{\phi }(\theta )\), to another random variable \(\epsilon\), that follows a non-parametric distribution, \(q(\epsilon )\), by reparameterizing \(\theta\) as a deterministic and differentiable function of the variational parameters \(\phi\) and \(\epsilon\), \(g(\phi ,\epsilon )\) such that \(\theta = g(\phi ,\epsilon )\). Therefore, we may compute the gradients \(\nabla _{\theta }l(\theta ,\phi )\) by backpropagating via \(\theta\), which is now non-stochastic (See Algorithm 2).

As a result, Blundell et al. [8] proposed that if \(q_{\phi }(\theta )d\theta = q(\epsilon )d\epsilon\), and for a differentiable function \(l(\theta ,\phi )\), we get:

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial \phi } {\mathscr {L}}({\mathscr {D}},\phi )&= \frac{\partial }{\partial \phi }E_{q_{\phi }(\Theta )}\Big [l(\theta ,\phi )\Big ] \\&= E_{q(\epsilon )}\Big [\frac{\partial l(\theta ,\phi )}{\partial \theta }\frac{\partial \theta }{\partial \phi } + \frac{\partial l(\theta ,\phi )}{\partial \phi }\Big ] \end{aligned} \end{aligned}$$
(11)

Where \(\frac{\partial \theta }{\partial \phi } = \frac{\partial g(\phi ,\epsilon )}{\partial \phi }\) in the last expression. For more details about the last formula, see [8].

As \(\frac{\partial }{\partial {\phi }}{\mathscr {L}}({\mathscr {D}},\phi )\) is also hard to compute, we can use Monte Carlo sampling to estimate it. Using the reparameterization trick, we first sample \(\epsilon\) from the non-parametric distribution \(q(\epsilon )\) and then apply the deterministic function g, such that \(\theta = g(\phi ,\epsilon ) \sim q_{\phi }(\theta )\).

As a result, we can approximate \(\frac{\partial }{\partial \phi }{\mathscr {L}}({\mathscr {D}},\phi )\) as follows:

$$\begin{aligned} \begin{aligned} {\frac{\partial }{\partial \phi }{\mathscr {L}}({\mathscr {D}},\phi )}&\approx {\frac{\partial }{\partial \phi }\hat{\mathscr {L}}(\theta ,\phi )} \\&= \frac{1}{T}\sum _{t=1}^{T}\Big [\frac{\partial l(g(\phi ,\epsilon ^{(t)}),\phi )}{\partial \theta ^{(t)}}\frac{\partial g(\phi ,\epsilon ^{(t)})}{\partial \phi } \\&\qquad + \frac{\partial l(g(\phi ,\epsilon ^{(t)}),\phi )}{\partial \phi }\Big ] \end{aligned} \end{aligned}$$
(12)

Where \(l(g(\phi ,\epsilon ^{(t)}),\phi ) = \log q_{\phi }(g(\phi ,\epsilon ^{(t)})) - \log p(g(\phi ,\epsilon ^{(t)})) - \log p(y|x, g(\phi ,\epsilon ^{(t)}))\), \(\epsilon ^{(t)} \sim q(\epsilon )\), T is the number of samples, and \(\frac{\partial }{\partial \phi }\hat{\mathscr {L}}(\theta ,\phi )\) is an unbiased estimator of \(\frac{\partial }{\partial \phi }\mathscr {L}(\mathscr {D},\phi ) (E_{q(\epsilon )}\Big [\frac{\partial }{\partial \phi }\hat{\mathscr {L}}(\theta ,\phi )\Big ] = \frac{\partial }{\partial \phi }\mathscr {L}(\mathscr {D},\phi )\)).

Algorithm 2
figure b

Bayes by Backprop Algorithm [8]

Full size image

3.4 Gaussian mixture model

A Gaussian Mixture Model (GMM) is a probability distribution defined as a linear convex combination of Gaussian distributions [13, 53]. Therefore, we can express a GMM composed of a K-component Gaussian density as follows:

$$\begin{aligned} p_{\phi }(\theta ) = \sum _{k=1}^{K}\pi _{k}\textrm{N}(\theta |\mu _{k},\Sigma _{k}) \end{aligned}$$
(13)

Where \(\mathbf {\theta }\) is a D-dimensional vector, \(\{ \pi _{k},k=1,2,...,K \}\) are the mixture weights that satisfy the constraint that \(\sum _{k=1}^{K}\pi _{k} = 1,with\quad 0< \pi _{k}< 1\), and \(\{ \textrm{N}(\theta |\mu _{k},\Sigma _{k}),k=1,2,...,K \}\) are the components distributions. Each component is a multivariate Gaussian distribution of the following form:

$$\begin{aligned} {\textrm{N}(\hspace{-0.03cm}\theta |\mu _{k},\Sigma _{k}) = \frac{1}{(2\pi )^{d/2} \vert {\Sigma _{k}}\vert ^{1/2}}\exp \Big (-\frac{1}{2}(\theta - \mu _{k})^{T}\Sigma _{k}^{-1}(\theta - \mu _{k})\Big )} \end{aligned}$$
(14)

Where \(\mu _{k}\) is a d-dimensional mean vector, \(\Sigma _{k}\) is a d\(\times\)d-dimensional covariance matrix of the corresponding Gaussian distribution. \(\phi = \{(\pi _{k},\phi _{k}=\{\mu _{k}, \Sigma _{k}\}), k=1,2,...,K \}\)

represents the full parameters of the Gaussian mixture model \(p_{\phi }(\theta )\).

For various theoretical and computational reasons, the Gaussian distribution is the most preferred unimodal distribution in real-world modelling. However, some challenging applications, such as image classification, require more sophisticated distributions to model them.

As a result, using a unimodal model in this situation is frequently ineffective [53],

[13]. To solve this issue, we can represent these applications using a GMM, which is a combination of several unimodal Gaussian distributions that can provide more statistical information about the problem than single-mode distributions.

4 Bayes by backprop using mixture models

A mixture model is a powerful tool that may be used in variational inference as an approximated posterior distribution. However, reparameterizing the parameters of mixture models is challenging since they combine component distributions using discrete-categorical variables

\(k \sim Cat(\{\pi _{k}\}_{k=1}^{K})\). To address this problem, Roeder et al. propose that the expectation over the mixture model be computed by taking the sum of the mixture weights outside the expectation and then sampling equally from each component distribution, [47, 55].

As a result, if each component distribution is reparameterizable, we may reparameterize the mixture models.

Let \(q_{\phi }(\theta ) = \sum _{k=1}^{K}\pi _{k}q_{\phi _{k}}(\theta )\) as a mixture distribution made up of K component distributions \(q_{\phi _{k}}(\theta )\), combined by K mixture weights \(\{ \pi _{k},k=1,2,...,K \}\).

If \(q_{\phi _{k}}(\theta _{k})d\theta _{k} = q(\xi _{k})d\xi _{k}\), and \(\theta _{k}=g(\phi _{k},\xi _{k})\), for \(k=1,2,...,K\), with g is a differentiable function, we can approximate the expectation \(E_{q_{\phi }(\theta )}[f(\theta )]\), as follows:

$$\begin{aligned} \begin{aligned} E_{q_{\phi }(\theta )}\Big [f(\theta )\Big ]&= \sum _{k=1}^{K}\pi _{k}E_{q(\xi _{k})}\Big [f(g(\phi _{k},\xi _{k}))\Big ] \\ {}&\approx \sum _{k=1}^{K}\frac{\pi _{k}}{T}\sum _{t=1}^{T}f(g(\phi _{k},\xi _{k}^{(t)})) \end{aligned} \end{aligned}$$
(15)

Where \(\xi _{k}^{(t)}\sim q(\xi _{k})\), and T is the number of samples.

Proof:

$$\begin{aligned} E_{q_{\phi }(\theta )}\Big [f(\theta )\Big ]&=\int _{\theta }\sum _{k=1}^{K}\pi _{k}q_{\phi _{k}}(\theta )f(\theta )d\theta \\ {}&= \sum _{k=1}^{K}\pi _{k}\int _{\theta }q_{\phi _{k}}(\theta )f(\theta )d\theta \\ {}&= \sum _{k=1}^{K}\pi _{k}\int _{\theta _{k}}q_{\phi _{k}}(\theta _{k})f(\theta _{k})d\theta _{k}\\&\text {(Linearity of integral)} \\ {}&= \sum _{k=1}^{K}\pi _{k}\int _{\xi _{k}}q(\xi _{k})f(g(\phi _{k},\xi _{k}))d\xi _{k}\\&\text {Reparameterization the parameters of each} \\&\text {component distribution as } \theta _{k} = g(\phi _{k},\xi _{k}) \\ {}&= \sum _{k=1}^{K}\pi _{k}E_{q(\xi _{k})}[f(g(\phi _{k},\xi _{k}))]\\&\approx \sum _{k=1}^{K}\frac{\pi _{k}}{T}\sum _{t=1}^{T}f(g(\phi _{k},\xi _{k}^{(t)}))\\&\hspace{6cm}\square \end{aligned}$$

With \(\xi _{k}^{(t)}\sim q(\xi _{k})\), for \(k=\{1,2,...,K\}\).

The latter expression is the result of applying Monte Carlo sampling to each component distribution \(q(\xi _{k})\), taking into account the independence of \(\xi _{k}\), resulting from the independence of parameters \(\theta _{k}\), for \(k = \{1,2,...,K\}\).

Furthermore, using this approximation, we obtain an unbiased estimator as shown below:

$$\begin{aligned}&E_{\prod _{k=1}^{K}q(\xi _{k})}\Big [\sum _{k=1}^{K}\frac{\pi _{k}}{T} \sum _{t=1}^{T}f(g(\phi _{k},\xi _{k}^{(t)}))\Big ]\\ {}&\hspace{1.5cm}= \sum _{k=1}^{K}\pi _{k}E_{q(\xi _{k})}\Big [\frac{1}{T}\sum _{t=1}^{T}f(g(\phi _{k},\xi _{k}^{(t)}))\Big ]\\&\hspace{1.5cm} = \sum _{k=1}^{K}\frac{\pi _{k}}{T}\sum _{t=1}^{T}E_{q(\xi _{k})} \Big [f(g(\phi _{k},\xi _{k}^{(t)}))\Big ] \\&\hspace{1.5cm}= \sum _{k=1}^{K}\pi _{k}E_{q(\xi _{k})}\Big [f(g(\phi _{k},\xi _{k}))\Big ]\\&\hspace{1.5cm}=\sum _{k=1}^{K}\pi _{k}E_{q_{\phi _{k}}(\theta _{k})}\Big [f(\theta _{k})\Big ]\\&\hspace{1.5cm}= E_{q_{\phi }(\theta )}\Big [f(\theta )\Big ] \end{aligned}$$
Fig. 1
figure 1

Bayesian convolution neural network

Full size image

Instead of sampling a discrete random variable

\(k \sim Cat(\{\pi _{k}\}_{k=1}^{K})\) and then sampling \(\theta\) from the associated component distribution \(q_{\phi _{k}}(\theta )\), the approach described above takes samples from each component distribution equally and then combines them using the mixture weights. Although the last method is more computationally expensive than the first since it requires K-implementations of the function f to obtain one Monte Carlo estimate of the expectation

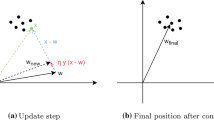
\(E_{q_{\phi }(\theta )}[f(\theta )]\), it allows us to reparameterize the parameters of the mixture model and also gives a differentiable estimate (See Fig. 2), which is not available in the first approach [15, 40].

Therefore, if all conditions are satisfied, we can apply the Bayes by Backprop method to the differentiable and continuous function l (Eq. 10), using a mixture model as an approximate distribution (Algorithm 3), as illustrated below:

for \(j= 1,2,...,K:\)

$$\begin{aligned} \frac{\partial }{\partial \phi _{j}} {\mathscr {L}}(D,\phi )&= \frac{\partial }{\partial \phi _{j}} {\mathscr {L}}(D,(\phi _{1},..,\phi _{j},..,\phi _{K}))\\ {}&=\frac{\partial }{\partial \phi _{j}}E_{q_{\phi }(\theta )}\Big [l(\theta ,\phi )\Big ] \\ {}&= \frac{\partial }{\partial \phi _{j}}\sum _{k=1}^{K}\pi _{k}E_{q_{\phi _{k}}(\theta )}\Big [l(\theta ,\phi )\Big ] \\ {}&= \frac{\partial }{\partial \phi _{j}}\sum _{k=1}^{K}\pi _{k}E_{q(\xi _{k})}\Big [l(g(\phi _{k},\xi _{k}),\phi )\Big ] \\&= \sum _{k=1}^{K}\pi _{k}E_{q(\xi _{k})}\Big [\frac{\partial l(g(\phi _{k},\xi _{k}),\phi )}{\partial \theta _{k}}\frac{\partial g(\phi _{k},\xi _{k})}{\partial \phi _{j}} \\&\hspace{2cm}+ \frac{\partial l(g(\phi _{k},\xi _{k}),\phi )}{\partial \phi _{j}}\Big ] \end{aligned}$$

Where \(q_{\phi }(\theta ) = \sum _{k=1}^{K}\pi _{k}q_{\phi _{k}}(\theta )\) is a mixture model,

\(l(\theta ,\phi )=\log q_{\phi }(\theta ) - \log p(\theta ) - \log p(y|x, \theta )\), and

\(q_{\phi _{k}}(\theta _{k})d\theta _{k} = q(\xi _{k})d\xi _{k}\), for \(k= 1,2,...,K\).

Since \(\frac{\partial }{\partial \phi _{j}} {\mathscr {L}}(\phi ,D)\) is also computationally intricate, we can estimate it using Eq. 15, as follows:

for \(j= 1,2,...,K:\)

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial \phi _{j}}{\mathscr {L}}(D,\phi )&\approx \frac{\partial }{\partial \phi _{j}}\hat{\mathscr {L}}(\mathbf {\theta ,\phi }) \\ {}&= \frac{1}{T}\sum _{k=1}^{K}\sum _{t=1}^{T}\pi _{k}\frac{\partial l(\theta _{k}^{(t)},\phi )}{\partial \theta _{k}^{(t)}}\frac{\partial g(\phi _{k},\xi _{k}^{(t)})}{\partial \phi _{j}}\\&+ \frac{1}{T}\sum _{k=1}^{K}\sum _{t=1}^{T}\pi _{k}\frac{\partial l(g(\phi _{k},\xi _{k}^{(t)}),\phi )}{\partial \phi _{j}} \end{aligned} \end{aligned}$$
(16)

Where \(\xi _{k}^{(t)} \sim q(\xi _{k})\) for \(t= 1,2,...,T\), and \(k= 1,2,...,K\),

\(l(g(\phi _{k},\epsilon ^{(t)}),\phi ) =\log \Big (\sum _{i=1}^{K}\pi _{i}q_{\phi _{i}}(g(\phi _{k},\xi _{k}^{(t)}))\Big ) - \log p(g(\phi _{k},\xi _{k}^{(t)})) - \log p(y|x, g(\phi _{k},\xi _{k}^{(t)}))\), and

\(\frac{\partial }{\partial \phi _{j}}\hat{\mathscr {L}}(\theta ,\phi )\) is an unbiased estimator of \(\frac{\partial }{\partial \phi _{j}}\mathscr {L}(\mathscr {D},\phi )\). \(\Big (E_{\prod _{k=1}^{K}q(\xi _{k})}\Big [\frac{\partial }{\partial \phi _{j}}\hat{\mathscr {L}}(\theta ,\phi )\Big ] = \frac{\partial }{\partial \phi _{j}}\mathscr {L}(\mathscr {D},\phi )\), for \(j= 1,2,...,K\Big )\).

Algorithm 3
figure c

Bayes by Backprop using mixture model

Full size image

4.1 Bayesian convolution neural network with GMM

In this section, we will try to apply the Bayes By Backprop method to convolutional neural networks using a Gaussian mixture model (BBGMM) as an approximate distribution of the true posterior, and we will show how to construct, train, and evaluate BCNN using this distribution.

A convolutional neural network is a deep learning model characterized by two basic steps. First, we extract the most significant features of inputs using kernels in convolutional layers, and second, we classify the inputs using fully connected layers and a softmax function in the output layer (See Fig. 1).

As a result, the CNN parameters are expressed as follows: \(\theta = \{F, b_{c}, \omega , b_{l}\}\), where \(F = \{\{f_{h_{i,p},w_{i,p},c_{i,p}}\}_{i,p=1}^{N_{c},p_{i}}\}, b_{c} =\{ \{b_{c_{i}}\}_{i=1}^{i=N_{c}} \}\) are the kernels and the biases of the convolutional layers, and \(\omega =\{\{W_{j}\}_{j=1}^{j=N_{l}}\}\), \(b_{l} = \{\{b_{l_{j}}\}_{j=1}^{j=N_{l}}\}\) are the weights and the biases of the fully connected layers.

Following the Bayesian approach, these parameters are represented as stochastic kernels in the convolution layers and as stochastic matrices in the fully connected layers. Before seeing the data, the Bayes by Backprop algorithm, like the other variational inference methods, requires setting a prior distribution for all CNN parameters \(p(\theta ) =\) \(p(F, b_{c}, \omega , b_{l})\) as prior beliefs about the possible parameters that fit the data. After seeing the data \(D = \{(x,y)\}\), we have to determine the model’s probability \(p(y| x, \theta )\) (the likelihood) for the outputs \(y = \{(y_{1}, y_{2},....,y_{N})\}\) given the inputs \(x = \{(x_{1}, x_{2},....,x_{N})\} \in \mathscr {R}^{H\textbf{x}W\textbf{x}C\textbf{x}N}\) and parameters

\(\theta = \{F, b_{c}, \omega , b_{l}\}\).

Then, we use a mixture of K fully-factorized normal distributions (i.e., with diagonal covariances) as a variational distribution of the CNN parameters, as shown below:

$$\begin{aligned} \begin{aligned} q_{\phi _{k}}(\theta )&= \sum _{k=1}^{K}\pi _{k} q_{\phi _{k}}(F, b_{c}, \omega , b_{l}) \\ {}&= \sum _{k=1}^{K}\pi _{k} \underbrace{q_{\phi _{k_{F}}}(F)q_{\phi _{k_{bc}}}(b_{c})}_{Convolution-layers} \underbrace{q_{\phi _{k_{\omega }}}(\omega )q_{\phi _{k_{bl}}}(b_{l})}_{Fully-Connected-layers} \end{aligned} \end{aligned}$$
(17)

Where

$$\begin{aligned}q_{\phi _{k_{F}}}(F) ={} & {} \prod _{i,p,h,w,c=1}^{N_{c},p_{i},h_{i},w_{i},c_{i}}\textrm{N} \Big (f_{i,p,h,w,c}|\mu _{k_{f_{i,p,h,w,c}}},\sigma ^{2}_{k_{f_{i,p,h,w}}}\Big )\\{} & {} q_{\phi _{k_{bc}}}(bc) =\prod _{i,p=1}^{N_{c},p_{i}} \textrm{N}\Big (bc_{i,p}|\mu _{k_{bc_{i,p}}},\sigma ^{2}_{k_{bc_{i,p}}}\Big )\\{} & {} q_{\phi _{k_{\omega }}}(\omega ) = \prod _{j,m,n=1}^{N_{l},L_{j},L_{j+1}}\textrm{N}\Big (w_{j,m,n}| \mu _{k_{w_{j,m,n}}},\sigma ^{2}_{k_{w_{j,m,n}}}\Big )\\{} & {} q_{\phi _{k_{bl}}}(b{l}) = \prod _{j,n=1}^{N_{l},L_{j+1}}\textrm{N}\Big (bl_{j,n}| \mu _{k_{bl_{j,n}}},\sigma ^{2}_{k_{bl_{j,n}}}\Big ) \end{aligned}$$

\(N_{c}\) is the number of convolutional layers, \(p_{i}, h_{i}, w_{i}\), and \(c_{i}\) represent, respectively, the number, width, height, and the channels number of kernels in the \(i^{th}\) convolutional layer, \(N_{l}\) is the number of fully connected layers, \(L_{j}\), and \(L_{j+1}\) denote the number of neurons in the \(j^{th}\) and the \(j+1^{th}\) layers, respectively.

Fig. 2
figure 2

Reparameterization trick on GMM using K Gaussian Components

Full size image

The Gaussian distribution \(\textrm{N}(\theta |\mu , \sigma ^{2})\) can be reparameterized to the unit Gaussian \(\textrm{N}(\epsilon |0, I)\) by using a differential transform of the parameters expressed as follows: \(\theta = \mu + \sigma \odot \epsilon\), where \(\odot\) is an element wise product, and \(\epsilon\) is a free-noise parameter of the unit Gaussian. To prevent receiving negative values for \(\sigma\), we can rewrite them as follows: \(\sigma = \log (1 + \exp (\sigma ))\). As a result, we can reparameterize the parameters of the Gaussian mixture model by reparameterizing them over each Gaussian distribution component (See Fig. 2), as shown below:

for \(k = 1,...,K.\)

$$\begin{aligned} \theta _{k} = g(\phi _{k},\epsilon _{k}) = \mu _{k} + \log (1 + \exp (\sigma _{k}))\odot \epsilon _{k} \end{aligned}$$
(18)

With \(\epsilon _{k}\sim \textrm{N}(\epsilon |0, I)\), and \(\phi _{k} = \{(\mu _{k},\sigma _{k})\}\).

This allows applying the Bayes by backprop algorithm using GMM to deep neural networks, including CNNs (see Algorithm 4), as follows:

for \(j = 1,...,K.\)

$$\begin{aligned}&\frac{\partial }{\partial \phi _{j}} {\mathscr {L}}({\mathscr {D}},\phi ) = \sum _{k=1}^{K}\pi _{k}E_{\textrm{N}(\epsilon _{k}|0, I)}\Big [\frac{\partial l(\mathbf {\theta _{k},\phi })}{\partial \theta _{k}}\frac{\partial g(\phi _{k},\epsilon _{k})}{\partial \phi _{j}} \nonumber \\&\qquad + \frac{\partial l(g(\phi _{k},\epsilon _{k}),\phi )}{\partial \phi _{j}}\Big ] \nonumber \\&\approx \frac{1}{T}\sum _{t=1}^{T}\sum _{k=1}^{K}\pi _{k}\Big [\frac{\partial l(\theta _{k}^{(t)},\phi )}{\partial \theta _{k}^{(t)}}\frac{\partial g(\phi _{k},\epsilon _{k}^{(t)})}{\partial \phi _{j}} \nonumber \\ {}&\qquad + \frac{\partial l(g(\phi _{k},\epsilon _{k}^{(t)}),\phi )}{\partial \phi _{j}}\Big ]\nonumber \\&\quad = \frac{\partial }{\partial \phi _{j}}\hat{\mathscr {L}}(\theta ,\phi ) \nonumber \\&{\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{\partial }{\partial \mu _{j}}{\mathscr {L}}(D,\phi ) \approx \frac{1}{T}\sum _{t=1}^{T}\Big [ \sum _{k=1}^{K}\pi _{k}\frac{\partial l(g(\phi _{k},\epsilon _{k}^{(t)}),\phi )}{\partial \mu _{j}} \\ &{}\qquad + \pi _{j}\frac{\partial l(\theta _{j}^{(t)},\phi )}{\partial \theta _{j}^{(t)}}\Big ] \\ &{}\quad = \frac{\partial }{\partial \mu _{j}}\hat{\mathscr {L}}(\mathbf {\theta ,\phi }) \\ &{}\quad \frac{\partial }{\partial \sigma _{j}}{\mathscr {L}}(D,\phi ) \approx \frac{1}{T}\sum _{t=1}^{T}\Big [\sum _{k=1}^{K}\pi _{k} \frac{\partial l(g(\phi _{k},\epsilon _{k}^{(t)}),\phi )}{\partial \sigma _{j}} \\ &{}\qquad + \pi _{j}\frac{\partial l(\theta _{j}^{(t)},\phi )}{\partial \theta _{j}^{(t)}}\frac{\epsilon _{j}^{(t)}}{1 + \exp (-\sigma _{j})} \Big ] \\ &{}\quad = \frac{\partial }{\partial \sigma _{j}}\hat{\mathscr {L}}(\theta ,\phi ) \end{aligned} \end{array}\right. } \end{aligned}$$
(19)

Where, \(\epsilon _{k}^{(t)}\sim {\textrm{N}}(\epsilon _{k}|0, I)\), for \(k = 1,...,K\), and \(t = 1,...,T\),

and \(l(\theta _{k},\phi ) = \log \Big (\sum _{i=1}^{K}\pi _{i}{\textrm{N}}(\theta _{k}| \mu _{i}, \sigma _{i}^{2})\Big ) - \log p(\theta _{k})- \log p(y|x, \theta _{k})\).

Algorithm 4
figure d

Training BCNN using Gaussian mixture model (BBGMM)

Full size image

Having obtained the optimal variational distribution, we can use it to estimate the predictive distribution \(p(y^{*}|x^{*},D)\) for an unseen data input \(x^{*}\) using the observed data \(D = \{(x,y)\}\), as follows:

$$\begin{aligned} \begin{aligned} p(y^{*}|x^{*},x,y)&\approx \int q_{{\hat{\phi }}}(\theta )p(y^{*}|x^{*},\theta )d\theta \\ {}&= \int \Big (\sum _{k=1}^{K}\pi _{k}{\textrm{N}}(\theta |{\hat{\mu }}_{k}, {\hat{\sigma }}_{k}^{2})\Big )p(y^{*}|x^{*},\theta )d\theta \\ {}&\approx \frac{1}{T}\sum _{t=1}^{T}\sum _{k=1}^{K}\pi _{k}p(y^{*}|x^{*},\theta _{k}^{(t)}) \\ {}&= q(y^{*}|x^{*}) \end{aligned} \end{aligned}$$
(20)

Since classification tasks have a discrete nature, the predictive distribution is estimated by an average of discrete functions, which are frequently categorical probabilities.

$$\begin{aligned} \begin{aligned} p(y^{*}|x^{*},x,y)&\approx \frac{1}{T}\sum _{t=1}^{T}\sum _{k=1}^{K}\pi _{k}p(y^{*}|x^{*},\theta _{k}^{(t)}) \\ {}&=\frac{1}{T}\sum _{t=1}^{T}\sum _{k=1}^{K}\pi _{k}Cat(y^{*}|f(x^{*},\theta _{k}^{(t)}))\\ {}&=\frac{1}{T}\sum _{t=1}^{T}\sum _{k=1}^{K}\pi _{k}\prod _{c=1}^{C} f^{c}(x^{*},\theta _{k}^{(t)})^{y_{c}^{*}} \end{aligned} \end{aligned}$$
(21)

With \(\theta _{k}^{(t)}\sim \textrm{N}(\theta |{\hat{\mu }}_{k},{\hat{\sigma }}_{k}^{2})\), for \(t= 1,2,...,T\), and

\(k= 1,2,...,K\), \(f(x^{*},\theta _{k}^{(t)})\) is the output function of CNN, \(f^{c}(x^{*},\theta _{k}^{(t)}) = p(y_{c}^{*} = 1|f(x^{*},\theta _{k}^{(t)}))\) with \(\sum _{c=1}^{C}f^{c}(x^{*},\theta _{k}^{(t)}) = 1\), and C is the number of classes in the output layer.

4.2 Uncertainty in CNN with GMM

Uncertainty estimation in deep neural networks is crucial for decision-making, especially in tasks that require a high degree of credibility and reliability. Generally, there are two types of uncertainty: aleatoric uncertainty and epistemic uncertainty. Aleatoric uncertainty is an irreducible quantity resulting from the noise generated by the data collection method. Regarding epistemic uncertainty, it results from model predictions when there is little observed data, but it can be reduced if more data are available. In general, Bayesian techniques provide an effective framework for estimating uncertainties by computing the variance of the predictive distribution over the variational posterior, as shown below:

$$\begin{aligned} \begin{aligned}&\mathbf {\textbf{V}_{q_{{\hat{\phi }}}(\theta )}[p(y^{*}|x^{*},x,y)]} {\mathbf {= \textbf{E}_{q_{{\hat{\phi }}}(\theta )}[y^{*}y^{*^{T}}]- \textbf{E}_{q_{{\hat{\phi }}}(\theta )}[y^{*}]\textbf{E}_{q_{\phi }(\theta )}[y^{*}]^{T} }} \\ \\ {}&{\mathbf {=\underbrace{\mathbf { \int _{\theta } \Big [diag\Big (\textbf{E}_{p(y^{*}|x^{*},\theta )}[y^{*}]\Big ) -\textbf{E}_{p(y^{*}|x^{*},\theta )}[y^{*}]\textbf{E}_{p(y^{*}|x^{*},\theta )} [y^{*}]^{T}\Big ]q_{{\hat{\phi }}}(\theta )d\theta }}_{{\hspace{0.7cm}Aleatoric-Uncertainty}}}}\\&{\mathbf {+ \underbrace{\mathbf {\int _{\theta } \Big (\textbf{E}_{p(y^{*}|x^{*},\theta )}[y^{*}] - \textbf{E}_{q_{{\hat{\phi }}}(\theta )}[y^{*}]\Big ) \Big (\textbf{E}_{p(y^{*}|x^{*},\theta )}[y^{*}] - \textbf{E}_{q_{{\hat{\phi }}}(\theta )}[y^{*}]\Big )^{T} q_{{\hat{\phi }}}(\theta )d\theta }}_{{\hspace{2cm}Epistemic-Uncertainty}}}} \end{aligned} \end{aligned}$$
(22)

For a review of the last formula’s proof, see: [36].

As seen in the last formula, the variance of the predictive distribution is the sum of the aleatoric and epistemic uncertainty. Despite this, calculating these two uncertainties remains difficult due to the intractability of the integrals in the last formula. To solve this problem, we can combine the approach described earlier in Sect. 1 (Eq. 15) with the method proposed by Kwon in [36] to estimate the uncertainty using a GMM, as illustrated below:

$$\begin{aligned} \begin{aligned} \textbf{V}_{q_{{\hat{\phi }}}(\theta )}[p(y^{*}|x^{*},x,y)]&\approx \underbrace{\frac{1}{T}\sum _{t=1}^{T}\sum _{k=1}^{K}\pi _{k} \Big [diag({\hat{p}}_{k}^{(t)})-{\hat{p}}_{k}^{(t)}{\hat{p}}_{k}^{(t)^{T}}\Big ]}_{Aleatoric-Uncertainty} \\ {}&+ \underbrace{\frac{1}{T}\sum _{t=1}^{T}\sum _{k=1}^{K}\pi _{k}({\hat{p}}_{k}^ {(t)}-\bar{p})({\hat{p}}_{k}^{(t)}-\bar{p})^{T}}_{Epistemic-Uncertainty} \end{aligned} \end{aligned}$$
(23)

Where, \(q_{{\hat{\phi }}}(\theta )=\sum _{k=1}^{K} \pi _{k}\textrm{N}(\theta |{\hat{\mu }}_{k},{\hat{\sigma }}_{k}^{2})\),

\(\bar{p}=\sum _{k=1}^{K}\pi _{k}\frac{1}{T}\sum _{t=1}^{T}{\hat{p}}_{k}^{(t)}\), \({\hat{p}}_{k}^{(t)}=f(x^{*}, \theta _{k}^{(t)})\) is the output function of CNN, and \(\theta _{k}^{(t)}\sim \textrm{N}(\theta |{\hat{\mu }}_{k},{\hat{\sigma }}_{k}^{2})\).

5 Experiments

In this section, we will apply the LeNet-5 network (as described in Appendix C, Table 9) to the MNIST and Fashion MNIST datasets. Additionally, we will use the CNN model defined in Appendix C (Table 10) for the CIFAR-10 and SVHN datasets (as specified in Appendix A, Table 8). To approximate the posterior distribution, we will employ the GMM as the variational distribution (BBGMM).

5.1 Experimental setup

Implementing the BCNN requires first defining the prior distribution of all CNN parameters. In this regard, we have adopted a fully factorized Gaussian distribution with a zero mean and a prior standard deviation \(\mathbf {\sigma _{0}>0}\) as a prior distribution of the parameters, as shown below:

$$\begin{aligned}{} & {} p(\theta )= p(F, b_{c}, \omega , b_{l})= \prod _{i=1}^{P}\textrm{N}(\theta _{i}|0,\sigma ^{2}_{0}) \end{aligned}$$
(24)
$$\begin{aligned}{} & {} \log p(\theta )= \log p(F, b_{c}, \omega , b_{l})= \sum _{i=1}^{P}\log \Big (\textrm{N}(\theta _{i}|0,\sigma ^{2}_{0})\Big ) \end{aligned}$$
(25)

Where P is the number of all CNN parameters.

After executing the CNN-feedforward on the dataset, we compute the log-likelihood as follows:

$$\begin{aligned} \begin{aligned} \log p(D|\theta )&= \log p(D|cnn(x,\theta )) \\ {}&= \sum _{n=1}^{N}\log p(y_{n}|cnn(x_{n},\theta ))\\ {}&=\sum _{n=1}^{N}\log Cat(cnn^{1}(x_{n}, \theta ),...,cnn^{C}(x_{n}, \theta )) \end{aligned} \end{aligned}$$
(26)

Where C is the number of classes in the output layer (C = 10 for all datasets).

Computing \(\log p(D|\theta )\) gets difficult when dealing with a huge dataset (N is large). To address this issue, the mini-batch optimization technique has demonstrated its efficiency in training time by randomly dividing the training data D into small partitions of equal size \(D_{1},...,D_{S}\) and using them to train the model at each epoch.

$$\begin{aligned} \log p(D_{s}|\theta ) = \sum _{n=1}^{M}\log p(y_{s_{n}}|x_{s_{n}},\theta ) \end{aligned}$$

Where \(\log p(D|\theta )= \sum _{s=1}^{S}\log p(D_{s}|\theta )\), \(D_{s}=\{(x_{s_{n}},y_{s_{n}})\}_{n=1}^{M}\), S is the number of partitions, and M is the size of each partition.

Next, we define the variational distribution that approximates the posterior distribution of parameters. In our situation, we considered it as a mixture of two factorized Gaussian distributions, as shown below:

$$\begin{aligned}{} & {} \begin{aligned} q_{\phi }(\theta )&= \pi \textrm{N}(\theta |\mu _{1},\sigma ^{2}_{1}) + (1-\pi )\textrm{N}(\theta |\mu _{2},\sigma ^{2}_{2})\\ {}&= \pi \prod _{i=1}^{P}\textrm{N}(\theta _{i}|\mu _{1_{i}},\sigma ^{2}_{1_{i}}) + (1-\pi )\prod _{i=1}^{P}\textrm{N}(\theta _{i}|\mu _{2_{i}},\sigma ^{2}_{2_{i}}) \end{aligned} \end{aligned}$$
(27)
$$\begin{aligned}{} & {} \begin{aligned} {\log q_{\phi }(\theta )= \log \Big (\pi \prod _{i=1}^{P}\textrm{N}(\theta _{i}|\mu _{1_{i}},\sigma ^{2}_{1_{i}}) + (1-\pi )\prod _{i=1}^{P}\textrm{N}(\theta _{i}|\mu _{2_{i}},\sigma ^{2}_{2_{i}})\Big )} \end{aligned} \end{aligned}$$
(28)

Where \(0<\pi < 1\) is the mixture weight considered as a hyperparameter.

Finally, we can approximate the cost function of this model as follows:

$$\begin{aligned} \begin{aligned} {\mathscr {L}}(D,\phi )&\approx {\hat{\mathscr {L}}}_{MB}(\theta ,\phi )\\ {}&\hspace{-1.3cm}= {\frac{1}{T}\sum _{t=1}^{T}\Big [\pi \Big (\log q_{\phi }(\theta _{1}^{(t)}) -\log p(\theta _{1}^{(t)}) - \frac{N}{M}\sum _{n=1}^{M}\log p(y_{n_{s}}|x_{s_{n}},\theta _{1}^{(t)})\Big )} \\&\hspace{-1.3cm}+{ (1-\pi )\Big (\log q_{\phi }(\theta _{2}^{(t)}) -\log p(\theta _{2}^{(t)}) - \frac{N}{M}\sum _{n=1}^{M}\log p(y_{s_{n}}|x_{s_{n}},\theta _{2}^{(t)})\Big )\Big ]} \end{aligned} \end{aligned}$$
(29)

Where \(\theta _{1}^{(t)} = \mu _{1} + \sigma _{1}\odot \epsilon _{1}^{(t)}\), and \(\theta _{2}^{(t)}=\mu _{2} + \sigma _{2}\odot \epsilon _{2}^{(t)}\),

where \(\epsilon _{1}^{(t)}\sim \textrm{N}(\epsilon _{1}|0,I)\), and \(\epsilon _{2}^{(t)}\sim \textrm{N}(\epsilon _{2}|0,I)\), for t = 1,...,T.

5.2 Results and analysis

This section provides an assessment of the performance of BBGMM method described in Algorithm 4 compared to existing methods (Frequentist approach, BBGaussian [58], and MC Dropout [18]) in classification tasks using MNIST, Fashion MNIST, CIFAR-10, and SVHN datasets (Appendix A, Table 6). We then evaluate the uncertainties associated with our proposed method for these datasets.

5.2.1 Datasets (Appendix A, Table 6)

We evaluate our method using the following datasets: 1. MNIST: This well-established benchmark dataset comprises grayscale images representing handwritten digits. It contains 70,000 samples, each image sized at \(1\times 28\times 28\) pixels. The dataset is strategically partitioned into training (50,000 samples), validation (10,000 samples), and test (10,000 samples) sets, facilitating essential aspects of model training, hyperparameter tuning, and performance evaluation.

2. Fashion MNIST: An alternative to MNIST, this dataset shifts focus to fashion products. Sharing structural similarities with MNIST, it encompasses 70,000 grayscale images of fashion items, each sized at \(1\times 28\times 28\) pixels. Like MNIST, it is partitioned into training, validation, and test sets, comprising 50,000, 10,000, and 10,000 samples, respectively.

3. CIFAR-10: Representing a more intricate challenge than MNIST and Fashion MNIST, CIFAR-10 consists of 60,000 color images, each with dimensions of \(3\times 32\times 32\). The dataset covers ten distinct object categories and is is split into training (40,000 samples), validation (10,000 samples), and test (10,000 samples) sets to support effective model development and evaluation.

4. SVHN: Focused on digit recognition within real-world images, the SVHN dataset captures house numbers from street views. Comprising 73,257 color images sized at \(3\times 32\times 32\) pixels. This dataset includes a range of digits from 0 to 9. The dataset is partitioned into training (53,257 samples), validation (20,000 samples), and test (26,032 samples) sets, enabling a comprehensive assessment of model performance.

5.2.2 Results on MNIST and fashion MNIST

Table 2 compares the training, validation, and test accuracies (in percent) of LeNet-5 on the MNIST and Fashion MNIST datasets, evaluating our method against frequentist, MC dropout, and BBGaussian models.

Table 2 Comparison of accuracies between Frequentist, MC dropout, BB-Gaussian, and BBGMM models on the MNIST, and Fashion MNIST datasets
Full size table
Fig. 3
figure 3

Comparison of validation accuracies on MNIST

Full size image
Fig. 4
figure 4

Comparison of validation accuracies Fashion MNIST

Full size image

Overall, the table shows comparable results between the models. On MNIST, the frequentist model obtained the highest training accuracy of 99.97% compared with the other models, with a test accuracy of 98.54%.

Table 3 Comparison of errors on the MNIST, and Fashion MNIST datasets
Full size table

On the other hand, our model achieved a training accuracy of 99.87% and a test accuracy of 98.85%. For Fashion MNIST, our model outperformed the others with a test accuracy of 89.02%, indicating that the BBGMM model is more accurate and reliable on Fashion MNIST test data.

Figs. 3 and 4 display the evolution of validation accuracy during LeNet-5 training on the MNIST and Fashion MNIST datasets, comparing previous approaches with our model. Notably, the validation accuracy curves for all models show comparable performance, but with a preference for the BBGMM model (blue lines).

Table 3 compares the training and validation errors obtained by training the LeNet-5 network on the MNIST and Fashion MNIST datasets using the BBGaussian and BBGMM models. The results indicate that our proposed model achieves lower training and validation errors than the BBGaussian model for both datasets. This suggests that incorporating a mixture model (GMM) within the Bayes by Backprop method for training CNN on the MNIST and Fashion MNIST datasets yields improved performance than using a single mode distribution, such as the Gaussian distribution.

5.2.3 Results on CIFAR-10 and SVHN

Table 4 Comparison of accuracies between Frequentist, MC dropout, BB-Gaussian, and BBGMM models on CIFAR-10, and SVHN datasets
Full size table

In this section, we have used a CNN network consisting of three blocks similar to the VGG blocks and two fully connected layers. Each block consists of two convolutional layers followed by max-pooling, and we adopted ReLu as an activation function (see Appendix C (Table 10)).

Table 4 presents a comparison of accuracies between the previous models (Frequentist, MC dropout, BB-Gaussian) and the BBGMM method, using the CNN model described in Appendix C (Table 10), on the CIFAR-10 and SVHN datasets. Table 4 shows that our method performed better than other models. For the CIFAR-10 dataset, after 100 epochs, our BBGMM model achieved the highest test accuracy of 80.60%, with a corresponding training accuracy of 83.76%. On the other hand, the MC dropout model achieved a test accuracy of 79.52% and a training accuracy of 81.08%. As for the BBGaussian method, it yielded a lower test accuracy of 78.68%. For the SVHN dataset, our BBGMM model achieved the highest test accuracy of 94.53%, outperforming the frequentist, MC dropout, and BBGaussian models, which achieved test accuracies of 93.21%, 93.16%, and 93.36%, respectively.

Figs. 5 and 6 illustrate the evolution of validation accuracies during CNN training on the CIFAR-10 and SVHN datasets, respectively. Generally, the results show comparable performance on the two datasets, with a slight improvement observed for our BGMM method, as indicated by the blue lines in the figures.

Fig. 5
figure 5

Comparison of validation accuracies on CIFAR 10

Full size image
Fig. 6
figure 6

Comparison of validation accuracies on SVHN

Full size image

Fig. 7 shows the progression of validation error during CNN training on the CIFAR-10 and SVHN datasets using two different variational distributions: the Bayes by Backprop method with a single Gaussian distribution (BBGaussian, orange lines) and the same method with a mixture model of two Gaussian distributions (BBGMM, bleu lines). The figure indicates that both methods converge as training progresses on both datasets. However, it is worth noting that the BBGMM model consistently achieves a lower validation error than the BBGaussian model. This lower validation error indicates that the BBGMM method performs more accurately on the validation set than the BBGaussian method.

Fig. 8 displays the evolution of the probability density of a weight taken from the last layer of the CNN over training iterations. The weight is sampled from the two Gaussian distributions employed in the mixture for classifying the CIFAR-10 images. Figure 9 shows that during the first ten training epochs, the weight density appears unimodal due to the proximity of the means of the two Gaussian distributions used.

Fig. 7
figure 7

Comparison of validation losses on CIFAR-10, and SVHN

Full size image

However, as the training progresses, the density is transformed into a bimodal distribution, with each mode corresponding to a different mean. This observation highlights the power of approximating the posterior distribution for this case using a mixture of Gaussian distributions rather than adopting an unimodal distribution such as the Gaussian distribution.

Fig. 8
figure 8

Probability density evolution

Full size image

Figures 9, and 10 depict the convergence of standard deviations \(\mathbf {\sigma _{1}}\) and \(\mathbf {\sigma _{2}}\) for the Gaussian mixture distribution represented in Fig. 8. It is noticed in Fig. 9 that the standard deviations of each component of the binary mixture of Gaussian distributions decrease over epochs, indicating that the uncertainty of the model reduces as more new data is received. Thus, the model gets more reliable with its training.

Fig. 9
figure 9

Standard deviation (\(\sigma _1\)) evolution

Full size image
Fig. 10
figure 10

Standard deviation (\(\sigma _2\)) evolution

Full size image
Fig. 11
figure 11

The image on the top left is an image of number 4 taken from the test set for MNIST. The image on the top right is an image of a dress (class 3) taken from the test set for Fashion-MNIST. The bottom left image shows the percentage of epistemic uncertainty for the BBGMM model predictions of the previous two pictures, where a high value of epistemic uncertainty appears between classes 1 and 8 for the image taken from Fashion-Mnist, as it is completely different from the MNIST set, but it has a high similarity between it and both numbers 1 and 8, so the BBGMM model predicts uncertain outputs for this image between these two classes. The picture at the bottom right presents the proportion of aleatoric uncertainty for the BBGMM model predictions in the previous two images, where varying values of this uncertainty appear between the two images resulting from the noise in these two images. For example, we can explain the appearance of aleatoric uncertainty between the numbers 4 and 9 for the image taken from MNIST by the presence of a significant similarity between these numbers in this image

Full size image

5.2.4 Uncertainty estimation

Figure 11 shows the BBGMM model prediction for two randomly selected images in the test set from the MNIST and Fashion-MNIST datasets and estimates the BBGMM model uncertainties using Eq. 23 for these two images. It illustrates that the BBGMM model can predict the classification of the picture extracted from MNIST, but with a percentage of aleatoric uncertainty owing to the noise in this image. However, the BBGMM model failed to correctly classify the picture taken from Fashion-MNIST since it differed from the MNIST dataset used during training, which explains the significant value of epistemic uncertainty in this image. Also, it shows a significant value of aleatoric uncertainty in the last image due to the noise present in this image.

Table 5 Uncertainty estimation
Full size table

Table 5 compares the average epistemic and aleatoric uncertainties for the BBGMM model applied to the MNIST, Fashion MNIST, CIFAR-10 and SVHN datasets using the LeNet-5 network. The results indicate that the aleatoric uncertainty of CIFAR-10 is over thirty times higher than that of MNIST, while the epistemic uncertainty of CIFAR-10 is more than thirteen times greater than that of MNIST. The variations in aleatoric and epistemic uncertainty between all datasets can be attributed to the performance of the LeNet5-BBGMM model on each specific dataset. In other words, the model’s accuracy on the test data directly affects its reliability, with lower uncertainty values indicating higher reliability.

5.3 Training time complexity

The training time of the BGMM for CNNs can be estimated as the training time required for a Bayesian CNN with a single Gaussian distribution having a similar structure, multiplied by K, where K represents the number of components in the mixture. It is important to note that this approach can be computationally expensive, especially for high-dimensional models like CNNs. However, the advantage of the BGMM lies in its ability to reparameterize the Gaussian mixture, providing differentiable estimates. This, in turn, leads to a reduction in the variance of the gradients for our objective function, resulting in more accurate and reliable predictions compared to other models.

6 Conclusion and discussion

The BBGMM model can be viewed as an extension of the Bayes by Backprop method for mixture models (Gaussian mixture model) to approximate the posterior distribution for convolutional neural networks. We followed how to reparameterize the mixture model if all of its components are reparametrizable, which is available in Gaussian mixture models. We then tried to estimate the aleatoric and epistemic uncertainties of mixture models for classification tasks.

Next, the experimental results showed that the BBGMM model performed well compared to the other methods, as it achieved significant test accuracy over all datasets.

We also saw that the BBGMM model increased the credibility of convolutional neural network outcomes by quantifying uncertainty in network weights from the mixture model.

Although the BBGMM method has produced positive results, it is crucial to note that the extent of these results is currently insufficient. This implies that while the BBGMM method is promising, there is still considerable potential to improve it to achieve more substantial and robust results. The second problem is that the BBGMM method doubles the number of parameters that vary as a function of the number of components in the mixture, which increases the complexity of the model and makes it inflexible or difficult to apply in practical applications, particularly when the number of mixture components increases.

This motivates us to improve the BBGMM model and discover complementary solutions to reduce the model’s complexity.