Introduction

Starting from the mid-1980s, concerns about environmental degradation have prompted many researchers and agencies to analyze the relation between energy intensity (energy per unit of output) and pollution intensity (emissions per unit of output) urging them to measure reduced level of carbon dioxide emissions as a result of increased energy efficiency. For example, McKinsey and Company (2009) estimate that through increased energy efficiency alone, United States (U.S) can reduce global emissions of carbon dioxide by one-third and hence meet its 2020 greenhouse gas emission goals. In the same vein, the International Energy Agency (2015) (IEA) have recently disclosed improvements in energy efficiency as a primary goal towards reaching energy-related carbon dioxide emissions by 2020 and 2050. Hence, improvements in energy efficiency (energy intensity) have become a priority area in sustainable development efforts of the governments, since this simultaneously confronts climate change and energy security concerns while sustaining economic growth and competitiveness. Consequently, since the early 1990s, almost all of the national statistics agencies as well as the environmental departments of the International AgenciesFootnote 1 have started to disseminate economy-wide energy efficiency indicators. However, researchers soon realized that simple ratios such as energy use per dollar of GDP are far from revealing the real energy efficiency improvements, since a substantial part of this improvement may have been occurring due to structural effects where the relative contributions of less energy intensive sectors (such as services) to GDP increase over time.

Driven by the prospect of measuring real efficiency improvements, the energy economics literature witnessed an influx of studies that decompose changes in aggregate energy intensity into a structural effect and a sectoral intensity effect. In the majority of studies, methodological approach pursued was either an index decomposition approach (IDA), similar to the one that decomposes a value change index to price and quantity indices, or a structural decomposition approach (SDA) which is based on input-output analysis with more demanding data requirements. Ang (1995) in a comprehensive review surveys 51 IDA studies conducted between 1987 and 1994, and Ang and Zhang (2000) survey an additional 124 studies published between 1995 and 1999 and conclude that the declining sectoral intensity effect is the main drive behind declining aggregate intensities. Contrary evidence is provided however by some more recent studies (see for example Huntington (2010) and Mulder and de Groot (2012)), where the contribution of structural change to the decline in aggregate energy intensity is substantial. Finally, Ang et al. (2010) compare accounting frameworks used for tracking energy efficiency trends and recommend common adoption of the Logarithmic Mean Divisia Index (LMDI) with its desirable index number properties.

On the SDA front, Rose and Casler (1996) provide a review of earlier studies, compare SDA and IDA, and offer a critical review. Hoekstra and van den Bergh (2003) present a more comprehensive comparison of two methods and show how each technique can be transferred to one other and suggest a more careful assessment of the axiomatic properties of the indices generated. In a more recent study, Su and Ang (2012) provide a review of the latest methodological developments along with 43 applied studies conducted between 1999 and 2010.

More recently, researchers inspired by the decomposition of Malmquist productivity index first proposed by Färe et al. (1994) have also adopted production-theoretical approach to decompose energy intensity changes over time into their subcomponents. These studies can be viewed as the extensions of Kumar and Russell (2002) and Zhou and Ang (2008a) who respectively decomposed labor productivity and aggregate CO2 emissions into their subcomponents. Realizing the need for multilateral comparisons of energy intensity levels across different energy consuming entities, Zhou and Ang (2008b) resort to data envelopment analysis (DEA) techniques to compare average energy utilization performance of the OECD countries. The DEA approach, which accounts for possible substitution effects among capital, labor, and energy inputs as well as for the possible substitution effect among different energy inputs, also allows for inclusion of the undesirable outputs as a by-product of desirable outputs. After comparing different contraction methods (radial versus non-radial) and existence of slacks (slack based versus non-lack based), they conclude that slack-based DEA model has a higher discriminatory power. Their results indicate that nine countries (Australia, France, Ireland, Italy, Norway, Portugal, Sweden, Switzerland, and the USA) are perfectly energy efficient among the OECD countries and that remaining inefficient countries have a potential to reduce energy consumption by 86 quadrillion Btu over a five-year period 1997–2001. In a more recent study, Wang (2013) using Shephard output distance functions decomposes energy intensity changes over time into five components: change in technical efficiency, technological progress, change in capital energy ratio, change in labor energy ratio, and changes in output structure.

Although these studies immensely contributed to our knowledge based on the evolution of energy efficiency trends over time, there are some considerable challenges in performing informative and fair comparisons between the energy efficiency levels of units considered. Even cross-country studies by Mulder and de Groot (2012) and Voigt et al. (2014) were limited to the comparison of efficiency trends over time where the authors proceed first by decomposing energy intensity trends within individual countries and only then do comparisons across countries. The only exceptions are the work of Duro et al. (2010) and Zhou and Ang (2008b) where the authors analyze the inequality of energy intensity between OECD countries.

Furthermore, regarding the IDA and SDA approaches, even after accounting for the effect of structural change, the resultant measure of energy intensity is still the inverse of a partial factor productivity measure (PFP), i.e., energy productivity, that does not take into consideration compositional differences between inputs of the units being compared (which are also subject to change over time) and that ignores the type of substitution among inputs and, hence, makes it a measure that disguises rather than illuminates.

Hence, the objective of this paper is to address the issues above by constructing an alternative multifactor input intensity index (an inverse of Multifactor Productivity Index (MFP)) that accommodates level comparisons as well as over-time multilateral comparisons and to show that special cases of this measure not only generate the traditional single input intensity measure (i.e., aggregate energy intensity as the inverse of PFP measure) but also lead to an energy intensity index that overcomes the shortcomings of the traditional measure. Unlike our predecessors, our productivity measure (or energy intensity measure) overcomes the shortcomings of the partial productivity measure by not only controlling for the compositional differences in outputs (both across the units being observed and over-time) but also by accounting for the compositional differences in inputs (both across the units being observed and over-time). Hence, this study can be viewed as the extension of the production-theoretical approaches, where DEA techniques are used to develop Malmquist quantity indices, a novel approach, first introduced in this paper, into the measurement of factor intensities (factor productivities).

All our measures will rely on computation of directional distance functions, which provide a valuable framework in modeling a technology with multiple outputs and inputs. An empirical application on the energy intensity of U.S state-level agricultural sectors further complements existing studies. Studying the U.S agriculture sector is particularly important due to its significant role in the consumption of fossil fuels and generation of greenhouse gases (GHG). Recent studies indicate that while agricultural production’s share in national energy consumption is only 2% (Canning et al. (2010)), it is responsible of over 9% of total GHG emissions (EPA (2014)). Hence, even the modest improvements in energy intensity at the production stage could result in meaningful societal benefits in terms of reduced cost to the producers and hence lower prices to the consumers, as well as helping the U.S to reach its environmental goals by 2050.

The paper unfolds as follows. The following section will introduce the methodology. The “Data” section describes the data used and the “Results” and “Discussion” sections are allocated to the results and discussion, respectively. Finally, the “Conclusions and policy implications” section concludes the study.

Methodology

Two commonly used productivity measures, PFP and MFP, are distinguished by their handling of inputs. While the ratio of output to a single input is called partial productivity of that particular input, the ratio of output to all inputs combined is called multifactor productivity. The inverses of these measures are called single input intensity measure (i.e., energy intensity, labor intensity) and multifactor input intensity measure respectively. In cases where there is more than one output, this of course requires the construction of a quantity index of outputs for both measures and a quantity index of inputs for the MFP measure. In developing PFP and MFP measures, a modeling technique developed in a series of papers by Färe et al. (2000, 2004), Zaim et al. (2001), and Zaim (2004) is adopted. While these papers made extensive use of output distance functions in constructing various quantity indices, this paper promotes the use of the directional technology distance function which allows for simultaneous expansion of output(s) and contraction of input(s) as the most appropriate choice in developing measures which allow for bilateral and multilateral comparisons of partial and multifactor productivity levels. We will also show that the productivity measures that are presented here can easily be extended to measure productivity growth over time.

The computation of productivity measures relies on the construction of quantity index of output(s) and quantity index of input(s). Intuitively, the quantity index of output(s) shows the relative success of an observation, say j, in expanding its output(s) and simultaneously contracting its input(s) while using the same level of input(s) as another observation, say i (or using some arbitrary level of inputs common to both i and j). One should note that, in constructing an output index, compositional differences in inputs are accounted for. The quantity index of input(s) on the other hand measures the relative success of observation, say j, in expanding its output(s) and simultaneously contracting its input(s) while producing the same level of output(s) as another observation, say i (or producing some arbitrary level of output(s) common to both i and j). Note this time that, in constructing an input quantity index, compositional differences in output(s) are accounted for.

To describe the theoretical underpinnings of the index used, suppose we observe a sample of K units each of which uses inputs \( x=\left({x}_1,..\dots, {x}_N\right)\in {R}_{+}^N \), to produce a vector of outputs \( y=\left({y}_1,.\dots, {y}_M\right)\in {R}_{+}^M \). With this notation at hand, the technology can be described as all feasible vectors (x, y), i.e., T = {(x, y) : x can produce y}. This technology satisfies standard regularity conditions like closedness and convexity. See Färe and Primont (1995) for details.

Among alternative approaches, directional technology distance functions prove to be a particularly useful tool not only to represent a technology with distinctive characteristics such as closedness and convexity but also as a perfect aggregator and a performance measure. Hence, to develop an MFP index, one may employ the directional technology distance function, \( {\overrightarrow{D}}_T\left(x,y;{g}_x,{g}_y\right)=\sup \left[\lambda :\left(x-\lambda {g}_x,y+\lambda {g}_y\right)\in T\Big)\right] \), where T is the technology defined as T = {(x, y) : x can produce y }.

To construct the output quantity index, consider the following two directional distance functions which show the success of two states j and i respectively in expanding their outputs and simultaneously contracting an arbitrary vector of inputs common to both with respect to a constant returns to scale (CRS) technology:

$$ {\displaystyle \begin{array}{l}{{\overrightarrow{D}}_{0T}}^j\left({y}^{\mathrm{j}},{x}^0\right)=\max {\lambda}_0^j\\ {}\\ {}\mathrm{such}\kern0.34em \mathrm{that}\\ {}\kern8.25em \sum \limits_{k=1}^K{z}_k{y}_{km}\ge {y}_m^j+{\lambda}_0^j{y}_m^j\kern1.5em m=1,\dots, M\kern7.75em \\ {}\kern8em \sum \limits_{k=1}^K{z}_k{x}_{kn}\le {x}_n^o-{\lambda}_0^j{x}_n^o\kern2.25em n=1,\dots, N\\ {}\kern8.5em {z}_k\ge 0\kern7.5em k=1,\dots, K\kern.2em \end{array}} $$
(1)

and

$$ {\displaystyle \begin{array}{l}{{\overrightarrow{D}}_{0T}}^i\left({y}^i,{x}^0\right)=\max {\lambda}_0^i\\ {}\\ {}\mathrm{such}\kern0.34em \mathrm{that}\\ {}\kern8.25em \sum \limits_{k=1}^K{z}_k{y}_{km}\ge {y}_m^i+{\lambda}_0^i{y}_m^i\kern1.5em m=1,\dots, M\\ {}\kern8.25em \sum \limits_{k=1}^K{z}_k{x}_{kn}\le {x}_n^o-{\lambda}_0^i{x}_n^o\kern2.25em n=1,\dots, N\\ {}\kern8.25em {\mathrm{z}}_{\mathrm{k}}\ge 0\kern8em k=1,\dots, K\end{array}} $$
(2)

where zk ' s are intensity variables.

Now defining \( {y}_j^{\ast}\;\mathrm{and}\;{y}_i^{\ast } \) as the maximum attainable outputs and \( {x}_j^{\ast}\;\mathrm{and}\;{x}_i^{\ast } \) as the minimum attainable inputs for the producing units j and i respectively, under CRS

$$ \frac{y_j^{\ast }}{y_i^{\ast }}=\frac{y_j\left(1+{\lambda}_0^j\right)}{y_i\left(1+{\lambda}_0^i\right)}=\frac{x_j\left(1-{\lambda}_0^j\right)}{x_i\left(1-{\lambda}_0^i\right)}=\frac{x_j^{\ast }}{x_i^{\ast }} $$
(3)

and restricting x j  = x i  = x 0 as required by the above linear programming problems, this yields a quantity index of outputs

$$ {Q}_y=\frac{y_j}{y_i}=\frac{\left(1+{\lambda}_0^i\right)\left(1-{\lambda}_0^j\right)}{\left(1+{\lambda}_0^j\right)\left(1-{\lambda}_0^i\right)} $$
(4)

This can be best explained by Fig. 1. Consider two observations/production units (x j , y j ) and (x i , y i ) for which a meaningful output comparison y j /y i is required. The first linear programming problem expands jth producing unit’s output (vector) y j and simultaneously contracts an input vector common to both, i.e., x j  = x i  = x 0, and the second program does the same thing for the ith producing unit. Simple geometry, i.e., similar triangles, allows one to write Eq. (3) which intuitively says that meaningful output comparisons can only be made between producing units which have the same input composition and amounts.

Fig. 1
figure 1

Illustration of directional technology distance function

Full size image

Now the next question is how to choose an input vector common to both. The trick is to choose a base production unit, for example production unit i in a given year, and then calculate the rate of difference between each production unit and the base production unit. By normalizing the base producing unit’s output to one, one can do all cross-section multilateral output comparisons.

If on the other hand the objective is to compute an output index for a panel of observations (i.e., panel of output index for 48 U.S states over 45 years from 1960 to 2004), one could still use the same approach by neglecting the fact that different producing units exist at different points in time. For example, input vectors for Alabama in 1970 could be chosen as a base, in which case one will construct an output index where Alabama in 1970 is equal to one. Moreover, since the output quantity index satisfies all the desirable properties due to Fisher (1922)—i.e., homogeneity, time reversal, transitivity, and dimensionality—and hence naturally passes the Fisher test, this allows all multilateral comparisons across space and time.

Now turning to the construction of the input quantity index, consider the following directional distance functions which show the success of two states j and i respectively in contracting their inputs while expanding an arbitrary vector of outputs which are common to both:

$$ {\displaystyle \begin{array}{l}{{\overrightarrow{D}}_{iT}}^j\left({y}^0,{x}^j\right)=\max {\lambda}_i^j\\ {}\\ {}\mathrm{such}\kern0.34em \mathrm{that}\\ {}\kern8.25em \sum \limits_{k=1}^K{z}_k{y}_{km}\ge {y}_m^0+{\lambda}_i^j{y}_m^0\kern1.25em m=1,\dots, M\\ {}\kern8.25em \sum \limits_{k=1}^K{z}_k{x}_{kn}\le {x}_n^j-{\lambda}_i^j{x}_n^j\kern1.75em n=1,\dots, N\\ {}\kern9.25em {z}_k\ge 0\kern6em k=1,\dots, K\end{array}} $$
(5)

and

$$ {\displaystyle \begin{array}{l}{{\overrightarrow{D}}_{iT}}^i\left({y}^0,{x}^i\right)=\max {\lambda}_i^i\\ {}\\ {}\mathrm{such}\kern0.34em \mathrm{that}\\ {}\kern8.25em \sum \limits_{k=1}^K{z}_k{y}_{km}\ge {y}_m^0+{\lambda}_i^i{y}_m^0\kern1em m=1,\dots, M\\ {}\kern8.25em \sum \limits_{k=1}^K{z}_k{x}_{kn}\le {x}_n^i-{\lambda}_i^i{x}_n^i\kern1.75em n=1,\dots, N\kern.2em \\ {}\kern9.25em {z}_k\ge 0\kern6em k=1,\dots, K\end{array}} $$
(6)

Now defining \( {x}_j^{\ast } \) and \( {x}_i^{\ast } \) as the minimum attainable inputs for states j and i respectively, and again relying on similar triangles in Fig. 1., yields

$$ \frac{x_j^{\ast }}{x_i^{\ast }}=\frac{x_j\left(1-{\lambda}_i^j\right)}{x_i\left(1-{\lambda}_i^i\right)}=\frac{y_j\left(1+{\lambda}_i^j\right)}{y_i\left(1+{\lambda}_i^i\right)}=\frac{y_j^{\ast }}{y_i^{\ast }} $$
(7)

Furthermore, restricting y j  = y i  = y 0 as required by the above linear programming problems yields a quantity index of inputs:

$$ {Q}_x=\frac{x_j}{x_i}=\frac{\left(1+{\lambda}_i^j\right)\left(1-{\lambda}_i^i\right)}{\left(1+{\lambda}_i^i\right)\left(1-{\lambda}_i^j\right)} $$
(8)

As for the output index, the output vector of Alabama in 1970 could be chosen as a base, in which case one will construct an input index where Alabama in 1970 is equal to one.

Finally, the MFP level index and its reciprocal multifactor input intensity index (MFII) can be defined as follows:

$$ \mathrm{MFP}=\frac{\frac{\left(1+{\lambda}_0^i\right)\left(1-{\lambda}_0^j\right)}{\left(1+{\lambda}_0^j\right)\left(1-{\lambda}_0^i\right)}}{\frac{\left(1+{\lambda}_i^j\right)\left(1-{\lambda}_i^i\right)}{\left(1+{\lambda}_i^i\right)\left(1-{\lambda}_i^j\right)}}\kern1.25em \mathrm{MFII}=\frac{\frac{\left(1+{\lambda}_i^j\right)\left(1-{\lambda}_i^i\right)}{\left(1+{\lambda}_i^i\right)\left(1-{\lambda}_i^j\right)}}{\frac{\left(1+{\lambda}_0^i\right)\left(1-{\lambda}_0^j\right)}{\left(1+{\lambda}_0^j\right)\left(1-{\lambda}_0^i\right)}} $$
(9)

Since both the output and the input quantity index satisfy all the desirable properties due to Fisher (1922)—i.e., homogeneity, time reversal, transitivity, and dimensionality—both MFP and MFII indices naturally pass the Fisher test.

A very nice feature of this model is that, for a single output (Y) and single input case (i.e., ignoring all other inputs while in fact they exist), it collapses into a measure that allows for bilateral (and multilateral) comparisons of traditional partial factor productivity (energy productivity), whose reciprocal is aggregate energy intensity (AEI):

$$ {\mathrm{PFP}}_E=\frac{\frac{Y_j}{E_j}}{\frac{Y_i}{E_i}}=\frac{\frac{Y_j}{Y_i}}{\frac{E_j}{E_i}} $$
(10)
$$ \mathrm{AEI}=\frac{\frac{E_j}{E_i}}{\frac{Y_j}{Y_i}} $$
(11)

This requires the computation of four linear programming problems, two of which are for the output index and the other two for the input index. The following two programming problems for example will compare outputs of j and i provided that their energy inputs are held constant at an arbitrary level common to both.

$$ {\displaystyle \begin{array}{l}{{\overrightarrow{D}}_{0T}}^j\left({Y}^J,{E}^0\right)=\max {\gamma}_0^j\\ {}\\ {}\mathrm{such}\kern0.34em \mathrm{that}\\ {}\kern8.25em \sum \limits_{k=1}^K{z}_k{Y}_k\ge {Y}^j+{\gamma}_0^j{Y}^j\kern8.5em \\ {}\kern8em \sum \limits_{k=1}^K{z}_k{E}_k\le {E}^o-{\gamma}_0^j{E}^o\kern2.25em \\ {}\kern8.25em {z}_k\ge 0\kern6.75em k=1,\dots, K\end{array}} $$
(12)

and

$$ {\displaystyle \begin{array}{l}{{\overrightarrow{D}}_{0T}}^i\left({Y}^i,{E}^0\right)=\max {\gamma}_0^i\\ {}\\ {}\mathrm{such}\kern0.34em \mathrm{that}\\ {}\kern8em \sum \limits_{k=1}^K{z}_k{Y}_k\ge {Y}^i+{\gamma}_0^i{Y}^i\kern1.25em \\ {}\kern8em \sum \limits_{k=1}^K{z}_k{E}_k\le {E}^0-{\gamma}_0^i{E}^0\kern1.75em \\ {}\kern8em {\mathrm{z}}_{\mathrm{k}}\ge 0\kern6.75em k=1,\dots, K\end{array}} $$
(13)

Similarly, the following two linear programming problems will compare energy inputs of j and i provided that their outputs are held constant at an arbitrary level common to both.

$$ {\displaystyle \begin{array}{l}{{\overrightarrow{D}}_{iT}}^j\left({Y}^0,{E}^J\right)=\max {\gamma}_i^j\\ {}\\ {}\mathrm{such}\kern0.34em \mathrm{that}\\ {}\kern8.25em \sum \limits_{k=1}^K{z}_k{Y}_k\ge {Y}^0+{\gamma}_i^j{Y}^0\kern1em \\ {}\kern8em \sum \limits_{k=1}^K{z}_k{E}_k\le {E}^j-{\gamma}_i^j{E}^j\kern1.75em \\ {}\kern8.25em {z}_k\ge 0\kern6.75em k=1,\dots, K\end{array}} $$
(14)

and

$$ {\displaystyle \begin{array}{l}{{\overrightarrow{D}}_{iT}}^i\left({Y}^0,{E}^i\right)=\max {\gamma}_i^i\\ {}\\ {}\mathrm{such}\kern0.34em \mathrm{that}\\ {}\kern7.75em \sum \limits_{k=1}^K{z}_k{Y}_k\ge {Y}^0+{\gamma}_i^i{Y}^0\kern1em \\ {}\kern7.75em \sum \limits_{k=1}^K{z}_k{E}_k\le {E}^i-{\gamma}_i^i{E}^i\kern1em \\ {}\kern7.75em {z}_k\ge 0\kern6.75em k=1,\dots, K\end{array}} $$
(15)

The level of energy input and output that are held constant at an arbitrary level in the linear programming problems above could easily be set to be equal to those of observation i. In this particular case, observation i is considered to be the base country (for which the PFP of energy is equal to unity) with respect to which all bilateral productivity comparisons can be made. Furthermore, since this index is transitive, it allows for all multilateral comparisons. Hence, our partial factor productivity measure and aggregate energy intensity measures are as follows:

$$ {\mathrm{PFP}}_{\mathrm{E}}=\frac{\frac{\left(1+{\gamma}_0^i\right)\left(1-{\gamma}_0^j\right)}{\left(1+{\gamma}_0^j\right)\left(1-{\gamma}_0^i\right)}}{\frac{\left(1+{\gamma}_i^j\right)\left(1-{\gamma}_i^i\right)}{\left(1+{\gamma}_i^i\right)\left(1-{\gamma}_i^j\right)}}\kern1.25em \mathrm{AEI}=\frac{\frac{\left(1+{\gamma}_i^j\right)\left(1-{\gamma}_i^i\right)}{\left(1+{\gamma}_i^i\right)\left(1-{\gamma}_i^j\right)}}{\frac{\left(1+{\gamma}_0^i\right)\left(1-{\gamma}_0^j\right)}{\left(1+{\gamma}_0^j\right)\left(1-{\gamma}_0^i\right)}}\kern0.5em $$
(16)

The most appealing feature of the general model presented is that its special case leads to a PFP index that overcomes the shortcomings of the traditional measure. The reciprocal of this index naturally results in the energy intensity index, which this study aims to obtain. The two following linear programming problems which will lead to the construction of an output quantity index reveal the success of two states j and i respectively in expanding their outputs and simultaneously contracting their energy input common to both while holding all other inputs at a constant level common to both.

$$ {\displaystyle \begin{array}{l}{{\overrightarrow{D}}_{0T}}^j\left({y}^j,{E}^0,{x}^0\right)=\max {\beta}_0^j\\ {}\\ {}\mathrm{such}\kern0.34em \mathrm{that}\\ {}\sum \limits_{k=1}^K{z}_k{y}_{km}\ge {y}_m^j+{\beta}_0^j{y}_m^j\kern1.5em m=1,\dots, M\\ {}\sum \limits_{k=1}^K{z}_k{E}_k\le {E}^o-{\beta}_0^j{E}^o\kern2.25em \\ {}\sum \limits_{k=1}^K{z}_k{x}_{k{n}_{-E}}\le {x}_{n_{-E}}^o\kern3.75em {n}_{-E}=1,\dots, N-1\\ {}{z}_k\ge 0\kern8em k=1,\dots, K\end{array}} $$
(17)
$$ {\displaystyle \begin{array}{l}{{\overrightarrow{D}}_{0T}}^i\left({y}^{\mathrm{i}},{E}^0,{x}^0\right)=\max {\beta}_0^i\\ {}\\ {}\mathrm{such}\kern0.34em \mathrm{that}\\ {}\sum \limits_{k=1}^K{z}_k{y}_{km}\ge {y}_m^i+{\beta}_0^i{y}_m^i\kern1.5em m=1,\dots, M\\ {}\sum \limits_{k=1}^K{z}_k{E}_k\le {E}^o-{\beta}_0^i{E}^o\kern2.25em \\ {}\sum \limits_{k=1}^K{z}_k{x}_{k{n}_{-E}}\le {x}_{n_{-E}}^o\kern3.25em {n}_{-E}=1,\dots, N-1\\ {}{z}_k\ge 0\kern7.25em k=1,\dots, K\end{array}} $$
(18)

Similarly, the following two programming problems compare energy inputs of j and i provided that their outputs are held constant at an arbitrary level common to both, while all other inputs except energy used by j and i are treated as fixed inputs.

$$ {\displaystyle \begin{array}{l}{{\overrightarrow{D}}_{iT}}^j\left({y}^0,{E}^J,{x}^j\right)=\max {\beta}_i^j\\ {}\\ {}\mathrm{such}\kern0.34em \mathrm{that}\\ {}\sum \limits_{k=1}^K{z}_k{y}_{km}\ge {y}_m^0+{\beta}_i^j{y}_m^0\kern1.25em m=1,\dots, M\\ {}\sum \limits_{k=1}^K{z}_k{E}_k\le {E}^j-{\beta}_i^j{E}^j\kern2em \\ {}\sum \limits_{k=1}^K{z}_k{x}_{k{n}_{-E}}\le {x}_{n_{-E}}^j\kern3.5em {n}_{-E}=1,\dots, N-1\\ {}{z}_k\ge 0\kern6.75em k=1,\dots, K\end{array}} $$
(19)
$$ {\displaystyle \begin{array}{l}{{\overrightarrow{D}}_{iT}}^i\left({y}^0,{E}^i,{x}^i\right)=\max {\beta}_i^i\\ {}\\ {}\mathrm{such}\kern0.34em \mathrm{that}\\ {}\sum \limits_{k=1}^K{z}_k{y}_{km}\ge {y}_m^0+{\beta}_i^i{y}_m^0\kern1.25em m=1,\dots, M\\ {}\sum \limits_{k=1}^K{z}_k{E}_k\le {E}^i-{\beta}_i^i{E}^i\kern2em \\ {}\sum \limits_{k=1}^K{z}_k{x}_{k{n}_{-E}}\le {x}_{n_{-E}}^i\kern3.5em {n}_{-E}=1,\dots, N-1\kern.2em \\ {}{z}_k\ge 0\kern6.5em k=1,\dots, K\end{array}} $$
(20)

As is the usual convention, if the levels of energy input, other inputs, and outputs that are held constant at an arbitrary level in the linear programming problems above are set to be equal to those of observation i, observation i becomes the base economy (for which the corrected PFP of energy (CPFP) is equal to unity) with respect to which all bilateral productivity comparisons can be made. Furthermore, since this index is transitive, it allows for all multilateral comparisons. The resultant indices are expressed as follows:

$$ {\mathrm{CPFP}}_{\mathrm{E}}=\frac{\frac{\left(1+{\beta}_0^i\right)\left(1-{\beta}_0^j\right)}{\left(1+{\beta}_0^j\right)\left(1-{\beta}_0^i\right)}}{\frac{\left(1+{\beta}_i^j\right)\left(1-{\beta}_i^i\right)}{\left(1+{\beta}_i^i\right)\left(1-{\beta}_i^j\right)}}\kern1.25em \mathrm{EI}=\frac{\frac{\left(1+{\beta}_i^j\right)\left(1-{\beta}_i^i\right)}{\left(1+{\beta}_i^i\right)\left(1-{\beta}_i^j\right)}}{\frac{\left(1+{\beta}_0^i\right)\left(1-{\beta}_0^j\right)}{\left(1+{\beta}_0^j\right)\left(1-{\beta}_0^i\right)}} $$
(21)

It is also worthwhile to state that the technique proposed here is rich enough to accommodate the joint production of good and bad outputs as demonstrated by Zaim (2004) in computation of carbon dioxide intensities. However, unavailability of data on bad outputs precluded us from such an attempt.

Data

The data used for the computation of intensity indices described above are obtained from the Economic Research Service (ERS) of the United States Department of Agriculture and have recently been made publicly available at http://www.ers.usda.gov/data-products/agricultural-productivity-in-the-us (2014). The data set consists of state-level observations of real quantities of three outputs: crop, livestock, and other farm-related outputs and real quantities of seven inputs: capital, land, labor, energy, pesticides, fertilizers, and materials all expressed in real terms in 1996 Alabama prices for all the years between 1960 and 2004. It is important to note that energy input is only the direct energy use, which is the real quantity of the sum of petroleum fuels, natural gas, and electricity. It is obtained as the ratio of total expenditures at each state to the corresponding price index (where Alabama 1970 = 1). Capital input is constructed by aggregating over different capital assets using as weights asset-specific rental prices. To obtain a constant-quality land stock, the value of land is deflated by an intertemporal land price index, where relative prices of land are obtained from hedonic regression results to account for quality differences. In constructing the labor input for each state for each year, demographically cross-classified hours and compensation data are used. Differences in marginal productivity of labor are accounted for by giving higher weights to labor hours with higher marginal productivity (wages). To construct the real quantity of pesticides and fertilizer inputs, first price indices are estimated by hedonic price functions to account for quality differences both across states and over the years, and then respective expenditures are deflated by their respective price indices. Material input consists of goods used in production during the calendar year, whether withdrawn from beginning inventories or purchased from outside. Open market purchases of feed, seed, and livestock inputs as well as a variety of purchased services such as contract labor services, custom machine services, machine and building maintenance and repairs, and irrigation from public seller of water are all included in material inputs. The output quantity for each crop and livestock category consists of quantities of commodities sold off the farm, additions to inventory and quantities consumed as a part of final demand in farm households during the calendar year. For the off-farms sales to farm sector in other states are also considered as off-farm sales. Full details of data definitions are available at the above URL.

Results

As is the usual convention in agricultural studies in the U.S, all the results will be summarized for ten regional aggregates: Northeast (CT, DE, MA, MD, ME, NH, NJ, NY, PA, RI, VT); Appalachia (KY, NC, TN, VA, WV); Southeast (AL, FL, GA, SC); Corn Belt (IA, IL, IN, MO, OH); Lake States (MI, MN, WI); Delta (AR, LA, MS); Northern Plains (KS, NE, ND, SD); Southern Plains (OK, TX); Mountain (AZ, CO, ID, MT, NM, NV, UT, WY), and Pacific (CA, OR, WA), but more detailed state-level results will be made available upon request. Table 1 shows the relative importance of these regions in U.S agricultural production. Accordingly, it demonstrates that five regions the Pacific, Corn Belt, Southern Plains, Lake States, and Northern Plains constitute over 74% of U.S aggregate output and 61% of U.S agricultural direct energy use over the period 1990–2004. However, Table 1 also shows that composition of outputs have undergone substantial changes in some regions. While in the Pacific, Corn Belt, Northern Plains, and Lake States, the share of crops was increased and the share of the livestock was decreased; just the opposite has occurred for Appalachia. The other states seem to have a more stable composition over-time.

Table 1 Average % share of outputs in U.S agriculture
Full size table

Figure 2 compares our MFP index as expressed in Eq. (9) to that reported by the ERS of the USDA, where both indices are expressed relative to the level of MFP in Alabama in 1970. Although the construction of quantity indices of outputs and inputs is quite different in both methods, and the ERS relies on Fisher quantity indices of outputs and inputs (i.e., Theil-Tornqvist index) after doing a transitivity correction by a method independently proposed by Eltetö and Köves (1964) and Szulc (1964), both MFP measures mirror each other perfectly not only with respect to levels but with respect to trend growth rates as well (except for the Lake States). This, once again, demonstrates that directional distance functions are perfect aggregators (without using information on prices).

Fig. 2
figure 2

Comparison of MFP index and Theil-Tornqvist index of ERS. The calculation of MFP (ERS) is based on Theil-Tornqvist index which is reported at http://ers.usda.gov/data-products/agricultural-productivity-in-the-us/findings,-documentation,-and-methods.aspx#intinput for indices of total factor productivity relative to Alabama 1996=1. a Comparison of MFP index and MFP (ERS) in Pacific. b Comparison of MFP index and MFP (ERS) in Southern Plains. c Comparison of MFP index and MFP (ERS) in Corn Belt. d Comparison of MFP index and MFP (ERS) in Lake States. e Comparison of MFP index and MFP (ERS) in Northern Plains

Full size image

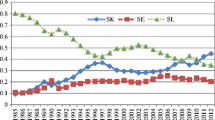
Reminding the reader once more time that our variable of concern is energy, now we turn to the comparison of AEI, EI, and MFII as computed by Eqs. (16), (21), and (9) across time and space. In computing AEI, the single output required is obtained by summing the real quantities of crop, livestock, and farm-related outputs and energy is considered to be the single input, ignoring the existence of all the other inputs. Figure 3 shows general trends for the five regions which constitute over 75% of agricultural production in the U.S. One should remember however that the bases for all these indices are Alabama 1970 (i.e., Alabama 1970 = 1). Therefore, in the figures, EI compares (geometric) average energy intensities of states in a particular region to that of Alabama in 1970 over the years, after accounting for the differences in outputs while energy use is being compared and for the differences in inputs while outputs are being compared. Hence, EI level of 1.93 in the Pacific region in 1960 indicates that energy use per unit of output in 1960 in the Pacific region was almost double that of Alabama in 1970 after accounting for the differences in output and input combinations of the Pacific region in1960 and that of Alabama in 1970. This, when compared with an AEI level of 1.16 implies that there emerges a substantial bias due to (i) aggregation of outputs while energy use is being compared and (ii) failure to hold non-energy inputs constant while output comparisons are being made. Furthermore, in the years where EI > AEI (EI < AEI), this indicates a structure of production where combinations of inputs and outputs use less (more) energy when compared to Alabama 1970.

Fig. 3
figure 3

Comparison of intensities. a Comparison of intensities in Corn Belt. b Comparison of intensities in Pacific. c Comparison of intensities in Southern Plains. d Comparison of intensities in Lake States. e Comparison of intensities in Northern Plains

Full size image

Comparison of figures reveals some further important results. First, there exist substantial level differences between energy intensity levels for both the AEI and EI which prior studies relying on index decomposition methods failed to show. For example, our results show while Southern Plains start off with relatively low levels of AEI (1.29) and EI (1.42) which are close to each other, the Pacific region has achieved the lowest EI level in the 1972–1976 period (0.59 in 1975). Second, improvements in energy intensity (energy productivity) will be underestimated if measured by AEI. Third, for all the five regions, although EI was higher than MFII during the initial years, rapid improvements in EI indicate that particular attention was paid to increase the energy efficiency and that energy efficiency has increased at a faster rate than the average rate of increase in the efficiency of all the inputs. Fourth, there has been a convergence of EI levels to somewhere between 0.26 and 0.55 (i.e., one-fourth to one-half of the levels in Alabama in 1970) towards the end of the first half of the 2000s.

More comprehensive level and growth comparisons are provided in Tables 2, 3, and 4. First, the results reveal that EI and AEI are not necessarily in agreement in ranking the states according to their energy intensity. For example in 1960, while the Northeast region is found to be the worst performer with respect to EI level, AEI measure ranks it as being the best performer with the lowest energy intensity. However, at the state-level comparisons, Florida is the only state which was consistently ranked as one of the best performers for all the selected years by both the measures. As for the other states, no consistency is observed with respect to the rankings of states. Second is the relation between EI and MFII. While EI has been consistently higher than MFII in 1960 (except for Florida, North Carolina, and Oklahoma), just the reverse is true in 2004 for all the states implying that there has been a special emphasis on reducing the energy intensity.

Table 2 Intensity level comparison
Full size table
Table 3 Average annual growth rates of intensity measures
Full size table
Table 4 Intensity rankings (measured with respect to Alabama 1970 = 1)
Full size table

Now turning to the growth rates of the indices computed, for all the regions, EI outperforms both MFII and AEI for the 1990–2004 and for the full 1960–2014 period implying that AEI is a measure that underscores the real achievement in reducing energy intensity and that reduction in energy intensity has been larger than the average rate of decline in the intensity of all inputs. Pacific, Corn Belt, and Northeastern regions have been the most successful states in reducing energy intensity (EI) with dramatic decline rates of − 4.46, − 4.25, and − 3.85% per annum respectively over the period 1960–2004.

Next we proceed to analyze the effect of relative energy price (energy price/output price index), capital intensity index, and labor intensity index (both computed with the models proposed in this study) on energy intensity using Arellano-Bond (1991) dynamic panel model in Table 5. We assumed relative price being exogenous to the producers. The panel estimates indicate that while the short run response of energy intensity to the increase in relative energy prices is positive (immediate response is insignificant), the intermediate response is negative (second and third lags). In fact, the long run relative energy price coefficientFootnote 2 estimate is − 0.30, indicating that farmers take energy conserving measure in response to relative energy price increase which induces a decline in energy intensity. The positive and significant coefficient of both capital intensity and labor intensity is an indication of complementary relation between energy and these two other inputs. That is, a fall in capital and labor intensities induces a fall in energy intensity. This actually is quite consistent with Fig. 3 where MFII is positively related to EI.

Table 5 Determinants of energy intensity—Arellano-Bond dynamic panel estimates with robust S.E’s
Full size table

Discussion

At this point, it is important to discuss the precision at which the “real energy intensity” is measured. But before we go into the details, still it is useful to reconsider how much we diverge from the traditional well-known approaches. It is important to reiterate that the approach pursued here is to provide an alternative to the preceding methods which either rely on IDA or SDA which decompose aggregate energy intensity into structural and intensity effects. The method proposed diverges from the traditional approach in a number of ways. First, unlike the preceding methods, which account for structural change only at the output side for a correct measurement of intensity, the method proposed here accounts for structural change both at the output and the input side. Second, while the traditional decomposition approaches do not allow for the level comparisons of intensity at a point in time and only allow for the growth comparisons, the approach pursued here allows for both the level and the growth comparisons. Third, unlike the previous methods, the structural effect can be obtained as a residual, i.e., AEI/EI.

Now, when we turn to the question of how precise our real energy estimates (and hence structural effects) are, the answer depends on how precisely could we account for the differences in combinations of outputs and inputs across the units being compared. This of course depends on the level of aggregation in the data with which the analysis is conducted. On the output side, the data provides the breakdown as crop, livestock, and other farm-related outputs (mostly vegetables and fruits) and the raw data highlight the fact that over time, there has been a major shift of production from livestock to crop production in some important agricultural regions such as Pacific, Corn Belt, Northern Plains, and Lake States (see Table 1). Given the priori information that the energy share of cost of production for crop activities is almost five times as much of that of livestock activities (Schnepf 2014), one would expect to see the structural effect reflecting over-time movement from less energy-consuming activities towards more energy-consuming activities. This is in fact the case for the regions portrayed in Fig. 2. Note that a large distance between EI and AEI during the initial years (where EI > AEI) is an indication of structure of production where combinations of inputs and outputs use less energy when compared to Alabama 1970, and that closure of this gap over the years reflects the fact that combination of outputs and inputs are moving in the direction towards using more energy input. It is evident that during the early 1960s, for all the regions, considerably higher energy intensities (than that of Alabama 1970) are offset by low energy using combination of inputs and outputs (again than that of Alabama 1970). On the other hand, the years where EI < AEI (which is most evident in the Pacific region after 1968) should be interpreted as those years that combination of inputs and outputs are more energy using than that of Alabama 1970. Pacific region in this case has shown a remarkable success in reducing its energy intensity by 4.46% per annum, offsetting the structural effect.

Could we have more precise estimates of energy intensity (and hence structural change)? The answer is yes, if the data were to allow a further breakdown of crop varieties since there exists a large variation in energy cost in the total cost of production across crop varieties which ranges from 13.9% for soybeans to 30.5% for rice (Schnepf 2014). Given the high sensitivity of American farmers to energy price fluctuations, a more disaggregated data would certainly be an improvement over an aggregate crop quantity, leaving aside the introduction and increasingly adopted less energy using genetically modified varieties.

A similar argument can be carried out for the input side. Direct energy use is mostly petroleum-based fuels to operate farm transportation vehicles and machinery as well as natural gas, liquid propane, and electricity that are used to operate crop dryers and irrigation equipment. Furthermore, petroleum-based fuels can be disaggregated into gasoline and diesel. Unfortunately, aggregated form of direct energy input precludes us from accounting for inter-substitution effects in energy. From the secondary sources (Schnepf 2014), we understand that there had been a substantial substitution of diesel for gasoline since diesel fuel is substantially cheaper especially when one considers that diesel-powered machinery outperforms its gasoline-powered peer in terms of miles per gallon. Inability to identify these inter-fuel substitution effects with the aggregated data will result in over-estimated decline in energy intensity over time, since what is/should be considered as structural effect is now measured as energy intensity.

As for the land input, perfectionism requires taking different tillage practices both across time and space into account, since different practices will inevitably affect energy consumption. Similar arguments may be developed for capital input and materials.

Conclusions and policy implications

This paper revisits an exhaustively studied area, measurement of energy intensity, and proposes an alternative method which overcomes the shortcomings of the index decomposition approach. In this paper, we regard energy intensity measure as the inverse of a partial factor productivity measure and consider index decomposition trials as an attempt to partially alleviate some but not all the weakness of the measure. First, while index decomposition method accounts for compositional differences in outputs among units being compared, it fails to take into consideration compositional differences between inputs. Second, while energy intensity measures provide a valuable information on the evolution of energy efficiency trends over time, there are some considerable challenges in using energy intensity measure to perform informative and fair comparisons between the energy efficiency levels of units (states) being considered.

In this paper, by relying on the computation of directional distance functions, which provide a valuable framework for modeling a technology with multiple outputs and inputs, we propose an alternative technique that expresses the energy intensity index as a ratio of input (energy) quantity index to output quantity index, both of which satisfy all the desirable properties due to Fisher (1922)—i.e., homogeneity, time reversal, transitivity, and dimensionality. Unlike our predecessors, our productivity measure (or energy intensity measure) overcomes the shortcomings of the partial productivity measure by not only controlling for the compositional differences in outputs (both across the units being observed and over-time) but also by accounting for the compositional differences in inputs (both across the units being observed and over-time).

Application of the proposed methodology to the U.S agricultural sector, an unexplored area with respect to energy intensity, reveals that there exist substantial differences between energy intensity levels for both the AEI and EI which prior studies relying on index decomposition methods failed to show and that improvements in energy intensity (energy productivity) will be underestimated if measured by AEI. The study also shows that, for all the regions, the level of EI was higher than the level of MFII during the initial years. EI improved faster indicating that particular attention is paid to increase energy efficiency and that energy efficiency has increased at a faster rate than the average rate of increase in the efficiency of all the inputs.

On the energy policy front, the indices developed in this study will provide a quick assessment tool for policy makers, based on meaningful analysis. This study’s research on energy intensity level differences across states can serve as the starting point in identifying good practices and developing region- or state-based policies. Furthermore, identification of the impact of energy policies requires a correct measurement of the outcomes of these policies. The methodology proposed in this study, through more accurate measurements, will help the policy makers do more sound judgments.