Optimal control of pump rotational speed in filling and emptying a reservoir: minimum energy consumption with fixed time

Abstract

An effective way to save energy in pumping systems with low static head is to control the pump’s rotational speed with a variable-speed drive (VSD), which allows changing of the rotational speed when necessary. VSDs can be utilized to control batch transfer systems, for example, in filling or emptying a tank or a reservoir. In the literature, such processes have been optimized only with respect to energy consumption, but the time limit has been ignored. This means that pumping time can be very long. Our paper deals with this optimization problem and considers both pumping time and energy demand, which are often conflicting criteria. We derived a general optimal control law for rotational speed, which can easily be implemented in existing VSDs in the market. Minimum energy and minimum time schemes are special cases of this general new scheme. A constant flow rate scheme, suggested in the literature, is verified to give an optimum solution if the efficiency of the pump remains constant during operation. In addition to energy consumption, rotational speed control can have a favorable effect on the pump’s lifetime, as pointed out in the paper.

Introduction

Pumps are commonly used, for example, for heating and air conditioning, wastewater treatment, and the processing of chemicals and food. Pumping consumes roughly one-fifth of the electricity produced in the world, and in the industrial sector, this figure is even greater (Hydraulic Institute, Europump, and US Department of Energy’s Office of Industrial Technologies 2001). Though over the last 20 years, some industries have considerably improved their energy efficiency (Schächtele and Schneider 2012), more energy could still be saved. For example, de Almeida et al. (2005) point out that considerable energy savings could be gained by applying variable-speed drives (VSD) in pumping systems.

To efficiently exploit VSDs in pumping systems, the operational point, i.e., flow rate and head, must be constantly available for the control system. With modern VSDs, system flow rate or pressure measurements are not required, because VSDs provide an accurate estimate of pump power. Flow rate can then be calculated using the affinity law for power (QP-method), and head from the affinity law for pump head (Hydraulic Institute, Europump, and US Department of Energy’s Industrial Technologies Program 2004, p. 75). Tamminen et al. (2014) have pointed out that the QP-method is inaccurate if the power curve flattens out, and they showed how accuracy could be improved.

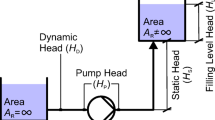
In batch transfer systems, for example in the process of Fig. 1 or in wastewater pumping (Kallesøe et al. 2011), a given volume of liquid is pumped from one reservoir or tank into another, and the liquid levels can change as a result of pumping. VSD control can be adopted in these kinds of processes to reduce energy consumption, when the static head H _s is considerably smaller than the frictional head, see, e.g., Casada (1999) and Hovstadius et al. (2005). Energy savings are possible also with a high static head component by using hybrid control proposed by Budris (2008). In hybrid control, VSD control is combined with a bypass line, which moves the pump operation point towards higher efficiency. This requires additional investment but leads to lower energy consumption and increased pump reliability even though pump rotational speed must be somewhat increased.

Fig. 1

Schematics of a pumping process where the surface level drops in reservoir 1 and rises in reservoir 2 as a function of time

Recently, the reservoir filling process in Fig. 1 was studied both analytically and experimentally. Bene and Hős (2012) derived an analytical expression for an optimal flow rate as a function of static head to minimize energy consumption in the process. In the derivation, they made simplifying assumptions about the shape of system and pump characteristics. Tamminen et al. (2013) performed an experimental study of reservoir filling with a VSD-controlled pump. The pump rotational speed was changed in small steps to constantly pump with minimum specific energy consumption. When the process time limit is ignored, as in the above studies, the pumping time can be excessively long. In practice, finishing pumping within a given time limit can be a more important objective than low-energy consumption. In another experimental study (Ahonen et al. 2014), the pump rotational speed was not changed during pumping, but the process energy consumption and time were determined for different fixed rotational speeds.

The time constraint of the reservoir filling process could easily be taken into account by maintaining a constant flow rate (Karassik et al. 2008, p. 11.15), but energy consumption might not then be minimal. This scheme obviously works well when surface levels do not change much, but it must be further evaluated in the case where static head increases a lot.

This paper introduces pumping of a given volume of fluid between two reservoirs at minimum energy consumption in a fixed time. The inverter and motor efficiencies are omitted from the analysis because they are nearly constant and much higher than the efficiency of the pump. They can be easily added to our model. With the calculus of variations, a simple equation is derived to determine how pump rotational speed should be controlled throughout the process. The equation can be used to calculate optimal operation with model equations or to control variable-speed driven pumping systems. To help make the method more comprehensible, we give examples that compare energy consumption and time in different control schemes.

Pump and system hydraulics

The delivered pump head (pressure rise divided by ρg) and consumed power depend on the rotational speed and flow rate through the pump. According to the affinity laws, the pump head H at a flow rate Q and rotational speed n can be obtained with the help of the reference head curve H _r (Q _r ), which is known at another rotational speed n _r :

$$ \frac{Q}{Q_r}=\frac{n}{n_r} $$

(1a)

$$ \frac{H\left(Q,n\right)}{H_r\left({Q}_r\right)}={\left(\frac{n}{n_r}\right)}^2 $$

(1b)

where the reference speed n _r is usually the maximum rotational speed. The reference head curve is typically a quadratic function as in Eq. (17).

Pumping power is linked to the operational point by the equation

$$ P\left(Q,n\right)=\frac{\rho gH\left(Q,n\right)Q}{\eta \left(Q,n\right)} $$

(2)

where η(Q, n) is the pump efficiency. In actual pumps, the losses, i.e., 1 − η, increase when rotational speed is reduced. This can be taken into account with the following model:

$$ \eta \left(Q,n\right)=1-\left(1-{\eta}_r\left({Q}_r\right)\right){\left(\frac{n_r}{n}\right)}^k $$

(3)

where the constant k depends on the pump type and takes values greater than 0.1 (Gülich 2003). In Eq. (3), η _r (Q _r) is the pump efficiency curve at the reference rotational speed n _r . Later on, Eq. (18) is used as the reference curve.

The total head that the pump must overcome can be divided into a static head H _s , which does not depend on flow rate, and a frictional head H _f , which does. The former is the vertical distance between the free surfaces in Fig. 1, when the reservoirs have the same pressure. Because industrial piping systems contain bends and valves, the frictional head can be assumed quadratic: H _f  = KQ ². The total head is the sum of static and frictional head:

$$ H={H}_s+K{Q}^2 $$

(4)

The operational point of the pump, i.e., flow rate and head, is determined by the intersection of Eq. (4) and the pump head-flow rate characteristics, which is obtained using Eqs. (1a) and (1b). Thus the possible values of flow rate and head are dictated by the shape of the system curve. It is easy to show that with a high static head component in Eq. (4), a small change in rotational speed can lead to a large change in flow rate.

Pumping power can also be expressed as work dE done in a short time interval dt as

$$ P=\frac{\mathrm{d}E}{\mathrm{d}t} $$

(5)

The time interval $\mathrm{d}t$ is related to a corresponding increase in the static head dH _s between the reservoirs in Fig. 1:

$$ \mathrm{d}t=\frac{\mathrm{d}{H}_s}{Q\left(\frac{1}{A_1}+\frac{1}{A_2}\right)} $$

(6)

where A ₁ and A ₂ are the free surface areas of the reservoirs at a given time.

Optimal rotational speed control in filling a reservoir

The purpose of the pumping process in Fig. 1 is to increase the static head of the system from H _s,min to H _s,max. Pumping should be performed with the minimum energy consumption E, while the process time $T$ is fixed at ${T}_0$. Energy consumption is obtained by combining Eqs. (5) and (6) and by integrating pumping power:

$$ E={\displaystyle {\int}_{H_{s, \min}}^{H_{s, \max }}\frac{P}{Q}{\left(\frac{1}{A_1}+\frac{1}{A_2}\right)}^{-1}\mathrm{d}{H}_s} $$

(7)

The pumping time $T$ is obtained from Eq. (6):

$$ T={\displaystyle {\int}_{H_{s, \min}}^{H_{s, \max }}\frac{1}{Q}{\left(\frac{1}{A_1}+\frac{1}{A_2}\right)}^{-1}\mathrm{d}{H}_s} $$

(8)

The free surface areas ${A}_1$ and ${A}_2$, i.e., the reservoir cross sectional areas, may vary with static head. This means that the reservoirs in Fig. 1 may have arbitrary shapes and sizes.

To meet the objective of minimum energy consumption and satisfy the time limit, pump rotational speed must be controlled optimally throughout the process according to the static head. Pump operation is limited to within the allowable operating region (AOR) shown as the shaded region in Figs. 2 and 4. The AOR is defined by the lower and upper limits of the rotational speed, n _min ≤ n ≤ n _max, and the flow rate, Q _min(n) ≤ Q ≤ Q _max(n). The flow rate limits shown are 50 and 130 % of the best efficiency point (BEP) flow rate of each rotational speed.

Fig. 2

Minimum energy (a), constant flow rate (b), and minimum time (c) control schemes on a QH-plane

When the rotational speed is changed, the operational point moves along the system curve and the flow rate changes. We assume that a time delay from the change of rotational speed to the corresponding change of flow rate is very short compared to the time of the whole process. Because of this one-to-one correspondence between flow rate and rotational speed, we can treat flow rate rather than rotational speed as the unknown function, and the problem is reduced to finding the flow rate as a function of the static head, Q(H _s ):

$$ \begin{array}{l}\\ {}\begin{array}{cc}\hfill \mathrm{find}\hfill & \hfill Q\left({H}_s\right),{H}_{s, \min}\le {H}_s\le {H}_{s, \max }\ \hfill \\ {}\hfill \mathrm{t}\mathrm{o}\ \mathrm{minimize}\hfill & \hfill E\hfill \\ {}\hfill \mathrm{subject}\ \mathrm{t}\mathrm{o}\hfill & \hfill T-{T}_0=0,\hfill \\ {}\hfill \hfill & \hfill {n}_{\min}\le n\le {n}_{\max}\hfill \\ {}\hfill \hfill & \hfill {Q}_{\min }(n)\le Q\le {Q}_{\max }(n)\hfill \end{array}\end{array} $$

(9)

Before solving problem (9), let us look at Fig. 2, which shows pump head curves at different rotational speeds and the contours of efficiency. Typical system characteristics from Eq. (4) with two different static heads are also shown. At the beginning of pumping, the static head is H _s,min, and the pumping ends at a static head of H _s,max. The desired fluid volume can be pumped in various ways by changing the rotational speed within the AOR. For instance, by following path (a), a small energy consumption is obviously obtained. In fact, the pump is initially at rest and is then accelerated smoothly to point 1 while gradually opening the system valve. When the process is completed at point 2, the pump is shut down in a similar manner. We ignore the pump startup and shutdown phases since they do not greatly affect the total performance. According to an alternative path, (b), the flow rate is kept constant. Also here 1 and 2 designate the process start and end. On the other hand, if the pumping time is minimized, the rotational speed should be as high as possible, e.g., equal to n _max. In that case, the process follows the pump QH-characteristic along path (c). Figure 2 does not show paths in the case where energy consumption is minimized and the process time is fixed. This problem will be tackled in the following.

Solution of minimum energy with fixed time

The energy consumption in Eq. (7) is a functional of the flow rate; i.e., it depends on flow rate values at every time instance during the process. Optimization problems involving functionals can be dealt with the Calculus of variations, which is an alternative method to Dynamic programming used by da Costa Bortoni et al. (2008) for optimal control of parallel pumps. Whereas in Dynamic programming the solution is broken down into a number of sub problems, which are solved recursively, the Calculus of variations may give an analytical solution. The basic theory of the Calculus of variations, presented by Smith (1998), is given in Appendix.

Rotational speed and flow rate limits may be active only over a part of the process and are thus difficult pointwise constraints of the variational problem. We do not treat them in the derivation of the control law, because the control law can be simply ignored if it attempts to steer the operation outside the limits. The solution of problem (9) is straightforward without these limits. The energy consumption $E$ in Eq. (7) corresponds to $F$ in Eq. (25), and the time constraint $T-{T}_0=0$ from Eq. (8) corresponds to G in Eq. (28). Thus the minimum energy-fixed time operation occurs when (see Eq. (30)):

$$ \frac{\mathrm{d}}{\mathrm{d}Q}\left(\left(\frac{P}{Q}+\frac{C}{Q}\right){\left(\frac{1}{A_1}+\frac{1}{A_2}\right)}^{-1}-C{T}_0\right)=0 $$

(10)

Because ${A}_1$, ${A}_2$, C, or ${T}_0$ do not depend on the flow rate, Eq. (10) is reduced to the following optimal control law:

$$ \frac{\mathrm{d}}{\mathrm{d}Q}{\left(\frac{P}{Q}\right)}_{H_s=\mathrm{const}.}=\frac{C}{Q^2} $$

(11)

where $P/Q=\mathrm{d}E/\mathrm{d}V$ is the instantaneous specific energy consumption.

The unknown Euler-Lagrange multiplier C in Eq. (11) represents the sensitivity of the process energy consumption to the process time. With C = 0, Eq. (11) gives d(P/Q)/dQ = 0, which is the special case of minimum specific energy consumption without a time constraint. When the pumping time is fixed to the value ${T}_0$, the Euler-Lagrange multiplier C is unknown and must be found iteratively by running the process several times both in actual VSD control and in numerical calculations. The iteration can be performed by minimizing the difference between realized and desired process times $T-{T}_0$ using some optimization algorithm. Care should be taken not to select too long a time, which might give $C<0$. A good initial guess for C to start optimization can be obtained from Eq. (16) derived below.

Equation (11) can be applied to VSD control using a similar algorithm, as did Tamminen et al. (2013), who had $C=0$. The rotational speed is increased or decreased in small steps $\Delta n$, which are sufficiently large to change the value of the power given by VSD. Equations (1), (2) and (3) combined with a known reference head and efficiency curves give the flow rate, and the derivative on the left of Eq. (11) can be estimated as ((P/Q) _n + Δn  − (P/Q) _n )/(Q _n + Δn  − Q _n ). If this value is greater than C/Q ² _n + Δn , the flow rate is too large, and the rotational speed must be decreased by $\Delta n$. In the opposite case, the flow rate is too small, and the rotational speed should be increased by $\Delta n$. However, the rotational speed limits must be obeyed. Another way to apply the algorithm is to calculate the optimal rotational speed as a function of time as shown in “Comparison of control schemes” and use that in VSD control without using the QP-method.

Constant flow rate control

Pumping at a constant flow rate is a simple scheme, which is applicable to the pumping process in Fig. 1, but its performance has not been proven theoretically. For example, Karassik et al. (2008), p. 11.15, stated that this process “can have a constant flow”. We will show that this is good advice, and that the constant flow rate scheme is optimal with respect to energy and time if efficiency remains constant during the process.

Let us assume again that the pump is operating inside the AOR, as, e.g., curve (b) in Fig. 2. When the head $H$ in Eq. (2) is expressed using the system curve in Eq. (4), the criterion for optimality in Eq. (11) becomes

$$ \frac{\mathrm{d}}{\mathrm{d}Q}{\left(\frac{\rho g\left({H}_s+K{Q}^2\right)}{\eta}\right)}_{H_s=\mathrm{const}.}=\frac{C}{Q^2} $$

(12)

Assuming that the pump efficiency remains constant during the process, we can perform differentiation in Eq. (12) and get

$$ \frac{\rho g}{\eta }2KQ=\frac{C}{Q^2} $$

(13)

and finally

$$ Q={\left(\frac{\eta C}{2\rho gK}\right)}^{1/3} $$

(14)

Equation (14) shows that if pump efficiency is constant and pumping time is fixed (C is fixed), the constant flow rate scheme yields minimum energy consumption. This result is valid regardless of the shape of the system curve. For example, the exponent of Q in Eq. (4) affects only the numerical constants in Eq. (14). In practice, Eq. (14) is not necessary, but a suitable flow rate is obtained from the volume of fluid V and the time limit ${T}_0$ as follows:

$$ Q=\frac{V}{T_0} $$

(15)

A good initial guess for the unknown C in Eq. (11) is obtained by combining Eqs. (14) and (15):

$$ C=\frac{2\rho gK}{\eta_{\mathrm{BEP}}}{\left(\frac{V}{T_0}\right)}^3 $$

(16)

where the pump efficiency has been approximated with ${\eta}_{BEP}$. The system friction constant $K$ can be estimated using friction factor formulae when the piping layout and fluid properties are known. In the numerical calculations below, we assume that $K$ is known.

Comparison of control schemes

This section presents calculation examples of the pumping system in Fig. 3, where water (ρ = 1000kg/m³) is pumped from a very large reservoir (${A}_1\approx \infty$) into a cylindrical tank (${A}_2=20\;{\mathrm{m}}^2$). Table 1 gives in detail the system characteristics in four different system setups, in which the volume of pumped water is the same V = A ₂(H _s,max − H _s,min) = 240 m³. The constant $K$ takes into account pipe friction in Eq. (4). The pump’s rotational speed is controlled according to

Fig. 3

Process layout in the examples

Table 1 System characteristics of examples

• 1. Minimum energy-fixed time scheme, Eq. (11)

• 2. Constant flow rate scheme, Eq. (15)

• 3. Constant rotational speed scheme.

To illustrate the performance of the control schemes, we present results for different time limits for each control scheme and system.

According to Mackay (2004), p. 79, a pump to fill a reservoir should be selected such that the pump’s BEP is halfway between the system curves. This minimizes the departure from the BEP during the process and increases the pump’s lifetime. Of course, the pump must also be able to deliver the maximum static head and flow rates high enough to reach the time limit. In two pumping systems in Table 1, the pump has been properly selected, and the static head is relatively small (System 1) or large (System 2) compared to the frictional head. In Systems 3 and 4, the pump’s BEP does not lie between the system curves but at smaller and larger flow rates, respectively.

The characteristic head and efficiency curves of a Sulzer AHLSTAR A32-100 pump used in the examples are shown in Fig. 4 together with the AOR. The minimum allowed rotational speed is n _min = 800 rpm and the maximum n _max = 1400 rpm, which is also used as the reference speed, n _r  = n _max. The reference curves are quadratic fits of the values at the reference speed:

$$ {H}_r\left({Q}_r\right)={a}_0+{a}_1{Q}_r+{a}_2{Q}_r^2 $$

(17)

$$ {\eta}_r\left({Q}_r\right)={b}_0+{b}_1{Q}_r+{b}_2{Q}_r^2 $$

(18)

where a ₀ = 36.26 m, a ₁ = 126.7 sm^− 2, a ₂ = − 3450 s²m^− 5, b ₀ = 0.2010, b ₁ = 22.00 sm^− 3, and b ₂ = − 201.65 s²m^− 6. The pump power as a function of rotational speed and flow rate is obtained by combining Eqs. (1a), (1b), (2), (3), (17) and (18):

$$ P=\rho g\frac{a_0Q{\left(\frac{n}{n_r}\right)}^2+{a}_1{Q}^2\left(\frac{n}{n_r}\right)+{a}_2{Q}^3}{1-\left(1-{b}_0-{b}_1Q\frac{n_r}{n}-{b}_2{\left(Q\frac{n_r}{n}\right)}^2\right){\left(\frac{n_r}{n}\right)}^{0.154}} $$

(19)

Fig. 4

Characteristics of the Sulzer AHLSTAR A32-100 centrifugal pump

Where k = 0.154 in Eq. (2) for this pump. In actual speed control, Eq. (19) should be further divided by the VSD and motor efficiencies, which can depend on power and rotational speed. However, in our examples, we assume that these efficiencies are constant and can be ignored. Because the pump power is calculated using Eqs. (17) and (18), which are valid only inside the AOR, Eq. (19) gives false results outside the AOR (see also (Ulanicki et al. 2008)).

When the QP-method is applied to an actual pumping system, the power and rotational speed are obtained from VSD, and the flow rate is solved from Eq. (19). On the other hand, in numerical calculations where the system curve is known, the rotational speed can be calculated by equating the pump and system heads, i.e., solving Eqs. (1a), (1b) and (4):

$$ \frac{n_r}{n}=\frac{1}{2}\left(\frac{a_1Q}{H_s-\left({a}_2-K\right){Q}^2}+\sqrt{\frac{{\left({a}_1Q\right)}^2}{{\left({Q}^2\left({a}_2-K\right)-{H}_s\right)}^2}-\frac{4{a}_0}{Q^2\left({a}_2-K\right)-{H}_s}}\right) $$

(20)

The rotational speed can now be eliminated from Eq. (19).

Minimum energy-fixed time scheme

The problem in applying the minimum energy-fixed time scheme, i.e., Eq. (11), is that the constant C corresponding to the desired process time is unknown. It can be found iteratively, as explained below Eq. (11). During a pumping process with a given C, Eq. (11) is solved as follows: First, Eq. (20) is inserted in Eq. (19) so that the pump power becomes a function of the flow rate only. Then the derivative in Eq. (11) can be expressed, e.g., by using a central difference scheme:

$$ \frac{{\left(P/Q\right)}_{Q+\Delta Q}-{\left(P/Q\right)}_{Q-\Delta Q}}{2\Delta Q}-\frac{C}{Q^2}=0 $$

(21)

where $\Delta Q$ is a small increment of the volume flow rate. We used the value ΔQ = 10^− 5 m³/s. Optimal flow rates are solved from Eq. (21) with many different static heads spaced evenly between H _s,min and H _s,max. The operation is limited to within the AOR. At the end, the process time and energy consumption are calculated by numerically integrating Eqs. (7) and (8) using the calculated flow rates and pump powers. If the process time is not sufficiently close to the desired value, the process is repeated using a different value of C, obtained from the selected optimization algorithm.

To show how the above theory is utilized, we calculated optimal pump operation with three time limits in each system. The time limits in these example processes, labeled P₁₁ to P₄₃, are given in Table 2. The calculation results are commented on below.

Table 2 Minimum energy consumption of processes in Fig. 5 with fixed time ${T}_0$

Let us first look at process P₁₁, where we have set $C=0$ to obtain the minimum energy process without a time limit. Because C is given, no iteration is needed, and the process time is not known in advance. Equation (21) is solved with sufficiently many static heads to get a good resolution of how the operation point (Q, $H$) changes during the process. In Fig. 5, this process starts from the lower system curve and follows the lower rotational speed limit (n _min = 800 rpm) until the static head is equal to H _s  = H − KQ ² = 9.68 m and the flow rate Q = 0.0167m³/s (see also Fig. 2). After that, both the rotational speed and flow rate start to increase. Figure 6 shows the corresponding rotational speed as a function of static head. The minimum energy consumption is 42.9 MJ, and the pumping time is equal to 11,168 s. Without a time limit, the minimum energy process requires a very long time. When the process time is fixed at 9000 and 6000 s, the corresponding minimum pumping energy is obtained by following paths P₁₂ and P₁₃ in Figs. 5 and 6.

Fig. 5

Process paths for minimum energy consumption with fixed time

Fig. 6

Rotational speed as a function of static head for the processes in Fig. 5

The minimum energy consumption as a function of the time limit is shown in Fig. 7. The results in Table 2 were selected for illustration and are found in the curves of Fig. 7. Figure 7 also shows the results of the other control schemes, which are explained below. Energy consumption and time are obviously conflicting criteria, since the minimum attainable energy consumption increases when the time limit is shortened. In short, minimum time corresponds to maximum energy consumption and vice versa.

Fig. 7

Energy consumption as a function of process time in different control schemes

The minimum energy scheme without a time limit ($C=0$) may not be the best in practice, because the time to complete the pumping may be long. The Euler-Lagrange multiplier C = 0 of this scheme indicates that when the time available is somewhat shortened, energy consumption does not increase significantly. For example, in System 1 it is possible to select process P₁₂ instead of P₁₁ and shorten the process time by 15 % with only a 6 % increase in energy consumption. This effect is pronounced in systems 2 and 4, where the static head is large.

It can be seen in Fig. 6 that in some cases the pump is operated most of the time at either the lower or the upper rotational speed limit. In process P₄₃ of System 4, the fixed process time limit equal to 5000 s is too short and cannot be reached even though the pump operates at its maximum speed throughout the process. The actual pumping time is given in parentheses in Table 2.

The constants for System 1 and System 2 in Table 1 were selected so that the minimum time processes have the same energy consumption. Figure 7 shows that in System 1, where the frictional head predominates, rotational speed control can even halve energy consumption compared to a pump running at maximum speed. However, in System 2, where the static head is larger than the frictional head, energy consumption is less reduced. The same applies to systems 3 and 4. In System 3, energy consumption can be considerably reduced by using speed control but not in System 4.

Constant flow rate and constant rotational speed schemes

The constant flow rate scheme suggested by Karassik et al. 2008, p. 11.15 is attractive because the required flow rate is given by Eq. (15). We show here that this scheme is also energy efficient. Because the flow rate must be constant and operation must remain within the AOR, the choice of flow rates may be limited. For example, in System 4 the admissible flow rates are within a narrow band, as shown in Fig. 8.

Fig. 8

Process paths on QH-plane with constant flow rate scheme

The energy consumption and time were calculated from Eqs. (7) and (8) for the processes in Fig. 8. These processes are controlled as curve (b) is controlled in Fig. 2. The circles in Fig. 7 give the energy consumption and time of the processes such that the leftmost circle corresponds to the rightmost line in Fig. 8. The constant flow rate control gives practically the same energy consumption as the minimum energy-fixed time scheme. The reason is that the pump efficiency changes only slightly in the example processes, which, according to Eqs. (12)–(14) makes the process paths of the minimum energy-fixed time scheme almost vertical on the QH-plane.

Tamminen et al. (2014) studied pumping experimentally at a constant rotational speed in a reservoir pumping process. As with the above constant flow rate scheme, the AOR limits the choice of rotational speeds, as is shown in Fig. 9. Especially System 4 has only a small range of feasible rotational speeds. This is the simplest type of “control”, but it is not efficient; the energy consumption shown in Fig. 7 is higher than in the two other schemes. The crosses in Fig. 7 are obtained using the constant rotational speeds in Fig. 9. Each of these processes is controlled as curve (c) is controlled in Fig. 2. At the maximum rotational speed, this scheme gives the same result as the minimum energy-fixed time scheme. The difference in energy consumption grows when the time limit becomes less strict and the rotational speed slower.

Fig. 9

Processes with different rotational speeds on QH-plane in constant rotational speed scheme

Effect of speed control on pump reliability

Figure 7 shows that the way in which the pump’s rotational speed is controlled has only a moderate effect on its energy consumption. For this reason we considered also pump reliability, which is often a more important objective than low energy consumption. Sudden pump failures can cause shut-downs of large facilities with costs exceeding those of pump operation. Pump reliability depends on several operating conditions, the most important being rotational speed, flow rate, and suction conditions. Because the selected pump has a low suction energy, we ignore the effect of suction conditions in this analysis.

To increase the pump’s lifetime, operating far from the BEP or at a high rotational speed is to be avoided. To quantify these effects, Bloch and Budris (2010), Ch. 5, analyzed the data from 119 actual pumps and determined how deviations from the maximum allowed speed and BEP flow rate affect pump reliability. Reliability calculations based on their data are only approximate, because pump types and other conditions may not correspond to those in the Bloch and Budris data set. However, we think that their data allows for at least a qualitative comparison of the reliability of the control schemes of this paper.

We have correlated the data of Bloch and Budris (2010) for the reliability factors of speed ${R}_n$ and flow rate ${R}_Q$ as

$$ {R}_n=1.16-0.75\frac{n}{n_{\max }} $$

(22a)

$$ {R}_Q=1-4.53{\left(\frac{Q}{Q_{\mathrm{BEP},n}}-0.89\right)}^2 $$

(22b)

where Q _BEP,n  = Q _BEP n/n _max is the BEP flow rate at a rotational speed n, and where Q _BEP = 0.0545m³/s is the BEP flow rate at ${n}_{max}$. A mean speed reliability factor is calculated as a time average of Eq. (22a) over the process

$$ {R}_{n,\mathrm{mean}}=\frac{1}{T}{\displaystyle {\int}_0^T{R}_n\mathrm{d}t} $$

(23)

where dt is obtained from Eq. (6) and $T$ from Eq. (8). R _Q,mean is defined with ${R}_Q$ in a similar way as R _n,mean in Eq. (23). The total reliability factor is the product of the mean reliability factors:

$$ {R}_{\mathrm{tot}}={R}_{n,\mathrm{mean}}{R}_{Q,\mathrm{mean}} $$

(24)

The total reliability factor can be used to compare the relative lifetime of a given pump under different control schemes, but not to make any conclusions about the actual pump’s lifetime. A large value of R _tot corresponds to good reliability. For example, if R _tot with control scheme 1 is 5 % higher than with control scheme 2, the mean time to the next failure is expected to be 5 % longer in scheme 1.

Figure 10 presents total reliability factors for all the studied processes. The constant rotational speed scheme has the lowest possible rotational speed that can be used to achieve a given time limit, and thus the speed reliability factors are high. However, the operational point is on average far from Q _BEP,n as shown in Fig. 9, and the flow rate reliability factors are low. As a result, the total reliability factor is the lowest of the three schemes. The pump operates near its minimum and maximum flow rates, especially when the fixed time is long. The energy consumption of this scheme in System 3 was up to 8 % higher than in the minimum energy-fixed time scheme, and the reliability was worse as much as 15 %. Since both energy consumption and reliability affect the lifetime costs, this scheme should be avoided.

Fig. 10

Total reliability factors for minimum energy-fixed time (−), constant flow rate (o) and constant rotational speed (+) schemes

The constant flow rate scheme has as low energy consumption and good reliability as the minimum energy-fixed time scheme. This scheme should be used whenever it is possible to have a constant flow rate throughout the process without operating outside the AOR. Unfortunately, the AOR considerably limits the range of feasible flow rates, especially when the system curve is very steep, see Fig. 8.

When a very short process time or very low energy consumption is required or the rise in static head is large, operation along some edges of the AOR might be necessary. For example, optimal operation might first follow the lower rotational speed limit and then go inside the AOR, or operation might start inside the AOR and reach the maximum allowed rotational speed before the end of pumping. Iteration is certainly necessary to find the optimal path for the operational point. Since the constant flow rate scheme cannot be used in this case, the minimum energy-fixed time scheme should be used instead.

Every control scheme has its reliability maximum at a certain process time. In systems 2 and 4, where the static head is large, the best reliability occurs near the minimum time solution, where the rotational speed is the highest and the flow rate is near the BEP flow. This shows that flow rate has a much greater impact on reliability than rotational speed. In systems 1 and 3, the best reliability is obtained with a low rotational speed and long process time, since reduced rotational speed does not lead to operation far from BEP flow rates. Thus when static head is small, VSD control can decrease energy consumption and at the same time increase the pump’s reliability.

Conclusions

Filling or emptying a reservoir or tank is a typical pumping process in various industries. Pump head increases during the process and also changes flow rate. Using the calculus of variations, we derived an optimal control law (Eq. (11)) for pump rotational speed or flow rate when a given amount of fluid must be pumped at minimum energy consumption while the process time is fixed. This result is new because earlier papers in the literature have discussed only cases with no time limit for pumping. The new minimum energy-fixed time scheme can be easily implemented in a VSD control system, and it can be extended to optimize the operation of unequal parallel pumps when combined pump-group characteristics are used (Lindstedt and Karvinen 2015).

If pump efficiency remains almost unchanged during the pumping process, constant flow rate control gives minimum energy consumption with a fixed process time and guarantees high pump reliability. Such a control scheme has been suggested in the literature, but now it has been verified. However, the range of permissible constant flow rates may be narrow because the pump must operate within the minimum and maximum flow rates and the rotational speeds recommended by the pump manufacturer.

Our example calculations show that process time can be very long if energy consumption is minimized without a time limit. In this case, the pump operates at low flow rates and its efficiency is low. By setting a reasonable time limit, the process time can be shortened significantly with only a small increase in energy consumption. This also improves the pump’s reliability because its flow rate is then closer to that at its highest efficiency.

The highest pump reliability occurs at low rotational speeds and at high pump efficiencies. When the static head component in the system is small, VSD control can help retain high pump efficiency during the process. Our calculations show that in this case also the pump’s reliability remains high. However, with a large amount of static head in the system, maximum pump reliability occurs when the pump is operated near its maximum allowed speed, where energy consumption is at its maximum. In this case, application of VSD control is not justified.

a, Nomenclatureb, Coefficients in Eqs. (17)–(18); A ₁ , A ₂ , Free surface areas, ${\mathrm{m}}^2$; AOR, Allowable operating region, see Figs. 2 and 4; VSD, Variable-speed drive; BEP, Best efficiency point; C, Euler-Lagrange multiplier; E, Energy consumption of pumping process, Eq. (7), J; g, Gravitational acceleration, $9.81{\mathrm{m}}^2/\mathrm{s}$; $H$, Total head, Eqs. (1b) and (4), m; H _f , Frictional head, m; H _s , Static head, m; H _s,min, Static head at the beginning of process, m; H _s,max Static head at the end of process, m; k Constant in Eq. (3), here k = 0.154; K Constant in Eq. (4), ${\mathrm{s}}^2/{\mathrm{m}}^5$; n, Rotational speed, $\mathrm{rpm}$; P, Pump power, Eqs. (2) and (5), W; Q, Flow rate, ${\mathrm{m}}^3/\mathrm{s}$; Q _BEP,n , BEP flow rate at rotational speed n, ${\mathrm{m}}^3/\mathrm{s}$; R _tot, Total reliability factor, Eq. (24); t, Time, s; T, Time of pumping process, Eq. (8), s; T ₀, Target time for pumping process, s; V Volume of fluid pumped, ${\mathrm{m}}^3$; Greek Letters; ρ, Density of fluid, $\mathrm{kg}/{\mathrm{m}}^3$; η Pump efficiency, Eq. (3); Subscripts; r Values at reference curve

Appendix

Calculus of variations

The following theory can be found, e.g., in chapters 1–3 in (Smith 1998).

Consider a functional $F(y)$ defined as a definite integral:

$$ F(y)={\displaystyle {\int}_a^bf\left(y(x)\right)dx} $$

(25)

where f is some known function. We seek to find the unknown function y(x) in the interval a ≤ x ≤ b to minimize F(y). Henceforth, we denote y(x) by y.

The variation of the functional $F(y)$ is defined as

$$ \updelta F\left(y;\Delta y\right)=\underset{\epsilon \to 0}{ \lim}\frac{F\left(y+\epsilon \Delta y\right)-F(y)}{\epsilon } $$

(26)

where Δy is an arbitrary function in the interval a ≤ x ≤ b. The minimum of F(y) occurs when the variation is δF(y; Δy) = 0 for every function Δy. By inserting Eq. (25) into Eq. (26) and changing the order of limit and integral, we get

$$ \updelta F\left(y;\Delta y\right)={\displaystyle {\int}_a^b\underset{\epsilon \to 0}{ \lim}\frac{f\left(y+\epsilon \Delta y\right)-f(y)}{\epsilon}\mathrm{d}x={\displaystyle {\int}_a^b\frac{\mathrm{d}f}{\mathrm{d}y}\Delta y\mathrm{d}x}} $$

(27)

Since Eq. (27) must be zero for every Δy, we specifically choose Δy = df/dy, and the integrand becomes (df/dy)². The integral of this non-negative function is zero only if df/dy = 0, which is the condition for a minimum of F(y).

Now consider the minimization of F(y) subject to the constraint

$$ G(y)={\displaystyle {\int}_a^bg\left(y(x)\right)\mathrm{d}x-{G}_0=0} $$

(28)

where ${G}_0$ is some constant. The necessary condition for y to be a minimum is that there is a Euler-Lagrange multiplier C such that

$$ \updelta F\left(y;\Delta y\right)+C\updelta G\left(y;\Delta y\right)=0 $$

(29)

for every $\Delta y$. We insert Eqs. (25) and (28) into Eq. (29) and continue as with Eq. (27) above, which finally gives

$$ \frac{\mathrm{d}f}{\mathrm{d}y}+C\frac{\mathrm{d}g}{\mathrm{d}y}=0 $$

(30)

The constrained problem is solved by finding a function y and constant C such that Eqs. (28) and (30) hold.