1 Introduction

The main mechanical function of bone is to provide rigid support to muscle against pull forces during activity and to remain as light as possible for efficient locomotion [1]. To achieve this, bone must adopt the shape, topology and internal micro-structure to efficiently use the material [2]. Since [3] proposed that external forces influence bone micro-structure adaptation, many researchers developed bone re-generation and growth models by considering different factors which can be categorized into three groups: biomechanical models, structural optimization models, and optimal response models. Biomechanical researchers mostly addressed the mechanism of stimulus sensing and tissue remodeling to develop new frameworks through experimental data [4,5,6,7,8,9]. Structural optimization researchers developed regulatory mechanisms by minimizing an objective function such as strain energy density to analyze the effect of various parameters on bone adaptation or to design prosthesis [10,11,12,13,14,15]. The models derived based on the optimal response hypothesis assumes that bone adaptation is a continuous process and highly affected by temporal conditions [16, 17].

One of the most studied bone to which above bone micro-structure growth models have been applied is the femur, compared to which other equal load bearing bones like the pelvic bone have received less attention [11, 18]. Most researchers focused on developing models to understand the micro-structure growth of the bone, whereas the design of the global geometry of the bone has received little attention probably due to the complexity of the problem.

Although the pelvic bone has not been the active target of bone micro-structure growth models, Finite Element (FE) analysis of the pelvic bone is an active area of research [19,20,21,22,23]. Starting from the early works of Goel et al [19, 24] to calculate stresses in the pelvic bone using 3D linear isoparametric elements, FE analysis has been used to study multiple conditions affecting the mechanical behavior of the pelvic bone [22, 23, 25]. However, it remains an open problem to determine the extent to which the pelvic bone geometry is an optimal structure to resist deformation under mechanical loads acting on it. We think that the most suitable way to test this is to design a structure having the similar material, boundary, and loading conditions as the pelvic bone and then compare the geometries of the designed structure and the pelvic bone. Using structural optimization principles, the suitable approach of designing such an optimal structure is by posing a compliance or strain energy minimization problem with appropriate loading and boundary conditions and under the constraint of an upper limit on the mass (or volume for constant density) of the designed structure. Since the pelvic bone geometry is quite complicated (an irregularly shaped spread out bone with a hole in it) compared to other bones like the femur, instead of using shape optimization we use topology optimization (TO) to determine the geometry of an optimal structure under same loading and boundary conditions of the pelvic bone under a chosen activity. Our recent work demonstrates that optimally stiff structures similar to the pelvic bone can be designed using TO under mechanical loads of walking [26]. TO has already been used to design optimally stiff prostheses [15, 27], and the methodology adopted in this work may be extended in designing of pelvic prosthesis that require replacement of the entire hemi-pelvis [28, 29].

This work explores the design space of the hemi-pelvis under running gait cycle loads to understand the influence of the mechanical loads on the evolution of the shape and topology of the hemi-pelvis. Running gait cycle is chosen since muscles are more activated in running than in walking, implying greater body support forces in running [30,31,32]. Our previous work on walking [26] finds the optimal geometries of the hemi-pelvis under the loads of eight phases of walking gait cycle, which gives eight optimal geometries for a single walking cycle. Identifying a best optimal geometry among the eight for a possible prosthesis application is difficult, since all eight geometries are optimal solution for each phase. This motivated us to solve a multiple-load case optimization problem that considers the effect of the loads of all phases simultaneously. The aim of the current work is to obtain a optimal geometry for a running gait cycle using multiple-load case formulation. Experiments are conducted to verify simulation results of the pelvic bone obtained using OptiStruct®.

2 Methods

Figure 1
figure 1

Seven phase of the running gait cycle. The corresponding muscle and hip joint forces are given in table 1.

Full size image
Table 1 Magnitude of muscle and hip joint forces acting on pelvic bone during seven phases of running gait cycle using the OpenSim model of [37] for a human of weight 650 N.
Full size table

2.1 Topology optimization formulation

Topology Optimization (TO) presents the most generalized structural optimization approach as it has capability of not only exploring varied shapes and sizes, but different topologies as well for a given design domain [33]. Compliance minimization with volume constraint formulation of TO gives the possible stiffest structure under specified loading and boundary conditions for a given volume [34]. Compliance of a structure is defined as the total work done due to the external forces acting on it [33] and the optimization formulation is given as:

$$\begin{aligned} \qquad \qquad \text {minimize:}&\quad c = \mathbf {f}^T \mathbf {u}\nonumber \\ \qquad \qquad \text {subject to:}&\quad V \le V_{max}\nonumber \\ \qquad \qquad \mathbf {K} \mathbf {u}&= \mathbf {f} \end{aligned}$$
(1)

where c is compliance, \(\mathbf {f}\) is force vector, \(\mathbf {K}\) is stiffness matrix, \(\mathbf {u}\) is displacement vector, V is the volume of the structure and \(V_{max}\) is the maximum allowable volume [35]. For this work, \(V_{max}\) is equal to the volume of the natural hemi-pelvis. Force vector \(\mathbf {f}\) contains both hip joint reaction force and muscle forces acting on the pelvic bone during running. The running gait cycle is divided into seven phases [36] based on the contact of heel with ground and shown in figure 1. First phase of running is when the heel is in contact with ground, and the stance phases are second and third. The heel is just off from the ground in fourth phase, while the fifth and sixth phases are swing phases. The last phase where heel makes contact with ground is seventh phase. The mechanical forces on the pelvic bone during these seven phases of the running is not available in literature directly; hence, we use Opensim 3.0 software to obtain them. The OpenSim model of Hamner et al [37] is used to calculate the forces during these seven phases, whereas to obtain the direction of these forces a plugin called ‘MuscleForceDirection’ is used [38, 39].

Joint angles are calculated using inverse kinematics to minimize the error between experimental marker positions and modeled markers in the simulation. Joint moments are computed with residual reduction algorithm using inverse dynamics. A static optimization problem is formulated to compute the muscle forces that minimized the sum of square of each muscle activation. The accuracy of the OpenSim model was tested by [37] by comparing joint angles, joint moments and ground reaction forces with the literature [40, 41], and muscle forces and activations with the Electromyography data. We used this model without any modifications for obtaining the muscle forces of seven phases of running. The direction of muscle forces is obtained from the ‘MuscleForceDirection’ plugin in OpenSim [38, 39]. Table 1 presents the forces acting on the pelvic bone during the seven phases of running. More details regarding the creation and validation of the OpenSim model can be found in [37].

Equation 1 gives one optimal geometry for each phase, and a total of seven optimal geometries for one running gait cycle. However, if a designer has to design a structure experiencing a number of loading conditions, then to consider the simultaneous effect of all the loading cases, multiple-load case optimization formulation is used [11, 42]. The objective function in multiple-load case optimization is weighted compliance of the load cases and instead of one set of governing equation constraints, there are as many sets of governing equation constraints as the number of load cases. The multiple-load case problem formulation is:

$$\begin{aligned} \text {minimize:}&\quad c^{m}=\sum _{q=1}^{N_L}w_q\mathbf {f}^T_q \mathbf {u}_q \\ \text {subject to:}&\quad V \le V_{max}\nonumber \\ \qquad \qquad&\mathbf {K} \mathbf {u}_q = \mathbf {f}_q ; \qquad q = 1,2,...,N_L \nonumber \end{aligned}$$
(2)

where \(c^m\) is weighted compliance, \(\mathbf {f}_q\), \(\mathbf {u}_q\), \(w_q\) are force vector, displacement vector and weight factor corresponding to the \(q^{th}\) phase respectively, \(N_L\) is the number of phases in the gait cycle. The weight factors should satisfy the condition \(\sum _q^{N_L} w_q =1\) [11]. In multiple-load case formulation, the objective function is dependent on the specification of weights. In this work, we are motivated to define the weights on some physical basis and choose different criteria to calculate the same. The most trivial set of weights is uniform distribution, i.e., average of the phases in running gait cycle, case (i) in table 2. Since the running gait cycle is divided into seven phases [36], the fraction of the gait cycle at which each stance occurs can be calculated. We then calculate the fraction-gap between each stance and consider it as the duration of each phase. This duration forms the second set of weights, case (ii) in table 2. The normalized hip joint force magnitudes at the acetabulum [37] during each stance form the third set of weights, case (iii) in table 2. Next, we calculate the product of duration of phase and the hip joint force, i.e., the impulse which is physically relevant considering the momentum change during running. Hence the normalized impulse forms the fourth set of weights, case (iv) in table 2. Finally, considering the jerking movement during running, i.e., sudden change in accelerations, we are also interested to incorporate this factor in the weights. Hence, we consider the force sensitivity with respect to time, and the normalized force sensitivity forms the last set of weights, case (v) in table 2.

Table 2 Weights used for multiple-load case optimization.
Full size table
Figure 2
figure 2

Natural hemi-pelvis bone along with its components (iliac-crest and obturator foramen) and three joints (sacro-iliac joint, acetabulum and pubic symphysis).

Full size image
Figure 3
figure 3

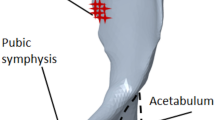
Design domain with boundary conditions, i.e., fixed boundary conditions (‘\(\Gamma _u\)’ shown in red hash), hip joint force (‘\(\Gamma _s\)’ shown in black dotted line), and muscle forces (‘balck dotted closed curves’). The muscle attachment areas (‘balck dotted closed curves’) and iliac-crest (‘\(\Omega _n\) shown in black solid curve), are non-design domains. The arrows represent forces acting on the pelvic bone (arrows are neither scaled to magnitude, nor show actual direction).

Full size image

2.2 Material modeling

Material modeling is required to define the stiffness and density (design variable) of the structure by using an interpolation technique. This work uses Solid Isotropic Material Penalization (SIMP) method [43]. The structure is discretized into finite elements and a penalization factor penalizes the density of each element to a continuous variable (that varies from 0 to 1) from a discrete variable (either 0 for void or 1 for solid). Using SIMP, the stiffness matrix can be defined as:

$$\begin{aligned} \mathbf {k}_e=\rho ^p \mathbf {k}_0, ~~0<\rho _{min}\le \rho \le 1 \end{aligned}$$
(3)

where \(k_e\) is modified elemental stiffness matrix, \(k_0\) is initial elemental stiffness matrix, p is penalization factor and \(\rho \) is design variable. The compliance using SIMP is given as,

$$\begin{aligned} c_e^m = \sum _{q=1}^{N_L}w_q (\mathbf {f}_e^T \mathbf {u}_e)_q&= \sum _{q=1}^{N_L}w_q (\mathbf {u}^T_e \mathbf {k}_e \mathbf {u}_e)_q\nonumber \\&=\sum _{q=1}^{N_L}w_q \rho ^p (\mathbf {u}^T_e \mathbf {k}_0 \mathbf {u}_e)_q \end{aligned}$$
(4)

where \(c_e^m\) is the elemental weighted compliance, \((\mathbf{f} ^T_e)_q\) is force vector of the \(e^{th}\) element for \(q^{th}\) phase and \((\mathbf{u} ^T_e)_q\) is displacement vector of the \(e^{th}\) element for \(q^{th}\) phase.

2.3 Sensitivity analysis

TO requires the calculation of sensitivities since many TO algorithms are based on convex optimization techniques [44]. Sensitivity analysis provides the variation of the objective function, i.e., compliance due to small change in the design variable, i.e., density and is defined as:

$$\begin{aligned} \frac{\partial c^m}{\partial \rho }&= \sum _{q=1}^{N_L}w_q\mathbf {f}^T_q \frac{\partial \mathbf {u}_q}{\partial \rho } = \sum _{q=1}^{N_L}w_q\mathbf{u} ^T_q \mathbf{K} \frac{\partial \mathbf {u}_q}{\partial \rho } \end{aligned}$$
(5)

From equation 2, the sensitivity of weighted compliance and weighted elemental compliance with respect to the design variable \(\rho \) is given as,

$$\begin{aligned} \frac{\partial \mathbf{K} }{\partial \rho } \mathbf{u} _q + \mathbf{K} \frac{\partial \mathbf{u} _q}{\partial \rho }&= 0 \Rightarrow \frac{\partial \mathbf{u} _q}{\partial \rho } = - \mathbf{K} ^{-1}\frac{\partial \mathbf{K} }{\partial \rho } \mathbf{u} _q \nonumber \\ \Rightarrow \frac{\partial c^m}{\partial \rho }&= -\sum _{q=1}^{N_L}w_q \mathbf{u} ^T_q \frac{\partial \mathbf{K} }{\partial \rho }{} \mathbf{u} _q \end{aligned}$$
(6)
$$\begin{aligned} \text {and} \quad \frac{\partial c_e^m }{\partial \rho }&= -\sum _{q=1}^{N_L}w_q (\mathbf{u} _e^T)_q \frac{\partial \mathbf{k} _e}{\partial \rho } (\mathbf{u} _e)_q \end{aligned}$$
(7)

Using SIMP method (equation 3), the sensitivity of the compliance \(c_e^m\) with respect to the design variable \(\rho \) is,

$$\begin{aligned} \frac{\partial c_e^m}{\partial \rho } = -\sum _{q=1}^{N_L}w_q p\rho _{e}^{p-1}(\mathbf{u} ^T_e)_q \mathbf{k} _0(\mathbf{u} _e)_q \end{aligned}$$
(8)

2.4 Filtering techniques

TO has numerical instabilities like mesh dependency and checker board problems [45, 46]. Filtering techniques are widely used to prevent these instabilities. This work uses the following filtering technique by modifying the sensitivities that are obtained from Eq. 8.

$$\begin{aligned} \frac{\partial \bar{c_e}^m}{\partial \rho _i} = \frac{1}{\rho _i \sum _{l=1}^{N} w_l} \sum _{l=1}^{N} w_l \rho _l \frac{\partial c_e^m}{\partial \rho _l} \end{aligned}$$
(9)

The weight factor \(w_l\) is defined as:

$$\begin{aligned}&w_l = r_{min} - dist(i,l),\nonumber \\&\{l\in N ~~|~~ dist(i,l)\le r_{min}\}, \quad l = 1,...,N \end{aligned}$$
(10)

where \(\frac{\partial \bar{c_e}^m}{\partial \rho _i}\) is the modified sensitivity of the \(i^{th}\) element that is obtained after using filtering technique, \(\frac{\partial c_e^m}{\partial \rho _l}\) is original elemental sensitivity of the \(l^{th}\) element, \(\rho _l\) is \(l^{th}\) element density, N is the total number of elements in the structure, dist(i, l) is the distance between the \(i^{th}\) and \(l^{th}\) elements and \(r_{min}\) is the filtering radius [33].

2.5 Design domain, boundary conditions, and optimization solver

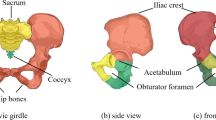
Pelvic bone is connected to three other bones through the sacro-iliac joint (with the sacrum), the acetabulum (with the femur) and the pubic symphysis (with the other pelvic bone) and these three joints are shown in figure 2. The design domain for topology optimization is shown in figure 3. The arrows represent the forces acting on the pelvic bone. In general, the topology optimization input is an arbitrary domain, but it is avoided in the current problem. The traction forces on the pelvic bone, i.e., muscle forces and hip joint force, are exerted through multiple muscle attachment areas and the acetabulum respectively (figure 3). Initial geometry of any arbitrary shape (for example, a cuboid) is avoided due to the following reasons:

  • Modeling the muscle attachment areas inside the cuboid involves the modeling of the replica surface of these muscle attachment areas; this increases the complexity of modeling; and meshing of these complex modeled areas is difficult.

  • The application of traction boundary conditions on inner elements is not allowed. The inner elements can take only body forces, while the boundary elements can take traction.

  • To avoid the convergence to a local optimal solution since OptiStruct®solver uses a convex optimization technique.

As explained earlier, the design domain (figure 3) is highly restricted by Dirichelt (fixed) and Neumann (force) boundary conditions. The Dirichelt boundary conditions are applied at the pubic symphysis and sacro-iliac joint since the joint deformations are negligible compared with that of the acetabulum. Neumann boundary conditions include two parts, i.e., hip joint force and muscle forces. The hip joint force is applied at the acetabulum [47]. Muscle applies active forces on pelvic bone through the muscle attachment areas and these areas also restrict the design domain. The muscle forces are obtained using the OpenSim running gait model of Hamner et al [37]. The direction of muscle forces are obtained from the ‘MuscleForceDirection’ plugin in OpenSim [38, 39]. The running gait cycle consists of seven phases [36]. Similar to our previous work [26, 48], the muscle attachment areas and iliac-crest are posed as non-design domains to prevent material removal from unwanted areas.

Figure 4
figure 4

Mesh convergence study of the input domain (figure 3) for topology optimization.

Full size image
Figure 5
figure 5

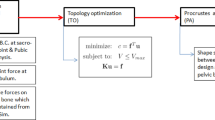
Schematic representation of the methodology used in this work. The input geometry and boundary conditions are supplied to topology optimization. Topology optimization generates the optimal geometries and these optimal geometries are compared with pelvic bone by measuring the shape similarity using Procrustes analysis. The top row shows the main steps (in bold boxes) involved in this work: Modeling input geometry and its boundary conditions, performing topology optimization, and measuring shape similarity using Procrustes analysis. The middle row shows inputs or outputs and formulations used in each step. The bottom row shows the pictorial representation of each step.

Full size image

The geometric model of the design domain from our previous works [49, 50] is used in the current work. The design domain is meshed with tetrahedral elements using Altair HyperMesh®software. Figure 4 presents the mesh convergence details of the design domain of the topology optimization. Based upon results from mesh convergence study, the design domain contains a total of 978, 112 tetrahedral elements and 163, 273 nodes. This work uses Altair OptiStruct ®software to solve Eqs. 1 and 2 [51]. The output from OptiStruct®is a density map over the design domain with densities for elements varying between 0-1, 0 for void, and 1 for a homogeneous isotropic solid. The final geometry is decided by the designer by selecting a threshold density below which everything is converted to void and above which everything is converted into solid. More details on the calculation of the threshold density are given in our previous work [26].

2.6 Procrustes analysis

This work uses Procrustes Analysis (PA) to calculate the shape similarity between two shapes (optimal geometry and natural hemi-pelvis) [52]. PA uses coordinate information of both optimal geometry and natural hemi-pelvis. The coordinates are obtained by meshing both the optimal geometry and natural hemi-pelvis. The coordinate data of either optimal geometry or natural hemi-pelvis is transformed as follows: 1) Removing translation component: The coordinates of the selected geometry (say optimal geometry) is subtracted by the mean of the coordinates. 2) Removing scaling component: The translated coordinate information is divided by the root mean squared distance of the coordinates to remove the scaling component. 3) Removing the rotational component: The coordinates obtained after removing the translation and scaling components is rotated with an optimal angle ‘\(\theta \)’ such that the sum of squared distance is the minimum between transformed optimal geometry and natural hemi-pelvis. The dissimilarity index ‘D’ is given as the normalized sum of squared distance between them. The compliment of ‘D’ is the similarity index ‘S’ and given as \(S=1-D\). The shape similarity value of the initial design domain is equal to 46.13%.

2.7 Combination of phases

In our previous work [26] we explored the design space of hemi-pelvis for walking gait loads by a user-feedback based design procedure which we termed as “combination of phases”. In this user-guided approach, the hemi-pelvis is considered an optimal structure that is the goal of optimization, and among the designs using topology optimization on each phase of gait cycle, the user selects those designs having high shape similarity with natural hemi-pelvis, and then applies loads of some other phase of gait cycle to get a new optimal design. In this work, we use the same procedure of combination of phases for seven phases of running gait cycle. Although, we had stated in our previous work [26] that achieving high shape similarity with natural hemi-pelvis is the objective for formulating an user-guided design procedure like “combination of phases”, a more physically reasoned explanation behind this design procedure is as follows: the timescale of the bone growth are in years whereas the timescale of activities of daily living like running are in seconds. During bone growth, the activities can occur many many times. It may be possible to have high influence of a few phases of an activity like running on bone growth compared to other phases of running, and these phases need not be sequential as the activity of running might occur many times over the period of bone growth. One can even extend this to specific phases of different activities that might occur many times during the overall period of bone growth. Thus, each of the seven phases of running lead to seven optimal geometries, among which the designer may select any one and apply load of remaining six phases to get a new geometry using optimization, and then further apply load of remaining five phases to get another optimal geometry, and so on. In this way, there can be \(7!=5040\) load sequences, from which only a very small set is selected based on high shape similarity of optimal geometries with the natural hemi-pelvis.

2.8 Summary of Methods

The pictorial summary of the methodology adopted in this work is presented in figure 5. The input design domain along with the boundary conditions are supplied to TO solver OptiStruct®. After successful convergence to a local optimum, OptiStruct®generates the optimal density plot as an output containing different values of the density ranging from void (\(\rho = 0.001\approx 0\)) to solid (\(\rho = 1\)). The optimal geometry is obtained from the optimal density plot by selecting a threshold density value (\(\rho _{th}\)) below which Optistruct®converts parts of the design to void and above which parts are converted to solid (\(\rho = 1\)). \(\rho _{th}\) is decided such that the volume of the optimal geometry is same as the volume of the hemi-pelvis. The obtained optimal geometry is compared with naural hemi-pelvis by measuring shape similarity between them using Procrustes analysis.

3 Results and discussions

This section presents the optimal design of pelvic bone for running gait cycle using topology optimization. The simulations are performed on a desktop computer with an Intel(R) Core i7, 3.60 GHz processor and 32 GB of RAM that consumes approximately 8 hours to converge to an optimal solution. In this work, material property of bone is assumed to be that of cortical bone with Young’s modulus = 17 GPa and Poisson’s ratio = 0.3.

3.1 Optimal design obtained from seven phases of running gait cycle

Figure 6(a) and (b) shows the optimal geometries and the stress distributions of the seven phases of the running gait cycle. Table 3 enlists the shape similarity index, compliance, maximum stress and maximum displacement of both the pelvic bone and optimal geometries. Phase I has the highest shape similarity index (70.88%), whereas phase II has the lowest shape similarity index (48.57%). Phases I, III and V create a hole in the lower portion of the pelvic bone and the remaining phases remove a layer of material. Phases I, III and V have a high magnitude of the hip joint force and the upper muscles (rectus femoris, iliacus, psoas and gluteus muscles), while the lower muscles (gemellus, semimembranosus, semitendinosus and adductor muscles) are inactive or have low magnitude. This creates high stresses in the upper portion than the lower portion (figure 6b). Hence, material removal occurs in the lower portion by creating a hole.

Figure 6
figure 6

(a) The optimal geometries of the pelvic bone obtained from topology optimization for each phase of running gait cycle. The red arrow represents the leg corresponding to which the muscle forces are calculated. (b) von-Mises stress distribution of the seven optimal geometries. The values in legend are in MPa.

Full size image
Table 3 Shape similarity index, compliance, maximum stress and maximum displacement of the seven optimal geometries and the pelvic bone during running gait cycle.
Full size table

Compliance of optimal geometries are lower than the pelvic bone, implying that optimal geometries are stiffer than the pelvic bone. Phase III has a high compliance value (405.91 N-mm) and phase II has a low compliance value (10.76 N-mm). Since phase III is a stance phase, the muscles and hip joint force are highly active and generates high-stresses throughout the optimal geometry, whereas the muscles are less active in phase IV and generates less number of high stress zones. From figure 6(b), it is clear that phase III and V have more high-stress zones (above 10 MPa) since these two are in stance phase, transfer of forces through the pelvic bone is high, resulting in high compliance values, whereas phase IV has less high-stress zones and produce low compliance. The hip joint force is low in phase V but compliance is high and the hip joint force in phase II is high but compliance is less. This is due to the presence of more high stress regions (red colour zones \(\sim 8.9-10\) MPa) in phase V and phase II has more number of low-stress zones (blue colour zones \(\sim 0-1\) MPa). As explained earlier, the hip joint force and the muscles are highly active in phases III and V that induces highest stresses in the optimal geometry, while phases II and IV has less number of active muscles and resulting in lowest values for both maximum stress and maximum displacement.

3.2 Multiple-load case optimization

The five optimal geometries obtained using the multi-load approach are shown in figure 7. The

shape similarity and compliance of the five optimal geometries using different weights in multi-load case optimization with the pelvic bone is presented in table 4. From the results (figure7, table 4), the optimal geometry obtained from case (ii) has the highest shape similarity (71.43%), whereas case (iii) has the lowest shape similarity (58.94%). For individual phases, I (70.88%), III (65.19%) and V (63.74%) have high shape similarity and weights of these phases are high in case (ii) that creates a hole in the lower portion. Even though case (iv) and (i) have a hole in the lower portion, the shape similarity is less than the case (ii) design due to the following reasons: Case (iv) design has a high number of surface dents in the ilium bone and, case (i) design hole is smaller in size than case (ii) hole. Case (ii) has the highest compliance (411.09 N-mm) and case (v) has the lowest compliance (164.75 N-mm). Compliance of the optimal geometry is also dependent on the weights of the phases. Phase III (405.91 N-mm) and V (396.66 N-mm) have high compliance values than the other phases. Since case (ii) has high weights for both phase III and phase V, it inherits higher compliance than all other cases.

Figure 7
figure 7

Five optimal geometries of the pelvic bone obtained from multiple-load case optimization of running gait cycle.

Full size image
Table 4 Shape similarity and compliance of the optimal geometries obtained from multiple-load case optimization along with the pelvic bone.
Full size table

3.3 Optimal design from combination of phases

We found that phases I, III, and V produce high shape similarity (70.88%, 65.19 %, and 63.74 % respectively) in the optimal geometries. In the “combination of phases” user-guided design approach, we select the design from one of the above phases (say phase I) and apply a load of another phase (say phase III) after patching the surface dents in the upper portion of the input to avoid convergence to local minimum [26]. For the running gait cycle, we have selected these three designs which give six loading sequences that are listed below:

  • (a): Phases I-III

  • (b): Phases I-V

  • (c): Phases III-I

  • (d): Phases III-V

  • (e): Phases V-I

  • (f): Phases V-III

The procedure for combination of phases I-III is explained pictorially in figure 8 which applies the loads of phase III on the output obtained from the loads of phase I. Figure 9 shows the six optimal geometries obtained from the combination of the phases (a)–(f). The shape similarity and compliance of both optimal geometries and the pelvic bone are presented in table 5. All six designs create a hole in the lower portion of the design since the individual phases I, III, and V have a hole in the optimal geometries. Phases I-III has high shape similarity value (76.23%). This might be because phase I and phase III have high shape similarity for individual loads. Phases V-I and phases V-III have low shape similarity values compared to other optimal geometries due to the presence of a large dent in the upper portion of the optimal geometries. The optimal geometry obtained from phases I-III has high compliance (403.52 N-mm) and phases III-I has low compliance (145.73 N-mm) since phase III and phase I generate high and low compliance respectively among the three phases (table 3 and figure 6b).

Figure 8
figure 8

Pictorial summary of optimal design under combination of phases I-III, i.e., loads of phase III are applied on the modified input obtained from phase I. The red arrow represents the leg corresponding to which the muscle forces are calculated. The shape similarity values are presented above the optimal geometries.

Full size image
Figure 9
figure 9

(a)-(f) are the six optimal geometries of the pelvic bone obtained from the combinations of phases of running.

Full size image
Table 5 Shape similarity and compliance of the optimal geometries obtained from combination of phases along with the pelvic bone.
Full size table

4 Experimental Validation

So far a computational procedure has been presented for optimal geometry of the pelvic bone for running gait. A detailed experimental validation using similar material, loading, and boundary conditions may be substituted by testing the hypothesis that the conclusions drawn using the computational procedure remain valid also in experiments. The testing hypothesis is:

“All the designs are based on compliance minimization and claim that these are stiffer than the pelvic bone geometry of same material.”

Figure 10
figure 10

Experimental setup for measuring stiffness of (a) pelvic bone and (b) optimal geometry (figure 9a). The fixed boundary conditions are imposed with cement mould at the upper part of the pelvic bone and load from the load cell is applied on the lower part of the pelvic bone.

Full size image
Figure 11
figure 11

Force vs. displacement plot for experimental data and simulation data using OptiStruct®for optimal geometry (figure9a) and the pelvic bone models made of PLA material.

Full size image

The chosen design for experimental testing is the optimal geometry given in figure 9(a) which we test for geometric stiffness and compare with the same of a pelvic bone model under the same loading and boundary conditions. Experiments are conducted on the Universal Testing Machine (UTM) for compression testing to measure the displacement for a given applied force. The details of the UTM (Model: SHIMADZU – AG-X plus) used in this work is as follows:

  • Loading Capacity: 50 kN

  • Load cells available: 50 kN

  • Testing speed range: 0.0005 to 1000 mm/min

  • Cross-head stroke measurement resolution: 1/48 \(\upmu \)m

  • Size (width \(\times \) depth \(\times \) height in mm): 955 \(\times \) 579 \(\times \) 1720

From the above specifications, it is clear that SHIMADZU – AG-X plus allows us to measure small displacements (order of microns) precisely. It is assumed that the cross-head stroke measurement to be a representative of deformation of the specimen under the loads.

The test specimens of the pelvic bone and optimal geometry (figure 9a) are fabricated with polylactic acid (PLA) using additive manufacturing (AM) with 100% infill density and 0.2 mm as the primary layer thickness. The experimental setup is shown in figure 10(a and (b) for pelvic bone and optimal geometry (figure 9a) respectively. The specimen is rigidly fixed at the upper part of the pelvic bone (near iliac-crest) by using a cement mould. The process of mould preparation is similar to mould preparation of casting process, except one difference. In casting, we keep the entire model (pattern) inside the sand mixture for making the exact replica of the model, whereas here only part of the model (where the fixed boundary conditions are applied) is kept inside the cement mixture.

A compression load of 12 N with 0.5 N/min as loading rate is applied from the UTM to the lower part of the pelvic bone. The same boundary condition and load are applied to both the pelvic bone and optimal geometry to measure the displacement. The experimental setup of this work is similar to the experimental setup of [21]. The measured displacement values are plotted against the applied force to calculate total stiffness which is the slope of the force vs. displacement (F-S) plot. Simulations are performed using OptiStruct®with the same loading and boundary conditions on both pelvic bone and optimal geometry (figure 9a) with PLA material properties. The F-S plots obtained from experiments are shown in figure 11 for both the pelvic bone and optimal geometry (figure 9a) after approximation with a straight line using linear regression analysis. The straight-line equation for pelvic bone is \(F=178.83 S\), and for the optimal geometry (figure 9a) the equation is \(F=254.06 S\). The overall stiffness value from the simulation and experiment for pelvic bone is 185.72 N-mm and 178.83 N-mm respectively, whereas for optimal geometry (figure 9a) total overall stiffness value is 274.21 N-mm and 254.06 N-mm for simulation and experiment respectively. The ratio of overall stiffness value between experiment and simulation is 0.93 for optimal geometry (figure 9a) and 0.96 for pelvic bone. The simulation results are in good agreement with experiments for both the optimal geometry (figure 9a) and the pelvic bone. From the results. it is concluded that the simulations are in good agreement with experiments, and the testing hypothesis “optimal geometries are stiffer than the natural pelvic bone geometry” is successfully verified.

5 Conclusions and future work

This work is the first attempt to explore the influence of mechanical loads on the evolution of shape and topology of the pelvic bone for running gait cycle. We try to understand this by posing a stiff structure design problem using TO. Our work is also among the first attempts to compare synthesized designs with its natural counterpart by measuring shape similarity. Two optimal design strategies are followed, the multiple-load case approach and the combination of phases approach. Our results show that optimal stiff structures can be designed having good shape similarity with the pelvic bone (highest shape similarity being 76.23%) and new topologies can be generated under running gait loads. The claim of optimal stiffness is validated using compression test experiment.

Future research will focus on following issues: Our immediate concern is to explore how to incorporate bone micro-structure models into our TO formulation. Current work is limited by capabilities of OptiStruct®software which uses a SIMP model from which the final geometry is obtained by converting all material to full solid above a user defined threshold density. In this method, all heterogeneity in the optimal designs are lost, which is contrary to bone micro-structure that is mostly heterogeneous. An alternative homogenization based approach may yield better results for hemi-pelvis bone micro-structure design. Thus, a combined local bone micro-structure optimization along with bone global geometry optimization as presented in current work would lead to more realistic exploration of the influence of mechanical loads on shape and topology of the pelvic bone. Further, different biologically relevant objective functions like metabolic cost which are not available in the standard objective function library of OptiStruct®software should be explored to consider more realistic design objectives. Combining the loads of different activities such as walking and running with suitable weights can also be explored to study the influence of muscle forces on evolution of global geometry of the pelvic bone.