Collision of nonlinear waves in logotropic system with a Coulomb-type friction

Abstract

In this article, we consider the logotropic system of gasdynamics with a Coulomb-type friction to explore all possible collisions of elementary waves. We discuss the elementary waves and their properties in the phase plane to describe the exact Riemann solution. Further, we analyze all possible cases of the elementary wave interactions between same and different families of waves in the phase plane employing the solution of the Riemann problem.

1 Introduction

The theory of hyperbolic quasilinear conservation laws has variety applications in the field of gas dynamics, oil industries, applied science, engineering physics, multiphase flows and etc. It can be noted that the conservation of mass, momentum and energy form a common starting point of this study. However, in terms of field variables these reduce to partial differential equations (PDEs) under quite natural assumptions. In most of the cases, these PDEs are either quasilinear or nonlinear with source terms. Therefore, it is not easy to understand the solution and their properties as in the context of linear theory. Conservation laws are system of PDEs which can be written in the form of divergence. There are many physical phenomena which are modeled by the systems of conservation laws those are hyperbolic in nature. Hence, it is very interesting and challenging task to study the mathematical theory of hyperbolic conservation laws. Nowadays, the study of Riemann problem and wave interactions becomes very much popular in the theory of hyperbolic quasilinear PDEs.

The Riemann problem is a particular case of the Cauchy problem where the initial data is piecewise constant and having a single jump discontinuity. In order to construct the solution to the general initial value problem by exploiting the random choice method [1], the solution of local Riemann problem plays a very important role. In general, the solution of Riemann problem consists of shock wave, rarefaction wave and contact discontinuity which are called as elementary waves. The study of Riemann problem exhibits some fundamental properties of the elementary waves and detailed picture of solution. Therefore, this study has its own significance due to its wide practical applications. So, the researchers are attracted towards this topic and analyze the solution to the Riemann problem for the system of conservation laws and it becomes a very important topic in the context of quasilinear hyperbolic conservation laws.

In the last few decades, many researchers have been attracted towards the study of wave interactions for hyperbolic system of conservation laws due to its wide practical applications. Minhajul et al [2] studied the Riemann problem and collision between weak shocks in two-phase flows which describes isentropic drift-flux model. Kuila and Raja Sekhar [3] established Von Neumann’s result related to overtaking of two weak shocks belong to same family in the context of drift-flux isothermal multi-phase flows. Raja Sekhar and Sharma [4] discussed the existence of vacuum state and wave interactions briefly in isentropic magnetogasdynamics. By exploiting characteristic analysis methodology, elementary wave interactions in ideal magnetogasdynamics have been analyzed by Liu and Sun [5]. Sen et al [6] discussed stability of Riemann solutions and their asymptotic behaviour for system of strictly hyperbolic conservation laws. Collision of weak discontinuity with contact discontinuity and shock in isothermal drift-flux model have been analyzed in [7].

There are several interesting ways to study the problem of wave interactions among which phase plane analysis and characteristic analysis are widely adopted by the researchers. For example, elementary wave interactions for diverse practical problems [8, 9] have been analyzed using the phase plane analysis. The collision of elementary classical waves and stability analysis of Riemann solution for various physical problems have been investigated in [10, 11] using the method of characteristic analysis. For basic concepts on analysis of nonlinear waves in the context of hyperbolic quasilinear systems we refer [12,13,14]. Sun [15] constructed solutions for one-dimensional traffic flow problem when initial data consist of three constant states. Singh and Jena [16] computed transmitted and reflected wave amplitudes after the interaction between strong shock and acceleration wave in reacting polytropic gases. Classes of exact solutions to generalized Riemann problem for traffic flow model have been developed in [17] by using differential constraint method. A class of double wave solutions to nonlinear model of extended thermodynamics with six fields is determined and nonlinear wave interactions have been illustrated by Curro and Manganaro [18]. Chaudhary and Singh [19] established existence and uniqueness of Riemann solution for isentropic dusty gas flows and wave interactions are discussed. Stability of Riemann solutions are proved in [20] for the chromatography system under the small perturbations of local Riemann data. Sen et al [21] studied stability of Riemann solution, which consists of classical waves and delta shock, for strictly hyperbolic conservation laws system. Nonlinear wave interactions for a Temple-class hyperbolic system of conservation laws consisting of three scalar equations have been analyzed by Wei and Sun [22]. Zhang and Zhang [23] constructed the global structure of solutions through the nonlinear wave interactions investigation.

In the current study, we are concerned with the elementary wave interactions for Euler system with logarithmic equation of state and Coulomb type friction terms. The system of PDEs can be expressed by balance laws of the following form [24]

$$\begin{aligned} \begin{aligned}&\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial x}(\rho v)=0,\\&\frac{\partial }{\partial t}(\rho v)+\frac{\partial }{\partial x}(\rho v^2+A\ln \rho )=\eta \rho , \end{aligned} \end{aligned}$$

(1)

where the independent variables x and t denote the space and time, respectively, while the dependent variables $\rho$ and v, respectively, denote the density and velocity of the gas. Here, A and $\eta$ are positive constant parameters. When $\eta = 0$, the system of PDEs has been introduced in the area of astrophysics to study various properties of molecular clouds which may not be well understood in general for the case of isothermal distribution.

The logarithmic equation of state is used to investigate the logotropic dark fluid as a unification of dark matter and dark energy [25,26,27]. The system (1) can be reduced to homogeneous conservative form through a new state variable $w(x,t)=v(x,t)-\eta t$ as done in [28] and the corresponding conservative form is given by

$$\begin{aligned} \begin{aligned}&\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial x}(\rho (w+\eta t))=0,\\&\frac{\partial }{\partial t}(\rho w)+\frac{\partial }{\partial x}(\rho w(w+\eta t)+A\ln \rho )=0. \end{aligned} \end{aligned}$$

(2)

The Riemann initial data for the system (2) is given by

$$\begin{aligned} {(\rho ,w)(x,0)}= {\left\{ \begin{array}{ll} {(\rho _l,w_l)}, &{} \text {if}\, x<0, \\ {(\rho _r,w_r)}, &{} \text {if}\, x>0, \end{array}\right. } \end{aligned}$$

(3)

where $\rho _l$, $w_l$, $\rho _r$ and $w_r$ are constants. For the system (2)-(3), an exact Riemann solver has been developed in [24]. Recently, the authors in [29] discussed the limiting behaviour of the solution to the Riemann problem (1) and (3). The solution of the original Riemann problem (1) and (3) can be determined from the solution of (2) and (3) by substituting the value of new variable $(\rho ,v)(x,t)=(\rho ,w+\eta t)(x,t)$. In the present work, our main objective is to study various possible wave interactions of the elementary waves of (2) in the phase plane. The motivation of this study is to analyse the wave interactions problems to the nonhomogeneous hyperbolic system with the logotropic equation of state because of its various practical applications in the field of aerodynamics, cosmology, engineering physics and astrophysics. To the best of our knowledge, no one has attempted this type of wave interactions for the system (1) till now.

Organization of the rest of this paper is as follows. In section 2, we recall the elementary waves of (2) and their properties very briefly. In section 3, we discuss in detail about the interactions between elementary waves for all possible cases in the phase plane. Finally, a brief conclusions are drawn in section 4.

2 Preliminaries

The quasilinear form of the system (2) can be written as

$$\begin{aligned} \frac{\partial V}{\partial t}+A(V)\frac{\partial V}{\partial x}=0. \end{aligned}$$

(4)

Here, the primitive variable V and the Jacobian matrix A(V) are, respectively, given by

$$\begin{aligned} V= \begin{pmatrix} \rho \\ w \end{pmatrix},\,\, A(V)= \begin{pmatrix} w+\eta t &{} \rho \\ \frac{A}{\rho ^2}&{} w+\eta t \end{pmatrix} \cdot \end{aligned}$$

The eigenvalues of the Jacobian matrix A(V) are given by

$$\begin{aligned} \lambda _1=w+\eta t-\sqrt{\frac{A}{\rho }}\,\,\, \, \text {and} \,\,\,\, \lambda _2=w+\eta t+\sqrt{\frac{A}{\rho }}. \end{aligned}$$

(5)

The respective eigenvectors corresponding to the eigenvalues are

$$\begin{aligned} r^1=\left( -\rho , \sqrt{\frac{A}{\rho }}\right) ^{Tr}\,\,\, \text {and} \,\,\,r^2=\left( \rho , \sqrt{\frac{A}{\rho }}\right) ^{Tr} \end{aligned}$$

(6)

where Tr denotes the transposition. It can be noted that both the characteristic fields are genuinely nonlinear as $\nabla \lambda _i\cdot r^i\ne 0 \, (i=1,2)$. Hence, the solution of the Riemann problem consists of either shock wave (bounded discontinuous solution) or rarefaction wave (continuous solution). The Riemann invariants corresponding to these characteristic fields are, respectively, given by

$$\begin{aligned} 1-Riemann \,invariant\, \Pi _1=w-2\sqrt{\frac{A}{\rho }}, \end{aligned}$$

(7)

$$\begin{aligned} 2-Riemann \,invariant\, \Pi _2=w+2\sqrt{\frac{A}{\rho }}. \end{aligned}$$

(8)

We have already seen from the characteristic analysis that the solution of the Riemann problem consists of shock and rarefaction waves. Now, we discuss some properties of these two elementary waves very briefly. For more details about the elementary waves corresponding to the system (2), one can refer [24].

2.1 Shock waves

Shock wave is a discontinuous solution of the system (2) satisfying the Rankine-Hugoniot jump conditions and Lax entropy conditions. Suppose $\sigma$ denotes the speed of shock then the Rankine-Hugoniot jump conditions across the shock wave are given by

$$\begin{aligned} \begin{aligned} \sigma [\rho ]=[(\rho (w+\eta t))],\\ \sigma [\rho w]=[\rho w(w+\eta t)+A\ln \rho ], \end{aligned} \end{aligned}$$

(9)

where $[V]=V_l-V_r$, $V_l = V(x(t)-0, t)$ and $V_r = V(x(t)+0, t)$, denotes the jump of V across the shock. Suppose $V=(\rho , w)$ and $V_l=(\rho _l,w_l)$ indicate the right and left-hand states respectively. If $\sigma =0$, then we get the trivial solution $V=V_l$. So, we assume $\sigma \ne 0$ and the 1-shock curve passing through $V_l$ is denoted by $S_1(V_l)$ which satisfies the following

$$\begin{aligned} {S_1(V_l):}= {\left\{ \begin{array}{ll} w=w_l-\sqrt{A(\frac{1}{\rho _l}-\frac{1}{\rho })(\ln \rho -\ln \rho _l)}, \\ \sigma =\frac{\rho w-\rho _lw_l}{\rho -\rho _l}+\eta t,\\ w<w_l, \rho _l<\rho . \end{array}\right. } \end{aligned}$$

(10)

Similarly, 2-shock curve passing through $V_l$ is represented by $S_2(V_l)$ which is given by

$$\begin{aligned} {S_2(V_l):}= {\left\{ \begin{array}{ll} w=w_l-\sqrt{A(\frac{1}{\rho _l}-\frac{1}{\rho })(\ln \rho -\ln \rho _l)}, \\ \sigma =\frac{\rho w-\rho _lw_l}{\rho -\rho _l}+\eta t,\\ w<w_l, \rho _l>\rho . \end{array}\right. } \end{aligned}$$

(11)

Figure 1

Elementary waves in $(\rho ,w)$-plane.

One can easily prove the following properties of the shock curve and we explore these properties in the succeeding sections.

Lemma 1

The 1-shock curve, $S_1$, is monotonically decreasing and convex whilst the 2-shock curve, $S_2$, is monotonically increasing and concave.

2.2 Rarefaction waves

Using the property of Riemann invariants (7)-(8) across the rarefaction wave region, the 1-rarefaction wave curve through $V_l$ is denoted by $R_1(V_l)$ and represented by

$$\begin{aligned} {R_1(V_l):}= {\left\{ \begin{array}{ll} w=w_l-2\sqrt{\frac{A}{\rho _l}}+2\sqrt{\frac{A}{\rho }}, \\ \frac{dx}{dt}=\lambda _1=w+\eta t-\sqrt{\frac{A}{\rho }},\\ w\ge w_l, \rho _l\ge \rho . \end{array}\right. } \end{aligned}$$

(12)

In the same manner, the 2-rarefaction wave curve through $V_l$ is represented by $R_2(V_l)$ and expressed as

$$\begin{aligned} {R_2(V_l):}= {\left\{ \begin{array}{ll} w=w_l+2\sqrt{\frac{A}{\rho _l}}-2\sqrt{\frac{A}{\rho }}, \\ \frac{dx}{dt}=\lambda _2=w+\eta t+\sqrt{\frac{A}{\rho }},\\ w\ge w_l, \rho _l\le \rho . \end{array}\right. } \end{aligned}$$

(13)

One can easily prove the following properties of the rarefaction wave curve and these can be exploited in the succeeding sections.

Lemma 2

The 1-rarefaction curve, $R_1$, is convex and monotonically decreasing whilst the 2-rarefaction curve, $R_2$, is concave and monotonically increasing.

Using the properties of elementary waves we can easily prove the following theorem.

Theorem 1

The curves of shock and rarefaction waves of same family, say, $S_1$ and $R_1$ (respectively, $S_2$ and $R_2$) have the second order contact at $V_l$.

2.3 Solution structure of Riemann problem

Let us consider the Riemann problem for (2) with initial data given by

$$\begin{aligned} {V(x,0)}= {\left\{ \begin{array}{ll} {V_l}, &{} \text {if}\, x<0, \\ {V_r}, &{} \text {if}\, x>0. \end{array}\right. } \end{aligned}$$

(14)

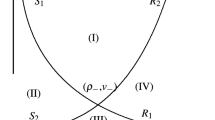
It is observed from figure 1 that the elementary waves divide the phase plane into four disjoint regions namely, I, II, III and IV. Depending on the position of $V_r$, the solution of Riemann problem can be constructed for a given $V_l$. For example, if $V_r$ lies in region I, then $V_l$ can be connected to $V_r$ by a 1-shock $S_1(V_l)$ followed by a 2-rarefaction wave $R_2(V_l)$, i.e., the Riemann solution involves 1-shock and 2-rarefaction wave. Similarly, if $V_r\in II$, solution of Riemann problem contains a 1-shock followed by a 2-shock. Consequently, if $V_r\in III$ then the solution of Riemann problem consists of a 1-rarefaction followed by a 2-shock wave. Finally, if $V_r\in IV$ then the Riemann solution possess of a 1-rarefaction followed by a 2-rarefaction wave. Therefore, we can state the following theorem without proof.

Theorem 2

If $V_l, V_r\in \mathbb {R}^+\times \mathbb {R}$ with $V_l$ fixed and $V_r$ is allowed to vary then the Riemann problem is solvable if and only if $V_r$ lies on any one of the four regions I, II, III and IV.

3 Elementary wave interactions

In order to determine all possible cases of wave interactions for the system (2), we consider the following initial data with three piecewise constant states

$$\begin{aligned} {V(x,0)}= {\left\{ \begin{array}{ll} {V_l}, &{} \,-\infty<x<x_{-}, \\ {V_m}, &{}\, x_{-}<x<x_{+},\\ {V_r}, &{}\, x>x_{+}, \end{array}\right. } \end{aligned}$$

(15)

where $x_{-}$, $x_{+}$ are arbitrary real numbers and we choose $V_m$ and $V_r$ with reference to $V_l$. Therefore, with this choice of data (15) with system (2) leads to two Riemann problems locally at $x_{-}$ and $x_{+}$. An elementary wave of the first Riemann problem may interact with an elementary wave of the second Riemann problem and at the time of interaction a new Riemann problem is formed. In this article, the symbol $S_2R_1\Rightarrow R_1S_2$ indicate that a 2-shock, $S_2$, associated with the first Riemann problem which connects $V_l$ to $V_m$, collide with 1-rarefaction wave, $R_1$, corresponding to the second Riemann problem which connects $V_m$ to $V_r$ and the collision generates a new Riemann problem with a left hand state $V_l$ and a right hand state $V_r$ and the solution of this new Riemann problem consists of a 1-rarefaction wave, $R_1$, and a 2-shock wave $S_2$ (i.e., $R_1S_2$). There are four possible cases of collisions of elementary waves corresponding to various families which are $R_2R_1$, $R_2S_1$, $S_2R_1$, and $S_2S_1$ whilst there are six possible cases of collisions of elementary waves corresponding to the same family which are $R_1S_1$, $S_1S_1$, $S_1R_1$, $S_2S_2$ $R_2S_2$ and $S_2R_2$.

Figure 2

Collision of $S_2S_1$.

3.1 Wave interactions between different families of elementary waves

• (i) Collision of two shocks ($S_2S_1$):

  Let us assume that $V_l$ and $V_m$ are connected by $S_2$ associated with the Riemann first problem and $V_m$ and $V_r$ are connected by $S_1$ corresponding to the second Riemann problem. Therefore, for a fixed given $V_l$, we choose $V_m$ and $V_r$ in such a way that $\rho _m<\rho _l$, $w_m= w_l-F(\rho , \rho _l)$ and $\rho _m < \rho _r, w_r = w_m-F(\rho _r, \rho _m)$ where $F(a,b)=\sqrt{A\left( \frac{1}{a}-\frac{1}{b}\right) (\ln b-\ln a)}$. One can verify from the Lax entropy condition that

  $$\begin{aligned} \sigma _2(V_l,V_m)>\lambda _2(V_m)>\lambda _1(V_m)>\sigma _1(V_m,V_r). \end{aligned}$$

  (16)

  Therefore, 2-shock corresponding to first Riemann problem moves faster than the 1-shock of the second Riemann problem. Hence, interaction will take place and $S_2$ overtakes $S_1$ after a finite time. In order to solve this problem, we need to determine the region in which $V_r$ lies with respect to $V_l$. Now, we show that for any given arbitrary state $V_l$, the curve $S_1(V_l)$ lies above the curve $S_1(V_m)$ which implies that the state $V_r\in II$. In order to prove this, it is enough to show that $F(\rho _m, \rho _l)+F(\rho _m, \rho )- F(\rho _l, \rho ) > 0$ for $\rho < \rho _l$ and $\rho _m < \rho$.

  We assume that $F(\rho _m, \rho _l)+F(\rho _m, \rho )- F(\rho _l, \rho ) \le 0$ and we prove the inequality by method of contradiction. Therefore, we have

  $$\begin{aligned} F^2(\rho _m, \rho _l)+F^2(\rho _m, \rho )+2F(\rho _m, \rho _l)F(\rho _m, \rho )\le F^2(\rho _l, \rho ) \end{aligned}$$

  which implies that

  $$\begin{aligned} \begin{aligned}&A\left( \frac{1}{\rho _l}-\frac{1}{\rho _m}\right) \big (\ln \rho _m-\ln \rho \big )+A\left( \frac{1}{\rho }-\frac{1}{\rho _m}\right) \big (\ln \rho _m-\ln \rho _l\big )\\ {}&+2F(\rho _m, \rho _l)F(\rho _m, \rho )\le 0. \end{aligned} \end{aligned}$$

  (17)

  For $\rho>\rho _l>\rho _m$, the left hand side of (17) is positive, which is a contradiction and therefore $F(\rho _m, \rho _l)+F(\rho _m, \rho )- F(\rho _l, \rho ) > 0$. Further, if $\rho _l>\rho >\rho _m$ then also the left hand side of inequality (17) is positive as $A\left( \frac{1}{\rho _l}-\frac{1}{\rho _m}\right) \big (\ln \rho _m-\ln \rho \big )>0$ and $A\left( \frac{1}{\rho }-\frac{1}{\rho _m}\right) \big (\ln \rho _m-\ln \rho _l\big )>0$. Therefore, $V_r$ lies in the region II and hence the interaction result is $S_2S_1\Rightarrow S_1S_2$. The graphical representation for this case is drawn in figure 2.

• (ii) Interaction of 2-shock and 1-rarefaction $(S_2R_1)$:

  Here, we consider $V_m$ and $V_r$ with reference to a given $V_l$ in such a way that $V_m\in S_2(V_l)$ and $V_r\in R_1(V_m)$. It follows that, $\rho _m<\rho _l$ , $w_m= w_l-F(\rho , \rho _l)$ and $\rho _r\le \rho _m$, $w_r=w_m-2\sqrt{\frac{A}{\rho _m}}+2\sqrt{\frac{A}{\rho _r}}$. One can evaluate that $\sigma _2(V_l,V_m)-\lambda _1(V_m)=\frac{\rho _l(w_l-w_m)}{\rho _l-\rho _m}+\frac{A}{\sqrt{\rho _m}}>0$. Therefore, 1-rarefaction has less speed compare to 2-shock which leads $S_2$ to overtake $R_1$ after a finite time. In order to prove that $V_r$ lies in the region III, it is enough to show that $F(\rho , \rho _l)-2\sqrt{\frac{A}{\rho _l}}+2\sqrt{\frac{A}{\rho _m}}>0$ for $\rho <\rho _m\le \rho _l$ which is in fact true as left hand side is always positive for $\rho <\rho _m\le \rho _l$. Therefore, $R_1(V_m)$ lies below the curve $R_1(V_l)$ and hence $V_r$ lies in region III. So, the result of interaction is $S_2R_1\Rightarrow R_1S_2$ as depicted in figure 3.

• (iii) Interaction between two rarefaction waves ($R_2R_1$):

  In this case, $V_m\in R_2(V_l)$ and $V_r\in R_1(V_m)$. Therefore, for a given fixed $V_l$, we choose $V_m$ and $V_r$ in such a way that $\rho \ge \rho _l$, $w_m=w_l+2\sqrt{\frac{A}{\rho _l}}-2\sqrt{\frac{A}{\rho _m}}$ and $\rho _r\le \rho _m$, $w_r=w_m-2\sqrt{\frac{A}{\rho _m}}+2\sqrt{\frac{A}{\rho _r}}$. Since, $\lambda _2(V_m)>\lambda _1(V_m)$, the tail of 2-rarefaction wave of first Riemann problem has greater speed than the head of 1-rarefaction wave of second Riemann problem. Hence, interaction will take place after a finite time. Here, we prove that curve $R_1(V_l)$ lies below $R_1(V_m)$. As, $4\left( \sqrt{\frac{A}{\rho _l}}-\sqrt{\frac{A}{\rho _m}}\right) >0$ whenever $\rho _m\ge \rho _l$, hence $R_1(V_l)$ lies below the curve $R_1(V_m)$ for any $\rho _r$ satisfying $\rho _m\ge \rho _l\ge \rho _r$ or $\rho _l\le \rho _r\le \rho _m$. Therefore, we can conclude that the result of interaction is $R_2R_1\Rightarrow R_1R_2$ and the computed result is illustrated in figure 4.

• (iv) Collision of 2-rarefaction and 1-shock ($R_2S_1$):

  Here, $V_m\in R_2(V_l)$ and $V_r\in S_1(V_m)$. Hence, we set $V_m$ and $V_r$ with reference to a given $V_l$ in such a manner that $\rho _m\ge \rho _l$, $w_m=w_l+2\sqrt{\frac{A}{\rho _l}}-2\sqrt{\frac{A}{\rho _m}}$ and $\rho _m < \rho _r , w_r = w_m-F(\rho _r , \rho _m)$. From Lax entropy condition we have, $\lambda _2(V_m)>\sigma _1(V_m,V_r)$, which follows that the trailing end of $R_2$ corresponding to the Riemann first problem has more speed compare to $S_1$ associated with Riemann second problem. Thus, $R_2$ overtakes $S_1$ and interaction will take place after a finite time. Now for a given $V_l$, we show that $V_r\in I$. In order to prove this, it is sufficient to show that $2\sqrt{\frac{A}{\rho _l}}-2\sqrt{\frac{A}{\rho _m}}+F(\rho ,\rho _l)-F(\rho ,\rho _m)>0.$ Clearly, $2\sqrt{\frac{A}{\rho _l}}-2\sqrt{\frac{A}{\rho _m}}>0$ for $\rho _m\ge \rho _l$ and an easy computation yields $F(\rho ,\rho _l)-F(\rho ,\rho _m)>0$. Therefore, $S_1(V_m)$ lies above the curve $S_1(V_l)$ and hence the result of interaction is $R_2S_1\Rightarrow S_1R_2$ and the computed result is exhibited in figure 5.

Figure 3

Collision of $S_2R_1$.

Figure 4

Collision of $R_2R_1$.

Figure 5

Collision of $R_2S_1$.

3.2 Interaction of elementary waves of same family

• (i) 1-rarefaction overtakes 1-shock ($R_1S_1$):

  In this case, $V_l$ and $V_m$ are connected by a 1-rarefaction of first Riemann problem while the states $V_m$ and $V_r$ are connected by 1-shock of second Riemann problem. In other words, for a given $V_l$, we choose $V_m$ and $V_r$ in such a way that $\rho _m\le \rho _l$, $w_m=w_l-2\sqrt{\frac{A}{\rho _l}}+2\sqrt{\frac{A}{\rho _m}}$ and $\rho _m<\rho _r$, $w_r=w_m-F(\rho _m,\rho _r)$. From Lax entropy inequality, we have $\lambda _1(V_m)>\sigma _1(V_l,V_m)$ which indicates that the trailing end of $R_1$ corresponding to Riemann first problem has more speed compare to $S_1$ associated with Riemann second problem. So, $R_1$ collides with $S_1$ and interaction occurs after a finite time. Now, we show that the curve $S_1(V_m)$ lies below the curve $R_1(V_l)$ for $\rho _m<\rho \le \rho _l$. In order to complete the argument, it is sufficient to establish that

  $$\begin{aligned} 2\left( \sqrt{\frac{A}{\rho _m}}-\sqrt{\frac{A}{\rho }}\right) -F(\rho ,\rho _m)<0, \end{aligned}$$

  (18)

  for $\rho _m<\rho \le \rho _l$ which is equivalent to the inequality

  $$\begin{aligned} 2\left( \sqrt{\frac{\rho }{\rho _m}}-1\right) -\sqrt{\left( 1-\frac{\rho }{\rho _m}\right) \ln \frac{\rho _m}{\rho }}<0. \end{aligned}$$

  (19)

  In order to prove (19), let $y=\frac{\rho }{\rho _m}$ then $\rho _m<\rho \le \rho _l$ implies $1<y\le \frac{\rho _l}{\rho _m}$. Therefore, we have to prove that $2(\sqrt{y}-1)-\sqrt{(y-1)\ln y}<0$ for $y>1$. One can show that $\ln y<y-1$ for $y>1$ using the monotonicity of the function $g_1(y)=y-\ln y$. Further, by applying Lagrange mean value theorem on the interval [1, y] to the function $g_2(y)=\sqrt{y}$, we obtain $\frac{\sqrt{y}-1}{y-1}<\frac{1}{2}$ and which implies the inequality (19) and hence (18) for $\rho _m<\rho \le \rho _l$.

  Next, we prove that the curve $S_1(V_l)$ lies above the curve $S_1(V_m)$ whenever $\rho _m<\rho _l\le \rho$. In order to prove this it is sufficient to show that

  $$\begin{aligned} 2\left( \sqrt{\frac{A}{\rho _m}}-\sqrt{\frac{A}{\rho _l}}\right) -F(\rho ,\rho _m)+F(\rho , \rho _l)<0. \end{aligned}$$

  (20)

  In order to prove (20), let $g_3(\rho )=2\left( \sqrt{\frac{A}{\rho _m}}-\sqrt{\frac{A}{\rho _l}}\right) -F(\rho ,\rho _m)+F(\rho , \rho _l)$. Then from (18), it is clear that $g_3(\rho _l)<0$. Moreover, $\frac{dg_3}{d\rho }=\frac{dF}{d\rho }(\rho , \rho _l)-\frac{dF}{d\rho }(\rho ,\rho _m)<0$ as $F(\rho ,\rho _m)$ is a decreasing function of $\rho _m$ for $\rho _m<\rho$. Therefore, $g_3(\rho )<g_3(\rho _l)<0$ which proves the inequality (20) and hence $S_1(V_m)$ lies below the curve $S_1(V_l)$ for $\rho _m<\rho _l\le \rho$.

  Lastly, we prove that $S_1(V_m)$ intersects $S_2(V_l)$ at some point, say, $V_1=(\rho _1,w_1)$ with $\rho _m<\rho _1\le \rho _l$. To prove this, let us consider the function $g_4(\rho )=2\left( \sqrt{\frac{A}{\rho _m}}-\sqrt{\frac{A}{\rho _l}}\right) -F(\rho ,\rho _m)+F(\rho , \rho _l)$ with $\rho _l\ge \rho \ge \rho _m$. Therefore, $g_4(\rho _l)<0$ and $g_4(\rho _m)>0$ and hence by applying monotonicity and the intermediate value theorem of the function we can find a unique $\rho _1$ such that $g_4(\rho _1)=0$ satisfying $\rho _m<\rho _1\le \rho _l$. Therefore, the point of intersection between $S_1(V_m)$ and $S_2(V_l)$ is uniquely obtained. Now, based upon the choice of $\rho _r$, there will be three possible cases which are

  • (a) When $\rho _r<\rho _1$ then $V_r\in III$ and the result of interaction is $R_1S_1\Rightarrow R_1S_2$.

  • (b) When $\rho _r=\rho _1$ then $V_r\in S_2(V_l)$ and the interaction results as $R_1S_1\Rightarrow S_2$, i.e., the wave of second family occurs after the collision of two 1-family waves.

  • (c) When $\rho _r>\rho _1$ then $V_r\in II$ and consequently the interaction leads to $R_1S_1\Rightarrow S_1S_2$. The corresponding configuration of wave interactions are illustrated in figure 6.

• (ii) 1-shock overtakes 1-rarefaction ($S_1R_1$):

  In this case, $V_l$ is connected to $V_m$ by 1-shock of first Riemann problem and $V_m$ is connected to $V_r$ by a 1-rarefaction wave of second Riemann problem. Therefore, for a given $V_l$, we choose $V_m$ and $V_r$ are such that $\rho _l<\rho _m$, $w_m=w_l-F(\rho _l,\rho _m)$ and $\rho _r\le \rho _m$, $w_r=w_m-2\sqrt{\frac{A}{\rho _l}}+2\sqrt{\frac{A}{\rho }}$. Lax entropy condition for 1-shock of first Riemann problem is given by $\lambda _1(V_m)<\sigma _1(V_l ,V_m) < \lambda _2(V_m)$ which follows that the trailing end of $R_1$ associated with Riemann second problem has less velocity compare to the velocity of $S_1$ corresponding to the Riemann first problem. Consequently, 1-shock collides with 1-rarefaction wave and interaction occurs after a certain time. Here, we prove that $S_1(V_l)$ lies above the curve $R_1(V_m)$ whenever $\rho _l<\rho <\rho _m$. To establish this, it is enough to show that

  $$\begin{aligned} F(\rho _m,\rho _l)-F(\rho ,\rho _l)+2\sqrt{\frac{A}{\rho _m}}-2\sqrt{\frac{A}{\rho }}>0. \end{aligned}$$

  (21)

  To prove (21), let us consider the function $g_5(\rho )=F(\rho _m,\rho _l)-F(\rho ,\rho _l)+2\sqrt{\frac{A}{\rho _m}}-2\sqrt{\frac{A}{\rho }}$ such that $g_5(\rho _m)=0$. An easy computation yields

  $$\begin{aligned} \frac{dg_5}{d\rho }=\frac{\sqrt{A}}{\rho ^2}\left( \sqrt{\rho }+\frac{\ln \frac{\rho _l}{\rho }+(1-\frac{\rho }{\rho _l})}{2\sqrt{(\frac{1}{\rho }-\frac{1}{\rho _l})\ln \frac{\rho _l}{\rho }}}\right) . \end{aligned}$$

  (22)

  Now, we claim that $\frac{dg_5}{d\rho }<0$ for $\rho _l<\rho <\rho _m$. In order to prove our claim, let us take $\xi =\frac{\rho }{\rho _l}>1$ and it is sufficient to prove that

  $$\begin{aligned} 2\sqrt{(\xi -1)\ln \xi }-\ln \xi +(1-\xi )<0. \end{aligned}$$

  (23)

  Applying the property of arithmetic mean (A. M.) and geometric mean (G. M.) between the two positive real numbers $\xi -1$ and $\ln \xi$, we get $(\xi -1)+\ln \xi >2\sqrt{(\xi -1)\ln \xi }$ (as $A. M. >G. M.$) which leads to the inequality (23). Therefore, $g_5(\rho )$ is decreasing function of $\rho$ and hence $g_5(\rho )>g_5(\rho _m)=0$ which implies that $R_1(V_m)$ lies below the curve $S_1(V_l)$ for $\rho _l<\rho <\rho _m$.

  Now, we show that $R_1(V_m)$ lies below the curve $R_1(V_l)$ for $\rho<\rho _l<\rho _m$. To prove this it is sufficient to establish that $0<F(\rho _m,\rho _l)+2\sqrt{\frac{A}{\rho _m}}-2\sqrt{\frac{A}{\rho _l}}$ for $\rho<\rho _l<\rho _m$. The right hand side of this inequality is same as $g_5(\rho _m)$ which is established already as positive quantity.

  Finally, we prove that the curve $R_1(V_m)$ intersects with $S_2(V_l)$ at some unique point say $(\rho _2,w_2)$. To establish this, we have to show that $g_5(\rho )=0$ has a unique root at $\rho =\rho _2$ satisfying $\rho _2<\rho _l$. Clearly, $g_5(\rho _l)>0$ and $g_5(\rho )$ is negative when $\rho$ is near zero. Hence by applying the monotonicity and intermediate value theorem to the shock and rarefaction wave curve there exist a unique root of $\rho =\rho _2$ with $\rho _2<\rho _l$. Now, depending upon the choice of $\rho _r$, there will be three possibilities which are

  • (a) When $\rho _r<\rho _2$ then $V_r\in III$ and the result of interaction is $S_1R_1\Rightarrow R_1S_2$.

  • (b) When $\rho _r=\rho _2$ then $V_r\in S_2(V_l)$ and the interaction results as $R_1S_1\Rightarrow S_2$, which means that after collision of two waves of 1-family provides a new wave of the other family.

  • (c) When $\rho _r>\rho _2$ then $V_r\in II$ and consequently the interaction leads to $S_1R_1\Rightarrow S_1S_2$. The configuration of wave interactions are depicted in figure 7.

• (iii) 1-shock overtakes 1-shock ($S_1S_1$):

  In this case, for a given $V_l$, we choose $V_m$ and $V_r$ in such a way that $V_l$ is connected to $V_m$ by 1-shock of first Riemann problem and $V_m$ to $V_r$ are connected by 1-shock of second Riemann problem. In other words, $\rho _l<\rho _m$, $w_m=w_l-F(\rho _l,\rho _m)$ and $\rho _m<\rho _r$, $w_r=w_m-F(\rho _m,\rho _r)$. From Lax entropy condition one can easily verify that $\sigma _1(V_l,V_m)>\lambda _1(V_m)>\sigma _1(V_m,V_r)$ and hence 1-shock of first Riemann problem overtakes 1-shock of second Riemann problem and interaction occurs after a finite time. Now, we show that the curve $S_1(V_m)$ lies above the curve $S_1(V_l)$ for $\rho _l<\rho _m<\rho$. In order to prove this, it is sufficient to show that

  $$\begin{aligned} F(\rho , \rho _l)-F(\rho _m,\rho _l)-F(\rho ,\rho _m)>0, \end{aligned}$$

  (24)

  for $\rho _l<\rho _m<\rho$. In order to prove (24), let us consider the function $g_7(\rho )=F(\rho , \rho _l)-F(\rho _m,\rho _l)-F(\rho ,\rho _m)$ such that $g_7(\rho _m)=0$. Differentiating $g_7(\rho )$ with respect to $\rho$ gives

  $$\begin{aligned} \frac{dg_7}{d\rho }(\rho )=\frac{dF}{d\rho }(\rho , \rho _l)-\frac{dF}{d\rho }(\rho ,\rho _m). \end{aligned}$$

  (25)

  Since, $\frac{dF}{d\rho }$ is a decreasing function of $\rho$ for $\rho >\rho _l$ which implies that $\frac{dg_7}{d\rho }(\rho )>0$ and hence $g_7(\rho )>g_7(\rho _m)>0$ which proves the inequality (24) for $\rho _l<\rho _m<\rho$. Therefore, $V_r\in I$ and the result of interaction is $S_1S_1\Rightarrow S_1R_2.$ The computed result is established in figure 8.

• (iv) 2-shock overtakes 2-shock ($S_2S_2$):

  Here, for a given $V_l$, we choose $V_m$ and $V_r$ in such a way that $V_l$ and $V_m$ are connected by a 2-shock of first Riemann problem and $V_m$ and $V_r$ are connected by 2-shock of second Riemann problem. It can be proved in a same manner as in previous case that $V_r\in III$ and the result of interaction is $S_2S_2\Rightarrow R_1S_2$. The computed result is characterized in figure 9.

• (v) 2-rarefaction overtakes 2-shock ($R_2S_2$):

  In this case, we choose $V_m$ and $V_r$ with respect to $V_l$ in such a way that $V_m\in R_2(V_l)$ and $V_r\in S_2(V_m)$. In other words, we have $\rho _m\ge \rho _l$, $w_m=w_l+2\sqrt{\frac{A}{\rho _l}}-2\sqrt{\frac{A}{\rho _m}}$ and $\rho _r<\rho _m$, $w_r= w_m-F(\rho _r, \rho _m)$. From Lax entropy condition, we have $\lambda _2(V_m)>\sigma _2(V_l,V_m)$ which implies that $R_2$ overtakes $S_2$ after a finite time. First we prove that $R_2(V_l)$ lies above $S_2(V_m)$ for $\rho _l\le \rho <\rho _m$. In order to show this, it is sufficient to prove

  $$\begin{aligned} 2\sqrt{\frac{A}{\rho _m}}-2\sqrt{\frac{A}{\rho }}+F(\rho ,\rho _m)>0 \end{aligned}$$

  (26)

  for $\rho _l\le \rho <\rho _m$. The inequality (26) can be written as

  $$\begin{aligned} \sqrt{\frac{A}{\rho }}\left[ 2\left( \sqrt{\frac{\rho }{\rho _m}}-1\right) +\sqrt{\left( 1-\frac{\rho }{\rho _m}\right) \ln \frac{\rho _m}{\rho }}\right] >0. \end{aligned}$$

  (27)

  Now, let $\tau =\frac{\rho }{\rho _m}<1$. To prove (27), it is sufficient to show that $g_8(\tau )=2(\sqrt{\tau }-1)+\sqrt{(\tau -1)\ln \tau }>0$ for $\tau <1$. Now, one can easily prove that $g_8(\tau )$ is a decreasing function of $\tau$ on the interval $[\tau ,1]$. Hence, we obtain that $g_8(\tau )>g_8(1)=0$ which implies our required inequality (27).

  Next, we show that $S_2(V_m)$ lies below the curve $S_2(V_l)$ for $\rho \le \rho _l<\rho _m$. In order to prove this it is sufficient to show that

  $$\begin{aligned} 2\sqrt{\frac{A}{\rho _m}}-2\sqrt{\frac{A}{\rho }}+F(\rho ,\rho _m)-F(\rho ,\rho _l)>0 \end{aligned}$$

  (28)

  for $\rho \le \rho _l<\rho _m$. To prove (28), let $g_9(\rho )=2\sqrt{\frac{A}{\rho _m}}-2\sqrt{\frac{A}{\rho }}+F(\rho ,\rho _m)-F(\rho ,\rho _l)$ such that $g_9(\rho _l)$ is nothing but the left hand side of the inequality (26) which is already shown to be positive, i.e., $g_9(\rho _l)>0$. Now,

  $$\begin{aligned} \frac{dg_9}{d\rho }(\rho )=\frac{dF}{d\rho }(\rho , \rho _m)-\frac{dF}{d\rho }(\rho ,\rho _l). \end{aligned}$$

  (29)

  Since, $\frac{dF}{d\rho }$ is a decreasing function of $\rho _m$ for $\rho _m>\rho _l$ which implies that $\frac{dg_9}{d\rho }(\rho )<0$. Therefore, $g_9(\rho )>g_9(\rho _l)>0$ which implies the inequality.

  Finally, we prove that $S_2(V_m)$ intersects with $S_1(V_l)$ uniquely at some point, say, $(\rho _3,w_3)$ with $\rho _l<\rho _3<\rho _m$. This can be proved using the same argument as done in preceding cases. Here also, depending upon the choice of $\rho _r$, there will be three cases which are

  • (a) When $\rho _r<\rho _3$ then $V_r\in II$ and the result of interaction is $R_2S_2\Rightarrow S_1S_2$.

  • (b) When $\rho _r=\rho _3$ then $V_r\in S_1(V_l)$ and the interaction results as $R_2S_2\Rightarrow S_1$, i.e., after interaction of two waves of 2-family gives rise to a wave of the 1-family.

  • (c) When $\rho _r>\rho _3$ then $V_r\in I$ and the result of interaction is $R_2S_2\Rightarrow S_1R_2$. The computed results are interpreted in figure 10.

• (vi) 2-shock overtakes 2-rarefaction ($S_2R_2$):

  Here, $V_l$ is connected to $V_m$ by a 2-shock of the first Riemann problem and $V_m$ is connected to $V_r$ by a 2-rarefaction wave of the second Riemann problem, i.e., $V_m\in S_2(V_l)$ and $V_r\in R_2(V_m)$. It follows that, for $\rho _m<\rho _l$, $w_m=w_l-F(\rho _l,\rho _m)$ and for $\rho _r\ge \rho _m$, $w_r=w_m+2\sqrt{\frac{A}{\rho _m}}-2\sqrt{\frac{A}{\rho _r}}$. Since $\sigma _2(V_l ,V_m)>\lambda _2(V_m)$, 2-shock overtakes 2-rarefaction after a finite time. First we show that the curve $S_2(V_l)$ lies above the curve $R_2(V_m)$ for $\rho _m< \rho < \rho _l$. In order to prove this, it is enough to show that

  $$\begin{aligned} 2\sqrt{\frac{A}{\rho _m}}-2\sqrt{\frac{A}{\rho }}+F(\rho ,\rho _l)-F(\rho _m,\rho _l)>0, \end{aligned}$$

  (30)

  for $\rho _m< \rho < \rho _l$. Now, we set a new function $g_{10}(\rho )=2\sqrt{\frac{A}{\rho _m}}-2\sqrt{\frac{A}{\rho }}+F(\rho ,\rho _l)-F(\rho _m,\rho _l)$ such a way that $g_{10}(\rho _m)=0$. Moreover, one can prove that $\frac{dg_{10}}{d\rho }(\rho )>0$ which implies that $g_{10}(\rho )>g_{10}(\rho _m)=0$ and hence the inequality (30). Thus, $S_2(V_l)$ lies above the curve $R_2(V_m)$ for $\rho _m< \rho < \rho _l$. Now, we prove that $R_2(V_m)$ lies below the curve $R_2(V_l)$ for $\rho> \rho _l> \rho _m$. To show this it is sufficient to prove that $0<2\sqrt{\frac{A}{\rho _m}}-2\sqrt{\frac{A}{\rho _l}}-F(\rho _m,\rho _l)$ for $\rho > \rho _l \le \rho _m$. But, the left hand side of the inequality is nothing but $g_9(\rho _m)$ which is already shown to be positive. Thus, $R_2(V_l)$ lies above the curve $R_2(V_m)$ for $\rho _m< \rho _l < \rho$.

  Finally, we prove that $R_2(V_m)$ intersects uniquely with $S_1(V_l)$ at some point, say, $(\rho _4,w_4)$ with $\rho _m<\rho _l<\rho _4$. In order to show this, it is sufficient to prove that $2\sqrt{\frac{A}{\rho _m}}-2\sqrt{\frac{A}{\rho }}+F(\rho ,\rho _l)-F(\rho _m,\rho _l)=0$ has a root for $\rho _m<\rho _l<\rho$ which can be proved similarly as done in preceding cases. Again, there will be three possible cases which are given by

  • (a) When $\rho _r<\rho _4$ then $V_r\in II$ and the result of interaction is $S_2R_2\Rightarrow S_1R_2$.

  • (b) When $\rho _r=\rho _4$ then $V_r\in S_1(V_l)$ and the interaction results as $S_2R_2\Rightarrow S_1$, i.e., after interaction of two waves of 2-family gives rise to a wave of the 1-family.

  • (c) When $\rho _r>\rho _4$ then $V_r\in I$ and the result of interaction is $S_2R_2\Rightarrow S_1R_2$. The computed results are represented in figure 11.

Figure 6

$R_1$ overtakes $S_1$.

Figure 7

$S_1$ overtakes $R_1$.

Figure 8

$S_1$ overtakes $S_1$.

Figure 9

$S_2$ overtakes $S_2$.

Figure 10

$R_2$ overtakes $S_2$.

Figure 11

$S_2$ overtakes $R_2$.

4 Conclusion

We studied characteristic analysis of logotropic system of gasdynamics with a Coulomb-type friction and established the properties of shocks and rarefaction curves of one-parameter family. For a given arbitrary state, we constructed the Riemann solution in phase plane. Further, we developed locally two Riemann problems by considering appropriate initial data and analyzed all possible interactions between shocks and rarefactions in the phase plane which provide the basic features of solution with rich geometric structure. It is observed that Riemann problem is uniquely solvable and no vacuum occurs in the solution.