1 Introduction

Due to the advancement of thermal devices in engineering systems, the utilization of nanofluids has been playing a vital role in the process of cooling electronic devices and heat transfer enhancement in many industrial manufacturing processes. Nanofluid is produced by mixing nanosized metallic or nonmetallic particles or nanofiber particles into conventional fluids in order to increase the thermal properties Gupta et al [1]. Among different researches on nanofluids, some works have been focused on a new kind of nanofluids called ferrofluids. Ferrofluids (Magnetic nanofluids) are a special class of nanofluids exhibiting both magnetic and fluid properties Bahiraei and Hangi [2]. Ferrofluids are defined as a solution comprising of colloidal mixtures of super-paramagnetic nanoparticles (Magnetite, Hematite, Cobalt Ferrite, or some other compounds containing iron) and a nonmagnetic base fluid Xuan et al [3]. In the occurrence of the magnetic field, the thermal conductivity of the magnetic nanofluid is affected by the orientation and the intensity of the applied magnetic field Odenbach [4]. Furthermore, ferrofluids and magnetic fields can also be used for fluid flow control and for improving the heat transfer process taking place in case of natural, forced, and mixed convection Gupta [5]. In order to maintain agglomeration of the magnetic nanoparticles formed due to the Van der Waals interaction and magnetic interaction between the particles, particles are coated with surfactants Tynjäl et al [6].

Using magnetic fluids have various use in different engineering processes and biomedical applications such as removing particles and contamination from drinking/wastewater streams, removing radioactive chemicals, MRI, drug delivery in cancer treatment, low-friction seals, dampening and cooling agents in loudspeakers, recovery of hazardous wastes, heat transfer, computer hardware, dynamic sealing, electronic packaging, aerospace, power electric transformers, solar collectors and magnetically controlled thermosyphons as mentioned by [7,8,9,10]. Following these facts, several works have been done experimentally and numerically to determine the fluid flow characteristic and heat transfer enhancement of a magnetic nanofluid by considering several aspects of the problem. For instance, Lajvardi et al [11] experimentally examined the convective heat transfer characteristics of the magnetic nanofluids with a magnetic field effect and obtained that the heat transfer rate upsurges with the magnetic nanoparticles concentration and the applied magnetic field. Sivakumar et al [12] numerically scrutinized the cumulative effects of viscous dissipation, thermal radiation, convective heating, and slip effect on the MHD ferrofluid flow past a permeable nonlinear stretching sheet and concluded that the heat transfer rate increases with the convective heating and the viscous dissipation while thermal radiation acts on the contrary.

Fluid flow caused by a stretching/shrinking sheet has many practical applications in the field of metallurgy, polymer technology, chemical engineering, industrial processes and etc. [13,14,15]. Fluid flow towards a shrinking case is possible whenever sufficient mass suction is imposed on the boundary [16] or with the consideration of stagnation point flow [17]. Due to the unconfined fluid flow occurring in the boundary layer of the shrinking case, no possible solution is found. However, the application of the adequate value of wall mass suction Miklavčič and Wang [16] or with an added stagnation flow Wang [17], a non-unique solution may exist. The governing system of differential equations may have a non-unique solution. Temporal stability analysis is a mathematical technique that is conducted to test the temporal stability of the non-unique solutions obtained. Though the lower branch solution cannot be produced experimentally, this solution is a part of the solution of the differential equations and therefore should be considered. Different works on stability analysis are documented in the literature [18,19,20,21,22]. Recently, such fluid flow problems have been investigated extensively by considering different aspects of the problem. For instance, Khashi’ie et al [23] numerically examined the combined effects of the controlling parameters such as magnetic field, suction, and Joule heating on fluid flow and heat transfer characteristics of a hybrid nanofluid past a permeable stretching/shrinking sheet. From the temporal stability analysis, they verified that only the upper branch solution is stable and physically realizable.

Investigations on the stagnation point flow of nanofluid or ferrofluid have gained more attention due to its immense applications in many industrial manufacturing processes such as aerodynamic, extrusion of plastic sheet, and the cooling and drying of papers as reported by Kamal et al [24]. Owing to this importance, such fluid flow problems have been extended in various ways. For example, Abbas and Sheikh [25] studied the stagnation point flow of a magnetic nanofluid past a flat sheet with the consideration of non-linear slip boundary condition and homogeneous–heterogeneous reactions and concluded that the skin friction obtained for water-based ferrofluid exceeds the kerosene-based ferrofluid. Makinde [26] numerically investigated hydrodynamic stagnation point flow of Fe3O4-water ferrofluid towards a permeable stretching or shrinking sheet with the effects of applied magnetic field. They perform hydrodynamic stability analysis to identify stable solutions among those solutions which exist within the specific range of stretching/shrinking parameter. Mohamed et al [27] numerically examined the combined effects of the magnetic field, velocity slip, nanoparticles volume fraction, stretching, and conjugate parameter on the boundary layer flow of a water-based magnetite ferrofluid. They reported that the heat transfer rate rises with the magnetite nanoparticles volume fraction, whereas the velocity slip diminishes the skin friction coefficient. Moreover, Jamaludin et al [28] explored a two dimensional hydromagnetic stagnation point flow of Fe3O4-water ferrofluid flow past a permeable non-linearly stretching/shrinking surface by considering the thermal radiation effect. They found that dual solutions exist in certain ranges of mixed convection parameter and thermal radiation diminishes the rate of heat transfer from the sheet surface. Besides all these, some researchers have investigated heat transfer enhancement process by considering hybridized nanoparticles. For instance, Waini et al [29] numerically examined buoyancy effects on stagnation point flow of hybrid nanofluid flow towards an exponentially stretching/shrinking vertical sheet and found that the heat transfer rate is greater for Al2O3-Cu/water hybrid nanofluid compared to Cu/water nanofluid.

Meanwhile, fluid flow and transport process in porous media have many applications in hydrology, agriculture, civil, petroleum engineering, environmental and industrial systems such as heat exchange design, catalytic reactors, geothermal energy systems, fermentation process, grain storage, groundwater pollution, groundwater systems, movement of water in reservoirs, crude oil production and recovery systems as explained by [30,31,32]. Owing to these importance, several works have been done based on Darcy’s law. However, in many practical applications, porous media with relatively high porosity and permeability are used, especially for reducing the pressure drop. Hence, the Reynolds number based on the pore size may be greater than unity and there is an impermeable boundary, making Darcy’s law inapplicable Muhammad et al [33]. For these reasons, it is important to incorporate the velocity-squared term in addition to Darcian velocity in the momentum equation in order to include the effect of inertia porous media resistance [34, 35]. Following this fact, an important analysis is done on the convective transport process in a porous medium with the inertial effect. To mention some, Bakar et al [36] numerically examined effects of velocity and thermal slip on stagnation point flow towards a shrinking sheet embedded in Darcy-Forchheimer porous medium. They obtained that dual solution exists in certain ranges of the velocity ratio parameter. Ali Lund et al [37] examined Darcy-Forchheimer’s flow of Casson type nanofluid past a non-linearly shrinking sheet to identify the effects of slip condition and viscous dissipation. They identified the existence of dual solution.For fluid flows in a porous medium, the inclusion of porous dissipation in the model equation modifies the viscous dissipation term in energy equation Kausar et al [38]. From the literature survey and to the best of our knowledge, more attention is required for problems of fluid flow and heat transfer past a stretching/shrinking sheet embedded in a Darcy-Forchheimer porous medium in the presence of frictional heating and porous dissipation.

Motivated by the above-cited works of literature, our main goal here is to examine carefully the characteristics of magnetohydrodynamic stagnation point flow of a magnetite ferrofluid past a permeable stretching/shrinking sheet in a Darcy-Forchheimer porous medium with viscous and porous dissipation, and convective heating. For such fluid flow problems, the existence of a dual solution is possible, and stability analysis is performed to identify stable and physically reliable solutions. To the best of our knowledge, no work has been done to analyze the combined effects of these parameters on the ferrofluid flow and heat transfer characteristics. The di- mensionless velocity, temperature, skin friction coefficient, and the Nusselt number are obtained numerically and pre- sented in graphs and tables.

2 Mathematical formulation and analysis

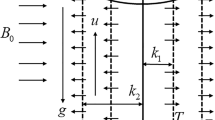
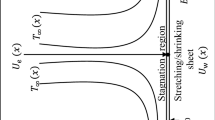
We consider a steady, laminar, viscous, and incompressible stagnation point flow of Fe3O4-H2O nanofluid towards a convectively heated permeable stretching/shrinking sheet which is kept in a two dimensional Darcy-Forchheimer porous med-ium. The flow is subjected to a constant magnetic field of strength \(B_{0}\) which is applied in the positive y-direction normal to the surface. The induced magnetic field is assumed to be small compared to the applied magnetic field. The ambient temperature of the fluid is taken as \(T_{\infty }\) while the surface below the stretching/shrinking sheet is heated by convection from a hot fluid having initial temperature \(T_{f}\) which provides a heat transfer coefficient \(h_{f}\). It is assumed that the porous medium is homogeneous and isotropic, and saturated with a nanofluid which is in local thermal equilibrium with the solid matrix. We choose the coordinate system so that x-axis along the permeable stretching/shrinking sheet and y-axis is normal to the sheet surface. Figure 1 shows the physical model and the coordinate systems.

Figure 1
figure 1

Flow diagram of the model.

Full size image

The flow equations for continuity, conservation of momentum and energy in the presence of magnetic field past a permeable stretching/shrinking sheet, under the Boussinesq approximation, with reference to a Cartesian coordinate \(x-y\) system is defined as( [35,36,37, 39]).

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y} = 0, \end{aligned}$$
(1)
$$\begin{aligned}&u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} = U_{\infty }\frac{\partial U_{\infty }}{\partial x}\nonumber \\&\quad +\frac{\mu _{nf}}{\rho _{nf}}\frac{\partial ^{2} u}{\partial y^{2}}\nonumber \\&\quad -\left( \frac{\sigma _{nf} B_{0}^{2}}{\rho _{nf}}+\frac{\mu _{nf}}{\rho _{nf}K_{1}}\right) (u-U_{\infty })\nonumber \\&\quad + \frac{F}{\rho _{nf}\sqrt{K_{1}}}(u-U_{\infty })^{2}, \end{aligned}$$
(2)
$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y} = \frac{k_{nf}}{(\rho C_{p})_{nf}}\frac{\partial ^{2} T}{\partial y^{2}}\nonumber \\&\quad +\frac{\mu _{nf}}{(\rho C_{p})_{nf}}\biggl (\frac{\partial u}{\partial y}\biggr )^{2}\nonumber \\&\quad +\biggl (\frac{\sigma _{nf} B_{0}^{2}}{(\rho C_{p})_{nf}}\nonumber \\&\quad +\frac{\mu _{nf}}{(\rho C_{p})_{nf}K_{1}}\biggr )(u-U_{\infty })^{2}\nonumber \\&\quad +\frac{F}{(\rho C_{p})_{nf}\sqrt{K_{1}}}(u-U_{\infty })^{3}, \end{aligned}$$
(3)

with the boundary conditions:

$$\begin{aligned} u(x,0)= & {} U_{w}(x),\quad v(x,0)=V_{0}, \quad \nonumber \\&-k_{f}\frac{\partial T}{\partial y}(x,0)=h_{f}(T_{f}-T(x,0)), \end{aligned}$$
(4)
$$\begin{aligned}&u(x,\infty )\rightarrow U_{\infty }(x),\quad T(x,\infty )\rightarrow T_{\infty }, \end{aligned}$$
(5)

where u and v are the velocity components along the x and y directions, respectively. The expressions \(U_{w}(x)=bx\) is the stretching/shrinking velocity of the sheet where \(b>0\) is for stretching case and \(b<0\) for shrinking case, \(U_{\infty }(x)=ax\) is the free stream velocity where \(a>0\) is the strength of stagnation flow, and \(T_{f}=T_{\infty } +nx^{2} \) is the temperature of the hot fluid below the sheet. The terms \(V_{0}\) is the sheet suction/injection velocity, \(K_{1}\) is the permeability of the porous medium, F is the non-uniform inertial coefficient of porous medium, \(\rho _{nf}\) is the nanofluid density, \(\mu _{nf}\) is the nanofluid dynamic viscosity, \(k_{nf}\) is the nanofluid thermal conductivity, \((\rho C_{p})_{nf}\) is heat capacity of the nanofluid at constant pressure and \(\sigma _{nf}\) is the nanofluid electrical conductivity are defined as follows:

$$\begin{aligned} \begin{aligned}&\rho _{nf}=(1-\phi )\rho _{f}+\phi \rho _{s},\\&( \rho C_{p} )_{nf}=(1-\phi )(\rho C_{p})_{f}+\phi (\rho C_{p})_{s},\quad \\&\mu _{nf}=\dfrac{\mu _{f}}{(1-\phi )^{2.5}},\quad \\&\dfrac{k_{nf}}{k_{f}}=\dfrac{k_{s}+2k_{f}-2\phi (k_{f}-k_{s})}{k_{s}+2k_{f}+\phi (k_{f}-k_{s})},\quad \\&r=\dfrac{\sigma _{s}}{\sigma _{f}},\quad \dfrac{\sigma _{nf}}{\sigma _{f}}=1+\dfrac{3(r-1)\phi }{(r+2)-(r-1)\phi }, \end{aligned} \end{aligned}$$
(6)

where \(\rho _{f}\) is the density of the base fluid, \(\rho _{s}\) is the density of the solid nanoparticle, \(k_{f}\) is the base fluid thermal conductivity, \(k_{s}\) is the nanoparticles thermal conductivity, \(\sigma _{f}\) is the base fluid electrical conductivity,\(\sigma _{s}\) is the nanoparticles electrical conductivity, \(\phi \) is the nanoparticles volume fraction, \(\mu _{f}\) is the base fluid dynamic viscosity \(C_{pf}\) is the base fluid specific heat capacity and \( C_{ps}\) is the nanoparticles specific heat capacity. The thermo-physical properties of \(Fe_{3}O_{4}\) nanoparticles and \(H_{2}O\) are listed in table 1 below;

Table 1 Nanoparticle and base fluid thermophysical properties.
Full size table

Introduce the following non-dimensional similarity variables in order to transform the governing equations.

$$\begin{aligned} \eta= & {} y\sqrt{\dfrac{a}{\nu _{f}}},\quad \psi (x,y)=f(\eta )x \sqrt{a\nu _{f}}, \quad \nonumber \\ \theta (\eta )= & {} \dfrac{T-T_{\infty }}{T_{f}-T_{\infty }}. \end{aligned}$$
(7)

The equation of continuity is satisfied for the chosen stream function \(\psi (x,y)\) such that

$$\begin{aligned} u= & {} \frac{\partial \psi }{\partial y},\quad and \quad v=-\frac{\partial \psi }{\partial x}. \end{aligned}$$
(8)

Now using the similarity transformation quantities, the nonlinear partial differential equations are transformed into nonlinear ordinary differential equations as:

$$\begin{aligned}&f'''-A_{1}((f')^{2}-ff''-1)-\left( MA_{2}+\frac{1}{Da}\right) (f'-1)\nonumber \\&-F_{n}A_{3}(f'-1)^{2}=0, \end{aligned}$$
(9)
$$\begin{aligned}&\theta ''- A_{4}Pr(2\theta f'-f\theta ')+A_{5}PrEc(f'')^{2}\nonumber \\&\quad +EcPr(A_{6}M+A_{5}\frac{1}{Da})(f'-1)^{2}\nonumber \\&+\quad A_{7}EcPrF_{n}(f'-1)^{3}\nonumber \\&\qquad =0. \end{aligned}$$
(10)

The boundary conditions in terms of the new variables become:

$$\begin{aligned}&\eta =0: \quad f(0)=S, \quad f'(0)=\lambda , \quad \theta '(0)=-Bi\left[ 1-\theta (0)\right] , \end{aligned}$$
(11)
$$\begin{aligned}&\eta \rightarrow \infty : \quad f^{'}(\infty )=1,\quad \theta (\infty )=0. \end{aligned}$$
(12)

Here a prime symbol denotes differentiation with respect to \(\eta \) and \(f',\theta \) and \(\eta \) are the dimensionless velocity, temperature and similarity variable respectively. The parameters, the dimensionless numbers and the variables are defined as follows:

$$\begin{aligned} \begin{aligned}&M\,=\,\dfrac{\sigma _{f}B_{0}^{2}}{a\rho _{f}},\quad Pr\,=\,\frac{\mu _{f}C_{pf}}{k_{f}},\quad \\&Ec\,=\,\dfrac{a^{2}}{nC_{pf}},\\&Da\,=\,\dfrac{aK_{1}}{\nu _{f}}, F_{n}\,=\,\dfrac{Fx}{\rho _{f}\sqrt{K_{1}}},\quad \\&\lambda \,=\,\dfrac{b}{a},\quad S\,=\,\frac{-V_{0}}{\sqrt{a\nu _{f}}},\\&Bi\,=\,\dfrac{h_{f}}{k_{f}}\sqrt{\frac{a}{\nu _{f}}}\quad \\&A_{1}\,=\,(1-\phi +\frac{\phi \rho _{s}}{\rho _{f}})(1-\phi )^{2.5}, \\&A_{2}\,=\,\frac{(1-\phi )^{2.5}}{\sigma _{f}}\sigma _{nf},\quad A_{3}\,=\,(1-\phi )^{2.5},\\&A_{4}\,=\,\frac{k_{f}}{k_{nf}}\left( 1-\phi +\frac{\phi (\rho C_{p})_{s}}{(\rho C_{p})_{f}} \right) ,\quad \\&A_{5}\,=\,\frac{k_{f}}{k_{nf}(1-\phi )^{2.5}}, \\&A_{6}\,=\,\frac{\sigma _{nf}k_{f}}{\sigma _{f}k_{nf}},\quad A_{7}\,=\,\frac{k_{f}}{k_{nf}}. \end{aligned} \end{aligned}$$
(13)

Where \(M,Pr,Ec,Da,F_{n},S, \lambda \) and Bi denote the magnetic field parameter, Prandtl number, Eckert number, the porous media parameter, porous medium inertia parameter, the constant mass flux parameter where \(S > 0\) for suction and \(S < 0 \) for injection or withdrawal of the fluid, stretching/shrinking parameter where \( \lambda > 0\) for a stretching sheet and \( \lambda < 0 \) for a shrinking sheet, and Biot number respectively. It is important to note that the porous medium inertia parameter (\( F_{n})\) is a local similarity parameter. Nonetheless, the parameter \( F_{n}\) may become a similarity parameter if the non-uniform inertial coefficient of porous medium is defined as \(F = \dfrac{C_{d}}{x}\) where \(C_{d}\) is drag coefficient. In this case, the expression for \( F_{n}=\dfrac{C_{d}}{\rho _{f}\sqrt{K_{1}}}\) is a similarity parameter since it is independent of x [30, 40, 41].

The important physical quantities of interest, in this problem, are the skin friction coefficient \(C_{f}\) and the Nusselt number Nu are defined as:

$$\begin{aligned} C_{f}= & {} \dfrac{\tau _{w}}{\rho _{f}U_{\infty }^{2}},\qquad \nonumber \\ Nu= & {} \dfrac{xq''_{w}}{k_{f}(T_{f}-T_{\infty })}, \end{aligned}$$
(14)

where \(\tau _{w}\) is the skin friction and \(q''_{w}\) is heat flux from the plate are given by

$$\begin{aligned} \tau _{w}= & {} \mu _{nf}\frac{\partial u}{\partial y}|_{y=0},\qquad \nonumber \\ q''_{w}= & {} -k_{nf}\frac{\partial T}{\partial y}|_{y=0}. \end{aligned}$$
(15)

In dimensionless form, the skin friction coefficient and reduced Nusselt number can be rewritten as:

$$\begin{aligned} C_{f}Re_{x}^{1/2}= \frac{f''(0)}{(1-\phi )^{2.5}}, \qquad NuRe_{x}^{-1/2}= -\frac{k_{nf}}{k_{f}}\theta '(0). \end{aligned}$$
(16)

The heat transfer enhancement (HTE) of the nanoparticles can be determined as

$$\begin{aligned} HTE = \frac{NuRe_{x}^{-1/2}(\phi \ne 0)-NuRe_{x}^{-1/2}(\phi = 0)}{NuRe_{x}^{-1/2}(\phi = 0)} *100 \end{aligned}$$
(17)

Where \(Re_{x}=\dfrac{U_{\infty }x}{\nu _{f}}\) is the local Reynold number.

3 Stability analysis

From the numerical result obtained, such fluid flow problem has dual solutions depending on the physical parameters under consideration. For such cases, it is substantial to perform stability analysis in order to examine which of the solutions is physically practicable and stable. The execution of the stability analysis is mathematically performed to validate the real solution among all the solutions. It is implemented by considering an unsteady (time dependent) problem Merkin [18]. Hence, for the present analysis, an unsteady form of equations  (2) and  (3) have to be inspected:

$$\begin{aligned}&\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} = U_{\infty }\frac{\partial U_{\infty }}{\partial x}\nonumber \\&\quad +\frac{\mu _{nf}}{\rho _{nf}}\frac{\partial ^{2} u}{\partial y^{2}}\nonumber \\&\quad -\left( \frac{\sigma _{nf} B_{0}^{2}}{\rho _{nf}}+\frac{\mu _{nf}}{\rho _{nf}K_{1}}\right) (u-U_{\infty })\nonumber \\&\quad +\frac{F}{\rho _{nf}\sqrt{K_{1}}}(u-U_{\infty })^{2}, \end{aligned}$$
(18)
$$\begin{aligned}&\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y} =\frac{k_{nf}}{(\rho C_{p})_{nf}}\frac{\partial ^{2} T}{\partial y^{2}}\nonumber \\&\quad +\biggl (\frac{\sigma _{nf} B_{0}^{2}}{(\rho C_{p})_{nf}} +\frac{\mu _{nf}}{(\rho C_{p})_{nf}K_{1}}\biggr )\nonumber \\&\quad (u-U_{\infty })^{2}+\frac{\mu _{nf}}{(\rho C_{p})_{nf}}\biggl (\frac{\partial u}{\partial y}\biggr )^{2}\nonumber \\&\quad +\frac{F}{(\rho C_{p})_{nf}\sqrt{K_{1}}}(u-U_{\infty })^{3}. \end{aligned}$$
(19)

Following Makinde [26], new transformations are applied to the unsteady equations  (18) and  (19) where \(\tau \) is the non-dimensional time variable:

$$\begin{aligned} \begin{aligned}&\eta =y\sqrt{\dfrac{a}{\nu _{f}}}, \quad u=ax\frac{\partial f}{\partial \eta }(\eta ,\tau ),\quad \\&v=-\sqrt{a\nu _{f}}f(\eta ,\tau ),\\&\psi =f(\eta ,\tau )x\sqrt{a\nu _{f}}, \quad \theta (\eta ,\tau )=\dfrac{T-T_{\infty }}{T_{f}-T_{\infty }},\quad \tau =bt. \end{aligned} \end{aligned}$$
(20)

Now using equation  (20), equation (18) and  (19) become

$$\begin{aligned}&\frac{\partial ^{3}f}{\partial \eta ^{3}}-A_{1}\Biggl (\frac{\partial ^{2}f}{\partial \tau \partial \eta }+\Biggl (\frac{ \partial f}{\partial \eta }\Biggr )^{2}\nonumber \\&\qquad -f\frac{\partial ^{2}f}{\partial \eta ^{2}}\Biggr )-\biggl (MA_{2}+\frac{1}{Da}\biggr )\Biggl (\frac{\partial f}{\partial \eta }-1\Biggr )\nonumber \\&\quad -F_{n}A_{3}\Biggl (\frac{\partial f }{\partial \eta }-1\Biggr )^{2} +A_{1}=0, \end{aligned}$$
(21)
$$\begin{aligned}&\frac{\partial ^{2}\theta }{\partial \eta ^{2}}-A_{4}Pr\Biggl (\frac{\partial \theta }{\partial \tau }+2\theta \frac{ \partial f}{\partial \eta }-f\frac{\partial \theta }{\partial \eta }\Biggr )\nonumber \\&\quad +A_{5}PrEc\Biggl (\frac{\partial ^{2} f}{\partial \eta ^{2}}\Biggr )^{2}\nonumber \\&+EcPr\biggl (A_{6}M+\frac{A_{5}}{Da}\biggr )\Biggl (\frac{\partial f }{\partial \eta }-1\Biggr )^{2}\nonumber \\&\quad +A_{7}EcPrF_{n}\Biggl (\frac{\partial f }{\partial \eta }-1\Biggr )^{3}=0, \end{aligned}$$
(22)

and the boundary conditions become:

$$\begin{aligned} \begin{aligned}&f(0,\tau )=S, \quad \frac{\partial f}{\partial \eta }(0,\tau )=\lambda , \quad \frac{\partial \theta }{\partial \eta }(0,\tau )=-Bi\left[ 1-\theta (0,\tau )\right] , \quad \\&\frac{\partial f}{\partial \eta }(\infty ,\tau ) \rightarrow 1, \quad \theta (\infty ,\tau ) \rightarrow 0. \end{aligned} \end{aligned}$$
(23)

Based on Harris et al [20], we test the stability of the steady flow solution \(f(\eta ) = f_{0}(\eta )\) and \(\theta (\eta ) = \theta _{0}(\eta )\) satisfying the set of boundary-value problem equation  (9)–(12) by writing

$$\begin{aligned} \begin{aligned}&f(\eta , \tau )=f_{0}(\eta )+ e^{-\beta \tau }F(\eta ,\tau )\\&\theta (\eta ,\tau )=\theta _{0}(\eta )+e^{-\beta \tau }G(\eta ,\tau ) \end{aligned} \end{aligned}$$
(24)

where \(\beta \) is an unknown eigenvalue parameter (a small disturbance of growth or decay) and \(F(\eta , \tau )\) and \(G(\eta , \tau )\) are small relative to \(f_{0}(\eta )\) and \(\theta _{0}(\eta )\), respectively. The following equations are obtained by substituting  (24) into  (21)–(23)

$$\begin{aligned}&\frac{\partial ^{3}F}{\partial \eta ^{3}}+A_{1}f_{0}\frac{\partial ^{2}F}{\partial \eta ^{2}}+A_{1}F\frac{\partial ^{2}f_{0}}{\partial \eta ^{2}}\nonumber \\&\quad +\frac{\partial F}{\partial \eta }\Biggl [\beta A_{1}-2A_{1}\frac{\partial f_{0}}{\partial \eta }\nonumber \\&\quad -A_{2}M-\frac{1}{Da}-2A_{3}F_{n}\Biggl (\frac{\partial f_{0}}{\partial \eta }-1\Biggr )\Biggr ]\nonumber \\&\quad -A_{1}\frac{\partial ^{2}F}{\partial \eta \partial \tau } =0, \end{aligned}$$
(25)
$$\begin{aligned}&\frac{\partial ^{2}G}{\partial \eta ^{2}}+\frac{\partial F}{\partial \eta }\Biggl [2EcPr\Biggl (A_{6}M+A_{5}\frac{1}{Da}\Biggr )\Biggl (\frac{\partial f_{0}}{\partial \eta }-1\Biggr )\nonumber \\&\quad +3A_{7}EcPrF_{n}\Biggl (\frac{\partial f_{0}}{\partial \eta }-1\Biggr )^{2}-A_{4}Pr\theta _{0}\Biggr ]\nonumber \\&\quad +2A_{5}PrEcf_{0}\frac{\partial ^{2}\theta _{0}}{\partial \eta ^{2}}\frac{\partial ^{2}G}{\partial \eta ^{2}}\nonumber \\&\quad +A_{4}Prf_{0}\frac{\partial G}{\partial \eta }\nonumber \\&\quad +A_{4}PrG\Biggl (\beta - 2\frac{\partial f_{0}}{\partial \eta }\Biggr )+A_{4}PrF\frac{\partial \theta _{0}}{\partial \eta }\nonumber \\&\quad -A_{4}Pr\frac{\partial G}{\partial \tau }=0, \end{aligned}$$
(26)

subjected to the boundary conditions:

$$\begin{aligned} \begin{aligned}&F(0,\tau )=0, \quad \frac{\partial F}{\partial \eta }(0,\tau )=0,\\&\quad \frac{\partial G}{\partial \eta }(0,\tau )=BiG(0,\tau ), \quad \\&\frac{\partial F}{\partial \eta }(\infty ,\tau ) \rightarrow 0,\quad G(\infty ,\tau ) \rightarrow 0. \end{aligned} \end{aligned}$$
(27)

Following Weidman et al [19], the initial growth or decay of the solution  (24) can be identified by setting \(\tau = 0 \) so that \(F = F_{0}(\eta )\) and \(G = G_{0}(\eta )\) in Equations  (25)–(27). Solutions of the eigenvalue problem give an infinite set of eigenvalues \(\beta _1< \beta _2 < \beta _{3} \cdots \) ; if \(\beta _1\) is negative, there is an initial growth of disturbances and the flow is unstable but when \(\beta _1\) is positive, there is an initial decay and the flow is stable. The linearized Eigenvalue problem are given by

$$\begin{aligned}&F'''_{0}+A_{1}f_{0}F''_{0}+A_{1}F_{0}f''_{0}+ F'_{0}\Biggl [\beta A_{1}-2A_{1}f'_{0}-A_{2}M\nonumber \\&\quad -\frac{1}{Da}-2A_{3}F_{n}\Biggl ( f'_{0}-1\Biggr )\Biggr ]=0, \end{aligned}$$
(28)
$$\begin{aligned}&G''_{0}+F'_{0}\Biggl [2EcPr\Biggl (A_{6}M+A_{5}\frac{1}{Da}\Biggr )\Biggl ( f'_{0}-1\Biggr )+3A_{7}EcPrF_{n}\nonumber \\&\Biggl ( f'_{0}-1\Biggr )^{2}-A_{4}Pr\theta _{0}\Biggr ]\nonumber \\&+2A_{5}PrEcf_{0}\theta ''_{0}G''_{0}+A_{4}Prf_{0} G'_{0}\nonumber \\&+A_{4}PrG_{0}\Biggl (\beta - 2f'_{0}\Biggr )+A_{4}PrF_{0} \theta '_{0}=0, \end{aligned}$$
(29)

with the new boundary conditions:

$$\begin{aligned} \begin{aligned}&F_{0}(0)=0, \quad F'_{0}(0)=0, \quad G'_{0}(0)=BiG_{0}(0), \qquad \\&F'_{0}(\infty ) \rightarrow 0, \qquad G_{0}(\infty ) \rightarrow 0. \end{aligned} \end{aligned}$$
(30)

As suggested by Harris et al [20], the range of possible eigenvalues can be obtained by relaxing one of the boundary conditions given in equation  (30), \( F'_{0}(\infty ) \rightarrow 0\) or \(G_{0}(\infty ) \rightarrow 0\). Thus, the boundary condition \(F'_{0}(\infty ) \rightarrow 0\) is relaxed and replaced with the normalizing boundary condition \(F''_{0}(0)=1 \), and the boundary conditions become:

$$\begin{aligned} \begin{aligned}&F_{0}(0)=0, \qquad F'_{0}(0)=0, \qquad G'_{0}(0)=BiG_{0}(0),\\&F''_{0}(0)=1, \qquad G_{0}(\infty ) \rightarrow 0. \end{aligned} \end{aligned}$$
(31)

Finally, Equations  (28) and  (29) are solved along the new boundary conditions  (31).

4 Numerical procedure

The non-linear system of equations  (9) and  (10) along with the boundary conditions (11) and  (12) are solved numerically using the shooting method with the help of Maple software. However, this system needs to be reduced to the equivalent system of first order ODEs as follows:

$$\begin{aligned} \begin{aligned} f'&= g ,\\ g'&=h,\\ h'&=A_{1}(( g )^{2}-fh-1)+\left( MA_{2}-\frac{1}{Da}\right) ( g -1)\\&\quad +F_{n}A_{3}( g -1)^{2},\\ \theta '&= p,\\ p'&= A_{4}Pr(2\theta g -fp)-A_{5}PrEc(h)^{2}\\&\quad -EcPr(A_{6}M+A_{5}\frac{1}{Da}) ( g -1)^{2}\\&\quad +A_{7}EcPrF_{n}( g -1)^{3}, \end{aligned} \end{aligned}$$
(32)

with boundary conditions

$$\begin{aligned} \begin{aligned}&f(0)=S, \quad g (0)=\lambda , \quad h(0)=\alpha _{1}, \quad \theta (0)= \alpha _{2},\\&p(0)= -Bi\left[ 1-\alpha _{2}\right] , \end{aligned} \end{aligned}$$
(33)

Here, \(\alpha _{1}\) and \(\alpha _{2}\) are unknown initial conditions. We have to shoot these initial conditions with some arbitrary slope such that the solution of the ODE system satisfies the given far-field boundary conditions. Thereafter, the resultant system of first-order ODEs is solved by employing the fourth-fifth order Runge-Kutta-Fehlberg method, and the accuracy of missing initial conditions is then checked by comparing calculated values with the given terminal points. The dual solutions are obtained by taking different initial guesses for the values of \(\alpha _{1}\) and \(\alpha _{2}\), where the far-field boundary conditions might be satisfied by all profiles asymptotically.

5 Results and discussions

In this study, the effects of shrinking/stretching parameter \(\lambda \), magnetic field parameter M, the porous medium parameter Da, porous medium inertia parameter \(F_{n}\), the constant mass flux parameter S, viscous dissipation and convective heating on the magnetite ferrofluid velocity and temperature are demonstrated in graphs. The range of parameters used in this study are \( 0.1\le M \le 1.1, 0\le \phi \le 0.1, 0.1\le Ec \le 0.3, 0.2 \le Da \le 2, 0.1 \le F_{n} \le 1.5, -1\le S \le 2 \) and \( Pr = 6.2 \) is used to signify the pure water as the base fluid. The existence of dual solutions for certain ranges of parameter variations are shown for the skin friction coefficient in the form of graphs and tables and also the variations of Nusselt number are illustrated in graphs for different values of the parameters change.

Equations  (9) and  (10) together with the boundary conditions  (11) and  (12) are solved numerically using the shooting method in Maple2018. Validation of the numerical method used in this study is checked by comparing the results obtained in the present study with the results from the previous study for different parameters, as shown in table 2.

Table 2 The computation showing \( Re_{x}^{1/2}C_{f}\) and \(Re_{x}^{-1/2}Nu \) for different stretching/shrinking parameter value with \(Pr=1\) for \(\phi =0\) (Regular fluid), \(M=0,S=0,Da=\infty ,F_{n}=0,Bi=\infty ,Ec=0\).
Full size table

As presented in the above table, it was found that the present results are in a good agreement with the solution obtained by Nazar et al [42] for a regular fluid case. This is our guarantee that the method used to tackle our problem is accurate and valid. In this study, the computations are done for different values of parameters involved in the governing flow equations. The velocity profiles, temperature profiles, the graph of skin friction and Nusselt number are plotted.

The variations of the skin friction for various values of the governing parameters are presented in figures 2, 3 and 4. From these figures, we observe that dual solutions with upper and lower branch solutions exist when \(\lambda > \lambda _{c}\), while no real solution is obtained when \(\lambda < \lambda _{c}\). The critical value \( \lambda _{c}\) is the value where the upper branch solution meets the lower branch solution. These figures also show that the magnitude of \( \lambda _{c}\) increases with each parameter \( \phi ,S, M\) and acts in opposite fashion with the porous resistance parameters, Da and \( F_{n}\). Hence, the intensification of the nanoparticle volume fraction, suction, injection, and the magnetic field parameter widen the range of \( \lambda \) for which the solution exists and narrow for the increment of the porous medium parameter and porous medium inertia parameter. There is no similarity solutions exist beyond this critical value due to the boundary layer separation from the surface and the solution based upon the boundary layer approximations are not possible.

Figure 2
figure 2

(a) Variation of skin friction for different values of magnetite nanoparticle volume fraction, \(\phi \). (b) Variation of skin friction for different values of suction parameter, S.

Full size image
Figure 3
figure 3

(a) Variation of skin friction for different values of porous media parameter, Da. (b) Variation of skin friction for different values of magnetic field parameter, M.

Full size image
Figure 4
figure 4

(a) Variation of skin friction for different values of second-order porous resistance parameter, \(F_{n}\). (b) Variation of skin friction for different values of injection parameter, S.

Full size image

Figure 2a illustrates that the value of the skin friction coefficient is intensified with the quantity of magnetite nanoparticle volume fraction for the upper branch solution, which come to an agreement with the results obtained in table 3. This indicates that an increase in nanoparticle volume fraction resulted in a stronger wall shear stress. Furthermore, it is noted that no skin friction is achieved when \( \lambda =1\) for all values of nanoparticles volume fraction. This is due to the fact that the fluid velocity is equal to the stretching/shrinking sheet velocity.

Table 3 The computation showing skin friction and critical shrinking parameter for various values of \(\phi \) and \(\lambda \) when \(M=0.1,S=1,Da=0.5,F_{n}=1\).
Full size table

As seen in figure 2b that for the upper branch solution, the skin friction coefficient rises with an increase in suction. This is because suction at the boundary slows down the fluid motion and hence increases the velocity gradient at the surface. Similar behavior of the skin friction coefficient is observed with an intensification of the magnetic field parameter as presented in figure 3b. An increase in the porous media parameter, porous medium inertia parameter, and injection parameter drops the skin friction coefficient as shown in figures 3a, 4a, and  4b, respectively. All the results obtained graphically agreed with the results mentioned in table 4.

Table 4 The computation showing impact of parameters variation on skin friction and critical shrinking parameter for Fe3O4 /H2O when \(\phi =0.1\) .
Full size table

The effects of various values of the governing parameters on fluid velocity are shown in figures 5, 6 and 7. In these figures, we noted that the existence of dual solutions with the upper and lower branches for certain values of the parameter variations and the far end boundary conditions are satisfied asymptotically. Furthermore, it is noted that the hydrodynamic boundary layer thickness for the upper branch solution is less than that of the lower branch solution. As displayed in figure 5a, the intensification of the quantity of the magnetite nanoparticle volume fraction leads to an increment in the fluid velocity for the upper branch solution and a decrement in the lower branch solution. It is also noticed that the hydrodynamic boundary layer thickness goes in the reverse pattern for the upper branch solution and the same pattern for the lower branch solution.

Figure 5
figure 5

(a) Dual solution for velocity profiles with nanoparticles concentration, \(\phi \). (b) Dual solution for velocity profiles with suction parameter, S.

Full size image
Figure 6
figure 6

(a) Dual solution for velocity profiles with porous media parameter, Da. (b) Dual solution for velocity profiles with magnetic field parameter, M.

Full size image
Figure 7
figure 7

(a) Dual solution for velocity profiles with shrinking parameter, \(\lambda \). (b) Dual solution for velocity profiles with second-order porous resistance parameter, \(F_{n}\).

Full size image

The effects of the suction parameter on ferrofluid velocity for the shrinking sheet are observed in figure 5b. This profile shows that the increment in the suction parameter resulted in an increment in fluid velocity for the upper branch solution and decrement for the lower branch solution. Further, we noted that the hydrodynamic boundary layer thickness decrease for the upper branch solution and, thus, increases the flow near the surface as the suction parameter intensifies. This is because of the reason that suction is one of the mechanisms used to reduce drag on bodies to control the boundary layer separation.

The variation of fluid velocity profile with the variation of the porous medium parameter is illustrated in figure 6a. It can be noted that the higher the value of the porous medium parameter, the lower the fluid velocity in the upper branch solution. However, a different result is obtained for the lower branch solution that the intensification in the value of porous media parameter initiated the velocity to upsurge. Moreover, the hydrodynamic boundary layer thickness gets diminished for lower values of the porous medium parameter for the stable solution meanwhile goes in the same pattern for the lower solution.

As illustrated in figure 6b, the magnetite ferrofluid is derived to the sheet surface due to the increment in the magnetic field in the porous medium for the upper branch solution. Further resistance to the flow and the magnetite nanoparticles are resulted due to the Lorentz force associated with the applied magnetic field. This resulting force leads to the thinning of the hydrodynamic boundary layer; however, the boundary layer thickens with the magnetic field parameter for the lower branch solution. Furthermore, it is found that the higher values of the magnetic field applied lead to the increment of the fluid velocity for the upper branch solution and the decrement of the fluid velocity for the lower branch solution.

Figure 7a displays the effects of the shrinking parameter on the fluid velocity. The graph exhibits that the existence of dual solution for increasing values of \(|\lambda |\) for some fixed parameters. We noted that the fluid velocity decreases as the magnitude of the stretching/shrinking parameter \(|\lambda |\) increases for the upper branch solution and it increases as \(|\lambda |\) increases for the lower branch solution. Figure 7b deals about effects of the porous medium inertia parameter on the fluid velocity. In many practical applications the non-Darcy behavior is important for characterizing fluid flow problems in a porous medium. To see the effect of this parameter, the velocity squared term is included in the momentum equation which is known as the Forchheimer’s extension of Darcy’s law. As we can see from the graph, for the upper branch solution the porous medium inertia parameter affects the the fluid velocity in opposite manner compared to the lower branch solution. It is also noted that the hydrodynamic boundary layer thickness increases with the porous medium inertia parameter for the upper branch solution.

The dual natures of the temperature profile with sensible numerical values to the governing parameters \( \phi , Ec, Da \) and \( F_{n}\) variations are illustrated in figures 8 and 9. For the chosen parameter in these figures, it seems that the difference between the upper branch and lower branch solutions is very small and dual solutions almost do not exist in the temperature profile.

Figure 8
figure 8

(a) Dual solution for temperature profiles with nanoparticles concentration, \(\phi \). (b) Dual solution for temperature profiles with viscous dissipation, Ec.

Full size image
Figure 9
figure 9

(a) Dual solution for temperature profiles with porous medium parameter, Da. (b) Dual solution for temperature profiles with second-order porous resistance parameter, \(F_{n}\).

Full size image

As shown in figure 8a, the effects of the ferrofluid particle concentration on the fluids temperature profile for other fixed parameters are manifested. It is obtained that an increase in magnetite nanoparticle volume fraction, increased fluid temperature, and also the thermal boundary layer increased with the magnetite nanoparticle concentration. This is because the enhanced thermal conductivity property of the magnetite nanoparticles promotes the thermal enhancement of the ferrofluid past the permeable shrinking surface. From this graph, we also noted that the value \(\phi = 0\) (regular fluids) implies that no magnetite nanoparticles in the base fluid which in turn tells us that the surface temperature obtained for the base fluid(water) is lower than that of the surface temperature provided by magnetite ferrofluid \(\phi > 0\). Figure 8b conveys the consequences of the viscous dissipation parameter on the fluid temperature. An escalation in this parameter gives rise to an increment in the fluid temperature. Since Eckert number has a major role in cooling the stretching or shrinking surface which in turn the heat acquired from this stretching/shrinking surface increased the fluid temperature. Additionally, the thermal boundary layer thickness gets thickens with the Eckert number because an increase in dissipation boosts the thermal conductivity of the flow which leads to an increase in the thermal boundary layer.

As we see from figure 9a, the effects of the porous medium parameter on the fluid temperature for the shrinking sheet are verified. This profile shows that the thermal boundary layer thickness decreases for increasing values of the porous medium parameter. Figure 9b displays the effects of the nonlinear porous medium inertia parameter on the variation of fluids temperature for other fixed parameters. It is obtained that an increase in porous medium inertia parameter increases the fluid temperature and also the thermal boundary layer decreases with the increment of this parameter.

Table 5 The computation of smallest eigenvalue ( \(\beta \) ) for both lower and upper branch solutions for Fe3O4 /H2O.
Full size table

The nature of dual solution occurrence is explicated by local Nusselt number graphs, figures 10 and 11, by taking sensible numerical values to the governing parameters to exploit their effects on the heat transfer processes and the intervals of the existence of the dual solution. Figure 10a shows the variation of the reduced local Nusselt number with \(\lambda \) for different values of the magnetite nanoparticles volume fraction. It can be seen that the reduced local Nusselt number upsurges with magnetite nanoparticles volume fraction which physically means that the heat transfer rate at the surface increases as \( \phi \) increases. The application of the magnetite nanoparticles volume fraction causes an increase in temperature gradient at the sheet surface and hence enhances the rate of heat transfer from the surface to the fluid. It is also noted that the heat transfer characteristics of the base fluid (water) are improved due to the application of the magnetite nanoparticles. It is also observed that the solution domain increases with the intensification of the magnetite nanoparticles volume fraction. The combined effects of the suction parameter and the shrinking sheet are presented in figure 10b. For flows past a shrinking sheet, dual solutions are found for up to some critical value \( \lambda _{c} \) beyond which the boundary layer separates from the surface and no solution is excepted in this region. For the upper branch solution, the intensification of suction assists the heat transfer processes from the shrinking sheet surface. This is because a rise in the rate of suction increases the ferrofluid particles on the shrinking surface which leads to an increase in the rate of heat transfer. It is also noted that the interval of existence of dual solution increases with the suction parameter. Figure 11a shows that opposite behavior is observed for local Nusselt numbers for varying values of the porous medium parameter. It is also observed that the solution domain decreases with the intensification of the porous medium parameter. Figure 11b shows the variability of the reduced local Nusselt number concerning the shrinking surface parameter for different values of second-order porous resistance parameter. From this graph, we observed that an inverse relationship exists between the local Nusselt number and the second-order porous resistance parameter. It is also noted that the interval of existence of dual solution diminishes with the slight increment of this parameter.

Figure 10
figure 10

(a) Variation of local Nusselt number for different values of magnetite nanoparticle volume fraction, \(\phi \). (b) Variation of local Nusselt number for different values of suction parameter, S.

Full size image
Figure 11
figure 11

(a) Variation of local Nusselt number for different values of porous media parameter, Da. (b) Variation of local Nusselt number for different values of second-order porous resistance parameter, \(F_{n}\).

Full size image

Moreover, the heat transfer enhancement (HTE) of the Fe3O4 nanoparticle for the cases of shrinking, fixed and stretching sheet are presented in figure 12. As we can see from the bar chart given, for the magnetite nanoparticles volume fraction \( \phi = 0.1 \), a maximum heat transfer enhancement with values of 75.86%, 97.24%,and 27.04% are obtained for shrinking sheet with \( \lambda = -0.2\), fixed sheet with \( \lambda = 0\) and stretching sheet with \( \lambda = 0.2\), respectively.

Figure 12
figure 12

Heat transfer enhancement rate with nanoparticles concentration when \( S =F_{n}=1, Bi=Ec=M=0.1,Da=0.5\).

Full size image

The numerical results obtained in this problem show the existence of a dual solution for certain ranges of the stretching/shrinking parameter \(\lambda \). To identify stable solutions stability analysis is done for the solutions. The smallest eigenvalue, \(\beta \), for the temporal development of small disturbances with respect to the basic steady flow is obtained for various values of \(\phi \) and \(\lambda \) when \(M=0.1,S=1,Da=0.5,F_{n}=1\) as shown in table  5. we noted that the eigenvalues, \(\beta \), obtained for the upper branch solution are positive while those of lower branch solutions are negative. This confirms that the upper branch solution is hydrodynamically stable and the solution is physically achievable whereas the lower branch solution is unstable and physically unrealistic.

6 Conclusion

A study on stagnation point flow of magnetite ferrofluid past a stretching/shrinking sheet in a Darcy-Forchheimer porous medium is carried out numerically to investigate the collective effects of viscous dissipation, magnetic field, suction or injection, porous medium, porous medium inertia parameter, and convective heating. A stability analysis is performed to identify stable and physically reliable solutions. The effect of various parameters on the dimensionless velocity and temperature, skin friction, and the Nusselt number are obtained numerically and presented in graphs and tables. Using a set of similarity transformations the governing boundary layer equations are transformed into a system of nonlinear differential equations and MAPLE software is used to generate the numerical solutions. The following are concluded based on the findings:

  • Dual solutions exist for certain ranges of the stretching/shrinking parameter \(\lambda \).

  • The upper branch solution is hydrodynamically stable and is physically achievable, whereas the lower branch solution is unstable and physically unrealistic.

  • The intensification of the magnetite nanoparticle volume fraction, suction/injection, and the magnetic field parameter widen the range of \( \lambda \) for which the solution exists and narrow for the increment of the porous media parameter and the porous medium inertia parameter.

  • The skin friction coefficient for the upper branch solution is intensified with an increase in the quantity of magnetite nanoparticle volume fraction, suction, and the magnetic field parameters but drops for the porous medium parameter, porous medium inertia parameter, and the injection parameter.

  • For the upper branch solution, the ferrofluid velocity increases with the quantity of magnetite nanoparticle volume fraction, suction, and the magnetic field parameters, whereas decreases with an increase in the shrinking parameter and porous medium parameter.

  • The momentum boundary layer thickness increases with the shrinking parameter and porous medium parameter but decreases with an increase in the magnetite nanoparticle volume fraction, suction, and magnetic field parameters.

  • The ferrofluid temperature and thermal boundary layer thickness are enhanced with an increase in the magnetite nanoparticle volume fraction and Eckert number but diminished with an increase in porous media parameter and porous medium inertia parameter.

  • The heat transfer rate increases with the magnetite nanoparticle volume fraction and suction parameters, whereas decreases with the porous media parameter and porous medium inertia parameter.