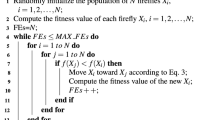1 Introduction

Meta-heuristic algorithms are approximate techniques for solving an optimization problem. They capitalize on intuitions along with randomness property in their search for improving solutions at hand through successive iterations. Nature has inspired the development of many meta-heuristic algorithms [1, 2]. The earliest of this kind, in the form of genetic algorithm (GA) [3, 4] was motivated by Darwin’s survival of the fittest by means of natural selection. Several researchers have shown there keen interests in this beautiful domain since then. As a result, numerous meta-heuristic algorithms have emerged over years [5, 6].

Different creatures communicate with each other through various unique modes of communication. Fireflies use their flashing lights of varying intensity to communicate for attracting mates or warning predators. A suitable mate would either communicate back mimicking the same pattern of flash or would produce response in a different flashing pattern. The intensity of the light which is the key source of attraction also depends on the distance between the source and the observer because of absorption in air. Environmental conditions like wind, darkness or fogginess also regulate the intensity. This phenomenon besides soothing the eyes of nature lovers in the darkness of summer nights has become the epitome of inspiration for many scientific researchers mainly dealing with optimization problems.

1.1 Standard firefly algorithm

Fireflies may be conceived as candidate solutions in the search space. The attraction and movements offer heuristic goals to achieve brighter fireflies i.e. better solutions. The standard firefly algorithm (FA) which has been developed by Yang [7] has two parts in the position updates as shown in Equation (1),

$$\begin{aligned} x_i = x_i + \beta _0^{(-\gamma \times r_{ij}^2)} (x_j - x_i) + \alpha (\varepsilon () - 0.5) \end{aligned}$$
(1)

where, \(x_i\) is the position of the firefly that is to be updated based on the difference of position of another firefly denoted by \(x_j\); in the first part, which is driven by attraction heuristic, \(\beta _0\) is the light intensity when the distance between them is 0, \(\gamma \) is the absorption coefficient and \(r_{ij}\) is the Euclidean distance between them; in the second part, which models random movement, \(\alpha \) is the coefficient of randomness and \(\varepsilon ()\) yields a random value in [0, 1].

1.2 Modifications of standard FA

FA is prone to premature convergence triggering efforts to relax the constant parameters used therein. Studies also show that this is comparatively slow and often suffers from problems of falling into local minima [8]. The movement update function solely depends on the present light intensity or fitness and no previous memory is preserved. Furthermore, the algorithm parameters are fixed for all the successive iterations making the step length of learning, constant, thereby foregoing the needed exploitation especially at the later stages. Enormous efforts have been channelled to boost the performance of the standard FA [9, 10]. The various modifications, in accordance with some broad categories are as follows.

1.2a Based on adaptive parameters: In this category, the parameters i.e. the user defined constants, used in like any other meta-heuristic algorithms, have been updated in the successive iterations. These constants control the degree of exploitation and exploration. The randomness coefficient \(\alpha \) has been tuned based on the current iteration number by Shakarami and Sedaghati [11]. Kavousi-Fard et al [12] have improvised the randomness part using crossover and mutation operators. Modification of attraction related parameters (\(\beta _0\), \(\gamma \) and \(r_{ij}\)) have been also explored by many researchers. Lin et al [13] have used a new concept of virtual distance, \(r'\), and computed the intensity of light \(\beta \) as \(\beta _0\gamma (1-r')\) to update the position of fireflies. Gandomi et al [14] have employed 12 different chaos functions which have non-repetition and ergodicity properties for updating the constant values of the algorithm (\(\beta \) and \(\gamma \)). Sulaiman et al [15] have introduced minimum variance distance replacing the Cartesian distance for the attraction part. The random part has been modified with a mutation operator. Wang et al [16] have handled the premature convergence by regulating all the constant parameters based on the difference of light intensity measured by a formula dependent on number of iteration. Yu et al [17] have proposed wise step length control specific to individual firefly based on its personal and global best position for updating its current position. A practical problem of optimizing droplet ejection speed in electro-hydrodynamic inkjet printing has been reportedly solved by using an improved FA [18]. The authors have used a new rule for updating the brightness instead of a constant initial brightness coefficient for getting comparatively better results.

Keeping in view the simple modifications in this approach, the results have been really encouraging. It has been proved that keeping updating strategy same may lead to stagnation. None of the cases in this line have considered the need for changing updating strategy in general. This method has also not considered the past memory. This method has not been able to reduce the search space to speed-up the convergence.

1.2b Based on update strategy: The second class of approaches for modification deals with changing the strategy of updating the position of the fireflies. Opposition based approach has been introduced by Roy et al [19] for solving high dimensional problems where opposite or reverse set of regularly achieved population has been determined in each iteration. The brightest one has been updated by \(x_{min} + x_{max} - x\) so that it can still improve from the initial local extremes. This method to some extent mimics the mutation operator in genetic algorithm which has eventually initiated many experiments with different methods and levels of incorporation. Yu et al [20] have defined a criterion of hazardous condition based on which a mutation can be operated on the weaker solutions to improve them. Additionally, the authors have preserved the historical performance in memory so that hitherto best cases are not left-out. Kazemzadeh-Persi [21] has added k newborn generations in each iteration with the help of mutation. The authors also have suggested updating the position based on the average directions of movement dictated by all the brighter fireflies. Another line of modification has been approached [12, 22] by employing five crossover operators and three mutation operators along with adaptive \(\alpha \). Three random solutions have been considered for generating the mutated solutions, one by applying \(x_{mute1} = x_{q1} + \varepsilon (x_{q2} - x_{q3})\), and another for any iteration number t by applying \(x_{mute2} = x_{mute1} + \varepsilon t(x_b - x_w)\). In other similar works [11, 23], the value of \(\alpha \) has been made adaptive by chaotic mapping or applying mutation operator. Mohammadi et al [23] have proposed the update of the position with respect to the brighter firefly \(x_j\), thereby adding more exploration capability. Hassanzadeh and Kanan [24] have used fuzzy attraction function represented by a Cauchy distribution from the selected top k brighter fireflies to impose the influence of a collection rather than an individual in order to explore towards the global best. In some literature [25, 26] , mutation has been used replacing the updating formula in Equation (1) or as an additional operator immediately after using the same updating formula. Wang et al [27] have introduced Cauchy distribution for performing mutation on the initially fitter fireflies known as good nodes set to obtain improved results on benchmark functions. In another recent work by Peng et al [28], a novel courtship learning strategy has been adopted where the updating of the position of the lower intensity male fireflies have been accomplished using the guidance from the relatively superior female fireflies. Tong et al [29] have proposed using several diverse sub-groups of FA and exchanging information for learning collectively about the global best more effectively. Zhou et al [30] have adopted partial attraction model which have been used to protect swarm diversity and utilize full individual information. Baykasouglu et al [31] have proposed a modification to FA to solve dynamic multidimensional knapsack problem by replacing pair-wise comparison by a specialized comparison based on a dynamic variable in each iteration. The authors have also used a probabilistic switch to decide whether to update the position or not for the firefly to avoid early convergence and reduce computational time.

This method of modification has been deemed very useful to specific problems. This has not considered the already improvement areas like adaptive control or changing the randomness characteristics for better explorations. This method has been not able to reduce the search space and the time complexity of convergence.

1.2c Based on solution space and randomness control: In the third category of approaches, two types of modification have been tried. Firstly, changing the solution space to an easy search space has been explored by Liu et al [32]. They have used quaternion representation for \(x_i(k) = \) \((y_1^i, y_2^i, y_3^i, y_4^i)\) for all components k. The update of position takes place in the quadruple-folded search space, while the computation of brightness is done in actual solution space using a norm transform function. Fister et al [33] have also used quaternion representation of the solution space for enhancing performance and avoiding stagnation. Wang et. al. [34] have used a predefined neighbourhood to overcome the problem of oscillation based on too much attractions happening during the search. Secondly, the randomness behaviour of the fireflies has been controlled by following certain probability distribution functions. For example, Farahani et al [35] have introduced Gaussian distribution, whereas Yang [36] has used Levy distribution for generating component wise product with the original random fraction. The randomness property has been improved by adding direction of movement of the fireflies using an additional sign vector in case of the later. Tighzert et al [37] have presented a set of new compact firefly algorithms involving levy functions, elitism or preservation of previous performances and opposition-based learning. They have tested on benchmark functions considering 30 dimensions. Wu et al [38] have also used adaptive logarithmic Levy distribution to improve over the global searching characteristics of FA using a probabilistic switch.

The best part about this method is the reduction of search space thereby minimizing the computational cost of the algorithm. This approach of modification has been proved beneficial in most of the cases though the use of other lines of modifications like adaptive control and changing the updating strategy along with it would have clearly achieved more robustness.

1.2d Hybrid approaches: There have been a few attempts of hybridization of the FA with other evolutionary algorithms. Luthra and Pal [39] have used genetic operators like crossover along with the standard FA for solving a monoalphabatic substitution cipher problem. Rahmani and MirHassani [40] have applied genetic crossover operator on the two fittest fireflies and mutation on the whole population based on the mutation probability after the pass of standard algorithm in each iteration. They have used this for solving a capacitated facility location problem. Sarangi et al [41] have modified the FA by integrating the formula used in particle swarm optimization (PSO). They have retained best positions for both individual and group in all successive iterations and have used it for the additional velocity component calculation. Aydilek et al [42] have enhanced hybrid FA and PSO by incorporating chaotic functions. Yelghi and Köse [43] have successfully incorporated the concept of tidal force for modifying the attraction component of the standard FA. Tomas et al [44] have introduced the concept of orthogonal learning to the hybridized FA and PSO algorithms to affect better performances than that obtained from the original hybridization. Huang et al [45] have used a hybridization of GA, FA and differential evolution (DE) to enable the maximum power point tracking for photovoltaic systems under partial shading conditions. The authors have created the hybridization framework by implementing DE mutation followed by FA attraction and finally carrying out GA crossover in each generation.

The hybrid methods of FA have been able to successfully make inroads to the hitherto unseen solution space. Nevertheless, a generic framework of integration of different independent meta-heuristics has not been standardized. There has been no such work reported which has partitioned the population and considered running different meta-heuristic algorithms in sub-groups.

1.3 Need and novelty of new algorithm

There have been numerous efforts for improving the standard FA to solve multiple optimization problems. At the same time they have added precious knowledge base to the literature in the process of different approaches of modifications. The key aspects that can be highlighted from the rigorous literature review are as follows:

  • Randomness part can be modified with controlled direction using genetic crossover and/or mutation or following other probability distributions for better exploration.

  • Records of past solutions and performance avoids probable loss of eligible solutions.

  • Adaptive \(\alpha \) comes handy especially at later stages for intensive exploitation.

Giving due respect to the previous modification efforts, it has been observed that there is no formal integration with any full fledged evolutionary algorithm as such. Genetic operators in parts have been tried as an alternate or additional update strategy of the standard FA. Their application has been targeted mainly on the fittest fireflies [40] for getting even better solutions. In some cases it has been purely application specific implementation of crossover using dominant genomes [39]. The modified algorithm in such case can not be used for solving any general optimization problems. If in any scenario it has been used to evolve the weaker solutions alone, additional evaluations of objective function fitness have been performed incurring more computational cost.

1.4 Motivation and inspiration

A single method of modification may not capture all the needed improvements of the existing FA. This may raise issues with premature convergence in problems with higher dimensionality. A very handful cases have concentrated on combining different approaches of modifications. A very few of the previous works reported has targeted hybridization of different meta-heuristics in true sense. Hence, this work aims to capitalize on the strengths of two algorithms viz. faster convergence of GA and better accuracy of FA so as to achieve a better performing algorithm.

In this approach, a novel methodology is formulated in the form of partition cum unification based genetic - FA (PUBG-FA) by integrating FA with GA. The initial population is partitioned into two compartments based on a weight factor, w set by user, which determines how much of the algorithm is dominated by FA. The first compartment which has the superior fireflies based on light intensity (fitness) runs a little improved version of standard FA, whereas the second chamber consisting of the weaker solutions runs the entire GA encompassing selection, crossover and mutation. After each iteration these two populations are again unified and the intensities of the new fireflies are computed. Based on that, the consolidated population is sorted and trimmed before going to the next iterative cycle for further partition, update and unification. The new algorithm in three variants of different w (30\(\%\), 50\(\%\) and 70\(\%\)) is tested and compared with the two constituents i.e. standard firefly and genetic algorithm and additionally with some state-of-the-art meta-heuristics namely PSO [46], cuckoo search (CS) [47, 48], flower pollination algorithm (FPA) [49], pathfinder algorithm (PFA) [50], bio-geography based optimization (BBO) [51] on 19 benchmark objective functions of different complexity, continuity, differentiability, mode, separability and scalability. This testing is carried-out considering several dimensionality of the problems viz. 2-D, 16-D, and 32-D. Further, the new algorithm is tested and compared with others on two real engineering optimization problems namely tension-compression spring [52, 53] and 3-bar truss problem [53, 54]. Non-parametric statistical tests, namely Wilcoxon rank-sum tests are conducted on the objective function values for each dimensional (scalability) test for all the algorithms from repeated independent experiments to statistically rule-out any significant deviations. One of the extensively used multi-criteria decision making (MCDM) tools, namely, technique for order of preference by similarity to ideal solution (TOPSIS) [55] is applied to statistically determine the best performing algorithm given the different multi-dimensional test scenarios and two assessment criteria - running time and objective function value.

Thus, the primal novel prospects and contributions of this article can be summarized as follows:

  • Seeking key improvement areas of FA from the past literature and combining them together for getting added advantages.

  • Envisaging a genetic strategy so as to achieve a faster convergence rate than conventional FA.

  • Partitioning the population for running two algorithms in two compartments and unification of the population derived from respective compartments.

  • Keeping the algorithmic parameter to tune to a single weight factor indicating the dominance of one algorithm over another.

  • Utilizing MCDM tool to strategically decide the final ranks of the competing optimization algorithms.

The rest of the paper is segmented as follows: section 2, where the methodology is described, presents the new algorithm elaborately and describes the objective functions and engineering optimization problems considered for testing. Results of all the testing are discussed in section 3. Finally, some concluding remarks are drawn in section 4.

2 Methodology

The basic idea of the new algorithm PUBG-FA is pretty simple. Dimmer fireflies get attracted towards the brighter ones and by virtue of their positions getting updated, their light intensities or objective fitness values are improved. The weaker section having feeble flashing intensity, instead of waiting for their turn for improving up the ladder of intensity through generations, are moved into a separate genetic compartment. In this space they get opportunities for further and faster improvement through explorations by applying standard genetic operators, namely selection, crossover and mutation. The remaining best part of the population having brighter fireflies undergo a little improved version of the standard FA in the primary compartment. Memory of the candidate solutions, random movement of the brightest firefly and adaptive \(\alpha \) constitute the improvement spectrum of FA as already successfully experimented in some previously reported works [19, 20, 36]. Figure 1 shows the flowchart of the new algorithm. After each iteration, the populations from two compartments along with the past memory are unified and ranked according to the light intensity meaning the objective fitness value before venturing for the next cycle. In the pseudo code presented in Algorithm 1, the new algorithm can be easily comprehended. Key improvement areas and features of PUBG-FA are discussed in the following subsection.

2.1 Features of PUBG-FA

2.1a Memory of past records: In the standard FA, the positions of all the fireflies are updated in a stochastic goal direction. Naturally, it may so happen that the intensity of the light meaning the objective fitness deteriorates from the previous value. Hence, it is changed to keep memory of the past records so that eligible candidates once found are never lost.

2.1b Random movement of the brightest: The position of the brightest firefly is not updated by the standard FA as because only dimmer fireflies update positions with respect to the brighter ones. Therefore, the algorithm is modified so that the brightest one is updated by the following Equation (2) involving only random term.

$$\begin{aligned} x_i = x_i + \alpha (\varepsilon () - 0.5) \end{aligned}$$
(2)
figure a
Figure 1
figure 1

Flowchart of the new algorithm.

Full size image

2.1c Adaptive random coefficient: It has been realized by the past researchers that an adaptive \(\alpha \) improves the exploration in the beginning and exploitation in the final stages of the FA. The following Equation (3) is used to update \(\alpha \) based on the value of initial randomness coefficient \(\alpha _0\) value and current generation/iteration counter iter.

$$\begin{aligned} \alpha = \alpha _0 \times 0.95^{iter} \end{aligned}$$
(3)

2.1d Partitioning the population: The initial population of size pop with randomly assigned positions is partitioned into two compartments based on w, which actually says \(w \times pop\) would go into FA compartment and the rest i.e. \((1-w) \times pop\) would go into the GA counterpart. This essentially makes the number of total functional evaluations same as that of the standard FA while improving the exploration capability by applying integrated GA.

2.1e Genetic operators: The specific implementations of genetic operators immensely influence the performance of GA. In this real coded GA, RouletteWheel selection mechanism is adopted. Uniform crossover as shown in Equations (4) and (5), is implemented. with a crossover probability of 0.8. Mutation operator is implemented by taking average of a random fraction \(\varepsilon ()\) in [0, 1] and previous value on the same dimension of position vector with a mutation probability of 0.2 as presented in Equation (6).

$$\begin{aligned} X_{child1}&= {} X_{parent1}\times \varepsilon () + X_{parent2}\times (1-\varepsilon ()) \end{aligned}$$
(4)
$$\begin{aligned} X_{child2}&= {} X_{parent1}\times (1-\varepsilon ()) + X_{parent2}\times \varepsilon () \end{aligned}$$
(5)
$$\begin{aligned} X_{mutated}&= {} \frac{1}{2} \times (X_{child}+ \varepsilon ()) \end{aligned}$$
(6)
Table 1 Benchmark objective functions.
Full size table

2.1f Unification before ranking: The position-updated populations from the two compartments are unified and ranked according to their newly computed light intensities or fitness values. This approach is better than parallel processing of FA and GA in two compartments without mixing. This is because the current scheme i.e. unification creates more chances to the newly evolved fireflies from GA compartment to come to the mainstream FA and thereby converge rapidly by following a local direction of search.

2.2 Objective functions for testing

The new algorithm in three variants with 30%, 50% and 70% of w is tested on 19 benchmark functions [56, 57] as illustrated in table 1 and the results are compared with that of the standard FA and GA and some five state-of-the-art meta-heuristic algorithms, namely PSO, CS, FPA, PFA, and BBO. Here, the different variants of this algorithm is used to study the impact of w on the overall performance. In this study, three main indices used for comparison are mean CPU time, mean number of functional evaluations and mean value of objective function presented by the best solution. The population size and maximum generation for termination for the 2-D functions (function 1 to 10 in table 1) are kept at 50 and 100 respectively. The respective values are chosen as 200 and 300 for all 16-D and 32-D functions (function 11 to 19 in table 1) for the enhanced complexity of the problems. The number of independent repeated trials is set at 30 for all the functions. The parameter settings for all the algorithms are fixed as per the values in table 2. To make the comparative study really unbiased, all the algorithms are started with the same initial random population set.

Table 2 Parameter settings for the algorithms.
Full size table
Figure 2
figure 2

Tension-compression spring mass problem.

Full size image
Figure 3
figure 3

3-bar truss structure problem.

Full size image

2.3 Engineering case study problems for testing

The algorithms have been also tested on some real world, engineering case study problems which are described in the following sub-sections:

3.1a Design optimization of tension/compression helical spring: In this case, the objective is to minimize the weight of a helical spring under tension/compression. Design variables for this case study are wire diameter (d), mean coil diameter (D), and the number of active coils (N) (figure 2). Here, the constraints on shear stress, surge frequency, and minimum deflection should be satisfied during the weight optimization. The objective function and the constraints of this problem can be formulated as follows:

$$\begin{aligned}&Consider \overrightarrow{x} = [x_1 x_2 x_3] = [d D N],\\&Minimize\, f (\overrightarrow{x}) = (x_3 + 2)x_2 {x_1}^2,\\&Subject \quad to\\&g_1(\overrightarrow{x}) = 1 - \frac{{x_2}^3 x_3}{71785 {x_1}^4} \quad \le 0,\\&g_2(\overrightarrow{x}) = \frac{{4x_2}^2 - x_1x_2}{12566(x_2{x_1}^3 - {x_1}^4)} + \frac{1}{5108{x_1}^2} - 1 \quad \le 0,\\&g_3(\overrightarrow{x}) = 1 - \frac{140.45{x_1}}{{x_2}^2 x_3} \quad \le 0,\\&g_4(\overrightarrow{x}) = 1 - \frac{x_1 + x_2}{1.5} \quad \le 0\\&Ranges\quad of\quad variables\\&0.05 \le d \le 2.00,\quad 0.25 \le D \le 1.30,\quad 2.00 \le N \le 15.00 \end{aligned}$$

Instead of choosing strict death penalty which often suffers stagnation, this problem has been formulated by a modified version of barrier penalty approach [58], which works by adding weighted penalty values computed from the deviations from all the constraints to the objective function value. The initial population has been generated considering the feasible solution space defined by only the individual bounds of the decision variables. The final solution has also been checked for feasibility. The candidate which lies in the last generation of solutions matching all the constraints with the best objective function value has been selected as the solution.

3.1b Design optimization of 3-bar truss structure: This problem can be regarded as one of the most studied cases in constrained optimization works for bench-marking. Figure 3 illustrates the shape of the formulated 3-bar truss and the related forces acting on this structure. Here, the design space constitutes of two parameters: the area of bars 1 and 3, which is \(A_1\) and the area of bar 2, which is \(A_2\). The objective of this problem is to minimize the total weight of the structure. While solving this, the optimal design has to satisfy several constraints including stress, deflection, and buckling.This problem can be formulated mathematically as follows:

$$\begin{aligned}&Consider \overrightarrow{x} = [x_1 x_2] = [A_1 A_2],\\&Minimize\,f (\overrightarrow{x}) = (2\sqrt{2}x_1 + x_2)\times L,\\&Subject \quad to\\&g_1(\overrightarrow{x}) = \frac{\sqrt{2}x_1+x_2}{\sqrt{2}{x_1}^2 +2x_1x_2}P -\sigma \quad \le 0,\\&g_2(\overrightarrow{x}) = \frac{x_2}{\sqrt{2}{x_1}^2 +2x_1x_2}P -\sigma \quad \le 0,\\&g_3(\overrightarrow{x}) = \frac{1}{\sqrt{2}x_2 +x_1}P -\sigma \quad \le 0\\&Ranges\quad of\quad variables\\&0.00 \le A_1 \le 1.00,\quad 0.00 \le A_2 \le 1.00\\&where \quad L = 100 \, cm, \quad P = 2 N/{cm}^2, \quad \sigma =2 N/{cm}^2 \end{aligned}$$

This problem has been similarly modelled by adding penalty values to the specific objective function value. The initial population has been generated considering the feasible solution space defined by both the individual bounds of the decision variables and all the constraints to be satisfied. The final solution has been checked for feasibility defined by the bounds and constraints.

2.4 Statistical tests

As per the recommendation by Derrac et al [59], the non-parametric Wilcoxon rank-sum statistical test with 95% degree of confidence (5% degree of significance) is performed along with experimental evaluations to detect any significant differences between the attained results of different algorithms.

TOPSIS is one of the most popular MCDM tool and has been successfully utilized for decision making across many engineering domains. There are grossly two criteria for relative comparison of all the meta-heuristic algorithms - mean CPU time and mean objective function value computed from 30 independent repeated runs with a specific algorithm. The lower the time and value, the better is the algorithm. The respective mean values for all the dimensions (2-D, 16-D and 32-D) including the engineering problems are used for comparative study.

3 Results and discussions

It should be mentioned that other than the improvement areas mentioned earlier all the remaining equivalent design and implementation is kept unaltered for all the algorithms in test. The user defined constant parameters are also same for all the algorithms. All the respective parameters and their values are shown in table 2. The results for benchmark objective functions and real engineering problems are discussed in the following subsections.

3.1 Results for benchmark objective functions

The population size and maximum number of iteration have been kept 50 and 100 respectively, for all the meta-heuristic algorithms for this lower dimension tests. It is clearly visible from comparison results of tests on 2D objective functions tabulated in table 3, the new PUBG-FA performs better in comparison with the standard FA and GA and it outperforms most of the state-of-the-art algorithms tested in this study. In case of Beale and Schaffer(6), FA3 has been found to be most accurate optimizer, while for Zettl function FA2 has been the topmost performer. For rest of the 2D functions, FA4 with the maximum (70%) weightage/dominance of FA has been proved to be the most suitable blender. It performs satisfactorily well for all the multimodal problems and specifically for functions like Carrom Table and Easom with nearly flat like surfaces containing very small central nadir area. In case of Acley (1) and Zakharov, PFA produces the least objective function value with the new algorithm closely following it. Figures 5 to 14 show the convergence plots of the algorithms for the 2-D objective functions. The convergence plots of the Carrom Table function and Easom function reveal that standard GA and standard FA get trapped at local minima, respectively. This clearly raises concerns about using any one specific standard algorithm for the two optimization problems. However, the new algorithm performs well and finds the global minima, converging pretty faster for both the optimization problems. It is clear from the plots that all the algorithms start with the initial same fitness dictated by the same initial population set design. Working with the higher dimensional 16-D benchmark function tests, the new algorithm is found to outperform all the algorithms except for Rastrigin function (table 4). Testing with the same group of functions on 32-D, has produced similar kind of results in favour of the new algorithm except for Rastrigin and Step (2) functions (table 5). The minimum objective values (global minimums) for all the functions tested are 0. For complexly scattered multi-modal functions like Rastrigin and Rosenbrock functions, where all the standard algorithms find it hard to converge to the global minima, the new PUBG-FA shows encouraging results. Figures 15 to 33 show the convergence plots for the 16-D and 32-D objective functions. Competitiveness of different algorithms for Alpine(1) and Rastrigin functions is studied from the respective graphs. They are complex, uniformly distributed multi-modal functions with a single global minimum at 0. The standard optimization algorithms are trapped at local minima whereas the proposed FA variants avoid trapping into local minima and converge rapidly. The impressive result is due to the seamless hybridization of the two standard algorithms enhancing both exploration and exploitation. The same happens with Step (2) and Sum Squares function, where the PUBG-FA is able to find competitive results while most of the other algorithms including the standard FA and GA seem to suffer from local optimization traps. In case of Rastrigin function alone when tested on 16-D, the new algorithm is preceded by FPA, PSO and BBO in the ascending order of superiority. In the further higher dimension of Rastrigin and Step (2) functions, BBO and FPA has been found the best performer respectively. In all the functions of higher dimensions too, PUBG-FA has outperformed the standard algorithms FA and GA quite consistently. The fast convergence rate of the new algorithm is very much evident from all the convergence plots. The success of PUBG-FA is due to the continuous exchange of useful information between two complete sets of different algorithms.

Even though, the variant with highest w (70%) as represented by FA4 is the overall best performer among all, FA2 with the least weightage of FA (30%) shows commendable performance when considered in terms of both accuracy and speed of convergence. FA2 has seen comparatively higher success rates in the higher dimensions. The most remarkable result is achieved while optimizing the 16-D and 32-D Sphere, Step (2) and Sum Squares functions, where it could draw a clear demarcation line of quality between itself and the two standard algorithms used as the constituents - FA and GA.

The average time taken and standard deviations are also far less than that of the standard FA and for lesser w variant it is very close to GA. The number of functional evaluations for all the algorithms is logged and found same for all the algorithms and it matches with the theoretically obtainable values (\(D\times N\)) i.e. 5000 and 60000 for the 2-D and higher dimensional functions (16-D and 32-D) respectively.

The time complexity of the new algorithm is studied by analytical method alongside plotting with a close watch on the reported time of execution in logs. Considering N as the population size the time complexity for the standard GA and FA are in the order of \(O(\frac{9N}{2} + 2N\log {(2N)})\) and \(O(\frac{N}{2}\times (N-1) + N\log (N))\) respectively. The newly developed PUBG-FA maintains an intermediate order of time as regards the standard algorithms, which can be computed as \(O(\frac{9N}{4} + \frac{N}{4}\times (\frac{N}{2}-1) + 2N\log {(2N)})\).

Figure 4 shows the plotting of time complexity of the new algorithm (FA3) along with that of the constituents used. It is evident from the mean CPU time tabulated in the table 4, all the variants of the new algorithm has an intermediate time complexity between standard GA and FA1 (standard FA). The fitness convergence plots against elapsed computation time for all the function tests and case studies are separately available as supplementary files (Figures. S1 to S30).

Figure 4
figure 4

Time complexity plot of the new algorithms and constituents.

Full size image

3.2 Results of engineering case study problems

The new algorithm has shown clear supremacy in dealing with constrained optimization problems when entrusted to solve two real engineering case studies. Population size and maximum number of iterations have been set as 200 and 300 respectively for the tension-compression spring problem having three variables. The FA4 variant of PUBG-FA has been able to expose the best solution with optimal weight satisfying all the constraints. The comparison results obtained in this study are tabulated in table 6. Similarly, the 3-bar truss optimization problem has been solved by all the algorithms using population size and maximum iteration number as 50 and 100 respectively. Here also, FA4 has been the topmost performer producing the least objective value. The results shown in table 7 indicate a total supremacy of all the variants of the new algorithm in the context of this particular case study. The performance plots for the engineering case studies are shown in figures 33 and 34. This proves that the new algorithm is aptly suitable in handling real world constraints besides achieving global optimization.

Table 3 Comparison results of 2-D functions (function 1 - 10).
Full size table
Figure 5
figure 5

Performance plot of Ackley (1) Function.

Full size image
Figure 6
figure 6

Performance plot of Beale Function.

Full size image
Figure 7
figure 7

Performance plot of Carrom Table Function.

Full size image
Figure 8
figure 8

Performance plot of Easom Function.

Full size image
Figure 9
figure 9

Performance plot of Goldstein-Price Function.

Full size image
Figure 10
figure 10

Performance plot of Michalewicz Function.

Full size image
Figure 11
figure 11

Performance plot of Schaffer (6) Function.

Full size image
Figure 12
figure 12

Performance plot of Xin-She-Yang (3) Function.

Full size image
Figure 13
figure 13

Performance plot of Zettl Function.

Full size image
Figure 14
figure 14

Performance plot of Zakharov (1) Function.

Full size image
Table 4 Comparison results of functions 11 - 19 for 16-D.
Full size table
Table 5 Comparison results of functions 11 - 19 for 32-D.
Full size table
Figure 15
figure 15

Performance plot of Alpine(1) Function for 16-D.

Full size image
Figure 16
figure 16

Performance plot of Alpine(1) Function for 32-D.

Full size image
Figure 17
figure 17

Performance plot of Dixon-Price Function for 16-D.

Full size image
Figure 18
figure 18

Performance plot of Dixon-Price Function for 32-D.

Full size image
Figure 19
figure 19

Performance plot of Levy Function for 16-D.

Full size image
Figure 20
figure 20

Performance plot of Levy Function for 32-D.

Full size image
Figure 21
figure 21

Performance plot of Rastrigin Function for 16-D.

Full size image
Figure 22
figure 22

Performance plot of Rastrigin Function for 32-D.

Full size image
Figure 23
figure 23

Performance plot of Rosenbrock Function for 16-D.

Full size image
Figure 24
figure 24

Performance plot of Rosenbrock Function for 32-D.

Full size image
Figure 25
figure 25

Performance plot of Sphere Function for 16-D.

Full size image
Figure 26
figure 26

Performance plot of Sphere Function for 32-D.

Full size image
Figure 27
figure 27

Performance plot of Step (2) Function for 16-D.

Full size image
Figure 28
figure 28

Performance plot of Step (2) Function for 32-D.

Full size image
Figure 29
figure 29

Performance plot of Sum Squares Function for 16-D.

Full size image
Figure 30
figure 30

Performance plot of Sum Squares Function for 32-D.

Full size image
Figure 31
figure 31

Performance plot of Xin-She-Yang (1) Function for 16-D.

Full size image
Figure 32
figure 32

Performance plot of Xin-She-Yang (1) Function for 32-D.

Full size image
Figure 33
figure 33

Performance plot of tension-compression spring problem.

Full size image
Figure 34
figure 34

Performance plot of 3-bar truss structure problem.

Full size image
Table 6 Comparison results of tension-compression spring problem.
Full size table
Table 7 Comparison results of 3-bar truss structure problem.
Full size table
Table 8 p-values obtained in Wilcoxon rank-sum tests on 2-D functions with 5% significance.
Full size table
Table 9 p-values obtained in Wilcoxon rank-sum tests on 16-D functions with 5% significance.
Full size table
Table 10 p-values obtained in Wilcoxon rank-sum tests on 32-D functions with 5% significance.
Full size table
Table 11 Results of TOPSIS conducted on all the algorithms. Equal weights for all functions. Weights for time:objective value = 1:3.
Full size table

3.3 Results of statistical tests

The results of non-parametric Wilcoxon rank-sum tests are tabulated in tables 8, 9, and 10 for 2-D, 16-D and 32-D benchmark functions respectively. The p-values are all below 0.05 (with 5% significance) and thus confirm that there is no significance differences in the results obtained in independent trials. The final ranks obtained by applying TOPSIS considering all the test scenarios are shown in table 11. It shows that FA2 and FA3 variants of PUBG-FA are the two top performing algorithms followed by PSO and GA. The other variant of the new algorithm - FA4 is assigned the 5th overall rank. Equal weights are given for all the objective functions and problems whereas ratio of weights of computation time to objective value is chosen as 1:3.

4 Conclusions

In this paper, a new algorithm PUBG-FA is proposed, which first partitions the population in two compartments for running a slightly modified FA and standard GA. Then it unifies the worked-upon sub-populations of two compartments and finally ranks the fireflies before going into next generation. The new algorithm is experimented with three variants of weightage, w which determines the percentage of total population belonging to FA chamber. This is tested on 19 different benchmark optimization functions, the first 10 of which are used as 2-D functions and the rest are run separately as 16-D and 32-D functions. The results, when compared with the standard FA and GA, show the algorithm is significantly more efficient with faster convergence than the standard FA and lower minimal values than the two. The new algorithm is also compared with some of the state-of-the-art meta-heuristic algorithms on the same functions and encouraging results are observed. A popular MCDM tool TOPSIS reveals that the new variants are very competitive and successfully outperform some renowned algorithms in majority of the cases.

Meta-heuristic algorithms are not panacea. It has been exhibited that different optimization problems suit different techniques ranging from simple classical optimization methods to complex meta-heuristic and population-based evolutionary algorithms. The methodology adopted in this study can be seen as a new approach of dealing with multiple population based meta-heuristic algorithms collaboratively for solving a particular optimization problem. This work has some prompting directions pertaining to the future works as follows:

  • The same hybridization schema can be rigorously explored in future considering other combination of some of the top performing evolutionary algorithms like PSO, FPA, BBO, etc.

  • The new PUBG-FA can be further tailored for new practical problems associated with social and engineering domain, e.g., preservation of privacy in social networks, the multicast vehicle routing, and parameter tuning in training of machine learning and artificial intelligence models.