A numerical study on the effect of aspect-ratio and density ratio on the dynamics of freely falling plate in the flutter-to-tumble transition regime

Abstract

The motion of a freely falling thin aluminium plate in water is studied using two-dimensional numerical simulations. The fluid-solid interface is treated using the diffuse interface immersed boundary method. Periodic side-to-side fluttering motion at the small dimensionless moment of inertia $(I^{*})$ becomes chaotic in the intermediate range which finally settles for pure tumbling at high $I^*$. Even the stable flutter trajectories exhibit significant sensitivity to incremental deviation in fluid forces brought in by inaccurate time marching. The maximum instantaneous inclination angle of the plate increases with $I^*$ during flutter with the uniform multilevel distribution. At larger $I^*$, such distribution collapses to nearly a single level indicating the ability of the plate to autorotate under the influence of turning moment created by the neighbouring fluid. The plate is observed to retain the initial orientation during its flight in the tumbling regime. The range of $I^{*}$ for chaotic motion is found to extend with the increase in initial inclination angle. Tests on the effect of initial conditions on the trajectories of the plate indicate while the chaotic regime is mostly affected by initial orientation and velocity of release, flutter and tumble motions converge for a variety of initial states. The chaotic motion transforms into a flutter or tumbles depending on the solid-to-fluid density ratio for a fixed geometry of the plate. However, with a fixed solid-to-fluid density ratio, aspect-ratio of the plate does not alter the stable trajectories appreciably.

1 Introduction

Objects like thin paper cards, plates, and leaves do not fall straight to the ground. Instead, they follow complex trajectories owing to the coupling between their motion and surrounding fluid. The forces which act on objects such as drag, lift, buoyancy and weight need to be accounted for to study their trajectories. The equations of motion of the freely falling objects under their own weight depend mainly on the solid-to-fluid density ratio $(\rho _{s}/\rho _{f})$ and thickness-to-width ratio $(\beta )$. The object undergoes different types of motions such as stable fall (straight downward), flutter (oscillating from one side to another), tumble (end-over-end rotation) or combination of any of these depending upon the above-mentioned ratios. Moreover, it is a classic example of two-way coupling between fluid and solid, which requires an understanding of aerodynamic forces, vortex shedding, and underlying Fluid-Structure Interaction (FSI). The complex motion of a plate finds direct relevance to various class of problems like wind pollination [1], effect of rising bubbles in two-phase flow [2], falling of ice crystals in cloud physics [3], hovering flight mechanism [4], pop-up effect of buoyant ball [5], and autorotation phenomenon in helicopters [6].

Study of natural flight of object under its weight has always been captivating owing to a complex interplay of forces. In one of the earliest studies, Maxwell [7] qualitatively described the direction of motion of a thin paper slip undergoing tumbling through the fluid resistance acting upon it. Since then, numerous experimental, and numerical studies [8,9,10] have been carried out to understand the motion of objects for the different dimensionless moment of inertia and Reynolds number range. Willmarth et al [8] conducted a series of experiments with thin disks of various thickness and diameter in different fluids and observed tumbling motion for large values of Reynolds number ($Re > 2000$), and moderate dimensionless moment of inertia ($I^{*} > 0.1$). In addition, phase diagrams for the disks undergoing steady descent and fluttering motion are also reported. In previous mapping [8, 11] of falling patterns, the Reynolds number is defined based on the average descent velocity of the plate or disk obtained after the experiments or numerical simulations, which does not give direct control over it. However, in recent studies [12, 13] Re is replaced by other non-dimensional numbers like Archimedes number (Ar), and Galileo number (G), in which fluid viscosity is effectively considered. Apart from different falling patterns, numerous attempts have been made to study the transition in trajectories of plate or disk by varying its geometry or the property of the fluid-solid system. Field et al [9] described the complex motion of falling disks with only one parameter, i.e., angle $\theta$ between the disk’s normal and the vertical axis. In an experimental study, Belmonte et al [14] showed that flutter to tumble transition depends mainly on the Froude number, which occurs at $Fr_{c} = 0.67 \pm 0.05$ for high Re. The transition of motion based on three non-dimensional parameters $I^{*}$, Re and $\beta$ is investigated by Andersen et al [15]. A quantitative description of the transition scenario for freely falling disk is also given by Chrust et al [13]. In their work, a limited number of bifurcating asymptotic states observed between stable periodic fluttering and tumbling motion.

Tumbling motion has prompted a number of works [6, 16] due to the aerodynamic importance in understanding various autorotation phenomena. Smith [6] experimentally observed free fall and fixed axis autorotation of a wing and found similar flow pattern and aerodynamic forces in both the cases. Contrary to autorotation of a wing, Skews [16] considered a rectangular plate in a wind tunnel in his experiment and found that the drag coefficient is independent of the thickness-to-chord ratio. Further, Mahadevan et al [17] investigated autorotation of the rectangular cards and proposed scaling for tumbling frequency ($\Omega$) as $\Omega$ $\sim$ $d^{1/2}w^{-1}$ where w and d are width and thickness of cards, respectively. Hirata et al [18] have experimentally investigated aerodynamic characteristics of a plate undergoing tumbling motion, and found lift-to-drag ratio is independent of the aspect ratio when it exceeds 10.

The vortex formation around the object plays a vital role in the falling pattern as it can alter the forces which act on the object by the surrounding fluid. Andersen et al [11] and Wan et al [19] have shown the vortex shedding and wake pattern during the rise and fall of a plate undergoing fluttering and tumbling motion. The lift generated from the boundary layer separation and vortex shedding is studied by Ern et al [20]. A different shedding pattern than the Kármán vortex street is reported by Zhong et al [21] in an experiment of freely falling disks in water for Reynolds number larger than 2000. Several theoretical models [11, 14, 22] have also been proposed to assess the unsteady aerodynamics, including lift and drag forces acting on the plate while descending. Andersen et al [11] proposed a different mathematical model than the classical Kutta-Joukowski theory by considering fluid circulation dependent on both translational and rotational velocity, and have shown that the rotational lift dominates during tumbling. Hu and Wang [22] have presented a quasi-steady aerodynamic model to study the effect of different aerodynamic coefficients on the falling patterns of plates. Fernandes et al [23] have used classical Kirchhoff equations to perform experimental measurements for rising disks with different aspect ratios and Reynolds number, to investigate the phase difference between vortical force and torque.

A summary of previous studies on the free fall of thin objects is shown in table 1. Though, much attention has been paid to study the various motions of the objects either by altering the geometrical parameters or physical properties of combine fluid-solid medium, the effect of initial conditions has not been explored in detail. Andersen et. al [11] studied the effect of initial conditions for thin plate of $I^{*} = 0.17$ and 0.36, and found apparent change in trajectories. Lau et al [24] have shown that only the initial inclination of the plate can completely change the trajectory of the falling plate from straight vertical to tumbling motion, for $I^{*} > 3$. The previous studies have reported the effect of initial conditions on the dynamics of the plate either for a particular value of $I^{*}$ [11] or for $I^{*} > 1$ [24]. Therefore, to find the effect of initial conditions on all possible regimes identified by $I^{*}$, a systematic study is carried out, which includes flutter, tumble and chaotic motion of the plate. In the current study, 2D numerical simulations are carried out for free fall of a rectangular plate in the range of $I^{*}$ that includes flutter, tumble and transition regimes. Linear and angular responses of the plate during its flight in these regimes are investigated in view of characterizing them in the parameter space. Effect of the initial conditions, owing to its importance on the final trajectory [11, 24] is studied in detail. Effect of density ratio and aspect ratio of the plate on the uncertainty of the final trajectory in the transition regime is investigated with the aim to shed light into this regime.

The paper is organized as follows. Section 2 contains the mathematical details which contain dynamical equations and boundary conditions. A brief description of the numerical set up is added for completeness. Effect of grid resolution and time increment are reported separately. In the results section, we first introduce the basic characteristics of the three most identified regimes, flutter in section 3.1, then moving to the transition regime in 3.2 followed by tumbling motion in 3.3. In section 3.4 PDF of descent, the angle is discussed with reference to a possible Froude number similarity. In a detailed discussion of the effect of initial velocity and orientation on the final trajectories in a wide range of $I^*$ can be found in section 3.5. Importance of the aspect-ratio of the plate and relative density ratio mainly in the transition regime is examined in section 3.6. The paper concludes with a brief summary of the principal findings in section 4.

Figure 1

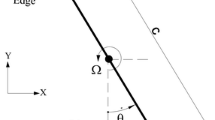
(Color online) Schematic diagram of the plate with its centerline trajectories showing (a) flutter, (b) tumble and (c) flutter-tumble combined chaotic motion in a fixed coordinate system where $\theta$ represents the instantaneous rotational angle measured from positive x-axis in anticlockwise direction. The top and bottom edges of the plate are drawn with different colors for better visualization of the rotation. Two particular positions of the plate during its flight, “broadside-on” and “edge-on”, which help in analyzing the dynamics of motion are indicated by arrows. On the extreme right, initial position of the plate having thickness t, width l and initial inclination angle $\theta _{0}$ is shown

Table 1 A brief review of previous studies on freely falling plate or disk in reverse chronological order.

2 Mathematical details

In this section, dynamical equations for the fluid flow and the body are written to address the ensuing FSI problem. The numerical method used to solve the coupled set of equations is also described briefly. To obtain the most suitable grid resolution and time-step, the convergence tests are conducted whose results are reported subsequently.

2.1 Dynamical equations

The present 2D numerical study primarily deals with the trajectories of a freely falling rectangular plate released in an otherwise quiescent medium. The geometric details, along with three well-known trajectory profiles, are shown in figure 1. Note, periodic side-to-side fluttering motion, shown in the frame (a) is characterized by mainly two orientations which are “broadside-on” and “edge-on”. On the other hand, cumulative rotation with slow horizontal march is identified as tumbling, shown in the frame (b) and a combination of these trajectories is identified as chaotic motion in the frame (c). It is apparent that the magnitude of the instantaneous angle $\theta$ in case of broadside-on position is either 0 or $\pi$, while for the edge-on position it is either $\pi /2$ or $3\pi /2$. Physical parameters that determine dynamics of the problem are width (l), thickness (t) and density $(\rho _s$) of the plate, density $(\rho _f$) and viscosity $(\nu$) of the surrounding fluid. The resulting non-dimensional parameters such as fluid-to-solid density ratio $\rho _{r} = \rho _{f}/\rho _{s}$ and length-to-thickness ratio $\beta = h/l$ or combinedly dimensionless moment of inertia $I^{*} = 8\beta (1 + \beta ^{2})/(3\pi \rho _{r})$ [11] are known to control the trajectories as they include all geometric and physical informations decisively. It should be noted that apart from the flow Reynolds number $Re = l_{r}u_{r}/\nu$, a relation of the inertial force with gravity is assessed through Froude number $Fr = u_r^2/gl$, which becomes important in view of the fact that the weight of the plate itself partly drives it. Though the length scale for the problem is fixed at $l_r = l$, velocity scale $u_r$ is a non-standard description which is taken as equivalent to the terminal velocity of the plate, $u_r=\sqrt{gl}$, that makes $Re=\sqrt{gl^3}/\nu$ and $Fr=1$. However, most of the previous studies have calculated Reynolds number based on the actual average descend velocity obtained from the experiments, and numerical simulations, defined as $Re_{v}=\langle u_y \rangle l/\nu$ where $\langle u_y \rangle$ [11] is the measured average descend velocity. To facilitate direct comparison of dimensionless parameters considered in previous and present study, $Re_{v}$ is also calculated, and values of these dimensionless variables are summarized in table 2.

Table 2 Summary of dimensionless parameters considered in the present and previous studies for freely falling rectangular plate.

Figure 2

Trajectories of the falling plate at various mesh and time resolution which are seen strongly sensitive to $\Delta t$, but only weakly dependent on the mesh resolution. The flutter case considered here assumes $l=1.134$ cm, $\beta =1/14$ and $\theta _{0} = 45^{\circ }$

Figure 3

(Color online) Time evolution of linear and angular velocities; on the left effect of progressively refined mesh and on the right sensitivity to time increment $\Delta t$

The mass and momentum conservation equations of the surrounding incompressible fluid are supplemented with dynamical equations for the three degrees of freedoms of the plate. The vertical motion is governed by the buoyancy force and the weight of the plate, while the horizontal and angular motion is governed by the drag and fluid torque, respectively. These equations when non-dimensionalized using the scales mentioned above take the following form

$$\begin{aligned}&\frac{\partial u_i}{\partial x_i} = 0 \end{aligned}$$

(1)

$$\begin{aligned}&{\frac{\partial u_i}{\partial t} + \frac{\partial (u_{i} u_{j})}{\partial x_{j}} = -\frac{\partial p}{\partial x_i} + \frac{1}{Re}\frac{\partial ^{2}u_i}{\partial {x_j}\partial {x_j}}} \end{aligned}$$

(2)

$$\begin{aligned}&\ddot{x} = \frac{\rho _{r}}{\beta }C_{x},\quad \ddot{y} = \frac{\rho _{r}}{\beta }C_{y} -(1 -\rho _{r}),\quad \ddot{\theta } = 12\rho _{r}\frac{1}{\beta ^{3} + \beta }C_{M} \end{aligned}$$

(3)

where force and moment coefficients, responsible for the solid-fluid interaction, are defined as $C_{x}=F_{x}/\rho _{f}u^{2}_{r}l$, $C_{y}=F_{y}/\rho _{f}u^{2}_{r}l$ and $C_{M} = M_{b}/\rho _{f}u^{2}_{r}l^{2}$. In the present study $\rho _{s}/\rho _{f}$ and $\beta$ range from $2.7-27$ and $1/14-1/5$, respectively, which corresponds to $0.16<I^{*}<3$. In line with available data, all three motions, flutter, tumble and chaotic, are observed in this range.

In each simulation listed in table 3, the plate is released at an angle $\theta _{0} = \pi /4$ in quiescent fluid (water) having $\rho _{f} = 1$ gm/cc and $\nu =0.0089$ $\hbox {cm}^2$/s which are taken from the experimental study of [11]. The convective velocity boundary condition is imposed at all the boundaries in order to facilitate the smooth passage of trailing wake created by the object during its descent. Since the extents of vertical fall and horizontal march widely differ in different regimes, a fixed domain for all the calculations were not possible. Thus, preliminary tests are carried out to determine the size of the domain for a range of $I^*$. The fixed size $-16l \le x \le 16l$ and $-50l\le y \le l$ were observed adequate for all the cases, though preliminary tests mentioned above did indicate a smaller domain for some cases.

2.2 Numerical method

The diffuse interface immersed boundary method [29] is used to solve the current FSI problem where a fluid-fluid Lagrangian boundary replaces the solid-fluid interface. A universal equation which combines momentum equation for the fluid domain and velocity of the rigid body through volume fraction is solved in the entire physical domain. The method starts with linearization of the plate, followed by a coupled solution of the conservation equation and the dynamical equation for the moving object. For solving the momentum equation, a $2^{nd}$-order predictor-corrector, finite volume formulation is used with velocity and pressure defined in a non-staggered fashion. For better numerical stability, implicit time integration is carried out. All the resulting sparse linear systems are solved using the BiCGSTAB technique pre-conditioned by a highly scalable diagonalized version of the SIP pre-conditioner. A uniform mesh of $\Delta x=\Delta y=0.01$ is used for all simulations with body resolution ($\delta _b$) kept in such a way that at least 8-10 computing cells are placed along the width, and $\delta _b/\Delta x$ does not become too small. The reason for such a choice is decided by the convergence tests. The plate is released from rest and is allowed to settle to a stable trajectory. All the simulations are carried out in a multi-processor environment with each case consumes approximately 12 hours to compute one free fall unit time on 50 computing cores.

2.3 Convergence: grid resolution and time-step

In order to determine the effect of mesh and time resolution on the trajectory of the plate, a fluttering case is considered. Physical data relevant to the case are width of the plate $l = 1.134$ cm, length-to-thickness ratio $\beta =1/14$, fluid viscosity $\nu = 0.0089$ $\hbox {cm}^2$/s and density ratio $\rho _{s}/\rho _{f} = 2.7$, which are taken from Andersen et al [11] to facilitate a direct comparison with experimental measurements. Simulations are carried out at in a domian $-12l \le x \le 12l, -31l \le y \le l$ with four progressively refined uniform meshes given by $M_{1}:1700 \times 2260(\Delta x,\Delta y=l/70)$, $M_{2}:2000 \times 2660(\Delta x,\Delta y=l/83)$, $M_{3}:2400 \times 3200(\Delta x,\Delta y=l/100)$ and $M_{4}:2760 \times 3680(\Delta x,\Delta y=l/115)$ keeping $\Delta t = 0.001$ and body resolution fixed at $\delta _b=l/125$. On the other hand, convergence of time-step is carried out by simulating on mesh $M_4$ at three different time steps, $\Delta t = 0.005, 0.002$ and 0.001 keeping $\delta _b = l/125$.

The trajectories of the plate for all the cases are shown in figure 2 which confirms the stable flutter motion with $\Delta t=0.001$ being the most appropriate time resolution. Larger $\Delta t$ is seen to be unreliable as owing to a numerically unstable time marching; different trajectory is obtained. However, such a difference is not evident at sufficiently coarse mesh where the basic trajectory turns out to be the same as for the finest one. Time evolution of linear and angular velocities, shown in figure 3, reveals only differences in phase at different grid resolution with amplitude remaining nearly the same. However, the effect of larger time-step is most evident from the time history of linear and angular velocities. The right column of figure 3 clearly shows significant departure to a wrong prediction of the motion of the plate at a larger $\Delta t$. Thus, to obtain the accurate trajectory of the plate, smaller time-step should be used. Based on these observations the uniform mesh resolution $\Delta x=\Delta y=0.01, \delta _b=0.008$ and time step $\Delta t=0.001$ are used in all subsequent simulations.

3 Results and discussion

Figure 4

A few selective trajectories of the falling plate with increasing normalized moment of inertia $I^{*}$. Note the flutter ($0.16 \le I^* \le 0.24$) and the first tumble regime ($0.48 \le I^* \le 0.6$) is separated by a chaotic regime which indicates a transition in motion

In the present study, numerical simulations are carried out by progressively increasing $I^{*}$ from 0.16 to 3. These simulations assist in analyzing the dynamics of the plate as it moves from one regime to another. The relevant input parameters, along with the corresponding computed average velocities and maximum inclination angle, are listed in table 3. Based on the obtained results with increasing $I^{*}$ in the selected range, four different types of motion of the plate are observed, as shown in figure 4. Fluttering is observed at lower values of $I^{*}$, i.e., in the range of $0.16-0.24$. Two distinct tumbling motions are observed: (a) tumbling along cusp like trajectories for $I^{*}$ = 0.48 and 0.6, and (b) tumbling along straight-line trajectories for $I^{*}$ = 2 and 3. A combination of flutter and tumble is termed as chaotic motion and obtained in the range $I^{*}$ = $0.28 - 0.4$. The current study is focused on finding the explanation of changing trajectories with an increase of $I^{*}$. The effect of initial conditions on the falling pattern in different regimes is also reported. Finally, the significance of density and aspect ratio in the transition regime is investigated.

3.1 Flutter regime

Flutter regime is usually defined for the range of $I^{*}$ in which the plate oscillates from one side to another while descending. This regime is clearly identified from the trajectories of the plate up to $I^{*}$ = 0.24 in figure 4. Quantitatively, the maximum value of inclination angle $(\theta _{max} < 90^{\circ })$ in table 3 indicates that the flutter regime continues until $I^{*}$ = 0.24. In this regime, it is observed that maximum inclination angle $(\theta _{max})$ and vertical descent height (d) in a cycle increase with $I^{*}$, as shown in figure 4. Such an increase can be explained from the horizontal and vertical velocity orbits of the plate with the angle of inclination during its flight, as shown in figures 5 (a, b). The maximum inclination angle in the frame (a) corresponds to the turning point of the plate where the magnitude of horizontal velocity changes its sign. It is important to note that vertical velocity is maximum near the turning point and also increases with increasing $I^{*}$ as shown in the frame (b). Thus, at the turning point, the plate falls with greater vertical velocity, and covers a larger descent height, as $I^{*}$ increases. A significant drop in number of completed side-to-side cycles from $I^{*} = 0.16$ to 0.24 is evident from figure 4. At $I^{*} = 0.24$, the maximum inclination angle reaches $85^{\circ }$, which is the highest among all the flutter cases. Thus, the effect of angular velocity is never observed to dominate the other two linear motions, and the plate never undergoes full rotation about its centroid. The two-lobe orbits of vertical velocity indicate that the periodicity of the vertical velocity is twice the horizontal motion. This suggests the plate has a greater tendency to return back to its position horizontally as the vertical velocity repeats itself at a rate twice the other. With further increase in $I^{*}$ under the same initial conditions, the motion of the plate will progress to the transition regime.

Table 3 Four characteristic parameters width l, thickness-to-width ratio $\beta$, dimensionless moment of inertia $I^{*}$, and Froude number ${\textit{Fr}}$ of the plate with obtained average velocities $<u>$, $<v>$ and $<\omega>$.

Figure 5

(Color online) Variation of (a) horizontal velocity, and (b) vertical velocity with the instantaneous inclination angle $(\theta )$ during the fluttering motion corresponding to $I^{*}$ = 0.16, 0.20 and 0.24. Note, while the horizontal velocity does not change appreciably, maximum vertical velocity which peaks near the turning point increases with $I^*$.

3.2 Transition regime

Figure 6

Time history of inclination angle ($\theta$), vertical velocity (v), and angular velocity ($\omega$) of the plate in the transition regime.

Figure 7

Time history of inclination angle $\theta$, horizontal velocity u, vertical velocity v and angular velocity $\omega$ of the plate for $I^{*} = 0.6$ and 2.0 in tumble regime. The symbol ‘$+$’ represents the edge-on position, where magnitude of inclination angle is either $\pi /2$ or $3\pi /2$. The dashed line is drawn for clear identification of positive vertical velocity

Figure 8

Probability density function (PDF) of instantaneous angle made by the falling plate during its course of trajectory for different $I^{*}$.

Figure 9

Variation of Froude number with $\sin (\theta _{max})$ for selected $I^{*}$ in different regimes listed in table 3.

Table 4 List of the combinations used to test the effect of initial condition in different regimes of descent.

In the transition regime, the plate undergoes a combination of fluttering and tumbling motion, as shown in figure 4 in the range $0.24 \le I^* \le 0.4$. Such a motion is also reported by Wang et al [25] for a relatively lower range ($0.21 \le I^* \le 0.31$), with an initial inclination angle $|\theta _{0}|=\pi /5$. However, they have reported that the transition regime can be extended by increasing $|\theta _{0}|$ which is in agreement with present data as we have used $|\theta _{0}|$ as $\pi /4$. With the increase in $I^{*}$ of the plate $\theta _{max}$ increases which is evident from the previous section. Therefore, a particular value of $I^{*}$ results in $\theta _{max} \simeq \pi /2$ which causes the plate to fall in a straight vertical path in an edge-on position to a large descent height due to the absence of drag force. Once the drag force develops sufficiently, the plate again starts to move slowly in the horizontal direction, as shown in figure 4 for $I^{*} = 0.36$. With further increase in $I^*$, the angular velocity of the plate tends to rotate it as it descends, leading to a tumble-like motion which changes its course owing to a switch in horizontal velocity.

The combination of flutter and tumble motion is depicted in figure 6, which shows variation of the inclination angle ($\theta$), vertical velocity (v), and angular velocity ($\omega$) with time for $I^{*}=0.28$ and 0.36. When the magnitude of inclination angle $\theta$ at the turning point becomes closer to $\pi /2$ or $3\pi /2$, the plate can either tumble or descend to a large vertical height, depending upon the magnitude of angular velocity at that point. Tumbling is observed for a relatively higher value of $\omega$, while the plate descends in edge-on position with increasing vertical velocity for lower $\omega$. For $I^{*}=0.36$, the time signal reveals that the vertical velocity reaches the maximum at $\theta =-\pi /2$, and the plate continues to fall with a constant vertical velocity until the angular velocity becomes greater than zero to cross over the edge-on position. The inclination angle increases gradually and reaches $\theta =\pi /2$ with sufficient positive angular velocity to cross the next edge-on position, resulting in the tumbling motion.

The intermediate tumbling stints between fluttering motion can also be explained in terms of energy interaction between the plate and the surrounding fluid. In this regime, $I^{*}$ lies in the range where the plate can not maintain the continuous rotation during its flight. After its release from the initial position, it acquires the edge-on position and descends to a large height. During the descent, fluid transfers energy to the plate which causes it to cross over the next edge-on position due to the large value of angular velocity, and thus the tumbling motion is obtained. After a short interval of time, the excess energy gained during the large descent loses its impact, owing to which plate starts fluttering again, and these cycle of events continue. Thus, the transition regime can be thought of as intermittent occurrences of tumbling while the plate can sustain its rotation, while a “cooling-off” period reflects fluttering in the horizontal direction.

3.3 Tumble regime

In the tumble regime, the plate undergoes complete rotation while drifting in the horizontal direction. This regime is obtained for $I^{*}>0.4$, however, two distinct tumbling motions are observed in the range $0.44<I^{*}<1.0$ and $I^{*}>1$. The motion in the former regime is along cusp like trajectories, whereas in the latter one it is along straight lines, as shown in figure 4. The obtained regimes are consistent with those reported by [24]. The transition from chaotic to pure tumbling motion is described by using the time history of velocity components and inclination angle, as shown in figure 7. Rotation of the plate in this regime is apparent from the time evolution of $\theta$, which changes continuously from 0 to $2\pi$. The angular velocity of the plate at the turning point in this regime is very high which causes a quick change in plate position from the vertical edge-on position, and thus it prevents the plate from falling vertically downward as in the transition regime. Moreover, figure 7 shows that the horizontal velocity never crosses the zero line, which indicates that the plate moves in a particular direction, unlike flutter regime where the plate oscillates from one side to another. For $I^{*}=0.6$, the formation of cusp at the turning point is attributed to the positive value of vertical velocity, whereas the large values of angular velocity and small range of fluctuations in vertical velocity explain the reason for tumbling in a straight line for $I^{*} = 2.0$.

3.4 PDF of instantaneous angle and Froude number similarity

Figure 10

Trajectories of the falling plate for different cases listed in table 4. It is shown that the effect of initial condition is important in flutter-to-tumble transition regime at $I^{*} = 0.4$ while the pure flutter and tumble motions retain the basic trajectories.

Figure 11

(Color online) Time signal of horizontal velocity u, vertical velocity v, angular velocity $\omega$ and rotational angle $\theta$ of the falling plate corresponding to four different cases i, ii, iiiand ivfor distinct $I^*$ listed in table 4.

Figure 12

Centerline trajectory of a freely falling plate in the transition regime for four different $\beta$ and constant $\rho _{s}/\rho _{f} = 2.7$.

Figure 13

(Color online) Time evolution of inclination angle of the plate for different $\beta$ in the transition regime, while inset shows the evolution for fluttering and tumbling motion.

Figure 14

Trajectory of the freely falling plate in the transition regime for four different $\rho _{s}/\rho _{f}$ at constant $\beta = 1/10$.

Figure 15

(Color online) Time evolution of inclination angle of the plate for different $\rho _{s}/\rho _{f}$ in the transition regime where the inset shows evolution for fluttering and tumbling motion.

The inclination angle of the plate, which continuously changes during its flight is found to be an important parameter to describe its motion. In the present study, probability density function (PDF) of the inclination angle is computed for a deeper insight into these complex motions, as shown in figure 8. The PDF denotes the time interval for which the plate stays at a particular inclination angle during its flight. It is observed that as $I^{*}$ increases, the plateau formed by the PDF gets flattened, and ultimately collapsed to zero in the tumble regime. The fall in the height of the plateau can be attributed to the increase in angular velocity of the plate, and consequently leads to a smaller PDF. Moreover, the maximum value of PDF in the tumble regime indicates that the plate descends at an angle approximately equal to the initial angle of inclination $(\theta _{0})$ for the maximum duration of descending motion. A multi-level uniform distribution during the flutter slowly breaks down as it passes through the transition zone where uniform distribution is punctured by high probability at certain angles which are completely unpredictable. Finally, nearly uniform distribution in the tumble regime indicates that the plate acquires all possible orientations as it rotates continuously.

For a freely falling plate, the Froude number similarity was proposed by Belmonte et al [14] to study the transition in the motion of a plate from a flutter to tumble regime. Since fluttering of a plate is very similar to the motion of a pendulum, they defined the Froude number as a ratio of the time scale for a buoyant pendulum to vertical descend in free fall. In their experimental study, they have only reported fluttering and tumbling motion of the plate. The transition between these two motions is observed at $Fr_{c} = 0.67 \pm 0.05$. In the present study, $\sin (\theta _{max}) - {Fr}$ similarity shows the flutter to tumble transition at $Fr_{c} = 0.7 + 0.05$, as shown in figure 9. The observed deviation in $Fr_{c}$ can be attributed to the sensitivity of motion of the plate towards initial conditions near the transition regime.

3.5 Effect of initial conditions

The effect of initial conditions on the motion of the plate plays a significant role, as discussed in the previous section. Four sets of initial conditions are tested which include a number of initial orientations. The plate is impulsively released in some cases while it is given horizontal and vertical velocity of varied magnitude in some other. Table 4 lists all the combinations with an average velocity of descending, and angular velocity is tabulated for a quantitative comparison. Their effect on the dynamics of the plate is examined from the trajectories and velocity histories of the plate, as shown in figures 10 and 11, respectively. It is evident from figures 10 (a, c) that the fluttering ($I^{*} = 0.16$) and tumbling ($I^{*} = 0.6$) at low $I^{*}$ are very stable as the trajectories of the plate remain nearly the same with different initial conditions. The variation in magnitude of average velocities is found to be very less for $I^{*} = 0.16$ and 0.6, as listed in table 4, which supports the above observation. Trajectories of the plate for $I^{*} = 0.4$, which lies between stable fluttering and tumbling motion of the plate are found to be dependent on initial conditions as shown in the frame (b). The motion of the plate for different initial conditions for this $I^{*}$ undergoes chaotic and tumbling with a single, and double period which is also reported Andersen et al [11]. Further, tumbling at high $I^{*}$ is also found to be independent of initial conditions as shown in the frame (d).

The time signal of velocity profiles and the inclination angle of the plate provides a better insight into its dynamics. Figure 11 shows the time signal of horizontal (u), vertical (v), angular ($\omega$) velocities and inclination angle ($\theta$) of the plate. It is noticed that the effect of initial conditions is not present for all distinct motion of the plate with a particular $I^{*}$. However, for $I^{*}$ = 0.4, it is observed that the velocity histories for case iare different than the other three cases, and they become more obvious as time increases. In case of fluttering and tumbling at $I^{*} = 0.16$ and 0.6, respectively, the time signals of velocity and inclination angle show similar increment with different initial conditions. Thus, the flutter and tumble regimes are found to be independent of initial conditions at low $I^{*}$. The velocity cycles for all cases except iattain steady-state rapidly. Apart from this, the angular velocity of the plate for case iiiabruptly changes its direction from the positive anti-clockwise to clockwise rotation. Thus, the initial conditions of the plate affect the chaotic and tumbling motion significantly at high $I^{*}$.

3.6 Significance of $\beta$ and $\rho _s/\rho _f$ in the transition regime

The previous section reveals the sensitivity of motion of the plate to initial conditions which pave the way to examine the effect of the other two parameters $\rho _{s}/\rho _{f}$ and $\beta$ in the transition regime. The effect of aspect ratio ($\beta$) is investigated keeping $\rho _{s}/\rho _{f}$ constant and vice-versa. Moreover, the inclination angle $(\theta _{0}= \pi /4)$ and initial velocity components $(u_{0}, v_{0} = 0)$ is kept constant for this investigation. It is observed that the trajectories of the plate for $\beta$ = 1/7 and 1/6 are a combination of flutter and tumble, as shown in figure 12. However, the trajectories are not sufficiently developed for $\beta = 1/8$ and 2/13 in the present domain, and it appears as a combination of flutter and tumble. Therefore, to identify the motion for $\beta = 1/8$ and 2/13, the time evolution of the inclination angle is investigated and presented in figure 13. Since the inclination angle crosses $2\pi$ for both the $\beta$ values, it implies the plate has completed one rotation. The time series of inclination angle for all $\beta$ seems to be a combination of fluttering and tumbling, as shown in the inset of figure 13. Thus, it can be claimed that the nature of the motion of the plate remains largely unaffected to a change in aspect ratio in the transition regime.

The effect of density ratio on the dynamics of the plate is examined similarly, and shown in figures 14 and 15. The time evolution of the inclination angle is similar to tumbling, as shown in the inset of figure 15 for all values of $\rho _{s}/\rho _{f}$ except for 3.5 which shows a fluttering behavior. Thus, the motion of the plate transforms from a flutter to tumble without passing through the chaotic regime for the considered density ratios at a fix aspect ratio. However, the average angular velocity increases with density ratio, except $\rho _{s}/\rho _{f} = 3.5$, which is evident from the increase in the slope of the inclination angle, as shown in figure 15. Therefore, the motion of the plate in transition regime is found to be sensitive to solid-to-fluid density ratio ($\rho _{s}/\rho _{f}$) while it remains insensitive to the aspect ratio ($\beta$) of the plate.

4 Conclusions

2D numerical simulations are carried out for free fall of a rectangular plate in water. The two dimensionless parameters that govern the motion of the falling object are solid-to-fluid density ratio ($\rho _{s}/\rho _{f}$) and thickness-to-width ratio ($\beta$). The dimensionless moment of inertia of the plate, which includes the effect of both $\rho _{s}/\rho _{f}$ and $\beta$ is found to control the dynamics of the plate effectively. In the selected range of density ratio, $2.7 \le \rho _{s}/\rho _{f} \le 27$, and thickness-to-width ratio, $1/14 \le \beta \le 1/5$, dimensionless moment of inertia lies in the range $0.16 \le I^{*} \le 3$. The motion of the plate changes from a flutter to tumble with an increase in $I^{*}$. In between these two regimes of motion, a transition regime is observed where the motion of the plate is chaotic, a combination of flutter and tumble. The reason for such a motion is explained in terms of the edge-on position, vertical descent height and energy interaction between the plate and the surrounding fluid. Froude number similarity predicts the transition from flutter to tumble which occurs at Froude number $Fr_{c} = 0.7+0.05$. Chaotic and tumbling ($I^{*}>1$) motions are found to be sensitive to the initial conditions. For the chaotic motion, the effect of initial conditions is found on the falling pattern of the plate. In case of tumbling motion at $I^{*}>1$, the initial conditions only affect initial transients of the trajectories and velocity histories, while final falling patterns of the plate are found to be independent of it. Study of PDF of instantaneous angle shows that in the tumble regime, the inclination angle of the plate is approximately equal to the initial angle of release for the maximum duration of motion. The effect of density ratio and thickness-to-width ratio on the dynamics of the plate in transition regime is investigated which reveals that the motion of the plate in the transition regime is more sensitive to the change in $\rho _{s}/\rho _{f}$ than $\beta$. For constant $\rho _{s}/\rho _{f} = 2.7$, with increase in $\beta$, the chaotic motion prevails in transition regime. On the other hand, for constant $\beta = 1/10$, with the increase in $\rho _{s}/\rho _{f}$ motion of the plate is found to change from a flutter to tumble without moving into the chaotic regime.