1 Introduction

In the recent years, a great deal of research attention has been paid to the area of microchannel flow and heat transfer due to developments in the electronic industry, microfabrication technologies, biomedical engineering, etc. In general, there is also a shift in the focus of published articles, from descriptions of the manufacturing technologies to discussions of the physical mechanisms of flow and heat transfer [1].

It is now well known that microscale fluid flow and heat transfer phenomena differ dramatically from those at macroscale. At macroscale, classical conservation equations are successfully coupled with the corresponding wall boundary conditions, usual no-slip for the hydrodynamic boundary condition and no-temperature-jump for the thermal boundary condition. These two boundary conditions are valid only if the fluid flow adjacent to the surface is in thermal equilibrium. However, they are not valid for rarefied gas flow at microscale [1]. For this case, the gas no longer reaches the velocity or the temperature of the surface, and therefore a slip condition for the velocity and a jump condition for the temperature should be adopted (the slip flow regime). The velocity slip and temperature jump are the main effects of rarefaction.

Axial conduction is an important and critical effect that should be taken into consideration at microscale. In existing literature, a criterion based on the Peclet number (Pe) is often used to decide whether the axial conduction in the fluid is included in the analysis or not. The axial conduction is usually considered as the dominant transport mechanism for low values of the Peclet numbers (Pe < 100). For macrochannels, this effect becomes critical especially for low-Pr fluids such as liquid metals [2]. However, for microchannels, since the characteristic lengths are very small, they lead to much lower Pe values even for gas flows.

The thermal entry region heat transfer problem that takes axial heat conduction into account, known as the extended Graetz problem, has been extensively studied in the literature for macrochannels. Hennecke [2] numerically analysed the hydrodynamically developed but thermally developing forced convection in a tube subjected to step change in wall heat flux. He disclosed that the temperature profile at the inlet of the heated region deviated considerably from a uniform value and received radial profile at low Peclet numbers. Hsu [3] studied the thermal entry region heat transfer problem in laminar flow through concentric annuli subjected to a step jump in the wall heat flux. His results indicated that disregarding the effect of axial conduction could lead to wrong results in the estimation of heat transfer coefficients, especially for small Peclet numbers. For the same boundary condition, Hsu [4] extended that analysis for pipe and parallel-plate channel flows. Jones [5] theoretically studied laminar flow inside a circular pipe with a step change in the wall temperature using the double-sided Laplace transform. He obtained that the incoming fluid from the adiabatic region was significantly pre-heated and, hence, the assumption of constant temperature at the inlet of heated region was not valid for low values of the Peclet number. Verhof and Fisher [6] numerically solved the extended-Graetz problem of laminar flow of heat transfer in a pipe with prescribed constant wall heat flux and temperature conditions by taking the effect of axial conduction into consideration. They solved the energy equation using a finite-difference technique. Papoutsakis et al [7] analytically studied the extended Graetz problem based on a self adjoint formalism obtained by decomposing the energy equation into a pair of first-order partial differential equations. Vick et al [8] employed finite integral transform technique to solve the thermal entrance region heat transfer problem with axial conduction. Ebadian and Zhang [9] analysed the effect of axial conduction on heat transfer characteristics of laminar gas flow in a circular pipe subjected to a step change in wall temperature. In another study, Ebadian and Zhang [10] extended their analysis by taking the effect of internal heat generation into consideration for the same problem. The thermal entrance length was found to be delayed to pipe exit with an increase in Peclet number. Bilir [11] numerically investigated the conjugate heat transfer problem for laminar pipe flow, taking wall and fluid axial conduction into consideration. He reported that the effect of wall conduction on heat transfer increased with increasing wall thickness while it decreased with decreasing Peclet number. The extended Graetz problem with piecewise constant temperature for pipe and channel flows is analytically studied by Lahjomri and Oubarra [12] and Weigand and Lauffer [13] over a wide range of Peclet number.

Although the extended Graetz problem has been extensively studied for macrochannels, few studies have been carried out for microchannels. Jeong and Jeong [14] analytically studied the effects of axial conduction and viscous dissipation in parallel-plate microchannel flow both for uniform wall temperature and uniform heat flux boundary conditions. In the presence of axial conduction, the local Nusselt number was found to decrease with a decrease in the Peclet number in the entrance region. Myong et al [15] analysed the convective heat transfer of rarefied gas flow in a micro-tube by taking the axial conduction effect into consideration. Slip corrections were made by employing a new Langmuir model based on the concept of absorption of gases on to solids as well as the conventional Maxwell model. Their results show that both models predicted the same reduction in heat transfer with increasing rarefaction, expect that the value of the energy accommodation was much smaller than that of the momentum accommodation. Dutta et al [16] obtained analytical solutions for temperature distributions and heat transfer characteristic of mixed electro-osmotic and pressure-driven flow in two-dimensional microchannels. Their results showed that the temperature profile in the fully developed region was independent of Peclet number. Cetin et al [17] analytically solved the extended Graetz problem inside a microtube including rarefaction, viscous dissipation and axial conduction effects in the analysis. The semi-infinite half of the tube wall was kept adiabatic while the other half was kept at a uniform wall temperature. The fully developed Nusselt number and thermal entrance length were found to increase with decreasing Peclet number. In another study, Cetin et al [18] extended their solution for the constant heat flux boundary condition. In their analysis, the effect of axial conduction was ignored in the adiabatic region. Aziz and Niedbalski [19] compared the first- and second-order slip flow model predictions for the thermal development of dilute gas flow in a microtube with axial conduction and viscous dissipation. The conventional slug flow problem in parallel-plate microchannel was analytically studied by Mecili and Mezaache [20] for constant wall temperature and constant heat flux boundary conditions, taking into consideration slip characteristics and axial conduction effect. Cole et al [21] analytically investigated the conjugate heat transfer problem in a parallel-plate microchannel in the slip flow regime. The effect of axial conduction both in the gas and wall is included in their analysis. In a very recent study, the combined effects of axial conduction, viscous dissipation and pressure work for a gaseous slip flow in a micropipe and a parallel-plate microchannel were studied by Haddout and Lahjomri [22]. The channel wall had a small part located at the centre, being kept at high temperature while the rest at lower temperature. In the presence of axial conduction, the local Nusselt number was found to increase with a decrease in the length of heated section. Balaj et al [23] numerically investigated the convective heat transfer of argon gas through a micro/nanochannel in both slip and transition flow regimes using the direct simulation of Monte Carlo (DSMC) method. They stated that the Nusselt number decreased with increasing Knudsen number in the transition flow regime and approached a constant value at high Knudsen numbers. In another study, Balaj et al [24] studied the effect of shear work on convective heat transfer in a microplane duct with constant heat flux imposed. For the wall cooling case, they observed some singularities in the local Nusselt number and discussed them in terms of energy balance.

Our group has contributed to the microscale heat and fluid flow phenomena literature with some articles [25,26,27,28,29], focusing our interest on the slip flow regime. All these articles have neglected the effect of axial conduction. In our very recent study [30], we included this effect for the problem of laminar forced slip flow in a microduct with a sinusoidally varying heat flux in an axial direction.

The cited literature review shows that the extended-Graetz problem inside a microtube under constant heat flux boundary condition has not been completely solved yet. The aim of this study is to numerically investigate the laminar convective heat transfer in the thermal entrance region of a microtube subjected to a step change in wall heat flux. The combined effects of the Knudsen number and the Peclet number on the axial wall and bulk temperature profiles and, in the following, on the Nusselt number, are determined and discussed.

2 Problem description and analysis

2.1 Governing equations and boundary conditions

Consider a laminar flow of rarefied gas in a microtube that is fully developed hydrodynamically but thermally developing. The fluid enters the tube with a uniform temperature, Te. The upstream region of the tube (–L ≤ x < 0) is externally well insulated, and the downstream region of the tube (0 ≤ x ≤ L) is subjected to a uniform axial and circumferential heat flux (figure 1). Thermophysical properties of the fluid are assumed to be constant, and the axial heat conduction in the wall is considered to be negligible.

Figure 1
figure 1

Schematic of the problem.

Full size image

For the continuum and slip flow regimes (0 ≤ Kn ≤ 0.1), under the afore-mentioned assumptions, the energy equation of a steady flow of an incompressible fluid and appropriate boundary conditions can be written as follows:

$$ u\,\frac{\partial \,T}{\partial \,x}\, = \,\frac{\upsilon }{\Pr }\left( {\frac{1}{r}\,\,\frac{\partial }{\partial \,r}\,\left( {r\frac{\partial T}{\partial r}} \right) + \frac{{\partial^{2} \,T}}{{\partial \,x^{2} }}} \right) $$
(1)
$$ x = - L,\,\,\,\,\,0 \le r \le r_{o} ,\,\,\,\,\,T = T_{e} $$
(2a)
$$ x = L,\,\,\,\,\,\,\,0 \le r \le r_{o} ,\,\,\,\,\,\partial T/\partial x = 0 $$
(2b)
$$ r = 0,\,\,\,\,\,\,\, - L \le x \le L,\,\,\,\,\,\partial T/\partial r = 0 $$
(2c)
$$ \begin{aligned} & r = r_{o} ,\quad - L \le x < 0,\quad \partial T/\partial r = 0 \\ & r = r_{o} ,\quad 0 \le x \le L,\quad \partial T/\partial r = q_{w}^{\prime \prime } /k \\ \end{aligned} $$
(2d)

Introducing the dimensionless variables

$$ U = \frac{u}{{u_{m} }},\,\theta = \frac{{T - T_{e} }}{{q_{w}^{{\prime \prime }} D/k}},\,R = \frac{r}{D},\,X = \frac{{{x \mathord{\left/ {\vphantom {x D}} \right. \kern-0pt} D}}}{{\text{Re} \,\Pr }},\,L^{*} = \frac{L/D}{{\text{Re} \,\Pr }},\,\text{Re} = \frac{{u_{m} D}}{\nu },\,Pe = \text{Re} \,\Pr $$
(3)

the energy equation and boundary conditions become

$$ U\,\frac{\partial \theta }{\partial \,X}\, = \,\frac{1}{R}\,\frac{\partial }{\partial R}\,\left( {R\,\frac{\partial \theta }{\partial R}} \right)\, + \,\frac{1}{{Pe^{2} }}\frac{{\partial^{2} \theta }}{{\partial X^{2} }} $$
(4)
$$ X = - L^{*} ,\,\,\,\,\,0 \le R \le 0.5,\,\,\,\,\,\theta = 0 $$
(5a)
$$ X = L^{*} ,\,\,\,\,\,\,\,0 \le R \le 0.5,\,\,\,\,\,\partial \theta /\partial X = 0 $$
(5b)
$$ R = 0,\,\,\,\,\,\,\, - L^{*} \le X \le L^{*} ,\,\,\,\,\,\partial \theta /\partial R = 0 $$
(5c)
$$ \begin{aligned} R = 0.5,\,\,\,\,\, - L^{*} \le X < 0,\,\,\,\,\,\partial \theta /\partial R = 0 \hfill \\ R = 0.5,\,\,\,\,\,\,\,\,\,0 \le X \le L^{*} ,\,\,\,\,\,\partial \theta /\partial R = 1 \hfill \\ \end{aligned} $$
(5d)

In the analysis, the usual continuum approach is integrated with the two main characteristics of the microscale phenomena: the velocity slip and the temperature jump. The first-order velocity slip boundary condition is given by [25] the relation

$$ u_{s} = - \frac{2 - F}{F}\lambda \left. {\frac{\partial u}{\partial r}} \right|_{{r = r_{0} }} $$
(6)

where \( \lambda \)(= KnD) is the molecular mean free path, and \( F \) is the tangential momentum accommodation coefficient, which has a value near unity for most engineering surfaces [25].

Considering the slip flow condition at the wall, the fully developed velocity profile is obtained as follows [25]:

$$ U = \frac{{2(1 - 4R^{2} + 4Kn)}}{(1 + 8Kn)} $$
(7)

where Kn is the Knudsen number, which equals \( \lambda /D \).

The first-order temperature jump boundary condition at the wall is given by a similar expression:

$$ T_{s} - T_{w} = - \frac{{2 - F_{t} }}{{F_{t} }}\frac{2\gamma }{\gamma + 1}\frac{\lambda }{\Pr }\left. {\frac{\partial T}{\partial r}} \right|_{{r = r_{0} }} $$
(8)

where \( T_{s} \) is the temperature of the gas at the wall, \( T_{w} \) is the wall temperature and \( F_{t} \) is the thermal accommodation coefficient, which depends on the gas and surface material. Particularly for air, it assumes typical values near unity [25]. For the rest of the analysis, \( F \) and \( F_{t} \) will be assumed to be 1. Introducing the dimensionless variables defined in Eq. (3), the temperature jump in the dimensionless form is written as follows:

$$ \theta_{s - w} = \frac{{T_{s} - T_{w} }}{{q^{\prime\prime}_{w} D/k}} = - \frac{2\gamma }{\gamma + 1}\frac{Kn}{\Pr }\left. {\frac{\partial \theta }{\partial R}} \right|_{R = 0.5} . $$
(9)

The fluid bulk temperature can be determined as follows:

$$ T_{b} = \frac{{\int\limits_{0}^{{r_{o} }} {uT2\pi rdr} }}{{\int\limits_{0}^{{r_{o} }} {u2\pi rdr} }}. $$
(10)

In terms of the dimensionless variables, the fluid bulk temperature becomes

$$ \theta_{b} = \frac{{T_{b} - T_{e} }}{{\frac{{q^{\prime\prime}_{w} D}}{k}}} = \frac{{\int\limits_{0}^{0.5} {U\theta RdR} }}{{\int\limits_{0}^{0.5} {URdR} }} = 8\int\limits_{0}^{0.5} {U\theta RdR} . $$
(11)

In the heated region, the local Nusselt number based on the difference between the wall and fluid bulk temperature is obtained using Newton’s cooling law as follows:

$$ Nu\, = \frac{hD}{k} = \,\frac{{\left. {\frac{\partial T}{\partial r}} \right|_{{r\, = \,r_{o} }} D}}{{T_{w} - T_{b} }}. $$
(12)

In terms of dimensionless variables defined in Eq. (3), Eq. (12) becomes

$$ Nu\, = \,\frac{{\left. {\partial \theta /\partial R} \right|_{R\, = 0.5} }}{{\theta_{w} - \theta_{b} }} = \frac{1}{{\theta_{w} - \theta_{b} }}. $$
(13)

The first term in the denominator of Eq. (13) indicates the dimensionless wall temperature, \( \theta_{w} \), which can be written as follows:

$$ \theta_{w} = \theta_{s} - \theta_{s - w} = \frac{{(T_{s} - T_{e} )}}{{q_{w}^{{\prime \prime }} D/k}} - \frac{{(T_{s} - T_{w} )}}{{q_{w}^{{\prime \prime }} D/k}}. $$
(14)

Here, \( \theta_{s} \) and \( \theta_{s - w} \) are the dimensionless fluid temperature at the wall and the temperature jump between the wall and fluid, respectively. Substituting Eq. (11) in Eq. (14) then gives

$$ \theta_{w} = \frac{{(T_{w} - T_{e} )}}{{q_{w}^{{\prime \prime }} D/k}} = \left. \theta \right|_{R = 0.5} + \frac{2\gamma }{\gamma + 1}\frac{Kn}{\Pr }\left. {\frac{\partial \theta }{\partial R}} \right|_{R = 0.5} . $$
(15)

Using Eqs. (11) and (15), the dimensionless temperature difference between the wall and fluid bulk temperature can be rearranged as follows:

$$ \theta_{w} - \theta_{b} = \frac{{(T_{w} - T_{b} )}}{{q_{w}^{{\prime \prime }} D/k}} = \left. \theta \right|_{R = 0.5} + \frac{2\gamma }{\gamma + 1}\frac{Kn}{\Pr }\left. {\frac{\partial \theta }{\partial R}} \right|_{R = 0.5} - 8\int\limits_{0}^{0.5} {U\theta RdR} . $$
(16)

Substituting Eq. (16) in Eq. (13), the local Nusselt number can written as follows:

$$ Nu\, = \,\frac{1}{{\theta_{w} - \theta_{b} }} = \frac{1}{{\left. \theta \right|_{R = 0.5} + \frac{2\gamma }{\gamma + 1}\frac{Kn}{\Pr }\left. {\frac{\partial \theta }{\partial R}} \right|_{R = 0.5} - 8\int\limits_{0}^{0.5} {U\theta RdR} }}. $$
(17)

2.2 Solution methodology, grid generation and code validation

The energy equation is discretized by the control volume discretization method in junction with the convection–diffusion formulation, as described by Patankar [31]. The set of discretized equations are solved by use of well-known ADI iterative solution procedure. The details of the solution procedure can be found in reference [24]. A uniform grid structure is used in the axial (x) and radial directions (r). To ensure that the solutions are grid-independent, several simulations are performed. Figure 2 shows the downstream variation of local Nusselt number for the tested grid configurations. It is evident from figure 2 that the relative percentage change in Nusselt number between the grid sizes of 2000×100 and 3000×100 is less than 1%. Therefore, all parametric runs are made with the 2000×100 grid.

Figure 2
figure 2

Grid independence test: The downstream variation of local Nu for Kn = 0.00 and Pe = 20.

Full size image

3 Results and discussion

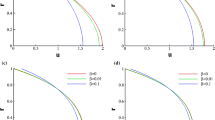
In this study, combined effects of the axial conduction and rarefaction on convective heat transfer for laminar flow inside a microtube are investigated. The upstream region of the tube (–L < x < 0) is externally well insulated while its downstream part (x ≥ 0) is subjected to a uniform axial and circumferential heat flux. The Prandtl number is assumed to be 0.71. At first, we validated our analysis by comparing some limiting results to those available in the existing literature, mainly by those of Hennecke [2] and Cetin et al [18] for the macroscale and microscale cases, respectively. As can be seen from figure 3, our results obtained for different values of Peclet and Knudsen numbers agreed very well with those for the macroscale case (figure 3a) and those for the microscale case without axial conduction effect (figure 3b).

Figure 3
figure 3

The downstream variation of local Nu for various values of Pe at Kn = 0.00 (a) and Kn at Pe = 500 (b).

Full size image

To understand the physical phenomena of axial conduction and rarefaction better, axial variations of the dimensionless wall and bulk fluid temperatures are illustrated in figure 4. Note that Kn = 0 represents the macroscale case while Kn > 0 holds for the microscale case and Pe = 500 represents the case with no axial conduction. For the macroscale case, it can be clearly seen from figure 4 that the axial temperatures considerably tend to deviate from the inlet temperature in the upstream region (X < 0) as the Peclet number becomes smaller. This behaviour can be explained by heat diffused backwards that is generated by axial conduction in the fluid. For lower values of Pe, due to the low velocities in the fluid, a certain amount of heat supplied from the heated wall can be easily diffused to the upstream region and, therefore, the magnitude and the extent of axial conduction increase in the upstream region, while the opposite is true for higher values of Pe. According to the degree of this reverse heat, a certain radial temperature profile is developed before the fluid reaches X = 0. For the case of Pe = 500, in which the effect of axial conduction is negligible, the wall and the bulk fluid temperatures get equal values and maintain their flat patterns until X = 0, in the upstream region of the tube. Similar trends were also observed by Hennecke [2].

Figure 4
figure 4

The downstream variations of the dimensionless wall and fluid bulk temperatures for various values of Pe.

Full size image

For a low value of the Peclet number (Pe = 5), the downstream variations of dimensionless wall fluid bulk temperatures for different values of Knudsen numbers are depicted in figure 5. An increase in Knudsen number results in a decrease in the wall temperature in the upstream region (X < 0) while it increases it in the downstream region (X > 0). Actually, this is an expected result when Eqs.(7) and (9) are closely examined. In the upstream region, the gas at the wall is in thermal equilibrium with the wall since no temperature jump occurs. In the presence of velocity slip at the wall, the velocity gradient decreases with increasing Knudsen number, which implies that high velocities occur near the wall region. As described later, these high velocities rapidly transfer the reverse heat to the upstream region, and therefore, the wall temperature gets lower values when compared with the macroscale case (Kn = 0). However, in the upstream region, temperature jump becomes dominant with increasing Knudsen number and leads to higher wall temperatures. From figure 5, it can be also seen that the dimensionless fluid bulk temperature is independent of Knudsen number in the two regions.

Figure 5
figure 5

The downstream variations of the dimensionless wall and fluid bulk temperatures for various values of Kn.

Full size image

The combined effect of rarefaction and axial conduction on heat transfer can be seen in figure 6, which shows the variation of local Nu number with Kn for different values of Pe. Generally, the local Nu shows a decrease until a certain entrance length, which then receives its fully developed value. For a fixed value of Pe, the local Nu decreases with an increase in Kn. This can be explained by the opposing effect of the temperature jump on heat transfer. As is shown in figure 5, an increase in Kn increases the temperature difference between the wall and the bulk, which weakens the driving potential for the heat transfer from wall to fluid. Therefore, for a given heat flux at the wall, an increase in the temperature difference will decrease the local Nu.

Figure 6
figure 6

The downstream variation of local Nu for various values of Kn at Pe = 5 (a), Pe = 10 (b), Pe = 20)(c), Pe = 50 (d) and Pe = 500 (e).

Full size image

Finally, figure 7 shows the influence of Pe on the local Nu for various values of Kn. As a general behaviour, for all values of Kn, the local Nu tends to decrease with a decrease in Pe until a certain axial distance, and then changes its behaviour in the opposite direction with decreasing Pe before reaching its fully developed value. The decrease with Pe near the entrance region is attributed to the augmentation of axial conduction to the upstream region. This causes higher temperature difference \( \theta_{w} - \theta_{b} \) at X = 0 than that for higher values of Pe (see figure 4). After this location (X > 0), due to the convection-dominated flow at larger values of Pe, the temperature difference between the wall and bulk fluid increases monotonically and gets higher values than those for lower values of Pe at a certain axial distance. Due to this fact, the trend of local Nu is changed in the opposite direction after this point before reaching its fully developed value. Similar tendencies were observed by Hsu [3] for conventional sizes of pipe and parallel-plate channels flows. The axial conduction also affects the thermal development length. As seen from figure 7, the thermal development length increases with decreasing Pe.

Figure 7
figure 7

The downstream variation of Nu for various values of Pe at Kn = 0.00 (a), Kn = 0.04 (b) and Kn = 0.10 (c).

Full size image

4 Conclusions

In this study, hydrodynamically developed, but thermally developing forced convection in a microtube subjected to a step change in wall heat flux has been analysed numerically. The slip velocity and temperature jump conditions at the wall and the axial conduction in the fluid have been included in the analysis. The combined effects of the Peclet number and the Knudsen number on the local Nusselt numbers as well as on the wall and bulk temperatures have been studied in detail. Main findings of the present study can be summarized as follows:

  • Either for the macroscale case or for the microscale case, the dimensionless wall and fluid bulk temperatures increase with decreasing Pe.

  • For the microscale case, the dimensionless wall temperature decreases with increasing Kn in the upstream region while it increases in the downstream region. The dimensionless fluid bulk temperature is independent of Kn.

  • The local Nu get lower values for low values of Pe in the entrance region than those for high values of Pe due to the axial conduction (i.e., for Pe changing from 500 to 5, the local Nu number decreases at least 20% at X = 0.001 for all values of Kn).

  • For Pe > 5, regardless of Kn, the effect of axial conduction on local Nu is insignificant at X ≥ 0.08.

  • The fully developed Nu is independent of Pe and decreases with increasing Kn due to higher slip velocities and temperature jumps at the channel wall. For a fixed value of Pe, the fully developed Nu are 4.363, 4.072, 3.748, 3.439, 3.155 and 2.904 for Kn = 0.00, 0.02, 0.04, 0.06, 0.08 and 0.10, respectively.

  • A decrease in Pe increases the thermal development length.