Homotopy classification of contact foliations on open contact manifolds

Abstract

We give a homotopy classification of foliations on open contact manifolds whose leaves are contact submanifolds of the ambient space. The result is an extension of Haefliger’s classification of foliations on open manifold in the contact setting. While proving the main theorem, we also prove a result on equidimensional isocontact immersions on open contact manifolds.

1 Introduction

The main contribution of the article is to show that contact forms on open manifolds do satisfy a weak form of stability though Gray’s stability theorem is not true.

Theorem 1.1

Let $\xi _{t}$, $t\in [0,1]$ be a continuous family of contact structures defined by the contact forms $\alpha _t$ on a compact manifold M with boundary. Let $(N,\tilde{\xi }=\ker \eta )$ be a contact manifold without boundary. Then every isocontact immersion $f_0:(M,\xi _0)\rightarrow (N,\tilde{\xi })$ admits a regular homotopy $\{f_t\}$ such that $f_t:(M,\xi _t)\rightarrow (N,\tilde{\xi })$ is an isocontact immersion for all $t\in [0,1]$.

In addition, if M contains a compact submanifold $V_{0}$ in its interior and $\xi _{t}=\xi _{0}$ on $\mathrm{Op}(V_{0})$ then $f_{t}$ can be chosen to be a constant homotopy on $\mathrm{Op}(V_{0})$.

Theorem 1.1, suggested as an exercise in [5], is an analogue of Ginzburg’s theorem on weak stability of symplectic forms on open manifolds [8]. The proof of Theorem 1.1 presented here is based on ideas that can be found in [5] and [8] and may be known to experts.

As a corollary to the above result, we prove that every open contact manifold admits an isocontact immersion into an arbitrary small neighbourhood of its core.

COROLLARY 1.2

Let $(M,\alpha )$ be an open contact manifold. Then it admits a regular homotopy of contact immersions $\varphi _t$, $t\in [0,1]$, such that $\varphi _0=id_M$ and $\varphi _1$ takes M into an arbitrary neighbourhood of a core of M.

Together with Gromov’s theorem for open invariant relations, this immediately leads to the following result of h-principle. In what follows below, $(M,\alpha )$ will denote an open contact manifold with contact structure $\xi =\ker \alpha$.

Theorem 1.3

Let $\mathcal {R}\subset J^{r}(M,N)$ be an open relation invariant under the action of the pseudogroup of local contactomorphisms of $(M,\alpha )$. Then the parametric h-principle holds for $\mathcal {R}$.

We refer the reader to [11] and [5] for the theory of h-principle. Having observed this, we proceed to obtain a homotopy classification of contact foliations on open contact manifold by adapting the techniques of Haefliger to the contact set up.

Suppose that N is any manifold with a foliation ${\mathcal {F}}_N$ of codimension 2q which is strictly less than the dimension of M. Then $\nu {\mathcal {F}}_N$ will denote the normal bundle $TN/T{\mathcal {F}}_N$ of ${\mathcal {F}}_N$ and $\pi :TN\rightarrow \nu {\mathcal {F}}_N$ will denote the canonical projection map. Let ${\mathcal {E}}_\alpha (TM,\nu {\mathcal {F}}_N)$ be the space of all vector bundle morphisms $F:TM\rightarrow TN$ such that

• (1) $\pi \circ F:TM\rightarrow \nu ({\mathcal {F}}_N)$ is an epimorphism,

• (2) $\ker (\pi \circ F)\cap \xi$ is a symplectic subbundle of $(\xi ,d'\alpha =d\alpha |_\xi )$.

Let $Tr_\alpha (M,{\mathcal {F}}_N)$ consist of all smooth maps $f:M\rightarrow N$ such that df belongs to ${\mathcal {E}}_\alpha (TM,\nu {\mathcal {F}}_N)$. The inverse images of ${\mathcal {F}}_N$ under an $f\in Tr_\alpha (M,{\mathcal {F}}_N)$, namely $f^{-1}{\mathcal {F}}_N$, is a contact foliation on $(M,\alpha )$. With $C^{\infty }$-compact open topology on $Tr_\alpha (M,{\mathcal {F}}_N)$ and $C^{0}$-compact open topology on $\mathcal {E}_\alpha (TM,\nu {\mathcal {F}}_N)$, we obtain the following result.

Theorem 1.4

Let $(M,\alpha )$ be an open contact manifold and $(N,{\mathcal {F}}_N)$ be any foliated manifold. Suppose that the codimension of ${\mathcal {F}}_N$ is even and is strictly less than the dimension of M. Then

$$\begin{aligned} \pi \circ d:Tr_\alpha (M,{\mathcal {F}}_N)\rightarrow \mathcal {E}_\alpha (TM,\nu {\mathcal {F}}_N) \end{aligned}$$

is a weak homotopy equivalence.

A foliation ${\mathcal {F}}$ on M will be called a contact foliation on M subordinate to $\alpha$ (or simply a contact foliation on $(M,\alpha )$) if the leaves of ${\mathcal {F}}$ are contact submanifolds of M. The tangent distribution $T{\mathcal {F}}$ of a contact foliation is transversal to the contact subbundle $\xi$; moreover, the intersection $T{\mathcal {F}}$ with $\xi$ is a symplectic subbundle of $\ker \alpha$ with respect to the symplectic structure $d'\alpha =d\alpha |_{\ker \alpha }$. In the above theorem, $f^{-1}({\mathcal {F}}_N)$ is a contact foliation for all $f\in Tr_\alpha (M,{\mathcal {F}}_N)$.

Theorem 1.4 is an exact analogue of Phillips’ theorem on homotopy classification of transversal maps to foliations [21], which was used by Haefliger to obtain a classification of foliations on open manifolds. Proceeding as in [12] we obtain a homotopy classification of contact foliations on open contact manifolds. To state the result, let $\Gamma _q$ be the groupoid of germs of local diffeomorphisms of ${\mathbb {R}}^q$ and $B\Gamma _q$ be the classifying space of $\Gamma _q$ structures with the universal $\Gamma _q$-structure $\Omega _q$. The homotopy classes of $\Gamma _q$ structures on M are in one-to-one correspondence with the homotopy classes of continuous maps $M\rightarrow B\Gamma _q$ (see [12]). Any $\Gamma _q$ structure on M is associated with a vector bundle over M, called the normal bundle of the structure. In particular, we have the normal bundle $\nu \Omega _q$ of the universal $\Gamma _q$-structure on $B\Gamma _q$. Theorem 1.4 leads to the following classification of contact foliations on open contact manifolds.

Theorem 1.5

The integrable homotopy classes of codimension 2q contact foliations on M subordinate to $\alpha$ are in one-to-one correspondence with the homotopy classes of bundle epimorphisms $(F,f):TM\rightarrow \nu \Omega _{2q}$ for which $\ker F\cap \ker \alpha$ is a symplectic subbundle of $\xi$.

The article is organized as follows. We include preliminaries of contact manifolds in section 2 in order to make the article self-contained. In section 3, we prove Theorem 1.1 and its corollary. In section 4, we recall some preliminaries of h-principle and then prove Theorem 1.3. In section 5, we prove Theorem 1.4 and Theorem 1.5. In the section 6, we relate the results of this article with those in [3] and give some examples of contact foliations on certain subsets of contact spheres. The article is partly expository in nature and we hope that it will fill up certain gaps in the existing literature.

2 Preliminaries of contact manifolds

In this section, we review basic definitions and results related to contact manifolds.

DEFINITION 2.1

Let M be a $2n+1$ dimensional manifold. A 1-form $\alpha$ on M is said to be a contact form if $\alpha \wedge (d\alpha )^n$ is nowhere vanishing.

If $\alpha$ is a contact form, then

$$\begin{aligned} d'\alpha =d\alpha |_{\ker \alpha } \end{aligned}$$

is a symplectic structure on the hyperplane distribution $\ker \alpha$. Also, there is a global vector field $R_\alpha$ on M defined by the relations

$$\begin{aligned} \alpha (R_\alpha )=1,\ \ \ i_{R_\alpha }\cdot \alpha =0, \end{aligned}$$

(1)

where $i_X$ denotes the interior multiplication by the vector field X. Thus, TM has the following decomposition:

$$\begin{aligned} TM=\ker \alpha \oplus \ker \,d\alpha , \end{aligned}$$

(2)

where $\ker \alpha$ is a symplectic vector bundle and $\ker \,d\alpha$ is the 1-dimensional subbundle generated by $R_\alpha$. The vector field $R_\alpha$ is called the Reeb vector field of the contact form $\alpha$.

A codimension 1 hyperplane distribution $\xi$ on M is said to be a contact structure on M if $\xi$ is locally defined as the kernel of a (local) contact form $\alpha$. Observe that the local contact form in this case is defined uniquely up to multiplication by a nowhere vanishing function f. Moreover, $d(f\alpha )|_\xi =f. d\alpha |_\xi$ and hence every contact structure is associated with a conformal symplectic structure.

If $\alpha$ is a contact form, then the distribution $\ker \alpha$ will be called the contact distribution of $\alpha$.

Example 2.2

• (1) Every odd dimensional Euclidean space ${\mathbb {R}}^{2n+1}$ has a canonical contact form given by $\alpha =dz+\sum _{i=1}^nx_i\,dy_i$, where $(x_1,\dots ,x_n,y_1,\dots ,y_n,z)$ is the canonical coordinate system on ${\mathbb {R}}^{2n+1}$.

• (2) Every even dimensional Euclidean space ${\mathbb {R}}^{2n}$ has a canonical 1-form $\lambda =\sum _{i=1}^n(x_idy_i-y_idx_i)$ which is called the Liouville form of ${\mathbb {R}}^{2n}$, where $(x_1,\dots ,x_n$, $y_1,\dots ,y_n)$ is the canonical coordinate system on ${\mathbb {R}}^{2n}$. The restriction of $\lambda$ on the unit sphere in ${\mathbb {R}}^{2n}$ defines a contact form.

A contact form $\alpha$ also defines a canonical isomorphism $\phi :TM\rightarrow T^*M$ between the tangent and the cotangent bundles of M given by

$$\begin{aligned} \phi (X)=i_X d\alpha +\alpha (X)\alpha , \quad \text { for } X\in TM. \end{aligned}$$

(3)

It is easy to see that the Reeb vector field $R_\alpha$ corresponds to the 1-form $\alpha$ under $\phi$.

DEFINITION 2.3

Let $(N,\xi )$ be a contact manifold. A monomorphisn $F:TM\rightarrow (TN,\xi )$ is called contact if F is transversal to $\xi$ and $F^{-1}(\xi )$ is a contact structure on M. A smooth map $f:M\rightarrow (N,\xi )$ is called contact if its differential df is contact.

If M is also a contact manifold with a contact structure $\xi _0$, then a monomorphism $F:TM\rightarrow TN$ is said to be isocontact if $\xi _0=F^{-1}\xi$ and $F:\xi _0\rightarrow \xi$ is conformal symplectic with respect to the conformal symplectic structures on $\xi _0$ and $\xi$. A smooth map $f:M\rightarrow N$ is said to be isocontact if df is isocontact.

A diffeomorphism $f:(M,\xi )\rightarrow (N,\xi ')$ is said to be a contactomorphism if f is isocontact.

If $\xi =\ker \alpha$ for a globally defined 1-form $\alpha$ on N, then f is contact if $f^*\alpha$ is a contact form on M. Furthermore, if $\xi _0=\ker \alpha _0$, then f is isocontact if $f^*\alpha =\varphi \alpha _0$ for some nowhere vanishing function $\varphi :M\rightarrow {\mathbb {R}}$.

DEFINITION 2.4

A vector field X on a contact manifold $(M,\alpha )$ is called a contact vector field if it satisfies the relaion ${\mathcal {L}}_X\alpha =f\alpha$ for some smooth function f on M, where ${\mathcal {L}}_X$ denotes the Lie derivation operator with respect to X.

Every smooth function H on a contact manifold $(M,\alpha )$ gives a contact vector field $X_H=X_0+\bar{X}_H$ defined as follows:

$$\begin{aligned} X_0=HR_\alpha \ \ \ \text { and }\ \ \ \bar{X}_H\in \Gamma (\xi ) \text { such that }i_{\bar{X}_H}d\alpha |_\xi = -dH|_\xi , \end{aligned}$$

(4)

where $\xi =\ker \alpha$; equivalently,

$$\begin{aligned} \alpha (X_H)=H\ \ \text { and }\ \ i_{X_H}d\alpha =-dH+dH(R_{\alpha })\alpha . \end{aligned}$$

(5)

The vector field $X_H$ is called the contact Hamiltonian vector field of H.

If $\phi _t$ is a local flow of a contact vector field X, then

$$\begin{aligned} \frac{d}{dt}\phi _t^*\alpha = \phi _t^*(i_X\cdot d\alpha +d(\alpha (X)))=\phi _t^*(f\alpha )=(f\circ \phi _t)\phi _t^*\alpha . \end{aligned}$$

Therefore, $\phi _t^*\alpha =\lambda _t\alpha$, where $\lambda _t=\mathrm{e}^{\int f\circ \phi _t \,dt}$. Thus the flow of a contact vector field preserves the contact structure.

Theorem 2.5

(Gray’s stability theorem [10]). If $\xi _t,\ t\in {\mathbb {I}}$ is a smooth family of contact structures on a closed manifold M, then there exists an isotopy $\psi _t,\ t\in {\mathbb {I}}$ of M such that

$$\begin{aligned} \psi _t:(M,\xi _0)\rightarrow (M,\xi _t) \end{aligned}$$

is isocontact for all $t\in {\mathbb {I}}$

Remark 2.6

Gray’s stability theorem is not valid on non-closed manifolds. We shall see an extension of Theorem 2.5 for such manifolds in Theorem 1.1 which is one of the main results of this article.

We end this section with the definition of a contact submanifold.

DEFINITION 2.7

A submanifold N of a contact manifold $(M,\xi )$ is said to be a contact submanifold if the inclusion map $i:N\rightarrow M$ is a contact map.

Lemma 2.8

A submanifold N of a contact manifold $(M,\xi =\ker \alpha )$ is a contact submanifold if and only if TN is transversal to $\xi |_N$ and $TN\cap \xi |_N$ is a symplectic subbundle of $(\xi ,d'\alpha )$.

3 Equidimensional contact immersions

We begin with the following simple observation.

Observation 3.1

Let $(M,\alpha )$ be a contact manifold. The product manifold $M\times {\mathbb {R}}^2$ has a canonical contact form given by $\tilde{\alpha }=\alpha - y\,dx$, where (x, y) are the coordinate functions on ${\mathbb {R}}^2$. We shall denote the contact structure associated with $\tilde{\alpha }$ by $\tilde{\xi }$. Now suppose that $H:M\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a smooth function which vanishes on some open set U. Define $\bar{H}:M\times {\mathbb {R}}\rightarrow M\times {\mathbb {R}}^2$ by $\bar{H}(u,t)=(u,t,H(u,t))$ for all $(u,t)\in M\times {\mathbb {R}}$. It is easy to note that $\bar{H}$ is transversal to $\tilde{\xi }$ on U.

PROPOSITION 3.2

Let M be a contact manifold with contact form $\alpha$. Suppose that H is a smooth real-valued function on $M\times (-\varepsilon ,\varepsilon )$ with compact support such that its graph $\Gamma$ in $M\times {\mathbb {R}}^2$ is transversal to the kernel of $\tilde{\alpha }=\alpha -y\,dx$. Then there is a diffeomorphism $\Psi :M\times (-\varepsilon ,\varepsilon )\rightarrow \Gamma$ which pulls back $\tilde{\alpha }|_{\Gamma }$ onto $f(\alpha \oplus 0)$, where f is a nowhere-vanishing smooth real-valued function on $M\times {\mathbb {R}}$.

Proof

Note that if $\Gamma$ is a codimension 1 submanifold of a contact manifold $(N,\tilde{\alpha })$ such that the tangent planes of $\Gamma$ are transversal to $\tilde{\xi }=\ker \tilde{\alpha }$, then there is a codimension 1 distribution D on $\Gamma$ given by the intersection of $\ker \tilde{\alpha }|_\Gamma$ and $T\Gamma$. Since $D=\ker \tilde{\alpha }|_\Gamma \cap T\Gamma$ is an odd dimensional distribution, $d\tilde{\alpha }|_D$ has a 1-dimensional kernel K. The integral curves of K are called characteristics of $\Gamma$ [1].

The main idea in the proof is to get a diffeomorphism $\Psi :M\times {\mathbb {R}}\rightarrow \Gamma$ which would map the lines $x\times {\mathbb {R}}$ onto the characteristics of $\Gamma$. The result can be proved by standard methods in the theory of contact fibration. Consider the trivial fibration $\pi :M\times {\mathbb {R}}\rightarrow {\mathbb {R}}$, where $M\times {\mathbb {R}}$ is endowed with the nowhere vanishing 1-form $\tilde{\beta }=\bar{H}^*\tilde{\alpha }=\alpha -H\,dt$, since $\bar{H}$ is transversal to $\tilde{\xi }$. Clearly, $\tilde{\beta }=\alpha - H\,dt$ restricts to a contact form on $M\times \{t\}$ for each $t\in {\mathbb {R}}$ and hence $\ker \tilde{\beta }$ is transversal to the distribution $\ker d\pi$. Hence $\pi$ is a contact fibration with the global 1-form $\tilde{\beta }$ on $M\times {\mathbb {R}}$ [15]. Therefore, the restriction of $d\tilde{\beta }$ to $\ker \tilde{\beta }$ has 1-dimensional kernel $\eta$. Thus, we get a connection $\eta$ on $M\times {\mathbb {R}}$. If we denote the parallel translations with respect to this connection by maps $P_t:M\times \{0\}\rightarrow M\times \{t\}$, $t\in {\mathbb {R}}$, then we have the following:

$$\begin{aligned} (\bar{P}_t)^*\alpha = f_t\alpha , \end{aligned}$$

where $\bar{P}_t:M\rightarrow M$ is defined by projecting $P_t$. Define a diffeomorphism $\Phi :M\times {\mathbb {R}}\rightarrow M\times {\mathbb {R}}$ by

$$\begin{aligned} \Phi (u,t)=P_t(u), \quad \text { for all } t\in {\mathbb {R}}\text { and } u\in M. \end{aligned}$$

It is a general fact that $\Phi$ preserves $\ker \tilde{\beta }\cap \ker d\pi$. Hence, $\Phi ^*(\tilde{\beta }|_{M_t})=f_t.(\tilde{\beta }|_{M_0})=f_t\alpha$. On the other hand, for a fixed $u\in U$, $P_t(u,0)$ is an integral curve of $\eta$ so that $\Phi (\frac{\partial }{\partial t})\in \eta$. Hence it follows that $\ker \Phi ^*\tilde{\beta }=p^*\xi \oplus {\mathbb {R}}$, where $p:M\times {\mathbb {R}}\rightarrow M$ is the projection map onto the first factor. Consequently, $(\bar{H}\circ \Phi )^*\tilde{\alpha }=f.(\alpha \oplus 0)$. Hence $\Psi =\bar{H}\circ \Phi$ is the desired map. $\square$

Remark 3.3

If there exists an open subset $\tilde{U}$ of M such that H vanishes on $\tilde{U}\times (-\varepsilon ,\varepsilon )$ then $\tilde{\beta }$ equals $p^*\alpha$ and therefore, $\eta$ is tangent to the lines $x\times {\mathbb {R}}$. Hence, $\Phi$ fixes the points of $\tilde{U}\times (-\varepsilon ,\varepsilon )$.

We shall now recall a result from [5] which will reduce Theorem 1.1 to the special case in which the contact forms $\alpha _t$ are piecewise primitive. In fact, we shall require the parametric form of this result which we state below in Lemma 3.4.

Lemma 3.4

Let $\alpha _{t}, t\in [0,1]$ be a continuous family of contact forms on a compact manifold $M$ $,$ possibly with non-empty boundary. Then for each $t\in [0,1],$ there exists a sequence of primitive 1-forms $\beta _t^l=r_t^l\,ds_t^l, l=1,\dots ,N$ such that

• (1) $\alpha _t=\alpha _0+\sum _1^N \beta _t^l$ for all $t\in [0,1],$

• (2) for each $j=0,\dots ,N$ the form $\alpha ^{(j)}_t=\alpha _{0}+\sum _{1}^{j}\beta _t^{l}$ is contact, 

• (3) for each $j=1,\dots ,N$ the functions $r_t^j$ and $s_t^j$ are compactly supported and supports are contained in a coordinate neighbourhood.

Furthermore,  the forms $\beta _t^l$ depends continuously on t.

If $\alpha _t=\alpha _0$ on an open neighbourhood of a compact subset $V_0$ contained in the interior of M,  then the functions $r^l_t$ and $s^l_t$ can be chosen to be equal to zero on some open neighbourhood of $V_0$.

Proof of Theorem 1.1

In view of Lemma 3.4, it is enough to prove the theorem for a family of contact forms $\alpha _t$, $t\in [0,1]$, satisfying

$$\begin{aligned} \alpha _{t}=\alpha _{0}+r_tds_t \end{aligned}$$

for some smooth real-valued functions $r_t,s_t$ which are (compactly) supported in an open set U of M. We shall first show that $f_{0}:(M,\xi _{0})\rightarrow (N,\tilde{\xi })$ can be homotoped to an isocontact immersion $f_{1}:(M,\xi _1)\rightarrow (N,\tilde{\xi })$ which will give a non-parametric version of the stated result.

For simplicity of notation, we write (r, s) for $(r_1,s_1)$ and define a smooth embedding $\varphi :U\rightarrow U\times {\mathbb {R}}^2$ by

$$\begin{aligned} \varphi (u)=(u,s(u),-r(u)) \,\text { for }\,u\in U. \end{aligned}$$

Since r, s are compactly supported, $\varphi (u)=(u,0,0)$ for all $u\in \mathrm{Op}\,(\partial U)$ and there exist positive constants $\varepsilon _1$ and $\varepsilon _2$ such that $\mathrm{Im}\,f$ is contained in $U\times I_{\varepsilon _1}\times I_{\varepsilon _2}$, where $I_\varepsilon$ denotes the open interval $(-\varepsilon ,\varepsilon )$ for $\varepsilon >0$. Clearly, $\varphi ^*(\alpha _0-y\,dx)=\alpha _0+r\,ds$ and so

$$\begin{aligned} \varphi :(U,\xi _{1})\rightarrow (U\times {\mathbb {R}}^2,\ker (\alpha _{0}- y\,dx)) \end{aligned}$$

(6)

is an isocontact embedding. The image of $\varphi$ is the graph of a smooth function $k=(s,-r):U\rightarrow I_{\varepsilon _{1}}\times I_{\varepsilon _{2}}$ which is compactly supported with support contained in the interior of U. Further note that $\pi (\varphi (U))$ is the graph of s and hence a submanifold of $U\times I_{\varepsilon _1}$. Now let $\pi :U\times I_{\varepsilon _{1}}\times I_{\varepsilon _{2}}\rightarrow U\times I_{\varepsilon _{1}}$ be the projection onto the first two coordinates. Since Im $\varphi$ is the graph of k, $\pi |_{\text {Im\,}\varphi }$ is an embedding onto the set $\pi (\varphi (U))$ which is the graph of s. Now observe that Im $\varphi$ can also be viewed as the graph of a smooth function, namely $h:\pi (\varphi (U))\rightarrow I_{\varepsilon _{2}}$ defined by $h(u,s(u))=-r(u)$. It is easy to see that h is compactly supported.

Fig. 1

.

In figure 1, the bigger rectangle represents the set $U\times I_{\varepsilon _{1}}$ and the central dotted line represents $U\times 0$. The curve within the rectangle stands for the domain of h, which is also the graph of s. We can now extend h to a compactly supported function $H:U\times I_{\varepsilon _{1}}\rightarrow I_{\varepsilon _{2}}$ (see [24]) which vanishes on the shaded region and is such that its graph is transversal to $\ker (\alpha _0- y\,dx)$. Indeed, since $\varphi$ is an isocontact embedding, it is transversal to $\ker (\alpha _0-y\,dx)$ and hence graph H is transversal to $\ker (\alpha _0-y\,dx)$ on an open neighbourhood of $\pi (\varphi (U))$ for any extension H of h. Since transversality is a generic property, we can assume (possibly after a small perturbation) that graph of H is transversal to $\ker (\alpha _0- y\,dx)$.

Let $\Gamma$ be the graph of H; then the image of $\varphi$ is contained in $\Gamma$. By Lemma 3.2, there exists a diffeomorphism $\Phi :\Gamma \rightarrow U\times I_{\varepsilon _1}$ with the property that

$$\begin{aligned} \Phi ^*(\ker (\alpha _{0}\oplus 0))=\ker ((\alpha _{0}- y\,dx)|_\Gamma ). \end{aligned}$$

(7)

Next, we use $f_0$ to define an immersion $F_{0}:U\times {\mathbb {R}}\rightarrow N\times \mathbb {R}$ as follows:

$$\begin{aligned} F_0(u,x)=(f_0(u),x)\hbox { for all }u\in U\hbox { and }x\in {\mathbb {R}}. \end{aligned}$$

It is straightforward to see that

• $F_{0}(u,0)\in N \times 0$ for all $u\in U$ and

• $F_0^*(\eta \oplus 0)$ is a multiple of $\alpha _{0}\oplus 0$ by a nowhere vanishing function on $M\times {\mathbb {R}}$.

Therefore, the following composition is defined:

$$\begin{aligned} U{\mathop {\longrightarrow }\limits ^{\varphi }} \Gamma {\mathop {\longrightarrow }\limits ^{\Phi }} U\times I_{\varepsilon _1} {\mathop {\longrightarrow }\limits ^{F_0}} N\times \mathbb {R} {\mathop {\longrightarrow }\limits ^{\pi _{N}}} N, \end{aligned}$$

where $\pi _{N}:N\times \mathbb {R}\rightarrow N$ is the projection onto N. Observe that $\pi _{N}^*\eta =\eta \oplus 0$ and therefore, it follows from equations (6) and (7) that the composition map $f_1=\pi _{N} F_{0}\Phi \varphi :(U,\xi _1)\rightarrow (N,\tilde{\xi })$ is isocontact. Such a map is necessarily an immersion.

Let $K=(\text {supp\,}r\cup \text {supp\,}s)$. Take a compact set $K_1$ in U such that $K\subset \text {Int\,}K_1$, and let $\tilde{U}=U\setminus K_1$. If $u\in \tilde{U}$, then $\varphi (u)=(u,0,0)$. This gives $h(u,0)=0$ for all $u\in \tilde{U}$. We can choose H such that $H(u,t)=0$ for all $(u,t)\in \tilde{U}\times I_{\varepsilon _1}$. Then by Remark 3.3, $\Phi (u,0,0)=(u,0)$ for all $u\in \tilde{U}$. Consequently,

$$\begin{aligned} f_1(u)=\pi _{N} F_{0}\Phi \varphi (u)=\pi _{N} F_{0}(u,0)=\pi _N(f_0(u),0)=f_0(u) \ \text {for all } u\in \tilde{U}. \end{aligned}$$

In other words, $f_1$ coincides with $f_0$ outside an open neighbourhood of K.

Now, if we have a continuous family of contact forms $\alpha _t$ as in equation (3), then define

$$\begin{aligned} \varphi _t(u)=(u,s_t(u),-r_t(u)) \,\text { for }\,u\in U. \end{aligned}$$

Since each $\varphi _t$ has compact support, it follows that $\cup _{t\in [0,1]}\varphi _t(U)$ is a compact subset of $U\times {\mathbb {R}}^2$ and therefore, there exist positive constants $\varepsilon _1$ and $\varepsilon _2$ such that $\varphi _t(U)\subset U\times I_{\varepsilon _{1}}\times I_{\varepsilon _{2}}$ for all $t\in [0,1]$. Proceeding exactly as before, we get a continuous family of smooth functions $H_t$ such that their graphs $\Gamma _t$ are transversal to $\ker (\alpha _0-y\,dx)$. By applying Proposition 3.2, we then get a continuous family of homeomorphisms $\Phi _t:\Gamma _t\rightarrow U\times I_{\varepsilon _1}$ which pull back $\ker (\alpha _{0}\oplus 0)$ onto $\ker (\alpha _{0}- y\,dx)|_{\Gamma _t}$. The desired homotopy $f_t$ is then defined by $f_t=\pi _{N} F_{0}\Phi _t \varphi _t$. This completes the proof of the theorem.$\square$

We shall now deduce from the above theorem, the existence of isocontact immersions of an open manifold M into itself which compress the manifold M into an arbitrary small neighbourhoods of its ‘core’. It is known that an open manifold admits a Morse function f without a local maxima. The codimension of the Morse complex of such a function is, therefore, strictly positive [16, 17]. The gradient flow of f brings the manifold into an arbitrary small neighbourhood of the Morse complex. In fact, one can get a polyhedron $K\subset M$ such that codim $K>0$, and an isotopy $\phi _t:M\rightarrow M$, $t\in [0,1]$ which fixes K pointwise and where $\phi _1$ takes M into an arbitrarily small neighborhood U of K. The polyhedron K is called a core of M.

COROLLARY 3.5

Let $(M,\xi =\ker \alpha )$ be an open contact manifold and let K be a core of it. Then for a given neighbourhood U of K in M there exists a homotopy of isocontact immersions $f_{t}:(M,\xi )\rightarrow (M,\xi ), t\in [0,1]$ such that $f_{0}=id_{M}$ and $f_{1}(M)\subset U$.

Proof

Since K is a core of M, there is an isotopy $g_t$ such that $g_0=id_M$ and $g_1(M)\subset U$. Using $g_t$, we can express M as $M=\bigcup _{0}^{\infty }V_{i}$, where $V_{0}$ is a compact neighbourhood of K in U and $V_{i+1}$ is diffeomorphic to $V_i\bigcup (\partial V_{i}\times [0,1])$ so that $\bar{V_i}\subset \text {Int}\,(V_{i+1})$ and $V_{i+1}$ deformation retracts onto $V_{i}$. If M is a manifold with boundary then this sequence is finite. We shall inductively construct a homotopy of immersions $f^{i}_{t}:M\rightarrow M$ with the following properties:

• (1) $f^i_0=id_M$

• (2) $f^i_1(M)\subset U$

• (3) $f^i_t=f^{i-1}_t$ on $V_{i-1}$

• (3) $(f^i_t)^*\xi =\xi$ on $V_{i}$.

Assuming the existence of $f^{i}_{t}$, let $\xi _{t}=(f^{i}_{t})^{*}(\xi )$ (so that $\xi _0=\xi$ and consider a 2-parameter family of contact structures defined by $\eta _{t,s}=\xi _{t(1-s)}$. Then for all $t,s\in {\mathbb {I}}$, we have

$$\begin{aligned} \eta _{t,0}=\xi _t,\ \ \eta _{t,1}=\xi _0=\xi \ \text { and }\ \eta _{0,s}=\xi . \end{aligned}$$

The parametric version of Theorem 1.1 gives a homotopy of immersions $\tilde{f}_{t,s}:V_{i+2}\rightarrow M$, $(t,s)\in {\mathbb {I}}\times {\mathbb {I}}$, satisfying the following conditions:

• (1) $\tilde{f}_{t,0},\tilde{f}_{0,s}:V_{i+2}\hookrightarrow M$ are the inclusion maps

• (2) $(\tilde{f}_{t,s})^*\xi _t=\eta _{t,s}$; in particular, $(\tilde{f}_{t,1})^*\xi _t=\xi$

• (3) $\tilde{f}_{t,s}=id$ on $V_i$ since $\eta _{t,s}=\xi _0$ on $V_i$.

We now extend the homotopy $\{\tilde{f}_{t,s}|_{V_{i+1}}\}$ to all of M as immersions such that $\tilde{f}_{0,s}=id_M$ for all s. By an abuse of notation, we denote the extended homotopy by the same symbol. Define the next level homotopy as follows:

$$\begin{aligned} f^{i+1}_{t}=f^{i}_{t}\circ \tilde{f}_{t,1} \qquad \text { for }\ t\in [0,1]. \end{aligned}$$

This completes the induction step since $(f^{i+1}_t)^*(\xi )=(\tilde{f}_{t,1})^*\xi _t=\xi$ on $V_{i+2}$ for all t, and $f^{i+1}_t|_{V_{i}}=f^i_t|_{V_{i}}$. To start the induction we use the isotopy $g_t$ and let $\xi _t=g_t^*\xi$. Note that $\xi _t$ is a family of contact structures on M defined by contact forms $g_t^*\alpha$. For starting the induction, we construct $f^{0}_{t}$ as above by setting $V_{-1}=\emptyset$.

Having constructed the family of homotopies $\{f^i_t\}$ as above, we set $f_t=\lim _{i\rightarrow \infty }f^i_t$ which is the desired homotopy of isocontact immersions. $\square$

4 An h-principle for open relations on open contact manifolds

We shall first briefly review some basic definitions and results from the theory of h-principle. For further details we refer to [11] and [5]. Suppose that M and N are smooth manifolds. Let $J^{r}(M,N)$ be the space of r-jets of germs of local maps from M to N [9]. The canonical map $p^{(r)}:J^r(M,N)\rightarrow M$ which takes a jet $j^r_f(x)$ onto the base point x is a fibration. We shall refer to $J^r(M,N)$ as the r-jet bundle over M. A continuous map $\sigma :M\rightarrow J^r(M,N)$ is said to be a section of the jet bundle $p^{(r)}:J^r(M,N)\rightarrow M$ if $p^{(r)}\circ \sigma =id_M$. A section of $p^{(r)}$ which is the r-jet of some map $f:M\rightarrow N$ is called a holonomic section of the jet bundle.

A subset $\mathcal {R} \subset J^{r}(M,N)$ of the r-jet space is called a partial differential relation of order r (or simply a relation). If $\mathcal {R}$ is an open subset of the jet space, then we call it an open relation. A $C^r$ map $f:M\rightarrow N$ is said to be a solution of $\mathcal {R}$ if the image of its r-jet extension $j^r_f:M\rightarrow J^r(M,N)$ lies in $\mathcal {R}$.

We denote by $\Gamma (\mathcal {R})$ the space of continuous sections of the bundle $J^r(M,N)\rightarrow N$ having images in $\mathcal {R}$. The space of $C^\infty$ solutions of $\mathcal {R}$ is denoted by $\mathrm{Sol}(\mathcal {R})$. If $\mathrm{Sol}({\mathcal {R}})$ and $\Gamma ({\mathcal {R}})$ are endowed with the $C^{\infty }$-compact open topology and the $C^0$-compact open topology respectively, then the r-jet map

$$\begin{aligned} j^r:\mathrm{Sol}({\mathcal {R}})\rightarrow \Gamma ({\mathcal {R}}) \end{aligned}$$

taking an $f\in \mathrm{Sol}({\mathcal {R}})$ onto the holonomic section $j^r_f$ is a continuous map which is clearly one to one. Therefore, we can identify $\mathrm{Sol}({\mathcal {R}})$ with the space of holonomic sections of ${\mathcal {R}}$.

DEFINITION 4.1

A differential relation $\mathcal {R}$ is said to satisfy the h-principle if every element $\sigma _{0} \in \Gamma (\mathcal {R})$ admits a homotopy $\sigma _{t}\in \Gamma (\mathcal {R})$ such that $\sigma _{1}$ is holonomic.

The relation ${\mathcal {R}}$ satisfies the parametric h-principle if the r-jet map $j^{r}:\mathrm{Sol}(\mathcal {R})\rightarrow \Gamma (\mathcal {R})$ is a weak homotopy equivalence.

We shall often talk about (parametric) h-principle for certain function spaces without referring to the relations of which they are solutions.

Remark 4.2

The space $\Gamma ({\mathcal {R}})$ is referred as the space of formal solutions of ${\mathcal {R}}$. Finding a formal solution is a purely (algebraic) topological problem which can be addressed with the obstruction theory. Finding a solution of ${\mathcal {R}}$ is, on the other hand, a differential topological problem. Thus, the h-principle reduces a differential topological problem to a problem in algebraic topology.

Next we define the notion of local h-principle near a subset K of M.

DEFINITION 4.3

Let K be a subset of M. We shall say that a relation ${\mathcal {R}}$ satisfies the h-principle near K if given an open set U containing K and a section $F:U\rightarrow \mathcal {R}|_U$, there exists an open set $\tilde{U}\subset U$ containing K such that $F|_{\tilde{U}}$ is homotopic to a holonomic section $\tilde{F}:\tilde{U}\rightarrow \mathcal {R}$ in $\Gamma ({\mathcal {R}})$.

The above h-principle will also be referred as an h-principle on $\mathrm{Op}\,K$. If K is a subset of M then by $\mathrm{Op}\,K$ we shall mean an unspecified open set in M containing K. The set $C^k(\mathrm{Op}\,K,N)$ will denote the set of all $C^k$ functions which are defined on some open neighbourhood of K.

DEFINITION 4.4

A function $F:Z\rightarrow C^k({\mathrm{Op}\,K},N)$ defined on any topological space Z will be called ‘continuous’ if there exists an open set U containing K such that each F(z) has an extension $\tilde{F}(z)$ which is defined on U and $z\mapsto \tilde{F}(z)$ is continuous with respect to the $C^k$-compact open topology on the function space. A relation ${\mathcal {R}}$ is said to satisfy the parametric h-principle near K if $j^r:\mathrm{Sol}({\mathcal {R}}|_{\mathrm{Op}\,K})\rightarrow \Gamma ({\mathcal {R}}|_{\mathrm{Op}\,K})$ is a weak homotopy equivalence.

Let $\text {Diff}(M)$ be the pseudogroup of local diffeomorphisms of M [7]. There is a natural (contravariant) action of $\text {Diff}(M)$ on $J^{r}(M,N)$ given by $\sigma .\alpha :=j^{r}_{f\circ \sigma }(x)$, where $\sigma$ is a local diffeomorphism of M defined near $x\in M$ and f is a representative of the r-jet $\alpha$ at $\sigma (x)$. Let ${\mathcal {D}}$ be a subgroup of $\text {Diff}(M)$. A differential relation $\mathcal {R}$ is said to be $\mathcal {D}$-invariant if the following condition is satisfied:

For every $\alpha \in {\mathcal {R}}$ and $\sigma \in {\mathcal {D}}$, the element $\sigma .\alpha$ belongs to ${\mathcal {R}}$ provided it is defined.

We shall denote the element $\sigma .\alpha$ by the notation $\sigma ^*\alpha$.

The following result, due to Gromov, is the first general result in the theory of h-principle.

Theorem 4.5

Every open,  Diff(M) invariant relation ${\mathcal {R}}$ on an open manifold M satisfies the parametric h-principle.

The above h-principle can be established in two steps. In the first place, one proves the local h-principle near the core K of M and then lifts the h-principle to M by a contracting diffeotopy.

If a relation is invariant under the action of a smaller pseudogroup of diffeomorphism, say ${\mathcal {D}}$, then the h-principle can still hold if ${\mathcal {D}}$ has some additional properties.

DEFINITION 4.6

[11]

Let $M_{0}$ be a submanifold of M of positive codimension and let $\mathcal {D}$ be a pseudogroup of local diffeomorphisms of M. We say that $M_0$ is sharply movable by $\mathcal {D}$, if given any hypersurface S in an open set U in $M_0$ and any $\varepsilon >0$, there is an isotopy $\delta _{t}$, $t\in {\mathbb {I}}$, in $\mathcal {D}$ and a positive real number r such that the following conditions hold:

(i):

$\delta _{0}|_U=id_{U}$,

(ii):

$\delta _{t}$ fixes all points outside the $\varepsilon$-neighbourhood of S,

(iii):

$\mathrm{dist}(\delta _{1}(x),M_{0})\ge r$ for all $x\in S$,

where ‘dist’ denotes the distance with respect to any fixed metric on M.

The diffeotopy $\delta _t$ will be referred as a sharply moving diffeotopy. A pseudogroup ${\mathcal {D}}$ is said to have the sharply moving property if every submanifold $M_0$ of positive codimension is sharply movable by ${\mathcal {D}}$. Eliashberg and Mishachev [5] have replaced sharply moving diffeotopies by capacious subgroup of diffeomorphism.

Recall now the following local h-principle result due to Gromov [11]; also see [5].

Theorem 4.7

Let $\mathcal {R}\subset J^r(M,N)$ be an open relation which is invariant under the action of a pseudogroup $\mathcal {D}$. If $\mathcal {D}$ sharply moves a submanifold $M_{0}$ in M of positive codimension,  then the parametric h-principle holds for $\mathcal {R}$ on $\mathrm{Op}(M_{0})$.

Remark 4.8

We remark here that the theory of h-principle extends to a more general situation, namely for sections of an arbitrary fibration. If $X\rightarrow M$ be a fibration, then we shall denote the r-jet space of sections of X by $X^{(r)}$. For the sake of simplicity, we have restricted ourselves in the above discussion to the case of smooth maps between manifolds. However, we shall consider a general relation in Example 5.8.

Proof of Theorem 1.3

Theorem 1.3 now follows by a direct application of Theorem 4.7 together with Corollary 3.5. It is known that the group $\mathcal {D}$ consisting of (compactly supported) contact diffeomorphisms of M has the sharply moving property [5]. To see this, let $M_0$ be a submanifold of M of positive codimension. Take a closed hypersurface S in $M_0$ and an open set $U\subset M$ containing S. We take a vector field X along S which is transversal to $M_{0}$. Let $H:M\rightarrow \mathbb {R}$ be a smooth function such that

$$\begin{aligned} \alpha (X)=H,\ \ \ \ i_X d\alpha |_\xi =-dH|_\xi , \ \ \text {at points of } S. \end{aligned}$$

The contact-Hamiltonian vector field $X_H$ is clearly transversal to $M_0$ at points of S. As transversality is a stable property and U is small, we can assume that $X_{H}\pitchfork U$. Now consider the initial value problem

$$\begin{aligned} \frac{d}{dt}\delta _{t}(x)=X_{H}(\delta _t(x)), \ \ \delta _0(x)=x. \end{aligned}$$

(8)

The solution to this problem exists for small time t, say for $t\in [0,\bar{\varepsilon }]$, for all x lying in some small enough neighbourhood of S. Moreover, since $X_H$ is transversal to S, there would exist a positive real number $\varepsilon$ such that the integral curves $\delta _t(x)$ for $x\in S$ do not meet $M_0$ during the time interval $(0,\varepsilon )$. Let

$$\begin{aligned} S_{\varepsilon }=\cup _{t\in [0,\varepsilon /2]}\delta _{t}(S). \end{aligned}$$

Take a smooth function $\varphi$ which is identically equal to 1 on a small neighbourhood of $S_{\varepsilon }$ and supp $\varphi \subset \cup _{t\in [0,\varepsilon )}\delta _t(S)$. We now replace $X_{H}$ in the initial value problem (8) by $X_{\varphi H}$. Since $X_{\varphi H}$ is compactly supported, the flow of $X_{\varphi H}$, say $\bar{\delta _{t}}$, is defined for all time t. Because of the choice of $\varphi$, the integral curves $\bar{\delta }_t(x_0)$, $x_0\in M_0$, cannot come back to $M_0$ for $t>0$. Hence, we have the following:

• $\bar{\delta }_0|_U=id_U$

• $\bar{\delta _t}=id$ outside a small neighbourhood of $S_{\varepsilon }$

• $\mathrm{dist}(\bar{\delta }_1(x),M_0)>r$ for all $x\in S$ and for some $r>0$.

This proves that $\mathcal {D}$ sharply moves any submanifold of M of positive codimension.

In fact, if K is a core of M, then ${\mathcal {D}}$ would also sharply move K. Since the relation ${\mathcal {R}}$ is open and invariant under the action of ${\mathcal {D}}$, we can apply Theorem 4.7 to conclude that ${\mathcal {R}}$ satisfies the parametric h-principle near K. Finally, to conclude the parametric h-principle for ${\mathcal {R}}$, we appeal to Corollary 3.5 which guarantees a homotopy of isocontact immersions $g_{t}:(M,\xi )\rightarrow (M,\xi )$ satisfying $g_{0}=id_{M}$ and $g_{1}(M)\subset U$, where U is any open neighbourhood of K. The argument for lifting of the local h-principle near K to a global one with the help of $g_t, t\in [0,1]$ is the same as that in the smooth case and so we omit the details of it. $\square$

We are now in a position to prove Theorem 1.4. We assume that $(M,\xi =\ker \alpha )$ is an open contact manifold and N is a foliated manifold with a smooth foliation ${\mathcal {F}}_N$ of even codimension. We shall denote the normal bundle of the foliation ${\mathcal {F}}_N$ by $\nu {\mathcal {F}}_N$ and the canonical projection map $TN\rightarrow \nu {\mathcal {F}}_N$ by $\pi$. We define a first-order differential relation ${\mathcal {R}}$ consisting of all 1-jets represented by triples (x, y, F), where $x\in M, y\in N$ and $F:T_{x}M\rightarrow T_{y}N$ is a linear map such that

• (1) $\pi \circ F:T_xM\rightarrow \nu ({\mathcal {F}}_N)_y$ is an epimorphism,

• (2) $\ker (\pi \circ F)\cap \ker \alpha _x$ is a symplectic subspace of $(\ker \alpha _x,d'\alpha _x)$.

Now we state the following obvious lemma noting the fact that non-degeneracy condition on 2-forms is an open conditon.

Lemma 4.9

The relation $\mathcal {R}$ defined above is an open relation and invariant under the action of the pseudogroup of local contactomorphisms of $(M,\alpha )$.

Proof of Theorem 1.4

In view of Theorem 1.3 and Lemma 4.9, it follows that the relation ${\mathcal {R}}$ satisfies the parametric h-principle, that is, $j^1:\mathrm{Sol} ({\mathcal {R}})\rightarrow \Gamma ({\mathcal {R}})$ is a weak homotopy equivalence. It is easy to see that the space of sections of ${\mathcal {R}}$ can be identified with ${\mathcal {E}}_\alpha (TM,\nu ({\mathcal {F}}_N))$. On the other hand, the solution space of ${\mathcal {R}}$ can be identified with the space $Tr_\alpha (M,{\mathcal {F}}_N)$. To see this, first note that $f:M\rightarrow N$ is transversal to ${\mathcal {F}}_N$ means that $\pi \circ df$ is an epimorphism. Further observe that the following two statements are equivalent:

• (S1) the leaves of the inverse foliation $f^*{\mathcal {F}}_N$ are contact submanifolds (immersed) of M.

• (S2) $\ker (\pi \circ df)\cap \ker \alpha$ is a symplectic subbundle of $(\ker \alpha ,d'\alpha )$.

This completes the proof of the theorem.$\square$

5 Classification of contact foliations

We shall now prove Theorem 1.5. The proof of Theorem 1.5 follows the same strategy as that in the smooth case. The existence of universal contact foliation is obtained by using the original construction of A. Haefliger and keeping track of the contact structure. We refer the reader to [6] as we closely follow the exposition for the theory of universal foliations and the proof of A. Haefliger’s theorem. In what follows, $\Gamma _q$ will denote the groupoid of germs of local diffeomorphisms of ${\mathbb {R}}^n$ and $B\Gamma _q$ the classifying space of $\Gamma _q$ structures; $\nu (\Omega _q)\rightarrow B\Gamma _q$ will denote the normal bundle of the universal $\Gamma _q$ structure $\Omega _q$ on $B\Gamma _q$.

As before M is an open manifold with contact structure $\xi =\ker \alpha$. Let $\mathrm{Fol}_\alpha ^{2q}(M)$ denote the space of contact foliations on M of codimension 2q subordinate to $\alpha$. Let ${\mathcal {E}}_{\alpha }(TM,\nu \Omega _{2q})$ be the space of all vector bundle epimorphisms $F:TM\rightarrow \nu \Omega _{2q}$ such that $\ker F$ is transversal to $\ker \alpha$ and $\ker \alpha \cap \ker F$ is a symplectic subbundle of $(\ker \alpha ,d'\alpha )$, where $d'\alpha =d\alpha |_{\xi }$.

If ${\mathcal {F}}\in \mathrm{Fol}^{2q}(M)$ and $f:M\rightarrow B\Gamma _{2q}$ is a classifying map of ${\mathcal {F}}$, then $f^*\Omega _{2q}= {\mathcal {F}}$ as $\Gamma _{2q}$-structure. We can define vector bundle epimorphisms $TM\rightarrow \nu \Omega _{2q}$ by the following (see [12]):

(9)

where $\pi _{{\mathcal {F}}}:TM\rightarrow \nu ({\mathcal {F}})$ is the projection map onto the normal bundle and $(\bar{f},f)$ represents a pull-back diagram. Note that the kernel of this morphism is $T{\mathcal {F}}$. If ${\mathcal {F}}\in \mathrm{Fol}^{2q}_\alpha (M)$, then $T{\mathcal {F}}\cap \ker \alpha$ is a symplectic subbundle of $\ker \alpha$ and therefore, $\bar{f}\circ \pi _{{\mathcal {F}}} \in {\mathcal {E}}_\alpha (TM,\nu \Omega _{2q})$. However, the morphism $\bar{f}\circ \pi _M$ is unique only up to homotopy. Thus, there is a function

$$\begin{aligned} H'_\alpha :\mathrm{Fol}^{2q}_\alpha (M)\rightarrow \pi _0({\mathcal {E}}_\alpha (TM,\nu \Omega _{2q})). \end{aligned}$$

DEFINITION 5.1

Two contact foliations ${\mathcal {F}}_0$ and ${\mathcal {F}}_1$ on $(M,\alpha )$ are said to be integrably homotopic relative to $\alpha$ if there exists a foliation $\tilde{{\mathcal {F}}}$ on $(M\times {\mathbb {I}},\alpha \oplus 0)$ such that the following conditions are satisfied:

• (1) $\tilde{{\mathcal {F}}}$ is transversal to the trivial foliation of $M\times {\mathbb {I}}$ by the leaves $M\times \{t\}$, $t\in {\mathbb {I}}$;

• (2) the foliation ${\mathcal {F}}_t$ on M induced by the canonical injective map $i_t:M\rightarrow M\times {\mathbb {I}}$ (given by $x\mapsto (x,t)$) is a contact foliation subordinate to $\alpha$ for each $t\in {\mathbb {I}}$;

• (3) the induced foliations on $M\times \{0\}$ and $M\times \{1\}$ coincide with ${\mathcal {F}}_0$ and ${\mathcal {F}}_1$ respectively,

Here $\alpha \oplus 0$ denotes the pull-back of $\alpha$ by the projection map $p_1:M\times {\mathbb {R}}\rightarrow M$.

Let $\pi _0(\mathrm{Fol}^{2q}_{\alpha }(M))$ denote the space of integrable homotopy classes of contact foliations on $(M,\alpha )$. Define

$$\begin{aligned} H_\alpha :\pi _0(\mathrm{Fol}^{2q}_\alpha (M))\rightarrow \pi _0({\mathcal {E}}_\alpha (TM,\nu \Omega _{2q})) \end{aligned}$$

by $H_{\alpha }([\mathcal {F}])=H_\alpha '({\mathcal {F}})$, where $[{\mathcal {F}}]$ denotes the integrable homotopy class of ${\mathcal {F}}$ relative to $\alpha$. To see that $H_\alpha$ is well-defined, let $\tilde{{\mathcal {F}}}$ be an integrable homotopy relative to $\alpha$ between two contact foliations ${\mathcal {F}}_0$ and ${\mathcal {F}}_1$. If $F:M\times [0,1]\rightarrow B\Gamma _{2q}$ is a classifying map of $\tilde{{\mathcal {F}}}$, then similar to (9) we have as follows:

Let $i_t:M\rightarrow M\times \{t\}\hookrightarrow M\times {\mathbb {R}}$ denote the canonical injective map of M into $M\times \{t\}$ and $f_t:M\rightarrow B\Gamma _{2q}$ be defined as $f_t(x)=F(x,t)$ for $(x,t)\in M\times [0,1]$. Since

$$\begin{aligned} \bar{F}\circ \bar{\pi }\circ di_t=\pi _{{\mathcal {F}}_t}\circ \bar{f}_t:TM\rightarrow \nu {{\mathcal {F}}_t}\rightarrow \nu \Omega _{2q} \end{aligned}$$

where ${\mathcal {F}}_t=f_t^*\Omega _{2q}$, it follows from the definition of $H'$ that

$$\begin{aligned} H'_\alpha ({\mathcal {F}}_t)=[\bar{F}\circ \bar{\pi }\circ di_t]. \end{aligned}$$

Thus we conclude that $H'_\alpha ({\mathcal {F}}_0)= H'_\alpha ({\mathcal {F}}_1)$. This proves that $H_\alpha$ is well-defined. We now restate Theorem 1.5 as follows.

Theorem 5.2

If M is open then $H_\alpha :\pi _0(Fol^{2q}_{\alpha }(M)) \longrightarrow \pi _0({\mathcal {E}}_{\alpha }(TM,\nu \Omega _{2q}))$ is bijective.

We first prove a lemma.

Lemma 5.3

Let N be a smooth manifold with a foliation ${\mathcal {F}}_N$ of codimension 2q. If $g:N\rightarrow B\Gamma _{2q}$ classifies ${\mathcal {F}}_N$, then we have a commutative diagram as follows : 

(10)

where the left vertical arrow is the isomorphism defined by Theorem 1.4. P is induced by a map which takes an $f\in Tr_\alpha (M,{\mathcal {F}}_N)$ onto the inverse foliation $f^{-1}{\mathcal {F}}_N$ and $G_*$ is induced by the bundle homomorphism $G:\nu {\mathcal {F}}_N\rightarrow \nu \Omega _{2q}$ covering g.

Proof

We shall first show that the horizontal arrows in (10) are well defined. If $f\in Tr_{\alpha }(M,\mathcal {F}_N)$, then the inverse foliation $f^{-1}{\mathcal {F}}_N$ belongs to $\mathrm{Fol}^{2q}_\alpha (M)$. Furthermore, if $f_t$ is a homotopy in $Tr_{\alpha }(M,\mathcal {F}_N)$, then the map $F:M\times {\mathbb {I}}\rightarrow N$ defined by $F(x,t)=f_t(x)$ is clearly transversal to ${\mathcal {F}}_N$ and so $\tilde{{\mathcal {F}}}=F^{-1}{\mathcal {F}}_N$ is a foliation on $M\times {\mathbb {I}}$. The restriction of $\tilde{{\mathcal {F}}}$ to $M\times \{t\}$ is the same as the foliation $f^{-1}_t({\mathcal {F}}_N)$, which is a contact foliation subordinate to $\alpha$. Hence, we get a map

$$\begin{aligned} \pi _0(Tr_{\alpha }(M,\mathcal {F}_N)){\mathop {\longrightarrow }\limits ^{P}}\pi _0(\mathrm{Fol}^{2q}_{\alpha }(M)) \end{aligned}$$

defined by

$$\begin{aligned}{}[f]\longmapsto [f^{-1}\mathcal {F}_N], \end{aligned}$$

where $[f^{-1}\mathcal {F}_N]$ denotes the integrable homotopy class of the foliation $f^{-1}\mathcal {F}_N$. On the other hand, since $g:N\rightarrow B\Gamma _{2q}$ classifies the foliation ${\mathcal {F}}_N$, we have the canonical projection map $G:\nu {\mathcal {F}}_N\cong g^*\nu \Omega _{2q}\rightarrow \nu \Omega _{2q}$ covering g. This induces a map

$$\begin{aligned} G_*: \pi _0({\mathcal {E}}_\alpha (TM,\nu {\mathcal {F}}_N))\rightarrow \pi _0({\mathcal {E}}_\alpha (TM,\nu \Omega _{2q})) \end{aligned}$$

which takes an element $[F]\in \pi _0({\mathcal {E}}_\alpha (TM,\nu ({\mathcal {F}}_N)))$ onto $[G\circ F]$. We now prove the commutativity of (10). Note that if $f\in Tr_{\alpha }(M,\mathcal {F}_N))$, then $g\circ f:M\rightarrow B\Gamma _{2q}$ classifies the foliation $f^{-1}{\mathcal {F}}_N$. Let $\widetilde{df}:\nu (f^{-1}{\mathcal {F}}_N)\rightarrow \nu ({\mathcal {F}}_N)$ be the unique map making the following diagram commutative:

where $\pi _M:TM\rightarrow \nu (f^{-1}{\mathcal {F}}_N)$ is the projection map onto the normal bundle of $f^{-1}{\mathcal {F}}_N$. Observe that $G\circ \widetilde{df}:\nu (f^{-1}{\mathcal {F}}_N)\rightarrow \nu (\Omega _{2q})$ covers the map $g\circ f$ and $(G\circ \widetilde{df},g\circ f)$ is a pullback diagram. Therefore, we have

$$\begin{aligned} H_\alpha ([f^{-1}{\mathcal {F}}_N])=[(G\circ \widetilde{df})\circ \pi _M]=[G\circ (\pi \circ df)]. \end{aligned}$$

This proves the commutativity of (10). $\square$

Proof of Theorem  5.2

The proof is exactly similar to that of Haefliger’s classification theorem. The main idea is to reduce the classification to Theorem 1.4 by using Lemma 5.3 and working along Haefliger.$\square$

We shall now see how the elements of $\pi _0({\mathcal {E}}_\alpha (TM,\nu {\mathcal {F}}_N))$ are related to homotopy liftings of the classifying map $\tau$ of $\ker \alpha$.

Theorem 5.4

Let $(M,\alpha )$ be an open contact manifold and let $\tau :M\rightarrow BU(n)$ be a map classifying the symplectic vector bundle $\xi =\ker \alpha$. Then there is a bijection between the elements of $\pi _0({\mathcal {E}}_{\alpha }(TM,\nu \Omega _{2q}))$ and the homotopy classes of triples $(f,f_0,f_1),$ where $f_0:M\rightarrow BU(q),$ $f_1:M\rightarrow BU(n-q)$ and $f:M\rightarrow B\Gamma _{2q}$ such that

• (1) $(f_0,f_1)$ is homotopic to $\tau$ in BU(n) and

• (2) $Bd\circ f$ is homotopic to $Bi\circ f_0$ in $BGL_{2q}$.

In other words,  the homotopy commutative diagrams are as follows : 

Proof

For the sake of simplicity, we shall denote $\Omega _{2q}$ by $\Omega$. An element $(F,f)\in {\mathcal {E}}_{\alpha }(TM,\nu \Omega )$ defines a (symplectic) splitting of the bundle $\xi$ as

$$\begin{aligned} \xi \cong (\ker F\cap \xi )\oplus (\ker F\cap \xi )^{d'\alpha } \end{aligned}$$

since $\ker F\cap \xi$ is a symplectic subbundle of $\xi$. Let $F'$ denote the restriction of F to $(\ker F\cap \xi )^{d'\alpha }$. It is easy to see that $(F',f):(\ker F\cap \xi )^{d'\alpha }\rightarrow \nu (\Omega )$ is a vector bundle map which is fibrewise isomorphism. If $f_0:M\rightarrow BU(q)$ and $f_1:M\rightarrow BU(n-q)$ are continuous maps classifying the vector bundles $\ker F\cap \xi$ and $(\ker F\cap \xi )^{d'\alpha }$ respectively, then the classifying map $\tau$ of $\xi$ must be homotopic to $(f_0,f_1):M\rightarrow BU(q)\times BU(n-q)$ in BU(n). Recall that the isomorphism classes of symplectic vector bundles are classified by homotopy classes of continuous maps into BU [14]. Furthermore, note that $(\ker F\cap \xi )^{d'\alpha }\cong f^*(\nu \Omega )=f^*(Bd^*EGL_{2q}({\mathbb {R}}))$; therefore, $Bd\circ f$ is homotopic to $f_0$ in BGL(2q).

Conversely, take a triple $(f,f_0,f_1)$ such that

$$\begin{aligned} Bd\circ f\sim Bi\circ f_0 \text { and } (f_0,f_1)\sim \tau . \end{aligned}$$

Then $\xi$ has a symplectic splitting given by $f_0^*EU(q)\oplus f_1^*EU(n-q)$. Further, since $Bd\circ f\sim Bi\circ f_0$, we have $f_0^*EU(q)\cong f^*\nu (\Omega )$. Hence there is an epimorphism $F:\xi {\mathop {\longrightarrow }\limits ^{p_2}} f_0^*EU(q) \cong f^*\nu (\Omega )$ whose kernel $f_1^*EU(n-q)$ is a symplectic subbundle of $\xi$. Finally, F can be extended to an element of ${\mathcal {E}}_\alpha (TM,\nu \Omega )$ by defining its value on $R_\alpha$ equal to zero. $\square$

DEFINITION 5.5

Let N be a contact submanifold of $(M,\alpha )$ such that $T_xN$ is transversal to $\xi _x$ for all $x\in N$. Then $TN\cap \xi |_N$ is a symplectic subbundle of $\xi$. The symplectic complement of $TN\cap \xi |_N$ with respect to $d'\alpha$ will be called the normal bundle of the contact submanifold N

The following result is a direct consequence of Theorem 1.5 and Theorem 5.4.

COROLLARY 5.6

Let $(M,\alpha )$ be an open contact manifold. Let B be a symplectic subbundle of $\xi$ with a classifying map $f_0:M\rightarrow BU(q)$. The integrable homotopy classes of contact foliations on M with their normal bundles isomorphic to B are in one-to-one correspondence with the homotopy classes of lifts of $Bi\circ f_0$ in $B\Gamma _{2q}$.

We end this article with an example to show that a contact foliation ${\mathcal {F}}$ on a contact manifold need not be transversally symplectic, though its normal bundle is a symplectic vector bundle.

DEFINITION 5.7

[12]

A codimension 2q-foliation ${\mathcal {F}}$ on a manifold M is said to be transversally symplectic if ${\mathcal {F}}$ can be represented by Haefliger cocycles which take values in the groupoid of local symplectomorphisms of $({\mathbb {R}}^{2q},\omega _0)$.

Thus the normal bundle of a transversally symplectic foliation has a symplectic structure. It can be shown that if ${\mathcal {F}}$ is transversally symplectic then there exists a closed 2-form $\omega$ on M such that $\omega ^q$ is nowhere vanishing and $\ker \omega =T{\mathcal {F}}$.

Example 5.8

Let us consider a closed almost-symplectic manifold $V^{2n}$ which is not symplectic (e.g., we may take V to be ${\mathbb {S}}^6$) and let $\omega _V$ be a non-degenerate 2-form on V defining the almost symplectic structure. Set $M=V\times \mathbb {R}^3$ and let $\mathcal {F}$ be the foliation on M defined by the fibres of the projection map $\pi :M\rightarrow V$. Thus the leaves are $\{x\}\times \mathbb {R}^3,\ x\in V$. Consider the standard contact form $\alpha =dz+x dy$ on the Euclidean space ${\mathbb {R}}^3$ and let $\tilde{\alpha }$ denote the pull-back of $\alpha$ by the projection map $p_2:M\rightarrow {\mathbb {R}}^3$. The 2-form $\beta =\omega _V\oplus d\alpha$ on M is of rank $2n+2$ and it is easy to see that $\beta$ restricted to $\ker \tilde{\alpha }$ is non-degenerate. Therefore $(\tilde{\alpha },\beta )$ is an almost contact structure on M. Moreover, $\tilde{\alpha }\wedge \beta |_{T\mathcal {F}}$ is non-zero on each fibre.

We claim that there exists a contact form $\eta$ on M such that its restrictions to the leaves of ${\mathcal {F}}$ are contact. Indeed, there exists a surjective map

$$\begin{aligned} (T^*M)^{(1)}{\mathop {\rightarrow }\limits ^{D}}\wedge ^1T^*M \oplus \wedge ^2T^*M \end{aligned}$$

such that $D\circ j^1(\alpha )=(\alpha ,d\alpha )$ for any 1-form $\alpha$ on M (see [4]). Let

$$\begin{aligned} r:\wedge ^1T^*M \oplus \wedge ^2T^*M\rightarrow \wedge ^1T^*\mathcal {F} \oplus \wedge ^2T^*\mathcal {F} \end{aligned}$$

be the restriction map defined by the pull-back of forms and let $A\subset T^*M \oplus \wedge ^2T^*M$ be the set of all pairs $(\eta ,\Omega )$ such that $\eta \wedge \Omega ^{n+1}$ is nowhere vanishing and let $B\subset T^*\mathcal {F} \oplus \wedge ^2T^*\mathcal {F}$ be the set of all pairs $(\alpha ,\beta )\in T^*\mathcal {F} \oplus \wedge ^2T^*\mathcal {F}$ whose restrictions to the fibres of $T\mathcal {F}$ are non-zero. Now set $\mathcal {R}\subset (T^*M)^{(1)}$ as

$$\begin{aligned} \mathcal {R}=D^{-1}(A)\cap (r\circ D)^{-1}(B). \end{aligned}$$

Since both A and B are open, so is $\mathcal {R}$. Now if we consider the fibration $M{\mathop {\rightarrow }\limits ^{\pi }}V$ then it is easy to see that the diffeotopies of M preserving the fibers of $\pi$ sharply moves $V\times 0$ and $\mathcal {R}$ is invariant under the action of such diffeotopies. Hence, by Theorem 4.7 there exists a contact form $\eta$ on $\mathrm{Op}(V\times 0)=V\times \mathbb {D}^3_{\varepsilon }$ for some $\varepsilon >0$, such that $\eta$ restricted to each leaf of the foliation ${\mathcal {F}}$ is also contact. Now take a diffeomorphism $g:\mathbb {R}^3\rightarrow \mathbb {D}^3_{\varepsilon }$. Then $\eta '=(id_V\times g)^*\eta$ is a contact form on M. Further, $\mathcal {F}$ is a contact foliation relative to $\eta '$ since $id_V\times g$ is foliation preserving.

But $\mathcal {F}$ can not be transversally symplectic; otherwise, there would exist a closed 2-form $\beta$ whose restriction to $\nu \mathcal {F}=\pi ^*(TV)$ would be non-degenerate. This would imply that V is a symplectic manifold contradicting our hypothesis.

6 Examples of contact foliations on contact manifolds

We shall first derive some corollaries of Theorem 1.4 related to simple foliations.

DEFINITION 6.1

A smooth submersion $f:(M,\alpha )\rightarrow N$ will be called a contact submersion if the level sets of f are contact submanifolds of M.

Let ${\mathcal {C}}_\alpha (M,N)$ denote the space of contact submersions $(M,\alpha )\rightarrow N$ and let ${\mathcal {E}}_\alpha (TM,TN)$ be the space of epimorphisms $F:TM\rightarrow TN$ for which $\ker F\cap \ker \alpha$ is a symplectic subbundle of $(\ker \alpha ,d'\alpha )$. Taking ${\mathcal {F}}_N$ to be the zero-dimensional foliation on N in Theorem 1.4, we get the following result.

COROLLARY 6.2

Let $(M,\alpha )$ be an open contact manifold. The derivative map

$$\begin{aligned} d:{\mathcal {C}}_\alpha (M,N)\rightarrow {\mathcal {E}}_\alpha (TM,TN) \end{aligned}$$

is a weak homotopy equivalence.

Remark 6.3

Suppose that $F_0\in {\mathcal {E}}_\alpha (TM,TN)$ and D is the kernel of $F_0$. Since M is an open manifold, the bundle epimorphism $F_0:TM\rightarrow TN$ is homotopic (in the space of epimorphism) to the derivative of a submersion $f:M\rightarrow N$ (see [20]). Hence the distribution $\ker F_0$ is homotopic to the tangent distribution of a foliation, namely the one given by the submersion. Since $D\cap \ker \alpha$ is a symplectic vector bundle, it then follows from a result in [4] that D is homotopic to the tangent distribution of a contact foliation ${\mathcal {F}}$ on M. Theorem 1.4 further guarantees that it is possible to get a foliation ${\mathcal {F}}$ which is subordinate to $\alpha$ and is defined by a submersion.

Next, we interpret Corollary 6.2 in terms of certain 2n-frames in M, when the target manifold is an Euclidean space. Recall that the tangent bundle TM of a contact manifold $(M,\alpha )$ splits as $\ker \alpha \oplus \ker \,d\alpha$. Let $P:TM\rightarrow \ker \alpha$ be the projection morphism onto $\ker \alpha$ relative to this splitting. We shall denote the projection of a vector field X on M under P by $\bar{X}$. For any smooth function $h:M\rightarrow {\mathbb {R}}$, $X_h$ will denote the contact Hamiltonian vector field defined.

Lemma 6.4

Let $(M,\alpha )$ be a contact manifold and $f:M\rightarrow {\mathbb {R}}^{2n}$ be a submersion with coordinate functions $f_1,f_2,\dots ,f_{2n}$. Then the following statements are equivalent : 

• (C1) f is a contact submersion.

• (C2) The restriction of $d\alpha$ to the bundle spanned by $X_{f_1},\dots ,X_{f_{2n}}$ defines a symplectic structure.

• (C3) The vector fields $\bar{X}_{f_1},\dots ,\bar{X}_{f_{2n}}$ span a symplectic subbundle of $(\xi ,d'\alpha )$.

Proof

If $f:(M,\alpha )\rightarrow {\mathbb {R}}^{2n}$ is a contact submersion, then the following relation holds pointwise:

$$\begin{aligned} \ker df\cap \ker \alpha =\langle \bar{X}_{f_1},\ldots ,\bar{X}_{f_{2n}}\rangle ^{\perp _{d'\alpha }}, \end{aligned}$$

(11)

where the right-hand side represents the symplectic complement of the subbundle spanned by $\bar{X}_{f_1},\dots ,\bar{X}_{f_{2n}}$ with respect to $d'\alpha$. Indeed, for any $v\in \ker \alpha$,

$$\begin{aligned} d'\alpha (\bar{X}_{f_i},v)=-df_i(v),\ \ \text { for all }i=1,\dots ,2n \end{aligned}$$

Therefore, $v\in \ker \alpha \cap \ker df$ if and only if $d'\alpha (\bar{X}_{f_i},v)=0$ for all $i=1,\dots ,2n$, that is, $v\in \langle \bar{X}_{f_1},\dots ,\bar{X}_{f_{2n}}\rangle ^{\perp _{d'\alpha }}$. Thus, the equivalence of (C1) and (C3) is a consequence of the equivalence between (S1) and (S2). The equivalence of (C2) and (C3) follows from the relation $d\alpha (X,Y)=d\alpha (\bar{X},\bar{Y})$, where X, Y are any two vector fields on M. $\square$

An ordered set of vectors $e_{1}(x),\dots ,e_{2n}(x)$ in $\xi _x$ will be called a symplectic 2n-frame in $\xi _x$ if the subspace spanned by these vectors is a symplectic subspace of $\xi _x$ with respect to the symplectic form $d'\alpha _x$. Let $T_{2n}\xi$ be the bundle of symplectic 2n-frames in $\xi$ and $\Gamma (T_{2n}\xi )$ denote the space of sections of $T_{2n}\xi$ with the $C^{0}$ compact open topology.

For any smooth submersion $f:(M,\alpha )\rightarrow \mathbb {R}^{2n}$, define the contact gradient of f by

$$\begin{aligned} \Xi f(x)=(\bar{X}_{f_{1}}(x),\dots ,\bar{X}_{f_{2n}}(x)), \end{aligned}$$

where $f_{i}$, $i=1,2,\dots ,2n$, are the coordinate functions of f. If f is a contact submersion then $\bar{X}_{f_{1}}(x),\dots ,\bar{X}_{f_{2n}}(x))$ span a symplectic subspace of $\xi _x$ for all $x\in M$, and hence $\Xi f$ becomes a section of $T_{2n}\xi$.

Theorem 6.5

Let $(M^{2m+1},\alpha )$ be an open contact manifold. Then the contact gradient map $\Xi :\mathcal {C}_\alpha (M,\mathbb {R}^{2n})\rightarrow \Gamma (T_{2n}\xi )$ is a weak homotopy equivalence.

Proof

As $T\mathbb {R}^{2n}$ is a trivial vector bundle, the map

$$\begin{aligned} i_{*}:\mathcal {E}_\alpha (TM,\mathbb {R}^{2n})\rightarrow \mathcal {E}_\alpha (TM,T\mathbb {R}^{2n}) \end{aligned}$$

induced by the inclusion $i:0 \hookrightarrow \mathbb {R}^{2n}$ is a homotopy equivalence, where $\mathbb {R}^{2n}$ is regarded as the vector bundle over $0\in \mathbb {R}^{2n}$. The homotopy inverse c is given by the following diagram. For any $F\in {\mathcal {E}}_\alpha (TM,T{\mathbb {R}}^{2n})$, c(F) is defined by as $p_2\circ F$,

$$\begin{aligned} \begin{array}{ccccc} TM &{} {\mathop {\longrightarrow }\limits ^{F}} &{} T\mathbb {R}^{2n}=\mathbb {R}^{2n}\times \mathbb {R}^{2n} &{} {\mathop {\longrightarrow }\limits ^{p_2}} &{} \mathbb {R}^{2n}\\ \downarrow &{} &{} \downarrow &{} &{} \downarrow \\ M &{} \longrightarrow &{} \mathbb {R}^{2n} &{} \longrightarrow &{} 0 \end{array} \end{aligned}$$

where $p_2$ is the projection map onto the second factor.

Since $d'\alpha$ is non-degenerate, the contraction of $d'\alpha$ with a vector $X\in \ker \alpha$ defines an isomorphism

$$\begin{aligned} \phi :\ker \alpha \rightarrow (\ker \alpha )^*. \end{aligned}$$

We define a map $\sigma :\oplus _{i=1}^{2n}T^*M\rightarrow \oplus _{i=1}^{2n}\xi$ by

$$\begin{aligned} \sigma (G_1,\dots ,G_{2n})=-(\phi ^{-1}(\bar{G}_1),\dots ,\phi ^{-1}(\bar{G}_{2n})), \end{aligned}$$

where $\bar{G}_i=G_i|_{\ker \alpha }$. Then noting that

$$\begin{aligned} \ker (G_1,\dots ,G_{2n})\cap \ker \alpha =\langle \phi ^{-1}(\bar{G}_1),\dots ,\phi ^{-1}(\bar{G}_{2n})\rangle ^{\perp _{d'\alpha }}, \end{aligned}$$

we get a map $\tilde{\sigma }$ by restricting $\sigma$ to ${\mathcal {E}}(TM,{\mathbb {R}}^{2n})$:

$$\begin{aligned} \tilde{\sigma }:{{\mathcal {E}}}(TM,\mathbb {R}^{2n})\longrightarrow \Gamma (M,T_{2n}\xi ), \end{aligned}$$

Moreover, the contact gradient map $\Xi$ factors as $\Xi = \tilde{\sigma } \circ c \circ d$:

$$\begin{aligned} \mathcal {C}_\alpha (M,\mathbb {R}^{2n}){\mathop {\rightarrow }\limits ^{d}}\mathcal {E}_\alpha (TM,T\mathbb {R}^{2n}){\mathop {\rightarrow }\limits ^{c}}\mathcal {E}_\alpha (TM,\mathbb {R}^{2n}){\mathop {\rightarrow }\limits ^{\tilde{\sigma }}}\Gamma (T_{2n}\xi ). \end{aligned}$$

(12)

To see this, take any $f:M\rightarrow {\mathbb {R}}^{2n}$. Then, $c(df)=(df_{1},\dots ,df_{2n})$, and hence

$$\begin{aligned} \tilde{\sigma } c (df)=(\phi ^{-1}(df_1|_\xi ),\dots ,\phi ^{-1}(df_{2n}|_\xi )) = (\bar{X}_{f_1},\dots ,\bar{X}_{f_{2n}})=\Xi (f) \end{aligned}$$

which gives $\tilde{\sigma } \circ c \circ d(f)=\Xi f$.

We claim that $\tilde{\sigma }: \mathcal {E}_\alpha (TM,\mathbb {R}^{2n})\rightarrow \Gamma (T_{2n}\xi )$ is a homotopy equivalence. To prove this, we define a map $\tau : \oplus _{i=1}^{2n}\xi \rightarrow \oplus _{i=1}^{2n} T^*M$ by the formula

$$\begin{aligned} \tau (X_1,\dots ,X_{2n})=(i_{X_1}d\alpha ,\dots ,i_{X_{2n}} d\alpha ) \end{aligned}$$

which induces a map $\tilde{\tau }: \Gamma (T_{2n}\xi ) \rightarrow \mathcal {E}(TM,\mathbb {R}^{2n})$. It is easy to verify that $\tilde{\sigma } \circ \tilde{\tau }=id$. In order to show that $\tilde{\tau }\circ \tilde{\sigma }$ is homotopic to the identity, take any $G\in {\mathcal {E}}_\alpha (TM,{\mathbb {R}}^{2n})$ and let $\hat{G}=(\tau \circ \sigma )(G)$. Then $\hat{G}$ equals G on $\ker \alpha$. Define a homotopy between G and $\hat{G}$ by $G_t=(1-t)G+t\hat{G}$. Then $G_t=G$ on $\ker \alpha$ and hence $\ker G_t\cap \ker \alpha =\ker G\cap \ker \alpha$. This also implies that each $G_t$ is an epimorphism. Thus, the homotopy $G_t$ lies in ${\mathcal {E}}_\alpha (TM,{\mathbb {R}}^{2n})$. This shows that $\tilde{\tau }\circ \tilde{\sigma }$ is homotopic to the identity map.

This completes the proof of the theorem since $d:\mathcal {C}(M,\mathbb {R}^{2n}) \rightarrow \mathcal {E}(TM,T\mathbb {R}^{2n})$ is a weak homotopy equivalence (Theorem 1.4) and c, $\tilde{\sigma }$ are homotopy equivalences.$\square$

We shall now relate the results of this article with those in [3] by means of the operations symplectization and contactization. If ${\mathcal {F}}$ is a contact foliation on a contact manifold $(M,\alpha )$, then the projection $p:M\times {\mathbb {R}}\rightarrow M$ pulls back ${\mathcal {F}}$ to a symplectic foliation on the symplectization $(M\times {\mathbb {R}}, d(e^s\alpha ))$. Thus, for any contact submersion $f:(M,\alpha )\rightarrow P$, $f\circ p:M\times {\mathbb {R}}\rightarrow P$ is a symplectic submersion on the symplectization. In fact, the symplectic submersions on $M\times {\mathbb {R}}$ which are lifts of contact submersions on M can be viewed as ${\mathbb {R}}$-invariant symplectic submersions. Note that ${\mathbb {R}}$ has a natural action on $M\times {\mathbb {R}}$ given by

$$\begin{aligned} \Phi :(t, (x,s))\mapsto (x,s+t), \ \ t\in {\mathbb {R}}, (x,s)\in M\times {\mathbb {R}}\end{aligned}$$

and $\varphi _t=\Phi (t,\ )$ pulls back the symplectic form $\omega =d(e^s\alpha )$ onto $e^t\omega$. The differentials of $\varphi _t$, $t\in {\mathbb {R}}$, define an action of ${\mathbb {R}}$ on the tangent bundle $T(M\times {\mathbb {R}})$. We can therefore interpret Corollary 6.2 as follows:

COROLLARY 6.6

Let $(M,\alpha )$ be an open contact manifold and $(M\times {\mathbb {R}},\omega )$ its symplectization. The derivative map

$$\begin{aligned} d:{\mathcal {S}}^\mathrm{inv}_\omega (M\times {\mathbb {R}},N)\rightarrow {\mathcal {E}}^\mathrm{inv}_\omega (T(M\times {\mathbb {R}}),TN) \end{aligned}$$

is a weak homotopy equivalence, where $S^\mathrm{inv}_\omega (M\times {\mathbb {R}},N)$ and $E^\mathrm{inv}_\omega (T(M\times {\mathbb {R}}),TN)$ respectively denote the space of symplectic submersions and symplectic epimorphisms which are invariant under ${\mathbb {R}}$-action.

On the other hand, if $(M,\omega )$ is a symplectic manifold with $\omega$ integral, then there is a circle bundle $q:\tilde{M}\rightarrow M$ over M which is referred as contact pre-quantization bundle. Boothby and Wang [2] proved the existence of a contact form $\alpha$ on $\tilde{M}$ satisfying the relation $q^*\omega =d\alpha$. The ${\mathbb {S}}^1$-action on $\tilde{M}$ preserves the contact structure $\xi =\ker \alpha$. If ${\mathcal {F}}$ is a symplectic foliation on M, then $q^{-1}({\mathcal {F}})$ is a contact foliation on $\tilde{M}$. Since the symplectic submersions on $(M,\omega )$ [3] are in one-to-one correspondence with the ${\mathbb {S}}^1$-invariant contact submersions on the contact pre-quantization $(\tilde{M},\alpha )$, we can deduce the following corollary from [3].

COROLLARY 6.7

Let $(M,\omega )$ be an open symplectic manifold and $\tilde{M}$ its contact prequantization. The derivative map

$$\begin{aligned} d:{\mathcal {C}}^\mathrm{inv}_\alpha (\tilde{M},N)\rightarrow {\mathcal {E}}^\mathrm{inv}_\alpha (T\tilde{M},TN) \end{aligned}$$

is a weak homotopy equivalence, where ${\mathcal {C}}^\mathrm{inv}_\alpha (\tilde{M},N)$ and ${\mathcal {E}}^\mathrm{inv}_\alpha (T\tilde{M},TN)$ respectively denote the space of contact submersions and contact epimorphisms which are invariant under ${\mathbb {S}}^1$-action.

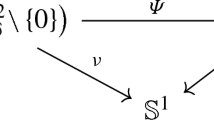
Thus we have the following commutative diagram in which the vertical arrows are weak homotopy equivalences and the horizontal arrows are inclusions.

(13)

We end this article with a family of contact foliations on certain open subsets of contact spheres.

Example 6.8

Let $\mathbb {S}^{2n+1}$ denote the unit sphere in ${\mathbb {C}}^{n+1}\cong {\mathbb {R}}^{2n+2}$,

$$\begin{aligned} \mathbb {S}^{2n+1}=\left\{ (z_{1},\ldots ,z_{n+1})\in \mathbb {C}^{n+1}: \sum _{1}^{n+1}|z_{i}|^{2}=1\right\} . \end{aligned}$$

The unit sphere has a canonical contact form $\alpha _0$ which is induced from the Liouville form $\lambda _0=\sum _{i=1}^{n+1} (x_i\,dy_i-y_i\,dx_i)$ on ${\mathbb {R}}^{2n+2}$. For $n>k$, we consider the open manifold ${\mathcal {S}}_{n,k}$ obtained from $\mathbb {S}^{2n+1}$ by removing a $(2k+1)$-sphere:

$$\begin{aligned} \mathcal {S}_{n,k}={\mathbb {S}}^{2n+1}\setminus \mathbb {S}^{2k+1}, \end{aligned}$$

where

$$\begin{aligned} \mathbb {S}^{2k+1}=\{(z_{1},\ldots ,z_{k+1},0,\ldots ,0)\in \mathbb {R}^{2n+2}: \Sigma _{1}^{k+1}|z_{i}|^{2}=1\}. \end{aligned}$$

Then $\mathcal {S}_{n,k}$ is a contact submanifold of ${\mathbb {S}}^{2k+1}$ which is homotopically equivalent to ${\mathbb {S}}^{2(n-k)-1}$.

The canonical projection map $q:{\mathbb {S}}^{2n+1}\rightarrow {\mathbb {C}}P^n$ defines ${\mathbb {S}}^{2n+1}$ as a circle bundle over the symplectic manifold ${\mathbb {C}}P^n$, where the symplectic form $\sigma$ on ${\mathbb {C}}P^n$ satisfies the relation $q^*\sigma =d\alpha$. As we have observed above, a foliation on ${\mathbb {C}}P^n$ is symplectic if and only if $q^{-1}({\mathcal {F}})$ is a contact foliation on ${\mathbb {S}}^{2n+1}$. It follows from [3] that ${\mathbb {C}}P^n\setminus {\mathbb {C}}P^k$ admits symplectic foliations for each k satisfying $0<k\le n$. In fact, these foliations are defined by submersions ${\mathbb {C}}P^n\setminus {\mathbb {C}}P^k\rightarrow {\mathbb {R}}^{2(k+1)}$. Hence, ${\mathbb {S}}^{2n+1}\setminus {\mathbb {S}}^{2k+1}$ admits contact foliations of codimension at most $2(k+1)$.

There are more direct constructions of contact foliations on ${\mathbb {S}}^{2n+1}\setminus {\mathbb {S}}^{2k+1}$. In the case of the standard 5-dimensional contact sphere $({\mathbb {S}}^5,\xi _0)$ we have the following two cases:

• (a) $({\mathbb {S}}^5\setminus \mathrm{Op}\,{\mathbb {S}}^3,\xi _0)$ and

• (b) $({\mathbb {S}}^5\setminus \mathrm{Op}\,{\mathbb {S}}^1,\xi _0)$.

The former is contactomorphic to $({\mathbb {S}}^1\times {\mathbb {D}}^4, d\theta +\lambda _0)$ and the latter is contactomorphic to $({\mathbb {S}}^3\times {\mathbb {D}}^2, \alpha _0+\lambda _0)$, where $\alpha _0$ is the standard contact form on odd spheres and $\lambda _0$ is the Liouville form on even dimensional Euclidean spaces.